Enhancing motion forecasting of ship sailing in irregular waves based on optimized LSTM model and principal component of wave-height

Irregular waves exhibit complex and erratic behavior, posing significant challenges for accurate short-term ship motion forecasting. Reliable ship navigation depends on precise motion predictions, necessitating effective feature extraction from wave data to enhance predictive models. This study proposes a hybrid model integrating a wavelet principal component analysis (WPCA) for dimensionality reduction with an optimized double circulation-long short-term memory (DC-LSTM) network. The WPCA method retains key variance components, reducing redundant data while preserving critical wave characteristics. The DC-LSTM model is optimized using both internal and external circulation mechanisms to enhance learning efficiency and stability. Numerical simulation data are used to train and validate the model. Compared with conventional LSTM and PCA-LSTM models, the proposed WPCA-DC-LSTM model improves R² by 14% and reduces RMSE by 12% in validation datasets. The model demonstrates robust generalization, effectively capturing nonlinear and high-dimensional wave features. The results indicate that the hybrid model effectively mitigates the influence of redundant data, reduces prediction randomness, and improves stability in handling wave-induced ship movements. The study highlights the broad applicability of the WPCA-DC-LSTM model for complex maritime data analysis and ship motion forecasting.

1 Introduction

With the global advancement of the shipping industry, the safety of ships sailing in the waves has become more critical. In particular, irregular waves will cause unstable motions of ships sailing in the sea, leading to difficulty maneuvering ships. Therefore, accurately predicting ship movements in irregular waves is vital for improving the stability of ships. However, the nonlinear and unpredictable nature of sea waves presents significant challenges to accurately forecasting the motion of ships at sea.

The prediction of ship motion in waves has been a research emphasis in ocean engineering for a long time. Early research emphasized using statistical models that considered external environmental factors and hydrodynamic parameters (Yoshimura, 1986; Khan et al., 2005). The Kalman filter, known for being a recursive, linear, and minimum variance filter, has found extensive application in dynamic ship positioning and short-term maneuver predictions (Rigatos, 2013; Perera, 2017). However, predicting motion using the ship's motion state equation and physical models is significantly affected by external environmental hydrodynamic parameters and computational fluid dynamics, making it less effective for short-term predictions. In contrast, autoregressive (AR) models have a simpler structure than Kalman filters, requiring consideration only of the autoregressive properties of time history data. Jiang et al. (2020) investigated the impact of scale on Autoregressive (AR) models for ship motion prediction in time. A common issue with these models is their assumption of a linear data distribution. However, ship motion exhibits strong nonlinearity, and this nonlinearity will impact the performance of the prediction models (Zhang et al., 2024).

With advancements in neural networks and computing power, recent years have seen an increasing number of studies using machine learning models to predict the ship’s attitude motion. Li et al. (2016) proposed a scheme to analyse and model ship sensor data for motion prediction. Additionally, various machine learning models have been utilized for this purpose, such as artificial neural networks (ANN) (De Masi et al., 2011), support vector machines (SVM) (Kawan et al., 2017), diagonal recurrent neural networks (DRNN) (Shen and Xie, 2005), and extreme learning machines (ELM) (Yin et al., 2014). Deep learning models have also demonstrated strong performance in improving the control of ships and predicting the attitude motion of ships. For example, the BP model has been applied to address the chaotic essence of ship motion time history data and enhance prediction accuracy (Peng et al., 2014). Recurrent Neural Networks (RNN) have been employed for nonparametric modelling to forecast ship manoeuvring motion (D'Agostino et al., 2021). Furthermore, the Long-Short-Term Memory (LSTM) neural network is one of RNN variants, has become widely used for capturing long-term dependencies and modelling complex temporal dynamics in predicting ship attitude motions or trajectory (Zhang et al., 2021; Xu et al., 2023, Xu et al., 2024).

Traditional models, such as Kalman filters and autoregressive (AR) models, have limitations in addressing the nonlinearity of ship motion. While Kalman filters offer recursive and linear filtering capabilities, they struggle with high randomness in wave-induced ship motion. AR models, despite their simplicity, fail to capture nonlinear dependencies inherent in wave-ship interactions. Recent advancements in deep learning models, like LSTM, have demonstrated significant improvements; however, these models face challenges in handling high-dimensional inputs and feature redundancy, especially in maritime environments. To avoid the limitations of the single model, many researchers have proposed hybrid methods that combine different models and algorithms. For example, the GPR-LSTM hybrid model effectively combines the high-accuracy point prediction capability of LSTM with the reliable interval prediction ability of GPR, demonstrating superior performance in accurately predicting ship motion attitudes for operational decision-making (Sun et al., 2022). The SHM-CNN-GRU-AM hybrid model, optimized using the GCWOA algorithm, demonstrates superior forecasting accuracy for ship motion, effectively addressing the complex nonlinear dynamics and variable periodicity inherent in ship motion time history data (Li et al., 2022). The EMD-PSO-LSTM hybrid model, utilizing intelligent algorithms with a sliding window approach, effectively predicts nonlinear and nonstationary ship motion attitudes (Geng et al., 2023). The R-LSTM hybrid method, which combines an LSTM model with a residual network and an attention mechanism, enhances prediction accuracy and generalization for ship maneuvers in challenging navigation conditions. This method ensures efficient and safe navigation by offering real-time trajectory forecasts (Zhou et al., 2023). These studies have improved the accuracy of ships’ motion attitude to a certain extent.

Although the work of ship motion prediction has been developed for a long time, the problem of high-dimension feature data still cannot be avoided, leading to the model failure to converge during training. The prediction of ships’ motion uses complex data that combines ship motion features and wave features as input. Determining the hyperparameters of the LSTM model effectively and achieving convergence of results have become challenging problems when dealing with the high dimension of input features. Principal component analysis (PCA) is a commonly used technique for dimension reduction that transforms high-dimensional datasets into low-dimensional subspaces while retaining most of the variation in the data (Greenacre et al., 2022). However, PCA may not always capture the most relevant or informative aspects of the data, especially if the features have complex interdependencies or nonlinear relationships.

The study ensured the effectiveness of data by utilizing simulation data generated through a hybrid method that combines the fully nonlinear potential flow method and the viscous flow method. First, motion data of the ship and wave height data at varying distances from the ship are selected. The correlation coefficients between wave height data at different distances from the ship’s bow are calculated using Pearson correlation, which are subsequently processed as weights for dimension reduction. To optimize the performance of the WPCA (Weighted Principal Component Analysis), an initial retained variance value is set prior to dimension reduction and is dynamically updated during the process. This approach enables the model to effectively capture the wave excitation acting on the ship while reducing dimensionality and eliminating redundant information. The motion data and the processed wave data are combined to form the input dataset for training the neural network model. The hyperparameters of the model are optimized through a double circulation process, consisting of internal and external circulation, to enhance predictive accuracy and generalization capability. The prediction results of the proposed hybrid model are compared with conventional models and models employing traditional data preprocessing methods, demonstrating the advantages and effectiveness of the proposed approach. This structured methodology highlights the innovative aspects of the work, including advanced data processing and robust model optimization, ensuring reliable and accurate ship motion prediction.

2 Principles and methods

2.1 Numerical methods

In previous work, the hybrid method has been applied and validated for the numerical simulation of motion in waves and manoeuvre of trimaran (Gong et al., 2020, Gong et al., 2021, Gong et al., 2022b), and here, a brief summary to ensure the paper’s completeness has been presented.

2.1.1 Numerical method

To accurately simulate surf-riding and broaching of a trimaran, nonlinear effects such as side hull emergence, bow diving, and transient draft variation are considered. The internal domain is solved using a viscous flow method, assuming incompressible flow with constant density and neglecting heat exchange. The incompressible URANS equations are:

$\begin{array}{ll}\frac{\mathbf{\partial }\rho }{\mathbf{\partial }\text{t}}+\frac{\mathbf{\partial }({\text{ρU}}_{\text{i}})}{\mathbf{\partial }{\text{x}}_{\text{i}}}=\mathbf{0}& (1)\end{array}$

$\begin{array}{ll}\frac{\mathbf{\partial }{\text{U}}_i}{\mathbf{\partial }\text{t}}+\frac{\mathbf{\partial }}{\mathbf{\partial }{\text{x}}_{\text{j}}}({\text{U}}_{\text{i}}{\text{U}}_{\text{j}})=-\frac{1}{\text{ρ}}\frac{\mathbf{\partial }\text{P}}{\mathbf{\partial }{\text{x}}_{\text{i}}}+\frac{1}{\text{ρ}}\frac{\mathbf{\partial }}{\mathbf{\partial }{\text{x}}_{\text{j}}}\mathbf{(}\text{μ}\frac{\mathbf{\partial }{\text{U}}_{\text{i}}}{\mathbf{\partial }{\text{x}}_{\text{j}}}+{\text{ρτ}}_{\text{ij}}\mathbf{)}& (2)\end{array}$

Where $\rho$ represents density, t denotes time, ${\tau }_{ij}=-\overline{u{\text{'}}_{i}u{\text{'}}_j}$ denotes the Reynolds Stress Tensor, P represents pressure, $U_i$ and $u{\text{'}}_i$ represent the time-averaged and fluctuation components of velocities, respectively, $\mu$ denotes the dynamic viscosity. The flow around the trimaran is accurately modelled using the Volume of Fluid (VOF) method combined with compression techniques. This approach effectively manages the Eulerian two-phase flow, ensuring precise simulation of the fluid dynamics near the trimaran. An artificial compression technique ensures a sharp interface between air and water (Rusche, 2002; Weller, 2002).

The external domain assumes ideal flow, governed by the Laplace equation. A wavemaker and adaptive wave absorption are implemented at opposite boundaries. Internal and external domains are coupled via interfaces, with more details on hybrid methods available in references (Ma and Yan, 2009; Yan and Ma, 2010; Hu et al., 2020; Gong et al., 2021).

2.1.2 Trimaran motion

The global coordinate system (x, y, z) is used for flow field solutions, while a local coordinate system (x', y', z'), centered at the trimaran’s center of gravity, is applied for motion calculations. The ship’s 6DOF motion includes linear velocities ($u_{x\text{'}}$, $u_{y\text{'}}$, $u_{z\text{'}}$) and angular velocities ($r_{x\text{'}}$, $r_{y\text{'}}$, $r_{z\text{'}}$), governed by:

$\begin{array}{ll}\{\begin{array}{l}\mathit{m}({\dot{\mathit{u}}}_{\mathbf{1}\text{'}}-{\mathit{u}}_{\mathbf{2}\text{'}}{\mathit{r}}_{\mathbf{3}\text{'}}+{\mathit{u}}_{\mathbf{3}\text{'}}{\mathit{r}}_{\mathbf{2}\text{'}})={\mathit{F}}_{\mathit{H}\mathbf{1}\text{'}}+{\mathit{F}}_{\mathit{W}\mathit{J}\mathbf{1}\text{'}}\hfill \\ \mathit{m}({\dot{\mathit{u}}}_{\mathbf{2}\text{'}}-{\mathit{u}}_{\mathbf{3}\text{'}}{\mathit{r}}_{\mathbf{1}\text{'}}+{\mathit{u}}_{\mathbf{1}\text{'}}{\mathit{r}}_{\mathbf{3}\text{'}})={\mathit{F}}_{\mathit{H}\mathbf{2}\text{'}}+{\mathit{F}}_{\mathit{W}\mathit{J}\mathbf{2}\text{'}}\hfill \\ \mathit{m}({\dot{\mathit{u}}}_{\mathbf{2}\text{'}}-{\mathit{u}}_{\mathbf{1}\text{'}}{\mathit{r}}_{\mathbf{2}\text{'}}+{\mathit{u}}_{\mathbf{2}\text{'}}{\mathit{r}}_{\mathbf{1}\text{'}})={\mathit{F}}_{\mathit{H}\mathbf{1}\text{'}}+{\mathit{F}}_{\mathit{W}\mathit{J}\mathbf{1}\text{'}}\hfill \\ {\mathit{I}}_{\mathbf{1}\text{'}}{\mathit{r}}_{\mathbf{1}\text{'}}+({\mathit{I}}_{\mathbf{3}\text{'}}-{\mathit{I}}_{\mathbf{2}\text{'}}){\mathit{r}}_{\mathbf{2}\text{'}}{\mathit{r}}_{\mathbf{3}\text{'}}={\mathit{M}}_{\mathit{H}\mathbf{1}\text{'}}+{\mathit{M}}_{\mathit{W}\mathit{J}\mathbf{1}\text{'}}\hfill \\ {\mathit{I}}_{\mathbf{2}\text{'}}{\mathit{r}}_{\mathbf{2}\text{'}}+({\mathit{I}}_{\mathbf{1}\text{'}}-{\mathit{I}}_{\mathbf{3}\text{'}}){\mathit{r}}_{\mathbf{1}\text{'}}{\mathit{r}}_{\mathbf{3}\text{'}}={\mathit{M}}_{\mathit{H}\mathbf{2}\text{'}}+{\mathit{M}}_{\mathit{W}\mathit{J}\mathbf{2}\text{'}}\hfill \\ {\mathit{I}}_{\mathbf{3}\text{'}}{\mathit{r}}_{\mathbf{3}\text{'}}+({\mathit{I}}_{\mathbf{2}\text{'}}-{\mathit{I}}_{\mathbf{1}\text{'}}){\mathit{r}}_{\mathbf{1}\text{'}}{\mathit{r}}_{\mathbf{2}\text{'}}={\mathit{M}}_{\mathit{H}\mathbf{3}\text{'}}+{\mathit{M}}_{\mathit{W}\mathit{J}\mathbf{3}\text{'}}\hfill \end{array}& (3)\end{array}$

where m is the trimaran’s mass, ($I_{x\text{'}}$, $I_{y\text{'}}$, $I_{z\text{'}}$) are moments of inertia, and ($F_{Hx\text{'}}$, $F_{Hy\text{'}}$, $F_{Hz\text{'}}$) and ($M_{Hx\text{'}}$, $M_{Hy\text{'}}$, $M_{Hz\text{'}}$) are forces and moments from the hull. Water-jet propulsion forces and moments ($F_{WJx\text{'}}$, $F_{WJy\text{'}}$, $F_{WJz\text{'}}$) and ($M_{WJx\text{'}}$, $M_{WJy\text{'}}$, $M_{WJz\text{'}}$) are modeled semi-empirically. After solving Equation 3, the changing rate of the Euler angle can be determined by

$\begin{array}{ll}\left[\begin{array}{ccc}\mathbf{1}& sin{\mathit{\xi }}_{\mathbf{4}}tan{\mathit{\xi }}_{\mathbf{5}}& cos{\mathit{\xi }}_{\mathbf{4}}tan{\mathit{\xi }}_{\mathbf{5}}\\ \mathbf{0}& cos{\mathit{\xi }}_{\mathbf{4}}& -sin{\mathit{\xi }}_{\mathbf{4}}\\ \mathbf{0}& sin{\mathit{\xi }}_{\mathbf{4}}/cos{\mathit{\xi }}_{\mathbf{5}}& cos{\mathit{\xi }}_{\mathbf{4}}/cos{\mathit{\xi }}_{\mathbf{5}}\end{array}\right]\left[\begin{array}{c}{\mathit{r}}_{\mathbf{1}\text{'}}\\ {\mathit{r}}_{\mathbf{2}\text{'}}\\ {\mathit{r}}_{\mathbf{3}\text{'}}\end{array}\right]& (4)\end{array}$

The target course of the autopilot is set to 0°, and PD (proportional derivative) control scheme is adopted. Autopilot control uses a PD controller, where the target nozzle deflection angle δ is:

$\begin{array}{ll}\mathit{\delta }=K_p{\xi }_{\mathbf{6}}+K_d{\dot{\xi }}_{\mathbf{6}}& (5)\end{array}$

Here, K_p=9.5, K_d=3.0, with δ_max=35° and $\dot{\delta }$=10°/s.

2.1.3 Domain and grid generation

The external domain grid is based on the QALE-FEM method (Yan et al., 2019), adjusted to the trimaran's navigation range. The internal domain dimensions are 4.5L×3.0L×2.0L, with water above and below set to 0.5L and 1.0L, respectively (ITTC, 2014). Grids are generated using OpenFOAM’s blockMesh and snappyHexMesh tools, following procedures in zigzag maneuver simulations (Gong et al., 2022a). The boundary definition of the hybrid method and the grid sketch are shown in Figure 1.

Figure 1

Figure 1. The sketch of the hybrid method's boundary.

The internal domain uses a k−ω SST turbulence model and the PISO method to solve pressure-velocity coupling. Boundary conditions are coupled with the external domain, transferring velocity and volume fraction at each time step. Diagrams of the grid and boundary conditions illustrate the setup.

The specific characteristic dimension of the trimaran form in this paper is shown in Table 1. The specific meanings of symbols in trimaran have been shown in Figure 2.

Table 1

Table 1. The specific parameters of incident waves and ship.

Figure 2

Figure 2. The sketch and dimensions of a trimaran.

2.2 Pearson correlation

Principal Component Analysis (PCA) is a highly effective statistical method used for dimension reduction, data visualization, and feature extraction. The Pearson correlation coefficient has been employed in calculating the linear correlations between ship motion dynamics and environmental conditions when analyzing ship motion (Zhang et al., 2023). In this paper, visualizing the relation between different distances of wave height will reinforce the understanding of the influence between waves and ship motion.

For two different features, ${\alpha }_1$ and ${\alpha }_2$, their correlation coefficient can be computed:

$\begin{array}{ll}\mathit{\rho }=\frac{cov({\mathit{\alpha }}_{\mathbf{1}},{\mathit{\alpha }}_{\mathbf{2}})}{\sqrt{var({\mathit{\alpha }}_{\mathbf{1}})}\sqrt{var({\mathit{\alpha }}_{\mathbf{2}})}}& (6)\end{array}$

where $cov({\alpha }_1,{\alpha }_2)$ is the covariance of the two features, $var({\alpha }_1)$, $var({\alpha }_2)$ is the variance of feature ${\alpha }_1$ and feature ${\alpha }_2$, respectively. The value of ρ ranges from -1 to 1. The closer the value is to 1, the more positive linear correlation between the two features, and the closer the value is to -1, the more negative linear correlation between the two features. When ρ is 1, it signifies a complete positive linear correlation; when ρ is -1, it signifies a complete negative linear correlation. A ρ value of 0 means there is no linear correlation between the variables.

In this paper, assuming that the time history of one feature is denoted as $X=\{x_1,x_2,\cdots ,x_n\}$, and another feature represent as $Y=\{y_1,y_2,\cdots y_n\}$. X and Y represent a whole time history of the feature with n nodes, then the correlation coefficient of the two features is (Cohen et al., 2009):

$\begin{array}{ll}\mathit{r}=\frac{{\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_{i=1}^n{(x_i-\overline{x})}^2{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}& (7)\end{array}$

2.3 Reduction of wave feature dimension

Suppose that each wave height feature is represented as $X^i=\{x_1^i,x_2^i,\cdots ,x_n^i\}$, where $x_n^i$ represents the n-th node in a time history of the i-th feature. The complete dataset of wave features can be represented as a matrix:

$\begin{array}{ll}\mathit{X}=\left[\begin{array}{ccc}{\mathit{x}}_{\mathbf{1}}^{\mathbf{1}}& \cdots & {\mathit{x}}_{\mathbf{1}}^{\mathit{i}}\\ ⋮& \ddots & ⋮\\ {\mathit{x}}_{\mathit{n}}^{\mathbf{1}}& \cdots & x_n^i\end{array}\right]=\mathbf{(}{\mathit{X}}^{\mathbf{1}},{\mathit{X}}^{\mathbf{2}},\cdots ,X^n\mathbf{)}& (8)\end{array}$

Combined with the Equation 8, the overall covariance S and each element in overall covariance were denoted as follows (Martinez and Kak, 2001):

$$\mathit{S}={\mathbf{(}{S}_{ij}\mathbf{)}}_{n\times n}, s_{ij}=\frac{\mathbf{1}}{\mathit{n}-\mathbf{1}}{\sum }_{\mathit{k}-\mathbf{1}}^{\mathit{n}}\mathbf{(}{x}_k-{\overline{x}}_i\mathbf{)}{\mathbf{(}{x}_k-{\overline{x}}_j\mathbf{)}}^{\mathit{T}}, {\overline{x}}_i=\frac{\mathbf{1}}{\mathit{n}}{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{n}}{x}_{ki}$$

The standard PCA treats all data points and features equally, and cannot capture the most relevant aspects of the data with complex interdependencies or nonlinear relationships. However, the influences between wave and ship change with the increasing distance (Torsvik, 2009). This paper will employ the WPCA with the Pearson correlation as the weight based on the reference (Xiao et al., 2023). Setting an initial value $\gamma$ of retained variance can be optimized in the model training process. Assign a weight $w_i$ to each feature i, reflecting its importance. Modify the computation of the covariance between features i and j to include weights:

$\begin{array}{ll}{s}_{ij}^{\prime }=\frac{\mathbf{1}}{{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{n}}{w}_k-\mathbf{1}}{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{n}}{w}_k\mathbf{(}{x}_{ki}-{\overline{x}}_i^{\prime }\mathbf{)}\mathbf{(}{x}_{kj}-{\overline{x}}_j^{\prime }\mathbf{)}, {\overline{x}}_i^{\prime }=\frac{{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{n}}{w}_k{x}_{ki}}{{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{n}}{w}_k}& (10)\end{array}$

$\begin{array}{ll}{w}_k={(\frac{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{m}}(x_{ki}-{\overline{x}}_i^{\prime })(x_{kj}-{\overline{x}}_j^{\prime })}{\sqrt{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{m}}{(x_{ki}-{\overline{x}}_i^{\prime })}^{\mathbf{2}}}\sqrt{{\sum }_{\mathit{j}=\mathbf{1}}^{\mathit{m}}{(x_{kj}-{\overline{x}}_j^{\prime })}^{\mathbf{2}}}})}^{\mathbf{2}}& (11)\end{array}$

The weighted covariance matrix $S^{\prime }$ is then used in place of the standard covariance matrix for PCA:

$\begin{array}{ll}{S}^{\prime }=\left[\begin{array}{ccc}{\mathit{S}}_{\mathbf{11}}^{\text{'}}& \cdots & {\mathit{S}}_{\mathbf{1}\mathit{n}}^{\text{'}}\\ ⋮& \ddots & ⋮\\ {\mathit{S}}_{\mathit{n}\mathbf{1}}^{\text{'}}& \cdots & S_{nn}^{\text{'}}\end{array}\right]& (12)\end{array}$

The eigenvalues and the eigenmatrix of $S^{\prime }$ are $\lambda$ and $a$, they satisfied the following formula:

$\begin{array}{ll}{S}^{\prime }{a}_i={\lambda }_i{a}_i,i=\mathbf{1},\mathbf{2},\cdots ,\mathit{n}& (13)\end{array}$

To adjust the eigenvalues and eigenvectors of $S^{\prime }$ and obtain the edge transformation matrix A, follow these steps:

$\begin{array}{ll}\mathit{A}=({\mathit{a}}_{\mathbf{1}},\cdots ,a_n)& (14)\end{array}$

Then, the principal component matrix can be expressed as:

$\begin{array}{ll}\mathit{P}=(\mathit{X}-{\overline{x}}_i)·\mathit{A}& (15)\end{array}$

The retention variance is the ratio of the retained variance to the total variance:

$\begin{array}{ll}\mathit{\gamma }=\frac{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\lambda }_k}{trace({\mathit{S}}^{\prime })}& (16)\end{array}$

2.4 LSTM model

LSTM models, also called Long Short-Term Memory models, are a specialized form of recurrent neural networks (RNNs) specifically designed to handle and learn from time sequential data. Their architecture allows them to effectively capture long-term dependencies, making them particularly suitable for tasks involving the understanding and forecasting of time-based patterns. With gated mechanisms, including input, forget, and output gates, LSTMs effectively manage information flow. In time series prediction, LSTMs excel in capturing complex patterns and long-term dependencies (Rithani et al., 2023), making them suitable for tasks like stock prices and weather forecasting. In maritime applications, LSTMs can predict vessel trajectories, detect anomalies, and monitor vessel operational status, thereby enhancing navigation safety and efficiency. The LSTM unit includes the LSTM cells, each of which includes an input gate, an output gate, and a forget gate, as shown in Figure 3.

Figure 3

Figure 3. Structure of LSTM cell.

The key principles of each gate in LSTM can be concluded as the following equations (the connotation of each symbol in LSTM cell is shown in Table 2):

$$i_t={\sigma }_g(W_f{x}_t+U_f{h}_{t-1}+b_f)$$

$$f_t={\sigma }_g(W_i{x}_t+U_i{h}_{t-1}+b_i)$$

$\begin{array}{ll}{o}_t={\sigma }_g(W_o{x}_t+U_o{h}_{t-1}+b_o)& (17)\end{array}$

$${\tilde{c}}_t=tanh(W_c{x}_t+U_c{h}_{t-1}+b_c)$$

$$c_t=f_t\odot c_{t-1}+i_t\odot {\tilde{c}}_t$$

$$h_t=o_t\odot {\sigma }_h(c_t)$$

Table 2

Table 2. The connotation of each symbol in LSTM cell.

2.5 The proposed model

Extracting valuable features from the waves and ship motions and reducing risks from the high dimension of features are the main problems in training the neural network. In this section, the specific model structure and algorithmic steps which are used to predict ship motion in this paper will be discussed.

The proposed model will divide the features into two groups. Then, the WPCA algorithm will be employed to extract the main information of waves and the reduce the dimension of the wave feature based on the feature weighting coefficients. This method reduces dimensionality while retaining critical information handles noisy data effectively, and adapts to varying conditions. The optimization process of the hybrid model hyperparameters is divided into external and internal circulation. And the internal and external circulations also form the Double-Circulation (DC) module. The internal circulation repeatedly improves the hyperparameters of the hybrid model based on the metrics of prediction results, while the external circulation optimizes the hyperparameters of the hybrid model based on the retained variance value of WPCA.

The workflow and steps of the proposed ship motion prediction model are shown in Figure 4. In the first step, the data on motion and wave features will be extracted from the results of the numerical simulation. In the second step, the Pearson coefficient between different distance waves is calculated as the weight of WPCA, and then the dimension of the wave feature is reduced based on the weight. In the third step, the proposed wave features and motion features are combined as the input dataset to train the model. In the fourth step, the hyperparameters will be improved through the internal and external circulation based on the prediction results. The detailed schematic diagram of the proposed model is shown in Figure 5. Table 3 shows specific hyperparameters of the neural network and the training setting of model architecture. Where is the number of final selected features which will be input to the proposed model, the number of the input features will change with the changes of dimension reduction schemes in this paper. The model is composed of seven layers which contains three LSTM layers, three dropout layers, and a dense output layer. All the layers are connected in the order shown in the Table 3. The inclusion of dropout layers aims to mitigate overfitting by forcing the network to learn more robust features that generalize well to new data. The prediction strategy employed involves using 1000 time steps of selected feature data as input to forecast the same feature data for the next fiftieth or more time step.

Figure 4

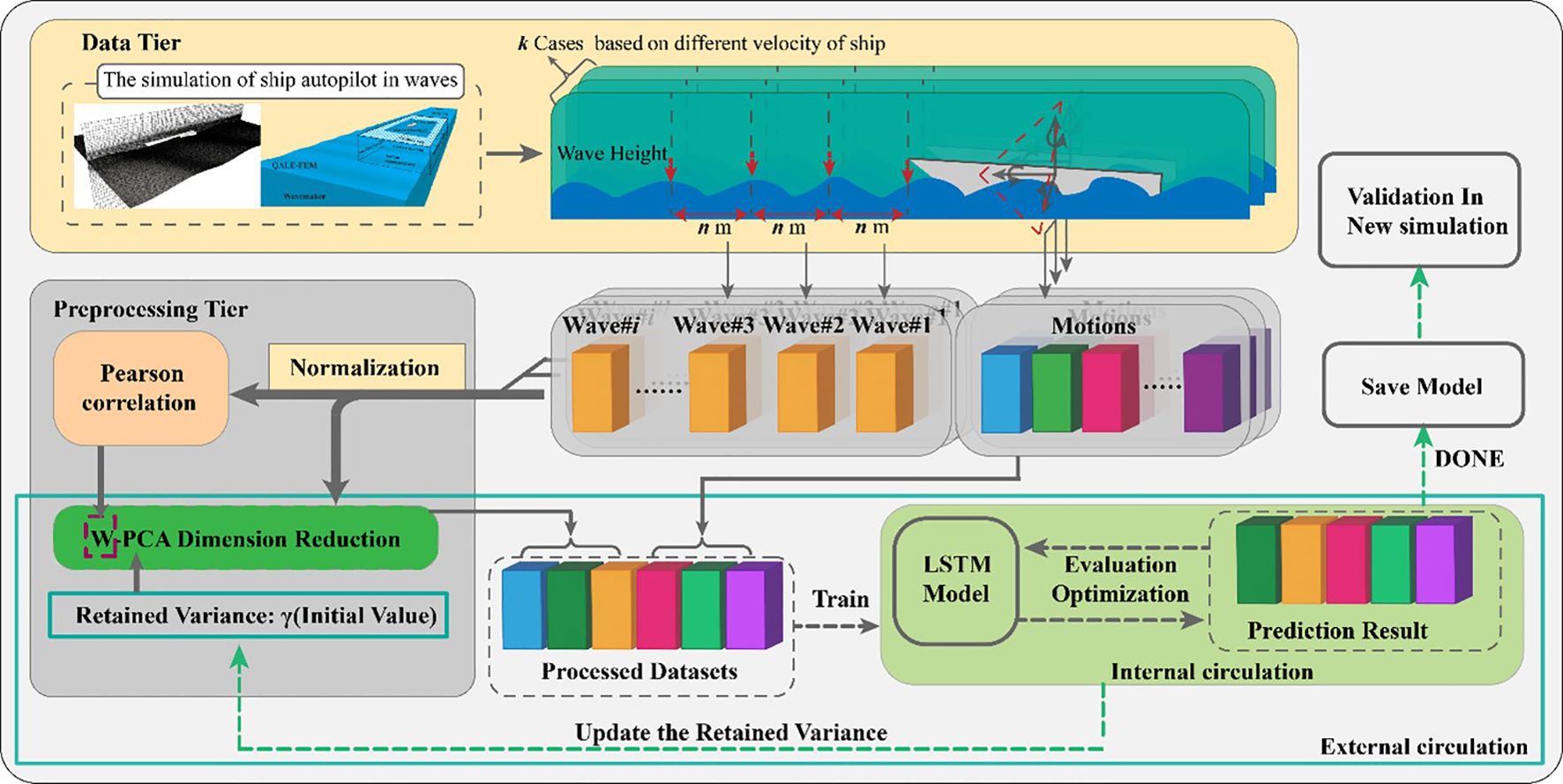
Figure 4. Schematic diagram of the proposed ship motion prediction in irregular waves based on the WPCA-DC-LSTM model.

Figure 5

Figure 5. Detailed information of the WPCA-DC-LSTM model.

Table 3

Table 3. The specific structure and parameters of the neural network.

2.6 Performance evaluation of model

Three metrics help evaluate the model’s performance in predicting ship movement in this paper, where R² indicates the proportion of the explained variance, RMSE indicates the typical size of the forecast error, and MAE provides a more interpretable measure of forecast accuracy.

$\begin{array}{ll}{R}^2=\sqrt{1-\frac{{\sum }_{i=1}^n{(y_i^{\prime }-y_i)}^2}{{\sum }_{i=1}^n{(\overline{y}-y_i)}^2}}& (18)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(y_i^{\prime }-y_i)}^2}& (19)\end{array}$

$\begin{array}{ll}MAE=\frac{1}{n}{\sum }_{i=1}^n|y_i^{\prime }-y_i|& (20)\end{array}$

3 Case study

3.1 The effect of each distance wave feature on the ship’s motion prediction

In this section, the data of wave height is selected every five meters from the bow of the trimaran to 20m ahead, as shown in Figure 4. Five datasets have been generated, each of which contains the data of wave and motion features. The specific conditions of each dataset have been shown in Table 4.

Table 4

Table 4. The specific conditions of the different cases.

The total time of the navigation under the condition of 0.35 Fn is 55s, and the data from 0s to 45s has been employed to train the proposed hybrid model, the rest of the data is used for verification. Notably, each time step of the dataset is 0.004s. Figure 6 shows the prediction results of the model trained by the different cases. Table 5 shows R², RMSE, and MAE for predicting the model trained by the different cases.

Figure 6

Figure 6. Comparison between the prediction and the original data.

Table 5

Table 5. R², RMSE, and MAE for prediction results.

In Figure 6, the datasets combining motion and wave features perform well in model training. Comparing the prediction results of the ship’s heave in Figure 6A, the results of Case1 and Case2 are more accurate than those from Case3 to Case5. In Figures 6B, D, there is an apparent bias between the original data and prediction results, suggesting that the introduced feature augmentation fails to uphold robust generalization across various features during model training. It can be seen that the dataset obtained by adding features cannot maintain good generalization for most features when training the model. In addition, the effect of waves at short distances on the ship's motion is greater than that of far waves.

In Table 5, the bias of R², RMSE, and MAE between these cases shows that waves in distances of 0m and 5m are more valuable in training the model. However, the slight variation in error indicates that these features of different distances cannot be ignored during training.

In general, different distances wave height features have different influences on the model's predictive capability. It can be found that the data set combining waves at short distances (0-5m in this case) performs better than the wave features at long distances. However, it also increases the burden of model learning, and if more wave features are added at one time, the problem of dimensional explosion will be generated.

3.2 Reduction of feature dimension based on WPCA

Due to the redundancy of wave height data at different distances, the feature dimension is too high, which increases the complexity of model training. To alleviate the dimensional disaster of the features and improve the efficiency of model training and performance of the model prediction, the wave feature data will be processed with the WPCA proposed in previous section. Figure 7 shows the Pearson coefficient between different features.

Figure 7

Figure 7. Visualization of correlation for the features.

Figure 7A shows the coefficients between wave features, and Figure 7B shows the coefficients between wave and ship motions. The Pearson coefficients between wave features and the ship’s trajectory are close to zero, so those effects can be ignored while calculating the weights before reducing the dimension. Pearson coefficients between other motion features and wave features were calculated respectively, and the expected value of the corresponding feature was taken as the weight of dimension reduction. In WPCA, the feature weights reflect their importance and correlation with the target variable. When a high retained variance (95%) is needed, the model must consider more details and complexity, thus requiring more principal components (WPCA_1, WPCA_2, and WPCA_3). When a lower retained variance (e.g., 85%) is acceptable, the model becomes simpler, requiring only two principal components (WPCA_1 and WPCA_2). The model is highly simplified at very low retained variance levels (below 75%), requiring only one principal component (WPCA_1), indicating that this single component is sufficient to explain the major variance and information.

3.3 Comparison of the hybrid model and conventional model

In this section, the performance of three models will be compared based on the prediction results. The models are the WPCA-DC-LSTM model, PCA-LSTM, and conventional LSTM model. The method of WPCA will generate three groups based on different retained variances. The specific features are shown in Table 6. A mark “√" indicates the feature data included at input, and the mark “x" indicates that this feature was not included at input.

Table 6

Table 6. The specific features of each selected dataset.

In Case#2.1, the PCA-LSTM model was employed. Cases from 2.2 to 2.4 utilized the WPCA-DC-LSTM model, while Case#2.5 and Case#2.6 utilized the conventional LSTM model.

Figure 8 shows the results of ship’s motion prediction in irregular waves. The first 45 seconds represent the training data used by the models, followed by the input data from 45 to 49 seconds. The last 6 seconds show the output predictions generated by the models compared against the true values of the prediction target. Table 7 shows the performance metrics of the models on both the training dataset and the validation dataset.

Figure 8

Figure 8. Comparison between the predicted results of different models and the original data.

Table 7

Table 7. R², RMSE, and MAE for prediction results.

In Figure 8, the three models have good performance of prediction on the selected dataset. Case#2.2 achieved high precision fit in predictions of heave, roll, pitch, and heading. With the decrease of retained variance, the performance of WPCA-DC-LSTM also decreases slightly. The PCA-LSTM model, which also reduces the wave features to three dimensions, has an apparent bias in motion prediction. The prediction results of the conventional LSTM model without adding wave features also shows poor performance.

In Table 7, the minimum values of RMSE and MAE appear in the results of dataset Case#2.3. The results indicate that while the prediction accuracy of the WPCA-DC-LSTM model shows certain limitations, particularly in comparison to more advanced or fine-tuned prediction frameworks, it allows for a clearer observation of the impact of different methodological variations. For instance, the performance of Case#2.2, with an R² value of 0.43612, significantly outperforms Case#2.3 (R² = 0.41673), despite their RMSE and MAE values being relatively close. This highlights that the retained variance of 95% in Case#2.2 is more effective in capturing meaningful information than the 85% retained variance in Case#2.3, especially in terms of model fit. Furthermore, the comparison between Case#2.5 and Case#2.6 emphasizes the positive effect of incorporating wave features, as the former shows better performance in all metrics, including a higher R² (0.33715 vs. 0.23079), demonstrating the importance of such features in enhancing prediction accuracy.

Overall, the WPCA-DC-LSTM model demonstrates that higher retained variances (above 85%) are critical for achieving reliable predictions, with performance converging at these levels. While the absolute predictive accuracy is moderate, the model effectively avoids overfitting and dimensionality issues observed in conventional methods. This allows a more controlled and interpretable evaluation of the influence of feature selection, dimensionality reduction, and wave feature inclusion on prediction outcomes. Future work should focus on further optimizing feature weighting before dimensionality reduction and incorporating more wave-related features to enhance the predictive capability for ship motion.

4 Prediction results and discussion

In this section, the trained model will be employed to predict the motion of the ship based on the new complete dataset, the F_n of which is 0.65. The retained variance of the WPCA-DC-LSTM is 95%. The other parameters of the model have been shown in section 2.6. The generalization ability of the model will be further discussed. In this section, the whole 55s prediction work will be implemented, excluding the first 1000-time steps.

4.1 Comparison of different advanced time steps based on 20m wave

Based on wave height data collected at distances of N (less than 20) m from the ship bow, these data are processed using Weighted Principal Component Analysis (WPCA). The processed wave height data, along with motion data, are then combined to input the hybrid model for predicting the ship’s motion. The specific features of the dataset are shown in Table 8. The features of wave height and 6DOF will be inputted the model.

Table 8

Table 8. Specific features of datasets.

The advanced time steps of prediction are 50, 75, 100, 125, and 150. Figure 9 illustrates the comparison between the time histories of predicted ship motion based on various input schemes and the original data. Figure 10 presents three metrics of the models on the selected validation datasets.

Figure 9

Figure 9. Comparison between the predicted results based on different input schemes and the original data.

Figure 10

Figure 10. RMSE, and MAE for prediction results.

In Figure 9, the model has good prediction effects on the selected dataset when the advanced time step is 50. With the increase in the advanced time step, the discrepancy between the predicted values and the original data is more apparent. In Figure 9A, the performance of the heave prediction is worse than that of other motion features. Especially the discrepancy between the prediction results and original values at the marked troughs and peaks is most affected by the increase of advanced time steps. In Figure 9B, there is a phenomenon of poor fitting to the periodic change data when the advanced time steps are more than 100. The prediction of pitch and heading met the expectation to some extent. The high accuracy of the short-term prediction reflects the ability of the WPCA-DC-LSTM hybrid model to extract the features of the ship’s motions and waves height.

In Figure 10, the RMSE and MAE achieved the minimum value when the advanced time steps were 50, it means the model is effectively minimizing large prediction errors when the advanced time is 50. Although the loss does not increase with the increase of the advanced time step, the overall trend is higher loss at the high advanced time step.

In general, the predictive capability of the model on the new data set is not too bad when the advanced time below 75, indicating that the proposed model has good ability of generalization. And the advanced time of single heading feature have room for testing. The accuracy of the heading prediction results is higher than the other features, showing that the features extracted from the waves have a more positive influence on the heading in the trained model.

4.2 Comparison of different advanced time steps based on 15m wave

The distance from the ship is reduced from 20 to 15 meters, and the wave height data at 0m,5m,10m, and 15m are taken. Then the wave height data processed by WPCA and motion data will be input into the model together to predict the ship’s motion. The advanced time steps of prediction are 50, 75, 100, 125, and 150. The different comparisons between the time history of the ship motion predicted based on different input database processing schemes and the original data is shown in Figure 11. Figure 12 shows the three final metrics of the models on the selected validation dataset.

Figure 11

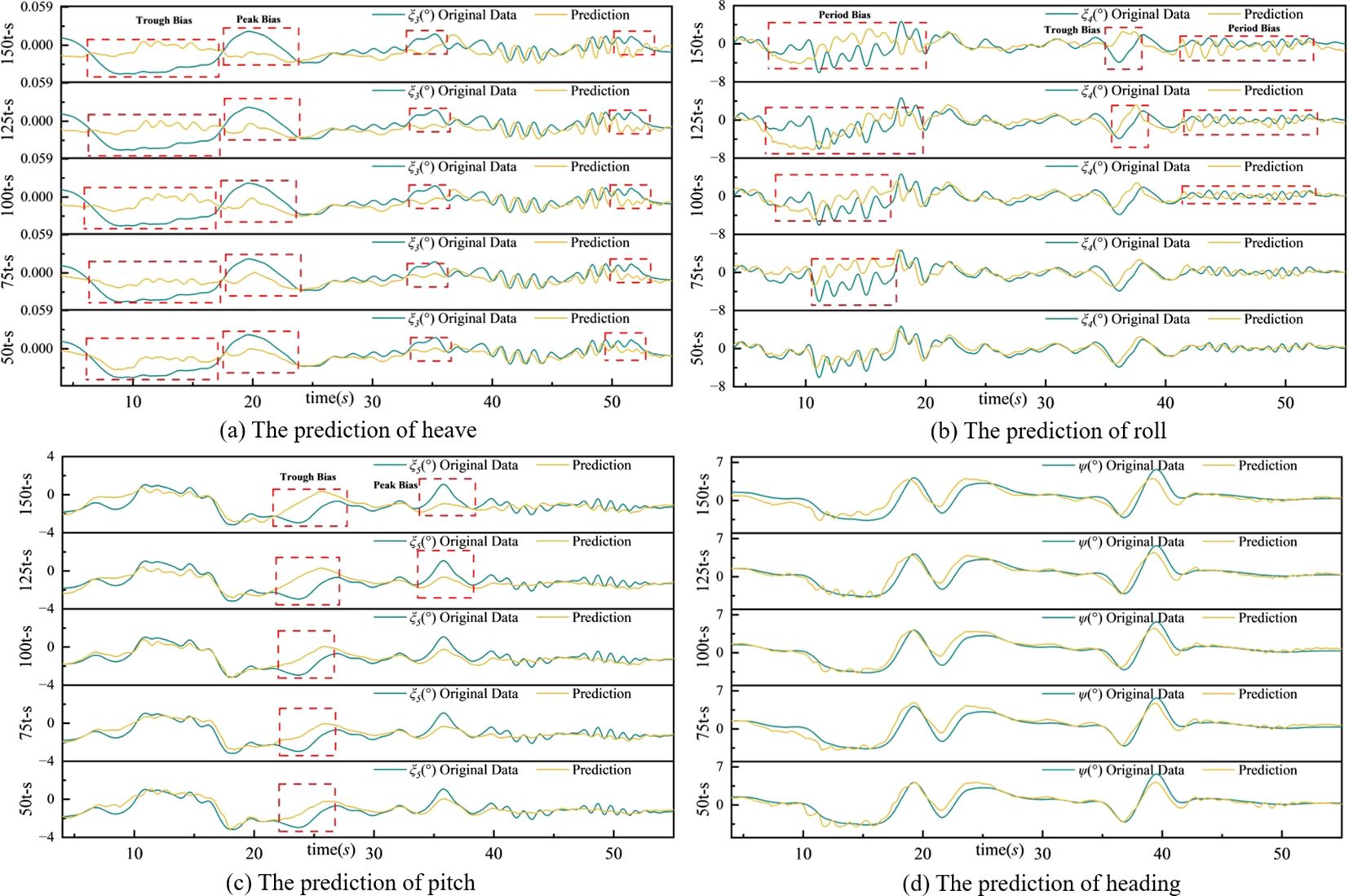
Figure 11. Comparison between the prediction results based on different input database processing schemes and the original data.

Figure 12

Figure 12. R², RMSE, and MAE for prediction results.

In Figure 11, the model has good prediction effects on the roll, pitch, and heading when the advanced time step is 50. The accuracy of the 50t-s in Figure 11 is similar to that of the 75t-s in Figure 9. With the increase in the advanced time step, the discrepancy between predicted values and original data is more apparent. In Figure 11A, the performance of the heave prediction is worse than that of other motion features. Apparent biases can be observed at some low advanced time steps. This means that the model’s ability to process long-term dependencies is declining compared to the results in section 4.1. However, the prediction of the heading also met the expectation.

In Figure 12, the values of RMSE and MAE at higher advanced time steps are larger than that at low higher times steps. The overall loss of Figure 12 is larger than that of the corresponding advanced time step in Figure 10. It shows that the contribution of the far wave height features to the prediction cannot be ignored during the process of reducing features dimension. When the wave height data at 20m is reduced, the prediction performance of the model worse overall, indicating that the model obtained the less information with the decrease of wave features.

In light of these observations, it is evident that the WPCA-DC-LSTM model's performance is highly dependent on the inclusion of comprehensive wave height data. The decline in prediction accuracy, particularly for heave at lower advanced time steps, underscores the model’s sensitivity to long-term dependencies. The increased biases and overall loss at higher advanced time steps, as shown in Figures 11 and 12, suggest that reducing the dimensionality of wave height features, especially those at greater distances like 20m, results in significant information loss. This highlights the critical role that distant wave features play in accurate motion prediction. Therefore, ensuring the retention of key wave height data during feature reduction is crucial for maintaining model performance. Furthermore, enhancing the model's capacity to capture long-term dependencies and incorporating advanced feature extraction methods could further improve its robustness and accuracy in predicting ship motion. Additionally, refining noise reduction techniques will help in preserving essential wave information, thereby enhancing the model's predictive capabilities even with fewer features.

4.3 Comparison of different advanced time steps based on 10m wave

Using wave height data from three points—0 m, 5 m, and 10 m from the ship bow—processed by WPCA, and combining these with motion data, input features were created to predict the ship’s motion. Figure 13 shows the comparison between the original data and the time history of ship motion predicted using different input schemes. Figure 14 shows three metrics of the models on the training dataset and validation dataset.

Figure 13

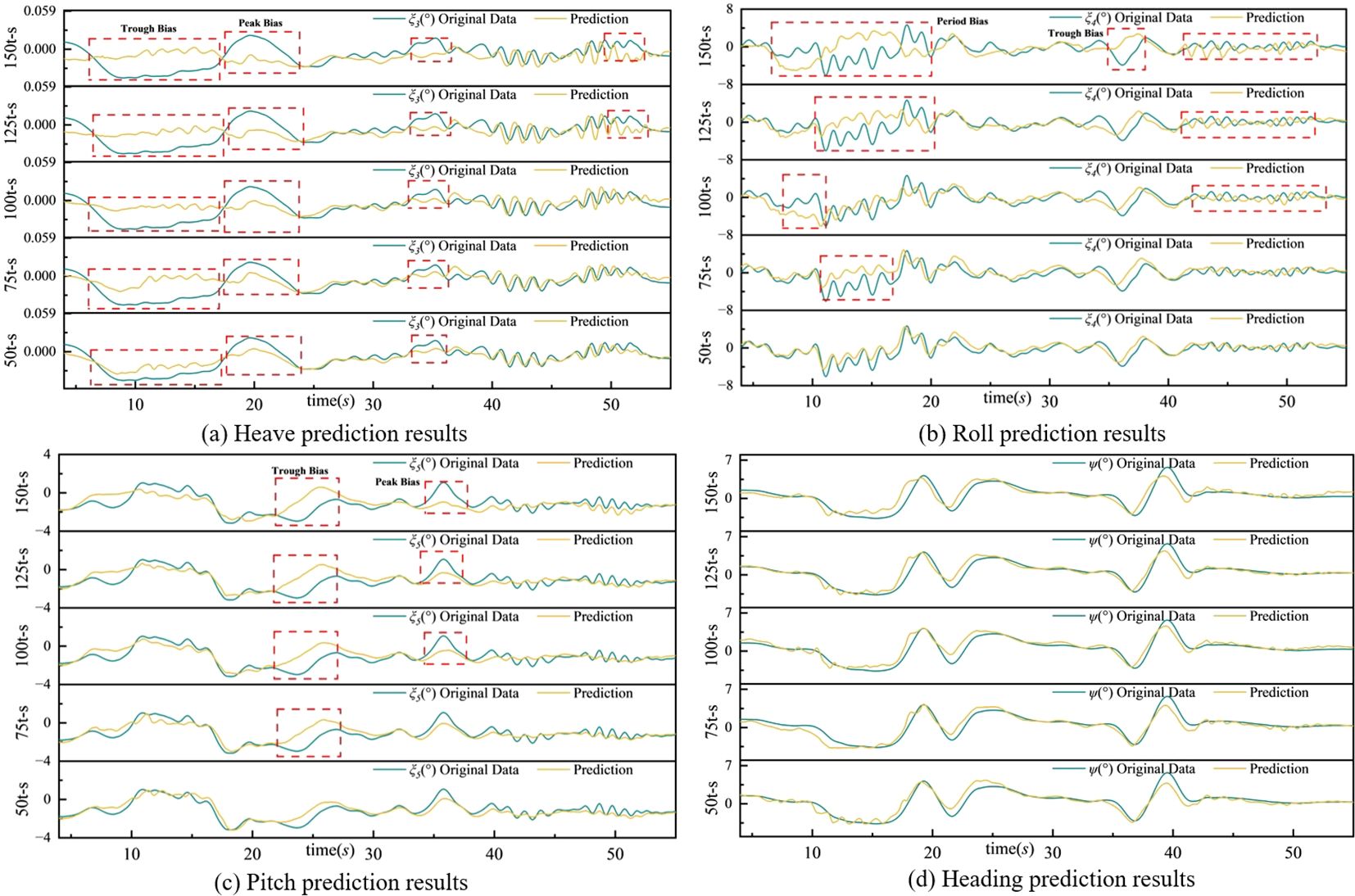
Figure 13. Comparison between the prediction results with different input schemes and the original data.

Figure 14

Figure 14. R², RMSE, and MAE for prediction results.

The trend of the prediction values in Figure 13 closely resembles that in Figures 9 and 11. However, the main distinction lies in the increasing bias between the predicted values and the original data at advanced time steps, particularly at marked points. In Figure 13D, the prediction of the heading shows significant fluctuations after 40 seconds, with a more pronounced bias compared to Figure 9D

In Figure 14, both RMSE and MAE values increase at higher advanced time steps, with overall losses exceeding those in Figures 10 and 12 at corresponding time steps. While MAE consistently rises with the time step, RMSE fluctuates around an intermediate value, highlighting its sensitivity to large errors and anomalies. Despite the fluctuations, the model's overall performance stabilizes as wave characteristics diminish. However, this stabilization does not imply improved prediction accuracy. The differing sensitivities of RMSE and MAE to factors such as error distribution, outliers, and skewness further explain these variations. Overall, the results indicate a decline in the model's generalization ability as fewer wave features are extracted.

Comparing predictions across the three datasets, the model's performance at advanced time steps deteriorates as wave features are reduced. Wave data may contain noise, but assigning higher weights to significant features during dimensionality reduction reduces the influence of noisy features. This process enhances data quality and model robustness. However, when key features critical to prediction are removed, the model loses essential information. Furthermore, the complementary relationships among wave features are disrupted, limiting the model's ability to capture complex wave patterns.

Overall, the WPCA-DC-LSTM model demonstrates strong generalization capabilities across new datasets. Although its predictive accuracy declines over time steps for certain motion features, such as heading and pitch, it excels in accurately predicting heave and roll motions. The reduction in wave features highlights the model's ability to capture essential information, but it also underscores the importance of comprehensive feature extraction for maintaining prediction accuracy. By assigning higher weights to significant features during dimensionality reduction, the model effectively mitigates the impact of noise and preserves critical wave patterns, even with fewer features. This capability ensures the model remains robust and adaptable, reinforcing its effectiveness in capturing and generalizing complex wave dynamics.

4.4 Comparison with other methods

To further validate the effectiveness of the proposed method, a comparative analysis was conducted against several widely used prediction models, including LSTM, BiLSTM, PSO-BiLSTM (BiLSTM optimized with traditional Particle Swarm Optimization), and ADPSO-BiLSTM (BiLSTM optimized with Adaptive Particle Swarm Optimization) (Cheliotis et al., 2020; Han et al., 2024). The goal of this comparison was to highlight the performance differences in terms of prediction accuracy and the ability to handle complex, high-dimensional wave-ship interaction data.

The LSTM and BiLSTM models were chosen as baseline methods due to their popularity in time-series prediction tasks. PSO-BiLSTM and ADPSO-BiLSTM represent more advanced techniques, incorporating optimization algorithms to enhance BiLSTM's predictive capabilities. These methods are frequently employed in the field to address nonlinear and complex dynamic systems. The training dataset consisted of sequential data combining wave features and motion features. The wave features included wave heights at distances of 0 m, 5 m, 10 m, 15 m, and 20 m from the vessel, while the motion features represented the six degrees of freedom (6DOF) of the ship’s movement (surge, sway, heave, roll, pitch, and yaw). These features were chosen to fully characterize the dynamic interactions between the vessel and the irregular wave conditions.

The comparison was performed on the same dataset, ensuring consistency in input features, training parameters, and evaluation metrics. Results were analyzed based on key performance indicators, including RMSE, MAE, and R².

From the Figure 15, the comparative evaluation of Model.4.1 to Model.4.5 (LSTM, BiLSTM, PSO-BiLSTM, ADPSO-BiLSTM, and WPCA-LSTM) reveals that WPCA-LSTM (Model.4.5) achieves the highest accuracy in predicting ship motion dynamics across all degrees of freedom. While all models capture the general trends of the original data, WPCA-LSTM consistently exhibits the closest alignment, particularly during steady-state oscillations (t>50 s). This performance highlights the effectiveness of combining WPCA for feature extraction with LSTM-based temporal modeling.

Figure 15

Figure 15. Comparison between the prediction results of different models and the original data.

In the transient phase (t=36–50s), WPCA-LSTM outperforms other models by minimizing deviations, handling rapid dynamic changes more effectively than earlier architectures. During the steady-state phase, its predictions demonstrate exceptional stability and precision, as evidenced by reduced deviations and accurate periodic oscillation capture. Across specific degrees of freedom, WPCA-LSTM shows superior performance in yaw, roll, heave, and pitch, particularly in capturing high-frequency and peak oscillations where other models falter.

The progressive improvement from Model.4.1 to Model.4.5 underscores the impact of advanced optimization techniques and architectural refinements. WPCA-LSTM leverages these advancements to provide the most accurate and robust predictions, though minor residuals in the transient phase suggest room for further enhancement through adaptive modeling techniques. Overall, WPCA-LSTM sets a new benchmark for predictive performance in complex ship motion dynamics, offering a promising approach for future applications.

In Table 9, LSTM and BiLSTM demonstrated reasonable performance but were less capable of capturing the full complexity of the dataset, particularly when dealing with irregular wave conditions. PSO-BiLSTM and ADPSO-BiLSTM achieved improved predictive accuracy compared to the baseline methods. However, their performance gains were limited when the dataset's dimensionality increased due to irregular wave data. The proposed method outperformed the baseline and optimization-based models in certain tasks, particularly in capturing the underlying dynamics of wave-ship interactions. Its performance was also more consistent across different prediction tasks.

Table 9

Table 9. R², RMSE, and MAE for prediction results.

This comparative analysis highlights the robustness and adaptability of the proposed approach in addressing the challenges posed by high-dimensional and irregular wave data. While optimization-based methods like PSO-BiLSTM and ADPSO-BiLSTM show promise, the proposed method provides a balanced solution, achieving competitive accuracy while maintaining interpretability and computational efficiency.

5 Conclusion

To improve the safety and stable navigation of ships in irregular waves, optimize the accuracy of ships’ motion prediction, and reduce the high dimension of feature, this paper proposed a WPCA-DC-LSTM prediction model based on wave height features. The dimension of wave height features was reduced with the WPCA. Then, the model employed internal and external circulation to optimize the hyperparameters of the LSTM structure based on the retained variance value of WPCA to improve the generalization capability of the model. The predictive capability of the proposed hybrid model has been discussed by comparing different models and methods. The advanced time step of prediction and the retained number of wave features have been compared. The proposed WPCA-DC-LSTM model is employed to process the motion and wave data from the autopilot trimaran. The key points of this paper can be concluded as follows.

1. Compared with the conventional LSTM model and PCA-LSTM hybrid model, the WPCA-DC-LSTM model achieves superior performance in predicting ship attitude motion, especially in generalizing to new datasets. The WPCA method enhances the ability to process nonlinear features like wave heights, while double circulation optimization improves model stability by dynamically adjusting the retained variance.

2. Incorporating wave height features at varying distances improves the model’s understanding of ship motion patterns, enabling more accurate and comprehensive motion predictions.

3. The WPCA-DC-LSTM model demonstrates strong generalization in new datasets. While prediction accuracy for some features declines with longer time steps, the model effectively captures overall motion trends.

4. The bias in prediction performance across different motion features highlights WPCA's limitations in fully capturing the relationship between wave and motion features.

5. Maritime Applications: The WPCA-DC-LSTM model offers practical value for maritime applications, including real-time autopilot systems for safer navigation, route optimization under varying wave conditions, and vessel design and performance analysis. Its accurate motion predictions enhance operational safety and efficiency in maritime environments.

Limitations and improvement:

1. The model’s performance shows a bias across different motion features, indicating limitations in addressing the complex interactions between ship motion and wave features.

2. The prediction accuracy declines as the advanced time step increases, particularly for features with higher nonlinearity, which might affect long-term predictions.

3. The computational cost of the double circulation optimization process is relatively high, which may limit the practical application of the model in real-time scenarios.

4. Incorporate temporal feature extraction methods, such as attention mechanisms, to better capture dynamic relationships and improve long-term prediction accuracy.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

JX: Data curation, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. JG: Conceptualization, Funding acquisition, Methodology, Resources, Supervision, Writing – original draft, Writing – review & editing. LX: Funding acquisition, Resources, Validation, Writing – review & editing. ZH: Data curation, Funding acquisition, Methodology, Resources, Validation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This project was supported by the National Key R&D Program of China (2022YFC2806600, 2022YFC2806604), the Science and Technology Commission of Shanghai Municipality, China (Grant number 22YF1415900), National Natural Science Foundation of China (Grant number 52401385).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cheliotis M., Lazakis I., Theotokatos G. (2020). Machine learning and data-driven fault detection for ship systems operations. Ocean Eng. 216, 107968. doi: 10.1016/j.oceaneng.2020.107968

Crossref Full Text | Google Scholar

Cohen I., Huang Y., Chen J., Benesty J. (2009). “Pearson correlation coefficien,” in Noise reduction in speech processing (Berlin Heidelberg: Springer-Verlag), 1–4.

Google Scholar

D'Agostino D., Serani A., Stern F., Diez M. (2021). Recurrent-type neural networks for real-time short-term prediction of ship motions in high sea state. arXiv 2105, 13102. doi: 10.48550/arXiv.2105.13102

Crossref Full Text | Google Scholar

De Masi G., Gaggiotti F., Bruschi R., Venturi M. (2011). Ship motion prediction by radial basis neural networks//2011 IEEE workshop on hybrid intelligent models and applications (Paris, France: IEEE), 28–32.

Google Scholar

Geng X., Li Y., Sun Q. (2023). A novel short-term ship motion prediction algorithm based on EMD and adaptive PSO–LSTM with the sliding window approach. J. Mar. Sci. Eng. 11, 466. doi: 10.3390/jmse11030466

Crossref Full Text | Google Scholar

Gong J. Y., Li Y. B., Cui M., Yan S., Ma Q. (2022a). Study on the surf-riding and broaching of trimaran in oblique stern waves. Ocean Eng. 266, 112995. doi: 10.1016/j.oceaneng.2022.112995

Crossref Full Text | Google Scholar

Gong J. Y., Li Y. B., Cui M., Fu Z., Zhang D. P. (2021). The effect of side-hull position on the seakeeping performance of a trimaran at various headings. Ocean Eng. 239, 109897. doi: 10.1016/j.oceaneng.2021.109897

Crossref Full Text | Google Scholar

Gong J. Y., Li Y. B., Yan S. Q., Ma Q. W. (2022b). Numerical simulation of turn and zigzag maneuvres of trimaran in calm water and waves by a hybrid method. Ocean Eng. 253, 111239. doi: 10.1016/j.oceaneng.2022.111239

Crossref Full Text | Google Scholar

Gong J. Y., Yan S. Q., Ma Q. W., Li Y. B. (2020). Added resistance and seakeeping performance of trimarans in oblique waves. Ocean Eng. 216, 107721. doi: 10.1016/j.oceaneng.2020.107721

Crossref Full Text | Google Scholar

Greenacre M., Groenen P. J., Hastie T., d’Enza A. I., Markos A., Tuzhilina E. (2022). Principal component analysis. Nat. Rev. Methods Primers 2, 100. doi: 10.1038/s43586-022-00184-w

Crossref Full Text | Google Scholar

Han P., Skulstad R., Zhang H. (2024). Deep autoregressive roll motion prediction of marine vessels (New York City: IEEE Transactions on Industrial Electronics).

Google Scholar

Hu Z., Yan S. Q., Greaves D., Mai T., Raby A., Ma Q. W. (2020). Investigation of interaction between extreme waves and a moored FPSO using FNPT and CFD solvers. Ocean Eng. 206, 107353. doi: 10.1016/j.oceaneng.2020.107353

Crossref Full Text | Google Scholar

ITTC M. C. (2014). “Recommended procedures and guidelines,” in 27th international towing tank conference (Copenhagen, Denmark: The International Towing Tank Conference).

Google Scholar

Jiang H., Duan S. L., Huang L., Han Y., Yang H., Ma Q. (2020). Scale effects in AR model real-time ship motion prediction. Ocean Eng. 203, 107202. doi: 10.1016/j.oceaneng.2020.107202

Crossref Full Text | Google Scholar

Kawan B., Wang H., Li G., Chhantyal K. (2017). Data-driven modeling of ship motion prediction based on support vector regression. Linköping Electronic Conference Proceedings. 2017 (138), 350–354. doi: 10.3384/ecp17138

Crossref Full Text | Google Scholar

Khan A., Bil C., Marion K. E. (2005). Ship motion prediction for launch and recovery of air vehicles//Proceedings of OCEANS 2005 MTS/IEEE (Washington, DC, USA: IEEE), 2795–2801.

Google Scholar

Li M. W., Xu D. Y., Geng J., Hong W. C. (2022). A hybrid approach for forecasting ship motion using CNN–GRU–AM and GCWOA. Appl. Soft Computing 114, 108084. doi: 10.1016/j.asoc.2021.108084

Crossref Full Text | Google Scholar

Li G., Zhang H., Kawan B., Wang H., Osen O. L., Styve A. (2016). Analysis and modeling of sensor data for ship motion prediction//OCEANS 2016-Shanghai (Shanghai, China: IEEE), 1–7.

Google Scholar

Ma Q. W., Yan S. Q. (2009). QALE-FEM for numerical modelling of non-linear interaction between 3D moored floating bodies and steep waves. Int. J. Numerical Methods Eng. 78, 713–756. doi: 10.1002/nme.v78:6

Crossref Full Text | Google Scholar

Martinez A. M., Kak A. C. (2001). Pca versus lda. IEEE Trans. Pattern Anal. Mach. Intell. 23, 228–233. doi: 10.1109/34.908974

Crossref Full Text | Google Scholar

Peng X., Men Z., Wang X., Jia S. (2014). The ship motion prediction approach based on BP neural network to identify Volterra series kernels//The 26th Chinese Control and Decision Conferenc CCDC) (Changsha, China: IEEE), 2324–2328.

Google Scholar

Perera L. P. (2017). Navigation vector based ship maneuvering prediction. Ocean Eng. 138, 151–160. doi: 10.1016/j.oceaneng.2017.04.017

Crossref Full Text | Google Scholar

Rigatos G. G. (2013). Sensor fusion-based dynamic positioning of ships using Extended Kalman and Particle Filtering. Robotica 31, 389–403. doi: 10.1017/S0263574712000409

Crossref Full Text | Google Scholar

Rithani M., Kumar R. P., Doss S. (2023). A review on big data based on deep neural network approaches. Artif. Intell. Rev. 56, 14765–14801. doi: 10.1007/s10462-023-10512-5

Crossref Full Text | Google Scholar

Rusche H. (2002). Computational fluid dynamics of dispersed two-phase flows at high phase fractions (London, UK: Imperial College).

Google Scholar

Shen Y., Xie M. (2005). Ship motion extreme short time prediction of ship pitch based on diagonal recurrent neural network. J. Mar. Sci. Appl. 4, 56–60. doi: 10.1007/s11804-005-0034-z

Crossref Full Text | Google Scholar

Sun Q., Tang Z., Gao J., Zhang G. (2022). Short-term ship motion attitude prediction based on LSTM and GPR. Appl. Ocean Res. 118, 102927. doi: 10.1016/j.apor.2021.102927

Crossref Full Text | Google Scholar

Torsvik T. (2009). Modelling of ship waves from high-speed vessels//Applied wave mathematics: Selected topics in solids, fluids, and mathematical methods (Berlin, Heidelberg: Springer Berlin Heidelberg), : 229–: 263.

Google Scholar

Weller H. G. (2002). “Derivation, modelling and solution of the conditionally averaged two-phase flow equations,” in Technical report TR/HGW/02 (Paris France: Nabla Ltd).

Google Scholar

Xiao Y., Zou C., Chi H., Fang R. (2023). Boosted GRU model for short-term forecasting of wind power with feature-weighted principal component analysis. Energy 267, 126503. doi: 10.1016/j.energy.2022.126503

Crossref Full Text | Google Scholar

Xu J., Gong J., Li Y., Fu Z., Wang L. (2024). Surf-riding and broaching prediction of ship sailing in regular waves by LSTM based on the data of ship motion and encounter wave. Ocean Eng. 297, 117010. doi: 10.1016/j.oceaneng.2024.117010

Crossref Full Text | Google Scholar

Xu J., Gong J., Wang L., Li Y. (2023). Integrating k-means clustering and LSTM for enhanced ship heading prediction in oblique stern wave. J. Mar. Sci. Eng. 11, 2185. doi: 10.3390/jmse11112185

Crossref Full Text | Google Scholar

Yan S. Q., Ma Q. W. (2010). QALE-FEM for modelling 3D overturning waves. Int. J. Numer. Meth. Fl. 63, 743–768. doi: 10.1002/fld.v63:6

Crossref Full Text | Google Scholar

Yan S. Q., Wang J. H., Wang J. X., Ma Q. W., Xie Z. H. (2019). “Numerical simulation of wave structure interaction using QaleFOAM,” in 29th international offshore and polar engineering conference(Honolulu, Hawaii, USA: International Ocean and Polar Engineering Conference).

Google Scholar

Yin J. C., Zou Z. J., Xu F., Wang N. N. (2014). Online ship roll motion prediction based on grey sequential extreme learning machine. Neurocomputing 129, 168–174. doi: 10.1016/j.neucom.2013.09.043

Crossref Full Text | Google Scholar

Yoshimura Y. (1986). Mathematical model for the manoeuvring ship motion in shallow water. J. Kansai Soc. naval architects 200, 41–51.

Google Scholar

Zhang L., Feng X., Wang L., et al. (2024). A hybrid ship-motion prediction model based on CNN–MRNN and IADPSO. Ocean Eng. 299, 117428. doi: 10.1016/j.oceaneng.2024.117428

Crossref Full Text | Google Scholar

Zhang M., Kujala P., Musharraf M., Zhang J., Hirdaris S. (2023). A machine learning method for the prediction of ship motion trajectories in real operational conditions. Ocean Eng. 283, 114905. doi: 10.1016/j.oceaneng.2023.114905

Crossref Full Text | Google Scholar

Zhang T., Zheng X. Q., Liu M. X. (2021). Multiscale attention-based LSTM for ship motion prediction. Ocean Eng. 230, 109066. doi: 10.1016/j.oceaneng.2021.109066

Crossref Full Text | Google Scholar

Zhou X., Zou L., Ouyang Z. L., Liu S. Y., Zou Z. J. (2023). Nonparametric modeling of ship maneuvering motions in calm water and regular waves based on R-LSTM hybrid method. Ocean Eng. 285, 115259. doi: 10.1016/j.oceaneng.2023.115259

Crossref Full Text | Google Scholar