Multi-AUV sediment plume estimation using Bayesian optimization

Sediment plumes created by dredging or mining activities have an impact on the ecosystem in a much larger area than the mining or dredging area itself. It is therefore important and sometimes mandatory to monitor the developing plume to quantify the impact on the ecosystem including its spatial-temporal evolution. To this end, a Bayesian Optimization (BO)-based approach is proposed for plume monitoring using autonomous underwater vehicles (AUVs), which are used as a sensor network. Their paths are updated based on the BO, and additionally, a split-path method and the traveling salesman problem are utilized to account for the distances the AUVs have to travel and to increase the efficiency. To address the time variance of the plume, a sliding-window approach is used in the BO and the dynamics of the plume are modeled by a drift and decay rate of the suspended particulate matter (SPM) concentration measurements. Simulation results with SPM data from a simulation of a dredge experiment in the Pacific Ocean show that the method is able to monitor the plume over space and time with good overall estimation error.

1 Introduction

The deep sea contains vast quantities of mineral resources that are currently being explored by mining companies, state entities, and scientists for their economic potential and their value as a habitat to be protected. Three main types of mineral resources exist, namely, polymetallic nodules, cobalt-rich ferromanganese crusts, and seafloor massive sulfides, of which the polymetallic nodules are of specific interest due to the enormous size of the resource and the leap in technology development to mine this resource in recent years. These nodules are small potato-shaped concretions of centimeter to decimeter sizes that lie on the seafloor in 3,000- to 6,000-m water depths and consist mainly of authigenic manganese and iron oxides that during their precipitation incorporated economically interesting metals such as nickel, copper, cobalt, and REE of a few weight percentages in total (Petersen et al., 2020). Demand for such minerals is growing rapidly as “green industries” producing, e.g., electric car batteries, wind turbines, and solar cells require much larger quantities of such minerals than their fossil counterparts (IEA, 2021). Intensive research has been conducted to study the impact of mining on the environment and ecosystem (Jones et al., 2017; Gillard et al., 2019; Spearman et al., 2020; Baeye et al., 2021; Elerian et al., 2022; Haalboom et al., 2022; Muñoz-Royo et al., 2022; Weaver et al., 2022; Haalboom et al., 2023; Lefaible et al., 2024; Mousadik et al., 2024). Although it is not clear how severe and spatially wide the damage to the ecosystem would be, recent studies suggest that the effects will last for a long period of time, as effects of the 1989 DISCOL disturbance experiment in the Peru Basin are still apparent 26 years later (Drazen et al., 2019; Simon-Lledó et al., 2019; Gausepohl et al., 2020; Vonnahme et al., 2020). One impact on the ecosystem is the sediment plume that is created when nodules are mined with a hydraulic mining vehicle that uses waterjets to lift up the nodules from the seabed, which also sucks up a few centimeters of the sediment (Muñoz-Royo et al., 2022). The generated plume from the exhausted sediment splits into two parts: a gravity current sediment plume and a suspension plume. The gravity current sediment plume occurs in the immediate vicinity of the collector vehicle. This plume contains most of the mobilized sediment but remains very close to the seafloor. The suspension plume forms close to the mining vehicle at the interface between the gravity plume and the undisturbed bottom water. Here, fine particles are detrained from the gravity current and made available for far-field transport by the background water currents. The suspension plume has significantly lower sediment concentrations than the gravity plume but spreads much further and higher (Muñoz-Royo et al., 2022; Mousadik et al., 2024). The suspension plume will affect much larger areas than the mining area itself; therefore, it is important to monitor the spreading of the plume to be able to quantify the impact of the mining on the adjacent environment. Due to the large extent of the plume and changing bottom currents, a stationary sensor network on the seafloor is not able to estimate its full extent, whereas autonomous underwater vehicles (AUVs) are ideal platforms for such tasks as they can operate for long periods of time and do not require constant human input like remotely operated vehicles (ROVs). Some monitoring studies already use AUVs but only in preplanned survey missions that are designed to densely map a specific region. Since this is time consuming and only yields limited information, adaptive mapping approaches should be used (Gazis et al., under revision)¹.

The utilization of adaptive mapping with AUVs to analyze and sample marine plumes is not a novel concept in general. However, the emphasis is frequently not on estimating the concentration or distribution of a measurand over a large, three-dimensional domain. In case of plumes originating from hydrothermal vents, the task is to detect the plume and track it to its source (see Tian et al., 2014; Hu et al., 2019; von See et al., 2022), whereas for algae blooms, oil spills, or other chemical pollutions, the task is to track and sample its boundary to monitor the extent of the pollution of the environment (see Petillo et al., 2011; Li et al., 2014; Fonseca et al., 2021). While the latter is important in the case of deep sea mining, it is also desirable to obtain an estimate of the suspended particulate matter (SPM) concentration to be able to quantify the amount of sediment. This task can be referred to as field estimation.

A popular approach in this context is to model the field to be estimated as a Gaussian process (GP) and to sample the environment in an intelligent way to estimate the GP hyperparameters. This is always a trade-off between exploring unknown regions and exploiting knowledge in known regions. The authors of Cui et al. (2015) propose a selective basis function Kalman filter to estimate the hyperparameters of the GP, and a mutual information-based multidimensional rapidly exploring random tree (RRT)^∗ algorithm is used to select new sampling locations. Simulation results and an experiment with four robotic fishes in an aquarium for a 2D static field are presented. Zhang et al. (2022) propose a method where some AUVs operate in an exploration mode and others in an exploitation mode. A differential evolution-based path planner is proposed to plan the individual AUV trajectories. Knowledge of the environment is shared via acoustic communication based on a sparse variation GP method. Simulation results for a scalar, static 3D field are presented. A reinforcement learning approach to select new sampling locations is used in Wang et al. (2018). To this end, a long-term reward function, which includes the AUV mobility cost, kinematic, communication, and sensing area constraints, is maximized by the deep deterministic policy gradient algorithm. Simulation results are presented for a static 2D field, and a comparison with a random walk method is performed.

In classical Bayesian optimization, so-called acquisition functions (AFs) are employed to balance between exploration and exploitation. The most common ones are probability of improvement (PI), expected improvement (EI), and upper confidence bound (UCB). In Samaniego et al. (2021), three modifications to these classical AFs are proposed to favor sampling locations close to the agents since the functions do not account for the distance between sample locations. Simulation results for an autonomous surface vessel (ASV) in a lake are presented and compared with classical monitoring approaches as, e.g., lawnmower patterns. Stankiewicz et al. (2021) propose two strategies based on the upper confidence bound (UCP) method to select new sampling locations. The first is based on branch-and-bound techniques, the other on cross-entropy optimization. Simulation results for an underactuated 6-degrees of freedom AUV model in a 3D marine environment as well as results from a field test are presented.

The abovementioned approaches are similar in that they all evaluate their methods on relatively smooth and static data, which is a valid assumption for many natural processes as, e.g., temperature or oxygen distributions in a water body. However, sediment plumes that arise from dredging or mining vehicles yield turbulent, heterogeneous and, due to water currents, also time-variant concentration distributions (Elerian et al., 2021; Muñoz-Royo et al., 2022; Peacock and Ouillon, 2023). To address these issues, we propose to use a sliding window UCB (SW-UCB) algorithm based on Cheung et al. (2019) for the hyperparameter estimation in combination with a traveling salesman problem (TSP) based approach for the selection of new sample locations. Instead of updating the GP after every sample, we use the N ∈ ℝ best sample locations based on the UCB function and calculate the shortest path along these locations by solving the TSP. Additionally, we adopt the split-path method from Samaniego et al. (2021) to also generate samples in specified distances between the sample locations. Furthermore, a simple drift model is proposed to artificially move the measurement samples with the water current to account for the main driver of the time variance of the sediment plume. Finally, a domain reduction scheme is proposed to reduce the search path lengths while making sure that the plume is captured completely.

2 Materials and methods

The objective of the sediment plume monitoring and estimation using AUVs as a sensor network is to sample the plume in an efficient way to estimate the suspended particulate matter concentration and track its change over time. To this end, a combination of Bayesian optimization for time-variant systems and the traveling salesman problem is utilized to achieve a small estimation error.

2.1 Assumptions

The assumptions that have been made for this study are as follows.

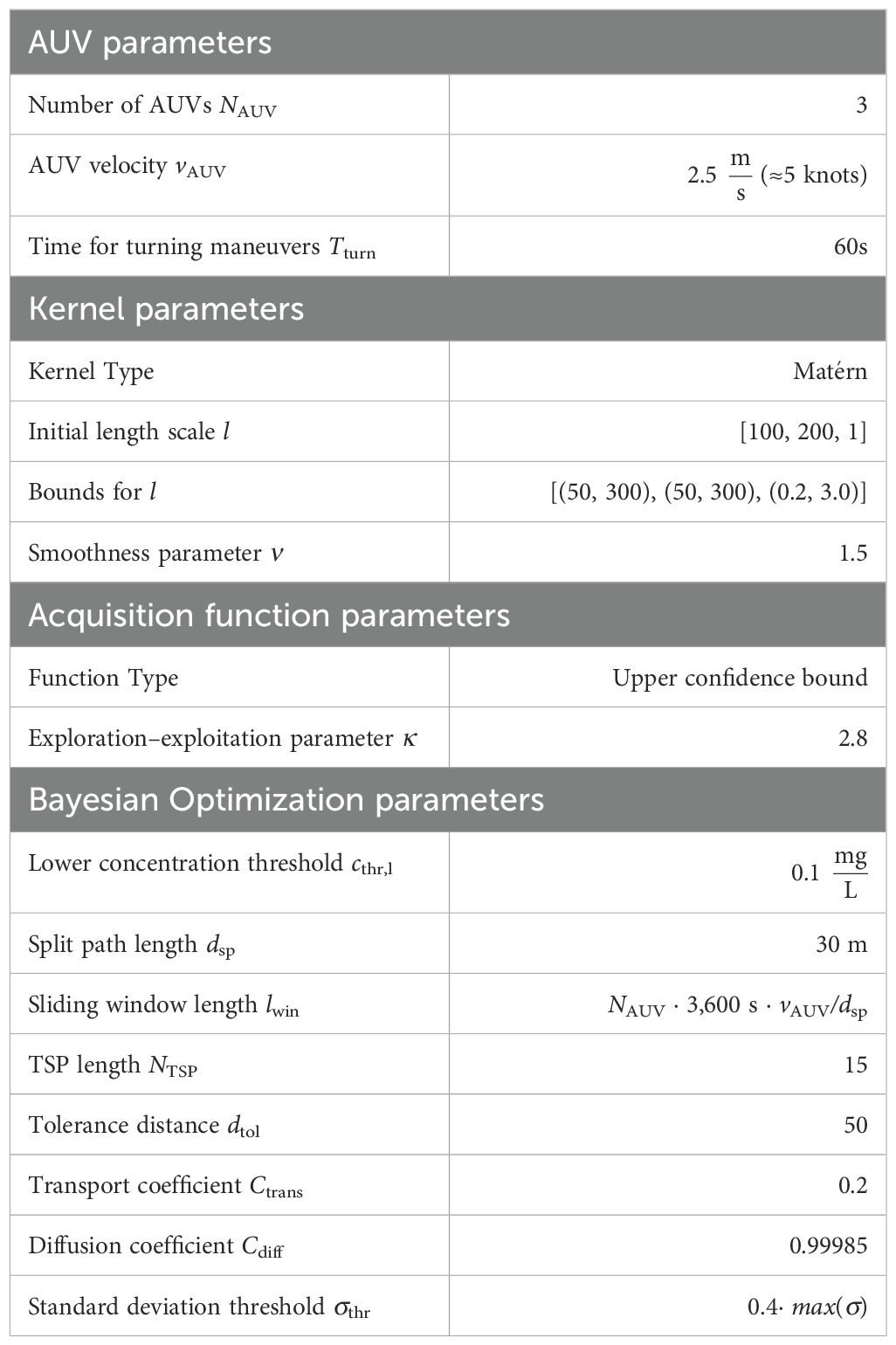
AUV dynamics. AUVs that can operate in depth up to 6,000 m are typically torpedo-shaped AUVs that are capable of flying at speeds of up to 5 knots and can reach mission durations of a day and more, making them feasible for long-term monitoring of a plume. They are equipped with one thruster at the back and fins to control the yaw and pitch; thus, they are underactuated. This means that they fly with almost constant velocity during the mission and need to perform turning maneuvers if waypoints lie too close to each other. Due to the large area, we model the AUV dynamics as a point mass. We assume a constant speed of 5 knots between two waypoints and add an extra amount of time T_turn for turns that are sharper than 90°.

Acoustic communication. The bandwidth underwater is very limited; thus, a decentralized approach where every AUV receives all information is not feasible. We consider a centralized approach, where all AUVs send their SPM concentration measurements with the corresponding locations to a centralized entity. This could be one of the AUVs or a stationary lander with high computation power and a large battery. The BO and calculation of new waypoints is performed by this entity, and only the new sampling locations are transmitted back to the AUVs. This reduces the communication drastically compared with sharing additionally all hyperparameters among all AUVs.

Current measurements. We assume that current measurements are available for the working area and time of the survey. This can be achieved by a lander (or lander array) equipped with upward-looking profiling acoustic current meters and a small computer and acoustic modem that broadcasts the mean water current values in fixed time intervals. This is an important consideration as the water current values are needed to model the change of the suspension plume over time.

Sensors. We assume that the AUVs are equipped with optical backscatter sensors (OBS), typically turbidity sensors. These have a very limited field of view of a few centimeters and hence provide point measurements. In stationary monitoring scenarios, acoustic backscatter sensors (ABS) are used additionally, typically Acoustic Doppler Current Profilers (ADCPs). Both sensor types do not measure the SPM concentration directly but use pre-calibration data to calculate the concentration from the backscatter signal. In the case of ADCPs, measurements along a line can be obtained which provide a larger coverage than OBS, but at the same time, the analysis of these measurements is more complex (Haalboom et al., 2022), so only OBS are considered here. They are known to work best at low suspended sediment concentrations and small particle sizes. Thus, they are ideally suited for monitoring the suspension plume. Other parameters that affect their accuracy include particle shape, near infrared radiation (NIR) reflectivity, and flocculation/aggregation, but these are less important than suspended sediment concentration and particle size (Downing, 2006). The speed of the AUV and the sampling rate of the sensor can also affect the accuracy of the measurements. In terms of localization, their influence is very limited, since typical sensors, such as those used in Haalboom et al. (2022), have high sampling rates of 8 Hz to 10 Hz, and thus, the measurements can be localized with an accuracy of approximately 30 cm, given the assumed AUV speed of 5 knots. Compared with the large scales of the suspension plume, this error can be neglected. A more detailed discussion of the interactions between the various factors that affect the sensitivity and accuracy of the sensor is beyond the scope of this paper. Here, we assume that the sensor readings are reliable and fast so that the samples can be located with negligible error.

2.2 Bayesian optimization

BO is a global optimization method that dates back to the 1960s and has been used intensively, (see Jones et al., 1998). It is very useful when obtaining new samples from an unknown blackbox function is expensive, e.g., due to complex experiments or computationally intensive simulations. In Figure 1, the general procedure of BO is shown as a flowchart. First, the surrogate model, a GP, is initialized. The AF, which provides a measure of the confidence of the model for all function values x, is evaluated and the next sample location is chosen as the location corresponding to the maximum value of the AF. The model is fitted through a Gaussian process regression (GPR), and the posterior probability distribution of the scalar filed can be calculated. Several termination criteria can be defined to evaluate whether the model reached a sufficient level of certainty, e.g., the maximum number of iterations or the maximum change in the hyperparameters or in the AF. If such a criterion is met, the procedure ends, and if it is not met, the AF is evaluated again to obtain new samples. In many cases, instead of just initializing the surrogate model, it is advantageous to acquire an initial set of samples and to fit the surrogate model before the optimization loop is started. Especially if taking samples is not only a matter of computational power, but also time or distance traveled between two measurements, it is advisable to acquire initial samples in a coordinated manner. In the context of plume monitoring with AUVs, the function values x refer to 3D points in the area of the plume. The AF is used to define new sampling locations, and the GPR calculates an estimate of the SPM concentration in the specified region. In the following, the individual parts of BO are explained in further detail.

Figure 1

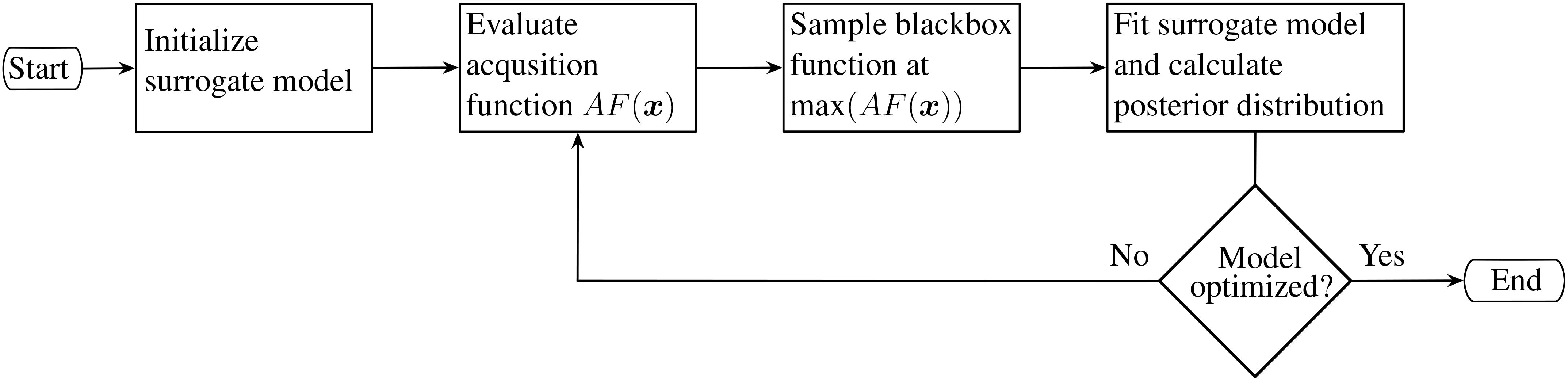
Figure 1. Flowchart of the Bayesian optimization without any prior knowledge of the unknown function.

2.2.1 Gaussian process regression

GPR is a Bayesian statistical technique to calculate an estimate of a function f(x) given some data. In the context of this paper, f(x) refers to the SPM concentration at the location x. The surrogate model used is a GP, which is defined by its mean function µ(x) and its covariance function, also called the kernel $k(\mathit{x},{\mathit{x}}^{\prime })$, given by

$\begin{array}{ll}\mu (x)=E[f(\mathit{x})]& \text{(1a)}\end{array}$

$\begin{array}{ll}k(\mathit{x},{\mathit{x}}^{\prime })=E[(f(\mathit{x})-\mu (\mathit{x}))(f({\mathit{x}}^{\prime })-\mu ({\mathit{x}}^{\prime }))].& \text{(1b)}\end{array}$

The blackbox function f(x) can be approximated by the GP as (Williams and Rasmussen, 2006)

$\begin{array}{ll}f(\mathit{x})\sim GP(\mu (\mathit{x}),k(\mathit{x},{\mathit{x}}^{\prime })).& (2)\end{array}$

Kernels can be written as a matrix K where the element K_i,j = k(x_i, x_j) represents the covariance between the inputs x_i and x_j. Given a set of training points X and a set of test points X_∗, the kernel matrix can be rewritten as

$\begin{array}{ll}K=\left[\begin{array}{cc}K(X,X)+{\sigma }_n^{2}I& K(X,X_{*})\\ K(X_{*},X)& K(X_{*},X_{*})\end{array}\right].& (3)\end{array}$

Here, K(X,X) is the covariance of the known data and ${\sigma }_n^{2}I$ is added to account for the noise in the observation data, where ${\sigma }_n^2$ is the variance of the noise and I is the identity matrix. The covariance between the known and the unknown data is given by K(X, X_∗) and K(X_∗, X) and the covariance of the unknown data is given by K(X_∗, X_∗). These submatrices can be used to predict the mean and covariance of unknown data by Williams and Rasmussen (2006)

$\begin{array}{ll}\overline{{\mathit{f}}_{*}}=E{[{\mathit{f}}_{*}|X,\mathit{y},X_{*}]=K(X_{*},X)[K(X,X)+{\sigma }_n^{2}I]}^{-1}\mathit{y}& \text{(4a)}\end{array}$

$\begin{array}{ll}\text{cov}({\mathit{f}}_{*})=K(X_{*},X_{*})-K(X_{*},X){[K(X,X)+{\sigma }_n^{2}I]}^{-1}K(X,X_{*}).& \text{(4b)}\end{array}$

Here, y is the vector containing the observation data at the training points X and f_∗ are the function values at the unknown test data X_∗. The quality of this prediction depends on how well the GP parameters match the unknown function. Especially the choice of the kernel is crucial since it defines the shape of the prior and posterior distribution of the GP. Assumptions about the underlying process such as periodicity, smoothness, or (non)linearity are encoded in the kernel. Common choices are the constant kernel, Radial Basis Function kernel, Rational Quadratic kernel, and the Matérn kernel. A detailed discussion of different kernels and their properties is beyond the scope of this paper, and the interested reader is referred to Duvenaud (2014) and Williams and Rasmussen (2006). In this paper, we use the Matérn kernel, which is defined as

$\begin{array}{ll}{k}_{\text{Matern}(\mathit{x},{\mathit{x}}^{\prime })=\frac{1}{\text{Γ}(\nu )2^{\nu -1}}{\left(\frac{\sqrt{2\nu }}{l}\left|\mathit{x}-{\mathit{x}}^{\prime }\right|\right)}^{\nu }{K}_{\nu }\left(\frac{\sqrt{2\nu }}{l}\left|\mathit{x}-{\mathit{x}}^{\prime }\right|\right),}& (5)\end{array}$

where | · | denotes the Euclidean distance, K_ν(·) is a modified Bessel function, and Γ(·) is the gamma function (Williams and Rasmussen, 2006). The positive parameters ν and l are the design parameters of the kernel. The larger ν, the smoother the correlation function will be. Typically, ν is chosen as half-integer ν = p + ½, p ∈ ℕ. The length scale l defines how far apart points are still correlated. The regression task is to vary the hyperparameters such that they best fit the data seen so far. This can be done in different ways as pointed out in Williams and Rasmussen (2006). Subsequently, this is done by maximizing the log-marginal-likelihood (LML) via a suitable optimizer, e.g., the L-BFGS-B algorithm (Zhu et al., 1997).

2.2.2 Acquisition functions

The AF provides a measure of how certain the model is about the estimate of the function at each function value x. Several functions have been proposed for this task of which the most widely used are PI, EI, and UCB (Brochu et al., 2010). They all include the possibility to focus more on exploration or exploitation and are explained below.

PI maximizes the probability of obtaining a function value that is better than the current best. It is computed based on the normalized surrogate model given by

$\begin{array}{ll}Z=\frac{f({\mathit{x}}^{*})-\mu (\mathit{x})-\xi }{\sigma (\mathit{x})},& (6)\end{array}$

where x^∗ is the location of the current best function value, σ(x) is the standard deviation of the predicted posterior distribution at x, and ξ is the design parameter that controls the ratio of exploration and exploitation (Snoek et al., 2012). High values for ξ favor exploration and low one’s exploitation. The PI is calculated as

$\begin{array}{ll}PI(\mathit{x})=\text{Φ}(Z)& (7)\end{array}$

with Φ(·) denoting the cumulative distribution function (CDF) Snoek et al. (2012).

EI extends PI in the sense that not only the PI is calculated, but also the magnitude of the potential improvement (Brochu et al., 2010). It reads

$\begin{array}{ll}EI(\mathit{x})=(f({\mathit{x}}^{*})-\mu (\mathit{x})-\xi )\text{Φ}(Z)+\sigma (\mathit{x})\varphi (Z),& (8)\end{array}$

where ϕ(·) is the probability density function (PDF) of the normal distribution.

UCB chooses to sample at the location where the upper bound on the confidence interval of the estimate is the largest. It is calculated by

$\begin{array}{ll}UCB(\mathit{x})=\mu (\mathit{x})+\kappa \sigma (\mathit{x})& (9)\end{array}$

with κ > 0 (Brochu et al., 2010). Similar to ξ in PI and EI, high values for κ favor exploration and low one’s exploitation.

2.3 Bayesian optimization for time-variant systems

While in many applications the scalar field can be assumed constant or at least very slowly changing, this is not true for sediment plume estimation in the context of dredging or mining activities. Thus, the application of the so far introduced methodology will yield suboptimal results. Some extensions to BO have been proposed to address time-variant systems. These include a regular reset of the learned hyperparameters (Bogunovic et al., 2016), an event-triggered reset of the learned hyperparameters (Brunzema et al., 2022a), separation of the kernel into a stationary and a time-variant covariance function and separate learning of the hyperparameters (Nyikosa et al., 2018), a sliding window for all measurements (Cheung et al., 2019), and weighting of the kernel (Bogunovic et al., 2016; Deng et al., 2022; Brunzema et al., 2022b). For the considered application, a complete reset of the hyperparameters implies gaps in the estimation during the initial sampling phase of the BO due to the large distances the AUVs have to travel. Therefore, these approaches are impractical for the use case. In this paper, we use the sliding-window approach of Cheung et al. (2019). This means that only the last l_win samples are considered in the GPR, where l_win is the sliding-window length, which has to be chosen based on the dynamics of the system, here the variability of the bottom currents. This approach has two distinct advantages. First, there is an upper bound for the size of the GPR, which prevents the optimization problem from becoming too large, and second, none of the other steps of the BO have to be adapted; thus, well-established libraries for BO can be used.

2.4 Traveling salesman problem

The traveling salesman problem (TSP) addresses the problem of finding the shortest path along a set of locations, where each location is visited only once. In the proposed approach, we do not only sample at one location per iteration as in classical BO, but at N_TSP locations per AUV, which is explained in more detail in the next section. The TSP is used in this context to minimize the AUV path lengths and thus increase the efficiency of the approach. Traditionally, the TSP is formulated as a closed loop so that start and end are the same location, but it can also be formulated as an open loop. The TSP belongs to the class of NP-complete problems (Hoffman et al., 2013). Even though no polynomial-time solution has been found, different algorithms have been proposed that can solve also problems with large numbers of locations in an efficient manner. For this study, the implementation of Mulvad (2022) is used, which implements the Held–Karp algorithm, a dynamic programming algorithm, for computing the exact solution of the TSP.

2.5 Proposed approach

We consider the case that a suspension plume shall be sampled by N_AUV AUVs such that a good estimate of the SPM concentration in the working area can be obtained. We extend the classical BO approach as depicted in Figure 1 to address the challenges in this special case. The approach is shown as a flowchart in Figure 2. An initial sampling is performed by flying lawnmower patterns. The patterns are oriented with the long segments parallel to the main water current direction because it can be assumed that this will be the main correlation axis. The GPR, termination criterion and evaluation of the AF are the same as in Section 2.2. In the classical BO, the sampling cost is assumed to be the same for all arguments x but this is not correct in the considered application because of the distances the AUVs have to travel between measurements. Therefore, instead of sampling the plume only at the location where max(AF(x)), we choose the N_TSP · N_AUV locations corresponding to the highest values of the AF. Here, N_TSP is the order of the TSP. The sampling locations are clustered into N_AUV groups based on their distance to the AUVs. Furthermore, not only the samples at these locations are taken into account but also samples at locations based on the split-path method proposed in Samaniego et al. (2021). In the split-path method samples are taken in equidistant intervals d_sp between two waypoints. For the GPR and the successive evaluation of the AF domain bounds have to be specified, which can be hard to estimate a priori. It is advisable to overestimate these bound to prevent cutting of the plume, especially in the direction of the bottom near currents. However, this can lead to very large AUV paths whenever the uncertainty of the prediction in the outer parts of the domain is high. Therefore, we adopt and modify the pan and zoom approach presented in Stander and Craig (2002). The aim for this approach is to converge to the optimum of a function by shifting and/or reducing the domain bounds of the optimization problem. However, in the case of plume estimation, the goal is not to converge to a maximum or minimum of the SPM concentration, but to shrink and pan the area so that only parts where no plume is present are discarded. Therefore, we propose a domain reduction by

Figure 2

Figure 2. Flowchart of the proposed Bayesian optimization scheme for sediment plume estimation with multiple AUVs.

$\begin{array}{ll}\left[\begin{array}{c}{x}_{k,\text{l}}\\ x_{k,\text{u}}\\ y_{k,\text{l}}\\ y_{k,\text{u}}\end{array}\right]=\left[\begin{array}{c}{x}_{k-1,\text{min}}-d_{tol}\\ x_{k-1,\text{max}}+d_{tol}\\ y_{k-1,\text{min}}-d_{tol}\\ y_{k-1,\text{min}}+d_{tol}\end{array}\right]& (10)\end{array}$

where k refers to the iteration of the optimization and the subscripts l and u refer to the lower and upper bound of the coordinates x and y, respectively. The coordinates $x_{k-1,\text{min}}$, $x_{k-1,\text{max}}$, $y_{k-1,\text{min}}$, and $y_{k-1,\text{max}}$ correspond to the smallest and largest coordinates at which the plume was measurable in the last iteration and d_tol is a tolerance distance that is added/subtracted to allow not only shrinking of the area but also widening as the plume evolves.

To address the dynamics of the plume, two measures are taken. First, as mentioned above, the sliding window approach proposed in Cheung et al. (2019) is used and second, all measurements are moved with the current to account for the main driver of the plume drift. This is done by the following model

$\begin{array}{ll}{\mathit{p}}_i={\mathit{p}}_i+{\overline{\mathit{v}}}_{\text{current},i}{C}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}}(t-t_i)& \text{(11a)}\end{array}$

$\begin{array}{ll}{c}_i=c_i{C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}}^{(t-t_i)}& \text{(11b)}\end{array}$

Here, the index i refers to the index in the array, p_i is a position vector of the SPM measurement, ${\overline{\mathit{v}}}_{\text{current},i}$ is the mean current vector in the time interval [t_i,t], where t represents the current time, C_trans is a transport coefficient, c_i is the SPM, and C_diff is a diffusion coefficient. Even though this is a simplified model where the diffusion is not modeled by a partial differential equation but only by a decay rate and a decrease of the current velocity, it provides a sufficient approximation on a short time horizon and is much less computationally expensive.

The posterior concentration distribution that can be calculated after the GPR is based on the mean value of the measurement samples µ_train and the learned correlation between them. In regions with maximum uncertainty, the predicted concentration will be equal to the mean value of the training samples. This is a valid assumption for many natural processes. However, in the case of sediment plume estimation, it is clear that there are regions without any plume. To account for this, we incorporate the standard deviation σ(x), which is calculated during the GPR, and the lower concentration threshold c_thr,l, which depends on the sensitivity of the considered sensor, to adapt the prediction of the posterior concentration distribution according to

$\begin{array}{ll}\widehat{f}(\mathit{x})=\{\begin{array}{ll}0\hfill & \widehat{f}(\mathit{x})\le {\mu }_{\text{train}}\text{\&}\sigma (x)>{\sigma }_{\text{thr}}\hfill \\ 0\hfill & \widehat{f}(\mathit{x})<c_{\text{thr},1}\hfill \\ \widehat{f}(\mathit{x})\hfill & else\hfill \end{array}& (12)\end{array}$

Herein, $\widehat{f}(\mathit{x})$ is the predicted SPM at the grid point x and σ_thr is the upper threshold for the standard deviation. This threshold is a design parameter that should be chosen based on the maximum value of σ(x). The first case in (12) describes the situation where the model is uncertain about a relatively small concentration, thus a situation where it is likely that there is no plume present but only background noise.

2.6 Model data

The data used in this study originate from a numerical simulation of sediment plume transport induced by a dredge experiment in the northeastern equatorial Pacific described in Purkiani et al. (2021). The dataset has been published by Purkiani et al. (2024). In the following, the dredge experiment and the data are briefly explained; for further details, the reader is referred to Purkiani et al. (2021) and Haalboom et al. (2022). The dredge experiment was conducted in the northeastern equatorial Pacific, and the sediment plume was created by towing a 1-m-wide geological chain dredge across the seafloor at velocities between 0.2 ms⁻¹ and 0.5 ms⁻¹ along 11 tracks between 450 m and 610 m in length. The modeled area for the plume dispersal is approx. 1,175 × 1,350 × 114 m (northing, easting, height/x, y, z) in steps of 20 × 23 × 6 m. The model uses an internal simulation time step length of 5 s and produces data at 300 time steps with intervals of 300 s so that the complete experiment can be covered. Even though the model area in the z-direction is relatively large, the main part of the measurable plume is present in the lowest three grid layers corresponding to a 12-m layer close to the seafloor. In the model data, the SPM is divided into three sediment classes based on the grain size. Purkiani et al. (2021) call these class 1 (D25: 70 µm), class 2 (D50: 340 µm), and class 3 (D75: 590 µm). In the simulation, we use the sum of all three classes as we assume measurements from an OBS, which cannot differentiate between these classes. To obtain continuous data from the discrete model grid, an interpolation between grid points via the piecewise cubic hermite interpolating polynomial method is used. Similarly, the time resolution is up-sampled to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$30$}\right.$ Hz and linearly interpolated. A visualization of the plume and its temporal evolution is shown in Figure 3. Here, a view on the X–Z plane of the plume is provided for the times (A) 0.5 h before and (B) 1 h, (C) 9 h, and (D) 16 h after the AUV mission start. The X–Z plane was chosen because the direction of the water current is mainly in the negative X-direction, so the change over time is best seen in this plane. Furthermore, in an interpolated 3D visualization, the high concentration in the inner part of the plume would not be visible because these voxels would be covered by the outer voxels. The SPM concentration is color coded and saturated at $5\raisebox{1ex}{$\text{mg}$}\!\left/ \!\raisebox{-1ex}{$\text{L}$}\right.$. The red circles indicate the original grid points, and the dense, connected points in the background show the interpolated plume. The concentration is averaged over all Y grid points at which the SPM concentration is larger than c_thr,l. It can be seen that there are large SPM concentrations at X ∈ [−150,50], which corresponds to the region where the dredge is towed across the seafloor.

Figure 3

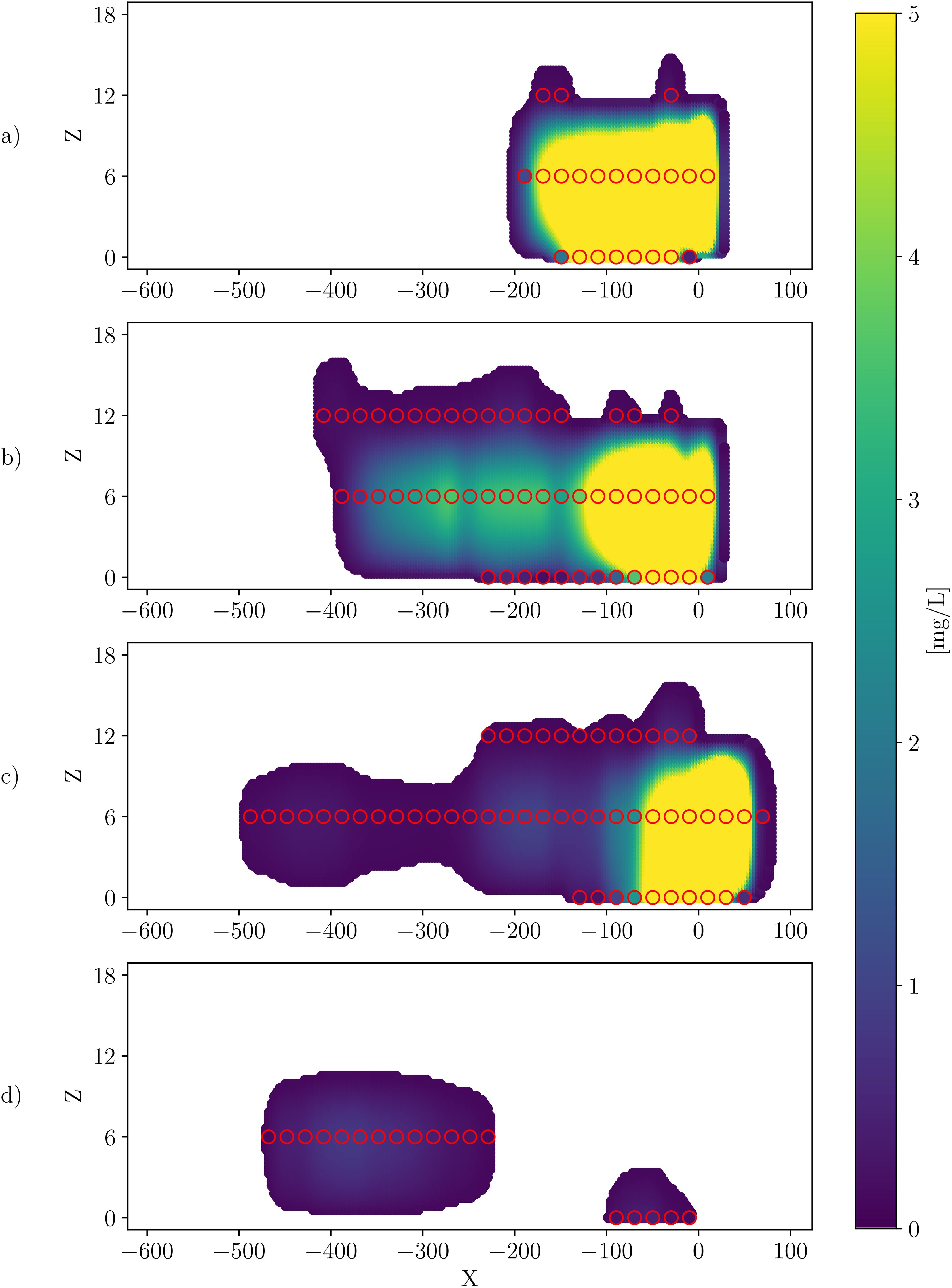
Figure 3. View on the X–Z (in meters) plane of the plume for times (A) 0.5 h before and (B) 1 h, (C) 9 h, and (D) 16 h after the AUV mission start. The red circles indicate the original grid points, and the dense points show the pchip-interpolated plume averaged over all y-voxels which contain a measurable suspended particulate matter concentration.

2.7 Quality measures

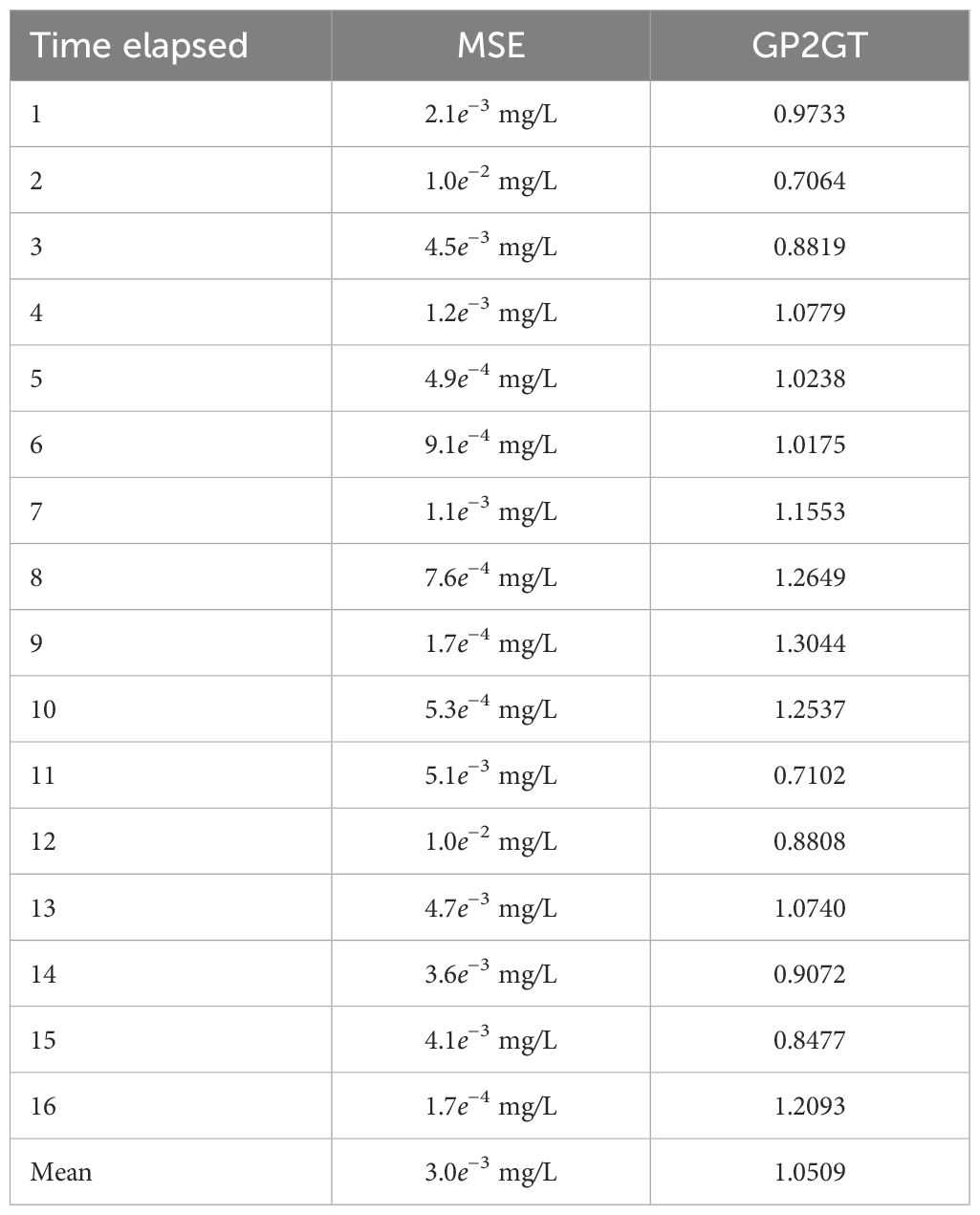
Finding a good quality measure for the estimation is difficult for this use case. On the one hand, it is important to get as close as possible to the overall SPM concentration, but on the other hand, also the distribution in space is important. A classical measure is the mean squared error (MSE), but this can yield misleading results in case of time-varying systems. Consider, e.g., the (extreme) case where the BO estimates the concentration of all voxels correct but they are shifted by 1 grid index in the opposite direction of the water current. This can be seen as a pure time delay in the estimation, and thus everything would be correct but 20 m off. In terms of the grid-based MSE, this can lead to a large error, depending on the distribution of the plume. Therefore, the MSE alone is not sufficient to measure the quality of the estimation. We propose to use the MSE alongside the ratio of the GP estimated to the ground truth summed SPM concentration, which we in the following call the GP2GT ratio. It is calculated as

$\begin{array}{ll}\text{GP}2\text{GT}=\frac{{\displaystyle \sum \widehat{f}(\mathit{x})}}{{\displaystyle \sum ^f(\mathit{x})}}.& (13)\end{array}$

A value GP2GT = 1 is the optimal case here. It describes the situation where the model estimates the summed concentration identical to the ground-truth concentration. A value smaller than 1 indicates an underestimation of the summed concentration and a value larger than 1 an overestimation.

3 Results

In Figure 4, the estimated SPM concentrations and those obtained from the model are shown as scatter plots for the time steps 1 h, 9 h, and 16 h after the start. These correspond to the beginning, mid, and end of the dredge experiment. For visualization purpose, the color coding is saturated at $9\raisebox{1ex}{$\text{mg}$}\!\left/ \!\raisebox{-1ex}{$\text{L}$}\right.$ for subplots a) and at $2\raisebox{1ex}{$\text{mg}$}\!\left/ \!\raisebox{-1ex}{$\text{L}$}\right.$ for subplots (b) and (c) in order to also make variations in areas of low concentrations visible. Additionally, the Z-scale is chosen such that there is some space between grid layers so that all three grid layers are fully visible. It can be seen that the rough shape of the plume was correctly estimated at all three time steps but also that in all three subplots there are some parts of the plume, which are not estimated correctly. The latter occurs mainly in regions with very low concentrations and at the edges of the plume or in the upper and lower depth layer where the plume is only present in small areas. Also, the concentration estimation provides good results in most parts of the plume. The most challenging area for the estimation is close to the upper domain bound of the x coordinate at approx. x ∈ [−150,−100]. The main current direction is in the negative x direction; hence, the plume enters the domain at this bound. Furthermore, due to the irregular swirling of the sediment, the plume entering the domain is strongly time-variable. Therefore, the largest deviations in the concentration estimate are in this region as can be seen in subplots a) and b). In subplots b) at approx. x ∈ [−600,−450] and in subplots a) at z = 12, it can be seen that the BO estimate misses the plume in an area almost completely. This is due to two reasons: first, the concentrations in these regions are smaller than the training mean of the respective BO iterations. Second, less samples in this region are taken because due to the higher uncertainty of the estimate at the upper domain bound of the x coordinate, as mentioned above, this area is sampled more frequently. As this leads to the combination of low expected concentrations and high standard deviation according to Equation 13, these grid cells are discarded.

Figure 4

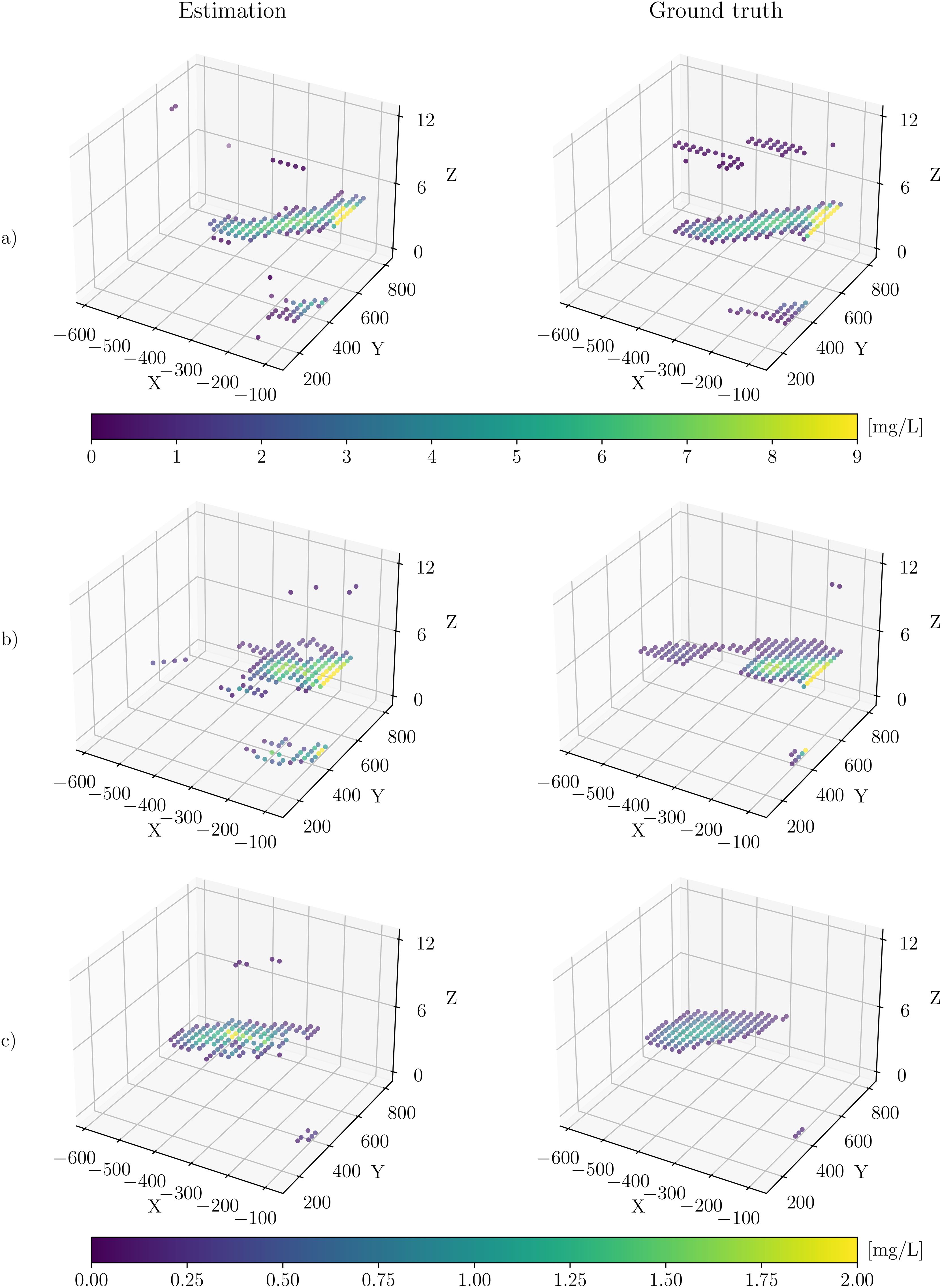
Figure 4. Scatter plots of the suspended particulate matter concentration for the time steps (A) 1 h, (B) 9 h, and (C) 16 h after the start. The left column shows the estimated concentration and the right column the ground-truth values. The concentration for the subplots (A) is color coded according to the upper color bar and for subplots (B, C) according to the lower color bar. The concentrations are shown on the original model grid resolution of 20 × 23 × 6 m voxels.

The quality metrics for the iterations corresponding to each full hour since the start of the estimation as well as the mean values over the complete simulation are listed in Table 1. It can be seen from the GP2GT ratio that there are distinct phases where the BO tends to underestimate or overestimate the concentration. On average, the BO is able to monitor the plume with only a 5% error in terms of the GP2GT ratio. The larger MSE at the beginning of the experiment is mainly related to the higher concentrations in the first hours of the experiment. The average MSE is two orders of magnitude lower than the considered lower concentration threshold c_thr,l. Both quality measures indicate a very good estimation performance. The slight variation in MSE and GP2GT over the time steps is a consequence of the plume changing and propagating over time due to the irregular sediment release. The parameters used in the simulation are listed in Table 2. A note on the choice of two parameters: First, the sliding window length l_win as it might be the least intuitive parameter: It must not be chosen close to or equal to zero as this essentially means that very few or no data are taken into account. On the other hand, it should not be chosen too large because the simple model (11) will not produce accurate results over long time scales. The lower bound of l_win should be chosen so that the AUVs are able to cover a significant part of the working area. The upper bound depends on the variability of the water currents. The model (11) works better for laminar flow than for turbulent flow, and thus larger values of l_win are feasible in the case of laminar flow. We chose l_win such that the measurement data of the last hour are considered but also values between approx. 0.5 h and 1.5 h resulted in reasonable performance metrics. Below and above these values, the performance decreased significantly. Second, the number of AUVs was chosen to be three because we believe that it is possible to operate three AUVs simultaneously and that in large-scale mining scenarios at least three AUVs are needed. However, the approach also works with one or two AUVs, but with reduced estimation quality. A visualization of the AUV paths is shown in Figure 1 in the Supplementary Files. It can be seen that the region has a higher sampling density at large X-values than at small X-values. At the end of the dredge experiment when the release of sediment stops, the AUV paths move toward smaller X values as is expected.

Table 1

Table 1. Quality metrics in hourly steps and mean values for the complete simulation.

Table 2

Table 2. Parameters used in the simulation.

4 Discussion

The BO domain bounds for the simulation results shown above are chosen as x ∈ [−600,−100], y ∈ [200,800], and z ∈ [0,12]; thus, they do not include the area of the dredge experiment, which is in the range of x ∈ [−100,50]. This is due to two reasons. First, in the dredging or mining area, there is at least one instrument or vehicle operated remotely from the ship via a cable, which can be hard to detect autonomously by an AUV thereby increasing the risk of collision in this area. Second, the SPM concentration in this area will be much higher and much more heterogeneous than further away and will likely include the beginning evolution of near-bottom gravity flows. Since the plume drifting farther away from the dredging or mining is more important for environmental monitoring, the dredge area was discarded in favor of the far-field plume. In addition, the bottom-near gravity plume produced by a mining vehicle is too shallow for monitoring with AUV, and hence also in this scenario, the focus is on the far-field plume.

BO is not designed for discontinuous problems, where the function is equal to zero in large areas, and hence, defining the boundaries of the plume is not straightforward. With Equation 13, we address this issue without losing too much information in areas of low function values. However, as shown in Section 3, a large concentration gradient across the domain may result in the BO not detecting the plume in areas of very low concentrations. In the considered use case, these plume parts can be neglected due to the very low concentrations and the short duration of the dredge experiment. In case of a long-term monitoring, it might be necessary to also monitor these very low concentrations as they add up over time. A possible extension is that an additional BO instance is created and the AUV(s) assigned to this instance operate only in the far field where low concentrations are assumed. The domain bounds of the two BO instances should be chosen such that they do not overlap in order to minimize the risk of AUV collisions.

The plume area considered in this study is relatively small compared with the area of a plume created by a mining vehicle. It is clear that the number of AUVs cannot be scaled up to yield the same AUV per area ratio as used in this study. However, the plume produced by a mining vehicle will probably be much more homogeneous than the plume produced by the dredge experiment. Therefore, less samples are needed since the correlation of neighboring locations will be much stronger than in the dredge scenario and thus the uncertainty of the prediction will be lower. Furthermore, it can be assumed that the time dependence will decrease because the mining vehicle will constantly bring sediment into suspension. In contrast, the dredge experiment released the sediment very irregularly. Thus, it can be argued that the time dependence of the suspension plume produced by mining will mainly be correlated with the water currents. Therefore, we believe that the method will also be applicable to larger plumes given a limited number of AUVs. Further simulations should be carried out with a dataset of a plume produced by a mining vehicle in order to investigate the influence of these factors in more detail. To the best of the authors’ knowledge, such data were not publicly available upon submission of this paper, although Gazis et al. (under revision)¹ describe such a scenario.

The presented study has to be seen as a feasibility study, and before the approach is used on real AUVs, further studies need to be conducted. This would involve implementation of a path planner, proper AUV dynamics, and a collision avoidance system in the simulation. Even though these aspects are not addressed in this study, we believe that the assumptions made in Section 2.1 are good estimates and the implementation of the mentioned parts will not change the performance of the system significantly. In addition, the clustering of the new sample locations based on the distances to the AUVs does in most cases result in AUV paths that are separated from each other, thus decreasing the probability of collisions.

To further improve the presented approach, not only source measurements from OBS and ABS but also a multibeam echosounder (MBES) could be included. The advantage of MBES systems is that they can sample large areas in a short amount of time, but their use for SPM concentration measurement is not yet as well studied as for OBS and ABS. Fromant et al. (2021) present data, which show a good correlation of MBES data with ABS and OBS for concentrations larger than approx. $40\raisebox{1ex}{$\text{mg}$}\!\left/ \!\raisebox{-1ex}{$\text{L}$}\right.$, which is significantly higher than the concentration considered in this paper. Nevertheless, a combination of both sensor types could be advantageous. An AUV equipped with an MBES system could, e.g., be used to fly above the plume to map its extent making use of the larger coverage. This map could be used to initialize the BO in a more intelligent way, or to update the plume boundaries and to check if new plume patches are covered by the new sample locations suggested by the AF, and if not, manually add waypoints in those regions. In addition, the integration of bathymetry in future simulations would be a valuable extension, as it influences the water current patterns and thus the plume behavior.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

TS: Data curation, Methodology, Software, Visualization, Writing – original draft, Writing – review & editing, Conceptualization. JG: Resources, Supervision, Writing – review & editing, Conceptualization, Funding acquisition. TM: Supervision, Writing – review & editing, Conceptualization, Funding acquisition.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The first author is funded through the Helmholtz School for Marine Data Science (MarDATA), Grant No. HIDSS-0005. Parts of the work of the first author have been performed at the Kiel University and at the Karlsruhe Institute of Technology (KIT).

Acknowledgments

This is publication 67 of the DeepSea Monitoring Group at GEOMAR Helmholtz Centre for Ocean Research Kiel.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1504099/full#supplementary-material

Footnotes

1. ^ Gazis, I., de Stigter, H., Thomsen, L., Mohrmann, J., Heger, K., Diaz, M., et al. Monitoring benthic plumes, sediment redeposition and seafloor imprints caused by deep-sea polymetallic nodule mining. Nat. Commun.

References

Baeye M., Purkiani K., de Stigter H., Gillard B., Fettweis M., Greinert J. (2021). Tidally driven dispersion of a deep-sea sediment plume originating from seafloor disturbance in the discol area (se-pacific ocean). Geosciences 12, 8. doi: 10.3390/geosciences12010008

Crossref Full Text | Google Scholar

Bogunovic I., Scarlett J., Cevher V. (2016). “Time-varying gaussian process bandit optimization,” in Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (New York, USA: PMLR) 51, 314–323.

Google Scholar

Brochu E., Cora V. M., De Freitas N. (2010). A tutorial on bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv preprint arXiv:1012.2599. doi: 10.48550/arXiv.1012.2599

Crossref Full Text | Google Scholar

Brunzema P., von Rohr A., Solowjow F., Trimpe S. (2022a). Event-triggered time-varying bayesian optimization. arXiv preprint arXiv:2208.10790. doi: 10.48550/arXiv.2208.10790

Crossref Full Text | Google Scholar

Brunzema P., Von Rohr A., Trimpe S. (2022b). “On controller tuning with time-varying bayesian optimization,” in 2022 IEEE 61st Conference on Decision and Control (CDC). (New York, USA: IEEE), 4046–4052.

Google Scholar

Cheung W. C., Simchi-Levi D., Zhu R. (2019). “Learning to optimize under non-stationarity,” in Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics (New York, USA: PMLR), 1079–1087.

Google Scholar

Cui R., Li Y., Yan W. (2015). Mutual information-based multi-auv path planning for scalar field sampling using multidimensional rrt. IEEE Trans. Sys. Man Cybernet.: Syst. 46, 993–1004. doi: 10.1109/TSMC.2015.2500027

Crossref Full Text | Google Scholar

Deng Y., Zhou X., Kim B., Tewari A., Gupta A., Shroff N. (2022). “Weighted gaussian process bandits for non-stationary environments,” in International Conference on Artificial Intelligence and Statistics. (New York, USA: PMLR), 6909–6932.

Google Scholar

Downing J. (2006). Twenty-five years with obs sensors: The good, the bad, and the ugly. Continent. Shelf Res. 26, 2299–2318. doi: 10.1016/j.csr.2006.07.018

Crossref Full Text | Google Scholar

Drazen J. C., Leitner A. B., Morningstar S., Marcon Y., Greinert J., Purser A. (2019). Observations of deep-sea fishes and mobile scavengers from the abyssal discol experimental mining area. Biogeosciences 16, 3133–3146. doi: 10.5194/bg-16-3133-2019

Crossref Full Text | Google Scholar

Duvenaud D. (2014). The kernel cookbook: Advice on covariance functions. Available online at: https://www.cs.toronto.edu/~duvenaud/cookbook/ (Accessed December 19, 2024).

Google Scholar

Elerian M., Alhaddad S., Helmons R., van Rhee C. (2021). Near-field analysis of turbidity flows generated by polymetallic nodule mining tools. Mining 1, 251–278. doi: 10.3390/mining1030017

Crossref Full Text | Google Scholar

Elerian M., Van Rhee C., Helmons R. (2022). Experimental and numerical modelling of deep-seamining-generated turbidity currents. Minerals 12, 558. doi: 10.3390/min12050558

Crossref Full Text | Google Scholar

Fonseca J., Aguiar M., de Sousa J. B., Johansson K. H. (2021). “Algal bloom front tracking using an unmanned surface vehicle: Numerical experiments based on baltic sea data,” in OCEANS 2021 (IEEE, San Diego–Porto), 1–7.

Google Scholar

Fromant G., Le Dantec N., Perrot Y., Floc’h F., Lebourges-Dhaussy A., Delacourt C. (2021). Suspended sediment concentration field quantified from a calibrated multibeam echosounder. Appl. Acoust. 180, 108107. doi: 10.1016/j.apacoust.2021.108107

Crossref Full Text | Google Scholar

Gausepohl F., Hennke A., Schoening T., Köser K., Greinert J. (2020). Scars in the abyss: Reconstructing sequence, location and temporal change of the 78 plough tracks of the 1989 discol deep-sea disturbance experiment in the Peru basin. Biogeosciences 17, 1463–1493. doi: 10.5194/bg-17-1463-2020

Crossref Full Text | Google Scholar

Gillard B., Purkiani K., Chatzievangelou D., Vink A., Iversen M. H., Thomsen L. (2019). Physical and hydrodynamic properties of deep sea mining-generated, abyssal sediment plumes in the clarion clipperton fracture zone (Eastern-central Pacific). Elem. Sci. Anth. 7, 5. doi: 10.1525/elementa.343

Crossref Full Text | Google Scholar

Haalboom S., de Stigter H. C., Mohn C., Vandorpe T., Smit M., de Jonge L., et al. (2023). Monitoring of a sediment plume produced by a deep-sea mining test in shallow water, Malagá bight, Alboran sea (Southwestern Mediterranean sea). Mar. Geol. 456, 106971. doi: 10.1016/j.margeo.2022.106971

Crossref Full Text | Google Scholar

Haalboom S., Schoening T., Urban P., Gazis I.-Z., de Stigter H., Gillard B., et al. (2022). Monitoring of anthropogenic sediment plumes in the clarion-clipperton zone, ne equatorial Pacific ocean. Front. Mar. Sci. 9, 882155. doi: 10.3389/fmars.2022.882155

Crossref Full Text | Google Scholar

Hoffman K. L., Padberg M., Rinaldi G. (2013). “Traveling salesman problem,” in Encyclopedia of operations research and management science. (Boston, MA: Springer New York), vol. 1, 1573–1578. doi: 10.1007/978-1-4419-1153-7_1068

Crossref Full Text | Google Scholar

Hu H., Song S., Chen C. P. (2019). Plume tracing via model-free reinforcement learning method. IEEE Trans. Neural Networks Learn. Syst. 30, 2515–2527. doi: 10.1109/TNNLS.5962385

PubMed Abstract | Crossref Full Text | Google Scholar

IEA (2021). The role of critical minerals in clean energy transitions.

Google Scholar

Jones D. O., Kaiser S., Sweetman A. K., Smith C. R., Menot L., Vink A., et al. (2017). Biological responses to disturbance from simulated deep-sea polymetallic nodule mining. PloS One 12, e0171750. doi: 10.1371/journal.pone.0171750

PubMed Abstract | Crossref Full Text | Google Scholar

Jones D. R., Schonlau M., Welch W. J. (1998). Efficient global optimization of expensive black-box functions. J. Global optim. 13, 455–492. doi: 10.1023/A:1008306431147

Crossref Full Text | Google Scholar

Lefaible N., Macheriotou L., Pape E., Molari M., Haeckel M., Zeppilli D., et al. (2024). Industrial mining trial for polymetallic nodules in the clarion-clipperton zone indicates complex and variable disturbances of meiofaunal communities. Front. Mar. Sci. 11, 1380530. doi: 10.3389/fmars.2024.1380530

Crossref Full Text | Google Scholar

Li S., Guo Y., Bingham B. (2014). “Multi-robot cooperative control for monitoring and tracking dynamic plumes,” in 2014 IEEE International Conference on Robotics and Automation (ICRA). (New York, USA: IEEE), 67–73.

Google Scholar

Mousadik S. E., Ouillon R., Muñoz-Royo C., Slade W., Pottsmith C., Leeuw T., et al. (2024). In situ optical measurement of particles in sediment plumes generated by a pre-prototype polymetallic nodule collector. Sci. Rep. 14, 23894. doi: 10.1038/s41598-024-72991-y

PubMed Abstract | Crossref Full Text | Google Scholar

Mulvad S. H. (2022). fast-tsp - A fast TSP solver with Python bindings.

Google Scholar

Muñoz-Royo C., Ouillon R., El Mousadik S., Alford M. H., Peacock T. (2022). An in situ study of abyssal turbidity-current sediment plumes generated by a deep seabed polymetallic nodule mining preprototype collector vehicle. Sci. Adv. 8, eabn1219. doi: 10.1126/sciadv.abn1219

PubMed Abstract | Crossref Full Text | Google Scholar

Nyikosa F. M., Osborne M. A., Roberts S. J. (2018). Bayesian optimization for dynamic problems. arXiv preprint arXiv:1803.03432. doi: 10.48550/arXiv.1803.03432

Crossref Full Text | Google Scholar

Peacock T., Ouillon R. (2023). The fluid mechanics of deep-sea mining. Annu. Rev. Fluid Mechan. 55, 403–430. doi: 10.1146/annurev-fluid-031822-010257

Crossref Full Text | Google Scholar

Petersen S., Haeckel M., Steffen J., Kersten C. (2020). Mineral resources of the deep sea: Formation, potential and risks.

Google Scholar

Petillo S., Schmidt H., Balasuriya A. (2011). Constructing a distributed auv network for underwater plume-tracking operations. Int. J. Distrib. Sensor Networks 8, 191235. doi: 10.1155/2012/191235

Crossref Full Text | Google Scholar

Purkiani K., Gillard B., Paul A., Haeckel M., Haalboom S., Greinert J., et al. (2021). Numerical simulation of deep-sea sediment transport induced by a dredge experiment in the northeastern pacific ocean. Front. Mar. Sci. 8, 719463. doi: 10.3389/fmars.2021.719463

Crossref Full Text | Google Scholar

Purkiani K., Paul M., Schulz A., Greinert T. B., von See J. (2024). Sediment concentration data calculated by numerical simulation of a dredge experiment in the northeastern pacific ocean.

Google Scholar

Samaniego F. P., Reina D. G., Marín S. L. T., Arzamendia M., Gregor D. O. (2021). A bayesian optimization approach for water resources monitoring through an autonomous surface vehicle: The ypacarai lake case study. IEEE Access 9, 9163–9179. doi: 10.1109/Access.6287639

Crossref Full Text | Google Scholar

Simon-Lledó E., Bett B. J., Huvenne V. A., Köser K., Schoening T., Greinert J., et al. (2019). Biological effects 26 years after simulated deep-sea mining. Sci. Rep. 9, 8040. doi: 10.1038/s41598-019-44492-w

PubMed Abstract | Crossref Full Text | Google Scholar

Snoek J., Larochelle H., Adams R. P. (2012). Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 25.

Google Scholar

Spearman J., Taylor J., Crossouard N., Cooper A., Turnbull M., Manning A., et al. (2020). Measurement and modelling of deep sea sediment plumes and implications for deep sea mining. Sci. Rep. 10, 5075. doi: 10.1038/s41598-020-61837-y

PubMed Abstract | Crossref Full Text | Google Scholar

Stander N., Craig K. J. (2002). On the robustness of a simple domain reduction scheme for simulationbased optimization. Eng. Comput. 19, 431–450. doi: 10.1108/02644400210430190

Crossref Full Text | Google Scholar

Stankiewicz P., Tan Y. T., Kobilarov M. (2021). Adaptive sampling with an autonomous underwater vehicle in static marine environments. J. Field Robot. 38, 572–597. doi: 10.1002/rob.22005

Crossref Full Text | Google Scholar

Tian Y., Zhang A., Li W., Yu J., Li Y., Zeng J. (2014). “A behavior-based planning strategy for deep-sea hydrothermal plume tracing with autonomous underwater vehicles,” in OCEANS 2014-TAIPEI (New York, USA: IEEE), 1–10. doi: 10.1109/OCEANS-TAIPEI.2014.6964302

Crossref Full Text | Google Scholar

Vonnahme T. R., Molari M., Janssen F., Wenzhöfer F., Haeckel M., Titschack J., et al. (2020). Effects of a deep-sea mining experiment on seafloor microbial communities and functions after 26 years. Sci. Adv. 6, eaaz5922. doi: 10.1126/sciadv.aaz5922

PubMed Abstract | Crossref Full Text | Google Scholar

von See T. B., Meurer T., Greinert J. (2022). Chemical plume tracking using an auv with ukf based extremum seeking. IFAC-PapersOnLine 55, 178–183. doi: 10.1016/j.ifacol.2022.10.428

Crossref Full Text | Google Scholar

Wang C., Wei L., Wang Z., Song M., Mahmoudian N. (2018). Reinforcement learning-based multi-auv adaptive trajectory planning for under-ice field estimation. Sensors 18, 3859. doi: 10.3390/s18113859

PubMed Abstract | Crossref Full Text | Google Scholar

Weaver P. P. E., Aguzzi J., Boschen-Rose R. E., Colaço A., de Stigter H., Gollner S., et al. (2022). Assessing plume impacts caused by polymetallic nodule mining vehicles. Mar. Policy 139, 105011. doi: 10.1016/j.marpol.2022.105011

Crossref Full Text | Google Scholar

Williams C. K., Rasmussen C. E. (2006). Gaussian processes for machine learning Vol. 2 (Cambridge, MA: MIT press) 2 (3).

Google Scholar

Zhang J., Liu M., Zhang S., Zheng R., Dong S. (2022). Multi-auv adaptive path planning and cooperative sampling for ocean scalar field estimation. IEEE Trans. Instrument. Measure. 71, 1–14. doi: 10.1109/TIM.2022.3167784

Crossref Full Text | Google Scholar

Zhu C., Byrd R. H., Lu P., Nocedal J. (1997). Algorithm 778: L-bfgs-b: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. softw. (TOMS) 23, 550–560. doi: 10.1145/279232.279236

Crossref Full Text | Google Scholar