An observation-based method to estimate carbonate system variations in the Labrador Sea

The ocean carbonate system consists of pH, alkalinity, inorganic carbon and the partial pressure of carbon dioxide, and during the current era of anthropogenic change, its dynamics are key for understanding changes in the ocean and its ecosystem over time. The focus of this study is to estimate the carbonate system in the Labrador Sea with time series methods, using direct observations from the ocean surface and interior, and chemical relationships between variables. Interior ocean observations are minimal for some of these variables, however, connections between the variables rooted in chemistry were used to create pseudo-observations using CO2SYS, increasing the information available. A state space model was designed that combined GLODAP and SOCAT observations along with pseudo-observations in a time series estimate of the carbonate system. The Labrador Sea between 1993 and 2016 shows increasing rates for DIC (0.57-1.16 µmol kg⁻¹ year⁻¹) and fCO₂ (0.70-2.45 µatm year⁻¹), as well as acidification via pH trends (0.0007-0.0018 year⁻¹). These ranges describe the scale of rates that are occurring at various depths through the water column, though they do not change linearly with depth. Largest rates are found at the surface for DIC, 500-1500 m for fCO₂, and 500-1500 m for pH. Total alkalinity also decreased and is correlated with the freshening of salinity. With the core carbonate variables estimated, other aspects of the carbonate system are calculated using CO2SYS, such as the aragonite and calcite saturation states, the Revelle factor, and the carbonate species. Our method also calculates uncertainties that vary over time and depth based on the availability of observations and their variance, which has lowered the uncertainty for pH by 71% and for fCO₂ by 64% compared to time-independent methods.

1 Introduction

In the current era of increased CO₂ emissions and ocean acidification, it is important to understand the temporal changes in the ocean carbonate system variables, i.e. dissolved inorganic carbon (DIC), total alkalinity (TA), pH, and the fugacity of carbon dioxide (fCO₂). Opportunistic sampling and sparse observations through space and time make it difficult to estimate the trends and variations in the ocean carbonate system, especially in the ocean interior. As a result, the literature has focused mainly on temporally averaged spatial climatologies (Bennington et al., 2022; Broullón et al., 2020; Lauvset et al., 2016; Takahashi et al., 2014; Sabine et al., 2004). Part of the reason for this emphasis is that carbonate variables are not consistently measured through time. Large data gaps in time induce large uncertainties, which favor estimation of decadal-scale trends, but not on finer time scales. We seek to improve the time resolution of the carbonate variables to a monthly scale by using observation-based methods. Here, we refer to observation-based, or observation-centric, methods as statistical approaches using direct observations of the ocean carbonate system from moorings, cruises, floats or underway sensors, as opposed to numerical model estimates. By amalgamating multiple observation sources and by using the chemical equilibrium relationships between variables, we can exploit the observation-based information to its fullest. We develop a methodology that produces a monthly time-depth gridded product of the carbonate system, with uncertainties that vary over time. Our application is focused on carbonate system variables in the Labrador Sea and how they have changed over the last 24 years.

The ocean carbonate variables (DIC, TA, pH, and fCO₂) have often been examined individually. Surface ocean fCO₂ is used to calculate the CO₂ air-sea flux, thus quantifying the magnitudes of the ocean carbon sink (Landschützer et al., 2016). Moving into the water column, DIC has been used to investigate the spatial distribution and storage rate of anthropogenic CO₂ (Müller et al., 2023; Gruber et al., 2019). With the increase of anthropogenic CO₂ in the ocean, pH measurements quantify ocean acidification and the impact on marine life (Rastrick et al., 2018). Finally, total alkalinity has been used to understand the ocean’s buffering capacity in response to changes in pH (Middelburg et al., 2020). TA is also often used with one of the other carbonate variables to then estimate the rest of the carbonate system (Carter et al., 2017).

A few studies have examined the carbonate variables from a multivariate perspective (Gregor and Gruber, 2021; Carter et al., 2021; Bittig et al., 2018; Sauzède et al., 2017). While these multivariate studies estimated the four carbonate variables, the variables themselves were analyzed independently, as in without correlation or connection between the carbonate variables. This is important since the carbonate variables are related (and constrained) through chemical equilibrium equations (Sarmiento and Gruber, 2006). CO2SYS is a family of algorithms with implementations in MATLAB (Sharp et al., 2020), Python (Humphreys et al., 2023) and R (Gattuso et al., 2022), that solves the chemical equilibrium equations to calculate the state of the carbonate system that consists of the four measurable variables (DIC, TA, pH, and fCO₂), but also includes the aragonite saturation state (Ω), DIC speciation and the Revelle factor. Few observation-based methods have incorporated the chemical connection between carbonate variables within the analysis method, but it is often done as a data processing step to fill in gaps in a set of observations prior to being analyzed (Lauvset et al., 2021; Mackay and Watson, 2021) to transform the results to another variable (Jiang et al., 2019), or as a consistency check (i.e. CONTENT, Bittig et al., 2018).

We used two observation-based data sources for carbonate variables: GLODAP with subsurface bottle sampled data (Lauvset et al., 2022) and SOCAT with surface fCO₂ data from underway systems on ships (Bakker et al., 2016). There is also BGC-ARGO profiling floats with subsurface pH data (Bittig et al., 2019). It is most common to use one data source (e.g. GLODAP) as input data for studies, and the others (e.g. SOCAT and/or BGC-ARGO) as validation or comparison data (Bittig et al., 2018). Few papers have incorporated multiple data sources as inputs into their analysis, with the exception of Feely et al. (2023); Iida et al. (2020); Gregor and Gruber (2021) and ECCO-Darwin, which is a data-assimilative biogeochemical model that used SOCAT, GLODAP, SOCCOM and BGC-ARGO data as observational constraints in their model (Carroll et al., 2022). Combining multiple data sources is challenging, as different observation types will have different measurement uncertainties, as well as spatial and temporal sampling schemes. Research on these carbonate variables often reflects the spatial distribution of their observations, with relatively little analysis on fCO₂ in the interior ocean (Fiedler et al., 2013), but significant work analyzing fCO₂ in the surface waters (Chau et al., 2024; Bennington et al., 2022; Gloege et al., 2022; Yasunaka et al., 2019; Du et al., 2015; Zeng et al., 2014; Landschützer et al., 2013).

In this study, we estimate monthly time series of the four carbonate system variables in the Labrador Sea from 1993-2016 using a fusion of GLODAP and SOCAT data. We used a state space model approach that produced time-varying uncertainties based on data availability and data type. We also improved our effective observation availability by combining direct observations with pseudo-observations derived from observation data with CO2SYS. This methodology could be generalized to different regions, temporal or spatial scales, with the caveat that data availability and its temporal resolution is a limiting factor for obtaining meaningful results.

2 Data

Our region of interest is the Labrador Sea, which we define as the region south of 65° N and west of 40° W within the Atlantic Arctic (ARCT) Longhurst biogeochemical province (Longhurst, 2007) (Figure 1). Within the Longhurst province, biogeochemical properties are assumed to be homogeneous. The Labrador Sea in the northwest Atlantic is a key area for anthropogenic carbon storage due to its association with deep convection (Raimondi et al., 2021).

Figure 1

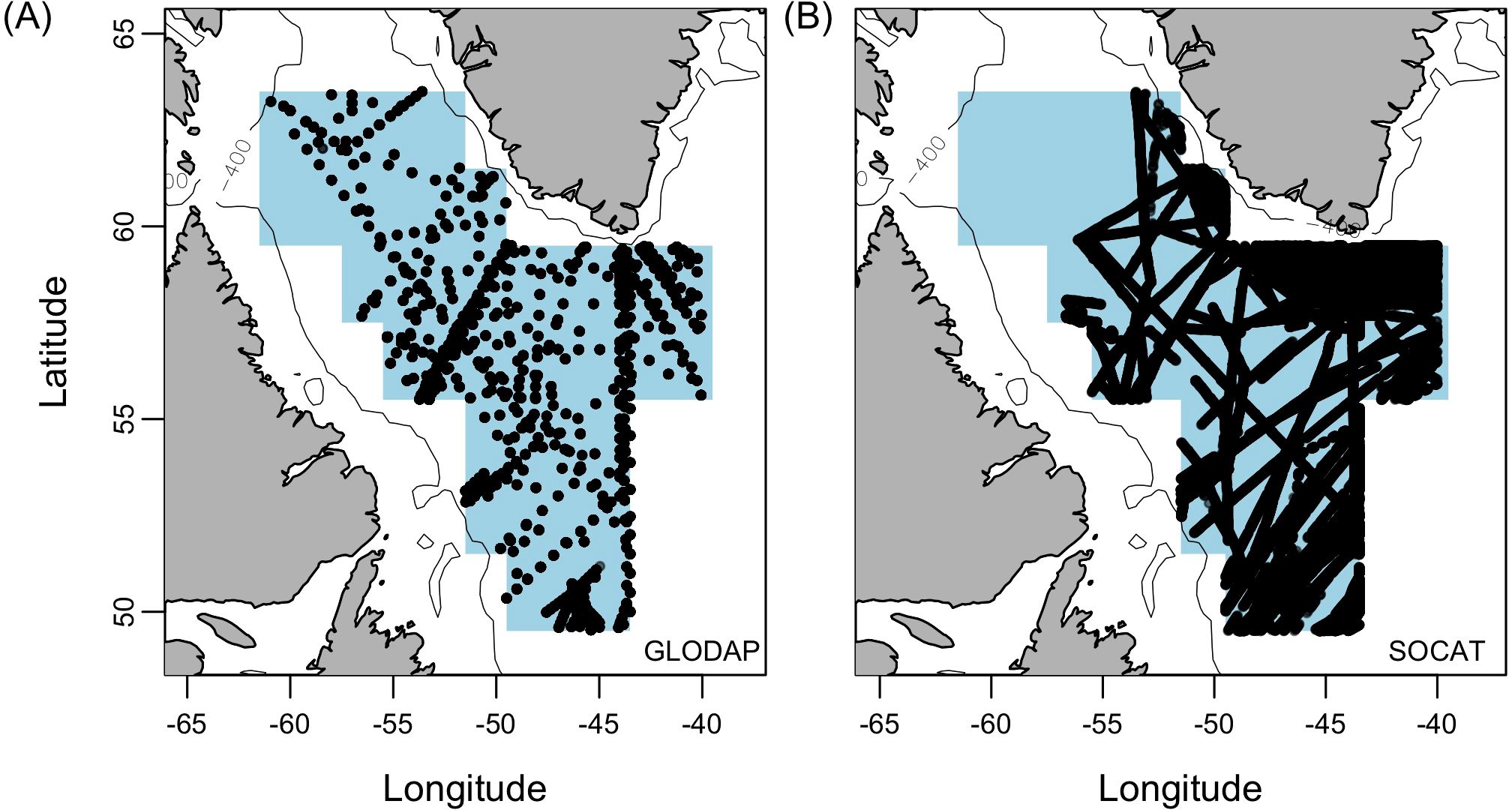
Figure 1. Geographical location of observations in the Labrador Sea study region: data within the Atlantic Arctic Longhurst Province and west of 40° W (blue shaded area). Two data sources used are: (A) GLODAPv2.2022 with profiles of observations (black dots) of at least one carbonate variable, and (B) SOCAT.2022 with fCO₂ data points. Data near the coast where bathymetry is less than 400 m were removed (grey line).

Two datasets were used in this study: GLODAPv2.2022 (Lauvset et al., 2022) and SOCAT2022 (Bakker et al., 2022, 2016). In our study region, these datasets provide complementary observations: GLODAP has direct observations of DIC, TA, pH, fCO₂, temperature, salinity and oxygen in the interior ocean for depths 0-4500 m from 1981-2021; and SOCAT has surface fCO₂ from 1990-2021. This version of GLODAP in the North Atlantic has large data gaps of multiple years before 1991 and after 2016. Our analysis will span 1993-2016 to minimize gaps larger than a year where no data for any carbonate variables exist. However, 1993 was chosen as a start date to mimic other oceanographic reanalysis data products with the same start date. Large gaps at the beginning and end of the time series will cause the overall decadal trend to be underestimated. We included SOCAT data from all cruises (flags A-D), but only GLODAP and SOCAT data with a WOCE flag 2 (good), thus removing the interpolated data for the GLODAP carbonate variables. The GLODAP and SOCAT observations within the Labrador Sea were separated into 20 depth layers and then averaged monthly. Layer divisions were chosen to have an approximately equal number (∼500) of individual DIC observations from GLODAP in each layer. This is related to near-surface DIC observations occurring in 40 months (14% of time series). The top of the depth layers in this study are: 0 m, 20 m, 53 m, 104 m, 209 m, 357 m, 505 m, 683 m, 890 m, 1100 m, 1360 m, 1580 m, 1830 m, 2090 m, 2370 m, 2590 m, 2810 m, 3000 m, 3200 m, and 3380 m.

Variables are sometimes reported for different ocean conditions, i.e. in situ ocean vs. laboratory temperature and pressure. Ocean conditions are defined by potential temperature (T), practical salinity (S) and pressure (P). We converted all variables to in situ ocean conditions to ensure compatibility across datasets. Subsurface ocean observations of fCO₂ are often standardized to laboratory conditions (P=0 dbar, T=20°C, and S=35 PSU), as is the case in the GLODAP dataset, since fCO₂ is not conservative to changes in T, S or P (Sarmiento and Gruber, 2006). Meanwhile, SOCAT reports surface fCO₂ at in situ conditions (P=0 dbar, T between −1.8 and 21.8°C, and S between 17.65 and 35.47 PSU). In order to make these two datasets comparable for use in the same analysis, GLODAP fCO₂ was converted to in situ conditions using chemical equilibrium equations (CO2SYS) and its corresponding input parameters: DIC, TA, T, S and P. The equilibrium constants used in CO2SYS are as described later in Section 3.1. pH was reported on total scale and in situ conditions by GLODAP.

GLODAP observations of the ocean interior are obtained from research cruises, and in our study region, observations are seasonally biased towards months May-July (63% of observations in the top 5 m are from May-July). The most sampled variable in GLODAP is DIC, followed by TA. Within GLODAPv2.2022, fCO₂ through the water column is rarely measured, but fCO₂ is more frequently available at the surface (notably between 2003-2012) owing to the ships of opportunity that collect the SOCAT data. The SOCAT data does not have a seasonal sampling bias (i.e. in the top 5 m there is a similar number of observations in each month). The sampling density of pH in GLODAP has been low at 0.08% of months, but with BGC-ARGO, pH availability since 2018 in the Labrador Sea has increased to a full 100% monthly coverage. Extra pH data from BGC-ARGO was considered to be included in the main results, but further investigation and quality control are needed, as we found the BGC-ARGO pH data has unexpected increasing trends in the Labrador Sea from 2018 to 2022. Instead, pH results with BGC-ARGO data are in the Supplementary Material (Supplementary Figure S19) and serve to demonstrate how the state space model is able to adapt to changes in time series characteristics present in observations.

We also carried out data augmentation, that when DIC and TA were available, fCO₂ and pH were calculated by CO2SYS, as denoted by CO2SYS(DIC, TA). CO2SYS solves the chemical equilibrium equations for the carbonate system (Lewis and Wallace, 1998) (see Section 3.1 for more details). The pseudo-observations fill in gaps when direct, monthly observations are not available, and this greatly increases the effective availability of fCO₂ information. Note, that the data augmentation was performed after monthly averaging the data, as further described in Section 3.2 Implementation.

Since the datasets differ in time range, depth range, and spatial and temporal sampling schemes (Figure 1), we checked how their T, S and fCO₂ data compared. The following comparisons were done as time series plots: (i) T and S of GLODAP and SOCAT, (ii) fCO₂ direct from SOCAT vs fCO₂ calculated via CO2SYS(DIC,TA) and GLODAP data. In the top 20 m, for temperature and salinity, SOCAT has a larger standard deviation than the others, but after being monthly averaged the three data sets have equivalent overall mean and standard deviations across our time period of interest (Supplementary Figure S20). The fCO₂ calculated from GLODAP DIC and TA were compared to fCO₂ observations from SOCAT, and the calculated fCO₂ had poor precision but were sufficient for our analysis. 37 observations were able to be co-located within a month, in the top 5 m and the closest points within 5° of one another. The differences (Supplementary Figure S16) showed an average bias of 1.56 µatm, with GLODAP calculated values slightly overestimating the fCO₂ on average and there is also a large RMSE of 50.26 µatm representing a large error between the calculated fCO₂ and the closest direct measurement within the month. Part of this bias would be due to measurement uncertainty of the input variables (DIC and TA) and the uncertainty in the equilibrium constants used in CO2SYS (Álvarez et al., 2020; Millero, 2007). The equilibrium constants are valid only for a set range of temperature and salinity values, however, in the subpolar region of the Labrador Sea, our temperatures do sometimes go below the recommended range.

3 Methods

The goal of the analysis is to estimate the state of ocean carbonate variables through time and over depth for the domain of interest of the Labrador Sea. $x_t$ is the state of the carbonate system at a given time t, and is as a column vector of length n_x = 4L, where L is the number of depths-layers (see Section 2). The state vector contains all the variables DIC, TA, pH and fCO₂ at each depth-layer through the water column (from surface to deep). The analysis times range from $t=1,\dots ,n_t$ on a regular interval (in our case, monthly). Estimation of the state vector over time makes use of all available observations, and the framework used for the analysis is a state space model. This is comprised of two equations: an observation Equation 1 and a persistence Equation 2, which are defined below. Once these are defined and their parameters specified, the carbonate state is then estimated through time using the Kalman filter/smoother algorithm (Anderson and Moore, 1979).

The observation equation relates the state ($x_t$) to available observations of the carbonate system through the following equation:

$\begin{array}{ll}{y}_t=A_t{x}_t+v_t.& (1)\end{array}$

Here, $y_t$is a column vector that contains the observations of the carbonate system at time t. This vector is of length $n_{y_t}$and the length varies at each time step with the number of observations available at time t. The $y_t$ vector includes observations of the different carbonate variables from multiple datasets including the pseudo-observations (see Supplementary Material). $A_t$ is an $n_{y_t}\times n_x$ observation indicator matrix comprising 1’s and 0’s to match each observation in $y_t$ with its corresponding term in the state vector, $x_t$. $A_t$ allows the simultaneous use of observations from multiple datasets, even observations at the same time t. It is also notable that $A_t$ varies over time, reflecting the fact the variables that are sampled will change over time. To complete the relationship between the mean state ($x_t$) and the direct observations ($y_t$), we include observation error, $v_t\sim N(0,{\text{Σ}}_{v,t})$, that follows a multivariate normal distribution with variance-covariance matrix Σ_v,t.

The persistence equation allows the carbonate state to have a memory (or be auto-correlated) in time. It is represented as a random walk process ${\text{Σ}}_{v,t}$

$\begin{array}{ll}{x}_t=x_{t-1}+w_t.& (2)\end{array}$

Specifically, this means that the new carbonate state ($x_t$) follows the previous state ($x_{t-1}$) but with some random perturbation or persistence error added. The persistence error $((w_t\sim N(0,{\text{Σ}}_w))$ follows a multivariate normal distribution with variance-covariance matrix ${\text{Σ}}_w$. The random walk, a widely used formulation in other statistical models (e.g. Markov Chain Monte Carlo), was chosen as the simplest model possible to achieve a non-parametric temporal persistence of the state that adapts to available observations, without the mean-reverting quantities of an auto-regressive model. The degree to which the state can change from one time to the next is controlled by the magnitude of the diagonal elements of ${\text{Σ}}_w$. This covariance matrix was structured to also allow for correlations between adjacent depth-layers, but not between the different carbonate variables (so it has a block-diagonal structure). Unlike the observation error covariance matrix ${\text{Σ}}_{v,t}$ which changes over time based on which observations are available, the persistence error covariance matrix ${\text{Σ}}_w$ is fixed in time.

The state space model is defined by Equations 1 and 2, both of which provide information for estimating the carbonate state through time. This linear, Gaussian framework is robust and reliable, and its properties are well understood and interpretable. The Kalman filter/smoother algorithm provides the optimal solution for the state space model and yields the state of the carbonate system ($x_t$). Specifically, it provides estimates for the monthly mean values of DIC, TA, pH, and fCO₂ at all depths, and each of their time-varying variances. The latter can then be used to produce error bars or confidence intervals. The algorithm uses Equations 1 and 2 in a sequential, or recursive, estimation procedure. This relies on the Kalman filter, which operates as a forward-in-time recursion such that at each time step t, an estimate of the new state vector (the four variables at the L depths) is available via a one-step ahead prediction using (2). This persistence estimate is then updated to be closer to any available observations. If there are no observations at time t, the observations Equation 1 is not used, only the persistence Equation 2. The Kalman smoother then further refines these estimates through a backwards-in-time recursion. The ratio of the variances for the observation error (diagonal elements of ${\text{Σ}}_{v,t}$) to the persistence error (diagonal elements of ${\text{Σ}}_w$) is a key quantity that dictates how closely the state estimates follow the observations. The smaller the ${\text{Σ}}_{v,t}:{\text{Σ}}_w$ ratio the closer our estimates are drawn to the observations otherwise the more the estimate will ignore the observations and predict a constant unchanging line. This is discussed in more detail in the Supplementary Material, along with details of the Kalman filter/smoother algorithm.

The ${\text{Σ}}_{v,t}$ matrix was estimated based on the variance of observations, and the ${\text{Σ}}_w$ matrix used maximum likelihood estimation. For details of how the matrix terms were estimated, the reader is referred to the Supplementary Material.

3.1 Pseudo-observations

We augmented our pH and fCO₂ data using chemical equilibrium relationships between carbonate variables to create pseudo-observations, designated $y_t^{*}$. These can be used together with direct observations, $y_t$, of other variables in the observation Equation 1. Pseudo-observations improve the state estimate for variables when direct observations are missing. The pseudo-observations for pH and fCO₂ at time t also implicitly act as a constraint that encourages the carbonate state estimates to be in a chemically balanced state with DIC and TA through time. The notation $y_t^{*}[\text{pH}]$ will be used throughout, where $y_t^{*}$ represents the vector of pseudo-observations, and inside the square brackets identifies the relevant variables being referenced from the vector (e.g. pH and/or fCO₂).

Given observations of DIC and TA (or $y_t[\text{DIC}, \text{TA}]$), CO2SYS calculates the remaining two variables, producing pseudo-observations of pH and fCO₂ $(y_t^{*}[\text{pH},{\text{fCO}}_2])$, i.e.

$\begin{array}{ll}{y}_t^{*}[\text{pH},{\text{fCO}}_2]=\text{CO}2\text{SYS}(y_t[\text{DIC},\text{TA}],{\psi }_t).& (3)\end{array}$

When calculating with CO2SYS, ${\psi }_t$ represents the set of in situ ocean parameters at time t: potential temperature, practical salinity and pressure/depth. To solve chemical equilibrium equations, CO2SYS used the following equilibrium constants: K₁ and K₂ from Lueker et al. (2000), K_f from Perez and Fraga (1987), K_s from Dickson (1990), and the concentration of total boron from Uppström (1974). Calculations were performed on the total scale for pH. In this work, the CO2SYS calculations were performed using the Seacarb package in R (Gattuso et al., 2022).

We also calculated pseudo-observations of TA with a regression relationship with salinity. The linear regression $y_t^{*}[\text{TA}]={\beta }_{\text{TA}:\text{S}}{S}_t$ was used with monthly salinity data ($S_t$) to predict pseudo-observations of TA $(y_t^{*}[\text{TA}])$ when direct observations of TA $(y_t[\text{TA}])$ were not available, time series showing their frequency of occurrence are in the Supplementary Material (Supplementary Figure S13). Least squares regression was used to estimate the conversion parameter ${\beta }_{\text{TA}:\text{S}}$ for each layer individually, though all values were found to be close to the average ${\beta }_{\text{TA}:\text{S}}$ of 66, (minimum 65.87, maximum 66.90). This is similar to the value (${\beta }_{\text{TA}:\text{S}}=67$) used by Olsen et al. (2020) for global data.

The pseudo-observation uncertainties within the matrix ${\text{Σ}}_{v,t}$ were determined with the error calculations from CO2SYS, except for the pseudo-observations of TA which used the regression prediction variance. Details of the ${\text{Σ}}_{v,t}$ matrix are in the Supplementary Material. Meanwhile, a key aspect to note is that the pseudo-observation errors are larger than the errors for direct observations, thus when estimating the state the Kalman smoother algorithm will favour (i.e. draw closer to) direct observations than pseudo-observations.

3.2 Implementation

To implement the methodology, the following steps were taken:

(i) Region selection and depth-layer assignment - pre-process the datasets by removing coastal and shelf regions (i.e. bathymetry less than 400 m), separating each dataset into L depth layers;

(ii) In situ observations - convert variables (i.e. fCO₂ from GLODAP) to in situ conditions with GLODAP data DIC, TA, T, S, and P as inputs, nutrients were set to 0;

(iii) Monthly average - use the individual observations in each layer to create monthly average time series for each layer;

(iv) Pseudo-observations - Predict TA from monthly salinity $(y_t^{*}[\text{TA}]=\beta S_t)$ when direct observations $(y_t[\text{TA}])$ are not available. Then use either direct or pseudo-observations of TA with DIC in CO2SYS to calculate pseudo-observations of pH and fCO₂ $(y_t^{*}[\text{pH},{\text{fCO}}_2]=\text{CO}2\text{SYS}(y_t[\text{DIC}, \text{TA}], {\psi }_t))$.

(v) Specify parameters - determine ${\text{Σ}}_{v_{\text{t}}}$ based on the variance of observations and determine ${\text{Σ}}_w$ using maximum likelihood with the Kalman filter. The initial mean state was set to the first monthly GLODAP observation, and this ideal scenario was used for DIC, T and S. For variables where there was no direct observation for a few years and where the observation variability was larger than the trend, such as for TA, the initial condition was the mean of the first 6 pseudo-observations. This also worked for fCO₂. For pH, and variables with a large gap of no direct observations and a prominent decadal trend, an initial analysis run was performed to determine an average trend 0.002 year⁻¹ and this was used with the first direct GLODAP observation, which was then used to trace back an appropriate initial mean state for pH. The initial variance for all variables was chosen by running the analysis with an arbitrary value, and then extracting the steady-state variance it approaches.

(vi) Kalman smoother - Using the Kalman filter results with optimal parameters determined from (v), the Kalman smoother algorithm implemented Equations 1 and 2 with observations ($y_t$) and pseudo-observations ($y_t^{*}$) to estimate the state of the carbonate system ($x_t$) monthly through time, as well as a time-varying uncertainty that is used for confidence intervals.

These steps are in more detail in the Supplementary Material. Note this analysis was performed with a monthly time step, but in principle, any time interval could be used. Also note that the state estimation for temperature, salinity and oxygen were also calculated following the same methodology.

Using a subset of the carbonate state estimates (DIC and TA) along with the state of temperature (T) and salinity (S), other aspects of the carbonate system were calculated: the aragonite saturation, calcite saturation, Revelle factor, as well as the carbonate, bicarbonate and carbonic acid concentrations. Furthermore, for each variable, the annual rate of increase was estimated from linear least squares regression, using bootstrapping to determine its significance (see Supplementary Material).

Finally, note that the analysis was also performed on total alkalinity but for interpretation and discussion, this was then converted to salinity-normalized Total Alkalinity (nTA)

$\begin{array}{ll}nTA=\frac{TA-T{A}^{S=0}}{S}{S}^{ref}+T{A}^{S=0}& (4)\end{array}$

where $S^{ref}=35$ PSU and $T{A}^{S=0}=728.3 \text{µ}{\text{mol kg}}^{-1}$ (Friis et al., 2003). We have also used the fugacity of CO₂ (fCO₂) instead of the partial pressure of CO₂ (pCO₂). pCO₂ is often analyzed rather than fCO₂ at near-surface, as their differences are usually <1.5 µatm. fCO₂ is, however, more appropriate for measurements through the water column as it is targeted at real gases, whereas pCO₂ is the equivalent for ideal gases. They are related via the fugacity coefficient, which is a function of the ocean state, thus accounting for the pressure effect with depth. At low pressure pCO₂ and fCO₂ are approximately equal.

The analysis was performed using R code (R Core Team, 2021) with RStudio (RStudio Teams, 2022), with the assistance of packages for date/time organization: lubridate (Grolemund and Wickham, 2011), and for assistance with plots: fields (Nychka et al., 2022), cmocean (Thyng et al., 2016), scales (Wickham and Seidel, 2021), and maps (Becker et al., 2021). For accessing and downloading BGC-ARGO data: argoFloats (Kelley et al., 2022a) and oce (Kelley et al., 2022b). CO2SYS calculations were performed with seacarb (Gattuso et al., 2022).

4 Results

The state of the carbonate system (i.e. the four variables DIC, TA, pH and fCO₂) was estimated monthly from 1993-2016 for the 20 depth-layers from 0 m - 3500 m using the state space model. These results are presented as time-depth plots for each variable (Figures 2-5). The estimated time series for the surface layer and an intermediate depth-layer were plotted in full to contrast their differences due to oceanic variability and observation sparsity, while all time series are presented Supplementary Figures S10-S13. Depth profiles of the calculated annual rates of increase (Supplementary Figure S18) visualizes the numbers that are listed on the right side of Figures 2A-5A. The results for each variable are presented in turn.

Figure 2

Figure 2. Results from analysis of DIC. (A) Time-depth plot of mean DIC concentration (µmol kg⁻¹). Note that the depth axis has nonlinear spacing. Observations in months 6-11 are indicated with a ‘S’ and months 12-5 with a ‘W’. The aragonite saturation horizon (Ω = 1) is shown by a thick black line. The depth-weighted column mean for each month is shown by the horizontal colorband at the top. The mean of each depth-layer is shown by the colorband to the right. The annual rates of increase shown on the right were calculated as linear least squares regression over 1993-2016, where black numeric slopes (µmol kg⁻¹ year⁻¹) are statistically significant, and grey slopes are not. (B) A time series of DIC at 0 m with the estimated mean (black line), 95% confidence intervals (grey area) and direct observations of monthly averaged GLODAP (red dots). Sampling times for the observations are shown along the x-axis (colored ticks). (C) A time series of DIC at 2090 m following panel (B).

DIC increases with depth, as expected, and there is a general increase of DIC over time as shown by the depth-weighted column mean (Figure 2). The time series of the near-surface waters (Figure 2B) have larger variability than the sub-surface waters (Figure 2C). The waters deeper than 100 m show linearly increasing trends of DIC at rates of 0.57 to 0.76 µmol kg⁻¹ year⁻¹. However, examining the individual time series for each depth (Supplementary Figure S10), for depths 200-800 m and for most below 1800 m the estimated DIC is unchanging in the 1990s and increasing after 2000. These deep water results are consistent with the anthropogenic increase presented in Boteler et al. (2023) and later shown by Olivarez et al. (2024) to be a delayed effect of the Pinatubo 1991 eruption. The intermediate waters however were unexpected, though a similar change in trend is seen in oxygen (Supplementary Figure S9a) which goes from a lack of trend in the 1990s to a decline in oxygen in the 2000s. Note also that the state space model is resistant to outliers with only a small divergent of the mean state towards the observation, as seen at the end of 2010 (Figure 2C). A list of cruises that contributed to outliers in monthly averaged DIC observations is provided in the Supplementary Material.

At the near surface (top 50 m), there is a small seasonal cycle in DIC with lower values in the summer due to biological production and a shallow mixed layer. There is also a pronounced 4-year cycle, which could be an artifact of the data, be actual inter-annual variability, or be a combination. The 4-year cycle is also seen in the near-surface temperature and oxygen time series (Supplementary Figures S7b, S9b). It could be related to biological activity as well as related to the North Atlantic Oscillation (NAO) and Atlantic Multidecadal Oscillation (AMO). The NAO and AMO have 4 year and 4-5 year periodic signals, respectively, as identified in a spectral analysis and F-test of the frequencies (Thomson, 1982). By visually comparing them, we see that high DIC values (years 2000 and 2004) coincide with moments of high NAO index. The other years of high DIC (years 1996, 2009, and 2014) are just a year out of phase with both the NAO and a high AMO index.

fCO₂ shows that it is steadily increasing over time at rates between 0.70 and 2.45 µatm year⁻¹ (Figure 3), which we generally attribute to the atmospheric CO₂ increase of ∼1.93 µatm year⁻¹ (Lebehot et al., 2019), with the near-surface fCO₂ increase being quite close to that of atmospheric CO₂. The time-depth plot also shows that fCO₂ increases with depth as a consequence of the increase in pressure, as expected. At the near-surface, fCO₂ is increasing at a rate of 1.48±0.04 µatm year⁻¹, which agrees with other ocean observation-based estimates (1.47 ± 0.06 µatm year⁻¹) and is close to the model-based estimates (1.9 ± 0.09 µatm year⁻¹) (Lebehot et al., 2019). It is however interesting to note that at depths of 1000-2000 m, the rate of fCO₂ increase is faster than the atmosphere, between 1.72 and 2.2 µatm year⁻¹. It is likely the deep convection in the Labrador Sea is taking the winterfCO₂ down to the intermediate waters.

Figure 3

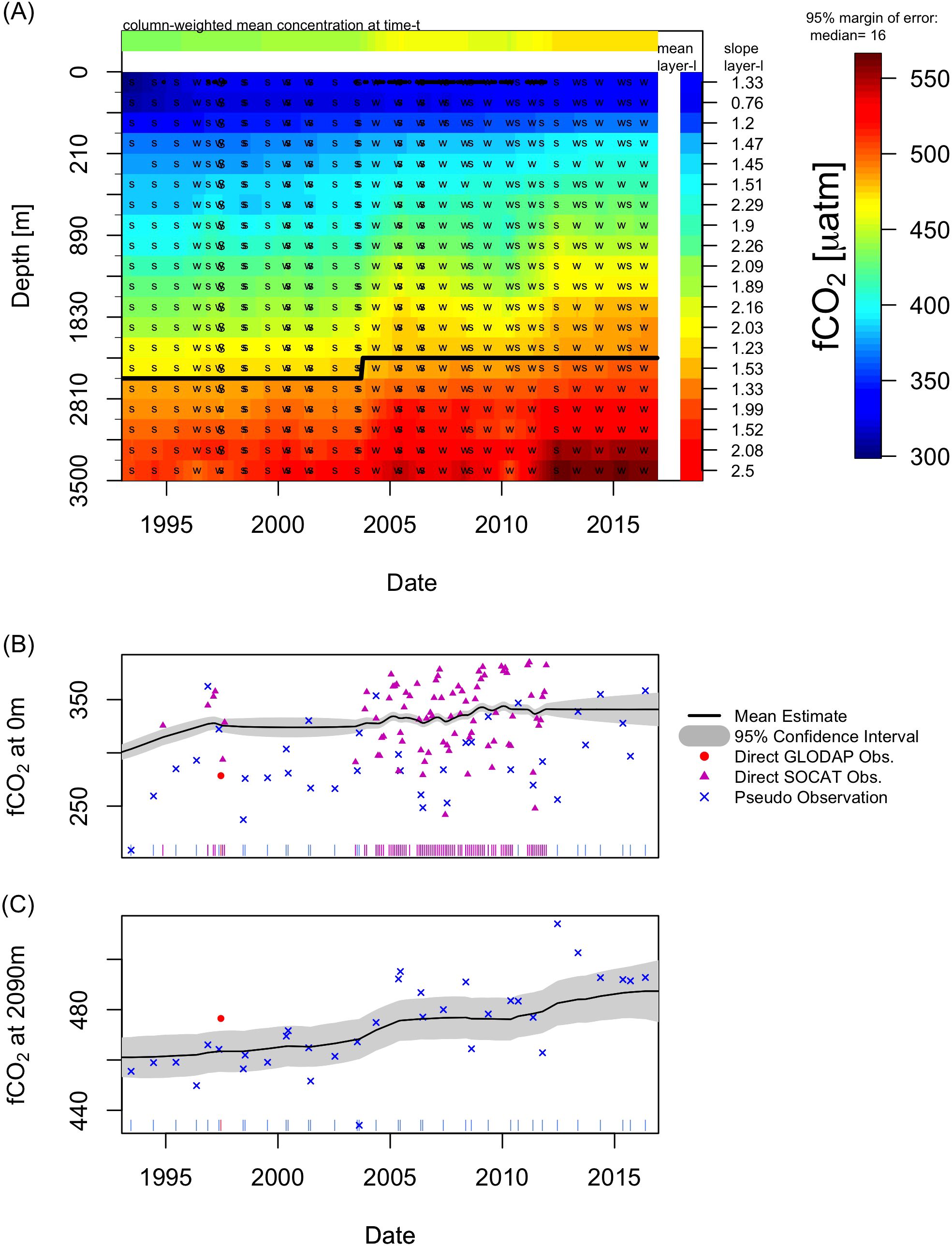
Figure 3. Results from analysis of fCO₂ (µatm). (A) Time-depth plot of fCO2, (B) time series of fCO2 at 0 m, and (C) time series of fCO2 at 2090 m. Format the same as Figure 2, with the addition in panels (B, C) of direct observations of monthly averaged SOCAT (purple triangles) and pseudo-observations (blue X).

The fCO₂ near-surface time series in Figure 3B shows the presence of direct observations from both GLODAP and SOCAT, as well as pseudo-observations. Between 2005 and 2012, the high frequency of SOCAT observations reveals a seasonal cycle peaking around February (Supplementary Figure S15), which is similar to other pCO₂ products in the Labrador Sea (Takahashi et al., 2002; Rödenbeck et al., 2013; Zeng et al., 2014; Arruda et al., 2024). The increasing trend in the near-surface is more obvious for fCO₂ than for DIC as the fCO₂ seasonal cycle presented here has an amplitude smaller than the increasing trend. This amplitude is however smaller than expected but it is based on the current data and the uncertainty parameters chosen. The monthly fCO₂ data between 2005 and 2012 have such a large scatter that a larger observation error would be preferred, but in that case the mean state estimate resulted in a linear line passing through them. We reduced the observation error to show that the seasonal cycle can be shown to be at the correct phase, though with an underestimated amplitude.

The width of the confidence interval shows the uncertainty of the mean state, but note that this uncertainty is not necessarily equal to the spread of the data. Figure 3B and Figure 4B show confidence intervals that are narrower than the spread of the data. The width of the confidence interval is based on three factors: frequency of data, observation error, and persistence error. The persistence error was estimated using maximum likelihood. The first two are based on the data and are illustrated in Figure 3B for the confidence interval narrow between 2005 and 2012 due to the increased frequency of SOCAT data and the small observation error for SOCAT within ${\text{Σ}}_{v,t}$(see Supplementary Material).

Figure 4

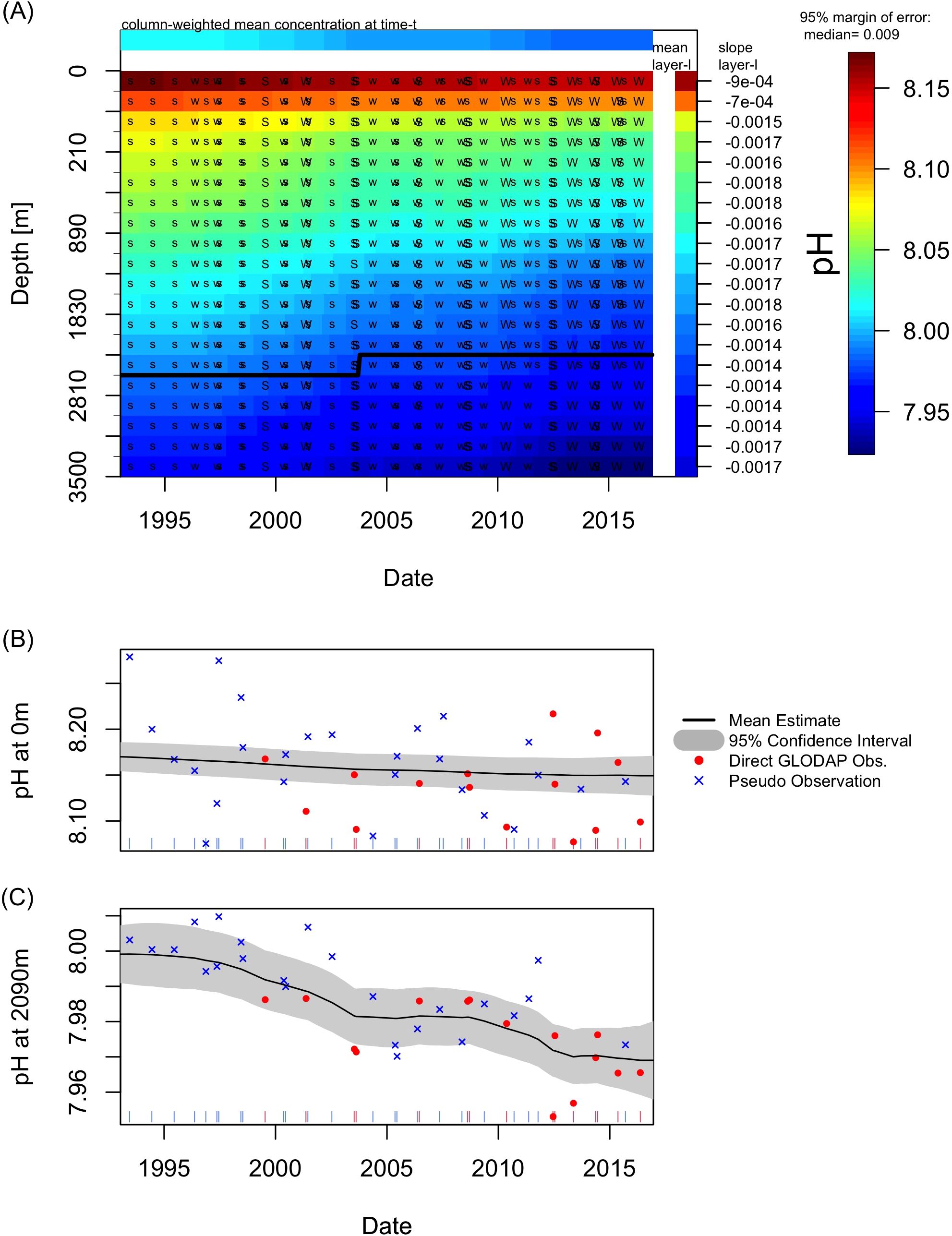
Figure 4. (A) Time-depth plot of pH, (B) time series of pH at 0 m, and (C) time series of pH at 2090 m. Format the same as Figure 2, with the addition in panels (B, C) of pseudo-observations (blue X).

Figure 5

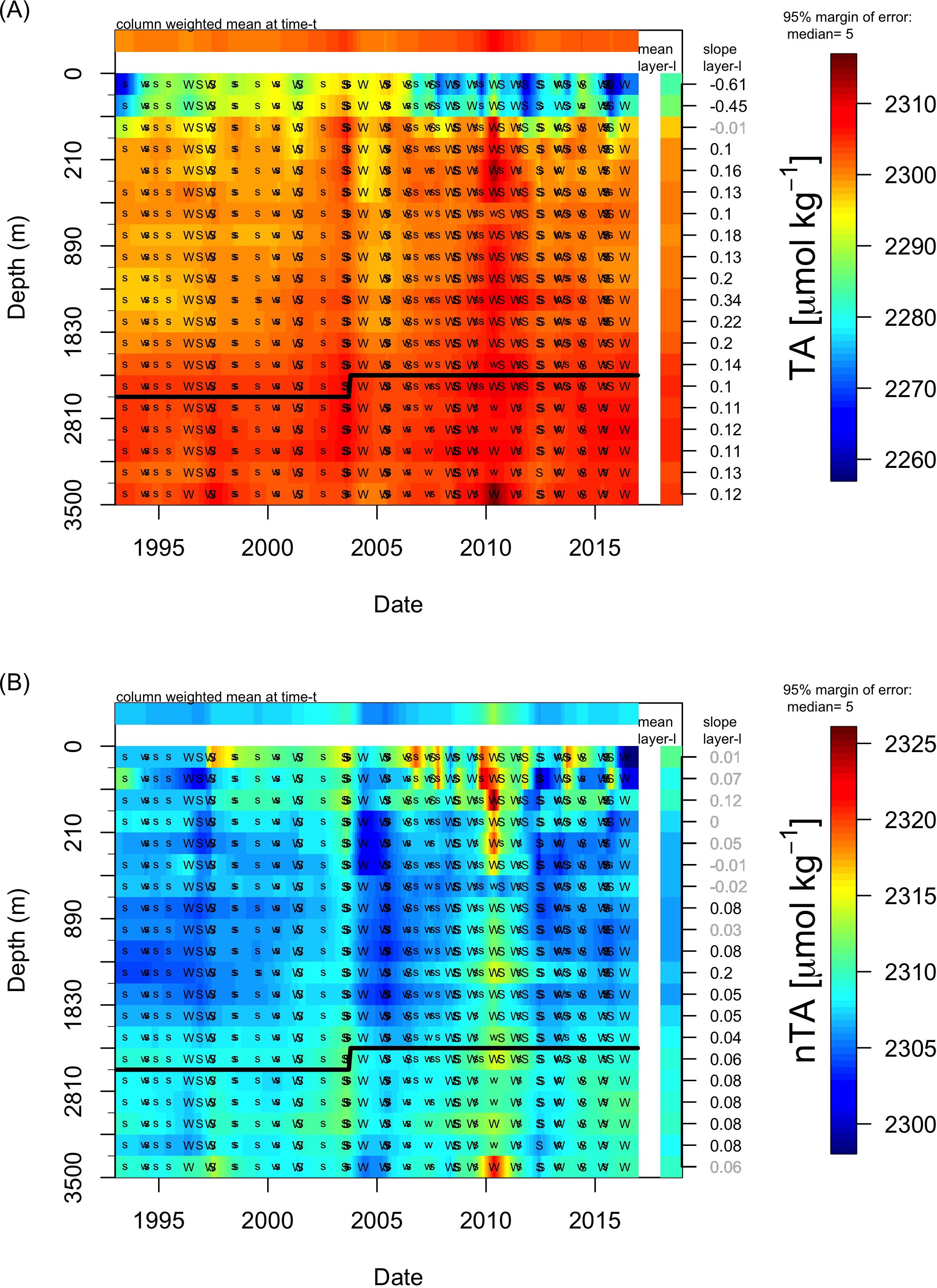
Figure 5. Results from the analysis of TA and salinity-normalized TA (nTA) (µmol kg⁻¹). (A) The time-depth plot of TA and (B) time-depth plot of nTA. Format the same as Figure 2A.

Of the four variables analyzed, fCO₂ sub-surface benefited the most from the use of pseudoobservations, and without them, the fCO₂ time series estimates would not be possible. In the deeper waters (Figure 3C) GLODAPv2 observations are available only one time, and the rest are pseudo-observations that were calculated using CO2SYS.

In the Labrador Sea, ocean acidification (i.e. declining pH) is occurring at rates between −0.0018 and −0.0007 year⁻¹ (Figure 4). In the near-surface (top 20 m) we see higher mean pH values (pH > 8.14), but of the lowest rate of ocean acidification. This rate is smaller than other estimates for the region and time frame (−0.0014 year⁻¹ Chau et al. (2024) and −0.002 year⁻¹ Lauvset et al. (2015)) and may be due to our data which has a larger variance than change over time. Through the water column, the pH value lowers with depth, but the rate of ocean acidification does not change linearly with depth (Supplementary Figure S18). The rate of ocean acidification is stronger for depths 50 to 2000 m. Below 2000 m around the aragonite saturation horizon (Ω = 1; solid line), the rate of ocean acidification is slower than the waters above or below it.

Total Alkalinity deeper than 50 m has minimal variability, but above 50 m lowers after 2006 (Figure 5A), which was found to be correlated with a decrease in salinity. This strong correlation between TA and salinity allowed us to calculate pseudo-observations of TA, but it also makes interpretation of TA difficult since its changes are related to salinity. Hence we use salinity-corrected alkalinity to aid in interpretation. Salinity normalized total alkalinity (nTA) (Friis et al., 2003) removes the expected variability of salinity, allowing us to distinguish changes in alkalinity that are not related to changes in salinity. After salinity-normalization, the trends in the top 50 m have been reduced by more than half, and in the top 20 m the trend is no longer statistically significant, indicating the trend was due to the changes in salinity (Figure 5B). Overall, nTA fluctuates less than ±10 µmol kg⁻¹ about the mean, which typically is considered a negligible variation. There are a few high nTA values (nTA >2315 µmol kg⁻¹) with most occurring around 2010 at 46°W and 52°N. Specifically, there is a single TA observation in May 9, 2010 (https://doi.org/10.25921/zp3g-cm29; doi: 10.5285/cf2d9ba9-d51d-3b7c-e053-8486abc0f5fd) that did not appear as an outlier when looking at the original GLODAP data as a time series (i.e. it was within the acceptable range of all the observations, Supplementary Figures S2–S5). However, by being a TA = 2315.8 µmol kg⁻¹ and no other observations in that month to balance it out, after monthly averaging the data it stood out as a potential outlier. There was enough variability in the surrounding years that we left this observation in, so as to not force the data into perfection. However, we note that this high TA value has cascading effects on other calculated quantities, as will be seen in the Revelle factor.

Using the estimated state for DIC and TA with CO2SYS, we calculated further derived quantities of the carbonate system: the aragonite and calcite saturation state, the Revelle factor and the speciation of DIC (Figure 6). We see in Figure 6E that for every depth-layer the aragonite saturation state is steadily decreasing. At the near-surface there is also some seasonality that is correlated with that of DIC. The same time-depth characteristics are also seen for calcite saturation. The calcite saturation has a range of 1.18 to 3.81, thus the saturation horizon (when Ω = 1) is not shown. The aragonite saturation horizon (Ω = 1), as shown on previous plots (Figures 2-5), is seen to go from our 16th depth-layer (2590-2810 m) to our 15th (2370-2590 m), with this shoaling between depth-layers occurring around 2003. Considering these depth-layers span 220 m each, the shoaling could be up to a max width of 440 m over 24 years, relating to an increase of 18 m year⁻¹.

Figure 6

Figure 6. Results of the carbonate species, Revelle factor and saturation states. The time-depth plots of the estimated mean (color intensity) for (A) carbonic acid $({\text{H}}_2{\text{CO}}_3^{*})$, (B) bicarbonate (HCO₃^–), (C) carbonate (CO₃^–2), (D) Revelle factor (E) aragonite saturation with the saturation horizons (Ω = 1) shown by a thick black line, and (F) calcite saturation.

The Revelle factor was calculated from the TA and DIC results, ${\gamma }_{DIC}$= $\frac{3TA·DIC-2DI{C}^2}{(2DIC-TA)(TA-DIC)}$ (Sarmiento and Gruber, 2006). For all depths after 2005, the Revelle factor increases, indicating that fCO₂ becomes more sensitive over time to changes in DIC. This increase is paused in 2010, but this is related to the anomalous high TA value. Time series of the top few layers (Supplementary Figure S14) show in more detail these changes in the Revelle factor. For the near-surface this implies a lowering of the ocean’s capacity to take up more atmospheric carbon. Since the Revelle factor is calculated from TA, this increased sensitivity is a reflection of the freshening in the area (Supplementary Figure S8). For the interior ocean, the Revelle factor has been used to determine the concentration of anthropogenic DIC (Terhaar et al., 2022; Sabine et al., 2004).

Our state space model also calculates 95% confidence intervals for all the carbonate variables. Hereafter, confidence intervals are referred to as uncertainties, though sometimes the related 95% margin of errors are reported instead (distance from mean estimate to upper uncertainty bound) as in Figure 7. The uncertainties produced from our time-correlated method are lower than the uncertainties from using CO2SYS on DIC and TA values which treat the carbonate variables as being independent through time, rather than auto-correlated (see Table 1 for a detailed comparison). Overall, our time-correlated method has lowered the uncertainty by more than 64%. Our uncertainty estimates are driven by the data distribution over time, as dictated by the opportunistic sampling protocol. In other words, the uncertainties varied over time based on the presence/absence of observations (Figure 7) and the average variability of observations within that depth-layer. In the near-surface waters of DIC, TA and pH the uncertainty is higher due to larger variability of the data. For fCO₂ at the surface, between 2005 and 2012 the uncertainty is reduced due to the presence of SOCAT data. The fCO₂ between 700-1600 m also has higher uncertainty than the waters above or below due to the pseudo-observations having larger variability.

Figure 7

Figure 7. The uncertainty estimate (95% margin or error) for (A) DIC, (B) fCO₂, (C) TA and (D) pH.

Table 1

Table 1. Comparing uncertainties from two methods for pH and fCO₂ (minimum, average, and maximum).

5 Discussion

We developed and implemented a multivariate, time series method to estimate the depth-time variability of the carbonate system in the Labrador Sea. This incorporated the four carbonate variables: DIC, TA, pH and fCO₂. Our method takes into account the temporal memory of the carbonate system, and as a consequence is able to considerably lower the uncertainty of pH by 71% and by 64% for fCO₂, compared to methods that assume independence in time. The estimated time series of DIC and TA were also used to calculate other aspects of the carbonate system, such as the aragonite and calcite saturation state, the Revelle factor and the speciation of DIC (i.e. carbonic acid, bicarbonate and carbonate). Our results for the carbonate system quantify their variations with depth and highlight temporal trends that are assumed to be due to anthropogenic sources: increases in DIC (0.57 to 1.16 µmol kg⁻¹ year⁻¹) and fCO₂ (0.70 to 2.45 µatm year⁻¹), as well as the acidification of pH (-0.0018 to -0.0009 year⁻¹).

We used a statistical time series method that amalgamates multiple data sources and takes account of their unique features. As well as direct observations from GLODAP and SOCAT, CO2SYS was used with DIC and TA observations to calculate pseudo-observations. The pseudo-observations more than doubled the amount of information on pH and fCO₂, which allowed for more detailed and realistic estimates of their depth-time variability, including the estimation of anthropogenic trends of pH and fCO₂. Using pseudo-observations also made pH and fCO₂ estimates chemically balanced with the rest of the carbonate system. DIC and TA were chosen to be in our CO2SYS calculation as we prioritized variables that were abundant over time, but as ARGO data continues to increase, pH could be considered instead of TA as the second input variable for CO2SYS. Using an input combination of one T, P-dependent (pH or fCO₂) and one non-dependent (DIC or TA) variable provides lower bias uncertainty for CO2SYS outputs (Raimondi et al., 2019). The distribution of data through time is also considered in the estimation of the uncertainties. Our time-varying uncertainties are smaller in the presence of observations, and larger in the data gaps. This is seen in Figure 7 where there are vertical bands of lower uncertainty at times when observations are present. Our results were on monthly time steps, but any interval could be used that is deemed reasonable given the observation distribution. If the gaps between observations are large (i.e. more than a year) then the state estimate will have flat unchanging sections between observations due to the Kalman filter based estimation procedure.

The mean and variance of the carbonate state are not constant over time due to anthropogenic sources of CO₂. DIC observations analyzed using a 1-year sliding window showed that not only is the mean state increasing over time and has inter-annual variability, but the standard deviation (or standard error) of those observations is also increasing over time in the near-surface and shows inter-annual variability for multiple depths (Supplementary Figure S17). This behavior could provide insight into the changes in the DIC seasonal cycle reported by Landschützer et al. (2018). The change of DIC standard error over time could be modelled by having our observation error (${\text{Σ}}_{v,t}$) change over time. Improvements can be made in the estimation of the observation error parameter (${\text{Σ}}_{v,t}$), a key quantity in the analysis.

While the Kalman Smoother is resistant to outliers (i.e. the state estimate does only a blimp towards them and does not go directly to them, Figure 2C), we found it was necessary to remove some extreme outliers. The motivation was because the small blip in our DIC estimates due to an outlier in 2015 around 700 m had a larger impact on our calculated quantities of the Revelle factor, bicarbonate and carbonate, which showed a local maximum at this depth. While no other outliers stood out after the monthly averaging, other suspected outliers in the original GLODAP data were removed as described in the Supplementary Material along with a list of the data and its cruise information.

Spatio-temporal estimates of the carbonate system have been produced by other methods, ranging from machine learning (Bittig et al., 2018) to Earth System Models (Carroll et al., 2020). The leading observation-based method for the estimation of the carbonate system is CANYON-B (Bittig et al., 2018). It uses a Bayesian neural network approach that employs non-linear relationships to estimate monthly spatial climatologies of the four carbonate variables and nutrients. Machine Learning methods are dependent on the data they are trained on. CANYON-B may find limitations in the training of their model in regions like the Labrador Sea, where the data has been mostly collected at the same time each year (e.g. AR7W from Labrador to Greenland each May). The CANYON-B framework employs year-to-year correlation whereas our method uses more localized time correlation (month-to-month). For validation of results, it is common to train the model on one data source (like GLODAP) and test on another (i.e. SOCAT or ARGO) (Bittig et al., 2018). Meanwhile, ECCO-Darwin (Carroll et al., 2020) used multiple data sources (i.e. GLODAP, SOCAT, ARGO) as observational constraints for their Earth System Model. Iida et al. (2020) also used multiple data sources (GLODAP, SOCAT, Satelite Data) with multiple linear regression and chemical relationships to estimate the carbonate system. Using multiple data inputs was a feature we also implemented in our observation-centric framework.

Our results yield time-varying uncertainties that are on average 64-71% lower compared to time independent methods such as calculations with CO2SYS on independent observations (see Table 1). There are multiple metrics for uncertainties. The time-varying uncertainties are defined as 95% confidence intervals that are calculated as part of the statistical model using the Kalman smoother algorithm. The time-independent CO2SYS calculates uncertainties using Gaussian propagation (Orr et al., 2018). From our method for the years 1993-2016, the carbonate system variables have the following average uncertainties: 5.14 µmol kg⁻¹ for DIC, 4.51 µmol kg⁻¹ for TA, 0.005 for pH and 8.36 µatm for fCO₂. When CO2SYS is used on time-independent observations, the estimated pH has an average uncertainty of 0.03 and fCO₂ uncertainty of 24 µatm. Carter et al. (2021) estimated spatial climatologies for the carbonate system using a mixed estimation of linear regression method (i.e. LIRv3) and neural networks, and in the North Atlantic their uncertainties averaged: 7.7 µmol kg⁻¹ for DIC, 5.0 µmol kg⁻¹ for TA, and 0.009 for pH. The neural network based Canyon-B uncertainty estimates averaged at: 8.6 µmol kg⁻¹ for DIC, 5.7 µmol kg⁻¹ for TA, and 0.008 for pH. Compared to our uncertainties, Carter et al. (2021) and Bittig et al. (2018) are slightly larger for DIC and lower for TA, but overall they are comparable values.

Our pH in the top 20 m shows the acidification in the Labrador Sea at a rate of 0.0009 year⁻¹, which is almost half the rate of other studies of the Labrador Sea of -0.0014 to -0.0016 year⁻¹ (Chau et al., 2024), meanwhile our sub-surface waters do have more comparable rates of -0.0015 to -0.0018 year⁻¹. With the large variance of surface pH observations, the signal-to-noise ratio is much higher in the surface waters than interior ocean (Figures 4B, C). This large observation variance paired with sporadic pH GLODAP observations, means our results are showing a steady decline as opposed to a seasonal cycle, as reported in the neighboring Irminger Sea, Bates et al. (2014) that peaks in the summer and spans 8.07 to 8.15 for years 1982-2006. The pseudo-observations we calculate for in the surface layer have larger uncertainty than the direct observations, which already have large variability themselves. This is an issue for pH and the fCO₂ seasonal cycle has a smaller amplitude than expected. A limitation of using pseudo-observations in the surface is that they add more uncertainty to a system, making it harder to distinguish process-driven variability like seasonal cycles from natural noise of observation; a limitation that other methods overcome by using global climatologies within their analysis. While the pseudo-observations have their surface limitations, their use in sub-surface hints at inter-annual variability, with a slow acidification between 2004 and 2010 before resuming (Supplementary Figure S12), though further analysis with more data should be performed.

Our estimated time series for the carbonate system in the Labrador Sea produces comparable results to others (Chau et al., 2024; Feely et al., 2023; Gregor and Gruber, 2021). The average across time of our near-surface layer is summarized in Table 2. The other studies ran global analyses but by extracting the Labrador Sea from their results, we find our DIC, TA, fCO₂, aragonite saturation and calcite saturation are close or overlapped with their values. Our average surface pH of 8.16 is on the high end of the other studies. These studies we compare with overlap in time span, and overlap with data inputs. Gregor and Gruber (2021) uses GLODAP TA, SOCAT pCO₂ and global climatologies to calculate the other variables using CO2SYS and Geospatial Random Cluster Ensemble Regression. Chau et al. (2024) uses SOCAT fCO₂, pCO₂ climatology and CMEMS data in CO2SYS and a neural network ensemble approach (CMEMS-LSCE-FFNN). Feely et al. (2023) uses SOCAT and DIC, TA and pH from GLODAP and the Common Online Data Analysis Platform in North America (CODAP-NA) and pools all into one observational database before it was interpolated using Data Interpolating Variational Analysis.

Table 2

Table 2. Average over time for near-surface carbonate variables for this study are compared against three other studies where the Labrador Sea values are extracted from presented results: Gregor and Gruber (2021) see their Figure 10, Chau et al. (2024) see their Figures 3, 6, 9, and A5 and Feely et al. (2023) see their Figures 3-5.

Our average TA results below 100 m were 2302 µmol kg⁻¹, which is the same as Broullón et al. (2019) reported for an annual mean TA in the Labrador Sea for X based on GLODAPv2.2019 data. In the surface layer, Broullón et al. (2019) reports a TA of 2300 µmol kg⁻¹, but our estimated TA is lower at 2278 µmol kg⁻¹. The variability seen in TA is correlated with salinity, as confirmed by the salinity-normalized TA (Figure 5). The freshening of the Labrador Sea in this timeframe has not been shown before, actually it has been described as having no change while the eastern North Atlantic in the 2010s had a notable freshening and cooling event (Holliday et al., 2020). We see cooler surface waters in the Labrador Sea in the 2010s compared to 2000s and these cooler waters are suggested to play a role in this eastern freshening Fox et al. (2022). But returning to the Labrador Sea, the freshening we see as of 2006 comes earlier than expected, as an ocean simulation has estimated around 13 years for the subpolar North Atlantic to adjust to the increase of annual Greenland freshwater discharge which increased as of 2000 (Dukhovskoy et al., 2021). Ocean simulations have also shown that freshwater from the Arctic could cause freshening in the Labrador Sea (Zhang et al., 2021).

Using an Earth System model, Jiang et al. (2019) predicts surface pH changing from 8.1 to 7.75 for 2000 to 2100 Jiang et al. (2019), see their Figure 6), implying a declining pH of 0.0035 year⁻¹, 4 times larger than our estimate. For a surface Revelle factor in the year 2000, our results agree with (Jiang et al., 2019) that the Revelle factor is around 15 in the Labrador Sea. Our aragonite saturation horizon in 2004 is found at 2370 m, which is very close to the 2300 m reported by Azetsu-Scott et al. (2010) using 2003-2005 Labrador Sea data. Our max increase of aragonite saturation horizon of 440 m from 1993-2016 agrees with Tanhua et al. (2007) who reported a 400 m increase in the North Atlantic from pre-industrial to 2004 and projected a 700 m increase from pre-industrial to 2050. The aragonite saturation horizon is increasing at a faster rate in the North Atlantic than in the Pacific, which was reported to have increased at 1-2 m year⁻¹ (Feely et al., 2012).

Carbonate (CO₃^–2) is rarely discussed in observation-based work. Using CO2SYS to calculate carbonate from our DIC and TA, our carbonate estimate for the year 1994 is 143 µmol kg⁻¹ in the top 20 m, which is similar to Orr et al. (2005), whose biogeochemical model estimated an average surface carbonate to be around 160 µmol kg⁻¹ at 60°N for the year 1994, and our 2010 carbonate estimate of 134 µmol kg⁻¹ is similar to the 120-140 µmol kg⁻¹ Jiang et al. (2023) estimated for the Labrador Sea. Our near-surface carbonate has a seasonal cycle but also a declining trend of -1.06 µmol kg⁻¹ year⁻¹ (intercept of 151.1), projected forward to the year 2100 would yield a carbonate value of 38 µmol kg⁻¹, which is close to the SSP3-7.0 projections of Jiang et al. (2023) (see their Figure 8).

Examining the individual time series of DIC for each depth (Supplementary Figure S10) we see the effects of the Pinatubo 1991 eruption. Our estimated DIC below 1800 m is unchanging in the 1990s and increasing after 2000. These deep-water results are consistent with anthropogenic carbon results in Boteler et al. (2023) and has since been shown by Olivarez et al. (2024) that the Pinatubo 1991 eruption had a delayed effect of not showing an increase in ocean carbon until after the year 2000 (using pCFC-12). This temporal pattern of an unchanging 1990s and increase after 2000 was also reported for our DIC between 200-800 m, which may have a separate biological reason for our oxygen results at those depths are also showing a change in trend around the year 2000. A longer time series would help in de-tangling its processes for the various depths, as this multi-decadal variability might also be in the surface layers but hidden within the seasonal cycle. The near-surface DIC as well as oxygen also have a 4-year cycle that seems related to the North Atlantic Oscillation (NAO) and Atlantic Multidecadal Oscillation (AMO).

The fCO₂ in the near-surface was estimated to be increasing at a rate of 1.48 µatm year⁻¹. This is lower than the atmospheric CO₂ increase of ∼1.9 µatm year⁻¹ but the same as other observation based estimates for the surface North Atlantic of 1.47 ±0.06 µatm year⁻¹ for years 1992-2014 (Lebehot et al., 2019) and Atlantic increase of 1.67 ±0.02 µatm year⁻¹ for years 1990-2018 (Gregor and Gruber, 2021). The near-surface fCO₂ values always remain below atmospheric partial pressure and with the ocean increasing at a slower rate, the gradient between atmospheric and ocean CO₂ is increasing. Moving to the deeper waters, sub-surface measurements of fCO₂ are rare, but they could prove useful for tracking the anthropogenic increase of CO₂ in the ocean. While DIC is a popular choice for estimating the anthropogenic change in the ocean interior, fCO₂ has a lower range of values and variability through the water column than DIC, making it more sensitive to anthropogenic changes through time and easier to identify variations within the ocean interior. Similar temporal variability to fCO₂ was also seen in the Revelle factor, which is described as the sensitivity of fCO₂ to the changes in DIC, and has been used to infer anthropogenic carbon in the ocean interior. The Revelle factor showed a steady rate of increase in the waters deeper than 100 m (Figure 6D). More sub-surface measurements of fCO₂ would be useful to further investigate the Revelle factor and fCO₂ and how their roles in quantifying anthropogenic change are distinctive or overlapping.

6 Conclusion

In summary, we present an observation-centric method to estimate the mean state carbonate system and its uncertainties for the Labrador Sea for the period of 1993-2016. The state space model framework allowed for the multivariate estimation of the carbonate system, and for the fusion of multiple data sources: GLODAP cruise data, SOCAT ships of opportunity, and calculated pseudo-observations via CO2SYS. Our analysis focused on estimating time-depth distributions and temporal trends at multiple depth layers through the water column in the Labrador Sea for carbonate system variables. Our analysis was transparent, making no assumptions or model constraints on the variables to let the data drive the estimation, the changes over time, the uncertainties, and thus the story of the carbonate system.

Data availability statement

Our carbonate system time series data product created in this study is freely available at https://doi.org/10.17632/jzp4dz77t4.1. Three data sources were used in this work and are available online. GLODAPv2.2022 data product (Lauvset et al., 2022; Olsen et al., 2016; Key et al., 2015) with data available at https://doi.org/10.25921/1f4w-0t92. SOCATv2022 data product (Bakker et al., 2016) with data available at https://www.socat.info/index.php/data-access/. BGC-ARGO (Bittig et al., 2019) has information regarding its data access at https://biogeochemical-argo.org/data-access.php, but we accessed the data via the R package argoFloats (Kelley et al., 2022a). For comparison we also used the North Atlantic Oscillation (NAO) Index values NAO (North Atlantic Oscillation, 2020) at https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/norm.nao.monthly.b5001.current.ascii and the Atlantic Multidecadal Oscillation (AMO) (AMO, 2020) at https://psl.noaa.gov/data/timeseries/AMO/. Some GLODAP were identified and removed as potential outliers, and a data file of the list is available in the Supplemental Material.

Author contributions

CB: Conceptualization, Formal analysis, Methodology, Visualization, Writing – original draft, Writing – review & editing. MD: Conceptualization, Funding acquisition, Supervision, Writing – review & editing. EO: Conceptualization, Funding acquisition, Supervision, Writing – review & editing. DW: Conceptualization, Funding acquisition, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Funding for this research was provided by the Ocean Frontier Institute, an NSERC Discovery Grant and an Nova Scotia Graduate Scholarship.

Acknowledgments

We would like to acknowledge Ricardo Arruda and Dariia Atamanchuk for their many helpful discussions about the carbonate system. We would also like to acknowledge the three data projects that were fundamental to this work: GLODAP, SOCAT and BGC-ARGO. The Global Ocean Data Analysis Project (GLODAP) is a synthesis activity for ocean surface to bottom biogeochemical data collected through chemical analysis of water samples. GLODAP is publicly available, discoverable, and citable. GLODAP enables quantification of the ocean carbon sink, ocean acidification and evaluation of ocean biogeochemical models. The Surface Ocean CO₂ Atlas (SOCAT) is an international effort, endorsed by the International Ocean Carbon Coordination Project (IOCCP), the Surface Ocean Lower Atmosphere Study (SOLAS) and the Integrated Marine Biosphere Research (IMBeR) program, to deliver a uniformly quality-controlled surface ocean CO₂ database. The many researchers and funding agencies responsible for the collection of data and quality control are thanked for their contributions to SOCAT. The BGC-ARGO data were collected and made freely available by the International Argo Program and the national programs that contribute to it. (https://argo.ucsd.edu, https://www.ocean-ops.org). The Argo Program is part of the Global Ocean Observing System.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1500225/full#supplementary-material

References

(2020). North Atlantic Oscillation (NAO). (Maryland, USA: NOAA National Weather Service - Climate Prediction Center). Available online at: https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/nao.shtml (Accessed 2020).

Google Scholar

Álvarez M., Fajar N. M., Carter B. R., Guallart E. F., P´erez F. F., Woosley R. J., et al. (2020). Global ocean spectrophotometric pH assessment: consistent inconsistencies. Environ. Sci. Technol. 54, 10977–10988. doi: 10.1021/acs.est.9b06932

PubMed Abstract | Crossref Full Text | Google Scholar

AMO (2020). AMO (Atlantic Multidecadal Oscillation) Index. (Boulder, Colorado, USA: NOAA Physical Sciences Laboratory). Available online at: https://psl.noaa.gov/data/timeseries/AMO/ (Accessed 2020).

Google Scholar

Anderson B. D. O., Moore J. B. (1979). Optimal Filtering. Prentice-Hall Information and System Sciences Series (Englewood Cliffs, N.J: Prentice-Hall).

Google Scholar

Arruda R., Atamanchuk D., Boteler C., Wallace D. W. R. (2024). Seasonality of pCO₂ and air-sea CO₂ fluxes in the Central Labrador Sea. Front. Mar. Sci. 11. doi: 10.3389/fmars.2024.1472697

Crossref Full Text | Google Scholar

Azetsu-Scott K., Clarke A., Falkner K., Hamilton J., Jones E. P., Lee C., et al. (2010). Calcium carbonate saturation states in the waters of the Canadian Arctic Archipelago and the Labrador Sea. J. Geophysical Res.: Oceans 115, 2009JC005917. doi: 10.1029/2009JC005917

Crossref Full Text | Google Scholar

Bakker D., Gritzalis T., Kadono K., Kozyr A., Lauvset S. K., Metzl N., et al. (2022). Surface Ocean CO₂ Atlas Database Version 2022 (SOCATv2022) (NCEI Accession 0253659). doi: 10.25921/1h9f-nb73

Crossref Full Text | Google Scholar

Bakker D. C. E., Pfeil B., Landa C. S., Metzl N., O’Brien K. M., Olsen A., et al. (2016). A multi-decade record of high-quality fCO₂ data in version 3 of the Surface Ocean CO₂ Atlas (SOCAT). Earth System Sci. Data 8, 383–413. doi: 10.5194/essd-8-383-2016

Crossref Full Text | Google Scholar

Bates N., Astor Y., Church M., Currie K., Dore J., González-Dávila M., et al. (2014). A time-series view of changing ocean chemistry due to ocean uptake of anthropogenic CO2 and ocean acidification. Oceanography 27, 126–141. doi: 10.5670/oceanog.2014.16

Crossref Full Text | Google Scholar

Becker R. A., Wilks A. R., Brownrigg R., Minka T. P., Deckmyn A. (2021). Maps: Draw Geographical Maps. CRAN R package version 3.4.0.

Google Scholar

Bennington V., Gloege L., McKinley, G A. (2022). Variability in the global ocean carbon sink from 1959 to 2020 by correcting models with observations. Geophysical Res. Lett. 49, e2022GL098632. doi: 10.1029/2022GL098632

Crossref Full Text | Google Scholar

Bittig H. C., Maurer T. L., Plant J. N., Schmechtig C., Wong A. P. S., Claustre H., et al. (2019). A BGC-argo guide: planning, deployment, data handling and usage. Front. Mar. Sci. 6. doi: 10.3389/fmars.2019.00502

Crossref Full Text | Google Scholar

Bittig H. C., Steinhoff T., Claustre H., Fiedler B., Williams N. L., Sauz`ede R., et al. (2018). An alternative to static climatologies: robust estimation of open ocean CO₂ variables and nutrient concentrations from T, S, and O₂ data using bayesian neural networks. Front. Mar. Sci. 5. doi: 10.3389/fmars.2018.00328

Crossref Full Text | Google Scholar

Boteler C., Dowd M., Oliver E. C. J., Krainski E. T., Wallace D. W. R. (2023). Trends of anthropogenic dissolved inorganic carbon in the northwest Atlantic ocean estimated using a state space model. J. Geophysical Res.: Oceans 128, e2022JC019483. doi: 10.1029/2022JC019483

Crossref Full Text | Google Scholar

Broullón D., Pérez F. F., Velo A., Hoppema M., Olsen A., Takahashi T., et al. (2019). A global monthly climatology of total alkalinity: A neural network approach. Earth System Sci. Data 11, 1109–1127. doi: 10.5194/essd-11-1109-2019

Crossref Full Text | Google Scholar

Broullón D., Pérez F. F., Velo A., Hoppema M., Olsen A., Takahashi T., et al. (2020). A global monthly climatology of oceanic total dissolved inorganic carbon: A neural network approach. Earth System Sci. Data 12, 1725–1743. doi: 10.5194/essd-12-1725-2020

Crossref Full Text | Google Scholar

Carroll D., Menemenlis D., Adkins J. F., Bowman K. W., Brix H., Dutkiewicz S., et al. (2020). The ECCO-darwin data-assimilative global ocean biogeochemistry model: estimates of seasonal to multidecadal surface ocean pCO₂ and air-sea CO₂ flux. J. Adv. Modeling Earth Syst. 12, e2019MS001888. doi: 10.1029/2019MS001888

Crossref Full Text | Google Scholar

Carroll D., Menemenlis D., Dutkiewicz S., Lauderdale J. M., Adkins J. F., Bowman K. W., et al. (2022). Attribution of space-time variability in global-ocean dissolved inorganic carbon. Global Biogeochemical Cycles 36. doi: 10.1029/2021GB007162

PubMed Abstract | Crossref Full Text | Google Scholar

Carter B. R., Bittig H. C., Fassbender A. J., Sharp J. D., Takeshita Y., Xu Y.-Y., et al. (2021). New and updated global empirical seawater property estimation routines. Limnol. Oceanogr.: Methods 19, 785–809. doi: 10.1002/lom3.10461

Crossref Full Text | Google Scholar

Carter B. R., Feely R. A., Mecking S., Cross J. N., Macdonald A. M., Siedlecki S. A., et al. (2017). Two decades of Pacific anthropogenic carbon storage and ocean acidification along Global Ocean Ship-based Hydrographic Investigations Program sections P16 and P02. Global Biogeochemical Cycles 31, 306–327. doi: 10.1002/2016GB005485

Crossref Full Text | Google Scholar

Chau T.-T.-T., Gehlen M., Metzl N., Chevallier F. (2024). CMEMS-LSCE: A global, 0.25°, monthly reconstruction of the surface ocean carbonate system. Earth System Sci. Data 16, 121–160. doi: 10.5194/essd-16-121-2024

Crossref Full Text | Google Scholar

Dickson A. G. (1990). Standard potential of the reaction: AgCl(s) + 12H2(g) = Ag(s) + HCl(aq), and and the standard acidity constant of the ion HSO4- in synthetic sea water from 273.15 to 318.15 K. J. Chem. Thermodynamics 22, 113–127. doi: 10.1016/0021-9614(90)90074-Z

Crossref Full Text | Google Scholar

Du Z., Fang L., Bai Y., Zhang F., Liu R. (2015). Spatio-temporal visualization of air–sea CO2 flux and carbon budget using volume rendering. Comput. Geosciences 77, 77–86. doi: 10.1016/j.cageo.2015.01.004

Crossref Full Text | Google Scholar

Dukhovskoy D., Yashayaev I., Chassignet E., Myers P., Platov G., Proshutinsky A. (2021). Time scales of the Greenland freshwater anomaly in the subpolar North Atlantic. J. Climate. 34, 8971–8987. doi: 10.1175/JCLI-D-20-0610.1

Crossref Full Text | Google Scholar

Feely R., Jiang L.-Q., Wanninkhof R., Carter B., Alin S., Bednaršek N., et al. (2023). Acidification of the global surface ocean: what we have learned from observations. Oceanography. 36, 120–129. doi: 10.5670/oceanog.2023.222

Crossref Full Text | Google Scholar

Feely R. A., Sabine C. L., Byrne R. H., Millero F. J., Dickson A. G., Wanninkhof R., et al. (2012). Decadal changes in the aragonite and calcite saturation state of the Pacific Ocean. Global Biogeochemical Cycles 26, 2011GB004157. doi: 10.1029/2011GB004157

Crossref Full Text | Google Scholar

Fiedler B., Fietzek P., Vieira N., Silva P., Bittig H. C., Körtzinger A. (2013). In situ CO2 and O2 measurements on a profiling float. J. Atmospheric Oceanic Technol. 30, 112–126. doi: 10.1175/JTECH-D-12-00043.1

Crossref Full Text | Google Scholar

Fox A. D., Handmann P., Schmidt C., Fraser N., Rühs S., Sanchez-Franks A., et al. (2022). Exceptional freshening and cooling in the eastern subpolar North Atlantic caused by reduced Labrador Sea surface heat loss. Ocean Sci. 18, 1507–1533. doi: 10.5194/os-18-1507-2022

Crossref Full Text | Google Scholar

Friis K., Körtzinger A., Wallace D. W. R. (2003). The salinity normalization of marine inorganic carbon chemistry data. Geophysical Res. Lett. 30, 57. doi: 10.1029/2002GL015898

Crossref Full Text | Google Scholar

Gattuso J.-P., Epitalon J.-M., Lavigne H., Orr J., Gentili B., Hagens M., et al. (2022). Seacarb: Seawater Carbonate Chemistry.

Google Scholar

Gloege L., Yan M., Zheng T., McKinley G. A. (2022). Improved quantification of ocean carbon uptake by using machine learning to merge global models and pCO2 data. J. Adv. Modeling Earth Syst. 35. doi: 10.1029/2021ms002620

Crossref Full Text | Google Scholar

Gregor L., Gruber N. (2021). OceanSODA-ETHZ: A global gridded data set of the surface ocean carbonate system for seasonal to decadal studies of ocean acidification. Earth System Sci. Data 13, 777–808. doi: 10.5194/essd-13-777-2021

Crossref Full Text | Google Scholar

Grolemund G., Wickham H. (2011). Dates and times made easy with lubridate. J. Stat. Software 40, 1–25. doi: 10.18637/jss.v040.i03

Crossref Full Text | Google Scholar

Gruber N., Clement D., Carter B. R., Feely R. A., van Heuven S., Hoppema M., et al. (2019). The oceanic sink for anthropogenic CO₂ from 1994 to 2007. Science 363, 1193–1199. doi: 10.1126/science.aau5153

PubMed Abstract | Crossref Full Text | Google Scholar

Holliday N. P., Bersch M., Berx B., Chafik L., Cunningham S., Florindo-López C., et al. (2020). Ocean circulation causes the largest freshening event for 120 years in eastern subpolar North Atlantic. Nat. Commun. 11, 585. doi: 10.1038/s41467-020-14474-y

PubMed Abstract | Crossref Full Text | Google Scholar

Humphreys M. P., Schiller A. J., Sandborn D., Gregor L., Pierrot D., van Heuven, et al. (2023). PyCO2SYS: Marine carbonate system calculations in Python. doi: 10.5281/ZENODO.3744275

Crossref Full Text | Google Scholar

Iida Y., Takatani Y., Kojima A., Ishii M. (2020). Global trends of ocean CO2 sink and ocean acidification: An observation-based reconstruction of surface ocean inorganic carbon variables. J. Oceanogr. 77, 323–358. doi: 10.1007/s10872-020-00571-5

Crossref Full Text | Google Scholar

Jiang L.-Q., Carter B. R., Feely R. A., Lauvset S. K., Olsen A. (2019). Surface ocean pH and buffer capacity: Past, present and future. Sci. Rep. 9, 18624. doi: 10.1038/s41598-019-55039-4

PubMed Abstract | Crossref Full Text | Google Scholar

Jiang L.-Q., Dunne J., Carter B. R., Tjiputra J. F., Terhaar J., Sharp J. D., et al. (2023). Global surface ocean acidification indicators from 1750 to 2100. J. Adv. Modeling Earth Syst. 15, e2022MS003563. doi: 10.1029/2022MS003563

Crossref Full Text | Google Scholar

Kelley D., Harbin J., Dunnington D., Richards C. (2022a). argoFloats: Analysis of Oceanographic Argo Floats.

Google Scholar

Kelley D., Richards C., Layton C., British Geological Survey. (2022b). Oce: Analysis of Oceanographic Data.

Google Scholar

Key R. M., Olsen A., van Heuven S., Lauvset S. K., Velo A., Schirnick C., et al. (2015). Global Ocean Data Analysis Project, Version 2 (GLODAPv2). Tech. rep.

Google Scholar

Landschützer P., Gruber N., Bakker D. C. E. (2016). Decadal variations and trends of the global ocean carbon sink. Global Biogeochemical Cycles 30, 1396–1417. doi: 10.1002/2015GB005359

Crossref Full Text | Google Scholar

Landschützer P., Gruber N., Bakker D. C. E., Schuster U., Nakaoka S., Payne M. R., et al. (2013). A neural network-based estimate of the seasonal to inter-annual variability of the Atlantic Ocean carbon sink. Biogeosciences 10, 7793–7815. doi: 10.5194/bg-10-7793-2013

Crossref Full Text | Google Scholar

Landschützer P., Gruber N., Bakker D. C. E., Stemmler I., Six K. D. (2018). Strengthening seasonal marine CO2 variations due to increasing atmospheric CO2. Nat. Climate Change 8, 146–150. doi: 10.1038/s41558-017-0057-x

Crossref Full Text | Google Scholar

Lauvset S. K., Gruber N., Landschützer P., Olsen A., Tjiputra J. (2015). Trends and drivers in global surface ocean pH over the past 3 decades. Biogeosciences 12, 1285–1298. doi: 10.5194/bg-12-1285-2015

Crossref Full Text | Google Scholar

Lauvset S. K., Key R. M., Olsen A., van Heuven S., Velo A., Lin X., et al. (2016). A new global interior ocean mapped climatology: The 1×1 GLODAP version 2. Earth System Sci. Data 8, 325–340. doi: 10.5194/essd-8-325-2016

Crossref Full Text | Google Scholar

Lauvset S. K., Lange N., Tanhua T., Bittig H. C., Olsen A., Kozyr A., et al. (2021). An updated version of the global interior ocean biogeochemical data product, GLODAPv2.2021. Earth System Sci. Data 13, 5565–5589. doi: 10.5194/essd-13-5565-2021

Crossref Full Text | Google Scholar

Lauvset S. K., Lange N., Tanhua T., Bittig H. C., Olsen A., Kozyr A., et al. (2022). GLODAPv2.2022: The latest version of the global interior ocean biogeochemical data product. Earth System Sci. Data 14, 5543–5572. doi: 10.5194/essd-14-5543-2022

Crossref Full Text | Google Scholar

Lebehot A. D., Halloran P. R., Watson A. J., McNeall D., Ford D. A., Landschützer P., et al. (2019). Reconciling observation and model trends in North Atlantic surface CO ₂. Global Biogeochemical Cycles 33, 1204–1222. doi: 10.1029/2019GB006186

Crossref Full Text | Google Scholar

Lewis E. R., Wallace D. W. R. (1998). Program Developed for CO2 System Calculations. Carbon Dioxide Information Analysis Center Oak Ridge National Laboratory, Oak Ridge, Tennessee. doi: 10.3334/CDIAC/otg.CO2SYSDOSCDIAC105

Crossref Full Text | Google Scholar

Longhurst A. (2007). Ecological Geography of the Sea (Elsevier). doi: 10.1016/B978-0-12-455521-1

Crossref Full Text | Google Scholar

Lueker T. J., Dickson A. G., Keeling C. D. (2000). Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: Validation based on laboratory measurements of CO2 in gas and seawater at equilibrium. Mar. Chem. 70, 105–119. doi: 10.1016/S0304-4203(00)00022-0

Crossref Full Text | Google Scholar

Mackay N., Watson A. J. (2021). Winter air-sea CO2 fluxes constructed from summer observations of the polar southern ocean suggest weak outgassing. J. Geophysical Res. 126. doi: 10.1029/2020jc016600

Crossref Full Text | Google Scholar

Middelburg J. J., Soetaert K., Hagens M. (2020). Ocean alkalinity, buffering and biogeochemical processes. Rev. Geophysics 58, e2019RG000681. doi: 10.1029/2019RG000681

PubMed Abstract | Crossref Full Text | Google Scholar

Millero F. J. (2007). The marine inorganic carbon cycle. Chem. Rev. 107, 308–341. doi: 10.1021/cr0503557

PubMed Abstract | Crossref Full Text | Google Scholar

Müller J. D., Gruber N., Carter B., Feely R., Ishii M., Lange N., et al. (2023). Decadal trends in the oceanic storage of anthropogenic carbon from 1994 to 2014. AGU Adv. 4, e2023AV000875. doi: 10.1029/2023AV000875

Crossref Full Text | Google Scholar

Nychka D., Furrer R., Paige J., Sain S., Gerber F., Iverson M., et al. (2022). Fields: Tools for Spatial Data.

Google Scholar

Olivarez H. C., Lovenduski N. S., Eddebbar Y. A., Fay A. R., McKinley G. A., Levy M. N., et al. (2024). How does the pinatubo eruption influence our understanding of long-term changes in ocean biogeochemistry? Geophysical Res. Lett. 51, e2023GL105431. doi: 10.1029/2023GL105431

Crossref Full Text | Google Scholar

Olsen A., Key R. M., van Heuven S., Lauvset S. K., Velo A., Lin X., et al. (2016). The Global Ocean Data Analysis Project version 2 (GLODAPv2) – an internally consistent data product for the world ocean. Earth System Sci. Data 8, 297–323. doi: 10.5194/essd-8-297-2016

Crossref Full Text | Google Scholar

Olsen A., Lange N., Key R. M., Tanhua T., Bittig H. C., Kozyr A., et al. (2020). An updated version of the global interior ocean biogeochemical data product, GLODAPv2.2020. Earth System Sci. Data 12, 3653–3678. doi: 10.5194/essd-12-3653-2020

Crossref Full Text | Google Scholar

Orr J. C., Epitalon J.-M., Dickson A. G., Gattuso J.-P. (2018). Routine uncertainty propagation for the marine carbon dioxide system. Mar. Chem. 207, 84–107. doi: 10.1016/j.marchem.2018.10.006

Crossref Full Text | Google Scholar

Orr J. C., Fabry V. J., Aumont O., Bopp L., Doney S. C., Feely R. A., et al. (2005). Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nature 437, 681–686. doi: 10.1038/nature04095

PubMed Abstract | Crossref Full Text | Google Scholar

Perez F. F., Fraga F. (1987). Association constant of fluoride and hydrogen ions in seawater. Mar. Chem. 21, 161–168. doi: 10.1016/0304-4203(87)90036-3

Crossref Full Text | Google Scholar

Raimondi L., Matthews J. B. R., Atamanchuk D., Azetsu-Scott K., Wallace D. W. R. (2019). The internal consistency of the marine carbon dioxide system for high latitude shipboard and in situ monitoring. Mar. Chem. 213, 49–70. doi: 10.1016/j.marchem.2019.03.001

Crossref Full Text | Google Scholar

Raimondi L., Tanhua T., Azetsu-Scott K., Yashayaev I., Wallace D. (2021). A 30 -year time series of transient tracer-based estimates of anthropogenic carbon in the central Labrador Sea. J. Geophysical Res.: Oceans 126, e2020JC017092. doi: 10.1029/2020JC017092

Crossref Full Text | Google Scholar

Rastrick S. S. P., Graham H., Azetsu-Scott K., Calosi P., Chierici M., Fransson A., et al. (2018). Using natural analogues to investigate the effects of climate change and ocean acidification on Northern ecosystems. ICES J. Mar. Sci. 75, 2299–2311. doi: 10.1093/icesjms/fsy128

Crossref Full Text | Google Scholar

R Core Team (2021). R: A Language and Environment for Statistical Computing. R version 4.1.3.

Google Scholar

Rödenbeck C., Keeling R. F., Bakker D. C. E., Metzl N., Olsen A., Sabine C., et al. (2013). Global surface-ocean pCO₂ and sea-air CO₂ flux variability from an observation-driven ocean mixed-layer scheme. Ocean Sci. 9, 193–216. doi: 10.5194/os-9-193-2013

Crossref Full Text | Google Scholar

RStudio Teams (2022). RStudio: Integrated Development Environment for R. Version 2022.02.1.

Google Scholar

Sabine C. L., Feely R. A., Gruber N., Key R. M., Lee K., Bullister J. L., et al. (2004). The oceanic sink for anthropogenic CO₂. Science 305, 367–371. doi: 10.1126/science.1097403

PubMed Abstract | Crossref Full Text | Google Scholar

Sarmiento J. L., Gruber N. (2006). Ocean biogeochemical Dynamics (Princeton: Princeton University Press).

Google Scholar

Sauzède R., Bittig H. C., Claustre H., Pasqueron de Fommervault O., Gattuso J.-P., Legendre L., et al. (2017). Estimates of water-column nutrient concentrations and carbonate system parameters in the global ocean: A novel approach based on neural networks. Front. Mar. Sci. 4. doi: 10.3389/fmars.2017.00128

Crossref Full Text | Google Scholar

Sharp J. D., Pierrot D., Humphreys M. P., Epitalon J.-M., Orr J. C., Lewis E. R., et al. (2020). CO2SYSv3 for MATLAB. doi: 10.5281/ZENODO.3950563

Crossref Full Text | Google Scholar

Takahashi T., Sutherland S., Chipman D., Goddard J., Ho C., Newberger T., et al. (2014). Climatological distributions of pH, pCO2, total CO2, alkalinity, and CaCO3 saturation in the global surface ocean, and temporal changes at selected locations. Mar. Chem. 164, 95–125. doi: 10.1016/j.marchem.2014.06.004

Crossref Full Text | Google Scholar

Takahashi T., Sutherland S. C., Sweeney C., Poisson A., Metzl N., Tilbrook B., et al. (2002). Global sea–air CO₂ flux based on climatological surface ocean pCO₂, and seasonal biological and temperature effects. Deep Sea Res. Part II: Topical Stud. Oceanogr. 49, 1601–1622. doi: 10.1016/S0967-0645(02)00003-6

Crossref Full Text | Google Scholar

Tanhua T., Kortzinger A., Friis K., Waugh D. W., Wallace D. W. R. (2007). An estimate of anthropogenic CO₂ inventory from decadal changes in oceanic carbon content. Proc. Natl. Acad. Sci. 104, 3037–3042. doi: 10.1073/pnas.0606574104

PubMed Abstract | Crossref Full Text | Google Scholar

Terhaar J., Frölicher T. L., Joos F. (2022). Observation-constrained estimates of the global ocean carbon sink from Earth system models. Biogeosciences 19, 4431–4457. doi: 10.5194/bg-19-4431-2022

Crossref Full Text | Google Scholar

Thomson D. J. (1982). Spectrum estimation and harmonic analysis. Proc. IEEE 70, 1055–1096. doi: 10.1109/PROC.1982.12433

Crossref Full Text | Google Scholar

Thyng K., Greene C., Hetland R., Zimmerle H., DiMarco S. (2016). True colors of oceanography: guidelines for effective and accurate colormap selection. Oceanography 29, 9–13. doi: 10.5670/oceanog.2016.66

Crossref Full Text | Google Scholar

Uppström L. R. (1974). The boron/chlorinity ratio of deep-sea water from the Pacific Ocean. Deep Sea Res. Oceanographic Abstracts 21, 161–162. doi: 10.1016/0011-7471(74)90074-6

Crossref Full Text | Google Scholar

Wickham H., Seidel D. (2021). Scales: Scale Functions for Visualization. CRAN R package version 1.1.1.

Google Scholar

Yasunaka S., Kouketsu S., Strutton P., Sutton A., Murata A., Nakaoka S., et al. (2019). Spatio-temporal variability of surface water pCO₂ and nutrients in the tropical Pacific from 1981 to 2015. Deep Sea Res. Part II: Topical Stud. Oceanogr. 169–170, 104680. doi: 10.1016/j.dsr2.2019.104680

Crossref Full Text | Google Scholar

Zeng J., Nojiri Y., Landschützer P., Telszewski M., Nakaoka S. (2014). A global surface ocean fCO₂ climatology based on a feed-forward neural network. J. Atmospheric Oceanic Technol. 31, 1838–1849. doi: 10.1175/JTECH-D-13-00137.1

Crossref Full Text | Google Scholar

Zhang J., Weijer W., Steele M., Cheng W., Verma T., Veneziani M. (2021). Labrador Sea freshening linked to Beaufort Gyre freshwater release. Nat. Commun. 12, 1229. doi: 10.1038/s41467-021-21470-3

PubMed Abstract | Crossref Full Text | Google Scholar