Numerical investigation of the effective receptive field and its relationship with convolutional kernels and layers in convolutional neural network

The receptive field (RF) plays a crucial role in convolutional neural networks (CNNs) because it determines the amount of input information that each neuron in a CNN can perceive, which directly affects the feature extraction ability. As the number of convolutional layers in CNNs increases, there is a decay of the RF according to the two-dimensional Gaussian distribution. Thus, an effective receptive field (ERF) can be used to characterize the available part of the RF. The ERF is calculated by the kernel size and layer number within the neural network architecture. Currently, ERF calculation methods are typically applied to single-channel input data that are both independent and identically distributed. However, such methods may result in a loss of effective information if they are applied to more general (i.e., multi-channel) datasets. Therefore, we proposed a multi-channel ERF calculation method. By conducting a series of numerical experiments, we determined the relationship between the ERF and the convolutional kernel size in conjunction with the layer number. To validate the new method, we used the recently published global wave surrogate model for climate simulation (GWSM4C) and its accompanying dataset. According to the newly established relationship, we refined the kernel size and layer number in each neural network of the GWSM4C to produce the same ERF but lower RF attenuation rates than those of the original version. By visualizing the gradient map at several points in West African and East Pacific areas, the high gradient value regions confirmed the known swell sources, which indicated effective feature extraction in these areas. Furthermore, the new version of the GWSM4C yielded better prediction accuracy for significant wave height in global swell pools. The root mean square errors in the West African and East Pacific regions reduced from approximately 0.3 m, in the original model to about 0.15 m, in the new model. Moreover, these improvements were attributed to the higher efficiency of the newly modified neural network structure that allows the inclusion of more historical winds while maintaining acceptable computational consumption.

1 Introduction

With the rapid development of deep learning, deep neural network models have achieved significant achievements in artificial intelligence (Ng et al., 2023). Convolutional neural networks (CNNs) are a type of deep feedforward network characterized by local connections and weight sharing (LeCun et al., 1989). They have been applied extensively to various algorithmic structures and domains, such as computer vision, image processing, semantic segmentation, and time series prediction (Gu et al., 2017). CNNs are composed of convolutional, pooling, and fully connected layers. Among these, the convolutional layer can perform local operations on input data via convolutional kernels to extract features. Each convolutional kernel moves across input datasets through a sliding window to generate feature maps. These feature maps signify abstract representations of certain characteristics. As the network deepens, these representations become increasingly complex and abstract, which facilitates the learning of nonlinear features.

The concept of the receptive field (RF) is crucial to the application and development of CNNs because the size of the RF directly affects the performance of CNNs (Duffy and Hubel, 2007; Chen et al., 2021). The RF typically refers to the projection area of neurons in a CNN layer of the original input data. As the number of network layers increases, the RF of subsequent layers becomes larger. The size of RF impacts the understanding and processing of the input datasets of a CNN. A smaller RF range is suited to capturing smaller spatial extent and other detailed information, whereas a larger RF captures contextual information with a wider spatial range and larger scope, which is important for understanding the complex structures and global information within an image. Therefore, different RF sizes can help CNNs to better capture features at different levels, which allows the network to perform well in tasks.

The RF range is determined by several factors: the size of the convolutional kernel, stride (convolutional steps), and pooling. In some tasks, a degree of feature information is lost in several strides or pooling. It is generally beneficial for the model to obtain a larger RF by increasing the number of layers in the convolutional neural network (i.e., by performing multiple convolution operations), increasing the size of the convolutional kernel, and using dilated convolution (Lei et al., 2019; Akhtar and Ragavendran, 2020). Theoretically, if the size of the convolutional kernel is constant during the training process, the RF will grow linearly with the number of convolutional layers.

However, some numerical experiments have found that the RF gradually decreases as the convolutional layer number increases (Gilbert and Wiesel, 1992; Lee, 1996; Schwartz et al., 2012). In these studies, they determined that all pixel points within the range have different contribution distributions. Therefore, there was some degree of attenuation of the RF for the CNNs. To characterize the decay process of the RF and determine the actual RF size, the concept of Effective Receptive Fields (ERFs) was proposed, which describes the effective range of influence of the input on the output (Luo et al., 2016). The variation of the target point output value on the different pixel points of the input part was investigated in a series of experiments using single-channel independent and identically distributed (IID) sample data, and the gradient value of the pixel points within 95.45% of the image (i.e., 2σ) was defined as the radius of the ERF. The contribution of different pixel points largely obeys a Gaussian distribution. But in the actual tasks, it is difficult to obtain single-channel and IID sample datasets (Zhou et al., 2017). For example, the color image processing task usually has three (i.e., R, G, and B) channels, and there will also be more than one channel when the datasets contain multiple variable features in certain scenarios.

In this study, we propose a new method to calculate ERF based on multi-channel and non-IID datasets. Specifically, the effective gradient range was modified according to the Gaussian distribution to determine the proportion of valid sample points within a larger confidence interval. Applying the method to GWSM4C (Jin et al., 2024), which is a fully convolutional neural network with a non-IID datasets. We optimized the GWSM4C model according to the new calculation method of ERF. Its practicality was verified by the characteristics of oceanic swell pools reported in previous studies and the final simulation effect of the model. Meanwhile, the structure of the improved model designed by the method we proposed is simpler and the running efficiency of the model is promoted.

The following sections are organized as follows. Section 2 details the calculation method for the multi-channel ERF. The variation in the ERF for different convolutional layers and kernel sizes is also provided in this section. The application of the proposed method in GWSM4C is described in Section 3. Section 4 details the results of the effective range of the gradient maps for the verification of swell characteristics and the simulation results for global SWH. In Section 5, the definition of the effective scope is discussed, followed by the conclusions in Section 6.

2 Multi-channel ERF for CNNs

2.1 Background

The growth rate of the RF decreases as the number of convolutional layers increases. The ERF can portray the actual size of the RF and its decay process. With IID single-channel sample data, the decay trend of the RF is thought to obey the Gaussian distribution by portraying the change of the target point to different pixel points in the inputs. The gradient values of the pixel points in the input within 95.45% of the image (2σ) are defined as the radius of the ERF.

The contribution distribution (i.e., gradient values) of all pixel points is considered when inscribing the ERF. These gradient values are calculated from the weights of the convolution kernels. For example, for a one-dimensional convolutional kernel, each kernel signal is denoted as.

$\begin{array}{ll}\ker ={\displaystyle \sum _{m=0}^{k-1}\omega (q)\delta (t-q),\delta (t)=\{\begin{array}{l}1,t=0,\\ 0,t\ne 0.\end{array}}& (1)\end{array}$

where k denotes the kernel size, $\omega$is the value of the convolution kernel, and q denotes the position of each number in a convolutional kernel. The output of the model is obtained using Equation 1 and multiple convolution operations. Each convolution operation is performed within a convolutional layer.

The pixel points of a single channel form a sequence in each convolutional layer. Each layer constitutes an independent mutually random sum of sequence based on IID data samples and layer normalization. According to the central limit theorem, the gradient values of different pixel points obey an asymptotic Gaussian distribution. The range of the ERF is the standard deviation of the gradient values of this sequence. The calculation formula is as follows:

$\begin{array}{ll}{\text{ERF}}_{\text{single\_channel}}={\displaystyle \sum _{i=0}^{n-1}\left[{{\displaystyle \sum _{q=0}^{k-1}{q}^2·\omega (q)-\left({\displaystyle \sum _{q=0}^{k-1}q·\omega (q)}\right)}}^2\right]}\propto k\sqrt{n}.& (2)\end{array}$

where n is the number of CNN layers. For multi-channel sample data, different channels can also constitute an IID sequence, which does not affect the result of Equation 2. However, this difference will eventually be reflected in the varying gradient values of the input sample data because of the varied assignment of importance among different channels. This directly affects the calculation of the ERF for multi-channel sample data. In addition, in some applications, the input sample data of the model do not satisfy the condition of IID data. Whether the 2σ range for a Gaussian distribution is reasonable requires further verification.

2.2 Calculation of multi-channel gradient map

Typically, the ERF of CNNs is the standard deviation encompassing the sum of all pixel point sequences. For multiple channels within a dataset, samples are merged into several convolutional modules depending on the specific task. In non-IID datasets and multi-module structures, the standard deviation of the sequence sum is defined in different modules by:

$\begin{array}{ll}\text{ERF =}\sqrt{{\displaystyle \sum _{i=1}^{m-1}Var(S_i)+{\displaystyle \sum _{j=1}^{m-1}{\displaystyle \sum _{k=1}^{m-1}\sqrt{Var(S_j)}·\sqrt{Var(S_k)}}·\rho (S_j,S_k)}}}.& (3)\end{array}$

where Var is the variance of the gradient from the convolutional module, S denotes the different convolutional modules in the model, and ρ is the correlation coefficient of any two diffusion modules. The subscripts i, j, and k for each S represent different numbers. Each module (S) contains several channels that are spliced together to produce an important feature combination in the CNN. Theoretically, the ERF can be defined in any CNN using Equation 3. However, calculating ρ between different modules is difficult because all neural networks use black-box training processes and structural operations. Therefore, when determining the ERF of a CNN, RF attenuation characteristics of different modules must be analyzed instead of directly obtaining it using Equation 3.

The decay of the CNN RF depends on the contribution of the inputs to the outputs (Luo et al., 2016). In deep learning, this contribution is called the credit assignment problem (CAP). CAP is usually solved using the backpropagation (BP) algorithm during the neural network training process. The BP algorithm constantly updates the parameters of the CNN with the gradient value of the loss function. Each gradient value reflects the effect of the loss function on different pixel points in the input datasets. We determined the range of the ERF by calculating the gradient value of the BP process.

Before calculating the gradient, the loss function L is set to have a gradient of 1 for the center target point and 0 for other points (Luo et al., 2016; Liu et al., 2018), which is written as Equation 4. This assumption is combined with the chain rule to ensure that the gradient from the output (y) to the input sample points (x) is equal to the error obtained by the loss function during the BP process.

$\begin{array}{ll}\frac{\partial L}{\partial x}=\frac{\partial L}{\partial y}·\frac{\partial y}{\partial x}=\frac{\partial L}{\partial y_{\text{center}}}·\frac{\partial y_{\text{center}}}{\partial x}=\frac{\partial y_{\text{center}}}{\partial x},\frac{\partial L}{\partial y}=\{\begin{array}{l}1,y\text{ is the central point,}\\ 0,\text{ others.}\end{array}& (4)\end{array}$

To determine the size of the ERF, the center point in each channel is selected from the model’s output by summing all channels to obtain φ. The gradient distribution can be computed using any pixel point as the target. Here, the center point of each channel (C) is selected as the study object to describe how the gradient is calculated. The calculation of the gradient of the input points in different channels and all the gradient values produces a gradient map, $g(h,w)$, where h and w denote the positions of the pixel points. The expression of the gradient maps for a convolutional module M = (M₁, M₂, … M_s), including s layers and p channels is as follows:

$\begin{array}{ll}\{\begin{array}{l}{g}_1(h,w)=\frac{\partial \phi }{\partial M_s(C_1(x))}·\frac{\partial M_s(C_1(x))}{\partial M_{s-1}(C_1(x))}·\cdots ·\frac{\partial M_2(C_1(x))}{\partial M_1(C_1(x))},\\ g_2(h,w)=\frac{\partial \phi }{\partial M_s(C_2(x))}·\frac{\partial M_s(C_2(x))}{\partial M_{s-1}(C_2(x))}·\cdots ·\frac{\partial M_2(C_2(x))}{\partial M_1(C_2(x))},\\ \cdots \cdots \cdots \cdots \\ g_p(h,w)=\frac{\partial \phi }{\partial M_s(C_p(x))}·\frac{\partial M_s(C_p(x))}{\partial M_{s-1}(C_p(x))}·\cdots ·\frac{\partial M_2(C_p(x))}{\partial M_1(C_p(x))}.\end{array}& (5)\end{array}$

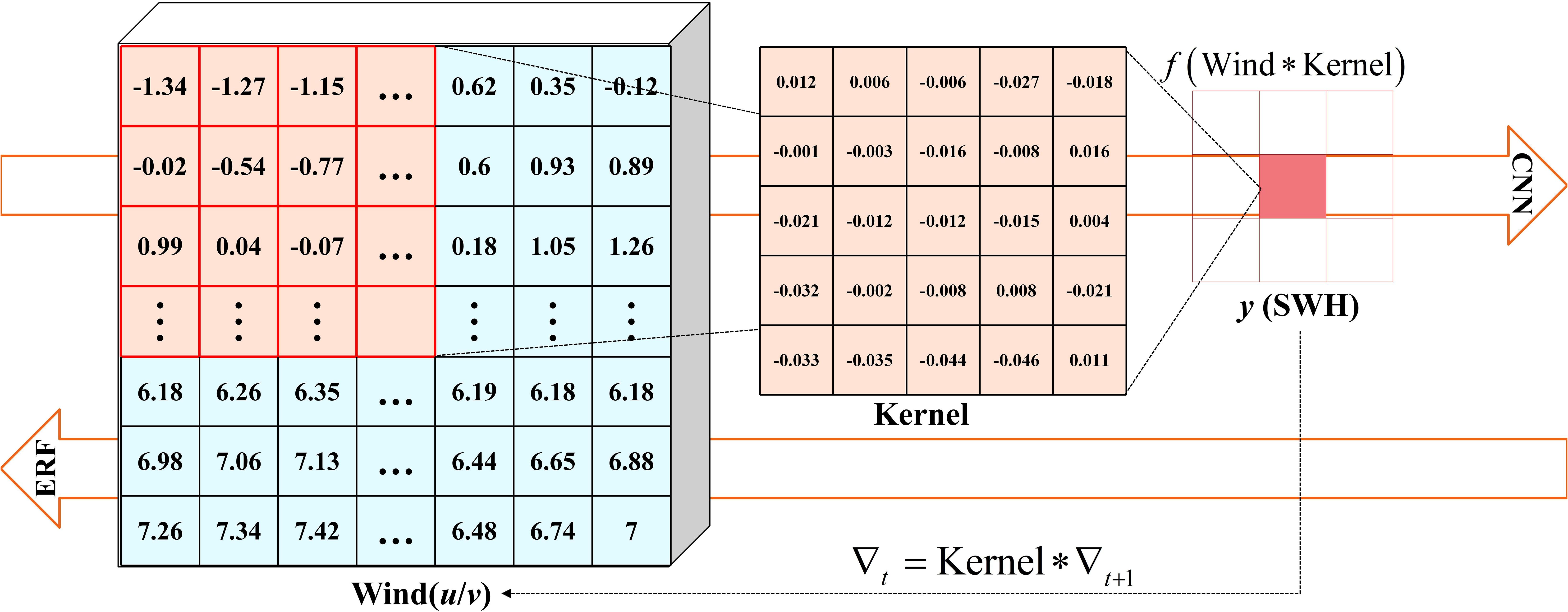
where each variable is a matrix containing multiple features. The subscripts of C are arranged from largest to smallest, corresponding to the BP process (Rumelhart et al., 1986). The simplified process is shown in Figure 1, which illustrates the outputs obtained for the input datasets using a 5 × 5 convolutional kernel. The first arrow indicates the CNN training process, and the second arrow depicts how the gradient map is updated. Negative gradient values are usually considered to be of no practical significance in image processing tasks. But these values reflect a negative feedback mechanism in many physical situations. They are also an important part for gradient contribution in CAP.

Figure 1

Figure 1. Obtaining a gradient map using the BP algorithm.

The ERF is usually calculated following two steps in the CNN: (1) the gradient maps take the sum of square according to the characteristics of different channels, which ensures that the effect of the negative gradient values is considered in the calculation of ERF. The ERF of a spatial point is then obtained by the square root of g. (2) All the gradients of the spatial point, G, in the model are summed and averaged by the number of samples N:

$\begin{array}{ll}G=\frac{1}{N}{\displaystyle \sum _{h=1}^H{\displaystyle \sum _{w=1}^W\sqrt{{(g_1(h,w))}^2+{(g_2(h,w))}^2+\cdots +{(g_p(h,w))}^2}}},g=[g_1,g_2,\cdots ,g_p].& (6)\end{array}$

where H and W denote the number of spatial points contained in the height and width of a gradient map, respectively. In some applications, especially image processing tasks, it is possible to convert the negative gradient values into zeros (Luo et al., 2016). The simplest approach to achieve this is to process the obtained gradient map using the rectified linear unit nonlinear function before using Equation 6.

2.3 Numerical testing of the multi-channel ERF and its relationship with convolutional kernel sizes and layers

From the gradient map obtained in Section 2.2, we need to take into account the correlation of different feature channels to determine the range of the ERF. If the effective range (95.45%) is used, a large amount of feature information about the target point is lost. However, with the target point, spatial points greater than 99.73% of the overall gradient value (i.e., a range of 3σ of the normal distribution) are selected to determine the final area.

Based on Equations 4-6, numerical experiments are designed to determine the ERF of multi-channel structures by modifying convolutional kernel size and network layer number. We constructed a random four-dimensional tensor with only one sample and multiple channels. Each experiment was performed within the same convolutional module. The ERF in the module was recorded by fixing the size of the convolutional kernel and changing the number of convolutional layers.

There are two ways to obtain the ERF: determining the maximum square range (Ding et al., 2022) containing the ERF based on Equation 6 or counting all pixel points within the range of the ERF in the experiment. To enable a comparison with the range of the RF, we chose the former scheme. We conducted the following experiments to determine the relationship among ERF, convolutional layer number, and kernel size. For the different convolutional kernel sizes, we tested the ERF, ERF/RF, and RF attenuation ratio (1-ERF/RF) for different convolutional layers. The results curves are shown in Figure 2.

Figure 2

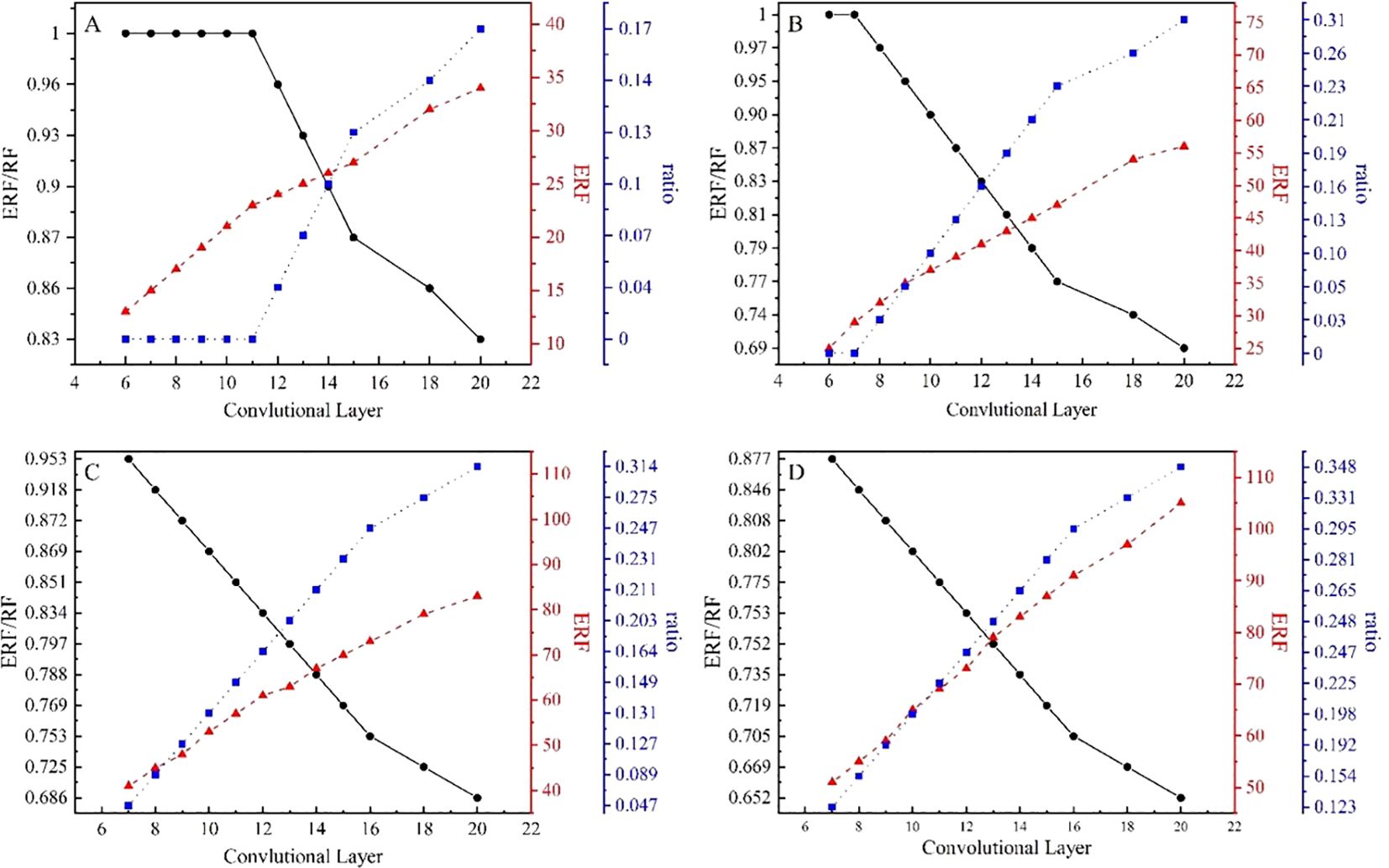
Figure 2. Results of the CNN for ERF, ERF/RF, and RF attenuation ratio for different layer numbers with kernel sizes. (A) 3 × 3, (B) 5 × 5, (C) 7 × 7, and (D) 9 × 9.

In all the experiments, the initial number of convolutional layers for each module was 6 (3 × 3 and 5 × 5) or 7 (7 × 7 and 9 × 9). The convolutional modules with fewer layers are not usually suited to local feature extraction (Alzubaidi et al., 2021) because they lack nonlinear characteristics. However, although a large convolutional kernel achieves the same range as several small kernels in the CNN, it comprises a larger number of parameters and thus increases computational power. Therefore, we selected the optimal combination of lower RF decay and fewer parameters.

3 Application to GWSM4C

3.1 Datasets

The theory of multi-channel ERF for CNNs mentioned above was applied to the designing of the improved GWSM4C. GWSM4C is a fully convolutional model. It takes same convolution (introducing Padding operation) to ensure that the size of the feature map is the same as the input datasets at each convolution. In addition, the model does not include pooling. The memory occupied by the feature map increases rapidly with the number of layers when simulating global waves. Our research area was 80° S–80° N and 0° E–359° E. The datasets were the same as the GWSM4C possessing the characteristic of non- independent and identically distribution. The wind speed data were obtained at an altitude of 10 meters above sea level and comprised two components: u and v. These data were obtained from ERA5 (fifth-generation reanalysis datasets produced by the European Centre for Medium-range Weather Forecasts; Hersbach et al., 2020; Bell et al., 2021) and had a spatial resolution of 0.25° × 0.25°. The SWH data were simulated by the third-generation Key Laboratory of Marine Science and Numerical Modeling-Wave Model (MASNUM-WAM) and had a spatial resolution of 0.5° × 0.5° (Yuan et al., 1991, 1992; Yang et al., 2005). We selected wind speed data from 2016 to 2020 as the training set for the simulation of global SWH, and data acquired in 2021 were used as the test set. The temporal resolution for all data was 1 hour.

3.2 Model structure and design based on the GWSM4C and ERF

The model framework is shown in Figure 3. Because the wind field x = [u₁₀, v₁₀] on the sea surface is the main source of wave energy, we made full use of the historical wind speed information at different moments (T – 168, T – 144, …, T – 12, T – 6) during the modeling process. In contrast to the GWSM4C, the interval of the wind field at different moments was modified rather than using only 6 hours, which allowed the accumulation of more wind features to portray energy diffusion features. This enabled the model to simulate the process of wave energy diffusion in the current moment. Based on this wave energy state, the wind field at the moment of T − 0 was combined with other moments to obtain the SWH in the ocean at any spatial scale.

Figure 3

Figure 3. Model structure based on the improved GWSM4C.

Crucially, the diffusion time of wave energy was defined to obtain the energy diffusion distance. Because the GWSM4C uses wind speed features at 6-hour intervals as inputs, the model is unable to incorporate more historical wind speed features. In our model, wind field data spanned 7 days, and we defined three time intervals, ΔT, for wind input at different historical moments. For wind speed data after 1 day, we used an interval of 6 hours. For historical wind field data on the second and third days, the time period spanned 12 hours. If the time range of historical wind speed data exceeded 3 days, an interval of 24 hours was chosen.

The process of wave energy diffusion is a crucial element in determining the wave state. In wave intelligent models, CNNs and convolutional structures can simulate regional wave states and avoid error accumulation caused by the iteration of network parameters during the training process. This lays the foundation for realizing global wave simulation. When designing the intelligent wave model, we tried to incorporate the range of wave energy diffusion to not only enhance the physical interpretation of the model but also improve the ability to simulate waves. Therefore, it is important to define the range of wave energy diffusion as well as establish the link between distance and the model’s ERF. Following previous studies on the relationship between dataset resolution and wave propagation (Jin et al., 2024; Zhang et al., 2024), our goal for the model’s ERF is represented by:

$\begin{array}{ll}\text{ERF}=\frac{c_g·\text{Δ}T}{111\text{km}}\times {\left(\frac{1}{r}\right)}^{-1}\times 2+1.& (7)\end{array}$

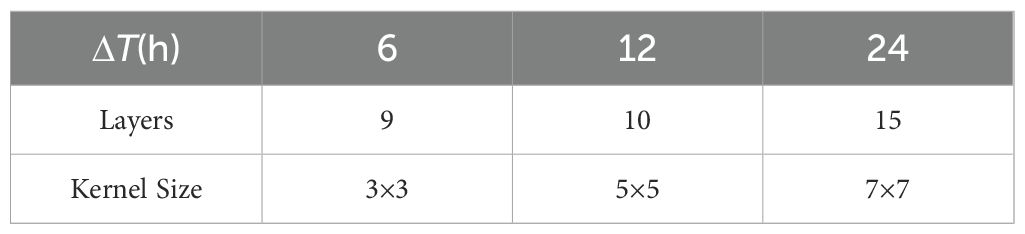
In Equation 7, the maximum diffusion distance of wave energy at different time intervals is c_g · ΔT, where c_g is wave group velocity, and ΔT indicates diffusion time. The unit length 111 km indicates the approximate distance of one arc-degree on the Earth’s surface, assuming the Earth’s radius to be 6371 km. Additionally, 1/r is the resolution of the dataset for SWH. When determining the maximum diffusion range of wave energy, c_g is the key element. We selected the maximum wind speed (36 m/s) within the datasets and calculated the wave group velocity (22.5 m/s) that corresponded to peak frequency. We anticipated that the model’s ERF would be equal to the model design goal in that it matches the range of wave energy diffusion as calculated using Equation 7. For the time intervals defined above, the range of wave energy diffusion (d) and the corresponding ERF are shown in Table 1.

Table 1

Table 1. Wave energy diffusion distance and the ERF at different intervals.

The structure of the energy confusion module in our model was designed to convert wind speed characterization information. This module became the driving force for wave energy diffusion. Each module could extract two features, u and v, for wind speed and generate 40 channels as the output. Importantly, the size of the convolution kernel of each convolutional layer was 1 × 1 (Szegedy et al., 2015), which ensured the completeness of the space feature information of the wind speed in the ocean.

As shown in Table 1, the wave energy diffusion distance corresponded to 19 for the model’s ERF when the time interval was 6 hours. Figure 2A illustrates that, based on Equation 5, nine convolutional layers are required when using 3 × 3 convolutional kernels. It is worth noting that there is no attenuation in the RF at this time. Similarly, the ERF of the model design goal was 36 with the 12-hour interval. At this point, we had two options for designing the module structure: (1) 22 convolutional layers are needed for 3 × 3 convolutional kernels (according to Figure 2A) with RF attenuation (0.2); (2) as shown in Figure 2B, we use 10 layers, so that the size of the convolutional kernel is 5 × 5. For the latter scheme, the decay ratio of the RF is 0.098. We compared the RF attenuation and convolutional layers for a kernel size of 3 × 3 with those for a kernel size of 5 × 5.

Specifically, when the interval is 24 hours, the goal of the ERF should be 71. There are three options to achieve this: (1) According to Figure 2B, more than 20 convolutional layers would be needed to use several convolutional kernels of 5 × 5, accompanied by RF attenuation (exceeding 0.3); (2) according to the statistical value in Figure 2C, 15 layers could be used with an RF attenuation rate of 0.23 when the convolutional kernel size is 7 × 7; (3) according to Figure 2D, if the convolutional kernel size is 9 × 9, 12 convolutional layers would be required with a decay rate of 0.25. The latter two schemes have fewer convolutional layers to obtain the ERF. The decay ratio of a 7 × 7 kernel size is lower than that of a 9 × 9 kernel size. In addition, the number of parameters for model training using scheme 2 would be 735 (only a one-feature channel), whereas the number of parameters for scheme 3 would be 972. For 40-feature channels, the number of parameters for a 9 × 9 kernel size would be 9480 more than that for a 7 × 7 kernel size. Such differences will impact the training efficiency of this model. The hyperparameters in the model energy diffusion module at different time intervals were set as shown in Table 2 throughout the above analyses.

Table 2

Table 2. Hyperparameter determination for the wave energy diffusion module.

3.3 Model training and evaluation indicators

The wind speeds, including the u and v components, were used as inputs at different moments during the training process. There were 12 energy diffusion modules in the wave energy diffusion model, consisting of wind speed features with intervals of 6, 12, and 24 hours at different historical moments. All the features are summarized in the energy conversion module at moment T – 0, and the model had 26 feature channels. In addition, because the wind speed datasets from ERA5 contain land wind data, the area related to land was set to 0 (increasing the mask).

Selecting an appropriate optimization method and learning rate for the neural networks is crucial because these factors enhance the network’s learning ability. In the improved model, we used the Adam optimizer (Kingma and Ba, 2014), which corrects the updating direction of the parameters and adaptively adjusts the learning rate during each iteration. The decay rates of the two moving averages are 0.9 and 0.99. In addition, the learning rate needs to be determined during the training process. Usually, the decay in the learning rate is set according to the number of epochs. However, the learning rate of our model was adjusted according to the cosine decay (Loshchilov and Hutter, 2016; Jin et al., 2024). The expression is shown in Equation 8.

$\begin{array}{ll}{\alpha }_{\text{epoch}}=\left[\left(\mathrm{1+}\frac{1}{2}\cos \left(\frac{\pi ·\text{epoch}}{400}\right)\right)\times \mathrm{0.9 + 0.1}\right]\times 0.001,\text{ epoch }=1,2,\cdots ,400.& (8)\end{array}$

To evaluate the simulation results of the model, we used three indicators to judge the accuracy of global SWH: the time correlation coefficient (TCOR), root mean square error (RMSE), and bias (BIAS). These indicators can be calculated using Equations 9-11.

$\begin{array}{ll}\text{TCOR = }\frac{1}{n}\frac{{\displaystyle \sum _{i=1}^n\left(\left(H_M-\overline{H_M}\right)\left(H_W-\overline{H_W}\right)\right)}}{\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(H_M-\overline{H_M})}^2}}·\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(H_W-\overline{H_W})}^2}}},& (9)\end{array}$

$\begin{array}{ll}\text{RMSE = }\frac{1}{n}\sqrt{{\displaystyle \sum _{i=1}^n{(H_M-H_W)}^2}},& (10)\end{array}$

$\begin{array}{ll}\text{BIAS = }\frac{1}{n}{\displaystyle \sum _{i=1}^n(H_M-H_w)},& (11)\end{array}$

where H_M and H_W represent the SWH calculated using the improved GWSM4C and the MASNUM-WAM, respectively. The line above the variable signifies that it is the mean value of that variable, and n is the number of sample points participating in the network test. For these evaluation metrics, if the value of TCOR is sufficiently high and the RMSE and BIAS are low, the model simulation is accepted.

4 Results

4.1 Gradient distribution in the West African and the East Pacific area

The ERF calculated by the model characterizes the distribution of different input sample point contributions; thus, it reflects the importance of different input samples to the output results. According to the model’s ERF mentioned in Section 3.2, the characteristics of regional swells can be verified via comparison with previous studies. The key element of the ERF is the gradient map of wind speed characteristics at different moments. Each gradient map portrays the importance of different output points relative to different modules and their input channels. Theoretically, the gradient values of different pixel points in the input should decay around the target point following a Gaussian distribution. The two-dimensional projections of the gradient values are circles. However, the gradient distribution at the target point varies because of many nonlinearities (e.g., nonlinear activation functions) in the network structure. Notably, the maximum value of the ERF at the earliest moment (i.e., T − 168) deviates from the center. The expressions are shown as Equations 12, 13, which demonstrate that the wind field in other sea areas impacts the SWH at this point. This is because the waves are susceptible to swells generated by storms from other sea areas. These swells are sufficient to propagate to the target point within 7 days and have a significant effect on wave height variations.

$\begin{array}{ll}\{\begin{array}{l}{g}_u(h,w)=\frac{\partial \phi }{\partial M^{(T-0)}(C_u(x))}·\frac{\partial M^{(T-0)}(C_u(x))}{\partial M^{(T-6)}(C_u(x))}·\cdots ·\frac{\partial M^{(T-144)}(C_u(x))}{\partial M^{(T-168)}(C_u(x))},\\ g_v(h,w)=\frac{\partial \phi }{\partial M^{(T-0)}(C_v(x))}·\frac{\partial M^{(T-0)}(C_v(x))}{\partial M^{(T-6)}(C_v(x))}·\cdots ·\frac{\partial M^{(T-144)}(C_v(x))}{\partial M^{(T-168)}(C_v(x))}.\end{array}& (12)\end{array}$

$\begin{array}{ll}G\text{ = }\frac{1}{M}{\displaystyle \sum _{h=1}^H{\displaystyle \sum _{w=1}^W\sqrt{{(g_u(h,w))}^2+{(g_v(h,w))}^2}}}.& (13)\end{array}$

The variables in Equations 12, 13 are subscripted with wind speed characteristics u and v. The upper right of each x is identified as the moment. Other variables are the same as those in Equations 5, 6. In our model, the values for H and W were 361 and 720, respectively, based on the characteristics of our datasets mentioned in Section 3.1.

The gradient distribution can verify the characteristics of oceanic swell. We selected the West African area, where the wave conditions are complex and dominated by swells (Allersma and Tilmans, 1993; Toualy et al., 2015; Almar et al., 2023). The swells primarily arise from cyclones in the North Atlantic or storms in the Subpolar Westerlies of the Southern Hemisphere (Southern Atlantic and Southern Ocean). To verify swell-related areas in the West African area according to the improved model, we selected three points (0°, 25° W; 15° S, 20° W; and 15° N, 25° W) and their average values of gradient maps corresponding to all T − 168 moments from 2021 (Figure 4).

Figure 4

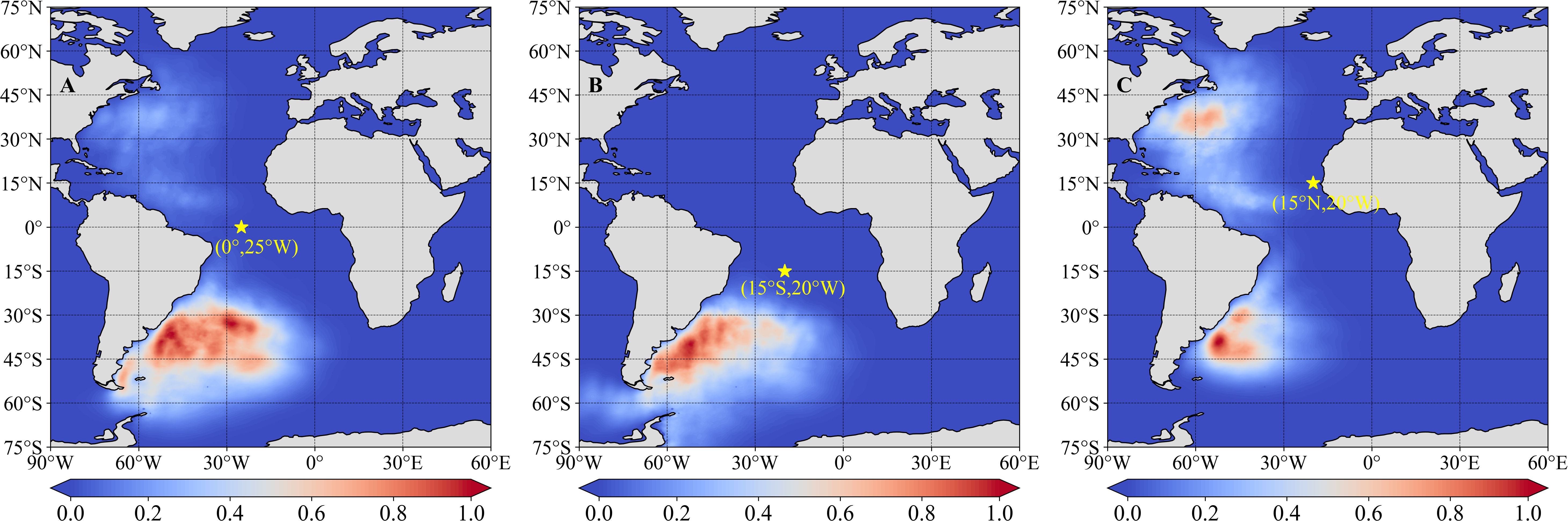
Figure 4. Gradient distribution at different points (A) 0°, 25°W; (B) 15°S, 20°W; and (C) 15°N, 25°W in the West African area-based ERF.

Similarly, the gradient distribution based on the improved GWSM4C can verify the characteristics of swells in the East Pacific area, which also has complex wave conditions that are dominated by swells (Jiang and Lin, 2019; Jiang et al., 2023; Zhang et al., 2023). For this area, the spatial points in the northern, central, and southern regions contain swells from the North Pacific, both the North and South Pacific, and South Pacific, respectively. To verify the swell-related areas in the East Pacific according to the improved GWSM4C, we selected three points (25° N, 120° W; 0°, 110° W; and 20° S, 95° W). Their average values of gradient maps corresponding to all T − 168 moments from 2021 are shown in Figure 5.

Figure 5

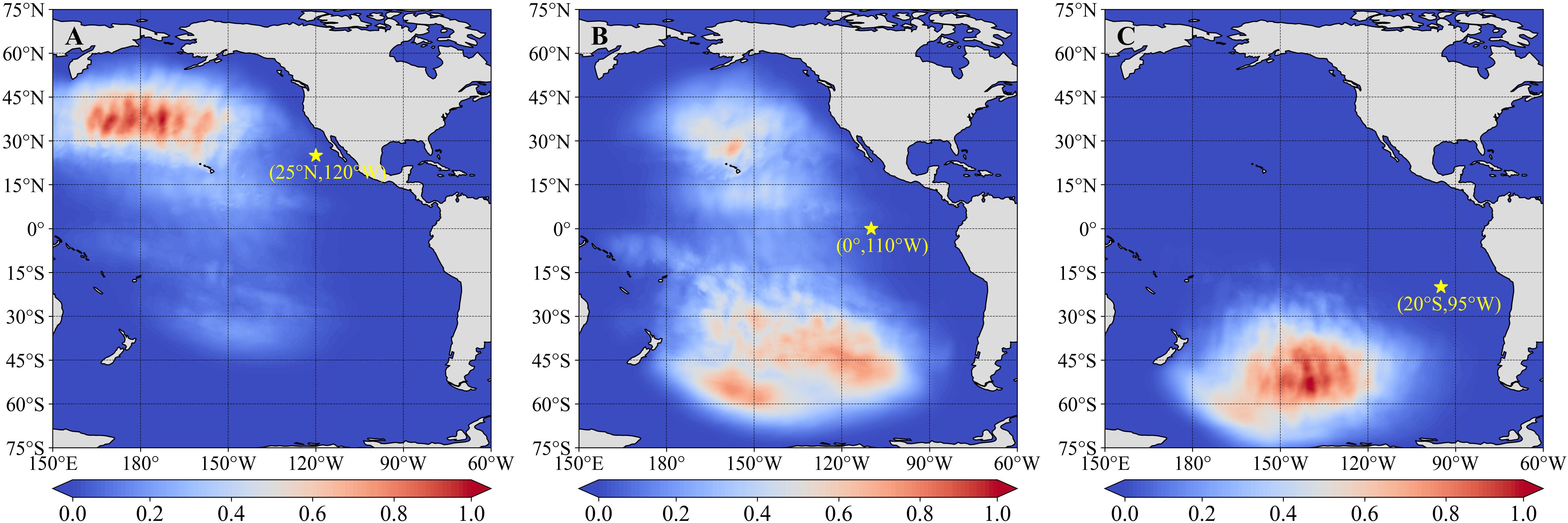
Figure 5. Gradient distribution at different points (A) 25°N, 120°W; (B) 0°, 110°W; and (C) 20°S, 95°W in the East Pacific area-based ERF.

According to the distribution of gradient values, the high correlation area of swells was largely consistent with the source of observation in the West African and East Pacific areas. This also indirectly justifies the use of our method for calculating the ERF and confirms that the improved GWSM4C is more reliable. In addition, this finding verified that our model can explain the results, which is particularly notable for furthering the development of deep learning models of ocean waves.

4.2 Improvement of SWH prediction in global swell pools

We compared the evaluation metrics of our model detailed in Section 3.3 with those of the MASNUM-WAM to validate the learning ability of the model. The comparison results of the seasonal distribution of SWH during 2021 are provided in Figure 6. Overall, the RMSE was less than 0.2 m (approximately 0.15 m), and the TCOR was more than 0.95 in most of the global ocean areas. The absolute value for BIAS mostly fell within the range of 0.15 m. These indicators showed that the simulation effect of the improved GWSM4C was similar to that of MASNUM-WAM.

Figure 6

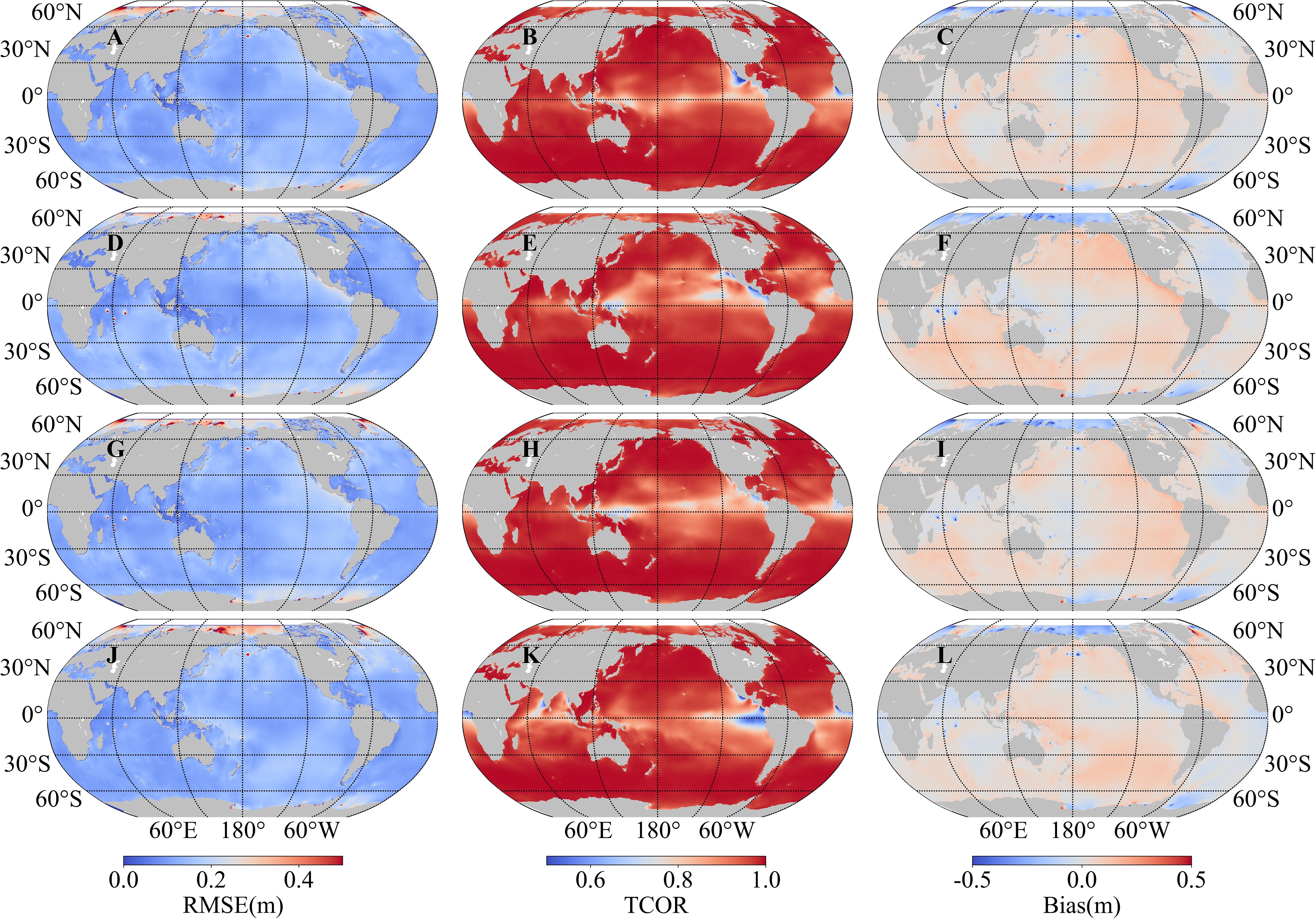
Figure 6. Comparison between our model and the MASNUM-WAM for SWH. RMSE, TCOR, and BIAS are shown in the left, center, and right columns, respectively. Seasonal distributions are shown for spring (A–C), summer (D–F), autumn (G–I), and winter (J–L).

Additionally, we found that the TCORs near the equator were lower than those of other areas; the TCORs fell between 0.7 and 0.8. In contrast, the RMSE and BIAS remained largely unchanged. The shorter time series of the wind fields could not effectively simulate the wave energy diffusion process because of a windless zone around the equator. Furthermore, swells propagating from different directions caused complex wave characteristics in this region that were similar to the eastern coast (Song and Jiang, 2023). The model structure was optimized by adding historical wind field data based on the ERF. Compared with that in the GWSM4C, the simulation effect was significantly better in swell pools. The spatial distribution of the annual SWH RMSE for both GWSM4C and the improved version is shown in Supplementary Figure 1. In particular, the RMSE reduced from 0.3 to 0.15 m in the West African and East Pacific swell pools. This demonstrates that adding historical wind field information benefits the model’s performance and its ability to learn the complex relationship between wind and waves. Although there were small gaps in the simulation of our model owing to the seasonal distribution of SWH during 2021, the overall results were acceptable, except for those in the equator and the eastern ocean. Compared with traditional artificial intelligence models for wave prediction, the simulation of SWH by our model is less impacted by seasonal climate events, such as cold-air outbreaks. Therefore, our model can be used to predict long-term wave characteristics and simulate wave climates.

It is also noted that the simulation results are less effective in the Arctic Oceans. It is because the computational grids adopted in GWSM4C are based on latitudes and longitudes, and the unit length 111 km presented in Equation 7 is acceptable to calculate the ERF for the vast majority of grid points in the global ocean, however, the distances between meridional grid points become much shorter than the preset unit length in polar regions, letting the supposed range of energy diffusion cannot be achieved and the ERF previously obtained and the convolutional neural network structure established be no more suitable. More detailed information about the poor performance of GWSM4C in higher latitudes can be referred to (Jin et al., 2024).

4.3 Test results and analysis of some points and areas

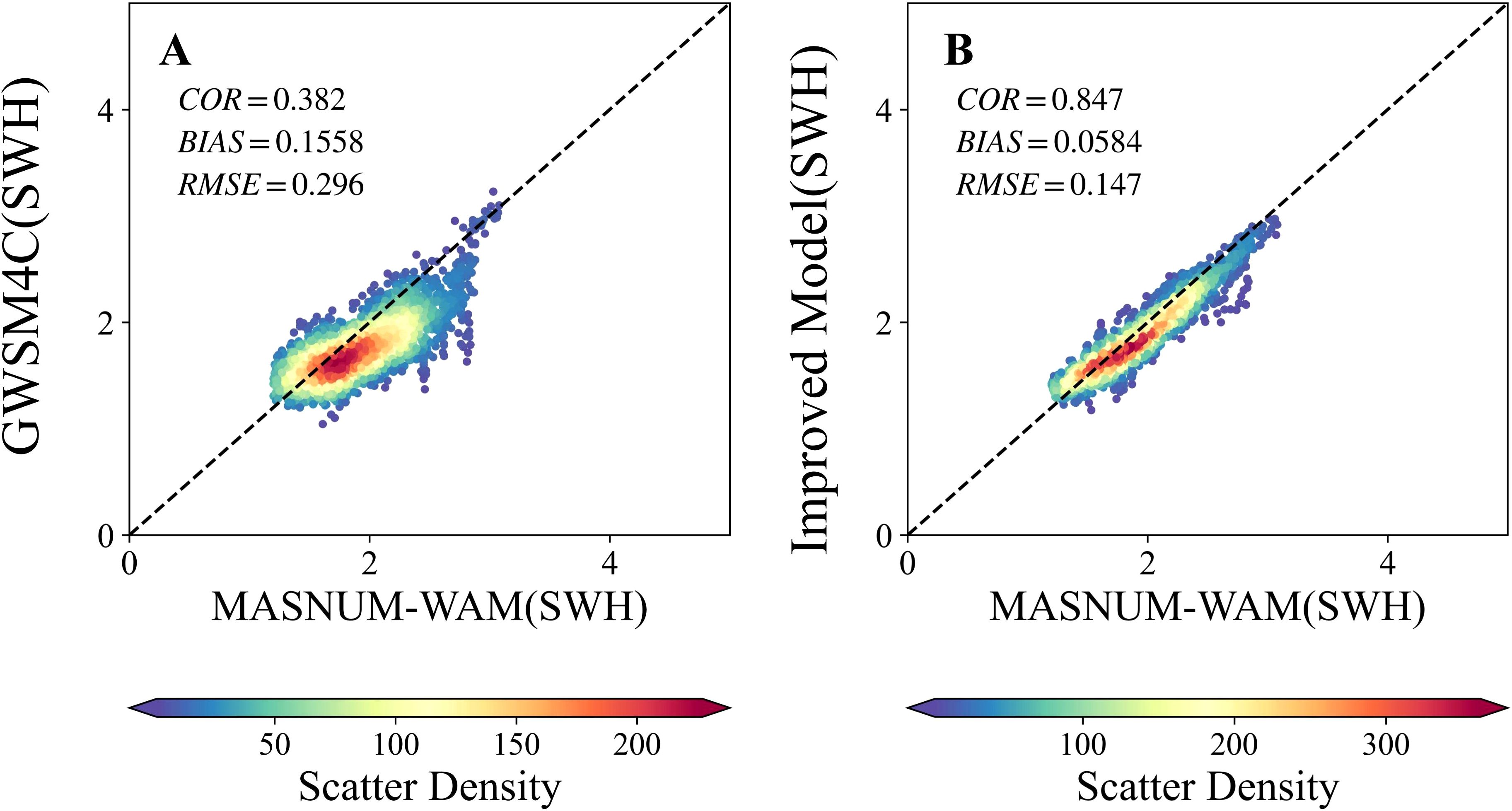
According to global ocean characteristics, we selected three points to verify the long-term simulation effect of the wave energy dispersion model. The three points were located in the South China Sea (an almost enclosed sea area), the East Pacific Ocean (dominated by several swells), and the Subpolar Westerlies of the Southern Hemisphere (no land obstruction). Overall, SWHs obtained from the GWSM4C and the improved model in areas dominated by wind waves were highly correlated (TCORs of 0.98 and 0.99, respectively) with the results of the MASNUM-WAM (The Scatter plot of two points is shown in Supplementary Figure 2). However, the GWSM4C performed poorly in the East Pacific swell pool whereas, the improved model performed significantly better in this region. The scatterplot distributions are shown in Figure 7. Taken together, the improved GWSM4C simulates swell pool areas better than the original model.

Figure 7

Figure 7. Scatter plot of SWH at 5° S, 90° W. (A) GWSM4C and (B) the improved model.

In addition to the several special points mentioned above, we divided the global ocean into seven regions to verify the generalizability of our model to different areas: Northern Indian, Southern Indian, Northern Atlantic, Tropical Atlantic, Northern Pacific, Tropical Pacific, and Southern Ocean. The latitude and longitude information is shown in Supplementary Table 1. For the Northern Atlantic region, the area 0°–15° N, 260° E–275° E was not included. The mean BIAS values of these areas in different seasons were less than 0.2 m for most SWHs (Supplementary Figure 3). Compared with the GWSM4C, the improved model showed a clear decline in BIAS values. The East Pacific and West African swell pools were included in the Tropical Pacific and Tropical Atlantic regions, respectively. Compared with the GWSM4C results, the improved model reduced the average BIAS in these two swell pools by approximately 0.1 m.

5 Discussion

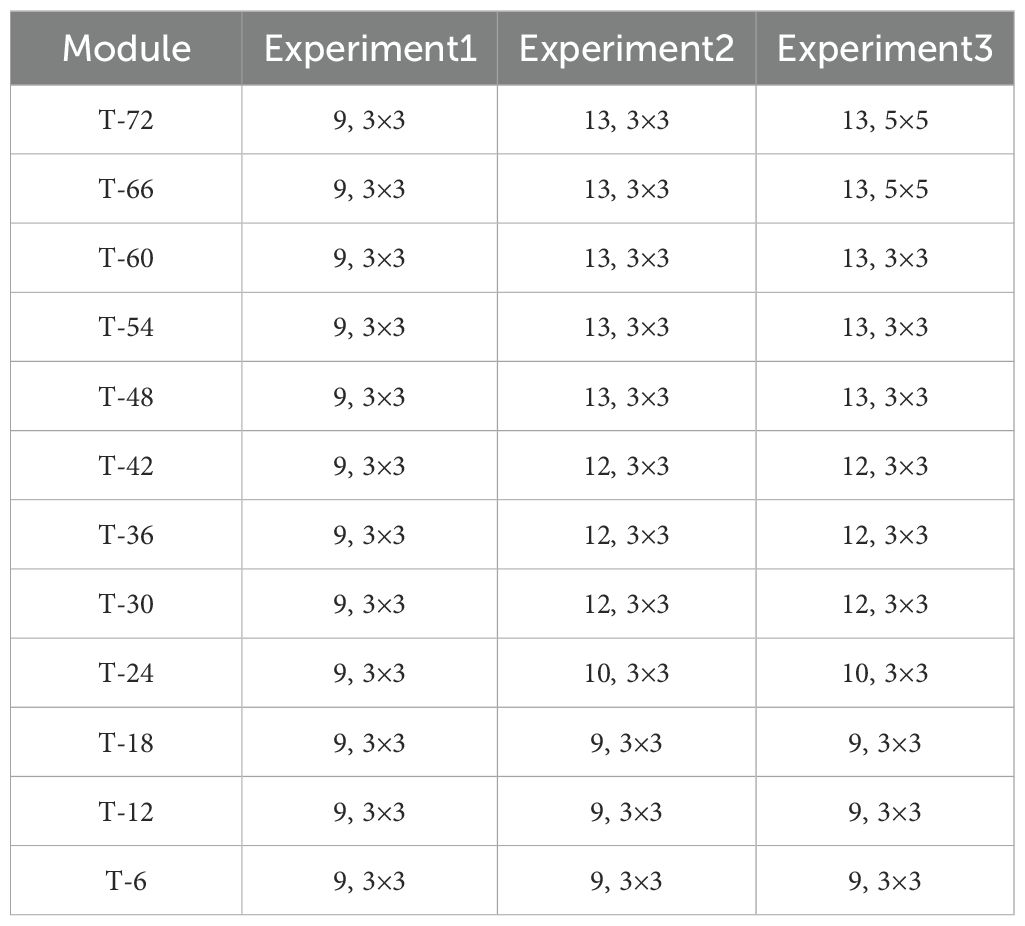
The effective range of the gradient map from the CNN directly determines the ERF. Global gradient values within 95.45% is widely used in image processing tasks. Its application presupposes that all trained samples are independent of each other. Therefore, this range cannot be applied to intelligent wave model datasets. The 3σ principle of normal distribution (99.73%) is defined for non-IID and multi-channel samples. To test the applicability of the effective range in wave modeling, we designed three fully convolutional models that were trained to simulate global waves. The earliest wind field of these three models was T − 72. The feature generated by the CNN was performed at 6-hour intervals, alongside wind field features at the subsequent moment. Twelve convolutional modules were used to realize wave energy diffusion at different moments. There was a total of 24 feature channels per data sample because the two components, u and v, were included in the wind field at each moment. The module parameters (e.g., 9, 3 × 3 represents the layers and convolutional kernel size, respectively) for these models are shown in Table 3.

Table 3

Table 3. Module parameters of the three experiments.

If the time span is too large, the wave energy propagation will be blocked by land. This will lead to dispersion of the ERF, which is not ideal for calculating the range. We selected the global center point (i.e., 0°, 180° E) to ensure that the wave energy propagated fully within a certain spatial range. The ERF of three models at different times, based on Equations 12, 13, are shown in Figure 8. We identified a significant gap between the ERF and the target RF based on the 2σ range up to moment T − 30. For Experiment 1, the model’s ERF was unstable under the 2σ principle. At moments T − 66 and T − 72, the ERF of Experiments 2 and 3 appeared to be upper bounded (135), which was not consistent with the ERF changes. Although the RF appeared to decay with the increase in the number of convolutional layers in the CNN, this did not necessarily signify that the ERF remained constant. If this principle was used according to the number of layers in the model feature extraction, model complexity, and consequently computational power, would become excessive. Therefore, improving the simulation performance of the model was deemed impractical.

Figure 8

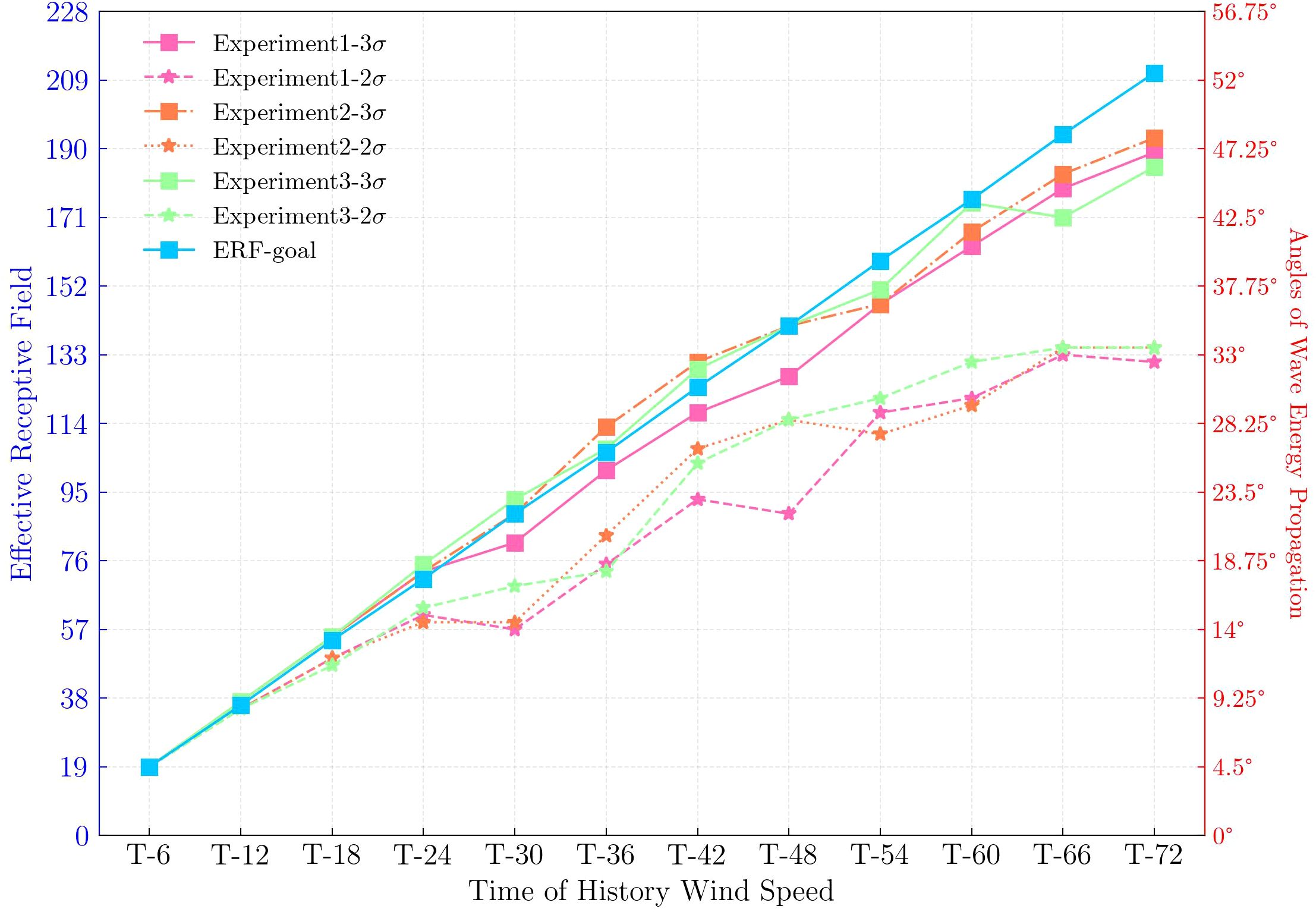
Figure 8. ERFs of historical wind speed characteristics under different models. The right axis represents the latitude and longitude of the wave energy diffusion corresponding to the ERF.

In contrast, the ERFs of the three models based on the 3σ principle were similar to the goal ERF. The gradient value of 99.73% could calculate the ERF of the models in different modules. It is worth noting that the similarity of the ERF to the goal range given was used only as a foundation for the model structure design. Specifically, we noticed that the ERFs of Experiment 3 did not increase at each moment; they both showed a decrease at moment T − 66, although they did not impact the ERF analysis. The ranges of the three models increased from previous moments. Overall, we considered using the 3σ principle for the wave simulation model because it will not result in a large amount of target point-related feature information loss.

6 Conclusions

Based on existing methods for determining the range of ERFs, we proposed a multi-channel ERF calculation method. We considered the correlation between different channels and the distribution characteristics of the general sample dataset. We then selected the gradient value of 99.73% of the global range as the effective range. By conducting numerical experiments, we determined the size of the ERF corresponding to different convolution kernel sizes and convolution layer numbers. Our method can be applied to the ERF calculation of any dimensional data (i.e., non-IID data samples).

The GWSM4C model was improved by targeting the range of the ERF and establishing its connection with the diffusion range of wave energy. We used the improved model’s ERF to explore the influence of other wind fields at different spatial points on SWH. This feature enabled us to use the gradient map of the ERF to investigate the influence of regional wind fields on the regional swell characteristics in the West African and East Pacific areas. Our results were largely consistent with previous observations. In addition, the improved model based on multi-channel ERF achieved better performance in simulating global SWH, especially in oceanic swell pools.

The gradient value of the ERF reflects the contribution of each spatial pixel point and illustrates the important features in the input datasets. Furthermore, the ERF can be used to examine the interpretability of the modules of the trained neural network model. In future research, based on the existing ERF theory, we plan to develop an evaluation method for an interpretable artificial intelligence model (Bommer et al., 2024) that can be applied to wave forecasting.

Data availability statement

The data that support the findings of this study are available on request from the corresponding author: Quan Jin, 21qjin@stu.edu.cn.

Author contributions

LJ: Formal analysis, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. QJ: Data curation, Funding acquisition, Methodology, Software, Supervision, Validation, Writing – review & editing. FeH: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing – review & editing. XJ: Formal analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing – review & editing. ZW: Data curation, Writing – review & editing. WG: Writing – review & editing. FuH: Writing – review & editing. CF: Writing – review & editing. YY: Funding acquisition, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key Research and Development Program of China (2022YFC3104801 & 2021YFC3101600), National Program on Global Change and Air-Sea Interaction (Phase II) “Parameterization assessment for interactions of the ocean dynamic system” (Grant No. GASI-04-WLHY-02), the Shantou University Scientific Research Funded Project (NTF21036), the Open Research Fund of Guangdong Provincial Key Laboratory of Marine Disaster Prediction and Prevention (GPKLMD2023005), and the General Project of Natural Science Research in Higher Education Institutions in Jiangsu Province(22KJB170009).

Acknowledgments

We hope the reviewers’ comments and suggestions to improve the quality of our manuscript. We thank Sarina Iwabuchi, PhD, from Liwen Bianji (Edanz) (www.liwenbianji.cn) for editing the language of a draft of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1492572/full#supplementary-material

References

Akhtar N., Ragavendran U. (2020). Interpretation of intelligence in CNN-pooling processes: a methodological survey. Neural Comput. Applic. 32, 879–898. doi: 10.1007/s00521-019-04296-5

Crossref Full Text | Google Scholar

Allersma E., Tilmans W. M. K. (1993). Coastal conditions in West Africa—A review. OCEAN. Coast. MANAGE. 19, 199–240. doi: 10.1016/0964-5691(93)90043-X

Crossref Full Text | Google Scholar

Almar R., Stieglitz T., Addo K. A., Ba K., Ondoa G. A., Bergsma E., et al. (2023). Coastal zone changes in West Africa: Challenges and opportunities for satellite earth observations. Surv. Geophys. 44, 249–275. doi: 10.1007/s10712-022-09721-4

Crossref Full Text | Google Scholar

Alzubaidi L., Zhang J., Humaidi A. J., Al-Dujaili A., Duan Y., Al-Shamma O., et al. (2021). Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J. Big. Data. 8, 53. doi: 10.1186/s40537-021-00444-8

PubMed Abstract | Crossref Full Text | Google Scholar

Bell B., Hersbach H., Simmons A., Berrisford P., Dahlgren P., Horányi A., et al. (2021). The ERA5 global reanalysis: preliminary extension to 1950. Q.J.R. Meteorol. 147, 4186–4227. doi: 10.1002/qj.4174

Crossref Full Text | Google Scholar

Bommer P. L., Kretschmer. M., Hedström. A., Bareeva. D., Höhne. M. M. (2024). Finding the right XAI method—A guide for the evaluation and ranking of explainable AI methods in climate science. Artif. Intell. Earth Syst. 3, e230074. doi: 10.1175/AIES-D-23-0074.1

Crossref Full Text | Google Scholar

Chen L., Li S., Bai Q., Yang J., Jiang S., Miao Y. (2021). Review of image classification algorithms based on convolutional neural networks. Remote Sens. 13, 4712. doi: 10.3390/rs13224712

Crossref Full Text | Google Scholar

Ding X., Zhang X., Han J., Ding G. (2022). Scaling up your kernels to 31x31: Revisiting large kernel design in CNNs (New Orleans, LA, USA: IEEE), 11963–11975. doi: 10.48550/arXiv.2203.06717

Crossref Full Text | Google Scholar

Duffy K. R., Hubel D. H. (2007). Receptive field properties of neurons in the primary visual cortex under photopic and scotopic lighting conditions. Vision Res. 47, 2569–2574. doi: 10.1016/j.visres.2007.06.009

PubMed Abstract | Crossref Full Text | Google Scholar

Gilbert C., Wiesel T. (1992). Receptive field dynamics in adult primary visual cortex. NATURE 356, 150–152. doi: 10.1038/356150a0

PubMed Abstract | Crossref Full Text | Google Scholar

Gu J., Wang Z., Kuen J., Ma L., Shahroudy A., Shuai B., et al. (2017). Recent advances in convolutional neural networks. Pattern Recognit. 77, 354–377. doi: 10.1016/j.patcog.2017.10.013

Crossref Full Text | Google Scholar

Hersbach H., Bell B., Berrosford P., Hirahara S., Horanyi A., Munoz-Sabater J., et al. (2020). The ERA5 global reanalysis. Quart. J. R. Meteor. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

Crossref Full Text | Google Scholar

Jiang H., Lin M. (2019). Wave climate from spectra and its connections with local and remote wind climate. J. Phys. Oceanogr. 49, 543–559. doi: 10.1175/JPO-D-18-0149.1

Crossref Full Text | Google Scholar

Jiang X., Xie B., Bao Y., Song Z. (2023). Global 3-hourly wind-wave and swell data for wave climate and wave energy resource research from 1950 to 2100. Sci. Data 10, 225. doi: 10.1038/s41597-023-02151-w

PubMed Abstract | Crossref Full Text | Google Scholar

Jin Q., Jiang X., Hua F., Yang Y., Jiang S., Yu C., et al. (2024). GWSM4C: A global wave surrogate model for climate simulation based on a convolutional architecture. Ocean. Eng. 309, 118458. doi: 10.1016/j.oceaneng.2024.118458

Crossref Full Text | Google Scholar

Kingma D. P., Ba J. (2014). Adam: a method for stochastic optimization. Comput. Sci. 30, 1272–1282. doi: 10.48559/arXiv.1412.6980

Crossref Full Text | Google Scholar

LeCun Y., Boser B., Denker J. S., Henderson D., Howard R. E., Hubbard W., et al. (1989). Backpropagation applied to handwritten zip code recognition. Neural Comput. 1, 541–551. doi: 10.1162/neco.1989.1.4.541

Crossref Full Text | Google Scholar

Lee B. B. (1996). Receptive field structure in the primate retina. Vision Res. 36, 631–644. doi: 10.1016/0042-6989(95)00167-0

PubMed Abstract | Crossref Full Text | Google Scholar

Lei X., Pan H., Huang X. (2019). A dilated CNN model for image classification. IEEE Access 7, 124087–124095. doi: 10.1109/ACCESS.2019.2927169

Crossref Full Text | Google Scholar

Liu Y., Yu J., Han Y. (2018). Understanding the effective receptive field in semantic image segmentation. Multimed. Tools Appl. 77, 22159–22171. doi: 10.1007/s11042-018-5704-3

Crossref Full Text | Google Scholar

Loshchilov I., Hutter F. (2016). SGDR: stochastic gradient descent with warm restarts. Comput. Sci. 32, 1–16. doi: 10.48550/arXiv.1608.03983

Crossref Full Text | Google Scholar

Luo W., Li Y., Urtasun R., Zemel R. (2016). Understanding the effectivereceptive field in deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 29, 1–9. doi: 10.48550/arXiv.1701.04128

Crossref Full Text | Google Scholar

Ng D. T. K., Lee M., Tan R. J. Y., Hu X., Downie J. S., Chu S. K. W. (2023). A review of AI teaching and learning from 2000 to 2020. Educ. Inf. Technol. 28, 8445–8501. doi: 10.1007/s10639-022-11491-w

Crossref Full Text | Google Scholar

Rumelhart D., Hinton G., Williams R. (1986). Learning representations by back-propagating errors. NATURE 323, 533–536. doi: 10.1038/323533a0

Crossref Full Text | Google Scholar

Schwartz G., Okawa H., Dunn F., Morgan J., Kerschensteiner D., Wong R., et al. (2012). The spatial structure of a nonlinear receptive field. Nat. Neurosci. 15, 1572–1580. doi: 10.1038/nn.3225

PubMed Abstract | Crossref Full Text | Google Scholar

Song Y., Jiang H. (2023). A deep learning–based approach for empirical modeling of single-point wave spectra in open oceans. J. Phys. Oceanogr. 53, 2089–2103. doi: 10.1175/JPO-D-22-0198.1

Crossref Full Text | Google Scholar

Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., et al. (2015). “Going deeper with convolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR). (Boston, MA, USA: IEEE), 1–9. doi: 10.1109/CVPR.2015.7298594

Crossref Full Text | Google Scholar

Toualy E., Aman A., Koffi P., Marin F., Wango T. E. (2015). Ocean swell variability along the northern coast of the Gulf of Guinea. Afr. J. Mar. Sci. 37, 353–361. doi: 10.2989/1814232X.2015.1074940

Crossref Full Text | Google Scholar

Yang Y., Qiao F., Zhao W., Teng Y., Yuan Y. (2005). MASNUM ocean wave numerical model in spherical coordinates and its application. Acta Oceanolog. Sin. 27, 1–7.

Google Scholar

Yuan Y., Hua F., Pan Z., Sun L. (1992). LAGFD-WAM numerical wave model-II. Characteristics inlaid scheme and its application. Acta Oceanolog. Sin. 14, 13–23.

Google Scholar

Yuan Y., Pan Z., Hua F., Sun L. (1991). LAGFD-WAM numerical wave model—I. Basic physical model. Acta Oceanolog. Sin. 13, 483–488.

Google Scholar

Zhang H., Jin Q., Hua F., Wang Z. (2024). GWSM4C-NS: improving the performance of GWSM4C in nearshore sea areas. Front. Mar. Sci. 11. doi: 10.3389/fmars.2024.1437043

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang X., Wu K., Li R., Li D., Zhang S., Zhang R., et al. (2023). Analysis of the interannual variability of pacific swell pools. J. Mar. Sci. Eng. 11, 1883. doi: 10.3390/jmse11101883

Crossref Full Text | Google Scholar

Zhou L., Pan S., Wang J., Vasilakos A. V. (2017). Machine learning on big data: Opportunities and challenges. NEUROCOMPUTING 237, 350–361. doi: 10.1016/j.neucom.2017.01.026

Crossref Full Text | Google Scholar