Coverage path planning for multi-AUV considering ocean currents and sonar performance

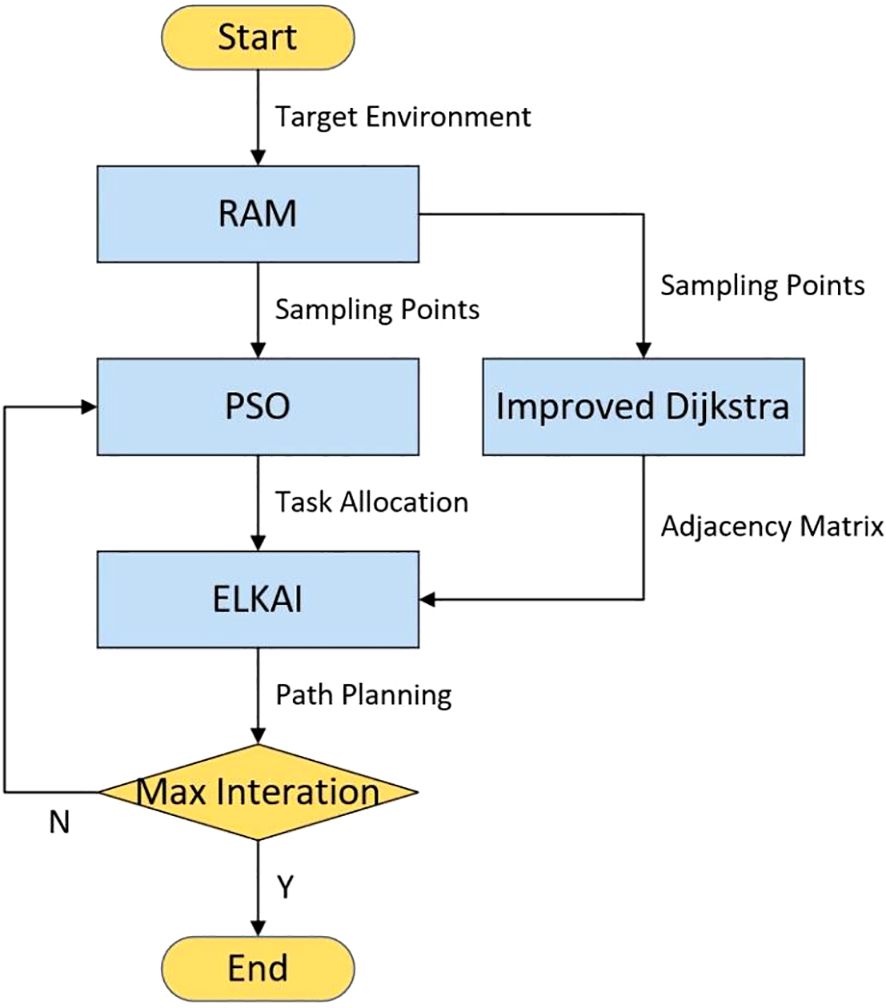
Coverage path planning (CPP) for target search by autonomous unmanned vehicle (AUV) involves two crucial aspects: (1) the sonar performance of the AUV is sensitive to ocean environment, such as changes in terrain; and (2) the ocean currents significantly influence AUV dynamics AUV dynamics. To address the CPP of multiple AUVs (multi-AUV) considering both sonar performance and ocean currents, we propose a new integrated algorithm based on the improved Dijkstra algorithm, Particle Swarm Optimization (PSO), and the ELKAI Solve. First, the necessary sampling points for the area coverage are identified based on the sonar detection range at different locations, which is calculated by combining the ocean acoustics model with the sonar equation. Second, an improved Dijkstra algorithm is presented to solve the adjacency matrix of the graph formed by all sampling points under the influence of ocean currents. Third, the PSO algorithm is utilized for task allocation, and the ELKAI solver determines the optimal path for each AUV. Finally, multi-AUV path planning is achieved through iterations of the PSO algorithm and the ELKAI solver. Simulation results demonstrate the outstanding performance and robustness of our integrated algorithm.

1 Introduction

Autonomous underwater vehicle (AUV) is an important tool in marine engineering, encompassing target coverage search (Yao et al., 2021a), man overboard search (Mou et al., 2021), ship oil spill detection (Vinoth Kumar et al., 2020), underwater topography scanning (Cai et al., 2023), and so on. A typical task scenario involves the utilization of sensors for target search, requiring the AUV to achieve complete coverage to minimize the probability of mission failure. Presently, the acoustic sensors on AUV enable static target search (e.g., sunken ships, relics) and dynamic target search (e.g., distressed individuals). This paper focuses on the coverage path planning problem for static target search using multi-AUV equipped with omnidirectional active sonar. Coverage path planning involves three main steps: firstly, determining the sampling points associated with the sonar detection range, traversing all the sampling points means achieving the coverage search of the whole area; secondly, calculating the shortest travel time between all sampling points, which involves solving the adjacency matrix of the graph formed by all sampling points in ocean currents; and finally, task allocation among multi-AUV and finding the optimal path for each AUV.

Figure 1

Figure 1. Flowchart of multi-AUV path planning.

Firstly, the determination of sampling points is influenced by the performance of sonar sensors. Sonar sensors possess two key features: they have a greater underwater detection range because sound waves can travel great distances underwater; they are easily affected by the terrain environment (Jensen et al., 2011). On a flat seafloor, omnidirectional active sonar has a circular detection range; however, on a sloping or irregular seafloor, the detection range may become elliptical or more complex in shape. Traditional AUV path planning typically assumes two specific forms for the sonar model: fan-shaped (Sun et al., 2019; Ai et al., 2021) and circular (Huang et al., 2023), both presuming a constant detection radius, i.e., assuming a stable and unchanging marine environment. However, the seafloor topography is often uneven. In such cases, AUV coverage path planning must consider the coupling effect between terrain undulations and the sonar model. One innovation of this paper is the combination of the acoustic simulation software RAM and the sonar equation to forecast the sonar detection range at different positions and in different directions at the same position when determining the sampling points for the task. The minimum detection range across all directions at a certain position is considered the final detection range for that position, acting as a constraint for path planning. This approach ensures comprehensive consideration of the coupling performance between sonar and the environment while minimizing the sampling points of the task area in complex terrain environments.

Secondly, calculating the adjacency matrix of the graph formed by all sampling points requires careful consideration of the influence of ocean currents. Currently, path planning for AUV in ocean currents is a prominent topic in marine engineering (Cao et al., 2019; Yao et al., 2021b). Numerous methods have been proposed and applied for shortest time path planning problem under currents. Traditional algorithms encompass the A* algorithm (Singh et al., 2018), Dijkstra’s algorithm (Wang et al., 2019), heuristic algorithms involve the Glasius Bio-Inspired Neural Network (GBNN) (Yao et al., 2020), improved particle swarm optimization (Chen et al., 2023; Li and Yu, 2023), Improved Artificial Jellyfish Search Algorithm (Guo et al., 2023), and genetic algorithms (Niu et al., 2020). However, these methods are primarily designed for the shortest time path planning between two given points. When directly applied to the problem presented in this paper, which involves a graph with numerous and unevenly distributed sampling points, they encounter the drawback of high computational complexity. An improved algorithm based on the traditional Dijkstra algorithm (Dijkstra, 1959) is proposed to increase the efficiency of solving the adjacency matrix. Unlike Dijkstra, which extracts the point with the smallest path distance from the starting point among the unprocessed grids each time, the improved Dijkstra algorithm updates all points adjacent to the already updated points simultaneously, significantly accelerating the search for the shortest path. However, updating the values of vast points simultaneously compromises the accuracy of the results. To address this issue, the concept of iteration is integrated into the update process, ensuring result accuracy through continuous iteration. Ultimately, the improved Dijkstra algorithm can calculate the adjacency matrix of the graph more rapidly than the traditional Dijkstra algorithm.

Ultimately, the core of multi-AUV path planning is addressing task allocation and determining the optimal path for each AUV. Multi-AUV path planning algorithms can be classified into two categories: centralized and distributed (Zhang et al., 2023). Due to the significant impact of the marine environment on communication among different AUVs, this paper focuses on distributed multi-AUV path planning. For small-scale tasks, heuristic algorithms like Ant Colony Optimization (ACO) (Pendharkar, 2015; Chen et al., 2022a), Genetic Algorithm (GA) (Patel et al., 2020; Dong et al., 2021), Particle Swarm Optimization (PSO) (Geng et al., 2021), and market-based auction algorithms (Zhang et al., 2017) can be used. In the case of large-scale task allocation, clustering methods (Tang et al., 2020) and allocation methods with custom constraint functions (DARP) (Kapoutsis et al., 2017) can be employed. In this study, the number of task points typically ranges in the hundreds. Heuristic algorithms and auction algorithms are slow and have poor convergence. Clustering methods and DARP methods can quickly process these problems, but they are mainly designed for Euclidean planes and perform poorly in non-Euclidean planes with ocean currents. To address this, the paper proposes a combination of the PSO (Kennedy and Eberhart, 1995) algorithm and the ELKAI solver to handle the task allocation problem. In the PSO algorithm, each particle represents a strategy for task allocation. Ensuring the accuracy of the particle fitness values is crucial to achieving optimal task allocation in the PSO algorithm, which requires precise determination of the optimal path for each AUV after task allocation. Determining the optimal path for a single AUV within a given subarea is a NP-hard (Trummel and Weisinger, 1986) problem. To accurately determine the fitness values for each particle, the paper introduces the ELKAI solver, a third-party Python library specifically designed for solving TSP problems. It is known to be capable of finding optimal solutions for problems with up to 315 points, which, considering the limited endurance of AUV, meets the task requirements in most scenarios.

In summary, this paper aims to achieve complete coverage of the task area in the shortest time and proposes a collaborative path planning method for multi-AUV. Building upon previous studies regarding the impact of ocean currents on AUV dynamics, this paper innovatively incorporates spatial heterogeneity of the sonar model into the coverage path planning for multi-AUV. The key benefit is the ability to achieve a more equitable task distribution among multi-AUV and decrease mission time. The main contributions of this paper are as follows:

1) In the coverage path planning for multi-AUV, the sonar model is no longer assumed to be circular or fan-shaped. Instead, this paper thoroughly considers the effects of the marine environment, especially the impact of terrain undulations on sonar detection range. The first step in determining sampling points for coverage path planning involves calculating the detection range at different positions by integrating the acoustic simulation software with the sonar equation. Finally, sampling points are determined based on the varying detection ranges at different positions.

2) An improved Dijkstra algorithm is proposed for calculating the adjacency matrix of numerous sampling points affected by ocean currents. Accurately determining the shortest path between any two sampling points and storing them as an adjacency matrix is essential to facilitate subsequent task allocation and optimal path planning. This paper modifies the search strategy of the Dijkstra algorithm, which exhibits high time complexity, to expedite the solution process and integrates the concept of iteration into it. While ensuring result accuracy, the improved Dijkstra algorithm is faster than the original algorithm and is better suited for solving problems based on the grid modeling approach.

3) The combination of the PSO algorithm and the ELKAI solver achieves task allocation for multi-AUV and path planning for single-AUV. In the PSO algorithm, each particle represents a task allocation strategy, and the ELKAI solver is utilized to determine the optimal paths for each AUV based on the given task allocation strategy. The solutions from the PSO algorithm are input into the ELKAI solver, which then returns the fitness values of the path solutions to the PSO algorithm. Ultimately, the multi-AUV path planning method, which integrates the PSO algorithm with the ELKAI solver, not only ensures an equitable distribution of tasks among multi-AUV but also minimizes the task time for each AUV.

The remainder of the paper is organized as follows: Section II describes the target search problem, including the basic assumptions, map model, sensor model, and problem formation. Section III introduces the consideration of sonar performance and ocean currents in path planning and the proposed method for multi-AUV path planning. Section IV shows the simulation results. We draw the conclusion in Section V.

2 Problem description

This section provides a detailed exposition of the critical issues in coverage path planning for multi-AUV, encompassing fundamental assumptions, map model, sensor model, and the problem formulation.

2.1 Basic assumptions

Figure 2A shows a three-dimensional (3-D) Cartesian workspace. Given that the dynamics of AUV are affected by ocean currents and the sonar detection range is linked to terrain undulation, this paper considers the combined effects of ocean currents and terrain on path planning. To simplify the problem of multi-AUV coverage path planning, this paper makes the following assumptions:

Figure 2

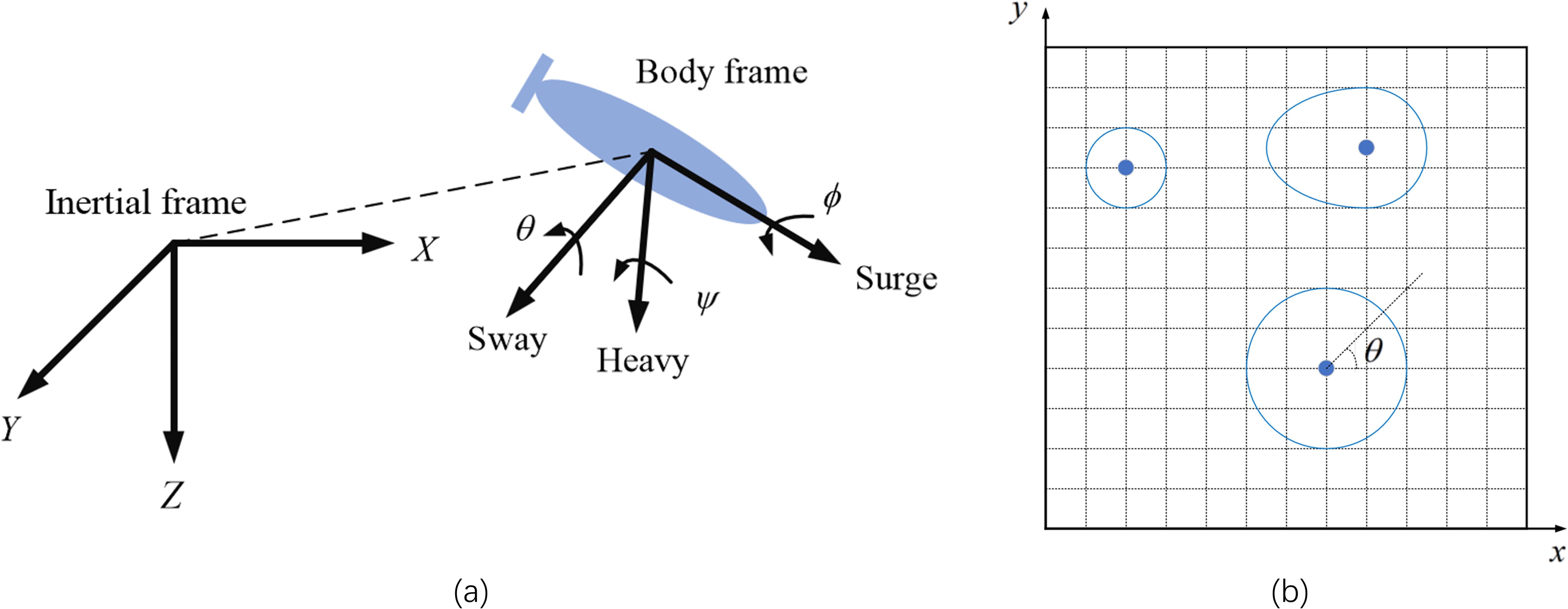
Figure 2. Basic Assumptions: (A) Coordinate systems, (B) Relationship between sonar detection range and variables x, y, θ.

1) Considering the temporal variation of the currents at the same location, the currents for task area is randomly selected from global currents data.

2) When the AUV moves between two adjacent grids, the magnitude and direction of the currents are assumed to be constant.

3) All AUVs have the same fixed output power.

4) All AUVs are equipped with identical acoustic sensors, with detection performance solely affected by seafloor terrain.

5) The sonar detection range at a given location is represented by a square area, with its radius being the minimum detection distance in all directions at that location.

2.2 Map model

The data of seafloor terrain are sourced from the ETOPO2022 dataset provided by the National Oceanic and Atmospheric Administration, and the data of ocean currents are derived from the Global Combined Currents Sample dataset provided by Tidetech. Given that many algorithms addressing coverage path planning problems are based on grid modeling (Zhu and Yang, 2022), for example, Tang (Tang, 2023) applied grid modeling to address the coverage problem of unmanned surface vehicles (USVs), and Shen (Shen et al., 2021) determined the optimal path by partitioning the task area into grids and using the grid information map as input to a neural network. This paper also adopts grid modeling, as depicted by the black dashed lines in Figure 2B, where each grid contains depth information $d(x,y)$ and currents information $\overrightarrow{v}(x,y)$. More information about the impact of ocean currents on AUV dynamics can be found in article (Franchi et al., 2020). In the case where the ocean current’s speed and direction are known, we can determine the AUV’s velocity in any direction at a specific position in space using the formulas provided in the article (Franchi et al., 2020).

2.3 Sensor model

This paper considers the AUV equipped with omnidirectional active sonar. The detection range at any given location can be represented as $r(\theta ,x,y),\theta \in [0,2\pi ],x\in [0,x_0],y\in [y,y_0]$, where $(x,y)$ represents the position, θ represents the angle in the horizontal direction, x₀ represents the length of the horizontal axis of the task area, and y₀ represents the length of the vertical axis of the task area. Many papers do not consider the variations in terrain, assuming $r(\theta ,x,y)=r_0$, where r₀ is a constant (Diniz and Calazan, 2023). However, in practice, terrain undulations are inevitable, leading to varying detection ranges at different locations. Particularly when the AUV is located on a sloping seafloor, the detection ranges in different directions are also different (Northrop et al., 1968; Rousseau et al., 1985), hence both $(x,y)$ and θ variables cannot be ignored. The sonar detection range, considering the three variables x, y, θ might be depicted by the blue curve in Figure 2B.

2.4 Problem formation

This paper aims to consider the sonar performance and currents in multi-AUV coverage path planning. Firstly, the sampling points determined based on the sonar detection range are shown in Figure 3A. All the sampling points $P_j,j=1,2,···,k$ in Figure 3A should satisfy the following requirements:

Figure 3

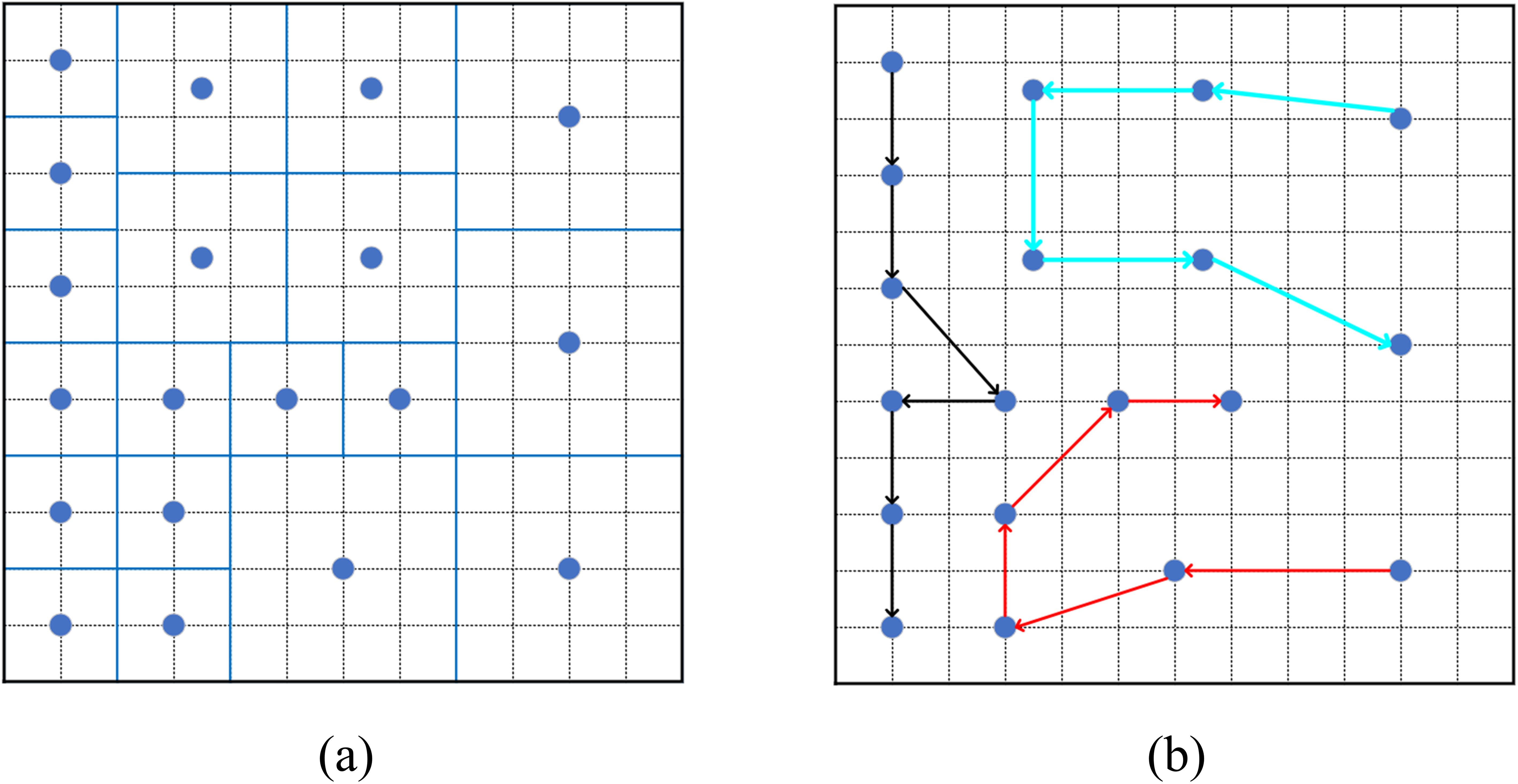
Figure 3. Illustration of coverage path planning based on grid modeling: (A) Complete coverage with different detection ranges (B) task allocation for multi-AUV and shortest time path for single-AUV.

$\begin{array}{ll}{P}_1{\cup }^{ }{P}_2{\cup }^{ }\cdots {\cup }^{ }{P}_k=P& (1)\end{array}$

$\begin{array}{ll}\text{min }(P_1{\cap }^{ }{P}_2{\cap }^{ }\cdots {\cap }^{ }{P}_k)& (2)\end{array}$

Equation 1 ensures that all sampling points completely cover the target area, while Equation 2 aims to minimize the overlap between sampling points. These two equations collectively guide the determination of sampling points based on sonar performance.

Once the sampling points are determined based on Equations 1 and 2, they need to be allocated to different AUVs, and the optimal paths for each AUV need to be identified. This requires a reasonable distribution of task points among all AUVs and ensuring that each AUV can find the shortest path within the designated sampling points. In Figure 3B, arrows of different colors represent the task points and corresponding paths for an AUV. Assuming the path corresponding to the ith robot is represented by $L_i,i=1,2,···,n$. The final path for all AUVs should satisfy:

$\begin{array}{ll}\left|L_1\right|\approx \left|L_2\right|\approx \dots \approx \left|L_n\right|& (3)\end{array}$

$\begin{array}{ll}\text{min }(\text{max }(\left|L_1\right|,\left|L_2\right|,\dots ,\left|L_n\right|)& (4)\end{array}$

$\begin{array}{ll}\forall L_k{\cap }^{ }{L}_m=\varnothing ,k,m=1,2,\dots ,n,k\ne m& (5)\end{array}$

$\begin{array}{ll}{L}_1{\cup }^{ }{L}_2{\cup }^{ }\dots {\cup }^{ }{L}_n=L& (6)\end{array}$

Equation 3 ensures an equitable distribution of workload among multi-AUV, enabling effective participation of all AUVs in the task; Equation 4 minimizes the workload of the AUV with the largest task, as the completion time depends on the AUV finishing last; Equation 5 prevents task area overlap for AUVs, reducing collision risk; Equation 6 guarantees complete coverage of the task area by ensuring the union of all AUV task areas covers the entire task area.

This paper aims to determine sampling points based on Equations 1 and 2 in conjunction with sonar performance, and then seeks to allocating sampling points to each AUV based on Equations 3–6 uniformly in ocean currents, ultimately achieving complete area coverage.

3 Proposed algorithm

This section provides a detailed introduction to solve the sonar performance, ocean currents, and multi-AUV path planning.

3.1 Sonar performance

Many papers overlook the fluctuation of sonar performance in different environments and assume a constant sonar detection radius. However, in reality, seafloor terrain is diverse and complex, significantly affecting the sonar performance. This section addresses the determination of sonar detection range and the selection of sampling points.

3.1.1 Determination of detection range

In the field of underwater acoustics, the sonar equation comprehensively incorporates the unique phenomena and effects related to sound propagation, as well as the influence of the target’s acoustic performance on the design and application of sonar equipment. This paper focuses on omnidirectional active sonar, encompassing parameters like the radiated sound source level (SL), receiving directivity index (DI), transmission loss from the sound source to the target (TL), target strength (TS), detection threshold of the temporal-spatial processor (DT), and background interference from environmental noise, characterized by a sound level of (TS). The active sonar equation is denoted as:

$\begin{array}{ll}SL-2TL+TS-(NL-DI)=DT& (7)\end{array}$

In reality, the parameters SL, DI, TS, DT, and NL are generally assumed to be constant. The sonar equation enables the estimation of the detection range by determining the transmission loss from the source to the target. This paper employs the acoustic software RAM (Collins, 2020) to calculate the transmission loss across different terrains. However, in ocean waveguides, fluctuations in transmission loss complicate the determination of the efficient detection range. So determining a unique propagation loss requires fitting the actual transmission loss, and an empirical formula for transmission loss in the ocean is:

$\begin{array}{ll}TL=a\text{ lg }r+\alpha r& (8)\end{array}$

The first term represents the spreading transmission loss, and the second term represents the absorption transmission loss, with a and α being constant coefficients related to the environment. Paper (Honghan et al., 2020) uses a Table lookup method to determine the coefficients, but this approach may lead to errors compared to actual values. As a result, in this paper, the method of fitting the simulation data by empirical formula is adopted, which can better adapt to the real ocean environment.

3.1.2 Determination of sampling points

After determining the sonar detection range, the next step is to identify sampling points in task area. This section demonstrates the process using the sea area defined by the coordinates N29.9979°N30.2062°, E124.0396°-E124.2479°, as shown in Figure 4A. Initially, a stratification of the seafloor is conducted. Figure 4A shows that the seafloor can be roughly categorized into two types: flat, and sloping, the stratified seafloor is shown in Figure 4B. The process of stratification can speed up the calculation without significantly affecting the accuracy of the results.

Figure 4

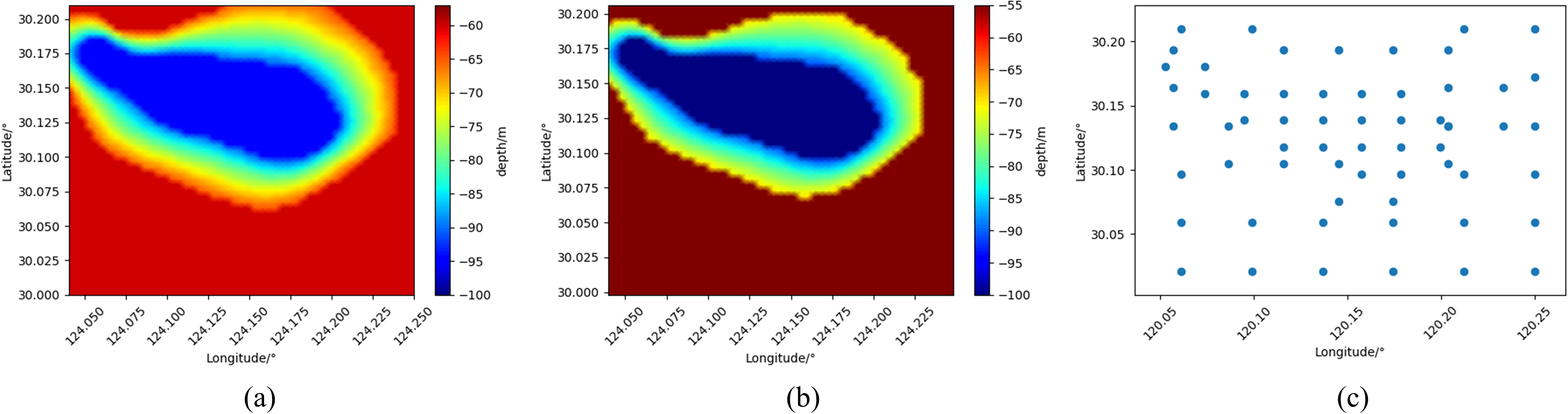
Figure 4. Determination of sampling points. (A) The actual seafloor (B) The simplified seafloor, (C) The task points.

Following the presentation of the simplified seafloor in Figure 4B, the subsequent step involves determining the sampling points corresponding to the three types of seafloors. The sonar detection ranges within these areas are calculated by combining the acoustic software RAM and the sonar equation. Due to the roughly uniform detection ranges within the same type of seafloor, we evenly sample across the entire seafloor area, corresponding to each type of detection range. Subsequently, the intersection of the first two columns is taken to obtain the final sampling points for each type of seafloor. Finally, the sampling points of the three types of seafloor are merged into a single map to obtain the sampling points based on sonar detection performance, as depicted on the right in Figure 4C.

3.2 Calculation of adjacency matrix

Once the distribution of sampling points within the task area, as shown in Figure 4C, is determined, furthermore, after the AUV’s movement speed between any two adjacent grids in the grid model is also determined, calculating the shortest time between any two sampling points becomes essential. Considering the influence of currents, this paper proposes the improved Dijkstra algorithm. At each step, the Dijkstra algorithm selects the node closest to the starting node from those whose shortest paths have not been determined, using this node as a hub to update the shortest path distances of other nodes. Nevertheless, the computational complexity of the Dijkstra algorithm is $O(n^2)$ (Verma et al., 2021), resulting in slower computation when handling a large number of sampling points. Therefore, this paper proposes an improved Dijkstra algorithm with reduced computational complexity to $O(n^{3/2})$.

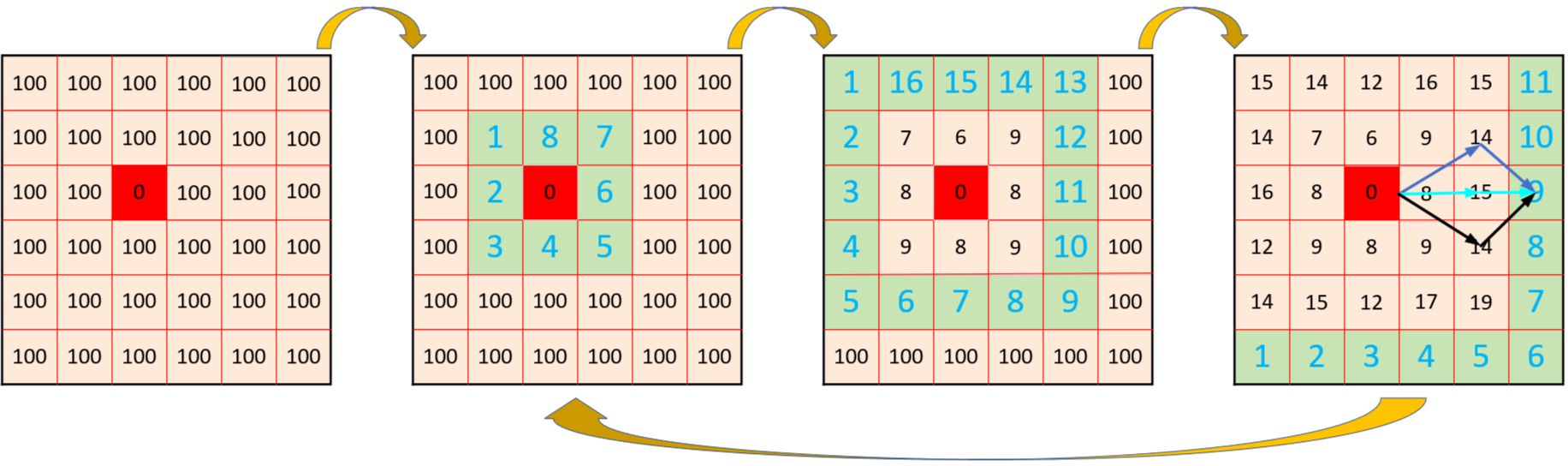
Figure 5 depicts the fundamental process of the improved Dijkstra algorithm. The figure on the left represents the initial state of the grid modeling after selecting the starting grid. The grid values indicate the shortest time from the starting grid. Initially, the value of the starting grid is set to 0, while the values of other grids are set to a significantly larger value than the actual value. The algorithm commences from the initial state, expanding one ring outward in each step, and computing the values of the new grids, as demonstrated by the green grids in the three figures on the right side of Figure 5. The numbers on the green grids denote the sequence of solution for all green grids in this step. The values of all grids in the entire area are updated by continuous stepping.

Figure 5

Figure 5. Improved Dijkstra algorithm.

The arrows in the right figure of Figure 5 illustrate how single grid values are updated. Each grid updates its value by using the neighboring updated grids as bridges, as shown by the three colored arrows. The minimum value among the three colored paths will be selected.

The improved Dijkstra algorithm updates the values of numerous grids with each step, greatly affecting the accuracy of the results. Therefore, we choose to re-update the results of the last iteration, as indicated by the leftward arrow in the lower part of Figure 5. Based on the results of the last iteration, we re-step from the initial position until the values of all grids are the same as in the last iteration. This paper introduces the adjacency matrix, which represents the connections between all vertices in a graph (Brede, 2012).

This study conducts simulation experiments to calculate the adjacency matrix using both the Dijkstra algorithm and the improved Dijkstra algorithm. The results indicate that the two methods produce consistent results, and multiple simulations demonstrate that the improved Dijkstra algorithm calculates the adjacency matrix faster. For example, with the sampling points and currents depicted in Figure 6C and Figure 6B, the improved Dijkstra algorithm takes 85.190563s to calculate, whereas the Dijkstra algorithm takes 2042.24464s.

Figure 6

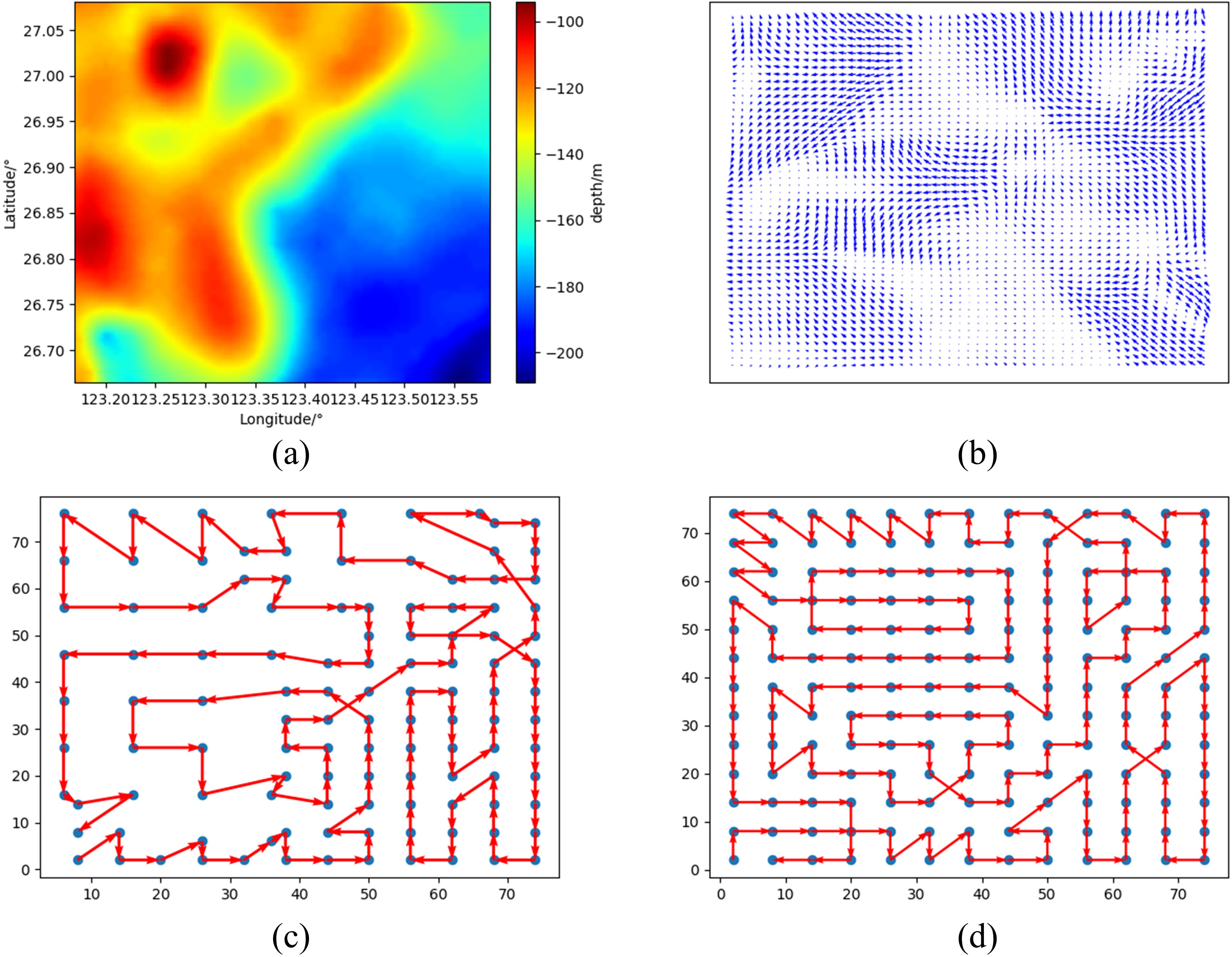
Figure 6. Environmental information for simulation 1: (A) Seafloor terrain, (B) Ocean currents, (C) Path for considering sonar performance, (D) Path for not considering sonar performance.

3.3 Task allocation and path planning for multi-AUV

After determining the sampling points and the adjacency matrix, the next step is the core of this paper,path planning for multi-AUV. Multi-AUV path planning can be divided into two parts: task allocation of multi-AUV and shortest time path solution of single-AUV. This paper combines the Particle Swarm Optimization (PSO) algorithm with the ELKAI solver to solve the task allocation for multi-AUV and to find the shortest time paths for single-AUV. Each particle in PSO is regarded as a task allocation strategy; the ELKAI solver solves a particle for the shortest time path corresponding to each AUV and feeds the path results back to the PSO algorithm for updating until convergence.

3.3.1 PSO for target allocation

In the PSO algorithm, individuals are referred to as particles, and each swarm consists of N particles randomly initialized in a D-dimensional search space (Roshanzamir et al., 2020). During the search process, $X_{id}^t$ represents the velocity and position of the ith particle in the d dimension at the t iteration. In this paper, it is assumed that each dimension of a particle corresponds to a ray, and any two adjacent rays form a sub-region, which corresponds to the task area of an AUV, as shown in Figure 7. The three rays divide the task area into three parts, each part corresponding to the task area of one AUV. By continuously adjusting the angles of the three rays through PSO, the task areas of the three AUVs are evenly distributed.

Figure 7

Figure 7. Region division by PSO.

To determine the best weighting factor, a set of randomly distributed points will be generated for testing different weighting factors. The range of values for the weighting factors is [0,4], ten sets of random initial values will be generated for the simulation, and the group with the best results will be selected as the weighting factor in subsequent simulations.

3.3.2 ELKAI solver for Shortest time path

After determining the method of task allocation, as shown in Figure 7, a key challenge is to find the shortest time path for the AUV within the sub-region. To address this issue, this paper introduces the ELKAI solver. The ELKAI solver is a traveling salesman problem (TSP) problem solver based on the LKH algorithm (Helsgaun, 2017), capable of solving TSP problems with a scale up to N=315 to find the optimal path. In the context of this paper, this refers to calculating the shortest time path that traverses all specified points. Considering the limited endurance and mobility of AUV, 315 points meet the requirements of the vast majority of cases.

3.3.3 Multi-AUV path planning

Figure 1 depicts the flowchart of the proposed method in this paper. Initially, the seafloor terrain is known and categorized into flat seafloor or sloping seafloor. This categorization simplifies the problem-solving process. Then, the acoustic software RAM is used to calculate the acoustic transmission loss, and the sonar detection range is determined based on transmission loss and the sonar equation. The sampling points are determined based on the different detection ranges at different locations. Subsequently, in marine environment with ocean currents, all target points form a directed and weighted graph. The improved Dijkstra algorithm is used to calculate the adjacency matrix of the graph Finally, the PSO algorithm is employed to conduct task allocation. The sub-adjacency matrix is extracted from the adjacency matrix for each divided sub-region and fed into the ELKAI solver to determine the optimal traversal sequence. Ultimately, through iterations of the PSO algorithm and the ELKAI solver, multi-AUV path planning problem is solved.

4 Simulation results

In subsequent simulation experiments, the acoustic simulation software and the improved Dijkstra algorithm run in the MATLAB environment. Task allocation and path planning, which integrate the Particle Swarm Optimization (PSO) algorithm with the ELKAI solver, are conducted in the PyCharm environment. Although the influence of currents on path planning has been extensively studied, the integration of sonar performance into path planning research remains relatively unexplored. Therefore, this section initially validates the importance of considering sonar performance in path planning and subsequently verifies the effectiveness of the proposed multi-AUV path planning method.

4.1 The importance of considering sonar performance

Currently, research on path planning that incorporates sonar performance is relatively limited. This research often assumes that the detection range of sonar is constant and neglects the relationship between sound waves and the marine environment. To validate the importance of considering the sonar performance in path planning, this section compares two scenarios: one that considers the influence of sonar performance, and another that does not. After determining the required sampling points for both scenarios, the optimal path for a single AUV is calculated using the ELKAI solver, and the path time is compared under the two assumptions. The shorter the path time, the more important it is to consider sonar performance.

The simulations were carried out using PyCharm and an Intel(R) Xeon(R) Gold 6226R CPU running at 2.90 GHz and 2.89 GHz, respectively, as well as 256 GB of RAM.

4.1.1 Simulation 1

In Simulation 1, the task area is N19.1646°-N19.4979° and E112.0813°-E112.4146°. Figure 6A illustrates the seafloor terrain of the task area, featuring a shallow sea area of 100-130m on the left and a deep sea area of 160-200m on the right. The sea depth is assumed to be 120m on the left and 180m on the right. Additionally, Figure 6B displays the corresponding currents. According to transmission loss at different depths, the sonar detection range is estimated to be approximately 2.25km for the shallow sea and 1.35km for the deep sea. The final sampling points, determined by the detection ranges, are depicted as blue dots in Figure 6C. The improved Dijkstra algorithm is used to calculate the adjacency matrix of the graph combining the Figures 6B, C. Figure 6D illustrates the sampling points needed to cover the entire area with a fixed detection range. The adjacency matrix is also obtained using the improved Dijkstra algorithm.

To compare the paths based on the two kinds of sampling points, this section employs the ELKAI solver to find the shortest path for a single AUV to traverse all sampling points. The resulting paths are depicted as red arrows in Figures 6C, D, with the final times for the paths in Figures 6C, D being 80.275h and 97.4h, respectively. Under the premise that both sampling points can cover the task area, the path time for the sampling points determined based on sonar performance is 21.3% less than that of equidistant sampling points. These results indicate that considering the sonar performance helps to reduce unnecessary sampling points and decrease the workload.

4.1.2 Simulation 2

In simulation 2, the task area exhibits significant variations in seafloor terrain, spanning geographic positions from N19.8729° to N20.2062°, and from E113.8313° to E114.1646°, as shown in Figure 8A, the depths of the task area range from 150m to 450m, and the currents are depicted in Figure 8B. Within this area, the seafloor was categorized into three types: shallower on the upper side, deeper at the lower right corner, and medium depth at the lower left corner. Similar to Simulation 1, the sampling points are represented as blue dots in Figure 8C, while those sampling points determined based on a constant sonar detection range are shown in Figure 8D. Employing a processing flow akin to Simulation 1, the resulting paths are depicted as red arrows in Figures 8C, D, displaying path times of 104.2h and 147.3h. The path time, considering sonar performance, was reduced by 29.3% compared to paths without considering sonar performance.

Figure 8

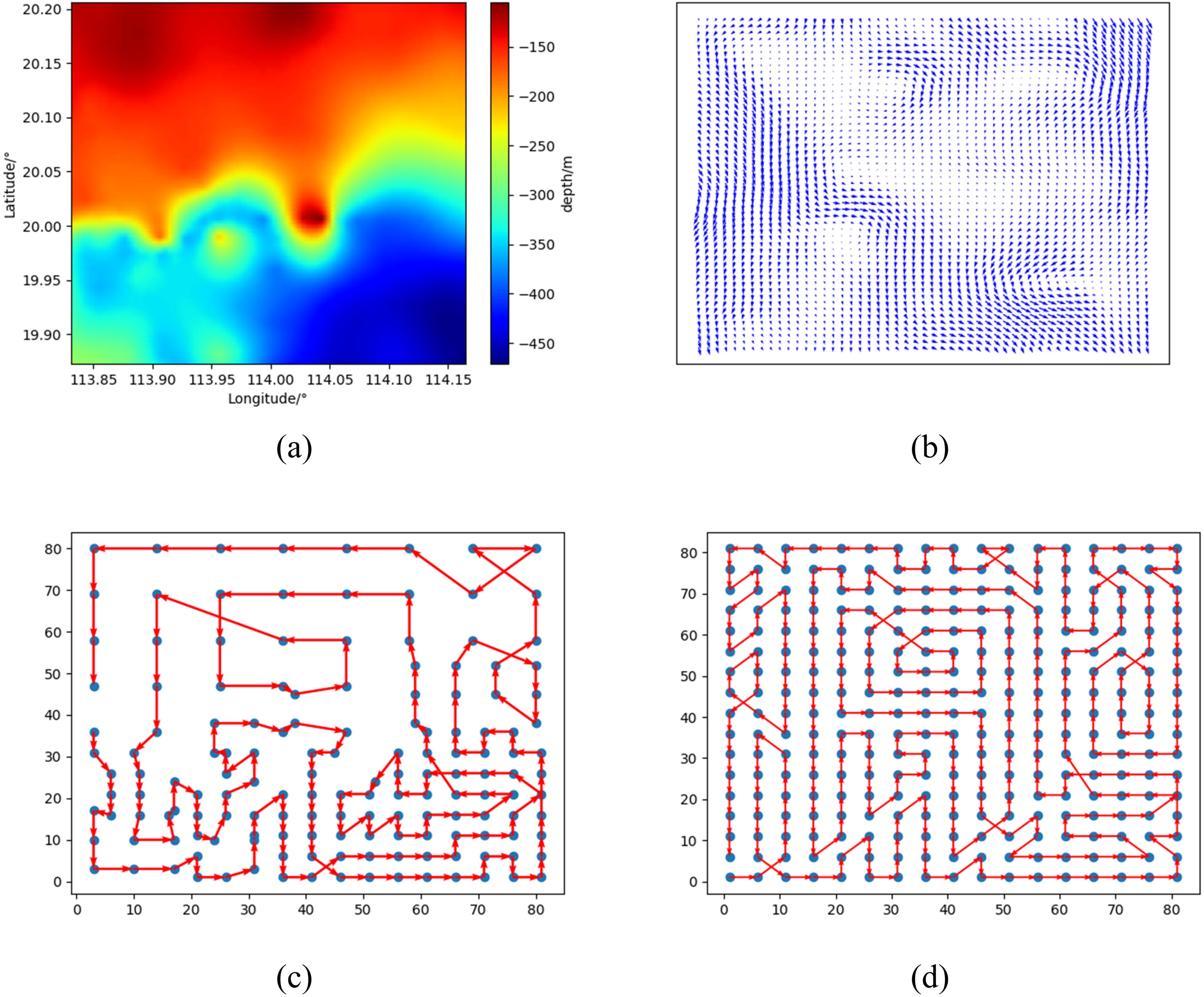
Figure 8. Environmental information for simulation 2: (A) Seafloor terrain, (B) Ocean currents, (C) Path for considering sonar performance, (D) Path for not considering sonar performance.

A comparative analysis of the two simulations reveals that a lower number of sampling points based on sonar performance can significantly decrease task times, especially in areas with substantial seafloor terrain changes. This analysis highlights the crucial role of considering sonar performance in enhancing the quality of path planning solutions and indicates that there is significant practical significance of incorporating sonar performance into AUV path planning.

4.2 Method proposed for multi-AUV path planning

Section 4.1 demonstrates the significance of integrating sonar performance into path planning. To validate the effectiveness of the multi-AUV path planning method proposed in this paper, it is compared with the hybrid genetic algorithm with variable neighborhood search from the literature (Cai et al., 2023) and the clustering method from the literature (Chen et al., 2022b). The effectiveness of these three methods is evaluated by comparing the path times planned for all AUVs within the same task area. These three methods will be abbreviated as PSO, GA and Clustering.

4.2.1 Simulation 3

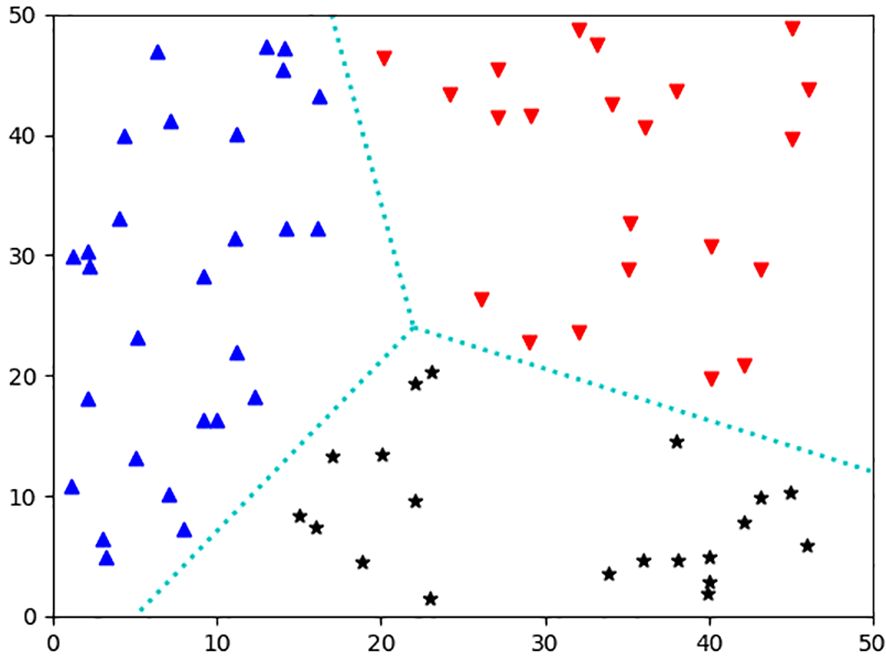
In Simulation 3, the task area spans N26.6646°-N27.0812°, E123.1687°-E123.5854°, the seafloor terrain is shown in Figure 9A, and the currents are shown in Figure 9B. In Figure 9A, the color map of the seabed depth can be roughly categorized into red, green, and blue. The simulation revealed that the sonar detection ranges in the green and blue depth regions are relatively similar. The sea depth within the area is categorized into two scenarios: shallower waters with a depth of 115m and deeper waters with a depth of 150m. The sonar detection ranges under these two conditions are determined, and all sampling points are identified based on these distances, as denoted by the blue dots in Figure 9C. By combining the sampling points with the currents in Figure 9B, the adjacency matrix of all sampling points is calculated using the improved Dijkstra algorithm. The resulting paths obtained by the three methods are depicted in Figure 9A, Figures 9B, C, where each color represents a path for an AUV (Ai et al., 2021).

Figure 9

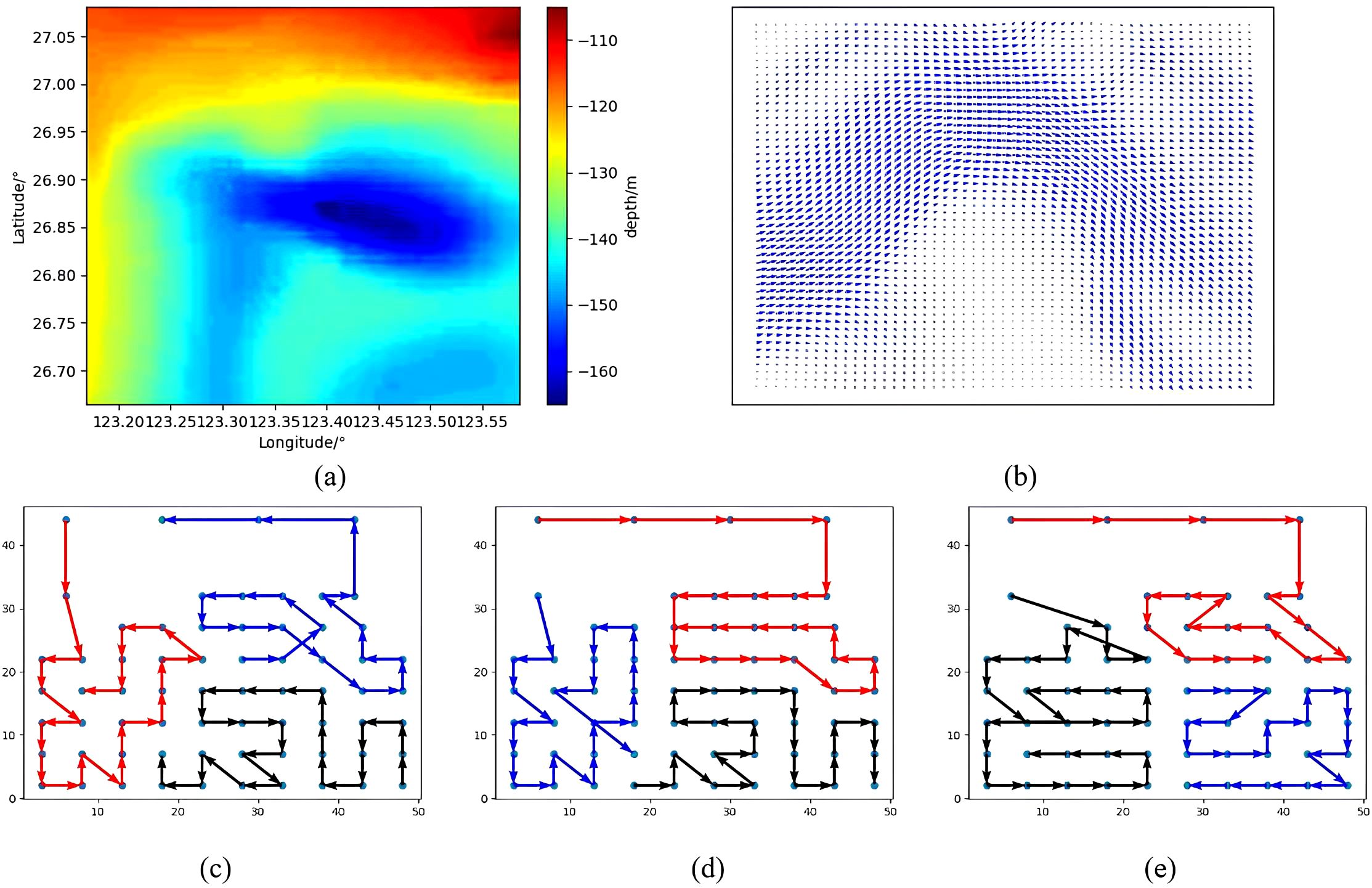
Figure 9. Environmental information for simulation 3: (A) Seafloor terrain, (B) Ocean currents, (C) Path planning results of PSO, (D) Path planning results of GA, (E) Path planning results of Clustering.

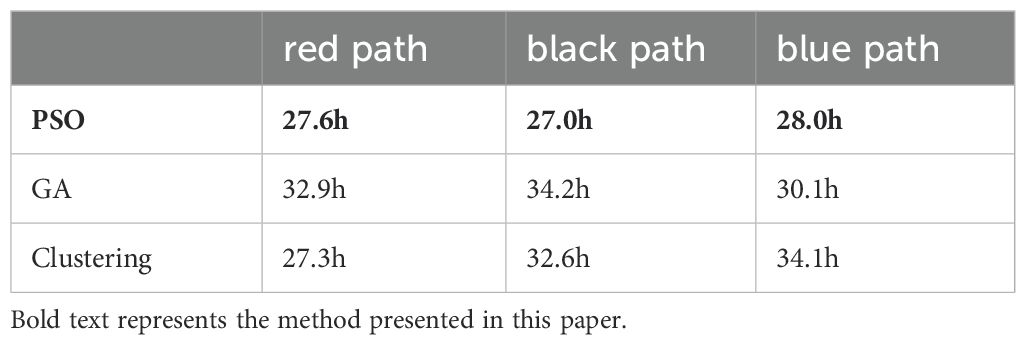
The detailed results of the path planning of the three methods are shown in Table 1. In Table 1, the task allocation method proposed in this paper has an average time of 27.5h, with the longest task taking 28h, representing a 3.7% increase compared to the shortest task time. The genetic algorithm has an average time consumption of 32.4h for three paths, with the longest task taking 34.3h, a 14.3% increase compared to the shortest task time. The clustering algorithm has an average time consumption of 31.3h for three paths, with the longest task taking 34.1h, a 24.9% increase compared to the shortest task time. The results in Table 1 demonstrate that the combination of the PSO and ELKAI solver achieves better results in speeding up tasks and minimizing the difference in tasks among different AUVs.

Table 1

Table 1. Results of simulation 3.

4.2.2 Simulation 4

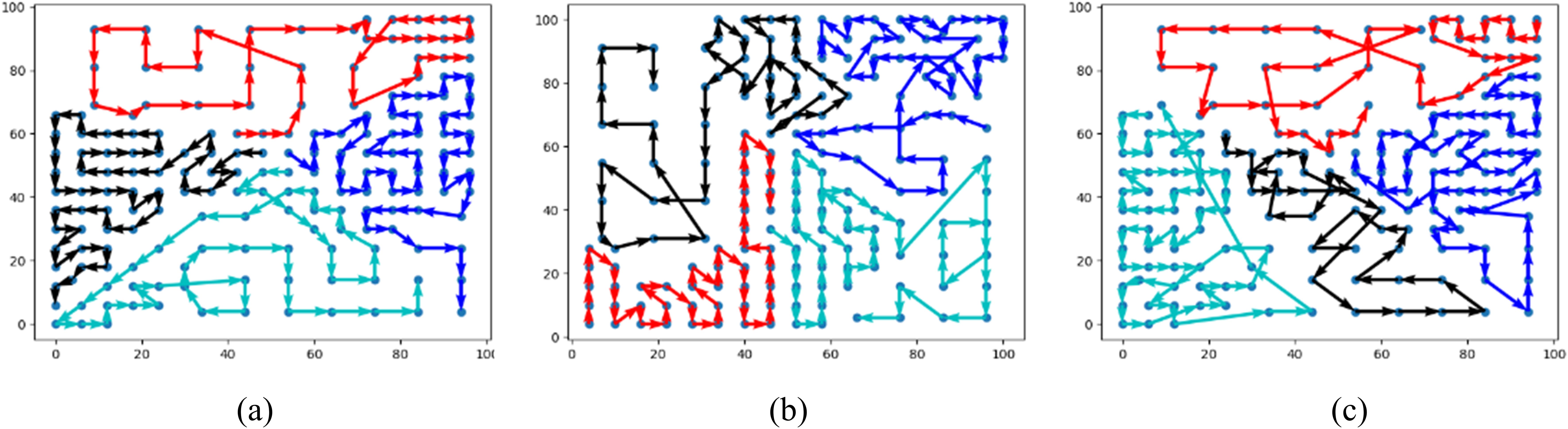
In Simulation 4, the task area spans from N26.2479° to N28.3313°, and from E122.4979° to E124.5813°. The seafloor terrain is shown in Figure 10A, and the corresponding currents are shown in Figure 10B. The water depth in this area can be divided into three layers: shallow waters (<90m), deep waters (>140m), and slope waters. Assuming average depths of 80m for shallow waters and 150m for deep waters, with a fixed slope between them. The sampling points are determined based on the detection range, as indicated by the blue dots in Figure 10C.

Figure 10

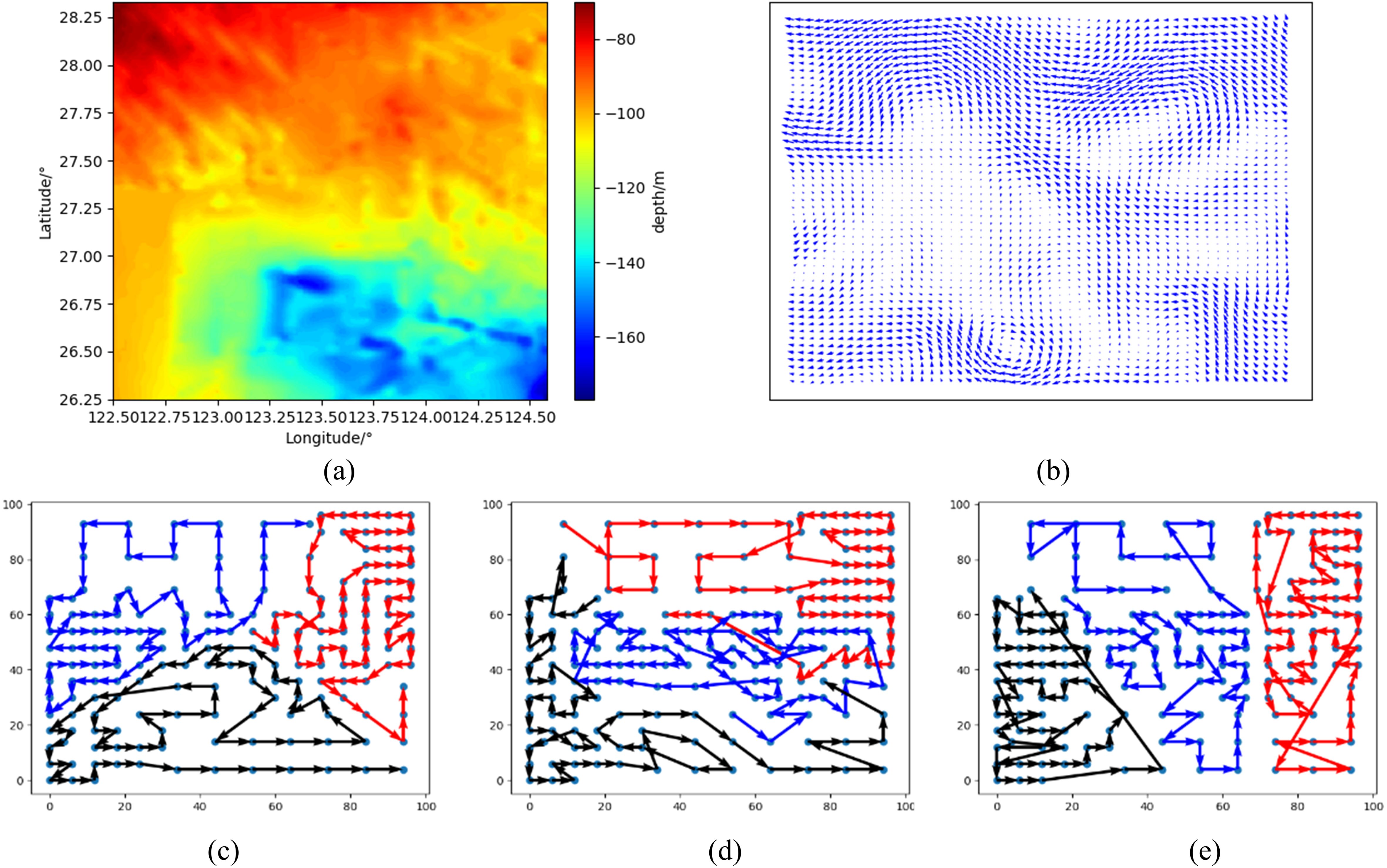
Figure 10. Environmental information for simulation 4: (A) Seafloor terrain (B) Ocean currents, (C) Path planning results of PSO, (D) Path planning results of GA, (E) Path planning results of Clustering.

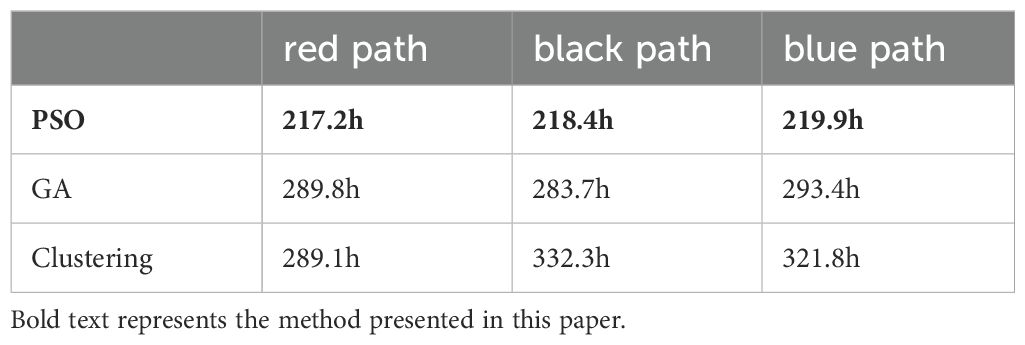
For Simulation 4, the time of the paths corresponding to the three methods is presented in Table 2. The task allocation method proposed in this paper has an average time of 218.5h, with the longest time consumption at 219.9h, reflecting a 1.2% increase compared to the shortest time. The genetic algorithm has an average time consumption of 289.0h for three paths, with the longest time consumption being 293.4h, reflecting a 4.1% increase compared to the shortest time. The clustering algorithm has an average time consumption of 314.4h for three paths, with the longest time consumption at 332.3h, reflecting a 15.0% increase compared to the shortest time. The results in Table 2 also demonstrate that the combination of PSO and ELKAI achieves better results in reducing task time and minimizing the difference in tasks among different AUVs.

Table 2

Table 2. Results of simulation 4.

4.2.3 Simulation 5

The simulations 3 and 4 focus on the path planning problem of three AUVs, while the simulation 5 focuses on the path planning problem of four AUVs. Simulation 5 utilizes uses the same environment as Simulation 4 but increases the number of AUVs. The final paths of the AUV is shown in Figure 11.

Figure 11

Figure 11. Path planning for four AUVs of Simulation 5: (A) PSO (B) GA (C) Clustering.

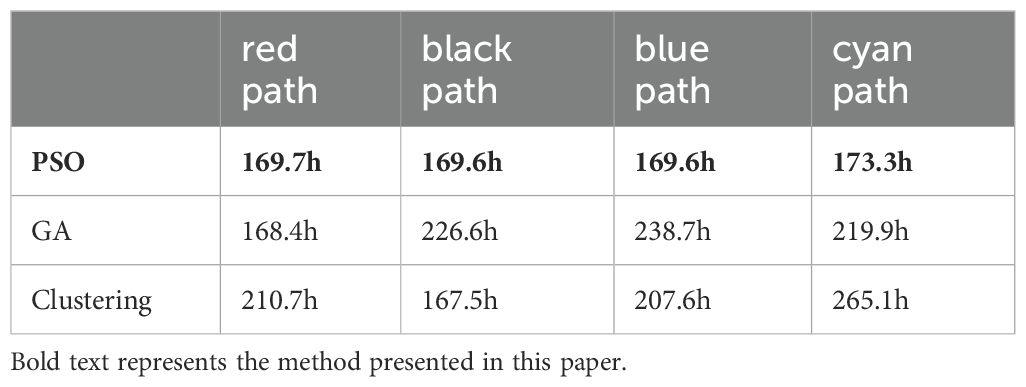
Table 3 presents the paths time for the three methods employed in Simulation 5. The task allocation method combining PSO and ELKAI has an average time of 170.6h, with the longest time at 173.3h, reflecting a 2.2% increase compared to the shortest time. The genetic algorithm has an average time of 213.4h, with the longest time at 238.7h, reflecting a 40.2% increase compared to the shortest time. The clustering algorithm has an average time of 212.7h, with the longest time at 265.1h, reflecting a 58.3% increase compared to the shortest time. The results in Table 3 intuitively demonstrate that the PSO-based optimization algorithm proposed in this paper achieves better performance in reducing average time consumption and minimizing the time difference between tasks of different AUVs, particularly showing robustness as the number of AUVs increases.

Table 3

Table 3. Results of simulation 4.

The aforementioned three groups of experimental simulations indicate that task allocation and path planning based on the combination of PSO and ELKAI ensures uniformity in allocation when dealing with the task allocation of multi-AUV and large-scale task points. This method also achieves the shortest path solution for a single AUV. On the contrary, the genetic algorithm is less effective than the proposed method due to poor convergence when dealing with large-scale task allocation and path planning, and the clustering algorithm is fails to guarantee the equal distribution of tasks when dealing with non-Euclidean space with ocean currents.

4.3 Statistical results in random scenarios

Simulations 3, 4, and 5, combined with actual seafloor terrain and currents, have preliminary validated the effectiveness of the proposed method. Further simulations are necessary to validate the robustness of the combination of PSO and ELKAI. This paper conducts two sets of random simulations to solve the multi-AUV path planning problem, one set for three AUVs and one set for four AUVs. The experimental process is roughly divided into two steps, the first step involves randomly generating sampling points within a given area, and the second step involves randomly extracting currents from the Global Combined Currents Sample dataset to combine with the generated sampling points. All task areas are assumed to be square regions with a width of 100km.

4.3.1 Simulation 6

Three AUVs were used to cover the task area, with the number of sampling points determined by the formula $n,n=130+5·i,i=0,1,\cdots ,29$. Path planning was conducted using the three methods mentioned above, and the statistical results are shown in Figures 12A, B. Figure 12A displays the maximum AUV task time for each method, reflecting the task completion time. Figure 12B illustrates the difference between the maximum and minimum task times, indicating the uniformity of task distribution. The most crucial factor is the maximum AUV task time, as it determines the overall task completion time when the last AUV finishes. From Figure 12A, it is clear that the maximum task time of the proposed method consistently outperforms the other two methods, indicating that the paths planned by this method achieve coverage earlier. Figure 12B shows that the difference between the maximum and minimum task times for the proposed method is the smallest, indicating a more balanced task distribution compared to the clustering method, which exhibits the largest discrepancy.

Figure 12

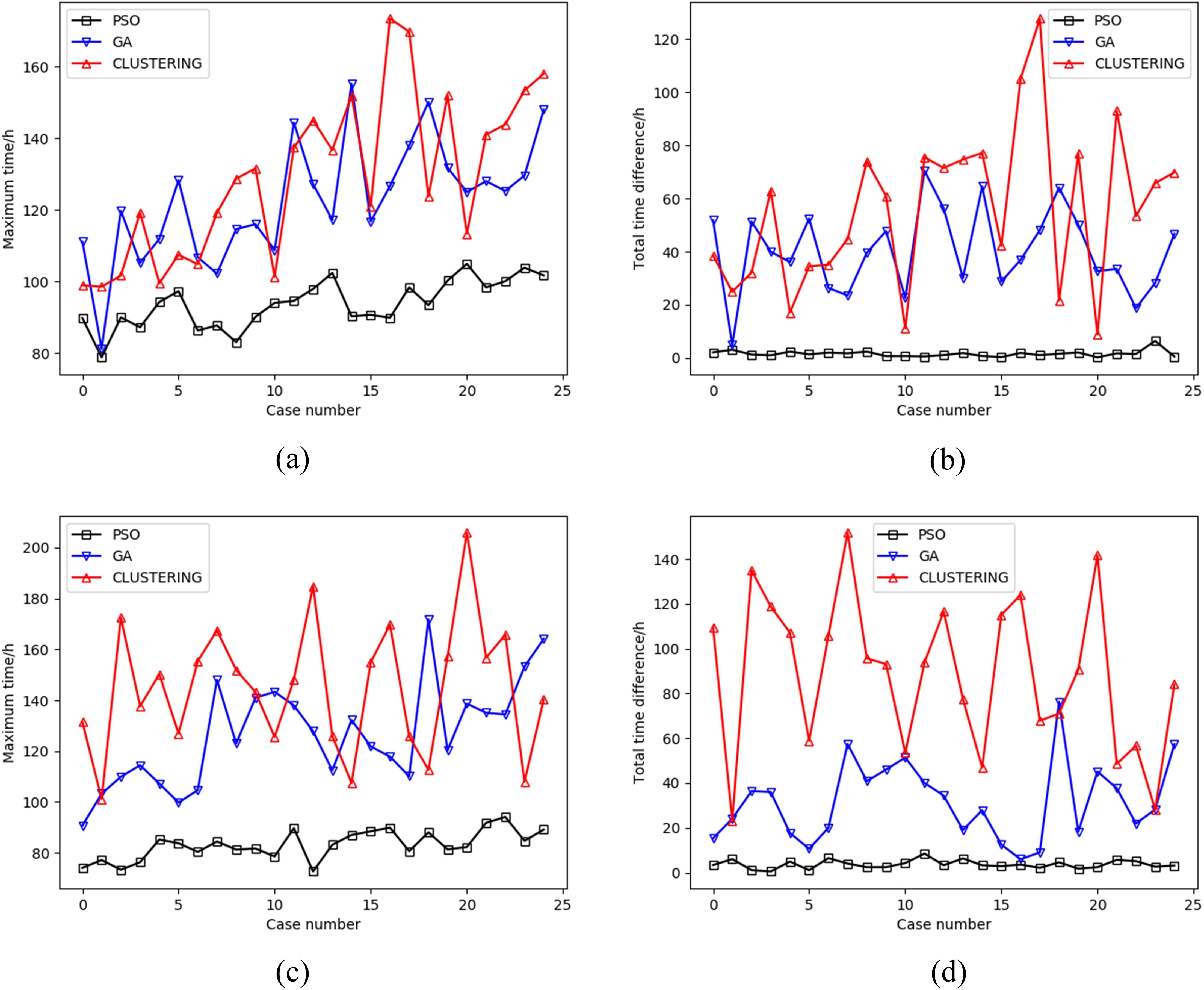
Figure 12. Statistical result of Simulation 6 and Simulation 7: (A) Maximum task time of Simulation 6, (B) The difference between the maximum task time and the minimum task time of Simulation 6, (C) Maximum task time of Simulation 7, (D) The difference between the maximum task time and the minimum task time of Simulation 7.

4.3.2 Simulation 7

Simulation 7 focuses on path planning for four AUVs, with a larger number of sampling points compared to simulation 6. It sets n satisfies $n=180+5·i,i=0,1\cdots 29$. The final paths for the four AUVs are carried out using the three methods mentioned above, and the statistical results for task allocation are shown in Figures 12C, D. Figure 12C shows that the method proposed in this paper consistently outperforms the other two methods, with a more pronounced advantage than in the scenario with four AUVs, highlighting the stronger robustness of the method when dealing with large sampling points. Figure 12D demonstrates that the task allocation proposed in this paper remains stable for four AUVs, whereas the clustering method exhibits more noticeable fluctuations when facing large populations.

According to the simulation results from Tables 1–3, and the statistical results from Figure 12, we draw the following conclusions: (1) The combination of PSO and ELKAI achieves a more balanced task distribution, ensuring efficient use of multi-AUV; (2) the combination of PSO and ELKAI consistently ensures that the maximum task time is less than that of other methods, allowing the completion of multi-AUV coverage tasks to be ahead of the other two methods; (3) the combination of PSO and ELKAI is more pronounced when dealing with multi-AUV and a large number of target points, indicating a wider range of applications for the method.

5 Conclusions

This paper proposes a multi-AUV path planning method that takes into account sonar performance and ocean currents. The core of this method involves using the PSO and ELKAI in combination to realize multi-AUV task allocation and path solving. The detailed solution steps of this method are as follows: Firstly, the sampling points required for target search are determined based on the sonar detection range. Secondly, the improved Dijkstra method is adopted to solve the adjacency matrix of the graph formed by the sampling points under the ocean currents. Finally, the PSO algorithm is used for task allocation, and the ELKAI solver is used to solve the shortest time path for each AUV, and multi-AUV path planning is realized through continuous iteration of PSO and ELKAI. The following conclusions can be drawn from the simulation results:

1) Incorporating sonar performance into the AUV path planning makes the sampling points needed to be traversed closer to reality, which is conducive to reducing the number of sampling points and finally reduces the mission time compared to not considering the sonar performance.

2) The improved Dijkstra algorithm updates a large number of grids under ocean currents simultaneously and introduces the idea of iterative updating to ensure the accuracy of the results, significantly improving solving speed of calculating the adjacency matrix compared to the traditional Dijkstra algorithm.

3) The method of combining PSO and ELKAI solver achieves a more balanced task allocation and finds the shortest time path for all AUVs, reducing the mission time compared to the hybrid genetic algorithm with variable neighborhood search and the clustering method.

Despite the above advantages, the method proposed in this paper has limitations, such as being inapplicable when the number of sampling points is low or the number of AUVs is particularly high. Expanding the applicability of our method to a broader range is a future research direction for this paper.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

XM: Conceptualization, Formal analysis, Methodology, Validation, Writing – original draft, Writing – review & editing. WG: Methodology, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China under Grant Nos. 52071309 and 52001296, the Taishan Scholars under Grant No. tsqn201909053, the Fundamental Research Funds for the Central Universities, Grant/Award Numbers: 202065005 and 862001013102.

Acknowledgments

I would like to thank my supervisor WG, for their invaluable guidance, encouragement, and patience throughout this research process. Their expertise and insights have been instrumental in shaping my work. The authors thank the reviewers for their suggestions and comments to improve the quality of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai B., Jia M., Xu H., Xu J., Wen Z., Li B., et al. (2021). Coverage path planning for maritime search and rescue using reinforcement learning. Ocean Eng. 241, 110098. doi: 10.1016/j.oceaneng.2021.110098

Crossref Full Text | Google Scholar

Brede M. (2012). Networks—an introduction. Mark E. J. Newman., (2010, Oxford University press.) $65.38, £35.96 (hardcover), 772 pages. Artif. Life 18, 241–242. doi: 10.1162/artl_r_00062

Crossref Full Text | Google Scholar

Cai W., Zhang S., Zhang M., Wang C. (2023). Improved binn-based underwater topography scanning coverage path planning for auv in internet of underwater things. IEEE Internet Things J. 10, 18375–18386. doi: 10.1109/JIOT.2023.3280035

Crossref Full Text | Google Scholar

Cao X., Sun C.-y., Chen M.-z. (2019). Path planning for autonomous underwater vehicle in time-varying current. IET Intelligent Transport Syst. 13, 1265–1271. doi: 10.1049/iet-its.2018.5388

Crossref Full Text | Google Scholar

Chen M., Guo S., Zhu D. (2023). Motion planning for an under-actuated autonomous underwater vehicle based on fast marching nonlinear model-predictive quantum particle swarm optimization. Ocean Eng. 268, 113391. doi: 10.1016/j.oceaneng.2022.113391

Crossref Full Text | Google Scholar

Chen J., Ling F., Zhang Y., You T., Liu Y., Du X. (2022a). Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evolution. Comput. 69, 101005. doi: 10.1016/j.swevo.2021.101005

Crossref Full Text | Google Scholar

Chen J., Zhang Y., Wu L., You T., Ning X. (2022b). An adaptive clustering-based algorithm for automatic path planning of heterogeneous uavs. IEEE Trans. Intelligent Transport. Syst. 23, 16842–16853. doi: 10.1109/TITS.2021.3131473

Crossref Full Text | Google Scholar

Collins M. D. (2020). User’s guide for ram versions 1.0 and 1.0p (Naval Research Lab).

Google Scholar

Dijkstra E. W. (1959). A note on two problems in connexion with graphs. Numerische Mathematik 1, 269–271. doi: 10.1007/BF01386390

Crossref Full Text | Google Scholar

Diniz P., Calazan R. (2023). Integrating modeled environmental variability into neural network training for underwater source localization. J. Acoust. Soc. America 153 6, 3201. doi: 10.1121/10.0019632

PubMed Abstract | Crossref Full Text | Google Scholar

Dong X., Zhang H., Xu M., Shen F. (2021). Hybrid genetic algorithm with variable neighborhood search for multi-scale multiple bottleneck traveling salesmen problem. Future Gen. Comput. Syst. 114, 229–242. doi: 10.1016/j.future.2020.07.008

Crossref Full Text | Google Scholar

Franchi M., Ridolfi A., Pagliai M. (2020). A forward-looking sonar and dynamic model-based auv navigation strategy: Preliminary validation with feelhippo auv. Ocean Eng. 196, 106770. doi: 10.1016/j.oceaneng.2019.106770

Crossref Full Text | Google Scholar

Geng N., Chen Z., Nguyen Q. A., Gong D. (2021). Particle swarm optimization algorithm for the optimization of rescue task allocation with uncertain time constraints. Complex Intelligent Syst. doi: 10.1007/s40747-020-00252-2

Crossref Full Text | Google Scholar

Guo S., Chen M., Pang W. (2023). Path planning for autonomous underwater vehicles based on an improved artificial jellyfish search algorithm in multi-obstacle ocean current environment. IEEE Access 11, 31010–31023. doi: 10.1109/ACCESS.2023.3257025

Crossref Full Text | Google Scholar

Helsgaun K. (2017). An extension of the lin-kernighan-helsgaun tsp solver for constrained traveling salesman and vehicle routing problems: Technical report. (Roskilde: Roskilde Universitet), 60.

Google Scholar

Honghan Z., Yanyang G., Yajie X., Benyin L., Zheping Y. (2020). Mission planning method of multi-uuv search submarine acoustic beacon. Chin. J. Ship Res. 15, 13–20. doi: 10.19693/j.issn.1673-3185.01641

Crossref Full Text | Google Scholar

Huang H., Liang Q., Hu S., Yang C. (2023). 3d search path planning for the blended-wing-body underwater glider. Ocean Eng. 276, 114219. doi: 10.1016/j.oceaneng.2023.114219

Crossref Full Text | Google Scholar

Jensen F. B., Kuperman W. A., Porter M. B., Schmidt H. (2011). Computational Ocean Acoustics (Springer New York).

Google Scholar

Kapoutsis A. C., Chatzichristofis S. A., Kosmatopoulos E. B. (2017). Darp: Divide areas algorithm for optimal multi-robot coverage path planning. J. Intelligent Robot. Syst. 86, 1–18. doi: 10.1007/s10846-016-0461-x

Crossref Full Text | Google Scholar

Kennedy J., Eberhart R. (1995). “Particle swarm optimization,” in Proceedings of ICNN’95 - International Conference on Neural Networks, Vol. 4. 1942–1948. doi: 10.1109/ICNN.1995.488968

Crossref Full Text | Google Scholar

Li X., Yu S. (2023). Three-dimensional path planning for auvs in ocean currents environment based on an improved compression factor particle swarm optimization algorithm. Ocean Eng. 280, 114610. doi: 10.1016/j.oceaneng.2023.114610

Crossref Full Text | Google Scholar

Mou J., Hu T., Chen P., Chen L. (2021). Cooperative mass path planning for marine man overboard search. Ocean Eng. 235, 109376. doi: 10.1016/j.oceaneng.2021.109376

Crossref Full Text | Google Scholar

Niu H., Ji Z., Savvaris A., Tsourdos A. (2020). Energy efficient path planning for unmanned surface vehicle in spatially-temporally variant environment. Ocean Eng. 196, 106766. doi: 10.1016/j.oceaneng.2019.106766

Crossref Full Text | Google Scholar

Northrop J. H., Loughridge M. S., Werner E. W. (1968). Effect of near-source bottom conditions on long-range sound propagation in the ocean. J. Geophys. Res. 73, 3905–3908. doi: 10.1029/JB073i012p03905

Crossref Full Text | Google Scholar

Patel R., Rudnick-Cohen E., Azarm S., Otte M. W., Xu H., Herrmann J. W. (2020). “Decentralized task allocation in multi-agent systems using a decentralized genetic algorithm,” in 2020 IEEE International Conference on Robotics and Automation (ICRA). 3770–3776.

Google Scholar

Pendharkar P. C. (2015). An ant colony optimization heuristic for constrained task allocation problem. J. Comput. Sci. 7, 37–47. doi: 10.1016/j.jocs.2015.01.001

Crossref Full Text | Google Scholar

Roshanzamir M., Balafar M. A., Razavi S. N. (2020). A new hierarchical multi group particle swarm optimization with different task allocations inspired by holonic multi agent systems. Expert Syst. Appl. 149, 113292. doi: 10.1016/j.eswa.2020.113292

Crossref Full Text | Google Scholar

Rousseau T. H., Jacobson M. J., Siegmann W. L. (1985). Ray transmissions over a sloping bottom in shallow water. J. Acoust. Soc. America 78, 1713–1726. doi: 10.1121/1.392757

Crossref Full Text | Google Scholar

Shen Z., Agrawal P., Wilson J. P., Harvey R., Gupta S. (2021). “Cppnet: A coverage path planning network,” in OCEANS 2021, vol. 1–5. (San Diego – Porto). doi: 10.23919/OCEANS44145.2021.9705671

Crossref Full Text | Google Scholar

Singh Y., Sharma S., Sutton R., Hatton D., Khan A. (2018). A constrained a* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 169, 187–201. doi: 10.1016/j.oceaneng.2018.09.016

Crossref Full Text | Google Scholar

Sun B., Zhu D., Tian C., Luo C. (2019). Complete coverage autonomous underwater vehicles path planning based on glasius bio-inspired neural network algorithm for discrete and centralized programming. IEEE Trans. Cogn. Dev. Syst. 11, 73–84. doi: 10.1109/TCDS.2018.2810235

Crossref Full Text | Google Scholar

Tang F. (2023). Coverage path planning of unmanned surface vehicle based on improved biological inspired neural network. Ocean Eng. 278, 114354. doi: 10.1016/j.oceaneng.2023.114354

Crossref Full Text | Google Scholar

Tang Y., Zhou R., Sun G., Di B., Xiong R. (2020). A novel cooperative path planning for multirobot persistent coverage in complex environments. IEEE Sensors J. 20, 4485–4495. doi: 10.1109/JSEN.2019.2963697

Crossref Full Text | Google Scholar

Trummel K. E., Weisinger J. R. (1986). The complexity of the optimal searcher path problem. Operations Res. doi: 10.1287/opre.34.2.324

Crossref Full Text | Google Scholar

Verma D., Messon D., Rastogi M., Singh A. (2021). “Comparative study of various approaches of dijkstra algorithm,” in 2021 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS). 328–336. doi: 10.1109/ICCCIS51004.2021.9397200

Crossref Full Text | Google Scholar

Vinoth Kumar S., Jayaparvathy R., Priyanka B. (2020). Efficient path planning of auvs for container ship oil spill detection in coastal areas. Ocean Eng. 217, 107932. doi: 10.1016/j.oceaneng.2020.107932

Crossref Full Text | Google Scholar

Wang H., Mao W., Eriksson L. (2019). A three-dimensional dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean Eng. 186, 106131. doi: 10.1016/j.oceaneng.2019.106131

Crossref Full Text | Google Scholar

Yao P., Qiu L., Qi J., Yang R. (2021a). Auv path planning for coverage search of static target in ocean environment. Ocean Eng. 241, 110050. doi: 10.1016/j.oceaneng.2021.110050

Crossref Full Text | Google Scholar

Yao X., Wang F., Yuan C., Wang J., Wang X. (2021b). Path planning for autonomous underwater vehicles based on interval optimization in uncertain flow fields. Ocean Eng. 234, 108675. doi: 10.1016/j.oceaneng.2021.108675

Crossref Full Text | Google Scholar

Yao P., Wei X., Qiu L., Liu Y. (2020). “Auv path planning for target search using bioinspired neural network,” in 2020 3rd International Conference on Unmanned Systems (ICUS). 575–580. doi: 10.1109/ICUS50048.2020.9274966

Crossref Full Text | Google Scholar

Zhang W., Li Z., Wu W., Yang Y. (2023). A bilevel task allocation method for heterogeneous multi-uuv recovery system. Ocean Eng. 274, 114057. doi: 10.1016/j.oceaneng.2023.114057

Crossref Full Text | Google Scholar

Zhang Z., Wang J., Xu D., Meng Y. (2017). “Task allocation of multi-auvs based on innovative auction algorithm,” in 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Vol. 2. 83–88.

Google Scholar

Zhu D., Yang S. X. (2022). Bio-inspired neural network-based optimal path planning for uuvs under the effect of ocean currents. IEEE Trans. Intelligent Vehicles 7, 231–239. doi: 10.1109/TIV.2021.3082151

Crossref Full Text | Google Scholar