AB-LSTM: a mesoscale eddy feature prediction method based on an improved Conv-LSTM model

Mesoscale eddies are the most important mesoscale phenomena in the oceans, and determining how to predict their spatial and temporal characteristics is a very challenging task. Most previous studies focused on the accuracy of full-domain prediction and ignored the accuracy of single-eddy prediction. To solve this problem, in this paper, we first apply multi-year sea surface height data to produce a spatiotemporal sequence sample dataset with a bidirectional prediction mechanism. Then, we introduce an adversarial generative mechanism through stacked spatiotemporal prediction blocks and rely on the strong generative ability of the generative adversarial network models to construct an adversarial bidirectional long- and short-term memory model (AB-LSTM). Next, the mesoscale eddy mixing algorithm is used to extract the matching eddy pair features from the real and predicted data, and several evaluation metrics are used to conduct error analysis. The experiments yield the following results. Prediction sequence days 1–7: the root mean square error (RMSE) values are 1.97–7.70 cm, the structural similarity index (SSIM) values are >0.61, the accuracy is >54.6%, and the eddy centre distance error is 6.34 km. The result is 11.61 km, which is consistent with many spatiotemporal prediction models and passes the generalisation test in many different sea areas. Finally, we carry out single eddy prediction on the basis of the evaluation of the entire prediction of the sea surface height and also obtain a more satisfactory experimental effect. This method has a better prediction ability than the original spatiotemporal method and has a certain reference significance for mesoscale eddy spatiotemporal feature prediction technology and subsequent underwater reconstruction.

1 Introduction

Mesoscale eddies (MEs) are a special phenomenon that widely occurs in the oceans. Their spatial scales are usually tens and hundreds of kilometres, and their lifetimes vary from tens of days to hundreds of days (Chelton et al., 2011). MEs are widely distributed in the global oceans and have become an important topic in research on ocean dynamics. According to the rotational direction of the eddy, mesoscale eddies can be divided into two categories: cold eddies (cyclonic eddies) and warm eddies (anticyclonic eddies). In the Northern Hemisphere, cyclonic eddies (CEs) rotate counterclockwise and anticyclonic eddies (AEs) rotate clockwise. In the Southern Hemisphere, these two types of eddies rotate in opposite directions (Zhang et al., 2013). These types of eddies are widely distributed in the global oceans. This rotation not only affects the fluid motion inside the eddy but also has a significant impact on the ocean’s thermohaline properties. Mesoscale eddies have an all-encompassing effect on the marine environment. By adjusting local water masses, they cause a huge difference in the thermohaline properties inside and outside of their area. This difference not only affects the pattern of ocean circulation but also influences the exchange of materials and energy transfer in the ocean (Dong et al., 2014). In addition, mesoscale eddies have a significant impact on marine environment variability and are important drivers of dynamic changes in marine ecosystems. The characteristics of mesoscale eddies are particularly evident in specific oceanic regions, such as the Kuroshio Extension (KE) region. Detailed statistics presented by Itoh et al. (Itoh and Yasuda, 2010) indicate that the northern side of the KE is dominated by a large number of anticyclonic eddies, and these eddies usually have long life cycles. However, on the southern side of the KE and near the flow axis, there are more CEs, and these eddies usually have stronger intensities. Further analysis has revealed that more than 85% of the anticyclonic eddies have high-salt warm cores, whereas only 15% of the anticyclonic eddies have cold cores. These features not only reveal the unique nature of the mesoscale eddies in the KE region but also provide important clues for understanding dynamic ocean processes in this region.

With the launch of ocean observation satellites, abundant large-scale, long time-series, and high-precision ocean remote sensing observation data have been obtained and processed, among which long time-series observation data accumulated through many years of observations have been widely used in analyses and forecasts of oceanic phenomena (Oka and Qiu, 2012; Qiu and Chen, 2013). Liu et al. (Liu et al., 2012) conducted a multi-year statistical analysis of the number, life cycle, amplitude, and radius of mesoscale eddies in the North West (NW) Pacific Ocean. Wang et al. (Wang et al., 2016) found that the interannual characteristics of the KE region may be affected by the instability of the main flow axis of the KE under the effect of the topography, and the results of their experiment were also affected by the instability of the main flow axis of the Kuroshio under the effect of the topography. Qiu et al. (Qiu and Chen, 2005) used the linear vorticity dynamics method to back-project the high- and low-pressure signals and reached the conclusion that the changes in the circulation characteristics of the KE are associated with the high- and low-pressure anomalies in the eastern North Pacific Ocean. In terms of prediction of the characteristics of mesoscale eddies, roughly classified, most scholars have adopted two approaches. The first is to make predictions using ocean numerical prediction models. Shriver et al. (Shriver et al., 2007) successfully improved the resolution of the prediction system by combining the Naval Layered Ocean Model (NLOM) with the optimal interpolation method, which in turn enhances the accuracy of the ME prediction. Trott et al. (Trott et al., 2023) used the hybrid coordinate ocean model (HYCOM) to simulate future sea-level anomaly (SLA) data and then adopted an SLA-based identification technique to identify MEs and predict their future distribution. The second method is to make predictions that are purely data-driven. This type of method can be subdivided into the direct prediction of ME features (often multi-feature one-dimensional sequence prediction). For example, Ashkezari et al. (Ashkezari et al., 2016) successfully predicted ME lifetimes under stable evolutionary conditions by employing an extreme random forest regression method. Wang et al. (Wang et al., 2020) combined extreme random trees and a long short-term memory (LSTM) network based on mesoscale eddy trajectory and feature datasets to predict several key features, including the latitude and longitude coordinates. Wang et al. (Wang et al., 2021) incorporated meso-historical latitude and longitude sequence data, sea surface height data, sea surface temperature data, and other additional information using a gated recurrent unit (GRU) network combined with a temporal attention mechanism to improve the prediction accuracy of the future centre coordinates of the ME. Ge et al. (Ge et al., 2023) developed a neural network for predicting the trajectory of an ME in compliance with the physical constraints, providing a more reliable and comprehensible method for the prediction of the trajectories of MEs. Another prediction method is to reconstruct a large sea surface height field (2-D) and accordingly to use a mesoscale eddy identification algorithm to obtain mesoscale eddy features in the predicted spatiotemporal sequence. For example, Ma et al. (Ma et al., 2019) obtained an accuracy higher than that of HYCOM for predicting the 7-day sea surface height field using a more mature convolutional LSTM. Nian et al. (Nian et al., 2021) proposed a neural network equipped with a Memory In Memory (MIM) model and a spatial attention module and obtained higher experimental results than those of many spatiotemporal prediction methods. However, according to the current state of research, the limitations of numerical modelling methods in terms of prediction performance should not be ignored. These limitations mainly stem from the nonlinear nature of MEs and the sensitivity of numerical models to initial conditions. Furthermore, these models mainly focus on the prediction of the marine environment rather than directly targeting the ME, so it is difficult to achieve a direct prediction. However, the pure data-driven approach has a lower demand for the initial field, and the current sea surface height observation data have the natural advantages of being large, continuous, and accurate, making the data sufficient to support the model computation. This also lays a solid foundation for the pure data-driven deep learning network prediction model.

The spatial and temporal smoothing properties of mesoscale eddy trajectory and feature prediction enable continuous observations with a high accuracy, which often causes the spatial and temporal properties between sequence units to have a nonlinear correlation. However, previous studies tended to focus on the predecessor sequence to the successor sequence prediction, which inevitably leads to the propagation of the errors generated by the predecessor prediction resulting in backward cumulative propagation. Although Nian et al. (Nian et al., 2021) utilized corresponding improvement measures for the non-stationary state and error accumulation problems in sea surface height anomaly (SLA) prediction, including optimising the memory and planned sampling methods, and achieved lower prediction errors, the error accumulation effect still occurred and was significant. This was due to the fact that the planned sampling method is only used to correct the weights via jump verification during the learning process, thus turning the continuous error into the accumulation of the stage error, rather than considering the entire range of errors in the prediction sequence as a whole. In addition, since most long-lived mesoscale eddies (more than 7 days) have strong continuity and physical interpretability of the sea surface height field with and without eddy features, we can make predictions from past measurements and can also make predictions from past measurements in the reverse direction. However, the related work has not been carried out so far. Currently, the models commonly used for spatiotemporal prediction are generally based on stacked recurrent neural network (RNN) models or LSTM models. Thus, the former links the correlation between the temporal and spatial attributes, while the latter is more prominent in solving the challenge of gradient explosion, leading to its wider use compared with the RNN. However, native LSTM models tend to focus more on non-Markovian attributes in the time series rather than spatial feature variations in dealing with long time-series prediction problems. For mesoscale eddy prediction tools that are time-varying and highly dependent on variations in spatial feature attributes (Yunbo Wang et al., 2017), one or the other is important. Second, the mesoscale eddy prediction process is often accompanied by eddy generation and elimination, as well as fusion, and existing prediction tools pay more attention to the description of high-value features rather than those of low-level features, which is acceptable in semantic recognition-related applications, but neither of them can be neglected in mesoscale eddy prediction. To solve the problem of the continuity of the prediction caused by unidirectional inputs and the problem of complex spatiotemporal feature description, in this paper, we propose an adversarial bidirectional LSTM (AB-LSTM) and a set of evaluation criteria for mesoscale eddy prediction, which obtained a good comparison effect compared with various spatio-temporal prediction models and numerical ocean prediction models.

2 Data and methods

2.1 Data

2.1.1 AVISO satellite altimeter data

The SLA data used in this paper were obtained from a gridded product provided by the Satellite Ocean Archive Data Centre (AVISO) of the Centre national d’études spatiales (CNES). This dataset combines altimetry data from several satellites, such as Jason-1, Topex/Poseidon, Envisat, GFO, and ERS-1&2, interpolated to a 1/4°×1/4° grid spatial resolution on the Mercator projection. The temporal resolution is interpolated from the original resolution of 7 d to 1 d, the spatial range of the selected data is 25–45°N, 150–170°E, and the time span is from January 1993 to December 2022. These data have been widely used by many scholars (Dong et al., 2014; Duo et al., 2019; Eden and Dietze, 2009), are the most important sample and training data used in this paper, and are also an important indicator for evaluating the quality of the prediction data.

2.1.2 Marine model data

The HYCOM is a data-assimilated hybrid isodensity sigma pressure (generalised) coordinate ocean model (Chassignet et al., 2009, 2007). The subset of HYCOM global sea surface height forecasts hosted in GEE (Google Earth Engine) has been plugged into a 1/12 degree latitude/longitude grid and has been widely used in several previous studies (Metzger et al., 2010; Wallcraft et al., 2007).

2.2 Research methods

2.2.1 Mesoscale eddy identification methods

Since the launch of the T/P satellite on 25 September 1992 and the output of data, the study of ocean mesoscale phenomena using ocean altimetry data has been taking place for more than 30 years. Mesoscale eddy identification algorithms have attracted the attention of several scholars, who have successively proposed physical parameters (Isern-Fontanet et al., 2004), flow field geometry (McWilliams, 2016; Nencioli et al., 2010), and machine vision algorithms (Franz et al., 2018; Xu et al., 2019). Each of the above-described algorithms has its own advantages, and in combination with the reality of this paper, in this paper, we refer to Ma et al (Ma et al., 2024).’s hybrid algorithm that combines flow field geometry and closed contours as the mesoscale eddy identification algorithm. Before carrying out the identification process of the hybrid algorithm, we need to convert the SLA data into the geostrophic flow field, which is calculated as follows:

$\begin{array}{ll}u=-\frac{g}{f}\frac{\partial h}{\partial y} , v=-\frac{g}{f}\frac{\partial h}{\partial x}& (1)\end{array}$

where u and v are the latitudinal and longitudinal components of the geostrophic anomalies, respectively, g is gravitational acceleration, f is the Koch parameter, and h is the height of the sea surface anomaly.

The flow field geometry method is based on the geometric characteristics of mesoscale eddies, which are defined as regions with rotating velocity vectors, a centre at the velocity extremum, and symmetrically rotating surrounding vectors. The SLA closure curve method focuses on the detection of sea surface altitude closure curves, which reduces the likelihood of non-closed eddies. To reduce the effect of the subjectivity of the sea surface height difference threshold and to balance the identification effect with the subjective threshold sensitivity, a hybrid algorithm that combines the two methods is used to analyse the sea surface flow field and the SLA data. When the goal is to detect mesoscale eddy pairs with the largest overlapping boundaries, the stable identification of the same eddy using both identification methods is determined by setting generic custom thresholds (intersecting area more than 50% and eddy centre distance of less than 1/12°). The eddy centre of this eddy determined using the flow field geometry method is considered the actual centre (Figure 1).

Figure 1

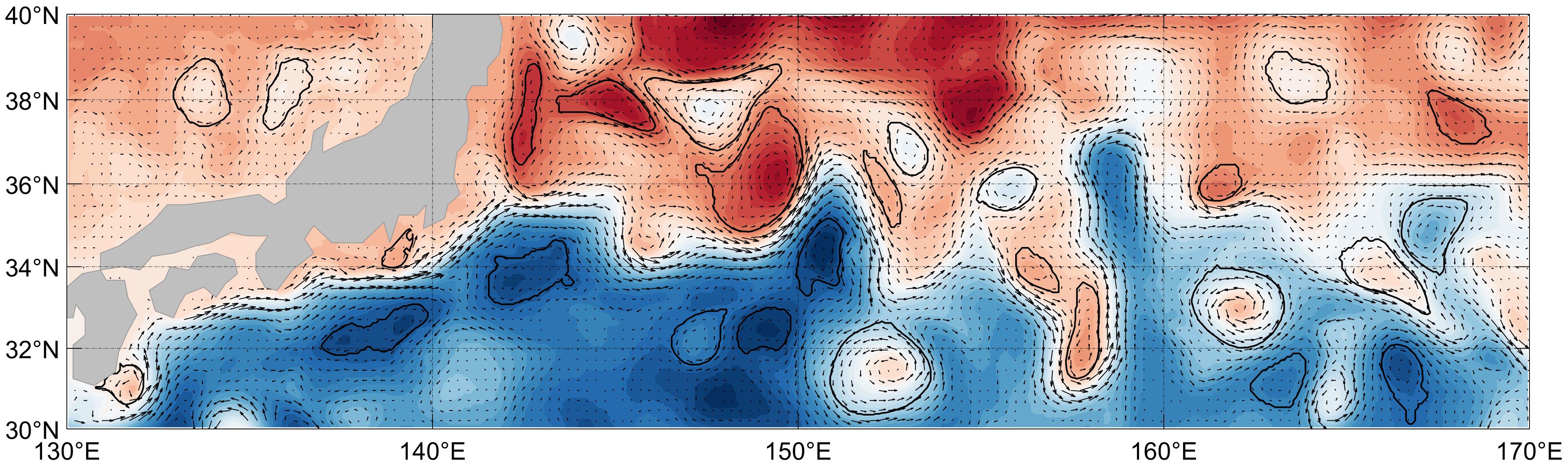
Figure 1. Schematic diagram of mesoscale eddy extraction in KE region utilizing the hybrid recognition algorithm.

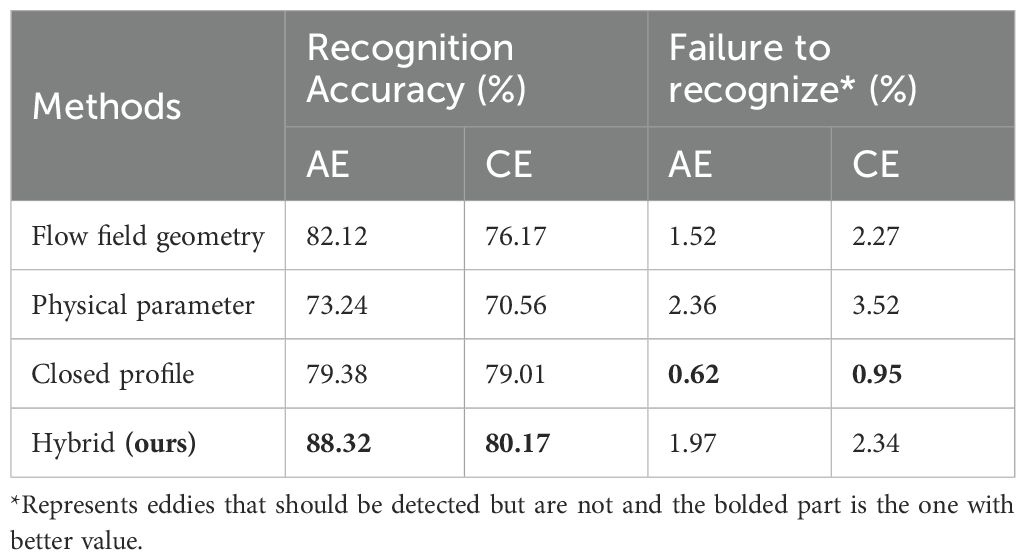
In addition, in order to demonstrate the advantages of the recognition effect of the hybrid algorithm, 1000 days were randomly selected from the sample data set (daily sea surface height data within the time span of the data), and the flow field geometry method, closed contour method and hybrid recognition algorithm were respectively adopted for recognition. In addition, most experts and scholars in this field conducted artificial recognition and judged the recognition effect. The recognition accuracy and the proportion that should be recognized but not recognized were evaluated by horizontal comparison. The results are shown in Table 1.

Table 1

Table 1. Results of horizontal comparison of recognition effects of various recognition methods.

2.2.2 Determination of input frame data resolution

For the identification of a mesoscale eddy, since all the current data-driven mesoscale eddy identification algorithms are based on feature identification of grid point data, the selection of the region and the determination of the data resolution play crucial roles, and too large or too small a resolution will have a great impact on the eddy identification results. Thus, in this paper, to ensure that the steps of the data extraction, model training, metric evaluation, and testing of the generalisation capability are characterised by continuity and referability, we fixed the study area as 25–45°N, 150–170°E. Since the resolution of the original altimetry data is 1/4°×1/4°, i.e., the dimension of the data in this part of the region is 80×80, to retain the details of the original data and facilitate the construction of the model, we interpolate all of the input–output data to 128×128 using the Akima (Akima, 1970) interpolation algorithm.

2.2.3 Evaluation metrics for predicting mesoscale eddy features

In previous mesoscale eddy predictions, most scholars have tended to use the sea surface height forecast error and the mesoscale eddy trajectory prediction as the evaluation metrics and have achieved better experimental results, but these two metrics cannot evaluate the sea surface height prediction in a complete way. Thus, in this subsection, we propose a mesoscale eddy prediction evaluation framework to evaluate the mesoscale eddy prediction metrics in a complete way. It should be noted that the evaluation metrics introduced in this subsection need to be predicated based on the basic information about the eddies obtained using the mesoscale eddy mixing identification algorithm described in Section 2.2.1, except for the root mean square error (RSME) and structural similarity index (SSIM), which is a metric for regional prediction results.

The characteristics of mesoscale vortices in the prediction can be expressed in a variety of ways, and the most important ones that can be obtained from the sea surface information field can be divided into three categories: The first type is the numerical error index of eddy prediction, which is reflected as the RSME index of sea surface height information, which intuitively reflects the overall error level of the predicted results and the real results. The second category is the representation of the number of vortices, because deep learning network is the best solution generated based on probability theory in two-dimensional space-time prediction process, while the application of mesoscale vortices may result in low numerical error and high distortion. For this reason, Num index, $Accuracy$ index and $Dist$ index are introduced. These three indexes can directly show whether the number and location of vortices in the prediction sequence can be accurately expressed without losing the target. The third category is the performance of the overall similarity. We use the $SSIM$ index to show the structural similarity of the whole selection area. This consideration is that not only the prediction level of the eddy itself needs to be reflected, but also the complex interaction field around it needs to be well predicted and expressed.

The first metric is the sea surface height prediction error. We use the two-dimensional $RMSE$ as the standard for this metric:

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{H\times W}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{(O_a(i,j)-P_a(i,j))}^2} i=1,2,3\dots H; j=1,2,3\dots W,& (2)\end{array}$

where H and W are the length and width of the data, respectively, and $P_a$ and $O_a$ are the predicted and original data, respectively.

The second metric is the mesoscale eddy prediction hit rate ($Accuracy$) and mesoscale eddy trajectory error (Dist). We take the distance of the same eddy centre (km) in the eddy identification results corresponding to the real dataset and the prediction dataset as the daily prediction trajectory error, in which the same eddy hit is discriminated by the fact that the area inside the two eddy profiles matches 75% or more of both the prediction results and real data in the same day. Then, we sum and average the matched eddy centre distances on that day to obtain the trajectory error indicator for that day, which is calculated as follows:

$$Dist=\frac{1}{n}{\displaystyle {\sum }_{m=1}^n}\sqrt{{(x_O(m)-x_P(m))}^2+{(y_O(m)-y_P(m))}^2},$$

$\begin{array}{ll}Accuracy=\frac{N_P}{N_O}*100\%,& (3)\end{array}$

Where n is the total number of identified matching eddies on that day, $x_O, y_O,$ $x_P,$ and $y_P$ are the horizontal and vertical coordinates in the real data identified eddy results, and $N_P$ and $N_O$ are the number of predicted eddies in the region and the number of real eddies, respectively.

The third metric is the sea surface prediction SSIM, which is one of the indicators used to measure the structural similarity of the data. When we have two datasets x, y, the structural similarity can be defined as follows:

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}$$

$\begin{array}{ll}{c}_1={(k_{1}L)}^2 , c_2={(k_{2}L)}^2 & (4)\end{array}$

where ${\mu }_x$ is the mean of $x, {\mu }_y$ is the mean of y, ${\sigma }_x^2$ is the variance of x, ${\sigma }_y^2$is the variance of y, and ${\sigma }_{xy}$ is the covariance of x and y. L is the dynamic range of the pixel value, which is set to 100 in this paper, and $k_1$ and $k_2$ are constants, which are set to 0.01 and 0.03, respectively, in this paper.

2.3 Data cleaning

Both ocean observation data and model prediction data have the advantages of wide coverage and clear grid, but they also often contain uncontrollable abnormal data. Due to the various data sources used in this paper, in order to ensure the quality of the data when forming the deep learning sample dataset, We will perform data cleaning on the data used for training, testing, verification and evaluation in this paper. Drawing on the experience of several atmospheric and oceanic researchers, we used the Mahalanobis denoising method (Eq. 5). First, the sequence data of sea surface height is obtained, and the Mahalanobis Distance ($D_M$) of each two-dimensional grid point in the sequence is calculated. When $D_M$ is greater than three standard deviations of the average distance, the grid point data is considered as “abnormal”; when the number of “abnormal” grid points exceeds 1% of the total grid points, the entire sequence including the two-dimensional grid point data is discarded.

$$\mu =\frac{1}{n}\sum _{i=1}^n{x}_i$$

$$S=\frac{1}{n-1}\sum _{i=1}^n(x_i-\mu ){(x_i-\mu )}^T$$

$\begin{array}{ll}{D}_M(x_i)=\sqrt{(x_i-\mu )S^{-1}(x_i-\mu )}& (5)\end{array}$

3 Model

3.1 Spatiotemporal Long Short-Term Memory Model

Suppose we are monitoring a dynamic system in which each measurement is recorded at all locations in a spatial region represented by an $M \times N$ grid. From a spatial point of view, these P measurements observed at any time can be represented by the tensor $X\in {ℝ}^{P\times M\times N}$ (Liu et al., 2018; Wang et al., 2021). From a temporal point of view, the observations at t time steps form a tensor sequence of $X_1,X_2,X_3,X_4,\dots ,X_t$. The spatiotemporal predictive learning problem is to predict the most probable $length-K$ sequence in the future given the two previous length-J sequences, including the current observation:

$\begin{array}{ll}{\widehat{X}}_{t+1},\dots , {\widehat{X}}_{t+k}=\underset{X_{t+1},\dots ,X_{t+k}}{argmax}p(X_{t+1},\dots ,X_{t+k}|X_{t-j+1},\dots ,X_t).& (6)\end{array}$

Sequence prediction has been a popular research topic in the field of machine learning, and LSTM, as an emerging RNN model with long- and short-term memory, has led to a breakthrough in dealing with the solution of long-term-dependent problems. Shi et al. (Shi et al., 2015) creatively used the input-to-state and state-to-state methods to visually extract the inputs using stacked LSTM layers and achieved pioneering research results in this field. However, the current problem is that this model needs to continue learning and predicting from the previous state. This means that the continuity prediction will be based on the previous prediction result, which will lead to the accumulation of error and feature bias. To solve this problem, several scholars have improved this model (Kalchbrenner et al., 2017; Patraucean et al., 2015; Villegas et al., 2017). In this paper, we utilize a spatiotemporal long- and short-term memory model (ST-LSTM) (Wang et al., 2022) as the basis of the generation of the model. Based on the stacking technique of the convolutional LSTM (Conv-LSTM), the model obtains higher experimental results than other models by proposing spatiotemporal memory flow and memory transfer across layers in several prediction results. The model’s architecture is shown in Figure 2.

Figure 2

Figure 2. Schematic diagrams of the ST-LSTM model (left) and the stacked sequence monolayer (the dark blue marks are space-time fluid cells different from the original Conv-LSTM).

The formulas are as follows:

$$G_t=tanh(W_{xG}\ast X_t+W_{HG}\ast H_{t-1}+b_G)$$

$$I_t=\sigma (W_{xI}\ast X_t+W_{HI}\ast H_{t-1}+b_I),$$

$$F_t=\sigma (W_{xF}\ast X_t+W_{HF}\ast H_{t-1}+b_F),$$

$$C_t=F_t⨀C_{t-1}+I_t⨀G_t,$$

$${\mathit{g}}_{\mathit{t}}\mathbf{=}\mathit{t}\mathit{a}\mathit{n}\mathit{h}({\mathit{W}}_{\mathit{x}\mathit{g}}\mathbf{\ast }{\mathit{X}}_{\mathit{t}}\mathbf{+}{\mathit{W}}_{\mathit{M}\mathit{g}}\mathbf{\ast }{\mathit{M}}_{\mathit{t}\mathbf{-}\mathbf{1}}\mathbf{+}{\mathit{b}}_{\mathit{g}})\mathbf{,}$$

$${\mathit{i}}_{\mathit{t}}\mathbf{=}\mathit{\sigma }({\mathit{W}}_{\mathit{x}\mathit{i}}\mathbf{\ast }{\mathit{X}}_{\mathit{t}}\mathbf{+}{\mathit{W}}_{\mathit{M}\mathit{i}}\mathbf{\ast }{\mathit{M}}_{\mathit{t}\mathbf{-}\mathbf{1}}\mathbf{+}{\mathit{b}}_{\mathit{i}})\mathbf{,}$$

$${\mathit{f}}_{\mathit{t}}\mathbf{=}\mathit{\sigma }({\mathit{W}}_{\mathit{x}\mathit{f}}\mathbf{\ast }{\mathit{X}}_{\mathit{t}}\mathbf{+}{\mathit{W}}_{\mathit{M}\mathit{f}}\mathbf{\ast }{\mathit{M}}_{\mathit{t}\mathbf{-}\mathbf{1}}\mathbf{+}{\mathit{b}}_{\mathit{f}})\mathbf{,}$$

$${\mathit{M}}_{\mathit{t}}\mathbf{=}{\mathit{f}}_{\mathit{t}}\mathbf{⨀}{\mathit{M}}_{\mathit{t}}\mathbf{+}{\mathit{i}}_{\mathit{t}}\mathbf{⨀}{\mathit{g}}_{\mathit{t}}\mathbf{,}$$

$${\mathit{O}}_{\mathit{t}}\mathbf{=}\mathit{\sigma }({\mathit{W}}_{\mathit{x}\mathit{O}}\mathbf{\ast }{\mathit{X}}_{\mathit{t}}\mathbf{+}{\mathit{W}}_{\mathit{H}\mathit{O}}\mathbf{\ast }{\mathit{H}}_{\mathit{t}\mathbf{-}\mathbf{1}}\mathbf{+}{\mathit{W}}_{\mathit{C}\mathit{O}}\mathbf{\ast }{\mathit{C}}_{\mathit{t}}\mathbf{+}{\mathit{W}}_{\mathit{M}\mathit{O}}\mathbf{\ast }{\mathit{M}}_{\mathit{t}}\mathbf{+}{\mathit{b}}_{\mathit{O}})\mathbf{,}$$

$\begin{array}{ll}{\mathit{H}}_{\mathit{t}}\mathbf{=}{\mathit{O}}_{\mathit{t}}\mathbf{⨀}\mathit{t}\mathit{a}\mathit{n}\mathit{h}({\mathit{W}}_{\mathbf{1}\mathbf{\times }\mathbf{1}}\mathbf{\ast }[{\mathit{C}}_{\mathit{t}}\mathbf{,}{\mathit{M}}_{\mathit{t}}])\mathbf{,}& (7)\end{array}$

where σ is the activation function, W corresponds to the process weight of the corner scale, b is the bias term (distinguished by the corner scale), X is the input sequence, C is the output cell, and H is the hidden state. The most important feature of the ST-LSTM model is that the memory cell is divided into two parts, namely, the classical C_t temporal cell and the M_t spatio-temporal cell, and they are distinguished in the level of the data flow. The C_t stream is passed continuously between the same corresponding layers of different stacks according to the classical Conv-LSTM. The M_t stream is first passed layer by layer in the same stack, repeated as the input of the next stack, and finally reduced to the same dimension by a 1×1 convolutional gate and outputted as H_t. This is different from the spatiotemporal memory transfer method of the classical Conv-LSTM to a large extent.

3.2 Generative adversarial network models

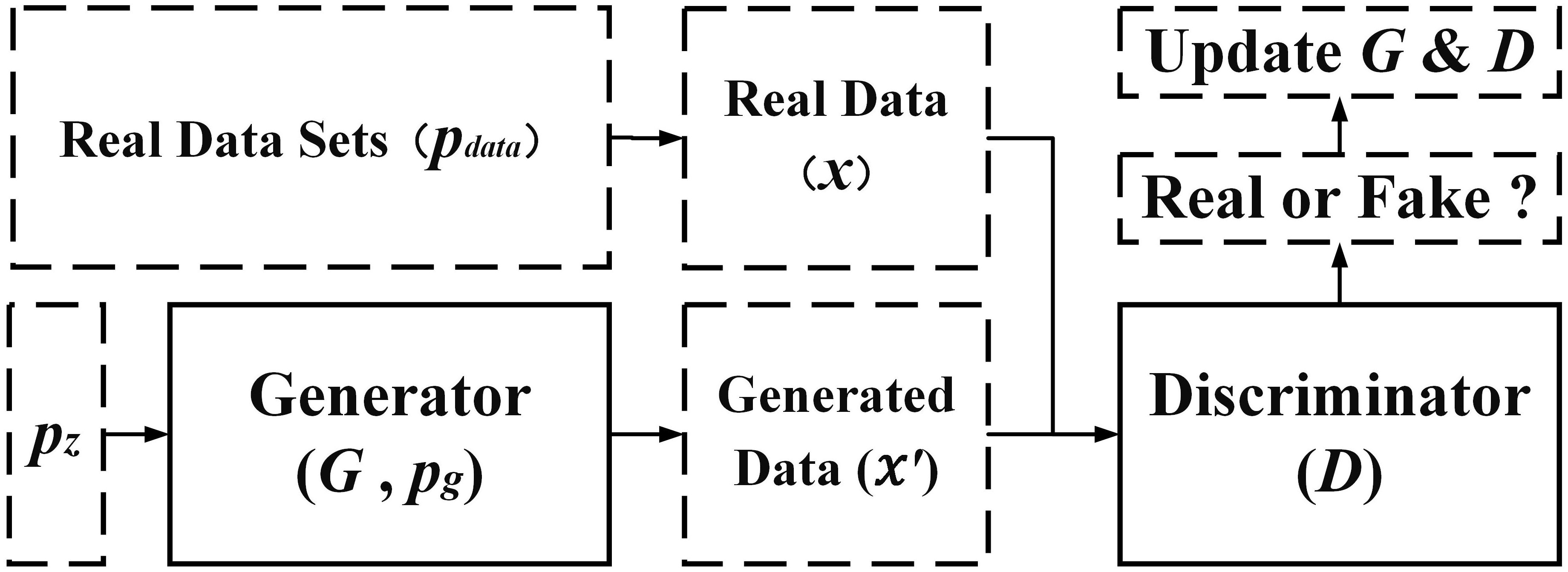
The main idea of the basic model of the generative adversarial network (GAN) is to make the two neural networks continuously play the binary extremely large and extremely small game, during which the model gradually learns the real sample distribution. In general, the training is considered complete when the two networks reach a Nash equilibrium in their want confrontation (Goodfellow et al., 2014).

The basic GAN model is shown in Figure 3. The input of the generator network (denoted as G) is a random variable (denoted as z) from the hidden space (denoted as $p_z$) and the output of the generator samples, the training goal of which is to improve the similarity between the generator samples and real samples, so that they are indistinguishable from those of the discriminator (denoted as D) network, i.e., to make the distributions of the generator samples (denoted as $p_{g }$) and real samples (denoted as $p_{data}$) as identical as possible. The training objectives of the native GAN network can be summarized as follows: to minimize the distance between $p_g$ and $p_{data}$ and to maximize the accuracy of the samples discriminated by D, i.e., the value of $D(x)$ tends to be 1 and the value of $D(x^{\prime })$ tends to be 0. This leads to the basic GAN network objective function expression:

Figure 3

Figure 3. Schematic diagram of the basic GAN model.

$\begin{array}{ll}\frac{min}{G}\frac{max}{D}{E}_{x~p_{data(x)}}[logD(x)]+E_{z~p_{z(z)}}[\log (1-D(G(z)))].& (8)\end{array}$

3.3 Adversarial bidirectional long- and short-term memory models

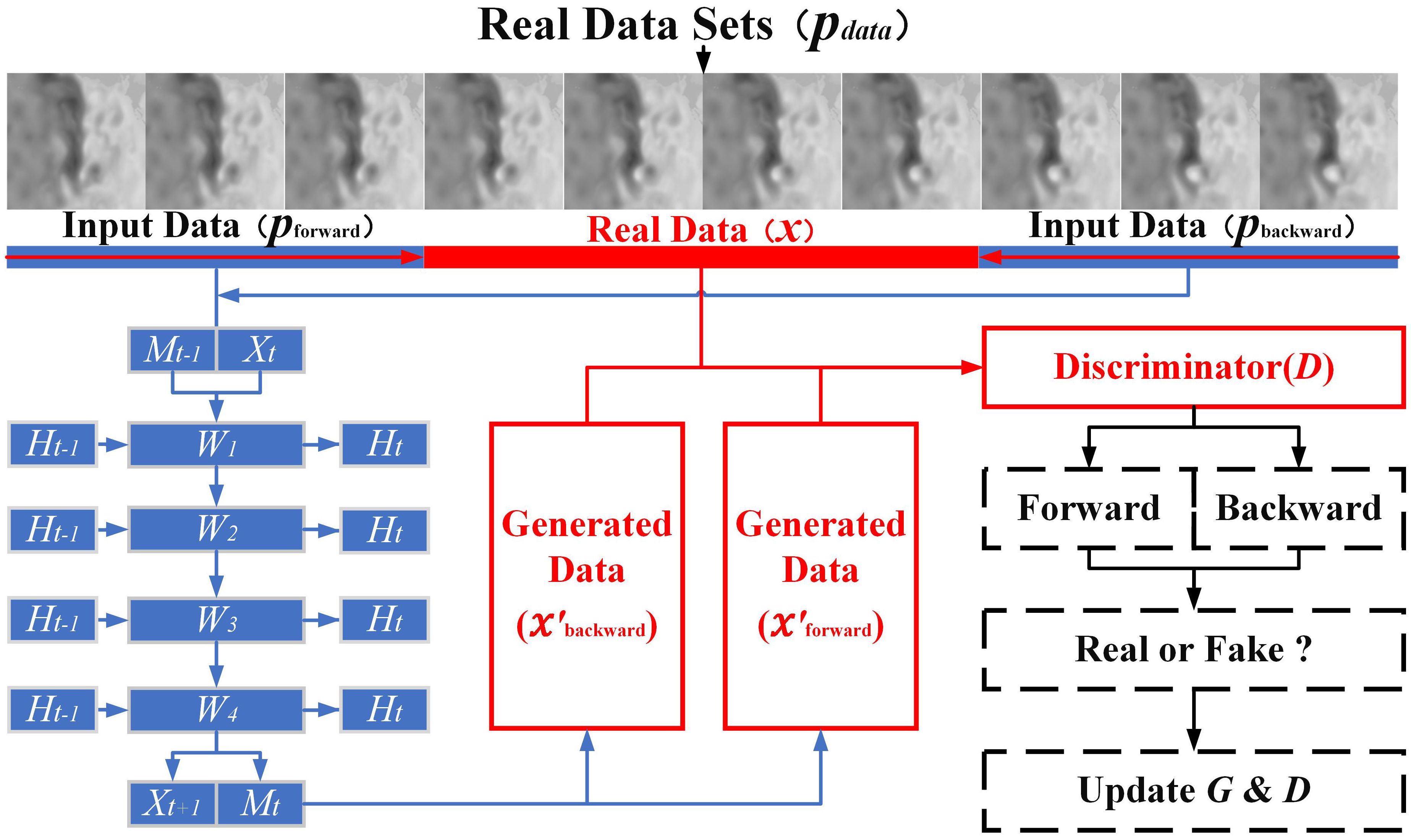
To solve the problems of the LSTM, namely, unidirectional prediction error and continuous accuracy of the spatiotemporal prediction, we embed a 4-layer stacked ST-LSTM model as the generative unit into the adversarial network model as the core of the generator. Then, we divide the generator inputs into forward spatiotemporal sequence inputs and inverse spatiotemporal sequence inputs and control the input streams of the two according to the discriminative results of the discriminators in a training cycle to achieve effective bi-directional training (Figure 4). To increase the learning ability of the overall trend, we train a global discriminator (Iizuka et al., 2017) to discriminate whether the output is true. The purpose of constructing the global discriminator is to strengthen the ability of the discriminator to identify the overall characteristics of the input region and to emphasise the importance of guiding the model to pay more attention to the overall trend of the sea surface data. The global discriminator consists of five consecutive convolutional layers, each of which has a step size of 2. It uses a fully connected layer and a sigmoid output layer to process the input data of size 128 × 128 into a high-dimensional vector, which is then transformed into a continuous and normalised real probability distribution by a fully connected layer and a sigmoid transfer function.

Figure 4

Figure 4. Overall schematic diagram of the AB-LSTM model.

In this paper, we use a total of 10,000 days of sea surface altimetry data from 1 January 1993 to 19 May 2020 as the training (first 90%) and validation datasets (second 10%), and the sea surface altimetry data from 20 May 2020 to 20 May 2022 as the model generalisation test datasets (validation and testing sets). We process each of the three datasets into time-series blocks with a length of 10 days (structure 3-4-3: the first number is the length of the forward input sequence, the second number is the length of the target prediction sequence, and the third number is the length of the reverse input sequence, as shown in $p_{data}$ in Figure 4), with 3 days of forward prediction input ($p_{forward}$) in each block, 7 days (including 3 days of reverse input) of target prediction data (x), and 3 days of reverse prediction input $p_{backward}$, corresponding to the generation results denoted as $x_{forward}$ and $x_{backward}$. The next batch of inputs in the generator is updated after the discriminator decides whether it is true or false and updates the current batch of generators (ST-LSTM cells) and the discriminator weights. The corresponding objective function is updated to

$\begin{array}{ll}\frac{min}{G}\frac{max}{D}{E}_{x~p_{data(x)}}[logD(x)]+E_{x~p_{forward}}[\log (1-D(G(p_{forward})))+E_{x~p_{backward}}[\log (1-D(G(p_{backward})))]& (9)\end{array}$

In the model proposed in this paper, we use the L1+L2 loss function and the Adam optimiser (Kingma and Ba, 2014) for the training, and in the actual training process we pre-train the GAN network and then access the ST-LSTM module. Regarding the setting of the hyperparameters, in general, the learning rate is set within 0.0001–0.1. A learning rate that is too high will make the model training effect poor, while a learning rate that is too low will make the model training convergence slow. Thus, through many adjustments, we determine the learning rate to be 0.0001, the batch is determined to be eight, and the corresponding epoch is appropriately increased to 100,000. If the dataset has a large amount of noise, we should try to minimise ${\beta }_1$ and ${\beta }_2$. Although the average coefficients converge faster, they are more susceptible to noise. In this paper, we set ${\beta }_1$ = 0.9 and ${\beta }_2$ = 0.999. All of the experiments are implemented in Pytorch = 3.10 (Paszke et al., 2019) and trained on an NVIDIA RTX4080. Additionally, it should be emphasized here that the parameter Settings of the Adam optimizer in this paper are determined by many attempts in the experiment process and previous experience of Adam optimizer parameters when applying deep learning models in the Marine field.

4 Model evaluation

In this subsection, first, we discuss the effect of different prediction lengths on prediction accuracy to confirm the optimal prediction range of the proposed model. Then, we conduct a multi-criteria comparison with the two modal datasets and a variety of existing spatiotemporal prediction models. Finally, we test the generalisation ability of the model using the day-by-day prediction history data from HYCOM. It should be noted that all input and output data used in this process are first interpolated to 128 × 128 using the interpolation method described in Section 2.2.2. Based on the conclusion of Ma et al. (Ma et al., 2019), the polarity of the mesoscale eddies has a limited effect on the smoothness, as well as the accuracy of the prediction process, so we do not take the issue of eddy polarity into account during the training process, but we do discuss it in the evaluation process.

4.1 Prediction effect

Figure 5 shows the trend of the training loss after 100,000 iterations. The black solid line in the figure is the real value of the training loss from iteration to iteration, and the red line is the higher-order smoothing curve of the black real loss. It can be seen from Figure 5 that the training loss of the model decreases rapidly during the initial training and stabilises at 10,000 iterations. After a long period of small and slow increase, it continues to decrease slowly after 40,000 iterations and finally converges slowly after 90,000 iterations.

Figure 5

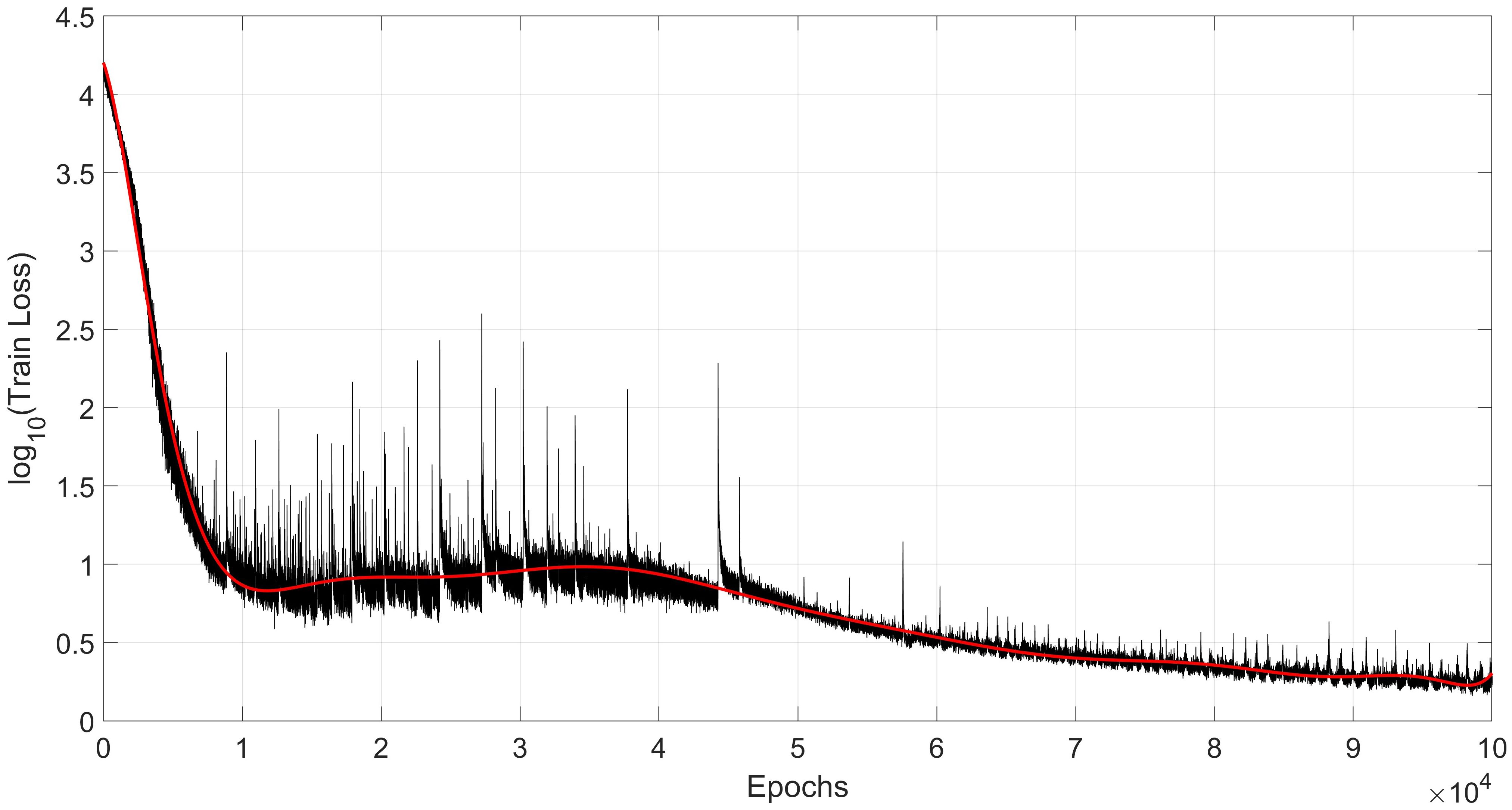
Figure 5. Plot of training loss versus number of iterations for the AB-LSTM and the AVISO sea surface height dataset. Due to the large span of the original training loss (Y-axis), to better show the trend of the change, we present it in logarithmic form, which results in the absence of some of the magnitude (the original magnitude is in cm), The black line is the original value of the training loss, and the red line is the error smoothing curve after 5-order Fourier fitting).

Figure 6 shows the effect of the prediction experiment for 7 days for different numbers of iterations. Intuitively, the prediction effect is good. As the number of iterations increases, the model prediction effect continues to improve. The effect tends to stabilise at 50,000 iterations, and the subsequent prediction results are not easily distinguished by the human eye. In addition, it can be seen that the prediction sequences for the different numbers of iterations exhibit good continuity of the overall trend, and the mesoscale eddy characteristics are more obvious, except for the test with 5000 iterations. This indicates that the training process is effective. Figure 7 shows the change trends of the RMSE and SSIM metrics for the AB-LSTM for the AVISO sea surface height dataset with increasing iteration numbers. It can be clearly seen that the results shown in Figure 7 are highly consistent with the prediction effect shown in Figure 6. This also shows that the selected metrics can accurately reflect the actual performance of the model in terms of the prediction process.

Figure 6

Figure 6. Schematic representation of the effect of the prediction experiment with different numbers of iterations. The predicted values are shown in the red boxes.

Figure 7

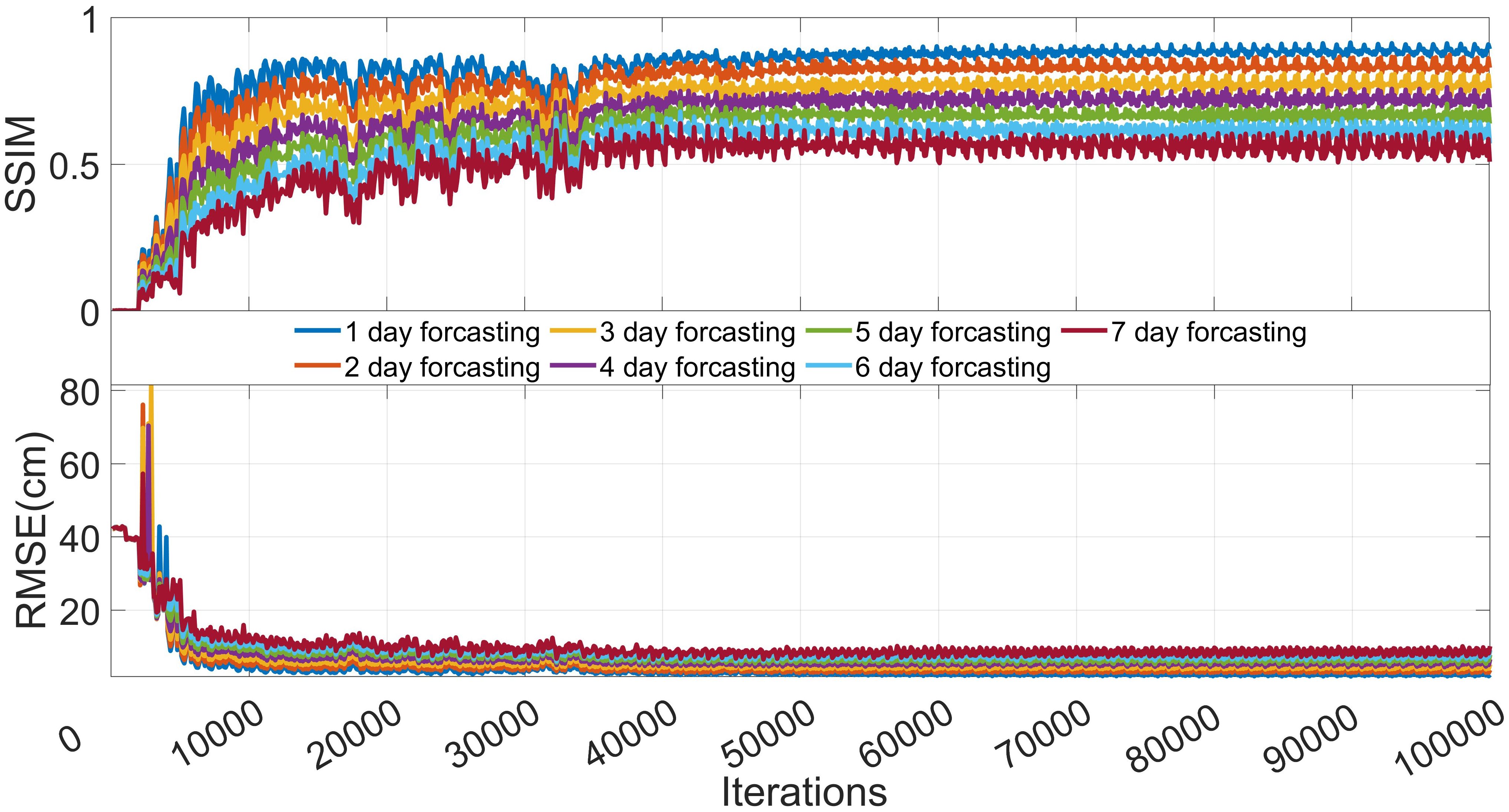
Figure 7. Plots of RMSE and SSIM metrics versus number of iterations for the AB-LSTM and the AVISO sea surface height dataset.

To discuss the effect of the forward and backward inputs on the model training in the AB-LSTM model, in this subsection we set up control experiment groups A (forward and backward) and B (forward only), randomly select 500 sets of experimental data from the sample dataset, which all have 3-4-3 structures, and make a 7-day prediction. The obtained results are averaged within each group according to the day-by-day prediction results (Table 2).

Table 2

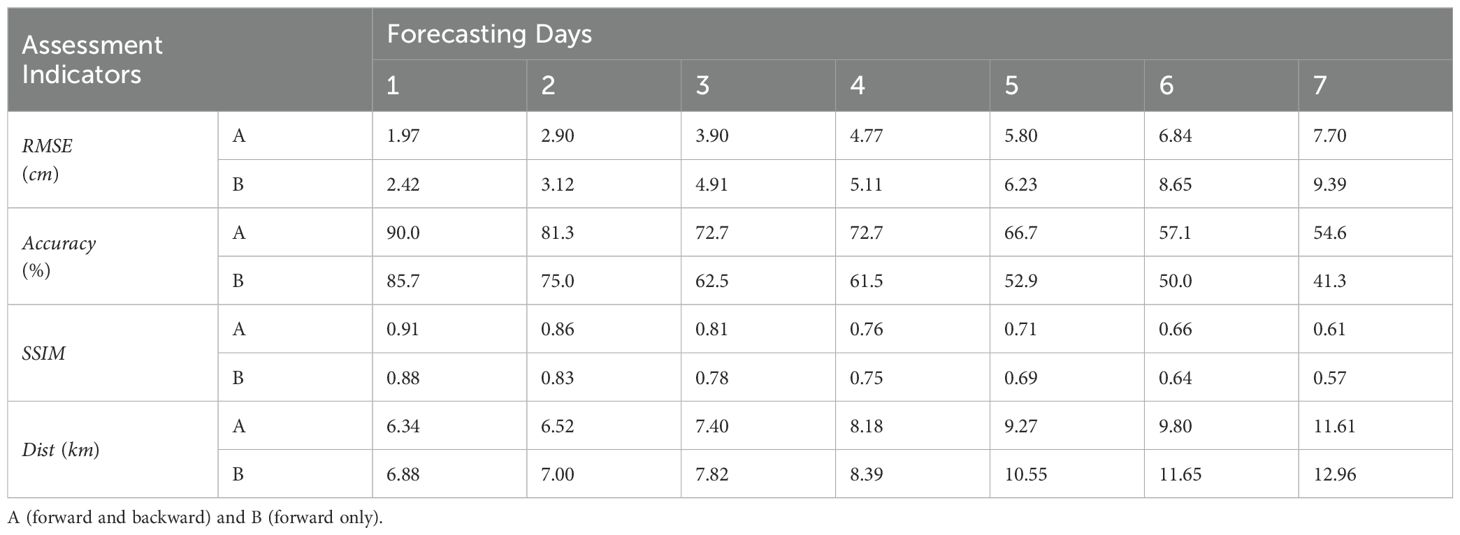
Table 2. Quantitative analysis of the effect of the forward and backward input conditions on the prediction.

4.2 Model comparison validation

In this subsection, to demonstrate the feasibility and the advantages of the model, we compare the AB-LSTM with the HYCOM model forecast and the FC-LSTM (Srivastava et al., 2015), PredRNN (Wang et al., 2022), and Conv-LSTM (Shi et al., 2015) spatiotemporal prediction methods under the 3-4-3 input block conditions described in Section 4.1 and using the evaluation metrics described in Section 2.2.3. It is worth emphasizing that the horizontal comparison verification of the model should be discussed in different scenarios. For mesoscale vortices, the different properties of vortices and the setting of the research area are very important elements for scene division. Therefore, we will reflect the model verification effect under different research areas in the subsequent regional generalization verification. The model generalization test for differentiating AE and CE in a single eddy prediction scenario is also presented.

Since the prediction results of AE and CE are similar, we consider the polarity of the eddy to be less influential on the comparison experiments, so we will not distinguish between them in this subsection. To avoid the high prediction effect caused by the use of the sample dataset and the inability to effectively compare the results of the experiments, we conduct the experiments on 1000 sets of sea-surface height data that are not included in the sample data. Data structure is still 3-4-3, and the metrics are averaged within the groups. We set the prediction area to the KE region of 25–45°N and 150–170°E. The results are shown in Figure 8.

Figure 8

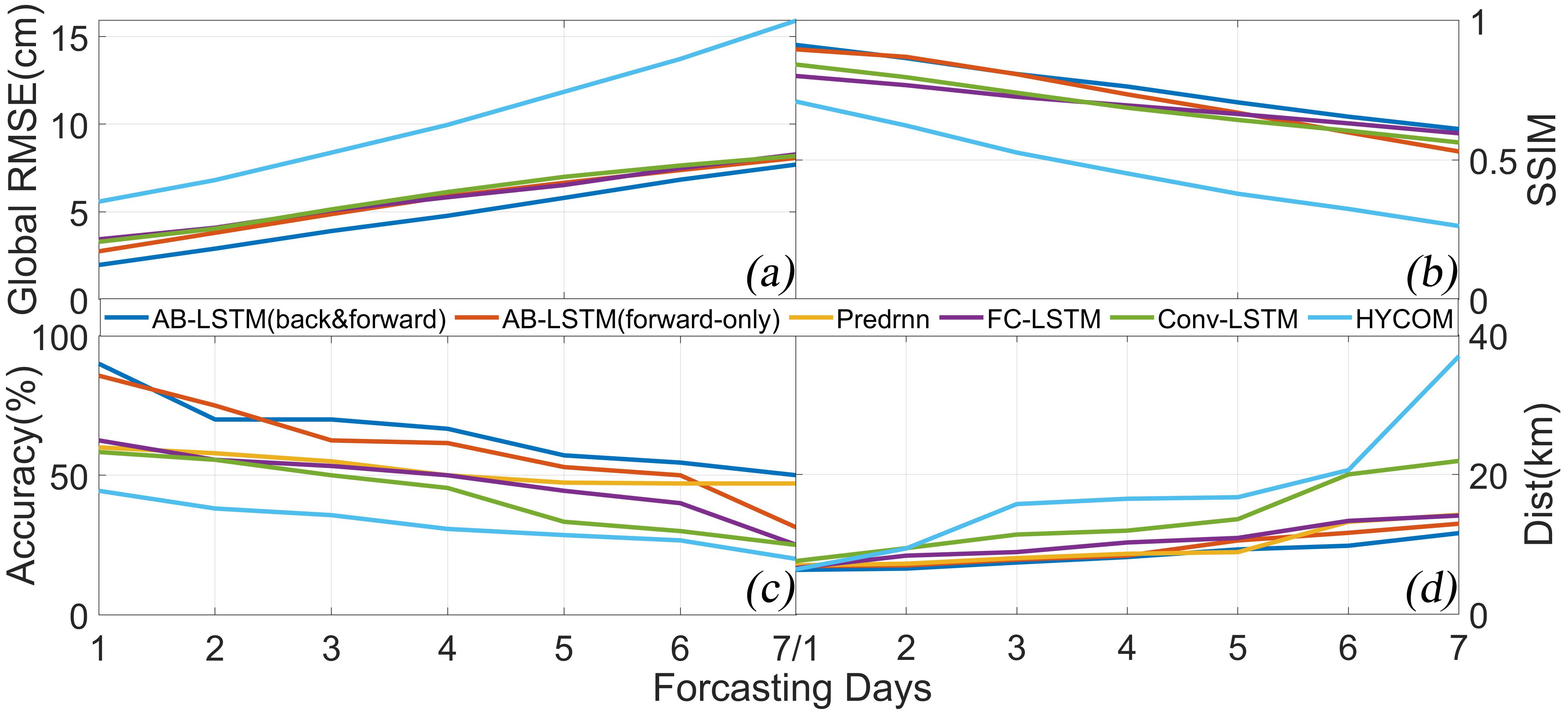
Figure 8. Plots of the (A) RMSE, (B) SSIM, (C) accuracy, and (D) Dist metrics for a 7-day forecast series for multiple forecasting methods and models.

As can be seen from Figure 7, according to all the computational indexes, the AB-LSTM yields better results. The AB-LSTM’s RMSE index increases from 1.97 cm on the first day to 7.70 cm on the seventh day, which is the same trend as the other methods, but the values are significantly lower than those of the other prediction methods. The AB-LSTM yields lower RMSE values than the unidirectional model in the control group, which distinguishes between positive and bidirectional inputs. Regarding the SSIM index, the AB-LSTM method has values similar to several of the prediction methods, except that the numerical prediction is within the range of 0.6–0.9 and only differs from the other prediction methods by about 0.05. This is since several of the deep learning-based spatial-temporal prediction models utilized as the control group in this paper are able to achieve very good results in terms of structural similarity, so it is not possible for this metric to clearly reflect the superiority of the AB-LSTM. The AB-LSTM has a much higher Accuracy, with a hit rate of more than 50% during the prediction sequence (days 1–7). This is 10–20% better than those of the other methods. On average, it achieves a 5% higher Accuracy in the control experiments and can distinguish between forward and reverse inputs. This suggests that the forward and reverse inputs are important for the model in the long mesoscale eddy time series prediction. The AB-LSTM model has a slightly better Dist value. The prediction distance error ranges from 6.34 to 11.61 km, which is generally 1–10 km lower than those of the other prediction methods for the 7-day prediction series. The AB-LSTM model with bidirectional input is more accurate in terms of the prediction results after the fourth day compared with the model with only forward input. After the fourth day, the prediction results of the AB-LSTM model with bi-directional inputs are lower, which suggests that the bi-directional inputs have a positive effect on the model in the long-term prediction of mesoscale eddies. Overall, compared with the traditional numerical prediction models’ results, the spatial and temporal prediction models that use deep learning algorithms have a greater advantage in terms of the overall prediction error and mesoscale eddy-related prediction indexes. For the sample dataset introduced in this paper, according to all the metrics, the AB-LSTM has the best performance, which directly proves the superiority of the AB-LSTM. In addition, by analysing the experimental results of the control experiment group, it was found that the two-way input training of the confrontation has more advantages and positive significance compared with the one-way input.

4.3 Model generalisation test

Model generalisability refers to the model’s ability to adapt to new data, i.e., whether the model can make accurate predictions for data that does not appear in the training set. A model with a strong generalisability can perform well on different datasets, not just on the training set. In summary, generalisability concerns the model’s ability to adapt to unknown situations (Liu and Aitkin, 2008). To explore the generalisability of our model, we experimentally validate the AB-LSTM using data from the same region as the data in the training sample set but that are not included in the training and testing sets. We also test the model on data for other sea areas. In this paper, we take the Oyashino Extension (OE, 35–45°N, 140–150°E) region and the North Pacific Subtropical Countercurrent (STCC, 15–25°N, 130–140°E) as the validation areas. It should be noted that in this subsection, the sea surface height data for the OE and STCC regions are processed into 128×128 grids using the data processing method described in Section 2.2.2, and the data span from January 1993 to 31 December 2022. The experimental data for the KE region, which are not included in the training and testing datasets, span from 1 to 30 October 2023 and are processed in the same manner.

As can be seen from Figure 8, the prediction results of the tested models are slightly poorer than the prediction results presented in Section 4.2, but the overall effects are similar, and all of the models yield more stable and good prediction results. The AB-LSTM is still better than the other models in terms of several metrics. For the prediction results for the three regions, the RMSE index remains within the range of 2.25–9.41 cm, which is slightly higher than the prediction results of 1.97–7.70 cm obtained in Section 4.2. The SSIM indicator remains within the range of 0.52–0.85, which is slightly lower than the range of 0.61–0.90 obtained in Section 4.2. The Accuracy remains within the range of 48.35–84.03%, which is slightly lower than the range of 54.60–90.00% obtained in Section 4.2. The Dist remains within the range of 6.71–12.89 km, which is slightly higher than the range obtained in Section 4.2. The possible reason for this result is that the OE region and STCC region are not within the region of the training set, and there may be motion features that are not fully fitted by the model, which may lead to the result that the AB-LSTM fits the KE region data better and the data for the other two regions slightly worse in terms of the prediction effect. The mesoscale eddy recognition algorithm used in this paper has a better recognition ability, but it still has a slightly worse recognition ability. In addition, it still has the possibility of identification error, and the mesoscale eddies identified from the predicted sea surface height data may have the intermittent appearance or disappearance of error, which would lead to problems in estimating the distance deviation of the centre of the mesoscale eddy and will make the error falsely high.

Based on the prediction results presented in Figure 9, several of the models achieve better prediction results in several sea areas, but the performance of the AB-LSTM is the best, which proves that the AB-LSTM model has an acceptable generalization ability for different sea surface height datasets.

Figure 9

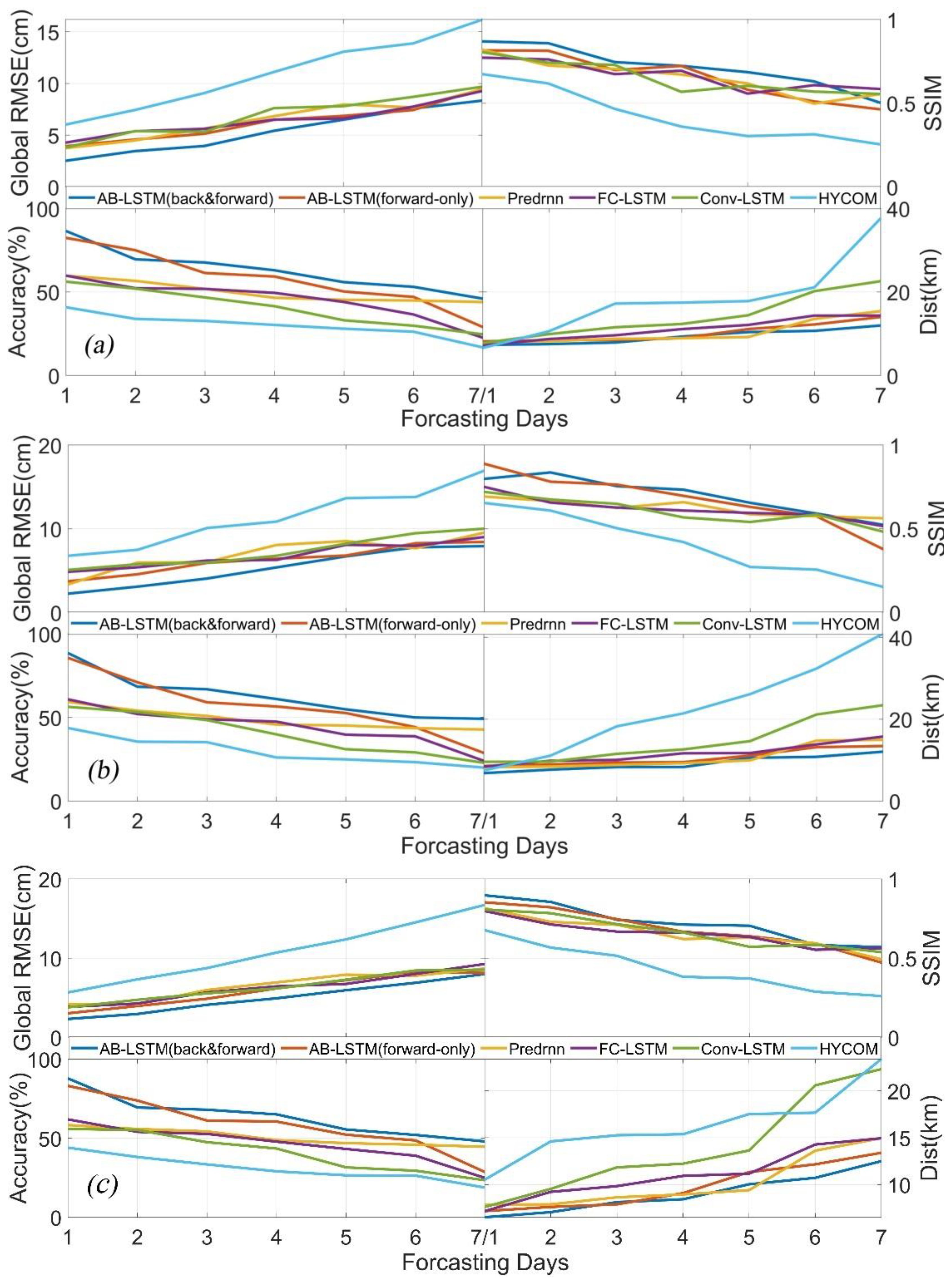
Figure 9. Generalisation test of the AB-LSTM model using data for the (A) OE region, (B) STCC region, and (C) KE region.

4.4 Single eddy prediction effect

Although regional sea surface prediction can reflect the overall prediction effect better, the prediction effect on single eddies is not fully reflected, so in this subsection, we predict multiple single eddies and use the strength at the centre of the eddy (denoted as the SSH in the centre of the eddy in this paper) and the eddy radius to describe them. Thus, the prediction effect of single eddies will be more clearly reflected in the form of data. Figure 10 shows a schematic representation of the evolution of a typical dipole pair over the course of its evolution.

Figure 10

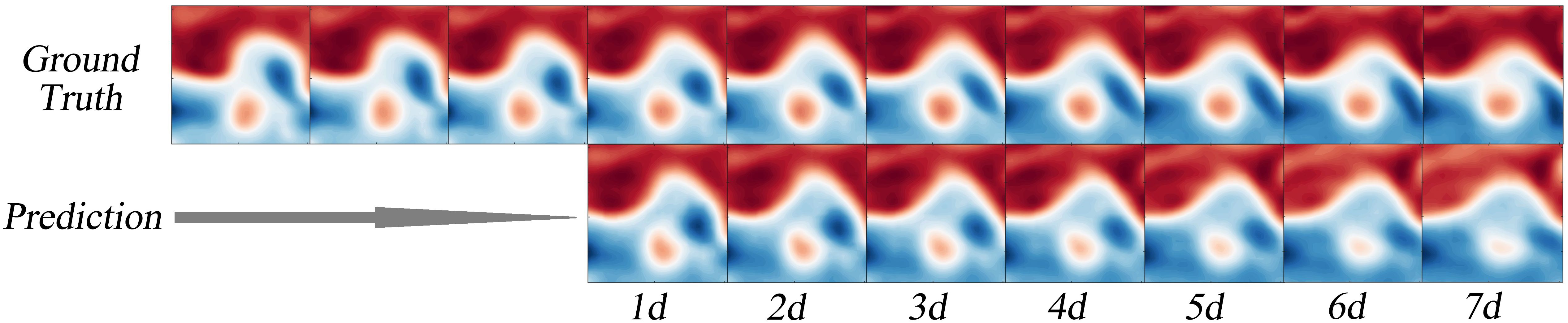
Figure 10. Schematic of the 7-day evolution of a pair of dipoles located in the KE region on 1 September 2017. To make the dipole evolution visually clearer, we converted the sea surface height data into a pseudo-colour map with an intercept area of 28–32°N, 146–150°E.

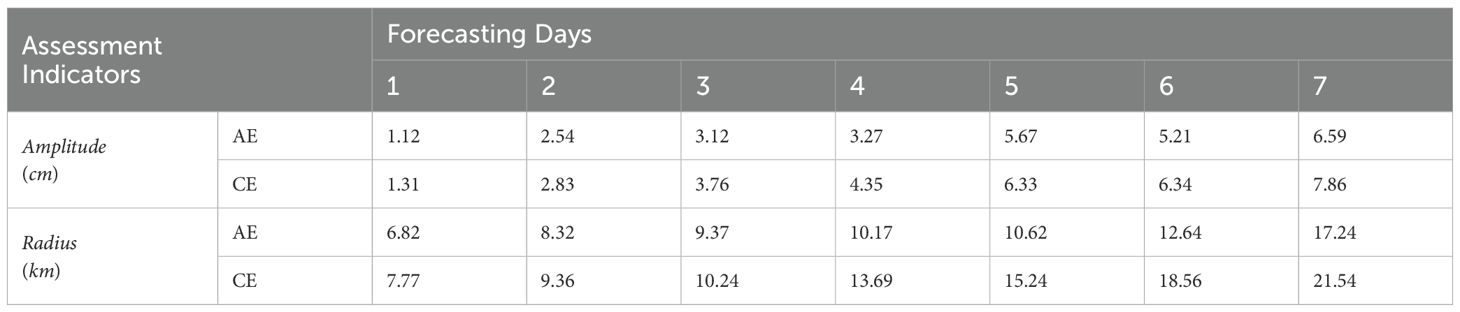
We randomly select 1000 days of data in the sea surface height sample dataset used in this paper as experimental samples, and then we use the AB-LSTM model to make predictions for a period of 7 days according to the 3-4-3 structure. We use the mesoscale eddy mixing identification algorithm to identify the matched eddy pairs (real vs. predicted). Then, we extract their centre eddy strengths and eddy radii as the control group for the experiments. To avoid the unmatched vortices and matching errors caused by the identification algorithms (described in the previous section) and thus to more effectively reflect the prediction effect, we exclude the matching error terms. Table 3 presents the single eddy prediction errors in the form of within-group averages and the distinction between AEs and CEs.

Table 3

Table 3. Quantification of single eddies during the 7-day forecast period.

The Radius metric is the equivalent radius of the identified eddy. As can be seen from Table 4, the AB-LSTM model also achieves relatively good prediction results in single-eddy prediction. In terms of the eddy centre height errors, the AE centre height errors are within the range of 1.12–6.59 cm, and the CE centre height errors are within the range of 1.31–7.86 cm. Overall, both increase as the prediction time increases. However, under the condition of distinguishing between the AEs and CEs, there is not a large difference in the overall errors of the two, which is similar to the conclusion of Wang et al (Wang et al., 2020). In terms of the eddy radius error, it also exhibits an overall prediction result with a trend similar to that of the eddy centre height error, which indicates that the model is more stable in the prediction process. In order to reflect the advantages of the AB-LSTM model in the single-eddy experiment, we conducted experiments according to the same sample collection method, and the results are shown in Table 4.

Table 4

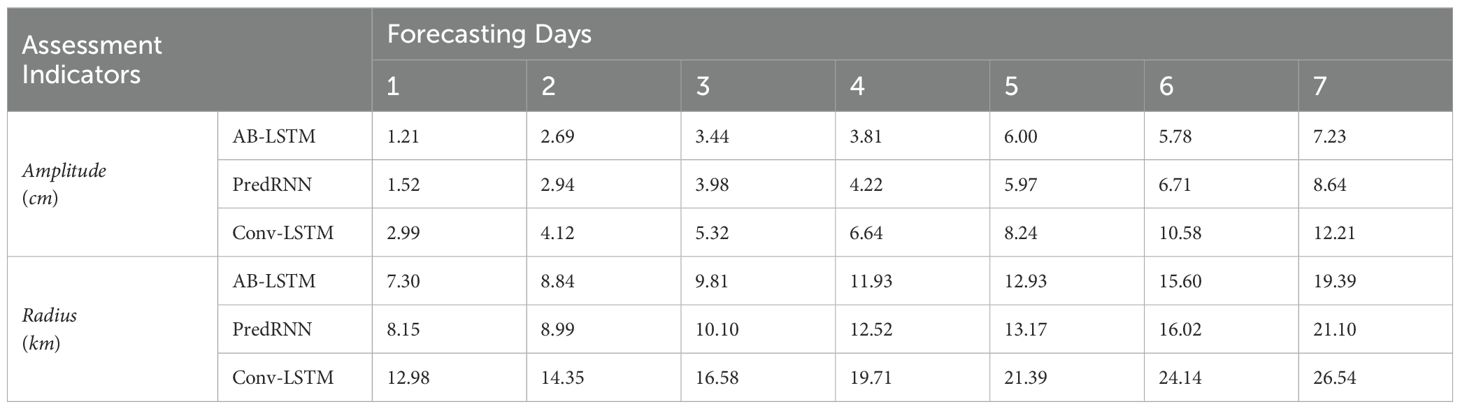
Table 4. Quantification of single eddies during the 7-day forecast period (different models and no distinction between AE and CE).

From Table 3, AB-LSTM is significantly better than the primary Conv-LSTM in single-eddy prediction results, and the experimental results of the AB-LSTM model are continued by the experimental results in Table 2. It is worth emphasizing that we have obtained the horizontal comparison results among multiple models above, so in the horizontal comparison experiment of single eddy prediction, we only compared the two models with similar performance as the AB-LSTM model.

4.5 Additional experiment

In the first few sections of this chapter, the AB-LSTM model proposed by us has achieved a small advantage in the image numerical evaluation index (SSIM, RMSE), and an even greater advantage in the feature prediction of mesoscale vorticity. However, its performance in the prediction error analysis results on the 7th day still makes us worried: Whether the trend of error change shown by AB-LSTM during the 7-day forecast will lead to more drastic changes over a longer forecast time horizon, making the prediction model worse than other spatio-temporal prediction models over a longer time horizon. Since the data input format we selected in the previous paper is 3-4-3 mode, which is not fully applicable for a longer prediction time, we use a longer data input mode here: 3-7-3. As a comparison, we still use RMSE, Accuracy, SSIM and Dist for error quantification (for longer forecast time series, a longer input should be selected).

After comparing the results of the two data input modes, we can find from Table 5 that there is no significant increase in prediction error on the whole. The 3-4-3 input mode has better prediction effect within 3 days, while the 3-7-3 input mode has better lasting prediction ability within a longer prediction period. This error is generally reversed on the fourth or fifth day of prediction, which also shows a relatively easy to understand trend, that is, different input data models are generated under different deep network models, and with the change of its application scenario, its prediction effect will also change.

Table 5

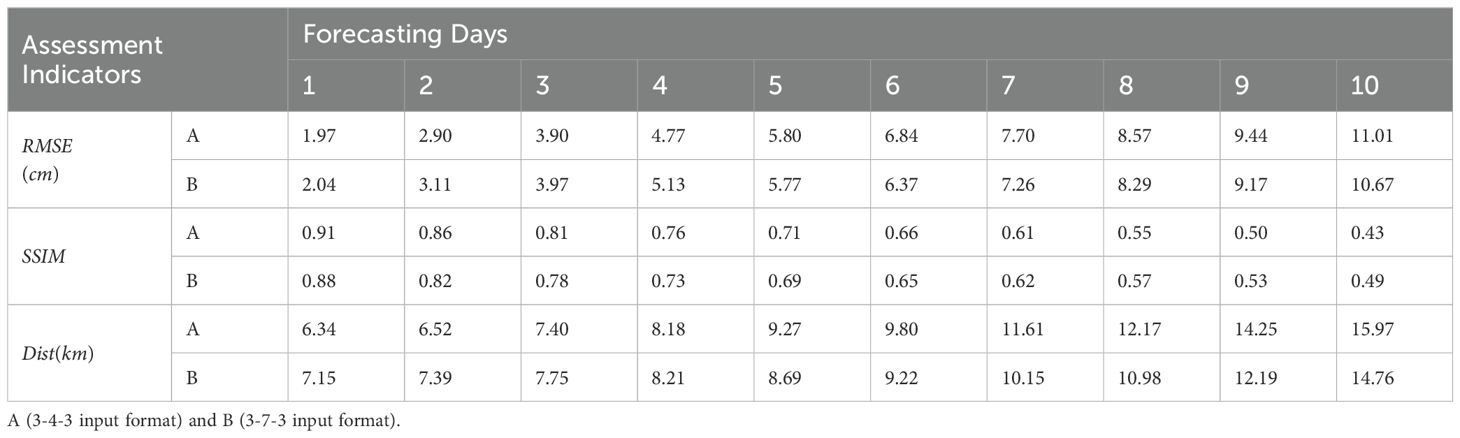
Table 5. Quantification of eddies over a 7-day forecast period (No distinction is made between AE and CE).

5 Summary and outlook

In this study, we acquired AVISO satellite altimeter data and HYCOM ocean model forecast data as the basis of our work. These data not only provide rich ocean information but also provide the necessary data support for the identification and characterization of mesoscale eddies. Then, we effectively identified and extracted the features of mesoscale eddies utilizing the hybrid mesoscale eddy identification algorithm, which has a better identification effect. We combined it with the sea surface height data and established an evaluation system for mesoscale eddy prediction, which includes four test metrics, namely, the RMSE, SSIM, Dist, and Num.

Subsequently, we combined the time-series prediction advantages of the LSTM model with those of previous studies, utilized the ST-LSTM model as the base generative model, and stacked them to form a prediction network in the same way as the Conv-LSTM. In addition to introducing the generative adversarial network model, which has a strong generative capability, the AB-LSTM model was constructed by embedding the ST-LSTM module into the generator therein. Considering that previous studies have mostly focused on unidirectional sequence prediction without using backward-assisted prediction, we incorporated backward sequence prediction into the input sequences based on the AB-LSTM model and obtained better results than when only unidirectional inputs were utilized. The RMSE was 1.97–7.70 cm, the SSIM was ≥0.61, the Accuracy was ≥54.6%, and the Dist was 6.34–11.61 km. All of the above indicators were better than those of the other models and numerical prediction products, thus achieving the goal of this study. In the training process, we used the Adam optimizer as the hyperparameter container, and through many experiments, we determined that the number of iterations should be 100,000 times and the number of batches should be 8. The experimental results show that the relevant parameters were set reasonably, and a relatively smooth trend was maintained in the training iteration loss. Then, we tested the model’s generalization ability using data for a different sea area and new data for the same sea area to achieve data expansion of the non-training testing set. The experimental results show that the AB-LSTM also has a good prediction ability for data that are different from the training test sample dataset. Its prediction ability is only slightly lower than the training sample prediction results according to the indicators, and it is still able to maintain a large improvement compared with the other models. Therefore, the results of the generalization test prove that the AB-LSTM has an acceptable generalization ability. Finally, to address the problem that the full-domain prediction error cannot directly describe the single-eddy prediction effect, we conducted single-eddy prediction analyses using randomly selected pairs of identified vortices. The results show that the eddy polarity has little effect on the prediction effect and that the single-eddy prediction error tends to be smaller than the full-domain prediction error.

Although the AB-LSTM model developed in this study preforms better than other prediction models in terms of the prediction error, it still has some shortcomings. First, the mesoscale eddy identification algorithm used in this paper was found to have discrepancies in terms of matching the real eddy with the predicted eddy, and there is no matching criterion that can be adopted, which leads to the fact that we have no choice but to eliminate the eddy pairs that are incorrectly matched in our single-eddy prediction analysis. To a certain extent, this is not possible in a single eddy prediction analysis. This may make our experimental results better than the real results to a certain extent. Second, more physical parameters should be introduced into the single-eddy prediction instead of only using the eddy centre height and radius to evaluate the error. In the future, we plan to introduce vorticity, shear deformation, and tensile deformation to improve the evaluation of the single-eddy prediction effect. Third, the computational redundancy of the AB-LSTM model is greater than those of several of the prediction models cited in the paper. To achieve better results, the AB-LSTM takes longer to run, occupies more memory, and has more training iterations, which means that our model still needs to be improved in terms of performance. In the next step, we will try to introduce more mesoscale eddy physics information to improve the prediction effect while improving the model.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: AVISO,JCOPE.

Author contributions

XM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. LZ: Conceptualization, Investigation, Software, Writing – review & editing. WX: Data curation, Methodology, Supervision, Writing – review & editing. ML: Formal analysis, Project administration, Validation, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We are grateful for the provision of the mesoscale eddy dataset from archiving, validation, and interpretation of satellite oceanographic data (AVISO) (https://www.aviso.altimetry.fr/en/data/products/value-added-products/global-mesoscale-eddy-trajectory-product.html) and the reanalysis data from the hybrid coordinate ocean model (HYCOM) (https://www.hycom.org/), We thank Wang et al. for providing the spatial–temporal long short-term memory (ST-LSTM) model, and other scholars and organizations that helped in the research process (https://github.com/thuml/predrnn-pytorch).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akima H. (1970). A new method of interpolation and smooth curve fitting based on local procedures. J. ACM (JACM) 17, 589–602. doi: 10.1145/321607.321609

Crossref Full Text | Google Scholar

Ashkezari M. D., Hill C. N., Follett C. N., Forget G., Follows M. J. (2016). Oceanic eddy detection and lifetime forecast using machine learning methods. Geophysical Res. Lett. 43, 12,234–212,241. doi: 10.1002/2016GL071269

Crossref Full Text | Google Scholar

Chassignet E. P., Hurlburt H. E., Metzger E. J., Smedstad O. M., Cummings J. A., Halliwell G. R., et al. (2009). US GODAE: global ocean prediction with the HYbrid Coordinate Ocean Model (HYCOM). Oceanography 22, 64–75. doi: 10.5670/oceanog.2009.39

Crossref Full Text | Google Scholar

Chassignet E. P., Hurlburt H. E., Smedstad O. M., Halliwell G. R., Hogan P. J., Wallcraft A. J., et al. (2007). The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 65, 60–83. doi: 10.1016/j.jmarsys.2005.09.016

Crossref Full Text | Google Scholar

Chelton D., Schlax M. G., Samelson R. M. (2011). Global observations of nonlinear mesoscale eddies. Prog. Oceanography 91, 167–216. doi: 10.1016/j.pocean.2011.01.002

Crossref Full Text | Google Scholar

Dong C., McWilliams J., Liu Y., Chen D. (2014). Global heat and salt transports by eddy movement. Nat. Commun. 5, 3294. doi: 10.1038/ncomms4294

PubMed Abstract | Crossref Full Text | Google Scholar

Duo Z., Wang W., Wang H. (2019). Oceanic Mesoscale Eddy detection method based on deep learning. Remote. Sens. 11, 1921. doi: 10.3390/rs11161921

Crossref Full Text | Google Scholar

Eden C., Dietze H. (2009). Effects of mesoscale eddy/wind interactions on biological new production and eddy kinetic energy. J. Geophysical Research: Oceans 114. doi: 10.1029/2008JC005129

Crossref Full Text | Google Scholar

Franz K., Roscher R., Milioto A., Wenzel S., Kusche J. "Ocean Eddy Identification and Tracking Using Neural Networks," IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium. (Valencia, Spain: IEEE). (2018) pp. 6887–6890. doi: 10.1109/IGARSS.2018.8519261

Crossref Full Text | Google Scholar

Ge L., Huang B., Chen X., Chen G. (2023). Medium-range trajectory prediction network compliant to physical constraint for oceanic eddy. IEEE Trans. Geosci. Remote Sensing. 61, 1–14, 2023. doi: 10.1109/TGRS.2023.3298020

Crossref Full Text | Google Scholar

Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., et al. (2014). Generative adversarial nets. Adv. Neural Inf. Process. Syst. 27.

Google Scholar

Iizuka S., Simo-Serra E., Ishikawa H. (2017). Globally and locally consistent image completion. ACM Trans. Graphics (ToG) 36, 1–14. doi: 10.1145/3072959.3073659

Crossref Full Text | Google Scholar

Isern-Fontanet J., Font J., García-Ladona E., Emelianov M., Millot C., Taupier-Letage I. (2004). Spatial structure of anticyclonic eddies in the Algerian basin (Mediterranean Sea) analyzed using the Okubo–Weiss parameter. Deep Sea Res. Part II: Topical Stud. Oceanography 51, 3009–3028. doi: 10.1016/j.dsr2.2004.09.013

Crossref Full Text | Google Scholar

Itoh S., Yasuda I. (2010). Water mass structure of warm and cold anticyclonic eddies in the western boundary region of the subarctic North Pacific. J. Phys. oceanography 40, 2624–2642. doi: 10.1175/2010JPO4475.1

Crossref Full Text | Google Scholar

Kalchbrenner N., Oord A., Simonyan K., Danihelka I., Vinyals O., Graves A., et al. (2017). “Video pixel networks,” in Proceedings of the 34th International Conference on Machine Learning, PMLR 70:1771–1779.

Google Scholar

Kingma D. P., Ba J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.

Google Scholar

Liu C. C., Aitkin M. (2008). Bayes factors: Prior sensitivity and model generalizability. J. Math. Psychol. 52, 362–375. doi: 10.1016/j.jmp.2008.03.002

Crossref Full Text | Google Scholar

Liu J., Zhang T., Han G., Gou Y. (2018). TD-LSTM: Temporal dependence-based LSTM networks for marine temperature prediction. Sensors 18, 3797. doi: 10.3390/s18113797

PubMed Abstract | Crossref Full Text | Google Scholar

Liu Y., Dong C., Guan Y., Chen D., McWilliams J., Nencioli F. (2012). Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Res. Part I: Oceanographic Res. Papers 68, 54–67. doi: 10.1016/j.dsr.2012.06.001

Crossref Full Text | Google Scholar

Ma C., Li S., Wang A., Yang J., Chen G. (2019). Altimeter observation-based eddy nowcasting using an improved Conv-LSTM network. Remote Sens. 11, 783. doi: 10.3390/rs11070783

Crossref Full Text | Google Scholar

Ma X., Zhang L., Xu W., Li M., Zhou X. (2024). A mesoscale eddy reconstruction method based on generative adversarial networks. Front. Mar. Sci. 11, 1411779. doi: 10.3389/fmars.2024.1411779

Crossref Full Text | Google Scholar

McWilliams J. C. (2016). Submesoscale currents in the ocean. Proc. R. Soc. A: Mathematical Phys. Eng. Sci. 472, 20160117. doi: 10.1098/rspa.2016.0117

PubMed Abstract | Crossref Full Text | Google Scholar

Metzger E. J., Hurlburt H., Xu X., Shriver J. F., Gordon A. L., Sprintall J., et al. (2010). Simulated and observed circulation in the Indonesian Seas: 1/12 global HYCOM and the INSTANT observations. Dynamics Atmospheres Oceans 50, 275–300. doi: 10.1016/j.dynatmoce.2010.04.002

Crossref Full Text | Google Scholar

Nencioli F., Dong C., Dickey T., Washburn L., McWilliams J. C. (2010). A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight. J. atmospheric oceanic Technol. 27, 564–579. doi: 10.1175/2009JTECHO725.1

Crossref Full Text | Google Scholar

Nian R., Cai Y., Zhang Z., He H., Wu J., Yuan Q., et al. (2021). The identification and prediction of Mesoscale Eddy variation via memory in memory with scheduled sampling for sea level anomaly. Front. Mar. Sci. 8, 753942. doi: 10.3389/fmars.2021.753942

Crossref Full Text | Google Scholar

Oka E., Qiu B. (2012). Progress of North Pacific mode water research in the past decade. J. Oceanography 68, 5–20. doi: 10.1007/s10872-011-0032-5

Crossref Full Text | Google Scholar

Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., et al. (2019). Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 32.

Google Scholar

Patraucean V., Handa A., Cipolla R. (2015). Spatio-temporal video autoencoder with differentiable memory. arXiv.

Google Scholar

Qiu B., Chen S. (2005). Eddy-induced heat transport in the subtropical north pacific from Argo, TMI, and altimetry measurements. Gayana 68, 499–501. doi: 10.1175/JPO2696.1

Crossref Full Text | Google Scholar

Qiu B., Chen S. (2013). Concurrent decadal mesoscale eddy modulations in the western North Pacific subtropical gyre. J. Phys. oceanography 43, 344–358. doi: 10.1175/JPO-D-12-0133.1

Crossref Full Text | Google Scholar

Shi X., Chen Z., Wang H., Yeung D.-Y., Wong W.-K., Woo W.-c. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 28.

Google Scholar

Shriver J., Hurlburt H. E., Smedstad O. M., Wallcraft A. J., Rhodes R. C. (2007). 1/32 real-time global ocean prediction and value-added over 1/16 resolution. J. Mar. Syst. 65, 3–26. doi: 10.1016/j.jmarsys.2005.11.021

Crossref Full Text | Google Scholar

Srivastava N., Mansimov E., Salakhudinov R. (2015). “Unsupervised learning of video representations using lstms,” in Proceedings of the 32nd International Conference on Machine Learning, PMLR 37:843–852.

Google Scholar

Trott C. B., Metzger E. J., Yu Z. (2023). Luzon strait mesoscale eddy characteristics in HYCOM reanalysis, simulation, and forecasts. J. Oceanography 79, 423–441. doi: 10.1007/s10872-023-00686-5

Crossref Full Text | Google Scholar

Villegas R., Yang J., Hong S., Lin X., Lee H. (2017). Decomposing motion and content for natural video sequence prediction. arXiv.

Google Scholar

Wallcraft A., Hurlburt H., Metzger E., Chassignet E., Cummings J., Smedstad O. M. (2007). “Global ocean prediction using HYCOM,” in Paper presented at the 2007 DoD High Performance Computing Modernization Program Users Group Conference. (Pittsburgh, PA, USA). 259–262. doi: 10.1109/HPCMP-UGC.2007.36

Crossref Full Text | Google Scholar

Wang X., Wang H., Liu D., Wang W. (2020). The prediction of oceanic mesoscale eddy properties and propagation trajectories based on machine learning. Water 12, 2521. doi: 10.3390/w12092521

Crossref Full Text | Google Scholar

Wang X., Wang X., Yu M., Li C., Song D., Ren P., et al. (2021). MesoGRU: Deep learning framework for mesoscale eddy trajectory prediction. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi: 10.1109/LGRS.2021.3087835

Crossref Full Text | Google Scholar

Wang Y., Long M., Wang J., Gao Z., Yu P. S. (2017). Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. Adv. Neural Inf. Process. Syst. 30.

Google Scholar

Wang Y., Wu H., Zhang J., Gao Z., Wang J., Philip S. Y., et al. (2022). Predrnn: A recurrent neural network for spatiotemporal predictive learning. IEEE Trans. Pattern Anal. Mach. Intell. 45, 2208–2225. doi: 10.1109/TPAMI.2022.3165153

PubMed Abstract | Crossref Full Text | Google Scholar

Wang Y., Yang X., Hu J. (2016). Position variability of the Kuroshio Extension sea surface temperature front. Acta Oceanologica Sin. 35, 30–35. doi: 10.1007/s13131-016-0909-7

Crossref Full Text | Google Scholar

Xu G., Cheng C., Yang W., Xie W., Kong L., Hang R., et al. (2019). Oceanic eddy identification using an AI scheme. Remote Sens. 11, 1349. doi: 10.3390/rs11111349

Crossref Full Text | Google Scholar

Zhang Z., Zhang Y., Wang W., Huang R. X. (2013). Universal structure of mesoscale eddies in the ocean. Geophysical Res. Lett. 40, 3677–3681. doi: 10.1002/grl.v40.14

Crossref Full Text | Google Scholar