Estimating fish stock biomass using a Bayesian state-space model: accounting for catchability change due to technological progress

The assessment of trends in fish stocks using long-term time-series data is important for effective fisheries resource management. Despite technological advancements in recent decades, the resulting increase in fisheries catch potential with applied effort is often not adequately considered in stock assessments. To address this gap, we developed a framework for simultaneously estimating catchability and biomass using a state-space population model. This model allows for the flexible integration of the timing and functional form of the uptake of technological innovations that are assumed to influence catchability. Our objective was to test the effectiveness of this framework by applying it to 48 years of skipjack pole-and-line fishery data in Japanese waters. We utilized two population models, the Ricker-type and Gompertz-type, under three different scenarios of technology-driven catchability changes: constant, exponential, and S-shaped. The results indicate that the calculations converged for the constant and S-shaped scenarios, and that both the Ricker and Gompertz models performed almost equally well in terms of the goodness of fit and prediction accuracy under the S-shaped scenario, which assumes time-varying catchability. Although time-varying catchability poses challenges for accurate biomass estimation due to the large range of uncertainty, the decreasing trend in stock status is still detected. The estimated recent decline in the skipjack stock around Japan provides a warning for stock assessments that do not incorporate technological progress, despite the species’ high natural population growth rate and presumed stable stock status. Our methodology, based on publicly available archived catch records (catch and effort), can be applied to other species with known timelines of technological innovation.

1 Introduction

Assessment of population trends is a cornerstone of fisheries management advice (Beddington et al., 2007; Mace, 2001). Accurate assessments are critical for implementing and measuring effectiveness of regulations that aim to prevent excessive declines in fish stocks, ensuring the sustainability of fisheries, and maintaining socioeconomic benefits and ecosystem functions (Costello et al., 2016; Hilborn et al., 2004; Worm et al., 2009). Hence, reliable population assessments are essential for supporting the ecosystem as well as fisheries-dependent livelihoods (Allison and Ellis, 2001; Crona et al., 2023).

Recent technological developments, such as sonar fish finders, radars, high resolution satellite imagery of ocean conditions (e.g., sea surface temperature), and improved inter-vessel communication, have enhanced the efficiency of locating and catching fish. These advancements have likely caused significant changes in catchability (catch effectiveness per unit effort), which are not adequately accounted for in many stock assessments (Eigaard et al., 2014; Hoyle et al., 2024; Kleiven et al., 2022; Rousseau et al., 2019). Accounting for rapid technology driven catchability changes in stock assessment is challenging because data on technology uptake are often not available at the vessel level. Even if available, the influence of technology uptake on catchability is difficult to quantify, as most vessels in a fishery are likely to adopt new technology simultaneously. This results in very few vessels actively fishing with old technology or gear alongside vessels using new technology for a sufficiently long period to quantify the effects of technology on catch rates and catchability. This situation can also make it difficult to standardize catch per unit effort (CPUE) data statistically to eliminate the effects of changes in fishing technology or practices. Because fishery-dependent CPUE provides the primary abundance indices for many stock assessments, it is essential to document changes in fishing gear, technology, and operational efficiency, which likely have strong effects on catchability, as well as the timing and rates of these changes. This basic knowledge can be derived from industry surveys, if not available from other sources, such as fishery logbooks or observer records, and provides a basis for further analysis of the implications of interpreting CPUE trends in relation to abundance.

Gear efficiency/technology effects are often accounted for in the catch equation C=qEN, where C is the number of fish caught, E is the amount of effort, N is the biomass or number of fish, and q is a coefficient of the catchability of fish (Hilborn and Walters, 1992; King, 2013). For example, if the catchability coefficient (q) increases by a factor of two over a certain period (perhaps because of technology uptake), a stock assessment that does not account for this may conclude that the biomass has doubled. Alternatively, doubling q may have compensated for the stock declining by half, such that the CPUE abundance index remained stable, while catches may have even increased. In this case, information on production based on the relationship between CPUE and catch is poor, which can create major problems in accurately estimating stock biomass.

Global fishing capacity has more than doubled since 1950 in all but the most developed regions (Rousseau et al., 2019). In combination with new technology and the modernization of fishing fleets, the implications for the sustainability of fisheries are profound (Rousseau et al., 2019). However, there are limited studies that considered rapid changes in fishing efficiency during stock assessments (Carvalho et al., 2014; Matsubara et al., 2022). For major pelagic fishery species, such as tuna and sardines, advances in radar and sonar technologies and improved information on ocean conditions are expected to improve fishing efficiency. However, catchability is often implicitly assumed to be constant in stock assessments that are conditioned on catch data and that use fishery-dependent CPUE as an abundance index. These assessments place strong faith in the standardized CPUE accounting for catchability changes, to provide a reliable index of abundance trends. Failure to adequately account for catchability changes can lead to severe biases in stock assessments and subsequent poor management advice (Arreguin-Sanchez, 1996; Hoyle et al., 2024).

Bayesian state-space models that estimate abundance by appropriately accounting for data uncertainty (observation error) have recently been developed and used in fisheries stock assessment and wildlife management (Best and Punt, 2020; Iijima et al., 2013; Scheuerell et al., 2021; Thorson and Minto, 2015; Yamamura et al., 2008; Zhou et al., 2011). In fisheries stock assessment, the Bayesian harvest-based state-space model is suggested as a useful method for estimating and evaluating population dynamics from fishery-dependent data records (catches and effort) that continually accumulate over time, such as fishery log sheets, even in the absence of detailed data such as size or age structure (Dichmont et al., 2016; Han et al., 2023). Studies have attempted to use such models to estimate abundance considering temporal changes in catchability due to technological development based on information from field manipulation experiments and existing literatures (Eigaard et al., 2014; Han et al., 2023; Kleiven et al., 2022). These studies emphasize the importance of properly estimating catchability, accounting for technology uptake, and adjusting CPUE estimates accordingly. Furthermore, a model incorporating specific catchability change points consistent with rapid technological uptake has been developed and applied to fishery stock assessments (Carvalho et al., 2014). However, there are still two critical issues: (1) many studies extrapolate catchability values from the existing literature and lack methods to estimate time-varying catchability, and (2) the statistical framework to explicitly distinguish between abundance (biomass) and catchability, while considering technological developments, requires further exploration (Bishop, 2006).

We hypothesized that these issues could be addressed simultaneously by integrating information on technology uptake into a Bayesian state-space model that explicitly addresses time-varying catchability. Here, information on technology introduction refers to the timing of introduction obtained through industry interviews and questionnaires, and Figure 1 shows a conceptual diagram of this approach. Since the state-space model draws out the potential information content of time-series data by considering the observation errors in the data, we considered that it may be able to capture changes in catchability before and after technological development. The objective of this study was to develop a statistical framework for integrating changes in catchability due to technological innovation into a Bayesian state-space model, and to test its effectiveness by applying it to long-term time series data from the Japanese skipjack tuna pole-and-line fishery (Figure 2). Using Ricker- and Gompertz-type state-space models, which are widely used as population models, we attempted to estimate the time-series changes in catchability and biomass from fishery data (catch and fishing effort). For changes in catchability, we assumed three scenarios (constant, exponential, and S-shaped increase), considering exponential and S-shaped increase as the functional forms used in previous studies (e.g., Kleiven et al., 2022; Han et al., 2023; Matsubara et al., 2022), in addition to the unlikely constant scenario assuming no change.

Figure 1

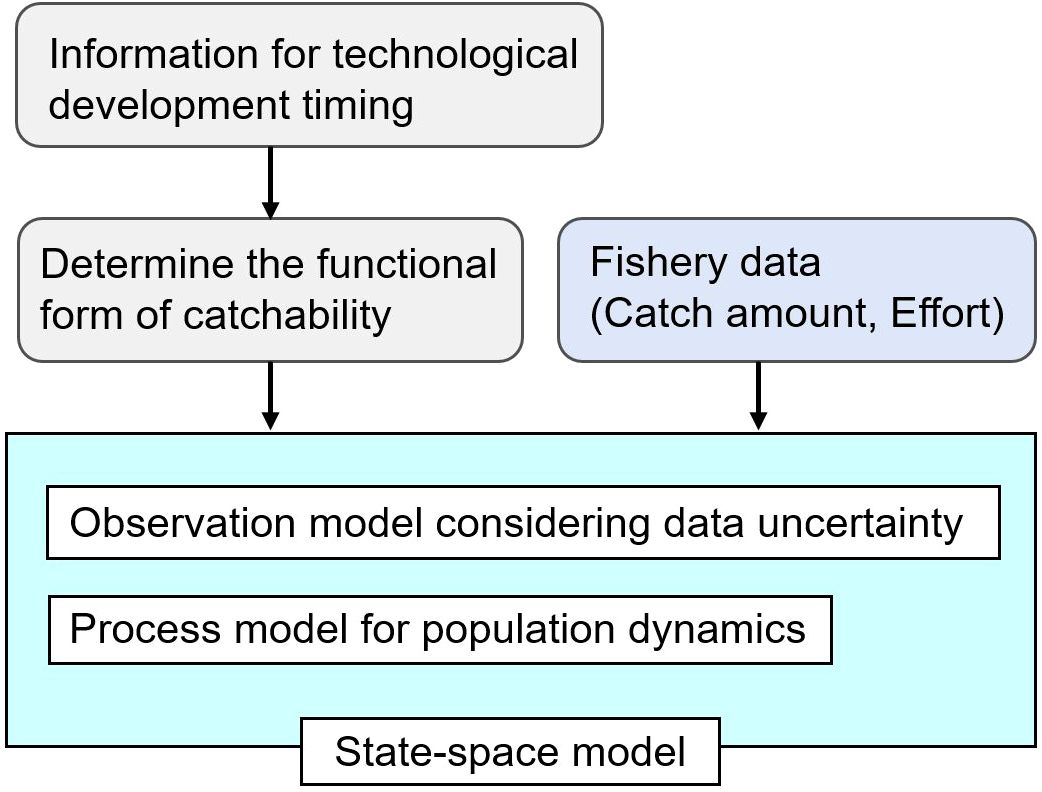
Figure 1. Conceptual diagram of a state-space model for estimating time-varying catchability. Catch and effort data are used to estimate population dynamics parameters. Utilizing the characteristics of the state-space model, which is hierarchical, the state and dynamics of the target species’ population are estimated by assuming a functional form of catchability based on information on the timing of technological uptake.

Figure 2

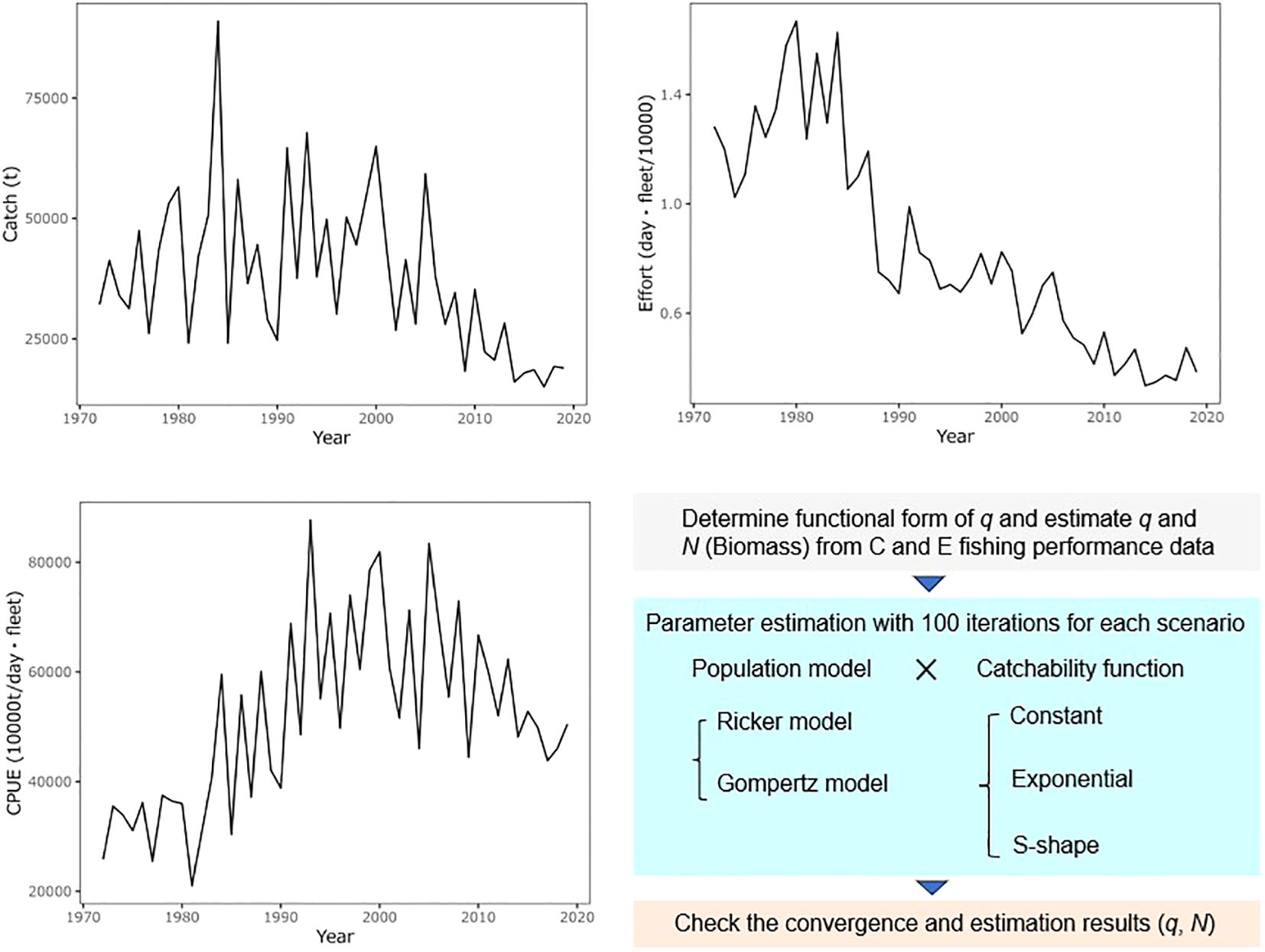
Figure 2. Time-series data of catch and effort (product of days and number of fleets) and workflow of this study. Effort is scaled to Effort/10,000. CPUE is the stock index of skipjack caught by Japanese pole-and-line fishing vessels, indicating the stock trend without considering technological uptake (i.e., when q = 1).

In this study, using skipjack pole-and-line fishery data, Bayesian estimation using MCMC calculations was performed for each case for a total of six combinations of two population models and three catchability scenarios. For each model combination, coefficients of determination were computed to assess the goodness of fit of the model, and leave-one-out cross-validation was also performed to examine prediction accuracy. We examined predictive accuracy in this study because we wanted to compare the performance of the two population models within a time constant q scenario or within a time-varying q scenario. Finally, although we expect q to change over time in an S-shape (logistic function) based on prior information on technological uptake in the skipjack pole-and-line fishery (Matsubara et al., 2022), the validity of the model for an S-shaped catchability change scenario is confirmed based on the results of this study, and a realistic approach for future work is discussed.

2 Materials and methods

2.1 Species and study area

Skipjack tuna (Katsuwonus pelamis) inhabits warm tropical waters and is of significant value in marine fisheries worldwide (Zhang et al., 2023). This species reaches sexual maturity in approximately 2 years and is known for its high population growth rate and density dependence (Ashida et al., 2010; Solari et al., 2003). Skipjack fisheries are conducted using a variety of fishing methods, although the catches are dominated by pole-and-line and purse-seine fisheries. In stock assessments of skipjack in the Western and Central Pacific, data from the Japanese pole-and-line fleet are used to construct CPUE abundance indices because they provide the longest time series of fishery-dependent data, dating back to the early 1970s. However, over such a long period, fishery operations have become more efficient and dependent on new technologies, such as bird radar and sonar, which are thought to have affected catch rate trends by improving catchability (Hamer et al., 2023; Matsubara et al., 2022). Although the stock status of this species in the western and central Pacific region has been assessed as stable and healthy in recent years (Castillo-Jordán et al., 2022), there is concern that this estimated stability is driven by long-term stable trends in the pole-and-line CPUE indices, used as the primary long-term abundance indices for stock assessment. It is possible that a stable CPUE has been influenced by technological innovations, such as bird radar and sonar, which have improved catchability and perhaps masked declines in true abundance. Given these considerations, we identified the Japanese skipjack pole-and-line fishery (JPPL) as an ideal case study for developing and applying a method to estimate temporal changes in catchability.

2.2 Data set

JPPL fisheries are mainly conducted in the northern western Pacific Ocean, predominately within the Japan exclusive economic zone. The study area focuses on pole-and-line fisheries in the waters around Japan (Figure 3). Therefore, the target population for this study was the Northwest Pacific population, that is thought to be part of a broader stock in the western and central Pacific Ocean. Long-term fishery data, including catch amount (t) and effort (vessel days), spanning 38 years from 1972 to 2019, were obtained from the Japanese logbook data records for analysis. The JPPL fishery comprises small (coastal), medium (offshore), and large (distant-water) vessels. Due to the large vessels covering the equatorial Pacific Ocean and the spatial sparsity and bias in sampling the target population, data from small and medium vessels were used in this study. Data from May to November, representing the season when skipjack are caught in the nearshore Japan pole-and-line fishery in the study area, were included in the analysis.

Figure 3

Figure 3. The study area encompasses the main region of the Japanese nearshore pole-and-line fishery in the northwestern Pacific Ocean. The colored area, indicated by the 2.5-degree grid in the figure, shows the total skipjack catch of pole-and-line fishing near Japan from 1972 to 2019. Areas with zero catch data are shown in gray.

The timing of technological development in this study was assumed to be similar to that previously determined for large-sized vessel fishing in distant waters (Matsubara et al., 2022) (Supplementary Data 2). However, since the introduction of equipment for medium-size vessels in Japan is thought to have been slightly later than that for large vessels, the technological innovations were assumed to have occurred in the 1990s (Hamer et al., 2024). For simplicity in this study, the inflection point of the S-shaped function was assumed to be in the middle of the 1972-2019 data set (i.e., 1996). Information on the timing of technology introduction was used only for the S-shaped scenario. Industry interview surveys, such as the one conducted by Matsubara et al. (2022), have the advantage of obtaining fishermen’s perceptions and opinions about the timing of past technology and gear improvements, which are not often available from logbook records required by management agencies. Furthermore, vessel skippers and crew can provide anecdotal support for changes in fishing effectiveness (i.e., catchability) associated with technological uptake (Marchal et al., 2007; Marriott et al., 2011).

2.3 Model description and estimation

To estimate the stock dynamics process, we extended the Bayesian state-space model to consider temporal variation in catchability. Bayesian state-space models, where the process model is a population model, are statistical frameworks that allow estimation of population dynamics while explicitly handling uncertainty and accounting for observation error and are commonly used in ecology to analyze nonlinear ecological processes from time-series data (Hostetler and Chandler, 2015). A state-space model comprises a state process model representing the stochastic transition of ecological states x_t (t = 1, 2, …, T), and an observation process model representing the data acquisition process. For analyzing population dynamics, a first-order Markov process, x_t | x_t-1, is applied sequentially, with the initial state defined by a random variable following a prior distribution. The observation process involves an observable vector y_t related to x_t, fluctuating with observation error. The Bayesian state-space model is a hierarchical model utilizing a set of three probability density functions (pdfs):

$${\text{g}}_{\text{t}}({\mathit{x}}_{\mathit{t}} \mathbf{|} {\mathit{x}}_{\mathit{t}\mathbf{-}\mathbf{1}} \mathbf{;} \mathit{\xi })\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}state process pdf,}$$

$${\text{g}}_1({\mathit{x}}_{\mathbf{1}} \mathbf{;}\mathit{\gamma })\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}initial state pdf,}$$

$\begin{array}{ll}{\text{f}}_{\text{t}}({\mathit{y}}_{\mathit{t}} | {\mathit{x}}_{\mathit{t}} ; \mathit{\psi })\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}observation process pdf,}& (1)\end{array}$

where, $\xi$, $\gamma$, and $\psi$ are vectors of model parameters.

In this study, the relationship between catch tonnage and population density over a 48-year period, from 1972 to 2019, was expressed as an observational process. In the t year (t = 1,2,3,…, T), the median catch C_t can be represented by the following equation, where q_t is the time-varying catchability parameter, E_t is the fishing effort (product of days and number of vessels), and N_t is the population density (e.g., Eigaard et al., 2014):

$\begin{array}{ll}{C}_t=q_t{E}_t{N}_t& (2)\end{array}$

Because skipjack catches are recorded in the logbooks in tonnage, which is a continuous value, the observed catch is assumed to follow the below log-normal distribution with variance σ² for the observation error:

$\begin{array}{ll}{C}_t~\text{lognormal}(\text{log}(q_t{E}_t{N}_t), {\sigma }^2)& (3)\end{array}$

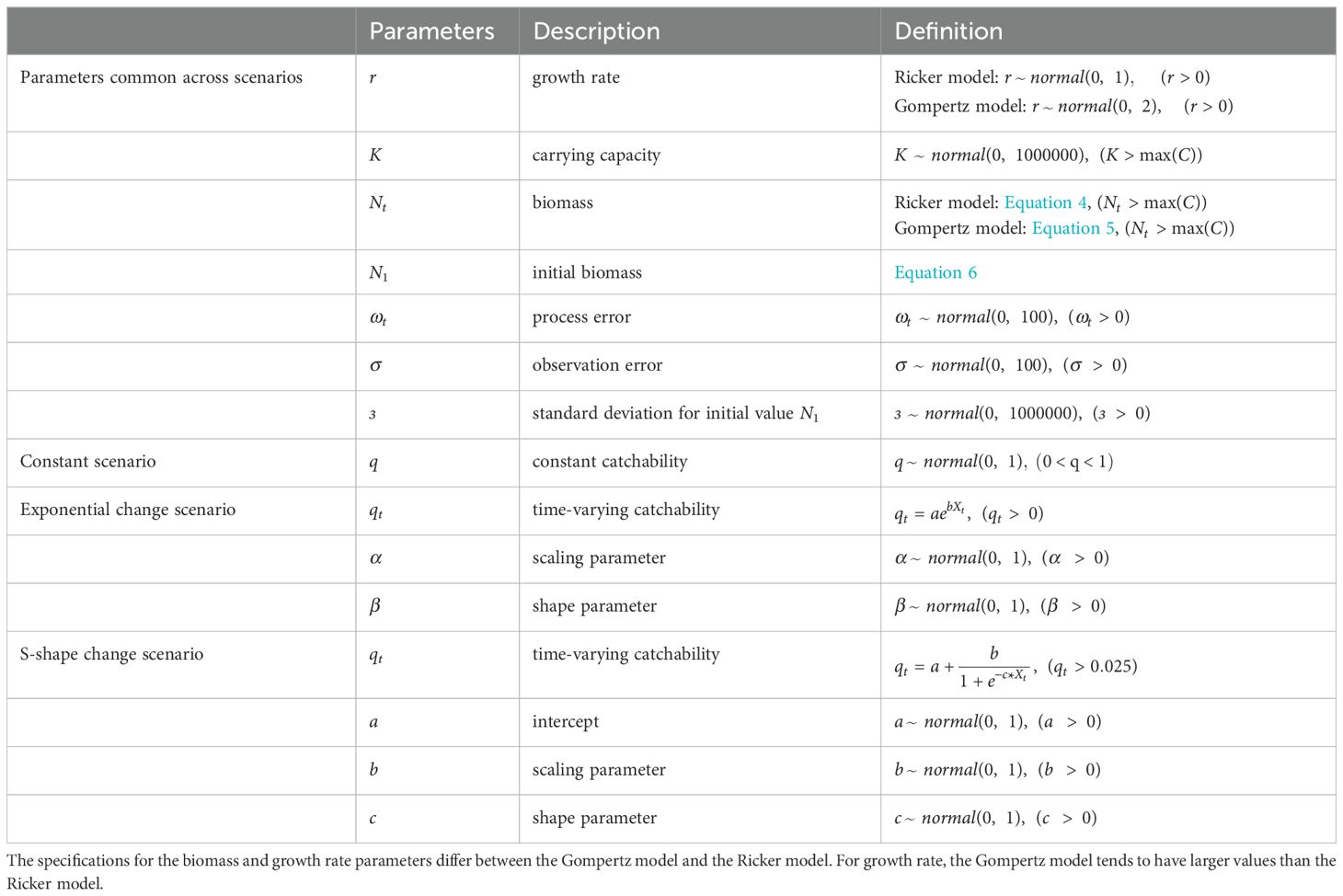
In this study, we assumed q_t to be represented by three models: a constant scenario ($q=\text{const}$), an exponential change scenario ($q_t=\alpha {\text{exp}}^{{\text{βX}}_t }$), and an S-shaped change scenario ($q_t=a+\frac{b}{1+e^{-c*X_t}}$), where X_t is discrete-time data (1972,1973,…2019) standardized to continuous values.

It is recommended to examine both the Gompertz and Ricker population models, depending on the species and operational mode being handled, and the assumed functional form of catchability. Hence, in the process model, following Hostetler and Chandler (2015), we applied the stochastic Ricker model and modified the stochastic Gompertz model (hereafter referred to as the Gompertz model), which accounted for the density dependence of population dynamics in the state process. The Ricker model is a density-dependent model that assumes an autoregressive formulation of population density N_t; moreover, it is more flexible than the discrete-time logistic model, including the case of overcompensation (where the population density goes from above carrying capacity K to below K) (Hostetler and Chandler, 2015). The Gompertz model behaves similarly to the Ricker model; however, overcompensation occurs only when the population growth rate is high (Dennis et al., 2006). In this study, we assumed the harvest-based Ricker model that estimates biomass and catchability by considering the annual catch amount C_t, and the dynamics of fish biomass N_t, described as follows:

$\begin{array}{ll}{N}_{t+1}=(N_t\left(\exp \left(r\left(1-\frac{N_t}{K}\right)\right)\right)-C_t)*\text{exp}({\omega }_t) ,& (4)\end{array}$

where r is the population growth rate and K is the carrying capacity. ω_t indicates the annual variation in the population growth rate for the stock, state and process errors were assumed to follow a log-normal distribution.

In the Gompertz model, the dynamics of fish species biomass, N_t, are described as follows (see Hostetler and Chandler (2015) for details):

$\begin{array}{ll}{N}_{t+1}=\left(N_t\left(\exp \left(r\left(1-\frac{\log (N_t+1)}{\log (K+1)}\right)\right)\right)-C_t\right)*\text{exp}({\omega }_t)& (5)\end{array}$

For the prior distribution of the initial state, the population density in the first year follows a zero-truncated normal distribution with mean 500,000 and variance ϵ² (ϵ$~ normal(0, 1,000,000)$) (N₁ > 0) to allow for a sufficiently wide range of values:

$\begin{array}{ll}{N}_1 ~ \text{Normal}(500,000, {ϵ}^2)& (6)\end{array}$

For prior distributions, a weakly informative prior was used for each parameter to ensure that the range of possible parameter values was adequately covered (Table 1). For the catchability parameter, we used a lower limit of 0.025 for the S-shaped change scenario. This prevents N from diverging and becoming impossible to estimate when q becomes extremely small during the MCMC random sampling when no lower limit is set in the S-shaped scenario. To analyze the real catch data, we devised a procedure to set this lower limit based on the available time series of catch data (number/volume of catches) and effort. Here, q was estimated once under the constant scenario using catch data for up to half of the time period, and then the lower limit of the 95% credible interval of the estimated q was used as the lower limit for setting parameters when estimating the S-shaped scenario for the full time period data (details in Supplementary Data 1).

Table 1

Table 1. Description of each parameter for the model equations and prior distributions.

In this study, we sampled from the posterior distribution using Markov Chain Monte Carlo (MCMC) with Stan, employing the No-U Turn Sampling algorithm which has a good sampling efficiency (Hoffman and Gelman, 2014). To improve the stability of sampling using MCMC, scaled-effort data (E/10,000) were used in the calculations. To eliminate the effects of the initial values and autocorrelation in the MCMC sample, the results were extracted every four iterations after discarding the first 5,000 iterations of 25,000 total iterations. This calculation is performed for four chains with different initial values to obtain the posterior distribution. The MCMC convergence was evaluated using R-hat with R-hat< 1.01, which is the convergence criterion (Gelman and Rubin, 1992; Vehtari et al., 2021). The MCMC method was implemented in Stan using the R package cmdstanr ver. 2.34.1 (Stan Development Team, 2021). The goodness of fit of the model was evaluated using the coefficient of determination, R-squared (R²), with observed and predicted values. Leave-one-out cross-validation, which examines out-of-sample pointwise prediction accuracy using log-likelihood evaluated at the posterior parameter distribution, was performed using the R package loo (Vehtari et al., 2017).

3 Results

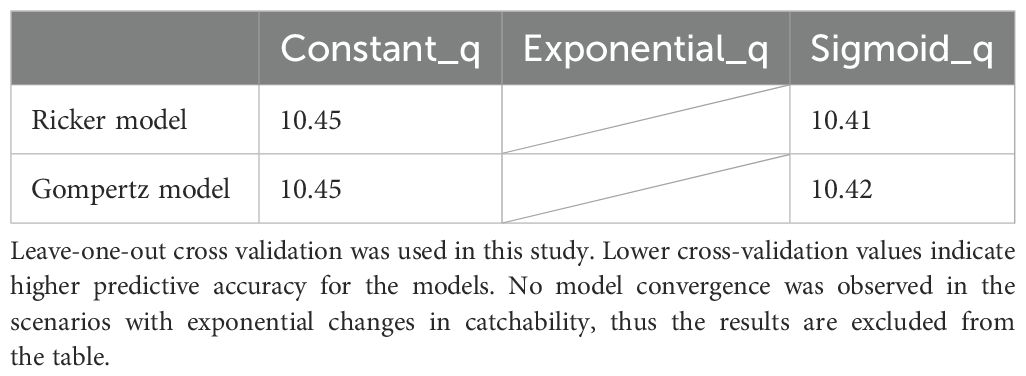
Application of Bayesian state-space models to skipjack JPPL data for each scenario confirmed convergence of MCMC calculations for both the Ricker and Gompertz models for the constant scenarios and S-shaped change scenarios in catchability with Rhat<1.01. However, the exponential change scenario did not converge for either the Ricker or Gompertz models.

Coefficients of determination were calculated for each of the scenarios for which convergence was confirmed, and no notable differences were found among the scenarios, which were generally comparable (Table 2). Similarly, cross-validation results indicated that the predictive accuracy of the Ricker and Gompertz models was comparable across all scenarios, including both the constant and variable catchability cases (Table 3). The differences between scenarios were very small, 0.04 at most, no particular scenario showed consistently higher forecasting accuracy than others.

Table 2

Table 2. R-squared (R²) results for the goodness of fit of the model in each scenario.

Table 3

Table 3. Cross validation results for each scenario.

When incorporating the functional form of catchability into the state-space model for each scenario, catchability was estimated to increase over time in S-shape change scenarios (Figure 4). The range of catchability uncertainty was wider in S-shape change scenario, and the uncertainty in biomass was also larger in this scenario. Compared to the time-constant scenario and the observed CPUE time series data, the S-shaped scenario showed an increase in catchability and a decreasing trend in biomass in the latter half of the time-series, resulting in a smaller biomass estimate. For the time varying scenario Ricker model the estimate of catchability increased by approximately 4.47 times from the start of the model period to the end (median value start = 0.058, median value end = 0.259), and for the Gompertz it increased by approximately 3.36 (median value start = 0.058, median value end = 0.195) (Figure 4). It should be noted that in the case of the Ricker model, the estimated change in median q is notably higher than for the Gompertz model, but empirically the MCMC convergence of the Ricker model is poor and the Gompertz model is more likely to be reliable in terms of reproducibility of the results. Although careful interpretation is required, we expect the estimation of q by the state-space model can help provide information on the level of effort creep in this JPPL skipjack fishery. The estimated median biomass (95% CI, lower–upper) in the S-shaped catchability scenario was as follows: Ricker: 522,000 tonnes (t) (163,000–1,203,000) and Gompertz: 532,000 t (167,000–1,207,000) in the first year; and Ricker: 207,000 t (105,000–1,023,000) and Gompertz: 277,000 t (112,000–1,119,000) in the latest year. Compared to the constant catchability scenario (Ricker: 779,000 t, Gompertz: 797,000 t), the estimated median biomass in the latest year was reduced by approximately 572,000 t (779,000–207,000) in the Ricker model and 520,000 t (797,000–277,000) in the Gompertz model.

Figure 4

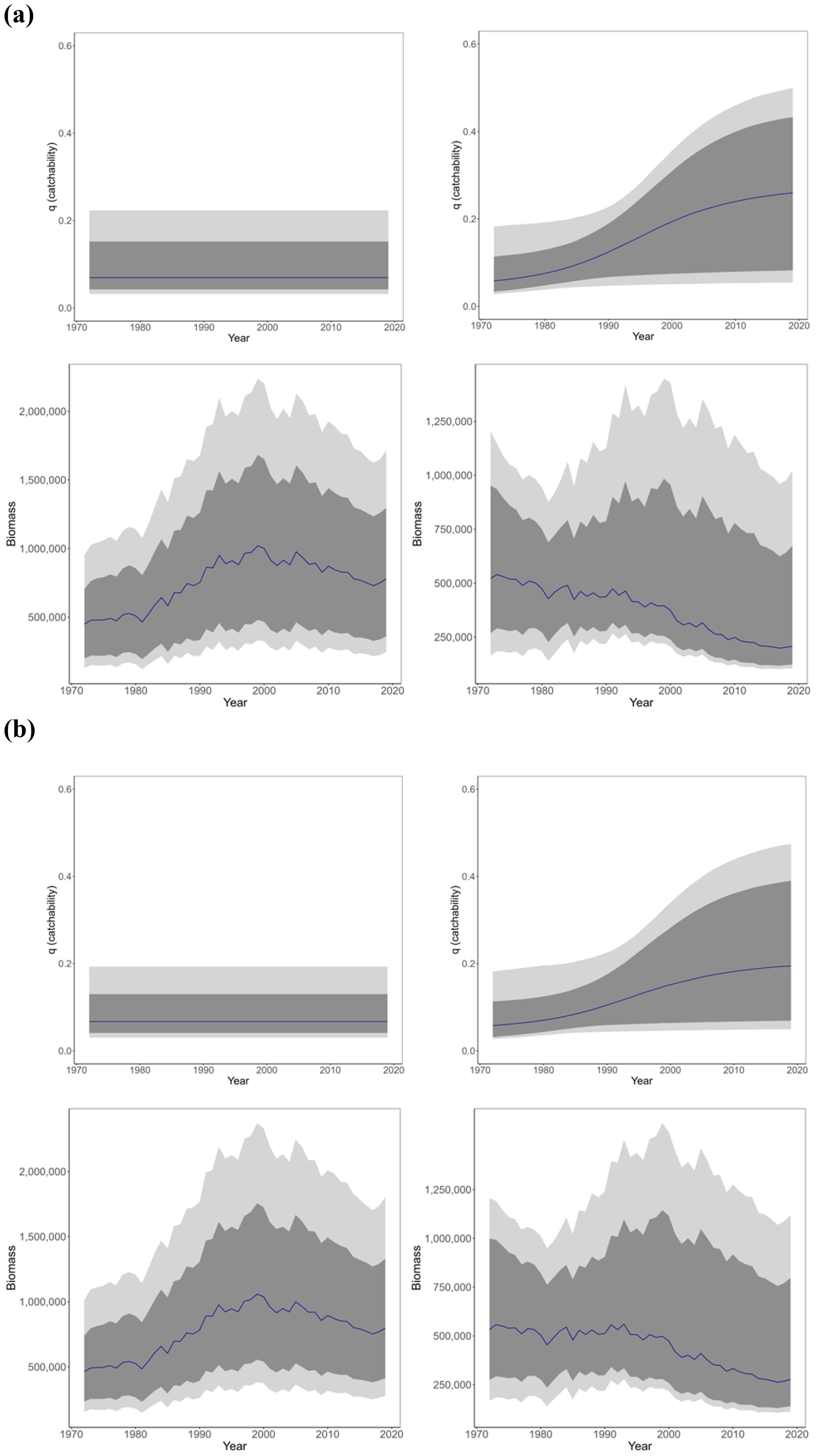
Figure 4. Estimated values of catchability parameter and biomass parameter for different scenarios for (A) Ricker model, (B) Gompertz model. The upper panel shows the estimated value for the catchability parameter, and the lower panel shows the estimated value for the biomass parameter. The blue solid line in the figures indicates the median, dark gray shading indicates the 80% CI, light gray shading indicates the 95% CI. Results for the exponential change scenario are not included because convergence was not observed in either population model.

Applying the approach of estimating the 95% CI lower bound of catchability in an S-shaped change scenario using the Gompertz state-space model, Rhat of all parameters converged to less than 1.01, indicating that the time-varying catchability and biomass could be estimated (Supplementary Data 1, Supplementary Figure 1). The 95% CI lower bound of the catchability parameter estimated in the first stage of estimation was 0.033, which is comparable to the 0.025 set in the same population model scenario (Table 1), supporting the validity of this approach.

Comparing the prior and posterior distributions for the growth rate and catchability parameters across scenarios revealed a shift from a broad prior distribution to a sharply peaked posterior distribution (Figure 5), indicating substantial information gain from the data in Bayesian estimation. For the growth rate parameter, the Ricker model exhibited sharper peaks compared to the Gompertz model. The catchability parameter showed similar shapes for both models, though the mode for the Gompertz model was slightly lower. When comparing time-varying and constant scenarios, the growth rate parameter in S-shaped scenarios exhibited a lower mode, likely reflecting population dynamics influenced by increased catchability and reduced biomass levels over time.

Figure 5

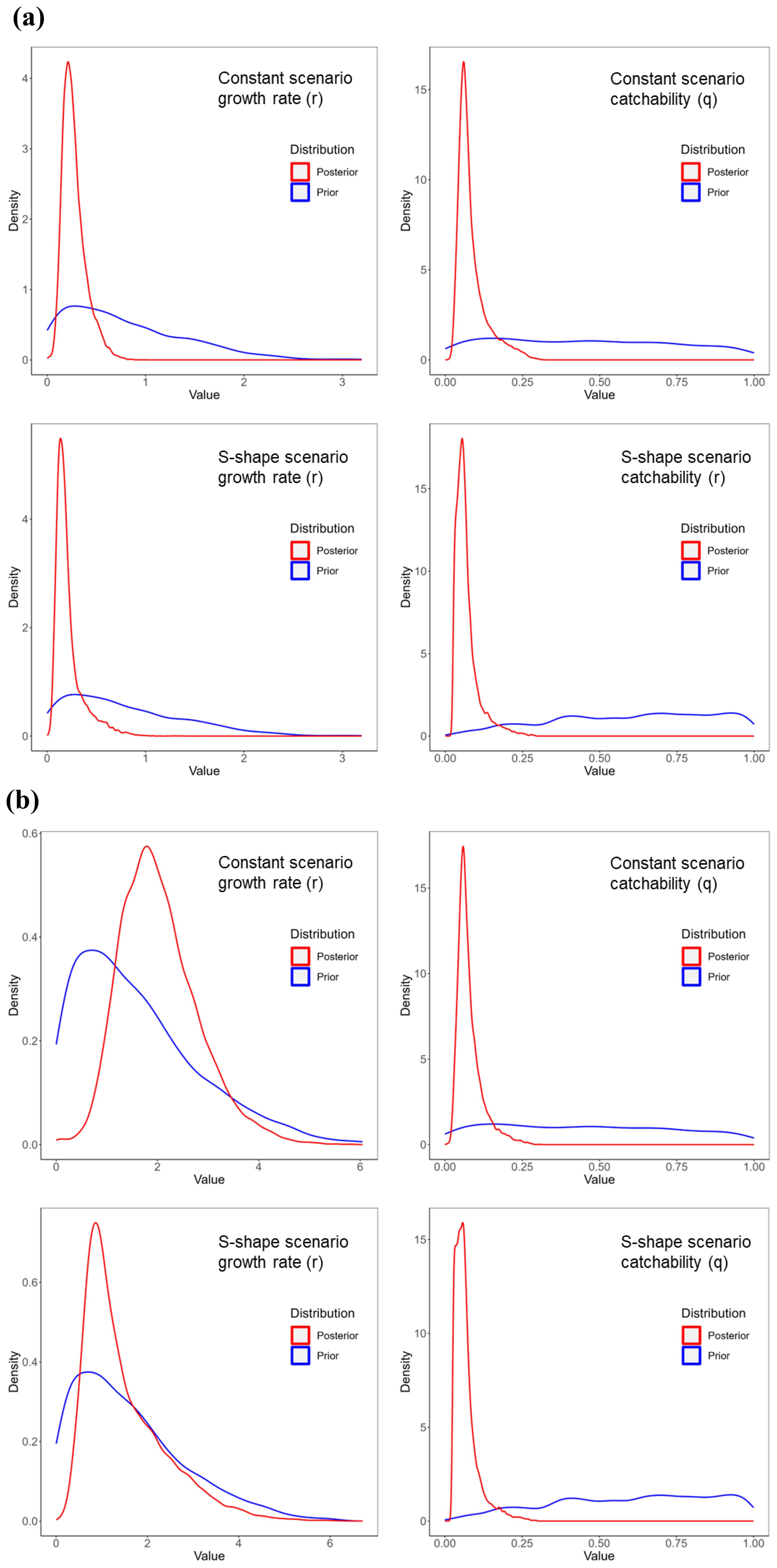
Figure 5. Prior and posterior distributions of the growth rate parameter and catchability parameter for different catchability scenarios for (A) the Ricker model and (B) the Gompertz model. The blue line shows the prior distribution, and the red line shows the posterior distribution. Results for the exponential change scenario are not included because convergence was not observed in either population model. The prior distribution in the figure was created by 1000 random numbers.

4 Discussion

We developed a method to simultaneously estimate population dynamics and time-varying catchability related to technological progress, and tested the validity of this method by applying it to skipjack catch data from the Japanese pole-and-line fishery using alternative catchability change scenarios. Our methodology represents two significant advancements compared to previous studies. First, it clearly distinguishes between catchability and abundance (biomass) estimates by considering natural rates of increase, density dependence, and temporal changes in catchability. This distinction resolves the confounding issue between population fluctuations and temporal changes in catchability (Arreguin-Sanchez, 1996; Szuwalski, 2022; Taylor and Methot, 2013), allowing for more accurate predictions and ecological understanding of population dynamics. Second, as a hierarchical Bayesian model, it provides a statistical basis for explicitly incorporating changes in catchability due to technological progress. These changes in catchability should not be ignored in long-term fishery catch rate data analysis, as modern technological progress has no doubt led to increases in catch efficiency (Eigaard et al., 2014; Marchal et al., 2007; Marriott et al., 2011; Rousseau et al., 2019).

In long-term fisheries stock assessment, ignoring temporal changes in catchability due to technological uptake can lead to overestimation of population abundance and risk-prone management advice (Eigaard et al., 2014; Kleiven et al., 2022). Tracking technological development in fisheries over time requires data on the development history and timing of equipment uptake. This understanding can provide support for hypothesis on historical catchability changes (Matsubara et al., 2022). While industry surveys can provide information on catchability changes (Rousseau et al., 2019), the data is often qualitative and underutilized in stock assessments due to a lack of statistical methods for integration. The state-space model introduced in the present study is flexible due to its hierarchical Bayesian framework, allowing the explicit incorporation of technological development timing from industry surveys as data and prior distributions. For example, future work could allow the timing of a technological innovation to vary within a range of ±1 standard deviation (SD) years, incorporating this into the prior distribution as a normal distribution. This approach would utilize the domain knowledge of fishers and experts, enhancing robustness of population dynamics estimation and resource management decision-making (Gorelli et al., 2016; Marriott et al., 2011).

The skipjack population in the northwestern Pacific Ocean is thought to be part of the broader west Pacific stock which has been considered healthy and stable in recent years (Castillo-Jordán et al., 2022; Matsubara et al., 2022). However, our estimations for the population around Japan indicate a downward trend when there is consideration of increased catchability due to technological development. Matsubara et al. (2022) suggested that the functional form of catchability changes in the JPPL skipjack fishery is likely to be S-shaped. When we assumed an S-shaped form, the goodness of fit and prediction accuracy was comparable between the Ricker and Gompertz models (Tables 2, 3). However, although it bears repeating, Gompertz estimation is likely to be more reliable in terms of reproducibility due to the empirically poor convergence of the MCMC in the Ricker model. This difference in convergence may be due to the Gompertz model being less prone to overcompensation than the Ricker model and estimates a smoother functional form (Certain et al., 2018; Hostetler and Chandler, 2015). In the Gompertz model, the exponential scenario had lower convergence than the S-shaped scenario, which may be due to the unrealistic assumption of an unlimited increase in catchability over time. Therefore, although exponential changes are often used in fisheries stock assessments when assuming a time-series change in catchability, it could be preferable to use the S-shaped function as presented in this study or a linear function that assumes a linear increase (Kim et al., 2024). The functional form of catchability should be carefully determined through industry surveys or other means. The study cautions against the constant catchability assumptions that encompasses low estimation uncertainty in long-term stock assessments. Even before conducting industry surveys, it may be useful to tentatively assume a linear increasing or S-shaped function or to estimate time-varying catchability as a random effect, if one wishes to mitigate the risk of overestimation of stock biomass (Kim et al., 2024).

Our analysis using catch and effort data under a time-varying catchability scenario showed converged calculations, suggesting a decreasing trend in abundance in recent years compared to that in the mid-1990s (Figure 4). The S-shaped scenario of the Gompertz model was able to capture an approximately threefold improvement in catchability from the beginning to the end of the time-series, indicating that the stock biomass may have been significantly overestimated, even in the most recent years. It should be noted that the timing of technology introduction was approximately set in this study considering previous studies, and this prior information can be refined by further work incorporating industry knowledge. In addition, for simplicity, environmental factors that might also influence sustained catchability changes in regional fisheries off Japan were not explicitly considered in this study. Because skipjack respond to water temperature (Kiyofuji et al., 2019), incorporating environmental factors such as annual minimum and average water temperatures into future models may improve estimation accuracy.

We presented a statistical framework that explicitly integrates changes in catchability due to technological uptake into a Bayesian state-space model. This framework enables the identification of changes in catchability using information on the timing of technological development and catch data, and estimates population dynamics, providing a more reliable representation of stock abundance trends. Application of the approach to the JPPL skipjack tuna fishery data showed that although accurate estimation of abundance is difficult under time-varying scenarios due to the wide credible intervals, it is likely to reveal trends in stock status (e.g., stable or declining). These wide credible intervals are primarily driven by uncertainties in time-varying changes in catchability. Further investigation of medium-sized vessel fisheries in offshore areas during periods of technological uptake could reduce the uncertainty in catchability estimates, improving the accuracy of skipjack tuna stock assessment in the waters around Japan, and supporting informed decision-making for sustainable resource management. The framework developed in this study is highly flexible and can be applied to various datasets by modifying the observation model. Therefore, it could be a useful method for assessing the implications of technology-driven catchability changes on the stock trends of various fish species.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics statement

Ethical approval was not required for the study involving animals in accordance with the local legislation and institutional requirements because the data used were generated during commercial practices.

Author contributions

MN: Writing – original draft, Writing – review & editing, Conceptualization, Formal Analysis, Investigation, Visualization. YA: Conceptualization, Investigation, Methodology, Validation, Writing – original draft, Writing – review & editing. NM: Conceptualization, Methodology, Writing – original draft, Writing – review & editing. PH: Conceptualization, Methodology, Writing – original draft, Writing – review & editing. YT: Conceptualization, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funding for this research project was provided by the Fisheries Agency of Japan and the Western and Central Pacific Fisheries Commission.

Acknowledgments

Hirotaka Ijima provided comments on an earlier version of the manuscript. We thank Keita Fukasawa and Kyuhan Kim for helpful advice and comments regarding statistical modeling. We are also grateful to Katsutoshi Nakata and Yoshikazu Myojin for providing helpful information on skipjack fisheries and fishing equipment for technological developments. We would like to express our gratitude to John Best and an reviewer for their valuable comments and suggestions, which have greatly improved the quality of this paper. We also acknowledge support for this work from the Western and Central Pacific Fisheries Commission under project 115.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1458257/full#supplementary-material

References

Allison E. H., Ellis F. (2001). The livelihoods approach and management of small-scale fisheries. Mar. Policy. 25, 377–388. doi: 10.1016/S0308-597X(01)00023-9

Crossref Full Text | Google Scholar

Arreguin-Sanchez F. (1996). Catchability: A key parameter for fish stock assessment. Rev. Fish Biol. Fish. 6, 221–242. doi: 10.1007/BF00182344

Crossref Full Text | Google Scholar

Ashida H., Tanabe T., Satoh K., Fukui A., Tanaka S., Suzuki N. (2010). Reproductive biology of male skipjack tuna Katsuwonus pelamis (Linnaeus) in the tropical western and central Pacific Ocean. Fish. Sci. 76, 785–793. doi: 10.1007/s12562-010-0282-y

Crossref Full Text | Google Scholar

Beddington J. R., Agnew D. J., Clark C. W. (2007). Current problems in the management of marine fisheries. Science 316, 1713–1716. doi: 10.1126/science.1137362

PubMed Abstract | Crossref Full Text | Google Scholar

Best J. K., Punt A. E. (2020). Parameterizations for Bayesian state-space surplus production models. Fish. Res. 222, 105411. doi: 10.1016/j.fishres.2019.105411

Crossref Full Text | Google Scholar

Bishop J. (2006). Standardizing fishery-dependent catch and effort data in complex fisheries with technology change. Rev. Fish Biol. Fisheries 16, 21–38. doi: 10.1007/s11160-006-0004-9

Crossref Full Text | Google Scholar

Carvalho F., Ahrens R., Murie D., Ponciano J. M., Aires-da-Silva A., Maunder M. N., et al. (2014). Incorporating specific change points in catchability in fisheries stock assessment models: An alternative approach applied to the blue shark (Prionace glauca) stock in the South Atlantic Ocean. Fish. Res. 154, 135–146. doi: 10.1016/j.fishres.2014.01.022

Crossref Full Text | Google Scholar

Castillo-Jordán C., Teears T., Hampton J., Davies N., Phillips J. S., McKechnie S., et al. (2022). Stock assessment of skipjack tuna in the Western and Central Pacific Ocean. Tech. Rep. WCPFC-SC, 2022 18–SA-WP-01.

Google Scholar

Certain G., Barraquand F., Gårdmark A. (2018). How do MAR (1) models cope with hidden nonlinearities in ecological dynamics? Methods Ecol. Evol. 9, 1975–1995. doi: 10.1111/2041-210X.13021

Crossref Full Text | Google Scholar

Costello C., Ovando D., Clavelle T., Strauss C. K., Hilborn R., Melnychuk M. C., et al. (2016). Global fishery prospects under contrasting management regimes. Proc. Natl. Acad. Sci. 113, 5125–5129. doi: 10.1073/pnas.1520420113

PubMed Abstract | Crossref Full Text | Google Scholar

Crona B. I., Wassénius E., Jonell M., Koehn J. Z., Short R., Tigchelaar M., et al. (2023). Four ways blue foods can help achieve food system ambitions across nations. Nature 616, 104–112. doi: 10.1038/s41586-023-05737-x

PubMed Abstract | Crossref Full Text | Google Scholar

Dennis B., Ponciano J. M., Lele S. R., Taper M. L., Staples D. F. (2006). Estimating density dependence, process noise, and observation error. Ecol. Monogr. 76, 323–341. doi: 10.1890/0012-9615(2006)76[323:EDDPNA]2.0.CO;2

Crossref Full Text | Google Scholar

Dichmont C. M., Deng R. A., Punt A. E., Brodziak J., Chang Y. J., Cope J. M., et al. (2016). A review of stock assessment packages in the United States. Fish. Res. 183, 447–460. doi: 10.1016/j.fishres.2016.07.001

Crossref Full Text | Google Scholar

Eigaard O. R., Marchal P., Gislason H., Rijnsdorp A. D. (2014). Technological development and fisheries management. Rev. Fish. Sci. Aqua. 22, 156–174. doi: 10.1080/23308249.2014.899557

Crossref Full Text | Google Scholar

Gelman A., Rubin D. B. (1992). Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472. doi: 10.1214/ss/1177011136

Crossref Full Text | Google Scholar

Gorelli G., Sardà F., Company J. B. (2016). Fishing Effort Increase and Resource Status of the Deep-Sea Red shrimp Aristeus Antennatus (Risso 1816) in the northwest Mediterranean Sea since the 1950s. Rev. Fish. Sci. Aqua. 24, 192–202. doi: 10.1080/23308249.2015.1119799

Crossref Full Text | Google Scholar

Hamer P., Senina I., Lehodey P., Nishimoto M., Aoki Y., Matsubara N., et al. (2024).Investigating long-term recruitment trends of skipjack tuna in the Western and Central Pacific Ocean and Effort Creep in the Japanese Pole and Line Skipjack Fishery (WCPFC Project: 115). WCPFC-SC20-2024/SC20-SA-WP-06. Available online at: https://meetings.wcpfc.int/node/23122 (accessed December 13, 2024).

Google Scholar

Hamer P., Teears T., Aoki Y., Nishimoto M., Tsuda Y. (2023).Project 115 progress update: Exploring evidence and mechanisms for a long-term increasing trend in recruitment of skipjack tuna in the equatorial Pacific and the development and modelling of defensible effort creep scenarios. Information Papers. WCPFC-SC19-2023/SA-WP-05. Available online at: https://meetings.wcpfc.int/libraries/pdf.js/web/viewer.html?file=https%3A%2F%2Fmeetings.wcpfc.int%2Fsystem%2Ffiles%2F2023-07%2FSC19-SA-IP-05%2520Progress%2520update_project115_skj_effort%2520creep_recruitment%2520trends_FNL.pdf (accessed December 13, 2024).

Google Scholar

Han Q., Shan X., Jin X., Gorfine H. (2023). Contrasting stock status trends obtained from survey and fishery CPUE, taking Larimichthys polyactis in Yellow Sea Large Marine Ecosystem as an example. Ecol. Indic. 147, 110032. doi: 10.1016/j.ecolind.2023.110032

Crossref Full Text | Google Scholar

Hilborn R., Stokes K., Maguire J. J., Smith T., Botsford L. W., Mangel M., et al. (2004). When can marine reserves improve fisheries management? Ocean Coast. Manage. 47, 197–205. doi: 10.1016/j.ocecoaman.2004.04.001

Crossref Full Text | Google Scholar

Hilborn R., Walters C. J. (1992). Quantitative Fisheries Stock Assessment: Choice, Dynamics, and Uncertainty (New York: Chapman & Hall).

Google Scholar

Hoffman M. D., Gelman A. (2014). The No-U-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623.

Google Scholar

Hostetler J. A., Chandler R. B. (2015). Improved state-space models for inference about spatial and temporal variation in abundance from count data. Ecology 96, 1713–1723. doi: 10.1890/14-1487.1

Crossref Full Text | Google Scholar

Hoyle S. D., Campbell R. A., Ducharme-Barth N. D., Grüss A., Moore B. R., Thorson J. T., et al. (2024). Catch per unit effort modelling for stock assessment: A summary of good practices. Fisheries Res. 269, 106860. doi: 10.1016/j.fishres.2023.106860

Crossref Full Text | Google Scholar

Iijima H., Nagaike T., Honda T. (2013). Estimation of deer population dynamics using a bayesian state-space model with multiple abundance indices. J. Wild. Manage. 77, 1038–1047. doi: 10.1002/jwmg.556

Crossref Full Text | Google Scholar

Kim K., Sibanda N., Arnold R., A’mar T. (2024). Enhancing data-limited assessments with random effects: A case study on Korea chub mackerel (Scomber japonicus). Can. J. Fish. Aquat. Sci. 81 (10), 1433–1455. doi: 10.1139/cjfas-2023-0358. Just-IN.

Crossref Full Text | Google Scholar

King M. (2013). Fisheries Biology, Assessment and Management (Chichester: John Wiley & Sons).

Google Scholar

Kiyofuji H., Aoki Y., Kinoshita J., Okamoto S., Masujima M., Matsumoto T., et al. (2019). Northward migration dynamics of skipjack tuna (Katsuwonus pelamis) associated with the lower thermal limit in the western Pacific Ocean. Prog. Oceanogr. 175, 55–67. doi: 10.1016/j.pocean.2019.03.006

Crossref Full Text | Google Scholar

Kleiven A. R., Espeland S. H., Stiansen S., Ono K., Zimmermann F., Olsen E. M. (2022). Technological creep masks continued decline in a lobster (Homarus gammarus) fishery over a century. Sci. Rep. 12, 3318. doi: 10.1038/s41598-022-07293-2

PubMed Abstract | Crossref Full Text | Google Scholar

Mace P. M. (2001). A new role for MSY in single-species and ecosystem approaches to fisheries stock assessment and management. Fish Fish. 2, 2–32. doi: 10.1046/j.1467-2979.2001.00033.x

Crossref Full Text | Google Scholar

Marchal P., Andersen B., Caillart B., Eigaard O., Guyader O., Hovgaard H., et al. (2007). Impact of technological creep on fishing effort and fishing mortality, for a selection of European fleets. ICES J. Mar. Sci. 64, 192–209. doi: 10.1093/icesjms/fsl014

Crossref Full Text | Google Scholar

Marriott R. J., Wise B., St John J. (2011). Historical changes in fishing efficiency in the west coast demersal scalefish fishery, Western Australia: Implications for assessment and management. ICES J. Mar. Sci. 68, 76–86. doi: 10.1093/icesjms/fsq157

Crossref Full Text | Google Scholar

Matsubara N., Aoki Y., Tsuda Y. (2022).Historical developments of fishing devices in Japanese pole-and-line fishery. WCPFC-SC18-2022/SA-IP-16. Available online at: https://meetings.wcpfc.int/node/16265 (accessed December 13, 2024).

Google Scholar

Rousseau Y., Watson R. A., Blanchard J. L., Fulton E. A. (2019). Evolution of global marine fishing fleets and the response of fished resources. Proc. Natl. Acad. Sci. 116, 12238–12243. doi: 10.1073/pnas.1820344116

PubMed Abstract | Crossref Full Text | Google Scholar

Scheuerell M. D., Ruff C. P., Anderson J. H., Beamer E. M. (2021). An integrated population model for estimating the relative effects of natural and anthropogenic factors on a threatened population of steelhead trout. J. Appl. Ecol. 58, 114–124. doi: 10.1111/1365-2664.13789

Crossref Full Text | Google Scholar

Solari A. P., Castro J. J., Bas C. (2003). On skipjack tuna dynamics: similarity at several scales. In Handbook of Scaling Methods in Aquatic Ecology. (CRC Press). 183–200

Google Scholar

Stan Development Team. (2021). CmdStanR: The R interface to CmdStan. Available online at: https://mc-stan.org/cmdstanr/index.html (accessed December 13, 2024).

Google Scholar

Szuwalski C. (2022). Estimating time-variation in confounded processes in population dynamics modeling: A case study for snow crab in the eastern Bering Sea. Fish. Res. 251, 106298. doi: 10.1016/j.fishres.2022.106298

Crossref Full Text | Google Scholar

Taylor I. G., Methot R. D. (2013). Hiding or dead? A computationally efficient model of selective fisheries mortality. Fish. Res. 142, 75–85. doi: 10.1016/j.fishres.2012.08.021

Crossref Full Text | Google Scholar

Thorson J. T., Minto C. (2015). Mixed effects: A unifying framework for statistical modelling in fisheries biology. ICES J. Mar. Sci. 72, 1245–1256. doi: 10.1093/icesjms/fsu213

Crossref Full Text | Google Scholar

Vehtari A., Gelman A., Gabry J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 27, 1413–1432. doi: 10.1007/s11222-016-9696-4

Crossref Full Text | Google Scholar

Vehtari A., Gelman A., Simpson D., Carpenter B., Bürkner P. C. (2021). Rank-normalization, folding, and localization: An improved R ̂ for assessing convergence of MCMC (with discussion). Bayesian Anal. 16, 667–718. doi: 10.1214/20-ba1221

Crossref Full Text | Google Scholar

Worm B., Hilborn R., Baum J. K., Branch T. A., Collie J. S., Costello C., et al. (2009). Rebuilding global fisheries. Science 325, 578–585. doi: 10.1126/science.1173146

PubMed Abstract | Crossref Full Text | Google Scholar

Yamamura K., Matsuda H., Yokomizo H., Kaji K., Uno H., Tamada K., et al. (2008). Harvest-based Bayesian estimation of sika deer populations using state-space models. Popul. Ecol. 50, 131–144. doi: 10.1007/s10144-007-0069-x

Crossref Full Text | Google Scholar

Zhang K., Zhang J., Zhang P., Su L., Hong X., Qiu Y., et al. (2023). This is what we know: Assessing the stock status of the data-poor skipjack tuna (Katsuwonus pelamis) fishery in the South China Sea. Front. Mar. Sci. 10. doi: 10.3389/fmars.2023.1095411

Crossref Full Text | Google Scholar

Zhou S., Punt A. E., Deng R., Bishop J. (2011). Estimating multifleet catchability coefficients and natural mortality from fishery catch and effort data: Comparison of bayesian state-space and observation error models. Can. J. Fish. Aquat. Sci. 68, 1171–1181. doi: 10.1139/f2011-052

Crossref Full Text | Google Scholar