A deep learning method for bias correction of wind field in the South China Sea

To address the systematic bias in the Global Forecast System (GFS) wind field forecasts, we utilize deep learning techniques. The developed MU - Diffusion framework, based on a diffusion model and MultiUnet (a multitasking Unet model), establishes a nonlinear relationship between GFS and the fifth-generation EC atmospheric reanalysis (ERA5) data. Focusing on the South China Sea region, this method corrects both wind speed and direction simultaneously. Using 2022 GFS data, we achieved average enhancements of 42% in wind speed and 38.3% in wind direction compared to the initial GFS data. Tests in typhoon conditions also confirm the excellent performance of this architecture.

1 Introduction

The South China Sea, situated at the intersection of East Asia and Southeast Asia, is a maritime region of significant geopolitical and ecological significance. The wind patterns in the South China Sea have a crucial influence on the climate in Southeast Asia and East Asia. The monsoon system exerts the most significant influence on the climate of the region, as it determines the intensity and direction of winds, which in turn affect the distribution of rainfall and fluctuations in temperature over the area. During periods of strong winds, waves and storms frequently result in significant coastal and maritime catastrophes. Over the last twenty years, these calamities have caused numerous fatalities and significant damage to properties (Moeller et al., 2008; Chang and Mori, 2021). Therefore, it is crucial and pressing to deliver precise predictions of wind patterns. Presently, the process of predicting weather conditions mostly depends on numerical weather prediction models (Rasp and Lerch, 2018). NWP models employ various initial circumstances and mathematical equations to replicate atmospheric and other environmental variables. Nevertheless, the predicting specifics of these simulations may be prone to mistakes as a result of constraints in processing capacity and the spatial and temporal resolution of models. Nonlinear properties of atmospheric systems and inaccuracies in physical parameters might lead to consistent biases in the forecasting process (Xu et al., 2021; Laloyaux et al., 2022). Therefore, in order to enhance the precision of NWP model predictions, it is necessary to employ efficient bias correction and post-processing techniques.

Over the past few decades, numerous post-processing techniques have been suggested to rectify biases in NWP models. Two commonly employed statistical techniques for predicting wind patterns and adjusting for biases are Model Output Statistics (MOS) (Glahn and Lowry, 1972), and Perfect Prognosis (PP) (Klein et al., 1959). MOS primarily utilizes observable data to align the results of NWP by building a linear regression to create corrective equations. However, its linear regression approach has limitations in handling nonlinear wind field data as it assumes a linear relationship. The PP approach is comparable to MOS. It utilizes a statistical screening process to identify pertinent variables from a vast pool and then constructs a linear regression equation for rectification. Similar to MOS, it also struggles with nonlinear wind field data due to its linear assumption. These methodologies have established a foundation for enhancing forecast skills. An instance of research involved the modification of the parameters of the f-ARIMA model to analyse and forecast long-term wind speed patterns, specifically over the upcoming 1-2 days (Kavasseri and Seetharaman, 2009). Peng et al. (2013) conducted a study that introduced the “Anomaly Numerical Correction” (ANO) approach. This method is based on the atmospheric variability decomposition theory developed by Qian (2012). This approach involves separating the observed data and numerical forecasts into two components: the climatic mean values and the perturbation values. The disparity in climate mean values between model forecasts and actual observations signifies the presence of systematic model bias.Traditional statistical models, with their linear assumptions, are limited in their ability to perform nonlinear fitting and struggle to accommodate nonlinear wind field data (Duan et al., 2021).

Deep learning technology has experienced significant achievements in various domains, including atmospheric sciences, in recent years. It has the ability to independently execute feature engineering and autonomously identify spatial structures in grid data, surpassing the capabilities of classical machine learning and statistical models. This is because it can adaptively learn the complex relationships between different variables, which is crucial for handling the nonlinear properties of wind fields, in contrast to statistical models with their linear assumptions. Several neural network architectures have been created, such as Convolutional Neural Networks (CNN) (Zhu et al., 2017), Long Short-Term Memory (LSTM) networks (Liu et al., 2018), and Convolutional Long Short-Term Memory (ConvLSTM) networks (Shi et al., 2015, 2017), among others. These models demonstrate robust autonomous learning abilities and are highly proficient in accurately fitting non-linear data (Liu et al., 2020). Harbola and Coors (2019) employed CNN to accurately model one-dimensional time series data for the purpose of forecasting wind speed and wind direction. A separate investigation examined the periodic properties of wind direction in order to construct a model for the fluctuating time series of wind direction (Solari and Losada, 2016). The Unet architecture exhibits significant capability in processing grid-based input data and producing grid-based output or predictions. In their study, Han et al. (2021) showcased the application of Unet for nonlinear modelling of several meteorological factors, such as wind fields.

Diffusion models belong to a category of generative models that produce data by imitating a process of diffusion (Ho et al., 2020). The fundamental concept is to extract significant information from random interference. Diffusion models differ from Generative Adversarial Networks (GANs) in that they do not depend on adversarial training involving a generator and a discriminator (Goodfellow et al., 2020). This characteristic helps to prevent the frequent problems of instability and mode collapse that are typically observed in GANs. Diffusion models have superior performance in terms of image creation quality and fidelity when compared to Variational Autoencoders (VAEs) (Kingma and Welling, 2013). Although diffusion models have achieved success in areas such as image restoration, image enhancement, and super-resolution, its application in oceanic and meteorological bias correction tasks is still in its early phases. As the areas of numerical weather prediction and ocean simulation strive for greater accuracy, diffusion models may become a valuable tool for correcting biases.

We have introduced a framework that addresses biases in ocean wind fields. This framework is based on a conditional diffusion model, which incorporates relevant oceanographic factors as conditional information. By doing so, the diffusion model is able to generate more accurate findings. We developed a multitasking Unet architecture called MultiUnet to provide guiding fields. Our bias correction technique employs a conditional diffusion model to incorporate wind fields and guidance fields, so indirectly forecasting wind field biases. We then merge the guidance field with the biases to simultaneously rectify wind speed and wind direction. Our study demonstrates that after conducting numerous trials using different correction procedures, this framework surpasses both single Unet and diffusion models in rectifying wind field biases. As a result, it provides enhanced efficacy and stability.

In contrast to existing methods such as traditional statistical models (MOS and PP) and some machine learning techniques, our proposed MU - Diffusion framework combines the power of the MultiUnet architecture and the diffusion model. The MultiUnet provides detailed guidance fields, while the diffusion model effectively models the spread and evolution of biases. This enables a more comprehensive and accurate bias correction compared to traditional approaches, especially in handling the nonlinear wind field data.

The remainder of this paper is organized as follows. Section 2 describes the data used in this study. Section 3 introduces the methodology, and section 4 analyzes the experimental results. Conclusions are presented in section 5.

2 Study area and data

In this study, we use historical data from the NCEP operational Global Forecast System from 2016 to 2022 (GFS for short) (National Centers for Environmental Prediction, National Weather Service, NOAA, U.S. Department of Commerce, 2015). The forecast grids are on a 0.25 by 0.25 global latitude longitude grid. Model forecast data are issued four times a day at 00, 06, 12, and 18 UTC daily. The ground truth used by the correction methods is the ERA5 dataset with the same grid resolution; this dataset has been widely used to replace the previous reanalysis dataset ERA-Interim (Hersbach et al., 2020). In addition, ERA5 is often used as the observation data in studies of numerical model bias correction (Dengxin He et al., 2019; Hersbach et al., 2020). It should be noted that GFS is a forecast model while ERA5 is a reanalysis model.

The study domain is located at 0°N-24°N and 100°E-124°E, which roughly covers the South Sea of China. The grid size is 96 × 96(lat × lon). In this paper, the GFS grid forecast data will also be referred to as the “forecast data”, which provides predictor variables; the ERA5 provides target variables.

3 Methods

3.1 Overview of model

We developed a wind field bias correction framework called MU-Diffusion, which consists of two channels. The system is illustrated in Figure 1 (right). This framework comprises two components: the MultiUnet model and the Diffusion model. MultiUnet is designed to capture the structural information of the wind field. Its unique architecture, with extended down - sampling steps for encoding the U and V components of the wind field and the insertion of Batch Normalisation layers, enables it to effectively extract and represent the spatial and deterministic features of the wind field. These features are then passed as conditional inputs to the diffusion model. The diffusion model, on the other hand, is based on the principle of imitating a process of diffusion to generate data. It takes the wind field data and the guidance fields from MultiUnet as inputs and models the spread and evolution of the wind field bias. By incorporating the structural information from MultiUnet, the diffusion model can better capture the spatial correlations and dependencies in the wind field bias, leading to more accurate bias correction. The Denoising Diffusion Probabilistic Model (DDPM) produces the refined wind field.

Figure 1

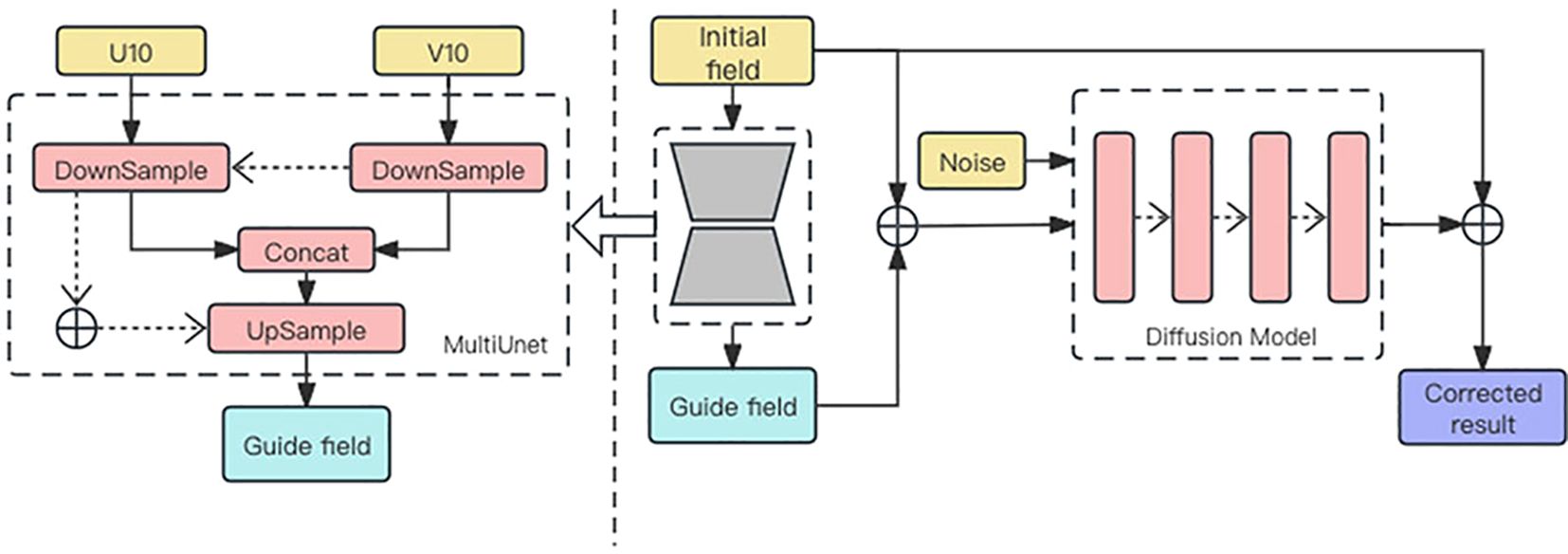
Figure 1. U10 and V10 represent the U and V components of the wind field at 10 meters above the surface. These components are used to describe the wind velocity vector in a a two - dimensional plane. Left: A simplified structure diagram of MultiUnet. Right: The graphic illustrates the structure of MU-Diffusion. The initial field is processed by MultiUnet to produce a guide field. The starting field and the guiding field are subsequently employed as conditional inputs in the Diffusion model, which produces the bias correction. The initial field is merged with the bias correction to generate the ultimate corrected outcome.

Initially, we employ MultiUnet to forecast the guidance field, which encompasses wind field data, as depicted in Figure 1 (left). The guiding field contains crucial structural and deterministic information regarding the wind field. We utilize this guidance condition as a spatial reference for the diffusion model. The encoding of the U and V components in MultiUnet preserves the spatial information of the wind field. The convolutional layers and blocks in MultiUnet process the wind field data in a way that maintains the spatial relationships between different grid points. When this spatially rich information is passed to the diffusion model as described above, it helps the diffusion model to understand how the bias varies across the wind field. For example, if there is a consistent bias pattern in a certain region of the wind field, the diffusion model can learn to correct it based on the spatial cues provided by MultiUnet. This process, which combines the spatial information from MultiUnet with the diffusion model, offers a more comprehensive understanding of the wind field bias and enables better control and guidance for bias correction. The diffusion model is employed to capture the spread of the initial wind field and produce the wind field bias. Ultimately, the original wind field is merged with the produced bias to acquire the adjusted wind field.

3.2 MultiUnet

The model used for generating the structural guidance field is a pre-trained MultiUnet, which is an enhanced version of the Unet (Ronneberger et al., 2015). The down-sampling step of MultiUnet is extended to include two channels, one for encoding the U component and the other for encoding the V component of the wind field. This approach offers an enhanced encoding mechanism for wind fields that have numerous components. A Batch Normalisation (BN) layer is inserted between every ReLU activation function in the convolutional layers and blocks. The BN layer constrains the variability of the input data within a defined range, enabling following layers to operate efficiently without the need for frequent adjustments to changing inputs. Engaging in independent learning enhances the speed and stability of the neural network.

Figure 2 depicts the configuration and information transmission of the MultiUnet. The dimensions of the input image are (2, 96, 96), where 96 represents the width and height, and 2 represents the number of channels, which correspond to the two components of the wind field. The Conv-Block, which is the fundamental unit of MultiUnet, consists of a 3 × 3 two-dimensional convolution layer, a BN layer, and a ReLU activation function. The dimensions of the input and output of the Conv-Block stay constant, but the number of convolution kernels determines the number of output channels. The encoding method consistently reduces the dimensions of the feature maps, hence improving the representation of higher-level characteristics. Upon completion of the decoding procedure, a feature map with dimensions of (64, 96, 96) is obtained. A 1 × 1 convolutional layer subsequently decreases the channel count to 2, resulting in the output of the model. The Mean Squared Error (MSE) is employed as the loss function for MultiUnet, as depicted in Equation 1.

Figure 2

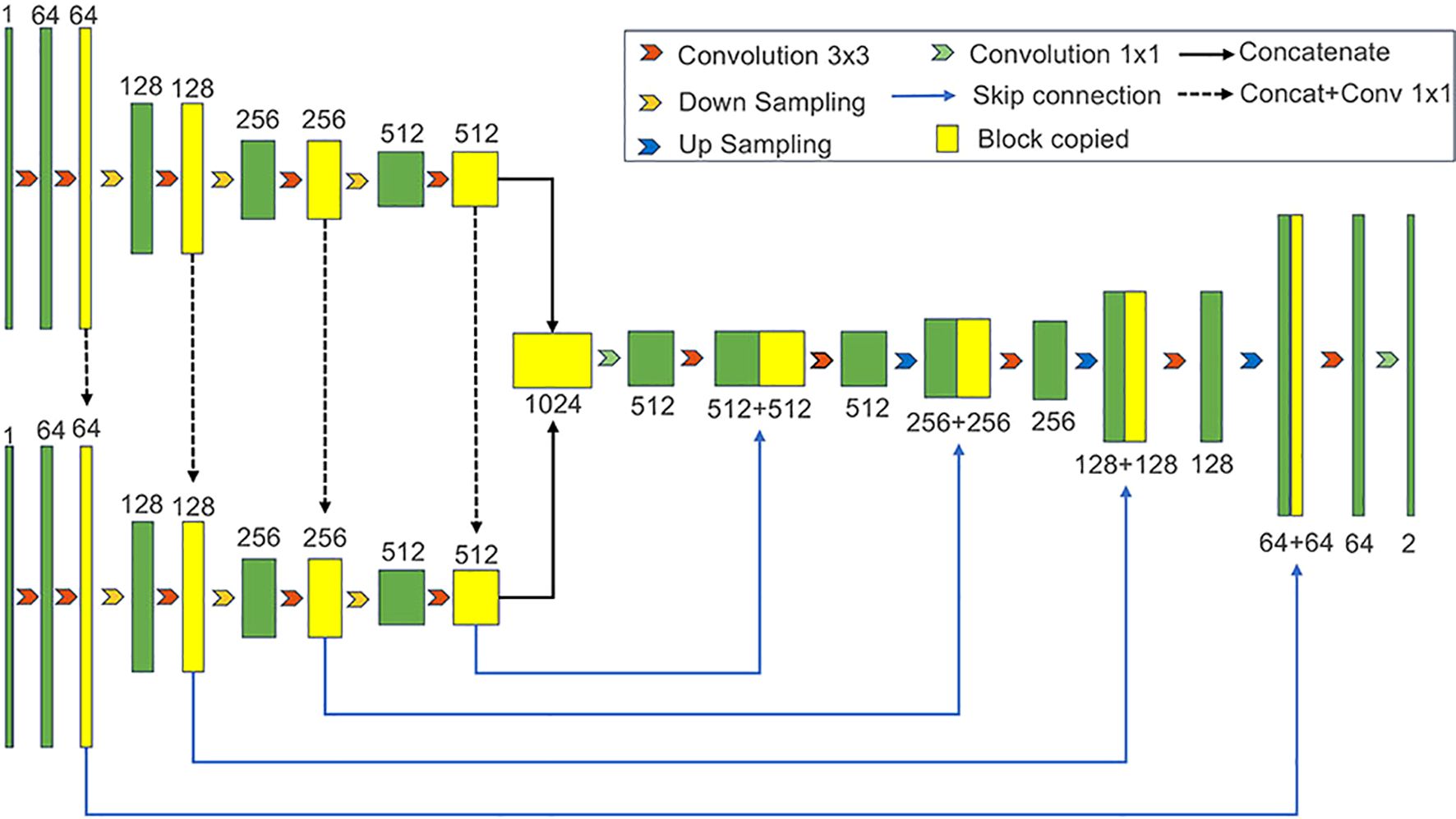
Figure 2. The diagram illustrates the structure of the multitasking Unet—MultiUnet. The down-sampling stage is split into two branches, with one branch encoding the U-component of the wind field and the other branch encoding the V-component. The up-sampling stage merges the two encoded blocks for decoding, with intermediate links to the matching encoding blocks in the down-sampling stage. The last convolutional block decreases dimensionality in order to produce the guide wind field.

$\begin{array}{ll}MSE=\frac{{\sum }_{i=1}^n{(f(x_i)-y_i)}^2}{n}& (1)\end{array}$

where n represents the number of samples. $f(x_i)$ is the predicted value of the i-th sample, and $y_i$ is the actual value of the i-th sample. MSE stands for Mean Squared Error, which measures the average squared difference between the predicted and actual values.

3.3 Conditional Denoising Diffusion Model

The Conditional Denoising Diffusion Probabilistic Model (DDPM) is employed for the purpose of rectifying wind field data. The prerequisites for wind field bias correction include the initial wind field bias y₀ and a guiding field x that encompasses structural information. We utilized Conditional DDPM to generate conditional wind fields, expanding upon the DDPM models introduced in (Ho et al., 2020). The Conditional DDPM model produces the target bias y₀ by going through T refining phases. The model begins with a random noise $y_T\sim N(0,I)$ and then repeatedly improves the output correction using the learnt conditional distribution. This process continues until a sequence is obtained that eventually converges to y₀ (refer to Figure 3).

Figure 3

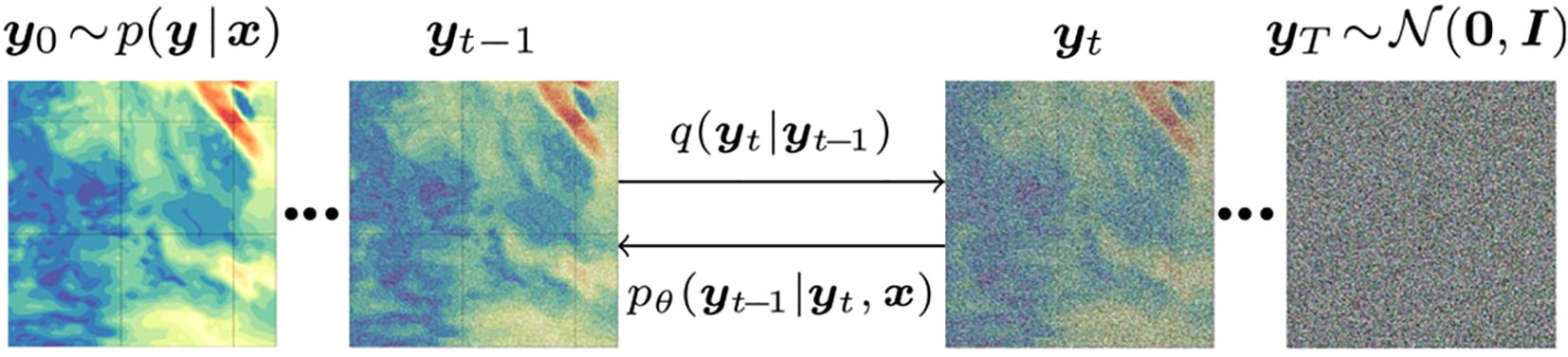
Figure 3. The forward diffusion process q, which occurs from left to right, progressively introduces Gaussian noise to the target image. The inverse procedure p (performed from right to left) systematically removes noise from the target image, taking into account the bias field x.

The forward diffusion process of DDPM gradually introduces Gaussian noise to the output by means of a stationary Markov chain q (Equations 2, 3).

$\begin{array}{ll}q({\mathit{y}}_{1:T}|{\mathit{y}}_0)=\prod _{t=1}^{T}q({\mathit{y}}_t|{\mathit{y}}_{t-1})& (2)\end{array}$

$\begin{array}{ll}q({\mathit{y}}_t|{\mathit{y}}_{t-1})=\mathcal{N}({\mathit{y}}_t|\sqrt{{\alpha }_t}{\mathit{y}}_{t-1},(1-{\alpha }_t)\mathit{I})& (3)\end{array}$

We employ a deep learning denoising model to acquire knowledge of the actual posterior $q(y_{t-1}|y_t)$. This model utilizes conditional information and Gaussian noise as inputs to estimate the noise using the following parameterization.

$\begin{array}{ll}{p}_{\theta }({\mathit{y}}_{t-1}|{\mathit{y}}_t,{\mathit{x}}_p,{\mathit{x}}_s)=\mathcal{N}({\mathit{y}}_{t-1};{\mu }_{\theta }({\mathit{y}}_t,t,{\mathit{x}}_p,{\mathit{x}}_s),{\text{Σ}}_{\theta }({\mathit{y}}_t,t,{\mathit{x}}_p,{\mathit{x}}_s))& (4)\end{array}$

We employ an Unet-based paradigm, akin to DDPM, incorporating self-attention and adjustments. The noise data y_t is merged with the beginning field x_p and the guidance field x_g. The denoising process is directed by x_p and x_g, guaranteeing that the intermediate noise and final wind field representation adhere to the provided structural information. In order to train the denoising algorithm, we initially create a noise sample $y_t\sim q(y_t|y_0)$ by introducing Gaussian noise to y₀. Next, we proceed to train a conditional denoising model $ϵ(y_t,t,x_p,x_g)$, which use the conventional loss function The Mean Absolute Error (MAE) to anticipate the new noise.

$\begin{array}{ll}{L}_{\text{mae}}={\mathbb{E}}_{t\sim [1,T],{\mathit{y}}_0\sim q({\mathit{y}}_{\text{o}}),ϵ}\Vert ϵ-{ϵ}_{\theta }({\mathit{y}}_t,t,{\mathit{x}}_p,{\mathit{x}}_s)\Vert & (5)\end{array}$

where T represents a certain number of phases (related to the diffusion process). y₀ is the initial wind field bias, and $q(y_{\text{o}})$ is a distribution related to y₀. ϵ is a variable related to noise. θ represents the parameters of the model. x_p and x_s are related to the beginning field and some other field (as described in the context). L_mae represents the Mean Absolute Error loss function, which is used to train the conditional denoising model to anticipate the new noise.

4 Results

4.1 Performance evaluation criteria

The MU-Diffusion framework comprises the MultiUnet and DDPM models, both operating in dual channels. In order to assess its performance, we selected the Unet model, which has exhibited efficacy in bias correction, and the DDPM model, an innovative method in image-based domains, as comparable models for our studies. The assessment of wind field bias correction is divided into two components: wind speed and wind direction. The corrective performance of each wind field variable is evaluated in respect to several seasons. The study classifies the months as follows: spring encompasses February, March, and April; summer encompasses May, June, and July; autumn encompasses August, September, and October; and winter encompasses November, December, and January.

MAE is employed to assess the accuracy of the corrective performance, and it is defined as follows:

$\begin{array}{ll}MAE=\frac{1}{T\ast H\ast W}\sum _{t=1}^T\sum _{i=1}^H\sum _{j=1}^W\left|y_{t,i,j}-{\widehat{y}}_{t,i,j}\right|& (6)\end{array}$

where T represents the number of samples in the testing dataset; H and W are the height and width of the study area, respectively. ${\widehat{y}}_{t,i,j}$ represents the forecast value or corrected value at $(i,j)$ at the forecast issue time t, and $y_{t,i,j}$ represents the observation value of $(i,j)$ at t. MAE stands for Mean Absolute Error, which measures the average absolute difference between the predicted and actual values.

Regarding the wind direction, 0° and 360° point in the same direction, even though their numerical values are very different; thus, we must consider the cyclic characteristics of wind direction. According to the “QXT 229–2014 Verification Method for Wind Forecast” (Han et al., 2021), the Mean Absolute Error of Direction (MAEd) represents a difference between the corrected and ground truth values of 180°, and is appropriate for wind direction assessment. Therefore, this metric was used for our evaluation; it is defined as follows:

$\begin{array}{ll}MA{E}_{\text{dir}}=\sqrt{\frac{1}{T\ast H\ast W}{\displaystyle \sum _{t=1}^T\sum _{i=1}^H\sum _{j=1}^W}{(\text{min }(\left|y_{t,i,j}-{\widehat{y}}_{t,i,j}\right|,360-\left|y_{t,i,j}-{\widehat{y}}_{t,i,j}\right|))}^2}& (7)\end{array}$

where T represents the number of samples in the testing dataset; H and W are the height and width of the study area, respectively. ${\widehat{y}}_{t,i,j}$ represents the forecast value or corrected value at $(i,j)$ at the forecast issue time t, and $y_{t,i,j}$ represents the observation value of $(i,j)$ at t. MAE_dir is used to evaluate the difference between the corrected and ground truth values of wind direction considering its cyclic characteristics (where 0° and 360° point in the same direction).

These criteria include commonly used metrics as well as a newly introduced metric, Mean Bias (MB), which provides valuable insights into the models’ ability to correct biases in the data.

$\begin{array}{ll}MB=\frac{1}{T\times H\times W\times N}\sum _{t=1}^T\sum _{i=1}^H\sum _{j=1}^W\sum _{n=1}^N(y_{t,i,j,n}-{\widehat{y}}_{t,i,j,n})& (8)\end{array}$

In this formula, T represents the number of time steps, H and W denote the latitude and longtitude of the spatial domain, N indicates the number of components of the wind field (there are two components, U10 and V10), $y_{t,i,j,n}$ is the true value of the n-th component of the wind field at time t and spatial location $(i,j)$, and ${\widehat{y}}_{t,i,j,n}$ is the predicted value of the n-th component of the wind field at time t and spatial location $(i,j)$. It should be particularly noted that due to the particularity of wind direction, the Mean Bias (MB) metric can only be used for calculations on the wind field as a whole. A positive mean bias indicates that the model tends to overpredict, while a negative value implies an underestimation. By analyzing the mean bias across different seasons and for different models, we can gain a deeper understanding of the models’ performance characteristics and their ability to correct biases in different climatic conditions.

These evaluation criteria are applied to each of the models considered in this study, namely the U-Net model, the diffusion model, and the U-Net diffusion combination model, as well as to the original data (origin) for comparison purposes. The results of these evaluations are presented and analyzed in subsequent sections to determine the relative performance of each model and to identify their strengths and weaknesses.

4.2 Corrected wind speed results for the four seasons

Figure 4 depicts the fluctuations in MAE across the seasons for various modes, as well as the respective models’ capacities to reduce errors. Figure 5 displays the correction outcomes of each model in several seasons, accompanied by visualised data from the GFS and ERA5.

Figure 4

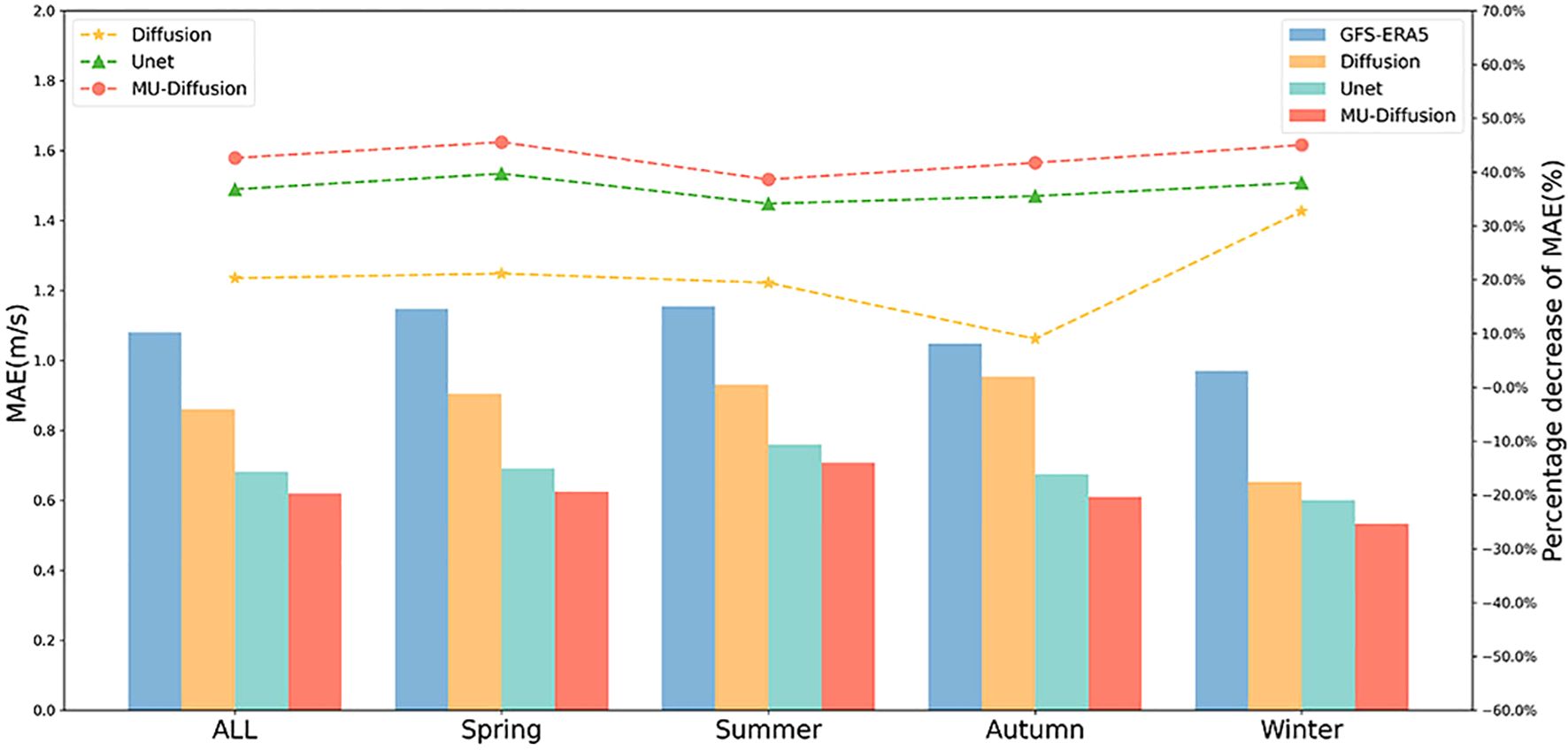
Figure 4. The MAE in metres per second for distinct modes for each of the four seasons in 2022. The initial column denotes the mean MAE of the model bias correction outcomes for the year 2022, while the next four columns reflect the outcomes for spring, summer, autumn, and winter, respectively. The coloured dashed lines represent the decrease in error of GFS-ERA5 wind speed for each respective model.

Figure 5

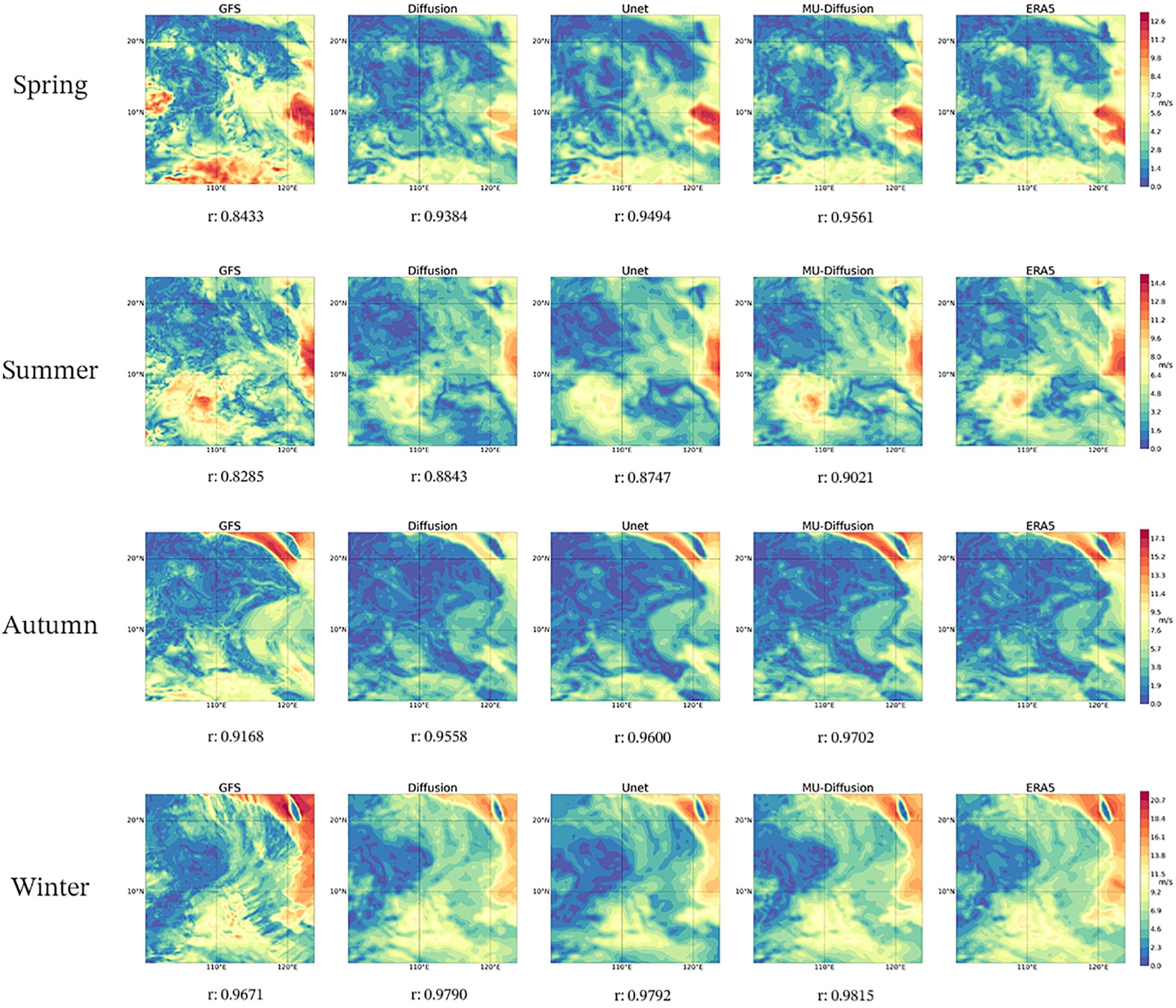
Figure 5. Correction results for wind speed in the South China Sea across the four seasons of 2022. The wind speed visualisation for spring, summer, autumn, and winter is represented in each row, from top to bottom. Each column in the visualisation reflects the wind speed for GFS, Diffusion, Unet, MU-Diffusion, and ERA5, respectively, from left to right. The Pearson correlation coefficients between the wind speed images of GFS, Diffusion, Unet, and MU-Diffusion and ERA5 are displayed below each image.

Figure 4 presents the Mean Absolute Error (MAE) estimates of wind speed for different models over different seasons. MU-Diffusion exhibits the lowest Mean Absolute Error (MAE) compared to the other two models, and it is also notably lower than GFS-ERA5. The MU-Diffusion model yielded a wind speed forecast for a duration of one year, with an average correction accuracy of 42%.The difference in performance between Unet and MU-Diffusion in relation to wind speed is negligible, and both models demonstrate comparable seasonal patterns with slight variations attributed to seasonality. Nevertheless, the Diffusion model exhibits significant fluctuations in inaccuracy over fall and winter, with a mere 10% adjustment in autumn and a potential enhancement of up to 32% in winter. In general, the MU-Diffusion model exhibits superior wind speed correction outcomes, surpassing Unet by around 4% to 7% in terms of correction accuracy.

In order to assess the accuracy of several models, we generated plots displaying the correction outcomes for wind speed in the South China Sea over the four seasons of 2022 for each model. The Pearson correlation coefficient between the model-generated results and ERA5 is displayed at the bottom of each figure. All three models demonstrate a certain level of ability to correct wind speed visually.MU-Diffusion offers a more precise and rational distribution of wind speed, along with enhanced visualisation and numerical enhancements. The areas with high wind speeds show a stronger correlation with ERA5 data. As an illustration, MU-Diffusion provides precise forecasts for two areas with strong wind speeds at 120°E and 124°E during the spring season. The Pearson correlation coefficients for each season indicate that the results obtained via MU-Diffusion exhibit the highest correlation with ERA5 data. With the exception of winter, the Pearson correlation coefficients demonstrate a notable enhancement, with an average augmentation of approximately 8%. The winter season exhibits a modest enhancement, with an only 1.4% rise.

4.3 Corrected wind direction results for the four seasons

Figure 6 depicts the fluctuations in MAEd. Figure 7 presents the correction outcomes for wind direction throughout the four seasons. Throughout all four seasons, MU-Diffusion consistently demonstrates the highest level of performance, with an average annual improvement rate of 38.3%. In comparison, the Unet and Diffusion models obtain improvement rates of 32.5% and 35.1% respectively. However, in terms of wind direction, Diffusion surpasses the Unet model by 2.5%, unlike wind speed. The three models all exhibit their lowest error rate throughout the summer, while seeing the greatest enhancement during the winter. The Unet and MU-Diffusion models display a comparable seasonal pattern, akin to wind speed. However, the Diffusion model is more susceptible to seasonal fluctuations.

Figure 6

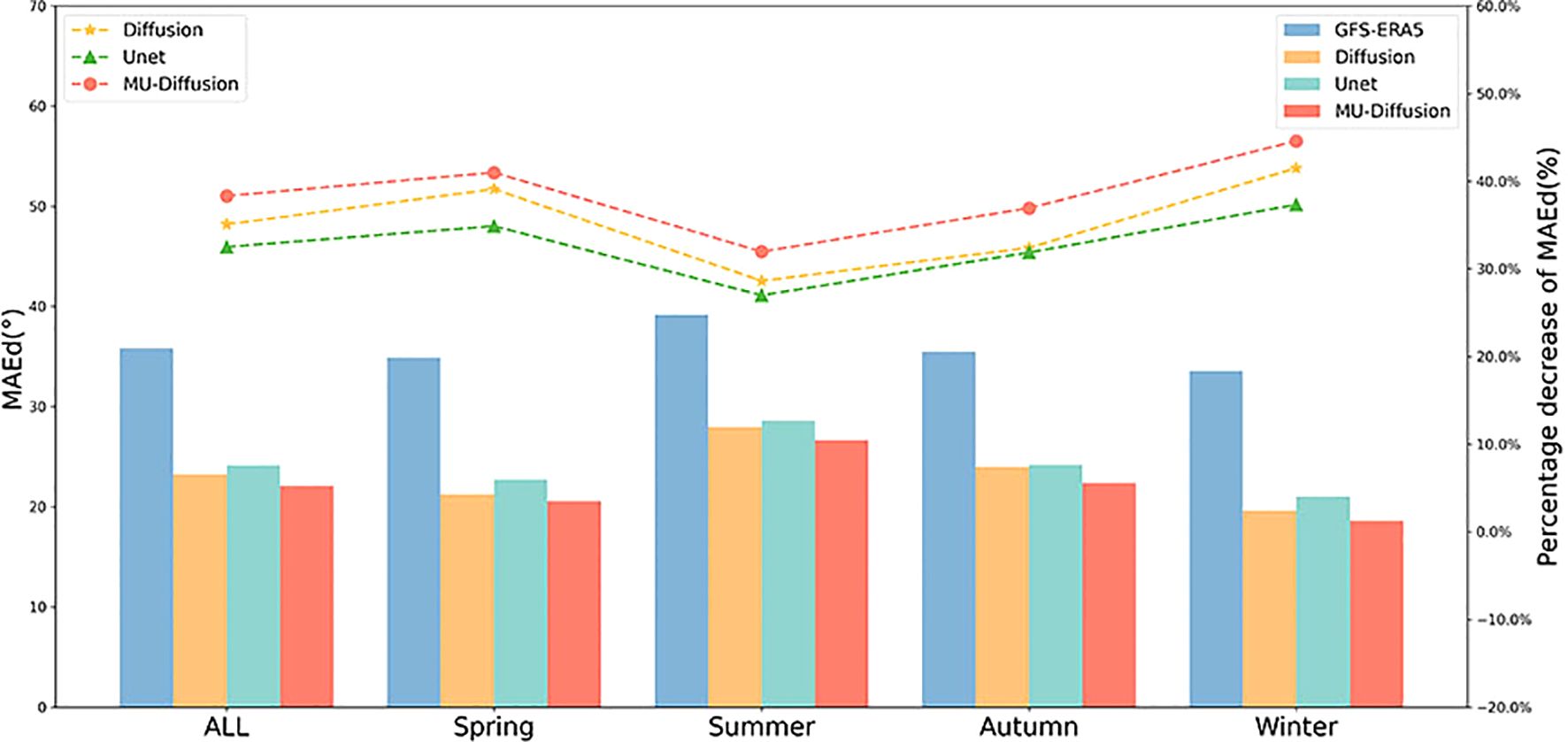
Figure 6. The fluctuation in MAEd for various modes across the four seasons of 2022. The initial column signifies the mean MAE for the outcomes of model bias correction in the year 2022, while the following four columns indicate the outcomes for spring, summer, autumn, and winter, correspondingly. The coloured dashed lines represent the extent to which the matching models have reduced errors in wind direction angle between GFS and ERA5.

Figure 7

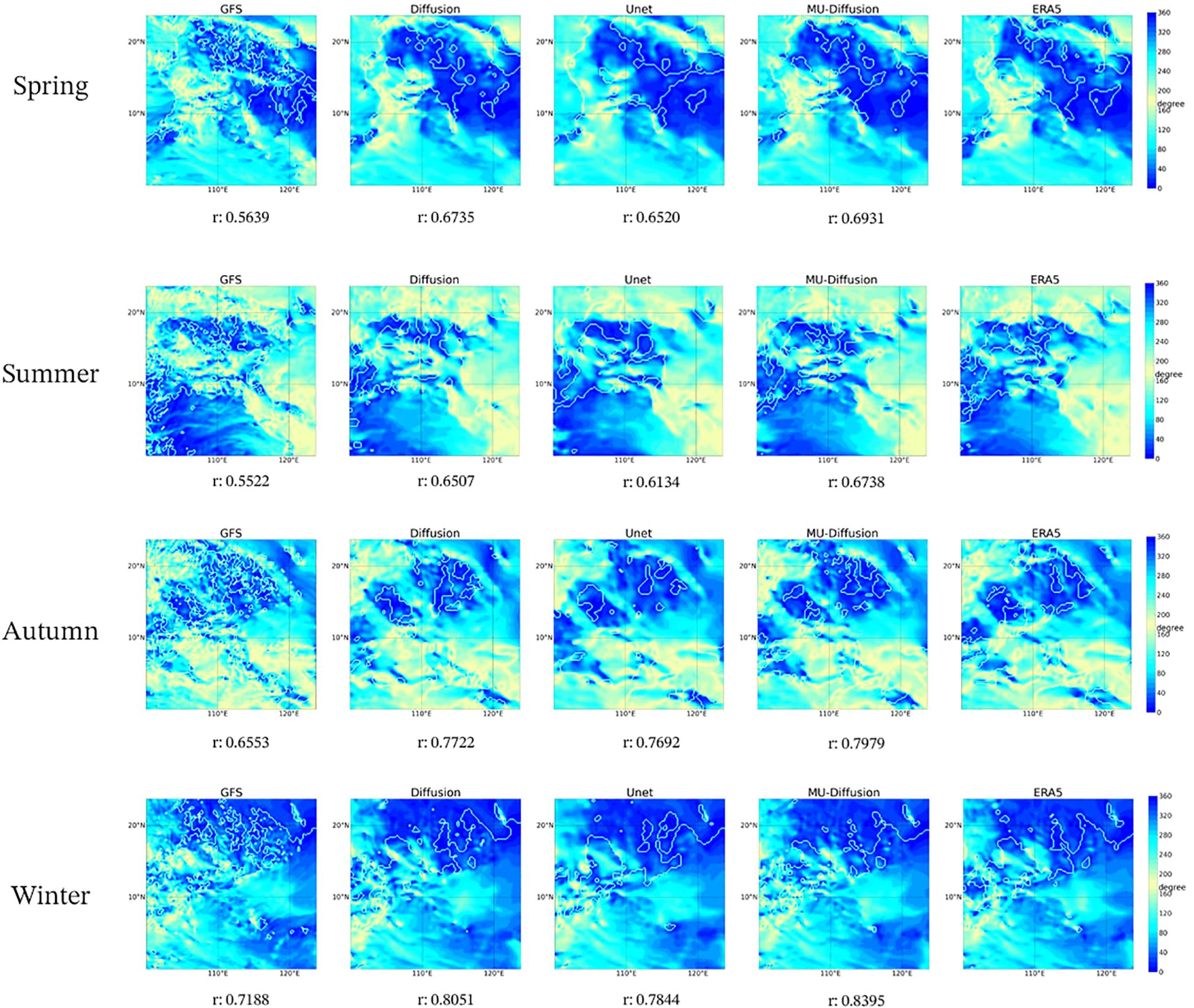
Figure 7. Correction results for wind direction in the South China Sea across the four seasons of 2022. Each row corresponds to the wind direction visualisation for the seasons of spring, summer, autumn, and winter, arranged from top to bottom. The wind direction visualisation for GFS, Diffusion, Unet, MU-Diffusion, and ERA5 is represented in each column from left to right. The wind direction graphics for GFS, Diffusion, Unet, and MU-Diffusion are accompanied by their respective Pearson correlation coefficients with ERA5.

Figure 6 displays the adjustment made to correct the bias in wind direction for each of the four seasons, using several models. The Figure 7 also includes the Pearson correlation coefficients associated with each model. From both a visual and numerical standpoint, all three models exhibit some ability to accurately predict wind direction. MU-Diffusion exhibits superior performance compared to Diffusion, but Diffusion demonstrates a greater improvement than Unet. These findings suggest that diffusion models are more effective in addressing wind direction bias.

The previously reported findings on the adjustment of wind speed and wind direction indicate that the Unet model and the Diffusion model possess distinct advantages in these specific domains. Nevertheless, the MU-Diffusion model amalgamates the benefits of both approaches, providing superior generalizability and robustness. The training data, utilizing the U and V components, can be employed to simultaneously rectify both wind speed and wind direction, thereby circumventing complications associated with the periodic nature of wind direction. In addition, the higher performance of MU-Diffusion serves as evidence for the usefulness of the suggested dual-channel system. The utilization of MultiUnet and Conditional Diffusion Models demonstrates an effective and resilient method for rectifying wind field bias. This strategy tackles both wind speed and wind direction inside a unified framework.

4.4 Bias correction for extreme weather

The South China Sea is a major hotspot for worldwide typhoon activity, seeing typhoons consistently throughout the year. This has a substantial influence on the safety of ships and offshore operations in the region. Hence, it is imperative to investigate the patterns and behavior of typhoons in the South China Sea, encompassing both those originating inside the region and those originating from the Northwest Pacific. For our wind field bias correction tests, we chose Typhoon Nalgae, the 22nd typhoon of 2022, which occurred in the South China Sea, as our test case. The objective of this study was to assess the effectiveness of several correction models in predicting the behavior of typhoons, considering their influence on marine safety and the requirement for precise forecasts during severe weather events.

We generated a graph illustrating the rectification findings for Typhoon Nalgae, which is the 22nd typhoon of the year 2022. The data corresponds to the 06 UTC time on October 30, 2022, as shown in Figure 8. The wind field patterns exhibited by the Diffusion, Unet, and MU-Diffusion models demonstrated more precise and rational distributions. The rectification results obtained via MU-Diffusion were superior. The initial MAEd was 38.2°, while the corrected MAEd was 18.5°.

Figure 8

Figure 8. Typhoon Nalgae, the 22nd typhoon of 2022, is seen in the wind field maps at 06 UTC on October 30, 2022. The colors correspond to the velocity of the wind, while the arrows indicate the direction in which the wind is flowing. The wind field maps displayed from left to right correspond to the GFS, Diffusion, Unet, MU-Diffusion, and ERA5 models.

Concurrently, we generated a scatterplot comparing the model-corrected data with the ERA5 (ground truth) data (Figure 9). The x-axis indicates the GFS forecast or the model-corrected outcome, while the y-axis represents the ERA5 data. A scatterplot displays data points that are clustered closer to the diagonal line, indicating a more pronounced linear relationship between two variables (Kim et al., 2021). This relationship facilitates the visualisation of the correspondence between the predicted or adjusted outcomes and the actual ground truth data, enabling an evaluation of the models’ accuracy in making corrections.

Figure 9

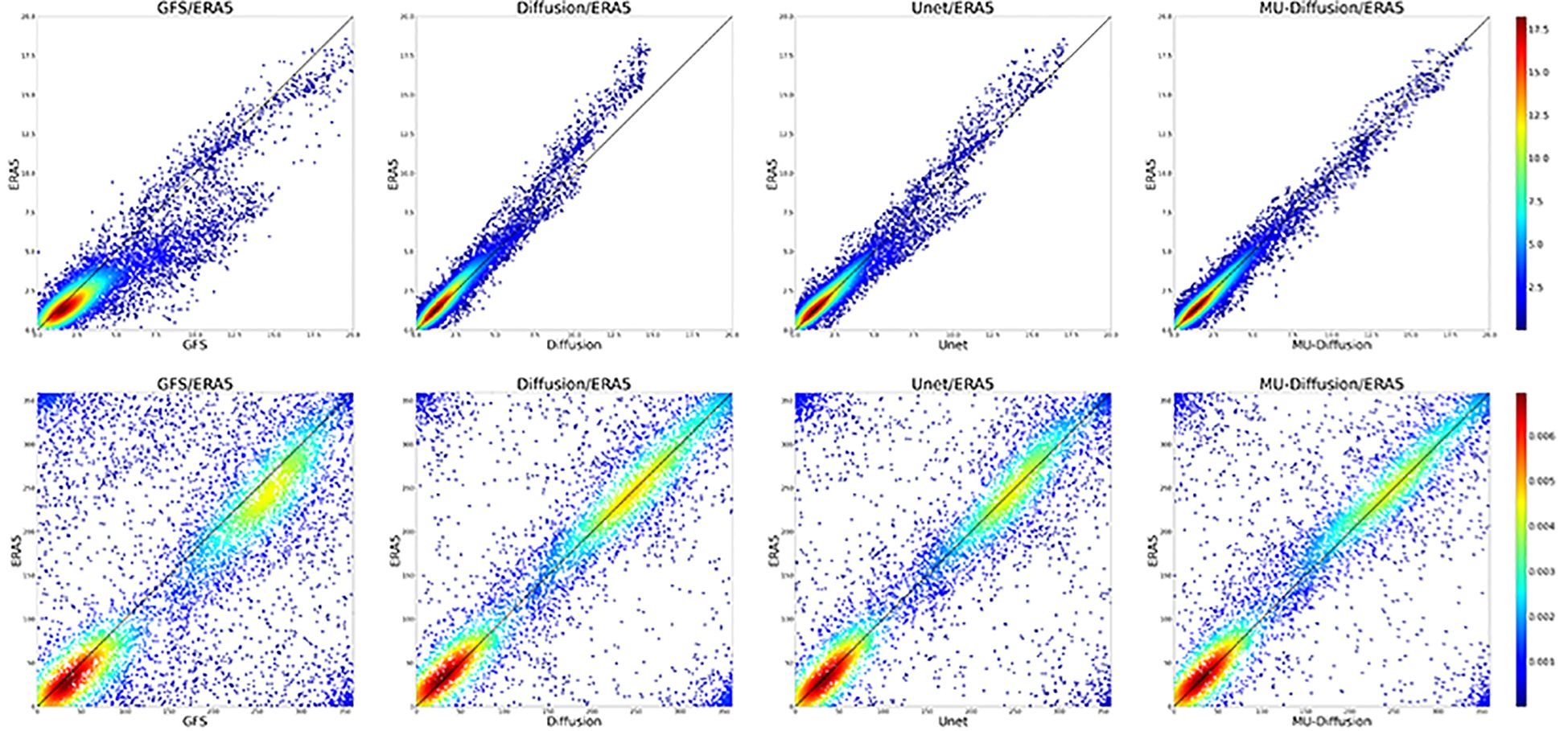
Figure 9. Typhoon Nalgae, the 22nd typhoon of 2022, is depicted in the scatter plots at 06 UTC on October 30, 2022. The initial row displays scatter plots representing wind speed, while the subsequent row showcases scatter plots representing wind direction. The charts, in order from left to right, depict the GFS, Diffusion, Unet, and MU-Diffusion.

4.5 Model performance evaluation using Mean Bias

In this section, we analyze the performance of different models using the Mean Bias (MB) metric. The MB values offer insights into the models’ tendencies to overestimate or underestimate the true values of the wind field. The data for these evaluations are presented in Table 1, with the origin data (GFS data) and labels (ERA5 data) used for calculations.

Table 1

Table 1. Wind field model performance evaluation index table, aiming to present the specific values of the mean bias (MB), a key indicator, of different models in different seasons, so as to conduct comprehensive and detailed analysis and comparison of the performance of each model.

Overall, the origin data shows an MB of 0.024, indicating a tendency to overpredict. Among the models, the Unet model has an MB of -0.023, suggesting a slight underestimation. The Diffusion model has an MB of -0.047, showing a more significant underestimation. The MU - Diffusion model has an MB of -0.018, which is closer to zero compared to the other models, indicating relatively better performance in terms of overall bias.

Seasonally, in spring, the origin data overpredicts. The Unet model underestimates, the Diffusion model has a small bias, and the MU - Diffusion model shows good performance. In summer, the origin data overpredicts. The Unet model slightly overpredicts, the Diffusion model underestimates, and the MU - Diffusion model has a better bias. In autumn, the origin data overpredicts. The Unet model underestimates, the Diffusion model underestimates, and the MU - Diffusion model shows good performance. In winter, the origin data overpredicts.

The Unet model underestimates, the Diffusion model underestimates, and the MU - Diffusion model has a relatively good bias.

The season differences may be attributed to various factors. Different seasons have distinct weather patterns and wind characteristics. For example, in spring and autumn, the temperature gradients and associated pressure systems may lead to more complex and variable wind fields, which pose greater challenges for the models to accurately capture the bias. In summer, the influence of large - scale weather systems such as monsoons can cause significant variations in wind speed and direction, affecting the model’s performance. In winter, cold fronts and jet streams can introduce sudden changes in wind conditions, making it difficult for the models to adapt and correct the bias effectively.

Overall, the MU - Diffusion model shows a more consistent performance across seasons with MB values closer to zero, indicating better bias correction capabilities compared to the other models. Its performance advantages may stem from its unique dual - channel framework structure. This structure can better integrate feature information at different levels, thus more accurately capturing the variation laws of the wind field and reducing the bias. At the same time, it may have stronger adaptability and robustness when dealing with complex weather patterns and changes in wind characteristics, enabling it to maintain a relatively good performance in different seasons.

5 Conclusion and discussion

Our research indicates that the data-driven dual-channel approach may effectively reduce biases in both wind speed and wind direction in model data. The MU-Diffusion model is constructed by combining the MultiUnet and Diffusion models. This framework can simultaneously correct wind speed and wind direction by modelling the spatio-temporal sequences of the u-direction and v-direction components of the wind field.MU-Diffusion algorithm effectively captures and combines characteristics from both the u-direction and v-direction wind components, resulting in accurate rectification outcomes even under severe weather conditions.

We utilized GFS model wind field forecast data spanning from January 2016 to December 2022, along with ERA5 reanalysis data, for the purposes of model training and testing. The model’s performance was evaluated using MAE and MAEd as performance metrics. The revised outcomes obtained from the MU-Diffusion model were contrasted with the forecasted outcomes of the GFS model, revealing an average enhancement of 42% in wind speed and 38.3% in wind direction. The empirical findings suggest that the MU-Diffusion model is capable of accurately adjusting wind speed and wind direction. When comparing the individual performance of Unet and Diffusion models, the MU-Diffusion model shown superior optimization in wind speed and wind direction. The test results collected under normal and typhoon conditions showed that the MU-Diffusion model performs equally well in correcting wind speed and wind direction across varied weather situations. This indicates that the model is highly generalizable and robust.

While the MU-Diffusion model has demonstrated significant effectiveness in deterministic bias correction, it is also important to consider its potential in providing probabilistic forecasts.

Currently, the MU-Diffusion model focuses on deterministic bias correction and does not directly generate probabilistic forecasts. However, the model’s architecture and the way it processes data provide some potential for future extensions towards probabilistic forecasting. One possible approach to introduce probabilistic forecasting could be to incorporate a Bayesian framework. By treating the model parameters as random variables with prior distributions, we could update these distributions based on the observed data and generate posterior distributions for the forecasts. Another option could be to use an ensemble of models, where multiple instances of the MU-Diffusion model are trained with different initializations or perturbations, and the resulting forecasts are combined to produce a probabilistic distribution.

Probabilistic forecasts are highly important in wind field prediction as they provide a more comprehensive understanding of the uncertainty associated with the forecasts. This allows meteorologists to make more informed decisions, especially in the context of severe weather events where the accuracy and reliability of the forecasts are crucial.

In the South China Sea, the climate is complex with strong Asian monsoon influence, bringing seasonal wind changes and frequent typhoons. Its topography further complicates the wind field. Compared to the North Atlantic, which has different dominant wind patterns due to the North Atlantic Oscillation and distinct oceanic interactions, the South China Sea shows unique characteristics. The MU-Diffusion model, with its combination of MultiUnet and diffusion model, has effectively corrected wind biases in the South China Sea. For application in other regions like the North Atlantic, its adaptability is crucial. Similar regions may need minor adjustments, while vastly different ones could require significant modifications considering factors like stronger currents and different temperature gradients. Globally, it has potential but requires extensive testing and calibration in diverse regions to handle the variety of climate and wind conditions, with the South China Sea study serving as a foundation for further exploration and improvement.

Although our study is based on the specific climate and data conditions of the South China Sea, the deep learning framework has a certain degree of universality. However, due to the significant differences in climate characteristics of different sea areas, direct application to other sea areas may face challenges. For example, in sea areas with relatively stable wind field changes and less typhoon influence, our model may need to be appropriately adjusted to adapt to the new environmental characteristics. Overall, our study provides an example for the application of deep learning in the field of wind field bias correction and offers a reference for subsequent research and improvement in other sea areas, contributing to the development of this field in a broader region.

In future extension research, we will investigate enhancing the model’s capacity to simultaneously manage several meteorological variables, including temperature, mean sea level pressure, air pressure, and others. By engaging in multitasking learning, the model has the potential to acquire additional environmental data, resulting in enhanced precision when correcting wind speed and wind direction. This study utilizes deep learning models to improve the predictive precision of NWP models, thereby enhancing the accuracy and dependability of weather forecasts. Additionally, the exploration of its potential for probabilistic forecasting opens up new avenues for future research and applications. As we have shown, there are viable approaches to extend the model towards generating probabilistic forecasts, which could greatly enhance its practical value in meteorological predictions. This not only highlights the versatility and adaptability of the model but also indicates the direction for further improvement and development in the field of wind field prediction. The objective is to provide meteorologists with enhanced instruments for forecasting future weather patterns and making well-informed choices when managing severe weather occurrences.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.5065/D65D8PWK.

Author contributions

CP: Conceptualization, Data curation, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. TS: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing. HS: Conceptualization, Formal analysis, Funding acquisition, Methodology, Resources, Software, Visualization, Writing – review & editing. XL: Conceptualization, Funding acquisition, Project administration, Software, Validation, Writing – review & editing. DX: Data curation, Funding acquisition, Investigation, Project administration, Resources, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by Natural Science Foundation of China (Grant: U1811464); National Key Research and Development Program (No. 2018YFC1406201 and No. 2018YFC1406204); Natural Science Foundation of Shandong Province(Grant No. 405 ZR2019MF012); Taishan Scholars Fund (Grant No. ZX20190157). Project Supported by Key Laboratory of Environmental Change and Natural Disaster of Ministry of Education, Beijing Normal University(Project No. 2022-KF-08), Project Supported by Key Laboratory of Marine Hazards Forecasting, Ministry of Natural Resources(No.LOMF2202), Innovation found project for graduate students of China University of Petroleum (East China)(CXJJ-2022-08); U21A6001, and the CAS Key Laboratory of Science and Technology on Operational Oceanography Open Project Funding No OOST2021-03.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer JW declared a shared affiliation with the authors CP, TS, HS, XL to the handling editor at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chang C.-W., Mori N. (2021). Green infrastructure for the reduction of coastal disasters: A review of the protective role of coastal forests against tsunami, storm surge, and wind waves. Coast. Eng. J. 63, 370–385. doi: 10.1080/21664250.2021.1929742

Crossref Full Text | Google Scholar

Dengxin He D., Zhou Z., Kang Z., Liu L. (2019). Numerical studies on forecast error correction of grapes model with variational approach. Adv. Meteorol. 2019. doi: 10.1155/2019/2856289

Crossref Full Text | Google Scholar

Duan J., Zuo H., Bai Y., Duan J., Chang M., Chen B. (2021). Short-term wind speed forecasting using recurrent neural networks with error correction. Energy 217, 119397. doi: 10.1016/j.energy.2020.119397

Crossref Full Text | Google Scholar

For Environmental Prediction/National Weather Service/NOAA/US Department of Commerce, N. C (2015). Ncep gfs 0.25 degree global forecast grids historical archive. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory.

Google Scholar

Glahn H. R., Lowry D. A. (1972). The use of model output statistics (mos) in objective weather forecasting. J. Appl. Meteorol. Climatol. 11, 1203–1211. doi: 10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2

Crossref Full Text | Google Scholar

Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., et al. (2020). Generative adversarial networks. Commun. ACM 63, 139–144. doi: 10.1145/3422622

Crossref Full Text | Google Scholar

Han L., Chen M., Chen K., Chen H., Zhang Y., Lu B., et al. (2021). A deep learning method for bias correction of ecmwf 24–240 h forecasts. Adv. Atmos. Sci. 38, 1444–1459. doi: 10.1007/s00376-021-0215-y

Crossref Full Text | Google Scholar

Harbola S., Coors V. (2019). One dimensional convolutional neural network architectures for wind prediction. Energy Conver. Manage. 195, 70–75. doi: 10.1016/j.enconman.2019.05.007

Crossref Full Text | Google Scholar

Hersbach H., Bell B., Berrisford P., Hirahara S., Horányi A., Muñoz-Sabater J., et al. (2020). The era5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.v146.730

Crossref Full Text | Google Scholar

Ho J., Jain A., Abbeel P. (2020). Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 33, 6840–6851.

Google Scholar

Kavasseri R. G., Seetharaman K. (2009). Day-ahead wind speed forecasting using f-arima models. Renewable Energy 34, 1388–1393. doi: 10.1016/j.renene.2008.09.006

Crossref Full Text | Google Scholar

Kim D.-K., Suezawa T., Mega T., Kikuchi H., Yoshikawa E., Baron P., et al. (2021). Improving precipitation nowcasting using a three-dimensional convolutional neural network model from multi parameter phased array weather radar observations. Atmos. Res. 262, 105774. doi: 10.1016/j.atmosres.2021.105774

Crossref Full Text | Google Scholar

Kingma D. P., Welling M. (2013). Auto-encoding variational bayes. CORR. abs/1312.6114

Google Scholar

Klein W. H., Lewis B. M., Enger I. (1959). Objective prediction of five-day mean temperatures during winter. J. Atmos. Sci. 16, 672–682. doi: 10.1175/1520-0469(1959)016<0672:OPOFDM>2.0.CO;2

Crossref Full Text | Google Scholar

Laloyaux P., Kurth T., Dueben P. D., Hall D. (2022). Deep learning to estimate model biases in an operational nwp assimilation system. J. Adv. Model. Earth Syst. 14, e2022MS003016. doi: 10.1029/2022MS003016

Crossref Full Text | Google Scholar

Liu Z., Jiang P., Zhang L., Niu X. (2020). A combined forecasting model for time series: Application to short-term wind speed forecasting. Appl. Energy 259, 114137. doi: 10.1016/j.apenergy.2019.114137

Crossref Full Text | Google Scholar

Liu H., Mi X., Li Y. (2018). Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, lstm network and elm. Energy Conver. Manage. 159, 54–64. doi: 10.1016/j.enconman.2018.01.010

Crossref Full Text | Google Scholar

Moeller D. P., Bunke M., Froese J., Schroer B., Harris G. (2008). “Ship-disaster and its impact on the transportation chain through simulation,” in Huntsville simulation conference (Huntsville). (Huntsville: The Society for Modeling and Simulation International)

Google Scholar

National Centers for Environmental Prediction, NationalWeather Service, NOAA, U.S. Department of Commerce. (2015). Ncep gfs 0.25 degree global forecast grids historical archive. last access: March 2024.

Google Scholar

Peng X., Che Y., Chang J. (2013). A novel approach to improve numerical weather prediction skills by using anomaly integration and historical data. J. Geophys. Res.: Atmos. 118, 8814–8826. doi: 10.1002/jgrd.v118.16

Crossref Full Text | Google Scholar

Rasp S., Lerch S. (2018). Neural networks for postprocessing ensemble weather forecasts. Month. Weather Rev. 146, 3885–3900. doi: 10.1175/MWR-D-18-0187.1

Crossref Full Text | Google Scholar

Ronneberger O., Fischer P., Brox T. (2015). “U-net: Convolutional networks for biomedical image segmentation,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. eds. Navab N., Hornegger J., Wells W. M., Frangi A. F. (Cham: Springer International Publishing), 234–241.

Google Scholar

Shi X., Chen Z., Wang H., Yeung D.-Y., Wong W.-K., Woo W.-c. (2015). Convolutional lstm network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 28.

Google Scholar

Shi X., Gao Z., Lausen L., Wang H., Yeung D.-Y., Wong W.-k., et al. (2017). Deep learning for precipitation nowcasting: A benchmark and a new model. Adv. Neural Inf. Process. Syst. 30.

Google Scholar

Solari S., Losada M. A. (2016). Simulation of non-stationary wind speed and direction time series. J. Wind Eng. Ind. Aerodynam. 149, 48–58. doi: 10.1016/j.jweia.2015.11.011

Crossref Full Text | Google Scholar

Wei-Hong Q. (2012). How to improve the skills of weather and climate predictions? Chin. J. Geophys. 55, 1532–1540. doi: 10.6038/j.issn.0001-5733.2012.05.010

Crossref Full Text | Google Scholar

Xu W., Liu P., Cheng L., Zhou Y., Xia Q., Gong Y., et al. (2021). Multi-step wind speed prediction by combining a wrf simulation and an error correction strategy. Renewable Energy 163, 772–782. doi: 10.1016/j.renene.2020.09.032

Crossref Full Text | Google Scholar

Zhu A., Li X., Mo Z., Wu R. (2017). “Wind power prediction based on a convolutional neural network,” in In 2017 International Conference on Circuits, Devices and Systems (ICCDS), 131–135. doi: 10.1109/ICCDS.2017.8120465

Crossref Full Text | Google Scholar