The golden batch-driven root cause analysis for anomalies in bioreactor fermentation process

Bioreactors are essential for the production of biopharmaceuticals and bioproducts, requiring continuous monitoring to ensure quality assurance. Manual processes in manufacturing plants often lead to anomalies such as out-of-trend and out-of-spec incidents, necessitating extensive root cause analysis that typically takes 2–8 weeks. This paper introduces an innovative methodology that uses the golden batch profile as a benchmark to identify deviations and root causes in subsequent industrial batches. The methodology involves normalizing the data and calculating the variances of a specified batch from the golden batch profile. By examining the contribution of each critical process parameter to these variances, the study highlights their importance in root cause analysis. The application of this methodology to the IndPenSim dataset demonstrated its effectiveness by significantly reducing false positives and negatives compared to traditional PCA-based methods. Emphasis on the deviations of critical quality attributes and critical process parameters from the specified batch compared to the golden batch profile offers valuable insights into industrial process analysis. This approach not only enhances anomaly detection accuracy but also improves the efficiency and reliability of biopharmaceutical and bioproduct manufacturing processes.

1 Introduction

In the realm of industrial batch processes, effective root cause analysis is paramount for maintaining product quality, ensuring process efficiency, and achieving overall operational excellence (Swim and Farach, 2023). Typically, engineers rely on their expertise and domain knowledge to identify the root cause by examining the system and specific processes. Throughout this process, a vast amount of data, including process features, in-line measurements, and final product information, is automatically recorded. While this extensive data collection can offer valuable manufacturing insights, the complexity and intricacy of the data structure make it difficult to process and interpret. As a result, identifying root causes becomes increasingly challenging, and solely relying on traditional methods and domain knowledge is inadequate (Chien and Chuang, 2014; He et al., 2019). This paper explores existing root cause analysis methods, shedding light on their advantages and limitations, and sets the stage for the introduction of an innovative golden batch-driven approach.

1.1 Industrial batch process root cause analysis methods

In our exploration of root cause analysis methods for industrial batch processes (Section 2), we thoroughly examine a range of established techniques. These include traditional approaches like the “5 Whys” method, Cause and Effect Fishbone diagram, Failure Mode and Effects Analysis (FMEA), and Fish Bone Diagram (Alliance Indian Pharmaceutical, 2019). Additionally, we investigate modern solutions such as AI based Automated Root Cause Analysis (RCA) Tools (Papageorgiou, et al., 2022; Oliveira et al., 2023), specifically delving into the functionalities of prominent tools like open library doWhy which are contributed lot of from Microsoft and Amazon (Sharma and Kiciman, 2020; Molak, 2023), ABS Group Consulting (Heuvel et al., 2008) and Fuzzy multi criteria decision making (Xu, et al., 2023). This detailed examination of diverse methodologies forms a comprehensive understanding that serves as the groundwork for the introduction of our innovative golden batch-driven approach.

1.2 Currently challenges in RCA of the bioreactor batch process

Despite its importance, root cause analysis in the bioreactor batch process faces challenges, primarily relying on manual processes that extend from 2 to 8 weeks for proper identification of root causes for complicated issues (White, 2022). This prolonged duration can lead to detrimental consequences, including wastage of valuable materials, increased costs, disruption of production schedules, and overall operational inefficiency. Addressing these challenges promptly through automation or data-driven processes is crucial for ensuring smoother and more efficient operations (Hornea et al., 2023).

1.3 Business value of advanced golden batch modeling driven root cause analysis

Introducing an advanced golden batch modeling-driven root cause analysis offers substantial business value. This approach accelerates the root cause analysis process by automating some manual procedures, reducing the time frame from 2 to 8 weeks to just days or even hours. The benefits include cost reduction through improved yield and resource utilization, decreased waste and downtime, increased revenue through enhanced product quality, and manufacturing consistency leading to market differentiation. The ease of implementation and focus on continuous improvement, exemplified by the utilization of a soft sensor (or “software sensor”) that combines process data (input) with a model to predict a target quantity (output), leveraging Generative AI, big data, XAI, and Causal Analysis, make it a strategic shift from reactionary to preventative analytics (Swim and Farach, 2023; White, 2022; Molak, 2023; Ahmed, et al., 2023; Brunner, et al., 2021; Menegozzo et al., 2022; Westerhuis et al., 2000; Yan et al., 2015; Rooney and Heuvel, 2004). This empowers the utilization of historical data to identify ideal manufacturing conditions, fostering a proactive approach towards operational excellence.

1.4 The contributions of this paper

This paper presents unique contributions to the field of bioprocess monitoring, particularly through the introduction of golden batch modeling and the integration of advanced analytical tools. Our key contributions are as follows:

• We introduce a data-driven golden batch profile framework that, when combined with automated root cause analysis, significantly reduces the manual process time for root cause identification from 2–8 weeks to mere days, or even less.

• Our methodology includes the automatic calculation of the primary contributors to deviations from the golden batch for current batches experiencing out-of-trend or out-of-spec nonconformance of critical quality attributes (CQAs).

• By leveraging deviations from the golden batch profile, our approach facilitates critical process parameter (CPP) anomaly detection, expediting the identification of root causes and precisely pinpointing the timing, location, and nature of critical quality attribute losses.

Overall, our proposed methodology, centered around the golden batch, aggregates data from multiple high-quality batches to establish a representative profile of the normal batch process enhancing transparency in analytical processes. Utilizing operator-defined CQAs and CPPs, our approach normalizes data and calculates deviations to provide relevant insights. This enables operators to swiftly identify the root causes of faults in the batch process.

This paper is organized as follows: Section 2 provides an overview of the methods related to the root cause analysis of nonconformance of industrial batch processes and outlines the strength and limitations of these methods. Section 3 introduces the golden batch profile framework, including the definition of the golden batch profile, normalization of batches, deviation of specified batches from the golden batch, contribution of the deviation of the specified batch to the golden batch techniques, and how to drill down to a critical process parameter with the highest contribution to identify when, where, and how the root cause occurs. In Section 4, we present experimental results derived from real-world applications of the proposed architecture.

2 Related work

2.1 Root cause analysis in manufacturing batch processes

RCA is a critical component in the optimization of manufacturing batch processes. In this section, we provide a detailed examination of various RCA methodologies, highlighting their strengths and limitations. The following table summarizes the current methods utilized for RCA in manufacturing settings:

From Table 1, current RCA methods each have unique strengths and limitations. The 5 Whys method is simple and quick but risks oversimplification and requires domain knowledge, while the Fish bone Diagram visually organizes complex information and encourages collaboration but may also oversimplify issues and be subjective. In contrast, our method automatically derives the contribution of critical process parameters to deviations of critical quality attributes, reducing dependency on domain knowledge, and is data-driven with dynamic interactions.

Table 1

Table 1. Current methods for root cause analysis.

FMEA (Failure Modes and Effects Analysis) offers a systematic and proactive approach but relies on assumptions and domain expertise, while Fuzzy Multi-Criteria Decision Making handles uncertainty well but is challenging to interpret and requires expertise. Conversely, our method is data-driven to determine when, where, and how the root cause occurs, and is easy to explain, reducing dependency on domain knowledge.

DoWhy, as an advanced causal discovery tool, leverages machine learning for causal inference but has a steep learning curve and is dependent on data quality. While SPC (Statistical Process Control) and PCA (Principal Component Analysis) detect process deviations early and identify control variable contributions but can produce false positives/negatives and are complex to explain. In comparison, our solution is based on statistical modelling and is data-driven, automatically deriving the contribution of CPPs to the deviations of CQAs, making it easy to understand and use, while effectively explaining the root cause.

The SOURCE^TM methodology provides professional consultancy but can be costly and dependent on external expertise. Instead, our solution leverages internal resources for RCA.

Finally, the Golden Batch Profile aids in identifying defect-free batches but may not meet multiple CQAs and lacks linkage between CQAs and CPPs, requiring manual processes and domain knowledge. Conversely, our method can analyze CQAs/conditions to identify the ideal batches to cultivate a golden batch. It establishes a linkage between CQAs and CPPs and automates and semi-automates processes to reduce dependency on domain knowledge.

From our comprehensive literature review and gathered insights, the ideal RCA solution should exhibit a data-driven approach, a user-friendly interface for seamless RCA exploration, minimized dependency on domain-specific knowledge, and automated or semi-automated functionality.

Based on the above analysis, we have identified that the golden batch profile offers a data-driven solution that is highly welcomed by manufacturing process engineers for root cause analysis. However, addressing the limitations and developing a method to construct the golden batch profile from numerous healthy batches, not just manually selecting a batch as the golden batch, considering multiple Critical Quality Attributes (CQAs) or quality Key Performance Indicator (KPI) thresholds or target values to data filter the batches under normal operational conditions, and automating the linkage between CQAs and Critical Process Parameters (CPPs) to facilitate the exploration of CPP contributions, would significantly enhance business value. This approach has the potential to expedite the root cause analysis (RCA) process by providing an automated or semi-automated RCA, allowing process engineers to explore where, when, and how the root cause occurred. This solution will speed up the RCA process, reduce dependence on domain knowledge, and contribute to overall operational efficiency.

2.2 RCA methods: customer insights

To gain more understanding of the root cause analysis (RCA) processes employed in the industry, we conducted interviews within Rockwell Automation engineering support and manufacturing team to understand their root cause analysis (RCA) process. Additionally, we gathered feedback from customers during our demo at the Automation Fair in 2023 in Boston (Rockwell Automation, 2023). The following questions were carried out:

• What methods or modeling do you use for root cause analysis?

• Is it a manual or automatic process?

• How long does it take to investigate root cause analysis?

• How much does it cost if a batch fails?

Based on customer feedback, we have identified that the most commonly employed root cause analysis (RCA) methodologies in various industries, including at Rockwell Automation, are the 5 Whys, Fishbone Diagram, A3, and Failure Mode and Effects Analysis (FMEA) (Gangidi, 2019; Reid and Smyth-Renshaw, 2012; Heher, 2017; Langer, 2008; Shook, 2009). These methods predominantly rely on manual processes. In industrial settings, executing an RCA can take between 2 and 8 weeks (White, 2022) and often involves multiple engineering teams. Domain experts have expressed a strong interest in leveraging advanced technologies such as Artificial Intelligence (AI), Machine Learning (ML), statistical modeling, and the golden batch concept to develop more sophisticated, automated RCA solutions. Such advancements are anticipated to reduce costs and enhance accuracy. In the biopharmaceutical industry, where batch costs range from $1 to $2 million (Langer, 2008), the ability to save even a single failed batch would result in substantial financial savings for businesses.

2.3 Apply golden batch in root cause analysis

The Golden Batch is the benchmark against which all other batches are measured. It can be created through first-principles models or by having expert engineers meticulously ensure the apparatus is clean and operate under optimal conditions (Yeh, et al., 2019). In practical scenarios, our approach involves the development of data-driven analytics. By analyzing historically successful batches, we learn the defining characteristics of a Golden Batch. This knowledge allows us to construct an ideal model based on the attributes of these previously high-performing batches.

The practice of establishing a golden batch and using its profile as a benchmark for evaluating current batches enables root cause identification, timely interventions and decisions about halting batch processes (Su and Yu, 2016; Hong et al., 2011). However, the industry often lacks automated tools for computing deviations. While many products allow the creation and editing of a golden batch, their functionality is generally restricted to these tasks. Users are typically expected to manually monitor the ongoing batch by visually comparing it to the golden batch, as suggested in training materials like TrendMiner’s videos, where the emphasis is on visual assessment against the golden standard (Yeh, et al., 2019).

3 Method

3.1 Definition of the golden batch profile

This section provides a comprehensive overview of defining golden batch modeling, a fundamental component of our approach. We elaborate on how this concept functions as a benchmark for identifying deviations and root causes of anomalies in subsequent batches.

A time series typically represents measurements of the same sample taken over time, establishing a connection between the samples in this type of data. In an industrial batch, numerous time series exist, some associated with Critical Quality Attributes (CQAs) and others with Critical Process Parameters (CPPs).

In the following equation, a variable X is repetitively sampled over time. The subscripts enumerate the sample points (sample 1 through sample n), and the entire series of samples is denoted as X:

$X=\{x_t\left.,t=1,2,\dots ,n\right\}(1)$

Assuming we have I batches under normal operational conditions, where i = 1, 2, …, I. For each batch i, and assuming there are J Critical Quality Attributes (CQAs), we will denote the j^th CQA time series as follows:

$Y^{\left(i,j\right)}=\left\{y_t^{\left(i,j\right)},t=1,2,\dots ,n\right\}(2)$

If there are K critical process parameters (CPPs), we will denote the k^th CPP time series as follows:

$X^{\left(i,k\right)}=\left\{x_t^{\left(i,k\right)},t=1,2,\dots ,n\right\}(3)$

We will define the golden batch time series for the j^th CQA as follows:

$G_{cqa}^{\left(j\right)}=\{g_t^{\left(j,cqa\right)},t=1,2,\dots ,n\}(4)$

where $g_t^{\left(j,cqa\right)}=\frac{1}{I}{\displaystyle \sum _{i=1}^I}{y}_t^{\left(i,j\right)},t=1,2,\dots ,n.$

Similarly, we will define the golden batch time series for the k^th CPP as follows:

$G_{cpp}^{\left(k\right)}=\left\{g_t^{\left(k,cpp\right)},t=1,2,\dots ,n\right\}(5)$

where $g_t^{\left(k,cpp\right)}=\frac{1}{I}{\displaystyle \sum _{i=1}^I}{x}_t^{\left(i,k\right)},t=1,2,\dots ,n.$

3.2 Normalized batches and golden batch profile

To measure the deviation between two time series, normalization is necessary to eliminate the unit factor and ensure comparability. For any batch i, where i = 1, 2, …, I, the normalized time series of the j^th Critical Quality Attribute (CQA) is denoted as follows:

$Y_{norm}^{\left(i,j\right)}=\{y_t^{\left(i,j,norm\right)},t=1,2,\dots ,n\}(6)$

If the distribution of the j^th CQA time series $Y^{\left(i,j\right)}\text{\hspace{0.17em}is similar to }\mathrm{a}\text{\hspace{0.17em}normal distrobtuinon\hspace{0.17em}with\hspace{0.17em}}\mathrm{a}$ mean ${\mu }^{\left(j\right)}$, and a standard deviation is ${\sigma }^{\left(j\right)}$, the normalization of j^th CQA time series is given by:

$y_t^{\left(i,j,norm\right)}=\frac{y_t^{\left(i,j\right)}-{\mu }^{\left(j\right)}}{{\sigma }^{\left(j\right)}},t=1,2,\dots ,n.(7)$

If the distribution deviates significantly from a normal distribution, Min-Max Scaling is employed:

$y_t^{\left(i,j,norm\right)}=\frac{y_t^{\left(i,j\right)}-{}_t{}^{\mathit{Min}}\left(y_t^{\left(i,j\right)}\right)}{{}_t{}^{\mathit{Max}}\left(y_t^{\left(i,j\right)}\right)-{}_t{}^{\mathit{Min}}\left(y_t^{\left(i,j\right)}\right)},t=1,2,\dots ,n.(8)$

Similarly, the k^th Critical Process Parameter (CPP) time series $X^{\left(i,k\right)},$ is normalized and denoted as $X_{norm}^{\left(i,k\right)}:$

$X_{norm}^{\left(i,k\right)}=\{x_t^{\left(i,k,norm\right)},t=1,2,\dots ,n\}(9)$

The time series $G_{cqa}^{\left(j\right)}$ is normalized and denoted as $G_{cqa,norm}^{\left(j\right)}$:

$G_{cqa,norm}^{\left(j\right)}=\{g_t^{\left(j,cqa,norm\right)}\left.,t=1,2,\dots ,n\right\}(10)$

Similarly, the time series $G_{cpp}^{\left(k\right)}$ is normalized and denoted as $G_{cpp,norm}^{\left(k\right)}$ , where k = 1, 2, …, K:

$G_{cpp,norm}^{\left(k\right)}=\{g_t^{\left(k,cpp,norm\right)}\left.,t=1,2,\dots ,n\right\}(11)$

3.3 Deviation from the golden batch profile

If the batch process analytics platform detects an anomaly with out-of-trend or out-of-spec non-conformance, it will trigger the root cause analysis process. To measure the deviation of the current batch from the golden batch profile, we will utilize the symmetric mean absolute percentage error (SMAPE), which is commonly used to measure the deviation between prediction values and actual values in machine learning model evaluations.

For the j^th Critical Quality Attribute (CQA) time series, where j = 1, 2, …, J, we define the deviation of the specified batch from the golden batch profile as follows:

${Deviation}^{\left(j,cqa\right)}=\frac{1}{n}{\displaystyle \sum _{t=1}^n}\frac{\left|y_t^{\left(i,j,norm\right)}-g_t^{\left(j,cqa,norm\right)}\right|}{\left|\left.y_t^{\left(i,j,norm\right)}\right|+\left|g_t^{\left(j,cqa,norm\right)}\right.\right|}(12)$

If $y_t^{\left(i,j,norm\right)}=0and{g}_t^{\left(j,cqa,norm\right)}=0$, The item in the sum of the right equation will be skipped, and n will be replaced with $n-1$.

For the k^th Critical Process Parameter (CPP) time series, where k = 1, 2, …, K, we define the deviation from the golden batch profile as follows:

${Deviation}^{\left(k,cpp\right)}=\frac{1}{n}{\displaystyle \sum _{t=1}^n}\frac{\left|x_t^{\left(i,k\right)}-g_t^{\left(k,cpp,norm\right)}\right|}{\left|\left.x_t^{\left(i,k\right)}\right|+\left|g_t^{\left(k,cpp,norm\right)}\right.\right|}(13)$

If $x_t^{\left(i,k\right)}=0and{g}_t^{\left(k,cpp,norm\right)}=0,\text{the\hspace{0.17em}item\hspace{0.17em}in\hspace{0.17em}the\hspace{0.17em}sum\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}right\hspace{0.17em}equation\hspace{0.17em}will\hspace{0.17em}be\hspace{0.17em}skipped}$ and n will be replaced with $n-1$.

3.4 Contribution of deviation of critical process parameters from golden batch profile

Emphasizing the importance of critical process parameters, we elucidate their role in contributing to deviations and the root cause of anomalies. Understanding these contributions is key to effective root cause analysis.

After calculating the deviations for all Critical Quality Attributes (CQAs), we will define the contribution to the deviation of the golden batch profile for the j^th CQA (j = 1, 2, …, J) as follows:

${Contribution}^{\left(j,cpp\right)}=\frac{{Deviation}^{\left(j,cqa\right)}}{{\displaystyle \sum _{j=1}^J}{Deviation}^{\left(j,cqa\right)}}(14)$

After computing the deviations for all CPPs, we will delineate the contribution to the deviation of the golden batch profile in the following manner:

${Contribution}^{\left(k,cpp\right)}=\frac{{Deviation}^{\left(k,cpp\right)}}{{\displaystyle \sum _{k=1}^K}{Deviation}^{\left(k,cpp\right)}}(15)$

3.5 Upper bound and lower bound of the golden batch profile

We generated the golden batch time series for the critical quality attributes and critical process parameters, such as penicillin concentration, temperature, by considering all selected normal operational batches (e.g., batch 61–90). For a critical quality attribute or critical process parameter, the bounds were determined using the normal distribution, ensuring that 99.7% of the data observed at sample time t falls within 3 standard deviations (σ_t) of the mean (μ_t) at that sample time. The upper bound is calculated as μ_t + 3σ_t, and the lower bound is calculated as μ_t − 3σ_t.

The upper and lower bounds at sample time “t” within the golden batch serve as indicators for detecting anomalies in the upcoming batch, initiating a quality anomaly alert. Subsequently, these bounds can be utilized to conduct a detailed analysis for each critical process parameter, pinpointing the occurrence, location, and nature of the root cause.

3.6 Root cause analysis method

We provide a detailed account of our root cause analysis method, encompassing the use of the golden batch profile, deviation from the golden batch for critical quality attributes, and contribution of deviation from the golden batch for critical process parameters. This section offers transparency into the analytical tools and processes employed.

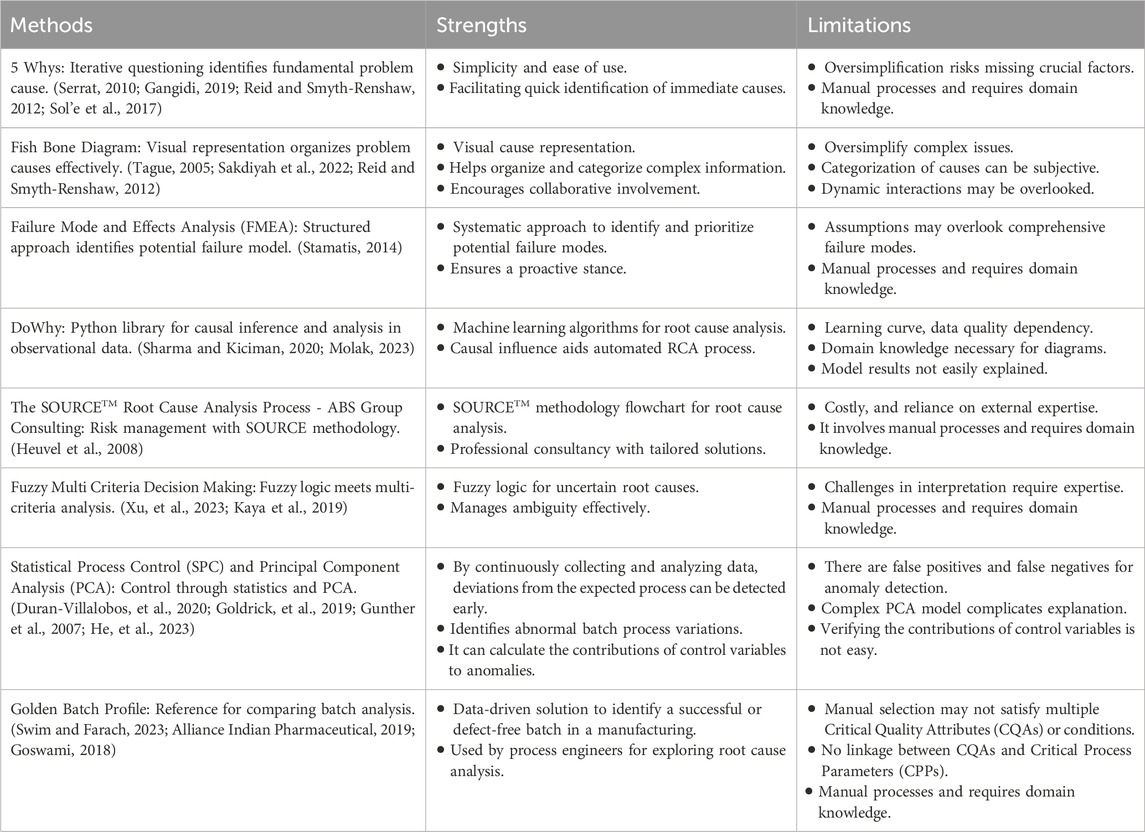
In the flow diagram depicted in Figure 1, the process for conducting root cause analysis on the golden batch profile unfolds as follows:

1) Establish a golden batch profile to embody the idealized notion of routine variation. This helps construct a controlled process with consistent outcomes over time. Also, see Sections 3.1–3.6.

2) Monitor the industrial batch system for exceptional variations in Critical Quality Attributes (CQA) or key quality Key Performance Indicators (KPI) to detect and quantify variation. If a process is identified as out of control in the Figure 1 flow diagram, it may lead to unpredictability over time. Additional details are available in Figure 2.

3) Analyze the contribution of Critical Process Parameters (CPPs) to identify trending or out-of-specification CPPs. For a more in-depth understanding, refer to Figure 3.

4) Delve into the CPP with the highest contribution to determine when, where, and how the root cause analysis occurred (refer to Figure). Further details can be found in Figure 4.

Figure 1

Figure 1. Illustrates the framework of root cause analysis guided by the golden batch profile.

Figure 2

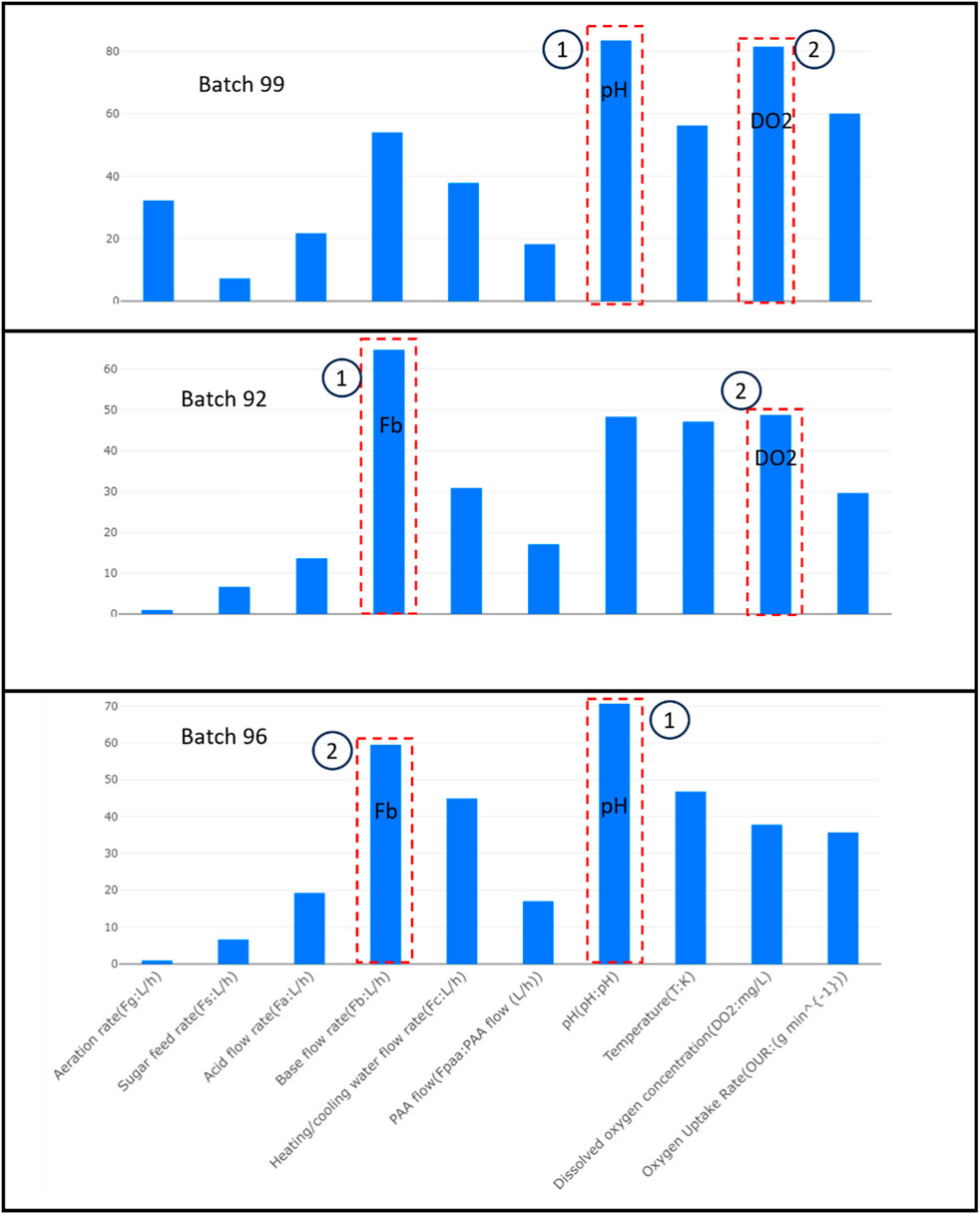
Figure 2. Comparison of penicillin production deviation across batches 99, 92, and 96 against golden batch standard.

Figure 3

Figure 3. Key contributors to deviation in penicillin production for batches 99, 92, and 96.

Figure 4

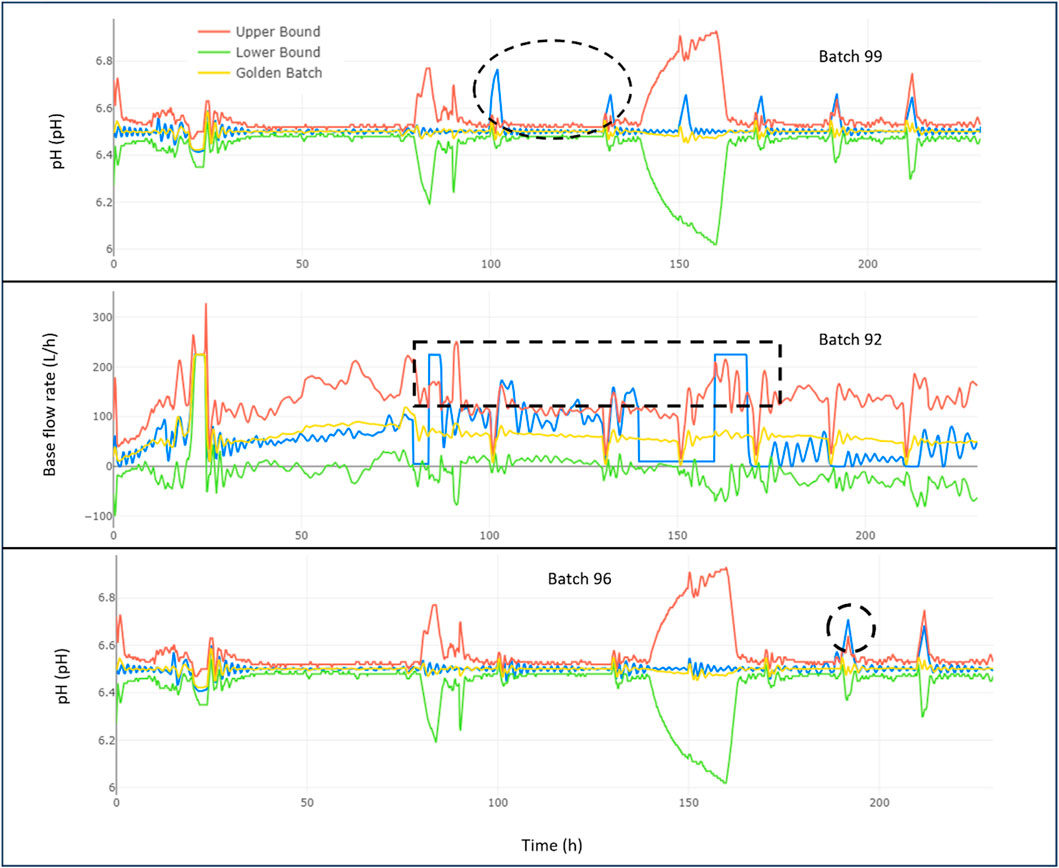
Figure 4. Analysis of topmost significant contributor to deviations over time for penicillin production batches 99, 92, and 96.

4 Experiment and results

4.1 Overview of IndPenSim data

The IndPenSim dataset comprises a comprehensive collection of time-series industrial process data, consisting of 100 distinct batches, each lasting approximately 230 h. Measurements were recorded at 12-min intervals, resulting in 113,934 observations across all batches. To ensure alignment for analysis purposes, each batch initiates at 0.2 h.

Within this dataset, 33 batches have been identified as unhealthy, characterized by penicillin concentration yields falling below the target threshold of 20 g/L. These specific batches are numbered 3, 4, 6, 9, 10, 18, 19, 24, 25, 28, 30, 33, 34, 36, 37, 40, 42, 43, 44, 45, 47, 49, 51, 54, 59, 60, 91, 92, 94, 95, 97, 99, and 100. Additionally, 67 batches, numbered 1, 2, 5, 7, 8, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 26, 27, 29, 31, 32, 35, 38, 39, 41, 46, 48, 50, 52, 53, 55, 56, 57, 58, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 93, 96, and 98, are labeled as healthy. To create the golden batch, we first determine the duration with the highest frequency (1,150) and subsequently truncate the healthy batches with a duration length greater than 1,150. This is done to add more consistency to the trend analysis.

4.2 Creation of the golden batch

For the IndPenSim dataset mentioned above, utilizing Equations 1–15, we construct the golden batch profile. We elaborate on the process of establishing a benchmark for normal operational conditions. This ensures a standardized reference for subsequent analyses.

4.3 Root cause analysis for batches with anomalies

We will utilize our golden batch profile to examine the problematic batches 92 and 99, identifying the root cause and determining when, where, and how it occurred. Additionally, we will explore the healthy batch 96 to investigate any deviations from the golden batch.

Figure 2 presents a comparison of penicillin production across three different batches, numbered 99, 92, and 96, against a Golden Batch profile, which serves as a quality standard. The golden batch is represented by the orange line in each graph, while the individual production batches are depicted in blue. Batch 99 shows the earliest and most considerable deviation from the golden standard starting around 100 h into production, resulting in a significant 54.03% overall deviation. Batch 92 begins to diverge from the expected results much later, around 160 h, and exhibits a lower overall deviation of 24.05%, indicating a closer adherence to the golden batch but still falling short of the quality benchmark. The last healthy batch, batch 96, exhibits the least deviation, starting around 180 h, with a final deviation of just 11.52%. Although this batch manages to stay within the acceptable quality threshold by the end of its production cycle, it does exhibit some minor inconsistencies when compared to the golden batch. These deviations are crucial for understanding the production quality and consistency of penicillin batches.

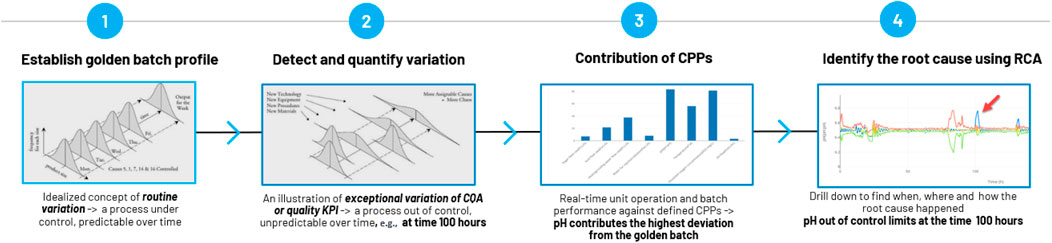
To understand the process variables that have the most significant contribution to these deviations, we present the contribution plots for the variables.

Figure 3 illustrates the main factors that affect the production quality of penicillin for three different batches when compared to the ideal production scenario (golden batch). In batch 99, the pH level and the amount of dissolved oxygen were the biggest issues, contributing 85 and 80 of the deviation, respectively. This indicates that these areas need to be closely examined to determine why they are so far off from the desired standard. For batch 92, the base flow rate and the amount of dissolved oxygen were the primary concerns, with contributions of 65 and 48. This suggests that adjustments in these parameters could bring the batch closer to the golden batch quality. Finally, batch 96, which did meet the overall quality threshold, still had notable variances in pH and base flow rate, at 70 and 60 contributions to deviation. Even though batch 96 was within the acceptable range, understanding why these deviations occurred is important for maintaining consistent quality in future batches.

Focusing on the top two contributors for each batch, we evaluate the trend of the batch with respect to the golden batch statistics. This analysis is critical for operators to pinpoint and rectify issues in the penicillin production process.

Figure 4 shows the trajectory over time of the top key variable, i.e., pH, base flow rate, and pH which significantly impact the quality of penicillin produced in batches 99, 92, and 96 respectively. For Batch 99, we notice that the pH levels (depicted in blue) rise well above the acceptable range (indicated by the red line) at approximately 100 and 135 h into the process. These surges are linked to the batch failing to meet the required penicillin concentration standards. The golden batch, which represents the target performance, is marked by an orange line, with the acceptable upper and lower limit shown in red and green.

In Batch 92, the base flow rate (also in blue) exceeds the upper limit of the golden batch (red line) multiple times between 80 and 180 h. These excessive rates are likely the reason why this batch’s penicillin quality was below the desired threshold. With this information, the production team can investigate specific stages in the manufacturing process that may be causing these deviations.

Lastly, Batch 96 (also in blue) exhibits a smaller, yet noticeable peak in pH above the golden batch’s upper bound around 190 h. Although this did not significantly affect the batch’s quality, identifying and understanding even these minor deviations can help refine the production process for future batches, ensuring a consistently high-quality product. This detailed tracking allows operators to focus on process improvement and maintain standards within the defined limits.

Figure 5 shows the trajectory over time of the second most Significant contributor to deviation for batches 99, 92, and 96. For Batch 99, it is clear that the oxygen levels (blue line) dipped below the minimum required (green line) quite early in the process, around 20 h, which may have caused the penicillin to be out of the desired specification. This is a matter of concern and could be a key area to investigate for quality improvement. For Batch 92, the oxygen levels slightly exceeded the golden batch’s maximum limit (red line) for a brief period at around 160 h. However, the deviation was minor and did not majorly impact the batch’s overall quality. Similarly, for Batch 96, the base flow rate remained mostly within the acceptable range defined by the golden batch, indicating that the process was well-controlled with respect to the base flow rate levels.

Figure 5

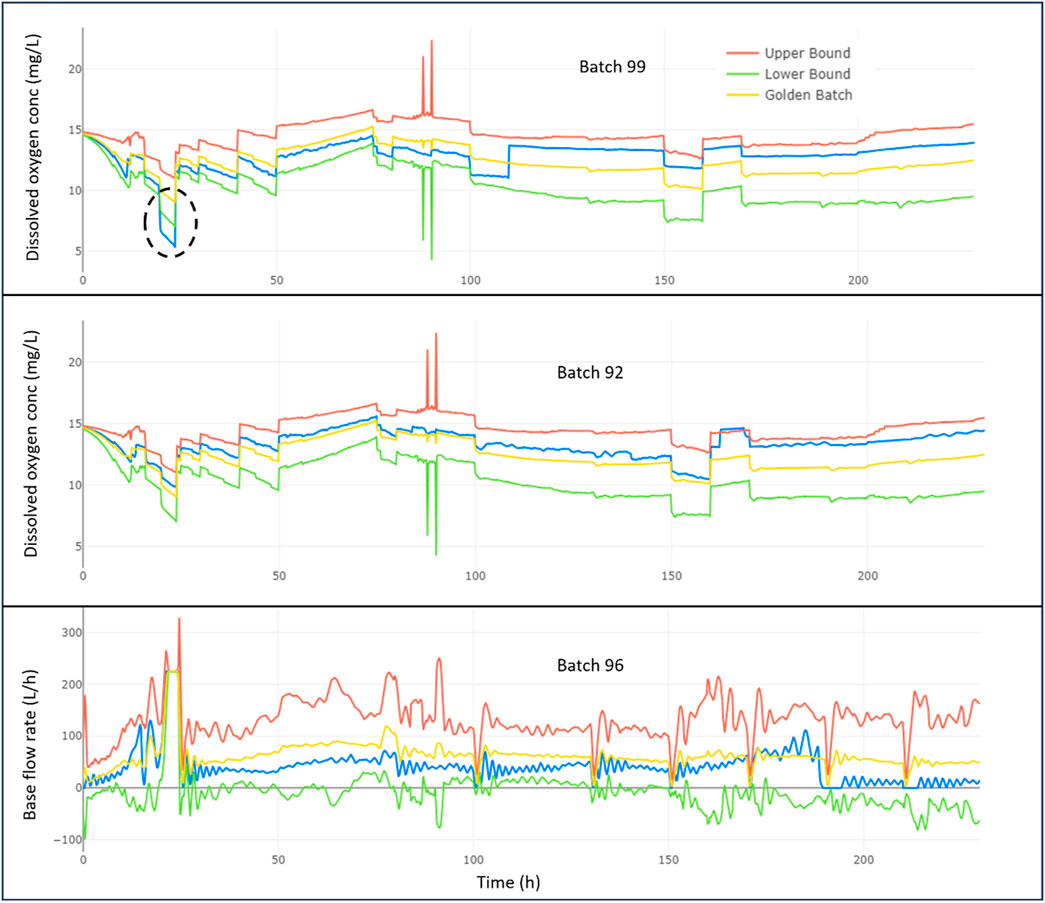
Figure 5. Analysis of second most Significant contributor to deviations over time for penicillin production batches 99, 92, and 96.

Since Batches 92 and 96 showed deviations that were mostly within the target range for their second most significant variable, it suggests that the production team should prioritize their efforts on investigating and optimizing the most significant contributing factor.

The above analysis uses a golden batch profile to investigate deviations in problematic batches 92, 99, and the healthy batch 96. Batch 99 deviates significantly early on, while Batch 92 shows a later but still considerable deviation. The healthy batch 96 exhibits the least deviation. Key contributors are identified for each batch, and the trajectory over time reveals critical points. Focusing on the most significant contributors is recommended for process improvement, with batches 92 and 96 showing deviations mostly within the target range for their second most significant variable.

4.4 Comparison with the existing methods

In Table 1, we list the strengths and limitations of current RCA methods. This section provides deeper dive in comparing Statistical Process Control (SPC) and Principal Component Analysis (PCA) methods with our solution (Gunther et al., 2007; Goldrick, et al., 2019; Duran-Villalobos, et al., 2020; Banner et al., 2021; Goldrick et al., 2014; Nomikos and MacGregor, 1995).

In the batch processing industry, analyzing and determining anomalies in a batch is a long and redundant process, especially executed manually and with significant gaps between test points. These anomaly detection processes rely on PCA-based Hotelling (T²) and Squared Prediction Error (SPE, also known as Q), comparing these KPIs with predetermined thresholds to detect anomalies during the batch process (Gunther et al., 2006, 2007; Goldrick, et al., 2019; Duran-Villalobos, et al., 2020). However, those approaches tend to produce some false positives and false negatives, which reduces anomaly detection accuracy (Gunther et al., 2007; Duran-Villalobos, et al., 2020). These limitations, along with the complexity of their method, made it challenging to explain their model results to operators for root cause analysis.

In contrast, our proposed methodology, centered around the golden batch, offers unique strengths. By aggregating around multiple good batches to identify the golden batch profile, we create a representative profile of the normal batch process and transparency into the analytical processes. Additionally, by using operator-defined CQAs and CPPs, normalizing the data, and calculating deviations, we provide only relevant insights that can quickly help operators identify the root cause of faults in the batch process. Finally, we calculate the contribution from each parameter to the calculated deviation, and demonstrate the significance of CPPs in root cause analysis.

5 Conclusion

The paper introduces a comprehensive methodology centered around the Golden Batch Profile, serving as a benchmark for identifying deviations and root causes in subsequent industrial batches. This involves defining time series for CQAs and CPPs, normalizing the data, and calculating deviations. The contribution of each parameter to the deviation is analyzed, emphasizing the significance of CPPs in root cause analysis. The detailed root cause analysis method provides transparency into the analytical tools and processes. Additionally, the integration of an innovative data-driven golden batch model and automated root cause analysis is highlighted for its potential to significantly reduce manual process time. The automated calculation of top contributions of deviation, especially in cases of the loss of a critical quality attribute, proves valuable. Moreover, the utilization of deviation of critical process parameters for anomaly detection expedites root cause identification, pinpointing where, when, and how the root cause occurs occurred.

The paper offers a robust approach for analyzing industrial batch processes, utilizing innovative concepts, and demonstrating effectiveness through the application to the IndPenSim dataset. By introducing golden batch modeling and leveraging advanced analytical techniques, we contribute to the ongoing efforts to enhance the reliability and efficiency of bioprocess monitoring and anomaly correction.

Although this research is based on rigorously-designed and well-controlled simulated data (Goldrick, et al., 2019) to establish the initial foundational understanding, we fully recognize the importance of validating our approach with real-world data, therefore, we are in the process of securing partnerships with industry collaborators to obtain real customer datasets. In the future work, we will carry out comprehensive experimental tests with non-simulated data and verify our method for real-world scenarios. We will publish these results in subsequent studies, providing a comprehensive evaluation of our method’s performance in practical applications.

Finally, in this work, we highlighted a simplistic approach of truncating the batch duration outside the batch duration with the highest frequency to bring batches into alignment before applying our proposed model. While this approach proved sufficient in our study, in future research we intend to investigate more established batch alignment methodologies such as Dynamic Time Warping (DTW) and Indicator Variable techniques (Brunner, et al., 2021; Chin-Chia Michael Yeh et al., 2019). DTW expands, contracts, or translates the time axis of the datasets in such a way that the shape of the variable trajectory is largely preserved, landmarks coincide in time and all datasets have a uniform number of measuring points. On the other hand, Indicator Variable techniques replace the time scale with an alternative scale, the indicator variable. This indicator variable can be either a real (physical) process variable or an estimated process progress, often referred to as a maturity index or percentage of completion.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://data.mendeley.com/datasets/pdnjz7zz5x/1.

Author contributions

DL: Writing–original draft, Writing–review and editing. MH: Writing–original draft, Writing–review and editing. JD: Writing–original draft, Writing–review and editing. FLS: Writing–original draft, Writing–review and editing. FM: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We would like to express our sincere gratitude to Rockwell Automation for their invaluable contributions and support, which greatly enriched the content and quality of this paper.

Conflict of interest

Authors DL, MH, JD, FLS and FM were employed by Rockwell Automation.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, T., Ghosh, S., Bansal, C., Zimmermann, T., Zhang, X., and Rajmohan, S. (2023). Recommending root-cause and mitigation steps for cloud incidents using large language models. arXiv:2301.03797. doi:10.1109/ICSE48619.2023.00149

CrossRef Full Text | Google Scholar

Alliance Indian Pharmaceutical (2019). Investigations for non-conformities guideline. Alliance Indian Pharm., 1–96.

Google Scholar

Banner, M., Alosert, H., Spencer, C., Cheeks, M., Farid, S. S., Thomas, M., et al. (2021). A decade in review: use of data analytics within the biopharmaceutical sector. Curr. Opin. Chem. Eng. 34, 100758. doi:10.1016/j.coche.2021.100758

CrossRef Full Text | Google Scholar

Brunner, V., Siegl, M., Geier, D., and Becker, T. (2021). Challenges in the development of soft sensors for bioprocesses: a critical review. Front. Bioeng. Biotechnol. 9, 722202–722221. doi:10.3389/fbioe.2021.722202

PubMed Abstract | CrossRef Full Text | Google Scholar

Chien, C.-F., and Chuang, S.-C. (2014). A framework for root cause detection of sub-batch processing system for semiconductor manufacturing big data analytics. IEEE Trans. Semicond. Manuf. 27, 475–488. doi:10.1109/tsm.2014.2356555

CrossRef Full Text | Google Scholar

Chin-Chia Michael Yeh, C. M. Y., Zhu, Y., Dau, H. A., Darvishzadeh, A., Noskov, M., and Keogh, E. (2019). “Online amnestic DTW to allow real-time golden batch monitoring,” in KDD '19: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data MiningJuly (Anchorage, AK: ACM), 2604–2612.

CrossRef Full Text | Google Scholar

Duran-Villalobos, C. A., Goldrick, S., and Lennox, B. (2020). Multivariate statistical process control of an industrial-scale fed-batch simulator. Comput. and Chem. Eng. 132, 106620. doi:10.1016/j.compchemeng.2019.106620

CrossRef Full Text | Google Scholar

Gangidi, P. (2019). A systematic approach to root cause analysis using 3 × 5 why’s technique. Int. J. Lean Six Sigma 10, 295–310. doi:10.1108/ijlss-10-2017-0114

CrossRef Full Text | Google Scholar

Goldrick, S., Duran-Villalobos, C. A., Jankauskas, K., Lovett, D., Farid, S. S., and Lennox, B. (2019). Modern day monitoring and control challenges outlined on an industrial-scale benchmark fermentation process. Comput. and Chem. Eng. 130, 106471. doi:10.1016/j.compchemeng.2019.05.037

CrossRef Full Text | Google Scholar

Goldrick, S., Mercer, E., Montague, G., Lovett, D., and Lennox, B. (2014). Control of an industrial scale bioreactor using a PAT analyser. IFAC Proc. 47, 6222–6227. doi:10.3182/20140824-6-za-1003.02589

CrossRef Full Text | Google Scholar

Goswami, M. D. (2018). Golden batch identification using statistical tools as a part of asset performance management. Int. J. Comput. Sci. And Technol. 9 (4), 69–72.

Google Scholar

Gunther, J. C., Conner, J. S., and Seborg, D. E. (2007). Fault detection and diagnosis in an industrial fed-batch cell culture process. Biotechnol. Prog. 23, 851–857. doi:10.1002/bp070063m

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunther, J. C., Seborg, D. E., and Baclaski, J. (2006). “Fault detection and diagnosis in industrial fed-batch fermentation,” in American Control Conference. IEEE, 6.

CrossRef Full Text | Google Scholar

He, F., Wang, C., and Fan, S.-K. S. (2019). Fault detection and root cause analysis of a batch process via novel nonlinear dissimilarity and comparative granger causality analysis. Industrial and Eng. Chem. Res. 58, 21842–21854. doi:10.1021/acs.iecr.9b04471

CrossRef Full Text | Google Scholar

He, M., Petering, M., LaCasse, P., Otieno, W., and Maturana, F. (2023). Learning with supervised data for anomaly detection in smart manufacturing. Int. J. Comput. Integr. Manuf. 36, 1331–1344. doi:10.1080/0951192x.2023.2177747

CrossRef Full Text | Google Scholar

Heher, Y. K. (2017). A brief guide to root cause analysis. Cancer Cytopathol. 125, 79–82. doi:10.1002/cncy.21819

PubMed Abstract | CrossRef Full Text | Google Scholar

Heuvel, L. N. V., Lorenzo, D. K., and Hanson, W. E. (2008). Root cause analysis handbook: a guide to efficient and effective incident management. 3rd Edition. Incorporated: Rothstein Associates.

Google Scholar

Hong, J. jin, Zhang, J., and Morris, J. (2011). Fault localization in batch processes through progressive principal component analysis modeling. Industrial and Eng. Chem. Res. 50, 8153–8162. doi:10.1021/ie1025387

CrossRef Full Text | Google Scholar

Hornea, S., Vera, M. D., Nagavelli, L. R., Sayeed, V. A., Heckman, L., Johnson, D., et al. (2023). Regulatory experiences with root causes and risk factors for nitrosamine impurities in pharmaceuticals. J. Pharm. Sci. 112, 1166–1182. doi:10.1016/j.xphs.2022.12.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaya, I., Çolak, M., and Terzi, F. (2019). A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 24, 207–228. doi:10.1016/j.esr.2019.03.003

CrossRef Full Text | Google Scholar

Langer, E. S. (2008). Biotech facilities average a batch failure every 40.6 weeks. BioProcess Int., 28–29.

Google Scholar

Menegozzo, G., Dall’Alba, D., and Fiorini, P. (2022). CIPCaD-bench: continuous industrial process datasets for benchmarking causal discovery method. arXiv:2208.01529. doi:10.1109/CASE49997.2022.9926420

CrossRef Full Text | Google Scholar

Molak, A. (2023). “Causal inference and discovery in Python – machine learning and pearlian perspective,” in Birmingham, B3 2PB. UK: Packt Publishing.

Google Scholar

Nomikos, P., and MacGregor, J. F. (1995). Multivariate SPC charts for monitoring batch processes. Technometrics 37, 41–59. doi:10.1080/00401706.1995.10485888

CrossRef Full Text | Google Scholar

Oliveira, E. E., Miguéis, V. L., and Borges, J. L. (2023). Automatic root cause analysis in manufacturing: an overview and conceptualization. J. Intelligent Manuf. 34, 2061–2078. doi:10.1007/s10845-022-01914-3

CrossRef Full Text | Google Scholar

Papageorgiou, K., Theodosiou, T., Rapti, A., Papageorgiou, E. I. E. I., Dimitriou, N., Tzovaras, D., et al. (2022). A systematic review on machine learning methods for root cause analysis towards zero-defect manufacturing. Front. Manuf. Technol. 2, 1–16. doi:10.3389/fmtec.2022.972712

CrossRef Full Text | Google Scholar

Reid, I., and Smyth-Renshaw, J. (2012). Exploring the fundamentals of root cause analysis: are we asking the right questions in defining the problem? Qual. Reliab. Eng. Int. 28, 535–545. doi:10.1002/qre.1435

CrossRef Full Text | Google Scholar

Rockwell Automation (2023). Automation Fair 2023. November. Available at: https://www.automation.com/en-us/events/automation-fair-2023.

Google Scholar

Rooney, J., and Heuvel, L. (2004). Root cause analysis for beginners. Qual. Prog. 37 (7), 45–53.

Google Scholar

Sakdiyah, S. H., Eltivia, N., and Afandi, A. (2022). Root cause analysis using fishbone diagram: company management decision making. J. Appl. Bus. Tax. Econ. Res. 1, 566–576. doi:10.54408/jabter.v1i6.103

CrossRef Full Text | Google Scholar

Serrat, O. (2010). The five ways technique. Washington, DC: Asian Development Bank.

Google Scholar

Sharma, A., and Kiciman, E. (2020). DoWhy: an end-to-end library for causal inference. arXiv:2011.04216 [stat.ME]. doi:10.48550/arXiv.2011.04216

CrossRef Full Text | Google Scholar

Shook, J. (2009). Toyota’s secret: the A3 report. MIT Sloan Management Review Summer Research Feature.

Google Scholar

Sol’e, M., Munt’es-Mulero, V., Rana, A. I., and Estrada, G. (2017). Survey on models and techniques for root-cause. arXiv:1701.08546. doi:10.48550/arXiv.1701.08546

CrossRef Full Text | Google Scholar

Stamatis, D. H. (2014). The ASQ pocket guide to failure Mode and Effect analysis (FMEA). 1st edition. Amer Society for Quality.

Google Scholar

Su, Y., and Yu, F. (2016). “Data mining applications for finding golden batch benchmarks and optimizing batch process control,” in 2016 12th World Congress on Intelligent Control and Automation (WCICA). Guilin, China: IEEE, 1058–1063.

CrossRef Full Text | Google Scholar

Swim, R., and Farach, R. (2023). “Achieving the ‘golden batch’ every time,” in Processing solutions for process manufacturers. Available at: https://www.processingmagazine.com/process-control-automation/article/53074467/achieving-the-golden-batch-every-time.

Google Scholar

Tague, N. R. (2005). The quality toolbox. Second Edition. ASQ Quality Press.

Google Scholar

Westerhuis, J. A., Gurden, S. P., and Smilde, A. K. (2000). Generalized contribution plots in multivariate statistical process monitoring. Chemom. intelligent laboratory Syst. 51, 95–114. doi:10.1016/s0169-7439(00)00062-9

CrossRef Full Text | Google Scholar

White, S. K. (2022). What is root cause analysis? A proactive approach to change management. CIO. Available at: https://www.cio.com/article/350219/what-is-root-cause-analysis-a-proactive-approach-to-change-management.html.

Google Scholar

Xu, S., Nupur, R., Kannan, D., Sharma, R., Kumar, P., Sharma, S., et al. (2023). An integrated fuzzy MCDM approach for manufacturing process improvement in MSMEs. Ann. Operations Res. 322, 1037–1073. doi:10.1007/s10479-022-05093-5

CrossRef Full Text | Google Scholar

Yan, B., Fang, Z., Shen, L., and Qu, H. (2015). Root cause analysis of quality defects using HPLC–MS fingerprint knowledgebase for batch-to-batch quality control of herbal drugs. Phytochem. Anal. 26, 261–268. doi:10.1002/pca.2559

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeh, C.-C. M., Zhu, Y., Hoang, A. D., Darvishzadeh, A., Noskov, M., and Koegh, E. (2019). Online amnestic dtw to allow real-time golden batch monitoring. Proc. 25th ACM SIGKDD Int. Conf. Knowl. Discov. and Data Min., 2604–2612. doi:10.1145/3292500.333065

CrossRef Full Text | Google Scholar