Parallel and scalable AI in HPC systems for CFD applications and beyond

This manuscript presents the library AI4HPC with its architecture and components. The library enables large-scale trainings of AI models on High-Performance Computing systems. It addresses challenges in handling non-uniform datasets through data manipulation routines, model complexity through specialized ML architectures, scalability through extensive code optimizations that augment performance, HyperParameter Optimization (HPO), and performance monitoring. The scalability of the library is demonstrated by strong scaling experiments on up to 3,664 Graphical Processing Units (GPUs) resulting in a scaling efficiency of 96%, using the performance on 1 node as baseline. Furthermore, code optimizations and communication/computation bottlenecks are discussed for training a neural network on an actuated Turbulent Boundary Layer (TBL) simulation dataset (8.3 TB) on the HPC system JURECA at the Jülich Supercomputing Centre. The distributed training approach significantly influences the accuracy, which can be drastically compromised by varying mini-batch sizes. Therefore, AI4HPC implements learning rate scaling and adaptive summation algorithms, which are tested and evaluated in this work. For the TBL use case, results scaled up to 64 workers are shown. A further increase in the number of workers causes an additional overhead due to too small dataset samples per worker. Finally, the library is applied for the reconstruction of TBL flows with a convolutional autoencoder-based architecture and a diffusion model. In case of the autoencoder, a modal decomposition shows that the network provides accurate reconstructions of the underlying field and achieves a mean drag prediction error of ≈5%. With the diffusion model, a reconstruction error of ≈4% is achieved when super-resolution is applied to 5-fold coarsened velocity fields. The AI4HPC library is agnostic to the underlying network and can be adapted across various scientific and technical disciplines.

1 Introduction

Artificial Intelligence (AI) has excelled tremendously in various scientific and technical disciplines, especially in the last decade with the advent of large-scale data and computing resources. In disciplines such as Computational Fluid Dynamics (CFD), conventional numerical methods are challenging to develop and computationally intensive, specifically if they want to make use of novel hardware architectures and fine-grained simulations are required. In this regard, AI-based models, for instance Neural Networks (NNs), have the potential to augment and accelerate solving such problems. NNs have been applied to CFD problems in various areas from heat transfer to aeronautics (Brunton et al., 2020; Scalabrin et al., 2006; Faller and Schreck, 1996), in turbulence modeling (Duraisamy, 2021; Ling et al., 2016; Maulik et al., 2019), and also in cases with complex flow physics. One of the applications is to augment the low-fidelity numerical models by Machine Learning (ML) models to achieve higher accuracy with a lower computational time compared to high-fidelity models—the work of Kochkov et al. (2021) provides a good example of this. For instance, an augmentation can be achieved by replacing or accelerating the iterative solvers employed in the physical solver (Obiols-Sales et al., 2020). In this regard, use of ML in hybrid models to provide error correction to under-resolved physical solvers is especially interesting for engineering problems (Um et al., 2020; Sirignano et al., 2020). The hybrid solver achieves computational savings while improving the simulation accuracy.

However, training AI models for such applications requires processing of large amounts of data and potentially feeding these data into large NN architectures. For example, a single CFD simulation with a computational mesh consisting of 512³ elements using only single precision representation of the flow variables can easily result in more than 500 MB of storage per variable and time step. Large-scale simulations in such domain sciences already exceed terabytes of data, such as the actuated Turbulent Boundary Layer (TBL) dataset employed in this study.¹ Furthermore, the models are also progressively increasing in size, especially with the large uptake in adoption of Large Language Model (LLM)-based architectures, where parameters are already in the range of hundreds of billions. High-Performance Computing (HPC) facilities provide the required infrastructure for training such large-scale models, especially with accelerators suitable for AI such as Graphical Processing Units (GPUs).

Efforts toward the development of AI frameworks targeted for HPC systems can already be found in literature with many of them addressing the implementation of workflows on HPC systems. In Lee et al. (2021), the authors develop scalable AI and HPC software tools able to execute distinct workflows concurrently, which is used to accelerate and enhance drug design in a hybrid simulation- and AI-based methodology. This tool exploits HPC systems and is based on a building blocks concept (Turilli et al., 2019). Libraries for the execution of workflows that couple large-scale simulations with an ML component on multi-GPU systems have also started emerging (Peterson et al., 2022) along with a support for online training (Meyer et al., 2023). The applicability of such libraries has already been demonstrated for various scientific disciplines, e.g., in molecular dynamics (Brace et al., 2022) and plasma physics (Stiller et al., 2022). These developments provide important contributions toward scaling and porting AI frameworks on HPC systems. However, migration of such workflows to HPC infrastructures is still tedious and requires significant development efforts.

In particular, the deployment of AI models on HPC systems requires many changes to a standard baseline implementation, e.g., to a code that runs serially on a local machine. The main challenges in this context are:

1. The serial code has to be distributed to enable exploitation of an HPC cluster. For distributed training, there exist different open-source frameworks that implement various levels of multi-worker parallelism in the form of model, pipeline and/or data parallelism (Li et al., 2020; Sergeev and Del Balso, 2018; Rasley et al., 2020; Götz et al., 2020). The performance and scalability of these frameworks may vary depending on the system and the NN architecture. A common library to test these and other community-added frameworks, which is easily-deployable, could largely benefit the wider AI and scientific community.

2. In addition to the variety of hardware architecture, the software configurations of HPC systems vary widely in terms of library and module versions. The AI user community requires extensive knowledge of the underlying software and system-specific hardware configurations to submit jobs successfully. This can significantly limit the use of HPC in the AI community. A library that automates the generation of HPC-specific job scripts to ease the access to and usage of such systems could be very useful for the wider community of users.

3. For the next generation of large-scale AI models, achieving optimized training performance on HPC systems is essential. The efficient utilization of an HPC system can be significantly improved by code optimization. Furthermore, training on large datasets with a high throughput is non-trivial and requires specific configurations to obtain good accuracy. Automating the implementation of these optimizations using only a single library that can interface different backends would make scalable and efficient algorithms available to all users.

To address these issues, this manuscript introduces the AI4HPC library,² which facilitates the efficient use of HPC systems by addressing all the identified challenges. The library is developed particularly for the CFD community. The developments are, however, generic for application in other scientific and technical domains. The innovative aspect of this library lies in the provision of a single solution to all the challenges 1–3, which are commonly encountered when scaling AI workflows to HPC systems.

This work analyzes the performance of AI4HPC using a large open-source CFD dataset to achieve dimensionality reduction and performing super-resolution on an actuated TBL flow problem. Large dataset sizes pose challenges with respect to associated mini-batch sizes, which may compromise the accuracy of the trained model. This can be mitigated with various strategies, such as learning-rate (Goyal et al., 2017) scaling and adaptive summation (Maleki et al., 2020), which are discussed in Section 3.2. Furthermore, scaling to a large number of workers using a relatively small dataset leads to lower GPU utilization and results in a communication/computation bottleneck. These aspects are discussed in detail and the solutions offered by AI4HPC are presented.

IN addition, first, the accuracy of the library is demonstrated on a dimensionality reduction network for the TBL CFD use case. Many popular compression algorithms, such as Proper Orthogonal Decomposition (POD) (Berkooz et al., 1993), Dynamic Mode Decomposition (DMD) (Schmid, 2010), Galerkin-projection-based methods (Carlberg et al., 2013), and system-identification-based auto-regressive models (Raveh, 2004; Sarma and Dwight, 2017) have been proposed in fluid dynamics. Among these methods, the model decomposition techniques such as POD and DMD are linear and are widely used in post-processing (Taira et al., 2017), while Galerkin projection-based POD can produce nonlinear evolution (Csala et al., 2022), but are intrusive in nature. Although autoregressive techniques are non-intrusive, high non-linearity impacts generalizability of the models. In this regard, deep NN-based models are known to exhibit high nonlinearity, making them suitable for application in fluid flows (Fu et al., 2023) which are complex and inherently non-linear in nature. In particular, convolutions can potentially learn both small- and large-scale structures through the kernel operations. Convolutional AutoEncoders (CAEs) have already been successful in extracting information from 3-D data (Wang et al., 2016). In this study, AI4HPC is employed to train a CAE-Neural Network (CAE-NN) to obtain an efficient and accurate dimensionality reduction model for the application to an actuated TBL flow case. The objective of the TBL study in Albers et al. (2019) is to find the actuation parameter configuration that maximizes two Quantities of Interest (QoIs), the drag reduction ΔC_d and the net power savings P_net. Hence, it is desirable that the trained CAE is able to reconstruct these physical quantities obtained by varying the actuation parameters for the TBL. These two QoIs are predicted and their reconstruction from the compressed latent space is enabled by coupling the CAE-NN to a novel, unique architecture of a regression-based network, named CAE-Prediction Network (CAE-PN).

A second application case shown in this manuscript is on the development of a super-resolution network (SRN) with a diffusion model to improve approximations from low-resolution CFD fields. A comprehensive review on application of SRN for fluid flows can be found in Fukami et al. (2023). Various NN-based methods have been explored in CFD for this task, including, but not limited to cycle-consistent adversarial Network known as CycleGAN (Kim et al., 2021), U-Net model based on Convolutional Neural Network (CNN) (Pant and Farimani, 2021), and with more recent networks such as diffusion-based models (Shu et al., 2023). In this study, a novel Convolutional Defiltering Model (CDM), based on the Diffusion Probability Model (DPM) is developed and applied to the TBL dataset. The application of this network is envisioned towards improving the approximations provided by Wall-Modeled Large Eddy Simulation (WMLES). In this manuscript, the super-resolution performance of CDM is evaluated by quantifying its ability to provide accurate reconstructions even with large filtering widths, through the use of the AI4HPC library.

The training dataset of the actuated TBL is generated using a high-fidelity Large Eddy Simulation (LES) approach with a sinusoidally moving geometry to actuate the TBL. Actuation parameters steer the movement of the geometry (Albers et al., 2019) and the simulations are carried out with the simulation software m-AIA code³, developed at RWTH Aachen University. The code is an extended version of the Zonal Flow Solver (Lintermann et al., 2020). The dataset size is ~8.3 TB. Through the TBL use case, the capabilities of AI4HPC are demonstrated in terms of data manipulation routines, support for multiple distributed backends and custom optimizations for efficient training on HPC systems, and through an intensive investigation of the performance of the CAEs and CDM on this dataset. The use case demonstrates that AI4HPC addresses the challenges 1 and 3 identified above. In terms of challenge 2, the library is already configured to directly run on several existing HPC systems, which are detailed in Section 2.

The manuscript is structured as follows: Section 2 introduces the details of the AI4HPC library and the available modules. In Section 3, the implemented optimizations and the performance of the library applied to the TBL usecase is investigated in detail. More details on the TBL use case using the CAE and CDM are presented in Section 4. Finally, Section 5 summarizes the main conclusions of these investigations and provides recommendations for further steps.

2 Method: distributed training with AI4HPC components

Training an ML model on large datasets in serial is time consuming. Hence, parallelization methods have to be employed to yield feasible runtimes. A common parallelization strategy is to distribute the (input) dataset to multiple separate workers, e.g., based on Central Processing Units (CPUs), GPUs, or Intelligence Processing Units (IPUs), where the trainable parameters between the workers are occasionally exchanged. This Data Distributed Training (DDT) method massively reduces the training duration and has the potential to scale up to an Exascale HPC system, i.e., systems that are capable of calculating at least 10¹⁸ IEEE 754 double precision (64-bit) operations (multiplications and/or additions) per second— exaFLOP. There exist many ML frameworks that integrate the DDT approach. Four common frameworks are integrated in AI4HPC, noting that Python is chosen as the host language; the PyTorch-DDP library as part of a PyTorch package (Li et al., 2020), Horovod (Sergeev and Del Balso, 2018), HeAT (Götz et al., 2020), and DeepSpeed (Rasley et al., 2020). In AI4HPC, the PyTorch library is chosen for consistency. To a certain degree, these frameworks operate similarly, however, for instance, PyTorch-DDP⁴ and HeAT use NVIDIA's Collective Communications Library (NCCL) or Gloo by Facebook for communication, whereas Horovod and DeepSpeed rely on the Message Passing Interface (MPI) for inter-node and NCCL for intra-node communication. Moreover, each framework is optimized (slightly) differently leading to varying scaling performance and training accuracy for individual cases. This raises the interest to test different frameworks, which is provided by AI4HPC. This DDT approach from the different backends in AI4HPC distributes the LES dataset equally amongst the workers.

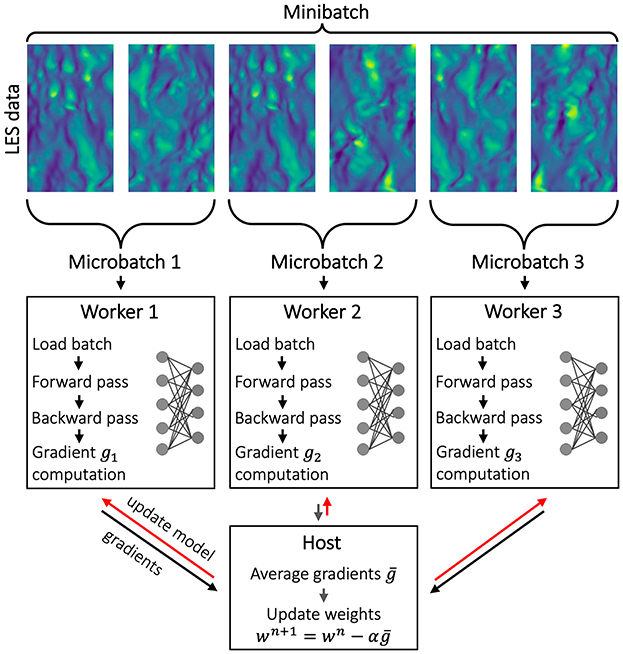
A general workflow of CAE training using the DDT approach is depicted in Figure 1. Each distributed dataset is initially transferred to a compute node and the node's host CPUs access the system's data storage to load the distributed dataset into the Random-Access Memory (RAM). The GPUs then transfer this distributed dataset from the system's RAM to their own RAM, which is local to the GPUs and optimized for specific operations, i.e., vectorizations for matrix-matrix or matrix-vector operations. For training exceptionally large datasets, this step is usually computationally expensive. A slow data transfer from disk storage to RAM, i.e., caused by CPU overhead, memory problems, and low transfer bandwidth, could potentially lead to idling GPUs and hence a waste of resources and energy.

Figure 1

Figure 1. Exemplary DDT workflow for an ML training using an LES dataset with three workers.

To train an NN, each worker works on a subset of the dataset, called the micro-batch B. In the DDT approach, the mini-batch then becomes the sum of the micro-batches across the workers. After each worker processes their respective micro-batches, the computed gradients and weights of the NN of each worker are transferred to a host worker, which is responsible for averaging the gradients and updating the weights via an AllReduce command. These quantities are transferred back to the rest of the workers, which requires worker-to-worker communication, known as node-based communication. The communication amount, which increases with size of the NN and the dataset, is a decisive factor in the performance of the DDT approach. For HPC systems with limited performance and unreliable communication networks, it is recommended to use a parameter server instead of the AllReduce command. This method is, however, not discussed in this work, since the configured systems in AI4HPC (as of 04/2024) have good performance with reliable communication networks. To reduce the communication overhead, it is also possible to postpone the communication to the non-consecutive iterations by skipping the AllReduce operation. It should be noted that the determination of the number of AllReduce operations to be skipped could affect the training accuracy and is also case-dependent. This approach is discussed for this case in Section 3.4.

AI4HPC is available in an open-access repository (under MIT License), which can be cloned with the following command.

  git clone https://gitlab.jsc.fz-juelich.de/

  CoE-RAISE/FZJ/ai4hpc/ai4hpc

The following code snippet provides the manual to compile AI4HPC, see also Appendix.

  python setup.py --help

The library has been tested on Linux-based operating systems at multiple HPC sites. The setup script of AI4HPC is pre-configured for five HPC systems (as of 04/2024): the Jülich Wizard for European Leadership Science (JUWELS) (Krause, 2019), the Jülich Research on Exascale Cluster Architectures (JURECA) (Jülich Supercomputing Centre, 2021), the Dynamical Exascale Entry Platform—Extreme Scale Technologies (DEEP-EST) (Suarez et al., 2021) systems at the Jülich Supercomuting Centre (JSC), the CTE-AMD⁵ system at Barcelona Supercomputing Center (BSC), and the Large Unified Modern Infrastructure (LUMI)⁶ system at the IT Center for Science (CSC). AI4HPC generates the configuration required in the job submission script for the respective HPC system. Moreover, configuring AI4HPC for other HPC systems is trivial and straightforward, which is provided in AI4HPC's documentation page.⁷

AI4HPC consists of five main components:

1. Data manipulation routines tailored for CFD datasets: AI4HPC implements a specific multi-process dataloader, which can process datasets with irregular dimensions and includes preprocessing, augmentation, and normalization methods. For instance, an irregularly-shaped input is reshaped into smaller patches to extract regularly shaped batches. This allows handling irregular CFD grids (e.g., non-equidistant meshes). The choice of smaller patches can be provided by the user as an optional parsing argument. It should be noted that when using the reshaping feature, the reconstruction of the cubes for post-processing needs to be handled by the code. An example of this operation is provided in the repository.⁸ For faster input, the data transfer between the CPU (host) and the GPU (device) uses page-locked (or pinned) memory; thus, cudaMemcpy operations can be skipped.

2. ML architectures: Several ML architectures, which are tailored for CFD applications, are available in AI4HPC. With some minimal changes, these models can easily be adapted to other tasks, e.g., coming from computer vision. The available architectures are:

• CAEs for compressing CFD fields to reduce local disk space requirements;

• CDM based on a DPM is used for super-resolution, i.e., to generate highly-resolved CFD fields from low-resolution data;

• CAE-PN, which is a fully-connected NN, is combined with a CAE to predict a QoI, e.g., the total power-saving of an actuated airfoil (as in Albers et al., 2019) as a function of operational conditions;

• Flow Transformer (FlT) is used for time-marching the CFD flow fields, replacing the expensive time-integration schemes.

3. Optimizations to handle distributed training on HPC systems: AI4HPC includes various optimization routines, which not only allow for more efficient training of ML models, but also for tuning the training with advanced options, such as mixed precision, gradient accumulation, etc. This is discussed in further details in Section 3.

4. HyperParameter Optimization (HPO) tool: Finding optimized hyperparameters increases the accuracy of an ML model significantly. AI4HPC includes a scalable HPO module with the Ray Tune library⁹ that features a smooth integration of PyTorch-based training scripts. Two levels of parallelism are possible: (i) run each trial (model with different hyperparameters) in parallel on multiple GPUs using the DDP strategy, and/or (ii) run several trials in parallel on an HPC system (via Ray Tune itself). An HPO implementation using the AI4HPC library involving mixed precision has already been published (Aach et al., 2023).

5. Monitoring and performance benchmarking tool: For monitoring AI4HPC, NVIDIA's system-wide performance analysis tool Nsight API¹⁰ and PyTorch's standard profiler are used. Important performance metrics are printed to the standard output file, such as the epoch runtimes, loss, or memory print. GitLab's CI routines continuously compiling and benchmarking AI4HPC are also implemented. Furthermore, AI4HPC includes a benchmarking tool, which enables to analyze the scaling behavior of the library on large HPC systems.

3 Optimizations and performance

AI4HPC implements many optimization routines, which augment the performance of the ML models. These are discussed in detail in this section. For the purpose of this study, the two frameworks PyTorch-DDP and Horovod are evaluated. To demonstrate the optimization choices, trainings of the CAE-NN on the TBL dataset is performed. Two HPC systems are chosen, the Booster module of JUWELS and the DC-GPU partition of JURECA. The JUWELS Booster module, at its current state (04/2024), consists of 936 compute nodes interconnected via four InfiniBand HDR adapters.¹¹ Each node is equipped with two 24-core AMD EPYC Rome 7402 CPUs¹² and four NVIDIA A100 GPUs.¹³ The JURECA DC module, at its current state (04/2024), consists of 192 accelerated compute nodes interconnected via two InfiniBand HDR adapters. Each node is equipped with two 64-core AMD EPYC 7742 CPUs¹⁴ and four NVIDIA A100 GPUs. Here, the scaling performance is measured in terms of speed-up s, which is the ratio of the reference average epoch duration using a reference number r of GPUs $\overline{t_e}(r)$ to the average epoch duration of the current training ${\overline{t_e}}^{*}(g)$, i.e.,

$\begin{array}{ll}s(r,g)=\frac{\overline{t_e}(r)}{{\overline{t_e}}^{*}(g)},& (1)\end{array}$

where g is the number of employed GPUs. The efficiency at g is then defined by

$\begin{array}{ll}e(r,g)=\frac{s(r,g)}{s^{*}(r,g)}·100\%,& (2)\end{array}$

where s^*(r, g) would be the ideal speed-up at g with baseline r.

The parallel performance of AI4HPC is analyzed in Section 3.1, both with and without input/output (IO) operations. Optimizations available in AI4HPC are then evaluated in terms of learning rate and adaptive summation (Section 3.2), mixed precision (Section 3.3) and gradient accumulation (Section 3.4). The effect of the dataset size on the error ϵ is evaluated in Section 3.5.

3.1 Parallel performance

To test the scaling performance of AI4HPC without IO, the training of a U-Net model is run on up to 916 compute nodes of the JUWELS system, which is equivalent to parallel usage of 3,664 NVIDIA A100s.¹⁵ The U-Net architecture (Ronneberger et al., 2015) is employed for super-resolution with over 52 million trainable parameters that occupy 90% of the available GPU memory per device (36/40 GB). A synthetically created CFD dataset (i.e., disabled IO) is employed with Horovod as communication backend in AI4HPC. The benchmark results in Figure 2 show the speed-up with g = 3, 664 and r = 4, leading to s(r, g) = 881.92 [ideal theoretical speed-up is s^*(r, g) = 916] and a scaling efficiency of e(r, g)>96%. It should be noted that this scaling performance is only possible using a significantly large dataset. With smaller datasets, the training suffers from a communication bottleneck due to insufficient data per device, which is further discussed below.

Figure 2

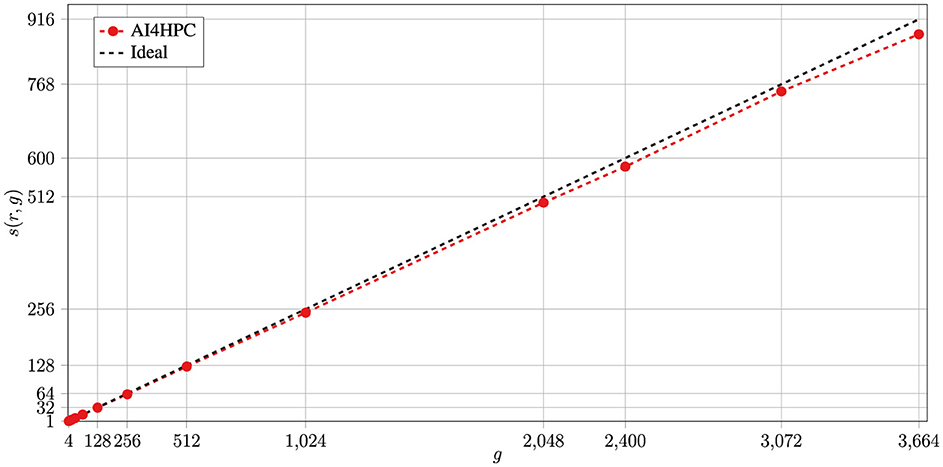
Figure 2. Benchmarking of AI4HPC on the JUWELS HPC system on up to 916 compute nodes (3,664 NVIDIA A100s) with Horovod. The NN is a U-Net model consisting of 52 million trainable parameters with 36 GB memory occupancy per GPU. The training is performed with a synthetically created dataset, which is expected to significantly affect the scaling. The black-dashed line depicts the ideal speed-up.

The parallel performance results of the CAE-NN training to reconstruct actuated TBL flow fields using the PyTorch-DDP and Horovod frameworks are depicted in Figure 3. Contrary to the experiments on JUWELS, IO is also considered in these CAE-NN trainings on JURECA. Around 90% (7.5 TB) of the dataset leading to around 2.7 million samples stored in HDF5¹⁶ format (30,614 files) is used for training. The remainder (0.8 TB) of the dataset, i.e., around 0.3 million samples in HDF5 format (3,402 files), is used for testing. The test dataset is ensured to include at least a single data sample per actuation parameter.

Figure 3

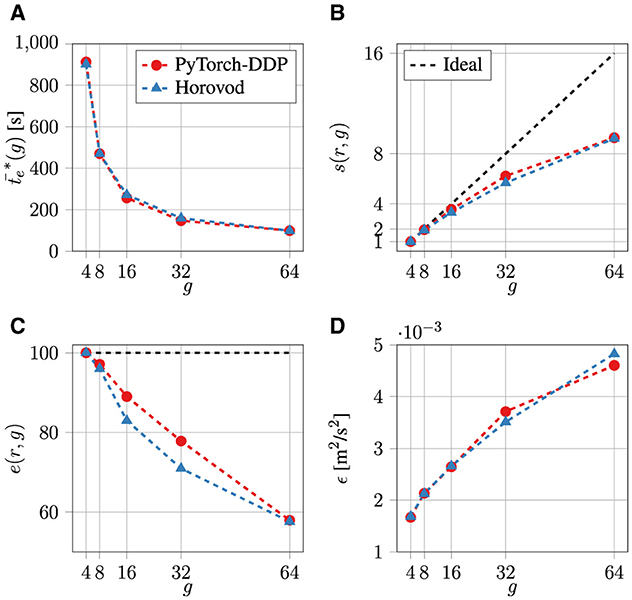
Figure 3. Performance comparison of the PyTorch-DDP and Horovod frameworks to train on actuated TBL data with hyperparameters E = 100, B = 2, and LR = 0.001 on the DC-GPU partition of JURECA (Jülich Supercomputing Centre, 2021). Depicted are the average epoch time ${\overline{t_e}}^{*}(g)$ (A), speed-up s(r, g) (B), efficiency e(r, g) (C), and the training error ϵ (D). The black dashed line represents the ideal scenario (perfect scaling).

For the trainings with g ≤ 64 and r = 4, the number of epochs is set to E = 100, the micro-batch size to B = 2, the fixed learning rate to LR = 0.001, and the SGD optimizer weight decay to W = 0.003. It is to be noted that the effective micro-batch size B_eff = B×88 is higher, since the velocity field slices in the wall-parallel direction are also included in the batch dimension during pre-processing. For the analyses in this manuscript, B is only used for reporting. Furthermore, the dataset is not shuffled after each epoch and no scheduler for LR is employed. In the experiments, shuffling did not improve the results and added (slight) computational overhead. Experiments showed E = 100 yielding an acceptably converged training. It is ensured that the findings of this and further tests are not dependent on E. The average epoch duration ${\overline{t_e}}^{*}(g)$ is averaged over the number of E. The first epoch duration is discarded from the statistics. The training error ϵ is computed during the test phase using the Mean-Squared Error (MSE) between the reference and the reconstructed velocity fields, which has been demonstrated to work well for canonical cases (Jin et al., 2018). Since in the distributed setting, all workers train on chunks of the dataset and consequently accumulate local errors, these are averaged over all the workers. Furthermore, the library also offers the possibility to allow deterministic runs for reproducibility. This can be activated with nseed as an optional parser argument to the code, which defaults to zero. This argument then uses the method torch.manual_seed¹⁷ provided by the PyTorch library. For the test runs in this study, the default seed of zero is used.

As shown in Figure 3A, the training duration for both frameworks is similar. From Figure 3B, it is evident that both frameworks achieve satisfactory scaling performance up to g = 64. The efficiencies are always higher than 58% (Figure 3D). From the behavior of the error ϵ in Figure 3C it is obvious that changing g indeed affects the quality of the reconstructions, noting that the learning rate is fixed at LR = 0.001. Both the PyTorch-DDP and Horovod frameworks suffer from worse ϵ values when more GPUs are used—the ϵ value increases by a factor of three when g is increased from four to 64.

In the DDT strategy, it is common practice to increase the number of workers to reduce the training time. In an ideal scenario, doubling the number of workers should halven the training time, leading to perfect scaling. In reality, distributing the total dataset to more workers causes an imbalance between the computation and communication—fewer data samples per worker are available, and the communication share increases, which (usually) negatively affects the scaling behavior. Exemplary, process monitoring results of three CAE-NN trainings with a single, two, and 16 nodes are depicted in Figure 4. The overall process shares between a single and two nodes are almost the same, but considerably different between two and 16 nodes. Comparing the results for two and 16 nodes, it is evident that a decrease in the share of CPU operations (denoted as Ops) is observed due to less data being available. In contrast, the share of the communication operations between GPUs (denoted as Comm) is increased. From these findings, it can be inferred that: (i) there is a limit to the maximum number of workers for a specific dataset size, and (ii) this limit extends for trainings with even larger dataset sizes.

Figure 4

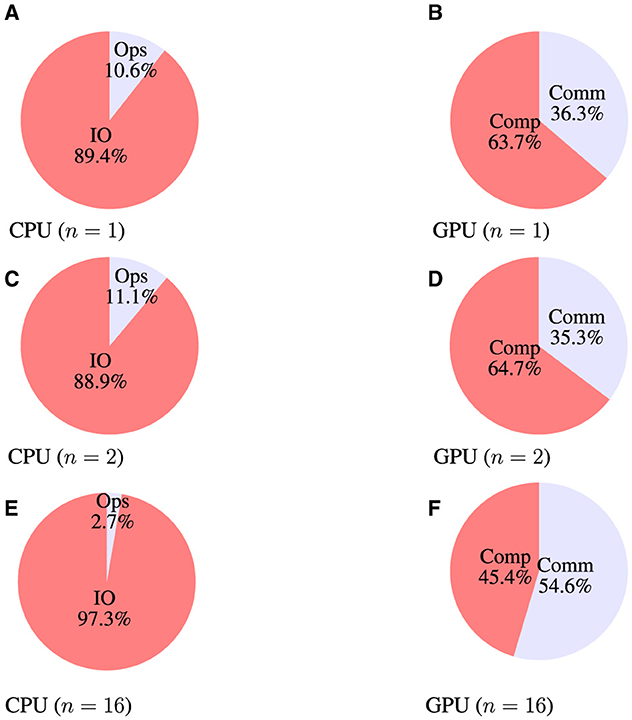
Figure 4. Process monitoring results on CPUs and GPUs for trainings with a number of nodes n. CPU's IO and basic arithmetic/logic/controlling operations (Ops), the GPU's computation (Comp) and communication (Comm) operations are shown. (A) CPU (n = 1). (B) GPU (n = 1). (C) CPU (n = 2). (D) GPU (n = 2). (E) CPU (n = 16). (F) GPU (n = 16).

Figure 5 shows the speed-up s(r, g) and efficiency e(r, g) results of the two trainings to test the effect of the dataset size on the scaling performance of the DDT approach in AI4HPC. For this purpose, the same CAE-NN training is repeated using the PyTorch-DDP framework with a 10 times larger dataset size compared to the original one. This larger size is achieved by rereading the same original dataset 10 times during the training, leading to an input of 83 TB of data. Note that due to file caching algorithms, the performance metrics of a training with an actual 83 TB might slightly differ from the results presented here. To compensate for the computational effort, the number of epochs is reduced to E = 10, while the other hyperparameters are kept the same (B = 2, LR = 0.001, W = 0.003). It is quite clear from Figure 5 that a better scaling performance can be achieved with a larger dataset size. However, it is also plausible to achieve better scaling performance for trainings with even larger dataset sizes.

Figure 5

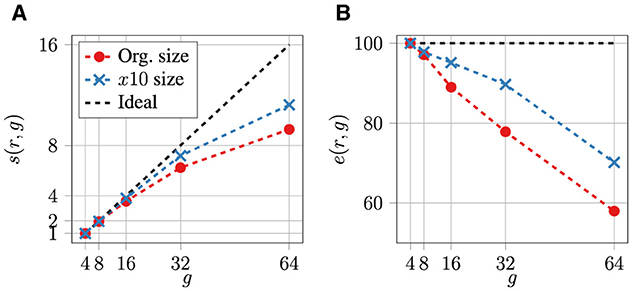
Figure 5. Effect of the dataset size on the scaling performance of the DDT approach in AI4HPC. The (A) speed-up s and (B) efficiency e of a training with 10 times larger dataset size (x10 size) using the PyTorch-DDP framework is compared to the same training on the original dataset size (Org. size). All hyperparameters are the same except for the lower number of epochs E = 10. The black dashed line represents the ideal scenario (perfect scaling).

3.2 Learning rate and adaptive summation

Another important issue that needs to be addressed when using the DDT approach is the loss in accuracy when the training is performed with a large number of workers. As each individual worker is set to a fixed micro-batch size, increasing the number of workers also increases the mini-batch size. If this mini-batch size is not adjusted accordingly, the scaling performance of the training becomes meaningless as the training accuracy turns out to be the decisive factor. This is addressed in AI4HPC using multiple strategies. The common strategy is to tune other hyperparameters keeping the accuracy of the training at an acceptable level, which has intensively been discussed in the literature (Goyal et al., 2017; You et al., 2017; Yamazaki et al., 2019), e.g., the learning rate can be proportionally scaled to the mini-batch size, i.e., the number of workers.

Another plausible strategy implemented in AI4HPC to reduce the ϵ values for a large-scale training is based on a summation algorithm, Adasum (Maleki et al., 2020). In this algorithm, the accumulation of gradients g₁ and g₂ from two workers are extended from the summation or averaging to:

$\begin{array}{ll}Adasum(g_1,g_2)=\left(1-\frac{g_1^T·g_2}{2||g_1|{|}^2}\right)g_1+\left(1-\frac{g_1^T·g_2}{2||g_2|{|}^2}\right)g_2,& (3)\end{array}$

where $g_1^T·g_2$ is their dot product. In synchronous SGD methods that are used to compute the gradients in parallel, the effective gradient is the average (g₁+g₂)/2. As a consequence, applying learning rate scaling (as discussed above), the effective gradient becomes the summation. Equation (3) reduces to a simple averaging if gradients g₁ and g₂ are parallel. In contrast, if the gradients g₁ and g₂ are orthogonal, Equation (3) reduces to a summation. Since during the training the gradients are neither perfectly parallel nor orthogonal, this equation simply sums these gradients after scaling with appropriate scalars. Thus, the sequential execution to compute both gradients g₁ and g₂ is approximated in a single execution. As presented in Maleki et al. (2020), the convergence properties of this algorithm do not require scaling of the learning rate and this algorithm does not add additional hyperparameters to be tuned. It can be recursively applied to combine the gradients in different workers.

The ϵ values of three CAE-NN trainings over g using Horovod are depicted in Figure 6A. All trainings have the same hyperparameters (B = 2, E = 100, W = 0.003), except for a varying LR. This quantity is either fixed at LR = 0.001, is scaled, or the adaptive summation algorithm Adasum is used with fixed LR = 0.004. It should be noted that this algorithm requires multiplying the base learning rate LR_b = 0.001 with the number of local GPUs per node¹⁸ i.e., LR(g) = LR_b·g. For JURECA, this results in a minimum of LR = 0.004 and a maximum of LR = 0.064 for g = 4 and g = 64. From Figure 6A, it becomes clear that the ϵ value is drastically lower when LR is scaled. When g = 4, the ϵ value is reduced by around 23%, whereas ϵ is reduced by around 64% when LR is scaled. Importantly, ϵ is highest when g = 32 and LR is scaled. It is evident that tuning hyperparameters, in this case LR, is of utmost importance when increasing g.

Figure 6

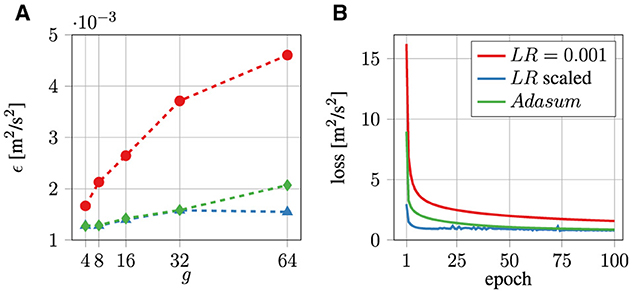
Figure 6. The ϵ value over g (A) and training loss over the number of epochs using g = 64 (B) for CAE-NN trainings with fixed LR = 0.001 (red), scaled LR = 0.001·g (blue), and Adasum algorithm with fixed LR = 0.004 (green).

The MSE training loss of the three CAE-NN trainings with g = 64 over the number of epochs is depicted in Figure 6B. The training with fixed LR is not fully converged after E = 100, whereas the scaled LR training converges for E≥7. Note that the training with a fixed LR could achieve similar training loss for a large number of E. The error in this case is still decreasing slowly until E = 100, but further epochs are not trained in this work.

The comparison of ϵ values and the training loss of the CAE-NN training using Adasum to both fixed and scaled LR is also depicted in Figures 6A, B. The Adasum algorithm leads to an ϵ value similar to using a scaled LR, except for g = 64. It is also possible to first optimize the LR value for this training, as suggested in Maleki et al. (2020). This requires, however, computationally costly HPO methods, which are out of scope of the present investigations. Notably, the training with Adasum shows a similar convergence rate as in the training with a fixed LR, see Figure 6B. A quantitative comparison of the training properties using either a fixed LR = 0.001, scaled LR, or Adasum with a fixed LR = 0.004 is summarized in Table 1. It is evident that the training with Adasum does not show any computational overhead. Horovod uses slightly less (around 10%) memory than PyTorch-DDP, hence, the lower memory results of Adasum are not a merit of this algorithm.

Table 1

Table 1. Summary of CAE-NN trainings with E = 100, B = 2, W = 0.003, and a fixed LR value, scaled LR, and using the Adasum algorithm with fixed LR.

3.3 Mixed precision

In the default implementation, frameworks such as PyTorch-DDP and Horovod use the single-precision floating-point format (commonly referred to as FP32), which occupies 32 bits per variable in memory for the dataset and the network parameters. As training on a large dataset is a memory-intensive process, it makes sense to use a half-precision floating-point format (commonly referred to as FP16) to reduce memory requirements. AI4HPC provides the option to test the mixed precision format for training ML models. For testing purposes, the same CAE-NN training using g = 64 is performed using various formats with the same hyperparameters as above (B = 2, E = 100, LR = 0.001, W = 0.003). Corresponding quantitative results are given in Table 2.

Table 2

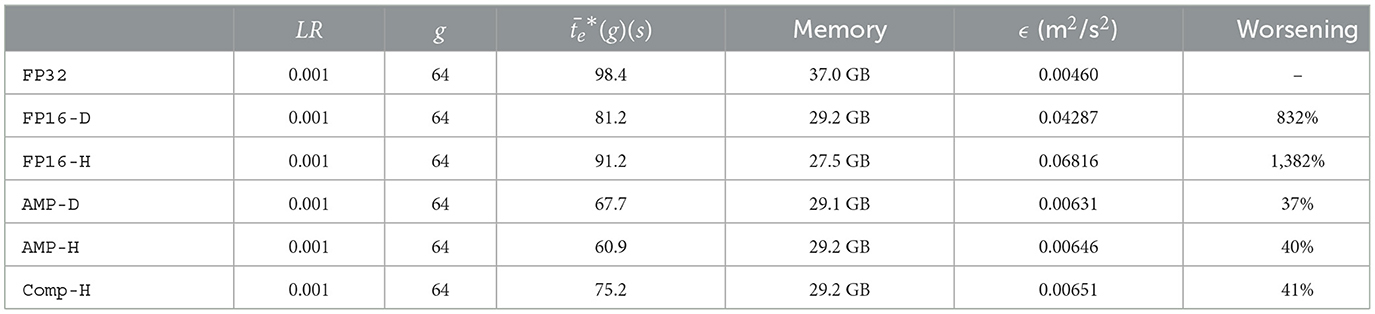
Table 2. Summary of the parameters and results of a CAE-NN trainings with E = 100, B = 2, W = 0.003, and a fixed LR value using various precision formats.

In the first test, only the format for the dataset in the memory is reduced to FP16 precision. This test is repeated twice, using PyTorch-DDP (FP16-D) and Horovod (FP16-H). In the second test, the format for the trainable parameters of the network and the dataset in the memory is chosen automatically using the Automatic Mixed Precision (AMP) package of PyTorch-DDP. This test is also repeated twice, using PyTorch-DDP (AMP-D) and Horovod (AMP-H). In the final test, the AMP package is combined with the compression algorithm of Horovod, which forces all of the gradients to be represented in FP16 precision during AllReduce operations (Comp-H).

In all tests, the memory requirements of the GPUs are reduced drastically, i.e., around 21% for FP16-D, AMP-D, AMP-H, and Comp-H, and around 26% for FP16-H. However, the ϵ error is an order of magnitude higher in the FP16-D and FP16-H tests compared to the FP32 test, where the ϵ is around 50% higher for FP16-H compared to FP16. The drastic worsening of ϵ is mainly due to the reduced precision format of the dataset, i.e., the smallest scales of the velocity components are lost using the FP16 format. Hence, employing AMP in AMP-D and AMP-H results in similar ϵ values, the values are, however, 37% higher than the one in FP32. Applying the compression algorithm of Horovod with AMP marginally affects the ϵ values.

Using FP16-D decreases the average epoch times by 17%, whereas using FP16-H decreases the average epoch times by only 7%. More importantly, AMP-D and AMP-H show 31 and 38% decreased average epoch times. Finally, Comp-H yields on average a longer epoch time than AMP-H, which has no compression algorithm enabled. From these findings it is clear that, as both the compression algorithm and AMP modifies the precision of the network parameters, the compression algorithm unnecessarily burdens the training by modifying the precision of the network parameters, causing longer average epoch times. It is worth mentioning that AMP would result in a major reduction of the memory footprint or of the training runtime for a larger network. However, AMP is not favorable for the CAE-NN due to high ϵ values.

The training loss of four CAE-NN trainings using g = 64 plotted over the number of epochs employing different precision formats is depicted in Figure 7. The hyperparameters are the same as above (B = 2, E = 100, LR = 0.001, W = 0.003). Interestingly, the training loss drops a second time in both the FP16-D and FP16-H cases after a few epochs. The FP16-D case is not converged, even after E = 100, whereas the FP16-H case is (almost) converged. The AMP-D case converges much faster than the other cases, noting that AMP-H and Comp-H show almost identical results than the one for AMP-D. They are therefore omitted for brevity. Interestingly, the cases with AMP converges even before 50 epochs and has the lowest final loss. However, the final loss of the training for each case does not represent the training errors achieved with the testing dataset, e.g, the AMP-D case has a higher training error but a smaller final loss than FP32.

Figure 7

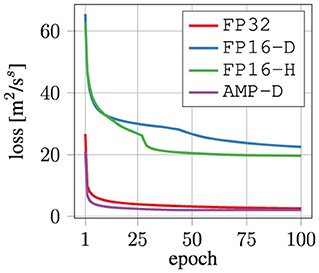
Figure 7. Training loss over the number of epochs for a CAE-NN trainings using g = 64 with different precision formats.

3.4 Gradient accumulation

Training a model using large datasets usually causes memory issues for large mini-batch sizes. A tiny micro-batch size is often preferable when using many GPUs in parallel. With an increasing number of GPUs, the mini-batch size inevitably scales as well, becoming infeasibly high for high GPU counts. One approach to achieve a large batch size regardless of the memory requirements is to accumulate the calculated gradients without issuing backpropagation, i.e., using gradient accumulation. This way, the next micro-batch is stacked into the previous one for the next epoch. For example, a training with B = 2 eventually is the same as a training with B = 4 but with a gradient accumulation step AS of 2, i.e., issuing backpropagation when Mod(E, AS = 2) = 0. Hence, gradient accumulation is a promising alternative to achieve larger batch sizes even with lower memory in GPUs. A small caveat of this approach is that the communication between the nodes becomes redundant if AS>2, since the parameters and weights are anyhow not updated locally. Here the effect of the use of gradient accumulation feature in AI4HPC on the training parameters is analyzed.

For the following analysis, the CAE-NN training using g = 64 is performed, and a range of gradient accumulation steps AS = 1 up to AS = 16 are executed. The parameters of the training and the quantitative results are given in Table 3. In all tests, the PyTorch-DDP framework is used and the hyperparameters are kept the same as above (B = 2, E = 100, LR = 0.001, W = 0.003), noting that certainly the same conclusions could be drawn if a different framework is used. In these tests, the effective mini-batch size is multiplied by up to 16 by considering AS = 16 without witnessing memory issues. Moreover, due to fewer backpropagation operations, considering a large AS slightly decreases the average epoch time by around 10%. The ϵ values for tests with a different AS value are slightly different due to different effective mini-batch sizes.

Table 3

Table 3. Summary of parameter and results of the CAE trainings with E = 100, B = 2, W = 0.003, and a fixed LR value using gradient accumulation steps AS∈{1, 2, 4, 8, 16}.

A common and sensible approach to alter the communication drawback of this approach is to skip AllReduce operations between the epochs, called batch per AllReduce BpA in AI4HPC. To test the impact of such a strategy, the same CAE-NN training using g = 64 is performed using BpA = 4 and BpA = 16. The findings are compared to those of a standard training using BpA = 1 in Table 4, where the Horovod framework is now used instead and the hyperparameters are B = 2, E = 100, LR = 0.001, W = 0.003. It is evident from this test that a high BpA yields similar ϵ values as with a low BpA. As most of the bottlenecks come from IO, thus, reducing communication between nodes barely reduces the average epoch times. It seems plausible that similar ϵ values are obtained as a consequence of the model parameters between the nodes not drifting apart significantly. But this might be dependent on the network and the dataset as well. Avoiding an update of the model parameters between nodes causes the training parameters in each node to continuously deviate per epoch, which is not desirable. However, with even larger g and importantly, worse inter-node communication in the HPC system, BpA>16 could be still useful in some cases.

Table 4

Table 4. Summary of the parameter and results of CAE-NN trainings with E = 100, B = 2, W = 0.003, and a fixed LR value using various micro-batch sizes per AllReduce step.

3.5 Dataset size

The influence of the dataset size on ϵ is investigated by conducting four CAE-NN trainings with different dataset sizes using 32 GPUs with Horovod, with E = 1000, B = 1, W = 0.003, and LR = 0.032. The chosen dataset sizes are based on a fraction, given by ℱ = 5, 10, 50, or 100% of the original (full) dataset, thus ranging from 0.415 TB (ℱ = 5%) to 8.3 TB (ℱ = 100%). The ϵ values obtained for these trainings values together with the dataset sizes are listed in Table 5.

Table 5

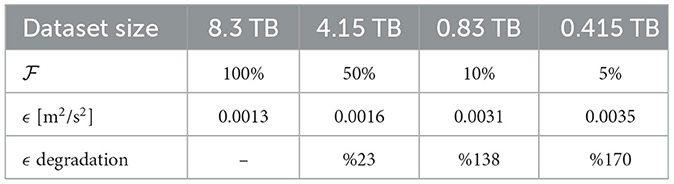
Table 5. Resulting ϵ values for four CAE-NN trainings with E = 1000, B = 1, W = 0.003, and a scaled LR with different dataset sizes using the Horovod framework.

It is evident that the increase in dataset size drastically reduces ϵ. The CAE-NN training with ℱ = 5% achieves an error of ϵ = 0.0035, which is 170% worse than the ϵ with ℱ = 100%. Meanwhile, doubling the dataset size to 0.83 TB (hence, ℱ = 10%) reduces ϵ by 12 percent, which is, however, still 138% worse than the ϵ value of ℱ = 100%. Moreover, using ℱ = 50% further reduces ϵ by 49%, which is yet again 23% worse than the ϵ with ℱ = 100%. Conclusively, the size of the dataset drastically affects the ϵ values, but a linear correlation between the dataset size and ϵ is not found.

It has been shown that the DDT method in AI4HPC drastically reduces the runtimes of training neural networks, which is also expected for other NN architectures. The library achieves satisfactory parallel efficiency, limited to the size of the dataset and the IO. The various optimizations presented provide implementation hints to AI users. For instance, among the two alternative solutions to circumvent the large mini-batches issue, Adasum algorithm and LR scaling, the latter should be preferred being the simpler-to-use solution. It is evident that for a CAE-NN training, especially in the context of CFD datasets, the input dataset requires a high-precision representation, e.g., in FP32, due to the importance of small-scale structures. Applying the AMP package should in such a case not be the option. However, other domains, such as computer vision, could benefit from AMP. It is also observed that large AS and BpA values can be selected for these trainings if a large B value is desired. High AS and BpA values only slightly reduce the training runtimes. Finally, the size of the dataset should be large enough to achieve low ϵ values.

4 Application case: reconstruction of TBL flow with AI4HPC

In this section, the reconstruction performance of the AI4HPC framework is investigated in detail for the actuated TBL flow case. The use case is defined briefly in Section 4.1, followed by an overview on the CAE-NN and CAE-PN network architectures and the accuracy of these networks for the TBL flow reconstruction shown in Section 4.2. The CDM network architecture and its performance for obtaining super-resolution is shown in Section 4.3.

4.1 Use-case specification—actuated TBL flow

The actuated TBL flow problem and the computational setup of the fluid solver (Albers et al., 2019, 2020; Albers and Schröder, 2021) are briefly explained. In this approach, an Active Drag Reduction (ADR) method introduces spanwise traveling transversal surface waves and is rigorously analyzed by high-fidelity LESs of compressible fluids. Figure 8A shows the computational setup. Here, periodic boundary conditions are employed in the spanwise direction. The friction REYNOLDS number based on the boundary layer thickness δ₉₉ is Re_τ = δ₉₉u_τ/ν = 360, where $u_{\tau }=\sqrt{{\tau }_w/\rho }$ is the friction velocity, ν is the dynamic viscosity, τ_w is the wall-shear stress, and ρ represents the density. The MACH number is Ma = 0.1 and is based on the freestream velocity and the local speed of sound. A Cartesian mesh is used to discretize the physical domain with a mesh resolution of Δx⁺ = 12 in the streamwise direction, $\Delta y^{+}{|}_{wall}=1$ in the wall-normal direction at the wall, and Δz⁺ = 4 in the spanwise direction. The plus sign denotes an inner scaling of the non-actuated reference case ${\Delta }^{+}=\Delta ·u_{\tau }/\nu$, i.e., the scaling is based on ν and u_τ, where Δ{x, y, z} is the cell size in the respective space dimension.

Figure 8

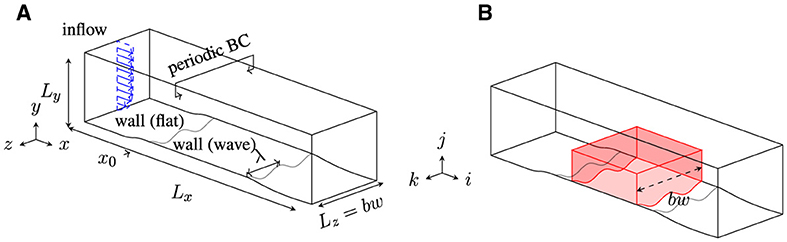
Figure 8. Full computational setup of the simulation of the actuated TBL and subvolume, where LES results are extracted (Albers et al., 2020). The quantity bw denotes the box-width of the computational domain. (A) Computational setup. (B) Three-dimensional subvolume.

At the lower x−z boundary, a moving no-slip wall boundary condition is applied, which allows the prescription of a space- and time-dependent sinusoidal wave motion, given by

$\begin{array}{ll}{y}^{+}{|}_{wall}(z^{+},t^{+})=A^{+}cos\left(\frac{2\pi }{{\lambda }^{+}}{z}^{+}-\frac{2\pi }{T^{+}}{t}^{+}\right).& (4)\end{array}$

Equation 4 features the time $t^{+}=t{u}_{\tau }/\nu$ and the actuation parameters in inner scaling, namely the wavelength ${\lambda }^{+}=\lambda u_{\tau }/\nu$, period $T^{+}=T{u}_{\tau }^2/\nu$, and the amplitude $A^{+}=A{u}_{\tau }/\nu$, where λ, T, and A are the wavelength, period, and amplitude in outer scaling.

Five spanwise widths are used to prescribe different wavelengths while keeping the same spanwise periodicity of the setup. In total, 79 parameter combinations with five non-actuated reference simulations are performed. The primitive flow velocity variables (u, v, w) are stored for the sub-volumes of the three-dimensional flow field shown by the highlighted red box in Figure 8B. Corresponding to the spanwise widths, the number of cells in the highlighted red box in the z-direction is 250, 300, 400, 450, or 750, while there are 192 and 98 cells in the x- and y-direction. For the different actuation parameter configurations, among various output quantities, ΔC_d and P_net are recorded. The expressions and details of the derivation of these quantities can be found in Albers et al. (2020), where the objective is to find the actuation parameter configuration that maximizes ΔC_d and P_net. Therefore, apart from the ability to attain a high compression of the data with high accuracy, the proposed NNs must also provide an accurate estimation of these quantities to allow the determination of optimized actuation parameters. This is achieved with two CAE networks, which are described in Section 4.2. Thereafter, an SRN is developed for increasing the resolution of the TBL fields, which is elaborated in Section 4.3.

4.2 CAE application to the TBL flow case

The first application case of AI4HPC with CAE is shown in this section. A discussion on the network architecture is provided, followed by an analysis of the performance of the networks for reconstructing the TBL flow field.

4.2.1 Network architectures

The architecture of the CAE-NN is shown in Figure 9A. It consists of four encoding and four decoding layers. Two of these layers, each in the encoder and the decoder, perform convolution along with compression (through striding), while the other two only perform convolution. This yields a compression ratio of 1:16. Comparatively, with a higher compression ratio of 1:64, the test error is found to be 3.3 times higher. Hence, the analysis here is restricted to a latent space compression of 1:16. The network is based on two-dimensional convolutional layers with a LeakyReLU activation function to introduce non-linearity. The convolution operation is applied along the wall-parallel direction. A batch-normalization is applied at the end of each activation layer. Down-sampling is performed with a stride argument in the convolution operation, which is the number of pixels/units that the convolutional filter moves at an iteration. For up-sampling in the decoder, the interpolation function in PyTorch is used subsequent to the convolutional layer. The network inputs are two-dimensional (u, w) velocity fields from the actuated TBL. The loss function is given by the MSE loss between the original and reconstructed fields. For training, about 2.7 million samples are used.

Figure 9

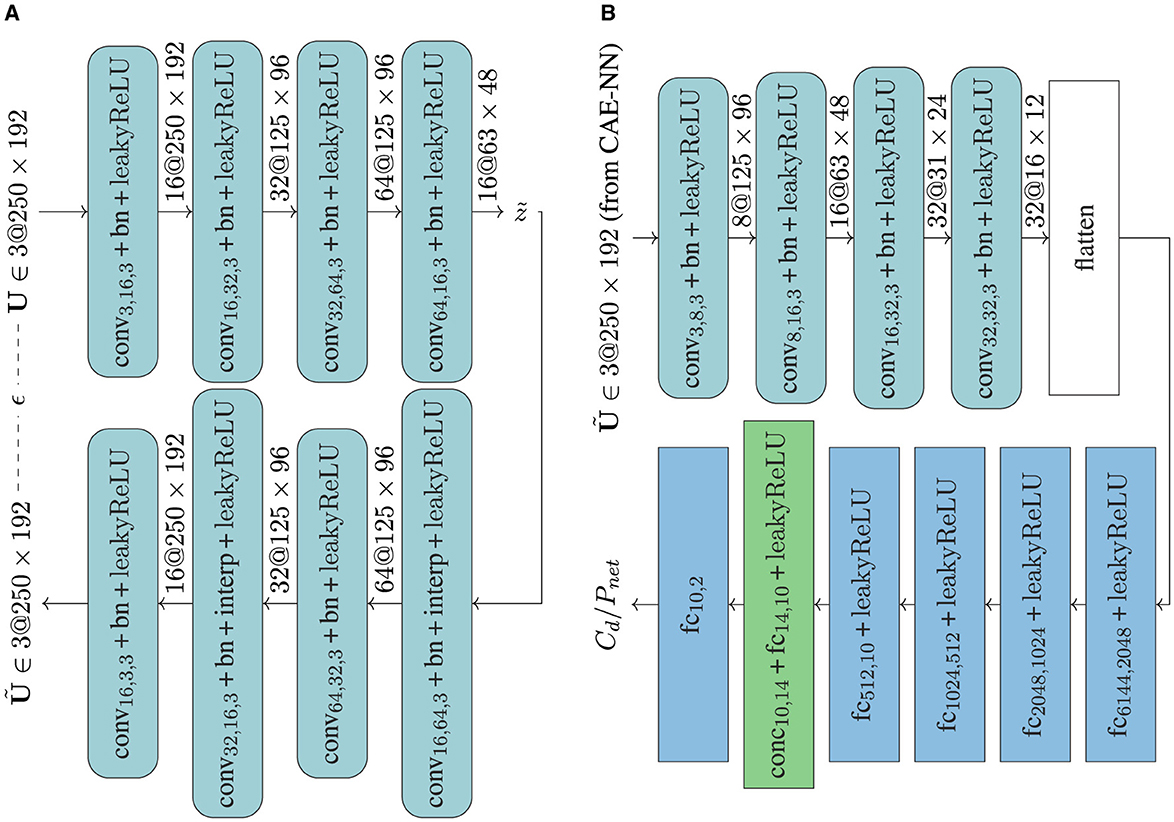
Figure 9. (A) CAE-NN architecture, where conv_{ifil, ofil, nk} denotes the convolution operation mapping ifil to ofil feature maps, and nk is the dimension of the filters, with batch-normalization (bn), interpolation (interp) function of PyTorch used for up-sampling and leakyReLU as the activation function. The dimension of the input and output tensors are mentioned after each of the operations. The quantities $\tilde{z}$, U, and $\tilde{\text{U}}$ are the latent space input velocity field and output velocity field tensors. (B) CAE-PN architecture, where the output $\tilde{\text{U}}$ from the CAE-NN is fed as input. The four convolutional layers (conv) are flattened, which are then passed through six fully-connected (fc) layers, and the final layer outputs the ΔC_d and P_net values, the QoIs. Note that the three actuation parameters and the additional parameter box-width are concatenated (conc) to the tensor after the fourth fc-layer (box shown in green).

The second network is the CAE-PN, whose objective is to predict relevant physical quantities from the latent space of the CAE-NN. In practice, for any given random slice of the velocity field reconstructed by the CAE-NN in the wall-normal direction and at any time-instance, the CAE-PN aims to predict the corresponding QoIs, ΔC_d and P_net. Furthermore, the corresponding three actuation parameters λ⁺, A⁺, and T⁺, see Equation 4, are used as input to the network. An additional parameter related to the computational setup for each velocity field, i.e., the spanwise size of the box (box-width bw) of the actuated region in the computational domain (see Figure 8B) is also concatenated to the network, which helps the NN to distinguish if an input field has been reshaped or not due to varying dataset dimension. The dependence of the network on the three actuation parameters facilitates the generalization of this network such that QoIs outside the trained actuation parameter range can be predicted accurately. The CAE-PN network is shown in Figure 9B, where $\tilde{\text{U}}$ is the velocity flow field of the actuated TBL reconstructed by the CAE-NN. Four convolutional layers are employed and the output tensor from the fourth convolutional layer is flattened. Subsequently, fully connected (fc) layers are employed. The three actuation parameters and the additional parameter, box-width are scaled based on their maximum value and concatenated to one of the hidden fc layers, see the green box in Figure 9B. Finally, the network yields the two QoIs. The loss function of the CAE-PN is given by two terms: the MSE between the original and reconstructed velocity fields from the CAE-NN, and the MSE between the predicted and target QoIs, which have been pre-computed during the run of the LES.

4.2.2 Performance of the NNs

An example of the reconstruction by the CAE-NN is shown in Figure 10 for the scaled streamwise (u^*) and wall-normal (v^*) velocity components in the wall-parallel plane closest to the wall at a certain time instance. The scaling of a scalar ϕ is defined by

$\begin{array}{ll}{\varphi }^{*}=n_{sc}·\frac{\varphi -{\varphi }_{min}}{{\varphi }_{max}-{\varphi }_{min}}-m_{sc},& (5)\end{array}$

Figure 10

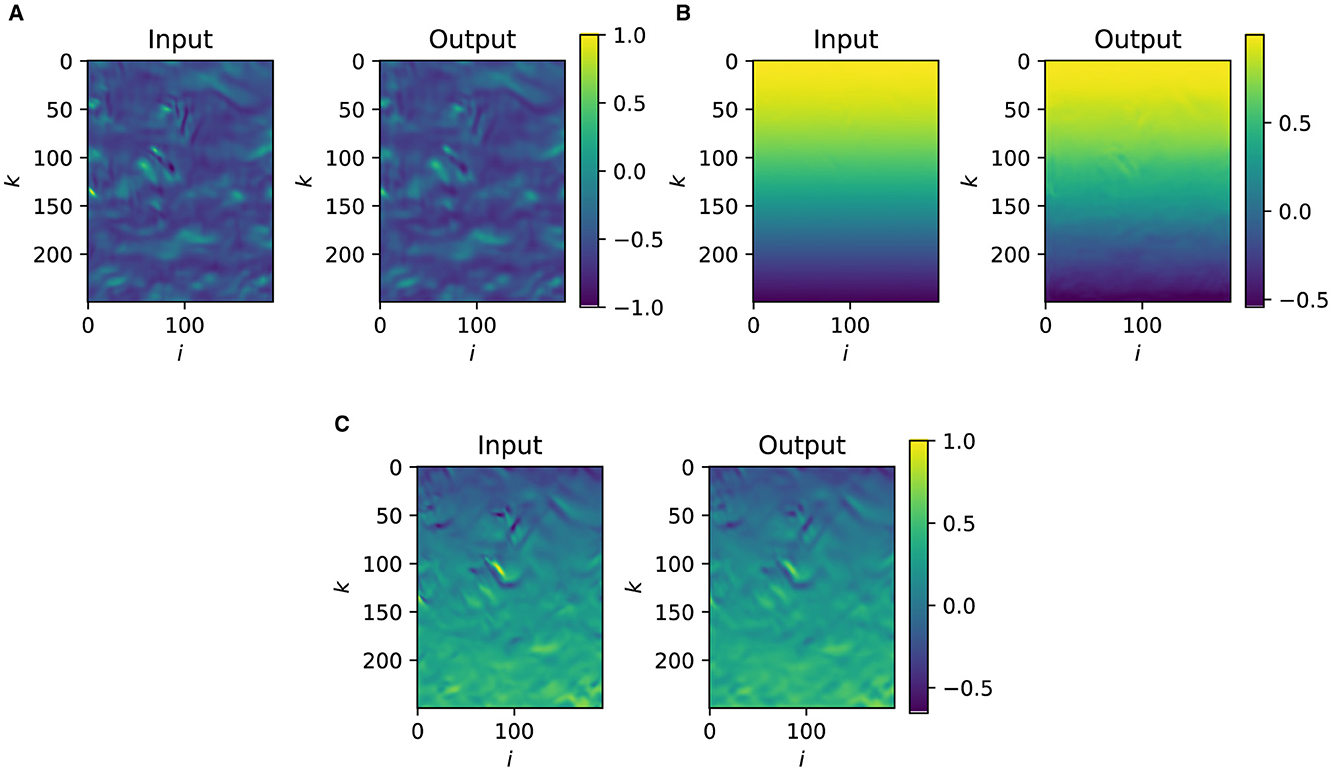
Figure 10. Cross-sections of the scaled velocity components from the LES (Input) and reconstruction by CAE-NN (Output). (A) Scaled streamwise (u^*) velocity. (B) Scaled wall-normal (v^*) velocity. (C) Scaled spanwise (w^*) velocity.

where n_sc = 2, m_sc = 1 is employed for the velocity fields, while n_sc = 1, m_sc = 0 is used for the QoIs. Qualitatively, the reconstructions are able to predict the general characteristics of the u, v and w fields. For all the components, the dominant flow features are well-reconstructed. However, when fine-scale details are compared, the reconstructions show qualitatively blurry images relative to the reference LES results, questioning the reconstruction performance of the CAE-NN toward the dissipative and plausibly energy-containing eddies. The two-dimensional Noise-Assisted Multivariate Empirical Mode Decomposition (NA-MEMD) (Mäteling and Schröder, 2022) method provides a quantitative measure of the CAE-NN's ability to reconstruct specific features based on their scale size. This data-driven decomposition method simultaneously decomposes the original and the reconstructed velocity data solely based on data-inherent features. The resulting Intrinsic Mode Functions (IMFs) are modal representations categorized with respect to flow features that share a certain range of scales. In total, five IMFs are obtained and an increasing mode number indicates larger scales (wavelengths) contained in the respective mode. For example, the first and the fifth IMFs from the simulated and the reconstructed velocity component u at an arbitrary time are depicted in Figure 11. It is visible that the large-scale flow features contained in IMF5 of the reconstructions are in satisfactory agreement with the original data. However, the agreement is lost for the small-scale structures visible from the first IMF1. This is even more clearly visible in Figure 12, where the scale-based energetic content of the reconstructions is compared to the characteristics of the original velocity fields using the pre-multiplied Power Spectral Density (PSD) of the individual IMFs. Pre-multiplication refers to the normalization of the PSD based on the streamwise (1/λ_x) and spanwise (1/λ_z) wavelengths. The distributions are averaged in space and over the instantaneous snapshots and are presented as a function of ${\lambda }_x^{+}$ and ${\lambda }_z^{+}$. It can be seen that the computed PSD values conditioned on IMF1 using the reconstructions are under-predicted, while for IMF5, the estimations are close to the original values. In order to be able to utilize this model for the TBL flow case, its ability to reconstruct the QoIs has to be determined, which is now analyzed with the CAE-PN.

Figure 11

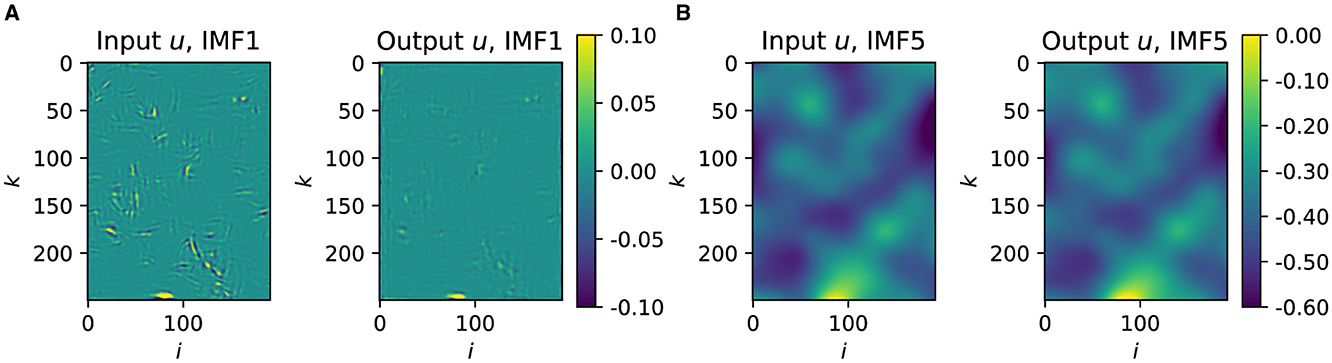
Figure 11. Exemplary intrinsic mode functions (IMFs) of the streamwise velocity component u from the LES (input) and the reconstruction by CAE-NN (output). (A) IMF1 for streamwise (u^*) velocity. (B) IMF5 for streamwise (u^*) velocity.

Figure 12

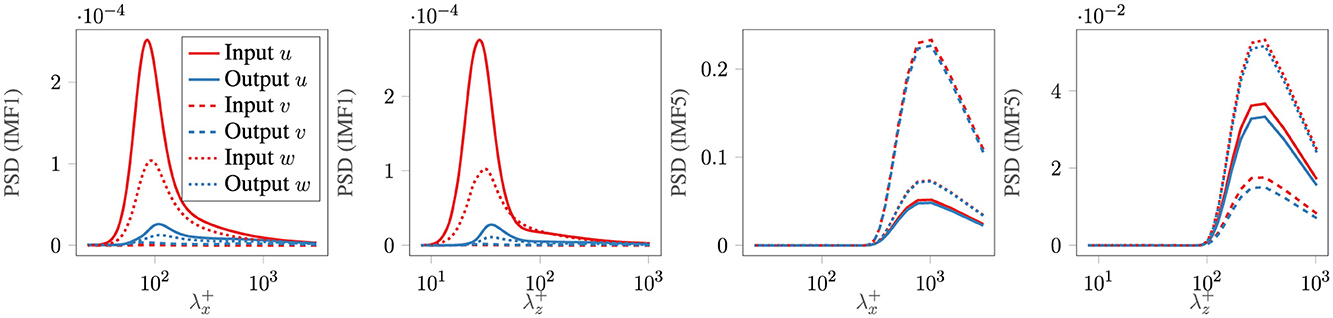
Figure 12. Comparison of pre-multiplied PSD of individual IMFs in the original and reconstructed velocity fields of the TBL.

To assess the performance of the CAE-PN for both interpolated and extrapolated states, the dataset is divided into two sets. For evaluating the interpolation performance, the training set is comprised of four box-widths bw∈{1, 000, 1, 200, 1, 600, 3, 000}, while the test set has box-width bw = 1, 800. To assess the extrapolation performance, the training set is comprised of box-widths bw∈{1, 000, 1, 200, 1, 600, 1, 800}, and the test set has box-width bw = 3, 000. The models are trained for E = 3, 200 epochs and E = 5, 140 epochs in interpolation and extrapolation cases, with a learning rate of LR = 0.001 and an SGD optimizer with a weight decay of W = 0.003.

The comparison of the statistics of the predicted and target values of the QoIs is shown in Table 6. A total of 6,784 and 2,240 different velocity fields in interpolation and extrapolation cases are fed to the CAE-PN as input to generate these statistics. The average values of ΔC_d in both the cases are accurately predicted with a deviation of only ≈5.71 and ≈3.57% for mean ΔC_d in interpolated and extrapolated cases, with a higher deviation for the predicted minimum value. In the case of P_net, the mean has a deviation of ≈7.14% in interpolated cases while this is much higher in the extrapolated case with ≈27.3%. The worse extrapolation performance with P_net can, however, be expected since there is higher variability in P_net (Albers et al., 2020). Furthermore, in Albers et al. (2020), no linear relationship between ΔC_d and P_net is observed, which is in agreement with the workflow that is employed here to train the QoI separately. Finally, the overall accuracy of the predictions is assessed with the Pearson correlation coefficient, which is given by

$\begin{array}{ll}r=\frac{cov(a,b)}{{\sigma }_a{\sigma }_b},& (6)\end{array}$

Table 6

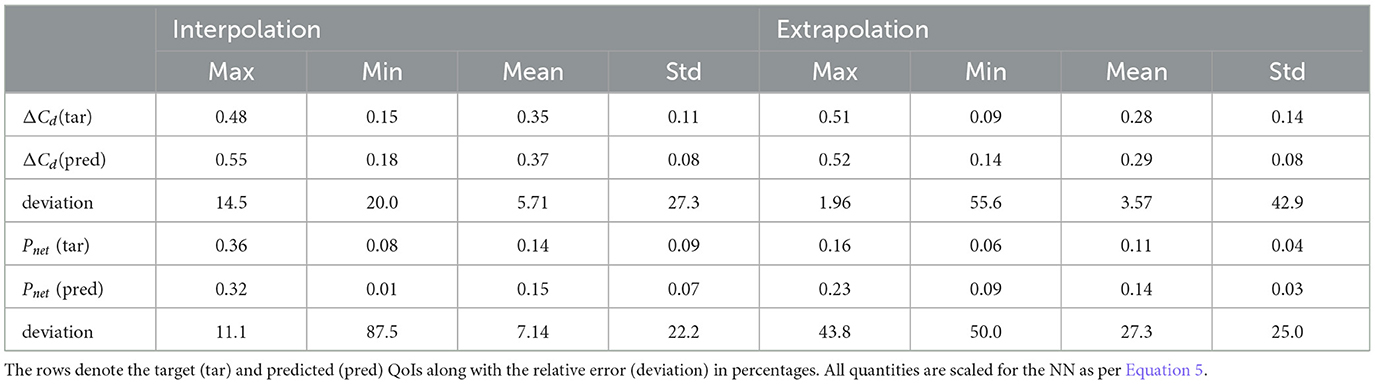
Table 6. Performance of the CAE-PN based on statistical properties of the estimated QoIs, namely maximum (max), minimum (min), average (mean), and standard deviation (std) values.

where cov(a, b) is the covariance between two datasets a and b, while σ_a and σ_b are the respective standard deviations. A value of r~1.0 signifies a high correlation, while r~0.0 implies uncorrelated quantities. It is observed that in the case of ΔC_d, r≈0.92 and r≈0.91 are achieved for interpolated and extrapolated states, while for P_net, the values are r≈0.89 and r≈0.69. To summarize, the CAE-PN is able to provide satisfactory reconstructions of ΔC_d in both cases, while for P_net the network provides reasonable performance for interpolation. Given the high variability of the target P_net, the obtained value of r for the extrapolation case can also be considered to be satisfactory.

4.3 CDM application to the TBL flow case

The second application case of AI4HPC is shown with a CDM network. The network architecture is initially depicted, followed by a performance analysis on a super-resolution task. The potential application of this network for augmenting the results of a WMLES solution is also discussed.

4.3.1 Network architecture

The CDM model is based on the Denoising DPM (Sohl-Dickstein et al., 2015; Ho et al., 2020) for reconstruction of near-wall quantities in wall-bounded turbulent flows, which can then be exploited for improving the approximation of the WMLES solution. The DPMs are unsupervised generative models which learn to denoise purely noisy data. The noise sampled from a distribution, e.g., Gaussian noise with a normal distribution is converted into the data sample, which is used as an input to the CDM model. The model then learns to defilter the filtered quantities. This could, for instance, be applied to locally filtered fields of an LES, to determine the distribution of the subgrid scale quantities close to the wall.

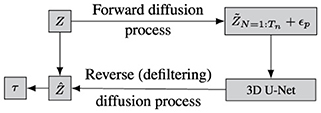
The workflow of the CDM is shown in Figure 13. In the CDM, the forward diffusion process filters an input Z with a Gaussian filter. The filter size N is iteratively increased, resulting in a linear increase of the standard deviation $\sigma =\sqrt{(N^2-1)/12}$. The size is increased from N = 1 corresponding to no filtering, up to a maximum of N = T_n. In each incremental step, a small amount of Perlin noise ϵ_p (Perlin, 1985) with 10 octaves and 1% amplitude compared to the filtered input is added to prevent the network from overfitting to a certain specified filter width. In this case, Perlin noise is preferred over Gaussian noise, as it produces computationally efficient turbulence-like structures (Perlin, 1985). This filtered and noised input ${\tilde{Z}}_N+{ϵ}_p$ is then fed into a “3D U-Net" which consists of three-dimensional convolutional operations. The U-Net architecture is similar to the work of Çiçek et al. (2016), where it is employed for volumetric medical data. The three-dimensional convolutional operations allow the network to evaluate the gradients in all the three directions, generally important to understand turbulent flow dynamics. The input to the network is the three-dimensional instantaneous velocity field Z = u_i, i∈{x, y, z}. Once trained, the network learns to defilter ${\tilde{Z}}_N$ to reconstruct the input such that $Ẑ\stackrel{!}{=}Z$, where the wall-shear stress τ can be computed from Ẑ.

Figure 13

Figure 13. Workflow of the CDM employed for super-resolution of TBL flow field.

For obtaining the training loss, a physics-constrained loss function ℒ is defined by incorporating physical constraints, given by:

$\begin{array}{ll}L={\beta }_1{L}_{\text{pixel}}+{\beta }_2{L}_{\text{grad}}+{\beta }_3{L}_{\text{cont}}& (7)\end{array}$

where, β₁ = 0.88994, β₂ = 0.06, and β₃ = 0.05 are the weights associated to the loss term contributions (Bode et al., 2021). Here, the pixel loss L_pixel and gradient loss L_grad are defined by MSE between the original and reconstructed field. The term, L_cont defines the continuity loss to enforce (close to) divergence-free condition. During the first 100 epochs, the terms L_grad and L_cont are scaled to avoid dominating L_pixel by:

$\begin{array}{ll}{L}_{\kappa }^{\text{scaled}}=L_{\kappa }/10^{\lceil log(L_{\kappa }/L_{\text{pixel}})\rceil },\kappa \in \left\{\text{grad},\text{cont}\right\}.& (8)\end{array}$

4.3.2 Performance and outlook of CDM

The CDM is applied to the non-actuated TBL dataset and trained for a maximum filter width of T_n = 5 for 20,000 epochs. The batch-size is set to one and the learning rate to 0.0001. The training is performed on the JURECA system with 32 GPUs for four days. The trainings for this network are expensive due to the iterative nature of the CDM and the large U-Net architecture. Reconstruction results close to the wall are shown in Figure 14. The instantaneous streamwise velocity contour plot u_i, i = x and line plots extracted at a randomly selected time step are shown. It can be seen from the contour and line plots that Z and Ẑ are in excellent agreement, with a reconstruction error of less then four percent. At locations with high gradients, the values are slightly underestimated. Overall, even with high filter widths (upto 5x), the CDM is able to reconstruct the velocity fields with high accuracy. Furthermore, the power spectrum of instantaneous velocity gradients is depicted in Figure 15, revealing the energy distribution across different scales in the flow and helping to identify dominant turbulent structures. To calculate this, a Fourier Transform is applied to the instantaneous velocity gradient in each direction, converting these gradients to the frequency domain and squaring the amplitude of the Fourier transform then yields the power spectrum. In Figure 15, the x-axis shows the distribution of turbulent structures, with increasing wave number κ denoting smaller eddies. The fully resolved flow fields are shown with the black line, whereas the filtering operation yields the red line, shifted to the left as filtering destroys small structures. After applying the CDM model, the blue line is achieved, which reconstructs the small structures, fitting the black line almost perfectly. In an extension to this work, the trained CDM will be coupled to an LES solver (achieved with a coupling framework) and the CDM-obtained results will be benchmarked against a standard wall models for near-wall flow reconstruction.

Figure 14

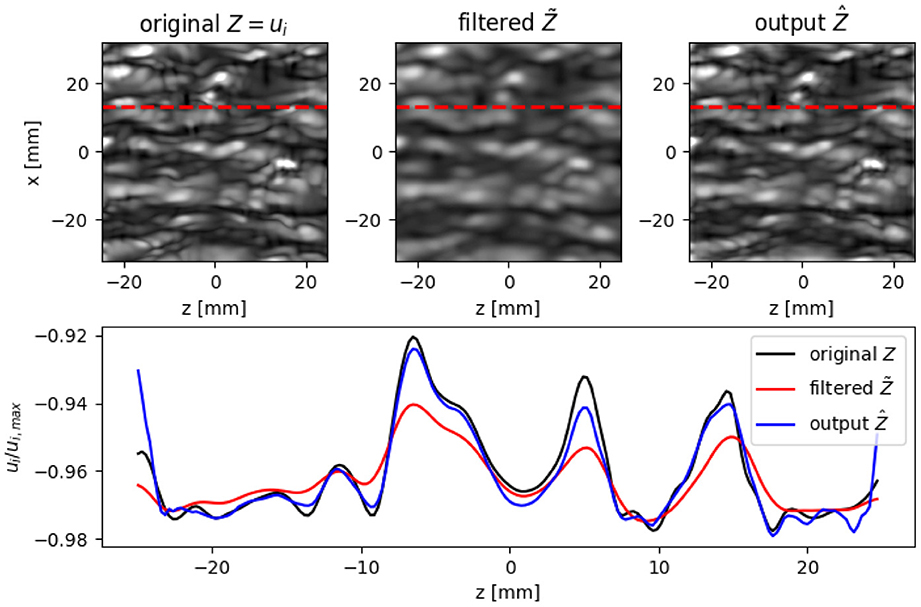
Figure 14. Performance of the CDM. Contours (Top row) and spanwise extractions (Bottom row) of the instantaneous streamwise velocity u_i with i = x for the original data Z, the filtered input $\tilde{Z}$, and the output Ẑ. Red dashed lines indicate the spanwise extraction location.

Figure 15

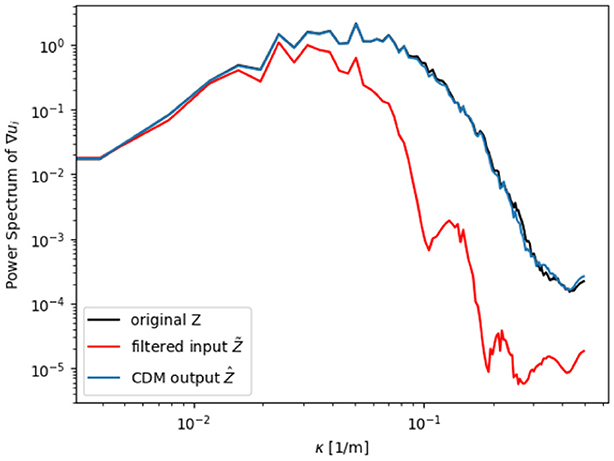
Figure 15. Power spectrum of instantaneous velocity gradients predicted by CDM and compared to the original and filtered inputs.

5 Discussion and conclusion

This manuscript detailed a comprehensive description of the AI4HPC library. The implementation, deployment, and integration of AI4HPC on leading HPC systems has been demonstrated along with its support for diverse communication libraries. Importantly, AI4HPC generates job scripts for multiple pre-configured HPC sites, which is expected to not only assist CFD users, but also popularize the exploitation of HPC infrastructure in the larger AI community. The custom data manipulation routines enables AI4HPC to be readily used for non-uniform mesh structures, which is commonly seen in CFD use cases. A benchmark on the JUWELS system highlights the scalability and performance enhancements of the library. The remarkable speed-up with a scaling efficiency of 96% achieved on up to 3,664 GPUs emphasizes the ability of the library to leverage the computational resources efficiently.

Furthermore, AI4HPC's performance is demonstrated for a large LES dataset. The training of this dataset employed up to 64 workers (in this case GPUs). Distributing the dataset to many workers converged to each worker having too few data samples leading to increased communication overheads. Hence, only a satisfactory parallel efficiency could be achieved. It was found that there was a limit to the maximum number of workers for a specific dataset size, and this limit was extended for trainings with even larger dataset sizes.

In addition, various performance optimization approaches available in AI4HPC for issues commonly encountered in AI training were presented. Two approaches to circumvent the issue of large mini-batches for a large number of workers using the DDT method were suggested. An effective solution was to apply an adaptive summation (Adasum) algorithm. Simply scaling the learning rate with the number of workers was a strong alternative. Several optimization schemes were tested to either reduce the training runtimes or to improve the accuracy. Applying a mixed precision format reduced the memory requirements but greatly increased the training error, and using gradient accumulation (with and without skipping AllReduce commands) only marginally improved the training runtimes, probably due to the small size of the network. Finally, correlating the dataset size to the training error showed no linear functional dependence between the dataset size and the training error, but a larger dataset size should be preferable to improve the generalizability of the trained NN.

Finally, the library was tested on two application cases. The first case investigated reconstruction of QoIs in the TBL flow case, combining two network architectures, a CAE-NN and CAE-PN. The CAE-NN accuracy was assessed with a mode decomposition method. The interpolation and extrapolation performance of the CAE-PN was found to be decent with ≈5% deviation in the predicted mean of ΔC_d. In the interpolation case, the P_net predictions were satisfactory with ≈7.14% deviation, while a lower but satisfactory performance of the CAE-PN was observed for P_net predictions in the extrapolation case due to the high variability in the target P_net. The workflow of the CAE-PN allowed the reconstruction of ΔC_d and P_net from low-dimensional velocity fields, which is a useful extension to the CAE-NN in terms of the ability to provide physically-relevant latent representations. The second application case was for development of an SRN with a novel NN termed CDM. This model was applied to the non-actuated TBL dataset. With an iterative increase in filter width and noise, and a loss function constrained with physical terms, the CDM learns to defilter the filtered and noised velocity fields. The network showed excellent reconstruction ability and <4% reconstruction error was obtained. This model is currently coupled to an LES solver to explore its application for providing data-driven corrections to WMLES estimations. Further investigations on these presented application cases will be performed by evaluating the performance of the presented models in terms of satisfaction of the conservation laws. In particular, to enable these investigations, a coupling framework to allow the synchronous execution of CFD and ML solvers is under active development.

AI4HPC provides a pivotal contribution to the fields of AI, CFD, and HPC. It holds the potential to drive cutting-edge research and applications in CFD and beyond. Although the library has been analyzed with respect to a CFD use case, other applications, e.g., from the computer vision and large language modeling community can easily adopt the framework and exploit HPC usage in their workflows. In this regard, the library consists of a transformer model architecture, which has already been integrated with the HPC systems. It should be noted that the backend frameworks and software configurations available at HPC sites are continuously updated and hence regular software releases are needed. Also the supported frameworks and HPC sites are non-exhaustive. However, AI4HPC already provides a wide array of options for new and advanced users. The idea of the developers of this open-source framework is to have a large community of users, which would automatically lead to an extension and support of the library across a wider spectrum. All the details and further updates on the library are available and can be accessed from the documentation¹⁹ and repository. page²⁰

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

RS: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. EI: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. MA: Data curation, Formal analysis, Investigation, Software, Writing – review & editing. AL: Formal analysis, Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research leading to these results has been conducted in the CoE RAISE project, which receives funding from the European Union's Horizon 2020—Research and Innovation Framework Programme H2020-INFRAEDI-2019-1 under grant agreement no. 951733. The authors gratefully acknowledge the computing time granted by the JARA Vergabegremium and provided on the JARA Partition part of the supercomputer JURECA (Jülich Supercomputing Centre, 2021) at Forschungszentrum Jülich, and by Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) and provided on the GCS Supercomputer Hazel Hen at Höchstleistungsrechenzentrum Stuttgart (www.hlrs.de).

Acknowledgments

The authors acknowledge the contribution of M. Albers, E. Lagemann, and W. Schröder from RWTH Aachen University for providing the LES dataset and contributing to the analysis and technical discussion of this work.

Conflict of interest

RS, EI, MA, and AL are employed by Forschungszentrum Jülich GmbH.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Available at: https://www.coe-raise.eu/od-tbl.

2. ^Available at: https://ai4hpc.readthedocs.io.

3. ^CFD solver m-AIA https://git.rwth-aachen.de/aia/m-AIA/m-AIA.

4. ^PyTorch-DDP. Available at: https://pytorch.org/docs/stable/distributed.html.

5. ^CTE-AMD. Available at: https://www.bsc.es/innovation-and-services/technical-information-cte-amd.

6. ^LUMI https://www.lumi-supercomputer.eu

7. ^AI4HPC. Available at: https://ai4hpc.readthedocs.io/en/latest/AI4HPC/HPCs.html.

8. ^Map Cubes. Available at: https://gitlab.jsc.fz-juelich.de/CoE-RAISE/FZJ/ai4hpc/ai4hpc/-/blob/master/Scripts/mapCubes.py.

9. ^Ray Tune. Available at: https://docs.ray.io/en/latest/tune/index.html.

10. ^Nsight API. Available at: https://developer.nvidia.com/nsight-perf-sdk.

11. ^Available at: https://www.mellanox.com/pdf/whitepapers/IB_Intro_WP_190.pdf.

12. ^Available at: https://www.amd.com/en/products/cpu/amd-epyc-7402.

13. ^Available at: https://www.nvidia.com/en-us/data-center/a100/.

14. ^Available at: https://www.amd.com/en/products/cpu/amd-epyc-7742.

15. ^NVIDIA A100. Available at: https://www.nvidia.com/en-us/data-center/a100.

16. ^https://www.hdfgroup.org/HDF5.

17. ^Manual Seed. Available at: https://pytorch.org/docs/stable/generated/torch.manual_seed.html.

18. ^Available at: https://horovod.readthedocs.io/en/stable/adasum_user_guide_include.html.

19. ^Available at: https://ai4hpc.readthedocs.io/en/latest/.

20. ^Available at: https://gitlab.jsc.fz-juelich.de/CoE-RAISE/FZJ/ai4hpc/ai4hpc.

References

Aach, M., Sarma, R., Inanc, E., Riedel, M., and Lintermann, A. (2023). “Short paper: accelerating hyperparameter optimization algorithms with mixed precision,” in SC-W '23 (New York, NY: Association for Computing Machinery), 1776–1779.

Google Scholar

Albers, M., Meysonnat, P. S., Fernex, D., Semaan, R., Noack, B. R., and Schröder, W. (2020). Drag reduction and energy saving by spanwise traveling transversal surface waves for flat plate flow. Flow Turbul. Combust., 105, 125–157. doi: 10.1007/s10494-020-00110-8

Crossref Full Text | Google Scholar

Albers, M., Meysonnat, P. S., Fernex, D., Semaan, R., Noack, B. R., Schröder, W., et al. (2023). CoE RAISE - Data for Actuated Turbulent Boundary Layer Flows. Espoo: EUDAT CDI.

Google Scholar

Albers, M., Meysonnat, P. S., and Schröder, W. (2019). Actively reduced airfoil drag by transversal surface waves. Flow Turbul. Combust. 102, 865–886. doi: 10.1007/s10494-018-9998-z

Crossref Full Text | Google Scholar

Albers, M., and Schröder, W. (2021). Lower drag and higher lift for turbulent airfoil flow by moving surfaces. Int. J. Heat. Fluid Flow 88:108770. doi: 10.1016/j.ijheatfluidflow.2020.108770

Crossref Full Text | Google Scholar

Berkooz, G., Holmes, P., and Lumley, J. L. (1993). The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575. doi: 10.1146/annurev.fl.25.010193.002543

Crossref Full Text | Google Scholar

Bode, M., Gauding, M., Lian, Z., Denker, D., Davidovic, M., Kleinheinz, K., et al. (2021). Using physics-informed enhanced super-resolution GANs for subfilter modeling in turbulent reactive flows. Proc. CI 38, 2617–2625. doi: 10.1016/j.proci.2020.06.022

Crossref Full Text | Google Scholar

Brace, A., Yakushin, I., Ma, H., Trifan, A., Munson, T., Foster, I., et al. (2022). “Coupling streaming AI and HPC ensembles to achieve 100–1000 × faster biomolecular simulations,” in 2022 IEEE International Parallel and Distributed Processing Symposium (IPDPS) (Los Alamitos, CA: IEEE Computer Society), 806–816.

Google Scholar

Brunton, S. L., Noack, B. R., and Koumoutsakos, P. (2020). Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 52, 477–508. doi: 10.1146/annurev-fluid-010719-060214

Crossref Full Text | Google Scholar

Carlberg, K., Farhat, C., Cortial, J., and Amsallem, D. (2013). The GNAT method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 242:623–647. doi: 10.1016/j.jcp.2013.02.028

Crossref Full Text | Google Scholar

Çiçek, Ö., Abdulkadir, A., Lienkamp, S. S., Brox, T., and Ronneberger, O. (2016). “3D U-Net: learning dense volumetric segmentation from sparse annotation,” in MICCAI (Athens), 424–432.

Google Scholar

Csala, H., Dawson, S. T. M., and Arzani, A. (2022). Comparing different nonlinear dimensionality reduction techniques for data-driven unsteady fluid flow modeling. Phys. Fluids 34:117119. doi: 10.1063/5.0127284

Crossref Full Text | Google Scholar

Duraisamy, K. (2021). Perspectives on machine learning-augmented Reynolds-averaged and large eddy simulation models of turbulence. Phys. Rev. Fluids 6:050504. doi: 10.1103/PhysRevFluids.6.050504

Crossref Full Text | Google Scholar

Faller, W. E., and Schreck, S. J. (1996). Neural networks: applications and opportunities in aeronautics. Prog. Aerosp. Sci. 32, 433–456. doi: 10.1016/0376-0421(95)00011-9

PubMed Abstract | Crossref Full Text | Google Scholar

Fu, R., Xiao, D., Navon, I., Fang, F., Yang, L., Wang, C., et al. (2023). A non-linear non-intrusive reduced order model of fluid flow by auto-encoder and self-attention deep learning methods. Int. J. Numer. Methods Eng. 124, 3087–3111. doi: 10.1002/nme.7240

Crossref Full Text | Google Scholar

Fukami, K., Fukagata, K., and Taira, K. (2023). Super-resolution analysis via machine learning: a survey for fluid flows. Theor. Comput. Fluid Dyn. 37, 421–444. doi: 10.1007/s00162-023-00663-0

Crossref Full Text | Google Scholar

Götz, M., Debus, C., Coquelin, D., Krajsek, K., Comito, C., Knechtges, P., et al. (2020). “HeAT-a distributed and GPU-accelerated tensor framework for data analytics,” in 2020 IEEE Int. Conf. on Big Data (Atlanta: IEEE), 276–287.

Google Scholar

Goyal, P., Dollár, P., Girshick, R. B., Noordhuis, P., Wesolowski, L., Kyrola, A., et al. (2017). Accurate, large minibatch SGD: training ImageNet in 1 hour. arXiv [prepint]. doi: 10.48550/arXiv.1706.02677

Crossref Full Text | Google Scholar

Ho, J., Jain, A., and Abbeel, P. (2020). Denoising diffusion probabilistic models. Adv. Neur. I. Proc. Sys. 33, 6840–6851. doi: 10.48550/arXiv.2006.11239

Crossref Full Text | Google Scholar

Jin, X., Cheng, P., Chen, W.-L., and Li, H. (2018). Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 30:047105. doi: 10.1063/1.5024595

Crossref Full Text | Google Scholar

Jülich Supercomputing Centre (2021). JURECA: data centric and booster modules implementing the modular supercomputing architecture at Jülich Supercomputing Centre. J. Large Scale Res. Facil. 7:A182. doi: 10.17815/jlsrf-7-182

Crossref Full Text | Google Scholar

Kim, H., Kim, J., Won, S., and Lee, C. (2021). Unsupervised deep learning for super-resolution reconstruction of turbulence. J. Fluid Mech. 910:A29. doi: 10.1017/jfm.2020.1028

Crossref Full Text | Google Scholar

Kochkov, D., Smith, J. A., Alieva, A., Wang, Q., Brenner, M. P., and Hoyer, S. (2021). Machine learning-accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. U. S. A. 118:e2101784118. doi: 10.1073/pnas.2101784118

PubMed Abstract | Crossref Full Text | Google Scholar

Krause, D. (2019). JUWELS: modular tier-0/1 supercomputer at the Jülich Supercomputing Centre. J. Large Scale Res. Facil. 5:A135. doi: 10.17815/jlsrf-5-171

Crossref Full Text | Google Scholar

Lee, H., Merzky, A., Tan, L., Titov, M., Turilli, M., Alfe, D., et al. (2021). “Scalable HPC & AI infrastructure for COVID-19 therapeutics,” in Proceedings of the Platform for Advanced Scientific Computing Conference, PASC '21 (New York, NY: Association for Computing Machinery).

Google Scholar

Li, S., Zhao, Y., Varma, R., Salpekar, O., Noordhuis, P., Li, T., et al. (2020). Pytorch distributed: experiences on accelerating data parallel training. arXiv [preprint]. doi: 10.14778/3415478.3415530

Crossref Full Text | Google Scholar

Ling, J., Kurzawski, A., and Templeton, J. (2016). Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 807, 155–166. doi: 10.1017/jfm.2016.615

Crossref Full Text | Google Scholar

Lintermann, A., Meinke, M., and Schröder, W. (2020). Zonal Flow Solver (ZFS): a highly efficient multi-physics simulation framework. Int. J. Comput. Fluid Dyn. 34, 458–485. doi: 10.1080/10618562.2020.1742328

Crossref Full Text | Google Scholar

Maleki, S., Musuvathi, M., Mytkowicz, T., Saarikivi, O., Xu, T., Eksarevskiy, V., et al. (2020). Scaling distributed training with adaptive summation. arXiv [preprint]. doi: 10.48550/arXiv.2006.02924

Crossref Full Text | Google Scholar

Mäteling, E., and Schröder, W. (2022). Analysis of spatiotemporal inner-outer large-scale interactions in turbulent channel flow by multivariate empirical mode decomposition. Phys. Rev. Fluids 7:034603. doi: 10.1103/PhysRevFluids.7.034603

Crossref Full Text | Google Scholar

Maulik, R., San, O., Rasheed, A., and Vedula, P. (2019). Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 858, 122–144. doi: 10.1017/jfm.2018.770

PubMed Abstract | Crossref Full Text | Google Scholar

Meyer, L., Schouler, M., Caulk, R. A., Ribés, A., and Raffin, B. (2023). “Training deep surrogate models with large scale online learning,” in 40th International Conference on Machine Learning (Honolulu: ICML), 202.

Google Scholar

Obiols-Sales, O., Vishnu, A., Malaya, N., and Chandramowliswharan, A. (2020). “CFDNet: a deep learning-based accelerator for fluid simulations,” in Proceedings of the 34th ACM International Conference on Supercomputing, ICS '20 (New York, NY: Association for Computing Machinery).

Google Scholar

Pant, P., and Farimani, A. B. (2021). Deep learning for efficient reconstruction of high-resolution turbulent DNS data. arXiv [preprint]. doi: 10.48550/arXiv.2010.11348

Crossref Full Text | Google Scholar

Perlin, K. (1985). An image synthesizer. ACM Siggraph Comp. Graph. 19, 287–296. doi: 10.1145/325165.325247

Crossref Full Text | Google Scholar

Peterson, J. L., Bay, B., Koning, J., Robinson, P., Semler, J., White, J., et al. (2022). Enabling machine learning-ready HPC ensembles with Merlin. Fut. Gener. Comp. Syst. 131, 255–268. doi: 10.1016/j.future.2022.01.024

Crossref Full Text | Google Scholar

Rasley, J., Rajbhandari, S., Ruwase, O., and He, Y. (2020). “Deepspeed: system optimizations enable training deep learning models with over 100 billion parameters,” in Proc. 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (New York, NY), 3505–3506.

Google Scholar

Raveh, D. E. (2004). Identification of computational-fluid-dynamics based unsteady aerodynamic models for aeroelastic analysis. J. Aircraft 41, 620–632. doi: 10.2514/1.3149

Crossref Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net: convolutional networks for biomedical image segmentation. arXiv [preprint]. doi: 10.1007/978-3-319-24574-4_28

Crossref Full Text | Google Scholar

Sarma, R., and Dwight, R. P. (2017). Uncertainty reduction in aeroelastic systems with time-domain reduced-order models. AIAA J. 55, 2437–2449. doi: 10.2514/1.J055527

Crossref Full Text | Google Scholar

Sarma, R., Inanc, E., Aach, M., and Lintermann, A. (2024). AI4HPC Performance and Applications. Zenodo.

Google Scholar

Scalabrin, G., Condosta, M., and Marchi, P. (2006). Modeling flow boiling heat transfer of pure fluids through artificial neural networks. Int. J. Therm. Sci. 45, 643–663. doi: 10.1016/j.ijthermalsci.2005.09.009

Crossref Full Text | Google Scholar

Schmid, P. J. (2010). Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28. doi: 10.1017/S0022112010001217

Crossref Full Text | Google Scholar

Sergeev, A., and Del Balso, M. (2018). Horovod: fast and easy distributed deep learning in TensorFlow. arXiv [preprint]. doi: 10.48550/arXiv.1802.05799

Crossref Full Text | Google Scholar

Shu, D., Li, Z., and Barati Farimani, A. (2023). A physics-informed diffusion model for high-fidelity flow field reconstruction. J. Comput. Phys. 478:111972. doi: 10.1016/j.jcp.2023.111972

Crossref Full Text | Google Scholar

Sirignano, J., MacArt, J. F., and Freund, J. B. (2020). DPM: a deep learning PDE augmentation method with application to large-eddy simulation. J. Comput. Phys. 423:109811. doi: 10.1016/j.jcp.2020.109811

Crossref Full Text | Google Scholar

Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., and Ganguli, S. (2015). “Deep unsupervised learning using nonequilibrium thermodynamics,” in Int. Conf. on ML (Lille: PMLR), 2256–2265.

Google Scholar

Stiller, P., Makdani, V., Pöschel, F., Pausch, R., Debus, A., Bussmann, M., et al. (2022). Continual learning autoencoder training for a particle-in-cell simulation via streaming. arXiv [preprint]. doi: 10.48550/arXiv.2211.04770

Crossref Full Text | Google Scholar

Suarez, E., Kreuzer, A., Eicker, N., and Lippert, T. (2021). The DEEP-EST Project. Schriften des Forschungszentrums Jülich IAS Series (Jülich: Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag), 9–25.

Google Scholar

Taira, K., Brunton, S. L., Dawson, S. T. M., Rowley, C. W., Colonius, T., McKeon, B. J., et al. (2017). Modal analysis of fluid flows: an overview. AIAA J. 55, 4013–4041. doi: 10.2514/1.J056060

Crossref Full Text | Google Scholar

Turilli, M., Balasubramanian, V., Merzky, A., Paraskevakos, I., and Jha, S. (2019). Middleware building blocks for workflow systems. Comp. Sci. Eng. 21, 62–75. doi: 10.1109/MCSE.2019.2920048

Crossref Full Text | Google Scholar

Um, K., Brand, R., Fei, Y. R., Holl, P., and Thuerey, N. (2020). “Solver-in-the-loop: learning from differentiable physics to interact with iterative pde-solvers,” in NIPS '20 (Red Hook, NY: Curran Associates Inc.).

Google Scholar

Wang, Y., Xie, Z., Xu, K., Dou, Y., and Lei, Y. (2016). An efficient and effective convolutional auto-encoder extreme learning machine network for 3d feature learning. Neurocomputing 174, 988–998. doi: 10.1016/j.neucom.2015.10.035

Crossref Full Text | Google Scholar

Yamazaki, M., Kasagi, A., Tabuchi, A., Honda, T., Miwa, M., Fukumoto, N., et al. (2019). Yet another accelerated SGD: ResNet-50 training on ImageNet in 74.7 seconds. arXiv [preprint]. doi: 10.48550/arXiv.1903.12650

Crossref Full Text | Google Scholar

You, Y., Gitman, I., and Ginsburg, B. (2017). Scaling SGD batch size to 32K for ImageNet training. arXiv [preprint]. doi: 10.48550/arXiv.1708.03888

Crossref Full Text | Google Scholar

Appendix

This section provides instructions to reproduce the application cases. After cloning the git repository as described in Section 2, the networks for each of these application cases can be loaded with the preferred distributed backend. For the applications shown here, PyTorch-DDP (fw 1) is used. For the CAE-NN network (model 1), AI4HPC can be built with the command:

  python setup.py --model 1 --fw 1

Similarly, for the CAE-PN and CDM cases, choosing model 3 and model 2 loads the corresponding networks. The installation generates the main Python script ai4hpc.py, startscript.sh for submitting the job and src folder with all the dependencies. A job can be submitted to an HPC system with:

  sbatch startscript.sh

The network states and all data related to the applications can be accessed from the open-access dataset (Sarma et al., 2024). The TBL dataset itself, which is used for all the trainings in this manuscript, is also open source and available from Albers et al. (2023).