Quantifying the long-term recovery of the protective effect of forests against rockfall after stand-replacing disturbances

Introduction: Increasing disturbances may significantly impact the long-term protective effect of forests against natural hazards. Quantifying the temporal development of the protective effect of forests is thus crucial for finding optimal management strategies.

Methods: In this study, we analyzed the long-term recovery of the protective effect of the secondary stands of spruce (Picea abies), fir (Abies alba), and beech (Fagus sylvatica) forests against rockfall after stand-replacing disturbances based on data of the Swiss National Forest Inventory (NFI). We therefore derived the age of the inventoried forest stands of those tree species based on a growth parametrization and quantified their energy dissipation capacity in rockfall processes as a function of stand age. We then analyzed the development of their protective factor for varying rockfall dispositions.

Results: Generally, it takes between 50 and 200 years to regain the maximum possible protective effect, depending from the site conditions and the rockfall disposition. This implies that the recovery of the protective effect after a severe disturbance may require more time than the decay of the protective effect from disturbance legacies, resulting in a long lasting gap of the provided protection.

Discussion: The here presented approach can serve as a basis to estimate the general range of recovery of the protective effect of beech, fir and spruce forests against rockfall provided by forest stands. Future research should analyse the effects of environmental and forest conditions as well as varying disturbance intensities and legacies to enable the assessment of specific trajectories of the short- and long-term recovery of the protective effect.

1 Introduction

European forests have been increasingly affected by natural disturbances, such as wind, fire, or insects, and this trend is likely to continue in the future given the ongoing climate change (IPCC, 2014; Senf and Seidl, 2021). The altering disturbance regimes may critically change the provision of ecosystem services provided by forests (Knoke et al., 2021; Stritih et al., 2021) and enhance the uncertainty in forest management (Polasky et al., 2011). In steep slope environments, the protective effect provided by forests against gravitational natural hazards, such as rockfall, avalanche, or landslide, is of great importance to affected communities. These forests can replace cost-intensive technical measures or reduce their installation and maintenance costs (Dorren and Moos, 2022). However, more frequent and severe disturbances are likely to impair their protective effect more often in future (Bebi et al., 2017; Irauschek et al., 2017; Sebald et al., 2019). Thus, quantifying the recovery of the protective effect of forests after disturbances is crucial for understanding the resilience of protective forests in the context of natural hazard and forest management. It can serve as basis for the planning of silvicultural measures and decisions on technical measures compensating for the protective effect of the forest.

Only a few studies quantified the post-disturbance recovery of the protective effect of forests against rockfall. Maringer et al. (2016) assessed the protective effect of fire-injured beech forests for different block volumes, slope inclinations, and forested slope lengths. They revealed a substantial reduction of the protective effect after moderate- to high-severity burns. Moos et al. (2019a) quantified the evolution of the risk reduction provided by a protective forest considering fire disturbances based on a probabilistic approach. Other studies analyzed the protective effect before and after windthrow events without monitoring its development (Costa et al., 2021; Ringenbach et al., 2022).

In the case of rockfall hazards, the protective effect of a forest is controlled by forest properties (tree density, basal area, tree species, forested slope length) as well as site properties (block volume, slope inclination, cliff height, slope curvature, surface roughness, soil compliance; Dupire et al., 2016; Moos et al., 2017). Accordingly, the duration of the recovery of the protective effect after a disturbance event critically depends on the disturbance severity and the site properties. While for low-severity disturbances, the loss in protective effect may be of short duration or even be compensated by disturbance legacies, such as standing or lying deadwood (Fuhr et al., 2015; Ringenbach et al., 2022), high-severity disturbance events and delayed reforestation may result in a long critical phase of reduced protective effect (Maringer et al., 2016).

In this study, we investigated the recovery of the protective effect against rockfall for the dominating tree species spruce (Picea abies), fir (Abies alba), and beech (Fagus sylvatica) in Switzerland after hypothetical severe, stand-replacing disturbance events based on data of the Swiss National Forest Inventory (NFI; Fischer and Traub, 2019). Thereby, we explicitly addressed the protective effect of the secondary stand, which we assumed as uniform in terms of age structure and species composition, and did not account for disturbance legacies from the primary stand. In order to be able to objectively assign an age to the stands of the NFI plots from tree density and basal area, we implemented an analytical growth parameterization similar to Flepp et al. (2021). We then coupled parameterized stand development with an empirically-based rockfall model developed by Berger and Dorren (2007) to calculate the energy dissipation capacity of forest stands. Based on this, we analyzed the long-term development of the total protective factor of the forest stands for varying rockfall dispositions (block volume, cliff height, slope inclination, slope length). Both variables, the energy dissipation capacity and the total protective factor are the basis for quantifying the recovery of the protective effect. Therefore, we define the recovery potential as the maximum possible energy dissipation capacity respectively protective factor and the recovery duration as the time required to reach it.

2 Methods

2.1 Study design

The methodological approach applied in this study consists of the following work steps (Figure 1). The underlying data sources are explained in detail in the following subsection.

1 Parametrization of diameter growth for spruce-, fir-, and beech-dominated stands for different site properties based on long-term data of the Swiss National Forest inventory (NFI) to derive a relationship between the mean stand diameter and stand age;

2 Calculation of the energy dissipation capacity of these stands as a function of stand age independent from the rockfall disposition;

3 Quantification of the development of the protective factor of these stands for different rockfall dispositions.

FIGURE 1

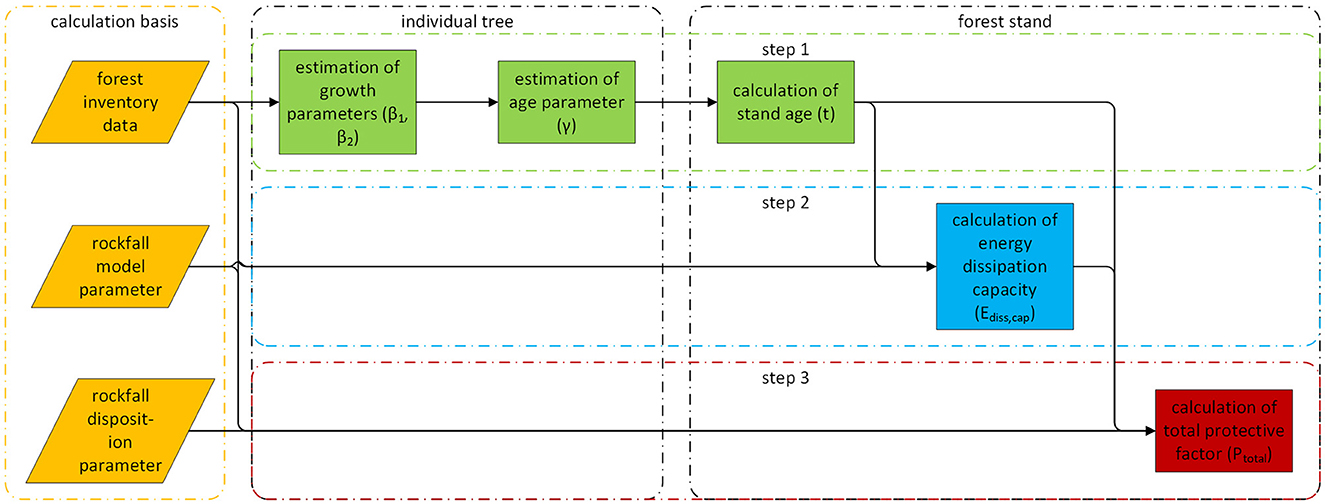
Figure 1. Schematic overview of the workflow applied in the study with three work steps and three data sources as well as their connection in the process.

2.2 Data basis

We used long-term stand data from the NFI to quantify the development of the protective effect of spruce-, fir-, and beech- dominated forests as function of stand age. The NFI comprises data for about 40 years, collected during four inventory periods (NFI1 1983–1985, NFI2 1993–1995, NFI3 2004–2006, NFI4 2009–2017; Fischer and Traub, 2019). Specifically, individual tree and forest stand data was systematically assessed in sample plots on a 1.4 km times 1.4 km grid (1 km times 1 km in the first inventory). In each plot, all trees with a diameter at breast height (1.3 m) D_bh (m) >12 cm were measured in an inner plot of 200 m² and all trees with a D_bh >36 cm in an outer circle of 500 m². The NFI thus provided stand data over the whole forest area of Switzerland (Figure 2).

FIGURE 2

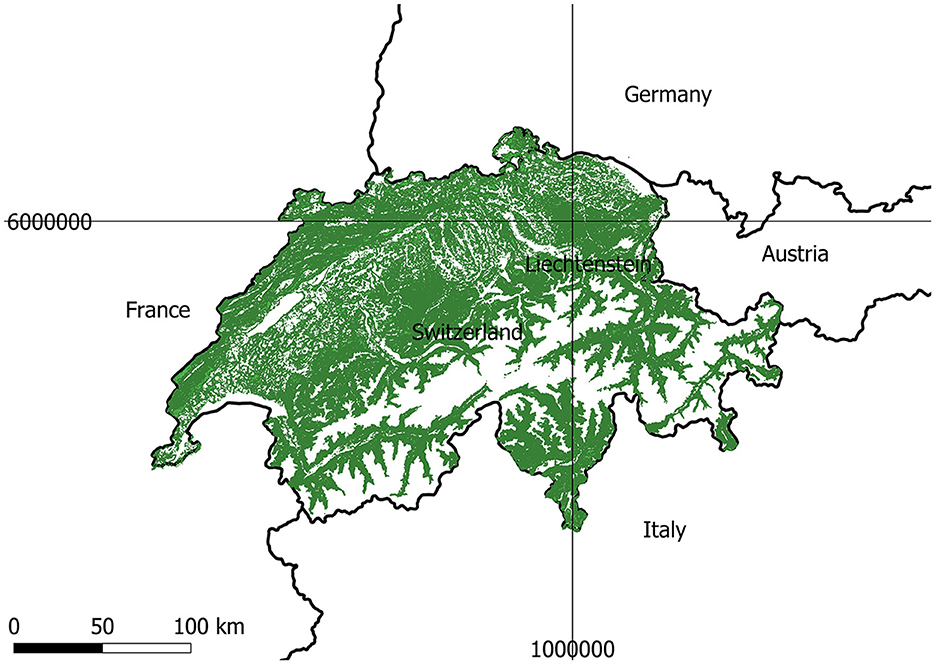
Figure 2. Geographic map of Switzerland (EPSG:3857 coordinates) with the current forest area according to the topografic landscale model (green color) where the NFI data was collected (Swisstopo, 2023).

Data about the tree diameter from all accessible NFI plots (except for shrub forest) that were re-sampled in at least two inventory periods were considered. The NFI data further include estimates of tree and stand age t (yr) based on tree ring counts on nearby stumps, whorl counts, forester survey, and expert appraisal. Topographic characteristics such as site elevation, slope aspect, and slope inclination were derived from the Swisstopo DHM25 digital elevation model (Fischer and Traub, 2019).

We applied parameter and concepts from the model RockforNET developed by Berger and Dorren (2007) to quantify the protective effect against rockfall hazards. Data on the energy dissipation capacity of the different species was based on Dorren and Berger (2005) and Moos et al. (2019b), who derived species-specific energy dissipation capacity based on real-size rockfall impact experiments and a discrete-element model of tree impacts. The parameter to characterize specific rockfall dispositions were derived from a study from Menk et al. (2023), which investigated 16 rockfall sites in Switzerland.

2.3 Growth parameterization

The concept for the parameterization of tree and stand growth was based on the approach presented in Flepp et al. (2021) for root reinforcement dynamics in spruce-dominated forests. It mainly aimed at deriving the stand age as a function of its quadratic mean diameter D_qm based on a more consistent and objective approach than the age estimates in the NFI data, which are based on various methods and also on expert opinion. It consisted of the parametrization of diameter increment of single trees to derive a model for the D_bh as function of tree age, which was then transferred to the stand level. In this study, we extended the approach of Flepp et al. (2021) for beech and fir forests and introduced a method to estimate also the initial conditions from the NFI data. We considered only data from approximately mono-species stands, which we defined as NFI plots with at least 80% of the basal area represented by the respective species.

We parameterized diameter growth of individual trees that were measured in at least two consecutive NFI inventories following Flepp et al. (2021). We therefore assumed a linear model (LM) of the diameter increment as function of the tree diameter (Equation 1). This linear differential equation can be solved obtaining an expression for D_bh as function of t (Equation 2).

$\begin{array}{ll}\frac{d{D}_{bh}}{dt}={\beta }_1+{\beta }_2\times D_{bh}& (1)\end{array}$

$\begin{array}{ll}{D}_{bh}=\frac{{\beta }_1\times (exp({\beta }_2\times (t-\gamma ))-1)}{{\beta }_2}& (2)\end{array}$

Thereby, the growth coefficients β₁ (m*yr^-1) and β₂ (yr^-1) were parameterized using a LM depending on the site elevation (above sea level) z (m), the slope aspect (squared sinus of the half north deviation angle) a (-) and the slope inclination (tangens of the inclination angle) s (-) (Equations 3 and 4). The age coefficient γ (yr) represents the integration constant and was defined as the age at which a tree reaches breast height, which corresponds by definition to a D_bh equal to 0 cm. It was also parameterized with a LM depending on site elevation, slope aspect and slope inclination based on available estimations of tree age in the NFI data (Equation 5). The linear functions allowed for using a robust linear regression which was conducted with the function lm() from the package stats (R Core Team, 2021).

$\begin{array}{ll}{\beta }_1=x_0+x_1\times z+x_2\times a+x_3\times s& (3)\end{array}$

$\begin{array}{ll}{\beta }_2=x_4+x_5\times z+x_6\times a+x_7\times s& (4)\end{array}$

$\begin{array}{ll}\gamma =y_0+y_1\times z+y_2\times a+y_3\times s& (5)\end{array}$

For the application of this growth parameterization from the individual tree level to the forest stand level, we assumed the case of an approximately uniform stand, which is feasible for the recovery after a stand-replacing disturbance on the scale of tree cohorts (Harvey et al., 2002; Angelstam and Kuuluvainen, 2004). Under this assumption, the D_bh of the individual trees is equal to the mean squared diameter D_qm (m) of the forest stand and the tree age corresponds to the stand age. This relation was then used to estimate the stand age from the mean squared diameter of the forest stands in the NFI data.

2.4 Rockfall model

To quantify the development of the protective effect of a forest against rockfall, we first calculated the energy dissipation capacity of a forest as a function of stand age. In a second step, we determined the total protective factor of a forest in terms of the proportion of stopped blocks as a function of stand age as well as other rockfall disposition parameters. For the total protective factor, required energy reduction and sufficient tree impacts are taken into account for specific rockfall dispositions (Figures 1, 3).

FIGURE 3

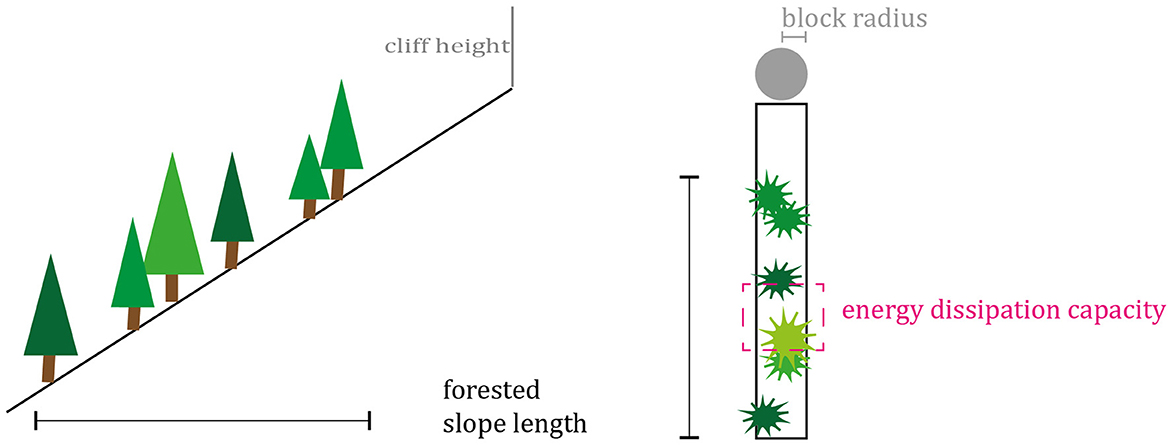
Figure 3. Conceptual scheme of the protective effect of a forest stand against rockfall that combines the energy dissipation capacity (E_diss,cap) as forest property with rockfall disposition (forested slope length, cliff height, and block radius, respectively block volume) to the total protective factor (P_total).

The energy dissipation capacity of a forest per area swept by a block E_diss,cap (J*m^-2) was calculated based on an empirical relationship depending on the quadratic mean diameter D_qm, the tree density N (m^-2), and the energy dissipation constant E_{diss, 0} (J) derived from the model RockforNET (Berger and Dorren, 2007; Equation 6). It corresponds to the maximum possible energy dissipation of a forest referred to the planimetric slope length independent of the specific rockfall disposition.

$\begin{array}{ll}{E}_{diss,cap}=E_{diss,0}\times N\times {(\frac{D_{qm}}{D_0})}^{2.31}& (6)\end{array}$

The energy dissipation constant E_{diss, 0} is a species-specific parameter (59,047 J for spruce, 65,607 J for fir, and 85,290 J for beech) and corresponds to the maximum possible energy that a tree can absorb from a block impact. The diameter constant D₀ served for normalization of the power relationship and was set to 25 cm (following Reineke, 1933), which means that the energy dissipation constant refers to a tree with this diameter.

The protective factor based on the energy reduction provided by the forest P_energy (-) was defined as the ratio of energy that a forest strip may potentially dissipate from a falling block and its total kinetic energy E_kin,tot (J) (Equation 7). Both, the forested slope length l_F (m) and the unforested slope length l_nF (m) contribute to the total kinetic energy but only the forested slope length contributes to the energy reduction due to tree impacts. The R_d (-) determines the maximum distance between the block and the tree which results from the multiplication with the block radius r (m) and was set to 0.95. E_kin,tot was calculated based on the energy line principle (assuming an energy line angle equal to 31°) following Berger and Dorren (2007).

$\begin{array}{ll}{P}_{energy}=\frac{2\times E_{diss,cap}\times l_F\times r\times R_d}{E_{kin,tot}}& (7)\end{array}$

We further calculated the protective effect with respect to the number of trees required for sufficient tree impacts P_impacts (-). It is based on the assumption of a minimum distance d_min (m) between two tree impacts, which is required to avoid that the falling block uptakes again the energy it had before the last tree impact. The d_min was set to 43 m following Berger and Dorren (2007) and must be corrected with the cosine of the slope inclination to the planimetric reference. The P_impacts was finally calculated as the ratio of the given tree density N and the required tree density for sufficient tree impacts (Equation 8).

$\begin{array}{ll}{P}_{impacts}=2\times d_{min}\times N\times r\times R_d\times cos(atan(s))& (8)\end{array}$

Calculated values of P_energy or P_impacts were limited to a range between 0 and 100 % since smaller or larger values are not reasonable in our definition of the protective factor. The total protective factor P_total (-) was calculated as the geometric mean of P_energy and P_impacts (Equation 9). It corresponds to the possible protection provided by a forest for a specific rockfall disposition.

$\begin{array}{ll}{P}_{total}=\sqrt{P_{energy}\times P_{impacts}}& (9)\end{array}$

2.5 Recovery quantification

Both variables, the energy dissipation capacity (E_diss,cap) and the total protective factor (P_total), were calculated for each NFI plot for a stand age up to 200 years while for P_total only plots with a slope inclination greater than the energy line angle of 31° were considered. We defined ranges for the forested slope length, cliff height and block volume based on data from 16 rockfall sites of the study from Menk et al. (2023) to get a realistic estimation of the variation for typical rockfall protective forests in Switzerland. Based on this study we also defined constant values for the unforested slope length, block density and shape factor (ratio of cubic block diameter to block volume; Table 1).

TABLE 1

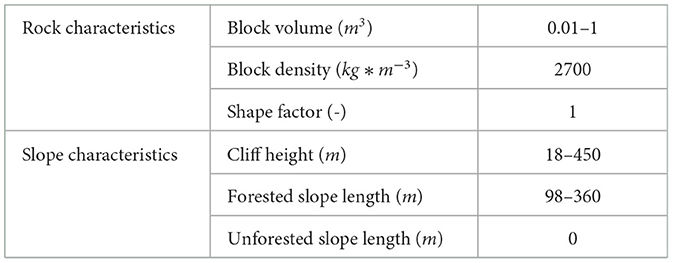
Table 1. Values of the parameters determining the rockfall disposition considered in the analysis of the development of the total protective factor (P_total) based on the investigation of 16 rockfall sites in Switzerland (Menk et al., 2023).

To derive the trend in the data and analyse the factors influencing the development of the protective factor, we fitted generalized additive models (GAM) to the calculated values of E_diss,cap and P_total. This approach allowed the modeling of non-linear relationships without the assumption of a specific function. In the GAM we implemented stand age as non-linear splines and the constant parameters (site elevation, slope aspect, slope inclination, forested slope length, cliff height, and block volume) as linear terms, whereby also interactions between stand age and the constant parameters were considered. The GAM was conducted with the function gam() from the package mgcv (R Core Team, 2021). To get robust results for the total protective factor, we applied a Monte-Carlo simulation approach. We repeated the calculation of the total protective factor per NFI plot 100 times with randomly selecting forested slope length, cliff height, and block volume from the considered ranges each time.

The curves derived from the GAM do not reflect effective trajectories of real disturbance events, but the statistical trend of the recovery of the protective effect that could be found in the NFI data combined with different rockfall dispositions. The application of the fitted GAM over the whole range of considered stand age enabled us to quantify the time required (recovery duration) to reach the maximum value (recovery potential) of E_diss,cap, and P_total. This allows to quantify the recovery of uniform forests after a stand-replacing disturbance depending on the site conditions and rockfall dispositions typical for Switzerland.

3 Results

3.1 Age estimation

For all considered tree species, beech, fir, and spruce, the quadratic mean diameter D_qm was an approximately linear function of the stand age t (Figure 4). This implies an almost constant growth rate for the individual trees of the assumed uniform stand in a range of 0.1–1 cm*yr^-1, which was more influenced by the site conditions than by the tree species.

FIGURE 4

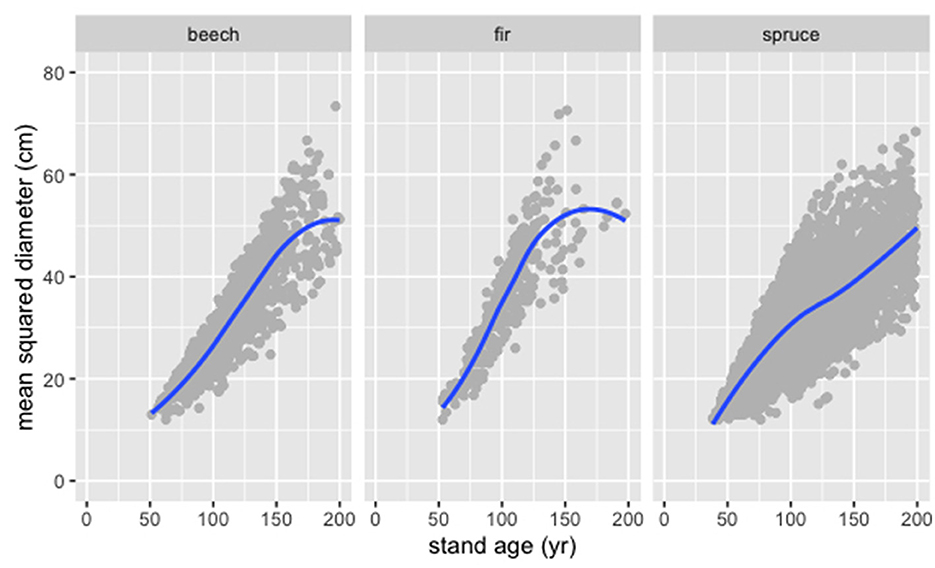
Figure 4. Quadratic mean diameter (D_qm) as function of stand age (t) derived from the fitted LM for all available NFI plots (gray dots) and the corresponding smoothed mean (blue lines) for the tree species beech, fir, and spruce.

The fitted LM to estimate t from the given D_qm is better for the growth coefficients than for the age coefficient while the model quality is similar for all considered tree species (Table 2). The application of this parameterization resulted in an error for the age estimation in the order of magnitude of 10 years. Further error may result from the assumption of an uniform stand, which can not be determined since the true age of the NFI stands is unknown.

TABLE 2

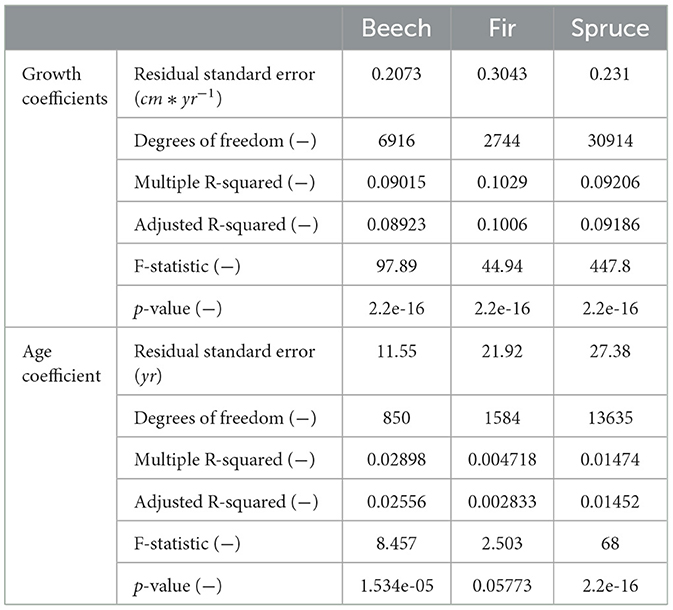
Table 2. Model output for the evaluation of the quality of the fitted LM for the growth coefficients and the age coefficient used for the age estimation.

3.2 Protective effect development

The energy dissipation capacity (E_diss,cap) increased continuously with stand age t and flattened toward a constant value for all considered tree species (Figure 5). The fitted GAM yields an approximately monotonic function of t that also considered site condition parameter and can represent a substantial part of the variability in the calculated values of E_diss,cap (Table 3).

FIGURE 5

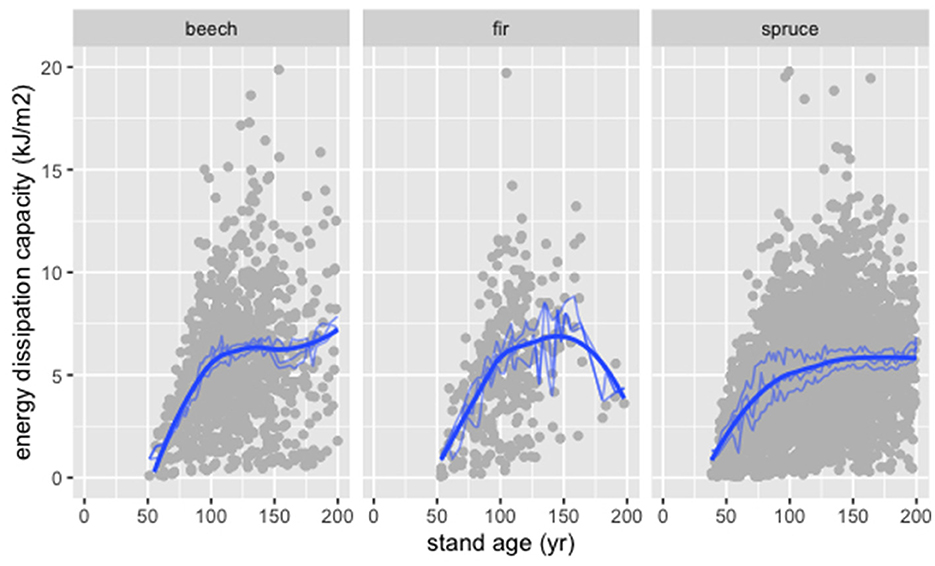
Figure 5. Energy dissipation capacity (E_diss,cap) as function of stand age (t) calculated for all available NFI plots (gray dots) and modeled with the fitted GAM (blue lines) for the tree species beech, fir, and spruce.

TABLE 3

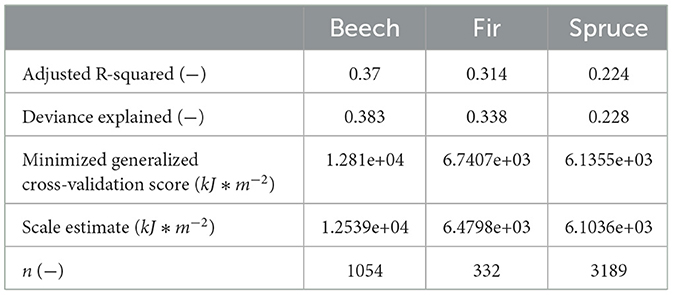
Table 3. Model output for the evaluation of the quality of the fitted GAM used for the development of energy dissipation capacity (E_diss,cap) as a function of stand age t and site condition parameter.

The total protective factor (P_total) generally increased with t, too, while it tended to decline again after reaching a maximum value for all considered tree species (Figure 6). The fitted GAM yields a non-monotonic function of t that also considers site condition as well as rockfall disposition parameter and can represent a substantial part of the variability in the calculated values of P_total (Table 4).

FIGURE 6

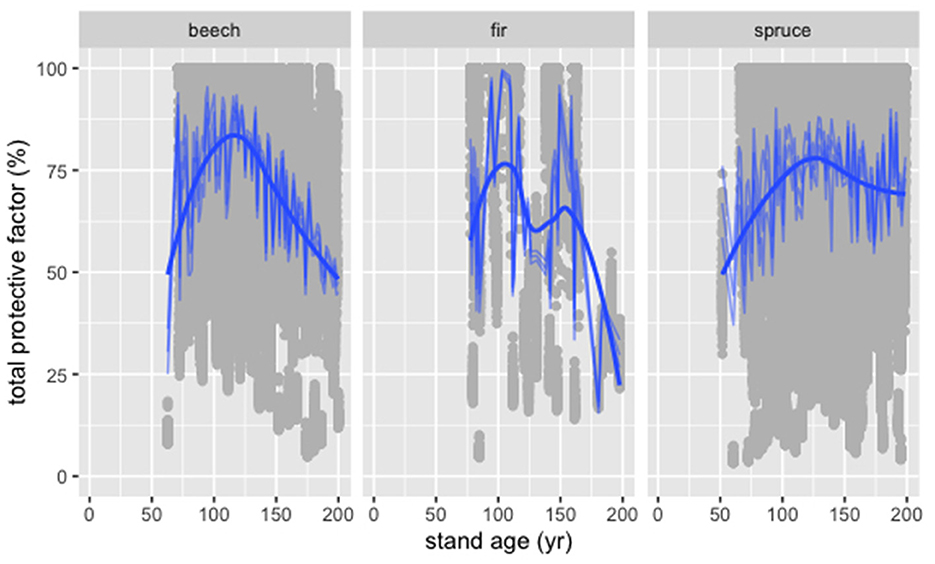
Figure 6. Total protective factor (P_total) as function of stand age (t) calculated for selected NFI plots with slope inclination s >31° (gray dots) and modeled with the fitted GAM (blue lines) for the tree species beech, fir, and spruce.

TABLE 4

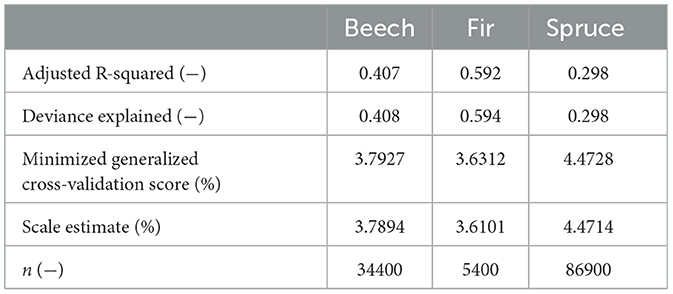
Table 4. Model output for the evaluation of the quality of the fitted GAM used for the development of total protective factor (P_total) as a function of stand age t as well as site condition and rockfall disposition parameters.

Based on the fitted GAM, the range of the recovery duration and recovery potential of E_diss,cap, and P_total could be estimated (Table 5). These values provide a quantitative overview of the recovery of the protective effect against rockfall after a severe disturbance. It must be noted that the recovery duration of E_diss,cap is limited due to the approximately monotonous increase through the considered time span at 200 years and the recovery potential of P_total is limited by the defined value range at 100%.

TABLE 5

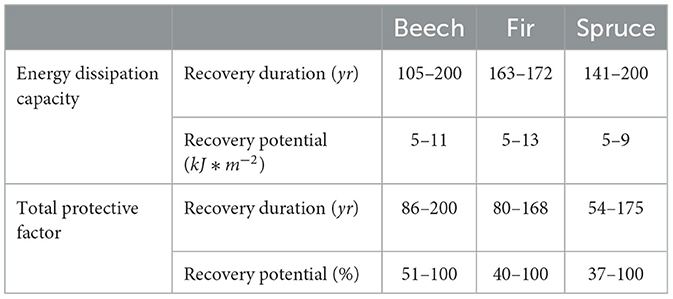
Table 5. Derived values for the recovery duration and the recovery potential to quantify the long-term recovery of the energy dissipation capacity (E_diss,cap) and the total protective factor (P_total) after a hypothetical stand-replacing disturbance.

4 Discussion

4.1 Recovery dynamics

This study provides a general estimation of the long-term recovery of the protective effect against rockfall of uniform forest stands based on a large data base from the Swiss NFI. The results show the trend of the possible recovery dynamics and can serve as a basis for assessing the resilience of protective forests after stand-replacing disturbances. We can show that the recovery duration in terms of the energy dissipation capacity (E_diss,cap) and the total protective factor (P_total) is in the order of magnitude of 100 years, whereby the maximum value of E_diss,cap is reached later (after 110–200 years) than of P_total (after 50–200 years). While E_diss,cap tends toward a constant value between 5 and 13 kJ*m^-2, P_total reaches values between 40 and 100% and has a turning point after a certain time. This difference is mainly attributed to the stronger influence of the decreasing stem density on the P_total than on E_diss,cap because of the entailing decrease in the number of tree impacts. Furthermore we can confirm that the recovery potential in terms of E_diss,cap and the P_total is limited and the possible protective effect of a forest depends from the rockfall disposition.

Only few studies investigated the recovery of the protective effect against rockfall hazards after severe disturbances, which is why the possibilities for a direct comparison of our findings are limited. Vacchiano et al. (2015) found for a forest disturbed by snow avalanches optimal protection against small blocks (volume equal to 0.05 m³) 50 years after the avalanche event. Another study showed that the protective effect against small blocks (volume equal to 0.05 m³) could be fully recovered within 40 years after severe fire events, while the protective effect against medium blocks (volume equal to 0.2 m³) was only recovered partially (Maringer et al., 2016). Both studies only considered few decades after the disturbance event, why conclusions on the long-term recovery are limited. Our study can at least partially bridge this gap.

The recovery dynamics of E_diss,cap showed a similar trend as those of the lateral root reinforcement derived by Flepp et al. (2021) for uniform spruce forests with a recovery duration in the same order of magnitude (about 100 years). The lateral root reinforcement is comparable to the energy dissipation capacity in the sense that both describe a general protective effect independent of the specific hazard disposition. This implies that typical protective forests in Switzerland require a time span up to 100 years after a stand-replacing disturbance to develop their maximum possible protective effect in terms of mechanical resistance against gravitational natural hazards.

Our study investigated only the protective effect of the secondary stand after a stand-replacing disturbance, without accounting for disturbance legacies from the primary stand, such as standing or lying deadwood, that can still have a significant protective effect for a few years (Olmedo et al., 2015; Ringenbach et al., 2022). Several studies investigated the decay of deadwood in general but not specific to its protective effect, which makes it difficult to compare the decay duration with the recovery duration derived in this study. The decay duration of deadwood related to its carbon stock in Swiss forests was estimated in the range of 30–290 years depending on the tree species and the climate conditions (Hararuk et al., 2020). Due to structural changes while the decomposition of the deadwood, it can be assumed that the decay duration of the energy dissipation capacity is smaller than of the carbon stock. The decay duration can be equal but also smaller than the recovery duration and the initial legacies do not necessarily provide the same protective effect as the original forest. Recent studies, however, show that lying deadwood after wind disturbances can even have a higher protective effect in case of small block volumes (Costa et al., 2021; Ringenbach et al., 2022). If this applies also to other disturbance types and for larger block volumes is subject to further research. Depending on site-specific conditions, the gap in the protective effect of a forest after a stand-replacing disturbance can be long lasting even if disturbance legacies are considered.

4.2 Modeling approach

The essential basis of the assessment of the protective effect of forests after disturbances in this study is the parameterization of stand growth of beech, fir, and spruce stands based on forest inventory data to derive a stand age that can be related to the energy dissipation capacity (E_diss,cap) and the total protective factor (P_total) based on the established model RockforNET. The variability in the underlying NFI data is high, which is only partly represented in the growth parameterization, while the trend of stand growth is well-captured.

The simplified consideration of the site properties assuming linear relations depending on the site elevation, slope inclination, and slope aspect may be a reason why our model captured the variability in the data only partially. This issue affects not only the LM for the age estimate but also the GAM for the development of the protective effect. Similar to Flepp et al. (2021), we used a reduced parameter set compared to other authors (Schelhaas et al., 2018). Including further site properties and also management effects as for example in the study of Rohner et al. (2018) could improve the representation of this variability. Furthermore, the model performance may be enhanced by including random effects accounting for further unknown site effects. Another potential for improvement may be the application of non-linear relations that potentially capture the effect of the site and environmental properties on the growth dynamic more appropriately (Stage and Salas, 2007).

The linear differential equation for diameter growth may be another reason why the variability of the data could not be fully represented. Although it generally captured the trend in the data well, it does not limit growth and, thus, its validity is only given for the considered data range. This concerns especially the early forest phase, for which no data is available in the NFI since only trees with a breast height diameter >12 cm are measured (Fischer and Traub, 2019), but also the late forest phase with natural decay since most of the Swiss forest stands are managed. Furthermore, the fact remains that the model is calibrated based on Swiss inventory data of the past 40 years. It can thus only be used within its own boundary conditions and it may not be applicable to distinctly different forest types and for changing environmental conditions (Lischke, 2001). This issue from the growth parameterization for the age estimation is also transferred to the modeling of the development of the protective effect. Still, the data basis in this study represents a vast spatial extent with a large variety of site conditions and, thus, provides a robust general estimation of the recovery of the protective effect, which, however, might be limited in its validity in a particular local context.

4.3 Factors influencing recovery

Considering additional factors influencing forest recovery in the growth parameterization would allow for deriving more specific scenarios of the recovery of the protective effect. Based on inventory data and analytical parameterization, this is well possible for static factors (concurrence effects, soil properties, topographical factors) but fraught with difficulties for dynamic factors (subsequent disturbances, silvicultural measures, climate change). Many of those factors are only implicit in the general trend presented here and require further investigation for an explicit consideration.

Delayed or missing regeneration due to subsequent disturbances can distinctly prolong the recovery of the protective effect. Ungulate browsing, for example, can substantially retard tree regeneration (Rammig et al., 2007; Wohlgemuth et al., 2017), but also other local effects, such as drought events (Anderson-Teixeira et al., 2013) or concurrence of herbaceous or alien species (Moos et al., 2019b). Moreover, the differences between managed and unmanaged stands were not considered in this study, but silvicultural measures are expected to critically influence stand growth (Krumm et al., 2011). Senf et al. (2019), for example, found distinctly faster recovery rates after disturbances in managed compared to unmanaged forests in a large-scale analysis, which was most likely due to advanced regeneration as result of management interventions as well as planting after natural disturbances. Finally, uncertainties regarding the dynamics of the protective effect critically increase with ongoing climate change. In future, shifts in forest structure and species distribution have to be expected (Albrich et al., 2020; Scherrer et al., 2020) and thus, the general trend of the recovery of the protective effect may be shifted in time and space (Hansen et al., 2018).

These variable factors can have a great influence on the recovery of protective forests, but their quantification is challenging. Dynamic forest models are a possible approach to consider dynamic factors in the recovery of the protective effect of protection forests. For example, Thrippleton et al. (2020) or Moos et al. (2021) applied dynamic forest models to assess the development of protective forests at case study sites under climate change. For a deeper understanding of possible recovery durations in protective forests, we suggest combining both approaches, empirical analyses, and numerical modeling, supplemented with additional long-term surveys of forest recovery after disturbances (Caduff et al., 2022; Cerioni et al., 2022).

5 Conclusions and outlook

The key findings of our study are that: (1) the energy dissipation capacity of uniform beech, fir, and spruce stands reaches a constant value after 100–200 years after a stand-replacing disturbance; (2) the recovery of the total protective factor against rockfall strongly depends on the rockfall disposition and reaches a maximum value after 50–150 years; and (3) the total protective factor decreases again as soon as the tree density falls below a critical value guaranteeing sufficient tree impacts to intercept the blocks.

Those findings show that stand-replacing disturbances can lead to a long lasting gap in the protective effect potentially causing a problematic risk increase without any additional measures. Furthermore, the study shows that the protective effect tends to decrease again with increasing stand age, which implies that silvicultural measures are required to maintain a certain level in the long term. The differences in the recovery dynamics between the energy dissipation capacity and the total protective factor reveal the importance of taking into account the specific rockfall disposition in the analysis of the development of the protective effect after a disturbance.

Our study presents a proof-of-concept using a simple and general quantitative basis to investigate the recovery of the protective effect of approximately uniform beech, fir and spruce forests after stand-replacing disturbances. An additional parameterization for the development of the stand tree density similar to the one for the tree diameter would allow for the estimation of potential trajectories of the recovery dynamics. In combination with the assessment of the rockfall release frequency, this could help to make a rough estimate of the potential change in the occurrence frequency of rockfall events at a specific element at risk after forest disturbances. Furthermore quantitative studies about the decay of the energy dissipation capacity of deadwood may provide models to take the protective effect of disturbance legacies into account. This could be particularly useful for quick assessments done by practitioners to assess the necessity of temporary protection measures.

While this study shows a general trend in the recovery of protective forests against rockfall after stand-replacing disturbances, several aspects that influence the recovery in specific situations were not considered. For this reason, a quantification of how for example subsequent disturbances, silvicultural measures, and climate change affect the recovery is not possible based on our results. This requires further research, which should include both, the analysis of data from disturbed forest stands and simulations with dynamic forest models. Thus, already available information from actually observed trajectories of forest recovery as well as from simulation models should be combined with rockfall models to better understand the effects on the recovery of the protective effect of protection forest.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: The data (i.e., output of the model and model code) can be received on request. Data from the Swiss National Forest Inventory is available from the responsible institution upon request (WSL Birmensdorf; https://lfi.ch/index-en.php). Requests to access these datasets should be directed to ZG9taW5pay5tYXkmI3gwMDA0MDtiZmguY2g=; https://lfi.ch/index-en.php.

Author contributions

DM: conceptualization, methodology, formal analysis, data curation, and writing original draft. CM: conceptualization, methodology, formal analysis, writing original draft, and visualization. LD: conceptualization and review and editing. EN: visualization and review and editing. CT: data curation and review and editing. MS: conceptualization, methodology, and review and editing. All authors contributed to the article and approved the submitted version.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was partly funded by the Waldbrandmanagement auf der Alpennordseite AWN-1 founded by the Wyss Academy Foundation for Nature at the University of Bern.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albrich, K., Rammer, W., and Seidl, R. (2020). Climate change causes critical transitions and irreversible alterations of mountain forests. Glob. Change Biol. 26, 4013–4027. doi: 10.1111/gcb.15118

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson-Teixeira, K. J., Miller, A. D., Mohan, J. E., Hudiburg, T. W., Duval, B. D., and DeLucia, E. H. (2013). Altered dynamics of forest recovery under a changing climate. Glob. Change Biol. 19, 2001–2021. doi: 10.1111/gcb.12194

PubMed Abstract | CrossRef Full Text | Google Scholar

Angelstam, P., and Kuuluvainen, T. (2004). Boreal forest disturbance regimes, successional dynamics and landscape structures: a European perspective. Ecol. Bull. 51, 117–136. doi: 10.2307/20113303

CrossRef Full Text | Google Scholar

Bebi, P., Seidl, R., Motta, R., Fuhr, M., Firm, D., Krumm, F., et al. (2017). Changes of forest cover and disturbance regimes in the mountain forests of the Alps. For. Ecol. Manage. 388, 43–56. doi: 10.1016/j.foreco.2016.10.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, F., and Dorren, L. K. (2007). Principles of the tool Rockfor.net for quantifying the rockfall hazard below a protection forest. Schweizer. Zeitsch. Forstw. 158, 157–165. doi: 10.3188/szf.2007.0157

CrossRef Full Text | Google Scholar

Caduff, M. E., Brožová, N., Kupferschmid, A. D., Krumm, F., and Bebi, P. (2022). How large-scale bark beetle infestations influence the protective effects of forest stands against avalanches: a case study in the Swiss Alps. For. Ecol. Manage. 514, 120201. doi: 10.1016/j.foreco.2022.120201

CrossRef Full Text | Google Scholar

Cerioni, M., Fidej, G., Diaci, J., and Nagel, T. A. (2022). Dynamics and drivers of post-windthrow recovery in managed mixed mountain forests of Slovenia. Eur. J. For. Res. 141, 821–832. doi: 10.1007/s10342-022-01475-3

CrossRef Full Text | Google Scholar

Costa, M., Marchi, N., Bettella, F., Bolzon, P., Berger, F., and Lingua, E. (2021). Biological legacies and rockfall: the protective effect of a windthrown forest. Forests 12, 1141. doi: 10.3390/f12091141

CrossRef Full Text | Google Scholar

Dorren, L., and Berger, F. (2005). Stem breakage of trees and energy dissipation during rockfall impacts. Tree Physiol. 26, 63–71. doi: 10.1093/treephys/26.1.63

PubMed Abstract | CrossRef Full Text | Google Scholar

Dorren, L., and Moos, C. (2022). Towards quantitative evidence of eco-DRR in mountains: a concise review. Ecol. Eng. 175, 106485. doi: 10.1016/j.ecoleng.2021.106485

CrossRef Full Text | Google Scholar

Dupire, S., Bourrier, F., Monnet, J.-M., Bigot, S., Borgniet, L., Berger, F., et al. (2016). Novel quantitative indicators to characterize the protective effect of mountain forests against rockfall. Ecol. Indic. 67, 98–107. doi: 10.1016/j.ecolind.2016.02.023

CrossRef Full Text | Google Scholar

Fischer, C., and Traub, B. (2019). Swiss National Forest Inventory-Methods and Models of the Fourth Assessment. Swiss National Forest Inventory.

Google Scholar

Flepp, G., Robyr, R., Scotti, R., Giadrossich, F., Conedera, M., Vacchiano, G., et al. (2021). Temporal dynamics of root reinforcement in European spruce forests. Forests 12, 815. doi: 10.3390/f12060815

CrossRef Full Text | Google Scholar

Fuhr, M., Bourrier, F., and Cordonnier, T. (2015). Protection against rockfall along a maturity gradient in mountain forests. For. Ecol. Manage. 354, 224–231. doi: 10.1016/j.foreco.2015.06.012

CrossRef Full Text | Google Scholar

Hansen, W. D., Braziunas, K. H., Rammer, W., Seidl, R., and Turner, M. G. (2018). It takes a few to tango: changing climate and fire regimes can cause regeneration failure of two subalpine conifers. Ecology 99, 966–977. doi: 10.1002/ecy.2181

PubMed Abstract | CrossRef Full Text | Google Scholar

Hararuk, O., Kurz, W., and Didion, M. (2020). Dynamics of dead wood decay in Swiss forests. For. Ecosyst. 7, 2197–5620. doi: 10.1186/s40663-020-00248-x

CrossRef Full Text | Google Scholar

Harvey, B. D., Leduc, A., Gauthier, S., and Bergeron, Y. (2002). Stand-landscape integration in natural disturbance-based management of the southern boreal forest. For. Ecol. Manage. 155, 369–385. doi: 10.1016/S0378-1127(01)00573-4

CrossRef Full Text | Google Scholar

IPCC (2014). Climate Change 2014 Impacts, Adaptation, and Vulnerability Part b: Regional Aspects: Working Group II Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change.

Google Scholar

Irauschek, F., Rammer, W., and Lexer, M. J. (2017). Evaluating multifunctionality and adaptive capacity of mountain forest management alternatives under climate change in the eastern ALPS. Eur. J. For. Res. 136, 1051–1069. doi: 10.1007/s10342-017-1051-6

CrossRef Full Text | Google Scholar

Knoke, T., Gosling, E., Thom, D., Chreptun, C., Rammig, A., and Seidl, R. (2021). Economic losses from natural disturbances in Norway spruce forests'a quantification using Monte-Carlo simulations. Ecol. Econ. 185, 107046. doi: 10.1016/j.ecolecon.2021.107046

CrossRef Full Text | Google Scholar

Krumm, F., Kulakowski, D., Spiecker, H., Duc, P., and Bebi, P. (2011). Stand development of Norway spruce dominated subalpine forests of the Swiss Alps. For. Ecol. Manage. 262, 620–628. doi: 10.1016/j.foreco.2011.04.030

CrossRef Full Text | Google Scholar

Lischke, H. (2001). New developments in forest modeling: convergence between applied and theoretical approaches. Nat. Resour. Model. 14, 71–102. doi: 10.1111/j.1939-7445.2001.tb00051.x

CrossRef Full Text | Google Scholar

Maringer, J., Ascoli, D., Dorren, L., Bebi, P., and Conedera, M. (2016). Temporal trends in the protective capacity of burnt beech forests (Fagus sylvatica l.) against rockfall. Eur. J. For. Res. 135, 657–673. doi: 10.1007/s10342-016-0962-y

CrossRef Full Text | Google Scholar

Menk, J., Berger, F., Moos, C., and Dorren, L. (2023). Towards an improved rapid assessment tool for rockfall protection forests using field-mapped deposited rocks. Geomorphology 422, 1–14. doi: 10.1016/j.geomorph.2022.108520

CrossRef Full Text | Google Scholar

Moos, C., Dorren, L., and Stoffel, M. (2017). Quantifying the effect of forests on frequency and intensity of rockfalls. Nat. Haz. Earth Syst. Sci. 17, 291–304. doi: 10.5194/nhess-17-291-2017

CrossRef Full Text | Google Scholar

Moos, C., Guisan, A., Randin, C. F., and Lischke, H. (2021). Climate change impacts the protective effect of forests: a case study in Switzerland. Front. For. Glob. Change 4, 6822923. doi: 10.3389/ffgc.2021.682923

CrossRef Full Text | Google Scholar

Moos, C., Thomas, M., Pauli, B., Bergkamp, G., Stoffel, M., and Dorren, L. (2019a). Economic valuation of ecosystem-based rockfall risk reduction considering disturbances and comparison to structural measures. Sci. Tot. Environ. 697:134077. doi: 10.1016/j.scitotenv.2019.134077

PubMed Abstract | CrossRef Full Text | Google Scholar

Moos, C., Toe, D., Bourrier, F., Knüsel, S., Stoffel, M., and Dorren, L. (2019b). Assessing the effect of invasive tree species on rockfall risk–the case of ailanthus Altissima. Ecol. Eng. 131, 63–72. doi: 10.1016/j.ecoleng.2019.03.001

CrossRef Full Text | Google Scholar

Olmedo, I., Bourrier, F., Bertrand, D., Berger, F., and Limam, A. (2015). “Felled trees as a rockfall protection system: experimental and numerical studies,” in Engineering Geology for Society and Territory, Volume 2 (Cham: Springer International Publishing), 1889–1893. doi: 10.1007/978-3-319-09057-3_335

CrossRef Full Text | Google Scholar

Polasky, S., Carpenter, S. R., Folke, C., and Keeler, B. (2011). Decision-making under great uncertainty: environmental management in an era of global change. Trends Ecol. Evol. 26, 398–404. doi: 10.1016/j.tree.2011.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2021). R: A Language and Environment for Statistical Computing. Vienna: R Core Team.

Google Scholar

Rammig, A., Fahse, L., Bebi, P., and Bugmann, H. (2007). Wind disturbance in mountain forests: simulating the impact of management strategies, seed supply, and ungulate browsing on forest succession. For. Ecol. Manage. 242, 142–154. doi: 10.1016/j.foreco.2007.01.036

CrossRef Full Text | Google Scholar

Reineke, L. (1933). Perfection a stand-density index for even-aged forest. J. Agric. Res. 46, 627–638.

Google Scholar

Ringenbach, A., Stihl, E., Bühler, Y., Bebi, P., Bartelt, P., Rigling, A., et al. (2022). Full-scale experiments to examine the role of deadwood in rockfall dynamics in forests. Nat. Haz. Earth Syst. Sci. 22, 2433–2443. doi: 10.5194/nhess-22-2433-2022

CrossRef Full Text | Google Scholar

Rohner, B., Waldner, P., Lischke, H., Ferretti, M., and Thuerig, E. (2018). Predicting individual-tree growth of central European tree species as a function of site, stand, management, nutrient, and climate effects. Eur. J. For. Res. 137, 29–44. doi: 10.1007/s10342-017-1087-7

CrossRef Full Text | Google Scholar

Schelhaas, M.-J., Hengeveld, G. M., Heidema, N., Thürig, E., Rohner, B., Vacchiano, G., et al. (2018). Species-specific, pan-European diameter increment models based on data of 2.3 million trees. For. Ecosyst. 5, 1–19. doi: 10.1186/s40663-018-0133-3

CrossRef Full Text | Google Scholar

Scherrer, D., Vitasse, Y., Guisan, A., Wohlgemuth, T., and Lischke, H. (2020). Competition and demography rather than dispersal limitation slow down upward shifts of trees–upper elevation limits in the Alps. J. Ecol. 108, 2416–2430. doi: 10.1111/1365-2745.13451

CrossRef Full Text | Google Scholar

Sebald, J., Senf, C., Heiser, M., Scheidl, C., Pflugmacher, D., and Seidl, R. (2019). The effects of forest cover and disturbance on torrential hazards: large-scale evidence from the eastern Alps. Environ. Res. Lett. 14, 114032. doi: 10.1088/1748-9326/ab4937

CrossRef Full Text | Google Scholar

Senf, C., Müller, J., and Seidl, R. (2019). Post-disturbance recovery of forest cover and tree height differ with management in central Europe. Landsc. Ecol. 34, 2837–2850. doi: 10.1007/s10980-019-00921-9

CrossRef Full Text | Google Scholar

Senf, C., and Seidl, R. (2021). Mapping the forest disturbance regimes of Europe. Nat. Sustain. 4, 63–70. doi: 10.1038/s41893-020-00609-y

CrossRef Full Text | Google Scholar

Stage, A., and Salas, C. (2007). Interactions of elevation, aspect, and slope in models of forest species composition and productivity. For. Sci. 53, 486–492. doi: 10.1093/FORESTSCIENCE/53.4.486

CrossRef Full Text | Google Scholar

Stritih, A., Bebi, P., Rossi, C., and Grêt-Regamey, A. (2021). Addressing disturbance risk to mountain forest ecosystem services. J. Environ. Manage. 296, 113188. doi: 10.1016/j.jenvman.2021.113188

PubMed Abstract | CrossRef Full Text | Google Scholar

Swisstopo (2023). Swiss TLM Wald.

Google Scholar

Thrippleton, T., Lüscher, F., and Bugmann, H. (2020). Climate change impacts across a large forest enterprise in the northern pre-alps: dynamic forest modelling as a tool for decision support. Eur. J. For. Res. 139, 483–498. doi: 10.1007/s10342-020-01263-x

CrossRef Full Text | Google Scholar

Vacchiano, G., Maggioni, M., Perseghin, G., and Motta, R. (2015). Effect of avalanche frequency on forest ecosystem services in a spruce–fir mountain forest. Cold Reg. Sci. Technol. 115, 9–21. doi: 10.1016/j.coldregions.2015.03.004

CrossRef Full Text | Google Scholar

Wohlgemuth, T., Schwitter, R., Bebi, P., Sutter, F., and Brang, P. (2017). Post-windthrow management in protection forests of the Swiss Alps. Eur. J. For. Res. 136, 1029–1040. doi: 10.1007/s10342-017-1031-x

CrossRef Full Text | Google Scholar