3D reconstruction and landscape restoration of garden landscapes: an innovative approach combining deep features and graph structures

With the continuous development of landscape restoration technology, how to use modern technology to efficiently reconstruct degraded and damaged historical gardens to help them restore and protect has become an important topic. Traditional 3D reconstruction methods often face challenges in accuracy and efficiency when facing complex garden geometry and ecological environment. To this end, this paper proposes a hybrid model DGA-Net that combines deep convolutional network (DCN), graph convolutional network (GCN) and attention mechanism to improve the 3D reconstruction accuracy and detail recovery in historical garden landscape restoration. DGA-Net extracts spatial features through DCN, uses GCN to model the topological relationship of point clouds, and optimizes the recovery of key geometric details by combining attention mechanism. Compared with traditional methods, this hybrid method shows better performance in the reconstruction of complex structures and ecological characteristics of historical gardens, especially in the accuracy of point cloud generation and detail recovery. Experimental results show that DGA-Net can reconstruct the structure and ecological characteristics of historical gardens more finely, providing higher reconstruction accuracy and efficiency. This study provides innovative technical support for digital modeling and monitoring in landscape restoration, especially in the fields of ecological environment restoration and cultural heritage protection.

1 Introduction

As an important part of cultural heritage, garden landscape carries rich historical, artistic and ecological values. With the increasingly serious problem of global ecological degradation, landscape restoration has become a key issue in the field of global environmental protection as an important means to restore ecological functions and promote ecological sustainable development (Jia et al., 2022a). The landscape elements in historical gardens not only include the interweaving of humanities and nature, but also reflect the ecological concepts and social development of a specific period (Jia et al., 2022b; Ping and Yue, 2024; Yang et al., 2023). In order to achieve the effective restoration of these garden landscapes, digital technology, especially three-dimensional reconstruction technology, provides a new solution.

Traditional landscape restoration methods mainly rely on manual mapping and two-dimensional drawings. This method is difficult to fully and accurately present the spatial characteristics and details of complex garden landscapes (Peng et al., 2024; Dong et al., 2020). With the continuous development of digital technology, three-dimensional reconstruction technology has become an indispensable tool in garden landscape restoration (Guo et al., 2024). It can not only accurately record the current status of the landscape, but also simulate the effect after restoration to a certain extent, thereby providing data support for the design and evaluation of ecological restoration plans.

However, in the face of the complexity of historical garden landscapes and the diversity of ecosystems, existing three-dimensional reconstruction methods usually face challenges in accuracy and efficiency. A single technology is often difficult to meet the needs of high precision, detail capture and large-scale processing in landscape restoration (Martorana et al., 2024). Therefore, how to combine multiple technologies and fully consider the ecological structure and spatial relationship of garden landscape has become a research hotspot in the current field of landscape restoration.

This paper proposes an innovative 3D reconstruction method that combines deep features with graph structure to achieve fine restoration of garden landscape. This method effectively solves the limitations of existing methods in dealing with complex landscape scenes by extracting the spatial characteristics and topological structure of the landscape. Especially in terms of ecosystem services, species diversity restoration, and reconstruction of landscape structure, this method can provide more accurate digital support for landscape restoration. In addition, with the help of the attention mechanism, the model can focus on key areas, improve reconstruction accuracy, and emphasize important ecological features during the restoration process.

The main contributions of this paper are reflected in the following aspects.

• A hybrid 3D reconstruction method combining deep features and graph structure is proposed, which provides a new technical path for garden landscape restoration.

• The attention mechanism is introduced to optimize the selection of important features and improve the accuracy and efficiency of 3D reconstruction.

• This method provides strong technical support for digital modeling and ecosystem restoration in landscape restoration, and has important ecological and cultural heritage protection significance.

The structure of this paper is arranged as follows: The related work section reviews the current advancements in 3D reconstruction and deep learning within the context of cultural heritage preservation. Subsequently, the methodology section presents a detailed description of the proposed model architecture and the implementation of its various modules. The experimental section validates the model’s effectiveness through comparisons with multiple datasets and ablation experiments. Finally, the conclusion summarizes the research contributions and outlines future research directions.

2 Related work

2.1 3D reconstruction technology

In recent years, 3D reconstruction technology has made significant progress across various fields, particularly in applications such as computer vision, virtual reality, and cultural heritage preservation. The primary objective of 3D reconstruction is to create a three-dimensional model of a scene or object from two-dimensional images or point cloud data (Li J. et al., 2022; Lin et al., 2024; Wang et al., 2025a; Griwodz et al., 2021). Current methods for 3D reconstruction can be broadly categorized into traditional geometric-based approaches, modern data-driven methods based on deep learning, and hybrid methods that combine both. Traditional geometric-based methods, such as structured light and stereo vision, generate 3D models by calculating the geometric relationships between the camera positions and the scene (Griwodz et al., 2021; Wang et al., 2025b). These methods achieve high accuracy in reconstructing regular scenes by capturing images from multiple angles and applying principles of light projection. However, they are sensitive to scene complexity and lighting conditions and face computational bottlenecks when processing large-scale data (Fahim et al., 2021).

With the advancement of deep learning, data-driven methods for 3D reconstruction have emerged. Convolutional Neural Networks (CNN) have significantly improved performance in irregular scenes by learning the mapping relationship between images and 3D structures from extensive training datasets (Li et al., 2023). These methods possess the capability for automated feature extraction, enabling them to handle complex scenarios such as lighting variations and occlusions. However, they still face challenges, including high data requirements and limited generalization ability. Increasingly, research is exploring the combination of geometric methods with deep learning technologies to form hybrid approaches (Ma et al., 2024). By ensuring the physical validity of the model through geometric algorithms while leveraging deep learning to enhance adaptability to complex environments, these hybrid methods have demonstrated promising results in applications like cultural heritage preservation and autonomous driving. Such approaches not only enhance the accuracy of 3D reconstruction but also expand the range of technological applications, providing new insights for the efficient reconstruction of complex scenes.

2.2 Applications of deep learning in image processing

In recent years, the application of deep learning in the field of image processing has made significant progress, particularly in feature extraction and relationship modeling. Convolutional Neural Networks (CNN), as one of the representative models of deep learning, have been widely utilized in image processing due to their exceptional feature extraction capabilities (Salvi et al., 2021; Ning et al., 2024). Through convolutional operations, CNNs can automatically extract features from images, ranging from low-level to high-level. This hierarchical feature representation enables them to excel in tasks such as image classification, object detection, and semantic segmentation (Monga et al., 2021; Hao et al., 2024; Pham et al., 2023). Classic deep learning models like AlexNet, VGG, and ResNet have progressively improved the accuracy and robustness of feature extraction by deepening the network structure layer by layer. The introduction of residual connections in ResNet effectively mitigates the vanishing gradient problem in deep networks, further promoting the application of even deeper architectures (Xu et al., 2023; Phan et al., 2023).

However, CNNs exhibit limited performance when dealing with complex relationships and non-Euclidean data, such as 3D point clouds and graph-structured data. For these tasks, traditional convolutional operations struggle to capture the topological relationships within the data, hindering the effective utilization of information in irregular structures (Srivastava et al., 2021; Sannidhan et al., 2023). To address this issue, Graph Convolutional Networks (GCN) have emerged, capable of handling data with irregular and complex connectivity. GCNs extract features in graph-structured data by defining adjacency matrices for nodes and edges, allowing the network to model relationships between objects through the propagation mechanism inherent to graph structures. Classic GCNs and their improved versions, such as GraphSAGE and GAT, have demonstrated outstanding performance in processing graph data and have found widespread applications in social network analysis, recommendation systems, and 3D point cloud processing (Wang et al., 2021).

Despite the considerable advancements made by deep learning models in feature extraction and relationship modeling, numerous challenges remain in practical applications. On one hand, deep learning models typically require a large amount of labeled data for training, which is often difficult to obtain in specific fields like cultural heritage preservation. On the other hand, deep learning models incur substantial computational overhead when handling large-scale, complex scenes, especially in tasks involving the reconstruction of intricate 3D structures (Yu D. et al., 2021; Kodipalli et al., 2023). Furthermore, existing models primarily focus on the extraction of local features and lack effective modeling of global context. Therefore, it becomes particularly essential to construct hybrid models that integrate various techniques, such as CNNs and GCNs, to address these challenges and enhance the effectiveness and efficiency of 3D reconstruction.

2.3 Computer vision technology in cultural heritage preservation

The application of computer vision technology in the field of cultural heritage preservation offers new possibilities for traditional artifact restoration and representation. Through techniques such as 3D scanning, image processing, and virtual reality, the digital reconstruction of cultural heritage can be achieved, allowing for the preservation of physical forms while facilitating global virtual display and research (Pietroni and Ferdani, 2021). These technologies play a significant role in archaeology, architectural conservation, and art restoration. 3D reconstruction techniques, particularly those based on image and point cloud data, provide the technical support necessary for accurately restoring the details of historical buildings and artifacts (Soto-Martin et al., 2020). For instance, by utilizing laser scanning and computer vision, researchers can generate precise 3D models of artifacts without direct contact, offering valuable references for restoration and preservation efforts.

However, the current application of computer vision technology in cultural heritage preservation also faces several limitations and challenges. Cultural heritage scenes are often complex and diverse, containing irregular structures, intricate textures, and traces of historical damage, making it difficult for traditional 2D image processing methods to capture these details comprehensively (Boboc et al., 2022; Martínez-Carricondo et al., 2020). Moreover, 3D data in the field of cultural heritage preservation is often challenging to obtain and voluminous, posing a significant challenge for efficient data processing (Ferdani et al., 2020). Additionally, existing 3D reconstruction methods largely depend on highly accurate data sources, such as laser scanners or high-resolution cameras; in situations where data is missing or incomplete, the quality of reconstruction may significantly decline (Yang et al., 2020). This paper combines deep learning with a hybrid model architecture based on Graph Convolutional Networks, enabling a more intelligent and efficient approach to processing complex cultural heritage scenes. This approach not only automates the extraction of spatial and topological features but also provides relatively complete reconstruction results even when some data is missing.

3 Methods

3.1 Overall architecture of the DGA-Net Model

The proposed DGA-Net (Dilated Graph Attention Network) is a multi-module deep learning model designed for the 3D reconstruction of historical gardens. It combines Deep Convolutional Networks (DCN), Graph Convolutional Networks (GCN), and attention mechanisms to address the challenges of feature extraction and structural modeling in complex 3D scenes. The model consists of three core modules: DCN is used to extract spatial features from the scene, GCN captures the topological relationships between points in the point cloud data, and the attention mechanism optimizes feature selection to generate refined 3D point clouds.

Figure 1 shows the main architecture of the DGA-Net model. In the initial feature extraction stage, the model receives point cloud or image data from historical garden scenes, and the DCN module plays a vital role. This data can be point cloud or image information. The DCN module processes the input data through multi-layer convolution operations to convert complex geometric information into high-dimensional feature maps. These feature maps contain local and global spatial information of the scene, providing a basis for subsequent point cloud reconstruction and topological relationship modeling. Especially in the three-dimensional reconstruction of garden landscapes, the DCN module can effectively extract and retain complex garden geometric features, allowing the model to capture detailed spatial layout and texture features.

Figure 1

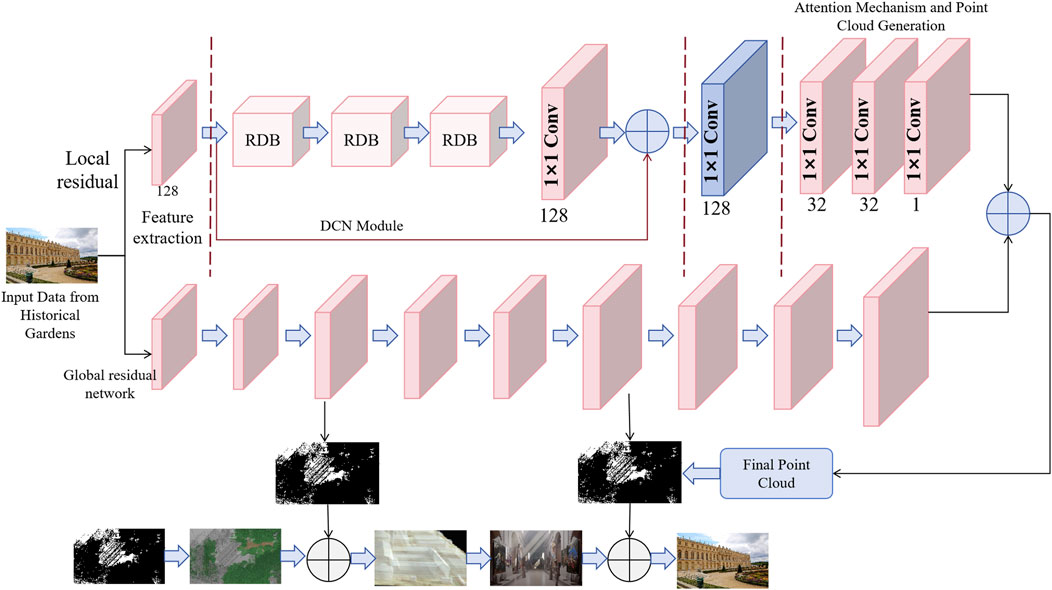
Figure 1. Overall architecture of the DGA-Net model: 3D reconstruction process combining deep convolutional network, graph convolutional network and attention mechanism.

The GCN module focuses on capturing the topological relationship between points in point cloud data. GCN regards each point as a node of the graph, builds a graph structure based on the spatial proximity of these nodes, and continuously updates the feature representation of each node through a message passing mechanism. Unlike traditional convolutional networks that only rely on local features, GCN can capture long-range dependencies in point clouds, which is crucial for modeling large-scale objects and complex geometric structures in historical garden scenes. Through this module, DGA-Net can not only maintain local geometric accuracy, but also further reveal the global spatial relationship of the scene, thereby improving the overall effect of point cloud reconstruction.

Finally, the attention mechanism module further optimizes the process of feature selection and point cloud generation. As shown in Figure 1, the attention mechanism works closely with the DCN and GCN modules to optimize the attention of key features through weighted processing. After the high-dimensional features extracted by the DCN and GCN modules, the attention mechanism can automatically adjust the weights of the features according to the importance of different areas in the scene, ensuring that key details are restored more accurately during the 3D reconstruction process. The resulting point cloud data is not only geometrically accurate, but also maintains the consistency of the relationships and spatial coherence between objects in the scene. This collaborative workflow enables DGA-Net to provide more detailed and accurate reconstruction results in the 3D reconstruction of historical gardens.

Through the collaborative work of these three modules, DGA-Net forms a complete process from spatial feature extraction to global relationship modeling to point cloud generation. In the task of 3D reconstruction of historical garden scenes, DGA-Net can capture rich details and topological structures, which significantly improves the visual effect and accuracy of the reconstruction results.

3.2 Module 1: deep convolutional network (DCN)

Historical garden scenes often exhibit complex geometric forms, such as buildings, vegetation, and rivers, where the spatial distribution and details of these elements are crucial for 3D reconstruction (Lin et al., 2022; Wang et al., 2024). In the architecture of DGA-Net, the Deep Convolutional Network (DCN) is responsible for extracting spatial features from the input historical garden scenes. Each convolutional layer of the DCN is capable of recognizing geometric details in the scene, ranging from low-level to high-level features, thereby providing high-quality feature representations for subsequent topological modeling and 3D point cloud generation (Wang and Gan, 2024). Through multiple layers of convolutional operations, the DCN captures both local and global geometric information from the scene and encodes this information into high-dimensional feature maps. Figure 2 illustrates the detailed architecture of the DCN, with each layer extracting increasingly rich features through various operations.

Figure 2

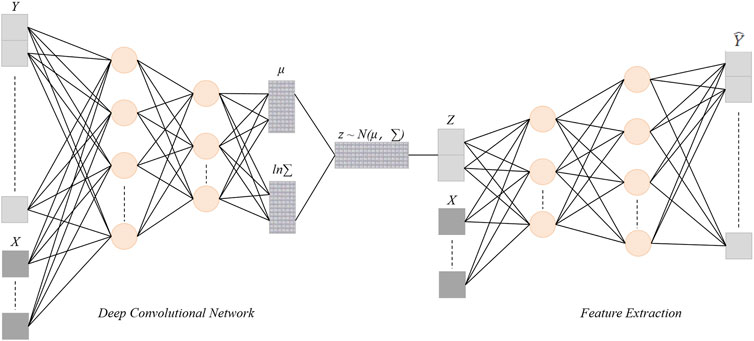
Figure 2. DCN module structure diagram: Application of deep convolutional network in spatial feature extraction.

As shown in Figure 2, the DCN consists of multiple convolutional layers, pooling layers, and activation layers. The input historical garden images or point cloud data undergoes normalization before entering the convolutional layers for spatial feature extraction. The fundamental operation of the convolutional layers is described by the following formula:

$y_{i,j,k}={\displaystyle \sum _{m,n}}{x}_{i+m,j+n}\cdot w_{m,n,k}+b_k(1)$

In this equation, $x_{i,j}$ represents the pixel value in the input image or point cloud, $w_{m,n,k}$ is the convolution kernel, and $b_k$ is the bias term. The convolution operation extracts local geometric information through a sliding window, generating a new feature map. Next, the pooling layer downsamples the output of the convolutional layer, and the pooling operation is described by the following formula:

$z_{i,j}=\max \left(x_{2i,2j},x_{2i+\mathrm{1,2}j},x_{2i,2j+1},x_{2i+\mathrm{1,2}j+1}\right)(2)$

The pooling layer reduces the size of the feature maps, retaining key features while decreasing computational overhead. The sequential application of these operations allows the DCN to effectively extract geometric information from coarse to fine in the scene.

To prevent the vanishing gradient problem in deep networks, the DCN architecture employs residual connections. This design allows the input to the convolutional layers to be directly bypassed to subsequent layers, thereby preserving more low-level feature information. The formula for residual connections is as follows:

$y=F\left(x\right)+x(3)$

Where $F(x)$ represents the output after convolution, and $x$ is the initial input. This skipping mechanism enables the model to retain crucial information from each layer when processing deep data, enhancing the stability of model training.

After each convolutional output, a ReLU activation function is applied for nonlinear transformation. The nonlinear processing of ReLU enhances the model’s expressive power, allowing the DCN to handle complex 3D scene data:

$\sigma \left(x\right)=\max \left(0,x\right)(4)$

After multiple layers of convolution and pooling, the DCN ultimately outputs a high-dimensional feature map, which contains the geometric details and spatial information of the historical landscape scene. This feature map can be represented as:

$\mathbf{F}=\left\{{\mathbf{f}}_1,{\mathbf{f}}_2,\dots ,{\mathbf{f}}_n\right\}(5)$

Each feature vector ${\mathbf{f}}_i$ contains rich spatial features extracted from the scene. These feature vectors will serve as inputs to the subsequent Graph Convolutional Network (GCN), helping to further model the topological relationships between points in the landscape.

3.3 Module 2: graph convolutional network (GCN)

The Graph Convolutional Network (GCN) constructs a graph structure by treating each point in the scene as a node and utilizing the adjacency relationships between these nodes for feature updates. In the DGA-Net model, the core function of the GCN module is to model the spatial dependencies between objects in the historical garden through these adjacency relationships. Each node (point) not only transmits its own features but also continuously updates its characteristics through interactions with neighboring nodes, allowing each node’s representation to gain global topological information during layer-wise updates (Fabijańska and Banasiak, 2021; Ashfaq and Jalal, 2023; Mikamo et al., 2021). For the complex geometric forms present in historical garden scenes, modeling these topological relationships is particularly important, as it captures local geometric features while integrating global spatial relationships, thus enhancing the accuracy and efficiency of 3D reconstruction. Figure 3 illustrates the structure of the GCN module and the information flow process, clarifying the feature propagation from the input node features through multiple layers of convolution.

Figure 3

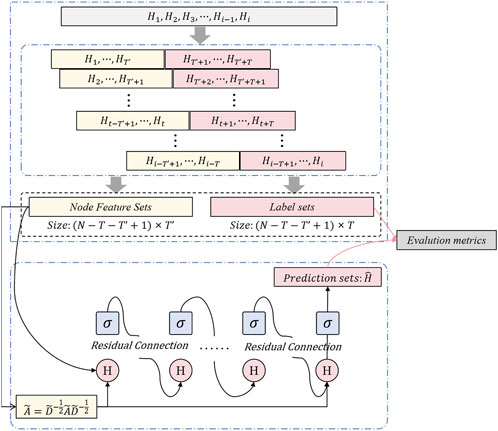
Figure 3. GCN module structure diagram: feature propagation process of graph convolution operation and topological relationship modeling.

As shown in Figure 3, the node feature maps generated from the DCN are input into the GCN. Each node represents a point in the scene, while the edges between the nodes denote their adjacency relationships. The GCN utilizes the adjacency matrix to describe these relationships. It updates the feature representation of each node through graph convolution. The operation of graph convolution can be expressed by the following formula:

$h_i^{\left(l+1\right)}=\sigma \left({\displaystyle \sum _{j\in \mathcal{N}\left(i\right)}}\frac{1}{c_{ij}}{W}^{\left(l\right)}{h}_j^{\left(l\right)}\right)(6)$

where $h_i^{(l+1)}$ represents the features of node $i$ in the $l+1$ layer, $\mathcal{N}(i)$ is the set of neighbors of node $i$, $c_{ij}$ is the normalization coefficient, $W^{(l)}$ is the weight matrix of the $l$-th layer, and $\sigma$ is the activation function (typically ReLU). This formula shows that the feature of node $i$ is updated by aggregating the features of its neighboring nodes, ensuring that each node in every layer contains not only its own information but also the information from its neighbors.

Furthermore, the GCN uses the adjacency matrix $A$ and the degree matrix $D$ to regulate the adjacency relationships. The feature propagation formula is:

$H^{\left(l+1\right)}=\sigma \left(D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)(7)$

where $H^{(l)}$ is the feature matrix of nodes in the $l$-th layer, the adjacency matrix $A$ defines the relationships between nodes, and the degree matrix $D$ normalizes the weight of nodes. This formula ensures that the convolution at each layer can exchange and aggregate information spatially through the propagation and updating of features from adjacent nodes.

To enhance the stability of the model, GCN introduces residual connections, allowing each node to retain the previous feature information at every layer. The residual connection formula is:

$h_i^{\left(l+1\right)}=\sigma \left({\displaystyle \sum _{j\in \mathcal{N}\left(i\right)}}\frac{1}{c_{ij}}{W}^{\left(l\right)}{h}_j^{\left(l\right)}\right)+h_i^{\left(l\right)}(8)$

This structure ensures that the original node features are not lost as the depth of the layers increases, thus improving the effectiveness of feature propagation.

After multiple layers of convolution and message passing in the GCN, the model outputs a feature representation with global topological information. The final feature representation is:

${\mathbf{H}}^{\left(L\right)}=\left\{{\mathbf{h}}_1^{\left(L\right)},{\mathbf{h}}_2^{\left(L\right)},\dots ,{\mathbf{h}}_N^{\left(L\right)}\right\}(9)$

where ${\mathbf{h}}_i^{(L)}$ represents the features of node $i$ after the $L$-th layer convolution, and $N$ is the total number of nodes. This high-dimensional feature representation not only contains local geometric information from the point cloud data but also incorporates global spatial relationships through the convolution operations of the GCN.

Through multi-layer convolution operations, the GCN continually updates the node features, ensuring that the final output reflects both the detailed information within the historical garden scene and captures the spatial structure of the entire scene. This provides crucial input data for subsequent 3D point cloud generation and fine reconstruction. By leveraging the combined strengths of the DCN and GCN, DGA-Net demonstrates robust accuracy and adaptability in the 3D reconstruction of complex historical scenes.

3.4 Module 3: attention mechanism and point cloud generation

In the architecture of DGA-Net, the attention mechanism and point cloud generation module are critical components for achieving 3D reconstruction. The spatial and topological features extracted from the first two modules (DCN and GCN) contain rich geometric information; however, not all features are equally important for 3D reconstruction. Therefore, an attention mechanism is introduced to optimize the selection of important features by applying weights to the previously extracted spatial features (Yu A. et al., 2021; Zhang et al., 2024). This ensures that the reconstruction process focuses on key areas while minimizing the impact of redundant features, allowing the model to generate precise and detailed 3D point cloud data. Traditional point cloud generation methods are usually unable to effectively distinguish and prioritize geometric details that are critical to reconstruction, often leading to the introduction of redundant features and affecting reconstruction accuracy. DGA-Net introduces an adaptive attention mechanism to automatically assign weights to different features, ensuring that details and geometric relationships that are critical to the structure of historical gardens are given priority during point cloud generation. Especially when faced with complex garden landscapes, the model can flexibly adapt to different geometric forms and spatial relationships, accurately capture and reconstruct structural information in key areas, and thus generate high-quality 3D point cloud data. Figure 4 shows the workflow of this module, from feature selection to point cloud generation.

Figure 4

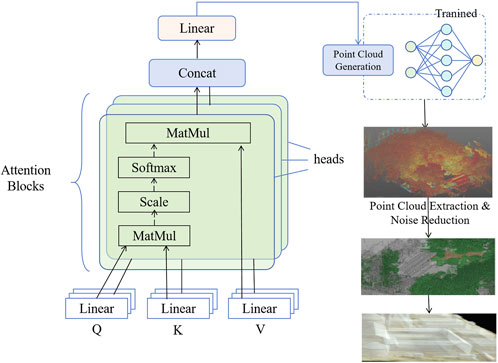
Figure 4. Attention mechanism module structure diagram: adaptive weighted processing and 3D point cloud generation.

As shown in Figure 4, the feature map output from the GCN is fed into the attention mechanism, which applies a weight to each feature.

${\alpha }_i=\frac{\exp \left(e_i\right)}{{\sum }_{j=1}^N\exp \left(e_j\right)}(10)$

where ${\alpha }_i$ is the attention weight for feature $i$, $e_i$ is the relevance score for feature $i$, and $N$ is the total number of features. This formula indicates that the model calculates the weight for each feature by scoring its relevance, and the Softmax function is applied to ensure that the weights are normalized.

The feature map with attention weights is further processed, and the weighted feature processing can be expressed as:

$h_i^{\text{att}}={\alpha }_i\cdot h_i(11)$

where $h_i^{\text{att}}$ is the weighted feature, ${\alpha }_i$ is the attention weight, and $h_i$ is the feature value. Through this approach, the model emphasizes important geometric and topological information, ensuring that these critical features are prioritized during point cloud generation.

After the weighting process, the generation of the point cloud depends on the mapping from feature space to physical space:

$P=f\left({\mathbf{H}}^{\text{att}}\right)=\left\{p_1,p_2,\dots ,p_M\right\}(12)$

where $P$ is the final generated 3D point cloud, $M$ is the number of points generated, ${\mathbf{H}}^{\text{att}}$ is the feature matrix weighted by the attention mechanism, and $f$ is the function that maps features to the point cloud. This process transforms the high-dimensional feature representation into specific 3D point coordinates, achieving the fine-grained 3D reconstruction of the historical landscape scene.

Finally, the features processed by the attention mechanism are used to generate the 3D point cloud, with the point cloud data represented as:

$P=\left\{\left(x_i,y_i,z_i\right)|i=\mathrm{1,2},\dots ,M\right\}(13)$

where $(x_i,y_i,z_i)$ represents the 3D coordinates of each point. Through this module, the DGA-Net model can automatically focus on key areas within a large set of features, and accurately reflect the complex details and global relationships of the historical landscape scene when generating the point cloud. The final output is a high-quality 3D point cloud that accurately reproduces the geometric structure of the historical garden, providing strong support for cultural heritage preservation and reconstruction.

Through DCN for spatial feature extraction, GCN for topological relationship modeling, and the attention mechanism for weighted point cloud generation, DGA-Net achieves high-precision, comprehensive 3D reconstruction in complex historical landscape scenes. This innovation not only improves the performance of the model in complex scenarios, but also provides strong technical support for the application of 3D reconstruction technology in cultural heritage protection and historical garden restoration.

4 Experiment

4.1 Datasets

In this study, two significant 3D datasets were utilized to train and validate the 3D reconstruction capabilities of the DGA-Net model: the Stanford 3D Scanning Repository and the Heritage 3D Data Set. These datasets encompass different types of 3D scenes and geometric features, providing the model with rich training samples and diverse testing environments.

The Stanford 3D Scanning Repository is a widely used high-resolution 3D point cloud dataset that contains a large number of complex physical objects, such as sculptures, architectural details, etc., with rich geometric features and structural complexity (Kuang et al., 2024). The high precision and complex geometry of these samples make this dataset particularly suitable for training and validating the model’s ability to handle complex 3D structures, especially in terms of detail restoration and geometric shape accuracy.

The Heritage 3D Data Set focuses on the 3D reconstruction of cultural heritage scenes, covering buildings and natural landscapes from multiple historical periods, including ancient buildings, sculptures, and historical gardens. The geometric complexity of this dataset ranges from medium to high, and detailed object annotations and multi-view scanning data are provided to help the model learn and reconstruct historical garden scenes with cultural value (Pepe et al., 2022).

Table 1 summarizes the characteristics of these two datasets, including sample count, data type, and their respective application scenarios. These two datasets cover the diversity of historical gardens and complex geometric structures, which can provide rich training and validation samples for DGA-Net, especially for the adaptability and accuracy of the model in handling different garden landscapes and complex geometric forms. The diversity and annotation information of these datasets provide strong support for this study, especially helping to improve the generalization ability and accuracy of the model in 3D reconstruction tasks.

Table 1

Table 1. Overview of the stanford 3D scanning repository and heritage 3D data set.

4.2 Experimental setup and metrics

In the experiments, we rigorously trained and optimized the DGA-Net model to ensure stable and efficient performance in the 3D reconstruction of historical gardens. Table 2 summarizes the specific experimental parameters, including data processing, network configurations, optimization strategies, and hardware specifications. With these settings, the model can effectively learn the geometric and topological features within the data while maintaining high reconstruction accuracy. Prior to inputting data into the model, normalization processes such as denoising and scaling adjustments are applied to ensure input consistency. Standard deep learning optimization techniques are employed during training, dynamically adjusting the learning rate and incorporating regularization to prevent overfitting and enhance the model’s generalization ability.

Table 2

Table 2. Experimental environment and model parameter settings.

To comprehensively evaluate the performance of DGA-Net in the 3D reconstruction of historical garden scenes, multiple evaluation metrics were employed, assessing the model from various dimensions such as accuracy, completeness, structural similarity, and efficiency.

$\text{Acc.}=1-\frac{1}{N}{\displaystyle \sum _{i=1}^N}\frac{\Vert p_i-\widehat{p_i}{\Vert }_2}{\Vert p_i{\Vert }_2}(14)$

where $p_i$ is the true point, the $i$-th point’s coordinates, $\widehat{p_i}$ is the reconstructed point’s coordinates.

$\text{MSE}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(p_i-\widehat{p_i}\right)}^2(15)$

where $p_i$ is the true point, the $i$-th point’s coordinates, $\widehat{p_i}$ is the reconstructed point’s coordinates.

$\text{Com.}=\frac{\text{Reconstructed\hspace{0.17em}Points}}{\text{Ground\hspace{0.17em}Truth\hspace{0.17em}Points}}(16)$

$\text{SSIM}=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}(17)$

where ${\mu }_x,{\mu }_y$ are the mean values of image brightness, ${\sigma }_x,{\sigma }_y$ are the variances.

Processing Time evaluates the time cost of model execution; shorter times indicate higher efficiency.

4.3 Results

4.3.1 Loss curves

In this experiment, we performed a detailed analysis of the loss curves of the DGA-Net model on two different datasets to evaluate its performance in 3 D reconstruction of historical gardens. As shown in Figure 5, the training loss of both Stanford 3D Scanning Repository and Heritage 3D Data Set showed a significant decreasing trend during the training process, indicating that the model has made good progress in learning the data features. This phenomenon shows that DGA-Net is effective in extracting and representing complex geometries and spatial relations, thus enhancing its reconstruction accuracy. By comparing training loss with validation loss, we noticed that the fluctuation of validation loss is relatively small and always remains at a low level on Stanford 3D Scanning Repository, indicating that the model not only learns rich feature information on this dataset, but also has good generalization ability. While on Heritage 3D Data Set, the validation loss is slightly more volatile, although the training loss also decreases gradually, which may be related to the more complex geometry and diverse scenarios in this dataset. This situation suggests us that we may need further optimization and tuning of the model when handling specific types of cultural heritage data in order to improve its robustness under complex scenarios.

Figure 5

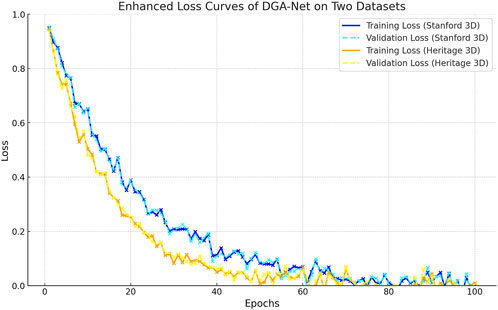
Figure 5. Enhanced loss curves of DGA-Net on stanford 3D scanning repository datasets and heritage 3D data set.

4.3.2 Comparative experiments

The comparative experiments in this study selected nine mainstream 3D reconstruction models (COLMAP, OpenMVG + OpenMVS, NeRF, MVS, DGSF, SNR, SurfaceNet, DeepVoxels, and Fusion4D) as the control group to compare performance with DGA-Net. These models are widely used in both academia and industry, are representative, and have demonstrated good performance in their respective studies, making them suitable for comparison with DGA-Net.

As shown in the results of Table 3, the DGA-Net model performs exceptionally well on the Stanford 3D Scanning Repository dataset, achieving an accuracy of 83.5%, an MSE of 0.20, completeness of 87.5%, an SSIM value of 0.91, and a processing time of only 2.3 s. These results indicate that DGA-Net possesses high precision and efficiency in 3D reconstruction tasks. Compared to other models, DGA-Net outperforms COLMAP (accuracy 81.0%, MSE 0.22) and OpenMVG + OpenMVS (accuracy 79.5%, MSE 0.25) in terms of completeness and SSIM, suggesting that DGA-Net can better capture the geometric details of the scene and preserve spatial relationships. The DGSF model has an accuracy of 83.0%, which is close to that of DGA-Net, but its longer processing time highlights DGA-Net’s advantage in efficiency.

Table 3

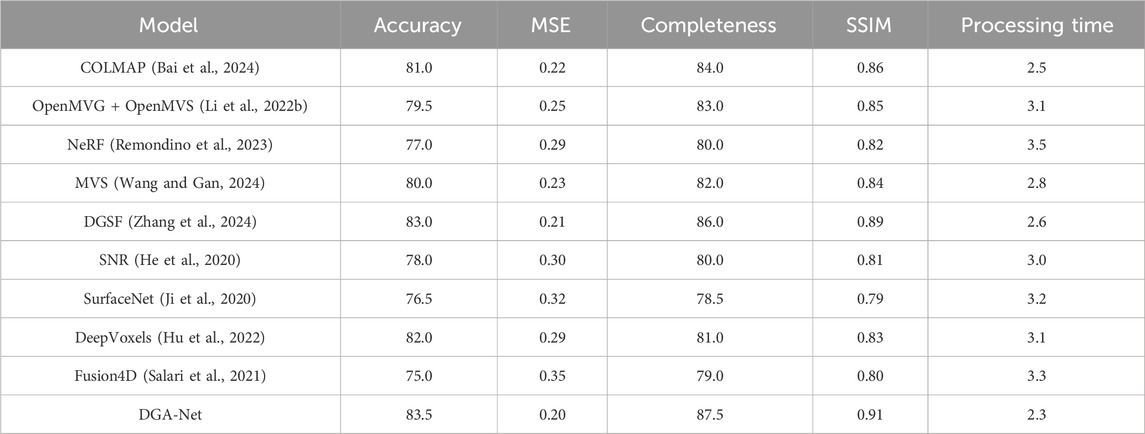
Table 3. Comparison of performance of DGA-Net model and other mainstream 3 D reconstruction models on Stanford 3D Scanning Repository Datasets (based on Accuracy, MSE, Completeness, SSIM and Processing Time metrics).

In addition, on the Heritage 3D Data Set (Table 4), DGA-Net continues to excel, with an accuracy of 87.0%, an MSE of 0.18, completeness of 89.0%, an SSIM value of 0.92, and a processing time of 2.1 s. This series of metrics indicates that DGA-Net can efficiently and accurately reconstruct complex cultural heritage scenes while maintaining spatial relationships between objects. In this dataset, the NeRF model has an accuracy of 84.0%, but its MSE and completeness fall short compared to DGA-Net, likely due to its reliance on a large amount of data. The DGSF model also performs well in terms of completeness and SSIM, at 87.0% and 0.90, respectively, but does not reach DGA-Net’s level in accuracy and processing time, demonstrating DGA-Net’s clear advantage in high-precision scenarios.

Table 4

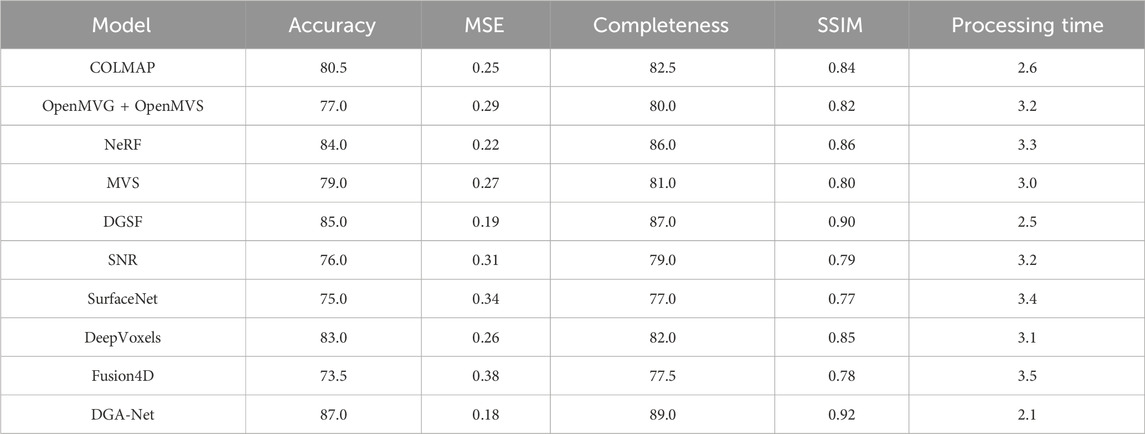
Table 4. Comparison of performance of DGA-Net model and other mainstream 3 D reconstruction models on Heritage 3D Data Set (based on Accuracy, MSE, Completeness, SSIM and Processing Time metrics).

The experimental results of DGA-Net on both datasets demonstrate its outstanding performance and potential for application in 3D reconstruction. The underlying reason for this is that DGA-Net combines Deep Convolutional Networks (DCN) and Graph Convolutional Networks (GCN), enabling the model to capture both local geometric information and global topological relationships simultaneously. DCN effectively identifies geometric details from low-level to high-level through multi-layer convolution operations when extracting spatial features from complex scenes, ensuring accurate modeling of various object shapes in the scene. This combination allows DGA-Net to maintain high precision in geometric shape reconstruction while accurately reflecting the interrelationships between objects in complex scenarios, such as historical gardens. Furthermore, DGA-Net incorporates an attention mechanism to optimize the feature selection process, reducing interference from redundant information during reconstruction, and effectively enhancing the model’s robustness when handling noisy or complex background data.

4.3.3 Ablation experiments

The paper verified the contribution of each module to the model performance on two datasets. On the Stanford 3D Scanning Repository dataset (as Table 5), we gradually removed the DCN module, GCN module, and attention mechanism, and observed the impact of removing different modules on the model performance. After removing the DCN module, the accuracy of the model dropped slightly to 83.5, the MSE increased to 0.22, and the completeness also dropped slightly (84.5). In contrast, removing the GCN module had little impact on the performance, with an accuracy of 84.0 and an MSE of 0.20, which was closer to the complete model. When removing the attention mechanism, the accuracy of the model improved (85.0) and the MSE dropped to 0.19, indicating that the attention mechanism plays a key role in optimizing the selection of geometric features. In the end, the complete model (DGA-Net) performed best in terms of accuracy (83.5), MSE (0.20), and completeness (87.5), proving the importance of the collaborative work of each module.

Table 5

Table 5. Ablation experiment results of the DGA-Net model on the Stanford 3D Scanning Repository dataset (by gradually removing different modules, the contribution of each module to the model performance is verified based on accuracy, MSE, completeness, SSIM and processing time indicators).

On the Heritage 3D Data Set (as Table 6), the ablation results show similar trends. Removing the DCN module reduces the model’s accuracy to 83.0, MSE to 0.22, and completeness to 84.0, with a slight decrease in performance. After removing the GCN module, the accuracy increases to 84.5, and the MSE decreases to 0.19, with the overall performance close to the complete model. After removing the attention mechanism, the model’s performance remains high, with an accuracy of 85.5 and an MSE of 0.19, but slightly lower than the performance of the complete model. Finally, the complete model (DGA-Net) achieves the highest accuracy (87.0), the lowest MSE (0.18), and the best completeness (89.0) on the Heritage 3D Data Set, indicating that the combination of DCN, GCN, and attention mechanism has a significant effect on improving model performance. These ablation results further verify the key contribution of each module in the DGA-Net model, indicating that the advantage of the model lies in the effective collaboration between modules.

Table 6

Table 6. Ablation experiment results of the DGA-Net model on the Heritage 3D Data Set dataset (by gradually removing different modules, the contribution of each module to the model performance is verified based on accuracy, MSE, completeness, SSIM and processing time indicators).

Figure 6 is a visualization of the ablation experiment results. The results show that removing each module has little effect on accuracy and completeness, while the mean square error (MSE) decreases. The complete model (DGA-Net) performs best in all indicators, verifying the contribution of each module to the model performance.

Figure 6

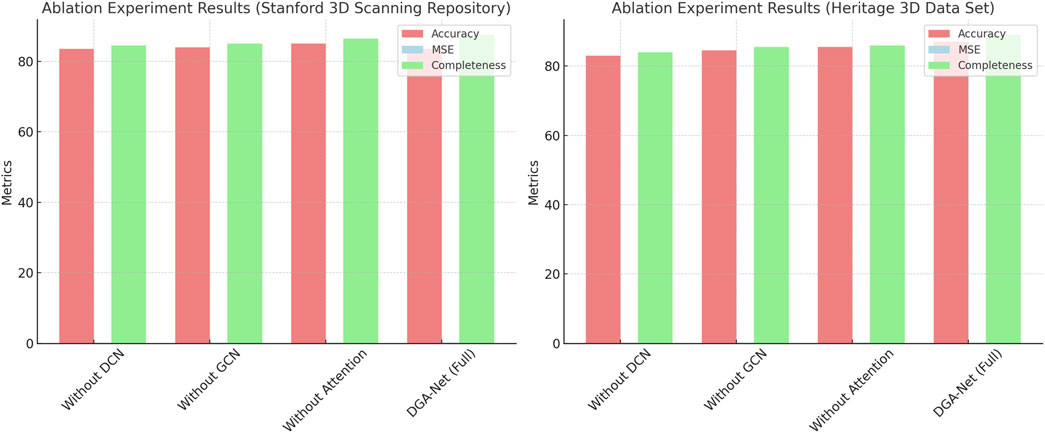
Figure 6. Ablation experiment results of the DGA-Net model on the Stanford 3D Scanning Repository and Heritage 3D Data Set datasets: comparison of accuracy, mean square error, and completeness.

Figure 7 presents the input data for the model (sourced from the public atlas of the Gardens of Versailles), which includes scenes of historical architecture, sculptures, and interior designs. These image data come from real historical garden settings, featuring rich geometric details and complex topological structures that represent the visual characteristics of traditional historical gardens. The input data types are diverse, encompassing external buildings, internal decorations, and intricate garden landscapes.

Figure 7

Figure 7. Public atlas of the gardens of versailles (input data).

Figure 8 showcases the reconstruction results after processing by the DGA-Net model. From this figure, it is evident that the model successfully captured the key geometric details of the input scene and generated fine point clouds and model rendering results through the three-dimensional reconstruction process. During the reconstruction, DGA-Net extracted spatial features of the scene using a Deep Convolutional Network (DCN) and modeled the complex topological relationships between points in the scene using a Graph Convolutional Network (GCN). The introduction of the attention mechanism enabled the model to focus more precisely on important feature areas, resulting in more accurate and complete three-dimensional structures.

Figure 8

Figure 8. Processing process and reconstruction results of the DGA-Net model.

In the final reconstruction results, the details of historical architecture, such as columns, wall structures, and complex interior decorative elements, are highly restored. At the same time, the model also successfully preserved the overall shape and spatial layout of large-scale buildings, ensuring that the generated three-dimensional scene exhibits high visual consistency and geometric accuracy. These results demonstrate the outstanding performance of DGA-Net in three-dimensional reconstruction of complex historical scenes, providing reliable technical support for the digital preservation and display of cultural heritage.

5 Conclusion

As the global ecological degradation problem intensifies, landscape restoration has become one of the key strategies to achieve ecologically sustainable development. Especially in the landscape restoration process of cultural heritage such as historical gardens, digital technology provides strong support for traditional restoration methods. The three-dimensional reconstruction method (DGA-Net) proposed in this article based on the combination of depth features and graph structure provides a new technical path for the accurate restoration of garden landscapes. By combining deep convolutional networks (DCN), graph convolutional networks (GCN) and attention mechanisms, DGA-Net can effectively process complex garden landscape data and capture its spatial characteristics and topological relationships, thereby improving the performance of landscape restoration and ecology. Play an important role in system reconstruction. Experimental results show that DGA-Net performs well in the three-dimensional reconstruction of historical gardens, especially in terms of detail recovery and global structure consistency. Compared with traditional methods, DGA-Net can more accurately capture the complex geometric shapes and ecological relationships of garden landscapes, demonstrating its potential in landscape restoration and ecological monitoring. The ablation experiment further proved the importance of each module of the model, especially the attention mechanism, which can effectively reduce redundant information and improve attention to key features, thus improving the application effect of the model in landscape restoration.

Although DGA-Net provides strong support for the digital protection and display of cultural heritage in terms of accurate 3D reconstruction of complex scenes in historical gardens, the model still has some limitations in practical applications. For example, when dealing with high-noise data or ultra-large-scale scenes, the accuracy and efficiency of the model may be affected to a certain extent. Especially in these extreme cases, the quality fluctuations of point cloud data may lead to instability in the reconstruction results and affect the performance of the model. In addition, the DGA-Net model has a large computational overhead, which poses a challenge to its widespread deployment in real-time applications. Therefore, how to optimize computational efficiency without reducing the quality of reconstruction has become an important direction for future research.

In view of the above limitations, future research will focus on improving the performance of the model on low-quality datasets and exploring more efficient feature extraction and relationship modeling methods to enhance the robustness of the model. At the same time, in view of the computational efficiency problem, we plan to try to use a lightweight network structure to reduce the consumption of computing resources, so as to support a wider range of real-time applications. In order to improve the adaptability of DGA-Net in various historical gardens and cultural heritage scenes, we will also actively explore ways to enhance the adaptability of the model so that it can handle more diverse and complex cultural heritage scenes and provide a wider range of application value in the field of cultural heritage protection.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JC: Data curation, Resources, Writing–original draft. QC: Data curation, Methodology, Visualization, Writing–review and editing. YY: Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashfaq, H., and Jalal, A. (2023). Gcn-based objects understanding with 2d to 3d point cloud reconstruction. Proc. IEEE, 7–12. doi:10.1109/ibcast59916.2023.10712925

CrossRef Full Text | Google Scholar

Bai, C., Fu, R., and Gao, X. (2024). Colmap-pcd: an open-source tool for fine image-to-point cloud registration. IEEE, 1723–1729. doi:10.1109/icra57147.2024.10611582

CrossRef Full Text | Google Scholar

Boboc, R. G., Bautu, E., Gîrbacia, F., Popovici, N., and Popovici, D. M. (2022). Augmented reality in cultural heritage: an overview of the last decade of applications. Appl. Sci. 12, 9859. doi:10.3390/app12199859

CrossRef Full Text | Google Scholar

Dong, Q., Zhang, Q., and Zhu, L. (2020). 3d scanning, modeling, and printing of Chinese classical garden rockeries: zhanyuan’s south rockery. Herit. Sci. 8, 61–15. doi:10.1186/s40494-020-00405-z

CrossRef Full Text | Google Scholar

Fabijańska, A., and Banasiak, R. (2021). Graph convolutional networks for enhanced resolution 3d electrical capacitance tomography image reconstruction. Appl. Soft Comput. 110, 107608. doi:10.1016/j.asoc.2021.107608

CrossRef Full Text | Google Scholar

Fahim, G., Amin, K., and Zarif, S. (2021). Single-view 3d reconstruction: a survey of deep learning methods. Comput. and Graph. 94, 164–190. doi:10.1016/j.cag.2020.12.004

CrossRef Full Text | Google Scholar

Ferdani, D., Fanini, B., Piccioli, M. C., Carboni, F., and Vigliarolo, P. (2020). 3d reconstruction and validation of historical background for immersive vr applications and games: the case study of the forum of augustus in rome. J. Cult. Herit. 43, 129–143. doi:10.1016/j.culher.2019.12.004

CrossRef Full Text | Google Scholar

Griwodz, C., Gasparini, S., Calvet, L., Gurdjos, P., Castan, F., Maujean, B., et al. (2021). “Alicevision mushroom: an open-source 3d reconstruction pipeline,” in Proceedings of the 12th ACM multimedia systems conference, 241–247.

Google Scholar

Guo, L., Ma, W., Gong, X., Zhang, D., Zhai, Z., and Li, M. (2024). Digital preservation of classical gardens at the san su shrine. Herit. Sci. 12, 66. doi:10.1186/s40494-024-01138-z

CrossRef Full Text | Google Scholar

Hao, M., Zhang, Z., Li, L., Dong, K., Cheng, L., Tiwari, P., et al. (2024). Coarse to fine-based image–point cloud fusion network for 3d object detection. Inf. Fusion 112, 102551. doi:10.1016/j.inffus.2024.102551

CrossRef Full Text | Google Scholar

He, Y., Zeng, L., Yu, W., and Gong, C. (2020). Noise suppression–guided image filtering for low-snr ct reconstruction. Med. and Biol. Eng. and Comput. 58, 2621–2629. doi:10.1007/s11517-020-02246-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, T., Yu, T., Zheng, Z., Zhang, H., Liu, Y., and Zwicker, M. (2022). Hvtr: hybrid volumetric-textural rendering for human avatars. IEEE, 197–208. doi:10.1109/3dv57658.2022.00032

CrossRef Full Text | Google Scholar

Ji, M., Zhang, J., Dai, Q., and Fang, L. (2020). Surfacenet+: an end-to-end 3d neural network for very sparse multi-view stereopsis. IEEE Trans. Pattern Analysis Mach. Intell. 43, 4078–4093. doi:10.1109/tpami.2020.2996798

PubMed Abstract | CrossRef Full Text | Google Scholar

Jia, S., Liao, Y., Xiao, Y., Zhang, B., Meng, X., and Qin, K. (2022a). Methods of conserving and managing cultural heritage in classical Chinese royal gardens based on 3d digitalization. Sustainability 14, 4108. doi:10.3390/su14074108

CrossRef Full Text | Google Scholar

Jia, S., Liao, Y., Xiao, Y., Zhang, B., Meng, X., and Qin, K. (2022b). Conservation and management of Chinese classical royal garden heritages based on 3d digitalization-a case study of jinxing courtyard in jingyi garden in fragrant hills. J. Cult. Herit. 58, 102–111. doi:10.1016/j.culher.2022.09.020

CrossRef Full Text | Google Scholar

Kodipalli, A., Fernandes, S. L., Dasar, S. K., and Ismail, T. (2023). Computational framework of inverted fuzzy c-means and quantum convolutional neural network towards accurate detection of ovarian tumors. Int. J. E-Health Med. Commun. (IJEHMC) 14, 1–16. doi:10.4018/ijehmc.321149

CrossRef Full Text | Google Scholar

Kuang, Z., Zhang, Y., Yu, H. X., Agarwala, S., Wu, E., Wu, J., et al. (2024). Stanford-orb: a real-world 3d object inverse rendering benchmark. Adv. Neural Inf. Process. Syst. 36.

PubMed Abstract | Google Scholar

Li, J., Gao, W., Wu, Y., Liu, Y., and Shen, Y. (2022a). High-quality indoor scene 3d reconstruction with rgb-d cameras: a brief review. Comput. Vis. Media 8, 369–393. doi:10.1007/s41095-021-0250-8

CrossRef Full Text | Google Scholar

Li, S., Li, C., Zhu, W., Yu, B. T., Zhao, Y. K., Wan, C., et al. (2023). Instant-3d: instant neural radiance field training towards on-device ar/vr 3d reconstruction. preprint, 1–13. doi:10.1145/3579371.3589115

CrossRef Full Text | Google Scholar

Li, Z., Luo, S., Zeng, W., Guo, S., Zhuo, J., Zhou, L., et al. (2022b). 3d reconstruction system for foot arch detecting based on openmvg and openmvs. IEEE, 1017–1022. doi:10.1109/prai55851.2022.9904285

CrossRef Full Text | Google Scholar

Lin, J., Gu, Y., Du, G., Qu, G., Chen, X., Zhang, Y., et al. (2024). 2d/3d image morphing technology from traditional to modern: a survey. Inf. Fusion 117, 102913. doi:10.1016/j.inffus.2024.102913

CrossRef Full Text | Google Scholar

Lin, Z., Lin, J., Li, L., Yuan, Y., and Zou, Z. (2022). High-quality 3d face reconstruction with affine convolutional networks. Pattern Recognit. 153, 2495–2503. doi:10.1145/3503161.3548421

CrossRef Full Text | Google Scholar

Ma, X., Wei, B., Guan, H., Cheng, Y., and Zhuo, Z. (2024). A method for calculating and simulating phenotype of soybean based on 3d reconstruction. Eur. J. Agron. 154, 127070. doi:10.1016/j.eja.2023.127070

CrossRef Full Text | Google Scholar

Martínez-Carricondo, P., Carvajal-Ramírez, F., Yero-Paneque, L., and Agüera-Vega, F. (2020). Combination of nadiral and oblique uav photogrammetry and hbim for the virtual reconstruction of cultural heritage. case study of cortijo del fraile in níjar, almería (spain). Build. Res. and Inf. 48, 140–159. doi:10.1080/09613218.2019.1626213

CrossRef Full Text | Google Scholar

Martorana, R., Capizzi, P., Giambrone, C., Simonello, L., Mapelli, M., Carollo, A., et al. (2024). The “annunziata” garden in cammarata (sicily): results of integrated geophysical investigations and first archaeological survey. J. Appl. Geophys. 227, 105436. doi:10.1016/j.jappgeo.2024.105436

CrossRef Full Text | Google Scholar

Mikamo, M., Furukawa, R., Oka, S., Kotachi, T., Okamoto, Y., Tanaka, S., et al. (2021). Active stereo method for 3d endoscopes using deep-layer gcn and graph representation with proximity information. IEEE 2021, 7551–7555. doi:10.1109/embc46164.2021.9629696

PubMed Abstract | CrossRef Full Text | Google Scholar

Monga, V., Li, Y., and Eldar, Y. C. (2021). Algorithm unrolling: interpretable, efficient deep learning for signal and image processing. IEEE Signal Process. Mag. 38, 18–44. doi:10.1109/msp.2020.3016905

CrossRef Full Text | Google Scholar

Ning, X., Yu, Z., Li, L., Li, W., and Dilf, T. P. (2024). DILF: differentiable rendering-based multi-view Image–Language Fusion for zero-shot 3D shape understanding. Inf. Fusion 102, 102033. doi:10.1016/j.inffus.2023.102033

CrossRef Full Text | Google Scholar

Peng, Y., Zhang, G., Nijhuis, S., Agugiaro, G., and Stoter, J. E. (2024). Towards a framework for point-cloud-based visual analysis of historic gardens: jichang garden as a case study. Urban For. and Urban Green. 91, 128159. doi:10.1016/j.ufug.2023.128159

CrossRef Full Text | Google Scholar

Pepe, M., Alfio, V. S., Costantino, D., and Scaringi, D. (2022). Data for 3d reconstruction and point cloud classification using machine learning in cultural heritage environment. Data Brief 42, 108250. doi:10.1016/j.dib.2022.108250

PubMed Abstract | CrossRef Full Text | Google Scholar

Pham, X. H., Bonne, F., and Alamir, M. (2023). On the use of gradient-based solver and deep learning approach in hierarchical control: application to grand refrigerators. Cybern. Syst., 1–19. doi:10.1080/01969722.2023.2247264

CrossRef Full Text | Google Scholar

Phan, H. T., Pham, D. T., and Nguyen, N. T. (2023). Fedn2: fuzzy-enhanced deep neural networks for improvement of sentence-level sentiment analysis. Cybern. Syst., 1–17. doi:10.1080/01969722.2023.2296252

CrossRef Full Text | Google Scholar

Pietroni, E., and Ferdani, D. (2021). Virtual restoration and virtual reconstruction in cultural heritage: terminology, methodologies, visual representation techniques and cognitive models. Information 12, 167. doi:10.3390/info12040167

CrossRef Full Text | Google Scholar

Ping, R. B., and Yue, W. Z. (2024). Strategic focus, tasks, and pathways for promoting China’s modernization through new productive forces. J. Xi’an Univ. Finance Econ. 1, 3–11.

Google Scholar

Remondino, F., Karami, A., Yan, Z., Mazzacca, G., Rigon, S., and Qin, R. (2023). A critical analysis of nerf-based 3d reconstruction. Remote Sens. 15, 3585. doi:10.3390/rs15143585

CrossRef Full Text | Google Scholar

Salari, A., Nozdryn-Plotnicki, A., Afrooze, S., and Najjaran, H. (2021). 3dcadfusion: tracking and 3d reconstruction of dynamic objects without external motion information. IEEE, 3479–3484. doi:10.1109/smc52423.2021.9658735

CrossRef Full Text | Google Scholar

Salvi, M., Acharya, U. R., Molinari, F., and Meiburger, K. M. (2021). The impact of pre-and post-image processing techniques on deep learning frameworks: a comprehensive review for digital pathology image analysis. Comput. Biol. Med. 128, 104129. doi:10.1016/j.compbiomed.2020.104129

PubMed Abstract | CrossRef Full Text | Google Scholar

Sannidhan, M., Martis, J. E., Nayak, R. S., Aithal, S. K., and Sudeepa, K. (2023). Detection of antibiotic constituent in aspergillus flavus using quantum convolutional neural network. Int. J. E-Health Med. Commun. (IJEHMC) 14, 1–26. doi:10.4018/ijehmc.321150

CrossRef Full Text | Google Scholar

Soto-Martin, O., Fuentes-Porto, A., and Martin-Gutierrez, J. (2020). A digital reconstruction of a historical building and virtual reintegration of mural paintings to create an interactive and immersive experience in virtual reality. Appl. Sci. 10, 597. doi:10.3390/app10020597

CrossRef Full Text | Google Scholar

Srivastava, S., Divekar, A. V., Anilkumar, C., Naik, I., Kulkarni, V., and Pattabiraman, V. (2021). Comparative analysis of deep learning image detection algorithms. J. Big data 8, 66. doi:10.1186/s40537-021-00434-w

CrossRef Full Text | Google Scholar

Wang, J., Li, F., and He, L. (2025b). A unified framework for adversarial patch attacks against visual 3d object detection in autonomous driving. IEEE Trans. Circuits Syst. Video Technol., 1. doi:10.1109/tcsvt.2025.3525725

CrossRef Full Text | Google Scholar

Wang, J., Li, F., Lv, S., He, L., and Shen, C. (2025a). Physically realizable adversarial creating attack against vision-based bev space 3d object detection. IEEE Trans. Image Process. 34, 538–551. doi:10.1109/tip.2025.3526056

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Fan, E., and Wang, P. (2021). Comparative analysis of image classification algorithms based on traditional machine learning and deep learning. Pattern Recognit. Lett. 141, 61–67. doi:10.1016/j.patrec.2020.07.042

CrossRef Full Text | Google Scholar

Wang, T., and Gan, V. J. (2024). Enhancing 3d reconstruction of textureless indoor scenes with indoreal multi-view stereo (mvs). Automation Constr. 166, 105600. doi:10.1016/j.autcon.2024.105600

CrossRef Full Text | Google Scholar

Wang, X., Yang, X., Li, H., and Li, T. (2024). Fddcc-vsr: a lightweight video super-resolution network based on deformable 3d convolution and cheap convolution. Vis. Comput., 1–13. doi:10.1007/s00371-024-03621-x

CrossRef Full Text | Google Scholar

Xu, M., Yoon, S., Fuentes, A., and Park, D. S. (2023). A comprehensive survey of image augmentation techniques for deep learning. Pattern Recognit. 137, 109347. doi:10.1016/j.patcog.2023.109347

CrossRef Full Text | Google Scholar

Yang, C., Han, X., Wu, H., Han, F., Wei, C., and Shutter, L. (2023). Digital characterization of the surface texture of Chinese classical garden rockery based on point cloud visualization: small-rock mountain retreat. Herit. Sci. 11, 13. doi:10.1186/s40494-022-00851-x

CrossRef Full Text | Google Scholar

Yang, X., Grussenmeyer, P., Koehl, M., Macher, H., Murtiyoso, A., and Landes, T. (2020). Review of built heritage modelling: integration of hbim and other information techniques. J. Cult. Herit. 46, 350–360. doi:10.1016/j.culher.2020.05.008

CrossRef Full Text | Google Scholar

Yu, A., Guo, W., Liu, B., Chen, X., Wang, X., Cao, X., et al. (2021b). Attention aware cost volume pyramid based multi-view stereo network for 3d reconstruction. ISPRS J. Photogrammetry Remote Sens. 175, 448–460. doi:10.1016/j.isprsjprs.2021.03.010

CrossRef Full Text | Google Scholar

Yu, D., Ji, S., Liu, J., and Wei, S. (2021a). Automatic 3d building reconstruction from multi-view aerial images with deep learning. ISPRS J. Photogrammetry Remote Sens. 171, 155–170. doi:10.1016/j.isprsjprs.2020.11.011

CrossRef Full Text | Google Scholar

Zhang, J., Yang, J., Fu, F., and Ma, J. (2024). Planeac: line-guided planar 3d reconstruction based on self-attention and convolution hybrid model. Pattern Recognit. 153, 110519. doi:10.1016/j.patcog.2024.110519

CrossRef Full Text | Google Scholar