Quantifying rain-driven NO3-N dynamics in headwater: value of applying SISO system identification to multiple variables monitored at the same high frequency

The nitrate–nitrogen (NO₃-N) concentration is a key variable affecting the ecosystem services supported by headwater streams. The availability of such data monitored continuously at a high frequency (in parallel to hydrometric and other water quality data) potentially permits a greater insight into the dynamics of this key variable. This study demonstrates how single-input single-output (SISO) system identification tools can make better use of these high-frequency data to identify a reduced number of numerical characteristics that support new explanatory hypotheses of rain-driven NO₃-N dynamics. A second-order watershed managed for commercial forestry in upland Wales (United Kingdom) provided the illustrative data. Fifteen-minute rainfall time series were used to simulate NO₃-N concentration dynamics and the potentially associated dynamics in dissolved organic carbon (DOC) and runoff, monitored at the same high resolution for two 30-day periods with a differing temperature regime. The approach identified robust, high-efficiency models needing few parameters. Comparison of only three derived dynamic response characteristics (DRCs) of δ, TC, and SSG for the three variables for the two different periods led to new hypotheses of rain-driven NO₃-N dynamics for further exploratory field investigation.

1 Introduction

With advances in sensor technology, more researchers and practitioners are continuously monitoring nitrate–nitrogen (NO₃-N) dynamics and other water quality variables at a high frequency, i.e., sub-daily or sub-hourly (Burns et al., 2019). For NO₃-N, this reveals the importance of diel and seasonal cycles (Halliday et al., 2013; Kermorvant et al., 2023) and complex short-term responses to rain events (Brunet et al., 2021). Time series of NO₃-N may also contain apparent interactions with other water quality variables, such as dissolved organic carbon (DOC) (Ledesma et al., 2022) or phosphate (Graeber et al., 2024).

As the accuracy and reliability of continuous in-field NO₃-N measurements have increased (Pellerin et al., 2013), so has the imperative to make the most of the information-rich time series that can now be collected (Burns et al., 2019). Improved evaluation of watershed models capable of simulating complex nitrate dynamics over wide time scales is possible with the higher-frequency data (Jiang et al., 2019). Where numerous water quality data streams are combined with synchronous data streams of potential controlling variables (e.g., solar radiation and rainfall), real-time “machine learning” can make rapid predictions of water quality changes for hazard mitigation (Tang et al., 2022; McGill and Ford, 2024). Similarly, numerical methods used for extracting 1) the dominant cycles and trends within NO₃-N time series; 2) quantifying the strength of dynamic relationships between a water quality variable and the controls on these dynamics; and 3) deriving dynamic response characteristics (DRCs) particular to the watershed, land use, or climate setting become credible. One such class of methods capable of extracting contained dynamics is system identification (SI) tools or models (Box et al., 2008). Typically, these methods differ from machine learning approaches or models built on biogeochemical–hydrological processes by the implicit goal of parsimony (Taylor et al., 2007). The goal is to simulate the dominant modes of behavior within a time series with the fewest number of model parameters in the least complex conceptual model structure. When the number of model parameters can be limited in this way (while still simulating outputs with high accuracy), uncertainty in the individual estimates of parameter values is constrained. The resultant reduced uncertainty may then lead to greater confidence in feasible interpretations of the process dynamics (Jones et al., 2014). Furthermore, by not “forcing” preconceived process dynamics to fit observed time series, new aspects of our perceptual understanding of water quality behavior may emerge from SI modeling (Burns et al., 2019).

Watercourses may have anthropogenically elevated concentrations of dissolved NO₃-N as a result of elevated nitrogen inputs to watersheds or through watershed disturbance. For example, in upland Wales (United Kingdom), soil and vegetation disturbances associated with commercial conifer forestry have been shown to lead to elevated NO₃-N losses to headwater streams (Neal et al., 2011; Halliday et al., 2013), risking acidification and eutrophication downstream. The instrumented headwater stream in upland Wales chosen for this illustrative study has been affected by such commercial forestry with its associated impacts on NO₃-N concentrations and other water quality variables (Ormerod and Durance, 2009; Jones and Chappell, 2014). This watershed is the 2-km² Trawsnant, with over 90% of its area covered by managed commercial conifer plantations. Lancaster University instrumented the watershed as part of the “Diversity of Upland Rivers for Ecosystem Service Sustainability” (DURESS) project within the Biodiversity and Ecosystem Service Sustainability (BESS) research program. The stream gauging station was installed at 52.12596° N, 3.74740° W, at a height of 322 m within the Welsh uplands. Approximately 44% of the watershed is covered by podzolic soil, 48% by histosol, and the remaining 9% by gleysol (Jones and Chappell, 2014). The geology comprises Ordovician sedimentary rocks (Cwmere and Yr Allt formations). A water quality station was located close to the stream gauge to collect parallel high-frequency time series of NO₃-N (dissolved and total), organic carbon (dissolved and total), water temperature, pH, and electrical conductivity. A network of automated rain gauges supported these stations. These parallel time series, all collected at a high frequency at every 15 min, permitted the comparison of rain-driven NO₃-N dynamics with those of DOC and hydrological dynamics. Previous studies have indicated that watershed hydrological responses to rainfall and DOC concentrations may help in understanding the rain-driven NO₃-N dynamics in similar low-order streams (Halliday et al., 2013; Koenig et al., 2017; Burns et al., 2019). A single-input single-output (SISO) form of system identification modeling (Taylor et al., 2007) was used in this study to quantify the rain-driven NO₃-N dynamics. The complexity of the accepted models was minimized (using numerical measures of efficiency and over-parameterization) to aid the hydrological/biogeochemical interpretation, as done by Jones and Chappell (2014), Jones et al. (2014), and Chappell et al. (2017a). The overall aim was to demonstrate the value of using a SISO system identification tool for quantifying rain-driven water quality dynamics, with the example of dissolved NO₃-N within a small stream emanating from a conifer plantation. The specific research objectives are to

1. Demonstrate the value of using SISO system identification to extract information from multiple water quality time series monitored at a high frequency along with parallel hydrometric data;

2. Quantify the degree of model complexity required to simulate rain-generated, dissolved NO₃-N concentration dynamics, along with reference dynamics of DOC concentration and streamflow; and

3. Gain consistent process interpretation (feasible hypotheses: following Beven and Chappell, 2021) from the identified values of SISO model parameters and their derivative DRCs from SISO model application to two periods differing in temperature.

2 Methods

The novelty of the approach illustrated comes from the combination of water quality and hydrometry monitored at a high frequency with SISO system identification modeling (Jones et al., 2014; Chappell et al., 2017a).

2.1 Monitoring dissolved NO₃-N and carbon plus hydrometric variables at a high frequency

A 430-L/s trapezoidal flume (Genesis Composites Ltd., Glenrothes) was used to generate the critical flow for discharge measurement. The water level was monitored at a tapping point installed within the throat of the flume using a CTWM82X5G4C3SUN pressure transmitter (Sensortechnics Ltd., Rugby). This was undertaken every 15-min and recorded using a CR1000 data logger (Campbell Scientific Ltd., Shepshed). Local deviation from the theoretical calibration was checked with salt dilution gauging. Rainfall was measured using two SBS500 rain gauges (Environmental Measurements Limited, South Shields) connected to the same CR1000 data-logging systems.

The water quality station was located 60 m upstream of the flume. The dissolved NO₃-N and organic carbon were measured continuously in the field at the same 15-min intervals as the hydrometric measurements (rainfall and discharge) using an in-field “Spectrolyzer” (version 2) with an optical path length of 35 mm (s::can Messtechnik GmbH, Vienna). To prevent the voltage from dropping below 12 vDC, which would deactivate the unit, a 24-vDC power supply was used. The optical windows of the spectrolyzer were cleaned twice weekly with 10% hydrochloric acid applied to a small brush. Then, once per week, the measurement windows were soaked in the same solution for 5 min as a further cleaning step. The station incorporated an auto-sampler so that water samples could be taken for laboratory analysis for NO₃-N and DOC by the accredited analytical laboratories of UKCEH. These samples were used for the adjustment of the s::can RIVCOL global calibrations to the local Trawsnant water (e.g., Jones et al., 2014). The regular cleaning regime minimized the magnitude of steps in the concentration time series before and after each cleaning episode. To remove these small steps, exponential development of precipitates and algal growth on the windows over the exact 3–4-day periods between cleaning was assumed and removed using 15 lines of code in MATLAB (Jones et al., 2014). Stream temperature at the water quality station was monitored in parallel to the other variables using a CS547A probe (Campbell Scientific Ltd.).

2.2 SISO system identification modeling of rain-driven dynamics

The SISO system identification tool used to quantify the rainfall to NO₃-N dynamics through a series of storm events was the Refined Instrumental Variable Continuous-time Box–Jenkins IDentification (RIVCBJID) algorithm within the CAPTAIN Toolbox for MATLAB (Taylor et al., 2007). This continuous-time variant of this Refined Instrumental Variable (RIV) method describes the SISO system with differential equations (Young, 2015) rather than different equations of the discrete-time variant. RIV methods gain their skill in capturing dynamics by incorporating

(i) an initial pre-filtering stage to remove high-order noise (i.e., dynamics much shorter than the shortest time constant of the system) that affects the identification of the true model structure and

(ii) the covariance matrix (Box et al., 2008) that is used explicitly to find the most robust model with the least uncertainty.

2.2.1 Model structure

To reiterate, the form of the model identified by RIVCBJID may be expressed in ordinary differential equation terms. The simplest form of the dynamic model identified (i.e., with the least number of hydrological/biogeochemical components) is called a first-order model. With rain-driven nitrate concentration as an example, this model would be (ignoring initial conditions)

$\frac{d{C}_{{NO}_3-N}\left(t\right)}{dt}+{\alpha C}_{{NO}_3-N}\left(t\right)=\beta r\left(t-\delta \right),$

where $C_{{NO}_3-N}$ is the stream nitrate–nitrogen concentration (mg/L monitored at a 15-min interval), $r$ is the total rainfall per 15-min period (mm/15 min), $\delta$ is the pure time delay between rainfall and an initial $C_{{NO}_3-N}$ response (number of 15-min periods in this study), $\alpha$ is the parameter capturing the rate of NO₃-N exhaustion (/15 min), $\beta$ is the parameter capturing the magnitude of NO₃-N production or gain (mg/L 15-min/mm), and t is time in 15-min periods. The SISO data being modeled that contain more complex dynamics than higher-order models (e.g., second-order) may be defined (Jones et al., 2014). Prior to interpretation (see Section 2.2.3), these are typically decomposed by partial fraction expansion into multiple first-order components.

Similarly, the first-order SISO model illustrated may be expressed as a first-order transfer function in continuous time (sometimes abbreviated to CT-TF):

${NO}_3-N=\frac{b}{s-a}{e}^{-s\delta }r;s\sim \frac{d}{dt},$

where s is the Laplace operator, $a=-\alpha$, and $b=\beta$. The structure of the CT-TF model identified (whether first-order or a higher order) is often shown in the form of a triad [den num del], where the number of denominators, den (i.e., number of $a$ terms in the lower part of a transfer function), number of numerators, num (i.e., number of $b$ terms in the upper part of a transfer function), and the number of time steps of pure time delay, del (where time-step length multiplied by del = $\delta$) are shown in square parentheses. For a first-order model, there is only one denominator (or $a$ term), so the triad would take the form [1 num del]. Rain-driven runoff dynamics sometimes exhibit nonlinearity, where the magnitude of a nonlinearity term (p) is sometimes shown with a superscript outside the parentheses, e.g., [den num del]^p (refer to Chappell et al., 2012 for example).

2.2.2 Application to high-frequency time series of NO₃-N, DOC, and runoff

RIVCBJID was applied to time series of dissolved NO₃-N concentration, DOC concentration, and stream discharge per unit area (i.e., runoff), with rainfall as the common input reference. A period of 234 days (09 January 2013 to 31 August 2013; in ISO 8601 ordinal date format 2012-374 to 2012-608) of synchronous 15-min time series was considered for analysis (Figures 1A, B).

Figure 1

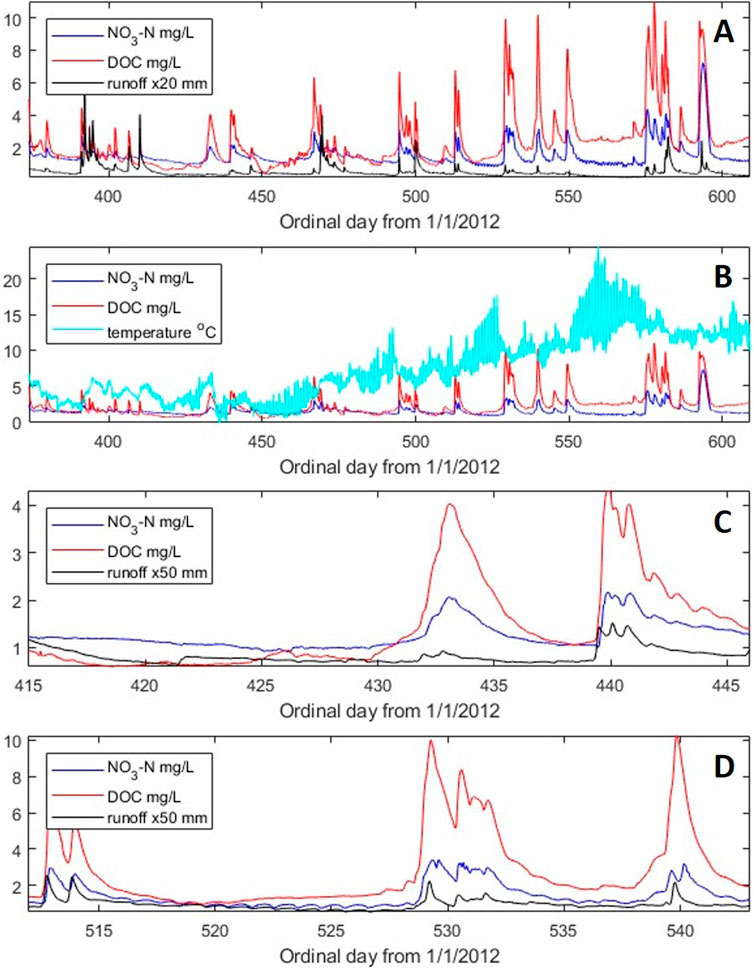
Figure 1. Time series of 234 days (09 January 2013 to 31 August 2013) at a 15-min resolution for the 2-km² Trawsnant stream in upland Wales (United Kingdom). Subplot (A) time series of dissolved NO₃-N concentration (mg/L), DOC concentration (mg/L), and unit area discharge (mm × 20); (B) time series of DOC concentration (mg/L) and stream temperature (°C); (C) 30-day “cold” (late winter–spring) period selected for SISO model identification; and (D) 30-day “warm” (early summer) period selected for SISO model identification.

Previous analysis of DOC time series from the Trawsnant watershed demonstrated differences in SISO chemograph responses between seasons (Jones et al., 2014). Thus, in this study with a NO₃-N focus, dynamics are quantified and compared between a 30-day period in late winter–spring (19 February–21 March; 2012-415 to 2012-445; Figure 1C) with those of a 30-day period in the early summer (27 May–26 June; 2012-512 to 2012-542; Figure 1D). The former had an average stream temperature of 2.8°C, and the latter, 9.4°C (see Figure 1B). The periods selected exhibit modest discharge responses but marked NO₃-N and DOC chemograph responses to rainfall (Figures 1A, C, D). The two periods also contrasted in their water balance. The discharge per unit area for the selected 30-day early-summer period was a much smaller proportion of the rainfall (i.e., 58 mm of 123 mm of rainfall) when compared with the late-winter–spring period (i.e., 49 mm of 51 mm of rainfall). The higher stream temperatures in the early-summer period are likely to have resulted from higher levels of net radiation (data available but not presented). These higher levels of net radiation are likely associated with higher wet-canopy evaporation rates (and transpiration) from the upland conifers in the early-summer period (Page et al., 2020). These higher rates of evaporation may explain the observed reduced discharge per unit rainfall input in the summer period.

2.2.3 Process interpretation of rain-driven dynamics within the identified model structures

The process of interpretation of key terms within identified transfer functions may be described by three DRCs (Jakeman et al., 1993). These DRCs are i) the time constant or TC; ii) the steady-state gain or SSG; and iii) the already identified pure time delay or δ. A time constant is derived directly from an identified value of $a$:

$TC=\frac{∆t}{a},$

where $∆t$ is the time step in the observations (15 min in this example). This derived TC is the rate of exhaustion (or recession) of the concentration (or runoff) response (expressed as time) following the unit input of rainfall (mm). The SSG is similarly derived directly from an identified value of $a$ and $b$:

$SSG=\frac{b}{a}.$

This derived SSG is, for example, the magnitude of the NO₃-N concentration increase (mg/L) for a unit input of rainfall (mm). For a model of runoff where the input and output units are identical, the SSG is simply the simulated runoff coefficient (Chappell et al., 2006). The identified parameter of the pure time delay ($\delta$) is the delay between a unit input of rainfall (mm) and a unit NO₃-N or DOC concentration (mg/L) response (or runoff response, mm).

3 Results

First-order SISO models (applied to 15-min resolution data) could describe most of the dominant modes of dynamics between a rainfall input and an output of either NO₃-N, DOC, or runoff (for either 30-day period; Figures 2, 3). Higher-order SISO models (e.g., more complex second-order models that may represent two parallel pathways with their own dynamics) could be identified. All of these higher-order models, however, failed the Young Information Criterion (YIC), indicating that higher model complexity was not justified by the information content of the data (refer to Chappell et al., 2012 for example).

Figure 2

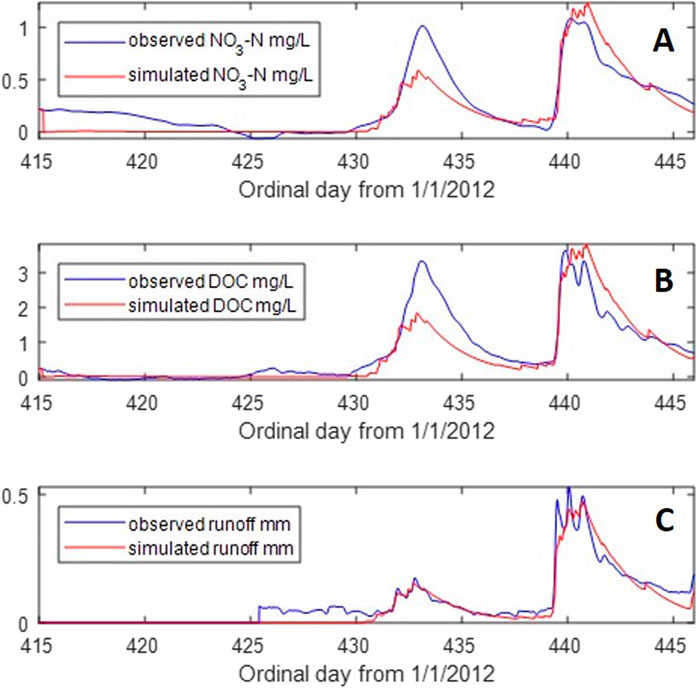
Figure 2. Observed and SISO-simulated time series for the 30-day “cold” period in late winter–spring (19 February–21 March 21 2013; ordinal date: 2012-415 to 2012-445). Subplot (A) NO₃-N concentration (mg/L); (B) DOC concentration (mg/L); and (C) runoff (mm, scaled by × 30 for model identification).

Figure 3

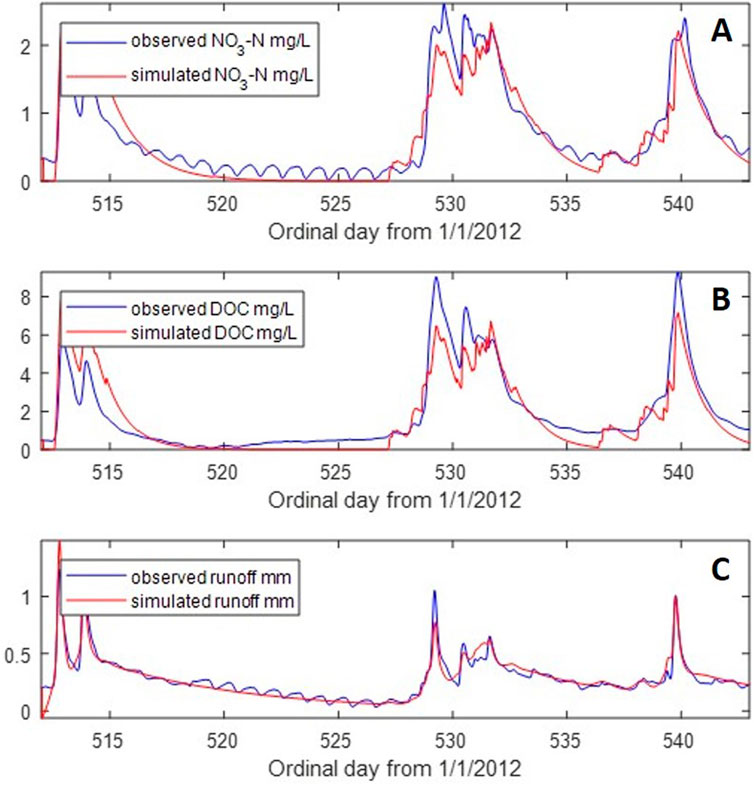
Figure 3. Observed and SISO-simulated time series for the 30-day “warm” period in the early summer (27 May–26 June 26 in 2023; ordinal date: 2012-512 to 2012-542). Subplot (A) NO₃-N concentration (mg/L); (B) DOC concentration (mg/L); and (C) runoff (mm, scaled by × 30 for model identification).

Table 1 shows the SISO transfer function parameters of the identified models and the derived estimates of the DRCs that may be interpreted in hydrological or biogeochemical terms (Jones et al., 2014). The efficiency of the identified models at capturing the output dynamics is given with the metric of R_t² (i.e., simplified Nash–Sutcliffe efficiency; Chappell et al., 2012). Although the models capture most of the dominant modes of rain-driven dynamics, they do not capture them all (i.e., R_t² < 1.0). Visual inspection of the simulated versus observed NO₃-N and DOC chemographs and runoff hydrographs (Figures 2, 3) provides the same finding. These apparent discrepancies provide additional insights beyond the interpretations gained from the DRCs and are therefore discussed.

Table 1

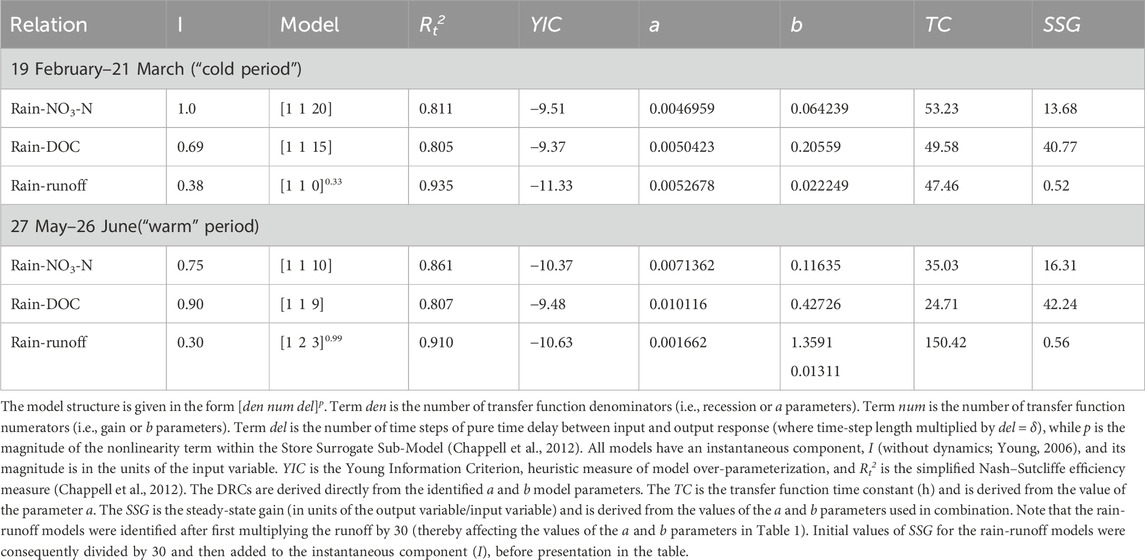
Table 1. Structure and parameters of the identified SISO first-order models applied to NO₃-N concentration, DOC concentration, and runoff data given a rainfall input.

4 Discussion

First, the interpretations of rain to NO₃-N concentration modeling are presented, followed by additional interpretations arising from parallel modeling of rain–DOC and rain–runoff dynamics.

4.1 Dissolved NO₃-N response to a unit input of rainfall in a cold versus warm period

A unit input of rainfall within the contiguous series of three early-summer storms delivered a similar unit increase in the dissolved NO₃-N concentration to that of the pair of contiguous winter–spring storms. In the early summer, a 16.3-mg/L increase in the NO₃-N concentration per mm rainfall (above the instantaneous response) was observed against a slightly smaller increase of 13.7 mg/L in the NO₃-N concentration per mm rainfall in the late winter–spring (Table 1). In some contrast, a large delay between the rainfall input and dominant mode of the concentration response of 5 h (i.e., 20 × 15-min time -steps) was observed in the case of late winter–spring storms. This was halved to 2.5 h (i.e., 10 × 15-min time steps) for the case of early-summer storms. With the storm pair in the winter period, the pulse of the NO₃-N concentration receded to two-thirds of its peak within 53.2 h (in the identified purely linear system). In contrast, in the summer period, the same rate of NO₃-N exhaustion was achieved in only 35.0 h, a 52% faster rate. Thus, the NO₃-N response per unit rainfall input appeared more quickly and depleted more quickly in the warmer, early-summer events than in the colder winter–spring events.

The antecedent runoff (a measure of catchment wetness: Chappell et al., 2017b) for the small events in the summer was slightly larger than that for the winter period (Figures 1C, D). This may have resulted in a reduced delay in developing a perched water table and, hence, lateral flow in the NO₃-N and DOC-rich organic surface layers of the forest floor (see Chappell et al., 1990; Winter et al., 2024) in these summer events. Drier antecedent conditions for the selected winter events may have additionally delayed the availability of NO₃-N in the upper soil through limits on mineralization and nitrification (Reynolds and Edwards, 1995; Rusjan et al., 2008; Koenig et al., 2017; Burns et al., 2019). Alternatively, the colder temperatures in the winter period may have limited the mineralization in the upper soil (Guntiñas et al., 2012). The faster exhaustion of the rain-driven NO₃-N signal at the water quality station in the headwater stream in the summer may be due to a higher rate of denitrification within the channel because of the higher temperatures (Figure 1B; Halliday et al., 2013; Kermorvant et al., 2023). Alternatively, if the size of the NO₃-N shallow source is limited and comparable for both periods, the faster responses in the summer period could have led to quicker exhaustion of the limited NO₃-N pool (e.g., Vaughan et al., 2017).

Clear diurnal cycles in the NO₃-N concentration time series emerge in the warmer period (Figures 1D, 3A). These have not been modeled with the SISO models utilized (negatively affecting model efficiency) but could be modeled using other SI models such as UCDHR (e.g., Halliday et al., 2013; Mindham et al., 2018). The greater sensitivity of the watershed to diurnal cycles in temperature (and its controlling net radiation) in the summer is interesting as it parallels the SISO modeling finding of greater sensitivity of NO₃-N response (“flashiness”) to rainfall inputs in this period.

4.2 Comparison with the DOC response

The dynamics of the rain-driven concentration response of DOC in the Trawsnant stream in the winter–spring and early-summer events was comparable to that of dissolved NO₃-N. The increase in the DOC concentration in the stream from the same unit input of rainfall was only marginally larger between the winter–spring and early-summer storms (i.e., an increase of 40.8–42.2 mg/L in the DOC concentration per mm rainfall). Similar to the NO₃-N response, the long delay before the initial response of the dominant DOC response of 3 h, 45 min in the winter–spring events reduced to 2 h, 15 min in the early-summer events (67% faster), and the storm-related pulse in the DOC concentration decreased more quickly in the summer months (i.e., TC 49.6 to 24.73 h: Table 1). This finding may imply that the dominant hydrological (i.e., antecedent conditions or water pathways) and/or biogeochemical controls affecting rain-driven NO₃-N dynamics between the two 30-day periods are the same for the DOC concentration.

Compared to NO₃-N, the magnitude of the response in the DOC concentration was considerably greater for the same unit input of rainfall. For example, in winter–spring, a 40.8 mg/L DOC increase per mm rainfall above the instantaneous response versus 13.7 mg/L increase per mm rainfall for the NO₃-N concentrations was observed. Thus, the Trawsnant watershed yielded more DOC than NO₃-N for the same rain event conditions. Figure 1B shows an increasing trend of the DOC concentration (starting on approximately day 2012-520), following the increase in stream temperature (starting approximately on day 2012-465). This may be caused by an increase in DOC production on the forest floor (Christ and David, 1996). Changing DOC:NO₃-N stoichiometry in the stream may have then given rise to the more rapid exhaustion of NO₃-N identified by the SISO modeling of the early-summer period (Ledesma et al., 2022). As a counter to this, the rate of exhaustion increased more with DOC than NO₃-N between the two periods (i.e., 50.1% reduction versus 34.2% reduction, respectively).

4.3 Comparison with streamflow generation

The SISO analyses yielded [1 1 15]^0.30 and [1 2 3]^0.99 rain-runoff models for the first and second periods, respectively (Table 1). This indicates that one hydrological pathway (or multiple paths combining to exhibit an apparent unitary behavior) dominates the Trawsnant hydrological response of the two studied periods with relatively small discharge events. The response, however, exhibited a marked increase in the residence time of the response from the winter–spring to the summer period, with the TC increasing by 217% from 47.5 to 150.4 h (Table 1). The dominant rainfall-runoff response had less than a 15-min initial delay (i.e., less than the time step of the data) in the winter–spring events, whereas the concentration responses had a pure time delay of 300 and 225 min for the NO₃-N and DOC, respectively (Table 1). These pure time delays in the dominant NO₃-N and DOC concentration response reduced to 150 and 135 min, respectively, while increasing to 45 min for the rainfall-runoff response in the early-summer period. These findings, using rainfall runoff as a reference, may support the idea that the changes in the dynamics between the two periods have a strong biogeochemistry control rather than a purely hydrological control.

It should be noted that the apparent diel cycle in the runoff between summer rainstorms (Figure 3C) has been experimentally measured to be an artifact of the pressure transmitters used (see also Mindham et al., 2018) rather than a natural diel cycle in the stream discharge (that can be present in other local watersheds; Kirchner, 2009). This contrasts with the natural diurnal cycle in the NO₃-N concentration time series (Figures 1D, 3A).

5 Conclusion

The SISO system identification tool of RIVCBJID identified models of rain-NO₃-N, rain-DOC, and rain-runoff over 30-day periods (each including 2–3 rain events) that have a high simulation efficiency (R_t²) of between 0.807 and 0.935 (Table 1). The water quality models comprised only four model parameters, namely, I (an instantaneous component with no dynamics; Young, 2006), δ, a, and b (Table 1). The runoff models required either five parameters, namely, p (a nonlinearity term), I, δ, a, and b or six parameters, namely, p, I, δ, a, and two b values (Table 1). The two b values provide a first-order model (i.e., one a parameter) in series. Water quality or hydrological models with such a small number of parameter values but high simulation efficiency are described as parsimonious (Chappell et al., 2017a). Slightly higher-order models (e.g., second-order models with two a values and two b values) were identified. These were, however, rejected as being “over-parameterized” (i.e., not justified by the dynamics in the data) for the selected Trawsnant events as the YIC values changed by more than +1 with higher model orders (Chappell et al., 2012).

Similarities and contrasts in behavior between rain-driven NO₃-N concentration dynamics between the two periods and with the other two variables (DOC concentration and runoff) were observed. For both water quality variables, the increase in the concentration per unit input of rainfall (SSG) remained similar in the cold and warm periods, as did the simulated runoff coefficient (i.e., SSG for the rain-runoff system). The SSG for the rain-DOC dynamics remained similar despite the increasing trend in the DOC concentration at times between storms (Figure 1B). In contrast, δ and TC for both water quality variables were much shorter (i.e., the system was more responsive) in the warmer period. This occurred as the hydrological system became more damped (i.e., δ and TC increased), perhaps highlighting the potential importance of the non-hydrological (e.g., biogeochemical) differences between the two periods.

The differences and similarities in the dynamics (between periods and variables) have feasible hydrological and biogeochemical interpretations based on the published findings of others. Whether these feasible interpretations are the dominant cause of the dynamics identified for the 2-km² Trawsnant stream (in upland Wales) , however, requires further field investigation (and subsequent numerical analysis). These further field investigations would benefit from high-frequency NO₃-N concentration time series at distributed locations within the watershed (Jones and Chappell, 2014; Burns et al., 2019), such as the litter layer, topsoil, upstream channels, and riparian zones. Similarly, improved rejection of feasible hypotheses would benefit from the collection and analysis of a greater number of potentially controlling variables at the watershed outlet (Burns et al., 2019; Li et al., 2022) and distributed throughout the watershed.

Additionally, the SISO models identified and interpreted in this study were for two 30-day periods with modest discharge responses but marked NO₃-N and DOC chemograph responses to rainfall. The robustness of the interpretations so far presented needs further evaluation by application to i) similar types of events in other years of record; ii) other seasons (e.g., autumn); iii) more complex storm periods with larger discharge responses; and iv) other water quality variables monitored in parallel (e.g., pH and electrical conductivity). These analyses are now planned.

Combining SISO system identification with high-frequency water quality and hydrometric data is, therefore, suggested as an approach to support more robust experimental designs of investigations into the rain-driven dynamics of NO₃-N and other important water quality variables.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

NC: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the UKRI Natural Environment Research Council grant NE/J014826/1.

Acknowledgments

The author acknowledges the Natural Resources Wales and Scottish Woodland for providing access to the research watershed and Natural Resources Wales for permission to install the flume and conduct dilution gauging. The considerable assistance of Tim Jones with the installation and maintenance of field instruments and subsequent data quality assurance is greatly appreciated. The author would like to thank the two reviewers for their constructive comments.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beven, K. J., and Chappell, N. A. (2021). Perceptual perplexity and parameter parsimony. WIREs Water 8 (4), e1530. doi:10.1002/wat2.1530

CrossRef Full Text | Google Scholar

Box, G. E. P., Jenkins, G. M., and Reinsel, G. C. (2008). Time series analysis: forecasting and control. 4th Edn. Hoboken, NJ, USA: Wiley.

Google Scholar

Brunet, C. E., Gemrich, E. R. C., Biedermann, S., Jacobson, P. J., Schilling, K. E., Jones, C. S., et al. (2021). Nutrient capture in an Iowa farm pond: insights from high-frequency observations. J. Environ. Manag. 299, 113647. doi:10.1016/j.jenvman.2021.113647

CrossRef Full Text | Google Scholar

Burns, D. A., Pellerin, B. A., Miller, M. P., Capel, P. D., Tesoriero, A. J., and Duncan, J. M. (2019). Monitoring the riverine pulse: applying high-frequency nitrate data to advance integrative understanding of biogeochemical and hydrological processes. WIREs Water 6, e1348. doi:10.1002/wat2.1348

CrossRef Full Text | Google Scholar

Chappell, N. A., Bonell, M., Barnes, C. J., and Tych, W. (2012). “Tropical cyclone effects on rapid runoff responses: quantifying with new continuous-time transfer function models,” in Revisiting experimental catchment studies in forest hydrology. Editors A. A. Webb, M. Bonell, L. Bren, P. N. J. Lane, D. McGuire, D. G. Nearyet al. (Wallingford: IAHS Press IAHS Publ), 353, 82–93.

Google Scholar

Chappell, N. A., Jones, T. D., and Tych, W. (2017a). Sampling frequency for water quality variables in streams: systems analysis to quantify minimum monitoring rates. Water Res. 123, 49–57. doi:10.1016/j.watres.2017.06.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Chappell, N. A., Jones, T. D., Tych, W., and Krishnaswamy, J. (2017b). Role of rainstorm intensity underestimated by data-derived flood models: emerging global evidence from subsurface-dominated watersheds. Environ. Model. Softw. 88, 1–9. doi:10.1016/j.envsoft.2016.10.009

CrossRef Full Text | Google Scholar

Chappell, N. A., Ternan, J. L., Williams, A. G., and Reynolds, B. (1990). Preliminary analysis of water and solute movement beneath a coniferous hillslope in mid-Wales, United Kingdom. J. Hydrology 116, 201–215. doi:10.1016/0022-1694(90)90123-f

CrossRef Full Text | Google Scholar

Chappell, N. A., Tych, W., Chotai, A., Bidin, K., Sinun, W., and Thang, H. C. (2006). BARUMODEL: combined Data Based Mechanistic models of runoff response in a managed rainforest catchment. For. Ecol. Manage. 224, 58–80. doi:10.1016/j.foreco.2005.12.008

CrossRef Full Text | Google Scholar

Christ, M. J., and David, M. B. (1996). Temperature and moisture effects on the production of dissolved organic carbon in a spodosol. Soil Biol. biochem. 28, 1191–1199. doi:10.1016/0038-0717(96)00120-4

CrossRef Full Text | Google Scholar

Graeber, D., McCarthy, M. J., Shatwell, T., Borchardt, D., Jeppesen, E., Søndergaard, M., et al. (2024). Consistent stoichiometric long-term relationships between nutrients and chlorophyll-a across shallow lakes. Nat. Commun. 15, 809. doi:10.1038/s41467-024-45115-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Guntiñas, M. E., Leiros, M. C., Trasar-Cepeda, C., and Gil-Sotres, F. (2012). Effects of moisture and temperature on net soil nitrogen mineralization: a laboratory study. Eur. J. Soil Biol. 48, 73–80. doi:10.1016/j.ejsobi.2011.07.015

CrossRef Full Text | Google Scholar

Halliday, S. J., Skeffington, R. A., Wade, A. J., Neal, C., Reynolds, B., Norris, D., et al. (2013). Upland stream water nitrate dynamics across decadal to sub-daily timescales: a case study of Plynlimon, Wales. Biogeosciences 10, 8013–8038. doi:10.5194/bg-10-8013-2013

CrossRef Full Text | Google Scholar

Jakeman, A. J., Littlewood, I. G., and Whitehead, P. G. (1993). An assessment of the dynamic response characteristics of streamflow in the Balquhidder catchments. J. Hydrol. 145, 337–355. doi:10.1016/0022-1694(93)90062-E

CrossRef Full Text | Google Scholar

Jiang, S. Y., Zhang, Q., Werner, A. D., Wellen, C., Jomaa, S., Zhu, Q. D., et al. (2019). Effects of stream nitrate data frequency on watershed model performance and prediction uncertainty. J. Hydrol. 569, 22–36. doi:10.1016/j.jhydrol.2018.11.049

CrossRef Full Text | Google Scholar

Jones, T. D., and Chappell, N. A. (2014). Streamflow and hydrogen ion interrelationships identified using Data-Based Mechanistic modelling of high frequency observations through contiguous storms. Hydrology Res. 45 (6), 868–892. doi:10.2166/nh.2014.155

CrossRef Full Text | Google Scholar

Jones, T. D., Chappell, N. A., and Tych, W. (2014). First dynamic model of dissolved organic carbon derived directly from high frequency observations through contiguous storms. Environ. Sci. Technol. 48, 13289–13297. doi:10.1021/es503506m

PubMed Abstract | CrossRef Full Text | Google Scholar

Kermorvant, C., Liquet, B., Litt, G., Mengersen, K., Peterson, E. E., Hyndman, R. J., et al. (2023). Understanding links between water-quality variables and nitrate concentration in freshwater streams using high frequency sensor data. PLoS ONE 18 (6), e0287640. doi:10.1371/journal.pone.0287640

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirchner, J. W. (2009). Catchments as simple dynamical systems: catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 45, W02429. doi:10.1029/2008WR006912

CrossRef Full Text | Google Scholar

Koenig, L. E., Shattuck, M. D., Snyder, L. E., Potter, J. D., and McDowell, W. H. (2017). Deconstructing the effects of flow on DOC, nitrate, and major ion interactions using a high-frequency aquatic sensor network. Water Resour. Res. 53, 10655–10673. doi:10.1002/2017WR020739

CrossRef Full Text | Google Scholar

Ledesma, J. L. J., Lupon, A., Martí, E., and Bernal, S. (2022). Hydrology and riparian forests drive carbon and nitrogen supply and DOC: NO₃⁻ stoichiometry along a headwater Mediterranean stream. Hydrol. Earth Syst. Sci. 26, 4209–4232. doi:10.5194/hess-26-4209-2022

CrossRef Full Text | Google Scholar

Li, C., Yue, F.-J., Li, S.-L., Ge, J.-F., Chen, S.-N., and Qi, Y. (2022). Land use as a major factor of riverine nitrate in a semi-arid farming-pastoral ecotone: new insights from multiple environmental tracers and molecular signatures of DOM. Front. Environ. Sci. 10, 1061857. doi:10.3389/fenvs.2022.1061857

CrossRef Full Text | Google Scholar

McGill, T., and Ford, W. I. (2024). Extreme learning machine predicts high-frequency stream flow and nitrate-N concentrations in a karst agricultural watershed. J. ASABE 67 (2), 305–319. doi:10.13031/ja.15747

CrossRef Full Text | Google Scholar

Mindham, D. A., Tych, W., and Chappell, N. A. (2018). Extended State Dependent Parameter modelling with a Data-Based Mechanistic approach to non-linear model structure identification. Environ. Model. Softw. 104, 81–93. doi:10.1016/j.envsoft.2018.02.015

CrossRef Full Text | Google Scholar

Neal, C., Reynolds, B., Norris, D., Kirchner, J. W., Neal, M., Rowland, P., et al. (2011). Three decades of water quality measurements from the Upper Severn experimental catchments at Plynlimon, Wales: an openly accessible data resource for research, modelling, environmental management and education. Hydrol. Process. 25 (24), 3818–3830. doi:10.1002/hyp.8191

CrossRef Full Text | Google Scholar

Ormerod, S. J., and Durance, I. (2009). Restoration and recovery from acidification in upland Welsh streams over 25 years. J. Appl. Ecol. 46, 164–174. doi:10.1111/j.1365-2664.2008.01587.x

CrossRef Full Text | Google Scholar

Page, T., Chappell, N. A., Beven, K. J., Hankin, B., and Kretzschmar, A. (2020). Assessing the significance of wet-canopy evaporation from forests during extreme rainfall events for flood mitigation in mountainous regions of the United Kingdom. Hydrol. Process. 34, 4740–4754. doi:10.1002/hyp.13895

CrossRef Full Text | Google Scholar

Pellerin, B. A., Bergamaschi, B. A., Downing, B. D., Saraceno, J. F., Garrett, J. A., and Olsen, L. D. (2013). Optical techniques for the determination of nitrate in environmental waters: guidelines for instrument selection, operation, deployment, maintenance, quality-assurance, and data reporting. U.S. Geol. Surv. Tech. Methods 1–D5, 37. doi:10.3133/tm1D5

PubMed Abstract | CrossRef Full Text | Google Scholar

Reynolds, B., and Edwards, A. (1995). Factors influencing dissolved nitrogen concentrations and loadings in upland streams of the United Kingdom. Agri. Water Manage. 27, 181–202. doi:10.1016/0378-3774(95)01146-a

CrossRef Full Text | Google Scholar

Rusjan, S., Brilly, M., and Mikoš, M. (2008). Flushing of nitrate from a forested watershed: an insight into hydrological nitrate mobilization mechanisms through seasonal high-frequency stream nitrate dynamics. J. Hydrology 354 (1–4), 187–202. doi:10.1016/j.jhydrol.2008.03.009

CrossRef Full Text | Google Scholar

Tang, Y., Deng, J., Zang, C., and Wu, Q. (2022). Chaotic modeling of stream nitrate concentration and transportation via IFPA-ESN and Turning Point Analyses. Front. Environ. Sci. 10, 855694. doi:10.3389/fenvs.2022.855694

CrossRef Full Text | Google Scholar

Taylor, C. J., Pedregal, D. J., Young, P. C., and Tych, W. (2007). Environmental time series analysis and forecasting with the Captain toolbox. Environ. Modell. Softw. 22, 797–814. doi:10.1016/j.envsoft.2006.03.002

CrossRef Full Text | Google Scholar

Vaughan, M. C. H., Bowden, W. B., Shanley, J. B., Vermilyea, A., Sleeper, R., Gold, A. J., et al. (2017). High-frequency dissolved organic carbon and nitrate measurements reveal differences in storm hysteresis and loading in relation to land cover and seasonality. Water Resour. Res. 53, 5345–5363. doi:10.1002/2017WR020491

CrossRef Full Text | Google Scholar

Winter, C., Jawitz, J. W., Ebeling, P., Cohen, M. J., and Musolff, A. (2024). Divergence between long-term and eventscale nitrate export patterns. Geophys. Res. Lett. 51, e2024GL108437. doi:10.1029/2024GL108437

CrossRef Full Text | Google Scholar

Young, P. C. (2006). “Rainfall-runoff modeling: transfer function models,” in Encyclopedia of hydrological sciences. Editors M. G. Anderson, and J. J. McDonnell doi:10.1002/0470848944.hsa141a

CrossRef Full Text | Google Scholar

Young, P. C. (2015). Refined instrumental variable estimation: maximum likelihood optimization of a unified Box-Jenkins model. Automatica 52, 35–46. doi:10.1016/j.automatica.2014.10.126

CrossRef Full Text | Google Scholar