
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci. , 06 August 2024
Sec. Environmental Informatics and Remote Sensing
Volume 12 - 2024 | https://doi.org/10.3389/fenvs.2024.1410741
This article is part of the Research Topic Advancements in Land Cover Classification and Machine Learning Techniques for Urban Areas Using Remote Sensing Big Data View all 5 articles
 Tadele Bedo Gelete1*†
Tadele Bedo Gelete1*† Pernaidu Pasala2
Pernaidu Pasala2 Nigus Gebremedhn Abay3
Nigus Gebremedhn Abay3 Gezahegn Weldu Woldemariam1,4†
Gezahegn Weldu Woldemariam1,4† Kalid Hassen Yasin1,4†
Kalid Hassen Yasin1,4† Erana Kebede5*†
Erana Kebede5*† Ibsa Aliyi5†
Ibsa Aliyi5†Land degradation from gully erosion poses a significant threat to the Erer watershed in Eastern Ethiopia, particularly due to agricultural activities and resource exploitation. Identifying erosion-prone areas and underlying factors using advanced machine learning algorithms (MLAs) and geospatial analysis is crucial for addressing this problem and prioritizing adaptive and mitigating strategies. However, previous studies have not leveraged machine learning (ML) and GIS-based approaches to generate susceptibility maps identifying these areas and conditioning factors, hindering sustainable watershed management solutions. This study aimed to predict gully erosion susceptibility (GES) and identify underlying areas and factors in the Erer watershed. Four ML models, namely, XGBoost, random forest (RF), support vector machine (SVM), and artificial neural network (ANN), were integrated with geospatial analysis using 22 geoenvironmental predictors and 1,200 inventory points (70% used for training and 30% for testing). Model performance and robustness were validated through the area under the curve (AUC), accuracy, precision, sensitivity, specificity, kappa coefficient, F1 score, and logarithmic loss. The relative slope position is most influential, with 100% importance in SVM and RF and 95% importance in XGBoost, while annual rainfall (AR) dominated ANN (100% importance). Notably, XGBoost demonstrated robustness and superior prediction/mapping, achieving an AUC of 0.97, 91% accuracy, 92% precision, and 81% kappa while maintaining a low logloss (0.0394). However, SVM excelled in classifying gully resistant/susceptible areas (97% sensitivity, 98% specificity, and 91% F1 score). The ANN model predicted the most areas with very high gully susceptibility (13.74%), followed by the SVM (11.69%), XGBoost (10.65%), and RF (7.85%) models, while XGBoost identified the most areas with very low susceptibility (70.19%). The ensemble technique was employed to further enhance GES modeling, and it outperformed the individual models, achieving an AUC of 0.99, 93.5% accuracy, 92.5% precision, 97.5% sensitivity, 95.4% specificity, 85.8% kappa, and 94.9% F1 score. This technique also classified the GES of the watershed as 36.48% very low, 26.51% low, 16.24% moderate, 11.55% high, and 9.22% very high. Furthermore, district-level analyses revealed the most susceptible areas, including the Babile, Fedis, Harar, and Meyumuluke districts, with high GES areas of 32.4%, 21.3%, 14.3%, and 13.6%, respectively. This study offers robust and flexible ML models with comprehensive validation metrics to enhance GES modeling and identify gully prone areas and factors, thereby supporting decision-making for sustainable watershed conservation and land degradation prevention.
Land degradation is a pressing global issue affecting agricultural production, the environment, and livelihoods by deteriorating soil health and productivity, with Sub-Saharan Africa experiencing 67% of land and two-thirds of productive land degradation (Gutema et al., 2023). Gully erosion is one of the most significant geo-hydrological land degradations characterized by the gradual formation of deep channels through concentrated surface and subsurface water flow within narrow paths, contributing to soil loss and deterioration (Arabameri et al., 2020b; Lei et al., 2020; Mohebzadeh et al., 2022). The interaction between natural phenomena (soil erodibility and rainfall erosivity) and anthropogenic factors (deforestation and unsustainable agricultural practices) exacerbates gully networks and soil erosion at various scales, posing socioeconomic and environmental challenges globally (Arabameri et al., 2020a; Igwe et al., 2020; Pourghasemi et al., 2020). Consequently, gully erosion is responsible for multifaceted destruction, such as habitat loss, ecosystem fragmentation, inundation and sedimentation, desertification, reduced soil fertility, diminished water tables, decreased crop production, and damaged infrastructure and facilities (Busch et al., 2021; Yazie et al., 2021).
Ethiopia is one of the developing sub-Saharan countries experiencing the most severe levels of land degradation, with over 85% of its terrain degraded to varying degrees (Gutema et al., 2023). In particular, the detrimental impacts of gully erosion are widespread in Ethiopia, where agriculture-dependent economies face substantial threats from the depletion of vital soil nutrients on farmlands resulting from the removal of topsoil by gullies (Belayneh et al., 2020; Amare et al., 2021; Setargie et al., 2023a). For instance, a prior study showed that water erosion severely impacts landscape features, ecological diversity, and agricultural productivity and sustainability in Ethiopia, with an estimated net soil erosion rate of 0.41 × 109 tons year−1, accounting for 22% of the 1.9 × 109 tons year−1 gross soil loss (Fenta et al., 2021). Furthermore, the increased frequency and intensity of rainfall, rising temperatures, and extreme events reinforced gully erosion and climate change, potentially worsening soil erosion processes and, hence, soil health and productivity deterioration, resulting in decreased agricultural productivity, food insecurity, and poverty (Ayanlade et al., 2022; Ebabu et al., 2023). To address these challenges, it is crucial to prioritize the restoration of degraded lands and implement measures to prevent further gully erosion by supporting and implementing sustainable land management practices (Gutema et al., 2023). Consequently, the study of soil erosion is gaining increasing attention, examining historical and current rates, fluctuations, and patterns to understand the extent, temporal changes, and quantitative and geographical severity of land susceptibility to erosion (Woldemariam et al., 2023).
The spatially explicit identification and prioritization of gully susceptible regions can provide valuable insights into the magnitude of hazards and risks in a given area of interest (Conoscenti, et al., 2013a; Rahmati et al., 2017a; Were et al., 2023). In this context, gully erosion susceptibility mapping (GESM) is a preliminary phase for targeted investment in sustainable management practices in highly affected landscapes. The GESM is based on advanced geospatial and remote sensing technologies, as well as state-of-the-art statistical modeling (Wang et al., 2016; Lei et al., 2020; Saha et al., 2021). Given the complex nature of gully erosion and its interrelationship with other hillslope processes, a systematic analysis of multiple contributing factors (rainfall, topography, lithology, soil characteristics, and land use) is essential for successful GESM (Conoscenti, et al., 2013b; Rahmati et al., 2017b; Saha et al., 2020; Were et al., 2023).
Recent scientific studies have revealed that integrated modeling approaches using geographic information system (GIS) tools and remotely sensed datasets combined with various MLAs could effectively capture the complex relationships between the ranges of predictive variables contributing to gully erosion (Wang et al., 2016; Rahmati et al., 2017a; Lei et al., 2020; Saha et al., 2020; Setargie et al., 2023b). These approaches have demonstrated superior performance compared to empirical, process-based, and conventional statistical methods, which often fail to account for complex feedbacks, thresholds, and nonlinear relationships that determine the formation of localized gullies (Al-Abadi and Al-Ali, 2018; Mohebzadeh et al., 2022; Pourghasemi et al., 2020; Woodward, 1999). However, few studies have been conducted on gully erosion modeling using MLAs in the Ethiopian context, with most studies focusing on the Blue Nile Basin (Belayneh et al., 2020; Amare et al., 2021; Setargie et al., 2023a) and only a few case studies being conducted in other vulnerable ecoregions of the country (Bouaziz et al., 2011; Busch et al., 2021).
The Erer watershed in the Wabi Shebele River Basin in Eastern Ethiopia is characterized mainly by agricultural activities and unsustainable exploitation of natural resources, leading to land degradation and gully erosion, which threaten the long-term viability of the region (Woldemariam and Harka, 2020). Despite the terrain complexity, diverse land-use patterns, and mixed agricultural practices within the Erer Watershed, which make it susceptible to gully erosion from concentrated surface runoff during peak rainfall periods, no prior studies have employed ML-based GESM approaches for this area. For instance, earlier studies within and around watersheds have investigated only rill and interrill erosion (Woldemariam and Harka, 2020; Woldemariam et al., 2023), and the spatial relationships between various natural and anthropogenic factors influencing gully formation have not been incorporated into gully erosion research. This study aims to evaluate the potential of integrating MLAs with GIS-based modeling techniques to develop the GESM and provide spatially disaggregated information to support sustainable land management practices, thereby mitigating the negative impacts of gully erosion in the Erer watershed of the upper Wabi Shebelle Basin in Ethiopia.
This study was conducted in the Erer Watershed in Eastern Ethiopia’s upper Wabi Shebelle Basin. The watershed covers a total land area of approximately 3,860 km2, with latitudes extending from 8°20′N to 9°20′N and longitudes extending from 41°40′E to 42°30′E (Figures 1A–C). With an altitudinal range from 800 m above sea level in the southwesternmost region to 2,920 m in the upperlands in the northern region (Woldemariam and Harka, 2020), the study area encompasses three dominant agroecological zones (Ministry of Agriculture, 2001): Kolla (500–1,500 m), Woinadega (1,500–2,300 m), and Dega (2,300–3,200 m). Moreover, the watershed is the source of the Erer River, which originates from the highlands in the northern portion of the country and flows southward as a tributary of the Wabi River, where it continues into Somalia to join the Shebelle River. According to the FAO (1995) classification, there are six dominant soil groups, namely, Eutric Nitosols, Calcaric Regosols, Eutric Regosols, Dystric Cambisols, Haplic Xerosols, and Humic Cambisols, with Haplic Xerosols being the most extensive, accounting for approximately 49% of the total watershed area.
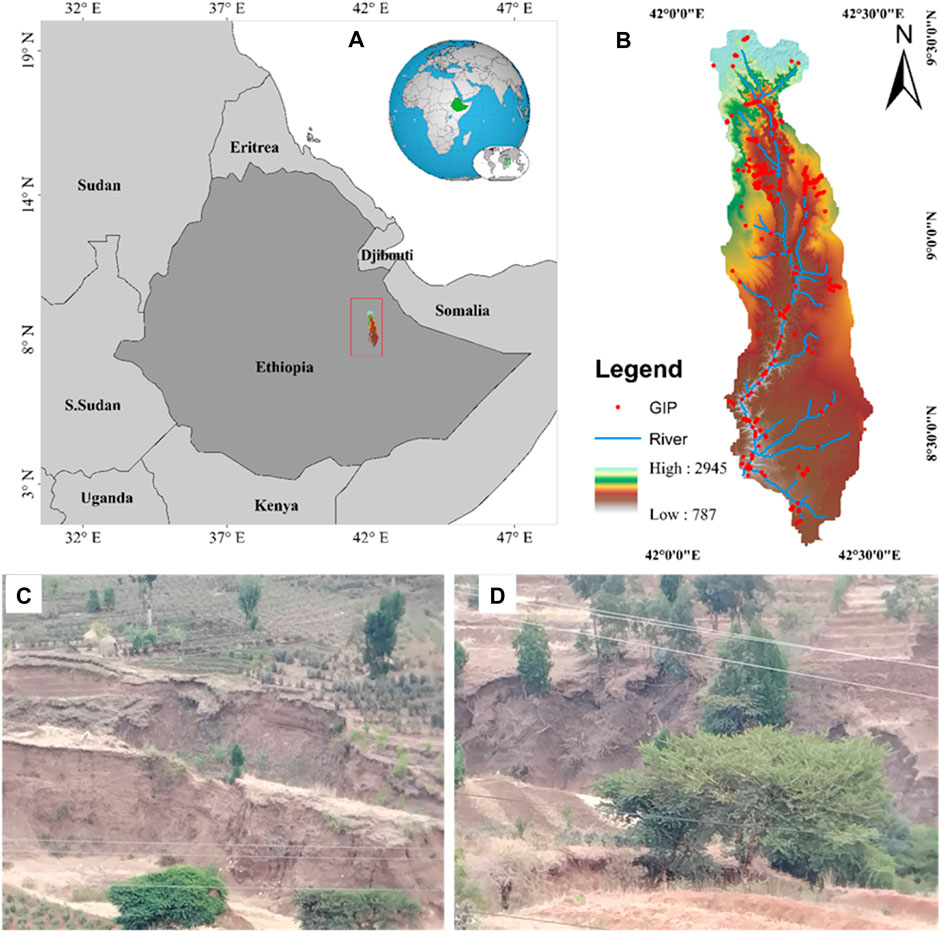
Figure 1. Map showing the location of the study area: (A) the Erer watershed delineated by a red polygon within the map of Ethiopia; (B) the basin alongside stream features, gully inventory points (GIPs), and elevations measured in meters above sea level; and (C,D) images illustrating gully erosion in the Erer watershed with geographical coordinates.
Gully erosion inventory preparation is a preliminary step in developing high-quality gully erosion susceptibility prediction models. This study generated a robust gully erosion inventory map (GEIM) to capture the spatial distribution of gullies across the Erer watershed. Field surveys enabled direct gathering of gully location coordinates via the Global Positioning System (GPS). Notably, the gullies studied had an average depth of 4 m (Figures 1C, D), indicating significant erosion. Furthermore, site visits have shown significant effects of gully erosion on the region’s local infrastructure and agricultural sector. High-resolution satellite imagery from Google Earth Pro was used to visually analyze and digitize gully locations as a complement to the field data, enabling the identification of additional gully locations. The digitized gully locations were converted into a shapefile format to extract predictor variable properties at the gully locations. Subsequently, an equal number of nongully (control) sites were randomly selected and merged with the identified gully locations, resulting in a balanced dataset of 1,200 inventory points. Of the inventory points, 42.92% were identified in bare land areas, 30.83% in shrubland, 24.33% in agricultural land, 1.17% in built-up areas, and 0.75% in forested areas. Furthermore, 79.25% were in low-slope areas, 16.33% were in medium-slope areas, and 4.42% were in high-slope areas.
The inventory points were divided into training 70% and testing 30% of the datasets to model gully erosion. MLAs use a curated training dataset to predict gully development areas based on geographical features (Pourghasemi et al., 2020). The reserved testing dataset was used to evaluate model performance by contrasting predictions to documented gully occurrences. Overall, the use of a multipronged data compilation strategy coupled with rigorous cross-validation procedures guaranteed the fidelity of the model outputs for directing gully erosion mitigation efforts in the study area (Azedou et al., 2021).
In this study, 22 factors that contribute to the conditioning and formation of gully erosion were identified based on a comprehensive literature review and analysis of publicly available data used to model GES (Roy and Saha, 2019; Yang et al., 2021; Aboutaib et al., 2023; Baiddah et al., 2023). QGIS-OSGeo4W (version 3.34.2) was used to generate maps of geoenvironmental factors and facilitate the transformation of the layers into a spatial database, as shown in Figure 2. Detailed descriptions of these geo-environmental factors are provided below.
In this study, twelve topographic factors were selected, considering their substantial impacts on hydrological conditions (Namous et al., 2021). These parameters included analytic hill shade (AH), slope (SLP), slope length (LS), elevation (ELV), relative slope position (RSP), aspect (ASP), plan curvature (PLC), profile curvature (PRC), convergence index (CI), topographic position index (TPI), topographic ruggedness index (TRI) and topographic wetness index (TWI) (Figures 2A–H, J–L). The maps for these topographic factors were created using a digital elevation model (DEM) from the Copernicus DSM’s open topographic database.
The ELV is a primary topographic factor (Figure 2I) in the GES due to its impact on climatic and vegetation variability (Conoscenti, et al., 2013a). The SLP considerably impacts runoff infiltration, water flow speed, and soil particle dissociation (Lei et al., 2020). The ASP represents the surface orientation of the slope, indirectly influencing erosion by changing the vegetation cover, solar incidence, and moisture (Figures 2F, H). The RSP (Figure 2J) measures the different terrain indices using the DEM. The CI and TPI (Figures 2B, K) describe the terrain’s form and its effects on flows. The AH, which indicates terrain exposure to sunlight, can influence soil moisture content and temperature, and increasing GES and AH values may result in distinct erosion patterns compared to low Hillshade values (Gayen and Saha, 2017), which are more shadowed (Figure 2G). The TWI (Figure 2A) depicts the regional distribution of soil moisture, erosion, and wetness conditions (Rahmati et al., 2017a) and is calculated using Eq. 1 as follows:
where
The LS is a parameter in the universal Soil Loss Equation (USLE) and Revised universal Soil Loss Equation (RUSLE) used to calculate soil erosion rates (Gayen et al., 2019) and is calculated using Eq. 2 developed by Moore and Burch (1986):
where LS is the slope length gradient factor, FAG (flow accumulation grid) represents the accumulated upslope contribution catchment region for a specific cell, cell size represents the grid cell size (for this research, 30 m spatial resolution), and the sin slope denotes the angle of the slope in degrees (Moore and Burch, 1986).
The TRI, which represents the elevation difference between adjacent cells in a DEM, determines the convexity and concavity of a slope (Figure 2C) and was calculated using Eq. 3 from Moreno-Ibarra et al. (2011):
where Cx is the cell under analysis and N8 is the set of eight neighbors of the cell.
Climate significantly impacts gully erosion, which occurs when rainwater penetrates ground fissures and expands gullies (Azareh et al., 2019; Hembram et al., 2019; Lei et al., 2020). Therefore, annual rainfall (AR) data from the Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) online database (https://data.chc.ucsb.edu/products/CHIRPS-2.0/) were gathered in the study area and resampled to a 30* resolution for compatibility. The rainfall map shows that the annual average range was between 526.24 and 705.55 mm/year. The northern and western regions of the basin had the highest average precipitation levels (Figure 2R).
The hydrological factors used in this study were drainage density (DD) and distance from stream (DS). Higher drainage densities are linked to lower infiltration and greater runoff in regions with lower infiltration and greater runoff (Conoscenti et al., 2013b; Arabameri et al., 2019). This study used the density tool in QGIS-OSGeo4W (version 3.34.2) to create a DD map based on stream features, illustrating the distribution of streams in the study area (Figure 2P). The DS was estimated using the Euclidean distance toolset in QGIS (version 3.34.2) software to determine the distance of the gully from the drainage system (Figure 2Q).
The geological criteria chosen for this study were lithology (LIT) and distance from the fault line (DF). This study assessed the impact of the LIT on gulling (Nhu et al., 2020; Baiddah et al., 2023) by identifying five types of units using 1/500,000 geological maps retrieved from the Geological Survey of Ethiopia (GSE) (GSE, 1972) (Figures 2S, T). The Euclidean distance is used to calculate the DF, which indicates a weak, highly permeable zone with low resistance, affecting slope stability and contributing to soil degradation (Gayen et al., 2019).
Three environmental parameters, which included land use/land cover (LULC), the normalized difference vegetation index (NDVI), and distance from road (DR), were developed to study runoff and infiltration in gullies (Negese, 2021). The Landsat 8 OLI satellite image for 2022 was obtained from the USGS Earth Explorer website using the Google Earth Engine (GEE) API to minimize the impact of transient landscape changes such as cloud cover, temporary land cover changes, and other anomalies (Loukika et al., 2021). Hence, the median value used offered a more accurate representation of the typical conditions that exist throughout the year, resulting in more robust and dependable land use/land cover classifications. Subsequently, the basin LULC map was generated in the GEE environment using a random tree-supervised classification technique. On the LULC map, the classification resulted in five classes: forest, shrubland, bare land, agricultural land, and built-up land (Figure 2O) and Supplementary Table S1, with a total accuracy of 90% (Supplementary Table S2). The DRs to gullies were selected due to their contribution to gully erosion by concentrating and intercepting runoff water, as shown in Figure 2M. (Igwe et al., 2020; Rahmati et al., 2022). To estimate distance features via Euclidean distance (ED) spatial analysis, road shapefiles were obtained from the Ethiopian Space Science and Geospatial Institute (SSGI) Geo-Portal (http://www.ethiosdi.gov.et/).
The NDVI was calculated using Eq. 4 and Landsat 8 OLI/TIRS images in the GEE platform to determine vegetation biomass (Okereke et al., 2012) and produce the NDVI map.
where NIR is the spectral reflectance of the near-infrared band and Red denotes the red spectral reflectance. The NDVI ranged from −0.32 to 0.76 in this study.
Soil type (ST) and soil organic matter (SOM) were chosen as the soil factors due to their significant impact on gully erosion (Aber et al., 2010; Li et al., 2019). The ST data were acquired from the Harmonized World Soil Database Version 2 (HWSDV2) (https://www.fao.org/), which identified six common soil types, namely, Calcaric Regosols, Eutric Nitosols, Eutric Regosols, Dystric Cambisols, Haplic Xerosols, and Humic Cambisols, which comprised 4%, 8%, 20%, 19%, 49%, and 16%, respectively (Figure 2V). The SOM protects soil aggregates from disruption caused by rainfall, with a higher SOM content lowering soil erosion (Figure 2U). The SOM data were obtained from the Soilgrid database (https://soilgrids.org/).
This study employed an approach of integrating ML models and geospatial analysis to understand gully erosion and develop susceptibility prediction maps using conditioning factors that are expected to influence the occurrence of identified erosion areas (Guisan et al., 2017), as depicted in Figure 3. Randomly selected pseudoabsence locations were also used to extract the values of the related conditioning factors. Both data forms were used to train algorithms, construct a prediction function hidden for ML, and identify the importance of each conditioning factor in the occurrence of gully erosion. The trained models were used to predict the occurrence probability of gullies across the entire study area, with gully absence and occurrence points randomly selected using the “random points” R function of the “spsample” package, followed by a 10-fold cross-validation for every ML technique (Barbet-Massin et al., 2012). The final modeling maps and performance measurements were generated by averaging ten replications, using independent (present and absence) data for training, and evaluating the performance of each replication separately.
The ML techniques used for modeling GES include XGBoost, random forest (RF), support vector machine (SVM), artificial neural network (ANN), the stacking method, and geospatial data processing. These models were generated in R 4.1.2 and in R Studio programming, and the GESM data were reclassified into five classes (very low, low, moderate, high, and very high) using the natural breaks method in QGIS software. Data normalization, which places the data within the 0–1 range (Eq. 5), was performed to enable ML estimation as described by (Davidson et al., 2008).
where Xmin is the lowest value of X, Xmax is the greatest value of X, X is the original value, and Xn is the normalized value.
By combining various decision tree models, RF is a nonparametric ensemble learning technique (Breiman, 2001). The input data were randomly divided into subgroups for each internal decision tree (Quevedo et al., 2022). A regression approach was employed in this study to provide numerical results for evaluating gully erosion susceptibility. The outcome is determined by averaging the three predictions. RF calculates the variable importance using the mean decrease in accuracy (Hitouri et al., 2022). For the primary node split, 200 trees were chosen for this study. In this model, the predictive variable is represented by the error, as stated in Eqs 6, 7 (Kim et al., 2016):
where M is the number of algorithm inputs computed for the mean square.
where ε represents the mean-square error of the algorithm, V observed is the observed data of the variable, and V response is the result of the variable.
The RF algorithm was used for several trees and predictive variables to regulate the split at each node (Naghibi et al., 2017). The average prediction of the tree was computed using Eq. 8 as follows:
where S denotes any forest prediction and K represents the individual trees in the model.
XGBoost is a boosting algorithm that generates a prediction model (Chen and Guestrin, 2016) by optimizing the loss function via gradient descent and increasing the ensemble of weak classification trees (Sahin, 2020). This algorithm generates top-to-bottom subtrees and then prunes them backward from bottom to top to eliminate local optimal solutions, making it more effective for regression and classification tasks. XGBoost contains three components: shrinkage and column subsampling to avoid overfitting, gradient tree boosting for additive training, and a regularized objective function for improved generalization (Cui et al., 2017; Dev and Eden, 2019). The best parameter combination was determined using a learning curve or grid search algorithm, and feature importance ranking was determined using the feature importance interface based on the Gini index, a standard parameter for GESM significance assessment (Arabameri et al., 2018). The rate at which variables contribute to fitting accuracy is known as feature importance, with the high importance of a specific feature indicating its significance. In this study, the XGBoost model was tuned across a comprehensive grid of hyperparameters, including the number of boosting rounds (nrounds), maximum tree depth (max_depth), learning rate (eta), minimum loss reduction (gamma), subsample ratio of columns (colsample_bytree), minimum sum of instance weights needed in a child (min_child_weight), and subsample ratio of the training instances (subsample). The values tested were 100, 200, and 300 for nrounds; 3, 6, and nine for max_depth; 0.01, 0.1, and 0.3 for eta; 0, 0.1, and 0.3 for gamma; 0.6, 0.8, and one for colsample_bytree; 1, 3, and five for min_child_weight; and 0.6, 0.8, and one for subsample.
The SVM algorithm is a supervised learning method that minimizes structural or empirical risk by dividing classes using kernel functions to fit an optimal separating hyperplane that maximizes the boundaries of two classes with minimal errors and complexity (Broséus et al., 2011). The original input data are transformed from a low-dimensional space where classes are linearly inseparable into a feature space of much greater dimensionality (Abdollahi et al., 2019). Classifying (or predicting) new information using the fitted nonlinear hyperplane is simple. We employed the Gaussian radial basis function kernel to transform the initial input data into a higher dimension (Eq. 9).
where K is the kernel function, x is the input vector, and σ is the bandwidth parameter (sigma), which controls the degree of nonlinearity in the hyperplane (Garosi et al., 2019). Sigma and the regularization (cost) parameter had to be specified. The SVM model with a radial basis function (RBF) kernel was optimized by tuning the cost parameter (C) and the RBF kernel parameter (sigma). The values tested for C were 0.1, 1, and 10, and for sigma, the values were 0.01, 0.05, and 0.1. The latter governs the tradeoff between the complexity of the model and empirical errors, which also controls overfitting. The optimal values for these two parameters were chosen through the grid search method with 10-fold cross-validation (Amiri et al., 2019).
The ANN algorithm can recognize patterns (Pourghasemi and Rahmati, 2018). This algorithm comprises node levels, including an input layer, one or more hidden layers, and an output layer. A weight and a threshold link the nodes together. When an individual node’s output surpasses a threshold value, it is activated and sends data to the next network layer. Otherwise, no data are sent to the following network layer (Alkhasawneh et al., 2014; Gholami et al., 2020). The ANN model was implemented in R 4.2.0 using this work’s “neuralnet” package, and we tuned the number of neurons in the hidden layer (size) and the weight decay parameter (decay). The values tested for size were 5, 10, and 15, while the values for decay were 0.01, 0.1, and 0.5.
Ensemble ML is an approach that integrates multiple base ML models to improve prediction accuracy and performance by reducing noise or error between observed and predicted data, as well as reducing model variance, bias, or both concurrently (Bouguerra et al., 2022). Ensemble approaches are typically classified as bootstrap aggregating (bagging), boosting, or stacking, with bagging and boosting primarily used for homogeneous models and stacking for combining heterogeneous models (Nguyen et al., 2021). This study employed stacking, also referred to as stacked generalization, an ensemble ML approach that utilizes a meta-model to integrate multiple heterogeneous base models. Here, 4 ML models, namely, the XGBoost, RF, SVM, and ANN models, were integrated as base models with the “caretEnsemble” package in R for implementation. The meta-model for stacking was trained using base model predictions from complete training data, allowing for the exploration of potential solutions with multiple models in the same scenario.
Multicollinearity analysis was used to identify information redundancy between parameters affecting the performance of ML models and the linearity among conditioning factors, thereby improving the results of GES mapping (Du et al., 2017; Arabameri et al., 2020a; Baiddah et al., 2023). In this study, the tolerance (TOL) and variance inflation factor (VIF) were calculated to test for multicollinearity among the factors influencing GES using Eqs 10, 11, respectively.
where
The integration of ML models and GIS techniques in this study assisted in leveraging spatial data and developing models that accurately predicted gully erosion susceptibility. This technique ensured a comprehensive analysis of the study area and provided valuable insights into multiple factors influencing erosion formation, suggesting the potential of their synergy in addressing complex environmental issues and supporting informed decision-making processes. In this study, we analyzed the importance of predictor factors to determine the relative significance of each factor in contributing to the GES models, aiming to prioritize and weigh the importance of different factors in the final susceptibility maps, ultimately improving the accuracy and effectiveness of the model predictions (Bouguerra et al., 2022).
In this study, validation metrics such as the receiver operating characteristic (ROC) curve and area under the curve (AUC), accuracy, precision, sensitivity, specificity, kappa coefficient, F1 score, and logarithmic loss were used to evaluate the performance of the ML models. These metrics were obtained from four possible methods, namely, true positive (TP), true negative (TN), false positive (FP), and false negative (FN), using a confusion matrix. The TP and FP represent the proportions of gully cells that are correctly classified as gully and nongully cells, respectively, while the TN and FN represent the numbers of gully cells classified correctly and incorrectly as nongully cells, respectively (Bui et al., 2019; Mohebzadeh et al., 2022).
The ROC curve was used to validate the goodness-of-fit and prediction performance of each model, with two-dimensional curves generated using the X-axis for sensitivity based on FP rates and the Y-axis for 1-specificity based on TP rates (Arabameri et al., 2020a; Bouguerra et al., 2022). The most commonly used area under the ROC curve (AUC), which ranges from 0.5 to 1, is a measure of the accuracy and reliability of the models in predicting gully erosion events, with a value closer to one indicating higher accuracy and a value closer to 0.5 indicating inaccuracy (Bammou et al., 2024). The AUC was calculated using Eq. 12 as follows:
The accuracy is the proportion of gully and nongully cells that are correctly classified and as high as possible (Baiddah et al., 2023). It is calculated using Eq. 13 as follows:
Precision predicts future classification performance by dividing the number of correct positive results by the number of predicted positive results, with higher precision values indicating better model performance (Nhu et al., 2020). It is calculated using Eq. 14 as follows:
Sensitivity is a metric that defines the number of correctly classified gully cells per total number of predicted gully cells, while specificity is the number of incorrectly classified gully cells per total number of predicted nongully cells (Bui et al., 2019; Lei et al., 2020). Higher sensitivity and specificity indicate greater predictive capability of the model in predicting gully erosion susceptibility cells and nongully susceptibility cells, respectively, and these metrics were computed using Eqs 15, 16 as follows:
The Kappa coefficient (κ) is a robust metric that measures the agreement between the predicted and true labels, accounting for the possibility of random agreement, and is useful in imbalanced datasets or multiclass classification problems (Rahmati et al., 2017b; Baiddah et al., 2023). The formula for calculating the kappa coefficient is presented in Eq. 17:
where κ is the kappa coefficient, po is the observed agreement between the predicted and true labels, and pe is the hypothetical probability of chance agreement.
The F1 score is a harmonic mean of precision and recall, providing a balanced measure of a model’s performance, which is particularly useful when dealing with imbalanced datasets, as it considers both false positives and false negatives (Nhu et al., 2020). The F1 score was computed using Eq. 18:
where precision is the ratio of true positives to the sum of true positives and false positives, and recall is the ratio of true positives to the sum of true positives and false negatives.
The log loss, also known as the cross-entropy loss, is a metric that measures the performance of a classification model by quantifying the uncertainty or confidence of the predictions, which is especially useful for probabilistic classifiers because it penalizes confident misclassifications more heavily.
The log loss was calculated as indicated in Eq. 19:
where N is the number of instances, yi is the actual class label (0 or 1) of the ith instance, and pi is the predicted probability that the ith instance belongs to the positive class.
Multicollinearity analysis is required to evaluate the intercorrelations between independent variables in a regression model, undermining the reliability and interpretability of the models (Liu et al., 2023; Were et al., 2023). Table 1 provides statistical comparisons of the multicollinearity analysis between the GES predictive factors using the VIF and TOL values. According to O'Brien (2007), multicollinearity occurs when the tolerance is less than 0.10 and the VIF is greater than 10. In this study, the multicollinearity test revealed that the TOL and VIF values of the factors were greater than 0.1 and less than 10, respectively. These findings suggest that there was no multicollinearity among the gully predictor factors studied, and all the factors could be used to model the spatial extent of GES in the Erer watershed.
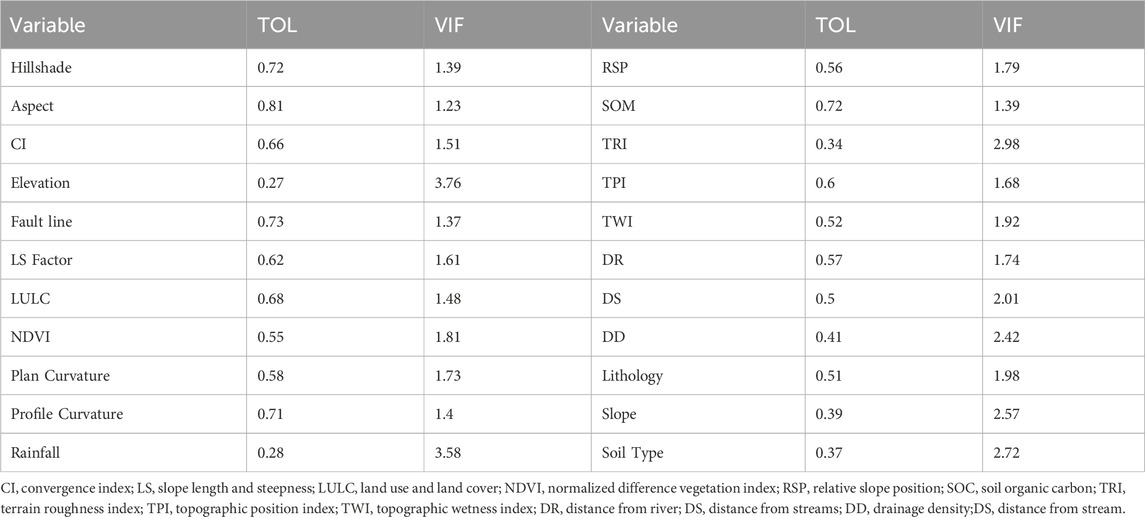
Table 1. Multicollinearity analysis for variables contributing to GES based on tolerance (TOL) and variance inflation factor (VIF) values.
Figures 4A–D demonstrate the importance of geoenvironmental factors in the ANN, SVM, RF, and XGBoost models for GES modeling, revealing similarities and differences in GES prediction in the study area, with varying rank orders and percentages. The XGBoost model also revealed that the RSP (94.97%) had the greatest influence on gully formation, followed by the NDVI (57.6%), SOM (28.03%), DS (17.03%), and AR (16.23%) (Figure 4A). The SVM results identified RSP (100%), SOM (52.922%), NDVI (42.759%), DD (42.03%), and DS (40.36%) as the most significant factors, while ST (0.73%), TRI (1.73%), ASP (2.73%), LS (2.82%), and AH (6.01%) were the least significant (Figure 4B). According to the RF model, the primary factors responsible for gully formation were RSP (100%), NDVI (85.45%), SOM (54.75%), DS (45.02%), and DR (39.43%), while the least significant factors were ASP, PRC, SLP, AH, TWI, TPI, TRI, CI, and ST, with importance scores ranging from 3% to 9.66% (Figure 4C). However, for ANN, rainfall (100%) had the greatest influence on gully formation, followed by LS (76.71%), ELV (56.88%), NDVI (50.36%), SOM (49.15%), RSP (47.39%), and CI (43.46%) (Figure 4D). All 4 ML modeling methods highlighted that several factor types collectively influence the formation and development of gully erosion. Were et al. (2023) used RF, SVM, and multivariate adaptive regression spline models to identify key gully erosion factors in Kenyan drylands, revealing slope, vegetation, rainfall, and drainage density as the most influential factors in GES modeling.
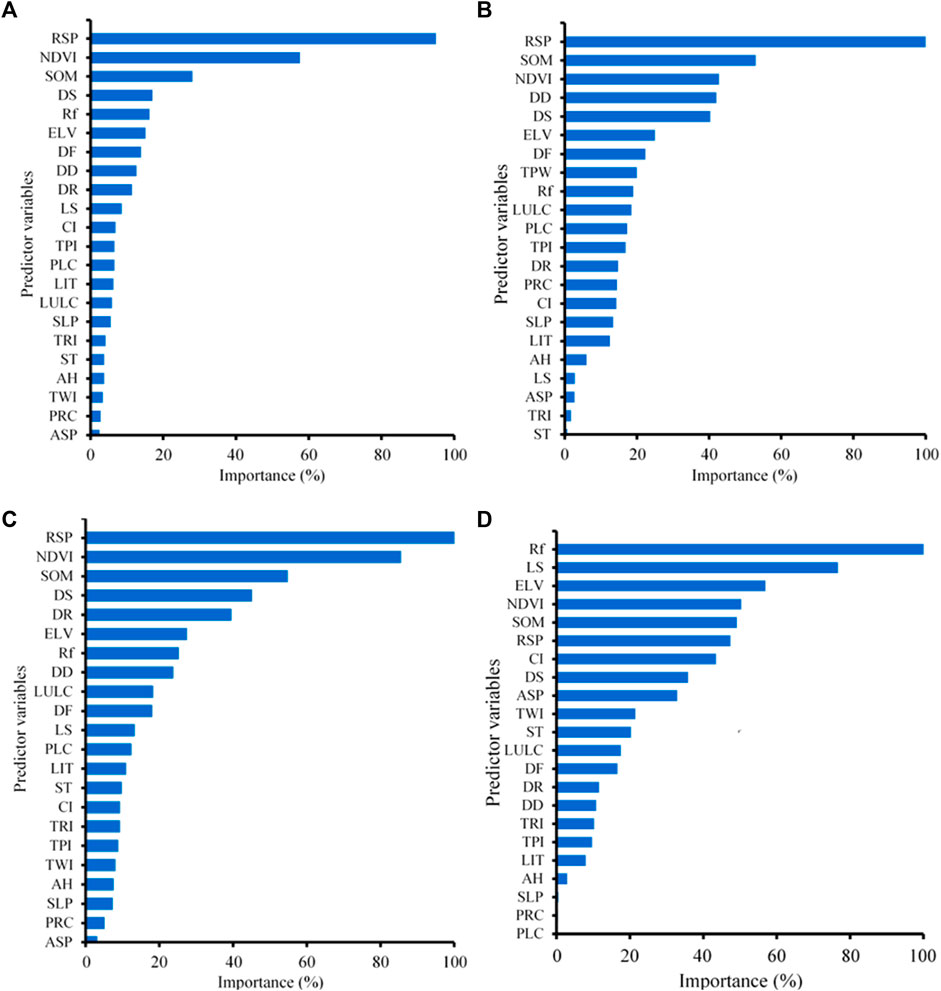
Figure 4. Predictor variables for gully erosion susceptibility modeling and their percentage importance ranked by machine learning models: (A) XGBoost, (B) support vector machine (SVM), (C) random forest (RF), and (D) artificial neural network (ANN).
The study revealed that RSP, NDVI, and SOM were highly important in all 4 ML models, indicating their robust predictive power and potential as driving factors. In particular, RSP was the most influential factor, with 100% importance for SVM and RF and 94.97% importance for XGBoost (Figures 4B–D), highlighting the importance of topographic characteristics in their framework. These findings align with the conceptual model of topographic threshold effects reported by Conforti et al. (2011), suggesting that certain landform sites become more susceptible to gully erosion when the slope length threshold is exceeded. Tebebu et al. (2010) reported that elevation, slope gradient, and DD are crucial for predicting gully formation in Ethiopian highlands, supporting the RSP, LS factor, and DD in selected ML models for GES modeling in watersheds; however, they did not consider the NDVI or SOM. Studies have shown that topographical factors significantly influence gully erosion, controlling surface runoff and other factors, highlighting the intricate relationships between topographical factors and rainfall, lithology, land use, soil, vegetation, and other variables (Gómez-Gutiérrez et al., 2015; Garosi et al., 2019; Al-Bawi et al., 2021). In addition, Mararakanye and Sumner (2017) highlighted that gully initiation is significantly influenced by local interactions between land use and environmental factors, requiring careful consideration of successful GES modeling.
The gully head of the Erer watershed lacks high surface vegetation cover, potentially affecting surface runoff and GES, especially in arable land, which can be disturbed by tillage practices (Jiang et al., 2021). Studies have also shown that vegetation can effectively reduce gully erosion where only dense vegetation provides protection from erosion, and for lower or moderate vegetation, topography is the major contributor (Sun et al., 2014; Jiang et al., 2021). Soil surface properties such as SOM and texture significantly influence erosion resistance, infiltration, and runoff rate in gully erosion susceptibility; hence, they are used as predictor variables in the GESM to understand their impact on erosion susceptibility (Garosi et al., 2019; Mohebzadeh et al., 2022). Yang et al. (2021) combined the RF, gradient boosting decision tree (GBDT), and XGBoost models with a statistical weight of evidence to map complex Chinese landscapes, and the dominance of rainfall, SOM, and slope factors closely aligns with our findings.
The ANN model, which prioritizes certain factors such as rainfall, may indicate model-specific behaviors that require validation before categorizing causally impactful behaviors, as it disproportionately weights variables compared to other algorithms (Saha et al., 2020). This finding is consistent with previous findings indicating that ML models may overestimate the significance of these predictors, such as rainfall, which is crucial for the development of ravines, gullies, and soil loss (Aboutaib et al., 2023). In contrast, rainfall was assigned much lower and insignificant importance values of 18.97%, 25.14% and 16.23% in the SVM, RF and XGBoost models, respectively. Studies have also suggested that topographic features (e.g., elevation, slope and plan curvature); hydrological factors, such as rainfall; and other factors, such as the NDVI and LULC, are among the influential factors that significantly impact the GES (Rahmati et al., 2017a; Arabameri et al., 2019; Mohebzadeh et al., 2022).
The findings on variable importance scores are consistent with the rationale offered by Hastie et al. (2009), who state that importance measures are relative, and it is typical to assign the highest score to 100 and then scale the others accordingly. As a result, the fact that two variables (RSP and AR) have high importance scores and others have significantly lower scores demonstrates their relative relevance in the ML models (Figures 4A–D). In this study, the ML models did not identify important variables such as AH, PRC, SLP, ST, TWI, PLC, LIT, or ASP as significant, suggesting a negligible role for these variables in the GES in the watershed. This could be due to the inability of the variable to explain the spatial distribution of GES, uncertainties in accurately defining factors or the impact of explanatory variables changing in different locations (Garosi et al., 2019; Saha et al., 2020). The contributions of different variables vary due to differences in underlying techniques and model sensitivities, highlighting the complex interplay between variables affecting GES (Rahmati et al., 2017a; Arabameri et al., 2018; Gayen et al., 2019). Studies have indicated that GES mapping is influenced by area-specific factors such as land use (Amiri et al., 2019), distance from rivers (Bui et al., 2019), slope (Arabameri et al., 2020a), elevation (Baiddah et al., 2023), rainfall (Nhu et al., 2020), and NDVI (Aboutaib et al., 2023), which cannot be reliably extrapolated to other regions, necessitating further research on different landscapes. These findings emphasize the significance of multiperspective variable importance analysis for understanding and interpreting broad explanatory relationships and for balancing ensemble-level information with model-specific details. Future research should also explore the use of influence functions to measure model sensitivity to individual predictors, allowing for a more comprehensive examination of unstable features and validating consensus relationships, as also suggested by Wei Koh and Liang (2017).
This study employed comprehensive validation metrics to evaluate the predictive capabilities of ML models for GES modeling, comparing their performance outcomes and effectiveness in GES modeling and delineating gully prone areas. The ROC-AUC analysis showed significant variation in the performance of the ML models, with the tree-based XGBoost model (AUC = 0.97) demonstrating exceptional performance and robustness, outperforming the RF (AUC = 0.96), SVM (AUC = 0.93), and ANN (AUC = 0.90) models (Figure 5). These findings suggested that the XGBoost model provided nearly perfect discrimination in predicting GES within the watershed, supporting findings by Arabameri et al. (2021) and Xu et al. (2023) but contrasting the findings of Rahmati et al. (2017b) and Amiri et al. (2019), who reported superior performance of RF and SVM for GES modeling. Previous studies have also shown XGBoost, with an AUC of ∼0.96, to be the most efficient model for GESM, outperforming the RF (AUC = 0.94) and SVM (AUC = 0.89) models in terms of performance, generalizability, and overfitting prevention (Arabameri et al., 2019; Yang et al., 2021).
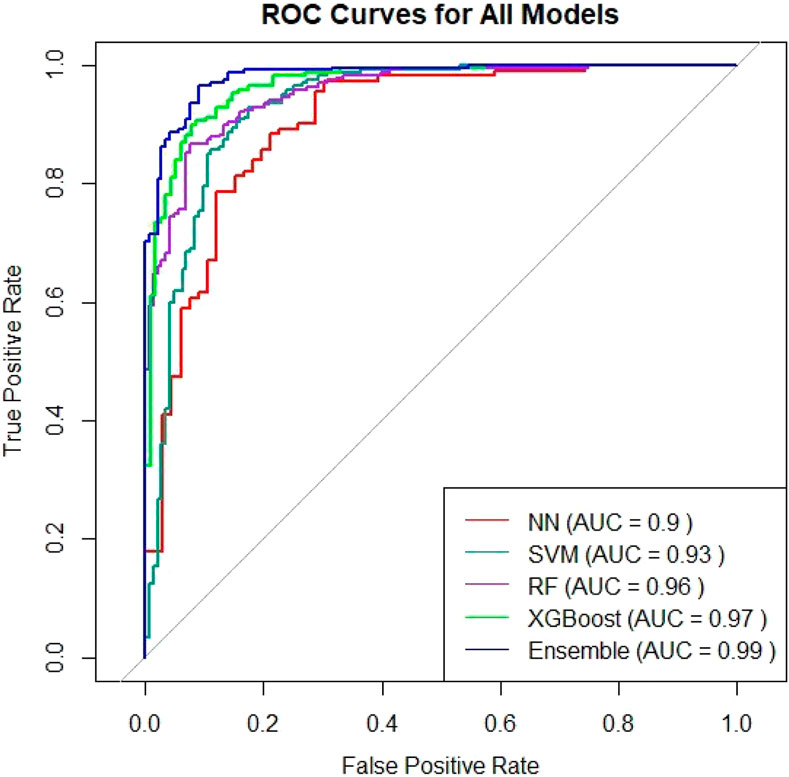
Figure 5. Receiver operating characteristic (ROC) curves of the artificial neural network (ANN), support vector machine (SVM), random forest (RF), XGBoost, and ensemble models in the study area.
The XGBoost model also achieved the highest accuracy (0.91), precision (0.92), and kappa value (0.81) (Table 2) with a low logloss (0.0482) (Figure 6D), indicating robustness and a high level of performance in GES predictions and mapping. These results are comparable to those reported by Pourghasemi et al. (2020) and Were et al. (2023), who reported that XGBoost had superior predictive accuracy over RF, SVM, and other models. The XGBoost model also had acceptable specificity (0.95) and F1 score (0.88) but was less effective in identifying areas resistant and susceptible to gully erosion than the SVM model, which had the highest sensitivity (0.97), specificity (0.98), and F1 score (0.91) (Table 2). Similarly, a study by Bammou et al. (2024) reported that the XGBoost model achieved outstanding results for various validation metrics, including the AUC-ROC (91.07%), accuracy (0.91), precision (0.93), sensitivity (0.89), specificity (0.95), sensitivity (0.89), and F1 score (0.91). As a result, the XGBoost model has been extensively utilized in studies for modeling landslides, flash floods, and groundwater susceptibility, demonstrating superior predictive potential for environmental risks (Arabameri et al., 2021; Xu et al., 2023; Zhuo et al., 2023; Meng et al., 2023).
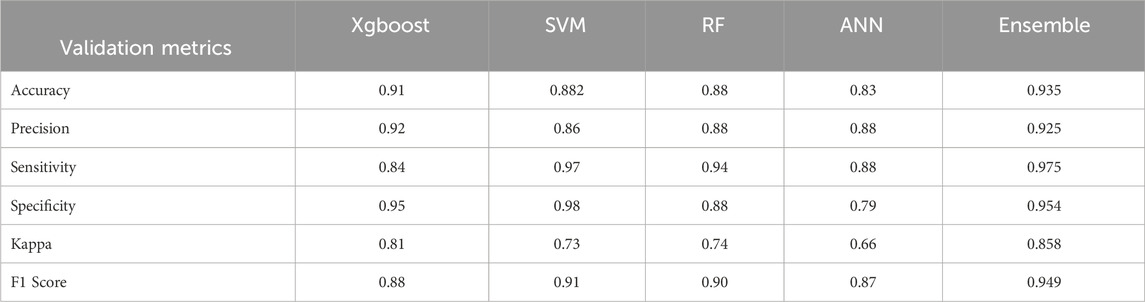
Table 2. Performance validation metrics of machine learning models and the ensemble technique for gully erosion susceptibility modeling.
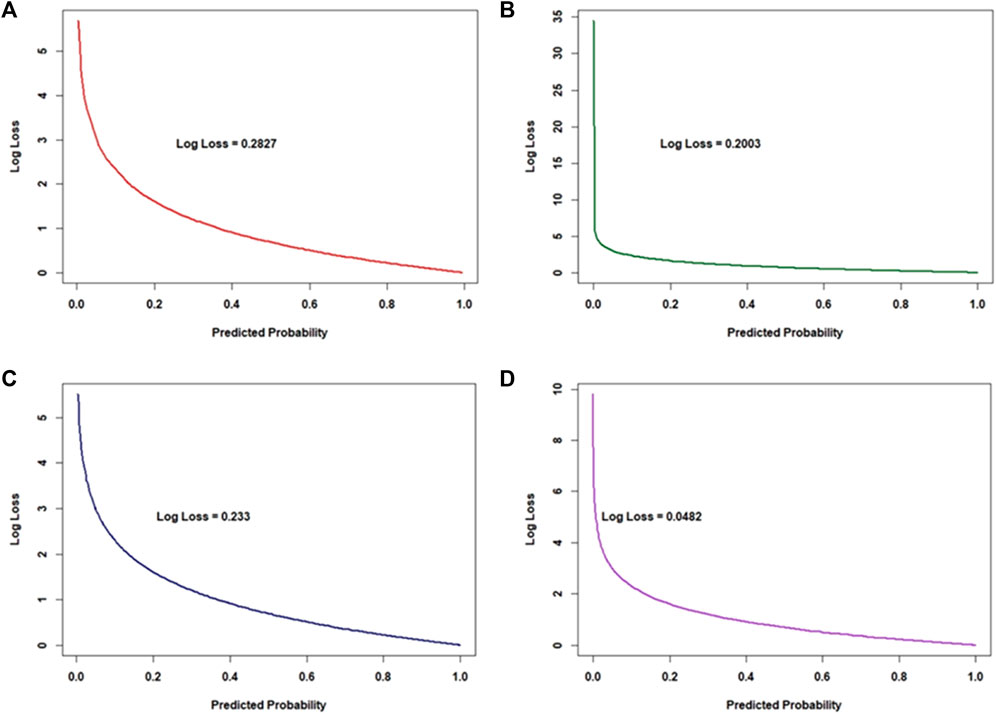
Figure 6. Performance validation of machine learning models for gully erosion susceptibility modeling using log loss: (A) artificial neural network (ANN), (B) support vector machine (SVM), (C) random forest (RF), and (D) XGBoost.
Nevertheless, the XGBoost model had the lowest sensitivity (0.84), supporting the findings of Garosi et al. (2019) that the model is more effective in predicting gullies but has lower sensitivity to complex nonlinear relationships and influential factors. In this study, the RF model showed better sensitivity (0.94), F1 score (0.90), Kappa value (0.74) and logloss (0.233) (Figure 6C), indicating its reasonable performance in predicting areas susceptible to gully erosion. The ANN model had the lowest performance in most metrics but still demonstrated a reasonable level of precision (0.88), sensitivity (0.88), and F1 score (0.87) (Table 2), with the highest level of confidence and a logloss value of 0.2827 (Figure aa). Bammou et al. (2024) also suggested that ML models, such as RF, SVM, and ANN, could perform well in identifying gully prone areas, with reasonable sensitivity, specificity, precision, accuracy, AUC, and F1 score values above 0.78. As Rouhani et al. (2021) stated, understanding the most relevant predictive factors is key to model performance, which may explain the superiority of the XGBoost model in this study. Therefore, the potential applicability of the XGBoost model in GES mapping makes it a promising tool for effective decision-making in sustainable soil and water management practices in watersheds, based on the current findings.
Currently, researchers are developing an ensemble model for large-scale GES modeling, combining predictions from multiple base models to enhance performance and arguing that it outperforms common statistical methods (Nhu et al., 2020; Arabamari et al., 2021). In this study, the ensemble approach, which integrated 4 ML models (ANN, SVM, RF, and XGBoost), achieved the highest AUC (0.99), accuracy (0.935), precision (0.925), sensitivity (0.975), specificity (0.954), kappa (0.858), and F1 score (0.949) values (Table 2). Similarly, earlier studies have shown that the ensemble approach enhances the GES mapping accuracy to 99% and the predictive capacity and reliability, especially when combined with XGBoost (Arabameri et al., 2019; Bouguerra et al., 2022). This study suggested that combining ML models, such as XGBoost, with geospatial analysis and/or implementing an ensemble approach can effectively predict gully erosion-prone areas, providing valuable insights for soil conservation solutions. Studies have also suggested that ensemble models are highly effective for local authorities in implementing countermeasures, land-use planning, and mapping global GES and natural hazards, producing accurate GES maps and outperforming individual models (Pourghasemi et al., 2017; Bui et al., 2019; Nhu et al., 2020).
Mapping the spatial distribution of GES and identifying high-risk areas based on geo-environmental factors are crucial for reducing soil erosion risks and promoting sustainable soil conservation, particularly in areas with high susceptibility or favorable conditions for gully development (Saha et al., 2021; Bouguerra et al., 2022). The current study classified GES using ML models at the broadest level, indicating significant variations in both the total areas within each GES class and their proportional distributions (Table 3; Supplementary Figure S1). The analysis of the spatial extent of gully erosion in the watershed revealed erosion-prone sites that were classified into five susceptibility groups using the Jenks natural break classification system, ranging from very low to very high GES (Amiri et al., 2019; Eloudi et al., 2023).
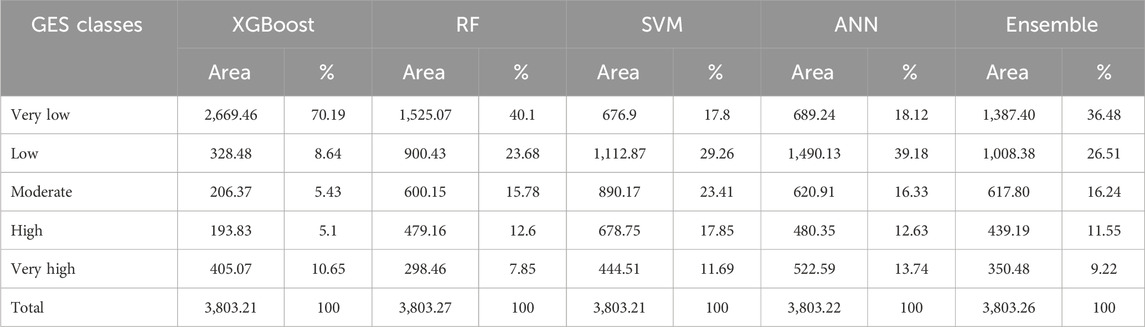
Table 3. Area and proportion of five gully erosion susceptibility (GES) classes in the four machine learning models and the ensemble technique.
The ML models and ensemble technique consistently projected that the Babile, Fedis, and Meyumuluke districts within the watershed would contain the largest areas classified under all GES classes, while the Gursum and Jarso districts were anticipated to encompass the smallest areas of land designated within the GES classes (Supplementary Tables S3–S7). In particular, the XGBoost model predicted the largest area (2,669.46 km2; 70.19%) to be in the ‘very low’ susceptibility class at the watershed scale, while the SVM model predicted the smallest area (676.9 km2; 17.80%) in this class (Table 3). In addition, the XGBoost model exhibited lower high-susceptibility areas in upland subwatersheds than did the other ML models while predicting lower risks for large subcatchments in southern regions. However, its focus on very low-GES risk areas might lead to an underestimation of higher-risk GES classes. These findings are consistent with those of Nhu et al. (2020), who hypothesized that gullies are mostly formed by extreme runoff associated with slope-area relationships. As a result, the GES map of the watershed developed by the XGBoost model accurately predicts the detected gullies along the subwatersheds and their tributaries.
The RF, ANN, and SVM models demonstrated greater spatial consistency in predicting low-risk GES areas than did XGBoost, resulting in greater area coverage (Figures 7A–D; Table 3). The ANN model predicted the largest area (522.59 km2; 13.74%) in the ‘very high’ GES class, while identifying an area of 1,490.13 km2 (39.18%) in the low-GES class, indicating areas with fewer erosion hazards. The RF model predicted the largest area in the “very low” GES class (1,525.07 km2; 40.1%), with notable allocations of 23.68, 15.78, and 12.6% to the low, moderate, and high GES classes, respectively, but more conservative estimations of the “very high” GES regions (298.46 km2; 7.85%) (Table 3). The SVM model, which included large areas (1,112.87 km2; 29.26%) as the low GES class, identified areas of 890.17 km2 (23.41%) as moderate, 678.75 km2 (17.85%) as high, and 444.51 km2 (11.69%) as very high GES classes, indicating its capacity to identify areas at significant gully erosion risk. These findings highlight the caution of SVM in identifying high-risk zones and the sensitivity of ANN in detecting vulnerable areas and that the predicted GES distribution (Figures 6A, B) is consistent with the quantitative results (Table 3). These findings support Arabameri et al. (2019), who found that gullies form in areas with high water concentrations, drainage densities, and arid conditions, particularly in plains and low-slope areas, where gypsum and salt minerals are evaporated and vegetation is overgrazed.
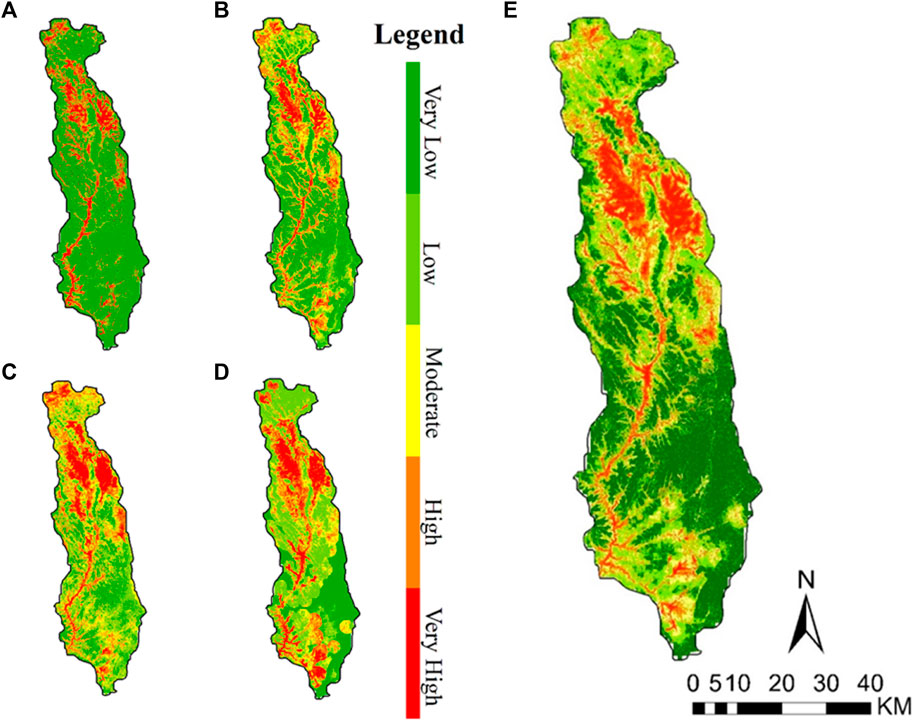
Figure 7. Spatial distribution of gully erosion susceptibility for four machine learning models: (A) XGBoost, (B) random forest (RF), (C) support vector machine (SVM), (D) artificial neural network (ANN), and (E) ensemble technique.
The ensemble approach comprehensively assessed GES distributions across watershed landscapes, providing a more powerful framework for predicting GES. The mapping identified watershed areas with very low, low, moderate, high, or very high erosion risk levels, accounting for 36.48%, 26.51%, 16.24%, 11.55%, and 9.22%, respectively, of the total area (Figure 7E; Table 3). As a result, this approach could offer decision makers insight into guiding land management strategies aimed at mitigating soil degradation in areas classified as possessing high or very high GES (Pourghasemi et al., 2017; Bui et al., 2019; Arabamari et al., 2021). Notably, the decrease in susceptibility was very low (36.48%), and XGBoost was predicted to constitute the largest area (70.19%) (Bui et al., 2019), with a more even distribution across the remaining GES classes, indicating a more accurate assessment of gully erosion risks across the watershed. Therefore, the development of ensemble models and advancements in GIS data collection, integration, and processing are crucial for improving the precision, reliability, and utility of ML-based erosion susceptibility assessments.
The results for the ML models (Section 3.3) showed that the XGBoost model achieved the highest prediction accuracy in differentiating erosion and nonerosion areas while revealing the reliability of district-level GES predictions and concentrated GES prediction clustering in critical areas (Table 3). Across all GES risk classes and ML models, districts located in the northern and southeastern positions within the watershed (along the Erer River) contained the greatest proportions of zones classified as being highly susceptible to gully erosion. At the district level, predictions indicated that the Harar, Fedis, Midega Tola, and Kombolcha districts would encompass the largest areas classified as having very high GES risk, while the Gursum and Jarso districts were anticipated to contain the smallest areas of land designated as having very high GES risk (Supplementary Tables S3–S7). Implementing preventative conservation efforts in these watershed hotspots could substantially reduce erosion risk. The GIS data-driven ML approaches in this study increased the accuracy of GES predictions by learning complex relationships between predictor variables compared to empirical prediction models used in similar catchments (Woldemariam and Harka, 2020). This approach predominantly aligns with the ensemble machine learning-GIS framework (Amiri et al., 2019), which outperforms individual ML models, and the XGBoost model (Lei et al., 2020), which showed exceptional performance and robustness for GES modeling compared to other ML models. These advanced ML approaches could also offer crucial information on concentrated and highly predicted GES areas in limited data regions, enabling the establishment of preventive measures to significantly reduce gully expansion (Woldemariam et al., 2023).
According to Baiddah et al. (2023), ML-based soil erosion susceptibility maps accurately identify vulnerable locations despite challenges in distinguishing between map errors and sensitive areas where erosion has not yet occurred. In this study, all ML models showed that the Erer watershed is prone to gully erosion; thus, the implementation of these ML models could help predict and map soil erosion, supporting policymakers in preventing soil erosion. Therefore, this study could benefit regional planners, especially in the rapidly changing arid to semiarid environments of Ethiopia, by offering accurate and reliable models, greater model flexibility, and comprehensive validation metrics to improve classification, method selection, and decision-making.
The current study focused on developing a novel and cost-effective methodology for GES modeling to identify areas susceptible to gully erosion and conditioning factors by integrating four MLAs with geospatial analysis within the Erer watershed in Ethiopia. The mapping method for GES proposed in this work can be applied in areas with comparable environmental and human activity, such as variable rainfall, steep slopes, and weak geology units. However, although the methods have shown excellent success in this context, it is important to note that certain limitations may impact their performance in other contexts. These limitations include reliance on single time-period data, exclusion of human activities as a factor, potential biases in individual MLAs, and utilization of coarse resolution data for specific variables due to the use of openly accessible datasets. The MLAs used in this study are sensitive to changes in specific input data and their accessibility and quality; thus, the findings may not be applicable in other regions with distinct geological features or environmental conditions. This is supported by recent studies by Baiddah et al. (2023) and Bammou et al. (2024), which revealed that conditioning factors for gully erosion are area-specific and cannot be reliably extrapolated to other regions, necessitating further investigation. This study relied on 30 m resolution data for the majority of geoenvironmental factors and 1 km resolution ARF data due to the lack of ground meteorology sites in the basin. Moreover, SOM data were obtained at a relatively low resolution. Although these resolutions were employed due to the availability of open-source data, future studies can leverage high-resolution imageries, including 3D Lidar point cloud data and commercial datasets, to enhance the precision of GES predictions. Furthermore, MLAs have been optimized using the available data; however, as suggested by Baiddah et al. (2023), applications in other regions require additional optimization according to the available data.
Although the study considered a diverse range of geospatial GES predictor variables, considering other variables, such as soil texture, electrical conductivity, and run-off speed, could further improve the identification of GES. In addition, the understanding of the factors influencing GES differs among models, which implies that less precise factors can lead to highly accurate models (Bouguerra et al., 2022). For a better understanding of this phenomenon and owing to the intrinsic relationships between gully erosion and its controlling factors, other types of MLAs, especially deep learning models (Baiddah et al., 2023), should be applied. A multitemporal geodatabase is also recommended for dynamic GES modeling and adaptive management strategies, incorporating socioeconomic data and human activities such as land management and agricultural activities as GES predictors.
Future climate change is expected to have an impact on gully erosion, with direct and indirect effects promoting or suppressing gullies; thus, climate change models should be combined with climate scenarios, land use models, and hydrologic models for accurate GES prediction and mapping. In particular, research on the long-term evolution of gully erosion and its interaction with climate change dynamics by combining MLAs and climate projections could provide more insights into the impacts of climate change on gully formation and guide adaptive prevention and mitigation strategies (Bouguerra et al., 2022; Bammou et al., 2024). Therefore, analyses of GES over longer time periods using climatic projection models could be recommended to provide valuable insights into the long-term impact of climate change and enable proactive measures to ensure the sustainability of soil resources.
Despite these limitations and gaps, the integration of MLAs and geospatial techniques, along with the ensemble technique, offers a promising approach to better delineate, visualize, and interpret erosion-prone areas. The reliable GES maps generated in this study serve as invaluable tools for decision-makers and government officials involved in erosion risk management. As a result, implementing soil and water conservation measures (e.g., check dams, contour bunds, gully plugs) in highly susceptible areas could effectively mitigate erosion processes. To mitigate soil erosion in watershed areas, which could be worsened by climate change, it is recommended that protection measures such as afforestation, conservation tillage, no-till, and planting drought-resistant cultivars be implemented (Arabameri et al., 2019; Bammou et al., 2024). In particular, recognizing the factors predictive of GES in this study, vegetation planting on borders and surrounding gullies can be one of the highest priority preventative strategies for controlling and reducing gully processes within watershed areas.
There is an apparent interplay between gullies, vegetation, and climate change, particularly extreme rainfall and heat events, which can exacerbate gully erosion; in particular, vegetation plays a protective role during extreme climate events (Bouguerra et al., 2022). In addition to the relationships between vegetative features (type, cover, and density) and soil factors (texture, compaction, porosity, etc.), which affect infiltration rates, runoff formation, and surface flow, vegetation also helps stabilize soils, gully walls, and potential gully nickpoints. Arabameri et al. (2019) suggested that planting around gullies in Iran can control erosion by increasing topsoil shear strength, slowing extreme rainfall runoff, reducing soil saturation, and adjusting overland flow and infiltration patterns. Furthermore, stakeholder engagement and community participation in implementing sustainable land management practices and monitoring gully erosion are crucial for long-term success.
The Erer watershed in Eastern Ethiopia faces significant challenges from extensive gullying, posing threats to agriculture, infrastructure, and communities. This study addresses the urgent need for evidence-based mitigation and management efforts by integrating machine learning (ML) models, including ANN, SVM, RF, and XGBoost, with geospatial analysis. This novel methodological framework effectively models and maps gully erosion susceptibility (GES) within a watershed. A comprehensive GIS database was developed to record gully erosion incidents, and 22 conditioning geoenvironmental factors were identified as predictive variables for assessing erosion conditions. The ML models demonstrated high accuracy and prediction performance for GES modeling. Notably, the XGBoost model outperformed the other models with an AUC of 0.97, achieving the highest accuracy (0.91), precision (0.92), and kappa value (0.81), indicating its robustness and superior performance. The SVM model excelled in detecting areas resistant and susceptible to gully erosion, exhibiting the highest sensitivity (0.97), specificity (0.98), and F1 score (0.91). An ensemble ML technique combining predictions from different base models further enhanced GES modeling, achieving the highest performance in terms of the AUC (0.99), accuracy (0.935), precision (0.925), sensitivity (0.975), specificity (0.954), kappa (0.858), and F1 score (0.949). This approach identified GES classes, highlighting areas with varying susceptibility levels within the watershed. Key factors such as RSP, NDVI, and SOM were identified as significant drivers of gully erosion. This study emphasizes the importance of optimal soil conservation measures and proposes planting around gullies to control and minimize gully processes. Overall, the integrated ML and geospatial analysis techniques provide valuable insights for sustainable management of the Erer watershed. Future research should focus on establishing a multitemporal geodatabase to iteratively update conditioning factors and enhance the GES map. Additionally, these findings can provide spatial support for future planning of sustainable land management practices and for mitigating losses and associated land degradation.
The following software packages were used in this study:
1. QGIS-OSGeo4W (version 3.34.2): QGIS is a free and open-source cross-platform desktop geographic information system (GIS) application that supports the viewing, editing, and analysis of geospatial data. It is available for download from the official QGIS website (https://qgis.org/en/site/forusers/download.html).
2. R Software (version 4.2.2): R is a free software environment for statistical computing and graphics. It is available for download from the Comprehensive R Archive Network (CRAN) (https://cran.r-project.org/).
3. Google Earth Engine (GEE): This is a cloud-based platform for planetary-scale environmental data analysis. It is accessible through the JavaScript or Python APIs, which are available with a Google account (https://earthengine.google.com/).
4. Google Earth Pro (version 7.3.4.8642): This is a desktop application for visualizing and exploring geographical data. It is available for download from the Google Earth website (https://www.google.com/earth/versions/).
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
TG: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. PP: Supervision, Validation, Writing–original draft, Writing–review and editing. NA: Supervision, Validation, Writing–original draft, Writing–review and editing. GW: Conceptualization, Formal Analysis, Validation, Writing–original draft, Writing–review and editing. KY: Conceptualization, Formal Analysis, Validation, Writing–original draft, Writing–review and editing. EK: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. IA: Conceptualization, Formal Analysis, Validation, Writing–original draft, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2024.1410741/full#supplementary-material
Abdollahi, S., Pourghasemi, H. R., Ghanbarian, G. A., and Safaeian, R. (2019). Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 78 (6), 4017–4034. doi:10.1007/s10064-018-1403-6
Aber, J. S., Marzolff, I., and Ries, J. B. (2010). “Gully erosion monitoring,” in Small-format aerial photography (Elsevier), 193–200. doi:10.1016/B978-0-444-53260-2.10013-4
Aboutaib, F., Krimissa, S., Pradhan, B., Elaloui, A., Ismaili, M., Abdelrahman, K., et al. (2023). Evaluating the effectiveness and robustness of machine learning models with varied geo-environmental factors for determining vulnerability to water flow-induced gully erosion. Front. Environ. Sci. 11, 1207027. doi:10.3389/fenvs.2023.1207027
Al-Abadi, A. M., and Al-Ali, A. K. (2018). Susceptibility mapping of gully erosion using GIS-based statistical bivariate models: a case study from Ali Al-Gharbi District, Maysan Governorate, southern Iraq. Environ. Earth Sci. 77 (6), 249. doi:10.1007/s12665-018-7434-2
Al-Bawi, A. J., Al-Abadi, A. M., Pradhan, B., and Alamri, A. M. (2021). Assessing gully erosion susceptibility using topographic derived attributes, multi-criteria decision-making, and machine learning classifiers. Geomatics, Natural Hazards and Risk 12 (1), 3035–3062. doi:10.1080/19475705.2021.1994024
Alkhasawneh, M. S., Ngah, U. K., Tay, L. T., and Isa, N. A. M. (2014). Determination of importance for comprehensive topographic factors on landslide hazard mapping using artificial neural network. Environ. Earth Sci. 72 (3), 787–799. doi:10.1007/s12665-013-3003-x
Amare, S., Langendoen, E., Keesstra, S., van der Ploeg, M., Gelagay, H., Lemma, H., et al. (2021). Susceptibility to gully erosion: applying random forest (RF) and frequency ratio (FR) approaches to a small catchment in Ethiopia. WaterSwitzerl. 13 (2), 216. doi:10.3390/w13020216
Amiri, M., Pourghasemi, H. R., Ghanbarian, G. A., and Afzali, S. F. (2019). Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 340, 55–69. doi:10.1016/j.geoderma.2018.12.042
Arabameri, A., Chandra Pal, S., Costache, R., Saha, A., Rezaie, F., and Seyed Danesh, A. (2021). Prediction of gully erosion susceptibility mapping using novel ensemble machine learning algorithms. Geomatics, Natural Hazards and Risk 12 (1), 469–498. doi:10.1080/19475705.2021.1880977
Arabameri, A., Chen, W., Loche, M., Zhao, X., Li, Y., Lombardo, L., et al. (2020a). Comparison of machine learning models for gully erosion susceptibility mapping. Geosci. Front. 11 (5), 1609–1620. doi:10.1016/j.gsf.2019.11.009
Arabameri, A., Pradhan, B., and Lombardo, L. (2019). Comparative assessment using boosted regression trees, binary logistic regression, frequency ratio and numerical risk factor for gully erosion susceptibility modelling. CATENA 183, 104223. doi:10.1016/j.catena.2019.104223
Arabameri, A., Rezaei, K., Pourghasemi, H. R., Lee, S., and Yamani, M. (2018). GIS-based gully erosion susceptibility mapping: a comparison among three data-driven models and AHP knowledge-based technique. Environ. Earth Sci. 77 (17), 628. doi:10.1007/s12665-018-7808-5
Arabameri, A., Saha, S., Roy, J., Chen, W., Blaschke, T., and Bui, D. T. (2020b). Landslide susceptibility evaluation and management using different machine learning methods in the Gallicash River Watershed, Iran. Remote Sens. 12 (3), 475. doi:10.3390/rs12030475
Ayanlade, A., Oluwaranti, A., Ayanlade, O. S., Borderon, M., Sterly, H., Sakdapolrak, P., et al. (2022). Extreme climate events in sub-Saharan Africa: a call for improving agricultural technology transfer to enhance adaptive capacity. Clim. Serv. 27, 100311. doi:10.1016/j.cliser.2022.100311
Azareh, A., Rahmati, O., Rafiei-Sardooi, E., Sankey, J. B., Lee, S., Shahabi, H., et al. (2019). Modelling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 655, 684–696. doi:10.1016/j.scitotenv.2018.11.235
Azedou, A., Lahssini, S., Khattabi, A., Meliho, M., and Rifai, N. (2021). A methodological comparison of three models for gully erosion susceptibility mapping in the rural municipality of el faid (Morocco). Sustainability 13 (2), 682. doi:10.3390/su13020682
Baiddah, A., Krimissa, S., Hajji, S., Ismaili, M., Abdelrahman, K., El Bouzekraoui, M., et al. (2023). Head-cut gully erosion susceptibility mapping in semi-arid region using machine learning methods: insight from the high atlas, Morocco. Front. Earth Sci. 11 (May), 1–19. doi:10.3389/feart.2023.1184038
Bammou, Y., Benzougagh, B., Abdessalam, O., Brahim, I., Kader, S., Spalevic, V., et al. (2024). Machine learning models for gully erosion susceptibility assessment in the Tensift catchment, Haouz Plain, Morocco for sustainable development. J. Afr. Earth Sci. 213, 105229. doi:10.1016/j.jafrearsci.2024.105229
Barbet-Massin, M., Jiguet, F., Albert, C. H., and Thuiller, W. (2012). Selecting pseudo-absences for species distribution models: how, where and how many? Methods Ecol. Evol. 3 (2), 327–338. doi:10.1111/j.2041-210X.2011.00172.x
Belayneh, M., Yirgu, T., and Tsegaye, D. (2020). Current extent, temporal trends, and rates of gully erosion in the Gumara watershed, Northwestern Ethiopia. Glob. Ecol. Conservation 24, e01255. doi:10.1016/j.gecco.2020.e01255
Bouaziz, M., Wijaya, A., and Gloaguen, R. (2011). Remote gully erosion mapping using aster data and geomorphologic analysis in the Main Ethiopian Rift. Geo-Spatial Inf. Sci. 14 (4), 246–254. doi:10.1007/s11806-011-0565-1
Bouguerra, H., Tachi, S. E., Bouchehed, H., Gilja, G., Aloui, N., Hasnaoui, Y., et al. (2022). Integration of high-accuracy geospatial data and machine learning approaches for soil erosion susceptibility mapping in the mediterranean region: a case study of the macta basin, Algeria. Sustainability 15 (13), 10388. doi:10.3390/su151310388
Broséus, J., Vallat, M., and Esseiva, P. (2011). Multi-class differentiation of cannabis seedlings in a forensic context. Chemom. Intelligent Laboratory Syst. 107 (2), 343–350. doi:10.1016/j.chemolab.2011.05.004
Bui, D. T., Shirzadi, A., Shahabi, H., Chapi, K., Omidavr, E., Pham, B. T., et al. (2019). A novel ensemble artificial intelligence approach for gully erosion mapping in a semi-arid watershed (Iran). Sensors 19 (11), 2444. doi:10.3390/s19112444
Busch, R., Hardt, J., Nir, N., and Schütt, B. (2021). Modeling gully erosion susceptibility to evaluate human impact on a local landscape system in tigray, Ethiopia. Remote Sens. 13 (2009), 2009. doi:10.3390/rs13102009
Chen, T., and Guestrin, C. (2016). “XGBoost: a scalable tree boosting system,” in Proceedings of the ACM SIGKDD international conference on knowledge discovery and data mining, 13-17-august-2016, 785–794. doi:10.1145/2939672.2939785
Conforti, M., Aucelli, P. P. C., Robustelli, G., and Scarciglia, F. (2011). Geomorphology and GIS analysis for mapping gully erosion susceptibility in the Turbolo stream catchment (Northern Calabria, Italy). Nat. Hazards 56 (3), 881–898. doi:10.1007/s11069-010-9598-2
Conoscenti, C., Agnesi, V., Angileri, S., Cappadonia, C., Rotigliano, E., and Märker, M. (2013a). A GIS-based approach for gully erosion susceptibility modelling: a test in Sicily, Italy. Environ. Earth Sci. 70 (3), 1179–1195. doi:10.1007/s12665-012-2205-y
Conoscenti, C., Angileri, S., Cappadonia, C., Rotigliano, E., Agnesi, V., and Märker, M. (2013b). Gully erosion susceptibility assessment by means of GIS-based logistic regression: a case of Sicily (Italy). Geomorphology 204, 399–411. doi:10.1016/j.geomorph.2013.08.021
Cui, Y., Cai, M., and Stanley, H. E. (2017). Comparative analysis and classification of cassette exons and constitutive exons. BioMed Res. Int. 2017, 1–8. doi:10.1155/2017/7323508
Davidson, L., Kline, K., Klein, S., and Windisch, K. (2008). “The normalization process,” in Pro SQL server 2008 relational database design and implementation (Apress), 117–175. doi:10.1007/978-1-4302-0867-9_4
Dev, V. A., and Eden, M. R. (2019). Formation lithology classification using scalable gradient boosted decision trees. Comput. Chem. Eng. 128, 392–404. doi:10.1016/j.compchemeng.2019.06.001
Du, G., Zhang, Y., Iqbal, J., Yang, Z., and Yao, X. (2017). Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mt. Sci. 14 (2), 249–268. doi:10.1007/s11629-016-4126-9
Ebabu, K., Taye, G., Tsunekawa, A., Haregeweyn, N., Adgo, E., Tsubo, M., et al. (2023). Land use, management and climate effects on runoff and soil loss responses in the highlands of Ethiopia. J. Environ. Manag. 326 (PA), 116707. doi:10.1016/j.jenvman.2022.116707
Eloudi, H., Hssaisoune, M., Reddad, H., Namous, M., Ismaili, M., Krimissa, S., et al. (2023). Robustness of optimized decision tree-based machine learning models to map gully erosion vulnerability. Soil Syst. 7 (2), 50. doi:10.3390/soilsystems7020050
FAO (Food and Agriculture Organization) (1995). The digital soil map of the World. Land Water Dev. Div. Available at: http://www.fao.org/geonetwork/.
Fenta, A. A., Tsunekawa, A., Haregeweyn, N., Tsubo, M., Yasuda, H., Kawai, T., et al. (2021). Agroecology-based soil erosion assessment for better conservation planning in Ethiopian river basins. Environ. Res. 195, 110786. doi:10.1016/j.envres.2021.110786
Garosi, Y., Sheklabadi, M., Conoscenti, C., Pourghasemi, H. R., and Van Oost, K. (2019). Assessing the performance of GIS- based machine learning models with different accuracy measures for determining susceptibility to gully erosion. Sci. Total Environ. 664, 1117–1132. doi:10.1016/j.scitotenv.2019.02.093
Gayen, A., Pourghasemi, H. R., Saha, S., Keesstra, S., and Bai, S. (2019). Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total Environ. 668, 124–138. doi:10.1016/j.scitotenv.2019.02.436
Gayen, A., and Saha, S. (2017). Application of weights-of-evidence (WoE) and evidential belief function (EBF) models for the delineation of soil erosion vulnerable zones: a study on Pathro river basin, Jharkhand, India. Model. Earth Syst. Environ. 3 (3), 1123–1139. doi:10.1007/s40808-017-0362-4
Gholami, H., Mohammadifar, A., Bui, D. T., and Collins, A. L. (2020). Mapping wind erosion hazard with regression-based machine learning algorithms. Sci. Rep. 10 (1), 20494. doi:10.1038/s41598-020-77567-0
Gómez-Gutiérrez, Á., Conoscenti, C., Angileri, S. E., Rotigliano, E., and Schnabel, S. (2015). Using topographical attributes to evaluate gully erosion proneness (susceptibility) in two mediterranean basins: Advantages and limitations. Nat. Hazards 79, 291–314. doi:10.1007/s11069-015-1703-0
Guisan, A., Thuiller, W., and Zimmermann, N. E. (2017) Habitat suitability and distribution models: with applications in R, 1–478. doi:10.1017/9781139028271
Gutema, T., Kebede, E., Legesse, H., and Fite, T. (2023). Integrating multiple soil management practices: a system-wide approach for restoring degraded soil and improving Brachiaria productivity. Agrosystems, Geosciences Environ. 6 (2), e20360. doi:10.1002/agg2.20360
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction, Second Edition. In Springer series in statistics (second). Springer New York, NY. doi:10.1007/978-0-387-84858-7
Hembram, T. K., Paul, G. C., and Saha, S. (2019). Comparative analysis between morphometry and geo-environmental factor based soil erosion risk assessment using weight of evidence model: a study on jainti River Basin, eastern India. Environ. Process. 6 (4), 883–913. doi:10.1007/s40710-019-00388-5
Hitouri, S., Varasano, A., Mohajane, M., Ijlil, S., Essahlaoui, N., Ali, S. A., et al. (2022). Hybrid machine learning approach for gully erosion mapping susceptibility at a watershed scale. ISPRS Int. J. Geo-Information 11 (7), 401. doi:10.3390/ijgi11070401
Igwe, O., John, U. I., Solomon, O., and Obinna, O. (2020). GIS-based gully erosion susceptibility modeling, adapting bivariate statistical method and AHP approach in Gombe town and environs Northeast Nigeria. Geoenvironmental Disasters 7 (1), 32. doi:10.1186/s40677-020-00166-8
Jiang, C., Fan, W., Yu, N., and Liu, E. (2021). Spatial modeling of gully head erosion on the Loess Plateau using a certainty factor and random forest model. Sci. Total Environ. 783, 147040. doi:10.1016/j.scitotenv.2021.147040
Kim, D., Jung, H. S., and Baek, W. (2016). Comparative analysis among radar image filters for flood mapping. J. Korean Soc. Surv. Geodesy, Photogrammetry Cartogr. 34 (1), 43–52. doi:10.7848/ksgpc.2016.34.1.43
Koh, P. W., and Liang, P. (2017). Understanding black-box predictions via influence functions. ArXiv. doi:10.48550/arXiv.1703.04730
Lei, X., Chen, W., Avand, M., Janizadeh, S., Kariminejad, N., Shahabi, H., et al. (2020). GIS-based machine learning algorithms for gully erosion susceptibility mapping in a semi-arid region of Iran. Remote Sens. 12 (15), 2478. doi:10.3390/RS12152478
Li, T., Zhang, H., Wang, X., Cheng, S., Fang, H., Liu, G., et al. (2019). Soil erosion affects variations of soil organic carbon and soil respiration along a slope in Northeast China. Ecol. Process. 8 (1), 28. doi:10.1186/s13717-019-0184-6
Liu, Y., Zhao, S., Du, W., Tian, Z., Chi, H., Chao, C., et al. (2023). Applying interpretable machine learning algorithms to predict risk factors for permanent stoma in patients after TME. Front. Surg. 10, 1125875. doi:10.3389/fsurg.2023.1125875
Loukika, K. N., Keesara, V. R., and Sridhar, V. (2021). Analysis of land use and land cover using machine learning algorithms on Google Earth engine for munneru River Basin, India. Sustainability 13 (24), 13758. doi:10.3390/SU132413758
Mararakanye, N., and Sumner, P. D. (2017). Gully erosion: a comparison of contributing factors in two catchments in South Africa. Geomorphology 288, 99–110. doi:10.1016/j.geomorph.2017.03.029
Meng, Y., Duan, Q., Jiao, K., and Xue, J. (2023). A screened predictive model for esophageal squamous cell carcinoma based on salivary flora data. Math. Biosci. Eng. MBE 20 (10), 18368–18385. doi:10.3934/mbe.2023816
Mohebzadeh, H., Biswas, A., Rudra, R., and Daggupati, P. (2022). Machine learning techniques for gully erosion susceptibility mapping: a review. Geosci. Switz. 12 (12), 429–523. doi:10.3390/geosciences12120429
Moore, I. D., and Burch, G. J. (1986). Physical basis of the length-slope factor in the universal soil loss equation. Soil Sci. Soc. Am. J. 50 (5), 1294–1298. doi:10.2136/sssaj1986.03615995005000050042x
Moreno-Ibarra, M., Torres, M., Quintero, R., Guzman, G., and Menchaca-Mendez, R. (2011). Semantic assessment of similarity between raster elevation datasets. Rev. Fac. Ing. 59, 37–46. doi:10.17533/udea.redin.13753
Naghibi, S. A., Ahmadi, K., and Daneshi, A. (2017). Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 31 (9), 2761–2775. doi:10.1007/s11269-017-1660-3
Namous, M., Hssaisoune, M., Pradhan, B., Lee, C. W., Alamri, A., Elaloui, A., et al. (2021). Spatial prediction of groundwater potentiality in large semi-arid and karstic mountainous region using machine learning models. WaterSwitzerl. 13 (16), 2273. doi:10.3390/w13162273
Negese, A. (2021). Impacts of land use and land cover change on soil erosion and hydrological responses in Ethiopia. Appl. Environ. Soil Sci. 2021, 1–10. doi:10.1155/2021/6669438
Nguyen, K. A., Chen, W., Lin, B.-S., and Seeboonruang, U. (2021). Comparison of ensemble machine learning methods for soil erosion pin measurements. ISPRS Int. J. Geo-Information 10 (1), 42. doi:10.3390/ijgi10010042
Nhu, V.-H., Shirzadi, A., Shahabi, H., Singh, S. K., Al-Ansari, N., Clague, J. J., et al. (2020). Shallow landslide susceptibility mapping: a comparison between logistic model tree, logistic regression, naïve bayes tree, artificial neural network, and support vector machine algorithms. Int. J. Environ. Res. Public Health 17 (8), 2749. doi:10.3390/ijerph17082749
O’Brien, R. M. (2007). A caution regarding rules of thumb for variance inflation factors. Qual. Quantity 41 (5), 673–690. doi:10.1007/s11135-006-9018-6
Okereke, C. N., Ubechu, B., and Okereke, C. N. (2012). Mapping gully erosion using remote sensing technique: a case study of okigwe area, southeastern Nigeria. Int. J. Eng. Res. Appl. 2 (3), 1955–1967.
Pourghasemi, H. R., and Rahmati, O. (2018). Prediction of the landslide susceptibility: which algorithm, which precision? CATENA 162, 177–192. doi:10.1016/j.catena.2017.11.022
Pourghasemi, H. R., Sadhasivam, N., Kariminejad, N., and Collins, A. L. (2020). Gully erosion spatial modelling: role of machine learning algorithms in selection of the best controlling factors and modelling process. Geosci. Front. 11 (6), 2207–2219. doi:10.1016/j.gsf.2020.03.005
Pourghasemi, H. R., Yousefi, S., Kornejady, A., and Cerdà, A. (2017). Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 609, 764–775. doi:10.1016/j.scitotenv.2017.07.198
Quevedo, R. P., Maciel, D. A., Uehara, T. D. T., Vojtek, M., Rennó, C. D., Pradhan, B., et al. (2022). Consideration of spatial heterogeneity in landslide susceptibility mapping using geographical random forest model. Geocarto Int. 37 (25), 8190–8213. doi:10.1080/10106049.2021.1996637
Rahmati, O., Kalantari, Z., Ferreira, C. S., Chen, W., Soleimanpour, S. M., Kapović-Solomun, M., et al. (2022). Contribution of physical and anthropogenic factors to gully erosion initiation. CATENA 210, 105925. doi:10.1016/j.catena.2021.105925
Rahmati, O., Tahmasebipour, N., Haghizadeh, A., Pourghasemi, H. R., and Feizizadeh, B. (2017a). Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: an integrated framework. Sci. Total Environ. 579, 913–927. doi:10.1016/j.scitotenv.2016.10.176
Rahmati, O., Tahmasebipour, N., Haghizadeh, A., Pourghasemi, H. R., and Feizizadeh, B. (2017b). Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion. Geomorphology 298, 118–137. doi:10.1016/j.geomorph.2017.09.006
Rouhani, H., Fathabadi, A., and Baartman, J. (2021). A wrapper feature selection approach for efficient modelling of gully erosion susceptibility mapping. Prog. Phys. Geogr. 45 (4), 580–599. doi:10.1177/0309133320979897
Roy, J., and Saha, D. S. (2019). GIS-Based gully erosion susceptibility evaluation using frequency ratio, cosine amplitude and logistic regression ensembled with fuzzy logic in hinglo River Basin, India. Remote Sens. Appl. Soc. Environ. 15, 100247. doi:10.1016/j.rsase.2019.100247
Saha, S., Roy, J., Arabameri, A., Blaschke, T., and Bui, D. T. (2020). Machine learning-based gully erosion susceptibility mapping: a case study of eastern India. Sensors Switz. 20 (5), 1313. doi:10.3390/s20051313
Saha, S., Sarkar, R., Thapa, G., and Roy, J. (2021). Modeling gully erosion susceptibility in Phuentsholing, Bhutan using deep learning and basic machine learning algorithms. Environ. Earth Sci. 80 (8), 295. doi:10.1007/s12665-021-09599-2
Sahin, E. K. (2020). Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. SN Appl. Sci. 2 (7), 1308. doi:10.1007/s42452-020-3060-1
Setargie, T. A., Tsunekawa, A., Haregeweyn, N., Tsubo, M., Fenta, A. A., Berihun, M. L., et al. (2023a). Random Forest–based gully erosion susceptibility assessment across different agro-ecologies of the Upper Blue Nile basin, Ethiopia. Geomorphology 431 (July 2022), 108671. doi:10.1016/j.geomorph.2023.108671
Setargie, T. A., Tsunekawa, A., Haregeweyn, N., Tsubo, M., Rossi, M., Ardizzone, F., et al. (2023b). Modeling of gully erosion in Ethiopia as influenced by changes in rainfall and land use management practices. Land 12 (5), 947. doi:10.3390/land12050947
Sun, W., Shao, Q., Liu, J., and Zhai, J. (2014). Assessing the effects of land use and topography on soil erosion on the Loess Plateau in China. CATENA 121, 151–163. doi:10.1016/j.catena.2014.05.009
Tebebu, T. Y., Abiy, A. Z., Zegeye, A. D., Dahlke, H. E., Easton, Z. M., Tilahun, S. A., et al. (2010). Surface and subsurface flow effect on permanent gully formation and upland erosion near Lake Tana in the northern highlands of Ethiopia. Hydrology Earth Syst. Sci. 14 (11), 2207–2217. doi:10.5194/hess-14-2207-2010
Wang, R., Zhang, S., Pu, L., Yang, J., Yang, C., Chen, J., et al. (2016). Gully erosion mapping and monitoring at multiple scales based on multi-source remote sensing data of the sancha river catchment, Northeast China. ISPRS Int. J. Geo-Information 5 (11), 200. doi:10.3390/ijgi5110200
Were, K., Kebeney, S., Churu, H., Mutio, J. M., Njoroge, R., Mugaa, D., et al. (2023). Spatial prediction and mapping of gully erosion susceptibility using machine learning techniques in a degraded semi-arid region of Kenya. Land 12 (4), 890. doi:10.3390/land12040890
Woldemariam, G. W., and Harka, A. E. (2020). Effect of land use and land cover change on soil erosion in erer sub-basin, northeast Wabi Shebelle Basin, Ethiopia. Land 9 (4), 111. doi:10.3390/land9040111
Woldemariam, G. W., Yasin, K. H., and Iguala, A. D. (2023). Water erosion risk assessment for conservation planning in the east hararghe zone, Ethiopia. Geosci. Switz. 13 (6), 184. doi:10.3390/geosciences13060184
Woodward, D. E. (1999). Method to predict cropland ephemeral gully erosion. CATENA 37 (3), 393–399. doi:10.1016/S0341-8162(99)00028-4
Xu, B., Tan, Y., Sun, W., Ma, T., Liu, H., and Wang, D. (2023). Study on the prediction of the uniaxial compressive strength of rock based on the SSA-XGBoost model. Sustainability 15 (6), 5201. doi:10.3390/su15065201
Yang, A., Wang, C., Pang, G., Long, Y., Wang, L., Cruse, R. M., et al. (2021). Gully erosion susceptibility mapping in highly complex terrain using machine learning models. ISPRS Int. J. Geo-Information 10 (10), 680. doi:10.3390/ijgi10100680
Yazie, T., Mekonnen, M., and Derebe, A. (2021). Gully erosion and its impacts on soil loss and crop yield in three decades, northwest Ethiopia. Model. Earth Syst. Environ. 7 (4), 2491–2500. doi:10.1007/s40808-020-01018-y
Keywords: machine learning, ensemble model, geospatial analysis, gully erosion, susceptibility modeling
Citation: Gelete TB, Pasala P, Abay NG, Woldemariam GW, Yasin KH, Kebede E and Aliyi I (2024) Integrated machine learning and geospatial analysis enhanced gully erosion susceptibility modeling in the Erer watershed in Eastern Ethiopia. Front. Environ. Sci. 12:1410741. doi: 10.3389/fenvs.2024.1410741
Received: 01 April 2024; Accepted: 01 July 2024;
Published: 06 August 2024.
Edited by:
Ionut Cristi Nicu, Norwegian Institute for Cultural Heritage Research, NorwayReviewed by:
Nitheshnirmal Sadhasivam, Virginia Tech, United StatesCopyright © 2024 Gelete, Pasala, Abay, Woldemariam, Yasin, Kebede and Aliyi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tadele Bedo Gelete, dGFkZWxlYmVkb0BnbWFpbC5jb20=; Erana Kebede, ZXJhbmFrLm5lZGFAZ21haWwuY29t
†ORCID: Tadele Bedo Gelete, orcid.org/0000-0001-5344-2580; Gezahegn Weldu Woldemariam, orcid.org/0000-0003-4649-5881; Kalid Hassen Yasin, orcid.org/0000-0001-6231-1312; Erana Kebede, orcid.org/0000-0002-3584-6757; Ibsa Aliyi, orcid.org/0000-0001-7675-6435
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.