
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci., 01 September 2022
Sec. Atmosphere and Climate
Volume 10 - 2022 | https://doi.org/10.3389/fenvs.2022.951468
This article is part of the Research TopicImpact of Climate Change on the Human Living EnvironmentView all 24 articles
Extreme rainfall can be affected by various climatic factors such as the large-scale climate patterns (LCPs). Understanding the changing LCPs can improve the accuracy of extreme rainfall prediction. This study explores the variation trend of extreme rainfall in the middle and lower reaches of the Yangtze River Basin (MLRYRB) and the telecorrelation with four LCPs, namely WPSHI (Western Pacific Subtropical High Index), EAMI (East Asia Monsoon Index), ENSO (El Niño-Southern Oscillation) and PDO (Pacific Decadal Oscillation), through modified Mann-Kendall (MMK) analysis, Pearson correlation coefficient, wavelet coherence analysis (WTC) and improved partial wavelet analysis (PWC). Previous studies have ignored the interdependence between these climate indices when analyzing their effects on precipitation. This study introduces the improved PWC, which can remove the correlations between them and reveal the influence of a single LCP. The results show that: 1) extreme rainfall in the MLRYRB has an obvious increasing trend and has a significant correlation with the LCPs; 2) the LCPs have a significant cyclical relationship with extreme rainfall, which can be significantly affected by the intergenerational variation of the LCPs; and 3) the improved PWC can accurately reveal the influence of a single LCP. EAMI is the main influencing factor in the 1-year cycle, while WPSHI is the main influencing factor in the 5-year cycle. ENSO and PDO can always influence extreme rainfall by coupling WPSHI or EAMI.
Due to climate change, the frequency and intensity of extreme weather events have increased. Extreme weather events will change the local characteristics of temperature and rainfall, posing a threat to natural systems. Rainfall is one of the most important climate variables, and its changes have an important impact on the local hydrological process and water resources management (Grimm and Tedeschi, 2008; Zhang et al., 2018; Ashcroft et al., 2019; Liu and Shi, 2019; Rao et al., 2020). The frequency increase in extreme rainfall often leads to more floods, which is one of the most serious water-related natural disasters. Since the 20th century, extreme rainfall has shown a significant and widespread increasing trend in most parts of the world (Chang et al., 2012; Syafrina et al., 2015; Shi et al., 2016), and more than 60% of floods are caused by extreme rainfall (Teegavarapu, 2012; Agilan et al., 2021). Extreme rainfall will have a huge impact on the local ecology, industry, and social economy, which has motivated more and more studies to emphasize the importance of extreme rainfall. However, the temporal and spatial distributions of extreme weather events in different regions are quite different (Sridhar et al., 2013; Weldegerima et al., 2018), normally, with different impact ranges, frequencies, durations, and severities (Swain et al., 2019; Fagnant et al., 2020; Tong et al., 2020; Ndlovu et al., 2021). Therefore, it is of great significance to investigate the spatiotemporal variations of extreme rainfall and its potential driving factors for different regions.
The middle and lower reaches of the Yangtze River Basin (MLRYRB) is located in the east of China, which is one of China’s important industrial and economic centers and also one of the most vulnerable areas threatened by heavy rainfall and floods. The floods in the MLRYRB are often attributed to the frequent occurrence of extreme rainfall (Jain and Lall, 2001; Su et al., 2005; Su et al., 2009; Chen et al., 2021). The characteristics of spatiotemporal distribution of extreme rainfall can be affected by many factors, such as the changes of large-scale climate patterns (LCPs), evaporation and underlying surface conditions (Fernández-Montes et al., 2014; Wang et al., 2017; Li et al., 2021; Zhou et al., 2021). Studies on its driving factors will help to conduct better flood disaster forecasting. Among all climatic and non-climatic factors, the LCPs are considered as important factors affecting extreme rainfall, and a number of studies have been focusing on the relationships between extreme rainfall and the LCPs (Ward et al., 2016; Wi et al., 2016; Liu et al., 2020). For example, East Asian monsoon has a significant variability on interannual and interdecadal time scales in the Yangtze River Basin (YRB), and has a unique impact on precipitation (Ding & Chan, 2005). Villarini and Denniston, 2016 illustrated that ENSO (El Niño-Southern Oscillation) has a significant control effect on extreme rainfall in Australia. Limsakul and Singhruck (2016) showed that PDO (Pacific Decadal Oscillation) is an important factor affecting extreme rainfall changes in Thailand. The results of Fu et al. (2013) indicated that ENSO activities have affected China’s extreme rainfall trends and changes. Zhang (2020) and Liu et al. (2019) have shown that WPSHI (Western Pacific Subtropical High Index) is one of the important drivers of extreme rainfall in summer in eastern China. Ayala (2019) supposed that AO (Arctic Oscillation) is one of the important causes of rainfall in Puerto Rico.
Most studies have used wavelet coherence and correlation coefficient methods to understand the distant link between the LCPs and extreme rainfall. However, it should be pointed out that none of these studies ever considered the correlations among the LCPs when assessing their effects on rainfall, which might lead to misinterpretation of the teleconnection (Huang et al., 2015; Wang et al., 2021; Zhou et al., 2020a, 2020b; Shi et al., 2020). The independent relationships between extreme rainfall and climate signals at the different time scales are rarely reported. Therefore, it is very important to find out the effect of an individual LCP on rainfall. Mihanovic et al. (2009) proposed the concept of partial wavelet coherence (PWC), providing a statistical method to estimate the dependence of two variables after removing the influence of one other potentially influencing variable. Hu and Si (2021) improved the PWC method so that the improved PWC could reveal the relation of two variables after removing the influence of multiple variables. Wavelet analysis also facilitates multi-scale signal analysis. Therefore, this study aims to understand the teleconnection between a given LCP and extreme rainfall with the improved PWC and cooperate with wavelet decomposition to understand their correlation at different scales. This will help to understand the effects of the LCPs on extreme rainfall in the MLRYRB.
The purpose of this study is to explore the spatiotemporal distribution of extreme rainfall in the MLRYRB from 1960 to 2020, and to study the teleconnection between extreme rainfall and the LCPs by wavelet analysis. The improved PWC method is used to explore the teleconnection relationship between extreme rainfall and individual LCP. This study mainly focused on the following aspects: 1) to analyze the characteristics of temporal variations and spatial distributions of extreme rainfall in the MLRYRB from 1960 to 2020; 2) to use wavelet coherence analysis to explore the temporal influences of multiple LCPs on extreme rainfall; and 3) to introduce the improved PWC method to quantify the interactions between different LCPs and their impacts on extreme rainfall.
The Yangtze River is the longest and largest river in China, which originates in the Tanggula Mountains, flows through 19 provinces from west to east, and eventually flows into the East China Sea. The YRB (24–35° N, 90–122° E), with a drainage area of about 1.8 million km2, is located in the subtropical and temperate climate zones dominated by the southeast monsoon. In this study, the MLRYRB (25–34° N, 108–122° E; Figure 1) are selected as the study area. The MLRYRB is one of the important water sources and economic centers in East China. The average annual temperature is between 14 and 18°C, and the average annual precipitation is between 1,000 and 1,400 mm. Affected by factors such as subtropical monsoons and typhoons, the MLRYRB is one of China’s heavy rain-prone areas and areas with the highest flood intensity.
The meteorological data used in this study are obtained from the China Meteorological Data Service Center (http://data.cma.cn/), and there are 62 meteorological stations with the complete sequence of daily rainfall from 1960 to 2020 in the MLRYRB (Figure 1). Stations with missing data for more than 15 days were deleted, and missing data for less than 15 days were interpolated with relevant neighboring stations to ensure the consistency and completeness of rainfall data. Missing rainfall data for 1–2 days were filled in with the average values of adjacent days. In addition, missing data for consecutive days were interpolated with the long-term average of the same day in other years. To find out the impacts of climate change in the MLRYRB, the correlations between the extreme rainfall indices and the LCPs are studied. The LCPs data can be obtained from Earth System Research Laboratory of the Physical Sciences Division of the National Oceanic and Atmospheric Administration in the United States (https://www.esrl.noaa.gov/psd/data/climateindices/list/). The WPSHI data can be obtained from the National Climate Center of China Meteorological Administration (https://cmdp.ncc-cma.net/Monitoring/cn_stp_wpshp.php) (Liu et al., 2019; Zhang, 2020). The East Asia Monsoon Index (EAMI) is based on the calculation method of EAMI given by China Meteorological Administration of (http://cmdp.ncc-cma.net/Monitoring/monsoon.php). Data such as sea level pressure (SLP) and wind vector are from NCAR (Kanamitsu et al., 2002). The specific calculation process can refer to Zhu et al. (2005).
Various extreme rainfall indices are defined to better understand the changing laws of extreme rainfall, according to the World Meteorological Organization (WMO) and the fifth assessment report of Intergovernmental Panel on Climate Change (IPCC, 2013). Previous studies have made different changes to the indices given by the WMO (Zhang et al., 2011; Lestari et al., 2016; Costa et al., 2020), and this study selected seven of them for analysis (Table 1). Data quality control and homogeneity testing for extreme rainfall index calculation refer to the RClimDex package provided by CCl/CLIVAR/JCOMM Expert Team (ET) on Climate Change Detection and Indices (ETCCDI) (http://etccdi.pacificclimate.org/software.shtml).
The original Mann-Kendall (MK) method is based on the assumption of random independence of sequences, but does not take into account the errors caused by sequence correlation. Hamed and Rao (1998) added a correction factor to the original MK method, and then, Hamed (2008) and Khaliq et al. (2009) further considered the lag-1 sequence relationship. The MMK method compensates for the influence of sequence correlation on the MK statistics by modifying the MK statistics. This study uses a modified Mann-Kendall (MMK) trend test method (Mann, 1945; Kendall, 1948; Hamed and Rao, 1998) to evaluate the trend of extreme rainfall in the MLRYRB. For the specific calculation process, please refer to Khaliq et al. (2009).
Pearson correlation analysis describes the degree of closeness by analyzing the linear relationship between two variables. When the correlation coefficient value is greater than zero, the two variables are positively correlated, when the correlation coefficient is less than zero, they are negatively correlated. The absolute value of the correlation coefficient close to 1 indicates that the correlation between the two variables is significant, and the correlation coefficient value close to zero indicates that the correlation is not significant. A correlation coefficient of zero means that there is no linear relationship between the two variables.
Wavelet Transform can perform wavelet decomposition of signals on multiple scales and the wavelet transform coefficients obtained from the decomposition on each scale represent the information of the signal at different resolutions. Wavelet coherence (WTC) can extend the time series to the time-frequency space, and find the local intermittent and periodic characteristics. This can be used to evaluate the correlation of two time series in the time-frequency domain, and find the significant differences between the two time series. WTC is widely used in the fields of hydrology and meteorology (Tan et al., 2016; Nalley et al., 2019; Zhou et al., 2021). For two time series x and y, the WTC (Hudgins et al., 1993; Torrence and Compo, 1998) of the two time series can be defined as follows:
where
where
where c1 and c2 are normalization constants and
Partial wavelet coherence (PWC) evaluates the correlation between two variables in the time-frequency (time series) domain by excluding the influence of other variables. It is more similar to partial correlation analysis, but it adds wavelet coherence analysis. Compared with the usual partial correlation analysis, it can reveal the time-frequency relationship between two variables more deeply, finding the interaction in the local time-frequency space and eliminating it. The PWC can be defined as follows:
Among them, the absolute value of Ryx,z is the PWC of x and y after removing the control variables, γ is the complex wavelet coherence between the two variables, Ry,z and Rx,z are the Bivariate wavelet coherency of the two variables. A more specific calculation process can refer to Hu and Si (2021) and Aguiar-Conraria and Soares (2014). The original PWC was limited to excluding one variable. Hu and Si (2021) modified the previous PWC and developed the improved PWC. The improved PWC between y and x after excluding variables Z at scale s and location
where symbol • is the notation for excluding variables. For the calculation of
Daubechies Wavelet is a wavelet decomposition method based on continuous wavelet transform, which can decompose the oscillation modes in different frequency bands. This study decomposes the LCP signals and rainfall sequences based on the Daubechies Wavelet and discusses their correlations in different frequency bands to help understand the results of the improve PWC. The 5th order Daubechies Wavelet (db5) will decompose the object signal into 7 bands. When the decomposed frequency band is greater than 7, the signal is very weak, and when it is less than 7, it cannot reflect the situation of all frequency bands. So db5 is selected to analyze the mutual interference of extreme rainfall and the LCPs in different frequency bands (Kumar & Foufoula-Georgiou, 1993).
Climate change and human activities led to changes in extreme rainfall events in the MLRYRB. Figure 2 shows the spatial distributions of the average values of RX1day, RX3days, SDII, R90D, R95D, CWD and CDD from 1960 to 2019. In addition, the temporal and spatial variation trends of rainfall in the MLRYRB were analyzed by the MMK trend test method. It illustrates that extreme rainfall was on the rise and had obvious regional characteristics in spatial distribution. The multi-year average values of RX1day, RX3days, SDII, R90D, and R95D were 102.12, 146.25, 9.43 mm/day, 14.45 days, and 4.91 days, respectively. These highest values all appeared in the Poyang Lake basin. This might be because of the climatic characteristics of the Poyang Lake that could be easily affected by the monsoon. Since the Poyang Lake area is closer to the Pacific Ocean, the East Asian monsoon will bring a large amount of water vapor to the coastal areas. At the same time, due to the combined effect of the Western Pacific Subtropical High in summer. The rainfall and humidity increase in the areas near the coast in summer, which in turn affects the annual average rainfall value. The mean values of the MMK statistics for RX1day, RX3days, SDII, R90D, and R95D are 1.43, 1.05, 2.88, 1.32, and 1.34, respectively, showing significant upward trends. The increase in extreme rainfall has led to an upward trend in the indicator of extreme rainfall in this region. Most of the stations showing a downward trend were concentrated in areas close to the middle reaches. It might be due to that the construction of the Three Gorges Reservoir and Gezhouba Reservoir has caused changes in the climate characteristics of these areas, thereby changing the trend of extreme rainfall. The multi-year average values of CWD and CDD were 10.61 and 21.92 days, respectively. For CWD, the mainstream of the Yangtze River was almost the dividing line. The difference between the north and the south was significant. The CWD in the north of the Yangtze River was significantly lower than the average value, and the CWD in the south was significantly higher than the average value. Both CWD and CDD showed downward trends in the MLRYRB, and the average values of their MMK statistics were −1.01 and −1.33, respectively. In the lower reaches of the Poyang Lake, the CWD showed an upward trend, almost overlapping with areas where extreme rainfall was significantly higher than the average value. In other regions, the CWD showed a downward trend. For CDD, upward trends could only be found in the southwestern part.
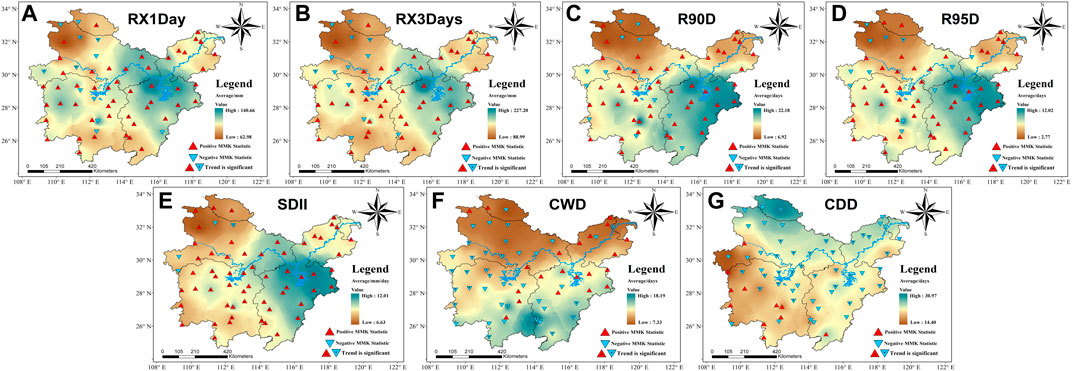
FIGURE 2. The trends and mean values of RX1day, RX3days, SDII, R90D, R95D, CWD and CDD across the MLRYRB.
Figure 3 shows the MMK trend test results of RX1day, RX3days, SDII, R90D, R95D, CWD and CDD from 1960 to 2019. In general, the results show a clear trend of increasing extreme rainfall in the MLRYRB over the past 60 years with five extreme rainfall indices (RX1day, RX3days, SDII, R90D, R95D) showing a clear upward trend. RX1day and RX3days fluctuated before 1990 and rose steadily after 1990, while R90D, R95D, SDII showed an increasing trend after 1970. RX1day, RX3days, R95D and SDII were mutated around 1990, while the mutation point of R90D was concentrated during 1970–1980. There were clear downward trends in CWD and CDD and no obvious mutation point could be found.
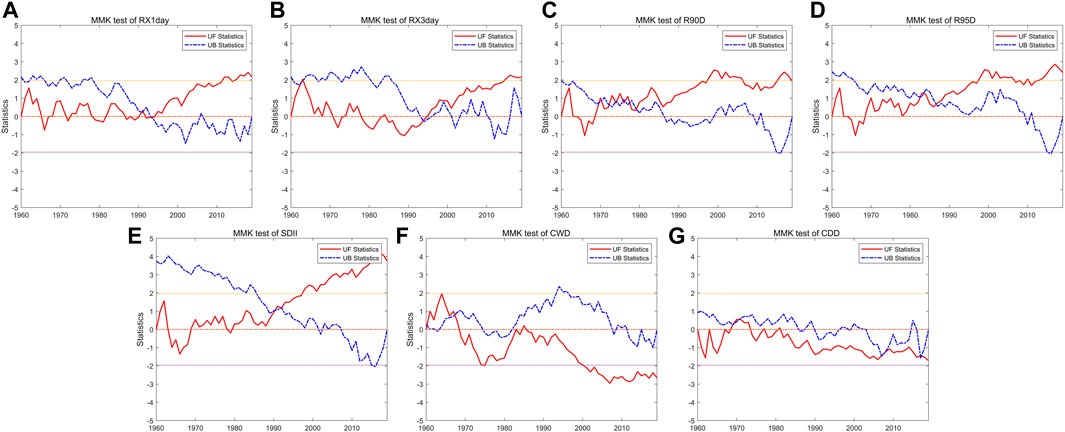
FIGURE 3. The MMK trend test results of RX1day, RX3days, SDII, R90D, R95D, CWD and CDD from 1960 to 2019.
To explore the correlations between extreme rainfall and the LCPs, Pearson correlation analysis was used for a preliminary analysis. Figure 4 shows the Pearson correlation coefficients between extreme rainfall indices and the LCPs, and the asterisk represents significant at the 95% confidence level. The results show that WPSHI, which had significant positive and the highest correlation with extreme rainfall. Most of the correlation coefficients between WPSHI and extreme rainfall indices exceed 0.3. Both ENSO and PDO had significant negative correlations with extreme rainfall and the correlation between PDO and extreme rainfall is slightly higher than ENSO. In comparison, EAMI and extreme rainfall also had a negative correlation, but the correlation coefficient and significance were lower. Among them, the correlation coefficients of WPSHI and PDO with 5 extreme rainfall indices all passed the 95% confidence level test. WPSHI and PDO had the largest correlations with extreme rainfall, followed by EAMI and ENSO, and AO had the smallest correlation with extreme rainfall. The correlation coefficients of CWD and CDD with extreme rainfall were low and failed the significance test, indicating that CWD and CDD were less relevant to the LCPs. In general, SDII, R90D, R95D, RX1day and RX3days had relatively consistent responses to the LCPs, but were significantly different from CWD and CDD.
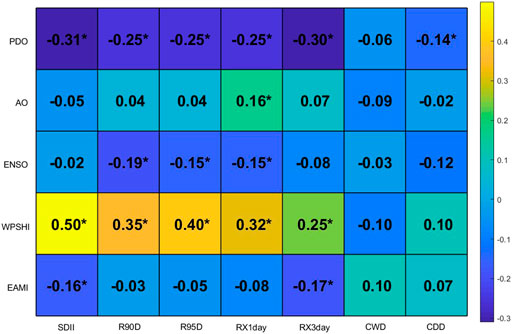
FIGURE 4. Pearson correlation coefficients between extreme rainfall indices and the LCPs. Note: the asterisk represents significant at the 95% confidence level.
The LCPs can directly or indirectly affect the occurrence and change of extreme rainfall, and are closely related to extreme rainfall. Exploring the teleconnection relationships between the LCPs and extreme rainfall helps to find out the response of extreme rainfall to changes in the LCPs, which is of great significance to extreme rainfall prediction. The previous section has shown the results of the Pearson correlation analysis between the LCPs and extreme rainfall. WTC was further used to find out the responses of extreme rainfall to the LCPs and their resonant frequencies and phase shifts in the time-frequency domain. Results with less relevance were not listed. Therefore, Figure 5 only presents the WTC analysis results between five selected extreme rainfall indices (i.e., SDII, R90D, R95D, RX1day, and RX3days) and four LCPs (i.e., WPSHI, EAMI, ENSO and PDO). The color bar represents the energy density, and the 95% confidence level of the red noise is shown as a thick outline. The relative phase relationship is expressed as an arrow (i.e., the opposite phase points to the left, and the same phase points to the right).
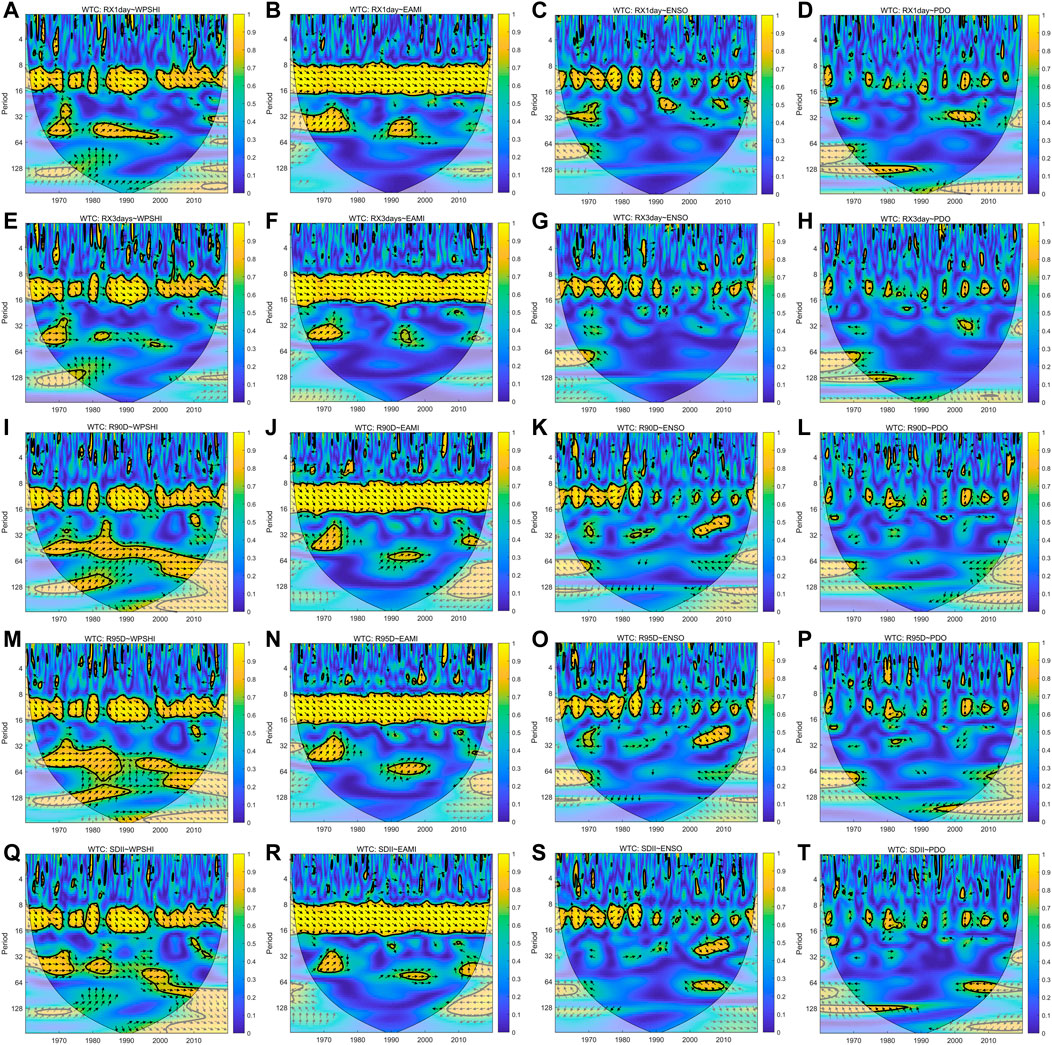
FIGURE 5. Wavelet coherence analysis results between the five selected extreme rainfall indices and four LCPs (i.e., WPSHI, EAMI, ENSO, and PDO).
In general, from the perspective of wavelet spectrum, the periodic correlations between WPSHI, EAMI and extreme rainfall were obvious, and the periodic signals of ENSO and extreme rainfall were significantly different for the periods before and after 2000. Although the correlation coefficient between PDO and extreme rainfall was high, the periodic signals were not significant. For WPSHI, it had a periodical signal of 8–16 months with RX1day, RX3days, R90D, and R95D, and the discontinuities were around 1975-1985 and 1995. WPSHI also had a periodical signal of about 32–64 months with RX1day and RX3days around 1970 and 1980-2000; however, the periodical signal around 1980-2000 was relatively weak for RX3days. The signal performances of WPSHI with R90D and R95D were similar, both having a periodical signal of 32–120 months from 1965 to 2019. The only difference was that the 32–64 months signal of WPSHI with R95D was interrupted around 1990. The signal performance of WPSHI with SDII was similar to that of WPSHI with R95D, but the signal period was shorter in the period of 32–64 months. For EAMI, the performance of different extreme rainfall indices was basically the same. All had 8–16 months of continuous uninterrupted periodic signals, 32 months periodic signals during 1970–1980, and 32–64 months periodic signals during 1990–2000. There were subtle differences in signal strength and duration between different extreme rainfall indicators.
ENSO had a negative correlation with extreme rainfall before 2000, but a positive correlation after 2000. The change in the positive-negative phase may be caused by the phase transition of ENSO around 2000. The periodical relationships of ENSO with the extreme rainfall indices were not as good as that of WPSHI. The difference was that, before 1990, there was a continuous cycle of 8–16 months between ENSO and extreme rainfall. After 1990, there were still some intermittent signals in the 8–16 months cycle, but the significant area of the signal decreased significantly. ENSO had periodical signals of about 20 months with RX1day around 1990-1995, 16–32 months with R90D, R95D, and SDII around 2000-2010, and 64 months with SDII around 2000-2020. Similar to ENSO, the relationships between PDO and the extreme rainfall indices were not as good as that of WPSHI. There was no long-term continuous signal between PDO and the extreme rainfall indices. PDO had significantly more periodical signals of 8–16 months with RX1day and RX3days after 1990, and 32 months periodical signals around 2000-2005. Moreover, the performance of PDO and the other 3 extreme rainfall indices (R90D, R95D, and SDII) did not change significantly.
Overall, it can be considered that WPSHI and EAMI had a major impact on extreme rainfall. The periodic relationships between the LCPs and extreme rainfall were not significant and had no obvious regularity in the periodic region of less than 8 months. During the 8–16 months cycle, EAMI played a leading role. In the cycles more than 32 months, different LCPs had different signal regions and less overlapping parts; however, the periodic relationship between WPSHI and extreme rainfall was significant.
In most cases, the impacts on rainfall are the results of the interaction among multiple LCPs; however, different LCPs may interfere with each other (Hu et al., 2017; Nalley et al., 2019; Su et al., 2019). Improved PWC can exclude multiple other influencing factors, and then find the main influencing factors. In this study, to explore the time domain of the impact of a single LCP on extreme rainfall, four LCPs with the greatest impacts on extreme rainfall of the MLRYRB were screened. For each LCP, PWC was used to eliminate the interaction of the other three LCPs (Figure 6). Table 2 shows the proportional change of the significant area in the cone region before and after the use of PWC, which is used to assist the judgment of the PWC results.
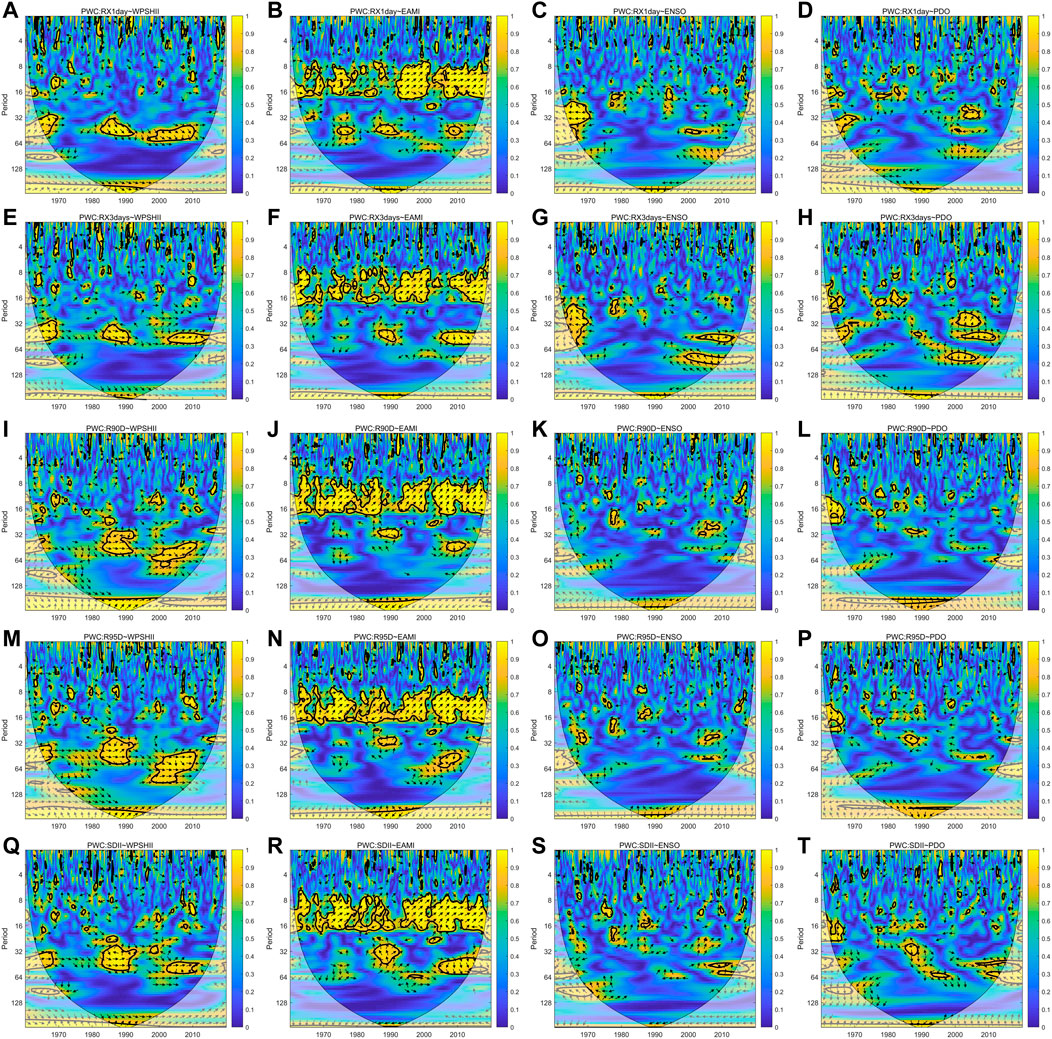
FIGURE 6. Partial wavelet coherence analysis results between a single LCP and extreme rainfall after removing other three LCPs impact.
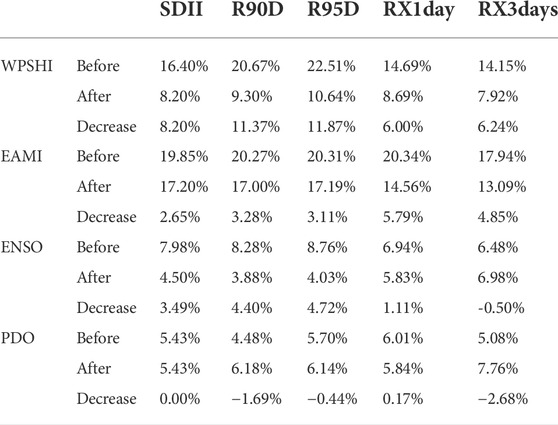
TABLE 2. Significant area changes in the partial wavelet coherence map before and after using improved PWC.
For WPSHI, the influence of the other three LCPs is eliminated. The continuous periodicity of WPSHI and extreme rainfall in the WTC disappeared, and the signals in the 16–128 months cycle were also significantly weakened, and the proportion of significant areas decreased by 6–11%. The continuous signal in the 8–16 months cycle disappeared completely, and the periodic signal in the 16–64 months cycle was also split into shorter cycles. The performance of different extreme rainfall indices on WPSHI was relatively consistent. For EAMI, the WTC results are similar to the PWC results. Although there was a decrease in signal continuity after using PWC, a continuous periodic signal in the 8–16 months cycle could still be found. There was a relatively small annual change in the medium and long periods other than 8–16 months, and the area of significant areas decreased by 2–5%. The areas with significant decrease in the signal area from 8 to 16 months were concentrated between 1980 and 1990 and around 2005, and the performance of different extreme rainfall indicators was basically the same. In the 16–64 months cycle, the 1970-1980 signal weakened and the 1990-2000 signal shifted to around 2010. The signal between ENSO and extreme rainfall indicators was significantly weakened after using the PWC, with a significant area reduction of about 4%. However, relationship between ENSO and RX1Day (as well as RX3Days) increased the signal at the edges of the impact cone, which were concentrated in 16–32 months. The long-period continuous signal almost completely disappeared, leaving only scattered small period signals. Most of these 16–32 months small period signals were concentrated around 1980 and 2005. The performance of PDO is abnormal. After using PWC, the area of the significant region was basically the same as that of WTC or slightly increased. However, the position of the significant area had great changes. The short 8–16 months cycle basically disappeared and was replaced by the longer 32–64 months cycle, which was distributed around 2000.
WPSHI and EAMI both played important roles in the periodicity impact of extreme rainfall in the MLRYRB. Since the MLRYRB is located in the area affected by East Asian monsoon, EAMI has maintained a relatively consistent oscillation cycle of about 1 year. After the use of PWC, the periodic effect of WPSHI on extreme rainfall has changed greatly, indicating that the performance of WPSHI would be affected by other LCPs.
In previous section, correlations between extreme rainfall and the LCPs were analyzed with WTC and improved PWC. At different times and frequency bands, there were different relationships and oscillation periods. To further understand these results, we used db5 wavelet to reconstruct extreme rainfall and the LCPs in different frequency bands. The reconstruction included 7 frequency bands, i.e., 0-2, 2-4, 4-8, 8-16, 16-32, 32-64, and 64–128 months. Taking SDII as an example, Figure 7 shows the reconstruction of SDII and four LCPs (i.e., ENSO, WPSHI, PDO and AO) based on wavelet coefficients. Table 3 shows the correlation coefficients of extreme rainfall and the LCPs in different frequency bands. The correlation coefficients in bold indicated that they could pass the 95% significance test.
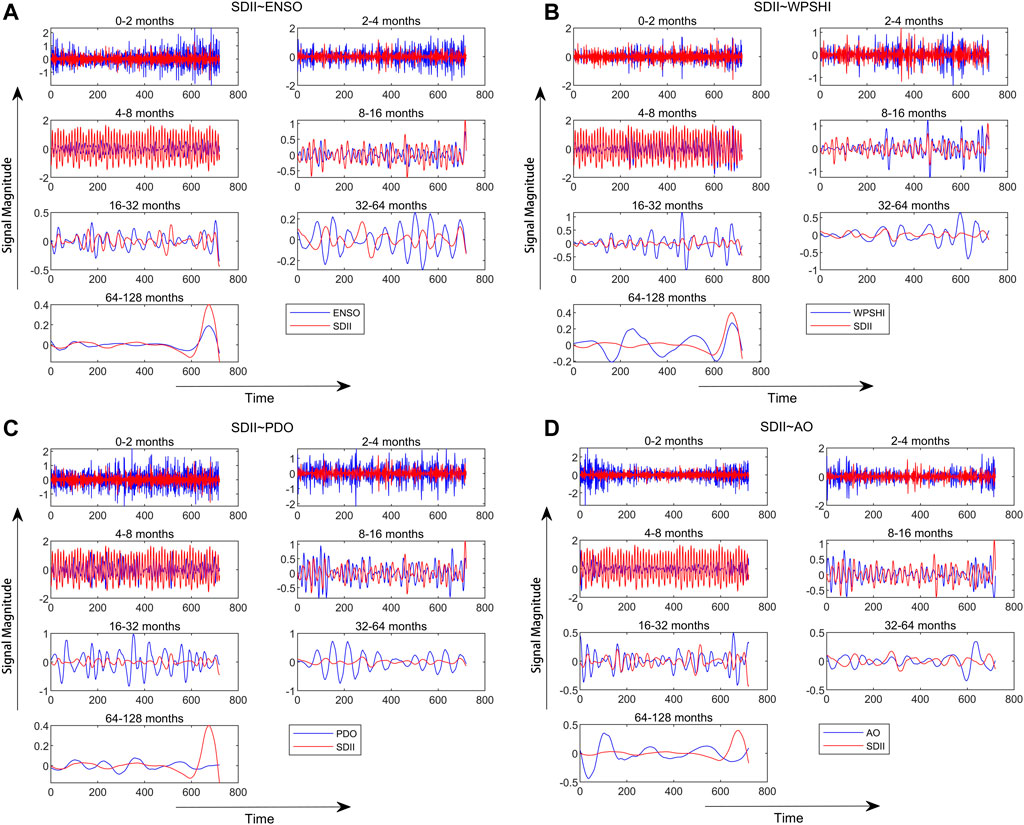
FIGURE 7. Wavelet reconstruction of SDII and the LCPs (i.e., ENSO, WPSHI, PDO and AO) in different frequency bands.
WPSHI was positively correlated with extreme rainfall in all frequency bands, while other LCPs had either positive or negative correlations with extreme rainfall in different frequency bands. The correlation between EAMI and extreme rainfall was mainly reflected in the 4–32 months, of which the correlation coefficients of the 4-8 and 8–16 months frequency bands both exceeded 0.5. Although the correlation of the 16–32 months frequency band was significant, the correlation coefficient was lower. PDO was positively correlated in the 0–2 months and 8–16 months frequency bands, and significantly negatively correlated in other frequency bands. ENSO was negatively correlated between 0-8 months and 32–64 months, but positively correlated in other frequency bands. The wavelet reconstruction again proved that AO had no significant effect on extreme rainfall in the MLRYRB.
In the frequency band of 0–4 months, the correlations between extreme rainfall and the LCPs were basically insignificant. In the 4–16 months band, the combined effect of WPSHI and EAMI was considered as the main driver. In the frequency band of 16–32 months, the main influencing factors were WPSHI and PDO. In the frequency band of 32–64 months, the effect of EAMI on extreme rainfall disappeared significantly, while the effects of other LCPs on extreme rainfall were all significant. In the 64–128 months frequency band, the signal strength began to weaken due to the characteristics of the db5 wavelet, so the correlation was very high. The reconstruction analysis results after wavelet decomposition were basically consistent with those of WTC and improved PWC. In the low frequency region (4–16 months), EAMI and WPSHI had the greatest correlations with extreme rainfall, and the correlation coefficient between EAMI and extreme rainfall was higher than that of WPSHI. For other LCPs, ENSO and PDO had some impacts on rainfall peaks in the 8–32 months band, but less on rainfall frequency and duration. In the frequency band over 32 months, ENSO and PDO had high correlations with the frequency and duration of extreme rainfall, possibly related to their long-term periodic oscillations.
Through the analysis of different frequency bands, it is found that there was a certain resonance period between the extreme rainfall indices and the LCPs. However, there were obvious differences in different time domains (Cheng et al., 2019; Yang and Li, 2020). These observations confirmed the complex nonlinear relationships between extreme rainfall and the LCPs. The influence of AO on extreme rainfall in the MLRYRB was almost negligible, while WPSHI and EAMI had great effects on extreme rainfall. These findings were consistent with the previous PWC results.
The intergenerational variation of the LCPs had important impacts on the climate of the MLRYRB. Cross wavelet and partial wavelet correlations were used to analyze the relationships between extreme rainfall and the LCPs. The results show that even though the correlation coefficient between EAMI and extreme rainfall was not significant, there was a clear periodic correlation. At the scale of 8–16 months, EAMI and WPSHI had significant and stable cyclical effects on extreme rainfall. For ENSO, although the correlation coefficient could pass the significance test, the periodic impact of ENSO on extreme rainfall around 1990 had a completely different performance. The results of the MK test also showed that most of the extreme rainfall indicators produced significant variation points around 1990 and corresponded to the results of WTC and PWC, confirming that the LCPs are indeed important factors affecting regional extreme rainfall.
The correlation between WPSHI and extreme rainfall changed greatly around 1990, and it is currently believed that WPSHI had a 2–3-year and around 5-year periodic oscillation before 1990. After 1990, the oscillation period was shortened from a quasi-5-year period to a 2–3-year oscillation (Gao et al., 2014; Huang et al., 2018, 2020). Therefore, the periodic signal on the 32–64 months scale around 1990 which could be seen in the WTC results was significantly weakened. The relationship between ENSO and extreme rainfall changed greatly around 1990. In the WTC results, ENSO and extreme rainfall also had a relatively stable periodic correlation of about 1 year before 1990. In contrast, after 1990, the correlations for the 1-year period or so weakened sharply, while the significance on the 32 months scale increased. The weakened signal of ENSO and extreme rainfall may be due to the change in the pattern of WPSHI, leading to the change in the correlation between ENSO and extreme rainfall around 1990. Around 1990, WPSHI significantly weakened and shifted. The change of WPSHI affected the interannual oscillation of ENSO, and ENSO had a phase change around 1990. So, after 1990 the periodic signal of ENSO and extreme rainfall changed into a higher frequency band but decreased the intensity. Combined with the PWC results, the effects of ENSO on extreme rainfall were coupled with WPSHI.
The advance and retreat of East Asian monsoon had significant correlations with the passage of the rainband and would have significant impacts on the rainfall of the MLRYRB together with WPSHI (Liu et al., 2013; Xu et al., 2021). In the WTC and PWC results, EAMI maintained a period of about 1 year on extreme rainfall, which corresponded to the inter-annual variation of East Asian monsoon. It significantly affected the rainy season of the MLRYRB from May to August and each annual cycle had a 10–20 weeks oscillation so EAMI and extreme rainfall in both WTC and PWC had a stable 8–16 months cycle correlation. The anomaly of East Asian monsoon would affect the drought and flood conditions in the MLRYRB so there would be scattered periodic signals in the 32–64 months frequency band.
The effects of WPSHI and EAMI on extreme rainfall were reflected at different signal scales. In the PWC results, the relationship between WPSHI and extreme rainfall completely disappeared at 8–16 months after excluding other LCPs, and other significant signals were found on the 32–64 months scale. This is consistent with the WPSHI’s own oscillation cycle of about 5 years, which confirmed the correctness of the PWC. In a cycle of about 1 year, the annual change and intensity of EAMI were the main factors affecting the rainfall of the MLRYRB (Li et al., 1991; Ding, 1992). WPSHI and EAMI could influence each other in summer, leading to the 8–16 months period of WPSHI in the WTC and the small-scale signal discontinuity of 8–16 months of EAMI in the PWC. So, it is considered that EAMI had the greatest impact on extreme rainfall in the 8–16 months cycle, while WPSHI played a major role in the 32–64 months cycle. ENSO and PDO had significant correlations with extreme rainfall; however, the PWC results suggested that the interannual oscillations of ENSO and PDO had no longer-term periodic effects on extreme rainfall. PDO and ENSO had certain coupling effects with WPSHI and EAMI in summer, when extreme rainfall was most likely to occur (Chan and Zhou, 2005; Matsumura and Horinouchi, 2016). Considering the results of wavelet reconstruction, the correlations between ENSO, PDO and extreme rainfall may come from the abnormal performances of ENSO and PDO.
A detailed understanding of the changing laws and driving factors of extreme rainfall is of great significance for future rainfall prediction and its corresponding response. This study used 7 extreme rainfall indices to examine the 60-year rainfall time series of the MLRYRB. Improved PWC was introduced to explore the correlations between extreme rainfall and the LCPs for the first time, which provided new ideas for subsequent extreme rainfall studies. The main findings of this study are summarized as follows:
1) The extreme rainfall in most areas of the MLRYRB was increasing, and the extreme values were mostly concentrated in the Poyang Lake area. A simple correlation analysis indicated that extreme rainfall had significant correlations with WPSHI, EAMI, ENSO, and PDO.
2) Analyzing the cyclical correlations between the LCPs and extreme rainfall using the WTC, the intergenerational variation of the LCPs had a significant impact on extreme rainfall in the MLRYRB. Even though the correlation coefficient between EAMI and extreme rainfall was not significant, EAMI had strong periodic impacts on extreme rainfall. On the 8–16 months scale, EAMI and WPSHI both had significant and stable periodic effects on extreme rainfall.
3) After the WTC analysis, the improved PWC was used to explore the influence of a single LCP on extreme rainfall after excluding other LCPs, and the WTC and PWC results were confirmed by wavelet decomposition. Using the improved PWC, it is found that the impact of WPSHI on extreme rainfall was mainly concentrated on the 32–64 months scale, and the impact of EAMI was mainly concentrated on the 8–16 months scale. There was a coupling between EAMI and WPSHI in the 1-year cycle. ENSO and PDO had no significant periodic effects on extreme rainfall, and the abnormal effects of ENSO or PDO would have greater impacts on extreme rainfall.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Conceptualization: SL, JC, and HS. Methodology: YW, HS, and ZZ. Formal analysis: YW. Validation: YW and ZZ. Supervision: HS and SL. Writing—original draft: YW. Writing—review and editing: HS, SL, and JC. Funding Acquisition: HS.
This study was supported by the National Natural Science Foundation of China (Grant No. 51909117), Natural Science Foundation of Shenzhen (JCYJ20210324105014039), Guangdong Provincial Key Laboratory of Soil and Groundwater Pollution Control (2017B030301012), and State Environmental Protection Key Laboratory of Integrated Surface Water-Groundwater Pollution Control.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Agilan, V., Umamahesh, N. V., and Mujumdar, P. P. (2021). Influence of threshold selection in modeling peaks over threshold based nonstationary extreme rainfall series. J. Hydrology 593, 125625. doi:10.1016/j.jhydrol.2020.125625
Aguiar-Conraria, L., and Soares, M. J. (2014). The continuous wavelet transform: moving beyond uni-and bivariate analysis. J. Econ. Surv. 28, 344–375. doi:10.1111/joes.12012
Ashcroft, L., Karoly, D. J., and Dowdy, A. J. (2019). Historical extreme rainfall events in southeastern Australia. Weather Clim. Extrem. 25, 100210. doi:10.1016/j.wace.2019.100210
Ayala, J. J. H. (2019). Atmospheric teleconnections and their effects on the annual and seasonal rainfall climatology of Puerto Rico. Theor. Appl. Climatol. 137 (3), 2915–2925. doi:10.1007/s00704-019-02774-3
Chan, J. C. L., and Zhou, W. (2005). PDO, ENSO and the early summer monsoon rainfall over south China. Geophys. Res. Lett. 32 (8), L08810. doi:10.1029/2004gl022015
Chang, C. P., Lei, Y., Sui, C. H., Lin, X., and Ren, F. (2012). Tropical cyclone and extreme rainfall trends in East Asian summer monsoon since mid-20th century. Geophys. Res. Lett. 39 (18), L18702. doi:10.1029/2012gl052945
Chen, Z., Zeng, Y., Shen, G., Xiao, C., Xu, L., and Chen, N. (2021). Spatiotemporal characteristics and estimates of extreme precipitation in the Yangtze River Basin using GLDAS data. Int. J. Climatol. 41, E1812–E1830. doi:10.1002/joc.6813
Cheng, Q., Gao, L., Zuo, X., and Zhong, F. (2019). Statistical analyses of spatial and temporal variabilities in total, daytime, and nighttime precipitation indices and of extreme dry/wet association with large-scale circulations of Southwest China, 1961–2016. Atmospheric Res. 219, 166–182. doi:10.1016/j.atmosres.2018.12.033
Costa, R. L., Baptista, G. M. D., Gomes, H. B., Silva, F. D. D., da Rocha, R. L., Salvador, M. D., et al. (2020). Analysis of climate extremes indices over northeast Brazil from 1961 to 2014. Weather Clim. Extrem. 28, 100254. doi:10.1016/j.wace.2020.100254
Ding, Y. H., and Chan, J. C. (2005). the East asian summer monsoon: an overview. Meteorol. Atmos. Phys. 89 (1), 117–142. doi:10.1007/s00703-005-0125-z
Ding, Y. (1992). Summer monsoon rainfalls in China. J. Meteorological Soc. Jpn. 70 (1B), 373–396. doi:10.2151/jmsj1965.70.1b_373
Fagnant, C., Gori, A., Sebastian, A., Bedient, P. B., and Ensor, K. B. (2020). Characterizing spatiotemporal trends in extreme precipitation in Southeast Texas. Nat. Hazards (Dordr). 104 (2), 1597–1621. doi:10.1007/s11069-020-04235-x
Fernández-Montes, S., Seubert, S., Rodrigo, F. S., Álvarez, D. R., Hertig, E., Esteban, P., et al. (2014). Circulation types and extreme precipitation days in the Iberian Peninsula in the transition seasons: Spatial links and temporal changes. Atmos. Res. 138, 41–58. doi:10.1016/j.atmosres.2013.10.018
Fu, G. B., Yu, J. J., Yu, X. B., Ouyang, R. L., Zhang, Y. C., Wang, P., et al. (2013). Temporal variation of extreme rainfall events in China, 1961–2009. J. Hydrology 487, 48–59. doi:10.1016/j.jhydrol.2013.02.021
Gao, H., Jiang, W., and Li, W. (2014). Changed relationships between the East Asian summer monsoon circulations and the summer rainfall in eastern China. J. Meteorol. Res. 28 (6), 1075–1084. doi:10.1007/s13351-014-4327-5
Grimm, A. M., and Tedeschi, R. G. (2008). ENSO and extreme rainfall events in South America. J. Clim. 22 (7), 1589–1609. doi:10.1175/2008jcli2429.1
Grinsted, A., Moore, J. C., and Jevrejeva, S. (2004). Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear process. geophys. 11 (5-6), 561–566. doi:10.5194/npg-11-561-2004
Hamed, K. H., and Rao, A. R. (1998). A modified Mann-Kendall trend test for auto-correlated data. J. Hydrology 204 (1-4), 182–196. doi:10.1016/s0022-1694(97)00125-x
Hamed, K. H. (2008). Trend detection in hydrologic data: the mann–kendall trend test under the scaling hypothesis. J. Hydrology 349 (3-4), 350–363. doi:10.1016/j.jhydrol.2007.11.009
Hu, W., Si, B. C., Biswas, A., and Chau, H. W. (2017). Temporally stable patterns but seasonal dependent controls of soil water content: Evidence from wavelet analyses. Hydrol. Process. 31, 3697–3707. doi:10.1002/hyp.11289
Hu, W., and Si, B. C. (2020). Matlab code for multiple wavelet coherence and partial wavelet coherency. doi:10.6084/m9.figshare.13031123.v4
Hu, W., and Si, B. C. (2021). Technical Note: Improved partial wavelet coherency for understanding scale-specific and localized bivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 25, 321–331. doi:10.5194/hess-25-321-2021
Huang, S. Z., Huang, Q., Chang, J. X., Zhu, Y. L., Leng, G. Y., and Xing, L. (2015). Drought structure based on a nonparametric multivariate standardized drought index across the Yellow River basin, China. J. Hydrology 530, 127–136. doi:10.1016/j.jhydrol.2015.09.042
Huang, Y., Wang, B., Li, X., and Wang, H. (2018). Changes in the influence of the Western Pacific subtropical high on Asian summer monsoon rainfall in the late 1990s. Clim. Dyn. 51 (1), 443–455. doi:10.1007/s00382-017-3933-1
Huang, Z., Zhang, W., Geng, X., and Jin, F. F. (2020). Recent shift in the state of the Western Pacific subtropical high due to ENSO change. J. Clim. 33 (1), 229–241. doi:10.1175/jcli-d-18-0873.1
Hudgins, L., Friehe, C. A., and Mayer, M. E. (1993). Wavelet transforms and atmopsheric turbulence. Phys. Rev. Lett. 71 (20), 3279–3282. doi:10.1103/physrevlett.71.3279
IPCC (2013). Summary for policymakers. Climate change 2013: The physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental Panel on climate change.
Jain, S., and Lall, U. (2001). Floods in a changing climate: Does the past represent the future? Water Resour. Res. 37 (12), 3193–3205. doi:10.1029/2001wr000495
Kanamitsu, M., Ebisuzaki, W., Woollen, J., Yang, S. K., Hnilo, J. J., Fiorino, M., et al. (2002). NCEP–DOE AMIP-II reanalysis (R-2). Bull. Am. Meteorological Soc. 83 (11), 1631–1643. doi:10.1175/bams-83-11-1631(2002)083<1631:nar>2.3.co;2
Khaliq, M. N., Ouarda, T. B. M. J., and Gachon, P. (2009). Identification of temporal trends in annual and seasonal low flows occurring in Canadian rivers: The effect of short-and long-term persistence. J. Hydrology 369 (1-2), 183–197. doi:10.1016/j.jhydrol.2009.02.045
Kumar, P., and Foufoula-Georgiou, E. (1993). A multicomponent decomposition of spatial rainfall fields: 1. Segregation of large- and small-scale features using wavelet transforms. Water Resour. Res. 29 (8), 2515–2532. doi:10.1029/93wr00548
Lestari, S., Hamada, J. I., Syamsudin, F., Sunaryo,, , Matsumoto, J., and Yamanaka, M. D. (2016). ENSO influences on rainfall extremes around sulawesi and maluku islands in the eastern Indonesian maritime continent. Sola 12, 37–41. doi:10.2151/sola.2016-008
Li, X. D., Dong, H. N., Wu, W., and Yan, J. P. (1991). The activity law of the East Asian monsoon and its difference from the South Asian monsoon. J. Northwest Normal Univ. Nat. Sci. Ed. 27 (4), 5. doi:10.16783/j.cnki.nwnuz.1991.04.019 (In Chinese).
Li, X., Zhang, K., Gu, P., Feng, H., Yin, Y., Chen, W., et al. (2021). Changes in precipitation extremes in the Yangtze River Basin during 1960–2019 and the association with global warming, ENSO, and local effects. Sci. Total Environ. 760, 144244. doi:10.1016/j.scitotenv.2020.144244
Limsakul, A., and Singhruck, P. (2016). Long-term trends and variability of total and extreme precipitation in Thailand. Atmos. Res. 169, 301–317. doi:10.1016/j.atmosres.2015.10.015
Liu, S. N., and Shi, H. Y. (2019). A recursive approach to long-term prediction of monthly precipitation using genetic programming. Water Resour. manage. 33 (3), 1103–1121. doi:10.1007/s11269-018-2169-0
Liu, S. N., Shi, H. Y., and Sivakumar, B. (2020). Socioeconomic drought under growing population and changing climate: A new index considering the resilience of a regional water resources system. J. Geophys. Res. Atmos. 125 (15), e2020JD033005. doi:10.1029/2020jd033005
Liu, Y., Ding, Y., Gao, H., and Li, W. (2013). Tropospheric biennial oscillation of the Western Pacific subtropical high and its relationships with the tropical SST and atmospheric circulation anomalies. Chin. Sci. Bull. 58 (30), 3664–3672. doi:10.1007/s11434-013-5854-7
Liu, Y. Y., Liang, P., and Sun, Y. (2019). The asian summer monsoon: characteristics, variability, teleconnections and projection. Cambridge, MA: Elsevier, p237.
Liu, Z. Y., Zhang, X., and Fang, R. H. (2018). Multi-scale linkages of winter drought variability to ENSO and the arctic oscillation: A case study in shaanxi, north China. Atmos. Res. 200, 117–125. doi:10.1016/j.atmosres.2017.10.012
Mann, H. B. (1945). Nonparametric tests against trend. Econometrica 13 (3), 245–259. doi:10.2307/1907187
Matsumura, S., and Horinouchi, T. (2016). Pacific Ocean decadal forcing of long-term changes in the Western Pacific subtropical high. Sci. Rep. 6, 37765. doi:10.1038/srep37765
Mihanovic, H., Orlie, M., and Pasaria, Z. (2009). Diurnal thermocline oscillations driven by tidal flow around an island in the Middle Adriatic. J. Mar. Syst. 78, S157–S168. doi:10.1016/j.jmarsys.2009.01.021
Nalley, D., Adamowski, J., Biswas, A., Gharabaghi, B., and Hu, W. (2019). A multiscale and multivariate analysis of precipitation and streamflow variability in relation to ENSO, NAO and PDO. J. Hydrology 574, 288–307. doi:10.1016/j.jhydrol.2019.04.024
Ndlovu, M., Clulow, A. D., Savage, M. J., Nhamo, L., Magidi, J., and Mabhaudhi, T. (2021). An assessment of the impacts of climate variability and change in KwaZulu-natal province, south Africa. Atmosphere 12 (4), 427. doi:10.3390/atmos12040427
Rao, G. V., Reddy, K. V., Srinivasan, R., Sridhar, V., Umamahesh, N. V., and Pratap, D. (2020). Spatio-temporal analysis of rainfall extremes in the flood-prone Nagavali and Vamsadhara Basins in eastern India. Weather Clim. Extrem. 29, 100265. doi:10.1016/j.wace.2020.100265
Shi, H. Y., Chen, J., Li, T. J., and Wang, G. Q. (2020). A new method for estimation of spatially distributed rainfall through merging satellite observations, raingauge records, and terrain digital elevation model data. J. Hydro-environment Res. 28, 1–14. doi:10.1016/j.jher.2017.10.006
Shi, H. Y., Li, T. J., Wei, J. H., Fu, W., and Wang, G. Q. (2016). Spatial and temporal characteristics of precipitation over the Three-River Headwaters region during 1961-2014. J. Hydrology Regional Stud. 6, 52–65. doi:10.1016/j.ejrh.2016.03.001
Sridhar, V., Jin, X., and Jaksa, W. T. A. (2013). Explaining the hydroclimatic variability and change in the Salmon River basin. Clim. Dyn. 40 (7-8), 1921–1937. doi:10.1007/s00382-012-1467-0
Su, B., Kundzewicz, Z. W., and Jiang, T. (2009). Simulation of extreme precipitation over the Yangtze River basin using wakeby distribution. Theor. Appl. Climatol. 96 (3), 209–219. doi:10.1007/s00704-008-0025-5
Su, B., Xiao, B., Zhu, D., and Jiang, T. (2005). Trends in frequency of precipitation extremes in the Yangtze River basin, China: 1960–2003. Hydrological Sci. J. 50 (3), 479–492.
Su, L., Miao, C., Duan, Q., Lei, X., and Li, H. (2019). Multiple wavelet coherence of world’s large rivers with meteorological factors and ocean signals. J. Geophys. Res. Atmos. 124, 4932–4954. doi:10.1029/2018jd029842
Swain, M., Sinha, P., Mohanty, U. C., and Pattnaik, S. (2019). Dominant large-scale parameters responsible for diverse extreme rainfall events over vulnerable Odisha state in India. Clim. Dyn. 53 (11), 6629–6644. doi:10.1007/s00382-019-04949-0
Syafrina, A. H., Zalina, M. D., and Juneng, L. (2015). Historical trend of hourly extreme rainfall in Peninsular Malaysia. Theor. Appl. Climatol. 120 (1), 259–285. doi:10.1007/s00704-014-1145-8
Tan, X., Gan, T. Y., and Shao, D. (2016). Wavelet analysis of precipitation extremes over Canadian ecoregions and teleconnections to large-scale climate anomalies. J. Geophys. Res. Atmos. 121, 14469–14486. doi:10.1002/2016jd025533
Teegavarapu, R. S. (2012). Floods in a changing climate: extreme precipitation. Cambridge University Press.
Tong, R., Sun, W., Han, Q., Yu, J., and Tian, Z. (2020). Spatial and temporal variations in extreme precipitation and temperature events in the beijing–tianjin–hebei region of China over the past six decades. Sustainability 12 (4), 1415. doi:10.3390/su12041415
Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79 (1), 61–78. doi:10.1175/1520-0477(1998)079<0061:apgtwa>2.0.co;2
Villarini, G., and Denniston, R. F. (2016). Contribution of tropical cyclones to extreme rainfall in Australia. Int. J. Climatol. 36 (2), 1019–1025. doi:10.1002/joc.4393
Wang, C., Ren, X., and Li, Y. (2017). Analysis of extreme precipitation characteristics in low mountain areas based on three-dimensional copulas—taking kuandian county as an example. Theor. Appl. Climatol. 128 (1-2), 169–179. doi:10.1007/s00704-015-1692-7
Wang, L. Y., Chen, S. F., Zhu, W. B., Ren, H., Zhang, L. J., and Zhu, L. Q. (2021). Spatiotemporal variations of extreme precipitation and its potential driving factors in China’s North-South Transition Zone during 1960–2017. Atmospheric Res. 252, 105429. doi:10.1016/j.atmosres.2020.105429
Ward, P. J., Kummu, M., and Lall, U. (2016). Flood frequencies and durations and their response to el Niño southern oscillation: Global analysis. J. Hydrology 539, 358–378. doi:10.1016/j.jhydrol.2016.05.045
Weldegerima, T. M., Zeleke, T. T., Birhanu, B. S., Zaitchik, B. F., and Fetene, Z. A. (2018). Analysis of rainfall trends and its relationship with SST signals in the Lake Tana Basin, Ethiopia. Adv. Meteorology 2018, 1–10. doi:10.1155/2018/5869010
Wi, S., Valdés, J. B., Steinschneider, S., and Kim, T. W. (2016). Non-stationary frequency analysis of extreme precipitation in South Korea using peaks-over-threshold and annual maxima. Stoch. Environ. Res. Risk Assess. 30 (2), 583–606. doi:10.1007/s00477-015-1180-8
Xu, B., Chen, H., Gao, C., Zeng, G., and Huang, Q. (2021). Abnormal change in spring snowmelt over Eurasia and its linkage to the East Asian summer monsoon: The hydrological effect of snow cover. Front. Earth Sci. 486.
Yang, S. Y., and Li, T. (2020). Cause for quasi-biweekly oscillation of zonal location of western Pacific subtropical high during boreal summer. Atmospheric Res. 245, 105079. doi:10.1016/j.atmosres.2020.105079
Zhang, A., Shi, H. Y., Li, T. J., and Fu, X. D. (2018). Analysis of the influence of rainfall spatial uncertainty on hydrological simulations using the bootstrap method. Atmosphere 9 (2), 71. doi:10.3390/atmos9020071
Zhang, C. (2020). Moisture sources for precipitation in Southwest China in summer and the changes during the extreme droughts of 2006 and 2011. J. Hydrology 591, 125333. doi:10.1016/j.jhydrol.2020.125333
Zhang, X., Alexander, L., Hegerl, G. C., Jones, P., Tank, A. K., Peterson, T. C., et al. (2011). Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Change 2 (6), 851–870. doi:10.1002/wcc.147
Zhou, Z. Q., Shi, H. Y., Fu, Q., Ding, Y. B., Li, T. X., Wang, Y., et al. (2021). Characteristics of propagation from meteorological drought to hydrological drought in the Pearl River Basin. JGR. Atmos. 126 (4), e2020JD033959. doi:10.1029/2020jd033959
Zhou, Z. Q., Shi, H. Y., Fu, Q., Li, T. X., Gan, T. Y., and Liu, S. N. (2020a). Assessing spatiotemporal characteristics of drought and its effects on climate-induced yield of maize in Northeast China. J. Hydrology 588, 125097. doi:10.1016/j.jhydrol.2020.125097
Zhou, Z. Q., Shi, H. Y., Fu, Q., Li, T. X., Gan, T. Y., Liu, S. N., et al. (2020b). Is the cold region in Northeast China still getting warmer under climate change impact? Atmos. Res. 237, 104864. doi:10.1016/j.atmosres.2020.104864
Keywords: extreme rainfall, large-scale climate patterns, partial wavelet analysis, yangtze river, driving factor
Citation: Wang Y, Liu S, Chen J, Zhou Z and Shi H (2022) Investigating the spatiotemporal variations of extreme rainfall and its potential driving factors with improved partial wavelet coherence. Front. Environ. Sci. 10:951468. doi: 10.3389/fenvs.2022.951468
Received: 24 May 2022; Accepted: 28 July 2022;
Published: 01 September 2022.
Edited by:
Yanfang Sang, Institute of Geographic Sciences and Natural Resources (CAS), ChinaReviewed by:
Xuezhi Tan, Sun Yat-Sen University, ChinaCopyright © 2022 Wang, Liu, Chen, Zhou and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Suning Liu, dTMwMDI5MDZAY29ubmVjdC5oa3UuaGs=; Haiyun Shi, c2hpaHlAc3VzdGVjaC5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.