State of charge estimation method for lithium-ion battery pack using BP-MDM-TEM

Addressing the fluctuating core temperatures during series battery pack operation that cause inconsistency in pack battery characteristics, the paper introduces a Battery-Pack Mean Difference-Method With Thermal-Electrical Coupled Model (BP-MDM-TEM). Thermal-electric coupling model describes the mean characteristics of battery pack, while the difference model quantifies variations among individual cells. A dual-time-scale method is employed to estimate State of Charge (SoC) of battery pack, reducing the computational load of the difference model.If the unique battery characteristics exceed system limits, a significant battery method is used to estimate SoC of pack battery. Building upon the BP-MDM-TEM framework,the paper employs the Improved Sage-Husa Adaptive Extended Kalman Filter (ISH-AEKF) to estimate SoC, mitigating the impact of process and measurement noise on system estimation. A hardware test platform is established in this paper, with a lithium-ion battery pack as the research subject.Compared with the traditional MDM method, the Mean Absolute Error (MAE) of soc estimation of BP-MDM-TEM is improved from 0.992% to 0.468%, and the Root Mean Square Error (RMSE) is improved from 1.279% to 0.982%.

1 Introduction

In recent years, the battery management system (BMS), as an important part of electric vehicles, is the technical bottleneck of electric vehicles, limited by its complex electrochemical reaction process, as well as temperature, load, inconsistency, performance degradation, etc., (Kumar et al., 2023). Due to the influence of deterministic application conditions, dynamic complex characteristics such as strong time-varying non-linearity and non-uniformity would appear when applied in battery packs, and its high-precision modeling and state estimation have always been hot and difficult in industry technology research (Hou et al., 2023). As the core function of BMS, the estimation of SoC provides an important basis for the energy management and safety management of electric vehicles. However, the accuracy of its estimate is influenced by two primary factors (Selvaraj and Vairavasundaram, 2023; Zhou et al., 2023). One is due to the limitation of electrode potential and materials, the voltage and capacity of a single battery cannot fully meet the requirements of electric vehicles, and a large number of batteries must be connected in series and parallel to form a battery pack. There are inconsistencies in the parameters of the batteries in the production and use process, which will lead to obvious differences between the batteries; the second is that the battery pack will generate heat during the working process, and the heat that is not released in time is absorbed by the battery itself. That leads to the increasement of operating temperature, and temperature will further affect the battery settings.

1.1 Battery pack model

Reliable assessment of the state of a lithium-ion battery is based on suitable battery models. Therefore, it is necessary to construct precise battery models that reflect both the internal and external characteristics of the battery accurately. These models can be categorized into electrochemical (Xin et al., 2020; Zhou et al., 2020; Hong et al., 2023; Yu et al., 2024), and equivalent circuit models (ECM) for batteries (Xu et al., 2024; Navas et al., 2023; Karimi et al., 2023; Cheng, 2024; Li et al., 2021).

Electrochemical models are mathematical frameworks used to describe the internal electrochemical processes of batteries. By simulating the reactions occurring at the electrodes, electrolyte, and interfaces, these models predict the battery’s performance, including voltage, capacity, energy efficiency, charge/discharge behavior, and aging characteristics. Common electrochemical models include the Pseudo-Two-Dimensional Model (P2D) and the Single Particle Model (SP). To adapt the SP model to high current conditions, an extended single-particle (ESP) model was proposed to improve model accuracy (Xin et al., 2020), but this method introduces complexity through curve fitting or approximate solutions to the differential equations (Zhou et al., 2020). Hong et al. (2023) integrated a portion of the equivalent circuit model with the SP model to effectively calculate the resistance in the electrolyte and utilized a second-order system dynamics approach to address the heat transfer delay from the center of the battery pack to the surface.

Equivalent circuit models can be used to simulate the external characteristics of the battery. A typical equivalent circuit model is the Thevenin model, which consists of an ideal voltage source, ohmic resistance, and an n-th order RC circuit. The accuracy of the model is directly proportional to the order of the RC circuit, while the model complexity is inversely proportional to the RC order. Model accuracy is proportionate to RC order, and model complexity is inversely proportional to RC order. The features of the various batteries can be accurately reflected by adjusting the order of the RC circuit (Li et al., 2021). Karimi et al. (2023) employed this model to develop an equivalent circuit model suitable for large currents, a wide temperature range, and various states of charge. Navas et al. (2023) used the same equations to simultaneously account for both the charging and discharging processes, resulting in a nonlinear relationship between the state of charge and the open-circuit voltage. This approach enabled the prediction of battery voltage and state of charge.

Although the equivalent circuit model can accurately simulate the electrical characteristics of the battery, it does not take into account the temperature increase due to the heat absorbed in the working process of the battery. Therefore, some researchers proposed to add a thermal model on the basis of the equivalent circuit model, so that the two models are coupled to each other to form a thermo-electric coupling model (Xu et al., 2024). At the same time, to describe the electrodynamic characteristics and thermal dynamic characteristics of the battery, providing the premise for the state prediction and performance optimization of the battery.

1.2 SoC estimation methods

SoC of batteries is a crucial parameter for electric vehicle battery management systems. Its accuracy directly impacts energy management control strategy and performance, subsequently affecting reliability and cost. Various algorithms can be used to estimate SoC, including state-space estimation methods, and machine learning approaches.

State-space estimation method usually uses a battery model combined with the measurement data to estimate SoC, including Kalman filter (Wang X. et al., 2024; Hosseininasab et al., 2023; Lin et al., 2023), particle filter (Wang J. et al., 2024; Jia et al., 2023), least square filter (Diep et al., 2024; Liu F. et al., 2023). Diep et al. (2024) proposed a method for real-time estimation of the state of charge of lithium-ion batteries using the Variable Forgetting Factor Recursive Least Squares (VFFRLS) combined with the Unscented Kalman Filter (UKF) algorithm, without the need for offline battery test data. The results showed an error of 1.5% compared to the reference values. The state space estimation method applied to battery SoC has not only good accuracy and convergence, but also small computational amount and strong adaptability.

Machine learning methods, often referred to as black-box models, capture the input-output relationship of a lithium-ion battery without relying on a physics or chemistry-based model. These methods are typically trained using measured data such as voltage, current, temperature, to accurately estimate SoC (Chen et al., 2024; Qian et al., 2024; Zhang et al., 2024). Qian et al. (2024) developed a hybrid neural network model (CNN-SAM-LSTM) that combines Convolutional Neural Networks (CNN), self-attention mechanisms, and Long Short-Term Memory (LSTM) networks for the joint estimation of state parameters in lithium-ion batteries. Although battery SoC estimation using machine learning methods can enhance accuracy, it often requires the establishment of an offline database and involves computationally intensive training processes, which may lead to overfitting and local optimum phenomena. Zhang et al. (2024) employed a stacked ensemble learning paradigm to estimate the state of lithium batteries. By utilizing base learners with different architectures, they enhanced adaptability to various features and reduced the risk of overfitting.

A battery pack is typically composed of hundreds of individual cells connected in series and parallel. Ideally, each cell leaving the production line would exhibit consistent performance over its lifespan. However, in practice, ensuring uniform initial performance parameters for each battery cell is challenging due to the manufacturing process and other factors. Inconsistencies during usage further exacerbate differences between batteries, complicating battery pack management over its service life. Additionally, the capacity and SoC of the battery are not intrinsic properties but must be determined based on individual cell behavior within the pack. Managing individual cell inconsistencies within a battery pack makes it difficult to accurately ascertain the capacity and SoC of the entire pack. The capacity of a series battery pack is determined by the sum of the minimum rechargeable capacity and the minimum discharge capacity of the individual cells in the group. Methods such as the large battery method, important battery method, and mean difference method are commonly used to estimate the SoC of the battery pack.

Large battery method treats a battery pack as a single large-capacity cell because individual cells within the battery pack exhibit similar characteristics, as proposed in reference (Ramachandran et al., 2019). Tian et al. (2023) considered large-scale battery systems as a unified entity and proposed an online capacity estimation method based on Extended Kalman Particle Filtering (EKPF). Additionally, they introduced an improved Gaussian mixture model to visualize the inconsistencies within the battery pack. Although the large battery method has a small amount of calculation, it ignores the inconsistency among individual cells in the group and cannot accurately estimate the battery SoC.

Important battery method is to use a single major battery in the group to represent battery pack performance (Liu et al., 2024; Trevizan et al., 2024). Typically, the lowest battery is selected, that is, the battery with the lowest voltage during discharge and the highest voltage during charging. The important battery method is often used in combination with different filtering algorithms. For example, Yu et al. (2023) employed cosine similarity to quantify the inconsistency among battery cells, identifying the representative cell within the battery pack based on the maximum cosine similarity value. They further utilized a multi-branch fusion approach to estimate SoC of the representative cell using Bayesian probability formulas. The important battery method can effectively protect the operation safety of the power battery pack, but when the SoC works in the range of 30%–80%, this method will reduce the energy efficiency of the battery pack.

Mean difference method treats the battery pack as both a mean model and a difference model, estimating the mean model SoC and the difference model $\mathrm{\Delta }$SoC, where $\mathrm{\Delta }$SoC represents the deviation of each cell from the mean model. This method typically utilizes an equivalent circuit model to determine model parameters through fitting measured cell data. Wu et al. (2023) designed a multi-layer balancing circuit capable of achieving both intra-group and inter-group balancing. This circuit topology ensures fast balancing while maintaining high balancing efficiency. Van and Vinh (2020) employs micro and macro time scales to estimate SoC for selected and unselected cells, respectively. Liu Z. et al. (2023) implemented a fusion of data-driven autoregressive (AR) models with ECM to enhance the dynamic characteristics of the battery pack model under complex operating conditions. They employed a differentiated update strategy to online update the parameters of the average differential model. However, this method does not consider the influence of battery operating temperature on SoC estimation.

Lai et al. (2022) proposed a joint estimation method for SoC and state of health (SOH) that takes temperature effects into account. In scenarios with temperature variations of up to 35°C, the joint estimator achieved a SoC error of 2%. Generally, the mean difference method usually estimates the SoC of the battery pack with good accuracy and low computational complexity.

The paper’s major contributions are as follows:

(1) First, a mechanistic model was developed to explore the characteristics of lithium-ion battery packs. Based on the analysis of battery pack characteristics, it was identified that temperature variations during the operation of series-connected battery packs could lead to internal inconsistencies in battery characteristics. To address this issue, BP-MDM-TEM was proposed. This model considers the thermal-electric coupling effect to describe the mean characteristics of the battery pack, enabling the characterization of the overall relationship between the battery pack and temperature changes. The difference model then describes the discrepancies between individual cell characteristics and the overall battery pack characteristics.

(2) On the basis of the BP-MDM-TEM, in order to realize the accurate estimation of SoC, this paper uses ISH-AEKF to estimate SoC of the battery pack, to overcome the influence of process noise and measurement noise on the system estimation.

(3) A dual-Time-Scale method was used to estimate SoC of battery pack based on the BP-MDM-TEM, reducing the amount of calculation of the differential model. When the characteristics of the single battery go beyond the limits allowed by the system, the system estimates the overall characteristics of the battery based on the important battery method.

2 Mean difference model based on thermal-electric coupling

2.1 Battery temperature features

Based on the operating conditions of the Hybrid Pulse Power Characterization (HPPC) (Belt, 2010), we found that the temperature of each individual cell in the battery pack rises during operation due to heat absorption.

When the battery is at rest, it no longer generates heat, and the temperature will slowly decrease. And, the temperature variation differs slightly due to the different positions of the cells. The temperature of the cells in the middle is slightly higher than those on the outer edges. This is because the heat generated by the middle cells is not dissipated as quickly, resulting in slightly higher heat absorption. However, this difference is minimal, and the overall temperature trend of the cells within the pack is consistent.

2.2 Thermal-electric coupling model of individual battery

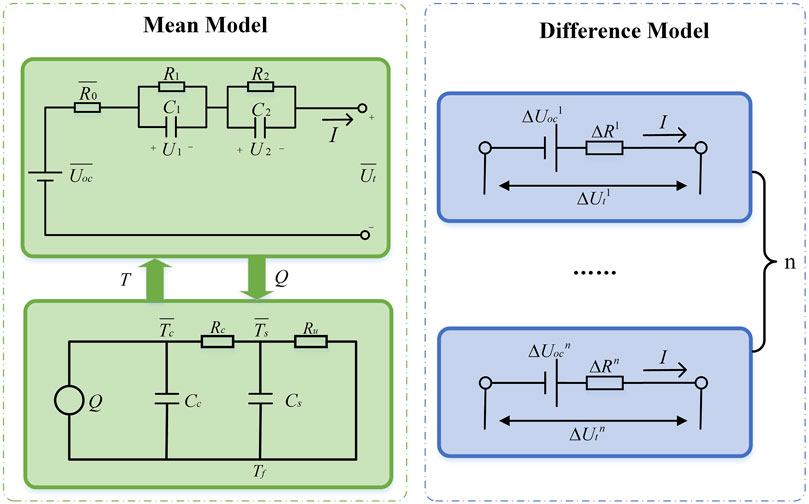
The basic operating principle for the thermal-electric coupling model is shown in the mean model section of the Figure 1, and the upper left section is the circuit model, as shown in Equation 1:

$\left\{\begin{array}{cc}\hfill & U_t=U_{oc}-U_1-U_2-I{R}_0\hfill \\ \hfill & {\dot{U}}_1=-\frac{1}{R_1{C}_1}{U}_1-\frac{1}{C_1}I\hfill \\ \hfill & {\dot{U}}_2=-\frac{1}{R_2{C}_2}{U}_2-\frac{1}{C_2}I\hfill \end{array}\right.(1)$

Figure 1

Figure 1. Battery-pack mean-difference method with thermal-electrical model.

Where, $U_{oc}$ is usually a nonlinear function of SoC and the battery operating temperature;$I{R}_0$ is the voltage difference across the ohmic resistance $R_0$; $R_1$ and $C_1$ are the internal resistance and capacitance of electrochemical polarization, respectively, with the voltage across the $R_1{C}_1$ circuit being the electrochemical polarization voltage is $U_1$; $R_2$ and $C_2$ are the internal resistance and capacitance of concentration polarization, respectively, with the voltage across the $R_2{C}_2$ circuit being the concentration polarization voltage is $U_2$. $R_1,C_1,R_2,C_2$ change with the operating temperature (Gu and Wang, 2000). A thermal model is illustrated in Equation 2.

$\left\{\begin{array}{cc}\hfill & C_c{\dot{T}}_c=Q+\frac{T_s-T_c}{R_c}\hfill \\ \hfill & C_s{\dot{T}}_{\text{s}}=\frac{T_f-T_s}{R_u}+\frac{T_s-T_c}{R_c}\hfill \end{array}\right.(2)$

Where, $T_s$ and $T_c$ represent the battery surface temperature and the battery core temperature; $T_f$ is the ambient temperature; $C_c$ and $C_s$ represent the heat capacity of the battery core and the battery surface; $R_c$ is the equivalent heat conduction resistance, and $R_u$ is the equivalent convective resistance used to simulate convective cooling of the battery surface, which is affected by the geometry of the battery pack, coolant type, and coolant flow; $Q$ represent the heat production during the battery operation.

Then from Bernardi equation, the heat production of the battery can be obtained as shown in Equation 3:

$Q=I*\left(U_{oc}-U_t\right)+I*T*\frac{d{U}_{oc}}{dT}(3)$

Using Equation 2, the battery core temperature and surface temperature are computed as the battery operating temperature $T$ as shown in Equation 4:

$T=\left(T_c+T_s\right)/2(4)$

Then, the battery operating temperature is used to modify the parameters in the Equation 1 to form a thermal-electrical coupling model with high simulation precision.

The thermal-electrical coupling model has the following three features:

First, the thermal-electrical coupling model, designed for real-time simulation with the control algorithm, can avoid the limitation of the finite element method, which cannot realize the real-time simulation of the battery temperature control algorithm. This effectively shortens the cycle of battery thermal management in the development of the control strategy, saving time.

Secondly, the thermal properties of the battery are very complex. The thermal-electrical coupling model can balance both the precision and computational complexity of the model. With appropriate computational intensity, the battery core temperature and battery surface temperature can be monitored more accurately simultaneously.

Thirdly, the thermal-electrical coupling model uses the equivalent circuit model and thermal model to describe the relationship between the thermal power of the battery and the current and voltage. Without considering the specific physical significance, the calculation is simple and easy to implement widely.

When the working temperature of the battery changes, the circuit model parameters related to the operating temperature of the battery will also change, making the identification of the thermal-electric coupling model very complex, and the identification accuracy cannot be guaranteed. In view of this problem, the identification of thermal-electric coupling model is regarded as an optimization process to find the optimal parameter values of a model under a specific open circuit voltage, SoC and battery operating temperature, so that the model output result and the measurement result are close.

2.3 Battery-pack mean-difference method with thermal-electrical model

The conventional MDM consists of CMM and CDM. CMM is used to describe the mean state of the battery pack, generally Thevenin model; CDM is used to describe the difference between the cell and mean state in the group, generally Rint model.

From the study of the temperature characteristics of the battery pack, it can be seen that the difference between the batteries in the group in the working process is relatively small, and the number of temperature sampling points set up in the actual packaging process of the automotive battery pack is limited, so only the temperature change of the battery pack as a whole needs to be taken into account in the estimation of the SOC of the battery pack.

Through the study of the open-circuit voltage characteristics of the battery pack, it can be seen that the open-circuit voltage of the batteries in the group under different ambient temperatures has small differences, and the overall trend of change is consistent, so the open-circuit voltage can be normalized;

Based on the model of the MDM, BP-MDM-TEM which proposed in the paper changes the Thevenin model used in the mean model to the thermal-electrical coupling model. Where $\bar{T}$ is the mean working temperature of the battery pack and ${\bar{U}}_{oc}$ is the mean open circuit voltage. The model can take into account the change in the operating temperature of the battery pack to obtain an accurate battery pack model.

For simplicity of the calculation, the difference model ignores the differences in polarized voltage and polarized capacitance. The mean differential model for thermal-electric coupling is shown in Figure 1.

2.3.1 Mean thermal-electrical coupling model

On the left side of Figure 1 is the mean thermal-electrical coupling model, which includes the mean equivalent circuit model and the mean thermal model. In the mean equivalent circuit model, the mean end voltage ${\bar{U}}_t$ of all series-connected batteries can be calculated from the measured end voltage of the battery pack and the number of batteries. The expression as shown in Equation 5:

$\overline{U_t}=\frac{1}{n}{U}_{\mathit{pack}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{U_t}^i(5)$

Where, $U_{\mathit{pack}}$ is the measuring end voltage of the series battery pack,${U_t}^i$ is the measuring end voltage of the $ith$ single cell in the series battery pack, and $n$ is the total number of the series battery pack. The parameters in the mean equivalent circuit have the following relationship as shown in Equation 6:

$\overline{U_t}=\overline{U_{\text{oc}}}-I\overline{R_0}-U_1-U_2(6)$

Where, $I$ is the current of the series battery pack; $\overline{U_{oc}}$ is the average open-circuit voltage, which can be obtained from MOCV; $\overline{R_0}$ is the average ohmic resistance; $U_1$ and $U_2$ represent the polarization voltages of the $R_1{C}_1$ and $R_2{C}_2$.

In the average thermal model, $\overline{T_s}$is the average surface temperature within the battery pack as shown in Equation 7.

$\overline{T_s}=\frac{1}{m}{\displaystyle \sum _{j=1}^m}{T}_s^j(7)$

Which can be obtained with the corresponding mean model parameters included Equation 3.

2.3.2 Difference model

According to the difference model on the right side of Figure 1, The difference model terminal voltage $\mathrm{\Delta }{U_t}^i$ of the $ith$ single cell is composed of the difference open-circuit voltage $\mathrm{\Delta }{U_{oc}}^i$ and the difference internal resistance $\mathrm{\Delta }{R}^i$. The expression for the difference model terminal voltage is shown in Equation 8.

$\mathrm{\Delta }{U_t}^i=\mathrm{\Delta }{U_{oc}}^i-I\mathrm{\Delta }{R}^i(8)$

The relationship between each parameter of the difference model and the mean model is shown in Equation 9.

$\left\{\begin{array}{cc}\hfill & \mathrm{\Delta }{U_t}^i={U_t}^i-{\bar{U}}_t\hfill \\ \hfill & \mathrm{\Delta }{U_{oc}}^i={U_{oc}}^i-\overline{U_{oc}}\hfill \\ \hfill & \mathrm{\Delta }{R}^i={R_0}^i-\overline{R_0}\hfill \end{array}\right.(9)$

Where, ${U_{oc}}^i$ is the open circuit voltage of the $ith$ cell in the series battery pack; and ${R_0}^i$ is the ohmic resistance of the $ith$ cell.

3 SoC estimation based on ISH-AEKF

3.1 ISH-AEKF method

If the object is modeled as shown in Equation 10:

$\left\{\begin{array}{cc}\hfill & x_k=f\left(k,x_{k-1}\right)+w_k\hfill \\ \hfill & y_k=h\left(k,x_{k-1}\right)+v_k\hfill \\ \hfill & F_k=\frac{\partial f}{\partial {\widehat{x}}_{k-1}}\hfill \\ \hfill & H_k=\frac{\partial h}{\partial {\widehat{x}}_{k-1}}\hfill \end{array}\right.(10)$

The algorithm steps of ISH-AEKF are as follows:

Step 1: Compute a priori estimates of the system ${\widehat{x}}_{k|k-1}$, and update the system covariance matrix ${\widehat{P}}_{k|k-1}$, as shown in Equation 11:

$\left\{\begin{array}{cc}\hfill & {\widehat{x}}_{k|k-1}=F_k{\widehat{x}}_{k-1}+{\widehat{P}}_{k-1}+q_{k-1}\hfill \\ \hfill & {\widehat{P}}_{k|k-1}=F_k{\widehat{P}}_{k-1}{F_k}^T+Q_{k-1}\hfill \end{array}\right.(11)$

Where $Q_k$ is the covariance of the process noise $w_k$.

Step 2: Adaptive measurement of noise covariance estimation, as shown in Equation 12:

$\left\{\begin{array}{cc}\hfill & d_k=\frac{1-b}{1-b^{k+1}}\hfill \\ \hfill & e_k=y_k-H_k{\widehat{x}}_{k|k-1}-r_{k-1}\hfill \\ \hfill & R_k=\left(1-d_k\right)R_{k-1}+d_k\left(e_k{e_k}^T\right)\hfill \end{array}\right.(12)$

Where $d_k$ is the adaptive factor; $b$ is forgetting factor, the value range is [0,1], usually set to [0.95,0.99];

Step 3: Calculate the Kalman gain matrix $K_k$, as shown in Equation 13:

$K_k=\frac{{\widehat{P}}_{k|k-1}{H_k}^T}{H_k{\widehat{P}}_{k|k-1}{H_k}^T+R_k}(13)$

Step 4: Adaptive process noise covariance estimation, as shown in Equation 14:

$Q_k=\left(1-d_{k-1}\right)Q_{k-1}+d_{k-1}\left(K_k{e}_k{e_k}^T{K_k}^T\right)(14)$

Step 5: Solving the optimal estimation of state variables ${\widehat{x}}_k$ and the optimal estimation of mean square error ${\widehat{P}}_k$, as shown in Equation 15:

$\left\{\begin{array}{cc}\hfill & {\widehat{x}}_k={\widehat{x}}_{k|k-1}+K_k{e}_k\hfill \\ \hfill & {\widehat{P}}_k=\left(I-K_k{C}_k\right){\widehat{P}}_{k|k-1}\hfill \end{array}\right.(15)$

Step 6: Adaptive measurement and calculation of mean Process Noise, as shown in Equation 16:

$\left\{\begin{array}{cc}\hfill & r_k=\left(1-d_k\right)r_{k-1}+d_k\left(y_k-C_k{\widehat{x}}_{k|k-1}\right)\hfill \\ \hfill & q_k=\left(1-d_k\right)q_{k-1}+d_k\left({\widehat{x}}_k-A_k{\widehat{x}}_{k-1}\right)\hfill \end{array}\right.(16)$

3.2 SoC estimation of battery pack

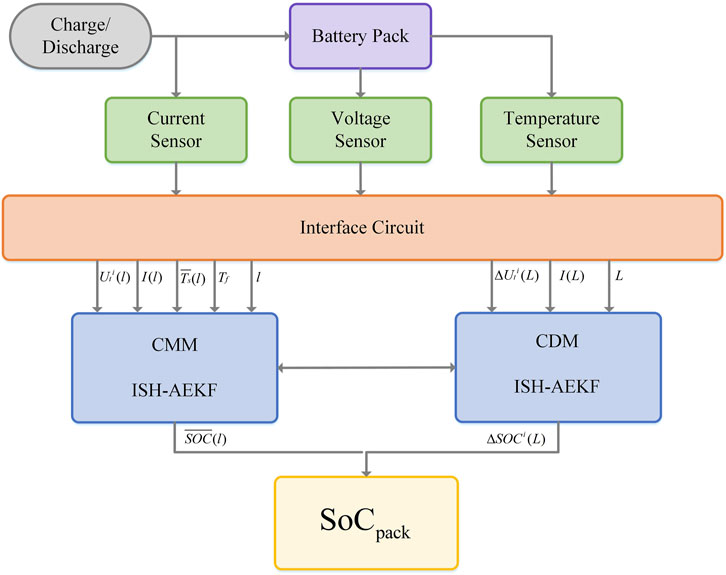
Due to the inconsistency within the battery pack, the remaining charge/discharge capacity of each cell varies. However, users are generally only interested in the SoC of the entire battery pack. Therefore, a method that can accurately estimate the SoC of the battery pack is needed. The paper proposes a method that combines the thermal-electrical coupling model with mean difference method (IMDM), which has the following characteristics:

First, The thermal-electrical coupling model is applied to the mean model to account for the effects of temperature variations in the battery pack.

Secondly, a dual-time scale is used to estimate the mean model and the difference model separately, which can reduce the estimation frequency of the difference model, thereby reducing the computational load of the system.

Thirdly, Based on this, the method integrates the significant battery method to monitor the charge level of each cell in the pack. When a cell’s charge is particularly high or low, a charge alert is set to prevent issues such as overcharging or over-discharging within the battery pack.

Taking into account the fact that certain batteries within the battery pack may experience overcharging or over-discharging when the pack is close to reaching its charging/discharging cut-off voltage, the paper proposed the important battery method and improve the mean difference model, real-time monitoring within the monomer battery, when a battery is high or low, set the power remind, avoid the group overcharged battery, etc. The process is illustrated in Figure 2.

Step 1: Measure the current of series battery pack $I(k)$, battery end voltage of each cell $U_t^i(k)$, ambient temperature of battery pack $T_f(k)$, and surface temperature of battery pack $T_s^j(k)$.

Step 2: Estimate pack mean SoC based on ISH-AEKF method.

Figure 2

Figure 2. SoC estimation based on ISH-AKEF.

Assuming the sampling period of the mean model CMM is $\mathrm{\Delta }T$.

Set up the following matrix as shown in Equations 17–23:

$x_k={\left[\begin{array}{ccccc}\hfill U_1\left(k\right)\hfill & \hfill U_2\left(k\right)\hfill & \hfill \overline{SoC}\left(k\right)\hfill & \hfill {\bar{T}}_c\left(k\right)\hfill & \hfill {\bar{T}}_s\left(k\right)\hfill \end{array}\right]}^T(17)$

$u_k={\left[\begin{array}{cc}\hfill I\left(k\right)\hfill & \hfill \begin{array}{cc}\hfill \bar{Q}\left(k\right)\hfill & \hfill T_f\left(k\right)\hfill \end{array}\hfill \end{array}\right]}^T(18)$

$y_k={\left[\begin{array}{cc}\hfill \overline{U_t}\left(k\right)\hfill & \hfill {\bar{T}}_s\left(k\right)\hfill \end{array}\right]}^T(19)$

$A_k=\left[\begin{array}{ccccc}\hfill e^{-\frac{\mathrm{\Delta }T}{R_1\left(k\right)C_1\left(k\right)}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{-\frac{\mathrm{\Delta }T}{R_2\left(k\right)C_2\left(k\right)}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{-\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_c\left(k\right)}}\hfill & \hfill e^{\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_c\left(k\right)}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_s\left(k\right)}}\hfill & \hfill e^{-\left(\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_s\left(k\right)}+\frac{\mathrm{\Delta }T}{R_u\left(k\right)C_s\left(k\right)}\right)}\hfill \end{array}\right](20)$

$B_k=\left[\begin{array}{ccc}\hfill R_1\left(k\right)\ast \left(1-e^{-\frac{\mathrm{\Delta }T}{R_1\left(k\right)C_1\left(k\right)}}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill R_2\left(k\right)\ast \left(1-e^{-\frac{\mathrm{\Delta }T}{R_2\left(k\right)C_2\left(k\right)}}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{\mathrm{\Delta }T}{C_N}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill R_c\left(k\right)\ast \left(1-e^{-\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_c\left(k\right)}}\right)\hfill & \hfill \frac{R_c\left(k\right)C_c\left(k\right)}{R_u\left(k\right)C_s\left(k\right)}\left(e^{\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_c\left(k\right)}}-1\right)\hfill \\ \hfill 0\hfill & \hfill \frac{R_c\left(k\right)C_s\left(k\right)}{C_c\left(k\right)}\left(e^{\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_s\left(k\right)}}-1\right)\hfill & \hfill \frac{R_c\left(k\right)}{R_u\left(k\right)+R_c\left(k\right)}\left(1-e^{-\frac{\mathrm{\Delta }T}{R_c\left(k\right)C_s\left(k\right)}-\frac{\mathrm{\Delta }T}{R_u\left(k\right)C_s\left(k\right)}}\right)\hfill \end{array}\right](21)$

$C_k=\left[\begin{array}{ccccc}\hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right](22)$

$D_k=\left[\begin{array}{c}\hfill -\overline{R_0}I\left(k\right)+\overline{U_{oc}}\left(k\right)\hfill \\ \hfill 0\hfill \end{array}\right](23)$

Then the mean model equation of state is shown in Equation 24:

$\left\{\begin{array}{cc}\hfill & x_k=A_k{x}_{k-1}+{\mathrm{B}}_k{u}_k+\omega \left(k\right)\hfill \\ \hfill & y_k=C_k{x}_{k-1}+{\mathrm{D}}_k+\nu \left(k\right)\hfill \end{array}\right.(24)$

Step 2.1: The mean voltage $\overline{U_t}(k)$ and mean surface temperature ${\bar{T}}_s(k)$ are calculated based on Equations 5, 7.

Step 2.2: Calculate the mean operating temperature of the battery pack based on Equation 4, as shown in Equation 25:

$\bar{T}\left(k-1\right)=\left(\overline{T_c}\left(k-1\right)+\overline{T_s}\left(k-1\right)\right./2(25)$

Step 2.3: Estimated based on the relationship obtained from the identification of Equation 10, as shown in Equation 26:

$y_k={\left[\begin{array}{c}\hfill \overline{U_t}\left(k\right){\bar{T}}_s\left(k\right)\hfill \end{array}\right]}^T(26)$

Step 2.4: Calculates the mean heat production of the current battery pack based on Equation 3, as shown in Equation 27:

$\bar{Q}\left(k\right)=I\left(k\right)*\left(\overline{U_{oc}}\left(k-1\right)-\overline{U_t}\left(k-1\right)\right)+I\left(k\right)*\bar{T}\left(k-1\right)\frac{\partial \overline{U_{oc}}\left(k-1\right)}{{\left.\partial T\right|}_{\bar{T}\left(k-1\right)}}(27)$

Step 2.5: Calculation Equations 28, 29:

$F_k=\left[\begin{array}{ccccc}\hfill a_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill a_{11}\frac{\partial a_{11}}{\partial T_c}{u}_1\left(k-1\right)+b_{11}\frac{\partial b_{11}}{\partial T_c}I\left(k\right)\hfill & \hfill a_{11}\frac{\partial a_{11}}{\partial T_s}{u}_1\left(k-1\right)+b_{11}\frac{\partial b_{11}}{\partial T_s}I\left(k\right)\hfill \\ \hfill 0\hfill & \hfill a_{22}\hfill & \hfill 0\hfill & \hfill a_{22}\frac{\partial a_{22}}{\partial T_c}{u}_2\left(k-1\right)+b_{12}\frac{\partial b_{12}}{\partial T_c}I\left(k\right)\hfill & \hfill a_{22}\frac{\partial a_{22}}{\partial T_s}{u}_2\left(k-1\right)+b_{12}\frac{\partial b_{12}}{\partial T_s}I\left(k\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill b_{42}\frac{\partial \bar{Q}\left(k\right)}{\partial \overline{SoC}\left(k\right)}\hfill & \hfill a_{44}+b_{42}\frac{\partial \bar{Q}\left(k\right)}{\partial T_c}\hfill & \hfill b_{42}\frac{\partial \bar{Q}\left(k\right)}{\partial T_c}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill b_{52}\frac{\partial \bar{Q}\left(k\right)}{\partial \overline{SoC}\left(k\right)}\hfill & \hfill a_{54}\hfill & \hfill a_{55}\hfill \end{array}\right](28)$

$H_k=\left[\begin{array}{ccccc}\hfill -1\hfill & \hfill -1\hfill & \hfill \frac{\partial {\bar{U}}_{oc}\left(k\right)}{\partial \overline{SoC}\left(k\right)}\hfill & \hfill \frac{\partial {\bar{U}}_{oc}\left(k\right)}{\partial \overline{T_c}\left(k\right)}-\frac{\partial {\bar{R}}_0\left(k\right)}{\partial \overline{T_c}\left(k\right)}I\left(k\right)\hfill & \hfill \frac{\partial {\bar{U}}_{oc}\left(k\right)}{\partial \overline{T_s}\left(k\right)}-\frac{\partial {\bar{R}}_0\left(k\right)}{\partial \overline{T_s}\left(k\right)}I\left(k\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right](29)$

Step 2.6: According to the ISH-AEKF method, ${\widehat{x}}_k$ can be calculated as shown in Equation 30:

${\widehat{x}}_k={\left[\begin{array}{ccccc}\hfill {\widehat{U}}_1\left(k\right)\hfill & \hfill {\widehat{U}}_2\left(k\right)\hfill & \hfill \widehat{\overline{SoC}}\left(k\right)\hfill & \hfill \widehat{\overline{T_c}}\left(k\right)\hfill & \hfill \widehat{\overline{T_s}}\left(k\right)\hfill \end{array}\right]}^T(30)$

Step 3: Estimation of single cell differential SoC based on ISHAEKF approach can be represented by Equations 31–33.

The sampling period of the Difference Model (CDM) is $\mathrm{\Delta }{T}_d$.

$\left\{\begin{array}{cc}\hfill & \mathrm{\Delta }So{C}^i\left(k\right)=\mathrm{\Delta }So{C}^i\left(k-1\right)-\frac{I\left(k\right)\mathrm{\Delta }{T}_d}{C_N}-\left[\overline{SoC\left(k\right)}-\overline{SoC\left(k-1\right)}\right]\hfill \\ \hfill & \mathrm{\Delta }{U_t}^i\left(k\right)=\mathrm{\Delta }{U_{oc}}^i\left(\overline{SoC\left(k\right)},\mathrm{\Delta }{SoC}^i\left(k\right)\right)-I\left(k\right)\mathrm{\Delta }{R}^i\hfill \end{array}\right.(31)$

Let:

$\left\{\begin{array}{cc}\hfill & x_k^i={\left[\mathrm{\Delta }So{C}^i\left(k\right)\right]}^T\hfill \\ \hfill & y_k^i={\left[\mathrm{\Delta }{U}_t^i\left(k\right)\right]}^T\hfill \end{array}\right.(32)$

For the difference model:

$F_k^i=\left[1\right],H_k^i=\left[\frac{\partial \mathrm{\Delta }{U}_{oc}^i}{\partial \mathrm{\Delta }So{C}^i}\right](33)$

Similarly, it can be obtained based on the ISH-AEKF method ${x_k}^i$.

Step 4: Monitor and handle battery pack SoC exceptions.

Due to the inconsistency of the battery pack, the battery is in danger of overcharging and overdischarge in the group, so when the battery pack is in a low/high power state, more attention should be paid to the two single batteries with the lowest/high remaining power in the battery pack. The open circuit voltage of the battery is higher and changes faster when the remaining power is higher than 80% and lower than 20%. Therefore, the paper proposes to set the monitoring module to remind the state of the important battery. When the battery with the lowest remaining power (high) in the process of battery discharge (charge) is low/above 20% (80%), that is$\min (So{C}^i)\le 20\%,\max (So{C}^i)\ge 80\%$ the monitoring module will remind the user and reduce the step size estimated by the difference model to avoid the problem of battery over discharge or overcharge.

Since the battery pack $So{C}_{\mathit{pack}}$ is used for calculation $\overline{SoC}$, the user is more concerned about the battery pack $\overline{SoC}$ than the individual monomer $\mathrm{\Delta }So{C}^i$,so the step size of the difference model can be set as shown in Equation 34:

$\mathrm{\Delta }{T}_d=M*\mathrm{\Delta }T,M>1(34)$

Which can effectively reduce the calculation amount. However, when the battery pack is calculated by two limit cells, the requirements for the difference model are increased, so the step size of the difference model needs to be changed $M=1$, so that the estimation accuracy can be effectively improved.

4 Experimental verification

4.1 Test platform setup

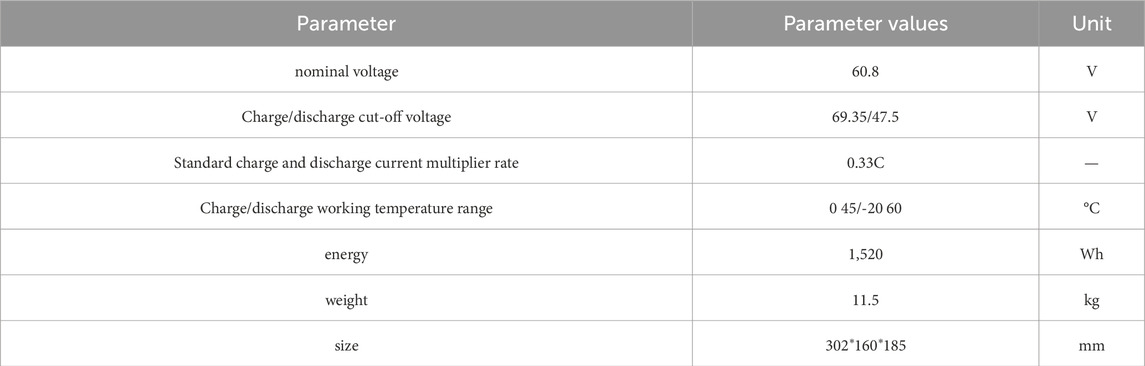
The test object of the paper is the rechargeable lithium-ion battery pack produced by Jiawei Longneng Solid State Energy Storage Technology Rugao Co. Ltd. with the model number JL60V25Ah, which consists of 19 single cells connected in series. The battery cells are model 90133200F25. The product specifications of the battery pack are shown in Table 1.

Table 1

Table 1. Specifications of lithium ion battery pack.

Battery pack uses RS485 communication, with a baud rate of 9,600, 8 data bits, and 1 stop bit, with no parity check. All data is requested by the charging and discharging device from the protection board, which sends responses including the total battery current (high and low), the voltage of individual cells (high and low), battery SoC, battery temperature, and battery series.

To charge the battery pack, a Chroma 62100H-1000 is used; for discharging, a Chroma 63210E-1200-400 programmable DC electronic load is chosen. The upper machine uses BMS test software provided by Hangzhou Xinwei Technology Co., Ltd., which can monitor the voltage, current, temperature, and other data of the battery pack in real time.

Based on the above devices, a hardware test platform for the battery pack is built, and the battery pack is tested under different working conditions. The charging test platform is shown in Figure 3A, and the discharging test platform is shown in Figure 3B.

Figure 3

Figure 3. Charging hardware test platform: (A) Charging test platform. (B) Discharge Test Platform.

4.2 Experimental design of the battery test

In order to establish the battery pack model and verify the accuracy of BP-MDM-TEM estimation of battery pack SoC method, the paper designed HPPC test, constant current constant voltage charging test and constant current discharge test experiments at different ambient temperatures. The purpose of the HPPC condition test is to establish the battery pack model and identify the parameters of the mean difference model. The advantage of the HPCC condition test is not removing the battery pack to obtain the characteristics of the constant current constant voltage charging test and constant current discharge test is to verify the BP-MDM-TEM to estimate the accuracy and robust of the battery SoC, which can effectively reflect the battery charge and discharge state.

(1) The HPPC test operating condition place the battery pack at the set ambient temperature for the following steps:

a. Fully charge the battery pack to the upper cut-off voltage 69.35 V with the constant current (8.25A) (0.33°C), and then charge the battery pack with a constant voltage until the charging current rate drops to 0.02°C;

b. Put the battery pack in an open state and stand for 1 h to depolarization, then the SoC is 100%;

c. Discharge the battery pack with the constant current (8.25A) of the standard discharge rate (0.33C) for 18min to the 10% SoC;

d. Repeat the test procedure in steps b and c. When the battery pack SoC has discharged to 0% or reached a low cut-off voltage, leave the battery pack still for 2 h.

In the HPPC test condition, in addition to recording the open circuit voltage value of the cell within [0%, 100%], the battery current, the battery voltage, the cell voltage and the mean temperature of the group measured in the experiment should also be recorded.

(2) Constant current and constant pressure charging test condition.

The test condition of constant current and constant voltage charging is the standard charging mode of the battery pack. First, the constant current charging is charged at 0.33°C rate, and when the charging stop voltage reaches 69.35 V, the charging is charged at constant voltage of 69.35 V until the current is less than 0.05°C.

(3) Constant current discharge test working condition.

The constant discharge test condition is the standard discharge mode of the battery pack. 0.33°C ratio is used to discharge the full battery pack until the discharge cut-off voltage reaches 47.5 V.

4.3 The HPPC experiment identified the model parameters

4.3.1 Parameter identification of the thermal-electric coupling mean model

Based on the HPPC test condition, the mean model open circuit voltage is identified according to the battery pack model parameter identification process.

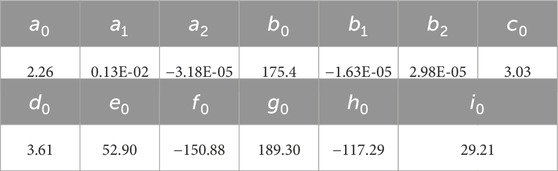
Setting as shown in Equation 35:

$\begin{array}{c}{U}_{oc}\left(SoC,T\right)=\left(a_0+a_1*T+a_2*T^2\right)+\left(b_0+b_1*T+b_2*T^2\right)*SoC+c_0*So{C}^2\hfill \\ +d_0*So{C}^3+e_0*So{C}^4+f_0*So{C}^5+g_0*So{C}^6+h_0*So{C}^7\hfill \\ +i_0*So{C}^8\hfill \end{array}(35)$

The obtained polynomial parameters are shown in Table 2.

Table 2

Table 2. Mean open-circuit voltage parameter identification results.

Based on the mean model RC parameters identified according to Equations 36–40, the result shown in Table 3.

$R_0\left(T\right)={\alpha }_0+{\alpha }_1*T+{\alpha }_2*T^2+{\alpha }_3*T^3(36)$

$R_1\left(T\right)={\beta }_0+{\beta }_1*T+{\beta }_2*T^2+{\beta }_3*T^3(37)$

$C_1\left(T\right)={\gamma }_0+{\gamma }_1*T+{\gamma }_2*T^2+{\gamma }_3*T^3(38)$

$R_2\left(T\right)={\delta }_0+{\delta }_1*T+{\delta }_2*T^2+{\delta }_3*T^3(39)$

$C_2\left(T\right)={\eta }_0+{\eta }_1*T+{\eta }_2*T^2+{\eta }_3*T^3(40)$

Table 3

Table 3. Mean model RC parameter identification results.

The identified mean model parameters are used to build the thermal-electric coupling model, and the voltage results output by the model are compared with the temperature results and the measured data. The Root Mean Square Error (RMSE) for the mean model end voltage is 6.55 mV, and the RMSE for the battery operating temperature is 0.12°C.

4.3.2 Parameter identification of the thermal-electric coupling difference model

In addition to the mean model, the differential resistance $\mathrm{\Delta }{R}^i$ in the differential model also needs to be identified by HPPC experiment. Because the differential resistance $\mathrm{\Delta }{R}^i$ changes slightly in the working process, the paper ignores the change, and the identification results are shown in Figure 4.

Figure 4

Figure 4. Differential resistance identification results of individual cells.

The criteria for differential voltage RMSE calculated from the difference model are shown in Table 4 in mV.

Table 4

Table 4. Differential model RMSE.

4.4 SoC estimation for individual cell

4.4.1 Effect of temperature on the SoC estimate

Considering the temperature of the charge-discharge state, the paper verifies the influence of temperature modification on SoC estimation results under DST and US06 conditions.

The paper compares the accuracy of SoC estimation with and without temperature correction using three methods: the EKF method without temperature correction, the EKF method with temperature correction, and the ISH-AEKF method. Initially, during SoC estimation, because the battery temperature change is not significant, the simulation results of the EKF method without temperature correction and the EKF method with temperature correction are similar. However, as the battery operating temperature increases, the estimation error of the former gradually becomes greater than that of the latter, and over time, the error becomes significantly higher. Compared with the ISH-AEKF method, the results of the latter are closer to the true value and have higher accuracy.

According to Figures 5A, B, the accuracy of the temperature correction model using the ISH-AEKF method is higher than that of the EKF method. The ISH-AEKF method achieves the highest accuracy among the methods tested, with an estimated Mean Absolute Error (MAE) of SoC at 0.489% and RMSE at 0.972% under DST conditions. Under US06 conditions, the estimated SoC MAE is 0.523% and RMSE is 0.991%. These results demonstrate that the ISH-AEKF method adopted in this paper ensures the accuracy of SoC estimation under varying temperature conditions, exhibiting good temperature adaptability.

Figure 5

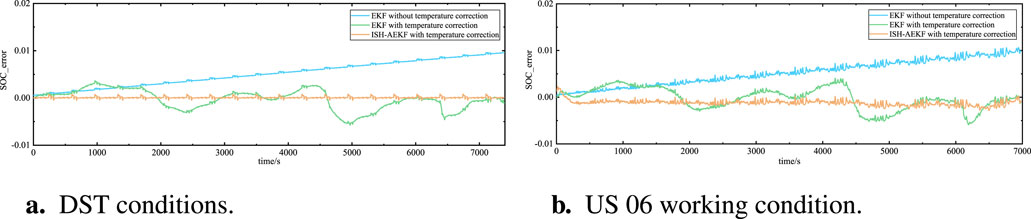
Figure 5. SoC estimation error under two different operating conditions: (A) DST conditions. (B) US 06 working condition.

4.4.2 Effect of different initial SoC value

This subsection will verify the initial SoC against the SoC of the ISH-AEKF. The initial value of deviation is defined based on the size of the difference from the reference value and is mainly divided into two categories: small deviation initial value and large deviation initial value.

The approach involves intentionally setting the initial SoC value to deviate from the reference value in the ISH-AEKF method for SoC estimation. Under different SoC conditions compared to the reference value, the algorithm is validated using two different driving cycles, DST and US06, to assess whether the ISH-AEKF algorithm can automatically correct the SoC, thus demonstrating the robustness of the ISH-AEKF method.

The paper validates the robustness using DST and US06 driving cycle data at an ambient temperature of 25°C. During the discharge process, the initial reference SoC is set to 1, while a slightly offset initial SoC of 0.9 is used. Through simulation experiments, the SoC estimation error results for the ISH-AEKF algorithm are depicted in Figures 6A, B.

Figure 6

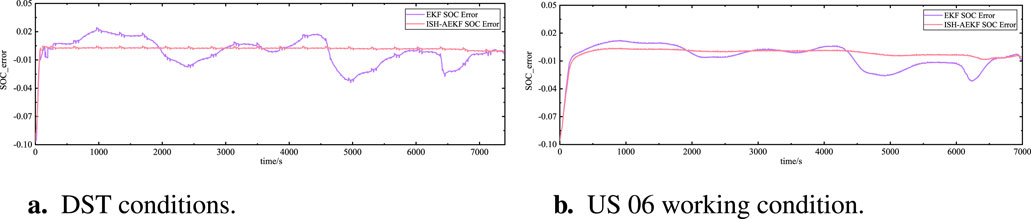
Figure 6. SoC estimation error under two different operating conditions when the initial error value is 0.9: (A) DST conditions. (B) US 06 working condition.

Using a slight initial deviation in SoC of 0.6, the ISH-AEKF algorithm’s SoC estimation error is evaluated through simulation experiments, with the results depicted in Figures 7A, B.

Figure 7

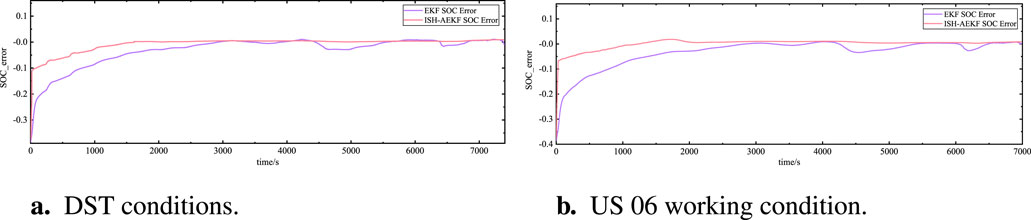
Figure 7. SoC estimation error under two different operating conditions when the initial error value is 0.6: (A) DST conditions. (B) US 06 working condition.

The results indicate that under conditions of an initial erroneous value, the ISH-AEKF algorithm is capable of automatically correcting the SoC estimation when there is an initial deviation in SoC. Once stabilized, the error range can be maintained within $\pm$0.004.

4.5 Charge and discharge experiment verification

In order to verify that BP-MDM-TEM has good SoC estimation accuracy in charge-discharge experiments, the paper tests standard charge-discharge of the battery pack and substitutes the SoC estimation data, such as measured voltage, measured current, and measured temperature obtained by the upper computer, into BP-MDM-TEM. The results are shown in Figures 8A, B.

Figure 8

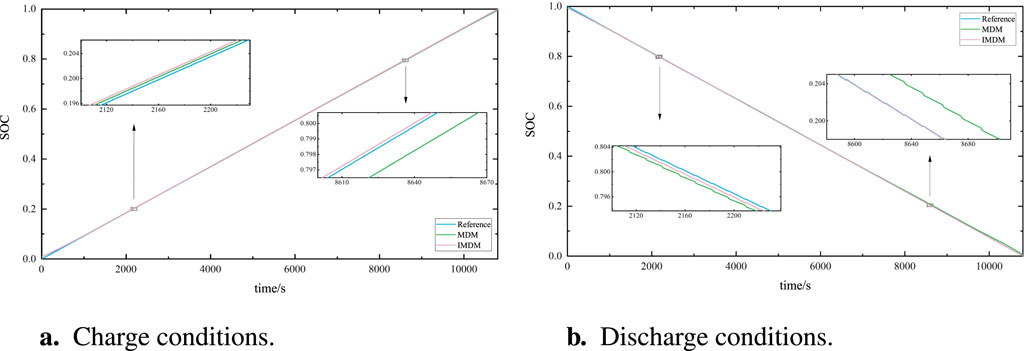
Figure 8. Battery pack SoC estimation results under charge-discharge conditions: (A) Charge conditions. (B) Discharge conditions.

The above figures compare the traditional MDM and the Battery Pack MDM with BP-MDM-TEM under constant current-constant voltage charging and constant current discharging conditions. The objective is to verify whether applying the thermal-electric coupling model to the mean model can effectively enhance the accuracy of SoC estimation for battery packs. Figures 9A, B depict error plots for this comparison.

Figure 9

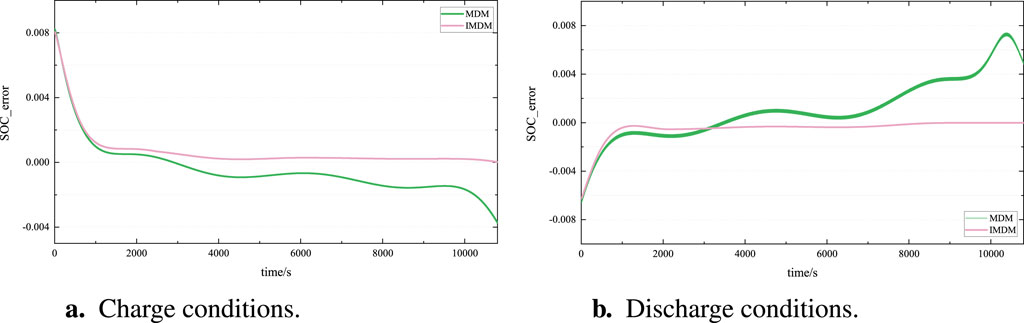
Figure 9. SoC estimation error of battery pack under charge-discharge conditions: (A) Charge conditions. (B) Discharge conditions.

As can be seen from the charge-discharge error diagrams in Figures 9A, B, the battery operating temperature of the model fluctuates throughout the SoC estimation. However, the BP-MDM-TEM applies the thermal-electric coupling model to the mean model and updates the model parameters with the battery’s operating temperature. Therefore, the BP-MDM-TEM shows a clear convergence trend in the early stages of estimation. This is because during the battery’s operation, part of the heat is not released in time and is absorbed by the battery itself, causing an increase in battery temperature. This temperature affects the battery parameters and changes its external characteristics, leading to a difference in temperature between MDM and the reference value. In the later stages of estimation, the BP-MDM-TEM’s SoC estimate can converge near the reference value.

According to the experimental results, the MAE of SoC estimated by the BP-MDM-TEM is 0.468% and RMSE is 0.982%, while the MAE of the traditional MDM method is 0.992% and RMSE is 1.279%. It is evident that the BP-MDM-TEM has higher accuracy, meeting the requirements for SoC estimation.

5 Conclusion

Based on the analysis of the battery pack characteristics, a thermal-electrical coupling mean-difference model for series-connected battery packs is proposed to address the issue of inconsistencies in battery characteristics due to changes in core temperature during operation. The thermal-electrical coupling model is used to describe the mean characteristics of the battery pack, thereby representing the overall relationship of the battery pack with temperature changes, while the difference model describes the discrepancies between each individual battery and the overall characteristics of the battery pack. The dual-time-scale method is employed to estimate the BP-MDM-TEM, reducing the computational load of the difference model. When the characteristics of an individual battery exceed the system’s allowable limits, the system estimates the overall characteristics of the battery pack based on the important battery method. To achieve accurate estimation of the battery pack’s SoC, the paper applies the adaptive EKF method to estimate the SoC of the battery pack, overcoming the impact of process noise and measurement noise on the system estimation. A hardware testing platform was constructed, and three battery pack testing condition experiments were designed. Based on HPPC conditions, the battery pack model was identified, and simulation models of the battery pack were constructed for both charge and discharge testing conditions to estimate the battery pack’s SoC. The experimental results demonstrate that this method can consider temperature changes during battery pack operation, estimate the battery pack’s SoC and temperature simultaneously, and update model parameters based on the operating temperature of the battery, effectively meeting the accuracy requirements for SoC estimation of the battery pack.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HY: Conceptualization, Funding acquisition, Resources, Writing–original draft, Writing–review and editing. YX: Funding acquisition, Resources, Writing–original draft, Writing–review and editing. QG: Methodology, Project administration, Validation, Writing–review and editing. YM: Project administration, Writing–original draft. XZ: Methodology, Writing–review and editing. JW: Validation, Writing–review and editing. YZ: Writing–original draft, Software. CW: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This paper was supported by the science and technology project of Zhejiang Dayou Group Co., Ltd. Under grant DY2023-31.

Conflict of interest

Authors HY, YX, QG, YM, XZ, and JW were employed by Hangzhou Electric Power Equipment Manufacturing Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from the science and technology project of Zhejiang Dayou Group Co., Ltd. The funder had the following involvement in the study: The funder participated in the project initiation of the paper: provided resources for data collection and provided technical support during the study.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Belt, J. R. (2010). Battery test manual for plug-in hybrid electric vehicles. Idaho Falls, ID (United States): Tech. rep., Idaho National Lab.

Google Scholar

Chen, X., Liu, Z., Sheng, H., Wu, K., Mi, J., and Li, Q. (2024). Transfer learning based remaining useful life prediction of lithium-ion battery considering capacity regeneration phenomenon. J. Energy Storage 76, 109798. doi:10.1016/j.est.2023.109798

CrossRef Full Text | Google Scholar

Cheng, Y.-S. (2024). Identification of parameters for equivalent circuit model of li-ion battery cell with population based optimization algorithms. Ain Shams Eng. J. 15, 102481. doi:10.1016/j.asej.2023.102481

CrossRef Full Text | Google Scholar

Diep, N., Trung, N., and Kiji, S. (2024). An online battery-state of charge estimation method using the varying forgetting factor recursive least square-unscented kalman filter algorithm on electric vehicles. Int. J. Electr. Comput. Eng. (IJECE) 14, 2541–2553. doi:10.11591/ijece.v14i3.pp2541-2553

CrossRef Full Text | Google Scholar

Gu, C. Y., and Wang, W. B. (2000). Thermal-electrochemical modeling of battery systems. J. Electrochem. Soc. 147, 2910. doi:10.1149/1.1393625

CrossRef Full Text | Google Scholar

Hong, C., Cho, H., Hong, D., Oh, S.-K., and Kim, Y. (2023). An improved thermal single particle model and parameter estimation for high-capacity battery cell. Electrochimica Acta 439, 141638. doi:10.1016/j.electacta.2022.141638

CrossRef Full Text | Google Scholar

Hosseininasab, S., Momtaheni, N., Pischinger, S., Günther, M., and Bauer, L. (2023). State-of-charge estimation of lithium-ion batteries using an adaptive dual unscented kalman filter based on a reduced-order model. J. Energy Storage 73, 109011. doi:10.1016/j.est.2023.109011

CrossRef Full Text | Google Scholar

Hou, J., Liu, J., Chen, F., Li, P., Zhang, T., Jiang, J., et al. (2023). Robust lithium-ion state-of-charge and battery parameters joint estimation based on an enhanced adaptive unscented kalman filter. Energy 271, 126998. doi:10.1016/j.energy.2023.126998energy.2023.126998

CrossRef Full Text | Google Scholar

Jia, X., Wang, S., Cao, W., Qiao, J., Yang, X., Li, Y., et al. (2023). A novel genetic marginalized particle filter method for state of charge and state of energy estimation adaptive to multi-temperature conditions of lithium-ion batteries. J. Energy Storage 74, 109291. doi:10.1016/j.est.2023.109291109291

CrossRef Full Text | Google Scholar

Karimi, D., Behi, H., Van Mierlo, J., and Berecibar, M. (2023). Equivalent circuit model for high-power lithium-ion batteries under high current rates, wide temperature range, and various state of charges. Batteries 9, 101. doi:10.3390/batteries9020101batteries9020101

CrossRef Full Text | Google Scholar

Kumar, R. R., Bharatiraja, C., Udhayakumar, K., Devakirubakaran, S., Sekar, K. S., and Mihet-Popa, L. (2023). Advances in batteries, battery modeling, battery management system, battery thermal management, soc, soh, and charge/discharge characteristics in ev applications. IEEE Access 11, 105761–105809. doi:10.1109/access.2023.33181213318121

CrossRef Full Text | Google Scholar

Lai, X., Yuan, M., Tang, X., Yao, Y., Weng, J., Gao, F., et al. (2022). Co-estimation of state-of-charge and state-of-health for lithium-ion batteries considering temperature and ageing. Energies 15, 7416. doi:10.3390/en15197416en15197416

CrossRef Full Text | Google Scholar

Li, H., Wang, S. L., and Zou, C. Y. (2021). Research on SOC estimation based on Thevenin model and adaptive Kalman. Autom. Instrum. 42, 46–51. doi:10.16086/j.cnki.issn1000-0380.2019100006

CrossRef Full Text | Google Scholar

Lin, Q., Li, X., Tu, B., Cao, J., Zhang, M., and Xiang, J. (2023). Stable and accurate estimation of soc using exogenous kalman filter for lithium-ion batteries. Sensors 23, 467. doi:10.3390/s230104673390/s23010467

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, F., Yu, D., Su, W., and Bu, F. (2023a). Multi-state joint estimation of series battery pack based on multi-model fusion. Electrochimica Acta 443, 141964. doi:10.1016/j.electacta.2023.141964

CrossRef Full Text | Google Scholar

Liu, X., Xia, W., Li, S., Lin, M., and Wu, J. (2024). State of charge estimation for lithium-ion battery pack with selected representative cells. IEEE Trans. Transp. Electrification 10, 4107–4118. doi:10.1109/tte.2023.3314532TTE.2023.3314532

CrossRef Full Text | Google Scholar

Liu, Z., Chen, J., Fan, Q., and Wang, D. (2023b). A key-term separation based least square method for hammerstein soc estimation model. Sustain. Energy, Grids Netw. 35, 101089. doi:10.1016/j.segan.2023.101089

CrossRef Full Text | Google Scholar

Navas, S. J., González, G. C., Pino, F., and Guerra, J. (2023). Modelling li-ion batteries using equivalent circuits for renewable energy applications. Energy Rep. 9, 4456–4465. doi:10.1016/j.egyr.2023.03.103

CrossRef Full Text | Google Scholar

Qian, C., Guan, H., Xu, B., Xia, Q., Sun, B., Ren, Y., et al. (2024). A cnn-sam-lstm hybrid neural network for multi-state estimation of lithium-ion batteries under dynamical operating conditions. Energy 294, 130764. doi:10.1016/j.energy.2024.130764130764

CrossRef Full Text | Google Scholar

Ramachandran, R., Ganeshaperumal, D., and Subathra, B. (2019). “Parameter estimation of battery pack in EV using extended kalman filters,” in 2019 IEEE international conference on clean energy and energy efficient electronics circuit for sustainable development (INCCES), 1–5. doi:10.1109/INCCES47820.2019.9167740

CrossRef Full Text | Google Scholar

Selvaraj, V., and Vairavasundaram, I. (2023). A comprehensive review of state of charge estimation in lithium-ion batteries used in electric vehicles. J. Energy Storage 72, 108777. doi:10.1016/j.est.2023.108777

CrossRef Full Text | Google Scholar

Tian, J., Liu, X., Chen, C., Xiao, G., Wang, Y., Kang, Y., et al. (2023). Feature fusion-based inconsistency evaluation for battery pack: improved Gaussian mixture model. IEEE Trans. Intelligent Transp. Syst. 24, 446–458. doi:10.1109/TITS.2022.3211002

CrossRef Full Text | Google Scholar

Trevizan, R. D., O’Brien, V. A., and Rao, V. S. (2024). “Adaptive battery state estimation considering input noise compensation,” in 2024 international symposium on power electronics, electrical drives, automation and motion (SPEEDAM), 223–228. doi:10.1109/SPEEDAM61530.2024.10609188

CrossRef Full Text | Google Scholar

Van, C. N., and Vinh, T. N. (2020). Soc estimation of the lithium-ion battery pack using a sigma point kalman filter based on a cell’s second order dynamic model. Appl. Sci.-Basel 10, 1896. doi:10.3390/app10051896

CrossRef Full Text | Google Scholar

Wang, J., Meng, J., Peng, Q., Liu, T., and Peng, J. (2024a). An electrochemical-thermal coupling model for lithium-ion battery state-of-charge estimation with improve dual particle filter framework. J. Energy Storage 87, 111473. doi:10.1016/j.est.2024.111473

CrossRef Full Text | Google Scholar

Wang, X., Gao, Y., Lu, D., Li, Y., Du, K., and Liu, W. (2024b). Lithium battery soc estimation based on improved iterated extended kalman filter. Appl. Sci. 14, 5868. doi:10.3390/app14135868

CrossRef Full Text | Google Scholar

Wu, T., Wang, Y., and Zhang, J. (2023). Research on multilayer fast equalization strategy of li-ion battery based on adaptive neural fuzzy inference system. J. Energy Storage 67, 107574. doi:10.1016/j.est.2023.107574

CrossRef Full Text | Google Scholar

Xin, K., Wei, S., and Hongtao, C. (2020). Parameter identification based on simplified electrochemical model of lithium ion battery. Energy Storage Sci. Technol. 9, 969. doi:10.19799/j.cnki.2095-4239.2019.0273

CrossRef Full Text | Google Scholar

Xu, Y., Zhang, Y., Zeng, M., Huang, X., and Wang, Z. (2024). An electrothermal coupling model for estimating the internal temperature of lithium-ion battery based on microthermal resistance method. Electrochem. Commun. 166, 107776. doi:10.1016/j.elecom.2024.107776107776

CrossRef Full Text | Google Scholar

Yu, Q., Huang, Y., Tang, A., Wang, C., and Shen, W. (2023). Ocv-soc-temperature relationship construction and state of charge estimation for a series– parallel lithium-ion battery pack. IEEE Trans. Intelligent Transp. Syst. 24, 6362–6371. doi:10.1109/TITS.2023.3252164

CrossRef Full Text | Google Scholar

Yu, Z., Tian, Y., and Li, B. (2024). A simulation study of li-ion batteries based on a modified p2d model. J. Power Sources 618, 234376. doi:10.1016/j.jpowsour.2024.234376234376

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, Y., Zhang, C., Qiao, X., Ge, Y., Li, X., et al. (2024). State-of-health estimation for lithium-ion battery via an evolutionary stacking ensemble learning paradigm of random vector functional link and active-state-tracking long–short-term memory neural network. Appl. Energy 356, 122417. doi:10.1016/j.apenergy.2023.122417apenergy.2023.122417

CrossRef Full Text | Google Scholar

Zhou, J., Xing, B., and Wang, C. (2020). A review of lithium ion batteries electrochemical models for electric vehicles. E3S Web Conf. 185, 04001. doi:10.1051/e3sconf/202018504001202018504001

CrossRef Full Text | Google Scholar

Zhou, L., Lai, X., Li, B., Yao, Y., Yuan, M., Weng, J., et al. (2023). State estimation models of lithium-ion batteries for battery management system: status, challenges, and future trends. Batteries 9, 131. doi:10.3390/batteries9020131

CrossRef Full Text | Google Scholar