- Shenzhen Audencia Financial Technology Institute, Shenzhen University, Shenzhen, China
This paper proposes a dynamic price-based demand response (DR) energy sharing model for peer-to-peer (P2P) transactions of photovoltaic (PV) prosumers in microgrids. First, a multi-subject dynamic game model is constructed between a retail electricity provider (REP), an energy sharing provider (ESP), and multiple prosumers participating in energy sharing transactions. The cost model of the prosumers is designed to reflect the DR from the perspectives of economic cost and the satisfaction of prosumers with electricity consumption patterns. Further, the effect of social learning (SL) among prosumers on multi-subject decision-making behavior is considered. The model is solved using a deep reinforcement learning algorithm, and the results show that: (1) SL reduces the volatility of electricity prices and provides more stable price signals for market participants. (2) When prosumers are unwilling to change their electricity consumption pattern, ESP and REP will increase the purchase price and reduce the sale price, encouraging prosumers to increase electricity consumption to some extent. (3) As the number of prosumers increases, the benefits to price setters increase, but the costs to prosumers rise accordingly. This study provides a valuable reference for promoting the development of the PV industry and the diffusion of sustainable energy.
1 Introduction
In recent years, the rapid development of photovoltaic (PV) technology has empowered households and small businesses to generate their own electricity through solar panels, creating a new category of energy users known as PV prosumers (Rathnayaka et al., 2013; Ma et al., 2016). A prosumer is an entity that has the capacity to produce, consume and possibly demand response (DR) at the same time (Kanchev et al., 2011). A group of prosumers can be integrated into a prosumer energy community (Paudel et al., 2018). Energy trading between neighboring prosumers can be considered as sharing of renewable energy (Liu N et al., 2018). The sharing of renewable energy has significant implications for the traditional energy industry and the broader energy system, as they have the potential to transform the way energy is generated, consumed, and traded (Fridgen et al., 2020; Rabaia et al., 2021; Sayed et al., 2021). Energy sharing trading among PV prosumers not only contribute to the decarbonization of the energy sector but also promote the democratization of energy, allowing individuals and communities to take control of their energy future (Y. Yang et al., 2022; Zhang et al., 2022). Hence, understanding the behavior and decision-making of PV prosumers and promoting the development of energy sharing models for them is of great importance in promoting sustainable and inclusive energy transition.
However, the uncertainty of PV energy makes it difficult to coordinate the sharing of PV energy between prosumers (Liu N et al., 2018). One of the main challenges is the stochastic, volatile and intermittent of PV energy, which means that prosumers do not always have the energy available to respond to demand signals from the grid (Rathor and Saxena 2020). This makes it challenging to balance supply and demand in real-time and create a stable grid. Energy sharing providers (ESPs) have emerged as agents to serve all PV prosumers involved in energy sharing transactions, with the goal of ensuring a balance of power and payments for the energy sharing community (Chen et al., 2020). They act as intermediaries, aggregating and selling the surplus PV energy produced by prosumers to retail electricity providers (REPs), and purchasing electricity from REPs when PV energy is scarce in the energy-sharing community. Hence, as microgrids become increasingly complex and different parties may have varying goals for power purchase, sale and consumption depending on their roles (Liu et al., 2017), it is significant to study the strategies of different actors in energy sharing communities. And a large number of studies have been conducted on energy sharing among multiple prosumers in smart grids, which can be broadly classified into two categories: integrated planning of energy sharing systems based on optimization methods and design of dynamic pricing strategies based on game theory.
Optimization methods are commonly used in the integrated planning of energy sharing systems for prosumers, aiming to find the optimal solution that satisfies the multiple objectives of the system. Alarcon-Rodriguez, Ault, and Galloway (2010) pointed out that the integrated planning of energy sharing systems for prosumers is a complex problem that involves optimizing multiple objectives, including minimizing energy costs, reducing greenhouse gas emissions, and ensuring a reliable supply of energy. Based on this, Pourakbari-Kasmaei et al. (2019) proposed a trilateral planning model for integrated community energy systems and PV-based prosumers to handle a joint master-slave operation-planning problem. Xiong, Qing, and Li (2022) designed a day-ahead and real-time P2P power transaction mechanism based on blockchain to meet the economic and security requirements of PV prosumer. Yang et al. (2023) established a bi-level planning model of DPV-energy storage systems in distribution network considering the uncertainty of DPV output power and the DR behavior of users under the background of coordinated operation of China’s electricity market and carbon market.
However, it is difficult to accurately and comprehensively analyze the P2P energy sharing transaction process at the individual level based on optimization methods alone, because they assume that all agents in the system have perfect information and behave rationally (Luo et al., 2022). This assumption may not hold in real-world situations, where agents may have incomplete information or may not behave rationally. In contrast, game theory provides a framework for modeling the behavior of agents in the system and analyzing the strategic interactions between them (Jiang, Yuan, and Li 2021). Game theory can capture the complexity and uncertainty of real-world situations, where agents may have different objectives and may behave strategically to achieve their goals. Game theory can also handle decentralized decision-making, where agents make decisions based on their own information and preferences (Soto et al., 2021).
Game theory has been extensively used in the design of dynamic pricing models for energy sharing systems of prosumers, including cooperative games, non-cooperative games, Stackelberg game, and other types. The cooperative game is essentially a benefit distribution problem, that is, when the prosumers shift from competition to cooperation, how to reasonably distribute the benefits of cooperation (Liu X et al., 2018). Han, Morstyn, and McCulloch (2018) used cooperative game theory to build an energy grand coalition and optimize the operation of distributed energy storage systems with the goal of minimizing coalition energy costs. Tushar et al. (2020) designed a coalition formation game to help prosumers determine how they can opportunistically participate in P2P transactions using their own batteries. Jiang, Yuan, and Li (2021) analyzed the economic interaction between the community energy manager and the PV prosumers based on Nash bargaining game, and developed an incentive mechanism to encourage the prosumers to actively participate in energy management.
The non-cooperative game focuses on the competitive behavior of market members, assuming that each market member is rational and will compete with others to maximize its own benefits (Nash 1950). Bhatti and Broadwater (2020) used a non-cooperative, infinite strategy, multiplayer game to model energy trading interactions among prosumers, which resulted in an increased payoffs for prosumers and higher reliability. He and Zhang (2020) formulated a non-cooperative game among all participants involved in the community energy sharing market consisting of distributed solar power prosumers and consumers to determine the double-sided auction market spot price. Luo et al. (2022) proposed a decentralized trading scheme based on noncooperative game theory to examine the impact of distributed energy ownership on the interests of prosumers in the P2P trading market.
The Stackelberg game, a branch of non-cooperative games, is most commonly used to study how stakeholders make optimal decisions when there is a leader-follower structure of energy trading relationships between community energy managers and prosumers (Erol and Filik 2022). Cui, Wang, and Liu (2018) formulated the energy sharing problem in a microgrid as a Stackelberg game, where the microgrid operator is the leader of the game and sets the internal buying and selling prices for energy sharing, and PV prosumers are the followers and decide their energy sharing allocation based on the internal prices. Ahmadi et al. (2020)modeled a bilevel retail market among an aggregator and multiple microgrids as a single-leader-multi follower game to determine the optimal demand scheduling for prosumers and the price-power bidding strategies for microgrids. Dong et al. (2022) proposed a P2P energy trading strategy in the blockchain environment and established a two-layer model of the leader and follower to determine prices using the Stackelberg game.
The existing literature has extensively studied the trading strategies of prosumers, microgrid operators, and other agents in energy-sharing communities using optimization, game theory, and other methods. However, these studies have not considered the impact of social learning (SL) among prosumers. SL among prosumers refers to the process by which individuals learn from the behavior and experiences of others in their social network (Hampton and Simon, 2013; Kendal et al., 2018). In the marketing literature, the SL theory has been widely used. Scholars have extensively studied the marketing strategies of companies under the influence of SL behavior, including quality disclosure strategy (Zhu et al., 2021), inventory ordering strategy (Zheng, Shou, and Yang 2021), return policies (B. Liu et al., 2022), and so on. They confirmed that SL behavior influences consumers’ purchase intention and decision-making process, thus changing the profitability of companies and the welfare of consumers.
The presence of the SL effect is often considered in the study of dynamic pricing. Papanastasiou and Savva (2017) investigated how the presence of SL affects the strategic interaction between a dynamic-pricing monopolist and a forward-looking consumer population, within a simple two-period model. Cao, Fang, and Wang (2021) investigated the impacts of SL on a real-time pricing scheme in the electricity market, and found that SL helps power companies balance the demand and supply. Wang, Fang, and Cao (2022) examined the influence of SL on customer behavior under time-of-use pricing implementation in electricity retail market, and showed that SL brings volatility to the market. These studies demonstrate that it is informative to consider consumer SL behaviors in dynamic-pricing design and inform. And in the spread of more efficient and sustainable energy consumption patterns, which ultimately benefits the entire microgrid. By considering the impact of SL on decision-making behavior, the energy sharing model can be more accurately designed and optimized, leading to more efficient and sustainable energy sharing transactions among PV prosumers.
To this end, this paper aims to address the problem of energy sharing transactions among PV prosumers, ESPs and RSPs in microgrids, taking into account the impact of SL on the agents’ decision making. The main contributions are as follows:
(1) A dynamic pricing model for energy sharing in microgrids based on a multi-subject dynamic game is proposed, in which the interaction of PV prosumers, ESPs and RSPs is considered.
(2) A cost model of the prosumers is designed to reflect the DR from the perspectives of economic cost and the satisfaction of prosumers with electricity consumption patterns.
(3) The effect of SL among prosumers on multi-subject decision-making behavior is investigated, and results show that SL reduces the volatility of electricity prices and decreases market risk.
The remainder of this paper is organized as follows. Section 2 describes the multi-subject dynamic game model, DR, and SL mechanisms. Section 3 presents the simulation results and sensitivity analysis. Section 4 concludes the full paper and suggests future research directions.
2 The model
2.1 Problem description
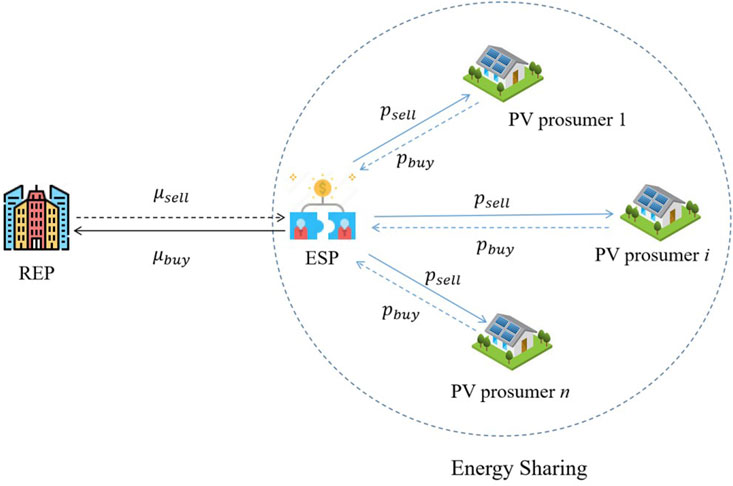
PV prosumers consist of PV systems, loads, customer energy management systems and smart meters. PV prosumers can share energy, and their additional PV energy can be shared among PV prosumers rather than traded directly with outside REPs. It is assumed that the ESP is the agent of PV prosumers and provides energy sharing services to all PV prosumers and is responsible for ensuring the balance of electricity in the energy sharing area. And the ESP trades directly with outside REPs. As indicated in Figure 1, self-consumption of PV energy is preferred by PV prosumers in the energy sharing area. If the PV energy does not meet the load demand, the PV prosumer will purchase energy from the ESP. If the demand of PV prosumer is less than PV’ production, the excess PV power will be sold to the ESP. In addition, if the power balance cannot be achieved within the shared area, the ESP will purchase or sell power from the REP depending on the internal power deviation.
2.2 Basic model
Suppose there are
Due to the priority trading within the shared area, for the ESP, if the electricity within the shared area cannot be balanced through the production consumers, then the electricity needs to be purchased or sold from the retailers to achieve the balance of supply and demand. The electricity
If
2.3 Demand response
It is assumed that all PV prosumers participating in energy sharing have a certain percentage of shiftable load. The REP sets prices
The adjusted electricity consumption can be denoted as
On the other hand, the variable electricity consumption is represented as
In addition, when implementing DR, it is important to consider not only the cost of electricity consumption by PV prosumers, but also PV prosumers’ satisfaction with the electricity consumption pattern (Lu and Zhang 2022). When the difference in electricity consumption before and after DR is large for PV prosumers, their satisfaction with the electricity consumption pattern will be lower and vice versa. Thus, the utility function of PV prosumer
where
In pursuit of cost minimization, PV prosumer
The relationship between adjusted electricity consumption and price is obtained after simplification as follows
According to Equation 6, when
Thus, when
This implies that by adjusting the value of
The ESP acts as an agent of PV prosumers, not for profit, but only as a bridge between PV prosumer. Therefore, the profit of the ESP can be denoted as Equation 7
Where
Equations 8, 9 has the meaning assigned as Equations 1, 2.
2.4 Social learning
Since consumers pay more attention to the decisions of friends around them when making decisions, this paper consider the impact of SL among production consumers on the decision-making behavior of multiple subjects such as retailers, ESPs, and production consumers in social networks. Assume that
The network of
After communicating with other neighbors, PV prosumer
Where
When implementing a peak shaving and valley filling strategy,
When implementing a load shifting strategy,
When implementing a load curtailment strategy,
3 Simulation
3.1 The algorithm
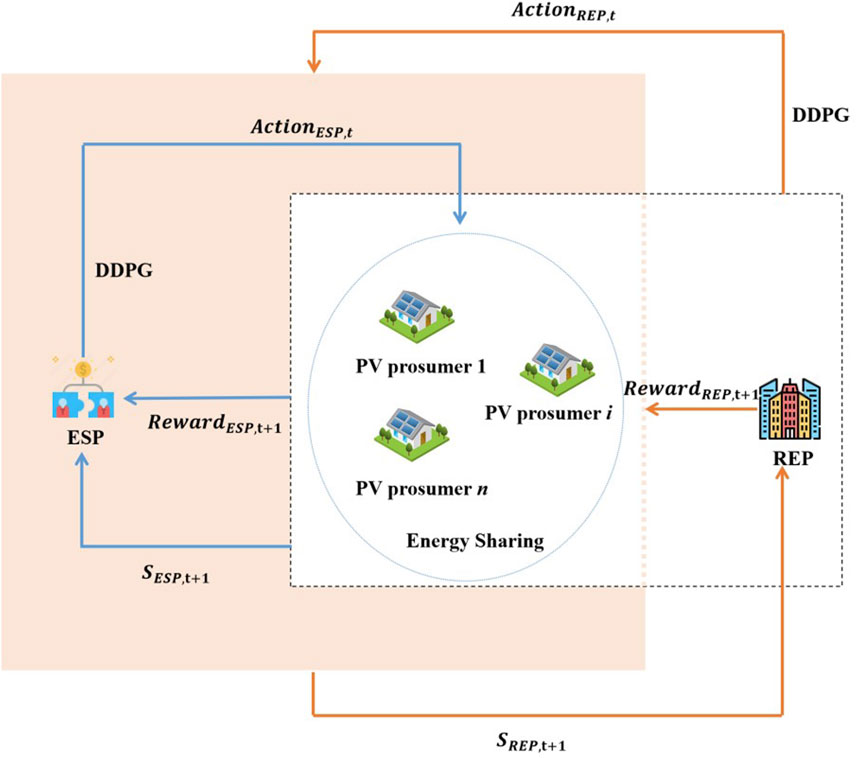
The deep deterministic policy gradient (DDPG) algorithm is a commonly used deep reinforcement learning algorithm, mainly for solving problems in continuous action space. The algorithm is based on a strategy gradient approach that uses a deep neural network to approximate the value function and the strategy function. Specifically, The DDPG algorithm uses an Actor network and a Critic network, where the Actor network is used to learn the optimal strategy, which receives the current state as input and outputs a continuous vector of actions. The Critic network is used to evaluate the goodness of the strategy, which receives the current state and the actions as input and outputs a Q value indicating the long-term cumulative reward. In addition, to improve learning, the DDPG algorithm utilizes an experience replay mechanism for storing past experiences in order to learn them repeatedly.
According to the real-time pricing model in Section 3, to test different demand response strategies and pricing methods, this paper adjusted the time intervals for price decision-making and designed multiple scenarios to evaluate the pricing decisions of the ESP and REP. In these settings, the effectiveness of various demand response schemes is assessed, and the DDPG algorithm is used to achieve dynamic pricing optimization, enabling better adaptation to supply and demand fluctuations in different market conditions. The specific details are as follows:
Real-Time Pricing Scheme (RTP Scheme): In this paper, a day is divided into
Time-Of-Use Pricing Scheme (TOU Scheme): A day is divided into three periods: peak, off-peak, and valley. In the simulation, the off-peak period is set from 8 a.m. to 4 p.m., the peak period is from 7 p.m. to 12 a.m., and the valley period is from 12 a.m. to 8 a.m., defined as the set
Fixed Pricing Scheme (FP Scheme): In this scheme, the REP only needs to make one fixed decision on
It is assumed that all PV prosumers participating in energy sharing have a certain percentage of shiftable load. The REP sets prices
The ESP has to consider the electricity consumption of all PV prosumers at different times, and its state information can be noted as
The REP mainly considers transactions with the ESP, whose status information can be noted as
The REP will reformulate prices
3.2 Parameter setting
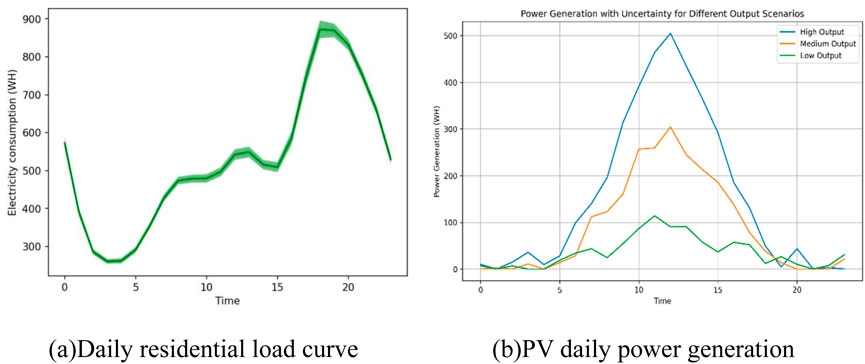
This paper utilizes daily residential energy consumption and PV generation data and applies cluster analysis to generate typical scenarios for PV generation (shown in Figures 3A, B, and the data is sourced from https://www.energymadeeasy.gov.au/). First, daily PV generation curves are constructed based on historical PV generation data, and cluster analysis is conducted according to the variations in generation across different time periods. Using the K-means clustering algorithm, the original PV generation data is divided into 3 clusters (There are three scenarios: high, medium and low), with each cluster representing a typical generation scenario. Then, the centroid or the point closest to the centroid is selected as the representative scenario for each cluster, ensuring that these scenarios capture the variability in PV generation under different weather conditions. Finally, corresponding probability weights are assigned to each representative scenario to construct a probabilistic scenario set for PV generation, thereby effectively capturing the uncertainties in generation for subsequent analyses.
Figure 3A shows the daily electricity consumption of PV prosumer. From about 5:00 a.m., their electricity consumption gradually increased and continued until 8:00 a.m. During the period from 8:00 a.m. to 4:00 p.m., electricity consumption basically remained in a stable state. Then, electricity consumption gradually increased until it reached a peak at 7:00 p.m., and then began to gradually decrease. This is in line with the characteristics of residential customers’ electricity consumption. Figure 3B shows the power generation of the PV panels in the producer-consumer households. Around 8:00 a.m., the power generation of PV panels starts to increase rapidly and continues until 12:00 noon. After 12:00 a.m., the power generation gradually decreases until it drops to 0 at night, indicating that the PV panels mainly work during the daytime and do not produce electricity at night.
3.3 Analysis of results
In this section, this paper explore the pricing of the ESP and REP and the benefits of different subjects under SL and no SL, respectively, to reveal the impact of SL on the decision-making behavior of multiple subjects.
3.3.1 Simulation results under no SL
Without considering the SL scenario, Figure 4A shows the average daily electricity sale and purchase prices of ESP and REP. This paper concludes that the average electricity sale price of ESP gradually increases and stabilizes around 24, and the average electricity purchase price gradually stabilizes around 2.58. The average daily electricity sales price of REP is stabilized around 9.5, and the average electricity purchase price is gradually stabilized around 7.6. Figure 4B shows the electricity prices set by ESP and REP at different times of the day. It exhibits two distinct phases. Firstly, from 8 p.m. to 10 a.m. the next day, the electricity sale price of ESP is approximately 20 and the electricity purchase price is about 5, while the electricity sale price of REP is approximately 9.7 and the electricity purchase price is about 7.5. Secondly, from 10 a.m. to 8 p.m., the electricity sale price of ESP is approximately 30 with a close-to-zero the electricity purchase price, while the electricity sale price of REP is about 9 and the electricity purchase price is about 8. Figure 4C shows the total daily revenue of the ESP and REP, and the daily electricity cost of PV prosumers. The total daily revenue of ESP eventually stabilizes at about 33,000,000, while the total daily revenue of REP eventually stabilizes at about 16,000,000. At the same time, the daily electricity cost of PV prosumers is about 30,000,000. Figure 4D further shows the revenue of the ESP and REP in 1 day. For the ESP, its revenue rises from about 500,000 at 4:00 a.m. to about 1,300,000 at 12:00 a.m., then drops to about 500,000, rises rapidly to about 3,800,000 after 3:00 p.m., and finally drops again. For the REP, its revenue rises from about 400,000 at 4 a.m. to about 700,000 at 12 a.m., then drops to about 200,000, rises rapidly to about 1,300,000 after 3 p.m., and finally drops again to about 400,000. The electricity cost of PV prosumers is 0 from 11 a.m. to 7 p.m., and in the range of 1,000–3,500 for the rest of the day.
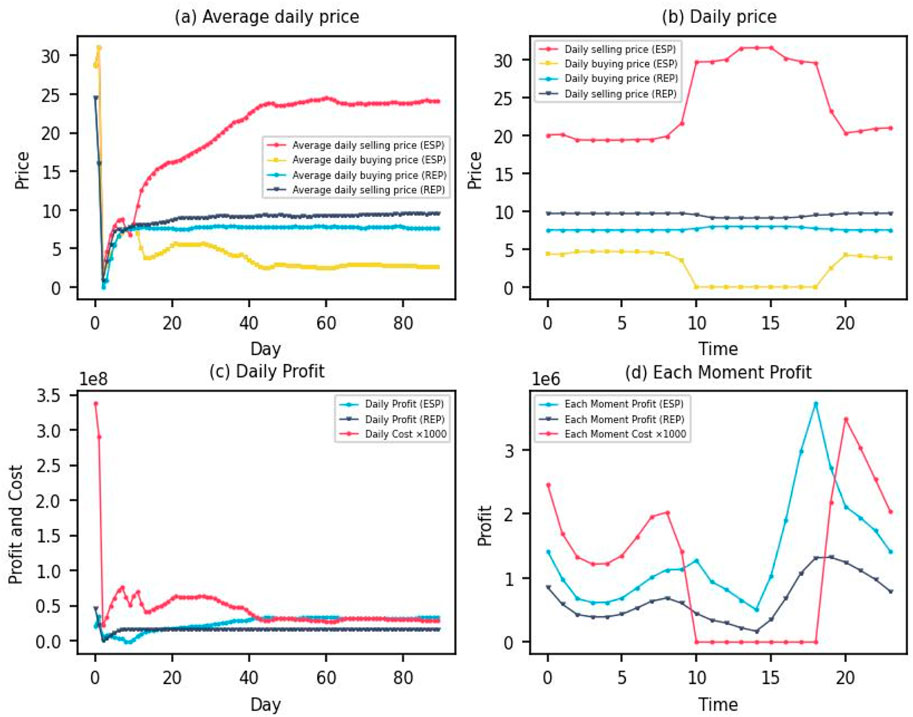
Figure 4. Decision-making results under no SL. (A) Average daily price. (B) Daily price. (C) Daily Profit. (D) Each Moment Profit.
In summary, first, the electricity price fluctuation for the ESP and REP reflects the supply and demand. During the period from 10:00 a.m. to 8:00 p.m., the electricity purchase price for ESP drops to close to zero and the electricity sale price is higher because of the high generation of PV panels, which leads to sufficient electricity supply. During the other hours, the electricity purchase price of ESP is relatively high due to the tight electricity supply caused by the low generation of PV panels. This price fluctuation encourages PV prosumers to use more electricity during the time when the electricity supply is sufficient, thus keeping the whole system in balance in terms of supply and demand. Second, the revenues fluctuations of the ESP and REP reflect their strategies at different times of the day. During the daytime, especially during peak PV generation periods, the ESP earns higher revenue by purchasing excess electricity from PV prosumers at lower prices and selling it to other PV prosumers who need electricity at higher prices. In turn, the REP purchases electricity during relatively low electricity demand periods to cope with electricity shortages during high demand periods. Finally, the electricity cost of PV prosumers is zero from 11 a.m. to 7 p.m. because the PV panels generate enough electricity to meet their electricity demand during this period. During the rest of the day, PV prosumers need to purchase electricity from the ESP because the PV panels are not generating enough electricity, thus incurring some electricity costs. This cost encourages PV prosumers to plan their electricity consumption more rationally and reduce their demand during non-peak PV generation periods.
3.3.2 Simulation results under SL
Considering the SL scenario, Figure 5A shows the average daily electricity sale and purchase prices for the ESP and REP. It can be observed that the average electricity sale price of the ESP gradually increases and stabilizes around 28, and the electricity purchase price gradually stabilizes around 2.4. While the average daily electricity sales price of REP stabilizes around 9.2, and the electricity purchase price gradually stabilizes around 8.1. Figure 5B shows the electricity prices for the ESP and REP at different times of the day under SL. Two distinct phases are presented. First, during the period from 8:00 p.m. to 10:00 a.m. the next day, the electricity sale price of the ESP is about 25 and the electricity purchase price is about 1.5. The electricity sale price of the REP is about 9.3 and the electricity purchase price is about 8.1. Second, during the period from 10:00 a.m. to 8:00 p.m., the electricity sale price of the ESP is about 34 and the electricity purchase price is about 4. The electricity sale price of the REP is about 9.3 with the electricity purchase price about 8.1. Figure 5C shows the total daily revenue of the ESP and REP and the daily electricity cost of PV prosumers under SL. The daily total revenue of the ESP eventually stabilizes around 40,000,000, while the daily total revenue of REP eventually stabilizes around 17,000,000. Meanwhile, the daily electricity cost of PV prosumers is about 23,000. Figure 5D further shows the revenue of the ESP and REP during the day under SL. For the ESP, its revenue rises from about 840,000 at 4:00 a.m. to about 1,500,000 at 12:00 p.m., then drops to about 500,000, rises rapidly to about 4,400,000 after 3:00 p.m., and finally drops again. For the REP, its revenue rises from about 400,000 at 4 a.m. to about 740,000 at 12 a.m., then drops to about 175,000, rises rapidly to about 143,000 after 3 p.m., and finally drops again to about 400,000. The electricity cost of PV prosumers rises from about 300 at 4:00 a.m. to about 1,150 at 12:00 a.m., then falls to about 400, rises rapidly to about 3,400 after 3:00 p.m., and then continues to fall again to about 300.
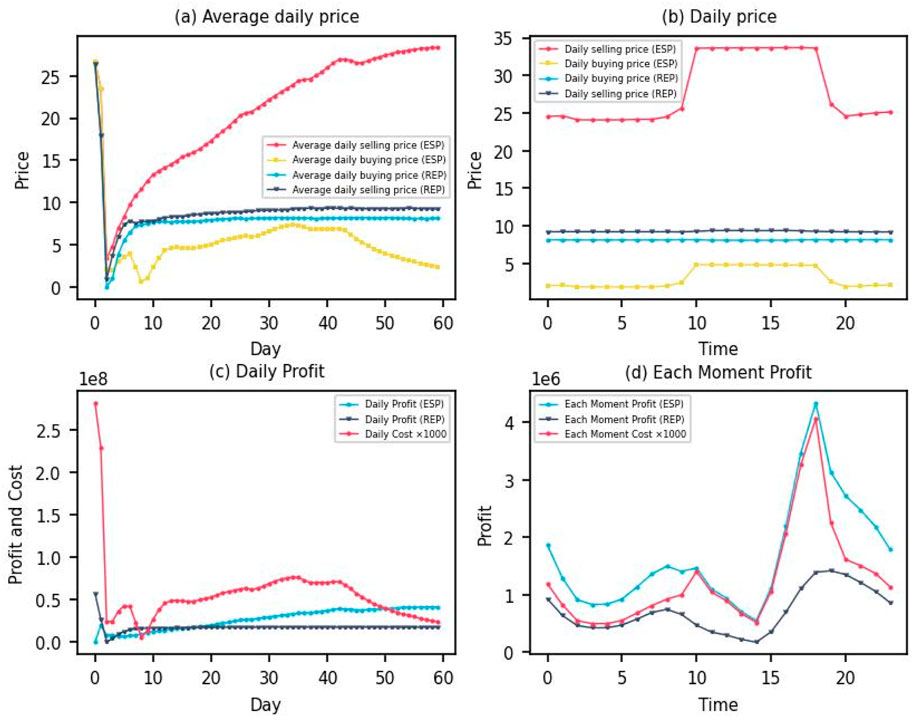
Figure 5. Decision-making results under SL. (A) Average daily price. (B) Daily price. (C) Daily Profit. (D) Each Moment Profit.
Compared to scenarios where SL does not exist, SL scenarios show advantages in the following areas: (1) Efficiency is improved. Through SL, PV prosumers can better understand and predict the dynamic changes of the electricity market, so as to reasonably adjust electricity consumption plans and generation strategies and improve the utilization rate of PV electricity generation. At the same time, ESP and REP can adjust the electricity purchase and sale price more flexibly according to the market demand, thus improving the operational efficiency of the whole system. (2) Costs are reduced. In the SL scenario, PV prosumers have lower daily electricity costs, which means they are able to meet their electricity needs at a lower cost. The lower cost is due to the fact that PV prosumers make better use of their own PV generation by communicating with other PV prosumers and adjusting their electricity consumption strategies, as well as buying electricity more rationally during the hours when electricity prices are low. (3) Revenue is increased. The total daily revenue of both ESP and REP increased under SL. This suggests that by better understanding and anticipating the dynamics of the market, both subjects can achieve higher economic efficiency in the electricity market. (4) Price volatility is reduced. The reduced electricity price volatility under SL compared to that without SL helps to reduce the overall market risk and provides a more stable price signal to market participants. (5) Promoting sustainable development. The pricing strategy under SL encourages PV prosumers to be more active in PV power generation and reduce carbon emissions through reasonable electricity consumption plans, thus promoting the popularity of renewable energy and helping to achieve the goals of energy transition and sustainable development.
In conclusion, the operational efficiency, economic efficiency, and sustainability of the overall electricity market are improved under SL. SL, as an information sharing and learning mechanism, helps market participants to better cope with the complexity and uncertainty of the electricity market and thus achieve optimization of the whole system. In addition, the model proposed in this paper demonstrates significant economic and environmental advantages compared to traditional energy systems. Firstly, by introducing DR and SL mechanisms, the model effectively reduces dependence on external electricity. PV prosumers can better meet their own electricity needs by sharing their self-generated power, thus lowering the costs of purchasing external electricity. This mechanism not only enhances the economic benefits for prosumers but also reduces the use of traditional fossil fuels, thereby lowering carbon emissions and environmental pollution. Secondly, the model promotes the utilization of distributed PV energy, fostering the widespread adoption of renewable energy and contributing to the achievement of sustainable development goals. Under this model, the power system becomes more flexible and efficient, meeting user demands while significantly reducing the environmental burden.
3.4 Sensitivity analysis
To further verify the validity of the method in this paper, this paper explored the influence of PV prosumers’ preference weights for electricity consumption satisfaction and the number of PV prosumers on the experimental results.
α indicates PV prosumers’ preference weights for electricity consumption satisfaction. Figure 6A shows that, in the absence of SL, the average daily purchase price of electricity for the ESP decreases from 12 to about 8 as α increases, while the average daily sale price increases from about 16.6 to about 17.3. The decrease in the purchase price is much larger than the increase in the sale price, economically encouraging PV prosumers to use more electricity. At the same time, the average daily purchase price of electricity for the REP increases from 8.4 to approximately 8.8, while the average daily sale price decreases from approximately 8.7 to approximately 8.3, indicating that the REP and ESP have the same objective of wanting PV prosumers to use more electricity. Figure 6B shows that, in the absence of SL, as α increases, the total daily benefit of the ESP increases from about 710,000 to about 740,000, the total daily benefit of REP increases from about 720,000 to about 770,000, and the cost of the producer-consumer decreases from about 4,500 to about 2,800. This indicates that when PV prosumers are reluctant to change their electricity consumption, the ESP and REP will set reasonable prices to help reduce the costs of PV prosumers, which in turn will encourage PV prosumers to increase their electricity consumption, indirectly increasing the benefits for both price setters.

Figure 6. Effect of α on decision results. (A) Average daily price without SL. (B) Daily Profit/Cost without SL. (C) Average daily price with SL. (D) Daily Profit/Cost with SL.
Figure 6C shows that under SL, the average daily electricity purchase price increases from 11.2 to about 11.4 and the average daily electricity sale price increases from about 8.3 to about 13.4 for the ESP as α increases. The average daily electricity purchase price increases from 8.1 to about 9.2 and the average daily electricity sale price decreases from about 8 to about 7.8 for the REP. This indicates that under SL, the electricity purchase price increases and electricity sales prices decrease, suggesting that SL among PV prosumers weakens the dominance of price setters. Figure 6D shows that under SL, as α increases, the total daily revenue of the ESP increases from about 37,000 to about 338,000, the total daily revenue of the REP increases from about 708,000 to about 798,000, but the cost of PV prosumers increases from about 1,300 to about 3,000. This indicates that under SL, the information sharing among PV prosumers makes the price setters both benefit. However, the cost to PV prosumers increases because the reduction in the electricity sale price increases PV prosumers’ electricity consumption, which in turn increases their costs.
Figure 7A shows that without SL, the average daily electricity purchase price of the ESP increases from 1.4 to about 14.3 and the average daily electricity sale price decreases from about 16 to about 14.3 as the number of PV prosumers increases. This is due to the fact that the increase in the number of PV prosumers increases market competition, causing the ESP to have to reduce the electricity sale price to attract more PV prosumers. In addition, the average daily electricity purchase price of the REP decreases from 9.2 to approximately 7.1 and the average daily sale price increases from approximately 7.8 to approximately 9.2. This is due to increased competition within the shared area causing outside REP to choose to adjust its pricing strategies to maximize its revenue. Figure 7B shows that as the number of PV prosumers increases, the total daily revenue of ESP increases from about 57,000 to about 1,650,000, the total daily revenue of REP increases from about 260,000 to about 1,600,000, and the cost of PV prosumers decreases from about 600 to about 5,000. This shows that in the absence of SL, as the market size increases, the benefits of price setters increase and costs of PV prosumers decrease in relative terms. Figure 7C shows that under SL, as the number of PV prosumers increases, the average daily purchase price for the ESP increases from 7 to about 14 and the average daily sale price increases from about 10 to about 19. Meanwhile, the average daily purchase price for the REP increases from 8.5 to about 9 and the average daily sale price decreases from about 9.7 to about 6.6. This reflects the fact that SL helps balance the shared regional internal supply and demand, weakening the price dominance of external REP. Figure 7D shows that as the number of PV prosumers increases, the total daily revenue of the ESP rises from about −188,000 to about 1,920,000, the total daily revenue of the REP rises from about 160,000 to about 1,960,000, and the cost of PV prosumers rises from about 1,200 to about 5,800. This suggests that under SL, as the market size increases, the benefits to price setters increase, but the costs of PV prosumers increase accordingly.
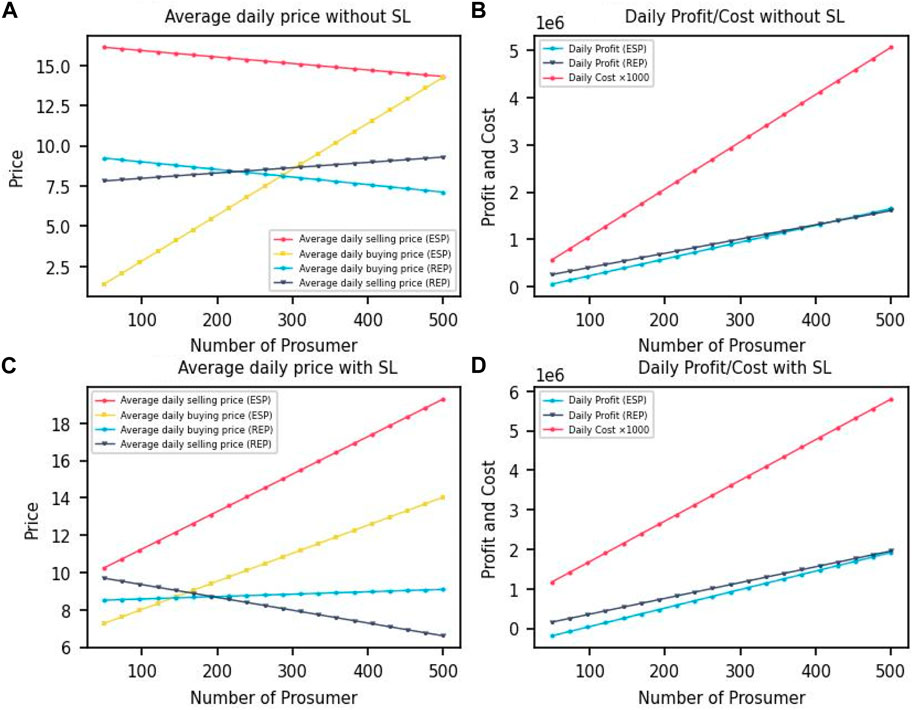
Figure 7. Effect of the number of PV prosumers on the decision results. (A) Average daily price without SL. (B) Daily Profit/Cost without SL. (C) Average daily price with SL. (D) Daily Profit/Cost with SL.
In summary, markets under SL exhibit greater efficiency, which means that resources are allocated and used more rationally, contributing to lower waste and higher overall welfare. However, it may also lead to higher costs for PV prosumers. Therefore, in practical applications, policymakers and market regulators need to weigh the interests of all parties in order to maximize economic efficiency and balance social welfare. In the absence of SL, the ESP may focus more on short-term benefits and lower electricity sales prices to gain more PV prosumers and thus increase its revenue. In this case, the costs of PV prosumers are reduced, but the overall efficiency of the market may not be as high as under SL. Hence, policymakers and regulators should encourage information sharing and collaboration among PV prosumers in order to promote market efficiency.
3.5 Comparative analysis
3.5.1 Comparison of different pricing schemes
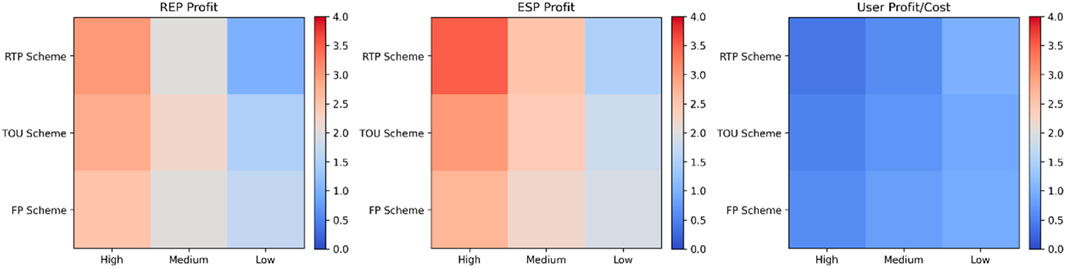
Figure 8 presents the profit and cost performance of ESPs, REPs, and users under three different pricing schemes: Real-Time Pricing Scheme (RTP Scheme), Time-Of-Use Pricing Scheme (TOU Scheme), and Fixed Pricing Scheme (FP Scheme) across high, medium, and low output scenarios. To effectively compare profits and costs across different scenarios, this paper standardized the original data. In the actual data, the profits of ESP and REP are in the range of millions or thousands, while the users’ costs are relatively smaller. A direct comparison would cause visual discrepancies. Through standardization, this paper scaled all the data to the same range (0–4), making the differences in performance across different pricing schemes more visible. This approach clarifies how profits and costs change under different output scenarios, allowing for a clearer understanding of the impact on market participants.
First, examining the heat map of REP profits, under the RTP Scheme, REP’s profits decrease significantly as output decreases, dropping from 3.0 in the high output scenario to 1.0 in the low output scenario. This indicates that when PV generation decreases, REPs need to purchase electricity at higher costs, reducing their profits. Although this pricing scheme can flexibly respond to market demand changes, it negatively impacts REP’s profitability under low output scenarios. In contrast, under the TOU Scheme, REP’s profits remain relatively stable, ranging from 2.8 in the high output scenario to 1.5 in the low output scenario, showing that this scheme adapts better to fluctuations in output levels. The TOU Scheme, by dividing peak and off-peak periods, mitigates large fluctuations in profits. The FP Scheme, on the other hand, shows the most stability but yields relatively lower profits. Particularly in the low output scenario, REP’s profits drop to only 1.7, demonstrating that the FP Scheme lacks flexibility in responding to output fluctuations, leading to overall poorer profit performance.
The ESP profit heat map reflects similar trends. ESP profits under the RTP Scheme fluctuate the most, with profits reaching 3.5 in the high output scenario but dropping to 1.5 in the low output scenario. The flexibility of the RTP Scheme allows ESPs to purchase electricity at lower costs when PV generation is abundant and sell it at higher prices, thereby generating higher profits. However, when output is low, ESP’s profits are constrained, showing the high-risk, high-reward nature of the RTP Scheme. Under the TOU Scheme, ESP’s profits fluctuate less, ranging from 3.0 to 1.8, indicating that this scheme provides more stable returns. Although the TOU Scheme does not deliver as high profits as the RTP Scheme, the balance between peak and off-peak periods makes ESP’s earnings relatively predictable. Under the FP Scheme, ESP’s profits are relatively lower, especially in the low output scenario where profits drop to 1.9, suggesting that this scheme lacks the flexibility to adapt to market fluctuations.
In the user cost heat map, although the variations in user costs are relatively moderate across all three pricing schemes, a clear trend can still be observed. In the high output scenario, user costs are the lowest, particularly under the RTP Scheme where costs are as low as 0.4. This indicates that users can reduce external electricity purchases by utilizing self-generated power, thereby effectively lowering their costs. As output decreases, user costs gradually increase, especially in the low output scenario where user costs under the RTP Scheme rise to 1.0. This suggests that users rely more on external electricity and their costs increase accordingly. In comparison, user costs under the TOU and FP Schemes are more stable, but user costs are slightly higher under the FP Scheme. Particularly in the low output scenario, user costs reach 0.95, highlighting the disadvantage of the FP Scheme in controlling costs when electricity supply is insufficient.
3.5.2 Comparison of different demand response strategies
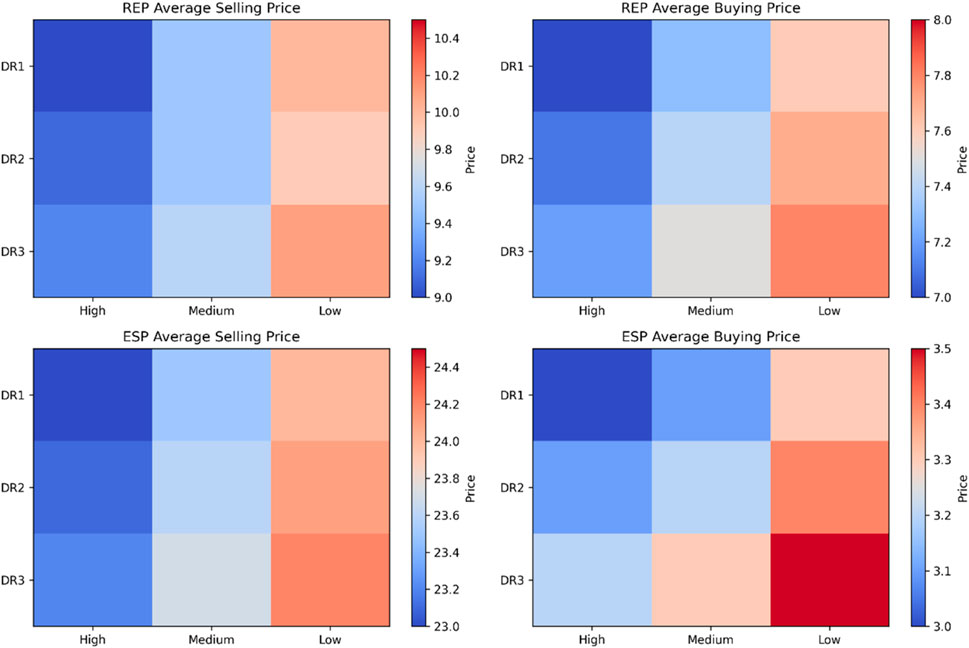
Figure 9 illustrates the changes in average selling and buying prices for REP and ESP under three demand response strategies (DR1, DR2, DR3) and three different output scenarios (high output, medium output, and low output). The figure clearly shows that different demand response strategies and output scenarios significantly impact the pricing of REP and ESP. Notably, as output decreases, electricity prices tend to rise, reflecting the changes in supply and demand.
Firstly, the average selling price of REP fluctuates significantly across different output scenarios. Under high output conditions, REP’s selling price remains relatively low, especially under DR1 and DR2 strategies, with prices ranging from around 9 to 9.3. This indicates that when the electricity supply is abundant, REP can sell electricity at lower prices to meet market demand. However, as output decreases, particularly in low-output scenarios, REP’s selling price rises sharply, reaching 10.1 under the DR3 strategy. This reflects the scarcity of electricity resources in low-output conditions, leading REP to raise selling prices to maintain profitability. Meanwhile, REP’s buying prices also adjust according to output changes. In high-output scenarios, REP’s buying price remains around 7.0 to 7.2, indicating sufficient electricity supply at lower costs. However, as output decreases, REP’s buying price rises significantly, especially in low-output scenarios, where it reaches 7.7 to 7.8. This suggests that under tighter electricity supply conditions, REP has to pay higher prices to procure electricity to meet its needs.
Similarly, ESP’s selling and buying prices are also affected by output changes. In high-output scenarios, ESP’s selling price is relatively low, around 23.0 to 23.2. This suggests that under high-output conditions, ESP can sell electricity at lower prices, attracting more users to consume electricity. However, as output decreases, ESP’s selling price gradually rises, particularly in low-output scenarios, reaching around 24.4. ESP’s buying price shows a similar trend. In high-output scenarios, ESP’s buying price remains around 3.0, but it increases to 3.5 under low-output conditions. This reflects that when electricity supply is constrained, ESP has to pay higher costs to purchase electricity to maintain operations.
Demand response strategies also have a significant impact on REP and ESP pricing. Under the peak shaving and valley filling strategy (DR1), price fluctuations are most pronounced, especially in low-output scenarios, where prices increase sharply. This strategy works by raising electricity prices during peak demand periods to encourage users to reduce consumption and balance supply and demand. Under the load shifting strategy (DR2), price fluctuations are relatively moderate, indicating that this strategy allows for flexible adjustments based on different time periods and demand changes, better managing imbalances in supply and demand. In contrast, under the load curtailment strategy (DR3), electricity prices are generally higher, especially in low-output scenarios, where both ESP and REP’s selling prices rise significantly. This suggests that the load curtailment strategy increases electricity prices to encourage users to reduce consumption and cope with the challenges of limited electricity supply.
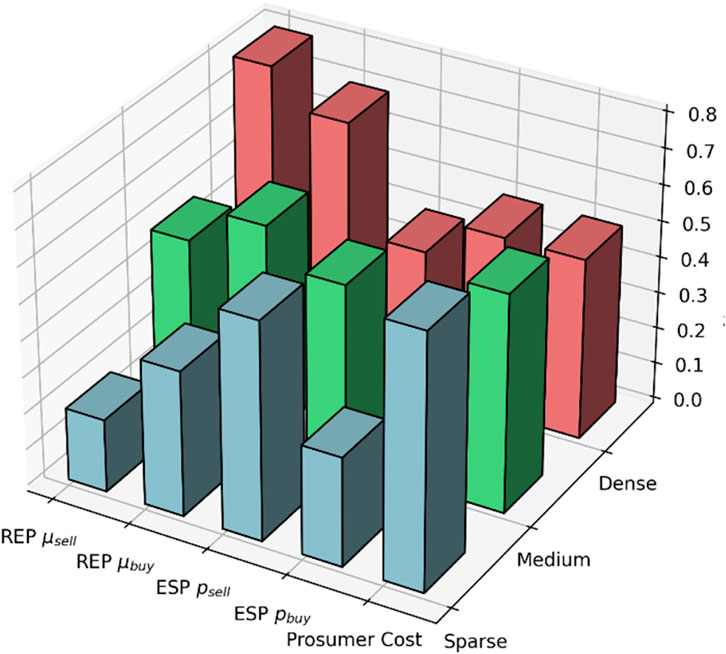
3.5.3 Comparison of different network structure
Network density refers to the ratio of the actual number of edges present in a network to the maximum possible number of edges. To reflect differences in network structures, this paper set three different network densities: 0.3, 0.6, and 0.9, representing sparse, medium-density, and dense networks, respectively. With these settings, this paper are able to explore how different network densities affect prosumers’ electricity consumption costs and the decision-making processes of REPs and ESPs. In networks with varying densities, the speed and scope of information dissemination differ, which in turn influences the decision-making behavior of market participants, leading to different market outcomes and economic efficiencies. To better compare the impact of different network structures on SL and decision-making behavior, this paper normalized all data to a range of 0–1, as shown in Figure 10:
In Figure 10, sparse, medium-density, and dense networks each illustrate how SL under different network structures influences consumer behavior, as well as REP and ESP pricing and consumer electricity costs. These differences in network density are reflected in the speed and scope of information dissemination, which significantly impacts market pricing and electricity costs.
First, in sparse networks (network density 0.3), the connections between consumers are few, meaning that information is exchanged only through a limited number of neighbors. Information dissemination is slow and limited in scope. In this situation, SL is less effective, and consumers are unable to respond quickly to price fluctuations, making their decisions more reliant on personal experience. As a result, both REP and ESP pricing tends to be conservative. The average daily selling price or REPs is relatively high, while the buying price is lower because demand is relatively stable and consumers lack the ability to adjust their electricity consumption through SL. Similarly, ESP selling prices remain high due to sluggish market demand, while buying prices remain relatively stable. Consumer electricity costs are higher in sparse networks because consumers cannot effectively adjust their consumption during peak periods, leading them to purchase more electricity during high-price periods. As a result, overall electricity costs for consumers remain elevated.
In medium-density networks (network density 0.6), the connections between consumers increase, allowing more information to be shared across a larger number of neighbors. Social learning becomes more effective, and information flows more smoothly. As a result, market demand becomes more sensitive, and consumers are able to adjust their electricity usage based on price fluctuations. REP and ESP pricing begins to reflect this increased flexibility. The selling price for REPs decreases slightly as consumers, with the help of SL, avoid peak periods and reduce demand pressure. The buying price increases, indicating that more consumers are shifting their electricity purchases to low-price periods. ESP pricing similarly reflects market demand fluctuations, with both selling and buying prices starting to show some volatility, suggesting that consumers are becoming more responsive to market prices and are able to plan their electricity usage more effectively. Consumer electricity costs decrease in medium-density networks, as SL helps them avoid high-price periods.
In dense networks (network density 0.9), consumers are highly connected, and information spreads rapidly and comprehensively throughout the network. Most consumers can quickly access market information and adjust their electricity consumption based on price changes, leading to the highest level of SL effectiveness. In this case, market demand fluctuations are much more pronounced. REP selling prices decrease significantly as most consumers reduce their electricity usage during peak periods, relieving market pressure. Meanwhile, REP buying prices increase as consumers collectively shift their electricity purchases to low-price periods, increasing demand during those times. ESP selling prices also decrease significantly as dense SL enables more consumers to fully utilize low-price electricity periods, reducing demand during peak periods. However, ESP buying prices exhibit greater volatility as demand concentrates in low-price periods, putting pressure on electricity supply. For consumers, the efficiency of SL allows them to avoid high-price periods more effectively, reducing overall electricity costs. However, as demand becomes overly concentrated during certain periods, there may be shortages of low-price electricity, preventing some consumers from fully lowering their costs in extreme cases.
In summary, as network density increases, consumers’ ability to learn socially improves significantly, allowing them to more accurately adjust their electricity usage, which in turn influences REP and ESP pricing strategies. In dense networks, SL intensifies supply and demand fluctuations, leading to lower consumer electricity costs and improved market efficiency. However, this may also result in excessive concentration of electricity demand during certain periods, affecting the balanced distribution of electricity resources.
4 Conclusion
Recent years, the global energy crisis and climate change issues have become increasingly severe, making renewable energy an urgent type of energy to develop. PV power generation, as a clean and renewable energy source, has received widespread attention. However, in the promotion of distributed PV power generation, the key issue is how to improve energy utilization efficiency, reduce costs, balance supply and demand, and achieve sustainable development. To address these challenges, researchers have begun to explore new market models and energy sharing mechanisms, such as P2P microgrids for PV prosumers. This study proposes a price-based DR energy sharing model, aiming to provide stable, efficient, and sustainable development paths for PV power users.
To achieve this goal, this paper first constructed a pricing model based on SL and energy sharing. SL is an information sharing and learning mechanism that helps consumers better cope with the complexity and uncertainty of the electricity market. Through SL, consumers can more accurately predict and assess market demand, thereby optimizing the entire system. In the pricing model, ESP and REP determine the purchase and sale prices of electricity based on market supply and demand, user behavior, and demand forecasts. This pricing mechanism, based on the market and user behavior, helps to achieve the operational efficiency, economic benefits, and sustainable development of the electricity market.
Secondly, this paper designed a prosumer cost model from the perspective of economic costs and user satisfaction with electricity consumption patterns. In this model, the cost of prosumers includes the cost of purchasing electricity, sales revenue, and equipment operation costs, among others. In addition, user satisfaction measures the subjective feelings of prosumers when using electricity and can be used to guide prosumers to adjust their electricity consumption patterns. By optimizing the prosumer cost model, we can maximize the economic benefits and satisfaction of electricity usage for prosumers.
Lastly, this paper employed reinforcement learning algorithms to solve the problem. Reinforcement learning is a machine learning method that obtains the best strategy through continuous trial and learning. In this study, the reinforcement learning algorithm learns the behavior and feedback of market participants, providing optimal solutions for the pricing model and prosumer cost model.
The research results show that: (1) SL can reduce electricity price fluctuations, decrease market risks, and provide more stable price signals for market participants. With SL, the operational efficiency, economic efficiency, and sustainability of the electricity market are improved. This helps to enhance the confidence and participation of market participants, promoting the healthy development of the electricity market. (2) When prosumers are unwilling to change their electricity consumption patterns, ESP and REP will increase the purchase price of electricity and reduce the sales price, encouraging prosumers to increase electricity consumption to some extent. This strategy is beneficial for PV power users to use more electricity when the power supply is sufficient, thereby maintaining the balance of supply and demand in the entire system. At the same time, this also helps to alleviate grid load and improve system stability. (3) As the scale of prosumers expands, the revenue of price setters increases, but the cost of prosumers correspondingly increases. This means that in practical applications, policymakers and market regulators need to weigh the interests of all parties to achieve the maximization of economic efficiency and the balance of social welfare, and encourage information sharing and cooperation among PV power users to improve market efficiency and promote sustainable development.
In summary, this study proposes a price-based DR energy sharing model for P2P PV prosumer microgrids. By constructing a pricing model based on SL and energy sharing, as well as designing a prosumer cost model from the perspective of economic costs and user satisfaction with electricity consumption patterns, provide an effective method to improve the energy utilization efficiency of PV power users, reduce system operation costs, promote market economic benefits, and support sustainable energy development. In addition, the application of reinforcement learning algorithms offers an effective means to solve the complex problems in pricing and cost models. This research would provide valuable references for policymakers and market regulators, promoting the development of the PV industry and the popularization of sustainable energy.
Nevertheless, this paper still has some limitations to be solved. Firstly, prosumers can be classified into three types, including those who only optimize their usage rate without directly connecting to the power grid, those who optimize their usage while maintaining their connection to the grid, and enterprises that provide flexible services at the system level (such as virtual power plants). And this study did not analyze multiple types of prosumers. Secondly, this study is limited to PV power generation prosumers, and has not conducted a comprehensive analysis of other renewable energy prosumers. Hence, future research can delve deeper into the following aspects: Firstly, the reduction in Distributed energy resources (DER) hardware, installation, and maintenance costs benefits both small-scale prosumers and utility level hardware buyers. This means that the types of prosumers will continue to increase, and the scale of DER will continue to expand. Hence, exploring how to adjust pricing strategies and optimize cost models based on the characteristics of different types of prosumers is of great practical significance. Secondly, future work can combine other types of renewable energy (such as wind energy, hydropower, etc.) and explore different market mechanisms to promote more efficient renewable energy sharing and trading between producers and consumers. Finally, future research should consider the potential impact of emerging technologies such as blockchain or artificial intelligence on energy sharing and demand response.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
JL: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmadi, F., Akrami, A., Doostizadeh, M., and Aminifar, F. (2020). Energy pricing and demand scheduling in retail market: how microgrids’ integration affects the market. IET Smart Grid 3 (3), 309–317. doi:10.1049/iet-stg.2019.0195
Alarcon-Rodriguez, A., Ault, G., and Galloway, S. (2010). Multi-objective planning of distributed energy resources: a review of the state-of-the-art. Renew. Sustain. Energy Rev. 14 (5), 1353–1366. doi:10.1016/j.rser.2010.01.006
Bhatti, B. A., and Broadwater, R. (2020). Distributed Nash equilibrium seeking for a dynamic micro-grid energy trading game with non-quadratic payoffs. Energy 202, 117709. doi:10.1016/j.energy.2020.117709
Cao, G. C., Fang, D., and Wang, P. (2021). The impacts of social learning on a real-time pricing scheme in the electricity market. Appl. Energy 291, 116874. doi:10.1016/j.apenergy.2021.116874
Chen, L., Liu, N., Li, C., and Wang, J. (2020). Peer-to-peer energy sharing with social attributes: a stochastic leader–follower game approach. IEEE Trans. Industrial Inf. 17 (4), 2545–2556. doi:10.1109/tii.2020.2999328
Cui, S., Wang, Y.-Wu, and Liu, N. (2018). Distributed game-based pricing strategy for energy sharing in microgrid with PV prosumers. IET Renew. Power Gener. 12 (3), 380–388. doi:10.1049/iet-rpg.2017.0570
Dong, J., Song, C., Liu, S., Yin, H., Zheng, H., and Li, Y. (2022). Decentralized peer-to-peer energy trading strategy in energy blockchain environment: a game-theoretic approach. Appl. Energy 325, 119852. doi:10.1016/j.apenergy.2022.119852
Erol, Ö., and Filik, Ü. B. (2022). A Stackelberg game approach for energy sharing management of a microgrid providing flexibility to entities. Appl. Energy 316, 118944. doi:10.1016/j.apenergy.2022.118944
Feldman, P., Papanastasiou, Y., and Segev, E. (2018). Social learning and the design of new experience goods. Manag. Sci. 65 (4), 1502–1519. doi:10.1287/mnsc.2017.3024
Fridgen, G., Halbrügge, S., Olenberger, C., and Weibelzahl, M. (2020). The insurance effect of renewable distributed energy resources against uncertain electricity price developments. Energy Econ. 91, 104887. doi:10.1016/j.eneco.2020.104887
Gillingham, K. T., and Bryan, B. (2021). Social learning and solar photovoltaic adoption. Manag. Sci. 67 (11), 7091–7112. doi:10.1287/mnsc.2020.3840
Hampton, G., and Eckermann, S. (2013). The promotion of domestic grid-connected photovoltaic electricity production through social learning. Energy, Sustain. Soc. 3, 23. doi:10.1186/2192-0567-3-23
Han, L., Morstyn, T., and McCulloch, M. (2018). Incentivizing prosumer coalitions with energy management using cooperative game theory. IEEE Trans. Power Syst. 34 (1), 303–313. doi:10.1109/tpwrs.2018.2858540
He, Li, and Zhang, J. (2020). A community sharing market with PV and energy storage: an adaptive bidding-based double-side auction mechanism. IEEE Trans. Smart Grid 12 (3), 2450–2461. doi:10.1109/tsg.2020.3042190
Jiang, A., Yuan, H., and Li, D. (2021). Energy management for a community-level integrated energy system with photovoltaic prosumers based on bargaining theory. energy 225, 120272. doi:10.1016/j.energy.2021.120272
Kanchev, H., Lu, Di, Colas, F., Lazarov, V., and Bruno, F. (2011). Energy management and operational planning of a microgrid with a PV-based active generator for smart grid applications. IEEE Trans. industrial Electron. 58 (10), 4583–4592. doi:10.1109/tie.2011.2119451
Kendal, R. L., Boogert, N. J., Rendell, L., Laland, K. N., Webster, M., and Jones, P. L. (2018). Social learning strategies: bridge-building between fields. Trends cognitive Sci. 22 (7), 651–665. doi:10.1016/j.tics.2018.04.003
Liu, B., Zhu, W., Shen, Y., Chen, Y., Wang, T., Chen, F., et al. (2022). A study about return policies in the presence of consumer social learning. Prod. Operations Manag. 31 (6), 2571–2587. doi:10.1111/poms.13703
Liu, N., Yu, X., Wang, C., and Wang, J. (2017). Energy sharing management for microgrids with PV prosumers: a Stackelberg game approach. IEEE Trans. Industrial Inf. 13 (3), 1088–1098. doi:10.1109/tii.2017.2654302
Liu N, N., Cheng, M., Yu, X., Zhong, J., and Lei, J. (2018). Energy-sharing provider for PV prosumer clusters: a hybrid approach using stochastic programming and stackelberg game. IEEE Trans. Industrial Electron. 65 (8), 6740–6750. doi:10.1109/tie.2018.2793181
Liu X, X., Wang, S., and Sun, J. (2018). Energy management for community energy network with CHP based on cooperative game. Energies 11 (5), 1066. doi:10.3390/en11051066
Lobel, I., and Sadler, E. (2015). Preferences, homophily, and social learning. Operations Res. 64 (3), 564–584. doi:10.1287/opre.2015.1364
Long, C., Zhou, Y., and Wu, J. (2019). A game theoretic approach for peer to peer energy trading. Energy Procedia 159, 454–459. doi:10.1016/j.egypro.2018.12.075
Lu, Q., and Zhang, Y. (2022). A multi-objective optimization model considering users' satisfaction and multi-type demand response in dynamic electricity price. Energy 240, 122504. doi:10.1016/j.energy.2021.122504
Luo, Xi, Shi, W., Jiang, Y., Liu, Y., and Xia, J. (2022). Distributed peer-to-peer energy trading based on game theory in a community microgrid considering ownership complexity of distributed energy resources. J. Clean. Prod. 351, 131573. doi:10.1016/j.jclepro.2022.131573
Ma, Li, Liu, N., Zhang, J., Tushar, W., and Yuen, C. (2016). Energy management for joint operation of CHP and PV prosumers inside a grid-connected microgrid: a game theoretic approach. IEEE Trans. Industrial Inf. 12 (5), 1930–1942. doi:10.1109/tii.2016.2578184
Palm, A., and Lantz, B. (2020). Information dissemination and residential solar PV adoption rates: the effect of an information campaign in Sweden. Energy Policy 142, 111540. doi:10.1016/j.enpol.2020.111540
Papanastasiou, Y., and Savva, N. (2017). Dynamic pricing in the presence of social learning and strategic consumers. Manag. Sci. 63 (4), 919–939. doi:10.1287/mnsc.2015.2378
Paudel, A., Chaudhari, K., Long, C., and Gooi, H. B. (2018). Peer-to-peer energy trading in a prosumer-based community microgrid: a game-theoretic model. IEEE Trans. Industrial Electron. 66 (8), 6087–6097. doi:10.1109/tie.2018.2874578
Pourakbari-Kasmaei, M., Asensio, M., Lehtonen, M., and Contreras, J. (2019). Trilateral planning model for integrated community energy systems and PV-based prosumers—a bilevel stochastic programming approach. IEEE Trans. Power Syst. 35 (1), 346–361. doi:10.1109/tpwrs.2019.2935840
Rabaia, M. K. H., Ali Abdelkareem, M., Sayed, E. T., Elsaid, K., Chae, K.-J., Wilberforce, T., et al. (2021). Environmental impacts of solar energy systems: a review. Sci. Total Environ. 754, 141989. doi:10.1016/j.scitotenv.2020.141989
Rathnayaka, A. J. D., Potdar, V. M., Dillon, T. S., Hussain, O. K., and Chang, E. (2013). A methodology to find influential prosumers in prosumer community groups. IEEE Trans. Industrial Inf. 10 (1), 706–713. doi:10.1109/tii.2013.2257803
Rathor, S. K., and Saxena, D. (2020). Energy management system for smart grid: an overview and key issues. Int. J. Energy Res. 44 (6), 4067–4109. doi:10.1002/er.4883
Sayed, E. T., Wilberforce, T., Elsaid, K., Rabaia, M. K. H., Ali Abdelkareem, M., Chae, K.-J., et al. (2021). A critical review on environmental impacts of renewable energy systems and mitigation strategies: wind, hydro, biomass and geothermal. Sci. total Environ. 766, 144505. doi:10.1016/j.scitotenv.2020.144505
Soto, E. A., Bosman, L. B., Wollega, E., and Leon-Salas, W. D. (2021). Peer-to-peer energy trading: a review of the literature. Appl. Energy 283, 116268. doi:10.1016/j.apenergy.2020.116268
Tushar, W., Kumar Saha, T., Yuen, C., Imran Azim, M., Morstyn, T., Vincent, H., et al. (2020). A coalition formation game framework for peer-to-peer energy trading. Appl. Energy 261, 114436. doi:10.1016/j.apenergy.2019.114436
Wang, P., Fang, D., and Cao, G. C. (2022). How social learning affects customer behavior under the implementation of TOU in the electricity retailing market. Energy Econ. 106, 105836. doi:10.1016/j.eneco.2022.105836
Xiong, X., Qing, G., and Li, H. (2022). Blockchain-based P2P power trading mechanism for PV prosumer. Energy Rep. 8, 300–310. doi:10.1016/j.egyr.2022.02.130
Xu, S., Zhao, Y., Li, Y., and Zhou, Y. (2021). An iterative uniform-price auction mechanism for peer-to-peer energy trading in a community microgrid. Appl. Energy 298, 117088. doi:10.1016/j.apenergy.2021.117088
Yang, S., Wang, X., Yang, Y., and Li, J. (2023). Bi-level planning model of distributed PV-energy storage system connected to distribution network under the coordinated operation of electricity-carbon market. Sustain. Cities Soc. 89, 104347. doi:10.1016/j.scs.2022.104347
Yang, Y., Lu, C., Liu, H., Wang, N., Chen, L., Wang, C., et al. (2022). Optimal design and energy management of residential prosumer community with photovoltaic power generation and storage for electric vehicles. Sustain. Prod. Consum. 33, 244–255. doi:10.1016/j.spc.2022.07.008
Zhang, L., Qian, Du, Zhou, D., and Zhou, P. (2022). How does the photovoltaic industry contribute to China's carbon neutrality goal? Analysis of a system dynamics simulation. Sci. Total Environ. 808, 151868. doi:10.1016/j.scitotenv.2021.151868
Zheng, R., Shou, B., and Yang, J. (2021). Supply disruption management under consumer panic buying and social learning effects. Omega 101, 102238. doi:10.1016/j.omega.2020.102238
Keywords: photovoltaic prosumers, energy sharing trading, dynamic pricing, demand response, social learning
Citation: Liu J (2024) Energy sharing trading among photovoltaic prosumers: a dynamic game considering social learning. Front. Energy Res. 12:1487408. doi: 10.3389/fenrg.2024.1487408
Received: 02 September 2024; Accepted: 16 October 2024;
Published: 29 October 2024.
Edited by:
Mostafa Esmaeili Shayan, University of Cagliari, ItalyReviewed by:
Abolfazl Sheybanifar, Isfahan University of Technology, IranFarzaneh Ghasemzadeh, Iran University of Science and Technology, Iran
Copyright © 2024 Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Junzhuo Liu, eWFuZ2xhbmx1b3lhbmdAMTYzLmNvbQ==
 Junzhuo Liu
Junzhuo Liu