Collaborative source–grid–load frequency regulation strategy for DC sending-end power grid considering electrolytic aluminum participation

As renewable energy sources are increasingly being integrated into power systems, traditional frequency regulation methods have faced challenges, such as reduced system inertia and diminished regulatory capacity. We present a source–grid–load collaborative control strategy for the participation of electrolytic aluminum in the frequency regulation of the DC sending-end power grid. First, the frequency response characteristics of the ultrahigh-voltage DC (UHVDC) sending-end system are analyzed, and an electrolytic aluminum load model is established. Then, a hierarchical source–grid–load control strategy is proposed. The upper-layer control assigns the frequency support tasks to synchronous generators, electrolytic aluminum stations, and UHVDC systems based on the frequency dead zones. The lower-layer control aims to minimize the cost of controlling the electrolytic aluminum loads by distributing power adjustment commands to each electrolytic aluminum series within the power station. Simulations were conducted, and the results validate the effectiveness and economic benefits of the proposed strategy in reducing the control costs while maintaining system stability.

1 Introduction

Comprehensive measures have been implemented in China to address carbon peaking and carbon neutrality, with particular focus on the strategic initiative of “accelerating the construction of a new energy system.” The aim of this initiative is to simultaneously ensure secure and stable energy supply while promoting green and low-carbon development efforts (Wang et al., 2023; Yang et al., 2023a). Traditionally, frequency regulation in a power system relies on the balancing control mode, where the generating units track the active power demand of the loads. However, given the increasing proportion of new energy generation on the supply side, challenges such as declining system inertia, reduced regulation capacity, and heightened instability have emerged (Han et al., 2021; Han et al., 2023; Han and Chen, 2024). These challenges render the traditional regulation methods inadequate for new operational scenarios, thereby necessitating the introduction of new regulation resources to alleviate the pressure on the active power reserves (Wang et al., 2023).

The ultrahigh-voltage direct current (UHVDC) system offers significant advantages, such as strong controllability, fast response time, and high degree of control flexibility. It enhances the ability of the system to integrate renewable energy by maintaining frequency stability at the sending-end and maximizing the new energy output. A multi-time-scale coordinated control strategy has been proposed to actively support the frequency stability of the sending-end system by optimizing the use of frequency regulation resources while improving the system stability (Xin et al., 2023). Similarly, measures to enhance renewable energy accommodation in the sending-end grids of UHVDC systems that address both frequency and voltage concerns have been validated through a planning example of the Qinghai power grid in 2025 (Zhang et al., 2022). Additionally, a control strategy has been developed for the double-terminal converter stations of UHVDC systems based on virtual synchronous generator technology. Under load mutation conditions, this strategy reduces the amplitude, speed, and overshoot of the frequency fluctuations, thereby suppressing voltage fluctuations and ensuring frequency regulation without deviations (Guo et al., 2022). The frequency limit controller (FLC) in the UHVDC transmission system also offers unique advantages for maintaining frequency stability in an islanded system. The causes of ultralow-frequency oscillations in a multi-DC sending-end system after asynchronous networking as well as the mechanism of the DC FLC in suppressing these oscillations were analyzed to propose a suppression scheme that effectively mitigates the ultralow-frequency oscillations of the transmitter grid (Li et al., 2019). A multiobjective double-layer optimization method was also introduced for the design of the DC FLC parameters to improve its performance and reduce its impact on the frequency of the receiving-end grid (Wang et al., 2022). Furthermore, in response to the operational safety requirements of the multiterminal DC systems of the Wudongde DC project, stability control measures and FLC settings were proposed to resolve the system instabilities caused by AC line faults near the Wudongde power station, thus enhancing the adaptability of the high-frequency generator tripping scheme in the Yunnan power grid (You et al., 2018).

However, adjusting the control strategy at the sending end of a UHVDC transmission line will inevitably impact the receiving-end power grid. This effect is particularly pronounced in scenarios with high proportions of wind and photovoltaic power sources as the volatility of renewable energy significantly influences the power system. The demand for real-time active power balancing in such systems is increasing; hence, relying solely on DC lines to compensate for power shortages can lead to large fluctuations in the receiving-end grid and may even exacerbate the system disturbances. Therefore, it is crucial to explore new regulation resources to alleviate the pressure of frequency regulation.

To improve the system regulation capacity, distributed resource (DR) and flexible loads are often used in frequency modulation auxiliary services to improve the overall performance of the system (Mo et al., 2023; Yang et al., 2021). When traditional generation units lack sufficient frequency modulation capacity, flexible loads can reduce their operating power or temporarily shut down electrical equipment without significantly impacting user experience. This alleviates the pressure on the load side of the power system and enhances the grid frequency stability (Yang et al., 2023b; Wang et al., 2024a). For instance, Wang et al. (2024b) proposed a stable control method incorporating the control parameters of an analogous virtual synchronous generator along with flexible load regulation; by utilizing resources such as virtual damping, virtual inertia, and flexible loads, this approach ensures that the initial steady-state point is included within the largest estimated domain of attraction of the target steady-state point. This method effectively eliminates the risk of instability due to oscillations and significantly improves the frequency stability of system operation.

Among the various types of flexible loads, electrolytic aluminum as a high-energy-consuming industrial load offers significant potential for frequency regulation owing to its power intensity and large thermal inertia. As a large-scale industrial load with a constant and substantial power demand, it plays a crucial role in energy-intensive industries. Despite its continuous power consumption, the aluminum electrolysis process allows short-term power modulation without disrupting production, making it an ideal candidate for demand-side frequency regulation. In regions with high renewable energy penetration, integrating such controllable loads becomes increasingly important. In particular, in high-voltage DC (HVDC) systems at the sending end where renewable power fluctuations are common, electrolytic aluminum can rapidly adjust its power consumption to provide essential flexibility while stabilizing the frequency and mitigating renewable generation variability. Thus, incorporating electrolytic aluminum not only enhances the reliability of the HVDC system but also addresses the operational challenges of modern grids with high renewable energy integration.

Considering the response of the electrolytic aluminum load, a source–grid–load coordinated active power and frequency control strategy is proposed herein by taking an industrial power grid including electrolytic aluminum loads as the sending-end system to provide power support to the receiving-end system via a flexible direct current transmission system (Bao, 2021; Nie et al., 2024). Additionally, the participation of high-energy-consuming electrolytic aluminum loads in frequency regulation and auxiliary services has been studied, and their fast dynamic regulation capabilities have been verified (Bao et al., 2020). A coordinated frequency modulation strategy for wind farms and electrolytic aluminum has also been proposed, although it lacks consideration of the entire power system (Luo et al., 2023). Another work proposed a secondary frequency control strategy using a virtual power plant with aluminum smelter loads for optimized power support via a voltage source converter (VSC)-HVDC link by focusing on secondary regulation and demand response under renewable energy uncertainty (Bao, 2023). A hierarchical control strategy for aluminum smelters was introduced to provide cost-efficient primary frequency support by utilizing a novel DC control scheme (Bao et al., 2022). These studies focus on the frequency regulation requirements of the power grid. In contrast, our proposed strategy emphasizes primary frequency regulation with comprehensive source–grid–load coordination by integrating synchronous generators, HVDC systems, and electrolytic aluminum loads. Furthermore, our approach addresses the physical constraints and economic impacts during the regulation process to provide a more detailed control structure at the electrolytic cell level, which has been insufficiently investigated in previous studies.

In response to the aforementioned issues, we propose a source–grid–load coordinated control strategy for the participation of electrolytic aluminum in the UHVDC sending-end system. The proposed strategy entails construction of power–frequency response models for both the UHVDC transmission system and electrolytic aluminum load along with analysis of the frequency modulation potential of the source–grid–load at the sending end. Additionally, a hierarchical control architecture was developed for the participation of electrolytic aluminum loads in primary frequency modulation. The upper layer of the control scheme establishes a coordinated frequency modulation scheme for source–grid–load interactions based on fixed-value coordination, whereas the lower-layer control scheme focuses on the economic aspects of electrolytic aluminum to formulate a decentralized frequency response strategy. The effectiveness and economic viability of the proposed control strategy are finally validated through simulations.

2 Frequency response model of the UHVDC sending-end system with electrolytic aluminum load

2.1 Frequency response characteristics of the UHVDC sending-end system

The topological structure of the sending-end system for large-scale wind power transmission via line-commutated converter (LCC)-HVDC is shown in Figure 1. Here, the traditional units are represented by synchronous units, wind turbines are represented by doubly fed induction generators, and the traditional LCC-HVDC system is adopted for the HVDC transmission line.

Figure 1

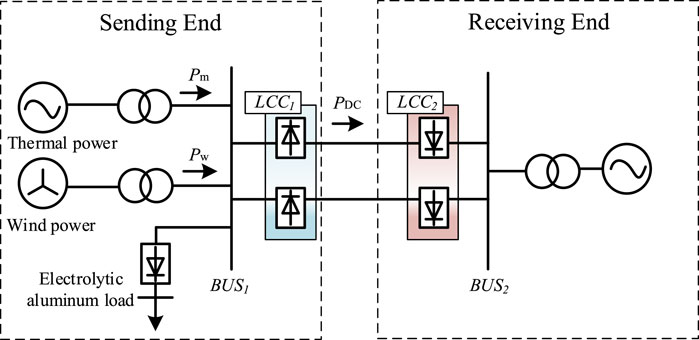
Figure 1. Structure of wind power unit with electrolytic aluminum load transmitted through the line-commutated converter high-voltage direct current (LCC-HVDC) system.

As shown in Figure 1, during stable operation, the active power of the sending-end system maintains equilibrium that can be expressed as Equation 1

$P_G=P_m+P_w=P_{ASL}+P_{LD1}+P_{dc}=P_L.(1)$

Considering the primary frequency regulation of the system, the system frequency deviation $\Delta f$ can be calculated by Equation 2:

$\Delta f=\frac{1}{s{H}_{sys}+D}\left(\Delta P_G-\Delta P_L\right).(2)$

It is seen from Equation 2 that when there is a disturbance in the system, the system frequency deviation is closely related to the system inertia. However, for the system in which large-scale new energy bases are transmitted through UHVDC links, the inertia of the sending-end system is low, and a small power disturbance will cause a large fluctuation in the system frequency. When the frequency deviation caused by the system load disturbance is within the primary frequency regulation range of the synchronous units, the system operates stably. However, once the system load disturbance exceeds the limit of the primary frequency regulation adjustment of the synchronous units, it will be difficult for the synchronous units to suppress the frequency fluctuations caused by the unbalanced power; thus, the system frequency will decrease rapidly and seriously threaten the system security (Li et al., 2024). At this time, relying only on the synchronous units to achieve frequency regulation no longer meets the demand for frequency stability. Hence, it is necessary to further introduce the sending-end electrolytic aluminum load and UHVDC transmission system for coordinated frequency regulation.

2.2 Model of the electrolytic aluminum load

The grid connection diagram of the rectification equipment for electrolytic aluminum is shown in Figure 2. By utilizing the rapid adjustment characteristics of thyristors, electrolytic aluminum can quickly regulate the active power of the electrolytic aluminum series according to the frequency regulation requirements, achieving a reduction of 0%–40% of the rated load and an increase of 0%–10% of the rated load within approximately 80 ms (Xu et al., 2014; Du et al., 2023).

Figure 2

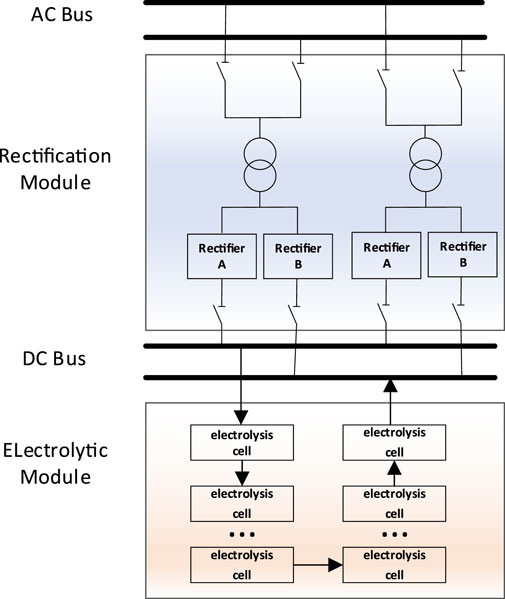
Figure 2. Schematic diagram showing the grid connection of rectification equipment for the electrolytic aluminum load.

The active power consumption of the $i$-th electrolysis cell $P_i^{ASL}$ is calculated as Equation 3

$P_i^{ASL}=U_i^{ASL}{I}_i^{ASL}.(3)$

The structure of the rectifier controller in the electrolytic aluminum load is shown in Figure 3. To eliminate the influences of external disturbances on $I_i^{ASL}$, the electrolytic aluminum load controller takes the difference between the reference value $I_{ref,i}^{ASL}$ of the DC of the electrolytic aluminum load and actual value $I_i^{ASL}$ as the input signal. Using the proportional–integral (PI) controller, a pulse-width modulation (PWM) signal is generated to change the duty cycle of the input switching circuit and change the output power of the electrolytic cell to achieve frequency support.

Figure 3

Figure 3. Structure of the rectifier controller in the electrolytic aluminum load.

3 Frequency control strategy for the UHVDC sending-end system with electrolytic aluminum load

3.1 Overall control structure

The frequency control structure of the UHVDC sending-end system with electrolytic aluminum load is divided into the upper and lower layers. The overall control structure is shown in Figure 4.

Figure 4

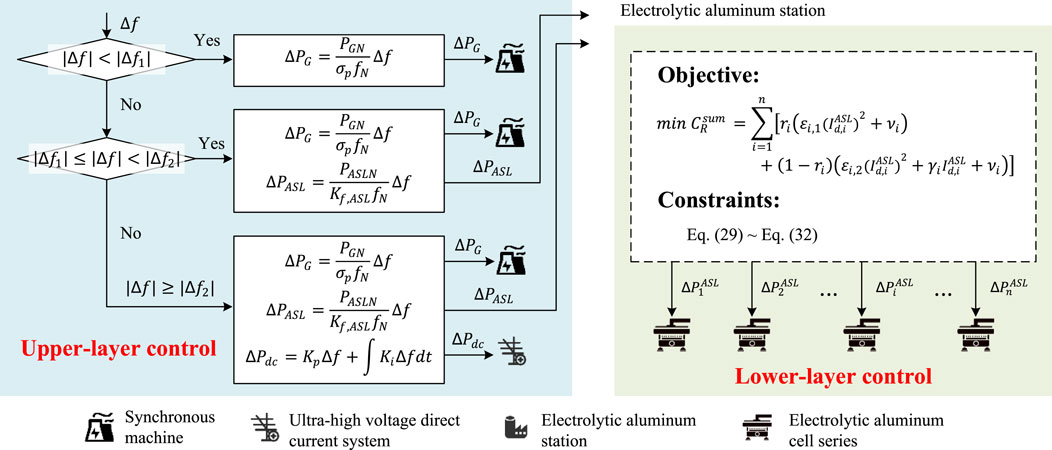
Figure 4. Overall control structure of the sending-end ultrahigh-voltage direct current (UHVDC) system.

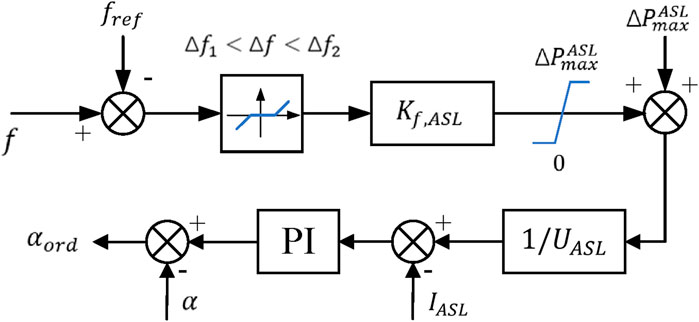
3.1.1 Upper-layer control

The upper layer is mainly focused on coordinating the synchronous machine, electrolytic aluminum station, and UHVDC system. Specifically, it determines the frequency regulation power allocation for the synchronous machines, electrolytic aluminum loads, and UHVDC system based on the magnitude of the frequency deviation. When $\left|\Delta \left.f\right|<\left|\Delta f_1\right|\right.$, the reserve capacity of the synchronous machine is sufficient to absorb the unbalanced power, and the frequency regulation task is handled exclusively by the synchronous machine to maintain system stability without engaging the electrolytic aluminum station. When $\left|\Delta f_1\right|\le \left|\Delta f\right|<\left|\Delta f_2\right|$, both the synchronous machine and electrolytic aluminum station share the burden of frequency regulation as the power disturbance exceeds the capabilities of the synchronous machine. When $\left|\Delta \left.f\right|\ge \left|\Delta f_2\right|\right.$, the frequency regulation task is jointly undertaken by the synchronous machine, electrolytic aluminum station, and UHVDC system. Specifically, under the circumstances of $\left|\Delta f_1\right|\le \left|\Delta f\right|<\left|\Delta f_2\right|$ and $\left|\Delta \left.f\right|\ge \left|\Delta f_2\right|\right.$, the frequency regulation power of the electrolytic aluminum station is transmitted to the lower-layer control.

3.1.2 Lower-layer control

The lower layer is mainly focused on coordinating the electrolytic aluminum cell series within the electrolytic aluminum station. Once the electrolytic aluminum station receives the command from the upper-layer control, the lower-layer control distributes the required regulation power to the individual electrolytic aluminum cell series by solving an optimization problem. This optimization considers the production state and control costs, including the production cost from output reduction and electrical energy cost during the heat preservation state when production is suspended. The lower-layer control must also meet the total regulated power constraint while ensuring that the combined regulation power of all cell series remains within their allowable limits. It also fine-tunes the self-saturable reactor to adjust the series current, maintaining it within the reactor’s voltage regulation capacity and minimum current limit.

3.2 Upper-layer source–grid–load coordinated control strategy

Frequent participation of the electrolytic aluminum load in system frequency regulation over a long period of time has a certain impact on the production efficiency of the high-energy-consuming load. Similarly, the power regulation of the UHVDC system also directly affects the power balance of the receiving-end power grid. Therefore, it is necessary to limit the ranges of participation of the electrolytic aluminum load and UHVDC system in frequency regulation to reduce the impacts of power disturbances on the loads and receiving-end power grid. Considering that different degrees of disturbance can lead to different amounts of unbalanced power, we divided the frequency support requirements into three scenarios based on the maximum reserve capacity and unbalanced power of the primary frequency regulation of the sending-end AC system.

Case 1. The power disturbance is small, and the absolute frequency deviation $\left|\Delta f\right|$ is less than the dead zone value of frequency regulation $\left|\Delta f_1\right|$, as shown in Equation 4. At this time, the reserve capacity of the synchronous machine completely absorbs the unbalanced power, and the frequency regulation task of the sending-end system is only undertaken by the synchronous machine, thus avoiding the influence of frequent participation of the electrolytic aluminum load in the system frequency on the stability of the equipment.

$\left|\Delta \left.f\right|<\left|\Delta f_1\right|\right.(4)$

Case 2. The absolute frequency deviation $\left|\Delta f\right|$ is between the dead zone values $\left|\Delta f_1\right|$ and $\left|\Delta f_2\right|$ of frequency regulation, as shown in Equation 5. At this time, the synchronous machine of the sending-end AC system cannot completely regulate the unbalanced power, and the frequency regulation task of the sending-end system is jointly undertaken by the synchronous machine and electrolytic aluminum station.

$\left|\Delta f_1\right|\le \left|\Delta f\right|<\left|\Delta f_2\right|(5)$

Case 3. The absolute frequency deviation $\left|\Delta f\right|$ is greater than or equal to the dead zone value of frequency regulation $\left|\Delta f_2\right|$, as shown in Equation 6. At this time, the frequency regulation task of the sending-end system is jointly undertaken by the synchronous machine, electrolytic aluminum station, and UHVDC system.

$\left|\Delta \left.f\right|\ge \left|\Delta f_2\right|\right.(6)$

It can be seen that the dead zone values $\left|\Delta f_1\right|$ and $\left|\Delta f_2\right|$ of frequency regulation determine the unbalanced power undertaken by the electrolytic aluminum load and UHVDC system in the process of frequency coordinated control.

3.2.1 Structure and parameter settings of the electrolytic aluminum load participating in primary frequency control

When the absolute frequency deviation $\left|\Delta f\right|$ is less than the dead zone value of frequency regulation $\left|\Delta f_1\right|$, the electrolytic aluminum load and UHVDC system do not participate in system frequency regulation, and the frequency is borne only by the synchronous generation units.

Here, the frequency regulation of the dead zone value $\left|\Delta f_1\right|$ is Equation 7

$\left|\Delta f_1\right|=\Delta P_{Gmax}{\sigma }_p.(7)$

When the absolute frequency deviation $\left|\Delta f\right|$ is between the dead zone values $\left|\Delta f_1\right|$ and $\left|\Delta f_2\right|$ of frequency regulation, the synchronous generation units and electrolytic aluminum load participate in frequency control. In this paper, a frequency droop control structure is introduced in the electrolytic aluminum station, as shown in Figure 5. The droop control coefficient of the electrolytic aluminum load is mainly related to the frequency regulation capacities of the synchronous generation units and electrolytic aluminum. The primary regulation amount of the synchronous generation units and system frequency change can be expressed as

$\Delta f={\sigma }_p\Delta P_G\frac{f_N}{P_{GN}}.(8)$

Figure 5

Figure 5. Structure of the frequency droop control scheme in the electrolytic aluminum load.

Then, the relationship between the regulation amount of the electrolytic aluminum load and system frequency deviation can be expressed as

$\Delta f=K_{f,ASL}\Delta P_{ASL}\frac{f_N}{P_{ASLN}}.(9)$

The power regulation undertaken by the electrolytic aluminum load is expressed as

$\Delta P_{ASL}=\Delta P_{unb}-\Delta P_G.(10)$

By substituting Equations 8, 9 into Equation 10, the droop control coefficient of the electrolytic aluminum load can be obtained as Equation 11

$K_{f,ASL}=\frac{{\sigma }_p\Delta P_{Gmax}{P}_{ASLN}}{\left(\Delta P_{unb}-\Delta P_{Gmax}\right)P_{GN}}.(11)$

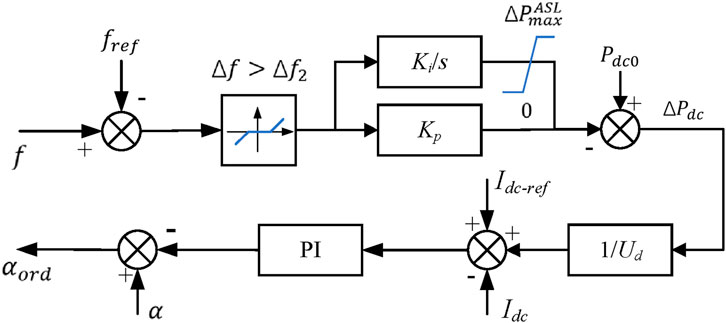
3.2.2 Parameter settings of the frequency regulation dead zone for the UHVDC system

When the absolute frequency deviation $\left|\Delta f\right|$ is greater than or equal to the dead zone value of frequency regulation $\left|\Delta f_2\right|$, the synchronous generation units, electrolytic aluminum loads, and UHVDC system participate in frequency control. The dead zone values of frequency regulation of the UHVDC system depend mainly on the upward and downward regulating capacities of the electrolytic aluminum load. The capacity of the electrolytic aluminum load depends on the depth of voltage regulation of the self-saturated reactors equipped to each electrolytic series and current power level of the electrolytic series.

The electrolytic aluminum station monitors the voltage, current, and power levels of the electrolytic series in real time. Based on the depth of voltage regulation of the self-saturated reactor equipped in the electrolytic series and current power level of the electrolytic series, the available active capacity of the $i$-th electrolytic series can be expressed as Equations 12–14

$\Delta P_{\mathit{max},i}^{ASL}=U_{\mathit{max},i}^{ASL}{I}_{\mathit{max},i}^{ASL}-U_{d,i}^{ASL}{I}_{d,i}^{ASL},(12)$

$I_{\mathit{max},i}^{ASL}=\frac{U_{\mathit{max},i}^{ASL}-E_{d,i}^{ASL}}{R_{d,i}^{ASL}},(13)$

$\Delta P_{\mathit{max}}^{ASL}={\displaystyle \sum _i}\Delta P_{\mathit{max},i}^{ASL}.(14)$

Combined with the reserve capacity of the primary frequency regulation of the synchronous generation unit, the dead zone parameter of the frequency regulation action of the UHVDC system is obtained as Equation 15

$\left|\Delta f_2\right|=\left(\Delta P_{\mathit{max}}^{ASL}+\Delta P_{Gmax}\right){\sigma }_p.(15)$

When the frequency deviation is greater than the dead zone value of frequency regulation $\left|\Delta f_2\right|$, the UHVDC sending-end system adopts DC frequency limit control to participate in frequency regulation, and its overall control structure is shown in Figure 6.

Figure 6

Figure 6. Structure of the frequency regulation model in the UHVDC sending-end system.

When the frequency change is greater than the dead zone value of frequency regulation $\left|\Delta f_2\right|$, the formula for the power modulation amount $\Delta P_{dc}$ is Equation 16

$\Delta P_{dc}=K_p\Delta f+\int K_i\Delta fdt.(16)$

3.3 Decentralized frequency response strategy of the electrolysis cell

Once the electrolytic aluminum station receives the upper-layer control command $\Delta P_{ASL}$, it decomposes the value among all the electrolysis aluminum cell series. Next, we simulate the control cost and power regulation command distribution architecture for the electrolytic aluminum load separately.

3.3.1 Modeling the control cost of the electrolytic aluminum load

The direct current series current value $I_i^{ASL}$ of the electrolytic cell is a key parameter in the electrolysis process. Under normal production conditions, the series current $I_i^{ASL}$ is maintained near its rated value $I_{i,0}^{ASL}$, and the electrolytic aluminum load is in normal production. However, when the electrolytic aluminum load is in the reduced load state, based on the magnitude of $I_i^{ASL}$, the production state of the electrolytic aluminum load can be divided into three types as production reduction, heat preservation, and cooling.

Under production reduction, the series current $I_i^{ASL}$ is 90%–100% of the rated value; in this state, the electrolytic aluminum load can still maintain production, but the output will be reduced. Under heat preservation, the series current $I_i^{ASL}$ is 70%–90% of the rated value; the electrolytic cell is energized for heat preservation to maintain the molten electrolyte from cooling; in this state, the production of electrolytic aluminum cannot be maintained but this will not cause equipment damage. Under cooling, the series current $I_i^{ASL}$ is 70% of the rated value; in this state, the electrolytic cell has difficulty maintaining the heat preservation state so that the molten electrolyte will cool gradually, and maintaining this state for a long time will cause equipment damage.

If the power consumed by the electrolytic aluminum load changes in response to frequency deviation, the production state will inevitably be affected. Compared to the normal production state of the electrolytic aluminum load, the economic loss caused by regulation due to the frequency response is the control cost and will be quantitatively analyzed.

Considering that a lengthy period of load reduction causes electrolyte cooling (8 h in summer and 4 h in winter), the duration of primary frequency regulation is relatively short. Therefore, the cost of damage to the electrolytic cell from maintaining electrolyte cooling for a long time can be ignored. Based on the different production states of the electrolytic aluminum load, the source of the control cost $C_R$ of the electrolytic aluminum load in this paper is divided into two parts as production and electrical energy costs.

Production cost $C_{PD}$ is the loss from production suspension or production reduction caused by the participation of the electrolytic aluminum load in regulation. This loss component is obtained by multiplying the difference between the original aluminum output under normal production and the original aluminum output after participating in regulation with the profit of the unit output of the original aluminum.

Electrical energy cost $C_{PW}$ refers to the large amount of electrical energy consumed in the absence of production of original aluminum in the heat preservation state under production suspension of the electrolytic aluminum load. This loss component is obtained by multiplying the electrical energy consumed under the production suspension state with the unit electricity cost.

Thus, $C_{R,i}$ can be expressed as

$\begin{array}{c}{C}_{R,i}=C_{PD,i}+C_{PW,i}\\ C_{PD,i}=\left\{\begin{array}{cc}\left(M_{0,i}-M_{R,i}\right)c_{prft}& I_i^{ASL}\ge 0.9I_{i,0}^{ASL}\\ M_{0,i}{c}_{prft}& I_i^{ASL}<0.9I_{i,0}^{ASL}\end{array}\right.\\ C_{PW,i}=\left\{\begin{array}{cc}0& I_i^{ASL}\ge 0.9I_{i,0}^{ASL}\\ \left(I_i^{ASL}{R}_{d,i}+E_{d,i}\right)I_i^{ASL}{c}_{free}& I_i^{ASL}<0.9I_{i,0}^{ASL}.\end{array}\right.\end{array}(17)$

The relationship between the primary aluminum output and DC series current value can be expressed as Equation 18

$M_{R,i}=\frac{0.3356\cdot {\eta }_{0,i}}{I_{i,0}^{ASL}}{\left(I_i^{ASL}\right)}^2.(18)$

To facilitate analysis of the piecewise function in Equation 17, the flag bit $r_i$ is introduced as follows:

$r_i=\left\{\begin{array}{cc}0& I_i^{ASL}<0.9I_{i,0}^{ASL},\\ 1& I_i^{ASL}\ge 0.9I_{i,0}^{ASL}.\end{array}\right.(19)$

By substituting Equation 19 in Equation 17, we obtain

$C_{PD,i}=r_i\left(M_{0,i}-\frac{0.3356{\eta }_{0,i}}{I_{i,0}^{ASL}}{\left(I_i^{ASL}\right)}^2\right)c_{prft}+\left(1-r_i\right)M_{0,i}{c}_{prft},(20)$

$C_{PW,i}=0\cdot r_i+\left(1-r_i\right)\left(I_i^{ASL}{R}_{d,i}+E_{d,i}\right)I_i^{ASL}{c}_{free}.(21)$

By substituting Equations 20, 21 in Equation 17, the control load cost of the electrolytic aluminum series can be obtained as

$C_{R,i}=r_i\left(M_{0,i}{c}_{prft}-\frac{0.3356{\eta }_{0,i}{c}_{prft}}{I_{d0,i}}{\left(I_i^{ASL}\right)}^2\right)+\left(1-r_i\right)\left[M_{0,i}{c}_{prft}+\left(I_i^{ASL}{R}_{d,i}+E_{d,i}\right)I_i^{ASL}{c}_{free}\right].(22)$

The control cost of the entire electrolytic aluminum station is the sum of the control costs of the $n$ electrolytic series:

$C_R^{sum}={\displaystyle \sum _{i=1}^n}{C}_{R,i}.(23)$

3.3.2 Power distribution control strategy for the electrolytic aluminum series

Considering the form of $C_{R,i}$ in Equation 22, Equation 23 can be written in the following compact form as shown in Equations 24–28:

${\mathit{min}C}_R^{sum}={\displaystyle \sum _{i=1}^n}\left[r_i\left({\epsilon }_{i,1}{\left(I_{d,i}^{ASL}\right)}^2+{\nu }_i\right)+\left(1-r_i\right)\left({\epsilon }_{i,2}{\left(I_{d,i}^{ASL}\right)}^2+{\gamma }_i{I}_{d,i}^{ASL}+{\nu }_i\right)\right],(24)$

where

${\epsilon }_{i,1}=-\frac{0.3356{\eta }_{0,i}{c}_{prft}}{I_{d0,i}},(25)$

${\epsilon }_{i,2}=c_{free}{R}_{d,i},(26)$

${\gamma }_i=c_{free}{E}_{d,i},(27)$

${\nu }_i=M_{0,i}{c}_{prft}.(28)$

The expression of $r_i$ is then constrained as Equation 29

$\frac{I_{d,i}}{0.9I_{d0,i}}-1<r_i\le \frac{I_{d,i}}{0.9I_{d0,i}}.(29)$

The model also needs to satisfy the total regulated power constraint, which can be expressed as Equations 30, 31

$\Delta P_{ASL}={\displaystyle \sum _i}\Delta P_i^{ASL},(30)$

${\displaystyle \sum _i}\Delta P_i^{ASL}\le {\displaystyle \sum _{i=1}^n}{U}_{\mathit{max},i}^{ASL}{I}_{\mathit{max},i}^{ASL}-U_{d,i}^{ASL}{I}_{d,i}^{ASL}.(31)$

Steady current control of the electrolytic series is achieved by fine-tuning the self-saturable reactor. Owing to the limited depth of voltage regulation of the self-saturable reactor, there are minimum values for both the voltage and series current of the electrolytic aluminum series. Therefore, the set series current should not exceed the voltage regulation capacity of the self-saturable reactor as shown in Equation 32:

$I_{\mathit{min},i}^{ASL}\le I_{d,i}^{ASL}\le I_{max,i}^{ASL}.(32)$

The above model is a mixed-integer quadratic programming problem. In each dispatch control cycle, the power adjustment sequence for each electrolytic aluminum series is calculated through optimization and distributed to the lower-layer electrolytic series $1$ to $n$. The lower electrolytic series respond automatically to system frequency deviation control by using the current command value as the input to the PI control link.

4 Case study

4.1 Simulation design

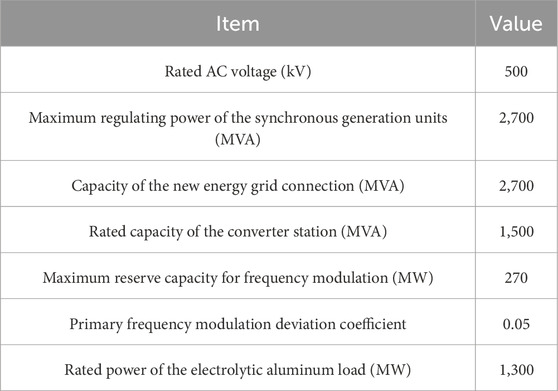
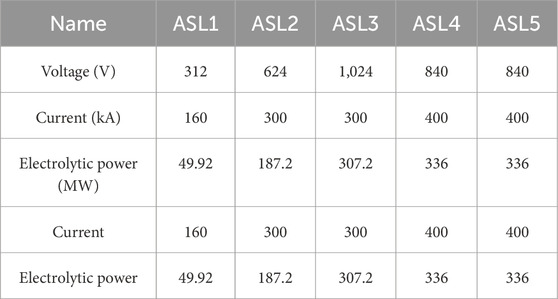
To verify the effectiveness of the abovementioned frequency regulation strategy, the UHVDC transmission system model with electrolytic aluminum load shown in Figure 1 was built and simulated in MATLAB/Simulink. The relevant simulation parameters are shown in Table 1. Among these, the load at the electrolytic aluminum station contains five electrolytic series ASL1–ASL5, all of which have the same type of self-saturable reactor with a voltage regulation depth of 70 V. The equipment parameters are shown in Table 2.

Table 1

Table 1. Parameters of the designed simulation experiment.

Table 2

Table 2. Parameters of the electrolytic aluminum series.

4.2 Source–grid–load coordinated frequency control experiment

In the simulations, two working conditions corresponding to frequency rise and frequency drop were set, and the dynamic response curves of the system frequency under participation or non-participation of the electrolytic aluminum load in the source–grid–load coordinated regulation were compared and analyzed to highlight the effectiveness and advantages of the proposed control strategy.

Condition 1: A wind farm failure occurs, resulting in a 450-MW power shortage in the system that causes the frequency of the sending-end power grid to drop.

Condition 2: A monopolar blocking fault occurs in the DC line, resulting in a 400-MW power surplus in the system that causes the frequency of the sending-end power grid to rise.

4.2.1 Simulation results under Condition 1

A 450-MW wind turbine generator was disconnected at $t=5s$, resulting in a 450-MW power shortage in the system. Since this shortage exceeds the primary frequency regulation reserve capacity of the synchronous units, the power shortage of the system should be compensated by the electrolytic aluminum station or UHVDC system after disturbance occurs. Under this working condition, we simulated the frequency and power variation curves for three control modes: 1) neither the electrolytic aluminum load nor the UHVDC system is involved in frequency regulation; 2) the electrolytic aluminum load does not participate in frequency regulation, but the UHVDC system participates in frequency regulation; 3) the proposed source–grid–load coordinated control strategy with the electrolytic aluminum load participates in frequency regulation. The results under these conditions are shown in Figure 7.

Figure 7

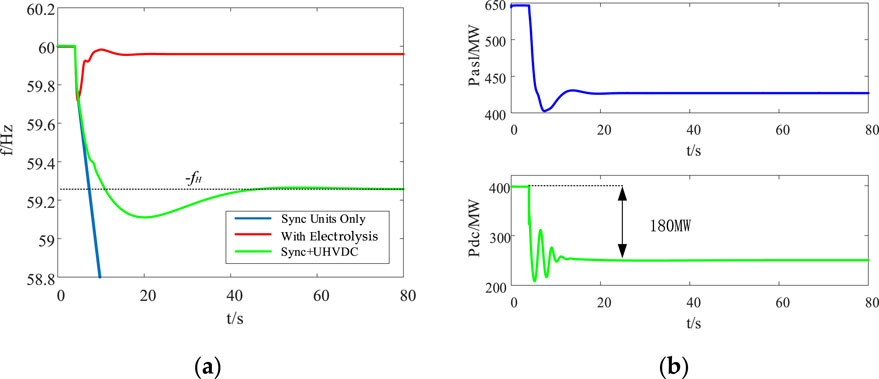
Figure 7. Simulation results under Condition 1 showing (A) a comparison of the effects of different frequency modulation methods and (B) the power consumed by the electrolytic aluminum station or delivered by the UHVDC grid.

As shown in Figure 7A, when only the synchronous units participate in frequency regulation without the electrolytic aluminum load or UHVDC system, the primary frequency regulation capacity of the synchronous generator units is maximum but still insufficient to compensate the unbalanced power of the system, eventually leading to rapid decline of the system frequency and to system collapse. As shown in Figure 7A, when the synchronous units and UHVDC system participate in frequency regulation, the final frequency will be stabilized near the frequency dead zone value of the UHVDC system. As seen in Figure 7B, during the adjustment process, there was a large power fluctuation in the receiving-end power grid; after reaching the steady state, the UHVDC system had a power transmission reduction of 180 MW that accounted for nearly 20% of the transmission capacity of the DC system and greatly reduced its utilization rate. In addition, although this scheme can suppress the frequency drop of the system, the frequency difference at steady state is large and there is much room for improvement.

As seen in Figure 7A, when the electrolytic aluminum load participates in grid frequency support through the source–grid–load fixed-value coordination strategy proposed in this paper, the power shortage reaches the action threshold of the electrolytic aluminum load that then participates immediately in the system frequency regulation control strategy. As seen in Figure 7B, under the proposed control strategy, the electrolytic aluminum station responds quickly to the frequency change and reduces the power of the entire station to that required by the dispatch control center within 2 s. Compared with the frequency regulation achieved with the control schemes of the participating units and UHVDC system, the proposed method increases the lowest point of frequency drop by 0.7 Hz. At the same time, compared with the UHVDC frequency regulation scheme, the frequency adjustment time of this strategy is significantly shorter, which has substantial advantages.

4.2.2 Simulation results under Condition 2

At $t=5s$, a monopolar blocking occurs in the UHVDC line, resulting in 400 MW of surplus power in the system that exceeds the primary frequency regulation capacity of the synchronous generator units. Once the disturbance occurs, the electrolytic aluminum load immediately responds to the unbalanced power of the system, and the corresponding simulation results are shown in Figure 8. As shown in Figure 8A, when only the synchronous units are used for frequency modulation, their electromagnetic power reaches the upper limit of regulation when the surplus power exceeds the maximum frequency modulation reserve capacity of the sending-end AC system owing to the limited frequency modulation resources of the system. At this time, if the electrolytic aluminum load does not participate in regulation, the frequency continues to increase, and it is ultimately difficult to maintain the frequency stability of the system.

Figure 8

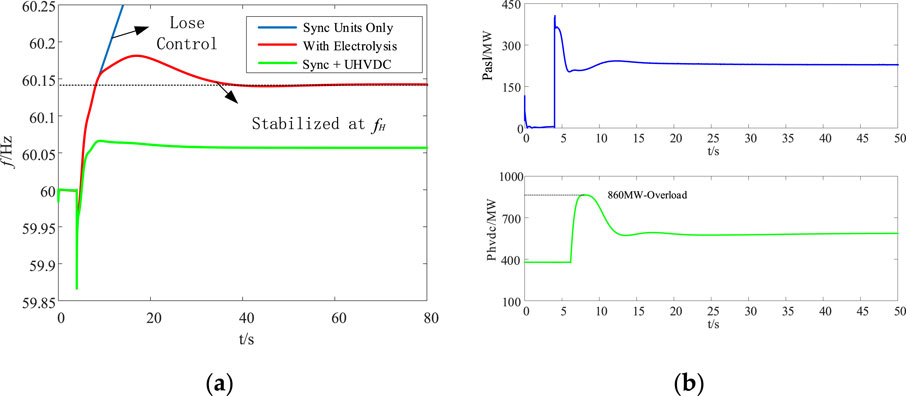
Figure 8. Simulation results under Condition 2 showing (A) a comparison of the effects of different frequency modulation methods and (B) power consumed by the electrolytic aluminum station or delivered by the UHVDC grid.

As shown in Figure 8B, when the electrolytic aluminum load participates in frequency regulation, the system power shortage reaches the action threshold of the electrolytic aluminum load that then immediately participates in system frequency modulation control and achieves rapid suppression of the frequency fluctuations within 20 s. At this time, the UHVDC line will have not reached the frequency action threshold yet and the transmission power remains unchanged, ensuring safe operation of the DC line. In addition, as shown in Figure 8A, the adjustment time, overshoot, and steady-state frequency difference of the proposed strategy have significant advantages compared to the frequency modulation scheme of the DC grid alone.

To further explore the influence of the participation degree of the electrolytic aluminum station in frequency modulation on the dynamic performance indicators of the system and operating process of the DC line, the processes causing frequency variations under different participation degrees of the electrolytic aluminum load in frequency modulation (100%, 90%, and 80%) were compared; these results are shown in Figure 9. As the participation degree of the electrolytic aluminum load in frequency modulation decreases, the system response speed gradually decreases, maximum point of frequency drop gradually decreases, and steady-state frequency difference gradually increases.

Figure 9

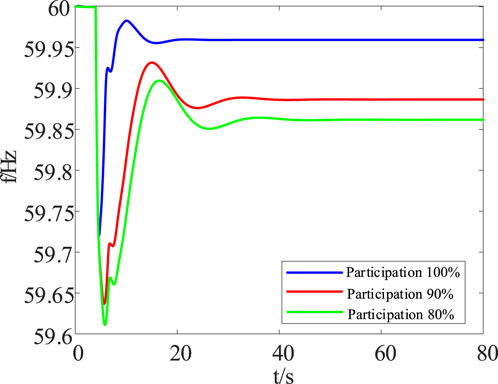
Figure 9. Comparison of the effects of the frequency adjustment process under different participation degrees of the electrolytic aluminum load.

By comparing the frequency variation curves of the DC grid participating in frequency modulation in Figures 8A, 9, it is understood that higher degrees of participation of the electrolytic aluminum load in frequency modulation result in lower adjustment power from the DC grid; moreover, both the dynamic and steady-state system performances are improved, fully demonstrating the superiority of the proposed method. With increase in the coordination degree of the electrolytic aluminum load, the system frequency can be quickly adjusted to the steady-state frequency with a small overshoot, thereby avoiding changes in the transmission power during the operation of the UHVDC line and effectively avoiding overload in the UHVDC grid while greatly improving the safety and reliability of the system.

4.3 Control cost analysis of the electrolytic aluminum station

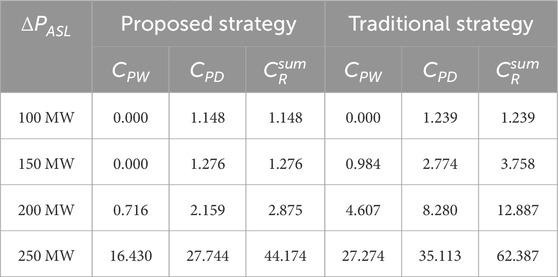
To verify the effectiveness of the proposed optimal control strategy in reducing the control cost of the electrolytic aluminum load, a contrastive method of proportional dispatch is designed. This scheme dispatches the required frequency regulation power proportionally among all operating generators based on their available regulation power, which can be expressed as Equation 33

$P_i^{ASL}=\frac{P_{\text{avail},i}^{ASL}}{{\displaystyle \sum _{i=1}^n}{P}_{\text{avail},i}^{ASL}}\Delta P_{ASL}.(33)$

The profit of each ton of primary aluminum is set at 71.4 $/MWh here, and the electricity fee is 57.1 $/MWh. By setting $\Delta P_{ASL}$ to 100, 150, 200, and 250 MW, we analyzed the production cost $C_{PD}$, electricity cost $C_{PW}$, and total cost $C_R^{sum}$ under the two methods, which are shown in Table 3.

Table 3

Table 3. Control costs (×10³ $/h) under different strategies.

According to the results in Table 3, the proposed method shows superior performance in reducing the control cost of the electrolytic aluminum load. When $\Delta P_{ASL}$ is 100 MW, the total costs of the proposed and comparable methods are 1.148 × 10³ $/h and 1.239 × 10³ $/h, respectively, and the total cost of the proposed method is slightly lower than that of the comparable method. As $\Delta P_{ASL}$ increases, the cost advantage of the proposed method becomes more obvious. When $\Delta P_{ASL}$ is 150 MW, the total cost of the proposed method is 1.276 × 10³ $/h while that of the comparable method is 3.758 × 10³ $/h, and the total cost with the proposed method is only about one-third of that of the comparable method. When $\Delta P_{ASL}$ is 200 MW, the total cost of the proposed method is 2.875 × 10³ $/h while that of the comparable method is as high as 12.887 × 10³ $/h, which is a significant difference. Finally, when $\Delta P_{ASL}$ is 250MW, the total cost of the proposed method is 44.174 × 10³ $/h while that of the comparable method is 62.387 × 10³ $/h; it can be seen that the total cost with the proposed method is always lower than that with the comparable method for all values of $\Delta P_{ASL}$ and especially at higher values of $\Delta P_{ASL}$. These data verify the significant superiority of the proposed optimal control strategy in reducing the control cost of the electrolytic aluminum load and prove its potential economic benefits in practical applications.

5 Conclusion

This paper presents a source–grid–load coordinated control strategy for the participation of electrolytic aluminum in frequency regulation at the DC sending-end grid. The proposed method effectively enhances system stability and reduces control costs. Simulation results confirm that this method significantly improves both the dynamic and steady-state performances of the power system. By leveraging the rapid response capabilities of electrolytic aluminum loads and the UHVDC system, the proposed strategy ensures efficient frequency regulation, minimizes power fluctuations, and prevents overload conditions. Additionally, the proposed method consistently demonstrates lower control costs compared to traditional proportional dispatch methods, particularly at higher regulation power levels. Thus, the proposed strategy offers substantial economic and operational benefits, underscoring its viability for practical applications in power system frequency regulation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

CX: conceptualization, methodology, and writing–original draft. XX: conceptualization, formal analysis, and writing–original draft. XH: formal analysis, investigation, validation, and writing–review and editing. CD: formal analysis, supervision, and writing–review and editing. MZ: resources, visualization, and writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors CX, XX, XH, CD, and MZ were employed by the Electric Power Research Institute of Yunnan Power Grid Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, P. (2021). Coordinated active power/frequency control from supply, network, and demand sides considering participation of aluminum smelter load. Shandong University. doi:10.27272/d.cnki.gshdu.2021.003789

CrossRef Full Text | Google Scholar

Bao, P., Zhang, W., Cheng, D., and Liu, M. (2020). Hierarchical control of aluminum smelter loads for primary frequency support considering control cost. Int. J. Electr. Power Energy Syst. 122, 106202. doi:10.1016/j.ijepes.2020.106202

CrossRef Full Text | Google Scholar

Bao, P., Zhang, W., and Zhang, Y. (2022). Secondary frequency control considering optimized power support from virtual power plant containing aluminum smelter loads through VSC-HVDC link. J. Mod. Power Syst. Clean Energy 11, 355–367. doi:10.35833/mpce.2021.000072

CrossRef Full Text | Google Scholar

Du, S., Han, S., Xu, L., Huang, Y., Wang, K., Zhang, Z., et al. (2023). Load frequency stabilization control and parameter optimization method in isolated electrolytic aluminum industrial microgrid. IEEE Power Energy Soc. General Meet. 11, 616–621. doi:10.1109/PSGEC58411.2023.10255878

CrossRef Full Text | Google Scholar

Guo, X., Zhang, J., Kang, P., Yang, G., Sun, Y., Yuan, T., et al. (2022). Virtual synchronization control strategy for UHVDC with secondary frequency modulation based on PI control. Electr. Power 55, 66–72. doi:10.11930/j.issn.1004-9649.202105025

CrossRef Full Text | Google Scholar

Han, J., and Chen, Z. (2024). An inertial control method for large-scale wind farm based on hierarchical distributed hybrid deep-reinforcement learning. J. Clean. Prod. 450, 142034. doi:10.1016/j.jclepro.2024.142034

CrossRef Full Text | Google Scholar

Han, J., Lyu, W., Song, H., Qu, Y., Wu, Z., Zhang, X., et al. (2023). Optimization of communication network for distributed control of wind farm equipped with energy storages. IEEE Trans. Sustain. Energy 14, 1933–1949. doi:10.1109/TSTE.2023.3264656

CrossRef Full Text | Google Scholar

Han, J., Miao, S., Chen, Z., Liu, Z., Li, Y., Yang, W., et al. (2021). Multi-view clustering and discrete consensus based tri-level coordinated control of wind farm and adiabatic compressed air energy storage for providing frequency regulation service. Appl. Energy 304, 117910. doi:10.1016/j.apenergy.2021.117910

CrossRef Full Text | Google Scholar

Li, C., Zhang, D., Han, J., Tian, C., Xie, L., Wang, C., et al. (2024). A multi-level operation method for improving the resilience of power systems under extreme weather through preventive control and a virtual oscillator. Sensors 24, 1812. doi:10.3390/s24061812

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Wang, B., Liu, C. Z., Wang, Y, Hu, X, and Han, L (2019). Suppression scheme for ultra-low frequency oscillation based on frequency limit controller. High. Volt. Eng. 45, 2126–2133. doi:10.13336/j.1003-6520.hve.20180822011

CrossRef Full Text | Google Scholar

Luo, Z., Gao, P., Nie, L., Tian, X., Shen, X., and Zhang, Z. (2023). Research on cooperative frequency control strategy of wind-aluminum combined system. Electr. Mach. Control Appl. 50, 49–57. doi:10.12177/emca.2023.035

CrossRef Full Text | Google Scholar

Mo, L., Lan, J., Zhou, L., Ye, M., Ma, L., and Chen, H. (2024). Multi-timescale frequency modulation control for flexible resources in virtual power plant. Automation Electr. Power Syst., 1–16. doi:10.7500/AEPS20230912004

CrossRef Full Text | Google Scholar

Nie, S., Huang, R., Chen, L., Min, Y., You, G., and Wu, C. (2024). Adaptive control of primary frequency regulation for electrolytic aluminum considering energy recovery. Automation Electr. Power Syst. 1, 13. doi:10.7500/AEPS20230821009

CrossRef Full Text | Google Scholar

Wang, C., Han, J., Jiang, D., Zhang, W., Yang, W., Song, H., et al. (2024a). Research on autonomous operation and mutual aid strategy of AC/DC hybrid microgrid cluster. Electr. Power Syst. Res. 231, 110302. doi:10.1016/j.epsr.2024.110302

CrossRef Full Text | Google Scholar

Wang, G., Shi, R., Cheng, W., Gao, L., and Huang, X. (2023). Bibliometric analysis for carbon neutrality with hotspots, frontiers, and emerging trends between 1991 and 2022. Int. J. Environ. Res. Public Health 20, 926. doi:10.3390/ijerph20020926

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Han, J., Jiang, D., Zhang, W., Yang, W., Song, H., et al. (2024b). Large signal stability control method of DC microgrid with analogous virtual synchronous generator and flexible load. Trans. China Electrotech. Soc. 1, 13.

Google Scholar

Wang, Y., Zhu, J., Zeng, Q., Tai, K., Yu, G., Yin, A., et al. (2022). Multi-objective bi-level optimization design method of DC frequency limiting controller parameters. Electr. Power Autom. Equip. 42, 189–196+224. doi:10.16081/j.epae.202205035

CrossRef Full Text | Google Scholar

Xin, Y., Zhang, J., Jiang, S., Wang, W., and Wang, T. (2023). Coordinated control strategy to improve frequency stability at sending terminal of ultra-high voltage direct current transmission system. Power Syst. Technol. 47, 5089–5097. doi:10.13335/j.1000-3673.pst.2022.2099

CrossRef Full Text | Google Scholar

Xu, J., Liao, S., Sun, Y., Ma, X., Gao, W., Li, X., et al. (2014). An isolated industrial power system driven by wind-coal power for aluminum productions: a case study of frequency control. IEEE Trans. Power Syst. 32, 22080. doi:10.1109/PESGM.2015.7286407

CrossRef Full Text | Google Scholar

Yang, W., Miao, S., Liu, Z., Han, J., Xiong, Y., and Tu, Q. (2021). Model predictive direct power control of grid-connected converters considering unbalanced filter inductance and grid conditions. J. Mod. Power Syst. Clean Energy 9, 1279–1288. doi:10.35833/MPCE.2021.000355

CrossRef Full Text | Google Scholar

Yang, Y., Yan, F., Yang, Y., and Chen, Y. (2023). Evaluating provincial carbon emission characteristics under China’s carbon peaking and carbon neutrality goals. Ecol. Indic. 151, 111146. doi:10.1016/j.ecolind.2023.111146

CrossRef Full Text | Google Scholar

Yang, Z., Han, J., Wang, C., Li, L., Li, M., Yang, F., et al. (2023). Emergency power supply restoration strategy for distribution network considering support of microgrids with high-dimensional dynamic correlations. Electronics 12, 3246. doi:10.3390/electronics12153246

CrossRef Full Text | Google Scholar

You, G., Li, L., and Zhu, X. (2018). Analysis on adaptability of Yunnan power grid to wudongde multi-terminal DC. Guangdong Electric Power 31 (09), 32–38.

Google Scholar

Zhang, X., Liu, F., Wang, S. B., and Li, Y. (2022). “Measures to improve the new energy consumption level of UHVDC sending-end power gird,” in Proceedings of the CSU - EPSA 2022 34 (06), 135–141. doi:10.19635/j.cnki.csu-epsa.000914

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

UHVDC ultrahigh-voltage direct current

FLC frequency limit controller

DC direct current

AC alternating current

DR distributed resources

VSC-HVDC voltage source converter high-voltage direct current

LCC-HVDC line-commutated converter high-voltage direct current

LCC line-commutated converter

ASL aluminum smelting line

PI proportional–integral

PWM pulse-width modulation

Frequency response model

LCC₁ rectifier station connecting the sending-end system including the wind farm, synchronous units, and electrolytic aluminum load

Bus₁ bus of the alternating current system on the rectifier side

R_d1 resistance of the direct current line

LCC₂ inverter station connecting the receiving-end alternating current power grid

Bus₂ bus of the alternating current system on the inverter side

P_m output of the synchronous unit

P_w output of the wind turbine unit

P_LD1 load power of the sending-end system

P_ASL power of the electrolytic aluminum load

P_dc transmission power of the high-voltage direct current line

P_G total generated output of the sending-end system

P_L total active load demand of the sending-end system

H_sys equivalent inertia of the sending-end power grid

ΔP_G active power of the primary frequency regulation response of the sending-end power grid

ΔP_L variation in the active load

D damping coefficient of the sending-end power grid

Δf frequency deviation of the sending-end power grid

f actual frequency of the sending-end power grid

f₀ rated frequency (50 Hz)

P_i^ASL active power consumption of the ith electrolysis cell

U_i^ASL voltage of the ith electrolysis cell

I_i^ASL current of the ith electrolysis cell

I_{ref, i}^ASL reference value of the current of the ith electrolysis cell

Frequency control strategy

|Δf| absolute frequency deviation

|Δf₁|, |Δf₂| dead zone values of the frequency regulation

σ_p droop coefficient of the primary frequency regulation of the synchronous generation units

P_Gmax maximum regulating power of the synchronous generation units

ɑ initial control angle of the converter

ɑ_ord command control angle of the converter

P_GN rated power of the generation unit

P_ASLN rated power of the electrolysis cell

K_f,ASL frequency droop coefficient of the electrolytic aluminum load

ΔP_ASL power deviation of the electrolytic aluminum station

ΔP_unb power disturbance generated by the system

ΔP_max,i^ASL available active capacity of the ith electrolytic aluminum series

U_{max, i}^ASL maximum voltage of the ith electrolytic aluminum series

I_{max, i}^ASL maximum current of the ith electrolytic aluminum series

ΔP_max^ASL available active capacity of the entire electrolytic aluminum station

K_p coefficients of the proportional links

K_i coefficients of the integral links

ΔP_max upper limit of the power adjustment amount

ΔP_dc0 reference value of the transmission power of the high-voltage direct current line

ΔP_dc transmission power value of the high-voltage direct current line after adjustment

I_i^ASL direct current series current value

I_i,0^ASL rated value of the direct current series current

C_R source of the control cost

C_PD production cost

C_PW electrical energy cost

C_R,I control cost of the ith electrolytic series

M_0,I output of the primary aluminum under normal production conditions

M_R,I output of the primary aluminum after load reduction or increase

c_prft profit of the primary aluminum per unit output

c_free unit electricity cost

ŋ_0,I rated current efficiency in the ith electrolytic series

r_i flag bit

ε_i,γ_i,ν_i coefficients of the piecewise quadratic function

P_i^ASL active power that the ith electrolytic series must generate

P_{avail, i}^ASL available reactive power of the ith electrolytic aluminum series at a specific moment

_R^sum total cost