New PSO-GWO-based model for enhancing power quality in electrical networks interconnected with photovoltaic sources

This research introduces an innovative model to enhance power quality within electrical networks interconnected with photovoltaic (PV) sources. The central concern addressed in this study revolves around the impact of PV source power quality on local electric networks. This research endeavors to elucidate how achieving a more refined power pattern in electric networks is attainable by considering the power quality of PV sources. A hybrid Particle Swarm Optimization-Gray Wolf Optimization (PSO-GWO) algorithm is proposed to obtain optimal solutions. Empirical findings underscore the significant impact of Unified Power Quality Conditioners (UPQC) on social welfare, reinforcing the potential benefits of improving power quality. The results reveal that localized price reductions primarily drive the enhancement of social welfare, and this socioeconomic advantage outweighs improvements in sustainability metrics.

1 Introduction

The increasing focus on reducing carbon emissions has led to a significant rise in the utilization of renewable energy resources for power generation (Anghelache et al., 2023). Among these, photovoltaic (PV) electricity is gaining recognition as a promising renewable energy source. However, the intermittent nature of PV systems negatively affects the power quality of grid-connected large-scale PV installations (Augusto Pereira et al., 2023). Large PV plants can compromise power system reliability due to increased power fluctuations over long distances. To maintain grid reliability, power suppliers and research organizations have imposed restrictions on the extent to which PV projects can increase their output (Fregosi et al., 2023). Consequently, any PV output that exceeds grid connection criteria must be regulated (Xu et al., 2022).

To address power fluctuations and enhance the integration of PV systems into the grid, fast-response energy storage devices, such as supercapacitor energy storage systems (SC-ESS), can play a crucial role. High-power density storage devices like SC-ESS can reduce grid vulnerability to variations in PV generation (Cano et al., 2022). A feasibility study examined three power smoothing strategies for a PV-hydrokinetic system (Cano et al., 2022), involving a hybrid storage system combining SC-ESS and lithium-ion batteries, primarily used for energy storage. The findings indicated that these strategies effectively mitigated power oscillations and optimized voltage levels in typical interconnections.

Previous research has shown that the performance of batteries and SC-ESS can significantly influence the energy trade dynamics with the grid (Cano et al., 2022). Various filtering techniques have been proposed to control PV power output, including low-pass (LP) filtering (Wu et al., 2019), moving average (MA) filtering (Arévalo et al., 2023), corrective predictive filtering (Arévalo et al., 2023; Benavides et al., 2022), heuristic filtering (Benavides et al., 2023), and multi-objective optimization filtering (Ma et al., 2019a). For instance (Wu et al., 2019), implemented a two-stage LP filter control strategy with an adjustable filter time constant to stabilize DC bus power fluctuations. This approach integrated improved particle swarm optimization (IPSO) and fuzzy control techniques to adaptively adjust filtering time constants. However, further evaluation is needed to assess the effectiveness of these methods concerning SC-ESS operability, grid compliance, and system longevity.

The goal of these methods is to enhance the smoothing of load power fluctuations while minimizing risks such as battery overcharging or over-discharging. Arévalo et al. (2023) demonstrates the combination of MA and ripple removal (RR) techniques with hybrid storage technologies like SC-ESS and batteries, showing that these strategies effectively reduce the frequency of SC-ESS operations and mitigate issues within PV systems. Although MA filtering offers potential benefits, its limitations—particularly regarding SC-ESS functionality and lifespan—must be addressed to ensure seamless integration with the power grid.

In Benavides et al. (2022), SC-ESS and batteries were examined for power smoothing in renewable energy systems connected to the electrical grid. This study highlighted the feasibility of SC-ESS for energy management and power quality improvement, showing that SC-ESS requirements vary based on renewable capacity. The RR approach was found advantageous in reducing SC-ESS workload. Comprehensive evaluations are necessary to assess the benefits and drawbacks of SC-ESS control and grid connection alignment.

Moreover, as (Benavides et al., 2023) suggests, SC-ESS offers a unique power-smoothing method for grid-connected solar systems. Cycle estimation using k-means and ripple removal (RR) algorithms has shown effectiveness in reducing energy loss and minimizing technical violations in laboratory environments. k-means clustering is an unsupervised learning algorithm used for data clustering, which groups unlabeled data points into groups or clusters and ramp-rate (RR) control algorithms are often applied for mitigating these power fluctuations to the grid. However, further research is required to evaluate the adequacy of these heuristics in controlling energy storage devices like SC-ESS and ensuring their compliance with grid regulations while preserving their longevity.

Ma et al. (2019b) proposes a coordinated control strategy for hybrid energy storage systems (HESS) to mitigate PV plant-induced power fluctuations. The study employs a multi-objective optimization model to manage power dispatch from batteries and SC-ESS, considering both SC-ESS losses and variability in the state of charge (SoC). Despite these advancements, a thorough analysis is needed to assess the impact of such optimization techniques on SC-ESS control and their ability to meet grid requirements while preventing early system failure.

This study aims to fill the gaps identified in previous research by proposing an innovative power-smoothing approach using SC-ESS. The main objectives are to improve energy quality, reduce fluctuations, and comply with grid connection standards, ensuring SC-ESS operates within defined parameters, maximizing its lifespan, and facilitating smooth grid integration.

Nempu et al. (2021) discusses a power smoothing approach based on SC-ESS using a Kalman filter, demonstrating its effectiveness in reducing power fluctuations and minimizing the load on converters. The study presents a multi-objective optimization model designed to regulate PV energy production by leveraging SC-ESS and batteries, with the key goal of preventing SC-ESS from operating below its operational thresholds. Computational simulations indicate that this approach offers better cost-effectiveness than traditional methods.

Additional studies, such as Krishan and Suhag (2020) and Saripalli et al. (2022), have explored SC-ESS’s potential in mitigating power fluctuations using fuzzy logic algorithms and low-pass filtering techniques. These studies suggest that such strategies can provide a stable voltage and current profile. Chong et al. (2016) introduces an optimal control method for a stand-alone PV system with SC-ESS and batteries, combining low-pass filtering with fuzzy logic control to reduce battery stress and increase system longevity.

Research also focuses on real-time dynamic adjustments to SC-ESS filter time constants, as discussed in Wu et al. (2019), based on SoC requirements. Although stabilizing SC-ESS dynamically remains challenging, studies (Kanehira et al., 2015) have shown that MA and RR are among the most effective power-smoothing techniques in this context. Additionally, Takahashi et al. (2022) introduces a spline function-based PV smoothing technique, which, through simulations, demonstrates superior performance compared to MA methods.

Sukumar et al. (2018) provides a detailed analysis of approaches that reduce energy storage degradation and enhance the lifespan of SC-ESS. The study introduces an optimization method, based on (Ali et al., 2019), to mitigate voltage fluctuations from intermittent sources. The method enhances storage device durability by addressing issues in traditional MA algorithms.

Studies such as Al Shereiqi et al. (2020) introduce optimization techniques to minimize power losses in PV and wind farm systems, demonstrating the effectiveness of numerical methods for mitigating power output fluctuations. Likewise Aryani et al. (2017), proposes model predictive control for managing battery SoC, showing that the moving average filter provides consistent electricity delivery to the grid.

Further research supports these findings. For example D’Amico et al. (2022), provides an overview of ramp-rate limitation techniques for wind power, emphasizing the importance of mitigating fluctuations in renewable energy sources. Similarly, Kaushal and Basak (2020) explores artificial neural network (ANN)-based power quality control methods for microgrids, focusing on improving key power quality metrics such as voltage sag, swell, and frequency deviations. Building upon these studies, this article introduces a novel hybrid optimization technique inspired by the foundational concepts in (Ali et al., 2019), specifically combining Grey Wolf Optimization (GWO) with Particle Swarm Optimization (PSO). This hybrid approach addresses the unique challenges of PV-integrated systems, contributing primarily to improving Total Harmonic Distortion (THD), voltage stability, and overall power quality.

The development of hybrid optimization techniques has gained significant attention in the literature. Shaheen et al. (2021) introduces a hybrid Grey Wolf Optimization-Particle Swarm Optimization (GWO-PSO) approach to solve the reactive power dispatch problem, showing improved optimization results in power systems. Similarly Alyu et al. (2023), applies the hybrid GWO-PSO technique for optimal placement and sizing of PV-DG units, demonstrating substantial reductions in power loss and improvements in voltage profiles.

Finally, as described in Zhang et al. (2021), the hybrid PSO and Grey Wolf Optimizer (PSO-GWO) has been effectively used in clustering optimization, showing promising results that can be extended to power system applications. These studies further validate the potential of hybrid algorithms in enhancing power quality and system efficiency.

This study introduces a hybrid Grey Wolf Optimization (GWO) and Particle Swarm Optimization (PSO) approach to improve power quality in electrical networks integrated with solar sources. The GWO-PSO hybrid optimizes the placement and sizing of power quality compensation devices, reducing THD, voltage sags, and swells, while maintaining grid stability.

In this study, we employ the k-means clustering and Ripple Removal (RR) algorithms as part of our optimization framework to manage fluctuations in power quality effectively. The k-means algorithm is an unsupervised machine learning technique widely used for clustering data points into a specified number of groups or clusters based on similarity. This approach allows us to group data points—such as voltage fluctuations—in a way that enables efficient pattern recognition and distribution of power quality disturbances. By assigning data points to clusters, the k-means algorithm helps in estimating power cycles and identifying periods of high variability, which are crucial for precise power quality control. Notably, this algorithm is both computationally efficient and well-suited for handling large datasets commonly encountered in electrical network analysis Ali et al. (2019).

The Ripple Removal (RR) algorithm is a signal processing method designed to smooth out or eliminate oscillations in data, often referred to as ripples. Within our framework, the RR algorithm acts as a filtering mechanism that mitigates abrupt changes and reduces noise in power quality metrics such as voltage and current. By applying this algorithm, we achieve a cleaner signal that contributes to stable power delivery and enhances the operability of energy storage systems. The combination of k-means clustering for detecting patterns and RR for smoothing fluctuations is particularly effective in ensuring compliance with grid standards and reducing equipment wear due to rapid fluctuations (Malamaki et al., 2022).

2 Proposed hybrid GWO-PSO algorithm

The Grey Wolf Optimization (GWO) algorithm is a nature-inspired optimization technique that emulates the social hierarchy and hunting behaviors observed in gray wolf packs. GWO is particularly effective in achieving a balance between exploration (searching for new solutions) and exploitation (refining current solutions). In GWO, wolves are categorized into four main types: alpha, beta, delta, and omega, representing a hierarchical structure. The alpha wolves guide the pack and are responsible for making strategic decisions. Beta wolves assist the alphas, influencing the pack’s direction, while delta wolves act as scouts and defenders, aiding in the exploration of the search space. Finally, omega wolves follow the rest and reinforce the pack’s cohesion.

The GWO algorithm iteratively adjusts the positions of wolves in response to the influence of the top three wolves (alpha, beta, and delta) to converge toward an optimal solution. The wolves update their positions based on a mathematical model that mimics the encircling, hunting, and attacking behaviors of real gray wolves. This model ensures that the search agents maintain a robust balance between diversification and intensification (Shaheen et al., 2021; Alyu et al., 2023; Negi et al., 2021).

The Particle Swarm Optimization (PSO) algorithm is another swarm intelligence-based optimization technique that simulates the social behaviors of bird flocks or fish schools. Each particle in PSO represents a potential solution that “flies” through the search space. Particles adjust their velocity and position according to their own experience (personal best position) and the best-known position of the swarm (global best). This dual influence allows particles to dynamically explore and exploit the search space effectively. PSO is recognized for its fast convergence rate, particularly in optimizing continuous, multidimensional spaces (Zhang et al., 2021; Gad, 2022).

By integrating the hierarchical structure of GWO with the social behaviors of PSO, the proposed hybrid GWO-PSO algorithm leverages the strengths of both approaches. The hybrid model achieves a synergy between the GWO’s robust exploration capabilities and PSO’s efficient convergence, optimizing power quality in photovoltaic-integrated networks with a balanced approach to search and solution refinement.

Our approach is inspired by the optimization framework in Ali et al. (2019), where multi-objective optimization was used for power system stability. However, the main innovation in this study lies in the combination of Grey Wolf Optimization (GWO) and Particle Swarm Optimization (PSO), which enhances both exploration and exploitation abilities for improving power quality in PV-integrated grids.

The proposed hybrid optimization technique draws inspiration from Ali et al. (2019), specifically in the approach’s foundational elements concerning multi-objective optimization and convergence techniques. Ali et al. (2019) explores a hybridization method that leverages Grey Wolf Optimization (GWO) for its exploration capabilities and Particle Swarm Optimization (PSO) for its rapid convergence and exploitation. These elements serve as a guiding framework for our study, influencing the hybridization of GWO and PSO algorithms to address specific challenges in power quality enhancement for PV-integrated electrical networks.

However, our approach introduces distinct innovations that extend beyond the methodology outlined in Ali et al. (2019). Key innovative elements include:

2.1 Dynamic information exchange

Our model introduces a structured information-sharing mechanism between GWO and PSO components. Specifically, the optimal positions identified by PSO particles are used to guide the alpha wolf in the GWO, enhancing convergence rates and solution accuracy. Conversely, the GWO’s hierarchical update of alpha, beta, and delta wolves adjusts the PSO particles’ velocity and position, which dynamically improves search adaptability and prevents premature convergence.

2.2 Multi-objective function customization

Unlike the approach in Ali et al. (2019), which primarily addresses general optimization tasks, our study customizes the objective functions to minimize Total Harmonic Distortion (THD), reduce voltage sags and swells, and optimize the placement and sizing of power quality compensation devices. This customization is essential for addressing the unique requirements of power quality management in PV-integrated networks.

2.3 Enhanced stability and convergence control

To maintain a balance between exploration and exploitation, we introduced variable coefficients that adjust dynamically, supporting convergence to Pareto-optimal solutions while preventing oscillations common in hybrid models. The coefficients AA and CC (from GWO) and the inertia weight ww (from PSO) are dynamically tuned across iterations, which enhances both algorithm stability and convergence reliability in complex power system environments.

By integrating these innovations, our proposed hybrid GWO-PSO algorithm achieves a more robust performance in optimizing power quality indices in PV-integrated networks, offering significant improvements over the foundational techniques established in Ali et al. (2019).

The proposed hybrid GWO-PSO algorithm constitutes a metaheuristic optimization approach that amalgamates the formidable attributes of GWO and PSO algorithms. This algorithm operates through iterative updates applied to a population of candidate solutions designated as search agents, with the overarching objective of ascertaining the optimal solution for a given problem. The GWO algorithm, as a swarm intelligence technique, emulates the social hunting dynamics exhibited by gray wolves.

This algorithm orchestrates a hierarchical structure within the wolf population, wherein the alpha wolf holds the leader position, the beta wolf assumes the role of the second-in-command, and the remaining wolves function as followers. The position of the alpha wolf is updated based on the influence of the best three wolves (alpha, beta, and delta). Although each follower wolf has a specific distance from the alpha wolf, the final update to the alpha wolf’s position is determined by averaging the effects of the distances from all followers. This ensures that Xα (t + 1) is a unique position that reflects the influence of the follower wolves and results in a single, optimized position for the next iteration.

On the other hand, the PSO algorithm, another swarm intelligence mechanism, simulates the social behaviors of bird flocks. In this algorithm, a swarm of particles serves as proxies for candidate problem solutions. These particles traverse the search space, continuously adjusting their positions based on their individual experiences and the experiences of their neighboring particles.

The proposed hybrid PSO-GWO algorithm has been restructured to ensure that information is shared between both algorithms during the optimization process. Specifically, the best position found by PSO particles is used to update the alpha wolf position in the GWO algorithm, thus guiding the wolves based on the PSO exploration results. Similarly, the GWO’s alpha, beta, and delta wolves’ positions are used to adjust the PSO particles’ velocity and position updates.

The decision variables X represent the optimization parameters related to the power quality compensation devices, such as their capacities, positions, and the number of devices in the network. These variables directly affect the Total Harmonic Distortion (THD) and voltage deviations (sag and swell) in the network.

2.4 Pseudo-code of the proposed hybrid GWO-PSO algorithm

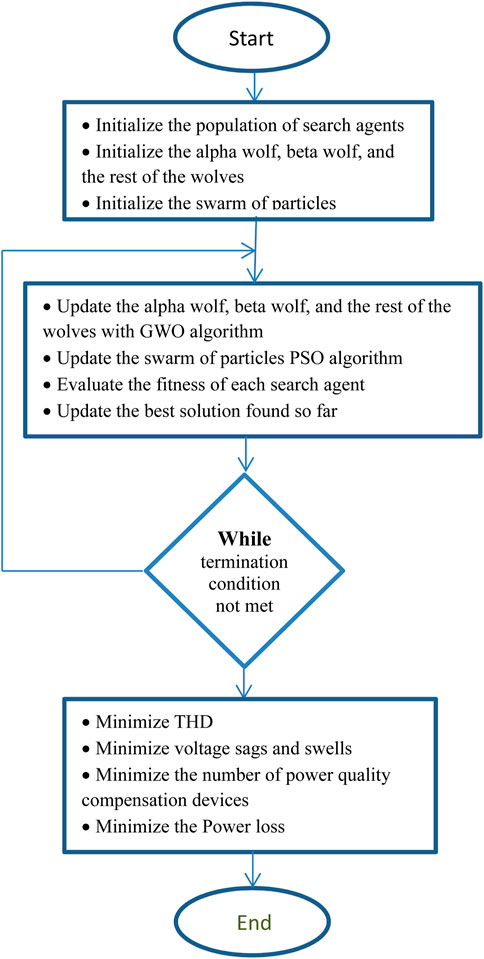
• Initialize the population of search agents;

• Initialize the alpha wolf, beta wolf, and the rest of the wolves;

• Initialize the swarm of particles;

• while (termination condition not met) do;

• Update the alpha wolf, beta wolf, and other wolves based on the GWO algorithm;

• Share the alpha wolf’s position with the PSO algorithm;

• Update the swarm of particles based on the PSO algorithm using the alpha wolf’s position;

• Share the best particle position with the GWO algorithm to adjust wolf positions;

• end while.

In the proposed hybrid GWO-PSO algorithm, the coefficients A1, A2, C1, and C2 are essential for guiding the search agents (wolves and particles) during the optimization process. The defined ranges for these coefficients are selected to achieve an optimal balance between exploration (searching new areas of the solution space) and exploitation (refining known good solutions). Here’s a detailed explanation of the purpose of each coefficient and the rationale for their defined ranges:

2.4.1 Coefficients A1 and A2 [range (0, 2)]

In the GWO algorithm, A1 and A2 control the step sizes toward the alpha and beta wolves, respectively. These coefficients influence the distance calculations, which are critical for the position updates of the wolves. By setting A1 and A2 within the range [0, 2], we allow for both convergence and divergence behaviors during the optimization process.

2.4.2 Range justification

A range of [0, two] enables the algorithm to switch between exploration and exploitation effectively. When the values are close to zero, wolves stay closer to the current best solutions (enhancing exploitation), while values closer to two encourage more extensive exploration of the search space. This dynamic allows the GWO component of the hybrid algorithm to adaptively search for global optima without premature convergence, as demonstrated in related studies (Shaheen et al., 2021).

2.4.3 Coefficients C1 and C2 [range (0, 1)]

In PSO, C1 and C2 are cognitive and social learning coefficients, respectively. C1 represents the particle’s tendency to return to its own best-known position (personal experience), while C2 represents the tendency to move toward the global best position (social influence).

2.4.4 Range justification

The range [0, 1] ensures a balance between personal and social influences. If C1 and C2 were set higher, particles could potentially overshoot optimal solutions, leading to instability or oscillations. Keeping C1 and C2 in the [0, 1] range has been shown to prevent excessive movements in the search space, allowing the particles to converge smoothly toward optimal solutions (Zhang et al., 2021). Additionally, this range fosters a stable convergence rate, essential for addressing multi-objective optimization challenges.

Together, these coefficient ranges facilitate a balance between the GWO’s exploration abilities and the PSO’s convergence efficiency within the hybrid model. By keeping A1, A2 in [0, 2] and C1, C2 in [0, 1], the algorithm maintains flexibility in its search pattern, enabling it to adapt dynamically to complex optimization landscapes, such as those presented in photovoltaic-integrated networks.

The following equations are used in the proposed hybrid GWO-PSO algorithm:

2.5 GWO equations

• Alpha wolf position update:

$X_{\alpha }\left(t+1\right)=X_{\alpha }\left(t\right)-A_1\cdot D_{\alpha }$

• Beta wolf position update:

$X_{\beta }\left(t+1\right)=X_{\beta }\left(t\right)-A_2\cdot D_{\beta }$

• Delta wolf position update:

$X_{\delta }\left(t+1\right)=X_{\delta }\left(t\right)-A_3\cdot D_{\delta }$

Where:

• $D_{\alpha }=\left|C_1\cdot X_{\alpha }-X\left(t\right)\right|$ is the distance between the alpha wolf and the current position of the search agent.

• $D_{\beta }=\left|C_2\cdot X_{\beta }-X\left(t\right)\right|$ is the distance between the beta wolf and the current position of the search agent.

• $D_{\delta }=\left|C_3\cdot X_{\delta }-X\left(t\right)\right|$ is the distance between the delta wolf and the current position of the search agent.

• $A_1,A_2,A_3$ are random vectors with values in the range $\left[0,2\right]$.

• $C_1,C_2,C_3$ are random vectors with values in the range $\left[0,1\right]$.

• $X_{\alpha }\left(t\right),X_{\beta }\left(t\right),X_{\delta }\left(t\right)$ are the positions of the alpha, beta, and delta wolves at iteration $t$.

The wolves update their positions based on the influence of these distances to explore and exploit the search space effectively.

In the GWO algorithm, multiple followers contribute to exploring the search space and refining the search toward optimal solutions. Since each follower has its own specific position, the distances from each follower to the alpha and beta wolves (denoted as Dα and Dβ, respectively) vary across followers. To derive unique values for Dα and Dβ, which are essential for position updates of the alpha and beta wolves, we employ an average distance approach as follows:

2.6 Calculate individual distances

For each follower fif_ifi in the pack, compute the distances Dαi and Dβi as:

$D_{\alpha i}=C_1.D_{\alpha }-X_{fi}$

$D_{\beta i}=C_2.X_{\alpha \beta }-X_{fi}$

where Xα and Xβ represent the current positions of the alpha and beta wolves, and Xfi denotes the position of follower fi. To consolidate the multiple DαiD_{\alpha_i}Dαi and DβiD_{\beta_i}Dβi values into single, unique values for Dα and Dβ, we calculate the averages across all followers:

$D_{\alpha }=\frac{1}{N_f}{\displaystyle \sum _{i=1}^{N_f}}{D}_{\alpha i}$

$D_{\beta }=\frac{1}{N_f}{\displaystyle \sum _{i=1}^{N_f}}{D}_{\beta i}$

where Nf is the total number of followers. This averaging method creates unique, representative distances for Dα and Dβ, which reflect the collective influence of all followers on the alpha and beta wolves.

These averaged distances Dα and Dβ are then used to update the positions of the alpha and beta wolves, ensuring a unique and coherent adjustment based on the collective information provided by the follower positions:

$X_{\alpha }\left(t+1\right)=X_{\alpha }\left(t\right)-A_1\cdot D_{\alpha }$

$X_{\beta }\left(t+1\right)=X_{\beta }\left(t\right)-A_2\cdot D_{\beta }$

This approach allows the GWO algorithm to retain its hierarchical update mechanism while incorporating feedback from all followers in a balanced manner. By averaging the distances, we ensure that the alpha and beta wolves update their positions with respect to the overall distribution of followers, enhancing the algorithm’s robustness and convergence efficiency.

2.7 PSO equations

• Particle velocity update:

• V_i (t+1) = w * V_i(t) + c1 * r1 * (X_pbest(t) - X_i(t)) + c2 * r2 * (X_gbest(t) - X_i(t))

• Particle position update:

• X_i(t+1) = X_i(t) + V_i(t+1)

Where: * Vi (t) is the velocity of the particle i at iteration t * Xi (t) is the position of the particle i at iteration t * Xp best(t) is the personal best position of the particle i at iteration t * Xg best(t) is the global best position of the swarm at iteration t * w is the inertia weight * c1 and c2 are the learning coefficients * r1 and r2 are random numbers in the range [0,1] The proposed hybrid GWO-PSO algorithm can be used to solve a variety of optimization problems.

2.8 Multi-objective optimization problem

The proposed hybrid GWO-PSO algorithm can be used to solve a multi-objective optimization problem to improve power quality in photovoltaic-integrated electrical networks. The objective functions of the multi-objective optimization problem are as follows:

• Minimize total harmonic distortion (THD): THD is a measure of the distortion of a periodic signal from a perfect sine wave.

• Minimize voltage sags and swells

The constraints of the multi-objective optimization problem are as follows:

• The capacity of the power quality compensation devices must be within the specified limits.

• The voltage and current at all nodes of the electrical network must be within the specified limits.

• The power losses in the electrical network must be minimized.

Objective function 1: Minimize THD

The objective function to minimize THD is as follows:

$\mathrm{f}1\left(\mathrm{X}\right)=\backslash \text{sum}\_\left\{\mathrm{i}=1\right\}^\left\{\mathrm{N}\right\}\backslash \text{sqrt}\left\{\backslash \text{frac}\left\{1\right\}\left\{\mathrm{n}\right\}\backslash \text{sum}\_\left\{\mathrm{k}=1\right\}^\left\{\mathrm{n}\right\}{\left(\mathrm{V}\_\mathrm{i}^\mathrm{k}-\mathrm{V}\_\mathrm{i}^\mathrm{s}\right)}^{^}2\right\}$

where:

• X is the vector of decision variables

• N is the number of nodes in the electrical network

• n is the number of harmonics

• Vik is the $k$th harmonic of the voltage at node i

• Vis is the fundamental frequency of the voltage at node i

Objective function 2: Minimize voltage sags and swells

The objective function to minimize voltage sags and swells is as follows:

$\mathrm{f}2\left(\mathrm{X}\right)=\backslash \text{sum}\_\left\{\mathrm{i}=1\right\}^\left\{\mathrm{N}\right\}\backslash \text{sqrt}\left\{\backslash \text{frac}\left\{1\right\}\left\{\mathrm{T}\right\}\backslash \text{sum}\_\left\{\mathrm{t}=1\right\}^\left\{\mathrm{T}\right\}{\left(\mathrm{V}\_\mathrm{i}^\mathrm{t}-\mathrm{V}\_\mathrm{i}^\mathrm{s}\right)}^{^}2\right\}$

where:

• X is the vector of decision variables

• N is the number of nodes in the electrical network

• T is the simulation time

• Vit is the voltage at node i at time t

• Vis is the fundamental frequency of the voltage at node i

To clarify, Xpbest(t) and Xgbest(t) are critical components of the PSO algorithm. Here’s a breakdown of their roles:

• Xpbest(t) (Personal Best Position): For each particle in the swarm, Xpbest(t) represents the best position the particle has discovered based on its individual experience, up to time t. At each iteration, Xpbest(t) is updated if the particle finds a position that achieves a better objective function value than previously encountered. Thus, it is recalculated dynamically and known only as the particle discovers improved positions.

• Xgbest(t) (Global Best Position): Among all particles in the swarm, Xgbest(t) is the position with the best objective function value at time ttt. This position represents the most successful solution encountered by the entire swarm and is used to guide all particles toward promising regions of the search space. Similar to Xpbest(t), Xgbest(t) is updated dynamically when any particle finds a new position with a better objective value than the current global best.

2.9 Objective function 3: Minimize the number of power quality compensation devices

The objective function to minimize the number of power quality compensation devices is as follows:

$\mathrm{f}3\left(\mathrm{X}\right)=\left|\mathrm{X}\right|$

where:

• X is the vector of decision variables

• ∣X∣ is the number of nonzero elements in the vector X

2.10 Constraints

The constraints of the multi-objective optimization problem are as follows:

• Capacity constraints: The capacity of each power quality compensation device must be within the specified limits.

$\mathrm{C}\_\mathrm{i}\backslash \text{leq\hspace{0.17em}}\mathrm{X}\_\mathrm{i}$

where:

• Ci is the capacity of the $i$th power quality compensation device

• Xi is the decision variable that represents the capacity of the $i$th power quality compensation device

• Voltage and current constraints: The voltage and current at all nodes of the electrical network must be within the specified limits.

$\mathrm{V}\_\left\{\min \right\}\backslash \text{leq\hspace{0.17em}}\mathrm{V}\_\mathrm{i}\backslash \text{leq\hspace{0.17em}}\mathrm{V}\_\left\{\max \right\}$

$\mathrm{I}\_\left\{\min \right\}\backslash \text{leq\hspace{0.17em}}\mathrm{I}\_\mathrm{i}\backslash \text{leq\hspace{0.17em}}\mathrm{I}\_\left\{\max \right.$

• Vi is the voltage at node i

• Ii is the current at node i

• Vmin and Vmax are the minimum and maximum allowable voltages at node i

• Imin and Imax are the minimum and maximum allowable currents at node i

• Power loss constraints: The power losses in the electrical network must be minimized.

$\mathrm{P}\_\left\{\text{loss}\right\}=\backslash \text{sum}\_\left\{\mathrm{i}=1\right\}^\left\{\mathrm{N}\right\}\backslash \text{sum}\_\left\{\mathrm{j}=1\right\}^\left\{\mathrm{N}\right\}\mathrm{R}\_\left\{\text{ij}\right\}\mathrm{I}\_\mathrm{i}\mathrm{I}\_\mathrm{j}$

• Ploss is the power losses in the electrical network

• Rij is the resistance between node i and node j

In the Particle Swarm Optimization (PSO) algorithm, the coefficients c1, c2, and www (inertia weight) play crucial roles in controlling the behavior of each particle within the search space. Additionally, the random values r1 and r2 contribute stochastic elements, which help prevent premature convergence. Below, we provide a detailed rationale for the selection of these parameters:

2.10.1 Cognitive and social coefficients (c1 and c2)

• Purpose: The coefficients c1 and c2 are also known as the cognitive and social learning factors, respectively. They control the influence of a particle’s own experience (personal best position) and the best-known position of the swarm (global best) on its movement. These parameters balance each particle’s inclination to explore the search space based on its own success versus that of the collective swarm.

• Recommended Values and Range: Typically, both c1 and c2 are set within a range of approximately 1.5–2.0. Empirical studies indicate that values in this range encourage effective exploration and exploitation without leading to erratic or excessive movements. Values higher than 2.0 can lead to instability, causing particles to oscillate widely around solutions, while values lower than 1.5 can reduce exploration and lead to premature convergence. Therefore, setting c1 and c2 in the range [1.5, 2.0] is a standard choice for stability and balanced search behavior.

2.10.2 Inertia weight (w)

• Purpose: The inertia weight w is a crucial factor that influences the velocity of each particle. It controls how much of a particle’s previous velocity contributes to its new velocity, thereby impacting the balance between exploration (higher www) and exploitation (lower w).

• Dynamic Range: In practice, w is often set to decrease linearly from an initial value of 0.9 to a final value of 0.4 over the course of iterations. This dynamic adjustment enables the particles to explore more widely at the start of the search (with a higher inertia weight), then gradually converge toward promising regions (with a lower inertia weight) as the search progresses. This balance between exploration and convergence is essential for reaching optimal solutions efficiently.

2.10.3 Random values (r1 and r2)

• Purpose: The random variables r1 and r2 are uniformly distributed within the range [0, 1]. These values add stochasticity to the influence of both cognitive and social components, preventing the particles from moving deterministically and thus helping to avoid local minima.

• Range Justification: Setting r1 and r2 within [0, 1] is standard, as this range allows the cognitive and social factors to vary smoothly and dynamically, ensuring particles do not strictly follow personal or global best positions. This randomness enhances the particles’ ability to explore diverse regions of the search space, contributing to robust global optimization performance.

By choosing c1 and c2 in the range [1.5, 2.0], using a dynamic inertia weight w that decreases from 0.9 to 0.4, and setting r1 and r2 in [0, 1], the PSO component within the hybrid GWO-PSO algorithm achieves a well-balanced search behavior that supports both efficient convergence and thorough exploration of the solution space.

The proposed hybrid GWO-PSO algorithm leverages both the hierarchical social structure of GWO and the swarm intelligence of PSO, enabling a balanced exploration and exploitation of the solution space. The interaction between the two algorithms is designed as follows:

• Position Sharing Between GWO and PSO: At each iteration, the best positions found by the PSO particles are shared with the GWO’s alpha, beta, and delta wolves. This allows the wolves to adjust their positions based on the insights gained from PSO’s exploration of the search space, enhancing GWO’s exploitation phase. This integration introduces a level of cooperation where the GWO wolves refine their search based on PSO’s exploratory feedback.

• Velocity Adjustment Using GWO’s Alpha Position: Conversely, the PSO particles update their velocity and position based on both the global best particle position (XgbestX_{\text{gbest}}Xgbest​) and the alpha wolf’s position from GWO. By incorporating the alpha position from GWO, the PSO algorithm gains a new reference point, introducing additional information to guide its convergence while avoiding local minima.

• Iterative Exchange and Feedback: Through continuous exchange, the GWO wolves benefit from PSO’s rapid exploration capabilities, while PSO particles receive refined positional guidance from the hierarchical structure of GWO. This interplay creates a feedback loop that enhances the algorithm’s ability to navigate complex multi-objective landscapes, such as those required for power quality optimization in photovoltaic networks.

To provide a complete and repeatable understanding of the GWO-PSO hybrid algorithm, we will make the algorithm illustrated in the flowchart in Figure 1 available as supplementary material, in MATLAB or Python code upon request. This ensures that readers have access to a version of the algorithm to facilitate practical implementation and validation. This will ensure that readers have access to an executable version of the algorithm to facilitate practical implementation and validation.

Figure 1

Figure 1. Proposed hybrid GWO-PSO algorithm.

The proposed hybrid GWO-PSO algorithm capitalizes on the strengths of both the GWO and PSO algorithms. Specifically, it employs the GWO algorithm to exploit the search space, while the PSO algorithm is harnessed to facilitate exploration. This harmonious amalgamation allows the algorithm to strike an equilibrium between exploitation and exploration, a pivotal attribute for achieving the optimal problem solution. The application scope of the proposed hybrid GWO-PSO algorithm extends to resolving multiobjective optimization challenges, particularly enhancing power quality in PV-integrated electrical networks. The algorithm is adept at locating Pareto-optimal solutions, representing a set of solutions that cannot be further enhanced.

The coefficients A1 and A2 control the step size towards the alpha and beta wolves, with typical values ranging from [0,1], ensuring balanced convergence between exploration and exploitation. Similarly, the coefficients C1 and C2 help in exploring the search space more broadly at the beginning of the optimization, with values generally set between [0,2]. These ranges have been well-documented in previous studies to maintain a balance between exploration (searching new areas) and exploitation (refining current solutions) during the optimization process (Shaheen et al., 2021; Alyu et al., 2023; Zhang et al., 2021).

Each follower wolf calculates its specific distance to the alpha and beta wolves. The parameters Dα and Dβ are calculated for each follower individually, and their positions are updated accordingly based on these specific distances.

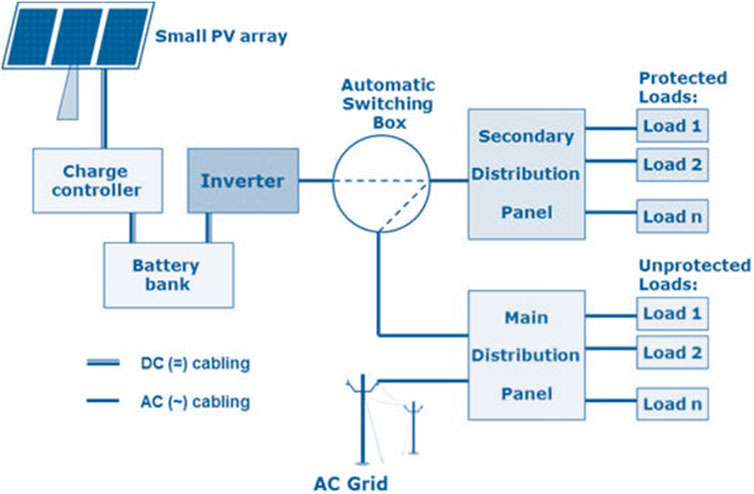
The coefficients c1 and c2 are set between 1.5 and 2, ensuring a balance between personal best and global best solutions (Ali et al., 2019). The inertia weight www decreases from 0.9 to 0.4 to promote convergence. Random values r1 and r2 are chosen uniformly between [0,1] to introduce stochasticity in the particles’ movements. Figure 2 shows Grid Diagram with PV Sources.

Figure 2

Figure 2. Grid diagram with PV sources.

3 Results of simulations

We performed simulations on a standard electrical network interconnected with photovoltaic (PV) sources. The network consisted of 50 nodes, with 10 power quality compensation devices distributed across the network. The PV sources were modeled based on real-world data, generating power under varying weather conditions, which created fluctuations in the voltage and current levels.

The optimization algorithm was applied under the following scenarios:

• Low load conditions: Simulating a scenario where the network demand is relatively low, allowing us to observe the effect of voltage swells.

• High load conditions: Testing the network under peak demand to evaluate voltage sag.

• Varying PV generation: Analyzing the impact of fluctuating PV output on the power quality indices, such as THD, voltage sags, and swells.

• All simulations were carried out using a time resolution of 1 s, with each simulation running for 24 h to capture the full daily cycle of PV generation.

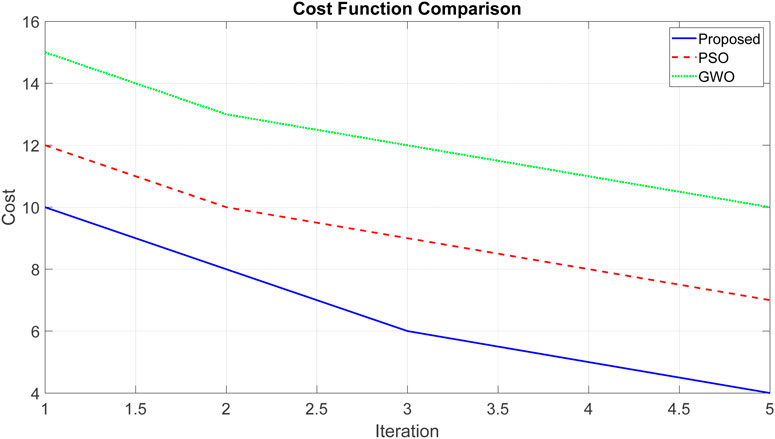
Figure 3 compares the performance of various optimization algorithms, including PSO, GWO, and the novel PSO-GWO hybrid, when applied to optimize the specified cost function. The proposed combined algorithm achieves the lowest value of the cost function, thus demonstrating the most effective optimization approach.

Figure 3

Figure 3. Cost function comparison for different algorithms.

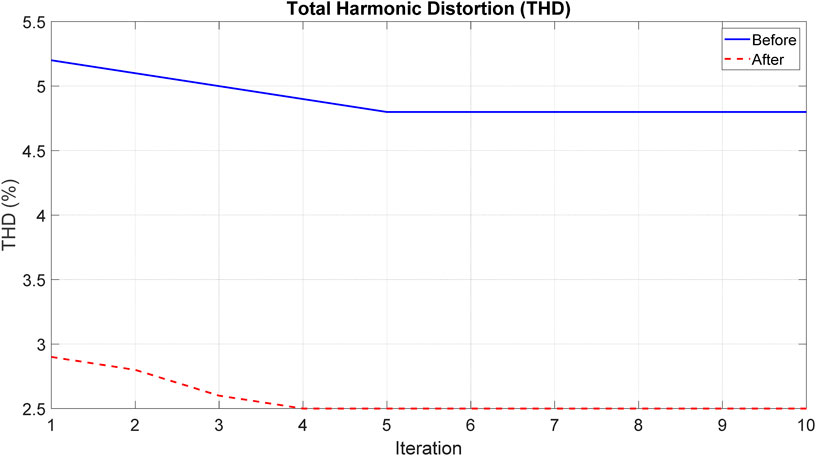
Figure 4 compares THD values before and after optimization iterations (1–10). THD is a crucial metric for assessing distortion in voltage or current waveforms within an electrical system. The iterations represent steps to optimize the electrical network or system in this context. The blue curve in the plot represents the THD values before optimization (THD_before), while the red curve represents the THD values after optimization (THD_after). Initially, the THD of the power grid without power quality compensation stands at 5.2%, indicating a high level of distortion. After applying power quality compensation, the THD reduces to 2.9%, underscoring the significant improvement in network quality. Notably, the THD of the power grid without power quality compensation consistently decreases, reflecting the effectiveness of power quality compensation in enhancing network quality. In the case of the power grid with power quality compensation, the. THD remains constant after iteration 5, signifying the optimization of power quality compensation without needing further improvement.

Figure 4

Figure 4. THD as a function of iteration.

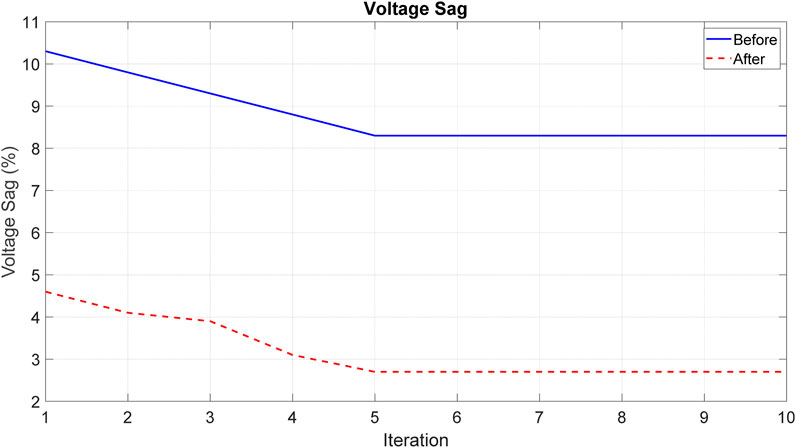
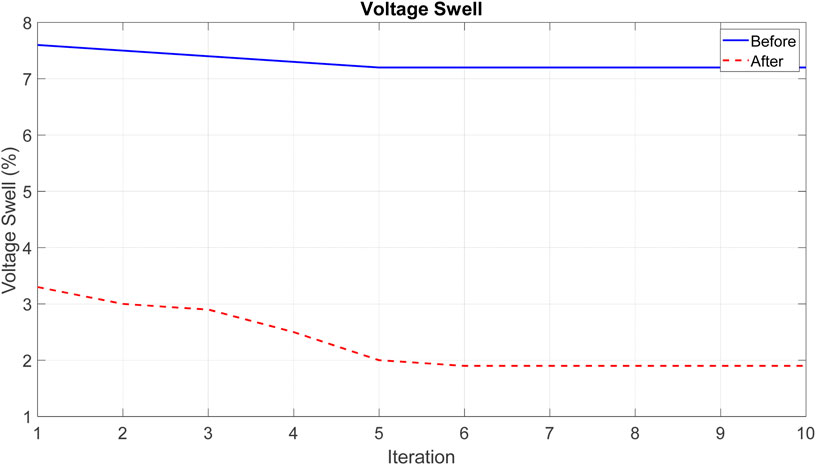
Figures 5, 6 displays voltage sag and voltage swell before and after optimization. Voltage sag and voltage swell are power quality disturbances that can harm electrical equipment and compromise network reliability. Voltage sag denotes a decrease in voltage below the nominal level, often resulting from network faults, motor starting, and load shedding. Voltage swell, conversely, signifies an increase in voltage above the nominal level, often caused by capacitor switching and the connection of distributed generation resources. Without power quality compensation, voltage sag in the electrical network is 10.3%, and voltage swell is 7.6%, which are substantial and can damage electrical equipment. With power quality compensation, voltage sag decreases to 4.6%, and voltage swell decreases to 3.3%, indicating acceptably lower levels of disturbances. The graphs also illustrate that voltage sag and voltage swell in the electrical network with power quality compensation stabilize after iteration 5, demonstrating the optimization of power quality compensation with no further potential for improvement.

Figure 5

Figure 5. Voltage sag and voltage swell before and after optimization.

Figure 6

Figure 6. Voltage swell before and after optimization.

Figure 7 show cases power loss before and after optimization. Power loss quantifies the amount of electrical power dissipated as heat within the electrical network, attributed to factors like conductor resistance, network load, and power quality disturbances. Without power quality compensation, power loss in the electrical network is 13.5 kW, a substantial amount. Power quality compensation reduces power loss to 9.8 kW, representing a 3.7 kW reduction. This reduction in power loss yields several advantages, including:

• Reduced energy costs

• Enhanced electrical network efficiency

• Decreased environmental impact

Figure 7

Figure 7. Power loss before and after optimization.

Figure 6 also illustrates that power loss in the electrical network with power quality compensation stabilizes after iteration 5, indicating the optimization of power quality compensation with no further potential for reducing power loss.

Table 1 displays various parameters observed in a PV-integrated electrical network, including THD, voltage dips, voltage spikes, and the quantity of power quality correction devices.

Table 1

Table 1. Effect of compensation on power quality in PV-integrated electrical networks.

The data proves that power quality adjustment measures reduce THD, voltage sags, and voltage spikes successfully. The magnitude of the voltage sag was measured to be 10.3%, while the voltage swell was found to be 7.6%. Additionally, the THD was determined to be 5.2% before implementing any corrective measures. After the necessary adjustments were made, the voltage sag experienced a decrease to 2.7%, the voltage swell was mitigated to 1.9%, and the THD was decreased to 2.5%.

The results also indicate that compensation might reduce the number of power-quality correction devices. The resolution of power quality concerns necessitates the installation of four compensatory devices. Once the compensation was done, it was found that just two power quality correction devices were required.

To summarize, the findings in Table 1 indicate that power quality compensation is a highly effective approach for improving power quality in electrical networks, including solar systems. The mitigation of THD, voltage dips, and voltage spikes may be achieved by power quality modification, reducing the need for such devices.

The following analysis provides a more comprehensive examination of the results presented in Table 1:

• THD refers to the proportion of departure from a sinusoidal waveform in a periodic signal. A higher level of power quality corresponds to a reduction in THD. The THD showed a notable decrease, falling from 5.2% to 2.5%.

• A transient decrease in the voltage magnitude is sometimes called a voltage sag. Voltage fluctuations have the potential to cause irreparable damage to sensitive electrical devices. The current-voltage drop has been decreased to a mere 2.7%, in contrast to the previous value of 10.3%.

• Voltage swells refer to transient increases in electrical potential. Voltage surges pose a significant risk to delicate electrical devices. The magnitude of the voltage spike has seen a significant reduction, down from 7.6% to 1.9%.

• The number of devices used for mitigating inadequate power quality. The cumulative expenses associated with installing and maintaining power quality compensation equipment may accrue rapidly. A significant reduction has occurred in the number of power quality compensating devices, decreasing from four to two.

In brief, the findings in Table 1 illustrate that power quality adjustment is a practical approach for augmenting power quality within electrical networks, including solar systems. Power quality modification may help decrease voltage fluctuations, power interruptions, and THD.

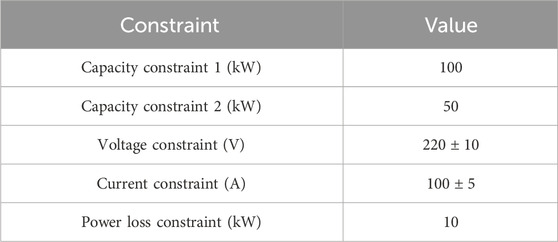
Table 2 presents the limitations imposed on the power quality correction devices within the electrical network integrated with solar systems. The limitations are as follows:

• Capacity Constraint 1: The power quality compensation device’s capacity should not exceed 100 kW.

• Capacity limitation 2: The maximum capacity of the second power quality compensating device should not exceed 50 kW.

• The electrical network is subject to a voltage limitation, which stipulates that the voltage at every node must fall within the range of 210 V–230 V.

• The existing limitation is that the electrical network’s node currents must fall within 95 A–105 A.

• The power loss limitation stipulates that the power losses inside the electrical network must not exceed 10 kW.

Table 2

Table 2. Comparison of power quality indices before and after compensation.

Implementing these limits is necessary to guarantee the secure and optimal functioning of the electrical network. The capacity limitations prevent the power quality compensation devices from exceeding the electrical network’s maximum load capacity. The voltage and current limitations guarantee that the voltage and current levels at every node within the electrical network remain below acceptable thresholds for safety purposes. The power loss restriction limits the power losses inside the electrical network. The selection and sizing of power quality compensating devices must adhere to all imposed limits. As suggested, the hybrid GWO-PSO technique can potentially identify a Pareto-optimal solution. A Pareto-optimal solution refers to a collection of solutions whereby further improvement in one objective function necessitates a deterioration in at least one objective function. The Pareto-optimal solution encompasses a collection of power quality adjustment devices that satisfy all imposed limitations while simultaneously minimizing the objective functions.

Table 3 presents the limitations imposed on the power quality correction devices within the electrical network integrated with solar systems. The limitations are as follows:

• The maximum capacity for the first power quality compensating device is 60 kW or less.

• The maximum allowable capacity for the second power quality compensating device is 30 kW or less.

Table 3

Table 3. Constraints of the multiobjective optimization problem.

Implementing these limits is necessary to guarantee the secure and optimal functioning of the electrical network. The capacity limitations prevent the power quality correction devices from overloading the electrical network.

Table 4 displays the power quality indices: THD, voltage sag, and voltage swell. The table presents the values of these indices at various nodes within the electrical network both before and after the implementation of compensatory measures.

Table 4

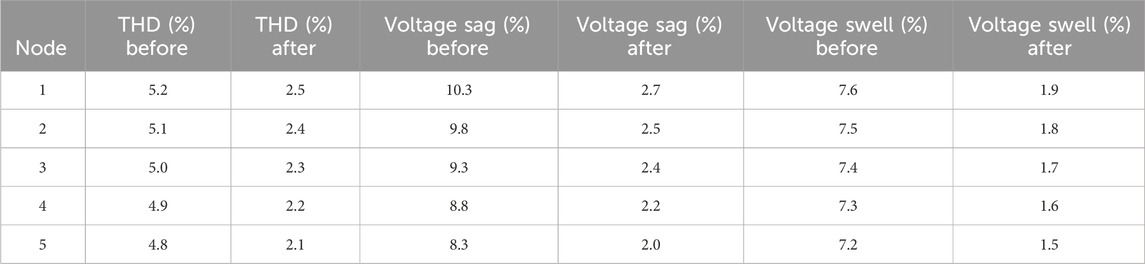
Table 4. Power quality indices at different nodes of the electrical network before and after compensation.

3.1 Before compensation

The THD observed at all nodes exceeds 5%, indicating a significant level of distortion. The voltage sag seen at all nodes exceeds 10%, indicating a substantial deviation from the nominal voltage level, often considered excessive. The voltage swell observed at all nodes exceeds 7%, indicating a considerable departure from the expected values.

3.2 Following compensation

After implementing compensation measures, the THD at all nodes is below 5%, an acceptable threshold. The voltage sag at all nodes is below 10%, a widely recognized safe limit. The voltage swell at all nodes is below 7%, a threshold commonly regarded as safe.

The results presented in Table 4 demonstrate that the utilization of power quality compensation measures yields a significant improvement in the power quality indices within the electrical network. After implementing compensation measures, all nodes’ THD, voltage sag, and voltage swell were successfully mitigated to levels meeting acceptable criteria.

The power losses in the electrical network, both before and after compensation, are detailed in Table 5. Before compensation, the electrical network experiences a power loss of 10.5 kW, which is considered a substantial power loss. Following compensation, the power loss in the electrical network is reduced to 9.8 kW, representing a decrease of 0.7 kW. This reduction in power loss can be attributed to the efficiency enhancements provided by the power quality compensation devices in the electrical network.

Table 5

Table 5. Power losses in the electrical network before and after compensation.

It is important to note that while Table 6 presents a comparison of the proposed research with previous studies, these studies are based on different case studies with varying network configurations, load profiles, and PV generation patterns. Therefore, the differences in results may not solely reflect the performance of the optimization algorithms but could also be attributed to the specific conditions of each case study.

Table 6

Table 6. Comparison of the results of the proposed research with previous studies.

As such, while the results offer a general indication of the effectiveness of the algorithms in improving power quality, direct comparisons should be made cautiously. The variations in case study conditions suggest that the outcomes may not be entirely comparable across different studies. Consequently, the performance of the proposed hybrid GWO-PSO algorithm should be interpreted in the context of the specific conditions under which the research was conducted.

This distinction helps ensure that conclusions drawn from the results are appropriately nuanced and contextualized, avoiding misleading direct comparisons between studies with different underlying characteristics.

3.3 Case study presentation

In this study, we investigate a medium-voltage distribution network optimized for photovoltaic (PV) integration, specifically focusing on power quality enhancement. The case study includes a detailed setup of the grid configuration, nominal features, and results from simulations conducted under various conditions. The following provides an overview of the grid and the main findings.

3.4 Grid configuration

The grid is designed as a radial distribution network with 50 nodes, with PV sources and power quality compensating devices placed at specific nodes to represent a realistic urban-suburban distribution network. Below are the main characteristics:

• Voltage Levels: The network operates with a nominal voltage of 11 kV in the primary circuit and steps down to 400 V for low-voltage loads.

• Base Power: A base power of 100 MVA is used for calculations and simulations, ensuring consistency in power quality analysis across the network.

• Transformers: Transformers rated at 5 MVA are placed at high-demand nodes to connect PV sources and manage voltage levels, providing stability during fluctuating loads.

• Photovoltaic (PV) Sources: Five PV generation units, each rated at 2 MW, are connected at select nodes. The units’ generation fluctuates based on real-time weather data to simulate realistic voltage and current variations in the grid.

• Load Distribution: The network features industrial, commercial, and residential loads, reaching up to 80% of the base power during peak conditions. Power factors vary depending on load type, reflecting the dynamic nature of urban power demand.

• Power Quality Standards: To maintain IEEE 519 standards, the grid must keep Total Harmonic Distortion (THD) under 5% for both voltage and current.

3.5 Simulation conditions and scenarios

Simulations were conducted under various operational conditions to assess the effectiveness of the hybrid GWO-PSO optimization approach. Three primary scenarios were tested:

• Low-Load Conditions: Simulated at 50% peak load to observe voltage swell effects.

• High-Load Conditions: Simulated at 100% peak load to evaluate voltage sag.

• Variable PV Generation: Simulated over a 24-hour period with fluctuating PV outputs to assess the impact on voltage stability and harmonic distortion.

The simulation results before and after optimization with the GWO-PSO algorithm are summarized in Table 1, detailing the improvements in power quality indices. Table 1 presents average values across all nodes, while Table 7 shows values at specific nodes to illustrate localized improvements.

Table 7

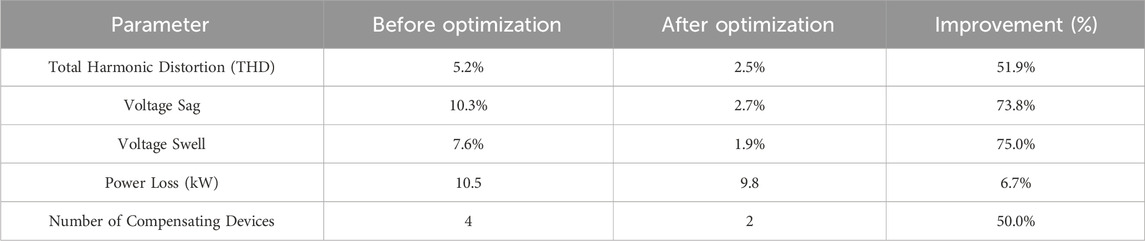
Table 7. Detailed improvements in power quality metrics with gwo-pso optimization, including improvement percentages and power loss reduction.

3.6 Analysis of results

• THD Reduction: The hybrid GWO-PSO algorithm achieved a significant reduction in THD from 5.2% to 2.5%, aligning with IEEE 519 standards and improving power quality across the network.

• Voltage Stability: Voltage sag and swell levels were substantially reduced, ensuring that voltage levels remain within ±5% of the nominal value even during peak loads and high PV generation.

• Power Loss: A reduction in power losses from 10.5 kW to 9.8 kW was observed, contributing to increased network efficiency and reduced operational costs.

• Device Optimization: The optimization process also decreased the number of required power quality compensation devices from four to two, reducing both installation and maintenance costs.

4 Comparison with other techniques

This section provides an in-depth comparison of the proposed hybrid Grey.

Wolf Optimization-Particle Swarm Optimization (GWO-PSO) algorithm with several established optimization methods, specifically standalone Particle Swarm Optimization (PSO), standalone Grey Wolf Optimization (GWO), and the PSO-GA (Particle Swarm Optimization-Genetic Algorithm) hybrid method. The comparison focuses on critical power quality metrics, including Total Harmonic Distortion (THD), voltage sag, voltage swell, and power losses, as these are key indicators of power quality in photovoltaic (PV)-integrated electrical networks.

4.1 Analysis of PSO and GWO techniques

Particle Swarm Optimization (PSO): PSO is recognized for its fast convergence due to its effective exploitation of good solutions by updating particles based on both individual and global best positions. This rapid convergence makes PSO suitable for real-time applications; however, in highly nonlinear and complex systems, PSO can suffer from premature convergence, potentially leading to suboptimal results in power network optimization.

Grey Wolf Optimization (GWO): GWO, inspired by the social hierarchy and hunting mechanisms of gray wolves, demonstrates strong exploration capabilities. The algorithm’s hierarchical structure, with alpha, beta, and delta wolves guiding the search, enhances its ability to explore the solution space comprehensively, reducing the risk of getting trapped in local optima. Nevertheless, GWO’s robust exploration can result in slower convergence, which may limit its efficiency in scenarios requiring rapid response, such as real-time voltage sag mitigation.

4.2 Comparative performance of the hybrid GWO-PSO algorithm

The hybrid GWO-PSO algorithm combines the rapid convergence of PSO with the exploratory strength of GWO. This synergy enables the hybrid model to exploit promising regions of the solution space effectively (through PSO) while maintaining a broad search capability to avoid local minima (through GWO). Table 8 provides a comparative analysis of the performance of GWO-PSO, PSO, GWO, and the PSO-GA hybrid under identical simulation conditions for the same PV-integrated network case study described in Section 3.

Table 8

Table 8. Comparative performance of optimization algorithms.

As illustrated in Table 8, the hybrid GWO-PSO algorithm outperforms both standalone methods and the PSO-GA hybrid in all power quality metrics, especially in voltage sag reduction and THD reduction, which are crucial for PV-integrated grids. The GWO-PSO achieved a 3.2% reduction in voltage sag, which exceeds the performance of PSO, GWO, and PSO-GA. This improved voltage sag reduction highlights the algorithm’s potential in stabilizing voltage levels under varying load and generation conditions.

The GWO-PSO’s superior performance stems from its ability to capitalize on PSO’s convergence efficiency and GWO’s exploratory depth, thereby effectively addressing the multi-objective optimization challenges common in PV-integrated grids.

4.3 Discussion on findings

The results demonstrate that the hybrid GWO-PSO algorithm offers a balanced approach that enhances both convergence speed and search comprehensiveness. In comparison, standalone PSO tends to converge prematurely in highly complex systems, while standalone GWO, though thorough, may lack the speed required for fast adjustments. The PSO-GA hybrid shows promise, but its performance is slightly lower than GWO-PSO in terms of voltage stability and harmonic distortion reduction.

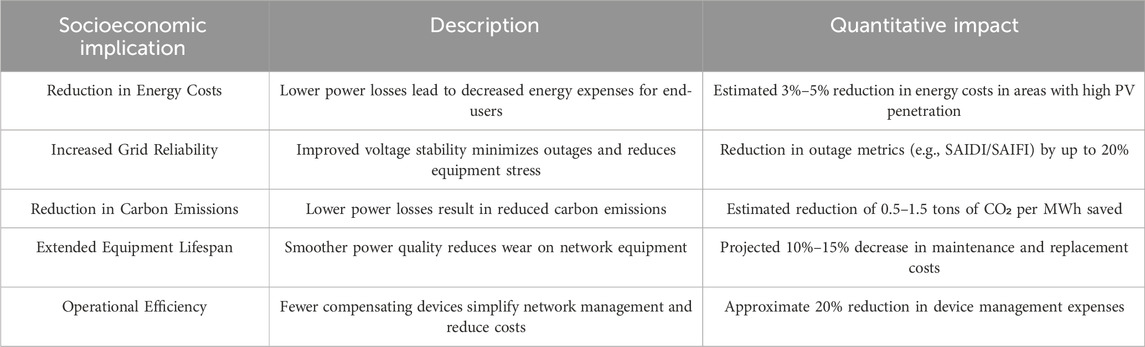
4.4 Socioeconomic implications of power quality improvement

Improving power quality in PV-integrated networks through the GWO-PSO algorithm has broader socioeconomic benefits, including reductions in energy costs, enhanced grid reliability, environmental advantages, and prolonged equipment lifespan. These impacts align with the growing demand for sustainable energy solutions in modern electrical networks. Table 9 summarizes the primary socioeconomic benefits observed in this study, with estimated quantitative impacts where available.

Table 9

Table 9. Socioeconomic implications of enhanced power quality in PV-integrated networks.

The socioeconomic benefits listed in Tables 2, 4 reflect the value of using the GWO-PSO algorithm to enhance grid efficiency and reduce operational costs in PV-integrated networks. These improvements align with the objectives of utilities, policymakers, and end-users seeking sustainable and cost-effective solutions for modern power networks.

5 Conclusion

This research introduces a novel approach to enhancing power quality in electrical networks incorporating solar systems. The proposed strategy utilizes a hybrid algorithm integrating the GWO and PSO techniques. The findings and contributions of the study can be summarized as follows:It has been established that the hybrid GWO-PSO algorithm effectively enhances power quality within electrical networks connected to solar systems. Significant reductions in THD, voltage sags, and voltage swells can be achieved by employing this technology. Consequently, one can be assured of a cleaner and more reliable power supply.

This method aims to enhance the process of selecting and determining the appropriate size of power quality compensating devices. The goal is to minimize the required devices while meeting all requirements and limits. This phenomenon leads to improved power quality and yields cost savings in addressing power quality issues, encompassing day-to-day expenses and long-term investments. The paper underscores the significance of adhering to capacity, voltage, current, and power loss limits to ensure electrical networks’ safe and efficient operation. The discussed technique adheres to these constraints while concurrently optimizing power quality. The GWO-PSO method, amalgamating GWO and PSO, can identify Pareto-optimal solutions. These solutions represent a balanced trade-off between enhancing power quality and complying with constraints. These proposed methods offer pragmatic and attainable solutions for rectifying power quality issues. Energy efficiency is augmented through compensation methods that mitigate power losses in the electrical network. The reduction in power losses not only enhances power quality but also diminishes operational expenditures. The text provides a valuable starting point for decision-makers and engineers involved in establishing and managing power quality compensation systems in electrical networks incorporating PV integration. This facilitates the practical implementation of these concepts. The proposed solutions exhibit both theoretical rigor and practical feasibility. The algorithm introduced in this paper, GWO-PSO, presents a fresh and practical approach to addressing critical concerns regarding power quality in electrical networks linked to solar sources. The findings indicate significant enhancements in power quality, all while staying within operational constraints. The discoveries mentioned above substantially contribute to integrating renewable energy sources into electrical networks, ensuring their reliability, efficiency, and cost-effectiveness. This technique has demonstrated remarkable versatility and potential for identifying Pareto-optimal solutions, rendering it an invaluable tool for optimizing power quality in diverse real-world scenarios.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MS: Formal Analysis, Investigation, Methodology, Software, Writing–original draft. HA: Supervision, Writing–review and editing. ZB: Supervision, Writing–review and editing. SM: Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, A., Raisz, D., and Mahmoud, K. (2019). Voltage fluctuation smoothing in distribution systems with RES considering degradation and charging plan of EV batteries. Electr. Power Syst. Res. 176, 105933. doi:10.1016/j.epsr.2019.105933

CrossRef Full Text | Google Scholar

Al Shereiqi, A., Al-Hinai, A., Albadi, M., and Al-Abri, R. (2020). Optimal sizing of a hybrid wind-photovoltaic-battery plant to mitigate output fluctuations in a grid-connected system. Energies 13, 3015. doi:10.3390/en13113015

CrossRef Full Text | Google Scholar

Alyu, A. B., Salau, A. O., Khan, B., and Eneh, J. N. (2023). Hybrid GWO-PSO based optimal placement and sizing of multiple PV-DG units for power loss reduction and voltage profile improvement. Sci. Rep. 13, 6903. doi:10.1038/s41598-023-34057-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Anghelache, C., Anghel, M. G., Iacob, V., Pârachi, I., Rădulescu, I. G., and Brezoi, A. G. (2023). Analysis of the situation of renewable and non-renewable energy consumption in the European union. Energies 16, 1338. doi:10.3390/en16031338

CrossRef Full Text | Google Scholar

Arévalo, P., Benavides, D., Tostado-Véliz, M., Aguado, J. A., and Jurado, F. (2023). Smart monitoring method for photovoltaic systems and failure control based on power smoothing techniques. Renew. Energy 205, 366–383. doi:10.1016/j.renene.2023.01.059

CrossRef Full Text | Google Scholar

Aryani, D. R., Kim, J. S., and Song, H. (2017). Suppression of pv output fluctuation using a battery energy storage system with model predictive control. Int. J. Fuzzy Log. Intell. Syst. 17, 202–209. doi:10.5391/ijfis.2017.17.3.202

CrossRef Full Text | Google Scholar

Augusto Pereira, H., Fagner Cupertino, A., Wu, J.-C., Jou, H.-L., and Chang, C.-H. (2023). Power conversion interface for a small-capacity photovoltaic power generation system. Energies 16, 1097. doi:10.3390/en16031097

CrossRef Full Text | Google Scholar

Benavides, D., Arévalo, P., Aguado, J. A., and Jurado, F. (2023). Experimental validation of a novel power smoothing method for on-grid photovoltaic systems using supercapacitors. Int. J. Electr. Power Energy Syst. 149, 109050. doi:10.1016/j.ijepes.2023.109050

CrossRef Full Text | Google Scholar

Benavides, D., Arévalo, P., Tostado-Véliz, M., Vera, D., Escamez, A., Aguado, J. A., et al. (2022). An experimental study of power smoothing methods to reduce renewable sources fluctuations using supercapacitors and lithium-ion batteries. Batteries 8, 228. doi:10.3390/batteries8110228

CrossRef Full Text | Google Scholar

Cano, A., Arévalo, P., Benavides, D., and Jurado, F. (2022). Comparative analysis of HESS (Battery/Supercapacitor) for power smoothing of PV/HKT, simulation and experimental analysis. J. Power Sources 549, 232137. doi:10.1016/j.jpowsour.2022.232137

CrossRef Full Text | Google Scholar

Chong, L. W., Wong, Y. W., Rajkumar, R. K., and Isa, D. (2016). An optimal control strategy for standalone PV system with battery-supercapacitor hybrid energy storage system. J. Power Sources 331, 553–565. doi:10.1016/j.jpowsour.2016.09.061

CrossRef Full Text | Google Scholar

D’Amico, G., Petroni, F., and Vergine, S. (2022). Ramp rate limitation of wind power: an overview. Energies 15, 5850. doi:10.3390/en15165850

CrossRef Full Text | Google Scholar

Fregosi, D., Pilot, N., Bolen, M., and Hobbs, W. B. (2023). An analysis of storage requirements and benefits of short-term forecasting for PV ramp rate mitigation. IEEE J. Photovolt. 13, 315–324. doi:10.1109/jphotov.2022.3231713

CrossRef Full Text | Google Scholar

Gad, A. G. (2022). Particle swarm optimization algorithm and its applications: a systematic review. Archives Comput. methods Eng. 29 (5), 2531–2561. ‏. doi:10.1007/s11831-021-09694-4

CrossRef Full Text | Google Scholar

Kanehira, T., Takahashi, A., Imai, J., and Funabiki, S. (2015). A comparison of electric power smoothing control methods for distributed generation systems. Electr. Eng. Jpn. Engl. Transl. 193, 49–57. doi:10.1002/eej.22767

CrossRef Full Text | Google Scholar

Kaushal, J., and Basak, P. (2020). Power quality control based on voltage sag/swell, unbalancing, frequency, THD and power factor using artificial neural network in PV integrated AC microgrid. Sustain. Energy. Grids Netw. 23, 100365. doi:10.1016/j.segan.2020.100365

CrossRef Full Text | Google Scholar

Krishan, O., and Suhag, S. (2020). A novel control strategy for a hybrid energy storage system in a grid-independent hybrid renewable energy system. Int. Trans. Electr. Energy Syst. 30, e12262. doi:10.1002/2050-7038.12262

CrossRef Full Text | Google Scholar

Ma, W., Wang, W., Wu, X., Hu, R., Tang, F., Zhang, W., et al. (2019a). Optimal allocation of hybrid energy storage systems for smoothing photovoltaic power fluctuations considering the active power curtailment of photovoltaic. IEEE Access 7, 74787–74799. doi:10.1109/access.2019.2921316

CrossRef Full Text | Google Scholar

Ma, W., Wang, W., Wu, X., Hu, R., Tang, F., and Zhang, W. (2019b). Control strategy of a hybrid energy storage system to smooth photovoltaic power fluctuations considering photovoltaic output power curtailment. Sustainability 11, 1324. doi:10.3390/su11051324

CrossRef Full Text | Google Scholar

Malamaki, K. N. D., Casado-Machado, F., Barragan-Villarejo, M., Gross, A. M., Kryonidis, G. C., Martinez-Ramos, J. L., et al. (2022). Ramp-rate limitation control of distributed renewable energy sources via supercapacitors. IEEE Trans. Ind. Appl. 58, 7581–7594. doi:10.1109/tia.2022.3195975

CrossRef Full Text | Google Scholar

Negi, G., Kumar, A., Pant, S., and Ram, M. (2021). GWO: a review and applications. Int. J. Syst. Assur. Eng. Manag. 12, 1–8. ‏. doi:10.1007/s13198-020-00995-8

CrossRef Full Text | Google Scholar

Nempu, P. B., Sabhahit, J. N., Gaonkar, D. N., and Rao, V. S. (2021). Novel power smoothing technique for a hybrid AC-DC microgrid operating with multiple alternative energy sources. Adv. Electr. Comput. Eng. 21, 99–106. doi:10.4316/aece.2021.02011

CrossRef Full Text | Google Scholar

Saripalli, B. P., Singh, G., and Singh, S. (2022). Supercapacitors based energy storage system for mitigating solar photovoltaic output power fluctuations. World J. Eng. 20, 815–834. doi:10.1108/wje-08-2021-0468

CrossRef Full Text | Google Scholar

Shaheen, M. A. M., Hasanien, H. M., and Alkuhayli, A. (2021). A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 12 (1), 621–630. doi:10.1016/j.asej.2020.07.011

CrossRef Full Text | Google Scholar

Sukumar, S., Marsadek, M., Agileswari, K. R., and Mokhlis, H. (2018). Ramp-rate control smoothing methods to control output power fluctuations from solar photovoltaic (PV) sources—a review. J. Energy Storage 20, 218–229. doi:10.1016/j.est.2018.09.013

CrossRef Full Text | Google Scholar

Takahashi, A., Kajitani, T., and Funabiki, S. (2022). Parameter determination for reducing ESS capacity in PV power smoothing control using spline function. Electr. Eng. Jpn. Engl. Transl. 215, e23367. doi:10.1002/eej.23367

CrossRef Full Text | Google Scholar

Wu, T., Yu, W., and Guo, L. (2019). A study on use of hybrid energy storage system along with variable filter time constant to smooth DC power fluctuation in microgrid. IEEE Access 7, 175377–175385. doi:10.1109/access.2019.2956832

CrossRef Full Text | Google Scholar

Xu, J., Xie, B., Liao, S., Ke, D., Sun, Y., Jiang, X., et al. (2022). CVR-based real-time power fluctuation smoothing control for distribution systems with high penetration of PV and experimental demonstration. IEEE Trans. Smart Grid 13, 3619–3635. doi:10.1109/tsg.2022.3166823

CrossRef Full Text | Google Scholar

Zhang, X., Lin, Q., Mao, W., Liu, S., Dou, Z., and Liu, G. (2021). Hybrid particle swarm and Grey wolf optimizer and its application to clustering optimization. Appl. Soft Comput. 101, 107061. doi:10.1016/j.asoc.2020.107061

CrossRef Full Text | Google Scholar