Optimal scheduling of distributed shared energy storage based on optimal SOC interval

Proposed within the framework of the sharing economy, Shared Energy Storage (SES) aims to enhance the efficiency of Energy Storage Systems (ESS) and drive down costs. This study focuses on an innovative approach to emphasize the multifaceted utilization of individual ESS units and the centralized use of dispersed ESS resources. Renewable Energy Power Plants (REPPs) collaborate to create SES pools, leveraging their ESS assets. Beyond meeting the needs of REPPs, these resources are shared for ancillary services like Secondary Frequency Regulation (SFR) to yield additional benefits. The paper delves into the scheduling techniques for SES. While conventional day-ahead robust optimization algorithms specify ESS power output for each period, they struggle to adjust schedules due to time-dependent constraints like renewable energy output and ESS state limitations. To address this, a distributed SES scheduling method based on optimal operating intervals is proposed. This method introduces an optimal interval variable for Energy Storage State of Charge (SOC) into the traditional three-layer optimization problem, effectively decoupling time-related constraints. Furthermore, a novel Nested Column and Constraint Generation (Nested C&CG) algorithm is presented to solve the mathematical model. Lastly, a revenue sharing model grounded in cooperative game theory is introduced, along with an illustrative example showcasing the efficacy of the proposed approach in managing uncertainties.

1 Introduction

In recent years, there has been a growing deployment of Energy Storage Systems (ESS) across various applications in different tiers of power systems, encompassing enhancements in reliability, peak-valley electricity price arbitrage, voltage and frequency regulation, renewable energy integration, and other functionalities (Zahedmanesh et al., 2021; Hou et al., 2020; Bitaraf and Rahman, 2018). Particularly on the generation-side, the increasing volatility, intermittency, and uncertainty associated with renewable energy sources have heightened the demand for flexible resources like ESS (Brouwer et al., 2015; Zeng et al., 2014; Dai et al., 2021). Despite the evident potential of ESS, their effective utilization encounters several challenges. Notably, a significant hindrance to widespread adoption is the considerable upfront investment required. Hence, the emergence of a Shared Energy Storage (SES) model, grounded in the principles of the sharing economy, is becoming increasingly pertinent. The SES model, as discussed below, can be categorized into two distinct setups proposed within this study:

(1) Independent SES operators providing storage services to diverse users.

(2) Users owning energy storage systems and engaging in collective utilization.

For the former model, research (Jo and Park, 2020) introduces the concept of energy capacity trading and operational games, alongside a 24-h ahead charging-discharging scheduling scheme aimed at minimizing energy operation costs. Furthermore, the advantages of centralized SES operations, particularly in terms of their cost-effectiveness, are meticulously examined in (Walker and Kwon, 2021). A pioneering energy trading system designed for demand-side management within a neighborhood network involving an SES provider, users with non-dispatchable energy sources, and an electricity retailer is outlined in (Mediwaththe et al., 2020). Additionally (Cao et al., 2021), presents an optimal economic dispatch method for microgrid owner/operators leveraging SES.

Exploring the latter model, investigations are conducted into user-owned structures in (Liu et al., 2021). Moreover, a cost-benefit-based approach to SES planning aimed at reducing electricity procurement costs for electricity retailers is proposed in (Zhong et al., 2020a). Furthermore (Zhong et al., 2020b), introduces an online control strategy for real-time energy management of distributed ESS, while (He and Zhang, 2021) suggests a double auction-based mechanism for a community energy sharing market where all participants possess ESS and engage in demand response activities.

Although previous studies have largely focused on delivering single services through SES, such as peak-valley electricity price arbitrage, renewable energy integration, and frequency regulation, the necessity for SES to cater to multiple service demands in order to enhance profitability has become apparent. Notably, limited attention has been given to the application of SES in the generation-side context. This paper introduces a novel application model focusing on the generation side, where Renewable Energy Power Plants (REPPs) join forces to utilize energy storage resources for Primary Frequency Regulation (PFR), penalty cost reduction, and increased earnings through Secondary Frequency Regulation (SFR) auxiliary services. The cooperative game involves independent REPPs, and the coalition’s revenue maximization is achieved through strategic SES scheduling decisions.

Addressing the uncertainties associated with renewable energy, this paper proposes a robust day-ahead scheduling approach to optimize ESS State of Charge (SOC) intervals, thereby decoupling time-coupled constraints. A novel nested C&CG (Column-and-Constraint generation) method is employed to address the proposed min-max-min three-layer optimization model. Additionally, a profit-sharing scheme grounded in cooperative game theory ensures financial rewards for all participants.

2 Distributed shared energy storage application mode

After forming an alliance of shared energy storage in new energy stations, a cooperative game will be played. As follows:

$P_{i,t}^{de}=P_{i,t}^{re}+P_{i,t}^d-P_{i,t}^{ex}-P_{i,t}^c+P_{i,t}^{tr}+P_{i,t}^s-P_{i,t}^{cur}(1)$

${\displaystyle {\sum }_{i=1}^n}{P}_{i,t}^{ex}={\displaystyle \sum _{i=1}^n}{P}_{i,t}^{tr}(2)$

where $P_{i,t}^{de}$ is the power generation plan reported by the new energy station i during time t; $P_{i,t}^{re}$ is the actual output of the new energy station i during time t; $P_{i,t}^d$ and $P_{i,t}^{ex}$ are the charging and discharging power of the energy storage system of the new energy station i during time t, respectively; $P_{i,t}^c$ is the provide power for the shared energy storage of the new energy station i during time t; $P_{i,t}^{tr}$ is the inject power for the new energy station i to share energy storage during time t; $P_{i,t}^s$ is the shortfall power of the new energy station i during time t; $P_{i,t}^{cur}$ is the abandoned wind or solar power of the new energy station i during time t.

The basic application of shared energy storage aims to reduce the cost of deviation assessment or wind/solar power abandonment. In addition, in the auxiliary service market, shared energy storage can serve as an independent market entity, utilizing the remaining capacity to provide primary or secondary frequency modulation services, thereby improving equipment utilization and energy storage investment returns. According to the regulations of the electricity market, the bidding capacity for secondary frequency regulation will be determined in advance. Therefore, the shared energy storage cloud platform needs to optimize the day ahead scheduling plan according to the needs of new energy stations.

2.1 Primary frequency modulation

This study assumes that each REPP is equipped with ESS. As the REPPs participating in the coalition are not far apart geographically and the electrical distance is close, the cost of line loss is small and is a certain value. As the REPPs participating in the coalition, the ESS of REPPs utilize the SES model. All the ESS of REPPs utilizing SES model is regarded as a whole. In this model, all REPPs utilizing SES model can meet the needs of primary frequency regulation (PFR), reduce punishment cost, and improve the information is provided to SES processing platform for centralized regulation by communication network.

China requires new energy stations to have a primary frequency regulation function. The droop characteristics of their primary frequency regulation are as follows:

$P=\left\{\begin{array}{l}{P}_0-\frac{1}{\delta \%}\ast P_{\mathrm{N}}\ast \frac{f-f_{\mathrm{d}}^{up}}{f_0},f>f_{\mathrm{d}}^{up}\\ P_0,f_{\mathrm{d}}^{low}\le f\le f_{\mathrm{d}}^{up}\\ P_0-\frac{1}{\delta \%}\ast P_{\mathrm{N}}\ast \frac{f-f_{\mathrm{d}}^{low}}{f_0},f<f_{\mathrm{d}}^{low}\end{array}\right.(3)$

$f_{\mathrm{d}}^{up}=f_0+\Delta f(4)$

$f_{\mathrm{d}}^{low}=f_0-\Delta f(5)$

where $f_{\mathrm{d}}^{up}$ and $f_{\mathrm{d}}^{low}$ respectively represent the upper and lower limits of the primary frequency modulation dead zone; _F0 is the rated frequency; Δ F is the dead zone range of primary frequency modulation; P_N is the rated power of the new energy station; δ% Adjust the frequency difference rate for primary frequency modulation; _P0 is the initial value of the active power of the new energy station; At that $f_{\mathrm{d}}^{low}\le f\le f_{\mathrm{d}}^{up}$ time, the system frequency was in the dead zone of primary frequency regulation, and the active power of the new energy station did not need to be changed; At that $f>f_{\mathrm{d}}^{up}$ time, the new energy station reduced the active power output and conducted a frequency modulation; At that $f<f_{\mathrm{d}}^{low}$ time, the new energy station increased active power output for primary frequency regulation.To illustrate this better, we add a graph.

When $f_{\mathrm{d}}^{up}$ and $f_{\mathrm{d}}^{low}$ are ±0.05 Hz, $\delta \%$ = 2%, the maximum power limit is set at 10% of the rated power, PFR droop curve of REPP is shown in Figure 1.

Figure 1

Figure 1. PFR droop curve of REPP.

2.2 Secondary frequency modulation

In the recent optimization stage, shared energy storage can not only reduce the penalty cost of new energy stations and assume the obligation of primary frequency regulation, but also participate in the auxiliary service market, use the remaining capacity to provide secondary frequency regulation services, thereby improving the utilization rate of shared energy storage and increasing the revenue of the new energy station alliance.

The secondary frequency regulation auxiliary service market in this chapter adopts the rule of compensating for bid winning capacity and mileage, with the decision variable being the secondary frequency regulation capacity tendered the day before each time period. Due to the fact that energy storage is a high-quality frequency modulation resource, it is assumed that its bidding quantity is the same as the winning bid quantity. There may be a deviation between the scalar quantity and the actual charging and discharging power. Deviation is reflected as a penalty term in the objective function. The secondary frequency modulation market recently conducted hourly bidding. The benefits of shared energy storage secondary frequency regulation include two parts: capacity and mileage benefits:

$\begin{array}{l}{R}_{sf}={\displaystyle \sum _i^n}{\displaystyle \sum _t^T}{c}^{cap}\cdot P_{i,t}^{cap}+c^{mil}\cdot P_{i,t}^{mil}\\ ={\displaystyle \sum _i^n}{\displaystyle \sum _t^T}\left(c^{cap}+c^{mil}\cdot \mathrm{m}\right)P_{i,t}^{cap}\end{array}(6)$

where $R_{sf}$ represents the shared energy storage secondary frequency regulation revenue; $c^{cap}$ and $c^{mil}$ are the secondary frequency regulation capacity and mileage benefit coefficients, respectively; $P_{i,t}^{cap}$ and $P_{i,t}^{mil}$ are the declared energy storage capacity and mileage of the i-th new energy station during time period t, respectively; M is the mileage benefit coefficient, which is an estimated value. For fast frequency modulation resources, based on experience, m = 3 can be taken.

2.3 Shared energy storage scheduling mode

The deviation between actual power generation and predicted values will result in deviation assessment and penalty costs for wind and solar curtailment. However, the energy storage SOC needs to maintain consistency throughout the scheduling cycle to cope with the scheduling plan for the next cycle, so its output power has a coupling relationship in time. In addition, due to the uncertainty of renewable energy and the limitations of energy storage capacity, the current shared energy storage scheduling decisions may not be efficient from an all day perspective, leading to the possibility of insufficient/excess energy storage capacity in the future, resulting in increased penalty costs. For example, in the daily scheduling, in order to meet the daily scheduling plan, the energy storage SOC is close to the maximum value. Due to the uncertainty of renewable energy output, new energy may experience a sudden increase in output during the next scheduling period, and energy storage will not be able to meet the usage needs of the next scheduling period.

This article proposes a robust scheduling method to obtain the SOC interval of shared energy storage in the worst-case scenario, in order to guide the daily operation of shared energy storage. This scheduling method aims to maximize the benefits of the new energy station alliance and improve the efficiency of renewable energy utilization. In the current stage, considering the uncertainty of renewable energy, determine the optimal SOC range. During the intraday phase, shared energy storage is optimized and scheduled within the SOC range based on short-term predictions. In addition, for real-time auxiliary service requirements, energy storage can be adjusted arbitrarily within the SOC range to improve economic efficiency. The proposed shared energy storage scheduling framework is shown in Figure 2.

Figure 2

Figure 2. Distributed shared energy storage scheduling framework for power generation.

3 Robust optimization scheduling method for min max min three-layer optimal SOC interval

3.1 Summary

The principle of robust optimization algorithms is to obtain optimized scheduling strategies in the worst scenario. This chapter obtains the optimal SOC interval for shared energy storage by solving the min max min three-layer robust optimization model, which can also be applied to intraday scheduling problems. The min max min three-layer optimization problem first takes the optimal interval of each energy storage SOC as a decision variable in the first stage, known as the “Here and Now” variable. Based on factors such as the predicted output of renewable energy, the optimal SOC interval for energy storage is determined. Solve the max min problem in the second stage. In the max problem, simulate the worst-case scenario of renewable energy output based on the SOC interval generated in the first stage, attempting to maximize the total cost. The min problem is based on the decision-making of the max problem in the first and second stages, to determine the actual output of shared energy storage in new energy stations, namely the “Wait and See” variable. The min problem attempts to maximize the benefits of the alliance. This process simulates the game process between the output power of new energy stations and the decision-making of shared energy storage cloud platforms. It is worth noting that the two-stage model is a unified whole. The SOC interval generated in the first stage will constrain the min problem in the second stage, thereby affecting the decision-making of the max problem in the second stage. Therefore, it is necessary to collaborate in these two stages to solve the problem. The overall scheduling framework of the min-max-min three-layer robust optimization scheduling algorithm considering the optimal SOC interval is shown in Figure 3.

Figure 3

Figure 3. Three layer robust optimization scheduling algorithm.

In real-time scheduling within the day, the obtained energy storage SOC interval is used as a constraint. Within this range, the adjustment of energy storage output will no longer incur penalty costs. Energy storage output can track real-time fluctuations in new energy and demand generated by frequency regulation, achieving greater benefits.

3.2 Phase Ι

The decision variable in the first stage is the optimal SOC operating interval for shared energy storage, which is the upper and lower bounds of the energy storage SOC for each time period. The goal of the first stage is to minimize the objective function of the second stage. The first stage objective function is:

$\underset{R}{\min }\underset{Z}{\max }\underset{P,\mathrm{o}}{\min }{C}_{pen}+C_{tr}-R_{sale}-R_{sf}(7)$

where R is the interval vector of the first stage shared energy storage SOC. The first stage constraints are as follows:

${SOC}_{i,\min }\le {SOC}_{i,t}^{low}\le {SOC}_{i,t}^{up}\le {SOC}_{i,\max }(8)$

${\text{SOC}}_{i,TT}^{low}={\text{SOC}}_{i,TT}^{up}={\text{SOC}}_{i,o}(9)$

${\text{SOC}}_{i,t}^{up}-{\text{SOC}}_{i,t-1}^{low}\le \frac{P_i^{\max }{\eta }_c\Delta t}{E_i^{\max }}(10)$

${\text{SOC}}_{i,t-1}^{up}-{\text{SOC}}_{i,t}^{low}\le \frac{P_i^{\max }\Delta t}{{\eta }_d{E}_i^{\max }}(11)$

where ${SOC}_{i,\min }$ and ${SOC}_{i,\max }$ are the upper and lower limits of the energy storage SOC of the i-th new energy station, respectively; ${SOC}_{i,t-1}^{low}$ and ${SOC}_{i,t-1}^{up}$ are the SOC intervals during the storage period t of the i-th new energy station, respectively; ${SOC}_{i,o}$ is the initial SOC value of the i-th new energy station’s energy storage; TT is the final scheduling period; _{Pmax i} and _{Emax i} are the rated power capacity and rated energy capacity of the i-th new energy station, respectively; η C and η D represents the efficiency of energy storage charging and discharging, respectively. The Formulas 5–8 stipulates that the upper bound of the shared energy storage SOC interval should be greater than the lower bound, and the energy storage SOC interval should be between the maximum and minimum SOC values; The Formula 9 ensures that the energy storage SOC recovers to its initial SOC value at the end of the scheduling period; In the Formula 10, it $SO{C}_{i,t}^{up}-SO{C}_{i,t-1}^{low}$ refers to the maximum amount of rechargeable energy that the i-th new energy station can charge within the SOC interval of time t; In the Formula 11, $SO{C}_{i,t-1}^{up}-SO{C}_{i,t}^{low}$ refers to the maximum amount of discharge that can be carried out by the i-th new energy station within the SOC interval of time t.

3.3 Phase Ⅱ

3.3.1 Objective function

$\underset{Z}{\max }\underset{P,o}{\min }{C}_{pen}+C_{tr}-R_{sale}-R_{sf}$

where Z represents the uncertainty set of renewable energy stations; P is a continuous variable in the second stage; O is a binary 0-1 variable in the second stage, referring to the charging and discharging state of energy storage; _Cpen is the penalty cost for the new energy station alliance; _Ctr is the cost of line loss; _Rsale represents the sales revenue of the alliance; _Rsf represents the revenue from the alliance’s secondary frequency modulation auxiliary services.

$\begin{array}{l}{C}_{pen}={\displaystyle \sum _i^n}{\displaystyle \sum _t^T}{P}_{i,t}^{pu}.{\partial }_1+P_{i,t}^{cur}\cdot {\partial }_2\\ +\left|P_{i,t}^{ff,pu}\right|\cdot {\partial }_3+\left|P_{i,t}^{sf,pu}\right|\cdot {\partial }_4\end{array}(12)$

$C_{tr}={\displaystyle \sum _i^n}{\displaystyle \sum _t^T}{\pi }_{tr}{P}_{i,t}^{tr}(13)$

$R_{sale}={\displaystyle \sum _i^n}{\displaystyle \sum _t^T}{\pi }_t^{sell}\left(P_{i,t}^{de}-P_{i,t}^{pu}\right)(14)$

$R_{sf}={\displaystyle {\sum }_i^n}{\displaystyle {\sum }_t^T}\left(C^{cap}{P}_{i,t}^{cap}+C^{mil}{P}_{i,t}^{mil}\right)(15)$

where $P_{i,t}^{pu}$ is the shortfall power of the i-th new energy station during period t; $P_{i,t}^{cur}$ is the wind/solar power curtailed by the i-th new energy station during time t; $P_{i,t}^{ff,pu}$ is the primary frequency regulation power shortfall of the i-th new energy station during time t period; $P_{i,t}^{sf,pu}$ is the secondary frequency regulation deficit power of the i-th new energy station during time t period; ${\partial }_1$, ${\partial }_2$, ${\partial }_3$, and ${\partial }_4$ Respectively represent the corresponding penalty cost coefficients; Selling electricity prices ${\pi }_t^{sell}$ for time period t; ${\pi }_{tr}$ is the cost coefficient of line loss.

3.3.2 Constraint condition

$P_{i,t}^{re}=P_{re,i,t}^{forecast}+z_{i,t}^u\Delta P_{re,i,t}^{forecast}-z_{i,t}^l\Delta P_{re,i,t}^{forecast}(16)$

$z_{i,t}^u+z_{i,t}^l\le 1(17)$

$P_{i,t}^{ch}-P_{i,t}^{tr}=P_{i,t}^{pf,c}+P_{i,t}^{sf,c}+P_{i,t}^{su,c}(18)$

$P_{i,t}^{dis}-P_{i,t}^{ex}=P_{i,t}^{pf,d}+P_{i,t}^{sf,d}+P_{i,t}^{su,d}(19)$

$P_{i,t}^{pf,c}-P_{i,t}^{pf,d}+P_{i,t}^{pf,pu}=P_{i,t}^{pf}(20)$

$P_{i,t}^{sf,c}-P_{i,t}^{sf,d}+P_{i,t}^{sf,pu}=P_{i,t}^{sf}(21)$

$SO{C}_{i,t+1}=\left(1-{\delta }_e\right)SO{C}_{i,t}+\left(P_{i,t}^{ch}{\eta }_c\Delta t-\frac{P_{i,t}^{dis}\Delta t}{{\eta }_d}\right)E_i^{\max }(22)$

$0\le P_{i,t}^{ch}\le {\epsilon }_{i,t}^{c}M(23)$

$0\le P_{i,t}^{dis}\le {\epsilon }_{i,t}^{d}M(24)$

${\epsilon }_{i,t}^c+{\epsilon }_{i,t}^d\le 1(25)$

$0\le P_{i,t}^{ch},P_{i,t}^{dis}\le P_i^{\max }(26)$

$SO{C}_{i,\min }\le SO{C}_{i,t}\le SO{C}_{i,\max }(27)$

where $P_{re,i,t}^{forecast}$ is the predicted power of the i-th new energy station in time period t; zu,i,t and zl,i,t are binary 0-1 variables that represent the fluctuation state of new energy output power; $\Delta P_{re,i,t}^{forecast}$ is deviation value from predicted power; δ _E is the self discharge rate of energy storage; P^pf,c_i,t, P^pf,d_i,t and P^pf,pu_i,t are storage charging and discharging power of the i-th new energy station during time t; P^sf,c_i,t, P^sf,d_i,t and P^sf,pu_i,t respectively represent the primary frequency regulation charging, discharging, and excess power of the i-th new energy station during time t; P^sf,c_i,t, P^sf,d_i,t and P^sf,pu_i,t respectively represent the secondary frequency regulation charging, discharging, and excess power of the i-th new energy station during time t; P^su,c_i,t and P^su,d_i,t are the charging and discharging power of the i-th new energy station to reduce penalty costs during time t; Charge ${\epsilon }_{i,t}^c$ and discharge status ${\epsilon }_{i,t}^d$ of the i-th new energy station during time t.

3.4 Intraday scheduling

After completing the optimization scheduling calculation, the optimal operating range of the distributed shared energy storage SOC can be obtained. Therefore, it is only necessary to optimize each time period. At various time periods during the day, the upper and lower bounds of energy storage SOC are known quantities, so the output power of renewable energy in the Formula 1 can also be measured using actual observations. The energy storage SOC can be obtained based on the execution situation in the previous period, which is a known quantity and achieves temporal decoupling. Therefore, it is unnecessary to consider the minimum deviation from the day ahead scheduling plan in the intra day scheduling phase. The output power of distributed shared energy storage can be flexibly adjusted according to the actual power output of renewable energy. As long as it is within the optimal SOC range, all constraints can be met.

4 Solution method

The mathematical model proposed in this chapter can be abbreviated as follows:

$\begin{array}{l}\underset{R}{\min }\underset{z}{\max }\underset{P,o}{\min }{A}^T\cdot P\\ \mathrm{s}.\mathrm{t}.C{R}_v\le d\\ F\cdot R_v+Y\cdot P+Q\cdot \mathrm{o}+z\cdot T\le \partial \\ z\in \left\{0,1\right\},o\in \left\{0,1\right\}\end{array}$

where R represents the optimal interval vector of the first stage distributed shared energy storage SOC; Z is the uncertain set of renewable energy output power; P is a continuous variable in the second stage; O is a binary variable in the second stage, referring to the charging and discharging status of energy storage in each new energy station; $C{R}_v\le d$ Constraints $F\cdot R_v+Y\cdot P+Q\cdot \mathrm{o}+z\cdot T\le \partial$ include Equations 8–11, constraints include Equations 1–6 and Equations 12–27. Due to the presence of 0–1 binary variables in the second stage, the Nested C&CG algorithm is used for solving in this chapter.

5 Case study

5.1 Case description

This chapter selects actual calculation examples of three renewable energy stations in a certain area of China, as shown in Figure 4. Among them, Station 1 is a photovoltaic power station, and Stations 2 and 3 are wind power stations. The scheduling period is 1 h. In the calculation example, the primary frequency regulation demand is calculated based on the actual frequency variation curve of the local power grid through droop characteristics. The dead zone of the primary frequency regulation is set to ± 0.02 Hz, and the rated frequency is 50 Hz. The declaration of secondary frequency modulation is in hours. The daily declared capacity of secondary frequency regulation is predicted based on historical data. The energy storage parameters are shown in Table 1. The online prices of new energy stations are shown in Table 2 (Zhang et al., 2015). π_tr is 0.1 $/kWh, π_pu is 1.5 times the real-time grid electricity price (Zhang et al., 2015), c^cap is 10 $/MW, and c^mil is 8 $/MWh. Other basic data can be found in (Available at).

Figure 4

Figure 4. Structural diagram of three renewable energy stations.

Table 1

Table 1. Distributed shared energy storage parameters.

Table 2

Table 2. Online electricity prices of new energy stations.

5.1.1 Results analysis

After calculation, the SOC range of distributed shared energy storage at various new energy stations in the worst-case scenario is shown in Figure 5. The worst-case scenario is shown in Figure 6. The output power of distributed shared energy storage is shown in Figure 7. The various costs of optimizing scheduling recently are shown in Table 3. The benefits of new energy station alliances with different sets are shown in Table 4. The results of income distribution using the Shapley value method are shown in Table 5.

Figure 5

Figure 5. SOC range of new energy station energy storage in the worst scenario.

Figure 6

Figure 6. Worst scenario of new energy stations.

Figure 7

Figure 7. Distributed shared energy storage output power.

Table 3

Table 3. Results of recent optimized scheduling.

Table 4

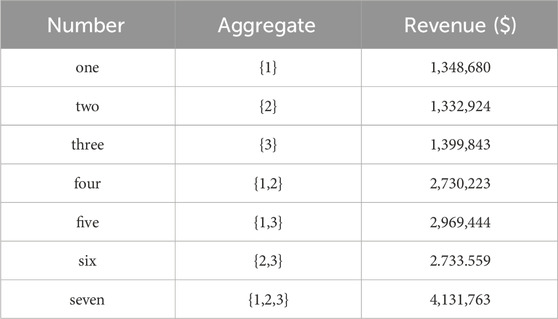
Table 4. Benefits of different collective new energy station alliances under shared energy storage mode.

Table 5

Table 5. Distribution results of alliance benefits.

5.2 Comparison with unshared energy storage mode

When the combination of members in the collection is {1}, {2}, {3}, each alliance has only one participant, that is, the shared energy storage mode changes to the unshared energy storage mode model. Alliance participants can only rely on their own energy storage equipment and optimize their own energy storage configuration to reduce deviation assessment costs and waste wind/solar costs, achieving maximum self benefits.

In this situation, compared to self built energy storage, adopting a shared energy storage model generates additional benefits. The total revenue of each alliance increased by 1.23%. The revenue of New Energy Station 1 increased by 33,889 $. The revenue of New Energy Station 2 increased by 7,180 $. The revenue of New Energy Station 3 increased by 7,095 $. The results verified the group rationality and individual rationality under the cooperative game model.

Comparison with traditional intraday rolling optimization algorithms.

Set the intra day rolling optimization algorithm as scenario 2, as shown in Figures 8.

Figure 8

Figure 8. Framework of rolling optimization algorithm within a day.

First of all, make a day ahead scheduling plan based on the predicted output of renewable energy. The intraday scheduling stage assumes that it can be obtained from the current time period to the future τ The accurate value of renewable energy output power for each time period, while the predicted values are still used for the remaining time periods, as shown in the prediction domain in Figures 6. Considering time coupling constraints, with the objective function of minimizing cost, an optimization calculation is performed for each scheduling cycle, and only the current time period strategy, i.e. the control domain time period, is executed until the scheduling cycle ends. And further use Monte Carlo simulation method to generate renewable energy output for optimization calculation, and change the forward-looking parameters in the intraday rolling optimization algorithm τ。 The results are shown in Table 6.

Table 6

Table 6. Different τ Value optimization calculation results.

It can be seen that with the prospective parameters τ The total revenue of rolling optimization within the day gradually increases with the increase of. This is because the more renewable energy output information is obtained, the less uncertainty in the subsequent period, the less impact it has on the scheduling plan, and the lower the cost of deviation penalty. τ It has a significant impact on the performance of intra day rolling optimization. The comparison results show that when τ = At 4 o’clock, its total revenue is slightly higher than Scenario 1, but in reality, it is difficult to accurately predict the renewable energy output power within 4 h.

The results indicate that although the scheduling method in Scenario 1 can only be based on the output of renewable energy in the current stage, compared with the method in Scenario 2, it lacks accurate prediction information for the output power of new energy stations in subsequent periods. Therefore, its scheduling method has more uncertain factors, but the total revenue is higher than that in Scenario 2. On the one hand, since Scenario 1 considers the worst scenario through robust optimization in the day ahead scheduling, the SOC optimal operation interval obtained has a stronger ability to deal with uncertainty. On the other hand, the scheduling method in Scenario 2 must track the previous day’s scheduling plan to meet time coupling constraints, resulting in limited adjustment intervals for energy storage. Scenario 1, after optimization, obtains the SOC operating range, which is no longer constrained by time coupling and can be adjusted arbitrarily within the range. Therefore, shared energy storage has greater flexibility, and the charging and discharging behavior of energy storage can be decided based on the real-time output of new energy and the real-time demand of the auxiliary service market, thereby obtaining more profits. This also indicates the economic viability of the scheduling method proposed in this article.

6 Conclusion

Considering the uncertainty of renewable energy, this chapter proposes an optimization scheduling method for distributed shared energy storage on the generation side based on the optimal SOC interval, decoupling the coupling constraints of energy storage time. And propose a mode of shared energy storage to participate in multiple auxiliary services, that is, to use idle capacity to participate in frequency regulation auxiliary services on the basis of reducing deviation assessment costs. To solve the min max min problem with binary variables in the second stage, the nested C&CG method is used for solving, and the Shapley value method is applied to develop a reasonable profit distribution plan. The specific conclusion is as follows:

(1) The distributed shared energy storage model can effectively improve the benefits of participants in the new energy station alliance.

(2) Considering the coupling relationship between the output power and time of energy storage during the scheduling cycle, in order to cope with the uncertainty of new energy, this chapter proposes an optimization scheduling method for distributed shared energy storage on the generation side based on the optimal SOC interval. The method used in this chapter is not limited by time coupling constraints and does not need to track the day ahead scheduling plan, so it has high flexibility and can further play the advantages of energy storage in the ancillary service market.

(3) The Shapley value method is used to allocate the benefits of the alliance, which satisfies both individual rationality and overall rationality, and is an effective method for distributing benefits.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TZ: Writing–original draft. LZ: Writing–original draft, Conceptualization, Methodology, Software. YC: Data curation, Resources, Writing–original draft. ZP: Supervision, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the project of State Grid Jiangsu Electric Power Co. Ltd. (J2024019).

Conflict of interest

Author LZ was employed by State Grid Jiangsu Electric Power Company.

Authors TZ and ZP were employed by State Grid Jiangsu Electric Power Co., Ltd.

Author YC was employed by Jiangsu Electric Power Co., Ltd.

The authors declare that this study received funding from State Grid Jiangsu Electric Power Co.Ltd.. The funder had the following involvement in the study: introducing an optimal interval variable for Energy StorageState of Charge.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Available at: https://www.jianguoyun.com/p/DSY6nOIQs7HYCxjsv4wFIAA (Accessed June 7, 2024).

Bitaraf, H., and Rahman, S. (2018). Reducing curtailed wind energy through energy storage and demand response. IEEE Trans. Sustain. Energy 9 (1), 228–236. doi:10.1109/tste.2017.2724546

CrossRef Full Text | Google Scholar

Brouwer, A. S., Van Den Broek, M., Seebregts, A., and Faaij, A. (2015). Operational flexibility and economics of power plants in future low-carbon power systems. Appl. Energy 156, 107–128. doi:10.1016/j.apenergy.2015.06.065

CrossRef Full Text | Google Scholar

Cao, S., Zhang, H., Cao, K., Chen, M., Wu, Y., and Zhou, S. (2021). Day-ahead economic optimal dispatch of microgrid cluster considering shared energy storage system and P2P transaction. Front. Energy Res. 9, 645017. doi:10.3389/fenrg.2021.645017

CrossRef Full Text | Google Scholar

Dai, R., Esmaeilbeigi, R., and Charkhgard, H. (2021). The utilization of shared energy storage in energy systems: a comprehensive review. IEEE Trans. Smart Grid 12 (4), 3163–3174. doi:10.1109/tsg.2021.3061619

CrossRef Full Text | Google Scholar

He, L., and Zhang, J. (2021). A community sharing market with pv and energy storage: an adaptive bidding-based double-side auction mechanism. IEEE Trans. Smart Grid 12 (3), 2450–2461. doi:10.1109/tsg.2020.3042190

CrossRef Full Text | Google Scholar

Hou, H., Xu, T., Wu, X., Wang, H., Tang, A., and Chen, Y. (2020). Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system. Appl. Energy 271, 115052. doi:10.1016/j.apenergy.2020.115052

CrossRef Full Text | Google Scholar

Jo, J., and Park, J. (2020). Demand-side management with shared energy storage system in smart grid. IEEE Trans. Smart Grid 11 (5), 4466–4476. doi:10.1109/tsg.2020.2980318

CrossRef Full Text | Google Scholar

Liu, J., Chen, X., Xiang, Y., and Huo, D. (2021). Optimal planning and investment benefit analysis of shared energy storage for electricity retailers. Int. J. Electr. Power & Energy Syst. 126, 106561. doi:10.1016/j.ijepes.2020.106561

CrossRef Full Text | Google Scholar

Mediwaththe, C. P., Shaw, M., Halgamuge, S., Smith, D. B., and Scott, P. (2020). An incentive-compatible energy trading framework for neighborhood area networks with shared energy storage. IEEE Trans. Sustain. Energy 11 (1), 467–476. doi:10.1109/tste.2019.2895387

CrossRef Full Text | Google Scholar

Walker, A., and Kwon, S. (2021). Analysis on impact of shared energy storage in residential community: individual versus shared energy storage. Appl. Energy 282, 116172. doi:10.1016/j.apenergy.2020.116172

CrossRef Full Text | Google Scholar

Zahedmanesh, A., Muttaqi, K. M., and Sutanto, D. (2021). A cooperative energy management in a virtual energy hub of an electric transportation system powered by PV generation and energy storage. IEEE Trans. Transp. Electrification 7 (3), 1123–1133. doi:10.1109/tte.2021.3055218

CrossRef Full Text | Google Scholar

Zeng, B., Zhang, J., Yang, X., Wang, J., Dong, J., and Zhang, Y. (2014). Integrated planning for transition to low-carbon distribution system with renewable energy generation and demand response. IEEE Trans. Power Syst. 29 (3), 1153–1165. doi:10.1109/tpwrs.2013.2291553

CrossRef Full Text | Google Scholar

Zhang, W., Wang, X., Wu, X., and Yao, Li (2015). An analysis model of power system with large-scale wind power and transaction mode of direct power purchase by large consumers involved in system scheduling. Proc. CSEE 35 (12), 2927–2935. doi:10.13334/j.0258-8013.pcsee.2015.12.002

CrossRef Full Text | Google Scholar

Zhong, W., Xie, K., Liu, Y., Yang, C., Xie, S., and Zhang, Y. (2020a). Online control and near-optimal 28algorithm for distributed energy storage sharing in smart grid. IEEE Trans. Smart Grid 11 (3), 2552–2562. doi:10.1109/tsg.2019.2957426

CrossRef Full Text | Google Scholar

Zhong, W., Xie, K., Liu, Y., Yang, C., Xie, S., and Zhang, Y. (2020b). Online control and near-optimal algorithm for distributed energy storage sharing in smart grid. IEEE Trans. Smart Grid 11 (3), 2552–2562. doi:10.1109/tsg.2019.2957426

CrossRef Full Text | Google Scholar