A synchronous compression and encryption method for massive electricity consumption data privacy preserving

The demand for fine-grained perception of electricity usage information in the new power system is continuously increasing, making it a challenge to address potential unauthorized data access while ensuring channel security. This paper addresses privacy in power systems requiring efficient source-load interactions by introducing a novel data compression synchronous encryption algorithm within a compressed sensing framework. Our proposed algorithm uses a ternary Logistic-Tent chaotic system for generating a chaotic measurement matrix, allowing simultaneous data compression and encryption of user-side voltage and current data. This mitigates high-frequency sampling overload and ensures data confidentiality. The implementation of a joint random model at both compression and reconstruction stages eliminates the need for key transmission, reducing management costs and leakage risks. The proposed algorithm was validated using the PLAID dataset, demonstrating that the time required for a single encryption-decryption operation can be reduced by up to 81.99% compared to the asymmetric RSA algorithm. Additionally, compared to the symmetric AES algorithm, the proposed method significantly enhances confidentiality.

1 Introduction

A significant number of distributed energy resources and load components have been integrated into the modern power system, resulting in increasingly stringent demands for accurate perception of electricity usage information on the load side (Schirmer and Mporas, 2023; Peng et al., 2022). However, the recording data of voltage and current on the user side contains extensive information about loads and electricity consumption. With the rise of non-intrusive load monitoring methods, this unencrypted private information may be illegally acquired during the data collection process through eavesdropping. Once such data is accessed by malicious actors, they can analyze various load profiles, occupancy rates, lifestyles, and behavioral patterns within a given area, potentially compromising users’ normal lives and property security (Wang et al., 2021). Therefore, safeguarding the privacy of the vast amounts of electricity usage information generated by smart terminals is of paramount importance.

Utilizing existing symmetric encryption algorithms such as DES, AES, and 3DES can efficiently encrypt electricity consumption information in non-intrusive load monitoring scenarios. However, there is a risk of leakage and decryption of keys during distribution and transmission (Alsuwaiedi and Alsuwaiedi, 2023). On the other hand, asymmetric encryption algorithms like RSA, and Elgamal can avoid the risk of key leakage, but they are computationally complex, with high key management costs, making it difficult for resource-constrained terminals in non-intrusive load monitoring scenarios to achieve and ensure data real-time (Okeyinka, 2015).

Furthermore, the transmission of electricity consumption information not only carries the risk of interception (Moon et al., 2019; Ding et al., 2020) but also incurs substantial communication costs due to the massive data generated by high-frequency sampling, especially in communication-constrained power user sides, such as those using Power Line Communication (PLC) mode. Therefore, efficient and secure transmission of electricity consumption information, including current and voltage waveform data, under terminal resource constraints, is crucial for improving the quality of electricity services and protecting customer privacy in the context of new power system requirements (Inayat et al., 2022; Mahmoud et al., 2021).

As the digitalization of power infrastructure accelerates, the privacy issues surrounding electricity consumption data are receiving increasing attention, with the security of the communication layer being crucial for protecting this data (Ashraf et al., 2021; Rafique et al., 2020). Regarding real-time collection of massive power big data, reference (Hasan et al., 2023) proposes a power user data compression algorithm based on improved atomic decomposition to reduce the volume of collected data. Reference (Khalid et al., 2023) proposed a state estimation based on the median regression function (MRF), which can accurately estimate the state and evaluate the measurement results affected by data injection and network attacks. For secure transmission of massive data, reference (Al-Kadhim and Al-Raweshidy, 2021) proposes a distributed AES real-time encryption algorithm for wide-area measurement systems of smart grids, which offloads AES blocks to the Storm computing platform to reduce encryption transmission delays. Reference (Zhai et al., 2022) designed two privacy-preserving outsourcing algorithms for modular exponentiation operations involved in multidimensional data aggregation, which allow these smart meter devices to delegate complex computing tasks to nearby servers for calculation. Reference (Meng et al., 2023) proposes a selective encryption algorithm for powering big data based on a Data Stream Manager (DSM). While these studies effectively enhance the confidentiality of electricity consumption data, the deployment of algorithms requires significant software and hardware resources and incurs substantial additional costs for key management.

In the context of non-intrusive load monitoring scenarios, existing research struggles to strike a balance between reducing transmission costs and key management expenses while addressing the dual challenges of key security and efficiency, thereby failing to meet the secure transmission demands of emerging power system electricity usage data. Compressive sensing, however, presents a novel signal-processing technique that rapidly reduces signal dimensions by observing them through measurement matrices. Given that signal observations can only be reconstructed through these measurement matrices, said matrices possess key encryption attributes, facilitating encryption, decryption, and secure transmission of sensitive data.

Therefore, this paper addresses the privacy protection needs of non-intrusive load monitoring (NILM) in the context of the new power system. We propose a novel algorithm for compressing and encrypting high-frequency electrical consumption data under terminal resource constraints. The algorithm enhances data security and confidentiality through the use of a ternary Logistic-Tent chaotic system and S-box techniques. Meanwhile, compressed sensing is employed to reduce the volume of front-end data, thereby improving the efficiency of data transmission. The main contributions of this paper are as follows:

1) A compressed sensing-based electricity consumption data compression and synchronous encryption algorithm is proposed. The algorithm effectively leverages the sparse characteristics of voltage and current waveform data, addressing the data overload problem caused by high-frequency sampling in residential electricity use. It enables the efficient and secure transmission of sensitive user data.

2) A joint random model for key generation and management is constructed based on a ternary Logistic-Tent chaotic system. Through coordination among three chaotic systems, the model parameters are automatically updated, diffused, and isolated, thereby defining a secure boundary for risk propagation. This greatly expands the key space and ensures the randomness of model parameters in the high-dimensional mapping space, thus guaranteeing the high security of data transmission.

2 Key generation of power consumption data measurement matrix based on compressed sensing framework

To solve the problem of massive data caused by high-frequency sampling of voltage and current recording data of power consumption information, and balance the security and efficiency of encryption algorithm, this paper proposes to use a compressed sensing framework to compress and synchronously encrypt power consumption data on the user side.

Compressed sensing is a technology that can project high dimensional signals x into low dimensional space y through measurement matrix Φ. High dimensional signal must be able to be converted into sparse signals α, and the observation matrix must meet the Restricted Isometry Property. The process of projection transformation can be mathematically expressed by Equation 1:

$\mathit{y}=\mathit{\Phi }\mathit{x}=\mathit{\Phi }\mathit{\Psi }\mathit{\alpha }(1)$

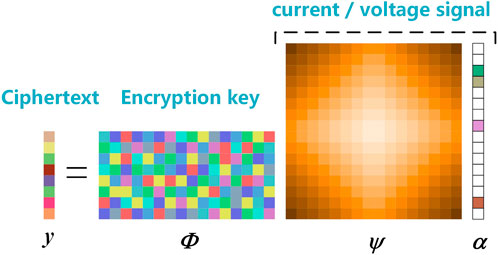
Using the measurement matrix Φ to observe the data sparse by the sparse basis Ψ, we can obtain the data after dimension reduction. If we treat the measurement matrix as a key to hide, we can encrypt the data.

It is proved in (Palczynska et al., 2020) that current and voltage recording data has sparsity under a DFT sparse basis. In the compressed sensing framework, we can use the measurement matrix Φ to observe the current and voltage recording signal x and obtain the observed value y. If we hide the measurement matrix Φ, we can regard the signal observation as signal encryption, and the observation value y can be regarded as ciphertext. If we need to decrypt the data, we still need the measurement matrix Φ. Therefore, compressed sensing can be regarded as a symmetric encryption algorithm. The power consumption information synchronous compression encryption process is shown in Figure 1.

Figure 1

Figure 1. Compression and encryption process of current/voltage recording signal.

The compressed sensing measurement matrix has a high selection space, which can increase the keyspace when used as a key. However, if the traditional deterministic measurement matrix is directly used as the key, there is still a risk of being decoded. Therefore, the power consumption information compression synchronous encryption scheme proposed in this paper uses the uncertainty measurement matrix as the key to ensure that each encryption is accompanied by a unique key.

From the above analysis, it can be seen that the measurement matrix Φ is the core of the compression synchronous encryption algorithm. If the current and voltage recording data is K sparse and the measurement matrix meets the RIP condition, the sparse coefficient can be accurately reconstructed from the observed value y. RIP condition definition is shown in Equation 2.

$\left(1-{\delta }_K\right){‖\alpha ‖}_2\le {‖\mathrm{\Phi }\alpha ‖}_2\le \left(1+{\delta }_K\right){‖\alpha ‖}_2(2)$

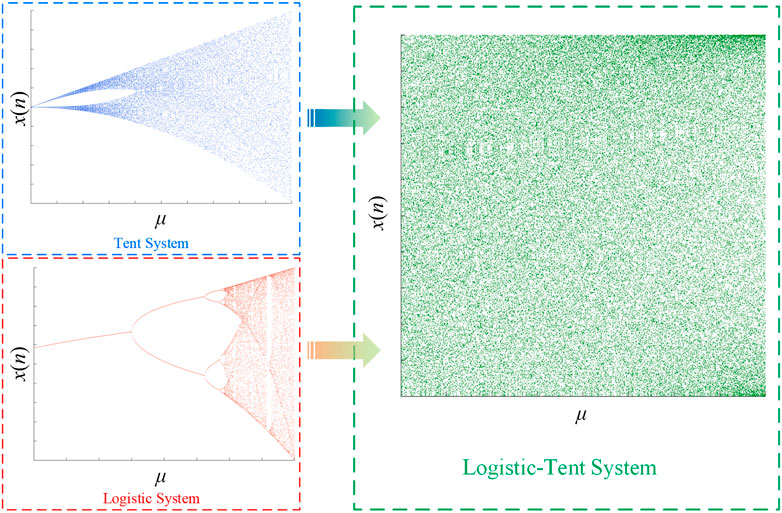
Research (Puthal et al., 2019) shows that the chaotic measurement matrix meets the RIP condition of compressed sensing and can be used for signal observation and reconstruction. Therefore, this paper selects the logistic tent chaotic system to generate the chaotic measurement matrix as the key to electricity consumption information of residents and enterprises encryption. Its mathematical model is shown in (3).

$x^{n+1}=\left\{\begin{array}{l}\begin{array}{l}\left[\mu x^n\left(1-x^n\right)+x^n\left(4-\mu \right)/2\right]\\ \mathrm{mod}1x^n<0.5\end{array}\\ \begin{array}{l}\left[\mu x^n\left(1-x^n\right)+\left(1-x^n\right)\left(4-\mu \right)/2\right]\\ \mathrm{mod}1x^n\ge 0.5\end{array}\end{array}\right.(3)$

where, the given initial value x⁰∈(0, 1) and control parameters μ∈(0,4). Logistic Tent chaotic system is a composite system of logistic and tent systems. With the control parameters μ The bifurcation diagram of its mapping is shown in Figure 2. It can be seen that the logistic tent chaotic system has a larger mapping space than the logistic or tent chaotic system. Therefore, using the logistic tent chaotic system to generate the uncertainty measurement matrix can not only realize its randomness by changing the control parameters and initial values but also further expand the security boundary of the key space and reduce the risk of key cracking.

Figure 2

Figure 2. Bifurcation diagram of Logistic-Tent chaotic system.

3 Compression and encryption of power consumption information based on a joint random model

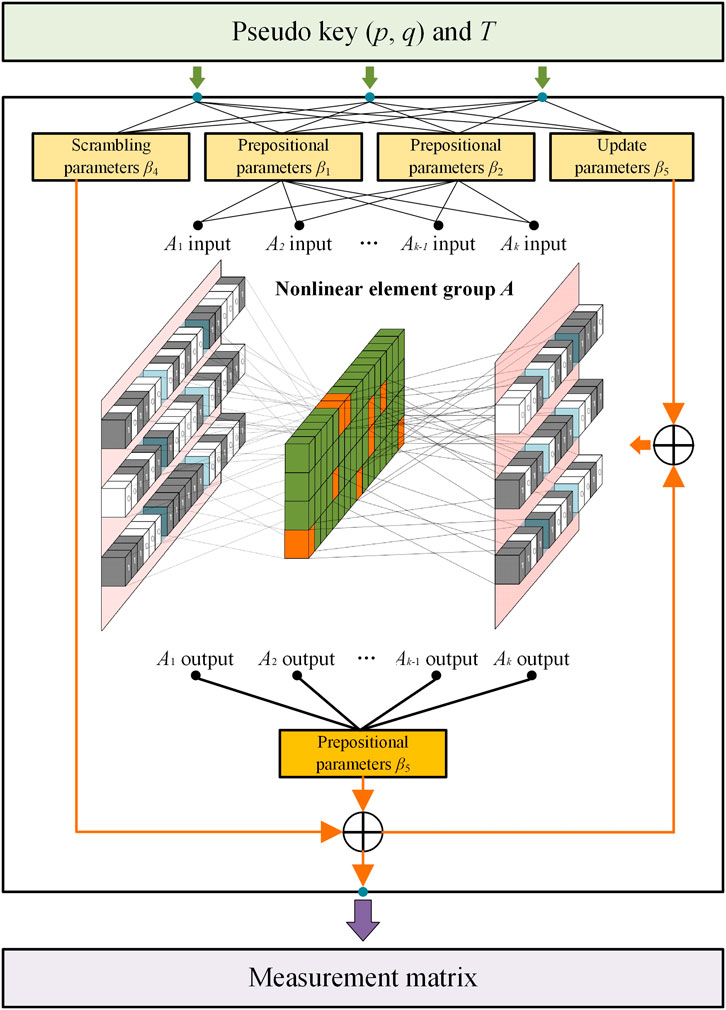
As mentioned above, based on the compressed sensing framework, this paper uses the logistic tent chaotic system to generate the uncertainty measurement matrix as the key to encrypt the user-side power consumption information, which improves security. The joint random model synchronous operation is realized at the compression sampling end and reconstruction end to avoid key transmission and reduce the key management cost and communication cost of the intelligent terminal. It also effectively eliminates the risk of leakage in the key transmission process and improves the confidentiality of the key. The working principle of the joint stochastic model is shown in Figure 3.

Figure 3

Figure 3. Working principle of a joint stochastic model.

3.1 Joint stochastic model initialization

Operation 1 (Logistic Tent chaotic sequence generation operation) For the given initial value x⁰ and control parameter μ, a Logistic Tent chaotic sequence l with length len is generated according to Equation 3, and the generation process is shown in Equation 4:

$l=LOGIS\left(x^0,\mu ,n=len\right)=\left\{x^1,x^2,x^3\cdots x^n\right\}(4)$

Operation 2 (nonlinear element group element generation operation) For the given initial value x⁰ and control parameter μ, an element sequence L with length d² is generated, and the L expression is shown in Equation 5:

$L=ELEMENT\left(x^0,\mu ,d^2\right)(5)$

ELEMENT (x⁰, μ, d²) is the element generation operation. The specific process is as follows:

ELEMENT (x⁰, μ, d²) is the generation operation of nonlinear element group elements. The specific process is as follows:

1) The state space of Logistic Tent chaotic system [0, 1] is equally divided into d² subspaces, which are expressed as [0, 1/d²), [1/d², 2/d²)…[(d²-1)/d², 1], and each interval is recorded as T_i, T_i = [(i-1)/d², i/d²], and the identifier L_i = i is defined.

2) Using the control parameter μ and according to the initial value x⁰, m-cycle iteration is carried out first to obtain L = LOGIS(x⁰, μ, n = m), to avoid the influence of the initial value, where m can be set according to the safety level. The higher the safety level, the greater the setting of m. Then select a new initial value of x⁰ = L [m], j = 1, Z = [](empty set).

3) Calculate x′ = LOGIS(x⁰, μ, n = 1), judge the situation of the subspace where x′ is located. If x′∈T_i, then y = L_i.

4) Judge whether j is greater than d². If it is greater than d², proceed to step 6, otherwise proceed to step 5.

5) y = (y mod d²) + 1, if y∈Z, then x⁰ = x′, return to step 3; Otherwise, Z [j] = y, j = j + 1, x⁰ = x′, return to step 3;

6) Let L = Z, then L is the sequence of elements, return L, and operation two ends.

Operation 3 (matrix filling operation) Through the element sequence L, a matrix A of size d × d is generated. The formation process is shown in Equation 6:

$\begin{array}{l}A=FILL\left(L,d,A\right)\\ \Rightarrow A\left[a\right]\left[b\right]=L\left[i\right]\\ \Rightarrow \left\{\begin{array}{l}\text{while\hspace{0.17em}}i\mathrm{mod}d\ne 0\langle \begin{array}{l}a=\left(i-i\mathrm{mod}d\right)/d+1\\ b=i\mathrm{mod}d\end{array}\\ \text{while\hspace{0.17em}}i\mathrm{mod}d=0\langle \begin{array}{l}a=i/d\\ b=d\end{array}\end{array}\right.\end{array}(6)$

Where A [a][b] is the element in row a and column b.

According to the above three operation definitions, the d × d nonlinear element groups A₁, A₂ … A_k can be initialized by the preset $x_1^0,x_2^0\dots x_k^0$ and the control parameters μ₁, μ₂ … μ_k according to Equation 7.

$A_k=FILL\left(ELEMENT\left(x_k^0,{\mu }_k,d^2\right),d,A_k\right)(7)$

The generated group is a nonlinear element, which can effectively resist differential analysis and linear cryptanalysis, and can effectively improve the robustness and security of constructing joint stochastic models.

3.2 Pseudo key pre parameter and mapping parameter generation

This section generates the pre parameters and mapping parameters of the pseudo key, realizes the dynamic update of the joint random model, and then completes the dynamic update of the measurement matrix to improve the security of the encryption algorithm.

On the intelligent terminal side, first calculate the Hash-256 value of the variable length string T, and define the operation process as h = HASH(T). Then, the string h is segmented to obtain H₁∼H₁₈ for subsequent parameter generation.

Perform bitwise operation on the split Hash-256 value H_i, and first obtain four 16-bit binary numbers B₁, B₂, B₃, B₄:

$B_i=BIN\left(H_i\right)(8)$

Shown as Equation 8, BIN(H_i) is an operation that converts the binary string H_i into a binary number.

Then the pre parameters β₁ and β₂ are obtained according to Equation 9.

$\left\{\begin{array}{l}{\beta }_1=\left[DEC\left(B_1\oplus B_2\oplus B_3\oplus B_4\right)+1\right]/65537\\ {\beta }_2=DEC\left(BIN\left(H_5^{\prime }\right)\right)+1\end{array}\right.(9)$

Where DEC(B_i) is the operation of converting the binary number B_i into a decimal number. $H_5^{\prime }$ is the (67-r)th to 66th place of H₅.

When the string T is randomly selected and the length is variable, the above operation ensures the pre parameter β₂ has random floating property, and the nonlinear element group generated from it has good anti-analysis performance.

Finally, according to β₂, (p, q) and equation ${\beta }_f=A_{{\beta }_2}\left[p\right]\left[q\right]/\left(d^2+1\right)$, we can calculate the mapping parameters of random frames.

Therefore, it can be seen that the pre parameters of the joint stochastic model β₁, β₂ and mapping parameters β_f are generated by Logistic-Tent chaotic system. Even if the transmitted pseudo key (p, q) is decoded, the pre parameters and mapping parameters will not be leaked, to ensure the high security of the real measurement matrix key.

The scrambling parameter β₄ is generated by Equation 10.

$\left\{\begin{array}{l}{\beta }_4^{\prime }=BIN\left(H_7\right)\oplus BIN\left(H_8\right)\oplus \\ BIN\left(H_9\right)\oplus BIN\left(H_{10}\right)\\ {\beta }_4=\left(e^{\left[DEC\left({{\beta }^{\prime }}_4\right)+1\right]/65537}-1\right)/\left(e-1\right)\end{array}\right.(10)$

3.3 Dynamic update of a joint stochastic model

The nonlinear mapping feature based on a logistic tent chaotic system improves the ability of the encryption algorithm to resist chosen plaintext attack (CPA) and known-plaintext attack (KPA). However, if a large number of plaintext-ciphertext pairs are leaked, it is still possible to analyze and decode, which will inevitably affect the confidentiality of the real key. To reduce the probability of being decoded, this paper introduces the third logistic tent chaotic system into the model for the dynamic update of the joint random model, that is, when the power consumption information is encrypted every time, the chaotic system is used to update the nonlinear element group immediately, maintain the dynamic change, and give the key timeliness at the same time.

This process is as follows: first, generate the scrambling parameter β₄ through Equation 10, then calculate and update parameter β₅ according to Equation 11.

$\left\{\begin{array}{l}{\beta }_{5x}=BIN\left(H_{11}\right)\oplus BIN\left(H_{13}\right)\oplus BIN\left(H_{15}\right)\oplus BIN\left(H_{17}\right)\\ {\beta }_{5y}=BIN\left(H_{12}\right)\oplus BIN\left(H_{14}\right)\oplus BIN\left(H_{16}\right)\oplus BIN\left(H_{18}\right)\\ {\beta }_5^{\prime }=DEC\left({\beta }_{5x}\right)\times DEC\left({\beta }_{5y}\right)\\ {\beta }_5=l_{Per}\left[{\beta }_5^{\prime }\right]/65537\end{array}\right.(11)$

After obtaining the updated parameter β₅, a new element group based on the Bernoulli matrix is generated by using the scrambling parameter β₄ and the control parameters μ_S and μ_Per, and the existing β 2-th element group is replaced and updated. The specific process is shown in Equations 12, 13.

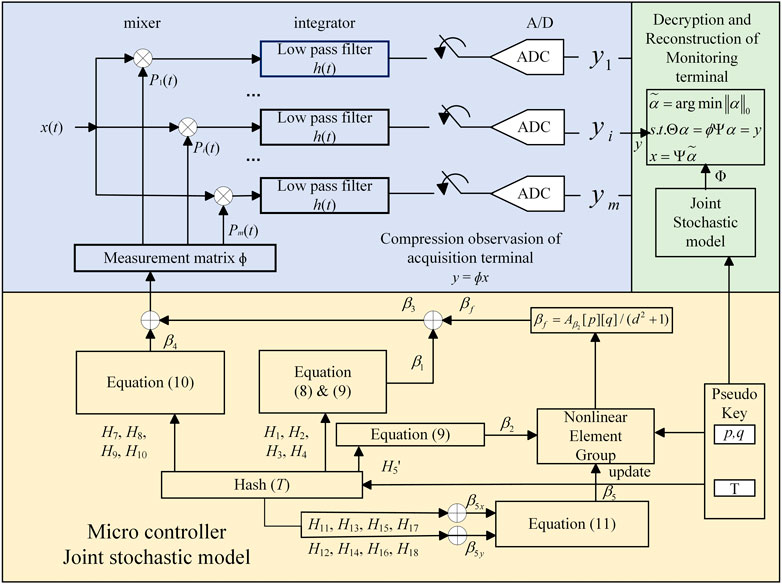
The local update strategy used in this paper can maintain the dynamic change of the element group while minimizing the computational overhead. Confusion of nonlinear element group by the Bernoulli matrix can improve the confidentiality. Figure 4 shows the hardware implementation structure of compression synchronous encryption.

$\left\{\begin{array}{l}{l}_A^{\prime }=INDEX\left(LOGIS\left({\beta }_4,{\mu }_{Per},n=d^2\right)\right)\\ l_A=\left\{\begin{array}{l}{l}_A^{\prime }\left[i\right]\mathrm{mod}2=1\Rightarrow l_A\left[i\right]=1\\ l_A^{\prime }\left[i\right]\mathrm{mod}2=0\Rightarrow l_A\left[i\right]=-1\end{array}\right.\end{array}\right.(12)$

$\left\{\begin{array}{l}{L}_A^{\prime }=ELEMENT\left({\beta }_5,{\mu }_A,d^2\right)\\ L_A=INDEX\left(L_A^{\prime }\otimes l_A\right)\\ A_{{\beta }_2}=A\prime =FILL\left(L_A,d,A\prime \right)\end{array}\right.(13)$

Figure 4

Figure 4. Hardware implementation of compression synchronization encryption.

4 Synchronous decryption of power consumption information reconstruction

The compressed sensing synchronous encryption proposed in this paper is essentially a symmetric encryption algorithm, but this algorithm is different from the traditional symmetric encryption algorithm. This algorithm deploys the same joint random model at the compression sampling terminal and the reconstruction terminal, and only performs a single exchange of pseudo keys. The reconstruction end can complete the reconstruction of the key under the dynamic synchronization of the joint random model, and then decrypt and recover the original signal through the reconstruction algorithm at the same time.

After receiving the pseudo key (p, q) and T, the reconstruction end regenerates β₁, β₂, β₃, β₄, β₅, β_f in the way of sections 2.1∼2.4. Then, the measurement matrix Φ′ is reconstructed according to Equation 14.

$\left\{\begin{array}{l}{l}_{Per}^{\prime }=INDEX\left(LOGIS\left({\beta }_4,{\mu }_{Per},n=M\times N\right)\right)\\ L_{Per}^{\prime }=\left\{\begin{array}{l}{l}_{Per}^{\prime }\left[i\right]\mathrm{mod}2=1\Rightarrow L_{Per}^{\prime }\left[i\right]=1\\ l_{Per}^{\prime }\left[i\right]\mathrm{mod}2=0\Rightarrow L_{Per}^{\prime }\left[i\right]=-1\end{array}\right.\\ l_{\mathrm{\Phi }}^{\prime }=LOGIS\left({\beta }_3,{\mu }_{\mathrm{\Phi }},n=M\times N\right)\\ {\mathrm{\Phi }}^{\prime }=FILL\left(l_{\mathrm{\Phi }}^{\prime }\otimes L_{Per}^{\prime },N,{\mathrm{\Phi }}^{\prime }\right)\end{array}\right.(14)$

After the reconstruction of the observation matrix Φ′ is completed, the terminal can reconstruct the original signal using the encrypted data y and the sparse basis Ψ sent by the sampling end according to Equation 15.

$\stackrel{\sim }{\alpha }=\arg \min {‖\alpha ‖}_0\mathrm{s}.\mathrm{t}y={\mathrm{\Phi }}^{\prime }\mathrm{\Psi }\alpha (15)$

The aforementioned expression necessitates exhaustive exploration of all potential outcomes to minimize the l₀ norm, a task known to be NP-hard. Nonetheless, given that the measurement matrix Φ′ satisfies the Restricted Isometry Property (RIP), Equation 15 can be reformulated into an equivalent convex optimization problem based on the l₁ norm, as demonstrated in Equation 16.

$\stackrel{\sim }{\alpha }=\arg \min {‖\alpha ‖}_1\mathrm{s}.\mathrm{t}y={\mathrm{\Phi }}^{\prime }\mathrm{\Psi }\alpha (16)$

Multiple algorithms exist for solving sparse coefficients. In this paper, the generalized orthogonal matching pursuit (gOMP) algorithm is used for this purpose. Following the derivation of the optimal solution of sparse coefficients using Equation 16, the inverse transformation $x^{\prime }=\mathrm{\Psi }\stackrel{\sim }{\alpha }$ is carried out to retrieve the decrypted current and voltage recording data.

Furthermore, the comprehensive encryption and decryption process of the synchronous encryption algorithm, tailored for compressing electricity consumption information of both residents and enterprises, is depicted in Figure 5.

Figure 5

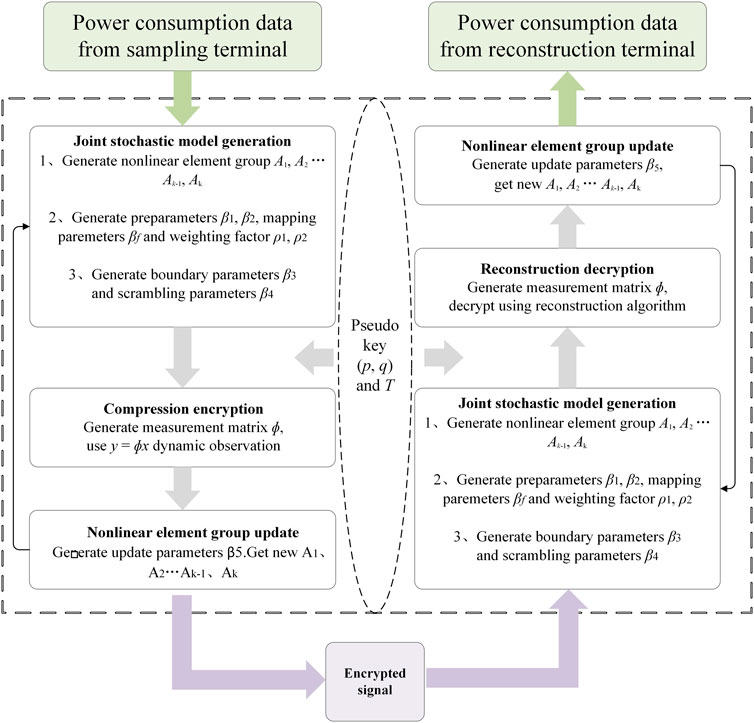
Figure 5. Power consumption information compression synchronous encryption and decryption algorithm flow.

5 Results and discussion

This section takes the PLAID household electricity data set as an example and analyzes and verifies the performance of the algorithm from four aspects: the feasibility of the electricity information compression synchronous encryption algorithm based on the compressed sensing framework, the key sensitivity, the encryption and decryption efficiency, and the anti-invasive analysis of the compressed and encrypted electricity data. The PLAID data set contains the current and voltage measurements of 11 different electrical appliances in more than 60 households in Pittsburgh, Pennsylvania, United States. The sampling frequency during data collection is 30 kHz, including a total of 1074 groups of samples. The simulation was conducted on a computer equipped with an Intel Core i7-13700KF processor, 12GB of RAM, and an NVIDIA RTX 4090 graphics card, running the Ubuntu 22.04.3 LTS operating system.

5.1 Algorithm feasibility

The operational dynamics and state transitions of various electrical devices on the user side often manifest substantial fluctuations and diverse current change patterns, while corresponding voltage fluctuations typically exhibit limited amplitude and a singular mode of change. Consequently, a comprehensive analysis of current recording data allows for the extraction of intricate and detailed power privacy information. To assess the practical viability of the proposed algorithm, this section leverages the PLAID dataset. Specifically, three distinctive current fluctuations associated with different electrical equipment—namely, current attenuation, current distortion, and current mutation—are selected. The reconstruction is performed using the g-OMP algorithm, and a comparative analysis is conducted with other algorithms integrated within the compressed sensing framework. These algorithms encompass the encryption algorithm based on the Bernoulli matrix (BM-CSE), the encryption algorithm based on a sparse random matrix (SRM-CSE), the encryption algorithm based on the partial Hadamard matrix (PHM-CSE), and the encryption algorithm based on Gaussian matrix (GM-CSE).

Firstly, the experimental evaluation focuses on the encryption and decryption of current fluctuation data under various scenarios with a compression ratio (CR) set at 0.3. The compression ratio (CR), a pivotal parameter indicating the extent of data compression, is defined in Equation 17. The assessment provides insights into the algorithm’s performance across diverse operational conditions, contributing to a thorough understanding of its applicability and effectiveness in real-world deployment scenarios.

$CR=y/x(17)$

Where y represents the length of the signal observation value, x represents the length of the original signal, and the reconstruction result is shown in Figure 6.

Figure 6

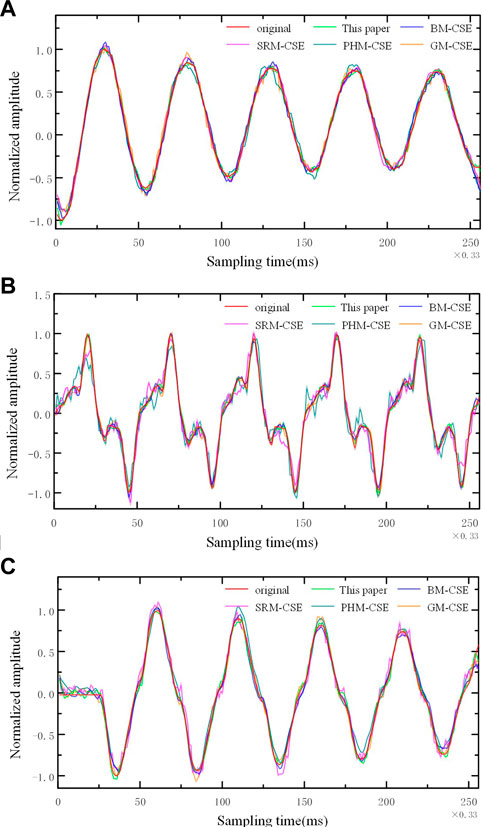
Figure 6. Comparison of reconstruction effects of different algorithms. (A) Current attenuation signal. (B) Current distortion signal. (C) Current mutation signal.

According to the results in Figure 6, when CR = 0.3, the reconstruction effect of this algorithm for the three current fluctuation signals is better than the other four comparison algorithms, and the decrypted waveform is consistent with the original signal. After normalizing the current, the mean square error of the decryption result of the current attenuation signal in this algorithm is MSE = 2.25 × 10⁻³, mean square error of decryption result of current distortion signal MSE = 1.53 × 10⁻³, mean square error of decryption result of current mutation signal MSE = 1.86 × 10⁻³, which ensures that the signal will not be distorted after compression sampling encryption and reconstruction decryption.

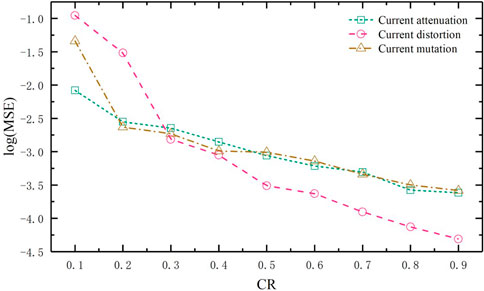
Furthermore, Figure 7 shows the MSE of the original signal and the reconstructed decrypted signal under different compression ratios after data normalization.

Figure 7

Figure 7. Signal decryption effect under different CR.

According to the experimental results, it is observed that as the depth of compression increases, i.e., the compression ratio (CR) decreases, the Mean Squared Error (MSE) gradually increases. Even with a depth compression scenario where CR = 0.3, the average deviation range of the current disturbance signal is only 2.7%.

When the compression ratio exceeds 0.5, the average deviation of the current disturbance signal is below 1%. The error still falls within the 5% error range specified by the Chinese national standard GB/T 19862-2016 “General Requirements for Power Quality Monitoring Equipment” (GB/T 19862, 2016), which adequately meets the accuracy requirements of non-invasive real-time monitoring data for residents and enterprises.

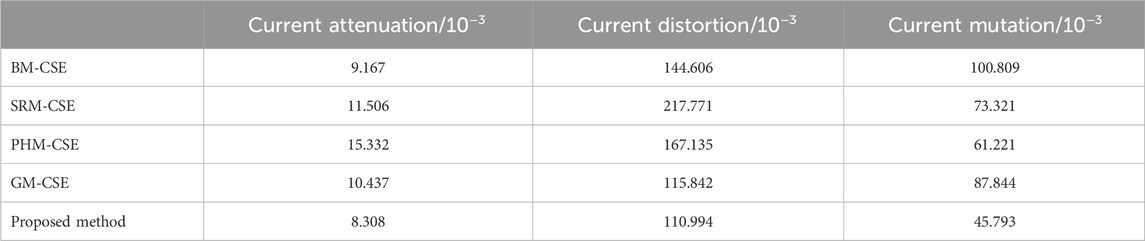
Simultaneously, to compare the comprehensive performance of the proposed algorithm, three types of current fluctuation signals are still selected. The performance differences of the proposed algorithm in compression, synchronous encryption, and reconstruction decryption processes are compared with other encryption algorithms using BM-CSE, SRM-CSE, PHM-CSE, and GM-CSE algorithms under different compression ratios. Table 1 presents the decryption accuracy of different algorithms at CR = 0.1.

Table 1

Table 1. The reconstruction effect of this scheme is compared with other schemes.

From the experimental results, it is evident that compared to the BM-CSE, SRM-CSE, PHM-CSE, and GM-CSE algorithms, the proposed algorithm demonstrates superior decryption accuracy for the three different signals. Under the condition of limited signal observation values, the decryption error of this algorithm can be reduced by up to 54.5% compared to other algorithms, making it particularly suitable for deployment in resource-constrained scenarios.

5.2 Comparison of reconstruction results

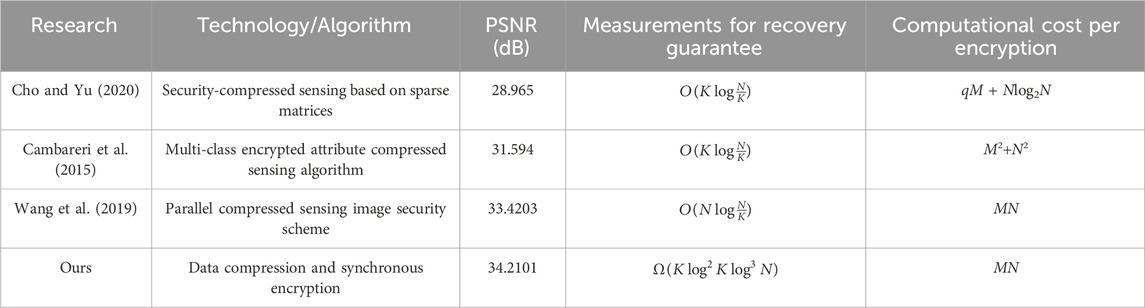
To clarify the research contributions and technological innovations of this paper, several mainstream power data encryption techniques in the current field, along with their limitations, are compared. As shown in Table 2, although these techniques each have advantages in data security, they fall short in terms of data reconstruction performance, resource efficiency, and computational complexity. The proposed solution in this paper integrates compressed sensing and chaotic systems, aiming to overcome these limitations and provide a novel approach to power data processing that is both secure and achieves a high data reconstruction rate. Two commonly used comparative metrics in these fields are first defined:

Table 2

Table 2. Comparison of existing related algorithms.

The Peak Signal-to-Noise Ratio (PSNR) is a commonly used metric for assessing the quality of image and signal reconstruction. It is defined based on the Mean Squared Error (MSE, defined by Equation 18) between the original signal x and the reconstructed signal $\widehat{x}$.

$\text{MSE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(x\left[i\right]-\widehat{x}\left[i\right]\right)}^2(18)$

Here, n is the length of the signal, and x [i] and $\widehat{x}\left[i\right]$ represent the values of the original signal and the reconstructed signal at position i, respectively. The PSNR is defined by Equation 19:

$\text{PSNR}=10\cdot {\log }_{10}\left(\frac{{\mathrm{MAX}}_x^2}{\text{MSE}}\right)(19)$

Here, MAX_x is the maximum value of the original signal, which is normalized to the range [0, 1], with MAX_x = 1. A higher PSNR indicates smaller error and better quality of signal reconstruction.

In this context, M represents the number of rows in the measurement matrix, N denotes the dimensionality of the signal, K indicates the sparsity of the signal, and q refers to the number of non-zero elements in each row of the measurement matrix for the corresponding algorithm.

5.3 Comparison of reconstruction accuracy and efficiency of different algorithms

Reconstruction algorithms are crucial to ensuring the accurate reconstruction of compressed sensing observation data. Currently, reconstruction algorithms are mainly divided into greedy algorithms and convex optimization algorithms. Compared to greedy algorithms, convex optimization algorithms have higher computational complexity and lower time efficiency, making them challenging to apply in NILM (Non-Intrusive Load Monitoring) scenarios, which require real-time data processing. Due to their good accuracy and efficiency, greedy algorithms have become the preferred choice for compressed sensing reconstruction in NILM contexts. However, there are many types of greedy algorithms, each with certain differences. The characteristics of common greedy algorithms are summarized below:

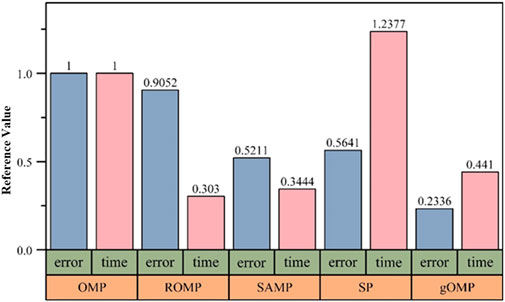
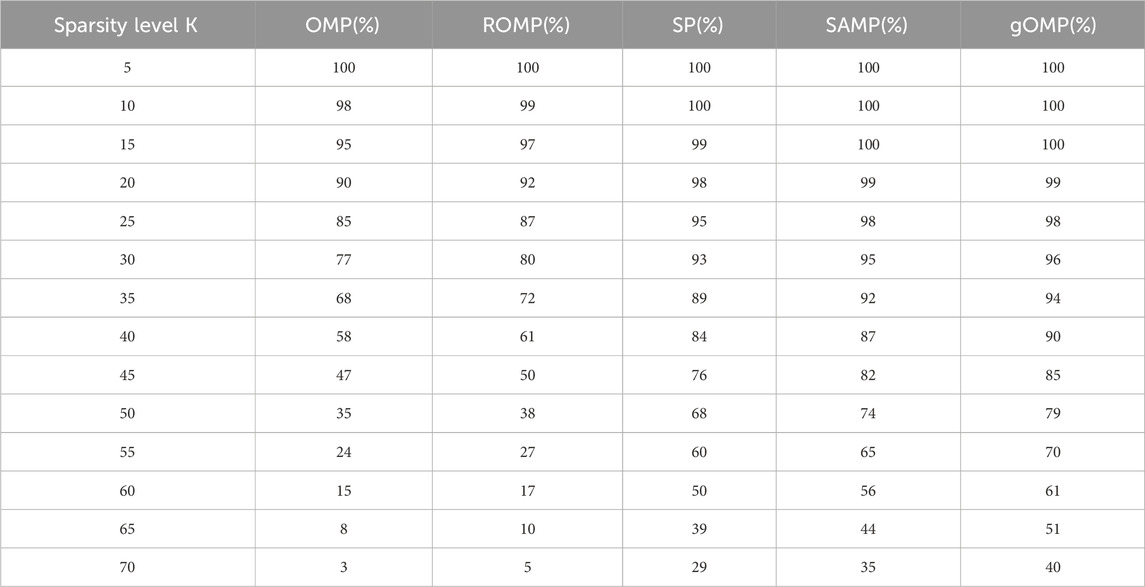
Reconstruction accuracy and execution efficiency are two key factors that must be considered in reconstruction algorithms. Therefore, in this paper, voltage, current, and power signals are used as examples. Multiple sets of controls are established, where the same observation matrix, sparse basis, and compression ratio (Compression Ratio, CR) are applied to test the reconstruction algorithms shown in Table 3. The compression ratio is a parameter that represents the degree of data compression, and is defined as: CR = y/x, where y represents the length of the signal observation vector, and x represents the length of the original signal. Based on the tests, the average reconstruction error (error) and execution time (time) for each reconstruction algorithm are obtained. Using the error and time values of the OMP algorithm as reference, the error and time values of the other algorithms are calculated for comparison, as shown in Figure 8.

Table 3

Table 3. Comparison of common greedy algorithms.

Figure 8

Figure 8. Comparison of reconstruction accuracy and efficiency of different algorithms.

As shown in the Figure 8 and Table 4, compared to the OMP algorithm, the ROMP, SAMP, and gOMP algorithms show improvements in both execution time and reconstruction accuracy. Although the execution efficiency of the gOMP algorithm is slightly lower than that of the SAMP algorithm, its reconstruction accuracy is much higher. Additionally, the SAMP algorithm requires a more sophisticated sparse optimization strategy to handle the complex and variable monitoring conditions, whereas the gOMP algorithm does not face this issue. Therefore, in this paper, the gOMP algorithm is chosen as the reconstruction algorithm for compressed observations of NILM real-time monitoring data.

Table 4

Table 4. Performance of different algorithms at different sparsity levels.

In this study, the Generalized Orthogonal Matching Pursuit (gOMP) algorithm is used for signal reconstruction. A performance comparison is made with several other algorithms. If the residual between the recovered signal $\widehat{x}$ and the original signal x is less than 1e-6, the reconstruction is considered successful.

The OMP algorithm shows a rapid decline in performance, indicating that as sparsity increases, its recovery success rate quickly decreases. ROMP performs similarly to OMP, but slightly better. SP outperforms both OMP and ROMP, maintaining relatively high performance even at moderate sparsity levels. The SAMP algorithm demonstrates a higher recovery success rate, maintaining good recovery performance even at higher sparsity levels. gOMP performs the best, maintaining a high recovery success rate even with high sparsity. This suggests that the gOMP algorithm has a significant advantage in handling highly sparse signals.

5.4 Key sensitivity analysis

A robust encryption algorithm should exhibit high sensitivity to the encryption key to thwart malicious decryption attempts using similar keys. In this paper, the proposed algorithm leverages a pseudo key and a chaotic system to establish a joint random model for generating the authentic key. The chaotic system, known for its strong sensitivity to initial values, ensures that even minor alterations in the pseudo key and key parameters result in propagated differences within the measurement matrix. This leads to amplification, ultimately yielding a completely distinct key and consequent decryption failure.

To assess the key sensitivity of the algorithm, three representative current fluctuation signals from the plaid power dataset are utilized. Specifically, when the compression ratio (CR) is set to 0.5, the data undergoes encryption, followed by decryption using both the original key and a tampered key with a single-bit modification. The experimental outcomes are illustrated in Figure 9.

Figure 9

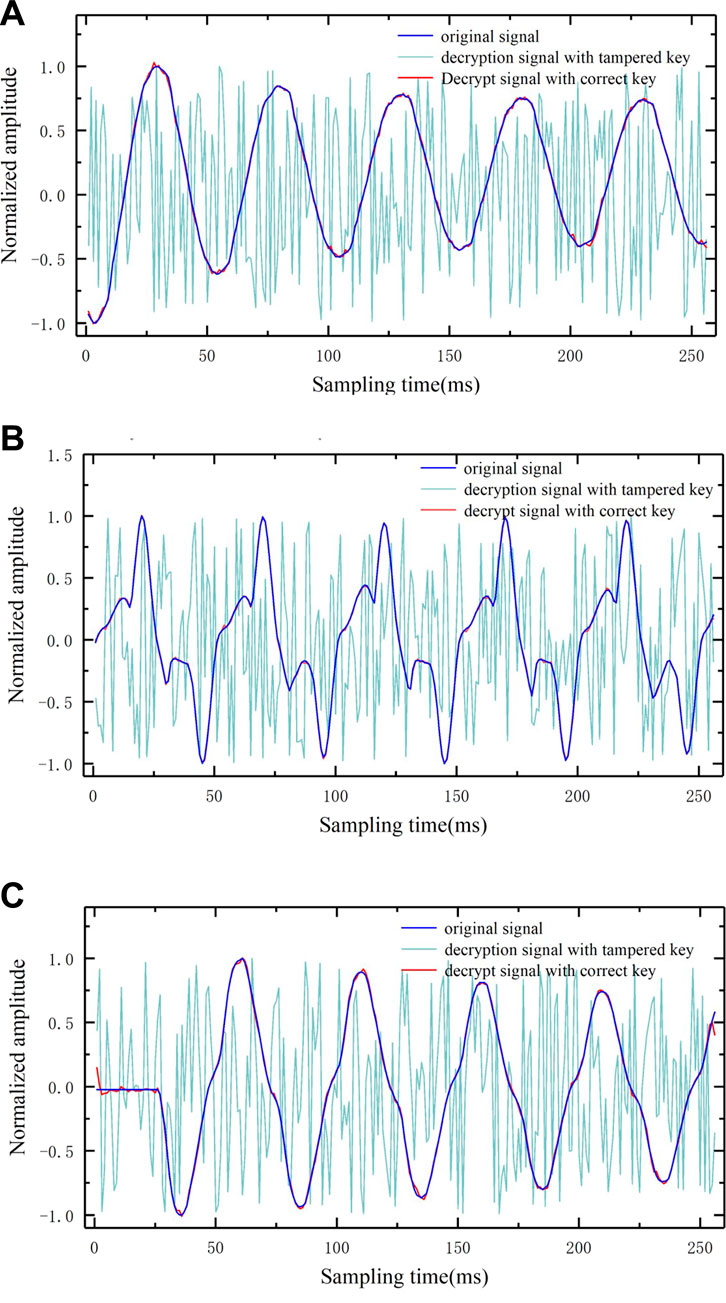
Figure 9. Comparison diagram before and after signal decryption. (A) Current attenuation signal. (B) Current distortion signal. (C) Current mutation signal.

It can be seen from Figure 9 that even if only 1 bit of the key is changed, the decrypted signal will become a noise signal, and its MSE reaches 0.61. It is completely impossible to obtain any useful information about the original signal, which verifies that the algorithm in this paper has high key sensitivity.

5.5 Encryption efficiency

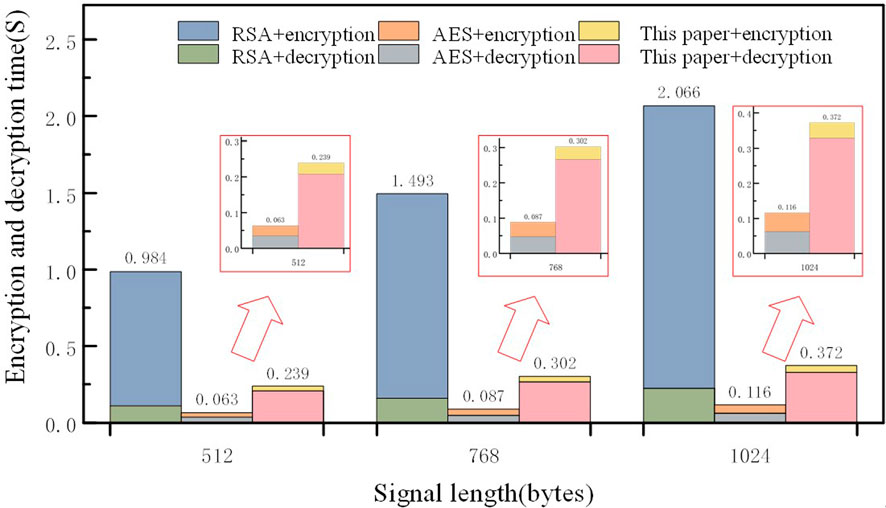
Effectiveness is another important requirement for non-invasive load monitoring of power consumption information, so the efficiency of the algorithm needs to be considered when compressing and encrypting data. Select current and voltage recording data of different lengths here, test the time required to complete one encryption and decryption when CR = 0.5, and compare it with RSA and AES encryption algorithms. The results are shown in Figure 10.

Figure 10

Figure 10. Comparison of encryption efficiency of different encryption algorithms.

As depicted in Figure 10, the encryption and decryption time required by the proposed algorithm for a given signal falls between that of the RSA and AES algorithms. Notably, compared to the RSA algorithm, the proposed algorithm achieves a maximum time reduction of 81.99%. Despite exhibiting slightly longer encryption and decryption durations compared to the AES algorithm, the proposed algorithm compensates by offering enhanced key space and heightened confidentiality, with only a marginal increase in time overhead. Moreover, as signal length increases linearly, the encryption and decryption time of the proposed algorithm experiences only modest growth. In contrast, the encryption and decryption time of the RSA and AES algorithms demonstrates a direct correlation with signal length. For instance, when transitioning from a signal length of 512 bytes–1024 bytes, the encryption and decryption time of the proposed algorithm increases by 55.65%, whereas the corresponding increases for RSA and AES algorithms are 110% and 84.13%, respectively. This divergence arises from the fixed length of data encrypted by RSA and AES, thereby making their encryption and decryption times contingent upon the number of encryptions performed. Conversely, the variable data length encrypted by the proposed algorithm results in the majority of time consumption being attributed to the reconstruction phase, a process less susceptible to fluctuations in the data length.

A detailed examination of the experimental outcomes presented in Figure 10 reveals noteworthy insights that the symmetric encryption algorithm AES exhibits equivalent encryption and decryption times, while the asymmetric encryption algorithm RSA predominantly allocates time during the encryption stage. In contrast, the compression encryption time of the algorithm proposed in this paper significantly surpasses the reconstruction decryption time. Specifically, when the signal length is 1024 bytes, the encryption time constitutes merely 13.41% of the decryption time. This algorithm demonstrates an asymmetric demand for encryption and decryption computing resources, rendering it particularly well-suited for the intricate operational conditions of power grid systems. To enhance operational efficiency, the field side implements a streamlined approach by employing a lightweight acquisition device coupled with a potent server endowed with robust computing capabilities. This strategic choice aligns with the algorithm’s resource utilization patterns, accommodating the distinct computational demands associated with encryption and decryption processes, as opposed to the more uniform resource requirements of traditional RSA and AES algorithms.

6 Conclusion

Aiming at the actual demand of load identification in the new power system source load interaction, this paper introduces a novel algorithm for compressing and encrypting data, tailored for the high-frequency acquisition of voltage and current data about residential and enterprise power consumption. This algorithm is designed to operate efficiently within the constraints of limited terminal resources while safeguarding data confidentiality. The proposed approach seamlessly integrates principles from compressed sensing and chaotic encryption techniques. Leveraging the logistic tent chaotic system and nonlinear element group, it establishes a coherent random model to generate a chaotic measurement matrix. By ensuring compressed sampling, the algorithm significantly expands the key space, thereby enhancing resistance against differential analysis. Moreover, a synchronized operation is implemented between the sending and receiving ends of data compression sampling, utilizing a joint random model. This facilitates the transmission of pseudo keys exclusively, mitigating the risk of real key leakage and thereby enhancing the confidentiality of the keys and the overall security of residential electricity data. Empirical validation using real-world data from the PLAID household electricity dataset demonstrates the heightened sensitivity of the proposed algorithm to cryptographic attacks such as CPA and KPA. Furthermore, the algorithm exhibits favorable feasibility and resistance against illicit analysis. In comparison to the RSA algorithm, this approach demonstrates superior efficiency in encryption and decryption processes, characterized by significant computational asymmetry. This attribute renders it particularly suitable for scenarios characterized by limited computational capacity at the front-end terminal and robust service computing architectures at the back-end master station, as encountered in wide-area non-invasive load monitoring applications. Therefore, this algorithm can well meet the security and real-time requirements of data in the new power system environment, and ensure the privacy and security of power users.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/jingkungao/PLAID.

Author contributions

RZ: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing. JL: Writing–original draft, Writing–review and editing. ZY: Writing–original draft, Writing–review and editing. KZ: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors RZ, JL, ZY, and KZ were employed by Guangdong Grid Co.

The authors declare that this study received funding from China Southern Power Grid Corporation under Grant (GDKJXM20210063). The funder had the following involvement in the study: study design, data collection and analysis, decision to publish, and preparation of the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Kadhim, H. M., and Al-Raweshidy, H. S. (2021). Energy efficient data compression in cloud based IoT. IEEE Sens. J. 21 (10), 12212–12219. doi:10.1109/jsen.2021.3064611

CrossRef Full Text | Google Scholar

Alsuwaiedi, H. K. A., and Alsuwaiedi, A. M. S. (2023). A new modified DES algorithm based on the development of binary encryption functions. J. King Saud. Univ.-Comput. Inf. Sci. 35 (8), 101716. doi:10.1016/j.jksuci.2023.101716

CrossRef Full Text | Google Scholar

Ashraf, S., Shawon, M. H., Khalid, H. M., and Muyeen, S. M. (2021). Denial-of-Service attack on IEC 61850-based substation automation system: a crucial cyber threat towards smart substation pathways. Sensors 21 (19), 6415. doi:10.3390/s21196415

PubMed Abstract | CrossRef Full Text | Google Scholar

Cambareri, V., Mangia, M., Pareschi, F., Rovatti, R., and Setti, G. (2015). Low-complexity multiclass encryption by compressed sensing. IEEE Trans. Signal Process. 63 (9), 1–2195, May 1. doi:10.1109/tsp.2015.2407315

CrossRef Full Text | Google Scholar

Cho, W., and Yu, N. Y. (2020). Secure and efficient compressed sensing-based encryption with sparse matrices. IEEE Trans. Inf. Forensic Secur. 15, 1999–2011. doi:10.1109/tifs.2019.2953383

CrossRef Full Text | Google Scholar

Ding, Y., Wang, B. Y., Wang, Y. J., Zhang, K., and Wang, H. Y. (2020). Secure metering data aggregation with batch verification in industrial smart grid. IEEE Trans. Ind. Inf. 16 (10), 6607–6616. doi:10.1109/tii.2020.2965578

CrossRef Full Text | Google Scholar

GB/T 19862-2016 General requirements for power quality monitoring equipment, GB/T 19862-2016, 2016.

Google Scholar

Hasan, M. K., Habib, A. A., Shukur, Z., Ibrahim, F., Islam, S., and Razzaque, M. A. (2023). Review on cyber-physical and cyber-security system in smart grid: standards, protocols, constraints, and recommendations. J. Netw. Comput. Appl. 209 (Jan), 103540. doi:10.1016/j.jnca.2022.103540

CrossRef Full Text | Google Scholar

Inayat, U., Zia, M. F., Mahmood, S., Khalid, H. M., and Benbouzid, M. (2022). Learning-based methods for cyber attacks detection in IoT systems: a survey on methods, analysis, and future prospects. Electronics 11 (9), 1502. doi:10.3390/electronics11091502

CrossRef Full Text | Google Scholar

Khalid, H. M., Flitti, F., Mahmoud, M. S., Hamdan, M. M., Muyeen, S. M., and Dong, Z. Y. (2023). Wide area monitoring system operations in modern power grids: a median regression function-based state estimation approach towards cyber attacks. Sustain. Energy Grids Netw. 34 (Jun), 101009. doi:10.1016/j.segan.2023.101009

CrossRef Full Text | Google Scholar

Mahmoud, M. S., Khalid, H. M., and Hamdan, M. M. (2021). Cyberphysical infrastructures in power systems: architectures and vulnerabilities[M]. Academic Press.

Google Scholar

Meng, S. P., Li, C. D., Peng, W., and Tian, C. L. (2023). Empirical mode decomposition-based multi-scale spectral graph convolution network for abnormal electricity consumption detection. Neural comput. Appl. 35 (13), 9865–9881. doi:10.1007/s00521-023-08222-8

CrossRef Full Text | Google Scholar

Moon, J., Lee, S. H., Lee, H., and Lee, I. (2019). Proactive eavesdropping with jamming and eavesdropping mode selection. IEEE Trans. Wirel. Commun. 18 (7), 3726–3738. doi:10.1109/twc.2019.2918452

CrossRef Full Text | Google Scholar

Okeyinka, A. E. (2015). “Computational speeds analysis of RSA and ElGamal algorithms on text data,” in Proceedings of the World Congress on Engineering and Computer Science I, 115–118. (WCECS 2015).

Google Scholar

Palczynska, B., Masnicki, R., and Mindykowski, J. (2020). Compressive sensing approach to harmonics detection in the ship electrical network. Sensors 20 (9), 2744. doi:10.3390/s20092744

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, B., Pan, Z., Yu, T., Qiu, X., Su, X., and Chen, Z. (2022). Graph data modeling and graph representation learning methods and their application in non-intrusive load monitoring problem. Proc. CSEE 42 (47), 6260–6273.

Google Scholar

Puthal, D., Wu, X. D., Surya, N., Ranjan, R., and Chen, J. J. (2019). SEEN: a selective encryption method to ensure confidentiality for big sensing data streams. IEEE Trans. Big Data 5 (3), 379–392. doi:10.1109/tbdata.2017.2702172

CrossRef Full Text | Google Scholar

Rafique, Z., Khalid, H. M., and Muyeen, S. M. (2020). Communication systems in distributed generation: a bibliographical review and frameworks. IEEE Access 8, 207226–207239. doi:10.1109/access.2020.3037196

CrossRef Full Text | Google Scholar

Schirmer, P. A., and Mporas, I. (2023). Non-Intrusive load monitoring: a review. IEEE Trans. Smart Grid 14 (11), 769–784. doi:10.1109/tsg.2022.3189598

CrossRef Full Text | Google Scholar

Wang, H., Xiao, D., Li, M., Xiang, Y. P., and Li, X. Y. (2019). A visually secure image encryption scheme based on parallel compressive sensing. Signal process. 155, 218–232. doi:10.1016/j.sigpro.2018.10.001

CrossRef Full Text | Google Scholar

Wang, H. X., Zhang, J. S., Lu, C. B., and Wu, C. Y. (2021). Privacy preserving in non-intrusive load monitoring: a differential privacy perspective. IEEE Trans. Smart Grid 12 (3), 2529–2543. doi:10.1109/tsg.2020.3038757

CrossRef Full Text | Google Scholar

Zhai, F., Yang, T., Zhao, B., and Chen, H. (2022). Privacy-preserving outsourcing algorithms for multidimensional data encryption in smart grids. Sensors 22 (12), 4365. doi:10.3390/s22124365

PubMed Abstract | CrossRef Full Text | Google Scholar