Performance assessment of subsea safety systems subject to heterogeneous failure modes and repair delays

Subsea production systems operate in harsh and hostile environments, making them subject to degradation that leads to failure. This is also the case for the final elements of safety-instrumented systems (SISs) that are installed to protect subsea production systems. As a result, the classic SIS performance assessment methods that assume constant failure rates may not be realistic for subsea elements, which may experience both random failures and natural degradation. The location of subsea production also provides challenges for accessing the system to perform repair, and this often results in delays before repair following revealed failures. In this paper, we explore all these issues by developing formulations that incorporate degradation and random failures as well as repair delays to assess the performance of the system. The degradation of the system is modeled with the Weibull distribution, while an exponential distribution is used to model the random failures. The impacts of different maintenance strategies on safety are also explored with case studies.

1 Introduction

Technical safety barriers have been widely used in different industries, such as oil and gas, nuclear, and chemical engineering sectors, to ensure safe operation, maximize production, and limit downtime. Popular among these are the safety-instrumented systems (SIS). An SIS is an independent protection layer installed to mitigate the risk associated with a specified hazard (Rausand, 2004). An SIS typically consists of one or more sensor(s), a logic solver, and one or more final element(s) (IEC 61511:2016). SISs are designed to detect the onset of hazardous situations and to act to prevent their occurrence or mitigate their consequences. The sensors monitor a process variable (e.g., flow pressure or temperature) and relay the measurement to a logic solver, which compares the measurement against a preset value. In a situation where there is a deviation, the logic solver will send a signal to activate the final element, such as cutting off flow in the case of a shutdown valve in a pipeline.

The use of SISs is heavily regulated due to its criticality to safety. Standards such as IEC61508 (IEC 61508:2010) and IEC61511 (IEC 61511:2016) govern the design, installation, and operation of such systems. To comply with the requirements of the standards, it is important to demonstrate by quantitative analysis that the performance of the system meets the minimum required level in terms of acceptable risk. The performance measure recommended by the International Electrotechnical Commission (IEC) standards is the average probability of failure on demand $({\mathrm{P}\mathrm{F}\mathrm{D}}_{\text{avg}})$ (IEC 61508:2010; IEC 61511:2016). The ${\mathrm{P}\mathrm{F}\mathrm{D}}_{\text{avg}}$ gives the average probability that the system will be unable to perform its required function when the need arises due to failures within the system.

Several studies have assessed the ${\mathrm{P}\mathrm{F}\mathrm{D}}_{\text{avg}}$ of SIS (IEC 61508:2010; Rausand, 2004; Torres-Echeverría et al., 2009; Liu and Rausand, 2011; Chebila and Innal, 2015). A common assumption is that the failure rates are constant for all subsystems of the SIS. This assumption is not very realistic, considering that certain subsystems, such as the final element, which often consists of mechanical parts working in a subsea environment, will experience deterioration and degradation due to the force and motion exerted when demand occurs (Rogova et al. (2017); Rausand, 2014; Rogova et al. (2017); Wu et al., 2018).

The multi-state Markov process has been used to address degradation within the SIS. Oliveira et al. (2016) and Oliveira (2018) developed models to evaluate the PFD considering degradation brought about by the test. This is a binary state model with a constant failure rate as degradation due to aging is not considered. Srivastav et al. (2020) considered degradation due to aging as well as the impact of testing. In the model, the failure rate is multiplied by a factor depending on the degraded state of the system following a test. Although this framework extends the binary state model by considering intermediate degraded states, it requires expert judgment to select initial parameters for changing the failure rate as well as to select the number of degraded states. There is also an exponential increase in the number of possibilities for the combination of system states and transition rates as the number of tests increases, making the assessment computationally intensive and time consuming.

The gamma process, a well-known process for modeling degradation, has also been applied to model the degradation of SIS. Zhang et al. (2019) analyzed the performance of redundant safety-instrumented systems subject to degradation and external demands using the gamma process. The natural aging of the component follows the gamma process. The external demand arrives following a homogeneous Poisson process, and its impact is assumed to be non-negative and gamma-distributed. The system fails if the combined accumulated damage exceeds a given threshold. Although this approach provides a more realistic assessment of the degradation of the system, a monitoring variable is required. In practice, the monitored parameter does not always follow the gamma process, and some computations and transformations must be done on the variable to suit the analysis. For example, considering the closing time of a shutdown valve as a monitored variable, this value fluctuates between tests and, therefore, cannot be used directly as the monitored value in the gamma process.

The Weibull distribution is another approach used to address the non-constant failure rate/degradation of SIS. The Weibull distribution offers flexibility, as the distribution parameters can be adapted to model the internal degradation and time to failure of the system. Jigar (2013) applied the Weibull distribution to develop analytical formulas based on the ratio between cumulative distribution functions for assessing the reliability of the SIS. Rogova et al. (2017) extended the model to incorporate common cause failures (CCFs) and diagnostic coverage (DC) for more complex systems with more than one component. Wu et al. (2018) developed approximation formulas based on the average failure rate in an interval to assess the performance of SIS while also considering the effect of partial tests (PT) on the reliability performance.

The above-mentioned works are based on the assumption that the system is repaired and put back into service immediately or almost immediately following the test, thereby ignoring the duration of the repair in their assessment. However, some other issues remain to be considered in the subsea context. These systems are not easily accessible, and thus, there is a delay following the test before the repair is carried out. This repair delay is non-negligible and should be considered in the assessment. Wu et al. (2019) addressed the problem of delayed restoration in their paper considering partial test and full test. However, they assumed that the system was as good as new following repair after a full test. This is often not the case with most mechanical systems unless there is a complete overhaul. Another issue to consider is that different failure modes may occur on the same system, and these can bring more challenges to the decision making with respect to testing and maintenance. The systems are often subject to random external shocks that may cause sudden failure to the system.

To address this issue, we analyze the performance of the SIS final element subject to failure due to different (heterogenous) failure modes in this paper. Subsea systems operate in a very hostile environment with harsh conditions. Aside from failures due to aging and degradation, the systems are also exposed to random shocks. We also consider the impact of delayed restoration on the unavailability/${\mathrm{P}\mathrm{F}\mathrm{D}}_{\text{avg}}$ of the system considering different testing strategies.

The main objective of this paper is to provide formulations for analyzing the unavailability of subsea SIS final elements subject to different (heterogenous) failure modes as well as the impact of delayed restoration. The main contribution/novelty in this paper is that we consider the impact of different failure modes with different failure distributions for the SIS final element in conjunction with delayed repair and formulate simple approximation formulas for assessing the system unavailability.

The rest of the paper is organized as follows: Section 2 presents a brief description of key concepts associated with SISs and performance analysis of SISs, as well as assumptions used in the analyses. Section 2 presents the analytical formulation of unavailability and average unavailability for different test intervals as well as the entire mission time of the system. Section 4 gives case studies and some numerical examples of applying the formulations to determine the unavailability as well as the effects of different parameters on the average unavailability. Section 6 provides a summary and conclusion of the paper. Suggestions for further work are also given in this section.

2 Definitions and assumptions

This section presents some definitions and assumptions for SIS performance assessment and lays the groundwork for the analytical formulation that follows.

2.1 Safety-instrumented system

A safety-instrumented system (SIS) is an independent protection layer installed to mitigate the risk associated with the operation of a specified hazardous system (Rausand, 2004). It consists of at least three subsystems: sensors, logic solvers, and the final element. The sensors monitor a pre-defined process variable (such as temperature or pressure). The measurement is transmitted to the logic solver, which compares it with a set value. In the event of a hazardous situation (temperature or pressure too high or too low, depending on the system and operation), the logic solver sends a signal to activate the final element. In this paper, we focus on the final element, specifically the shutdown valve. In the oil and gas industry, the shutdown valve is a very common final element used to cut off flow in pipelines or other processes. They are often set up in a 1oo1 or 1oo2 configuration. The 1oo2 is thought to have higher reliability because both valves need to fail for the system to fail, but where the risk to safety is not high, the 1oo1 set-up can be useful and more economical in terms of capital investment. Demand for these valves is low, and accordingly, they are classified by the IEC standards as a SIS with a low-demand mode of operation. Typical demand is less than once per year on average (IEC 61508:2010; IEC 61511:2016). Because these valves are inactive for a long period of time, any failure is not known until they are activated either through demand or a test. Such failures are referred to as dangerous undetected (DU) failures.

2.2 Safety unavailability

The safety unavailability of a safety system is the probability that the system is not able to perform its required function on demand (Rausand, 2004). The main contributions to safety unavailability include (Hauge et al., 2013):

$•$ Noncritical safety unavailability (NSU) of the item mainly caused by functional testing.

$•$ Probability of failure of demand (PFD). The unknown safety unavailability is due to DU failures during the test interval when it is not known that the function is unavailable.

$•$ Safety unavailability of the item due to restoration actions after failure has been revealed.

$•$ The probability that a systematic failure will prevent the item from performing its intended function.

In this paper, we focus on safety unavailability due to DU failures and safety unavailability due to restoration actions. In offshore and subsea installations, there is often a delay after failure is detected in the valve until the valve is restored. This kind of delay poses a different kind of risk to the operation. Quantifying these risks enables appropriate risk reduction actions to be put in place.

${\mathrm{P}\mathrm{F}\mathrm{D}}_{\text{avg}}$ is the recommended measure of safety unavailability caused by DU failures in the test interval (IEC 61508:2010; IEC 61511:2016).

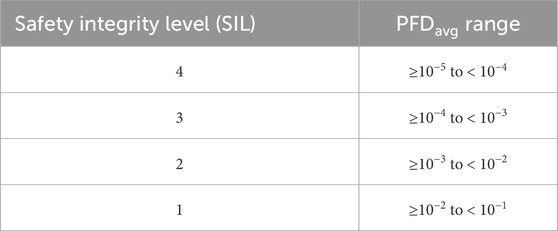
Safety integrity is a fundamental concept in the IEC standards. According to the international electrotechnical vocabulary (IEV 821-12-54), safety integrity is the ability of a safety-related system to achieve its required safety functions under all the stated conditions within a stated operational environment and within a stated duration (IEC, 2017). The safety integrity is classified into four discrete levels called safety integrity levels (SILs), which is, in turn, defined by the $\mathrm{P}\mathrm{F}{\mathrm{D}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$. Table 1 shows the range of values of $\mathrm{P}\mathrm{F}{\mathrm{D}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$ corresponding to each SIL, with SIL4 having the highest safety integrity and lowest range of values of $\mathrm{P}\mathrm{F}{\mathrm{D}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$ and SIL1 having the lowest safety integrity and the highest range of values of $\mathrm{P}\mathrm{F}{\mathrm{D}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$.

Table 1

Table 1. Safety integrity levels.

SIL targets are typically assigned to safety functions during the planning and design stage. Components and subsystems are then selected along with configurations to meet the required SIL targets in operation.

2.3 Assumptions for analysis

The following assumptions are made to further facilitate the formulations in this paper:

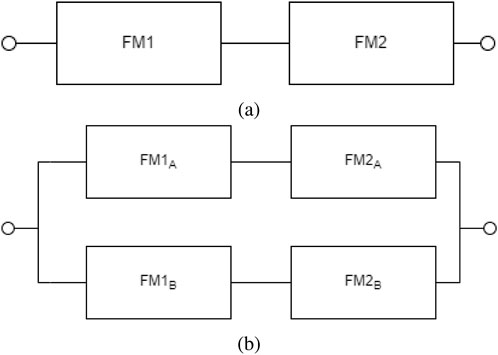
1. The system is subjected to two kinds of failure modes: 1. Failures due to degradation (failure mode 1, or FM1) and 2. Failures due to random external shocks to the system (failure mode 2, or FM2).

2. The degradation of the system follows the Weibull distribution with probability density function (PDF):

$f\left(t\right)=\alpha {\lambda }_1^{\alpha }{t}^{\alpha -1}{e}^{-{\left({\lambda }_{1}t\right)}^{\alpha }},(1)$

where $\alpha$ is the shape parameter, and ${\lambda }_1$ is the rate parameter of the Weibull distribution. The cumulative density function (CDF) is given as:

$F\left(t\right)=\mathrm{P}\mathrm{r}\left(T\le t\right)=1-e^{-{\left({\lambda }_{1}t\right)}^{\alpha }}.(2)$

3. External shocks causing sudden failures to the system are assumed to arrive following a homogeneous Poisson process with a pdf given by

$f\left(t\right)={\lambda }_2{e}^{-\left({\lambda }_{2}t\right)},(3)$

where ${\lambda }_2$ is the rate parameter of the exponential distribution. The cumulative density function is given as

$F\left(t\right)=\mathrm{P}\mathrm{r}\left(T\le t\right)=1-e^{-\left({\lambda }_{2}t\right)}.(4)$

4. The components and failure modes are assumed to be stochastically independent. However, the probability of having more than one failure mode present in the same component at any given point in time is considered low and negligible.

5. The system is regularly proof-tested. Tests are non-destructive and have no negative impact on the system. The tests are performed simultaneously for the final elements, and the testing duration is considered negligible. See, for example, Torres-Echeverría et al. (2009), Hauge et al. (2013), or Rausand (2014) for how to quantify the average unavailability of non-negligible test times.

6. Following proof tests, revealed failures are repaired. However, there will be a delay before the repair is carried out. The delay is the same regardless of number of items to repair. With respect to FM 1, repairs are assumed to be minimal, thereby making the entire system not as good as new following repairs.

7. Common cause failures (CCF) for a 1oo2 configuration, as well as the effects of dangerous detected (DD) failures for both configurations, are excluded. This is to keep the focus on quantifying the impact of the different failure modes, as well as the impact of delayed restoration on safety unavailability, while keeping the analysis relatively simple.

3 Safety unavailability analysis

This section presents the formulations for assessing the unavailability and ${\mathrm{P}\mathrm{F}\mathrm{D}}_{\text{avg}}$ for the final element of a SIS with delayed restoration. Consider the final element of a SIS with two failure modes. The system can either be configured as a 1oo1 system or as a 1oo2 system. A simple reliability block diagram representation of the 1oo1 system shows the system as two components in series, with each component representing a failure mode, and a diagram for the 1oo2 system shows it as two subsystems in parallel, with each subsystem consisting of two series components (Figure 1). This means that for the 1oo1 system, the presence of one failure mode in the system is sufficient to cause a system failure. For the 1oo2 system, both components must fail for the system to fail. At least one failure mode must be present in each component to cause system failure. This is further illustrated in the fault tree representation of the failure modes in Figure 2.

Figure 1

Figure 1. Reliability block diagram (RBD) representation of the (A) 1oo1 and (B) 1oo2 systems.

Figure 2

Figure 2. Fault tree representation of failure modes of the (A) 1oo1 and (B) 1oo2 systems.

3.1 Unavailability formulation

The unavailability of the system is defined for the system as the instantaneous inability to fulfil its intended function due to failure. The unavailability of the system can be analytically evaluated in different testing intervals.

3.1.1 Failure and conditional failure probability

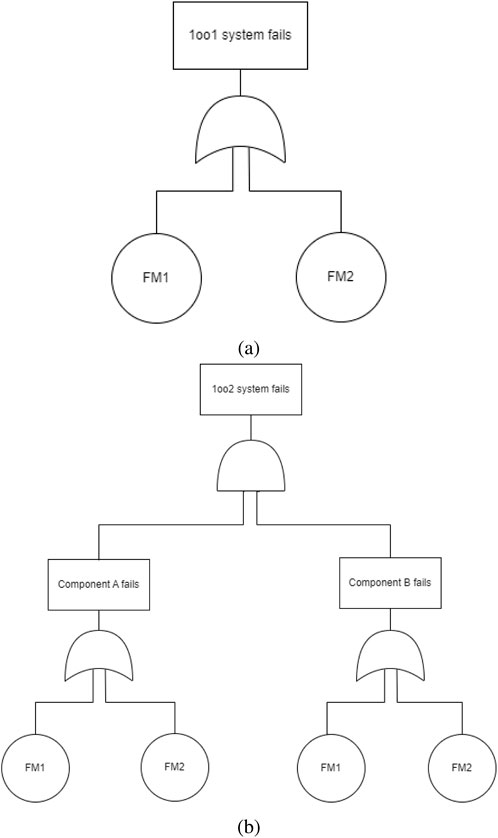
A 1oo1 system will fail if either of the two failure modes is present in the system. Let ${\mathrm{T}}_{\mathrm{1}}$ be the time to occurrence of failure mode 1 (FM1) and ${\mathrm{T}}_{\mathrm{2}}$ be the time to occurrence of failure mode 2 (FM2), the time to failure of the system is given as:

$T_s=min\left\{T_1,T_2\right\}.(5)$

The CDF of the system, which is the probability that the system is in a failed state at a given point in time, is given as:

$\begin{array}{cc}\hfill F_{s,1oo1}\left(t\right)& =\mathrm{P}\mathrm{r}\left(T_s\le t\right)=1-\mathrm{P}\mathrm{r}\left(T_s>t\right)\hfill \\ \hfill & =1-\left[\mathrm{P}\mathrm{r}\left(T_1>t\right)\cdot \mathrm{P}\mathrm{r}\left(T_2>t\right)\right]\hfill \\ \hfill & =1-\left(e^{-{\lambda }_{2}t}\cdot e^{-{\lambda }_1^{\alpha }{t}^{\alpha }}\right)=1-e^{-\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)}\hfill \\ \hfill & \approx {\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }.\hfill \end{array}(6)$

Note this approximation takes low values (i.e., ${\lambda }_1^{\alpha }{t}^{\alpha }$ and ${\lambda }_{2}t<0.01$).

For a 1oo2 system, failure will occur only when both components are in a failed state. Let $T_A$ and $T_B$ represent the time to failure of components A and B, respectively; the time to failure of the system assuming no repair is

$\begin{array}{cc}\hfill T_s& =max\left\{T_A,T_B\right\}\hfill \\ \hfill & =max\left[min\left\{T_{A1},T_{A2}\right\},min\left\{T_{B1},T_{B2}\right\}\right].\hfill \end{array}(7)$

The probability that the system is in a failed state at time, t, is given as

$\begin{array}{cc}\hfill F_{s,1oo2}\left(t\right)& =\mathrm{P}\mathrm{r}\left(T_s\le t\right)=\mathrm{P}\mathrm{r}\left(T_A\le t\cap T_B\le t\right)\hfill \\ \hfill & =\mathrm{P}\mathrm{r}\left(T_A\le t\right)\cdot \mathrm{P}\mathrm{r}\left(T_B\le t\right)\hfill \\ \hfill & =F_A\left(t\right)\cdot F_B\left(t\right).\hfill \end{array}(8)$

Assuming both components are identical

$\begin{array}{cc}\hfill \mathrm{P}\mathrm{r}\left(T_s\le t\right)& =F_{s,1oo2}\left(t\right)=F_A\left(t\right)\cdot F_B\left(t\right)\hfill \\ \hfill & \approx {\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)}^2\hfill \\ \hfill & ={\left({\lambda }_{2}t\right)}^2+\left(2{\lambda }_{2}t{\lambda }_1^{\alpha }{t}^{\alpha }\right)+{\left({\lambda }_1^{\alpha }{t}^{\alpha }\right)}^2\hfill \end{array}(9)$

for low values of ${\lambda }_1$ and ${\lambda }_2$ (i.e., ${\lambda }_1^{\alpha }{t}^{\alpha }$ and ${\lambda }_{2}t<0.01$).

Given that the system is functioning at time, $x$, the probability that the system fails before time $t$ for a 1oo1 system is (Rausand, 2021)

$\begin{array}{cc}\hfill & \mathrm{P}\mathrm{r}\left(T_s\le t|T_s>x\right)=\frac{\mathrm{P}\mathrm{r}\left(T_s\le t\right)-\mathrm{P}\mathrm{r}\left(T_s\le x\right)}{\mathrm{P}\mathrm{r}\left(T_s>x\right)}\hfill \\ \hfill & =\frac{\left(1-\left(Pr\left(T_1>t\right)\cdot Pr\left(T_2>t\right)\right)\right)-\left(1-\left(Pr\left(T_1>x\right)\cdot Pr\left(T_2>x\right)\right)\right)}{Pr\left(T_1>x\right)\cdot Pr\left(T_2>x\right)}\hfill \\ \hfill & =\frac{\left(1-\left(e^{-{\lambda }_{1}t}{e}^{-{\lambda }_2^{\alpha }{t}^{\alpha }}\right)\right)-\left(1-\left(e^{-{\lambda }_{2}x}{e}^{-{\lambda }_1^{\alpha }{x}^{\alpha }}\right)\right)}{\left(e^{-{\lambda }_{2}x}{e}^{-{\lambda }_1^{\alpha }{x}^{\alpha }}\right)}\hfill \\ \hfill & =\frac{\left(e^{-{\lambda }_{2}x}{e}^{-{\lambda }_1^{\alpha }{x}^{\alpha }}\right)-\left(e^{-{\lambda }_{2}t}{e}^{-{\lambda }_1^{\alpha }{t}^{\alpha }}\right)}{\left(e^{-{\lambda }_{2}x}{e}^{-{\lambda }_1^{\alpha }{x}^{\alpha }}\right)}\hfill \\ \hfill & =1-\frac{\left(e^{-{\lambda }_{2}t}{e}^{-{\lambda }_1^{\alpha }{t}^{\alpha }}\right)}{\left(e^{-{\lambda }_{2}x}{e}^{-{\lambda }_1^{\alpha }{x}^{\alpha }}\right)}\hfill \\ \hfill & =1-e^{-\left({\lambda }_2\left(t-x\right)+{\lambda }_1^{\alpha }\left(t^{\alpha }-x^{\alpha }\right)\right)}\hfill \\ \hfill & \approx {\lambda }_2\left(t-x\right)+{\lambda }_1^{\alpha }\left(t^{\alpha }-x^{\alpha }\right)\hfill \end{array}(10)$

and for a 1oo2 system

$\begin{array}{cc}\hfill & \mathrm{P}\mathrm{r}\left(T_s\le t|T_s>x\right)=\frac{\mathrm{P}\mathrm{r}\left(T_s\le t\right)-\mathrm{P}\mathrm{r}\left(T_s\le x\right)}{\mathrm{P}\mathrm{r}\left(T_s>x\right)}\hfill \\ \hfill & \approx \frac{{\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)}^2-{\left({\lambda }_{2}x+{\lambda }_1^{\alpha }{x}^{\alpha }\right)}^2}{1-{\left({\lambda }_{2}x+{\lambda }_1^{\alpha }{x}^{\alpha }\right)}^2}.\hfill \end{array}(11)$

Equations 1–11 provides formulas for the failure probability, conditional failure probability and lays the foundation for the unavailability formulation in the next section.

3.1.2 Analytical formulation of unavailability

Given $n$ testing intervals denoted as $[T_0=0,T_1]$, $[T_1,T_2],\dots ,[T_{n-1},T_n]$, if $t$ is within the first interval $[T_0=0,T_1]$, the unavailability for a 1oo1 system can be found as

$\begin{array}{cc}\hfill {UA}_{1_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)& =\mathrm{P}\mathrm{r}\left(T_s\le t\right)\hfill \\ \hfill & \approx {\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\hfill \end{array}(12)$

and for a 1oo2 system as

$\begin{array}{cc}\hfill {UA}_{1_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)& =\mathrm{P}\mathrm{r}\left(T_s\le t\right)\hfill \\ \hfill & \approx {\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)}^2.\hfill \end{array}(13)$

If t is in the second interval $[T_1,T_2]$, we need to consider the possibility of a repair in this interval. A repair will be carried out if failures are revealed during the test at time $T_1$, subject to delay before repair. Let $T_r$ denote the duration of the delay. The second interval consists of two distinct intervals $[T_1,T_1+T_r]$ and $[T_1+T_r,T_2]$.

In the interval $[T_1,T_1+T_r]$, the unavailability consists of two parts. The first part is the unavailability due to repairs that were subject to failure revealed during the test. The second part is unavailability due to the unreliability of the system subject to no failure revealed at the test

$\begin{array}{cc}\hfill {UA}_{2,1_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)& =\mathrm{P}\mathrm{r}\left(T_s\le T_1\right)+\mathrm{P}\mathrm{r}\left(T_s\le t\right)\cdot \mathrm{P}\mathrm{r}\left(T_s>T_1\right)\hfill \\ \hfill & =\left\{\begin{array}{c}\approx {\lambda }_1^{\alpha }\left(T_1^{\alpha }+t^{\alpha }\right)+{\lambda }_2\left(T_1+t\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \\ 0,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\hfill \end{array}\right.\hfill \end{array}(14)$

and for a 1oo2 system

$\begin{array}{cc}\hfill & {UA}_{2,1_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)=\mathrm{P}\mathrm{r}\left(T_s\le T_1\right)+\mathrm{P}\mathrm{r}\left(T_s>T_1\right)\cdot \mathrm{P}\mathrm{r}\left(T_s\le t\right)\hfill \\ \hfill \\ \hfill & =\left\{\begin{array}{c}{\left({\lambda }_1^{\alpha }{T}_1^{\alpha }+{\lambda }_2{T}_1\right)}^2+\left[\left(1-{\left({\lambda }_1^{\alpha }{T}_1^{\alpha }+{\lambda }_2{T}_1\right)}^2\right)\cdot {\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2\right],\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \\ 0,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\hfill \end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{c}\approx {\lambda }_1^{2\alpha }\left(T_1^{2\alpha }+t^{2\alpha }\right)+{\lambda }_2^2\left(T_1^2+t^2\right)+2{\lambda }_1^{\alpha }{\lambda }_2\left(T_1^{\alpha +1}+t^{\alpha +1}\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \\ 0,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0.\hfill \end{array}\right.\hfill \end{array}(15)$

For the interval $[T_1+T_r,T_2]$, the unavailability is due to the unreliability of the system, given we know the system is functioning at the beginning of the interval, at $t=T_1+T_r$ following the elapsed repair time

$\begin{array}{cc}\hfill & U{A}_{2,2_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)=\mathrm{P}\mathrm{r}\left(T_s\le t|T_s>T_1+T_r\right)\hfill \\ \hfill & \approx \left\{\begin{array}{c}{\lambda }_1^{\alpha }\left(t^{\alpha }-{\left(T_1+T_r\right)}^{\alpha }\right)+{\lambda }_2\left(t-T_1-T_r\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \\ \hfill \\ {\lambda }_1^{\alpha }\left(t^{\alpha }-T_1^{\alpha }\right)+{\lambda }_2\left(t-T_1\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0,\hfill \end{array}\right.\hfill \end{array}(16)$

and for a 1oo2 system

$\begin{array}{cc}\hfill & U{A}_{2,2_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)=\mathrm{P}\mathrm{r}\left(T_s\le t|T_s>T_1+T_r\right)\hfill \\ \hfill & \approx \left\{\begin{array}{c}\frac{{\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2-{\left[{\lambda }_1^{\alpha }{\left(T_1+T_r\right)}^{\alpha }+{\lambda }_2\left(T_1+T_r\right)\right]}^2}{1-{\left[{\lambda }_1^{\alpha }{\left(T_1+T_r\right)}^{\alpha }+{\lambda }_2\left(T_1+T_r\right)\right]}^2},\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \\ \hfill \\ \frac{{\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2-{\left[{\lambda }_1^{\alpha }{T}_1^{\alpha }+{\lambda }_2{T}_1\right]}^2}{1-{\left[{\lambda }_1^{\alpha }{T}_1^{\alpha }+{\lambda }_2{T}_1\right]}^2},\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0.\hfill \end{array}\right.\hfill \end{array}(17)$

For subsequent intervals $[T_{n-1},T_n]$, we also need to consider the possibility of repairs as with the second interval. However, before the test at time $T_{n-1}$ and possible delay before repair following the test, we know the last time the system was known to be in a functioning state was at time $T_{n-2}+T_r$. The unavailability in the interval $[T_{n-1},T_{n-1}+T_r]$ is therefore conditioned on this last known functioning time of the system

$\begin{array}{cc}\hfill & U{A}_{n,1_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)=\mathrm{P}\mathrm{r}\left(T_s\le T_{n-1}|T_s>T_{n-2}+T_r\right)\hfill \\ \hfill & +\mathrm{P}\mathrm{r}\left(T_s>T_{n-1}|T_s>T_{n-2}+T_r\right)\cdot \mathrm{P}\mathrm{r}\left(T_s\le t|T_s>T_{n-2}+T_r\right)\hfill \\ \hfill & \approx \left\{\begin{array}{c}\begin{array}{c}\hfill {\lambda }_2\left(t+T_{n-1}-2\left(T_{n-2}+T_r\right)\right)+{\lambda }_1^{\alpha }\left(t^{\alpha }+T_{n-1}^{\alpha }-2{\left(T_{n-2}+T_r\right)}^{\alpha }\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0,n\ge 3\end{array}\hfill \\ 0,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0,\hfill \end{array}\right.\hfill \end{array}(18)$

and for a 1oo2 system

$\begin{array}{cc}\hfill & U{A}_{n,1_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)\hfill \\ \hfill & =\mathrm{P}\mathrm{r}\left(T_s\le T_{n-1}|T_s>T_{n-2}+T_r\right)+\mathrm{P}\mathrm{r}\left(T_s>T_{n-1}|T_s>T_{n-2}+T_r\right)\cdot \mathrm{P}\mathrm{r}\left(T_s\le t|T_s>T_{n-2}+T_r\right)\hfill \\ \hfill \\ \hfill & \approx \left\{\begin{array}{c}\begin{array}{c}\hfill \frac{{\lambda }_2^2\left(t^2+T_{n-1}^2-2{\left(T_{n-2}+T_r\right)}^2\right)+{\lambda }_1^{2\alpha }\left(t^{2\alpha }+T_{n-1}^{2\alpha }-2{\left(T_{n-2}+T_r\right)}^{2\alpha }\right)+2{\lambda }_1^{\alpha }{\lambda }_2\left(t^{\alpha +1}+T_{n-1}^{\alpha +1}-2{\left(T_{n-2}+T_r\right)}^{\alpha +1}\right)}{1-2{\lambda }_1^{2\alpha }{\left(T_{n-2}+T_r\right)}^{2\alpha }-2{\lambda }_2^2{\left(T_{n-2}+T_r\right)}^2-4{\lambda }_1^{\alpha }{\lambda }_2{\left(T_{n-2}+T_r\right)}^{\alpha +1}}\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0,n\ge 3\end{array}\hfill \\ 0,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\hfill \end{array}\right.\hfill \\ \hfill & \approx \left\{\begin{array}{c}\begin{array}{cc}\hfill & {\lambda }_2^2\left(t^2+T_{n-1}^2-2{\left(T_{n-2}+T_r\right)}^2\right)+{\lambda }_1^{2\alpha }\left(t^{2\alpha }+T_{n-1}^{2\alpha }-2{\left(T_{n-2}+T_r\right)}^{2\alpha }\right)\hfill \\ \hfill & +2{\lambda }_1^{\alpha }{\lambda }_2\left(t^{\alpha +1}+T_{n-1}^{\alpha +1}-2{\left(T_{n-2}+T_r\right)}^{\alpha +1}\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0,n\ge 3\hfill \end{array}\hfill \\ 0,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0.\hfill \end{array}\right.\hfill \end{array}(19)$

In the interval $[T_{n-1}+T_r,T_n]$, the unavailability is similar to that of the corresponding second interval because the last known time of the system being in a functioning state now becomes $t=(T_{n-1}+T_r)$:

$\begin{array}{cc}\hfill & U{A}_{n,2_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)=\mathrm{P}\mathrm{r}\left(T_s\le t|T_s>\left(T_{n-1}+T_r\right)\right)\hfill \\ \hfill \\ \hfill & \approx \left\{\begin{array}{c}{\lambda }_1^{\alpha }\left(t^{\alpha }-{\left(T_{n-1}+T_r\right)}^{\alpha }\right)+{\lambda }_2\left(t-T_{n-1}-T_r\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0,n\ge 3\hfill \\ \hfill \\ {\lambda }_1^{\alpha }\left(t^{\alpha }-T_{n-1}^{\alpha }\right)+{\lambda }_2\left(t-T_{n-1}\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0,n\ge 3\hfill \end{array}\right.\hfill \end{array}(20)$

$\begin{array}{cc}\hfill & U{A}_{n,2_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)=\mathrm{P}\mathrm{r}\left(T_s\le t|T_s>T_{n-1}+T_r\right)\hfill \\ \hfill \\ \hfill & \approx \left\{\begin{array}{c}\frac{{\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2-{\left[{\lambda }_1^{\alpha }{\left(T_{n-1}+T_r\right)}^{\alpha }+{\lambda }_2\left(T_{n-1}+T_r\right)\right]}^2}{1-{\left[{\lambda }_1^{\alpha }{\left(T_{n-1}+T_r\right)}^{\alpha }+{\lambda }_2\left(T_{n-1}+T_r\right)\right]}^2},\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \\ \hfill \\ \frac{{\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2-{\left[{\lambda }_1^{\alpha }{T}_{n-1}^{\alpha }+{\lambda }_2{T}_{n-1}\right]}^2}{1-{\left[{\lambda }_1^{\alpha }{T}_{n-1}^{\alpha }+{\lambda }_2{T}_{n-1}\right]}^2},\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0.\hfill \end{array}\right.\hfill \end{array}(21)$

Equations 12–21 provide formulas for calculating the unavailability in different test intervals for a 1oo1 and a 1oo2 system. The intervals may be constant or non-constant, depending on the operational requirements of the system. It is important to note that the first two intervals are unique in their formulations, particularly when we consider delays before repair. If we assume no delays before repair, then only the first interval has a unique formulation. The repair delay is deterministic and can include the actual repair duration.

3.1.3 Average unavailability formulation

The average unavailability gives the average proportion of time the system is unable to fulfill its intended function in a given time interval. In the previous section, we established the instantaneous unavailability for the system in the different testing intervals. Likewise, we can find the average unavailability for the system in the different testing intervals. The average unavailability for a system in a given interval can generally be expressed as

$\begin{array}{cc}\hfill \mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g}}& =\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}UA\left(t\right)dt\hfill \\ \hfill & \approx \frac{1}{t_2-t_1}{\displaystyle \sum _{t=t_1}^{t_2}}UA\left(t\right).\hfill \end{array}(22)$

The approximation applies if we consider a time unit increment of $t$ by 1 (i.e., $\mathrm{\Delta }t=1$).

So, considering the first test interval, $t\in [T_0=0,T_1]$, the average unavailability for a 1oo1 system will be

$\begin{array}{cc}\hfill \mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g},{\mathrm{1}}_{\mathrm{1oo1}}}& =\frac{1}{T_1}{\int }_0^{T_1}U{A}_{1_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt=\frac{1}{T_1}{\int }_0^{T_1}\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)dt\hfill \\ \hfill \\ \hfill & \approx \frac{1}{T_1}{\displaystyle \sum _{t=0}^{T_1}}\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha },\right)\hfill \end{array}(23)$

and for a 1oo2 system

$\begin{array}{cc}\hfill \mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g},{\mathrm{1}}_{\mathrm{1oo2}}}& =\frac{1}{T_1}{\int }_0^{T_1}U{A}_{1_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt=\frac{1}{T_1}{\int }_0^{T_1}\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)dt\hfill \\ \hfill \\ \hfill & \approx \frac{1}{T_1}{\displaystyle \sum _{t=0}^{T_1}}{\left({\lambda }_{2}t+{\lambda }_1^{\alpha }{t}^{\alpha }\right)}^2.\hfill \end{array}(24)$

For the second interval, $t\in [T1,T2]$:

$\begin{array}{cc}\mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g},{\mathrm{2}}_{\mathrm{1oo1}}}=\hfill & \left\{\begin{array}{c}\begin{array}{c}\frac{1}{T_2-T_1}\left({\int }_{T_1}^{T_1+T_r}U{A}_{2,1_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt+{\int }_{T_1+T_r}^{T_2}U{A}_{2,2_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt\right),\hfill \\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \frac{1}{T_2-T_1}{\int }_{T_1}^{T_2}U{A}_{2,2_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill \approx & \left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T_2-T_1}\left({\displaystyle \sum _{t=T_1}^{T_1+T_r}}\left({\lambda }_1^{\alpha }\left(T_1^{\alpha }+t^{\alpha }\right)+{\lambda }_2\left(T_1+t\right)\right)\right.\\ \hfill +\left.{\displaystyle \sum _{t=T_1+T_r}^{T_2}}\left({\lambda }_1^{\alpha }\left(t^{\alpha }-{\left(T_1+T_r\right)}^{\alpha }\right)+{\lambda }_2\left(t-T_1-T_r\right)\right)\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \frac{1}{T_2-T_1}{\displaystyle \sum _{t=T_1}^{T_2}}\left({\lambda }_1^{\alpha }\left(t^{\alpha }-T_1^{\alpha }\right)+{\lambda }_2\left(t-T_1\right)\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0,\hfill \end{array}\right.\hfill \end{array}(25)$

and for a 1oo2 system

$\begin{array}{cc}\hfill & \mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g},{\mathrm{2}}_{\mathrm{1}\mathit{oo}\mathrm{2}}}=\left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T_2-T_1}\left({\int }_{T_1}^{T_1+T_r}U{A}_{2,1_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt+{\int }_{T_1+T_r}^{T_2}U{A}_{2,2_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \frac{1}{T_2-T_1}{\int }_{T_1}^{T_2}U{A}_{2,2_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill \approx & \left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T_2-T_1}\left({\displaystyle \sum _{t=T_1}^{T_1+T_r}}\left({\lambda }_1^{2\alpha }\left(T_1^{2\alpha }+t^{2\alpha }\right)+{\lambda }_2^2\left(T_1^2+t^2\right)+2{\lambda }_1^{\alpha }{\lambda }_2\left(T_1^{\alpha +1}+t^{\alpha +1}\right)\right)\right.\\ \hfill +\left.{\displaystyle \sum _{t=T_1+T_r}^{T_2}}\left(\frac{{\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2-{\left[{\lambda }_1^{\alpha }{\left(T_1+T_r\right)}^{\alpha }+{\lambda }_2\left(T_1+T_r\right)\right]}^2}{1-{\left[{\lambda }_1^{\alpha }{\left(T_1+T_r\right)}^{\alpha }+{\lambda }_2\left(T_1+T_r\right)\right]}^2}\right)\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \hfill \\ \frac{1}{T_2-T_1}{\displaystyle \sum _{t=T_1}^{T_2}}\left(\frac{{\left({\lambda }_1^{\alpha }{t}^{\alpha }+{\lambda }_{2}t\right)}^2-{\left[{\lambda }_1^{\alpha }{T}_1^{\alpha }+{\lambda }_2{T}_1\right]}^2}{1-{\left[{\lambda }_1^{\alpha }{T}_1^{\alpha }+{\lambda }_2{T}_1\right]}^2}\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0.\hfill \end{array}\right.\hfill \end{array}(26)$

With respect to subsequent intervals, $[T_{n-1},T_n]$, the average unavailability is given as:

$\begin{array}{cc}\hfill & \mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g},{\mathrm{n}}_{\mathrm{1oo1}}}=\left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T_n-T_{n-1}}\left({\int }_{T_{n-1}}^{T_{n-1}+T_r}U{A}_{n,1_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt+{\int }_{T_{n-1}+T_r}^{T_n}U{A}_{n,2_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \hfill \\ \frac{1}{T_n-T_{n-1}}{\int }_{T_{n-1}}^{T_n}U{A}_{n,2_{\mathrm{1}\mathit{oo}\mathrm{1}}}\left(t\right)dt,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill \approx & \left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T_n-T_{n-1}}\left({\displaystyle \sum _{t=T_{n-1}}^{T_{n-1}+T_r}}\left({\lambda }_1^{\alpha }\left(t^{\alpha }-{\left(T_{n-1}+T_r\right)}^{\alpha }\right)+{\lambda }_2\left(t-T_{n-1}-T_r\right)\right)\right.\\ \hfill +\left.{\displaystyle \sum _{t=T_{n-1}+T_r}^{T_n}}\left({\lambda }_1^{\alpha }\left(t^{\alpha }-{\left(T_{n-1}+T_r\right)}^{\alpha }\right)+{\lambda }_2\left(t-T_{n-1}-T_r\right)\right)\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \hfill \\ \frac{1}{T_2-T_1}{\displaystyle \sum _{t=T_{n-1}}^{T_n}}\left({\lambda }_1^{\alpha }\left(t^{\alpha }-T_{n-1}^{\alpha }\right)+{\lambda }_2\left(t-T_{n-1}\right)\right),\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0,\hfill \end{array}\right.\hfill \end{array}(27)$

and for a 1oo2 system

$\begin{array}{cc}\hfill & \mathrm{U}{\mathrm{A}}_{\mathrm{a}\mathrm{v}\mathrm{g},{\mathrm{n}}_{\mathrm{1oo2}}}=\left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T_n-T_{n-1}}\left({\int }_{T_{n-1}}^{T_{n-1}+T_r}U{A}_{n,1_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt+{\int }_{T_{n-1}+T_r}^{T_n}U{A}_{n,2_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt\right),\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\end{array}\hfill \\ \frac{1}{T_n-T_{n-1}}{\int }_{T_{n-1}}^{T_n}U{A}_{n,2_{\mathrm{1}\mathit{oo}\mathrm{2}}}\left(t\right)dt,\mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0.\hfill \end{array}\right.\hfill \end{array}(28)$

The above formulations (Equations 23–28) give the average unavailability for the system in different test intervals. However, we may be interested in finding the total average unavailability for a given mission time $(0,T)$. This is particularly the case with subsea systems that require a complete overhaul after a certain number of years in operation. To find the total average unavailability for a given mission time $\mathrm{U}{\mathrm{A}}_{{\mathrm{T}}_{\mathrm{avg}}}$, we add the individual unavailability in each test interval and divide by the mission time:

$\begin{array}{cc}\hfill & \mathrm{U}{\mathrm{A}}_{{\mathrm{T}}_{\mathrm{avg}}}=\frac{1}{T}{\int }_0^{T}UA\left(t\right)dt\hfill \\ \hfill & =\left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T}\left[{\int }_0^{T_1}U{A}_1\left(t\right)dt+{\int }_{T_1}^{T_2}U{A}_2\left(t\right)dt+\cdots +{\int }_{T_{n-1}}^{T_n}U{A}_n\left(t\right)dt\right],\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\end{array}\hfill \\ \hfill \\ \frac{1}{T}\left[{\int }_0^{T_1}U{A}_1\left(t\right)dt+{\int }_{T_1}^{T_1+T_r}U{A}_{\mathrm{2,1}}\left(t\right)dt+{\int }_{T_1+T_r}^{T_2}U{A}_{\mathrm{2,2}}\left(t\right)dt+\cdots \right.\hfill \\ +\left.{\int }_{T_{n-1}}^{T_{n-1}+T_r}U{A}_{n,1}\left(t\right)dt+{\int }_{T_{n-1}+T_r}^{T_n}U{A}_{n,2\left(t\right)}dt\right],\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill & \approx \left\{\begin{array}{c}\begin{array}{c}\hfill \frac{1}{T}\left[{\displaystyle \sum _0^{T_1}}U{A}_1\left(t\right)dt+{\displaystyle \sum _{T_1}^{T_2}}U{A}_2\left(t\right)dt+\cdots +{\displaystyle \sum _{T_{n-1}}^{T_n}}U{A}_n\left(t\right)dt\right],\\ \hfill \mathrm{f}\mathrm{o}\mathrm{r}{T}_r=0\end{array}\hfill \\ \hfill \\ \frac{1}{T}\left[{\displaystyle \sum _0^{T_1}}U{A}_1\left(t\right)dt+{\displaystyle \sum _{T_1}^{T_1+T_r}}U{A}_{\mathrm{2,1}}\left(t\right)dt+{\displaystyle \sum _{T_1+T_r}^{T_2}}U{A}_{\mathrm{2,2}}\left(t\right)dt+\cdots \right.\hfill \\ +\left.{\int }_{T_{n-1}}^{T_{n-1}+T_r}U{A}_{n,1}\left(t\right)dt+{\displaystyle \sum _{T_{n-1}+T_r}^{T_n}}U{A}_{n,2\left(t\right)}dt\right],\mathrm{f}\mathrm{o}\mathrm{r}{T}_r>0.\hfill \end{array}\right.\hfill \end{array}(29)$

4 Case studies and performance analysis

The shut-in pressure in new oil and gas fields exceeds the design pressure capacity for flowlines and risers. Without a pressure protection system, the flowline and risers would be overpressured and could rupture upon topside shutdown or other flow blockage. The subsea high-integrity pressure protection system (HIPPS) is an important part of the overall pressure protection system in subsea production. The system is typically designed to withstand adverse operating conditions, namely, high pressure and temperature, as well as harsh environmental conditions that may promote erosion and corrosion of the system parts. A HIPPS is subjected to different test and maintenance strategies in accordance with relevant standards to promote improved dynamic performance. It is typically configured in a basic 1oo1 or 1oo2 set-up. Due to its operating conditions, the mechanical components are subject to gradual degradation leading up to failures but also may experience random instantaneous failures. Access to any failures revealed during a test is difficult due to their location and requires planning before repair is carried out, resulting in a delay before repair. The reservoir pressure decays rapidly when the field is producing. After 4–5 years, the shut-in pressure is expected to be below the capacity of the flowlines and risers, and the HIPPS valves can be locked open Bak and Roald Sirevaag (2007). Based on this consideration, the HIPPS will serve as an application case for the proposed approach.

The HIPPS system is designed to comply with the IEC61508/IEC61511 standards to fulfill the safety integrity level requirements for a system in low-demand mode at SIL3 (NOG GL-070:2018).

To apply the proposed approach, the relevant parameters for the HIPPS are chosen as: $\alpha =3$, ${\lambda }_1=4e-06$, ${\lambda }_2=1e-6$. The value for $\alpha$ is chosen for a situation where two or three failure mechanisms can lead to failure (Vatn, 2007). In the case of HIPPS, this may include insufficient actuator force, excessive erosion, corrosion due to an unclean medium, etc. The value of ${\lambda }_1$ is then estimated using the formula for mean time to failure (MTTF) of the Weibull distribution $\left({\lambda }_1=\frac{\mathrm{\Gamma }\left(\frac{1}{\alpha }+1\right)}{MTTF}\right)$ with data from a reliability data handbook (Hauge et al., 2013). The value of ${\lambda }_2$ is also selected based on data from a reliability data handbook for similar installations (Hauge et al., 2013). Typical repair delays can range between 1 week and 2 months. For the purpose of this analysis, $T_r$ is assumed to be 1 month (730 h). The mission time is set as 5 years, $T$, as discussed above. We also consider a periodic and non-periodic testing strategy for a period of 5 years:

$•$ Periodic testing is carried out with constant intervals between the tests.

$•$ Non-periodic testing is carried out with non-constant intervals between the tests.

To keep the assessment of unavailability consistent, we consider the time of the first test to be the same for both periodic and non-periodic testing. This is to ensure consistency from the second interval because the unavailability due to repairs of revealed failures in the first interval is carried over and considered a part of the second interval (Equation 14; Equation 15). The first test is assumed to be after 6 months (4,380 h).

For periodic testing with intervals of 1 year (8,760 h), the following are the test times: T1 = 4,380 h, T2 = 13,140 h, T3 = 21,900 h, T4 = 30,660 h, T5 = 39,420 h, and T6 = 43,800 h. For non-periodic testing, we consider decreasing test intervals of 17,520 h, 13,140 h, and 8,760 h after the first test as follows: T1 = 4,380 h, T2 = 21,900 h, T3 = 35,040 h, and T4 = 43,800 h.

4.1 Instantaneous unavailability analysis

We analyze the unavailability of the system for both 1oo1 and 1oo2 systems using Equations 12–21. We consider different cases as follows:

$•$ Case 1. 1oo1 configuration tested with periodic and non-periodic test strategies without repair delays

$•$ Case 2. 1oo2 configuration tested with periodic and non-periodic test strategies without repair delays

$•$ Case 3. 1oo1 configuration tested with periodic and non-periodic test strategies with repair delays

$•$ Case 4. 1oo2 configuration tested with periodic and non-periodic test strategies with repair delays

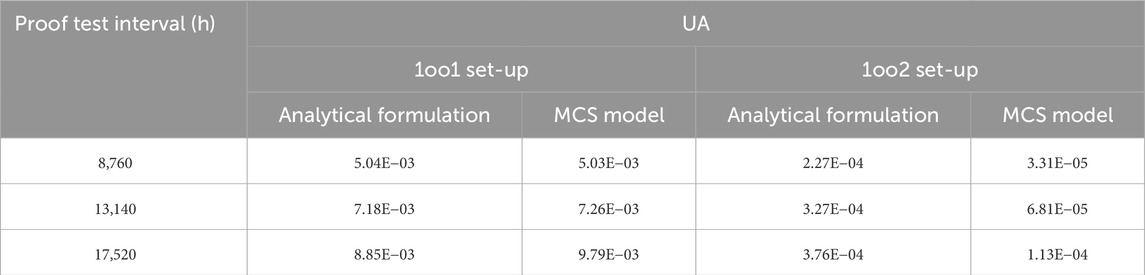
From Figure 3, we observe the general trend for the unavailability as a linear increase for a 1oo1 system and a non-linear increase for a 1oo2 system.

Figure 3

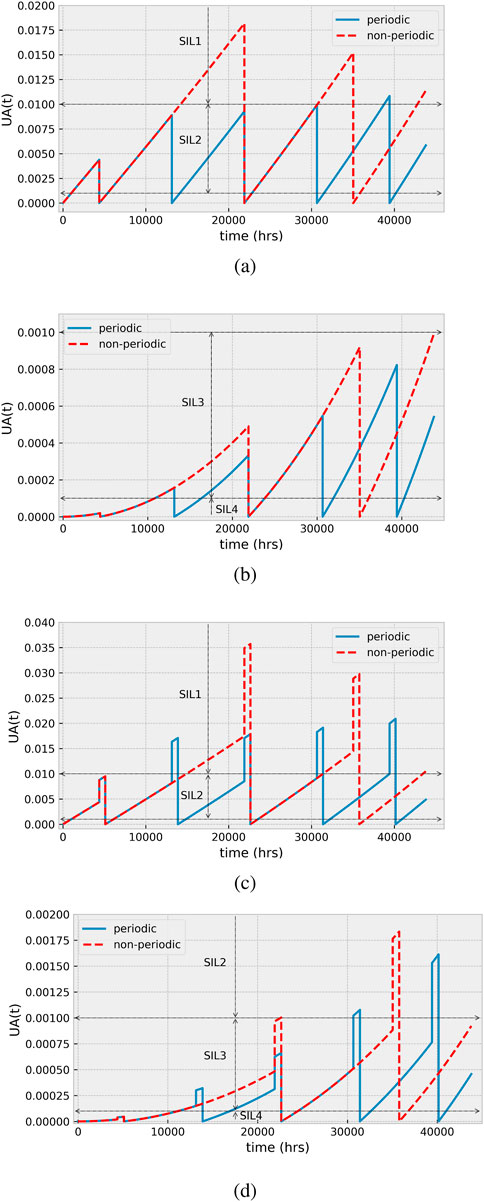
Figure 3. Comparison of instantaneous unavailability for periodic and non-periodic test intervals for (A) Case 1, (B) Case 2, (C) Case 3, and (D) Case 4.

For the 1oo1 configuration, the instantaneous unavailability increases with subsequent test intervals, with the highest point reached just before the fifth test at 39,420 h with periodic testing. On the other hand, the non-periodic testing has a decreasing instantaneous unavailability in subsequent intervals after the second interval in keeping with the decreasing test intervals, with the highest point reached just before the second test (Figures 3A, C).

For a 1oo2 system, the trend is similar for both periodic and non-periodic test intervals. The instantaneous unavailability increases with subsequent test intervals, with the peak coming just before the fifth test for the periodic test and at the end of the mission time for non-periodic testing with no repair delays (Figure 3B). However, in the case with repair delays, both periodic and non-periodic reach their peak unavailability just before the repair is completed following the last test within the mission time (Figure 3D).

In terms of reliability, the 1oo1 configuration with no repair delays achieves SIL 2 for all the intervals except the fifth test interval with periodic testing. With non-periodic testing, SIL 2 is achieved only within the first interval, with the rest of the interval reaching SIL 1. On the other hand, considering repair delays, both test strategies achieve SIL 1 for all intervals except the first (both strategies) and the last (periodic testing only) intervals.

For a 1oo2 system, SIL 3 is achieved for all intervals for both periodic and non-periodic test intervals without repair delays. With repair delay, SIL 2 is reached from the third and fourth test intervals for non-periodic and periodic test strategies, respectively, and it returns to within SIL 3 for the remainder of the mission time following the penultimate test.

4.2 Average unavailability analysis

Although the instantaneous unavailability shows the trend for unavailability, the average unavailability gives a measure of the expected proportion of time the system is unavailable within a given period. We consider two analyses of the average unavailability:

1. Test intervals. As we saw in Section 4.1, the rate of increase of the instantaneous unavailability is different for different test intervals influenced by the test strategy. Therefore, we analyze the average unavailability for the different intervals.

2. Mission time. It could also be interesting to consider the entire mission time for the system. This is particularly useful for selecting a strategy that gives an overall lower unavailability.

4.2.1 Test intervals

We analyze the average unavailability for both 1oo1 and 1oo2 configurations for different test intervals using Equations 23–28 and for the same cases as in Section 4.1.

The results show that generally, the periodic test strategy gives lower average unavailability than the non-periodic testing strategy (Figure 4); however, both strategies achieve a minimum SIL2 for a 1oo1 system and a minimum SIL3 for a 1oo2 system for all intervals.

Figure 4

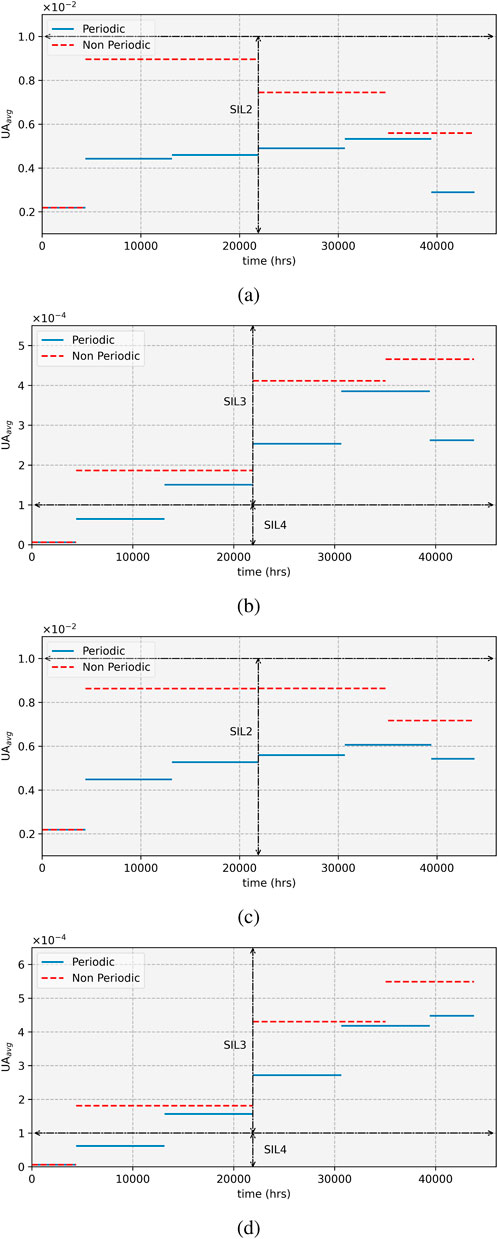
Figure 4. Comparison of average unavailability for periodic and non-periodic test intervals for (A) Case 1, (B) Case 2, (C) Case 3, and (D) Case 4.

The decreasing test intervals of the non-periodic strategy are reflected in the decreasing average unavailability from the second interval for subsequent intervals for a 1oo1 set-up, as illustrated in Figures 4A, C. However, this is not the case with the 1oo2 set-up, as the average unavailability increases for subsequent intervals, albeit the difference gradually reduces with the decreasing non-periodic test intervals (Figures 4B, D).

Given a SIL target of SIL2 for a 1oo1 and SIL3 for a 1oo2 set-up, the non-periodic testing strategy gives a better option from an economic perspective, as the number of tests is reduced. On the other hand, a target $\mathrm{P}\mathrm{F}{\mathrm{D}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$ may be given, and more frequent testing may therefore become necessary to meet the target. In this case, the periodic testing strategy becomes desirable.

4.2.2 Mission time

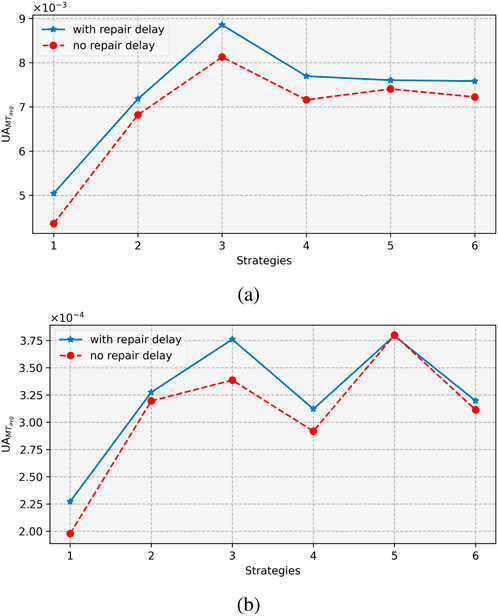
In this section, we consider the entire mission time for the system. We analyze the average unavailability for the entire mission time, considering different testing strategies using Equation 29. We also compare for repair delays and with no repair delays. The following testing strategies are used:

$•$ Strategy 1. Periodic test intervals (1 year): T1 = 4,380 h, T2 = 13,140 h, T3 = 21,900 h, T4 = 30,660 h, T5 = 39,420 h, and T6 = 43,800 h

$•$ Strategy 2. Periodic test intervals (1.5 years): T1 = 4,380, T2 = 17,520, T3 = 30,660, and T4 = 43,800

$•$ Strategy 3. Periodic test intervals (2 years): T1 = 4,380 h, T2 = 21,900, T3 = 39,420, and T4 = 43,800

$•$ Strategy 4. Non-periodic test intervals (decreasing). T1 = 4,380 h, T2 = 21,900 h, T3 = 35,040 h, and T4 = 43,800 h.

$•$ Strategy 5. Non-periodic test intervals (increasing). T1 = 4,380 h, T2 = 13,140, T3 = 26,280, and T4 = 43,800

$•$ Strategy 6. Non-periodic test intervals (mixed). T1 = 4,380, T2 = 21,900, T3 = 30,660, and T4 = 43,800

Strategies 1–3 are variants of periodic testing with intervals of 1 year, 1.5 years, and 2 years, respectively. Strategies 4–6 are variants of non-periodic testing with decreasing test intervals (i.e., intervals between subsequent tests decrease, $T_n-T_{n-1}<T_{n-1}-T_{n-2}$ for $n\ge 3$), increasing test intervals (i.e., intervals between subsequent tests increase, $T_n-T_{n-1}>T_{n-1}-T_{n-2}$ for $n\ge 3$) and mixed test intervals (i.e., the interval between subsequent tests increases, then the following interval decreases, $T_1-T_0<T_2-T_1>T_3-T_2$), respectively.

Figure 5 shows the results for the different strategies. Generally, with periodic testing, the unavailability increases with the length of the interval between the tests for both 1oo1 and 1oo2 configurations and for both delays before repair and without delays. For non-periodic testing, the three strategies (4–6) have similar performance trends for the 1oo2 set-up and for the 1oo1 set-up without repair delays. For this group, the decreasing test interval (Strategy 4) gives the lowest unavailability, while the increasing test (Strategy 5) interval gives the highest unavailability. For a 1oo1 set-up with a repair delay, the decreasing interval (Strategy 4) gives the highest unavailability, while the mixed test interval (Strategy 6) gives the lowest.

Figure 5

Figure 5. Average unavailability for the entire mission time for (A) 1oo1 and (B) 1oo2 systems.

4.3 Effect of parameters on unavailability

In this section, we examine the effect of different parameters on the average unavailability of the system for both 1oo1 and 1oo2 configurations with periodic and non-periodic testing strategies. Based on their performance, Strategy 1 is selected for periodic testing, and Strategy 4 is selected f or non-periodic testing. The strategies are described in Section 4.2.2.

4.3.1 Combined effect of ${\lambda }_1$ and repair delay $(T_r)$

We examine the combined effect of ${\lambda }_1$ and repair delay $T_r$ on the average unavailability of the system. The value of ${\lambda }_1$ ranges from $10^{-7}$ to $10^{-5}$, while the value of $T_r$ ranges from 0 h to 1,460 h. Other parameters are given in Section 4.

Figure 6 shows the result of the analysis. On the y-axis, we have ${\lambda }_1$, and on the x-axis, we have $T_r$. The color bar indicates the range of the average unavailability (log scaled).

Figure 6

Figure 6. Effect of ${\lambda }_1$ and repair delay $(T_r)$ on average unavailability for (A) a 1oo1 set-up with periodic testing, (B) a 1oo2 set-up with periodic testing, (C) a 1oo1 set-up with non-periodic testing, and (D) a 1oo2 set-up with non-periodic testing.

For periodic testing strategies (Figures 6A, B), a change in SIL occurs at high values of ${\lambda }_1$ for the given range of $T_r$. For instance, for the 1oo1 set-up, the unavailability changes from SIL 2 to SIL1 at ${\lambda }_1>9.7\cdot 10^{-6}$ when $T_r=0$ and at ${\lambda }_1>8.3\cdot 10^{-6}$ when $T_r=\mathrm{1,460}$. For a 1oo2 set-up, the change from SIL 3 to SIL 2 occurs at ${\lambda }_1>9.6\cdot 10^{-6}$ when $T_r=0$, similar to the 1oo1 set-up, and it changes at ${\lambda }_1>8.9\cdot 10^{-6}$ when $T_r=\mathrm{1,460}$. Based on these values, repair delays of up to 2 months (1,460 h) can be tolerated when employing the periodic test strategies as long as ${\lambda }_1<8.3\cdot 10^{-6}$ for a 1oo1 set-up and ${\lambda }_1<8.9\cdot 10^{-6}$ for a 1oo2 set-up, given that all other parameters are maintained.

For non-periodic test strategies (Figures 6C, D), the threshold for ${\lambda }_1$ is lower for changes in SIL. For a 1oo1 set-up, the threshold is at $7.1\cdot 10^{-6}$ for $T_r=0$ and $6.1\cdot 10^{-6}$ for $T_r=\mathrm{1,460}$. For a 1oo2 set-up, $T_r$ appears to have little effect on average unavailability with the threshold at $8.7\cdot 10^{-6}$ for $T_r=0$ and at $8.4\cdot 10^{-6}$ for $T_r=\mathrm{1,460}$. Based on these values, repair delays up to 2 months (1,460 h) are tolerable with non-periodic test strategies as long as ${\lambda }_1<6.1\cdot 10^{-6}$ for a 1oo1 set-up and ${\lambda }_1<8.4\cdot 10^{-6}$ for a 1oo2 set-up, given that all other parameters are maintained.

In summary, for the 1oo1 set-up, while the non-periodic strategy reduces the number of tests, which in turn reduces the number of stoppages, saves costs, and reduces production losses, the threshold for ${\lambda }_1$ is much lower than it is for periodic testing. In deciding the strategy for this set-up, the operator must make a trade-off from an economic perspective. If ${\lambda }_1$ exceeds the given threshold for the non-periodic strategy, some risk-reducing measure can be put in place to compensate for the increase in ${\lambda }_1$. First, the length of the repair delay can be reduced; however, this can be expensive as the length of delays is often tied to the availability of maintenance resources. For instance, having a repair vessel on standby, whether needed or not, can reduce repair delays but comes at an extra cost compared to booking one when needed, which will be subject to availability and thus can lengthen repair delays. Another measure can be a partial upgrade of parts of the system to reduce the failure rate. The cost of implementing these measures is then compared to the cost of switching to the periodic test strategy, which will involve more testing, resulting in more test costs, stoppages, and production loss. For a 1oo2 set-up, non-periodic testing seems more desirable from an economic perspective as the number of tests is reduced while also maintaining a high threshold for ${\lambda }_1$.

4.3.2 Combined effect of ${\lambda }_2$ and repair delay $(T_r)$

Here, we look at the effect of ${\lambda }_2$ and $T_r$ on average unavailability while keeping ${\lambda }_1$ constant. As with the previous section, ${\lambda }_2$ ranges from $10^{-7}$ to $10^{-5}$ while $T_r$ ranges from 0 to 1,460.

From Figure 7, we see that average unavailability is more sensitive to changes in ${\lambda }_2$ than ${\lambda }_1$ in the previous section, with values ranging from SIL 1 to SIL 3 for a 1oo1 set-up with periodic testing, SIL 1 to SIL 2 for a 1oo1 set-up with non-periodic testing, and SIL 1 to less than SIL 4 for a 1oo2 set-up with both testing strategies. Assuming a minimum requirement of SIL2 for a 1oo1 set-up and a minimum requirement of SIL3 for a 1oo2 set-up, adopting periodic testing requires a maximum threshold for ${\lambda }_2$ between $2.5\cdot 10^{-6}$ to $1.9\cdot 10^{-6}$ as $T_r$ increases from 0 h to 1,460 h for a 1oo1 set-up and between $2.3\cdot 10^{-6}$ to $2.0\cdot 10^{-6}$ for a 1oo2 set-up.

Figure 7

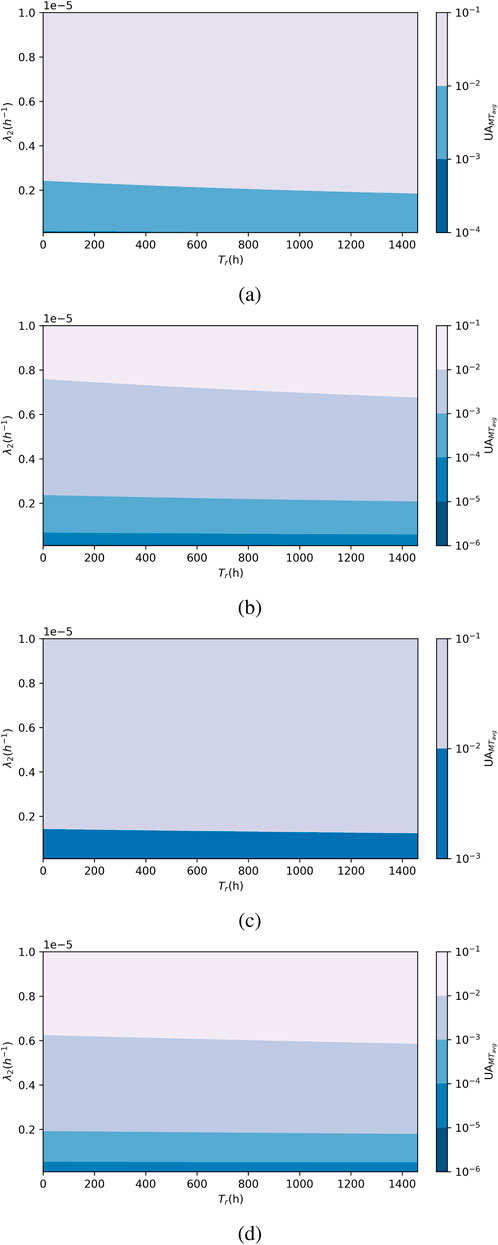
Figure 7. Effect of ${\lambda }_2$ and repair delay $(T_r)$ on average unavailability for (A) a 1oo1 set-up with periodic testing, (B) a 1oo2 set-up with periodic testing, (C) a 1oo1 set-up with non-periodic testing, and (D) a 1oo2 set-up with non-periodic testing.

The threshold is lower for the non-periodic test strategy and requires ${\lambda }_2$ to be less than values between $1.5\cdot 10^{-6}$ to $1.3\cdot 10^{-6}$ as $T_r$ increases from 0 h to 1,460 h for a 1oo1 set-up and between $2.0\cdot 10^{-6}$ and $1.9\cdot 10^{-6}$ for a 1oo2 set-up.

A lower threshold for ${\lambda }_2$ means lower tolerance for failure occurrence. For selection of test strategy, the non-periodic test strategy can tolerate repair delays of up to 2 months as long as ${\lambda }_2$ can be kept below $1.3\cdot 10^{-6}$ and $1.9\cdot 10^{-6}$ for a 1oo1 and a 1oo2 set-up, respectively. The periodic test strategy, on the other hand, has a threshold of $1.9\cdot 10^{-6}$ and $2.0\cdot 10^{-6}$ for a 1oo1 and a 1oo2 set-up, respectively, for the same conditions. Therefore, the non-periodic test strategy is desirable for a 1oo2 set-up because the threshold is similar to that of the periodic strategy. For a 1oo1 set-up, a trade-off must be made between implementing measures to reduce ${\lambda }_2$ (occurrence of fFM2) or switching to periodic testing. It must be noted, however, that switching to periodic testing does not offer a significant improvement in terms of increased threshold for ${\lambda }_2$, and it is only desirable to switch if improving the reliability of the component with respect to FM2 is more expensive than running more tests.

4.3.3 Combined effect of ${\lambda }_1$ and ${\lambda }_2$

In this section, we analyze the effect of ${\lambda }_1$ and ${\lambda }_2$ on average unavailability while keeping $T_r$ constant. Both ${\lambda }_1$ and ${\lambda }_2$ range from $10^{-7}$ to $10^{-5}$. The range of values for these parameters is chosen arbitrarily to encompass the relevant parameters of the study case. These values serve to illustrate how changes in the said values will affect the resulting average unavailability.

The result in Figure 8 shows average unavailability ranging from SIL 1 to SIL 3 for a 1oo1 set-up and from SIL 1 to below SIL 4 for a 1oo2 set-up.

Figure 8

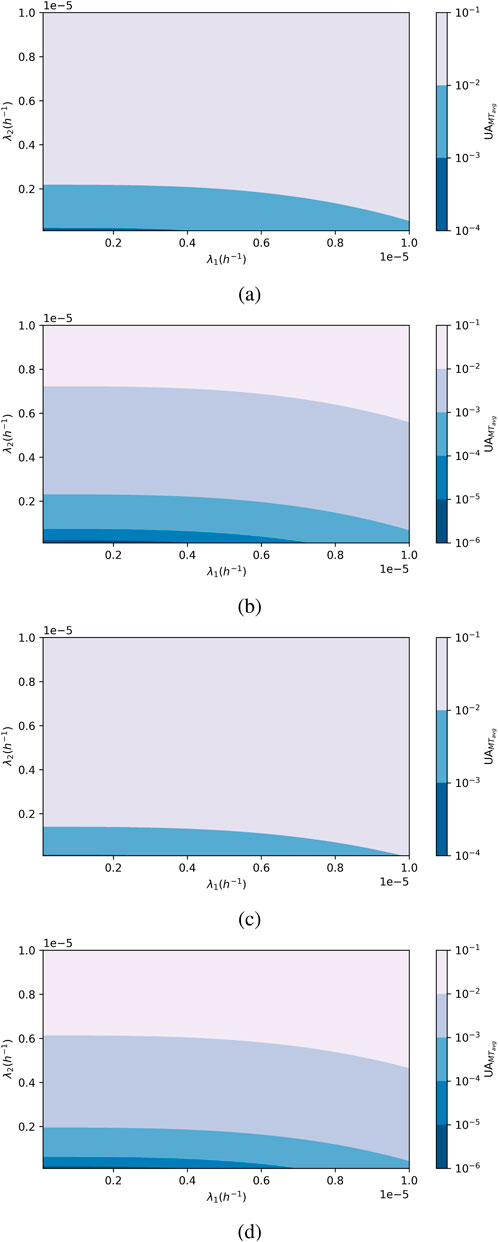
Figure 8. Effect of ${\lambda }_1$ and ${\lambda }_2$ on average unavailability of (A) a 1oo1 set-up with periodic testing, (B) a 1oo2 set-up with periodic testing, (C) a 1oo1 set-up with non-periodic testing, and (D) a 1oo2 set-up with non-periodic testing.

To determine the threshold for minimum SIL requirement, we first look at the maximum tolerable value for ${\lambda }_2$ at the lowest value of ${\lambda }_1$ in our range. This value is $2.1\cdot 10^{-6}$ for a 1oo1 and $2.3\cdot 10^{-6}$ for a 1oo2 set-up, respectively. Next, we look at the maximum tolerable value for ${\lambda }_1$ at these values of ${\lambda }_2$. We have $3.8\cdot 10^{-6}$ and $2\cdot 10^{-6}$ for a 1oo1 and a 1oo2 set-up, respectively. This means given $T_r=730$, we will always meet the minimum SIL requirement with periodic testing as long as ${\lambda }_1\le 3.8\cdot 10^{-6}$ and ${\lambda }_2\le 2.1\cdot 10^{-6}$ for a 1oo1 set-up and ${\lambda }_1\le 2\cdot 10^{-6}$ and ${\lambda }_2\le 2.3\cdot 10^{-6}$ for a 1oo2 set-up. It is important to note that the minimum SIL requirement can still be met at higher values of ${\lambda }_1$ but will require significantly lower values of ${\lambda }_2$. On the other hand, exceeding the given threshold of ${\lambda }_2$ will result in failure to meet the required target.

For a non-periodic test strategy, the threshold is at ${\lambda }_1\le 2.1\cdot 10^{-6}$, ${\lambda }_2\le 1.4\cdot 10^{-6}$ for a 1oo1 set-up and ${\lambda }_1\le 3.3\cdot 10^{-6}$, ${\lambda }_2\le 1.9\cdot 10^{-6}$ for a 1oo2 set-up.

This result shows that FM2 has a significantly higher impact on average unavailability than FM1. In terms of reliability performance improvement, efforts should be made to reduce the occurrence of FM2; otherwise, more frequent testing should be adopted. On the other hand, if ${\lambda }_2$ can be kept low, a non-periodic test strategy will be suitable to meet the required target while reducing costs.

5 Monte Carlo simulation for verification

A Monte Carlo simulation (MCS) is applied to verify the proposed analytical formulations. The simulation is performed with codes written using the Python programming language. The simulation procedures for a 1oo1 and a 1oo2 system are briefly described below.

5.1 Monte Carlo simulation model for a 1oo1 system

We define the following variables for the simulation: t (global simulation time), TFM1 and TFM2 (time of occurrence of FM1 and FM2, respectively), Ttest (time of test), TI (test intervals), Tr (calendar time of repair), TFail (calendar time of system failure), sysFailed (logical state of the system; 0 if the system is working and 1 if the system failed), CumFail (cumulative time system spends in a failed state).

1. Initialize the system and system characteristics and relevant variables: sysFailed = 0, t = 0, Ttest = TI, and Tr = inf (infinity).

2. Draw time until occurrence of each failure mode: TFM1 = T $\sim Weib(\alpha ,{\lambda }_1)$ and TFM2 = T $\sim Expon({\lambda }_2)$.

3. Select the next transition time: t = min{TFM1, TFM2, Ttest, Tr}

4. Update the variables and system statistics as relevant depending on the selected event as follows:

i. if t = TFM1 or t = TFM2, the system will fail if it is not already in a failed state. Thus, if sysFailed = 0, then sysFailed = 1, TFail = t, and TFM1 or TFM2 = inf.

ii. if t = Ttest: we check if the system is in a failed state and activate repair. Thus, if sysFailed = 1, then Tr = t + repairDelay. The next test time then becomes Ttest = t + TI.

iii. if t = Tr, the repair is completed, and sysFailed = 0. Next, the repair time is set to infinity (Tr = inf). We update the time the system spent in a failed state: CumFail = CumFail + (t − TFail). Finally, we draw next time until failure occurrence of each failure mode: TFM1 = t + T $\sim Weib(\alpha ,{\lambda }_1)$, TFM2 = t + T $\sim Expon({\lambda }_2)$.

5. We repeat steps 3 and 4 until the simulation time, t, is greater than the time horizon (mission time) under consideration.

6. Then, we repeat all the steps for a sufficient number of simulations, N.

7. The average unavailability is then calculated as the total time the system spends in the failed state divided by the product of the mission time and number of simulations (N), $U{A}_{\mathit{MCS}}=\frac{CumFail}{missionTime\cdot N}$

5.2 Monte Carlo simulation model for a 1oo2 system

The model for the 1oo2 system is similar to that of 1oo1 except with added variables to reflect the added component in the system. In addition to the variables defined above, we introduce the following variables: C1Failed and C2Failed to represent the logical state of the components similar to the variable sysFailed. In addition, we have TC1FM1 and TC1FM2 (for time to occurrence of FM1 and FM2, respectively) for component 1 and TC2FM1 and TC2FM2 (for time to occurrence of FM1 and FM2, respectively) for component 2.

The steps are as follows:

1. Initialize the system and system characteristics and the relevant variables: C1Failed = 0, C2Failed = 0, sysFailed = 0, Ttest = TI, and Tr = inf.

2. Draw time until occurrence of the failure modes for each component: TC1FM1 $\sim Weib(\alpha ,{\lambda }_1)$, TC1FM2 $\sim Expon({\lambda }_2)$, TC2FM1 $\sim Weib(\alpha ,{\lambda }_1)$, and TC2FM2 $\sim Expon({\lambda }_2)$.

3. Select the next transition time: t = min{TC1FM1, TC1FM2, TC2FM1, TC2FM2, Ttest, Tr}.

4. Update the variables and system statistics as relevant depending on the selected event as follows:

i. if t = TC1FM1 or t = TC1FM2, then if C1 = 0, C1 then becomes 1, and TC1FM1 or TC1FM2 is set to infinity as relevant.

ii. if t = TC2FM1 or t = TC2FM2, then if C2 = 0, C2 then becomes 1, and TC2FM1 or TC2FM2 is set to infinity as relevant.

iii. if t = Ttest: we check for component failure and activate repair if any component is in a failed state. Thus, if C1Failed = 1 or C2Failed = 1, then Tr = t + repairDelay. The next test time then becomes Ttest = t + TI.

iv. if t = Tr, the repair is completed. The time of the next repair is set to infinity (Tr = inf) and:

$•$if sysFailed = 1, then sysFailed = 0, and CumFail = CumFail + (t − Tfail)

$•$if C1Failed = 1, then C1Failed = 0, and we draw time until the occurrence of the next failure of component 1.

$•$if C2Failed = 1, then C2Failed = 0, and we draw time until the occurrence of the next failure of component 2.

v. we check for system failure: if C1Failed = 1 and C2Failed = 1 and sysFailed = 0, then sysFailed = 1, and Tfail = t.

vi. we repeat steps 3 to 5 until simulation time, t, is greater than the time horizon (mission time) under consideration.

vii. then we repeat all steps for a sufficient number of simulations, N.

viii. we calculate the average unavailability as described in the previous section.

The results of the simulation are shown in Table 2. The number of simulations for a 1oo1 and a 1oo2 set-up is kept fixed at $N=1x10^7$. The results from the simulations are closed to that of the numerical results from the analytical formulas for a 1oo1 set-up. For the 1oo2 set-up, the analytical formulas are slightly higher but provide a conservative result. Compared to MCS, the analytical formulas provide faster computation time.

Table 2

Table 2. Average unavailability (UA) for different test intervals.

6 Conclusion and further works

In this paper, we have explored the analysis of unavailability for the final element of an SIS operating in a subsea environment and subject to heterogeneous failure modes. Analytical formulations have been developed to incorporate degradation and random failures in the assessment. Furthermore, delays following tests have been incorporated in these formulations to examine the impact of delayed repair on system unavailability. The Weibull distribution has been adopted to model the degradation of the component, while the exponential distribution has been adopted to model random failures.

We focus on the HIPPS valves in the case study. Analyses are done for the time-dependent unavailability and average unavailability for different testing strategies. The results show that the periodic testing strategy generally gives lower unavailability, although it requires more testing to be carried out than a non-periodic testing strategy. However, both strategies are likely to meet a given SIL target, making the non-periodic strategy a more desirable option from an economic perspective. The effects of the parameters were also studied for both strategies. The selection of a strategy should be made based on the reliability of the valves in terms of failure occurrence, paying particular attention to random failures (FM2). Another issue to consider is the availability of maintenance resources, which will impact the length of the repair delay.

The work done in this paper is limited to full-proof tests only. Partial tests have been shown to improve the reliability performance of an SIS. An extension of this work will be to incorporate partial tests into the formulation. Another issue that can be considered is the incorporation of common cause failures, as the components in this work are assumed to be independent.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

ED: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. YL: conceptualization, funding acquisition, methodology, project administration, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research receives support from the IKTPLUSS program (Project No. 309628) and the NORGLOBAL2 program (Project No. 322410) of the Research Council of Norway.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bak, L., and Roald Sirevaag, H. S. (2007). Hipps protects subsea production in hp/ht conditions. Available at: https://www.offshore-mag.com/subsea/article/16760889/hipps-protects-subsea-production-in-hp-ht-conditions.

Google Scholar

Chebila, M., and Innal, F. (2015). Generalized analytical expressions for safety instrumented systems’ performance measures: pfdavg and pfh. J. Loss Prev. Process Industries 34, 167–176. Available at: https://www.sciencedirect.com/science/article/pii/S0950423015000480doi:10.1016/j.jlp.2015.02.002

CrossRef Full Text | Google Scholar

Hauge, S., Hokstad, P., Corneliussen, K., and Sikkerhet, S. (2013). Reliability prediction method for safety instrumented systems: PDS method handbook. Technical Report. Trondheim: SINTEF Technology and Society.

Google Scholar

IEC (2017). Internationa electrotechnical vocabulary. Available at: https://std.iec.ch/iev/iev.nsf/display?openformievref=821-12-54.

Google Scholar

IEC 61508 (2010). Functional safety of electrical/electronic/programmable electronic safety-related systems – Part 1-7. Geneva: International Electrotechnical Commission.

Google Scholar

IEC 61511 (2016). Functional safety-safety instrumented systems for the process industry sector. Geneva: International Electrotechnical Commission.

Google Scholar

Jigar, A. A. (2013). Quantification of reliability performance: analysis methods for safety instrumented system. Master’s thesis. Trondheim: NTNU.

Google Scholar

Liu, Y., and Rausand, M. (2011). Reliability assessment of safety instrumented systems subject to different demand modes. J. Loss Prev. Process Industries 24, 49–56. doi:10.1016/j.jlp.2010.08.014

CrossRef Full Text | Google Scholar

NOG GL-070:(2018). Application of IEC 61508 and IEC 61511 in the Norwegian petroleum industry. Guideline. Norwegian oil and gas. Stavanger.

Google Scholar

Oliveira, F. (2018). General theory of evaluation of pfd of sis subject to periodic testing. DNV-GL Intern. Guidel.

Google Scholar

Oliveira, F., Domingues, J., Hafver, A., Lindberg, D., and Pedersen, F. (2016). “Evaluation of pfd of safety systems with time-dependent and test step-varying failure rates,” in Risk, reliability and safety: innovating theory and practice: proceedings of ESREL 2016, 413.

CrossRef Full Text | Google Scholar

Rausand, M. (2004). System reliability theory: models, statistical methods, and applications.

Google Scholar

Rausand, M. (2014). Reliability of safety-critical systems: theory and applications. John Wiley and Sons.

Google Scholar

Rausand, M. (2021). System reliability theory: models, statistical methods, and applications.

Google Scholar

Rogova, E., Lodewijks, G., and Lundteigen, M. A. (2017). Analytical formulas of pfd and pfh calculation for systems with nonconstant failure rates. Proc. Institution Mech. Eng. Part O J. Risk Reliab. 231, 373–382. doi:10.1177/1748006X17694999

CrossRef Full Text | Google Scholar

Srivastav, H., Barros, A., and Lundteigen, M. A. (2020). Modelling framework for performance analysis of sis subject to degradation due to proof tests. Reliab. Eng. and Syst. Saf. 195, 106702. Available at: https://www.sciencedirect.com/science/article/pii/S0951832019301450doi:10.1016/j.ress.2019.106702

CrossRef Full Text | Google Scholar

Torres-Echeverría, A., Martorell, S., and Thompson, H. (2009). Modelling and optimization of proof testing policies for safety instrumented systems. Reliab. Eng. and Syst. Saf. 94, 838–854. Available at: https://www.sciencedirect.com/science/article/pii/S0951832008002287doi:10.1016/j.ress.2008.09.006

CrossRef Full Text | Google Scholar

Vatn, J. (2007). “Veien frem til world class maintenance: maintenance optimisation,” in A course in railway maintenance optimisation arranged (Trondheim, Norway: the Norwegian University of Science and Technology NTNU).

Google Scholar

Wu, S., Zhang, L., Lundteigen, M. A., Liu, Y., and Zheng, W. (2018). Reliability assessment for final elements of siss with time dependent failures. J. Loss Prev. Process Industries 51, 186–199. Available at: https://www.sciencedirect.com/science/article/pii/S0950423017305430doi:10.1016/j.jlp.2017.12.007

CrossRef Full Text | Google Scholar

Wu, S., Zhang, L., Zheng, W., Liu, Y., and Lundteigen, M. A. (2019). Reliability modeling of subsea siss partial testing subject to delayed restoration. Reliab. Eng. and Syst. Saf. 191, 106546. doi:10.1016/j.ress.2019.106546

CrossRef Full Text | Google Scholar

Zhang, A., Barros, A., and Liu, Y. (2019). Performance analysis of redundant safety-instrumented systems subject to degradation and external demands. J. Loss Prev. Process Industries 62, 103946. Available at: https://www.sciencedirect.com/science/article/pii/S0950423019305741doi:10.1016/j.jlp.2019.103946

CrossRef Full Text | Google Scholar