- 1Laboratoire de Maitrise des Energies Renouvelables, Faculté de Technologie, Université de Bejaia, Bejaia, Algeria
- 2Institute of Sustainable Energy, Universiti Tenaga Nasional, Kajang, Malaysia
- 3Department of Electric Energy, Norwegian University of Science and Technology, Trondheim, Norway
- 4School of Physics, Engineering and Technology, University of York, York, United Kingdom
- 5Fukushima Renewable Energy Institute, National Institute of Advanced Industrial Science and Technology (AIST), Koriyama, Japan
This study investigates strategies for enhancing the performance of dual-star induction generators in wind power systems by optimizing the full control algorithm. The control mechanisms involved include the PID (Proportional-Integral-Derivative) controller for speed regulation and the PI (Proportional-Integral) controller for flux, DC-link voltage, and grid connection control. The primary objective is to optimize the entire system by fine-tuning PID and PI controllers through the application of meta-heuristic algorithms, specifically Grey Wolf Optimization (GWO) and Particle Swarm Optimization (PSO). These algorithms play a crucial role in estimating the optimal values of Kp, Ki, and Kd for the PID speed controller, as well as Kp and Ki for the PI controller used in the flux, DC-link voltage, and grid connection for wind energy conversion system based dual-star induction generator. This comprehensive optimization ensures accurate parameter tuning for optimal system performance. A comparative analysis of the optimization results has been conducted, focusing on the outcomes obtained with the GWO algorithm. The findings reveal a notable reduction in steady-state error, signifying improved stability, and an overall enhancement in the wind power system’s performance. This study contributes valuable insights into the effective application of meta-heuristic algorithms for optimizing dual-star induction generators in wind power systems.
1 Introduction
Renewable energy sources are increasingly seen as a key solution to meet the growing demand for energy while addressing the challenges of global climate change. This need is further driven by industrialization and the vital role that electrical energy plays in satisfying basic human needs (Hamoudi et al., 2023a)- (Chauhan et al., 2021). As part of this transition, renewable sources like wind energy are replacing traditional energy options, helping to create a greener, more sustainable world. Among these renewable sources, wind energy stands out, with the capability to produce 200 times the global electricity demand (Dey et al., 2020)- (Barik et al., 2021).
Wind energy’s role in the global energy transition has spurred various technological innovations. One notable advancement is the use of multiphase drive systems in wind turbines, offering several benefits over conventional three-phase systems. These include enhanced power distribution, reduced current per phase, improved system reliability, lower rotor current harmonics, and decreased torque pulsation. Multiphase systems are particularly advantageous in high-power applications such as electric ship propulsion, locomotive traction, and hybrid vehicles. Recent research has increasingly focused on integrating multiphase systems into wind turbines, particularly through the use of double-star (double three-phase) induction machines (DSIM), which feature two sets of three-phase windings offset by 30 electrical degrees (Ulutas et al., 2020)- (Amimeur et al., 2012).
Effective control of such advanced drive systems relies on vector control techniques, which were introduced by Blascke in 1972. With the advent of microelectronics, these methods became feasible for practical application. This paper employs direct vector control, where flux is controlled through feedback, estimated using stator currents and pulsation (Amimeur, 2008). This approach enhances the efficiency and accuracy of wind turbine performance.
Moreover, modern wind turbines are increasingly adopting variable-speed operation, which provides several advantages over fixed-speed turbines. Variable-speed systems maximize energy capture through techniques like Maximum Power Point Tracking (MPPT), improving overall efficiency and reducing voltage spikes on components. These turbines also allow more precise control over the active and reactive power fed into the grid (Mesai-Ahmed et al., 2021).
In addition to these advancements, PID (Proportional-Integral-Derivative) controllers are widely used for controlling the speed and position of wind turbines (Solihin et al., 2011). As wind power systems grow more complex, there has been a shift toward intelligent optimization techniques to enhance performance. Particle Swarm Optimization (PSO) and Grey Wolf Optimizer (GWO) have emerged as popular metaheuristic algorithms, inspired by nature and applied successfully to wind power systems (Latif et al., 2020). These algorithms have been used for applications such as:
• Control of pitch angles (Hussain et al., 2020a)- (Safiullah et al., 2022).
• Grid connection (Hussain et al., 2020b)- (Iqbal and Singh, 2021).
• Variable wind speed (Sule et al., 2021).
• Hybrid approaches (Hassan et al., 2020)- (Zhang et al., 2019).
• Optimal turbine placement (Shaheen et al., 2021)- (Yasin et al., 2022).
This paper aims to evaluate the application of direct vector control, PSO, and GWO in dual-star induction generators for wind turbines. The study examines the advantages of multiphase drive systems, vector control techniques, variable-speed turbines, PID controllers, and the growing impact of smart optimization methods on improving wind power systems.
The rest of the paper is structured as follows: Section 2 presents the modelling of the wind power system, including the dual-star induction generator and power control strategies. Section 3 explores the use of metaheuristic algorithms to optimize control parameters. Section 4 offers validation studies to benchmark the optimized parameters and evaluate the overall performance of the wind power system, including the dual-star induction generator. Finally, Section 5 provides conclusions and outlines future research directions.
2 Modelling of the wind power system
The wind energy conversion system consists of both mechanical and electrical elements (Basu et al., 2022). The mechanical components involve a wind turbine and gearbox, while the electrical section encompasses the generator, control system, and other interconnected devices.
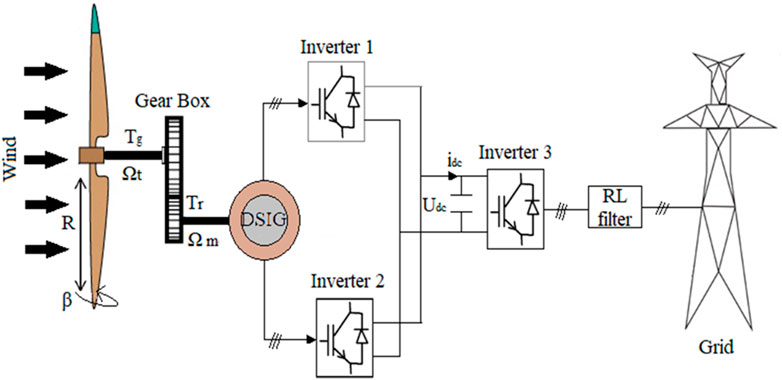
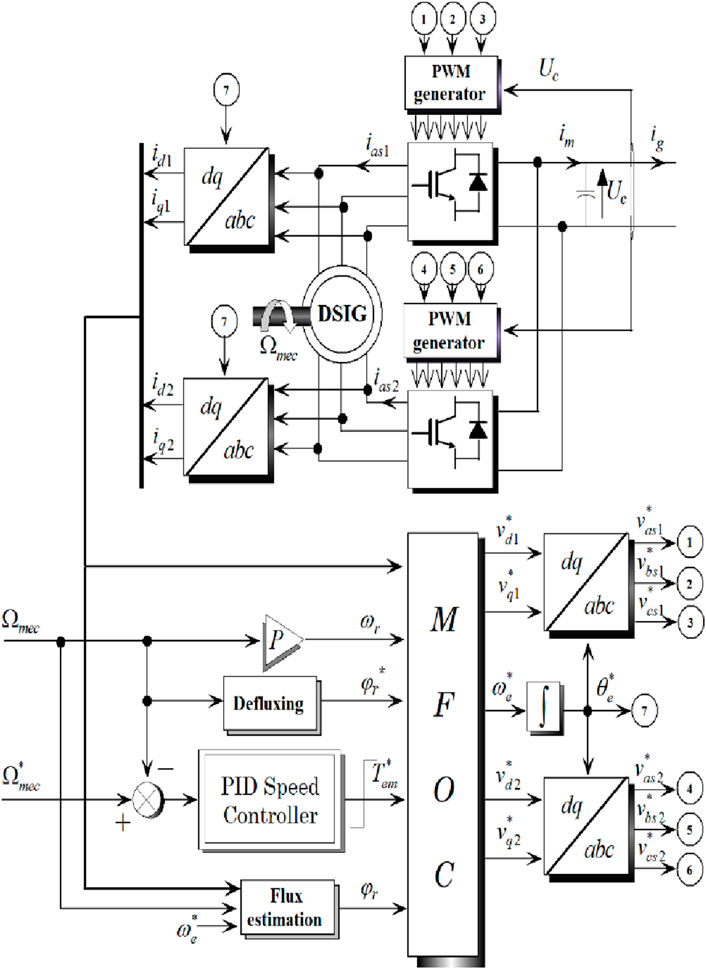
The investigated wind energy conversion system comprises several components, including the Dual Star Induction Generator (DSIG), inverters 1 and 2, the DC link voltage, inverter 3, and the connection to the grid facilitated by a filter. Inverters 1 and 2 are utilized for controlling the speed and flux of the generator, with the control strategy relying on the Maximum Power Point Tracking (MPPT) algorithm. Inverter 3 is responsible for regulating the DC link voltage, managing the active and reactive power exchanged with the grid, and adjusting the current to the correct frequency using Proportional-Integral (PI) controllers. The overall system configuration is depicted in Figure 1.
2.1 Modelling of the wind turbine
The expression (1) defines the transmitted power, Pt, harnessed by the wind turbine.
Here, Cp represents the power coefficient, S denotes the area swept by the blades, ρ represents air density, and V represents wind speed. The turbine’s torque is defined as the ratio of transmitted power to the shaft speed, Ωt, and is expressed as in Equation 2:
The gearbox is employed to match the generator to the turbine. The generator torque Tg and the speed Ωt are given by Equation 3:
The mechanical equation can be defined as in Equation 4:
The power coefficient Cp signifies the aerodynamic efficiency of a wind turbine, and its variation is specific to each turbine and wind speed. It is affected by the blade pitch angle β and the speed ratio λ, which is defined by Equation 5:
Where R denotes the blade radius.
With,
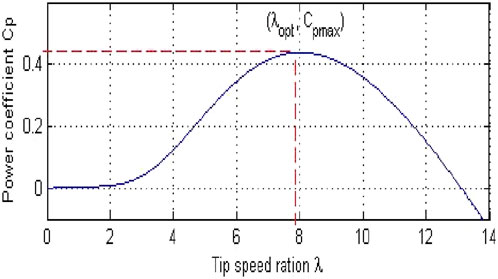
When the pitch angle (β) is set to 0, the graph of Cp (λ), as depicted in Figure 2, is generated using expression (6). The conversion device extracts less power than theoretically recoverable because of the non-zero speed of the air masses upstream of the turbine. This sets a theoretical limit referred to as the Betz limit, corresponding to Cpmax (Benakcha et al., 2017).
The utilization of the MPPT algorithm aims to optimize the power extracted from the wind, thereby improving the efficiency of the conversion process. The power coefficient Cp displays a parabolic shape, reaching its maximum at the optimal speed ratio λopt (Djoudi et al., 2023). The reference speed
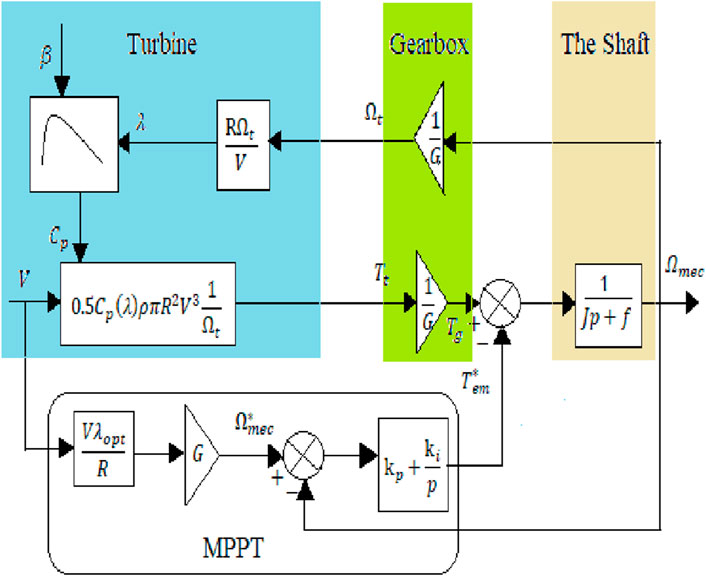
Figure 3 illustrates the block diagram of the turbine model, which includes speed control. The diagram illustrates how wind energy is converted into mechanical energy by the turbine, adjusted by the gearbox, and transferred through the shaft. The MPPT system optimizes the power extraction by controlling the voltage and current, ensuring the turbine operates at its most efficient point.
2.2 Modelling of the dual star induction generator
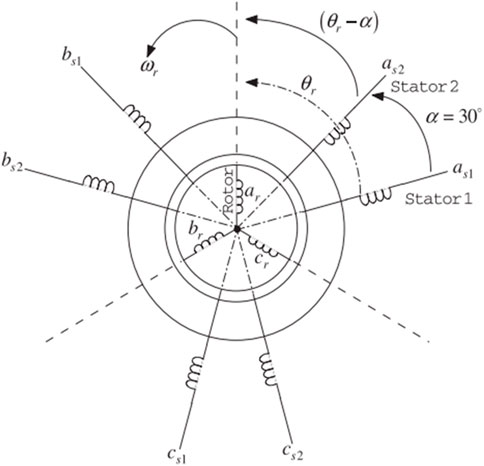
In the traditional arrangement, the stator winding of the DSIG is composed of two identical and balanced three-phase windings. These windings are offset by an electrical angle of α = 30° and possess an equal number of poles. Conversely, the rotor can be characterized as a simplified squirrel cage, resembling a short-circuited three-phase winding. Figure 4 provides a visual representation of the equivalent circuits for both the stator and rotor windings (Sellah et al., 2022)- (Hamoudi et al., 2023b). The mathematical model of the generator is derived by applying Park’s theory to simplify the differential equations. The electrical equations for the DSIG along the direct and quadrature axes (d, q) concerning the field are expressed as in Equation 8 (Benamara et al., 2023):
Where
The expressions for stator and rotor flux linkages are given in Equation 9:
Where
The electromagnetic torque is evaluated as in Equation 10:
Where
The active and reactive power at the stator, as well as those delivered to the grid, are defined as in Equation 11:
2.3 Direct field-oriented control of DSIG
Modified Field Oriented Control (MFOC) is an advanced strategy used in electric motor drives, particularly for three-phase AC motors. It enhances traditional Field Oriented Control (FOC) by optimizing magnetic field orientation to achieve superior torque and speed control, improving efficiency, performance, and precision. MFOC refines control algorithms and parameter tuning to handle varying conditions and external disturbances better, resulting in reduced energy losses, enhanced dynamic response, and precise control. This makes MFOC ideal for applications where high performance and energy efficiency are critical.
Vector control achieves an inherent separation of flux and torque control, resembling the arrangement found in a separately excited DC machine. The control strategy is specific to a drive and a given load specification (Benalia, 2010). through flux, orientation involves regulating the flux using one component of the current and controlling the torque using the other component.
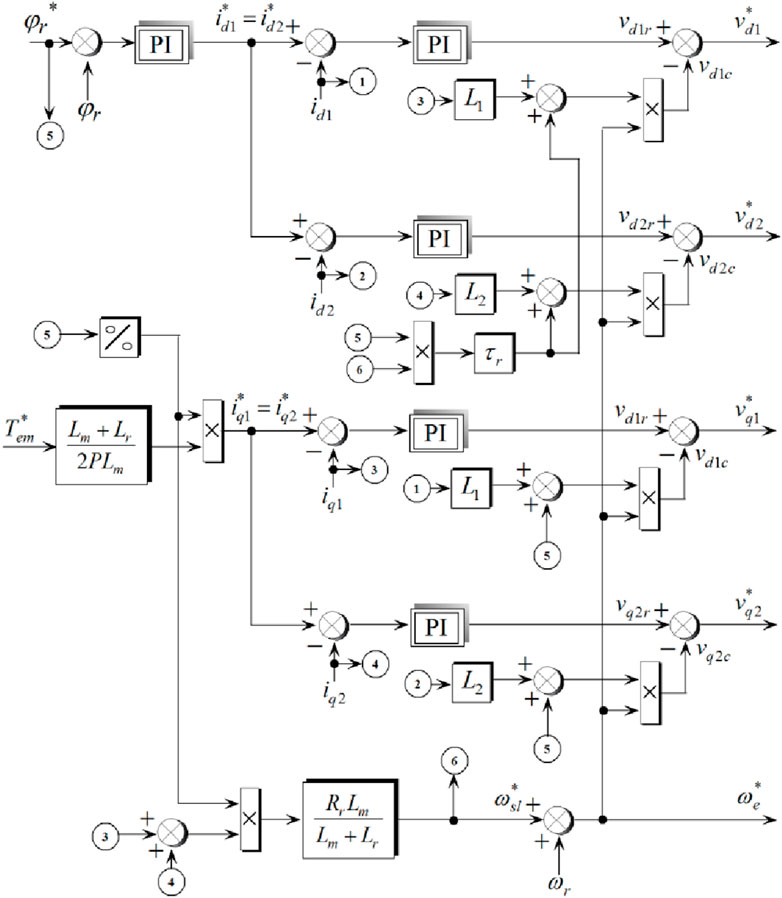
To do this, we need to choose a control law and a system of axes that will ensure the decoupling of flux and torque. Knowing that the expression for the electromagnetic torque (Equation 10) is dependent on both the stator currents and rotor flux.
However, by aligning the rotor flux along the d axis (φdr = φr and φqr = 0), the electromagnetic torque is given by Equation 12:
With:
For the choice of flux orientation in the MASDE, we opt for the choice of rotor flux orientation
For direct vector control, the rotor flux module will be controlled by feedback. To this end, a rotor flux estimator φr is implemented from measurements of id and iq and the rotor current pulsation ωr imposed on the machine (Benalia, 2010).
The proposed control scheme is a cascade structure at is shown in Figure 5. The bloc diagram of the MFOC is presented in Figure 6, the three-phase stator currents are transformed into the d-q reference frame using Park transformations and Proportional-Integral (PI)/Proportional-Integral derivative (PID) controllers are used to regulate the d-axis and q-axis currents to their reference values.
2.4 Power control on the grid side
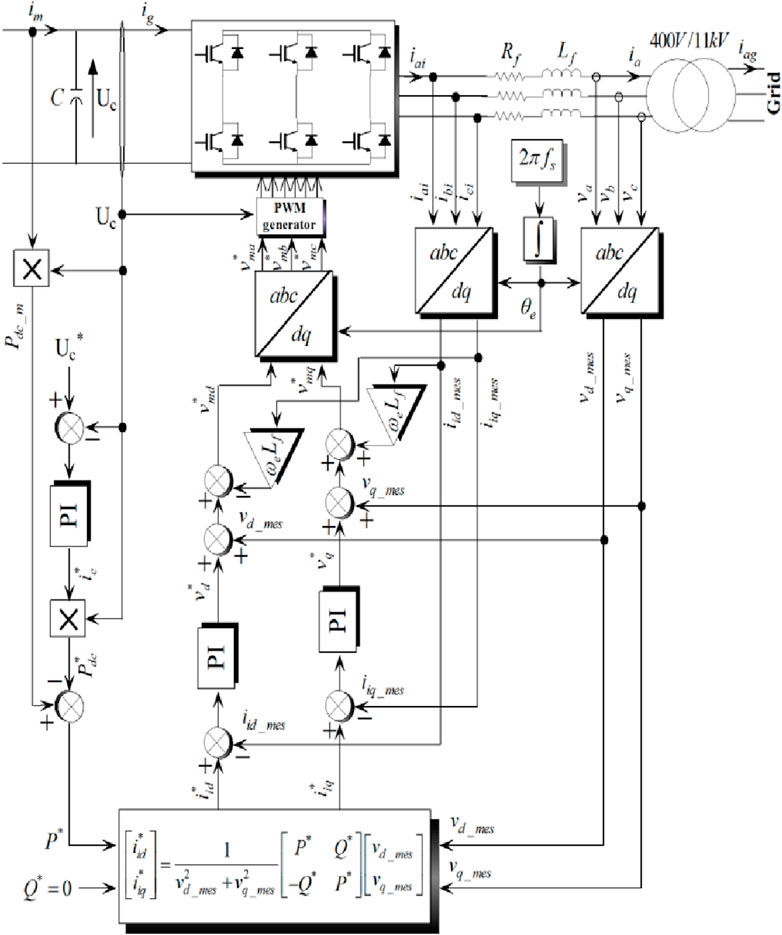
In grid-connected control mode, the aim is to transmit the entirety of the obtainable power derived from the wind generator to the grid Setting the reference reactive power (Q∗) to zero is necessary to align the grid current vector with the grid voltage vector. The regulation of the reference active power involves the control of the DC link voltage. The output from the current controllers determines the voltage reference in an average conversion control method, subsequently governing the switches of the grid inverter (Benamara et al., 2023). The DC link voltage is controlled by Equation 13.
The determination of the reference active power injected into the electrical supply network is dictated by Equation 14:
Where
The PI controller is incorporated to maintain a constant DC link voltage.
The control block of the grid connection conditioning system is shown in Figure 7.
3 Tunning proportional-integral-derivative controller using grey wolf optimization
3.1 Presentation of grey wolf optimization technique
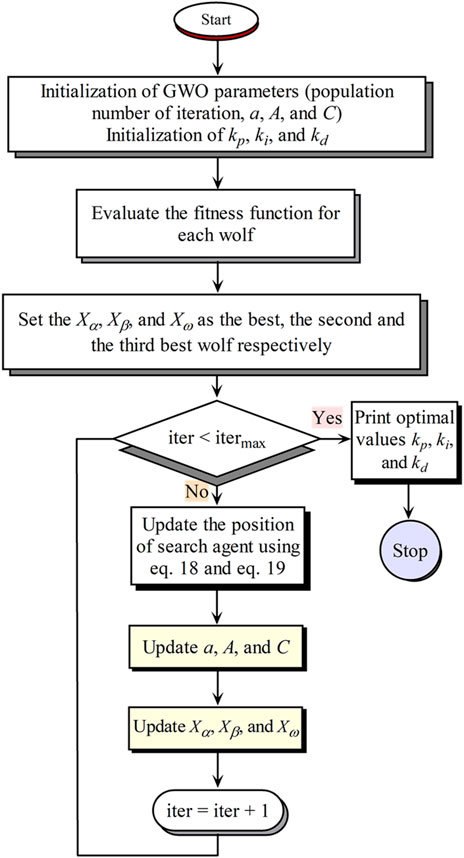
Proposed in 2014 by Mirjalili et al., the GWO algorithm is a novel meta-heuristic that emulates the natural leader hierarchy and hunting behavior observed in wild wolves.
The approach emulates the social structure and hunting dynamics within the gray wolf society. The grey wolf hierarchy is represented by four distinct simulations: Alpha (α), Beta (β), Delta (δ), and Omega (ω), as depicted in Figure 8. Assuming leadership of the entire group, the Alpha wolf (α) plays a primary role in decision-making regarding hunting, sleeping locations, wake-up times, and other collective activities. The Beta wolf (β), positioned as the second in the hierarchy and subordinate to the Alpha (α), functions as an assistant in decision-making, particularly in tasks such as hunting and other collective activities. The Omega (ω) wolf, the lowest-ranking member, follows the Alphas (α) and Betas (β) but exerts dominance over other Omegas (ω). Wolves not classified as Alpha (α), Beta (β), or Omega (ω) are referred to as Delta (δ) wolves. In the GWO algorithm, the search commences with a population of randomly generated wolves, representing potential solutions. These wolves, through an iterative hunting process during optimization, estimate the location of the prey (optimum). The Alpha (α) serves as the primary solution, with the Beta (β) and Delta (δ) representing the second and third-best solutions, respectively. The other solutions, considered less significant, are denoted as Omega (ω) and Delta (δ).
The following Equations 15 and 16 are introduced to mathematically represent the encircling action during the hunting process:
In the equations, t represents the current iteration,
where
In the GWO algorithm, the initial three best solutions are retained, exerting influence on the remaining search agents, including the omegas, to adjust their positions based on the location of the best solution. To implement this, the following formulas Equations 18–20, are proposed (Şen and Kalyonnu, 2018)- (Wang and Liu, 2022)- (Sidea et al., 2021).
The GWO algorithm, a metaheuristic optimization approach, draws inspiration from the collaborative hunting behavior of grey wolves. The sequence of the GWO algorithm is outlined as follows:
- Initiate the population of grey wolves, constituting a collection of potential solutions.
- Compute the objective function for each grey wolf in the population.
- Designate the best-performing, second-best, and third-best grey wolves as alpha, beta, and delta, respectively.
- Update the position of each grey wolf using Equations 18, 19.
- Update a, A, and C, and update the best-performing, second-best, and third-best grey wolves as alpha, beta, and delta, respectively.
- Iterate through steps 4 to 7 until the specified stopping criteria are satisfied, such as reaching a maximum number of iterations or achieving a desired level of convergence.
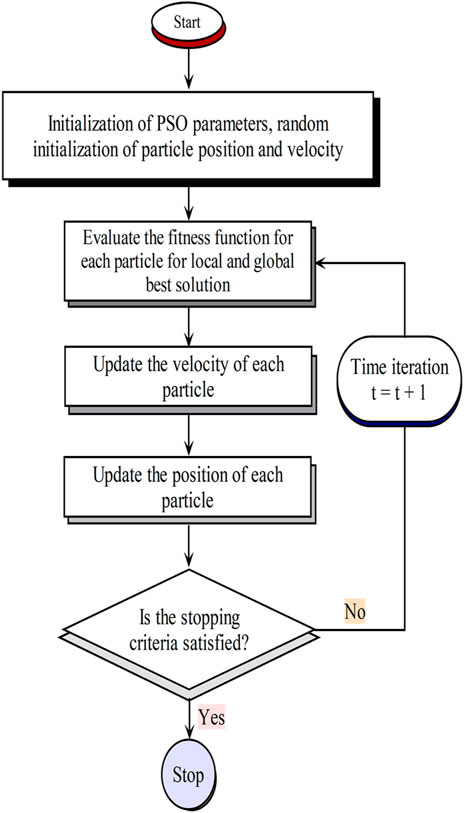
To assess the efficacy of the GWO in comparison to another optimization algorithm, it is essential to choose a suitable algorithm for the comparative analysis. We suggest PSO as a viable candidate for this evaluation (Abdolrasol et al., 2023) - (Bekakra and Ben Attous, 2014). The flowcharts for both the GWO and the basic algorithm are presented in Figures 9, 10 respectively.
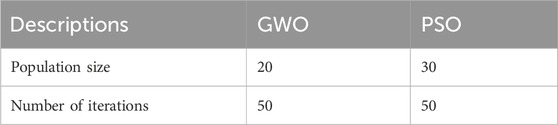
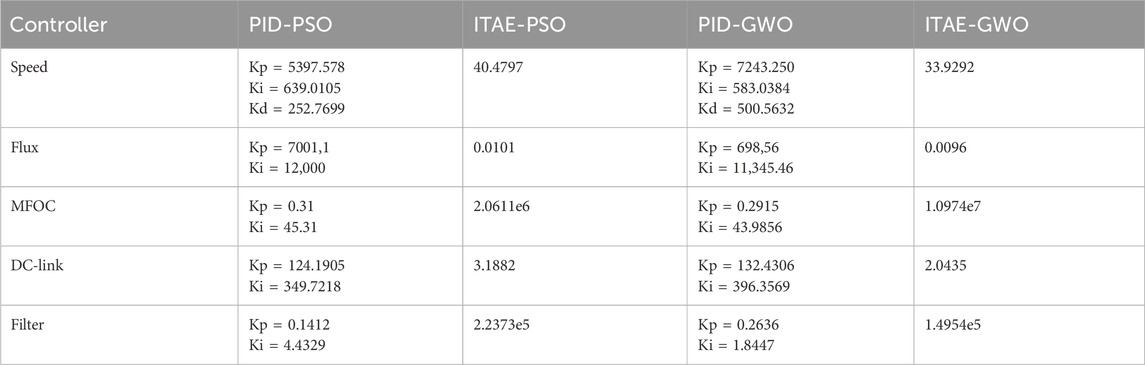
The parameters of the GWO and PSO algorithms used in this work are shown in Table 1.
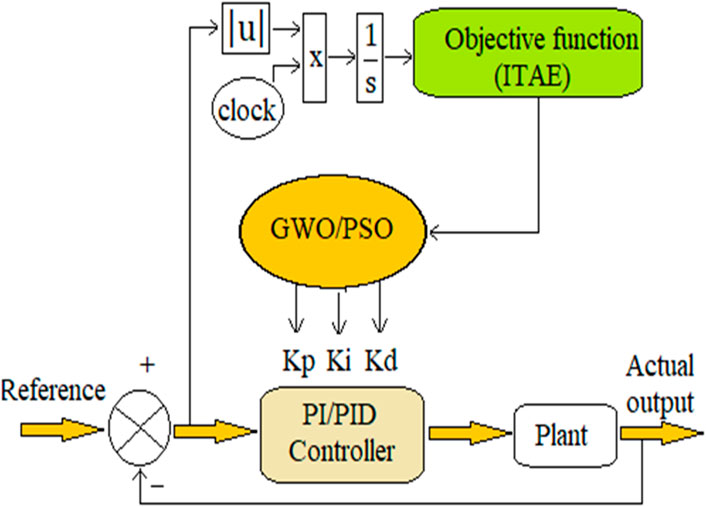
Figure 11 shows the use of the PSO and GWO optimization algorithms in our DSIG-based wind power system, changing the reference value and search interval each time, and carrying out several simulation runs until the desired result is achieved.
3.2 PI/PID controller
The PID controller is widely recognized for its effectiveness in machine control, albeit with the requirement of a known mathematical model for the system. To tackle challenges within the overall system, several methods have been introduced to fine-tune the parameters of PID controllers. The proposed approach utilizes both PSO and GWO methods to determine the optimal values for controller parameters (Kp, Ki, and Kd). This method aims to enhance the performance and adaptability of the PID controller in diverse machine control scenarios by dynamically optimizing its tuning parameters using evolutionary algorithms.
3.3 Objective function
A function identified as a potential objective is termed a candidate objective function. This mathematical function accepts one or more input variables and generates a singular output value. The optimization process entails seeking input values that yield the maximum or minimum output, contingent on the specific problem under consideration (Abdolrasol et al., 2021).
When designing PID controllers, essential performance benchmarks involve metrics such as the Integrated Time Absolute Error (ITAE), which is employed to assess how effectively a control system minimizes errors over time. This criterion is frequently applied when both response speed and steady-state accuracy are of significance. The Integrated Absolute Error (IAE) is another metric utilized to evaluate control system performance by considering the integral of the error over time. Similar to ITAE, it assists in evaluating the system’s ability to minimize errors. The Integrated Time-weighted Square Error (ITSE) is employed to analyze and quantify control system performance, placing greater emphasis on larger errors due to the inclusion of squared error terms in the integral. This criterion is often preferred when minimizing overshoot and settling time is crucial. The Integrated Squared Error (ISE) serves as a straightforward measure of the overall performance of a control system and is commonly used when both transient and steady-state responses are important. The respective formulas for ITAE, IAE, ISE, and ITSE performance criteria are provided below in Equation 21:
In this article, ITAE was used in both algorithms to minimize the error, which is crucial for optimizing the controller’s performance in the wind power system described in Section 2.
Figure 11 shows the use of the PSO and GWO optimization algorithms and ITAE calculation in matlab simulink in our DSIG-based wind power system, changing the reference value and search interval each time, and carrying out several simulation runs until the desired result is achieved. The parameters of PID controller are calculated using Matlab Simulink functions that we have programmed based on the flowcharts shown in Figures 9, 10, and the Pseudo code of the GWO algorithm is shown in Figure 12.
The system’s performance, including the wind turbine’s mechanical power and torque (as defined in Equations 1, 2), and the DSIG electromagnetic torque and speed (outlined in Equations 10, 4), directly affects the error signal
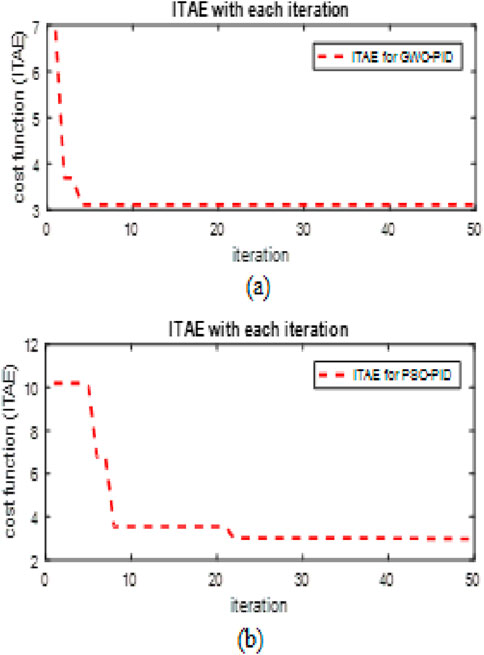
Figure 13 shows the variation of speed error (fitness). It is worth noting that the GWO method outperforms the PSO method.
4 Results
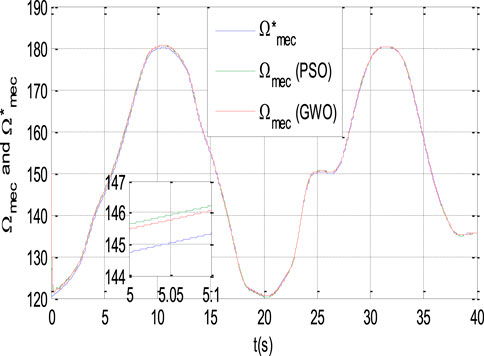
To validate this study, multiple simulations were carried out to analyze the performance of the DSIG under direct field-oriented control. The simulations incorporated the application of optimization algorithms that is PSO and GWO, implemented using MATLAB/Simulink. To acquire a more profound insight into the outcomes obtained through different methodologies, such as PID-PSO and PID-GWO, it is imperative to undertake a thorough comparison of their static and dynamic characteristics. This comparison should occur under identical operating conditions (which encompass references, and disturbance loads) and within the same simulation configuration. Simulation results were acquired for reactive power of Q* = 0 and a DC link voltage of Uc* = 1130V. In Figure 14, the angular speed controlled by two controllers (PSO and GWO), both tracking the same reference, demonstrates commendable performance. Notably, the GWO controller exhibits superior performance by precisely following the reference, evident in its reduced steady-state error of 0.62, in comparison, the PID-PSO controller exhibits a steady-state error of 0.82. The remainder of this article will delve into the presentation of additional results obtained through the implementation of the proposed PID/PI-PSO and PID/PI-GWO controllers.
Table.2 lists the gains of the controllers obtained by the two optimization methods, PSO and Grey Wolf, as well as ITAE.
The error obtained for all PSO controllers is slightly higher compared to the GWO adjustment method.
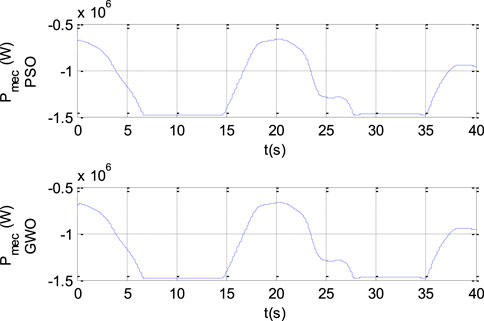
The progression of mechanical power on the DSIG shaft is depicted in Figure 15. The subtle fluctuation in operational phases at mechanical speeds below the rated speed is constrained by the power-limiting device when operating at speeds above the rated speed.
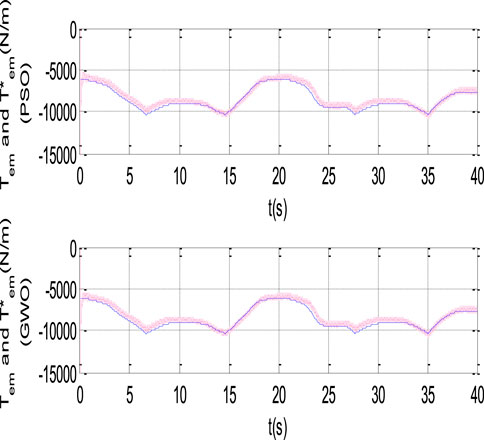
Figure 16, illustrates the electromagnetic torque response of the DSIG by the two proposed methods. However, PI-PSO and PI-GWO bring the necessary corrections to the system’s operation, the torque oscillations represent the generator’s dynamic response to varying wind conditions.
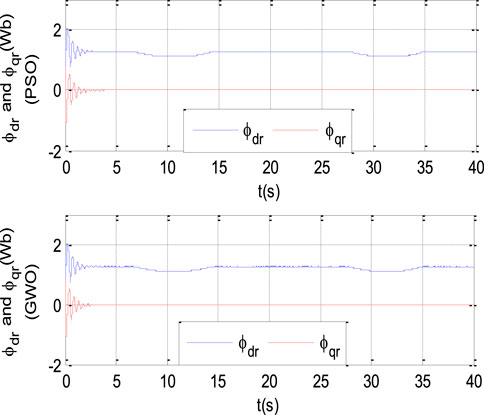
Moving to Figure 17, the decoupling of the direct and quadrature fluxes of the DSIG rotor is apparent, with the quadratic rotor flux registering a zero value following the principles of direct field-oriented control, the application PI-PSO and PI-GWO techniques help in optimizing the PI controller parameters, resulting in improved stability and response of the system under varying operating conditions.
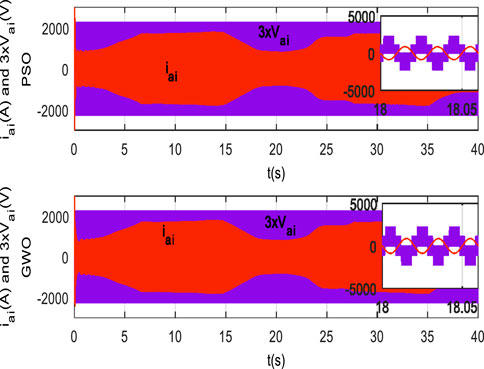
Figure 18A shows the stator voltages and currents for the first star, and the second star results are similar to those for the first one. It indicates that voltage and current are almost 180° out of phase. The consistent pattern of voltage and current observed in the figure is a direct outcome of the effective tuning of the PI controllers using PI-PSO and PI-GWO. These optimization techniques ensure precise adjustments to the PI controller parameters, thereby achieving a stable and efficient control of the stator voltages and currents.

Figure 18. (A). Stator current and voltage (phase as1). (B) Stator currents (phases as1 and as2). (C) Stator active and reactive powers.
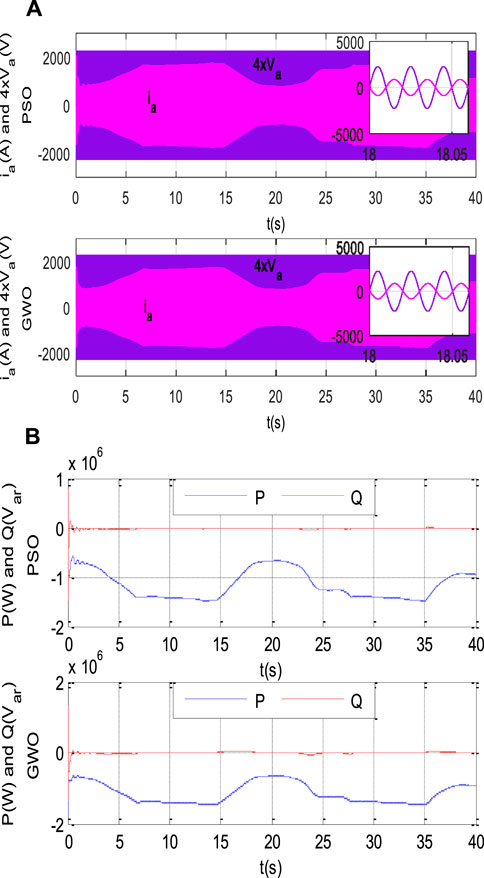
Figure 18B illustrates the sinusoidal shape of the stator currents highlighting the significant improvement in current quality achieved with the PI-PSO and PI-GWO techniques. The figure demonstrates that these optimization algorithms effectively reduce current ripple, resulting in smoother current waveforms. This reduction in ripple is crucial for enhancing the efficiency and performance of the DSIG. The results reveal that the PI-PSO and PI-GWO algorithms are particularly well-suited for tuning the gains of PI/PID controllers, offering superior performance in maintaining sinusoidal currents and minimizing undesirable fluctuations.
Figure 18C illustrates the profiles of active and reactive power for the DSIG stator. The negative sign associated with active power indicates that the DSIG generates this power, whereas the positive sign of reactive power signifies that the machine absorbs the energy required for its magnetization.
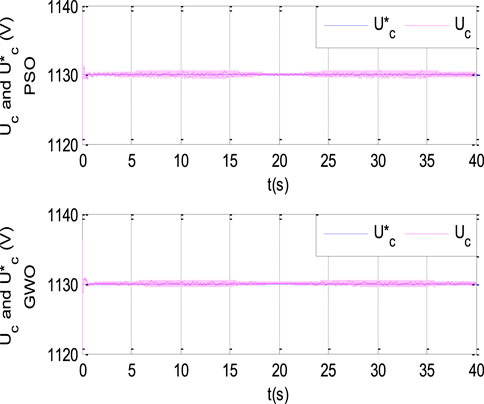
Figure 19 portrays the trend of the DC bus voltage and its reference. It is noticeable that the voltage Uc remains constant and precisely tracks its reference, this precise tracking is achieved through the effective application of optimization algorithms, (PSO) and (GWO). These algorithms are used to fine-tune the control parameters, ensuring that the DC bus voltage is stable and accurately follows the desired reference trajectory. The consistent voltage profile demonstrates the robustness and efficiency of the optimization techniques in maintaining voltage regulation and system stability.
The voltage and current profiles at the output of inverter 3 of the 1st star are presented in Figure 20. The phase shift between the supply current and voltage is 180°, indicating that the line-side converter is delivering real power to the electrical network.
Figure 21A displays the voltage and current profiles at the grid connection. The sinusoidal shape of the current, coupled with its phase being opposite to that of the voltage, indicates that power is flowing from the wind generator to the grid. This phase opposition suggests that the current is delivering power to the grid, which aligns with the operational characteristic of a wind generator supplying power. The smooth, sinusoidal current profile confirms the effective power transfer and integration of the wind generator with the grid, reflecting stable and efficient operation.
Figure 21B illustrates that the active and reactive powers of the network consistently track their references values throughout the simulation. This indicates effective control and regulation, with the system maintaining the desired power levels. The precise tracking of both active and reactive power highlights the success of the control strategies implemented in ensuring stable and reliable performance of the network.
5 Conclusion
In conclusion, this research significantly contributes to the enhancement of dual-star induction generator (DSIG) performance within wind power systems by regulating speed and various parameters. By employing PID controllers for speed regulation and PI controllers for flux estimation, DC-link voltage, Modified Field Oriented Control (MFOC), and grid filter, the study aims to optimize the entire system by fine-tuning these controllers. The optimization process is facilitated by utilizing meta-heuristic algorithms, specifically Grey Wolf Optimization (GWO) and Particle Swarm Optimization (PSO). The simulation results show that the GWO algorithm is slightly more efficient than the PSO algorithm in the speed controller, for an ITAE (33.9292 for PID-GWO and 40.4797 for PID-PSO), PI of the flux (0.0096 PID-GWO and 0.0101 PID-PSO), PI of the MFOC (1.0974e7 PID-GWO and 2.0611e7 PID-PSO), PI DC-link ensuring accurate parameter tuning for optimal system performance.
Appendix parameters
Turbine:
Diameter = 60m.
Number of Blades = 3.
Hub height = 85m.
Gearbox = 90.
DSIG: 1.5MW.
400V.
50Hz.
2 pole pairs.
r1 = r2 = 0.008Ω.
L1 = L2 =0.134mH.
Lm = 0.0045H.
Rr = 0.007Ω.
Lr = 0.067mH.
J = 30 kg.m2: inertia (turbine+ DSIG).
f = 2.5N.m.s/rd: viscous coefficient (turbine+ DSIG).
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
KB: Writing–original draft, Writing–review and editing. HA: Writing–original draft, Writing–review and editing. YH: Writing–original draft, Writing–review and editing. MA: Writing–original draft, Writing–review and editing. UC: Writing–original draft, Writing–review and editing. TU: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdolrasol, M. G. M., Ayob, A., Mutlag, A. H., and Ustun, T. S. (2023). Optimal fuzzy logic controller based PSO for photovoltaic system. Energy Rep. 9, 427–434. doi:10.1016/j.egyr.2022.11.039
Abdolrasol, M., G. M., Hannan, M. A., Hussain, S. M. S., Ustun, T. S., Sarker, M. R., and Ker, P. J. (2021). Energy management scheduling for microgrids in the virtual power plant system using artificial neural networks. Energies 14, 6507. doi:10.3390/en14206507
Amimeur, H., Aouzellag, D., Abdessemed, R., and Ghedamsi, K. (2012). Sliding mode control of a dual-stator induction generator for wind energy conversion systems. Int. J. Electr. Power Energy Syst. 42 (1), 60–70. doi:10.1016/j.ijepes.2012.03.024
Amimeur, H. (2008). “Contribution to the control of the double star induction machine by sliding mode control,” in French, Magister dissertation (Algeria: Hadj Lkhdar’s University).
Barik, A. K., Das, D. C., Latif, A., Hussain, S. M. S., and Ustun, T. S. (2021). Optimal voltage–frequency regulation in distributed sustainable energy-based hybrid microgrids with integrated resource planning. Energies 14, 2735. doi:10.3390/en14102735
Basu, J. B., Dawn, S., Saha, P. K., Chakraborty, M. R., and Ustun, T. S. (2022). Economic enhancement of wind–thermal–hydro system considering imbalance cost in deregulated power market. Sustainability 14, 15604. doi:10.3390/su142315604
Bekakra, Y., and Ben Attous, D. (2014). Optimal tuning of PI controller using PSO optimization for indirect power control for DFIG based wind turbine with MPPT. Int. J. Syst. Assur. Eng. Manag. 5 (3), 219–229. doi:10.1007/s13198-013-0150-0
Benakcha, M., Benalia, L., Ameur, F., and Tourqui, D. E. (2017). Control of dual stator induction generator integrated in wind energy conversion system. J. Energy Syst. 1 (1), 21–31. doi:10.30521/jes.351269
Benalia, L. (2010). Voltage control of double-fed induction motors. Algeria: Hadj Lkhdar’s University.
Benamara, K., Amimeur, H., and Hamoudi, Y. (2023). “Control of a dual stator induction generator integrated in a wind power system,” in 1st international conference on renewable solutions for ecosystems: towards a sustainable energy transition, September 4, 2017.
Chauhan, A., Upadhyay, S., Khan, M. T., Hussain, S. M. S., and Ustun, T. S. (2021). Performance investigation of a solar photovoltaic/diesel generator based hybrid system with cycle charging strategy using BBO algorithm. Sustainability 13, 8048. doi:10.3390/su13148048
Dey, P. P., Das, D. C., Latif, A., Hussain, S. M. S., and Ustun, T. S. (2020). Active power management of virtual power plant under penetration of central receiver solar thermal-wind using butterfly optimization technique. Sustainability 12, 6979. doi:10.3390/su12176979
Djoudi, O., Belaid, S. L., and Tamalouzt, S. (2023). Multilevel converter and fuzzy logic solutions for improving direct control accuracy of DFIG-based wind energy system. Period. Polytech. Electr. Eng. comput. Sci. 67 (2), 136–148. doi:10.3311/PPee.21047
Hamoudi, Y., Amimeur, H., Aouzellag, D., Abdolrasol, M. G. M., and Ustun, T. S. (2023a). Hyperparameter bayesian optimization of Gaussian process regression applied in speed-sensorless predictive torque control of an autonomous wind energy conversion system. Energies 16 (12), 4738. doi:10.3390/en16124738
Hamoudi, Y., Amimeur, H., and Nacef, S. (2023b). Finite-set model predictive power control with common mode voltage elimination for an asymmetrical double-star induction generator wind energy conversion system. Majlesi J. Electr. Eng. 17 (3). doi:10.30486/mjee.2023.1983159.1102
Hassan, S., Abdelmajid, B., Mourad, Z., Aicha, S., and Abdennaceur, B. (2020). PSO-Backstepping Controller of a grid-connected DFIG based wind turbine. Int. J. Electr. Comput. Eng. 10 (1), 856–867. doi:10.11591/ijece.v10i1.pp856-867
Hussain, I., Das, D. C., Sinha, N., Latif, A., Hussain, S. M. S., and Ustun, T. S. (2020b). Performance assessment of an islanded hybrid power system with different storage combinations using an FPA-tuned two-degree-of-freedom (2DOF) controller. Energies 13, 5610. doi:10.3390/en13215610
Hussain, S. M. S., Aftab, M. A., Nadeem, F., Ali, I., and Ustun, T. S. (2020a). Optimal energy routing in microgrids with IEC 61850 based energy routers. IEEE Trans. Industrial Electron. 67 (6), 5161–5169. doi:10.1109/tie.2019.2927154
Iqbal, A., and Singh, G. K. (2021). PSO based controlled six-phase grid connected induction generator for wind energy generation. CES Trans. Electr. Mach. Syst. 5 (1), 41–49. doi:10.30941/CESTEMS.2021.00006
Latif, A., Paul, M., Das, D. C., Hussain, S. M. S., and Ustun, T. S. (2020). Price based demand response for optimal frequency stabilization in ORC solar thermal based isolated hybrid microgrid under salp swarm technique. Electronics 9, 2209. doi:10.3390/electronics9122209
Mesai-Ahmed, H., Bentaallah, A., Cardoso, A. J. M., Djeriri, Y., and Jlassi, I. (2021). Robust neural control of the dual star induction generator used in a grid-connected wind energy conversion system. Math. Model. Eng. Probl. 8 (3), 323–332. doi:10.18280/mmep.080301
Safiullah, S., Rahman, A., Lone, S. A., Hussain, S. M. S., and Ustun, T. S. (2022). Novel COVID-19 based optimization algorithm (C-19BOA) for performance improvement of power systems. Sustainability 14, 14287. doi:10.3390/su142114287
Sellah, M., Kouzou, A., and Rezaoui, M. M. (2022). Investigation of SVPWM based sliding mode control application on dual-star induction motor and dual open-end winding induction motor. Period. Polytech. Electr. Eng. comput. Sci. 66 (1), 80–98. doi:10.3311/PPEE.17910
Şen, M. A., and Kalyonnu, M. (2018). Optimal tuning of PID controller using grey wolf optimizer algorithm for quadruped robot. Balk. J. Electr. Comput. Eng. 6 (1), 29–35. doi:10.17694/bajece.401992
Shaheen, M. A. M., Hasanien, H. M., and Alkuhayli, A. (2021). A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 12 (1), 621–630. doi:10.1016/j.asej.2020.07.011
Sidea, D. O., Picioroaga, I. I., and Bulac, C. (2021). Optimal battery energy storage system scheduling based on mutation-improved grey wolf optimizer using GPU-accelerated load flow in active distribution networks. IEEE Access 9, 13922–13937. doi:10.1109/ACCESS.2021.3051452
Solihin, M. I., Tack, L. F., and Kean, M. L. (2011). Tuning of PID controller using particle swarm optimization (PSO). Int. J. Adv. Sci. Eng. Inf. Technol. 1 (4), 458. doi:10.18517/ijaseit.1.4.93
Sule, A. H., Mokhtar, A. S., Bin Jamian, J. J., and Arfeen, Z. A. (2021). Optimal rotor blade control using Grey Wolf Optimizer for small signal stability of SCIG Wind Turbine. IOP Conf. Ser. Mater. Sci. Eng. 1051 (1), 012035. doi:10.1088/1757-899x/1051/1/012035
Ulutas, A., Altas, I. H., Onen, A., and Ustun, T. S. (2020). Neuro-Fuzzy-based model predictive energy management for grid connected microgrids. Electronics 9, 900. doi:10.3390/electronics9060900
Wang, X., and Liu, R. (2022). Ultra-short-term wind power prediction based on LVDBN. 2022 4th Int. Conf. Power Energy Technol. ICPET 9, 644–648. doi:10.1109/ICPET55165.2022.9918396
Yasin, Z. M., Salim, N. A., and Mohamad, H. (2022). Optimal location and sizing of wind-turbine generation using grey wolf optimizer. IEEE, ICPEA, Shah Alam, Malays., 1–6. doi:10.1109/icpea53519.2022.9744673
Zhang, Y., Sun, H., and Guo, Y. (2019). Wind power prediction based on pso-svr and grey combination model. IEEE Access 7, 136254–136267. doi:10.1109/ACCESS.2019.2942012
Glossary
Ωmec mechanical speed of the DSIG
Ω*mec mechanical speed reference
Ωt turbine speed
Pmec_opt mechanical optimal
Taer aerodynamic torque
Tg generator torque
Cp power coefficient
λ tip speed ratio
β pitch angle
ρ air density
R turbine radius
V wind velocity
G gear ratio
ʋd1, ʋd2, ʋq1, ʋq2 ‘‘d–q’’ stators voltages
id1, id2, iq1, iq2 ‘‘d–q’’ stators currents
φd1, φd2, φq1, φq2 ‘‘d–q’’ stators flux
ʋdr, ʋqr ‘‘d–q’’ rotor voltages
idr, iqr ‘‘d–q’’ rotor currents
φdr, φqr ‘‘d–q’’ rotor flux
ωe speed of the synchronous reference frame
ωr rotor electrical angular speed
r1, r2 per phase stators resistances
rr per phase rotor resistance
L1, L2 per phase stators leakages inductances
Lr per phase rotor leakage inductance
Lm magnetizing inductance
P number of pole pairs
p derivative operator
J inertia
ƒ viscous friction
Tem electromagnetic torque
Ps, Qs active and reactive stator powers
C DC bus capacitor capacity
im The current supplied by the DSIG and modulated by inverters1 and 2
ig current modulated by inverter 3
ic capacitive DC bus current
Pdc active power in the DC bus capacitor
PI Proportional Integrator controller
PID Proportional Integrator-Derivative controller
GWO Grey Wolf Optimizer
PSO Particle Swarm Optimization
ITAE Integral Time Absolute Error
IAE Integrated Absolute Error
ITSE Integrated Time-Squared Error
ISE Integrated Squared Error
WECS Wind Energy Conversion System
Keywords: field oriented control, dual star induction generator, grey wolf optimization, particle swarm optimization, wind energy
Citation: Benamara K, Amimeur H, Hamoudi Y, Abdolrasol MGM, Cali U and Ustun TS (2024) Grey wolf optimization for enhanced performance in wind power system with dual-star induction generators. Front. Energy Res. 12:1421336. doi: 10.3389/fenrg.2024.1421336
Received: 22 April 2024; Accepted: 16 September 2024;
Published: 21 October 2024.
Edited by:
Juan Carlos Jauregui, Autonomous University of Queretaro, MexicoReviewed by:
Mohammad Samiullah, King Fahd University of Petroleum and Minerals, Saudi ArabiaStephanie Camacho Gutierrez, Autonomous University of Queretaro, Mexico
Copyright © 2024 Benamara, Amimeur, Hamoudi, Abdolrasol, Cali and Ustun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Katia Benamara, a2F0aWEuYmVuYW1hcmFAdW5pdi1iZWphaWEuZHo=; Taha Selim Ustun, c2VsaW0udXN0dW5AYWlzdC5nby5qcA==; Umit Cali, dW1pdC5jYWxpQG50bnUubm8=
 Katia Benamara
Katia Benamara Hocine Amimeur
Hocine Amimeur Yanis Hamoudi1
Yanis Hamoudi1 Taha Selim Ustun
Taha Selim Ustun