Cooperative energy interaction for neighboring multiple distribution substation areas considering demand response

With the growing integration of renewable energy into medium- and low-voltage distribution networks, the distribution substation area (DSA) has emerged, encompassing energy storage and loads. This paper introduces an energy interaction framework for multiple DSAs aimed at enhancing local renewable energy consumption. The energy interaction issue among various DSAs is modeled as a Nash bargaining problem to encourage energy exchanges. However, the variability in pricing and internal demand response may influence scheduling decisions, necessitating further investigation. To address price forecast errors, scenarios are developed using a stochastic programming approach to represent price uncertainties while adjusting the DSA’s load accordingly. Optimal power flow constraints are integrated into the model to bolster power system operation security. Additionally, the transmission capacity can impact scheduling outcomes and operational costs. The influence of transmission limitations on operational strategies is examined within the allowable capacity. To solve this issue, the bargaining model is divided into two subproblems, and an enhanced alternating direction multiplier method (ADMM) is used to maintain the privacy of DSAs. The simulation results obtained using the IEEE-33 bus system indicate that energy interaction among multiple DSAs significantly lowers operating costs and facilitates the integration of renewable energy.

1 Introduction

The integration of distributed renewable energy is a key challenge within distribution networks. To facilitate energy interaction, a distribution substation area (DSA), comprising a renewable power station, energy storage, and loads, can support local consumption and reduce disturbances in the network (Hirsch et al., 2018). Using energy storage, the DSA can adjust the load demand and better accommodate renewable generation. However, the inherent unpredictability of renewable sources may lead to energy shortages or surpluses. To optimize renewable energy efficiency, DSAs can interconnect with neighbors to facilitate energy exchanges (Kumar and Saravanan, 2017). Guided by the time-of-use (TOU) pricing set by the distribution network operator, energy interaction among multiple DSAs is encouraged, forming a small-scale interconnected DSA energy market (Vieira and Zhang, 2021). Given the shared interests, it is crucial to develop an interactive mechanism that incentivizes energy exchanges while maintaining economic viability and reliability within the region (Tushar et al., 2020).

A game theory-based mechanism is instrumental in studying and analyzing interactive strategies among multiple DSAs (Tushar et al., 2018). Generally, the game theory approach to interaction processes among participants can be categorized into non-cooperative and cooperative games (Tushar et al., 2019). In a non-cooperative game, buyers and sellers negotiate to establish interaction prices and quantities, achieving market clearing while maintaining the supply–demand balance (Paudel et al., 2019). A Stackelberg game-based negotiation process between buyers and sellers, which considers participant competition and achieves market clearing, is detailed by Jiang et al. (2022). Although Nash equilibrium solutions can be obtained in non-cooperative games, the decision-making processes are typically self-centered, and these solutions are not necessarily unique local optima (Chen et al., 2019).

To balance individual and collective interests, a cooperative game theory-based energy interaction model is proposed to achieve global optimization in energy sharing (Luo et al., 2022). The Nash bargaining game theory is well suited for energy interactions among multiple DSAs, ensuring equitable benefit allocation (Dehghanpour and Nehrir, 2017; Wang and Huang, 2016). Building on this cooperative model, optimal power flow constraints are incorporated into the system operation to enhance the model’s practicality (Li et al., 2018). However, these studies often overlook the impact of the demand response on energy interaction, which could potentially increase operational costs.

The demand response is an effective and promising approach that shifts electricity demand to periods when renewable generation is more abundant or the demand is lower. By leveraging load baselines, the demand response aids in the integration of renewable generation and reduces operational costs, thereby facilitating energy interaction (Sarker et al., 2020). A bi-level optimization model has been introduced for energy storage planning and operation, considering the electricity–heat demand response while utilizing Nash bargaining methods for benefit allocation (Alizadeh et al., 2024). However, these studies often distribute cooperative benefits equally among participants, which may lead to fairness concerns (Luo et al., 2022). To address this, a generalized Nash bargaining theory is adopted to incentivize energy interaction among multiple DSAs and allocate cooperative benefits based on the quantities of energy interaction (Kim et al., 2019).

The aforementioned studies formulate energy interaction models based on deterministic optimization, often overlooking forecast errors in TOU prices. Price uncertainty significantly impacts the economic and security aspects of an energy system. Generally, stochastic programming (Li et al., 2022) and robust optimization (Wei et al., 2021) are two prevalent methods used for addressing uncertainties. Considering the conservative nature of robust optimization, a stochastic optimization model is developed for unpredictable prices, aiming to achieve optimal scheduling (Baharvandi et al., 2019) and effective energy management (Chang et al., 2020). However, the influence of uncertain prices on energy interaction, as well as Nash bargaining-based operation decisions, is often neglected in these studies. Given the uncertain prices, DSAs schedule their demand to respond dynamically, which may alter their final decisions and operational costs. Considering the interdependent relationship between prices and demand response, the decisions of DSAs should integrate these influencing factors to devise optimal strategies.

Another aspect investigated in energy interaction is the consideration of physical constraints. Voltage fluctuations at each node (Jin et al., 2020) and power losses resulting from energy interaction (Khorasany et al., 2020) are modeled as costs paid to the operator. Although these factors are considered costs, further analysis is needed to understand strategy changes when transferring power to neighbors within the specified capacity limits. In other words, the congestion of transmission lines is directly addressed during the energy interaction process. Therefore, an energy interaction model is established that incorporates uncertain prices, demand response, and transmission capacity during energy interaction.

To sum up, the main contribution of this paper is to derive optimal operation strategies by considering the interdependent relationship between uncertain prices and the demand response of DSAs. Specifically, this paper investigates the effect of price uncertainty on the Nash bargaining theoretical model, analyzing both operation costs and the internal decision-making strategies of DSAs. To mitigate these adverse effects, the demand response combined with energy storage is proposed to enhance the flexibility of DSAs by shifting the load demand to periods of lower prices. The final operation strategies should account for the interconnected nature of price uncertainty and demand response. Additionally, optimal power flow is integrated into the optimization model to improve its practicality. Transmission limitations are also included to examine the impact of capacity restrictions on operation costs. Finally, the cooperative benefits are allocated based on the interaction of DSAs, ensuring a fair distribution that reflects the contribution of each participant to the energy interaction process.

2 Problem description

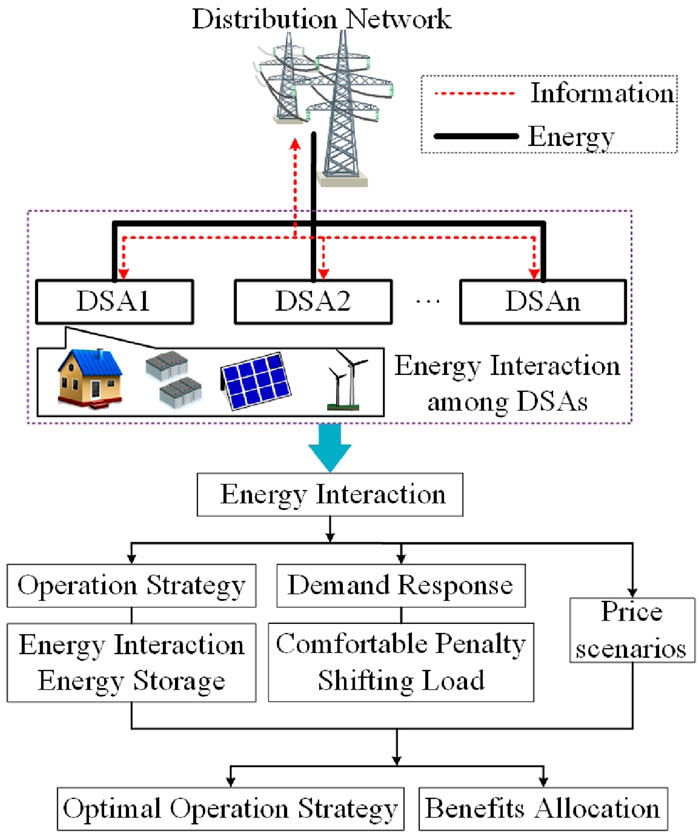
As illustrated in Figure 1, an energy interaction problem with $\mathcal{M}$ DSAs is considered, formulated as an interaction set $\mathcal{M}=1,\dots ,M$. Each DSA, which consists of PV/wind generation, energy storage, and loads, interacts with others to maintain the balance between supply and demand. Supported by the distribution network, these interconnected DSAs participate in energy interactions to share electricity with neighboring entities. In this process, electricity is transferred from one bus to another, which can be described as an AC power flow. To address the volatility of electricity prices, a stochastic programming approach is incorporated into the model, capturing price uncertainty through discrete scenarios.

Figure 1

Figure 1. System with interconnected DSAs.

Given the price scenarios, DSAs negotiate with each other and respond to the prices by shifting load demands. To this end, the energy interaction problem is formulated as a generalized Nash bargaining game model to incentivize energy interaction and achieve fair benefit allocation. Additionally, a penalty for DSAs caused by the demand response is incorporated into the model to account for comfort levels. DSAs develop optimal operation strategies to maximize cooperative benefits and allocate these benefits based on their respective contributions. Congestion may occur during the process of energy transmission, especially considering the energy interaction among DSAs. To address this issue, we adjust the operation strategies of DSAs and analyze the impact on operation costs.

3 Energy interaction model

An independent operation model of a DSA and an energy interaction model among multiple DSAs are established for the comparative analysis of the operation costs of DSAs. Compared to independent operations, DSAs achieve cost savings through energy interaction with neighbors, which includes energy sharing, renewable generation integration, energy storage scheduling, and load shifting. Then, based on the generalized Nash bargaining theory, cooperative benefits are allocated by leveraging the bargaining power parameters.

3.1 Basic operation optimization model of the individual DSA

The objective function of a DSA is to minimize operational costs in the face of uncertain pricing. To achieve this, the DSA uses demand response strategies and manages the charging and discharging of energy storage systems. The model, accounting for various price scenarios, is structured as follows:

$\begin{array}{c}{C}_{\mathit{Non}}^i={\min }_{{\mathit{x}}_{\mathit{Non}}^{\mathit{i},\mathit{t},\mathit{w}}}{\displaystyle \sum _{w=1}^{\mathcal{W}}}{\displaystyle \sum _{t=1}^{\mathcal{T}}}\frac{1}{\mathcal{W}}\left[{\mu }_{Pb}^{t,w}{P}_{Pb}^{i,t,w}-{\mu }_{Ps}^{t,w}{P}_{Ps}^{i,t,w}+c_E\left(P_{Ec}^{i,t,w}+P_{Ed}^{i,t,w}\right)\right.\hfill \\ \left.+c_{\mathit{Load}}{\left(P_{\mathit{Load}}^{i,t,w}-P_{\mathit{Load,Pre}}^{i,t}\right)}^2\right],\hfill \end{array}(\mathrm{1a})$

$s.t.P_{Pb}^{i,t,w}+P_{\mathit{Gen}}^{i,t,w}+P_{Ed}^{i,t,w}=P_{Ps}^{i,t,w}+P_{\mathit{load}}^{i,t,w}+P_{Ec}^{i,t,w},\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(\mathrm{1b})$

$0\le P_{Pb}^{i,t,w}\le P_{Pb,i}^{\mathit{max}},\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(\mathrm{1c})$

$0\le P_{Ps}^{i,t,w}\le P_{Ps,i}^{\mathit{max}},\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(\mathrm{1d})$

$0\le P_{Ec}^{i,t,w}\le P_{Ec,i}^{\mathit{max}},\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(1e)$

$0\le P_{Ed}^{i,t,w}\le P_{Ed,i}^{\mathit{max}},\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(\mathrm{1f})$

$SO{C}_i^{\mathit{min}}\le SO{C}^{i,t,w}\le SO{C}_i^{\mathit{max}},\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(\mathrm{1g})$

$\begin{array}{c}SO{C}^{i,t,w}Ca{p}^i=SO{C}^{i,t-1,w}Ca{p}^i+{\eta }_{Ec}^{i,t,w}{P}_{Ec}^{i,t,w}-1/{\eta }_{Ed}^{i,t,w}{P}_{Ed}^{i,t,w},\hfill \\ \forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },\hfill \end{array}(\mathrm{1h})$

$SO{C}^{i,24,w}=SO{C}_{\mathit{exp}}^i,\forall i\in \mathcal{M},\forall w\in \mathrm{\Omega },(\mathrm{1i})$

$\left(1-{\alpha }_L\right)P_{\mathit{Load,Pre}}^{i,t}\le P_{\mathit{Load}}^{i,t,w}\le \left(1+{\alpha }_L\right)P_{\mathit{Load,Pre}}^{i,t},(\mathrm{1j})$

${\displaystyle \sum _{t=1}^{\mathcal{T}}}{P}_{\mathit{Load}}^{i,t,w}={\displaystyle \sum _{t=1}^{\mathcal{T}}}{P}_{\mathit{Load,Pre}}^{i,t},(\mathrm{1k})$

where the objective function (1a) represents the individual operation cost $C_{\mathit{Non}}^i$ of DSA $i\in \mathcal{M}$, which includes the interaction cost with the distribution network, degradation cost of the energy storage, and comfortable penalty cost. The purchasing and selling prices denoted as ${\mu }_{Pb}^{t,w}$ and ${\mu }_{Ps}^{t,w}$, respectively, and quantities $P_{Pb}^{i,t,w}$ and $P_{Ps}^{i,t,w}$ in scenarios $w\in \mathrm{\Omega }$ are used to calculate the operation cost with the distribution network. The degradation cost of energy storage consists of the unit cost $c_E$ and charging/discharging variables ($P_{Ec}^{i,t,w}$ and $P_{Ed}^{i,t,w}$, respectively). The comfort penalty cost is expressed as the product of the unit cost $c_{\mathit{Load}}$ and load regulation quantities. The power balance constraint (Equation 1b) involves the forecast renewable generation $P_{\mathit{Gen}}^{i,t,w}$ and load demand $P_{\mathit{load,pre}}^{i,t}$ at time $t\in \mathcal{T}$, as well as the actual load demand $P_{\mathit{load}}^{i,t}$ during the decision process. Constraints in Equations 1c, d define the lower and upper bounds ($P_{Pb,i}^{\mathit{max}}$ and $P_{Ps,i}^{\mathit{max}}$, respectively) for purchasing/selling energy from/to a distribution network. The charging and discharging limitation of a battery is indicated by constraints in Equations 1e, f with upper bounds $P_{Ec,i}^{\mathit{max}}$ and $P_{Ed,i}^{\mathit{max}}$. The state of charge (SOC) is limited by constraints in Equations 1g, i, based on the storage capacity. The constraint in (1g) defines the minimum and maximum SOC values, while the constraint in (1h) specifies its balance expression. To ensure continuity in energy storage, the expected SOC must adhere to the constraint in (1i). For the demand response, the power reduction offered by each DSA $i$ should satisfy the constraint in Equation 1j, where ${\alpha }_L$ represents the load shifting ratio. Given that load shifting is considered, the total daily demand should match the predicted value $P_{\mathit{Load,Pre}}^{i,t}$, as specified by the constraint in Equation 1k. The decision variables in the individual operation model are represented by the vector ${\mathit{x}}_{\mathit{Non}}^{\mathit{i},\mathit{t},\mathit{w}}=\left[P_{Pb}^{i,t,w},P_{Ps}^{i,t,w},P_{Ec}^{i,t,w},P_{Ed}^{i,t,w}\right.$, $\left.SO{C}^{i,t,w},P_{\mathit{Load}}^{i,t,w}\right]$.

3.2 Branch power-flow formulation

Following Farivar and Low (2013), the power flow model is established in a radial network using angle and conic relaxation. Additionally, quadratic terms in the power flow constraints are neglected since the branch powers $p_{j,t,w}$ and $q_{j,t,w}$ are significantly larger than the quadratic terms in the branch flow equation. Consequently, the expression is simplified as follows:

$p_{j,t,w}=-{\displaystyle \sum _{i:i\to j}}{P}_{i,j,t,w}+{\displaystyle \sum _{k:j\to k}}{P}_{j,k,t,w},\forall \left(i,j\right)\in \mathcal{E},(\mathrm{2a})$

$q_{j,t,w}=-{\displaystyle \sum _{i:i\to j}}{Q}_{i,j,t,w}+{\displaystyle \sum _{k:j\to k}}{Q}_{j,k,t,w},\forall \left(i,j\right)\in \mathcal{E},(\mathrm{2b})$

$p_{i,t,w}=P_g^{i,t,w}-\left(P_{Pb}^{i,t,w}-P_{Ps}^{i,t,w}\right),(\mathrm{2c})$

$q_{i,t,w}=Q_g^{i,t,w}-Q_{L,pre}^{i,t},(\mathrm{2d})$

$-P_{\mathit{max}}^{i,j}\le P_{i,j,t,w}\le P_{\mathit{max}}^{i,j},\forall \left(i,j\right)\in \mathcal{E},(2e)$

$-Q_{\mathit{max}}^{i,j}\le Q_{i,j,t,w}\le Q_{\mathit{max}}^{i,j},\forall \left(i,j\right)\in \mathcal{E},(\mathrm{2f})$

$-P_{g,max}^i\le P_g^{i,t,w}\le P_{g,max}^i,(\mathrm{2g})$

$-Q_{g,max}^i\le Q_g^{i,t,w}\le Q_{g,max}^i,(\mathrm{2h})$

$U_{j,t,w}=U_{i,t,w}-2\left(P_{i,j,t,w}{r}_{i,j}+Q_{i,j,t,w}{x}_{i,j}\right),\forall \left(i,j\right)\in \mathcal{E},(\mathrm{2i})$

$U_{\mathit{min}}^i\le U_{i,t,w}\le U_{\mathit{max}}^i,\forall i,j\in \mathcal{N},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega },(\mathrm{2j})$

where the active and reactive powers in a branch are defined by constraints in Equations 2a, b, while the injection power of node $i\in \mathcal{N}$ can be obtained using constraints in Equations 2c, d. Constraints in Equations 2e, f set the limitation of branch flow for all branches $(i,j)\in \mathcal{E}$. The active and reactive bounds supported by the distribution network are specified by constraints in Equations 2g, h. The square of magnitudes of nodal voltage is provided by Equation 2i, and the constraint in Equation 2j ensures that $U_{i,t,w}$ always remains within the interval $\left[U_{\mathit{min}}^i,U_{\mathit{max}}^i\right]$.

3.3 Operation cost for cooperative DSAs

Supported by the distribution network, DSAs engage in energy interaction with neighbors to share idle energy while reducing disturbance to the main grid. Taking into account the impact of uncertain prices and the demand response, their cooperative formulation is expressed as follows:

$\begin{array}{c}{C}_{\mathit{Tra}}^i={\min }_{{\mathit{x}}_{\mathit{Tra}}^{\mathit{i},\mathit{t},\mathit{w}}}{\displaystyle \sum _{w=1}^{\mathcal{W}}}{\displaystyle \sum _{t=1}^{\mathcal{T}}}\frac{1}{\mathcal{W}}\left({\mu }_{Pb}^{t,w}{P}_{Pb}^{i,t,w}-{\mu }_{Ps}^{t,w}{P}_{Ps}^{i,t,w}+c_E^i\left(P_{Ec}^{i,t,w}+P_{Ed}^{i,t,w}\right)\right.\hfill \\ \left.+c_{\mathit{Load}}{\left(P_{\mathit{Load}}^{i,t,w}-P_{\mathit{Load,Pre}}^{i,t}\right)}^2\right),\hfill \end{array}(\mathrm{3a})$

$\begin{array}{ll}\hfill s.t.& \left(1c\right)-\left(1k\right),\left(2a\right)-\left(2b\right),\left(2d\right)-\left(2j\right)\hfill \\ \hfill & P_{Pb}^{i,t,w}+P_{\mathit{Res}}^{i,t}+P_{Ed}^{i,t,w}+P_{\mathit{Tra}}^{i,t,w}=P_{Ps}^{i,t,w}+P_{\mathit{Load}}^{i,t}+P_{Ec}^{i,t,w},\hfill \end{array}(\mathrm{3b})$

${\displaystyle \sum _i^{\mathcal{M}}}{P}_{\mathit{Tra}}^{i,t,w}=0,(\mathrm{3c})$

$p_{i,t,w}=P_g^{i,t,w}-\left(P_{Pb}^{i,t,w}+P_{\mathit{Tra}}^{i,t,w}-P_{Ps}^{i,t,w}\right),(\mathrm{3d})$

$\forall i\in \mathcal{M},\forall t\in \mathcal{T},\forall w\in \mathrm{\Omega }.$

Unlike the individual operation in model (1), the interaction variable $P_{\mathit{Tra}}^{i,t,w}$ is introduced by the constraint in Equation 3b. Considering energy interaction, DSAs maintain the supply–demand balance through energy exchange with the main grid and neighboring DSAs. The constraint in Equation 3c ensures that the total power output equals the power imported from neighbors’. Additionally, the net injection at node $i$ incorporates energy interaction among DSAs, as detailed by the constraint in Equation 3d. The decision variables in cooperative mode are represented by the vector ${\mathit{x}}_{\mathit{Tra}}^{\mathit{i},\mathit{t},\mathit{w}}=\left[P_{Pb}^{i,t,w},P_{Ps}^{i,t,w},P_{Ec}^{i,t,w},P_{Ed}^{i,t,w},SO{C}^{i,t,w},P_{\mathit{Tra}}^{i,t,w},P_{\mathit{Load}}^{i,t,w}\right]$.

3.4 General Nash bargaining game-based energy interaction

The general Nash bargaining game-based scheduling strategy is proposed to incentivize energy interaction among DSAs and ensure that benefits are allocated according to the contribution of each participant.

$\max {\displaystyle \prod _{i=1}^{\mathcal{M}}}{\left(C_{\mathit{Non}}^i-\left(C_{\mathit{Tra}}^i+C{e}_{\mathit{Pay}}^i\right)\right)}^{{\alpha }_i},(\mathrm{4a})$

$\underset{C_{\mathit{Total}}^i}{\underbrace{C_{\mathit{Tra}}^i+C{e}_{\mathit{Pay}}^i}}\le C_{\mathit{Non}}^i,\forall i\in \mathcal{M},(\mathrm{4b})$

${\displaystyle \sum _i^{\mathcal{M}}}C{e}_{\mathit{Pay}}^i=0.(\mathrm{4c})$

DSAs engage in energy interaction with neighbors to maximize social welfare, as expressed in the objective function (Equation 4a). The constraint in Equation 4b ensures that the cooperation cost does not exceed the cost of individual operation, thereby encouraging DSAs to participate in energy interactions. The purchasing cost of a DSA in an energy interaction must equal be to the selling income of neighbors, as represented by the constraint in Equation 4c. Additionally, the contribution of each participant is calculated using the coefficient ${\alpha }_i$, and the expression is

$\begin{array}{c}\hfill {\alpha }_i=\frac{\frac{1}{\mathcal{W}}{\sum }_{w=1}^{\mathcal{W}}{\sum }_t^{\mathcal{T}}|P_{\mathit{Tra}}^{i,t,w}|}{\frac{1}{\mathcal{W}}{\sum }_{w=1}^{\mathcal{W}}{\sum }_i^{\mathcal{M}}{\sum }_t^{\mathcal{T}}|P_{\mathit{Tra}}^{i,t,w}|},\end{array}(5)$

where the bargaining power ${\alpha }_i$ is determined by the ratio of net energy transmission of a DSA to the total energy transmission of all participants.

3.5 Decomposition and solution of the general Nash bargaining problem

According to the proposition put forward by Wang and Huang (2016), the optimal solution of the Nash bargaining problem is equivalent to the cost minimization of DSAs. By combining the individual rationality condition with the constraint in Equation 4b, a feasible payment allocation $C{e}_{\mathit{Pay}}^i$ always exists, which enhances cost reduction. Consequently, the general Nash bargaining-based energy interaction problem can be decomposed into two subproblems: the operation cost minimization problem (P1) and the bargaining problem (P2) (Kim et al., 2019). The optimal results are obtained by solving these two subproblems sequentially. Considering whether DSAs participate in energy interaction or not, the operation cost minimization problem (P1) encompasses both the individual operation model (1) and the cooperative operation model (3). Since the operation optimization problem (P1) consists of a quadratic objective and linear constraints, the optimal solution can be obtained by directly solving the convex problem. This optimal solution is then used to calculate the bargaining problem (P2), utilizing the value of ${\alpha }_i$ in (5):

$\begin{array}{c}\hfill \max {\displaystyle \prod _i^{\mathcal{M}}}{\left({\eta }^{i*}-C{e}_{\mathit{Pay}}^i\right)}^{{\alpha }_i}\\ \hfill s.t.\left(4b\right),\left(4c\right),\end{array}(6)$

where ${\eta }^{i*}=C_{\mathit{Non}}^{i*}-C_{\mathit{Tra}}^{i*}$ represents the cost saving of cooperative DSA $i$ through energy interaction. To allocate the benefits, the bargaining problem (P2) is transformed into a convex problem by taking the logarithm of (6):

$\begin{array}{c}\hfill \min {\displaystyle \sum _i^{\mathcal{M}}}-{\alpha }_{i}ln\left({\eta }^{i*}-C{e}_{\mathit{Pay}}^i\right)\\ \hfill s.t.\left(4b\right),\left(4c\right).\end{array}(7)$

According to Zhong et al. (2020), since the objective function $ln(•)$ increases monotonically, the optimal solution can be obtained by solving the model (7). An improved alternating direction multiplier method (ADMM) algorithm is proposed to solve the energy interaction problem in a distributed manner. To avoid updating the multiplier in a centralized way, each DSA interacts with its neighbors to share local information. For operation problem (P1), it is decomposed by introducing auxiliary variables $P_{\mathit{Tra,i}}^{j,t,w}$ and $P_{\mathit{Tra,j}}^{i,t,w}$. The details of the algorithm are shown in Algorithm 1. The couple constraint in Equation 3c is decomposed as:

$\begin{array}{c}\hfill P_{\mathit{Tra}}^{i,t,w}=P_{\mathit{Tra,i}}^{j,t,w}:{\lambda }^{i,t}\\ \hfill P_{\mathit{Tra}}^{j,t,w}=P_{\mathit{Tra,j}}^{i,t,w}:{\lambda }^{j,t},\end{array}(8)$

where ${\lambda }_i$ and ${\lambda }_j$ represent the Lagrangian multipliers. The augmented Lagrangian function of the energy interaction model is then expressed as follows:

$\begin{array}{c}\hfill L_i^{\mathit{DSA}}=C_{\mathit{Tra}}^i+{\displaystyle \sum _j^{\mathcal{M}}}{\displaystyle \sum _t^{\mathcal{T}}}{\lambda }^{i,t}\left(P_{\mathit{Tra}}^{i,t,w}-P_{\mathit{Tra,i}}^{j,t,w}\right)\\ \hfill +{\displaystyle \sum _j^{\mathcal{M}}}{\rho }_j/2{\displaystyle \sum _t^{\mathcal{T}}}\Vert P_{\mathit{Tra}}^{i,t,w}-P_{\mathit{Tra,i}}^{j,t,w}{\Vert }_2^2,\end{array}(9)$

where ${\rho }_j$ is the penalty parameter for DSA $i$. After each iteration, the updated expression of ${\lambda }^{i,t}$ at iteration $k$ is

$\begin{array}{c}\hfill {\lambda }^{i,t}\left(k\right)={\lambda }^{i,t}\left(k-1\right)+{\rho }_i\left(k\right)\left(P_{\mathit{Tra}}^{i,t,w}-P_{\mathit{Tra,i}}^{j,t,w}\right).\end{array}(10)$

The iteration converges when the primal and dual residues satisfy the following conditions (${ϵ}^{\mathit{Pri}}$ and ${ϵ}^{\mathit{Dual}}$):

$\begin{array}{c}{P}_{\mathit{Tra}}^{i,t,w}-P_{\mathit{Tra,i}}^{j,t,w}\le {ϵ}^{\mathit{Pri}},\hfill \\ P_{\mathit{Tra}}^{i,t,w}\left(k-1\right)-P_{\mathit{Tra}}^{i,t,w}\left(k\right)\le {ϵ}^{\mathit{Dual}}.\hfill \end{array}(11)$

Algorithm 1.An improved ADMM algorithm for solving the energy interaction problem of the DSA.

Input: Set iteration index $k\in [0,K]$, primal residue ${ϵ}^{\mathit{Pri}}$, dual residue ${ϵ}^{\mathit{Dual}}$, and step size ${\rho }_i(k)$.

1:repeat

2:   Each DSA solves the local energy interaction problem (9).

3:   Update the multipliers ${\lambda }^{i,t}(k)$ in (10).

4:   Each DSA $i$ computes the primal and dual residues. If the stopping criteria are satisfied, terminate; otherwise,repeat Step 4.

5:until Stopping criteria (11) are satisfied,terminate.

4 Case study

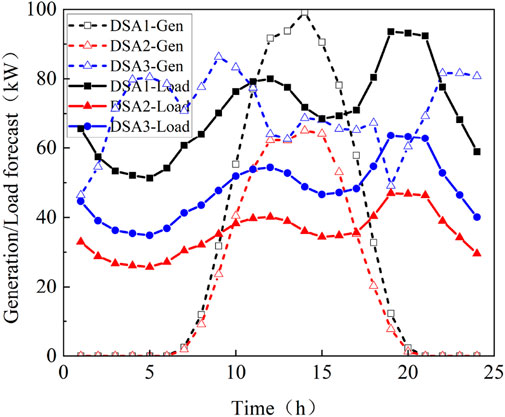
Numerical simulations are conducted in a distribution network to evaluate the effect of the demand response and uncertain prices on energy interaction. The system aims to verify the performance of the operation strategy based on the general Nash bargaining game theory. In the case study, simulations are performed on an IEEE 33-bus system with three DSAs located at buses 11, 23, and 29. The operation data, including the forecast value of price, generation, and load demand, are obtained from the study by Chen et al. (2017) and Lu et al. (2020). All simulations are solved using the Gurobi solver (Gurobi Optimization, 2020) in the Python environment on an Intel Core i7 computer.

4.1 Operation cost considering the stochastic prices and demand response

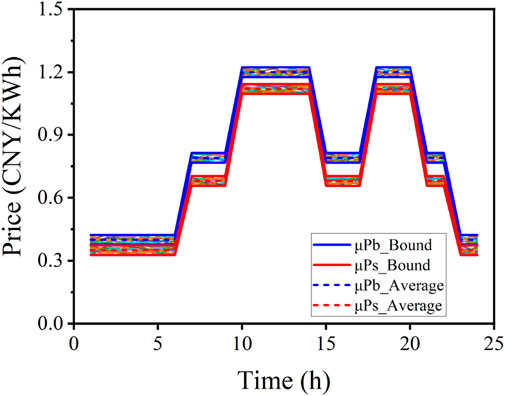
The effect of stochastic prices on the operation strategy is analyzed by comparing the operation costs under multiple price scenarios with the forecast value. The fluctuation in the market prices is modeled using the given probability distribution function, which is assumed to obey the Gaussian distribution. As shown in Figure 2, the forecast values of TOU prices are selected as the mean value with a variance of $1\times 10^{-4}$. Although large-scale scenarios are necessary to characterize random factors, they impose a heavy computational burden. To address this, a scenario reduction method is applied to decrease the number of scenarios. A total of 1,000 scenarios are generated by using Monte Carlo sampling, and K-means-based clustering reduction is utilized to generate 10 typical scenarios (Wang et al., 2021). The expected values of these multiple scenarios are selected as a result of the stochastic optimization, while the cost in the deterministic optimization is determined by the reaction of the DSAs to the predictable price. A general Nash bargaining-based interaction scheme is adopted to allocate the benefits when DSAs participate in energy interaction. To analyze the effect of the price on energy interaction, as shown in Figure 3, we assume that the predicted values of renewable generation and load demand are accurate. Since two important factors, energy interaction and demand response, affect the operation strategy, this paper analyzes the impact of these factors on the optimal operation strategy.

Figure 2

Figure 2. TOU price scenario with the distribution network.

Figure 3

Figure 3. Forecast of renewable generations and loads.

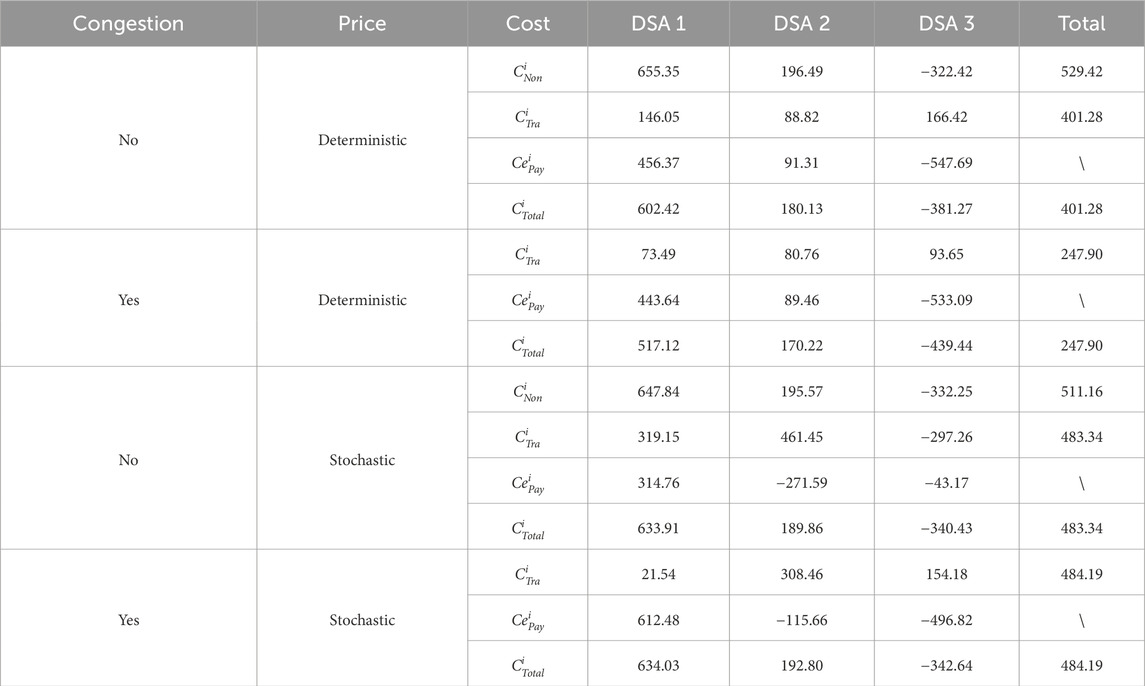
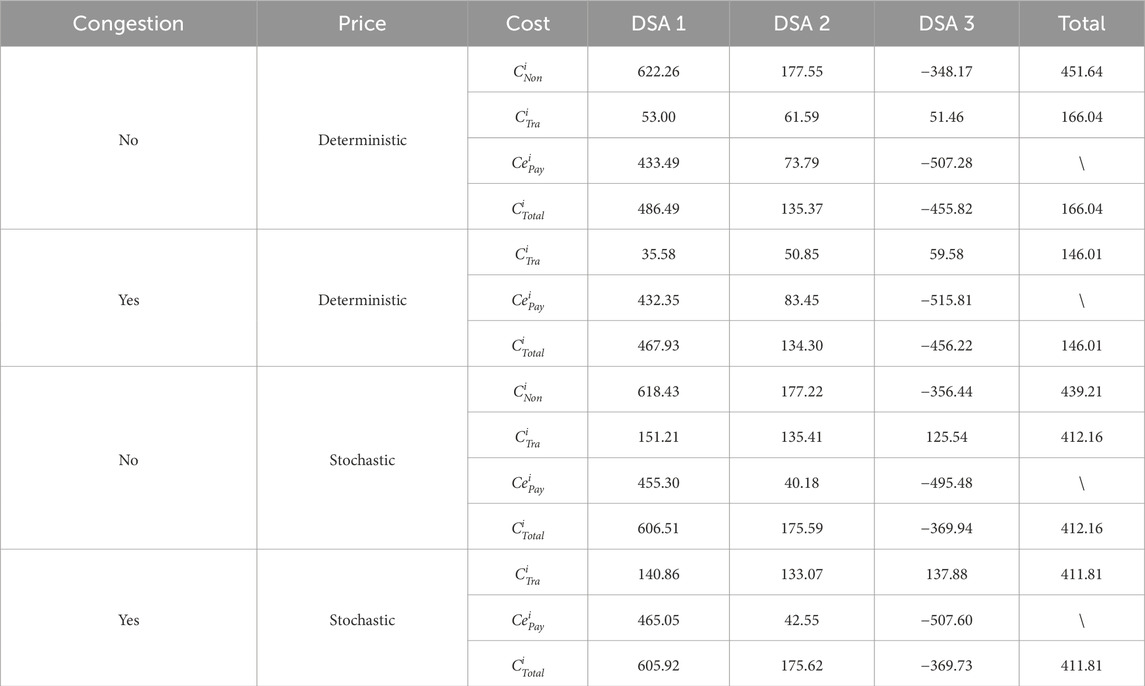
The deterministic and stochastic optimization results without/with the demand response are shown in Tables 1, 2, respectively. A negative value indicates the benefit that DSAs gain from selling energy to the distribution network or neighbors. It can be observed that DSAs reduce their operation cost when they participate in energy interaction. Considering the stochastic prices given in Table 1, the total operation cost of three DSAs is reduced by 24.20% under deterministic pricing, while the cost is reduced by 5.44% under uncertain pricing. In other words, compared with deterministic pricing, cooperative profit in energy interaction decreases by 16.98% in stochastic scenarios. The reason may be that, compared to deterministic prices, cooperative costs vary with the price scenarios, ultimately increasing the expected costs.

Table 1

Table 1. Operation costs without the demand response (CNY).

Table 2

Table 2. Operation costs with the demand response (CNY).

Considering the demand response, DSAs shift loads to periods of plentiful generation or lower demand through price adjustments or monetary incentives. They also enhance the efficiency of renewable energy utilization by coordinating the charging and discharging decisions of energy storage systems. As shown in Table 2, DSAs respond to prices through peak shaving and valley filling, which decreases the load demand during peak price periods. Consequently, operation costs—whether for individual or cooperative operations—significantly decrease compared to those given in Table 1. In other words, energy interaction among multiple DSAs enhances adaptable performance when considering the demand response.

The operation costs in energy interaction among DSAs will vary if the transmission lines have limitations within the distribution network. For simplicity, a maximum capacity of 100 kWh is considered for the line between nodes 2 and 3. This constraint causes decision changes for DSAs during the process of energy transactions with the distribution network and their neighbors. It can be observed that cooperative costs are always less than those of individual operations, and the demand response further reduces these operation costs.

Congestion impacts the operation decisions and, subsequently, the cooperative costs of DSAs. It restricts energy transmission for DSAs regardless of whether the demand response is considered. For deterministic prices, DSAs schedule battery usage to alleviate congestion, resulting in lower operation costs. However, stochastic prices compel DSAs to respond dynamically, leading to similar final operation costs with normal energy interaction since the total demand remains consistent.

4.2 Energy interaction with the distribution network

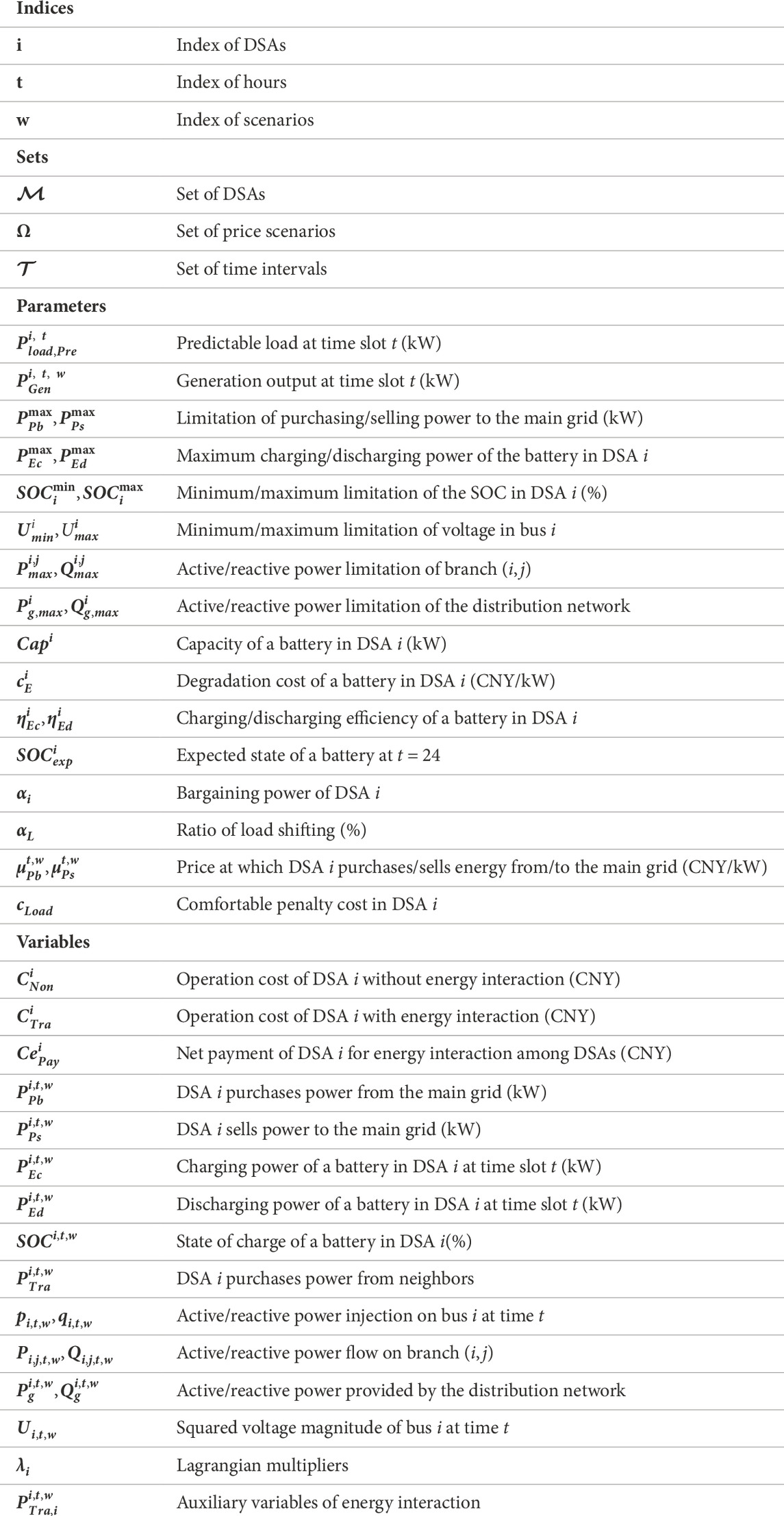
Figures 4, 5 illustrate the energy interaction results between the distribution network and DSAs over the course of a day. The positive/negative values represent the energy purchased/sold from/to the distribution network, respectively. We comparatively analyze the interaction quantities between the distribution network and multiple DSAs, regardless of their participation in energy interaction. Given the price scenarios, DSAs adjust their demand for purchasing/selling electricity to achieve cost minimization.

Figure 4

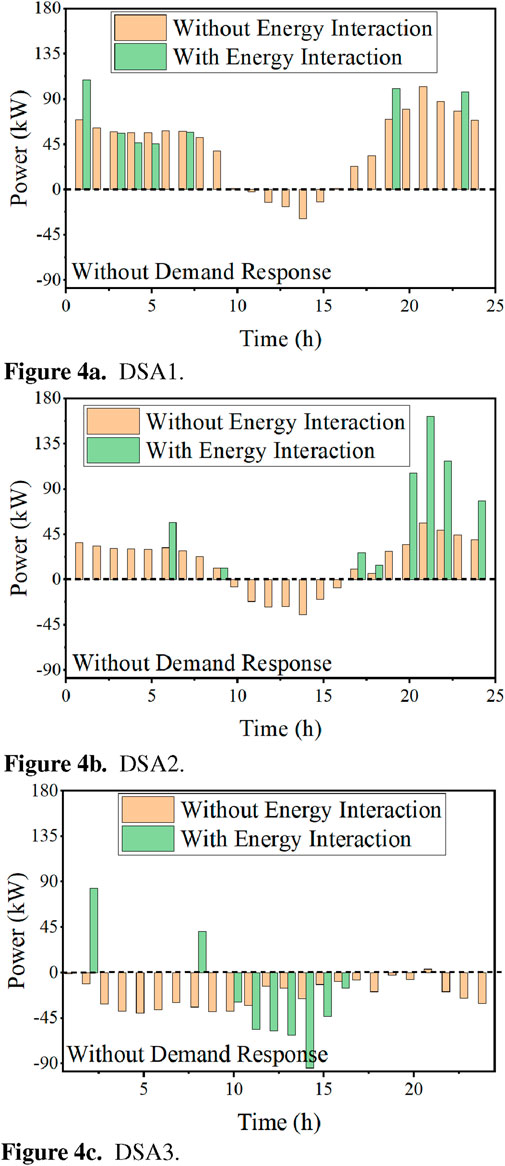
Figure 4. Interaction between the distribution network and DSAs ignoring the demand response. (A) DSA 1, (B) DSA 2, and (C) DSA 3.

Figure 5

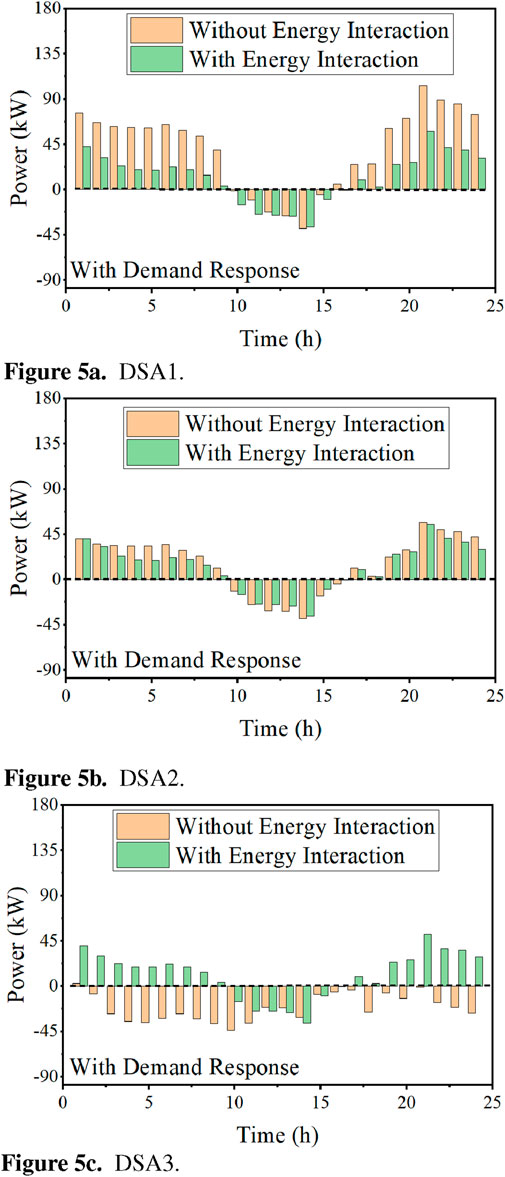
Figure 5. Interaction between the distribution network and DSAs considering the demand response. (A) DSA 1, (B) DSA 2, and (C) DSA 3.

Figure 4 shows the comparison of the effects of individual versus cooperative operation among DSAs on energy interactions with the distribution network. An individual DSA satisfies power balance by leveraging the distribution network and energy storage. Due to the scheduling limitation of the battery, the individual DSA may need to purchase electricity at a high price, increasing the operation costs. In contrast, cooperative DSAs form a group and share idle energy to balance their energy needs. DSAs purchase energy at 0:00–5:00 and 20:00–24:00 while selling energy at 10:00–15:00 to maximize their cooperative benefits during energy interactions. The load regulation capability of DSAs is enhanced when considering the demand response. As shown in Figure 5, DSAs achieve peak shaving and valley filling by leveraging the demand response and energy interactions.

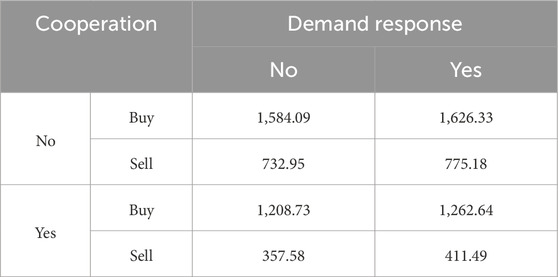
To further analyze the energy interaction, the total interaction quantity between DSAs and the distribution network is summarized in Table 3. The data show that the interaction between DSAs and the distribution network is influenced by both the interactive behavior of DSAs and demand response. We observed that the energy interaction among DSAs can reduce their dependence on the distribution network, enhancing their ability to cope with price uncertainty. To maintain energy balance, they purchase less energy from the distribution network and reduce the quantity of energy sold. Since the demand response is closely tied to electricity prices, DSAs increase their demand when the prices are lower, effectively responding to price uncertainties.

Table 3

Table 3. Total interaction quantity between DSAs and the distribution network (kWh).

4.3 Analysis of optimal results of the energy storage

The scheduling results of energy storage without/with the demand response are given in Figures 6, 7, respectively. The positive values represent storage discharging, while the negative values indicate storage charging. These figures demonstrate that energy storage can be utilized to satisfy the supply–demand balance through an internal scheduling strategy. As shown in Figure 6, the depth of charge/discharge is higher for the DSA operating individually without a demand response as energy storage is the primary means of shifting energy demand to other periods. This is particularly evident for DSA 1 at 10:00 and DSA 3 at 19:00. Although cooperative DSAs reduce the depth of charging/discharging, energy storage still works in conjunction with energy interaction to maintain energy balance.

Figure 6

Figure 6. Scheduling result of the energy storage without the demand response. (A) DSA 1, (B) DSA 2, and (C) DSA 3.

Figure 7

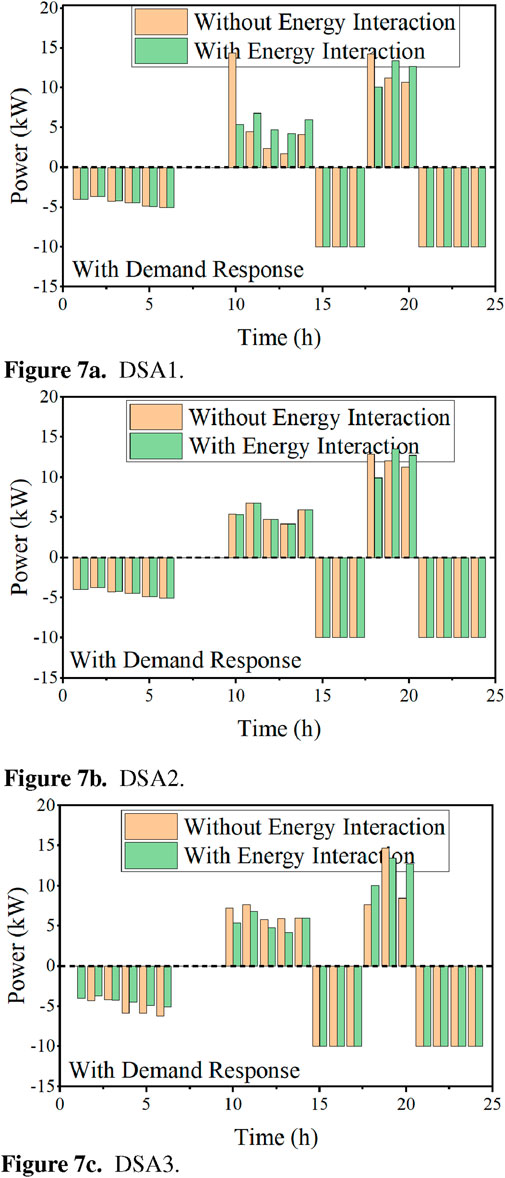
Figure 7. Scheduling result of the energy storage with the demand response. (A) DSA 1, (B) DSA 2, and (C) DSA 3.

The scheduling results of the energy storage considering the demand response are shown in Figure 7. We can observe that the reliance on energy storage decreases as supply–demand balance can be achieved through load shifting. Consequently, the charging and discharging depth of the energy storage for DSA 1 and DSA 3 is reduced, which, in turn, lowers the degradation costs in the objective function.

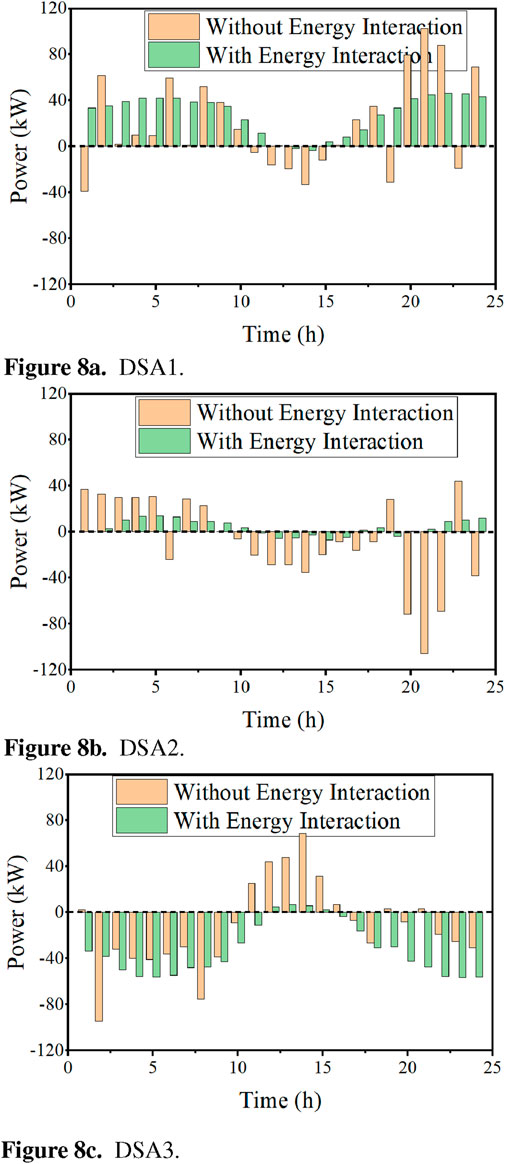
4.4 Analysis of energy interaction among DSAs

The energy interaction quantities among DSAs are given in Figure 8 when they cooperate with neighbors to share idle energy. The positive values indicate DSA $i$ purchasing energy from neighbors, while the negative values represent selling energy to others. Compared to individual operation, DSAs achieve energy balance by combining energy interaction, load shifting, and energy storage scheduling. This approach enhances energy self-sufficiency through energy interaction, potentially reducing the reliance on the distribution network.

Figure 8

Figure 8. Interaction among DSAs. (A) DSA 1, (B) DSA 2, and (C) DSA 3.

4.5 Distribution of the node voltage

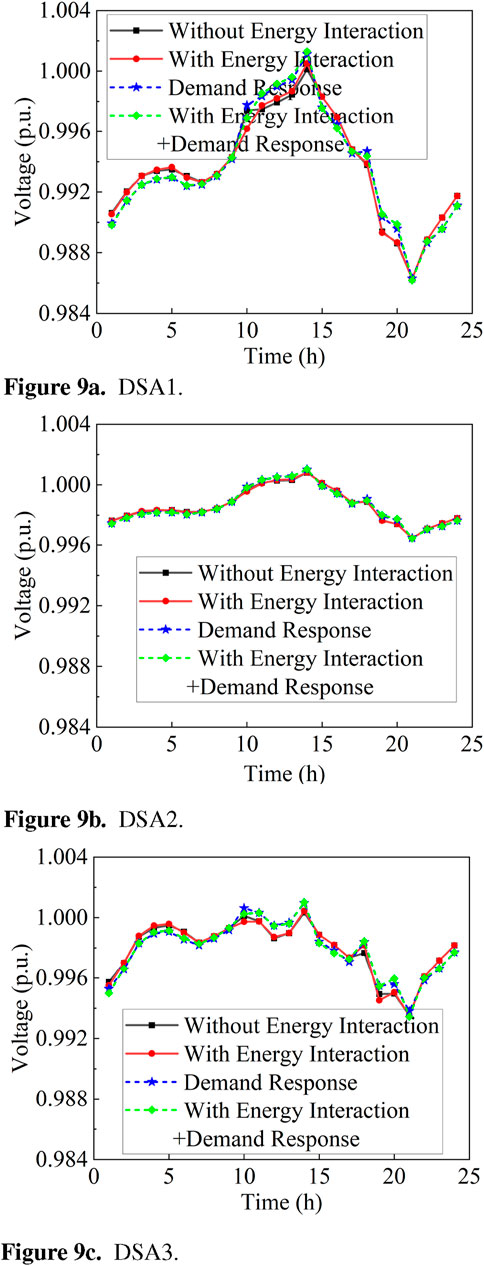
The node voltage varies with the energy interaction and demand response. Nodes 11, 23, and 29, connected to DSAs, serve as examples, and their voltages are shown in Figure 9. Although the voltage fluctuates across various simulation scenarios and periods, it always remains within the boundary limits. DSA 1, which has the highest load demand, experiences the largest voltage fluctuation, ranging from 0.986 p.u. to 1.001 p.u. Conversely, DSA 2, with the smallest load demand, exhibits relatively smooth voltage fluctuations. The demand response also leads to significant voltage fluctuations at different times. As shown in Figures 9A, C, DSAs shift loads to maintain the supply–demand balance, thereby altering the voltage distribution within the network.

Figure 9

Figure 9. Voltage of the node connected to multiple DSAs. (A) DSA 1, (B) DSA 2, and (C) DSA 3.

5 Conclusion

This paper presents an energy interaction framework for DSAs to enhance the local consumption of renewable generation. A general Nash bargaining theoretic model is established, taking into account the effect of uncertain prices and demand response. The typical price scenarios are depicted via Monte Carlo sampling and clustering. Given the price scenarios, DSAs make the optimal decisions by shifting loads to the plentiful generation or lower demand time through prices or monetary incentives. To solve the energy interaction model, it is decomposed and transformed into a traceable problem by leveraging the logarithmic transformation. In addition, the optimal power flow constraints are incorporated to improve the model’s practicality. The limitation of transmission capacity alters the operation strategies, which affects the operation costs. It decreases the energy exchange with the distribution network and increases the energy interaction among DSAs. An improved ADMM is proposed to solve the energy interaction problem using local information. Numerical simulations are conducted on an IEEE-33 bus system, demonstrating that uncertain prices may increase the total operation costs, while the demand response improves scheduling flexibility. Future work will focus on addressing energy transmission insufficiency due to capacity limitations during energy interactions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

FW: investigation and writing–original draft. XW: conceptualization and writing–original draft. JL: software and writing–original draft. YL: methodology and writing–original draft. HY: conceptualization and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Research on key technologies to improve application capability of distribution automation in new power system (2023A-016).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alizadeh, A., Esfahani, M., Dinar, F., Kamwa, I., Moeini, A., Mohseni-Bonab, S. M., et al. (2024). A cooperative transactive multi-carrier energy control mechanism with p2p energy+ reserve trading using nash bargaining game theory under renewables uncertainty. Appl. Energy 353, 122162. doi:10.1016/j.apenergy.2023.122162

CrossRef Full Text | Google Scholar

Baharvandi, A., Aghaei, J., Nikoobakht, A., Niknam, T., Vahidinasab, V., Giaouris, D., et al. (2019). Linearized hybrid stochastic/robust scheduling of active distribution networks encompassing pvs. IEEE Trans. Smart Grid 11, 357–367. doi:10.1109/tsg.2019.2922355

CrossRef Full Text | Google Scholar

Chang, X., Xu, Y., Gu, W., Sun, H., Chow, M.-Y., and Yi, Z. (2020). Accelerated distributed hybrid stochastic/robust energy management of smart grids. IEEE Trans. Industrial Inf. 17, 5335–5347. doi:10.1109/tii.2020.3022412

CrossRef Full Text | Google Scholar

Chen, S., Wei, Z., Sun, G., Cheung, K. W., Wang, D., and Zang, H. (2017). Adaptive robust day-ahead dispatch for urban energy systems. IEEE Trans. Industrial Electron. 66, 1379–1390. doi:10.1109/tie.2017.2787605

CrossRef Full Text | Google Scholar

Chen, Y., Mei, S., Zhou, F., Low, S. H., Wei, W., and Liu, F. (2019). An energy sharing game with generalized demand bidding: model and properties. IEEE Trans. Smart Grid 11, 2055–2066. doi:10.1109/tsg.2019.2946602

CrossRef Full Text | Google Scholar

Dehghanpour, K., and Nehrir, H. (2017). Real-time multiobjective microgrid power management using distributed optimization in an agent-based bargaining framework. IEEE Trans. Smart Grid 9, 6318–6327. doi:10.1109/tsg.2017.2708686

CrossRef Full Text | Google Scholar

Farivar, M., and Low, S. H. (2013). Branch flow model: relaxations and convexification-part i. IEEE Trans. Power Syst. 28, 2554–2564. doi:10.1109/tpwrs.2013.2255317

CrossRef Full Text | Google Scholar

Gurobi Optimization (2020). Gurobi optimizer reference manual.

Google Scholar

Hirsch, A., Parag, Y., and Guerrero, J. (2018). Microgrids: a review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 90, 402–411. doi:10.1016/j.rser.2018.03.040

CrossRef Full Text | Google Scholar

Jiang, Q., Mu, Y., Jia, H., Cao, Y., Wang, Z., Wei, W., et al. (2022). A stackelberg game-based planning approach for integrated community energy system considering multiple participants. Energy 258, 124802. doi:10.1016/j.energy.2022.124802

CrossRef Full Text | Google Scholar

Jin, Y., Choi, J., and Won, D. (2020). Pricing and operation strategy for peer-to-peer energy trading using distribution system usage charge and game theoretic model. Ieee Access 8, 137720–137730. doi:10.1109/access.2020.3011400

CrossRef Full Text | Google Scholar

Khorasany, M., Paudel, A., Razzaghi, R., and Siano, P. (2020). A new method for peer matching and negotiation of prosumers in peer-to-peer energy markets. IEEE Trans. Smart Grid 12, 2472–2483. doi:10.1109/tsg.2020.3048397

CrossRef Full Text | Google Scholar

Kim, H., Lee, J., Bahrami, S., and Wong, V. W. (2019). Direct energy trading of microgrids in distribution energy market. IEEE Trans. Power Syst. 35, 639–651. doi:10.1109/tpwrs.2019.2926305

CrossRef Full Text | Google Scholar

Kumar, K. P., and Saravanan, B. (2017). Recent techniques to model uncertainties in power generation from renewable energy sources and loads in microgrids–a review. Renew. Sustain. Energy Rev. 71, 348–358. doi:10.1016/j.rser.2016.12.063

CrossRef Full Text | Google Scholar

Li, G., Li, Q., Liu, Y., Liu, H., Song, W., and Ding, R. (2022). A cooperative stackelberg game based energy management considering price discrimination and risk assessment. Int. J. Electr. Power and Energy Syst. 135, 107461. doi:10.1016/j.ijepes.2021.107461

CrossRef Full Text | Google Scholar

Li, J., Zhang, C., Xu, Z., Wang, J., Zhao, J., and Zhang, Y.-J. A. (2018). Distributed transactive energy trading framework in distribution networks. IEEE Trans. Power Syst. 33, 7215–7227. doi:10.1109/tpwrs.2018.2854649

CrossRef Full Text | Google Scholar

Lu, S., Gu, W., Zhang, C., Meng, K., and Dong, Z. (2020). Hydraulic-thermal cooperative optimization of integrated energy systems: a convex optimization approach. IEEE Trans. Smart Grid 11, 4818–4832. doi:10.1109/tsg.2020.3003399

CrossRef Full Text | Google Scholar

Luo, C., Zhou, X., and Lev, B. (2022). Core, shapley value, nucleolus and nash bargaining solution: a survey of recent developments and applications in operations management. Omega 110, 102638. doi:10.1016/j.omega.2022.102638

CrossRef Full Text | Google Scholar

Paudel, A., Chaudhari, K., Long, C., and Gooi, H. B. (2019). Peer-to-peer energy trading in a prosumer-based community microgrid: a game-theoretic model. IEEE Trans. Industrial Electron. 66, 6087–6097. doi:10.1109/tie.2018.2874578

CrossRef Full Text | Google Scholar

Sarker, E., Seyedmahmoudian, M., Jamei, E., Horan, B., and Stojcevski, A. (2020). Optimal management of home loads with renewable energy integration and demand response strategy. Energy 210, 118602. doi:10.1016/j.energy.2020.118602

CrossRef Full Text | Google Scholar

Tushar, W., Saha, T. K., Yuen, C., Morstyn, T., McCulloch, M. D., Poor, H. V., et al. (2019). A motivational game-theoretic approach for peer-to-peer energy trading in the smart grid. Appl. energy 243, 10–20. doi:10.1016/j.apenergy.2019.03.111

CrossRef Full Text | Google Scholar

Tushar, W., Saha, T. K., Yuen, C., Smith, D., and Poor, H. V. (2020). Peer-to-peer trading in electricity networks: an overview. IEEE Trans. Smart Grid 11, 3185–3200. doi:10.1109/tsg.2020.2969657

CrossRef Full Text | Google Scholar

Tushar, W., Yuen, C., Mohsenian-Rad, H., Saha, T., Poor, H. V., and Wood, K. L. (2018). Transforming energy networks via peer-to-peer energy trading: the potential of game-theoretic approaches. IEEE Signal Process. Mag. 35, 90–111. doi:10.1109/msp.2018.2818327

CrossRef Full Text | Google Scholar

Vieira, G., and Zhang, J. (2021). Peer-to-peer energy trading in a microgrid leveraged by smart contracts. Renew. Sustain. Energy Rev. 143, 110900. doi:10.1016/j.rser.2021.110900

CrossRef Full Text | Google Scholar

Wang, H., and Huang, J. (2016). Incentivizing energy trading for interconnected microgrids. IEEE Trans. Smart Grid 9, 2647–2657. doi:10.1109/tsg.2016.2614988

CrossRef Full Text | Google Scholar

Wang, L., Zhang, Y., Song, W., and Li, Q. (2021). Stochastic cooperative bidding strategy for multiple microgrids with peer-to-peer energy trading. IEEE Trans. industrial Inf. 18, 1447–1457. doi:10.1109/tii.2021.3094274

CrossRef Full Text | Google Scholar

Wei, C., Shen, Z., Xiao, D., Wang, L., Bai, X., and Chen, H. (2021). An optimal scheduling strategy for peer-to-peer trading in interconnected microgrids based on ro and nash bargaining. Appl. Energy 295, 117024. doi:10.1016/j.apenergy.2021.117024

CrossRef Full Text | Google Scholar

Zhong, W., Xie, S., Xie, K., Yang, Q., and Xie, L. (2020). Cooperative p2p energy trading in active distribution networks: an milp-based nash bargaining solution. IEEE Trans. Smart Grid 12, 1–1276. doi:10.1109/tsg.2020.3031013

CrossRef Full Text | Google Scholar

Nomenclature