Quantum-inspired deep reinforcement learning for adaptive frequency control of low carbon park island microgrid considering renewable energy sources

The low carbon park islanded microgrid faces operational challenges due to the high variability and uncertainty of distributed renewable energy sources. These sources cause severe random disturbances that impair the frequency control performance and increase the regulation cost of the islanded microgrid, jeopardizing its safety and stability. This paper presents a data-driven intelligent load frequency control (DDI-LFC) method to address this problem. The method replaces the conventional LFC controller with an intelligent agent based on a deep reinforcement learning algorithm. To adapt to the complex islanded microgrid environment and achieve adaptive multi-objective optimal frequency control, this paper proposes the quantum-inspired maximum entropy actor-critic (QIS-MEAC) algorithm, which incorporates the quantum-inspired principle and the maximum entropy exploration strategy into the actor-critic algorithm. The algorithm transforms the experience into a quantum state and leverages the quantum features to improve the deep reinforcement learning’s experience replay mechanism, enhancing the data efficiency and robustness of the algorithm and thus the quality of DDI-LFC. The validation on the Yongxing Island isolated microgrid model of China Southern Grid (CSG) demonstrates that the proposed method utilizes the frequency regulation potential of distributed generation, and reduces the frequency deviation and generation cost.

1 Introduction

Distributed power supply has strong randomness and weak controllability, and its output mode is highly intermittent. Moreover, the load demand-side response is uncertain and the grid interconnection factors are sudden. These all affect the balance of supply and demand and the quality of power in the power system, leading to various problems for industrial and agricultural production and daily life. They cause economic losses and may even endanger the safe operation of the power grid. Frequency is an important measure of power quality. As one of the key indicators of power quality, frequency can directly reflect the balance between the load power on the demand side and the generator’s power generation in the power system. Therefore, maintaining the frequency stability is a feasible way to ensure the dynamic stability of the system under strong random disturbances. LFC 1 is a kind of ultra-short-term frequency regulation technology. The LFC controller uses closed-loop feedback control to adjust the output power of the LFC unit according to a certain control strategy. It senses a series of state indicators such as frequency, area control error (ACE), contact line exchange power, and output power of the unit. This achieves the dynamic balance of the power generation and the load power, and then keeps the grid frequency at the specified value and the contact line exchange power at the planned value. Thus, LFC control technology has been widely used in power system operation control. However, the traditional centralised LFC system (Li et al., 2020; Sun et al., 2023) always prioritises the optimal control performance of its own region, and the information synergy between regions is low. It is hard to meet the control performance demand of a high proportion of large-capacity new energy grid-connected mode with the traditional centralised AGC as a vital means of grid scheduling. Moreover, the control performance of LFC largely depends on the control strategy 4, while the traditional LFC control strategy 5 is no longer adequate to cope with the regulation and control tasks under the trend of large-scale new energy grid-connectedness and the stochastic fluctuation of uncertain loads on the customer side (Ferrario et al., 2021; Li et al., 2022). Therefore, from the perspective of distributed LFC, it is of great significance to seek a class of optimal LFC control strategies for large-scale grid integration of new energy sources based on modern control theory and intelligent optimization methods. These strategies can meet the control performance and operation requirements of power grids under strong stochastic perturbations in the new type of power systems. The traditional methods include two types: the centralised hierarchical LFC strategy and the fully distributed LFC strategy.

1.1 Centralized hierarchical LFC strategy

Some notable examples of this strategy include Model Predictive Control (MPC) (Zheng et al., 2012), Adaptive Control (AC) (Wen et al., 2015), Learning-Based Control (LBC) (Qadrdan et al., 2017), and Adaptive Proportional-Integral (PI) Control (El-Fergany and El-Hameed, 2017). Zheng et al. (Zheng et al., 2012) introduced a Distributed Model Predictive Control (DMPC) strategy that relies on the mutual coordination of global performance optimization metrics. Wen et al. (Wen et al., 2015) proposed a Composite Adaptive Centralized Load Frequency Control (CALFC) strategy for regulating the frequency of source-net-load systems, addressing the challenge of source-load cooperative frequency regulation. Qu et al. (Qadrdan et al., 2017) developed a Data-Driven Centralized Load Frequency Control (DLCFC) method, treating load frequency control as a stochastic dynamic decision-making problem for source-load cooperative frequency regulation. Qadrdan et al. (El-Fergany and El-Hameed, 2017) designed an LFC method based on the “Social Spider” Genetic Optimization Algorithm to tackle the tuning of PI parameters in microgrids.

However, these methods do not adequately consider load modeling or the time series dependence of random disturbances from sources like wind power and photovoltaic systems. Furthermore, their impact on the system’s frequency control performance is relatively limited.

Centralized LFC control offers the advantage of reflecting the entire network’s state, but it also comes with drawbacks. Firstly, the controller and power distributor employ distinct algorithms for control and optimization, resulting in independence and differing objectives, potentially compromising frequency control performance. Secondly, concentrated communication within the microgrid dispatch center can lead to inconsistencies and delays in frequency control due to communication overload, and may even trigger frequency collapse in some instances. Lastly, centralized LFC control makes it challenging to consider the consistent performance of regulation service providers in the performance-based regulation market across different regions, potentially leading to providers prioritizing local units over those in other areas and grid operators.

1.2 Fully distributed LFC strategy

Research on fully distributed Load Frequency Control (LFC) structures primarily centers on the multi-agent control framework. This framework comprises agent layers that analyze and process received information, determine suitable control strategies, and cooperate with other agent layers to ensure seamless LFC operation. The prevailing methods in this context are multi-agent collaborative consistency and stochastic consistency methods.

Li et al. (Qing et al., 2015) introduced a Collaborative Consistent Q-Learning (CCQL) algorithm that leverages a distributed power dispatch model to swiftly and optimally dispatch power commands for distributed LFC control, even in scenarios with high communication demands among units. Xi et al. (Xi et al., 2016b) proposed a Wolf-Pack Hunting Strategy (WPHS) to handle topological changes arising from power constraints. Wang et al. (Wang and Wang, 2019) devised a discrete-time robust frequency controller for islanded microgrids, capable of achieving frequency restoration and precise active power dispatch through an iterative learning mechanism. Lou et al. (Lou et al., 2020) aimed to reduce the operational costs of isolated microgrids by considering the active output costs. They implemented a distributed LFC control strategy based on the consistency approach, leading to an optimal LFC strategy that benefits both global and self-reliance aspects through effective communication among various units. This approach facilitates coordination between controllers and distributors, akin to centralized LFC, while ensuring smooth frequency control and minimizing conflicts of interest among different units. However, it relies heavily on communication among units and areas, making it less suitable for multi-area islanded microgrids.

Reinforcement Learning (RL) is a machine learning technique (Yu et al., 2011; Wiering and Otterlo, 2012) that operates without precise knowledge of the model. It offers the advantages of self-learning and dynamic stochastic optimization. RL does not rely on predefined systematic knowledge but continually adapts and optimizes strategies by interacting with the environment and learning through trial and error. This allows RL to find optimal solutions for sequential problems. RL-based control algorithms excel in decision-making, self-learning, and self-optimization, primarily due to the relatively straightforward design of reward functions. As the Load Frequency Control (LFC) process follows a Markov Decision Process (MDP), RL based on MDP can enhance LFC control strategies by crafting suitable reward functions to translate contextual information into appropriate control signals. It also aids in selecting control signals for optimal sequential decision-making iterations, improving aspects such as data processing, feature expression, model generalization, intelligence, and sensitivity of the LFC controller.

This paper explores optimal LFC control strategies for new energy grid integration using RL algorithms, focusing on multi-region collaboration and addressing issues arising from the high proportion of large-capacity new energy sources, which introduce strong random disturbances. This approach aims to enhance the compatibility between new energy sources and the power system, ultimately promoting the development of the new power system. RL is a pivotal topic in Artificial Intelligence, with Imthias et al. (Ahamed et al., 2002) being among the first to apply it to power system LFC. RL is favored for its high control real-time capabilities and robustness, as it responds primarily to the evaluation of the current control effect. It has found extensive use in ensuring the safe and stable control of power systems.

In addition to RL, classical machine learning algorithms have been widely adopted in Automatic Generation Control (AGC) strategies. Yinsha et al. (Yinsha et al., 2019) introduced a multi-agent RL game model based on MDP, capable of handling single-task multi-decision game problems, which enhances agent intelligence and system robustness. Sause et al. (Sause, 2013) proposed an algorithm combining Q-learning and SARSA time variance within the collaborative reinforcement learning framework of “Next Available Agent,” effectively addressing resource competition among multiple agents in a virtual environment. This improves agents’ exploration abilities in both static and dynamic environments. An algorithm integrating deep deterministic policy gradients and preferred experience replay is presented in (Ye et al., 2019), rapidly acquiring environmental feedback in a multi-dimensional continuous state-action space. Yin et al. (Yin et al., 2018) introduced an algorithm based on Double Q Learning (DQL) to mitigate the positive Q bias issue in Q learning algorithms through underestimation of the maximum expected value.

Ensemble learning, a specialized type of machine learning algorithm that enhances decision-making accuracy through collective decision-making, is less commonly applied in AGC. However, Munos et al. (Munos et al., 2016) introduced an Ensemble Bootstrapping for Q-Learning algorithm, which combines Q-learning within ensemble learning to correct the positive Q-value bias problem in Q-learning algorithms. This algorithm addresses high variance and Q-value deviation in the Q-learning iteration process, achieving effective control.

The methodologies employed for value function estimation in reinforcement learning algorithms are fundamentally divided into two distinct categories, predicated on the alignment between the target policy (the policy under evaluation) and the behavior policy (the policy enacted by the intelligent agent during environmental interaction). These categories are identified as in-policy and off-policy algorithms. In-policy algorithms undertake the evaluation of the target policy through the utilization of sample data directly derived from the target policy itself, a process typically exemplified by the Sarsa algorithm. Conversely, off-policy algorithms engage in the assessment of the target policy via sample data procured from the behavior policy, a method commonly exemplified by the Q-learning algorithm. Within the context of real-world engineering applications, in-policy algorithms may encounter challenges in efficiently generating requisite sample data or may incur elevated operational costs, which can severely restrict their applicability in complex decision-making scenarios. Off-policy algorithms emerge as a solution to these constraints, offering broad utility in practical Load Frequency Control (LFC) engineering projects. Nevertheless, these algorithms are not without their limitations, primarily due to their reduced robustness and the discrepancies in data distribution between the sample data utilized for target policy evaluation and that required for the off-policy algorithm’s evaluation process. Such disparities can lead to phenomena known as “overestimation” or “underestimation” of action values, which adversely affect the decision-making precision and convergence efficiency of off-policy algorithms. This issue represents a substantial impediment to the broader application of off-policy reinforcement learning algorithms, especially in the domain of frequency control for islanded microgrids.

In the contemporary landscape of science and technology, where interdisciplinary integration is increasingly becoming a norm, the borrowing and application of concepts from the natural world to information processing technologies are gaining momentum. Among these integrations, the incorporation of quantum physics principles into information processing technologies stands out, promising substantial performance improvements. The amalgamation of quantum physics with artificial intelligence algorithms, in particular, has shown to yield significant enhancement effects. The introduction of quantum characteristics into the frameworks of reinforcement learning algorithms, especially within the deep reinforcement learning experience replay mechanism, has attracted considerable academic interest. By integrating quantum features, the robustness of reinforcement learning algorithms can be significantly improved, offering a promising avenue for enhancing algorithmic performance in complex applications such as LFC in islanded microgrids. This innovative approach demonstrates the potential to mitigate the challenges posed by traditional off-policy algorithms, thereby advancing the field of reinforcement learning and its application in critical engineering solutions.

This paper introduces the Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) algorithm, which incorporates quantum-inspired principles and the maximum entropy exploration strategy into the original actor-critic algorithm. It transforms experiences into a quantum state and utilizes quantum properties to enhance the experience replay mechanism in deep reinforcement learning. Consequently, this enhancement improves the algorithm’s data efficiency and robustness, leading to an overall enhancement in the quality of Data-Driven Intelligent Load Frequency Control (DDI-LFC).

Building upon this algorithm, we have developed a Data-Driven Intelligent Load Frequency Control (DDI-LFC) method. This method replaces the conventional LFC controller with an intelligent agent based on a deep reinforcement learning algorithm. This agent is capable of handling the complex environment of isolated island microgrids and achieving adaptive multi-objective optimal frequency control.

Verification using the South Grid Yongxing Island isolated island microgrid model demonstrates the effectiveness of the proposed method. It fully leverages the frequency regulation capabilities of distributed power sources and energy storage, resulting in minimized frequency deviation and generation costs.

The innovations in this paper can be summarized as follows:

1) This paper introduces a novel approach known as Data-Driven Intelligent Load Frequency Control (DDI-LFC) to tackle the problem at hand. Instead of the traditional LFC controller, this method employs an intelligent agent built upon a deep reinforcement learning algorithm.

2) Furthermore, this paper puts forward the Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) algorithm, which seamlessly integrates quantum-inspired principles and the maximum entropy exploration strategy into the actor-critic algorithm.

Section 2 provides an in-depth description of the islanded microgrid system model. In Section 3, we present a novel method, presenting its comprehensive framework. Section 4 is dedicated to conducting case studies that assess the effectiveness of the proposed approach. Finally, in Section 5, we conclude the paper by summarizing key insights and discussing the primary research findings.

2 Model for island microgrid

2.1 Microgrids and distributed power sources

An islanded microgrid is a small-scale system that generates and distributes power using various distributed sources, storage devices, converters, loads, and monitoring and protection devices. Microgrids can operate autonomously and independently, with self-control, protection and management functions. The purpose of microgrid is to enable the flexible and efficient use of distributed sources and to address the challenge of connecting a large number and variety of distributed sources to the grid. Microgrid can utilize renewable energy and cogeneration, among other forms of energy, to enhance energy efficiency and power reliability, to lower grid losses and pollution emissions, and to facilitate the transition to smart grid. Photovoltaic, wind, internal combustion engines, fuel cells, and storage devices are some of the common distributed sources in microgrids. A quick and effective control strategy is needed to ensure the safe and stable operation of the microgrid, by maintaining the balance of voltage, frequency and power. The transfer function of an islanded microgrid is shown in Figure 1.

Figure 1

Figure 1. Model for Island microgrid.

2.2.1 Photovoltaic systems

To model the electrical behavior and power production of the PV power generation system, the mathematical model incorporates the PV array, the MPPT controller, the DC-DC converter, and other components. The following equations express the mathematical model of the PV array: Details as Eq. 1.

$I=I_{ph}-I_S\left(e^{\frac{q\left(V+I{R}_s\right)}{AkT}}-1\right)-\frac{V+I{R}_S}{R_p}(1)$

where I is the PV array output current, V is the PV array output voltage, I_ph is the photogenerated current, I_S is the reverse saturation current, q is the electron charge, A is the diode quality factor, k is the Boltzmann’s constant, T is the cell temperature, R_S is the series resistor, R_p is the parallel resistor.

2.2.2 Wind power systems

The mathematical model of the wind power system includes wind turbine, wind wheel, generator, inverter etc. to simulate the mechanical and electrical characteristics of the wind power system. The mathematical model of the wind turbine can be represented by the following equations. Details as Eq. 2.

$P_w=\frac{1}{2}\rho A{C}_p\left(\lambda ,\beta \right)v_w^3(2)$

where P_w is the wind turbine output power, ρ is the air density, A is the swept area of the wind turbine, C_p is the wind turbine power coefficient, λ is the wind turbine rotational speed ratio, β is the wind turbine blade inclination angle, v_w is the wind speed.

2.2.3 Fuel cells

The mathematical model of a fuel cell includes electrochemical reactions, thermodynamics, hydrodynamics, mass transfer, heat transfer, etc. to simulate variables such as voltage, current, temperature, concentration, etc. of the fuel cell. The mathematical model of a fuel cell can be represented by the following equations. Details as Eq. 3.

$V_{fc}=E_0-{\eta }_a-{\eta }_c-{{\eta }_o}_{hm}(3)$

Where V_fc is the fuel cell output voltage, E₀ is the fuel cell open circuit voltage, η_a is the anode polarisation loss, η_c is the cathode polarization loss and η_ohm is the ohmic loss.

2.2.4 Micro gas turbine modelling

Conventional power generators used in microgrids are generally microfuel generators. Compared with diesel generators, these generators have cleaner emissions and lower operation and maintenance costs, so they are mostly used for daily power supply. According to the analysis of (Xi et al., 2016b), the frequency control model of microfuel generator can be represented by the model in Figure 1 Details as Eqs. 4, 5.

$C_{MT,OM}={\displaystyle \sum _{t=1}^T}{k}_{MT,OM}{P}_{MT}\left(t\right)(4)$

$C_{MT,fuel}=C_{MT}\Delta t\frac{1}{LHV}{\displaystyle \sum _{t=1}^T}\frac{P_{MT}\left(t\right)}{{\eta }_{MT}}(5)$

where C_MT is the maintenance cost of the power consumption, the value of C_MT,fuel is the unit price of MT fuel gas, LHV is the low calorific value of natural gas, and P_MT is the operating efficiency of MT.

2.2.5 Diesel generators

Sag control is a technique that enables diesel generators to keep their frequency and voltage output stable. With sag control, each unit can adjust its power output to the voltage sag, without requiring any communication or coordination with other units. With sag control, each unit can adjust its power output to the voltage sag, without requiring any communication or coordination with other units. This enhances the reliability and flexibility of the distributed generation system. Details as Eqs. 6, 7.

$C_{DG,OM}={\displaystyle \sum _{t=1}^T}{k}_{DG,OM}{P}_{DG}\left(t\right)(6)$

$C_{DG,fuel}=\alpha +\beta {\displaystyle \sum _{t=1}^T}{P}_{DG}\left(t\right)+\gamma {\displaystyle \sum _{t=1}^T}{P}_{DG}^2\left(t\right)(7)$

where C_DG,OM is the cost of the DG, k_DG,OM is the DG maintenance factor; P_DG is the fuel cost of the DG, and α, β, and γ are the fuel cost coefficients.

2.2.6 Electrochemical energy storage devices

Energy storage device: the mathematical model of the energy storage device includes charge/discharge characteristics, energy management system, voltage control, etc. to simulate the charge/discharge process and power output of the energy storage device. The mathematical model of the energy storage device can be represented by the following equations. Details as Eqs. 8–10.

$E=P_{ch}-P_{dis}(8)$

$SOC=\frac{E}{E_{\max }}(9)$

$V_{\text{bat}}=E_{oc}-R_{\mathrm{int}}{I}_{\text{bat}}(10)$

where E is the energy change rate of the energy storage device, P_ch is the charging power of the energy storage device, P_dis is the discharging power of the energy storage device, SOC is the state of charge of the energy storage device, E_max is the maximum energy of the energy storage device, V_bat is the output voltage of the energy storage device, E_oc is the open-circuit voltage of the energy storage device, R_int is the internal resistance of the energy storage device, I_bat is the output current of the energy storage device.

2.2 Objective functions and constraints

The traditional LFC method for microgrids only focuses on reducing the frequency error of the isolated microgrid, without taking the cost into account. This paper presents a DD-LFC method that achieves both objectives: minimising the frequency variation and the power generation cost of the units. The DD- LFC method employs an integrated multi-objective optimization, such that the frequency error of the isolated microgrid is reduced to a minimum. LFC method employs an integrated multi-objective optimization, such that the sum of the absolute values of the frequency variation and the power generation cost is minimized. The constraints are shown below. Details as Eqs. 11, 12.

$\min {\displaystyle \sum _{t=1}^T}\left|\Delta f\right|+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^n}\left({\alpha }_i\Delta P_{\mathrm{G}i}^2+{\beta }_i\Delta P_{\mathrm{G}i}+{\gamma }_i\right)(11)$

$\left\{\begin{array}{l}{\displaystyle \sum _{i=1}^n}\Delta P_i^{\text{in}}=\Delta P_{\text{order}-\sum }\\ \Delta P_{\text{order}-\sum }*\Delta P_i^{\text{in}}\ge 0\\ \Delta P_i^{\min }\le \Delta P_i^{\text{in}}\le \Delta P_i^{\max }\\ \left|\Delta P_{\mathrm{G}i}\left(t\right)-\Delta P_{\mathrm{G}i}\left(t+1\right)\right|\le \Delta P_i^{\text{rate}}\end{array}\right.(12)$

where ΔP_order-∑ is the total command, ΔP_i^max and ΔP_i^min are the limits of the ith unit, ΔP_i^rate is the ramp rate of the ith unit, and ΔP_iⁱⁿ is the command of the ith unit.

3 Training for proposed method

3.1 MDP modelling of DDI-LFCs

RL aims to determine the optimal policy for a Markov Decision Process (MDP) where an agent engages in continuous exploration. The policy function, denoted as π, maps the state space (S) to the action space (A). The optimal policy is the one that maximizes the cumulative reward.

In the context of microgrid Load Frequency Control (LFC), Markov Decision Process modeling involves the utilization of MDP, a mathematical framework, to characterize and optimize load dispatch and frequency stabilization problems within microgrids. MDP serves as a discrete-time stochastic control process that models decision-making in situations with uncertainty and partial control. It comprises four key components: the state space, action space, state transition probability, and reward function.

The primary objective of modeling using MDP is to identify an optimal strategy for the microgrid. This strategy is essentially a mapping function from the state space to the action space, designed to maximize or minimize the cumulative rewards over the long term for the microgrid. The cumulative reward G_t from time t is defined as. Details as Eq. 13.

$G_t={\displaystyle \sum _{i=0}^n}{\gamma }^i{r}_{t+i}=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots {\gamma }^n{r}_{t+n}(13)$

where λ is the discount factor, which value lower than 1 is typically used to avoid the endless accumulation of expected rewards that causes the learning process to diverge. The distributor employs the PROP allocation method to guarantee the reasonableness of the power distribution for each unit.

3.1.1 Action space

The agent generates the total command that determines the unit’s output. The only variable that the agent can control is its action, which accounts for 10% of this command. The only variable that the agent can control is its action, which accounts for 10% of this command. Details as Eq. 14.

$\left[\Delta P_{\text{order}-\sum }/10\right](14)$

where $\Delta P_{\text{order}-\sum }$ is the total command.

3.1.2 State space

The microgrid system has two state variables: the frequency error and its integral. The frequency error measures the difference between the actual and the target frequency of the microgrid, while the integral accumulates the error over time. The frequency error measures the difference between the actual and the target frequency of the microgrid, while the integral accumulates the error over time. The output variable is the total power generated by the distributed energy sources in the microgrid. Details as Eq. 15.

$\left[\Delta f{\int }_0^t\Delta fdt\Delta P_G^{total}\right](15)$

where $\Delta P_G^{total}$ is the total output.

3.1.3 Reward functions

The controller aims to reduce both the frequency variation and the production cost. To encourage the agent to find the best policy, a penalty for control actions is included in the reward function. The reward function is defined as follows. Details as Eqs. 16, 17.

$r=-{\mu }_2\left|\Delta f\right|+{\mu }_3{\displaystyle \sum _{i=1}^n}{C}_i(16)$

$T=\left\{\begin{array}{ll}0& \left|\Delta f\right|<0.01HZ\\ -3& \left|\Delta f\right|\ge 0.01HZ\end{array}\right.(17)$

where r is the reward and A is the punishment function.

3.2 Quantum-inspired QIS-MEAC algorithm framework

3.2.1 QIS-MEAC foundation framework

This paper proposes a novel experience replay mechanism for quantum-inspired deep reinforcement learning algorithms, which leverages some quantum properties and applies them to reinforcement learning. The aim of this improvement is to offer a natural and user-friendly experience replay method that transforms experiences into quantized representations that correspond to their importance and sampling priority, thereby altering their likelihood of being sampled.

Current deep reinforcement learning algorithms still have some room for improvement in terms of data utilization efficiency, reference adjustment complexity, and computational cost, especially as the reinforcement learning application scenarios become more complex and dynamic, making the interaction with the environment very expensive. Therefore, the demand for data utilization efficiency and robustness of the algorithms is also increasing. By incorporating quantum properties into the experience replay mechanism of deep reinforcement learning, we can achieve better results with less effort in practical control tasks. The DDI-LFC method proposed in this paper improves the experience replay mechanism of deep reinforcement learning by using quantum properties, which enables it to effectively learn more samples and prior knowledge, thus enhancing its robustness and allowing the LFC to perform better under various complex load disturbances and achieve multi-objective optimal control.

Figure 2 above illustrates the experience replay process of the quantum-inspired deep reinforcement learning algorithm, and Figure 2 shows its overall structure. In each training iteration cycle, the agent interacts with the environment and reads the required state and reward information at step t, and then generates a state transition et based on its chosen actions. This state transition is first transformed into a quantum state representation, or more precisely, a mathematical expression of the kth qubit in the quantum integrated system, where k is the index of the qubit in the cache pool. Next, the qubit undergoes a quantum preparation operation and becomes a quantum in a superposed state. Then, by observation, the quantum state representation of the experience collapses into either an acceptance or a rejection state, with a probability that reflects its importance, and a small data batch is drawn from the accepted experience and fed into the neural network for training. Moreover, after each training, the extracted experience is returned to the experience pool and converted back into the quantized representation of the experience. This conversion process involves a combination of two kinds of western operations: quantum preparation operation and quantum depreciation operation. The quantum preparation operation adjusts the probability amplitude of the quantized representation of the experience to match its TD-error, and the quantum depreciation operation considers the number of times the experience is replayed, and adding the replay frequency of the experience will diversify the sampled experience, so as to make the experience replay more balanced. The whole process repeats until the algorithm stops, and the following sections will explain the operations in more detail.

Figure 2

Figure 2. Experience pool quantum operations.

The QIS-MEAC algorithm aims to maximize both the cumulative reward and the entropy. Entropy quantifies the uncertainty of stochastic strategies, and in deep reinforcement learning, higher entropy implies more diverse and exploratory strategies. Therefore, the QIS-MEAC algorithm has a greater ability to explore. The following is the optimal policy function of the QIS-MEAC algorithm with entropy. Details as Eq. 18.

$\left\{\begin{array}{l}{\pi }^{*}={\mathrm{argmax}}_{\pi }{s}_{\left(s_t,a_t\right){\tau }_{\pi }}\left[{\displaystyle \sum _{t=0}^T}{\gamma }^t\left(r\left(s_t,a_t\right)+\alpha \mathcal{H}\left(\pi \left(\cdot \mid s_t\right)\right)\right)\mid s_0=s\right]\\ \mathcal{H}\left(\pi \left(a_t\mid s_t\right)\right)=-{\displaystyle \sum _{s_t}}\pi \left(a_t\mid s_t\right)\log \pi \left(a_t\mid s_t\right)\end{array}\right.(18)$

where ${\pi }^{*}$ denotes the optimal policy function, s_t denotes the t momentary state, a_t denotes the t momentary action, ${\tau }_{\pi }$ denotes the distributional trajectory under the policy π, r is the reward, γ denotes the discount factor, H denotes the entropy, and α is the parameter used to determine the degree of importance of the entropy.

3.2.2 Quantitative representation of experience

In quantum theory, a quantum can be realised by a two-level electron, a rotating system or a photon. For a two-level electron, |0> can represent the ground state and, in contrast, |1> the excited state. For a rotating system, |0> can represent accelerated rotation, while |1> represents decelerated rotation. For a photon, |0> is considered as a quantum system, and its two eigenstates |0> and |1> represent the acceptance or rejection of the empirical quantum bit, respectively. In order to better demonstrate the empirical quantum bit and its eigenstates, their details are shown in Figure 3.

Figure 3

Figure 3. Experience pool quantum operations.

Throughout the learning process, the agent continuously tries to interact with the environment, and this learning process can be modelled as a Markov decision process. For each time step t, the state of the agent can be written as s_t, at which the agent chooses an action a_t according to the action strategy and a specific exploration strategy, and after the action, it moves to the next state s_t+1, and obtains a reward r_t from the environment. Eventually, the four elements together make up a state transfer, and are put into the experience cache pool after being assigned with the new index k. The state transfer process is converted into a state transfer process by converting it into an experience cache. By converting this state transfer process into a quantum representation, we define acceptance and rejection of a state transfer as two eigenstates. The state transfer is then considered as a quantum bit.

Since the quantised expression of the kth experience in the experience pool is of the form ${\left|\psi \right.}^{\left(k\right)}>$ , the state of the experience cache pool consisting of M experience quantum bits can be expressed as a tensor product of M quantum subsystems of the form. Details as Eq. 19.

$\left|{\psi }^{\text{total}}\right.〉=\left|{\psi }^{\left(1\right)}\right.〉\otimes \left|{\psi }^{\left(2\right)}\right.〉\otimes \dots \left|{\psi }^{\left(M\right)}\right.〉(19)$

3.3.3 Replay mechanisms for quantized experiences

The following page shows the pseudo-code for an integrated quantum-inspired deep reinforcement learning algorithm. At each time step, the agent produces a state transition by interacting with the environment. Since a new state transition does not have associated TD-errors, we assign it the TD-error with the highest priority in the experience pool, which means giving it a higher replay priority. This ensures that every new experience will be sampled at least once with the highest priority. This experience is then transformed into a quantum bit. A quantum preparation operation that uses Grover iteration as the fundamental operation is applied to the quantum representation of the experience in the uniform state until it reaches the final state. When the experience pool is full, the state transition is sampled with a probability amplitude that is proportional to the probability amplitude of its quantum representation, and the chosen experiences form a small data batch that is fed into the neural network for training. For those chosen experiences, when they are returned to the experience pool and prepared as uniform states again, their corresponding quantum representations are also subject to a quantum preparation operation to adjust to the new priority of the experience, and a quantum depreciation operation to adapt to the change in the number of times the experience is replayed. This operation is repeated until the algorithm converges.

An experience pool is established in deep reinforcement learning to store the experience data that are utilized to train and adjust the neural network parameters of an agent. The agent interacts with the environment once more under the direction of the neural network with the new parameters after training it with a small amount of data, and simultaneously produces new empirical data. Hence, the data in the experience pool have to be renewed and replaced periodically to attain better training outcomes. For this purpose, the experience pool has a fixed size, and when the pool is full (as shown by k>M in the algorithm’s pseudo-code) and new experience data are created, the oldest experience is removed to accommodate the new experience (as shown by k reset to 1 in the pseudo-code of the algorithm). Moreover, the neural network parameters are only updated after the experience pool is full, which corresponds to after LF is set to True in the pseudo-code.

4 Experiment and case studies

This paper validates the proposed algorithm in the LFC model of an isolated island microgrid on Yongxing Island. This refers to a smart energy system consisting of diesel power generation, photovoltaic power generation, and energy storage, built on Yongxing Island, the largest island among the South China Sea islands. This system can be connected to or disconnected from the main power grid as needed. The size and parameters of the microgrid on Yongxing Island are as follows. The microgrid has a total installed capacity of 1.5 MW, including 1 MW from the diesel generator, 500 kW from the photovoltaic power generation, and 200 kWh from the energy storage system. The microgrid can achieve 100 per cent priority use of clean energy sources such as photovoltaic, and it can also flexibly access a variety of energy sources in the future, such as wave energy and portable power. The completion of this microgrid increases the power supply capacity of Yongxing Island by eight times, making the power supply stability of the isolated island comparable to that of a city. In this paper, we also perform simulations and tests on the DDI-LFC that employs the QIS-MEAC algorithm and compare it with other control algorithms, such as DDI-LFC based on SQL algorithm (Li et al., 2021), DDI-LFC based on SAC algorithm (Xi et al., 2016), DDI-LFC based on PPO algorithm (Xi et al., 2016b), DDI-LFC based on TRPO algorithm (Xi et al., 2021), DDI-LFC based on MPC algorithm Xi et al., 2021), DDI-LFC based on Fuzzy-FOPI algorithm (Xi et al., 2021), TS-fuzzy-PI (Xi et al., 2022), PSO-PI (Li and Zhou, 2024), and GA-PI (Li and Zhou, 2023). To run the simulation models and methods that we present in this paper, we use a computer with 2 CPUs of 2.10 GHz Intel Xeon Platinum processor and 16 GB of RAM. The simulation software package that we use is MATALB/Simulink version 9.8.0 (R2020 a).

4.1 Case 1: step disturbance

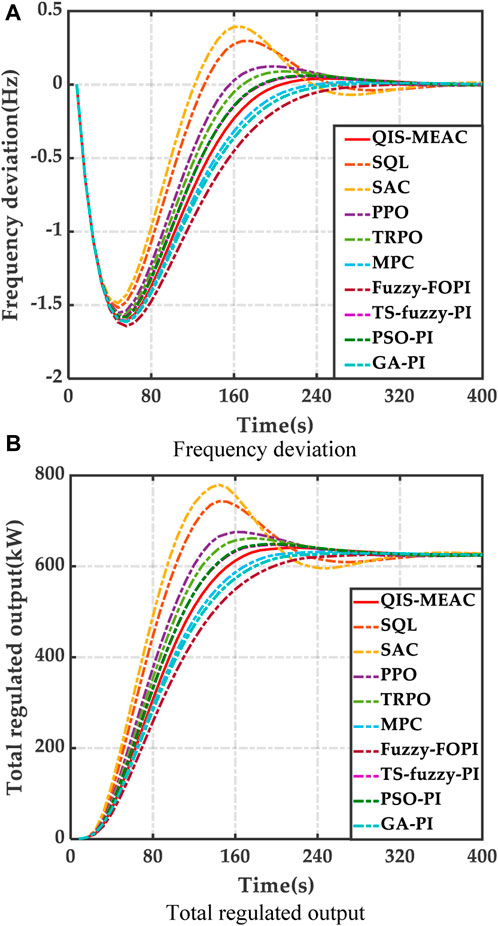
As displayed in Table 1, the Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) algorithm outperforms the other algorithms significantly, resulting in a substantial reduction in frequency deviation ranging from 9.65% to 75.55% and a decrease in generation cost ranging from 0.0004% to 0.012%. The microgrid’s frequency response and diesel generator’s output power are both affected by various control methods.

Table 1

Table 1. Statistical results for Case 1.

The simulation outcomes unequivocally highlight QIS-MEAC as the leading performer among the four intelligent algorithms, with soft Q-learning following closely. This can be attributed to the fact that both QIS-MEAC and soft Q-learning possess the capability of maximum entropy exploration. This enables them to dynamically adjust the learning pace, continuously update the function table through shared experiences, and determine the relative weight of each region. Consequently, each control region can adapt its control strategy effectively, enhancing control flexibility.

Unlike soft Q-learning, QIS-MEAC doesn't require averaging strategy evaluations. Instead, it can directly make decisions based on dynamic joint trajectories and historical state-action pairs. Additionally, it exhibits strong adaptability to the learner’s instantaneous learning rate, leading to improved coordinated Load Frequency Control (LFC). QIS-MEAC demonstrates remarkable adaptability and superior control performance under varying system operating conditions, thereby confirming the algorithm’s effectiveness and scalability.

RL offers advantages over many methods due to its straightforward and universally applicable parameter settings. Nevertheless, the application of RL theory encounters new challenges. Firstly, for large-scale tasks, determining an optimal common exploration goal for the reinforcement learning of multiple individual intelligences becomes complex. Secondly, each intelligence must record the behaviors of other intelligences (leading to reduced stability) to interact with them and attain joint behaviors, consequently slowing down the convergence speed of various methods. In light of these issues, multi-intelligence reinforcement learning techniques with collective characteristics have emerged and gained widespread adoption. The core concern of reinforcement learning is how to solve dynamic tasks in real-time using intelligent entities’ exploration techniques in dynamic planning and temporal difference methods. The Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) proposed in this paper is innovative and efficient, thanks to its precise independent self-optimization capabilities.

In Figure 4A below, the illustration demonstrates how the total power output of the unit effectively manages load variations, including scenic and square wave fluctuations. The active output curve of the LFC unit exhibits overshooting to counteract the effects of random power fluctuations. Figure 4B presents the output regulation curves for different LFC unit types. As shown in the figure, when the load increases, smaller hydro and micro-gas units with lower regulation costs are preferred for increasing output. Conversely, when the load decreases, biomass and diesel units with higher regulation costs are prioritized to reduce output, leading to improved frequency control. The LFC output allocation adheres to the equal micro-increment rate principle, ensuring that the final active output of each unit aligns with the economic allocation principle. Other Deep Reinforcement Learning (DRL) algorithms face challenges in producing satisfactory curves due to the lack of performance enhancement techniques. Furthermore, model-based control algorithms encounter difficulties in demonstrating effective control capabilities due to their heavy reliance on models.

Figure 4

Figure 4. Results for case 1. (A) Frequency deviation. (B) Total regulated output.

New energy units offer distinct advantages, including rapid start and stop capabilities, high climb rates, and extensive regulation ranges compared to diesel units. They play a pivotal role in the system, taking on most of the output tasks to address power grid load fluctuations. The controller’s online optimization results highlight the smoother and more stable regulation process achieved by the proposed method. This ensures that unit outputs quickly stabilize under new operational conditions, enabling optimal collaboration in response to sudden load changes in the power system.

4.2 Case 2: step disturbance and renewable disturbance

This study presents a smart distribution network model that integrates various new energy sources, including Electric Vehicles (EVs), Wind Power (WP), Small Hydro (SH), Micro-Gas Turbines (MGTs), Fuel Cells (FCs), Solar Power (SP), and Biomass Power (BP). The model is employed to assess the control effectiveness of Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) in a highly stochastic environment.

Electric vehicles, wind power, and solar power are considered as stochastic load disturbances due to their significant uncertainty in output. Consequently, they are excluded from the Load-Frequency Control (LFC) analysis. The output of the wind turbine is determined by simulating stochastic wind speed, using finite bandwidth white noise as input. The solar power model derives its output from the simulated variations in sunlight intensity throughout the day.

To comprehensively investigate the intricate effects of random load variations within a power system experiencing uncertain large-scale integration of new energy sources, we introduce random white noise load disturbances into the smart distribution network model. Our objective is to evaluate the performance of Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) under challenging random perturbations.

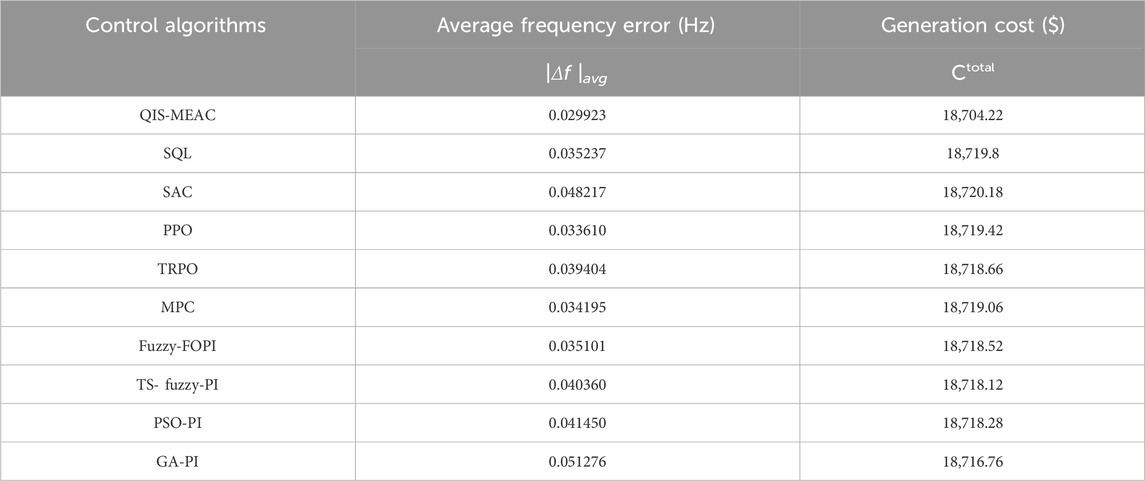
We utilize 24 h of random white noise disturbance as the evaluation criterion to gauge QIS-MEAC’s long-term performance in the face of significant random load disturbances. QIS-MEAC demonstrates remarkable accuracy and rapid responsiveness in tracking these random disturbances. The statistical results of the simulation experiments are presented in Table 2, where the generation cost represents the total regulation cost of all generating units over 24 h.

Table 2

Table 2. Data of case 2.

The distribution network data reveals that the frequency deviation in other algorithms is 1.12–1.71 times higher than that in the QIS-MEAC algorithm, while the QIS-MEAC algorithm reduces the generation cost by 0.067%–0.085%. Analysis of control performance metrics underscores QIS-MEAC’s superior economy, adaptability, coordination, and optimization control performance compared to other intelligent algorithms.

Furthermore, we conducted tests involving various disturbance types, including step waves, square waves, and random waves. The experimental outcomes demonstrate that Multi-Intelligence Actor-Critic exhibits strong convergence performance and high learning efficiency. Notably, in a random environment, it displays exceptional adaptability by effectively suppressing random disturbances and enhancing dynamic control performance in interconnected grid environments. It establishes a balanced relationship between the output power of different unit types and the load demand across a 24-h period. Consequently, it ensures that the total power output of the units accurately tracks load variations, achieving complementary and synergistic optimal operation among multiple energy sources in each time period.

5 Conclusion

The manuscript delineates the development and implementation of a Data-Driven Intelligent Load Frequency Control (DDI-LFC) strategy, aimed at facilitating adaptive, multi-objective optimal frequency regulation through the application of a Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) algorithm. The salient contributions of this research are articulated as follows:

1) Integration Challenges of Distributed Energy Resources: The manuscript identifies the complexity introduced into islanded microgrid operations by the large-scale integration of distributed, renewable energy sources. These sources exhibit high degrees of randomness and intermittency, resulting in severe random perturbations that compromise the frequency control performance and elevate regulation costs, thereby posing significant challenges to the system’s safety and stability. In response, the DDI-LFC method is introduced, replacing traditional Load Frequency Control (LFC) mechanisms with a deep reinforcement learning algorithm-based agent, aimed at enhancing frequency regulation amidst these challenges.

2) Quantum-Inspired Algorithmic Enhancement: To navigate the intricate environment of the islanded microgrid and achieve adaptive, multi-objective optimal frequency control, the research proposes the Quantum-Inspired Maximum Entropy Actor-Critic (QIS-MEAC) algorithm. This innovative algorithm integrates quantum-inspired principles and a maximum entropy exploration strategy with the conventional actor-critic algorithm framework. By transforming experiences into quantum states and exploiting quantum properties, the algorithm significantly enhances the efficiency and robustness of data utilization within the deep reinforcement learning experience replay mechanism, thereby augmenting the effectiveness of the DDI-LFC approach.

3) Empirical Validation and Impact: The efficacy of the proposed DDI-LFC method is empirically validated using the Yongxing Island isolated microgrid model within the South China Grid. Results demonstrate the method’s proficiency in leveraging the frequency regulation capabilities of distributed power sources and energy storage systems. Consequently, it substantially mitigates frequency deviations and reduces generation costs, underscoring the potential of the DDI-LFC strategy to improve the operational reliability and economic efficiency of islanded microgrids.

Through these contributions, the manuscript not only addresses critical challenges associated with the integration of renewable energy sources into microgrids but also showcases the potential of quantum-inspired algorithms in enhancing the landscape of intelligent load frequency control.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XS: Methodology, Writing–original draft, Conceptualization, Formal Analysis, Software. JT: Methodology, Writing–original draft, Funding acquisition, Investigation. FP: Formal Analysis, Supervision, Validation, Writing–review and editing. BQ: Validation, Visualization, Formal Analysis, Resources, Writing–review and editing. YZ: Validation, Visualization, Data curation, Investigation, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the support of the China Southern Power Grid Technology Project (YNKJXM20222402).

Conflict of interest

Authors XS and YZ were employed by Measurement Center, Yunnan Power Grid Co., Ltd. Authors JT and BQ were employed by CSG Electric Power Research institute Co., Ltd. Author FP was employed by Metrology Center of Guangdong Power Grid Co., Ltd.

The authors declare that this study received funding from China Southern Power Grid. The funder had the following involvement in the study: study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahamed, T. P. I., Rao, P. S. N., and Sastry, P. S. (2002). A reinforcement learning approach to automatic generation control. Electr. Power Syst. Res. 63, 9–26. doi:10.1016/s0378-7796(02)00088-3

CrossRef Full Text | Google Scholar

El-Fergany, A. A., and El-Hameed, M. A. (2017). Efficient frequency controllers for autonomous two-area hybrid microgrid system using social-spider optimiser. IET Generation, Transm. Distribution 11, 637–648. doi:10.1049/iet-gtd.2016.0455

CrossRef Full Text | Google Scholar

Ferrario, A., Bartolini, A., Manzano, F., Vivas, F., Comodi, G., McPhail, S., et al. (2021). A model-based parametric and optimal sizing of a battery/hydrogen storage of a real hybrid microgrid supplying a residential load: towards island operation. Adv. Appl. Energy 3, 100048. doi:10.1016/j.adapen.2021.100048

CrossRef Full Text | Google Scholar

Li, J., and Zhou, T. (2023). Evolutionary multi agent deep meta reinforcement learning method for swarm intelligence energy management of isolated multi area microgrid with internet of things. IEEE Internet of Things Journal. doi:10.1109/JIOT.2023.3253693

CrossRef Full Text | Google Scholar

Li, J., and Zhou, T. (2024). Prior Knowledge Incorporated Large-Scale Multiagent Deep Reinforcement Learning for Load Frequency Control of Isolated Microgrid Considering Multi-Structure Coordination. IEEE Transactions on Industrial Informatics. doi:10.1109/TII.2023.3316253

CrossRef Full Text | Google Scholar

Li, J., Yu, T., and Zhang, X. (2022). Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 306, 117900. doi:10.1016/j.apenergy.2021.117900

CrossRef Full Text | Google Scholar

Li, Q., Yang, W., Yin, L., and Chen, W. (2020). Real-time implementation of maximum net power strategy based on sliding mode variable structure control for proton-exchange membrane fuel cell system. IEEE Trans. Transp. Electrif. 6, 288–297. doi:10.1109/TTE.2020.2970835

CrossRef Full Text | Google Scholar

Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021). Efficient experience replay based deep deterministic policy gradient for AGC dispatch in integrated energy system. Appl. Energy 285, 116386. doi:10.1016/j.apenergy.2020.116386

CrossRef Full Text | Google Scholar

Lou, G., Gu, W., Lu, X., Xu, Y., and Hong, H. (2020). Distributed secondary voltage control in islanded microgrids with consideration of communication network and time delays. IEEE Trans. Smart Grid 11, 3702–3715. doi:10.1109/tsg.2020.2979503

CrossRef Full Text | Google Scholar

Mahboob, Ul H. S., Ramli, M. A. M., and Milyani, A. H. (2022). Robust load frequency control of hybrid solar power systems using optimization techniques. Front. Energy Res. 10, 902776. doi:10.3389/fenrg.2022.902776

CrossRef Full Text | Google Scholar

Munos, R., Stepleton, T., Harutyunyan, A., Bellemare, G., et al. (2016). “Safe and efficient off-policy reinforcement learning,” in Advances in neural information processing systems 29. Editors D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett (Barcelona, Spain: Curran Associates, Inc), 1054–1062.

Google Scholar

Qadrdan, M., Cheng, M., Wu, J., and Jenkins, N. (2017). Benefits of demand-side response in combined gas and electricity networks. Appl. Energy 192, 360–369. doi:10.1016/j.apenergy.2016.10.047

CrossRef Full Text | Google Scholar

Qing, L., Zhang, J., Liu, Y., Liang, J., Li, Y., and Wang, Z. (2015). “Decentralised reinforcement learning collaborative consensus algorithm for generation dispatch in virtual generation tribe,” in 2015 IEEE Innovative Smart Grid Technologies - Asia (ISGT ASIA). IEEE, Bangkok, Thailand, 3-6 November 2015, 1197–1201. doi:10.1109/ISGT-Asia.2015.7387139

CrossRef Full Text | Google Scholar

Sause, W. (2013). “Coordinated reinforcement learning agents in a multi-agent virtual environment,” in 2013 IEEE 13th International Conference on Data Mining Workshops. IEEE, Dallas, Texas, USA, 7-10 December 2013, 227–230. doi:10.1109/ICDMW.2013.156

CrossRef Full Text | Google Scholar

Sun, L., Tian, Y., Wu, Y., Huang, W., Yan, C., and Jin, Y. (2023). Strategy optimization of emergency frequency control based on new load with time delay characteristics. Front. Energy Res. 10, 1065405. doi:10.3389/fenrg.2022.1065405

CrossRef Full Text | Google Scholar

Tang, F., Niu, B., Zong, G., Zhao, X., and Xu, N. (2022). Periodic event-triggered adaptive tracking control design for nonlinear discrete-time systems via reinforcement learning. Neural Netw. 154, 43–55. doi:10.1016/j.neunet.2022.06.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., and Wang, J. (2019). A practical distributed finite-time control scheme for power system transient stability. IEEE Trans. Power Syst. 35, 3320–3331. doi:10.1109/tpwrs.2019.2904729

CrossRef Full Text | Google Scholar

Wen, G., Hu, G., Hu, J., Shi, X., and Chen, G. (2015). Frequency regulation of source-grid-load systems: a compound control strategy. IEEE Trans. Industrial Inf. 12, 69–78. doi:10.1109/tii.2015.2496309

CrossRef Full Text | Google Scholar

Wiering, M., and Otterlo, M. V. (2012). Reinforcement learning: state of the art. Springer Publishing Company, Incorporated.

Google Scholar

Xi, L., Xi, T., Yang, B., Zhang, X., and Qiu, X. (2016a). A wolf pack hunting strategy based virtual tribes control for automatic generation control of smart grid. Appl. Energy 178, 198–211. doi:10.1016/j.apenergy.2016.06.041

CrossRef Full Text | Google Scholar

Xi, L., Zhang, Z., Yang, B., Huang, L., and Yu, T. (2016b). Wolf pack hunting strategy for automatic generation control of an islanding smart distribution network. Energy Convers. Manag. 122, 10–24. doi:10.1016/j.enconman.2016.05.039

CrossRef Full Text | Google Scholar

Xi, L., Wu, J., Xu, Y., and Sun, H. (2021). Automatic generation control based on multiple neural networks with actor-critic strategy. IEEE Trans. Neural Networks Learn. Syst. 32, 2483–2493. doi:10.1109/TNNLS.2020.3006080

PubMed Abstract | CrossRef Full Text | Google Scholar

Xi, L., Zhang, L., Xu, Y., Wang, S., and Yang, C. (2022). Automatic generation control based on multiple-step greedy attribute and multiple-level allocation strategy. CSEE J. Power Energy Syst. 8, 281–292. doi:10.17775/CSEEJPES.2020.02650

CrossRef Full Text | Google Scholar

Ye, Y., Qiu, D., Sun, M., Papadaskalopoulos, D., and Strbac, G. (2019). Deep reinforcement learning for strategic bidding in electricity markets. IEEE Trans. Smart Grid 11, 1343–1355. doi:10.1109/tsg.2019.2936142

CrossRef Full Text | Google Scholar

Yin, L., Yu, T., and Zhou, L. (2018). Design of a novel smart generation controller based on deep Q learning for large-scale interconnected power system. J. Energy Eng. 144, 04018033. doi:10.1061/(asce)ey.1943-7897.0000519

CrossRef Full Text | Google Scholar

Yinsha, W., Wenyi, L., and Zhiwen, L. (2019). “Research on PSO-fuzzy algorithm optimised control for multi-area AGC system with DFIG wind turbine,” in 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA). IEEE, Xi'an, China, 19-21 June 2019, 877–881. doi:10.1109/ICIEA.2019.8834127

CrossRef Full Text | Google Scholar

Yu, T., Zhou, B., Chan, K. W., and Lu, E. (2011). Stochastic optimal CPS relaxed control methodology for interconnected power systems using Q-learning method. J. Energy Eng. 137, 116–129. doi:10.1061/(asce)ey.1943-7897.0000017

CrossRef Full Text | Google Scholar

Zheng, Y., Li, S., and Qiu, H. (2012). Networked coordination-based distributed model predictive control for large-scale system. IEEE Trans. Control Syst. Technol. 21, 991–998. doi:10.1109/tcst.2012.2196280

CrossRef Full Text | Google Scholar