Non-cooperative game-based electricity pricing method for data centers

Data centers are characterized by high energy consumption, with operating costs being extremely sensitive to electricity prices. Therefore, modern data centers are often equipped with microgrids for power supply, which adjust their operational strategies based on the given electricity prices to minimize costs. However, existing research has overlooked the flexible pricing potential of electricity retailers, prompting this study to propose a non-cooperative game theory-based optimization method for data center electricity procurement negotiation. A two-layer optimization model is established for data center electricity pricing. The upper layer focuses on electricity price optimization, modeling price negotiation as a Stackelberg game and adopting a weighted average cost approach to describe the electricity procurement prices. The lower layer addresses data center operational optimization, formulated as a nonlinear programming problem. To enable rapid solution convergence, a hybrid problem-solving method combining a genetic algorithm and branch-and-cut algorithm is proposed. Finally, a simulation is conducted using a data center located in California, United States, to validate the proposed method. The results demonstrate that the proposed method can reduce data center operational costs by 3% and increase the revenue for electricity retailers by 17%, achieving a win–win outcome.

1 Introduction

With the rapid advancement of next-generation information technologies such as 5G communication, industrial Internet of Things (IoT), and artificial intelligence (AI), the scale of big data and cloud computing industries continues to expand. Data centers, serving as the fundamental infrastructure for information processing, play an indispensable role in the realms of big data and cloud computing, leading to a continuous increase in their industrial scale and quantity (Yu and Song, 2019). However, during the flourishing development of the data center industry, challenges pertaining to high energy consumption and elevated costs have gradually surfaced. According to statistics, in 2019, the energy consumption of data centers in China accounted for approximately 0.8%–1% of the total national electricity usage (Guo et al., 2020). In 2020, data centers in the US consumed approximately 140 billion kilowatt-h of electricity, resulting in a power cost of 13 billion US dollars (The Natural Resources Defense Council, 2015). The issues of high energy consumption and operational costs have become critical problems throughout the development of the global data center industry.

Existing methods for optimizing data center energy consumption and electricity cost can be broadly categorized into three classes: load scheduling methods that optimize computational workloads; hardware optimization approaches that focus on air conditioning, power supply units, and other equipment to reduce data center operational energy consumption; and microgrid planning and operation optimization methods that aim to reduce energy consumption and operational costs. Specifically, optimizing data center computational workloads and power supply plans can effectively reduce energy consumption. Beloglazov and Abawajy (2012), Qin (2020), and Wu and Ishikawa (2019) studied the allocation of tasks within data centers to reduce the number of active servers and decrease the overall energy consumption. Muhammad and Mekhilef (2017) and Ohn and Yu (2020) used novel circuit topologies and advanced power semiconductor devices to optimize the design of uninterruptible power supply (UPS) and other power supply equipment, thereby improving the data center power efficiency and reducing the energy consumption of power supply devices. Khalaj Habibi and Halgamuage (2017) and Orkowski and Krzysztof (2022) optimized the design of data center cooling equipment to reduce electrical losses associated with cooling system operations. Cao and Wang (2019) and Al-Hazemi et al. (2018) proposed load scheduling methods considering data center supporting equipment to make full use of the load scheduling flexibility and the nonlinear characteristics of device energy consumption to reduce data center energy consumption.

However, most of the aforementioned research mainly focuses on optimizing the energy consumption of data center devices, essentially addressing load optimization. The collaborative operation between data centers and power distribution sides is ignored, leaving room for further optimization.

Introducing renewable energy and storage devices to establish data center microgrids can enable the adjustment of data center power supply methods and electricity purchasing behavior, thereby reducing data center operational costs. The Institute for Energy Economics and Financial Analysis (IEEFA, 2020) reported that Google data centers have adopted photovoltaic and battery storage-coordinated power supply approaches to reduce their electricity bill. Several data centers in China, such as the Guangzhou Foshan data center, have also implemented energy storage and photovoltaic systems to reduce electricity costs (Peter, 2017; Luo and Andresen, 2019; Guangdong Provincial Development and Reform Commission, 2020). Qi and Li (2019) employed linear programming to optimize the capacity of data center microgrids. Ding et al. (2018) combined the flexibility of data center workload scheduling to optimize the operation of data center microgrids. However, the aforementioned optimization methods are based on fixed electricity prices and ignore the feasibility of data centers to further engage in electricity pricing to reduce operational costs in electricity trading.

In electricity trading between data centers and electricity retailers, the real-time electricity price plays a crucial role. In this process, the retailers purchase electricity from the generation side and sell it to data centers at specific prices, thereby earning revenue from the transaction. Data centers, on the other hand, adjust their behaviors such as load scheduling, energy storage device charging and discharging, and generator start–stop operations based on the given electricity prices to reduce electricity expenses. Thus, it is evident that real-time electricity prices directly impact the interests of both retailers and data centers, and therefore, optimizing the electricity prices in transactions can benefit both sides. For example, optimizing electricity prices can prevent phenomena like starting backup generators and frequent charging and discharging of energy storage devices due to excessively high electricity prices, thereby reducing operational costs for data centers. It can also enable data centers to coordinate with electricity retailers in scheduling microgrids, avoiding high electricity consumption during periods of power supply shortage or high electricity purchasing price of retailers, thus reducing operational and electricity purchasing costs for retailers and increasing their revenue.

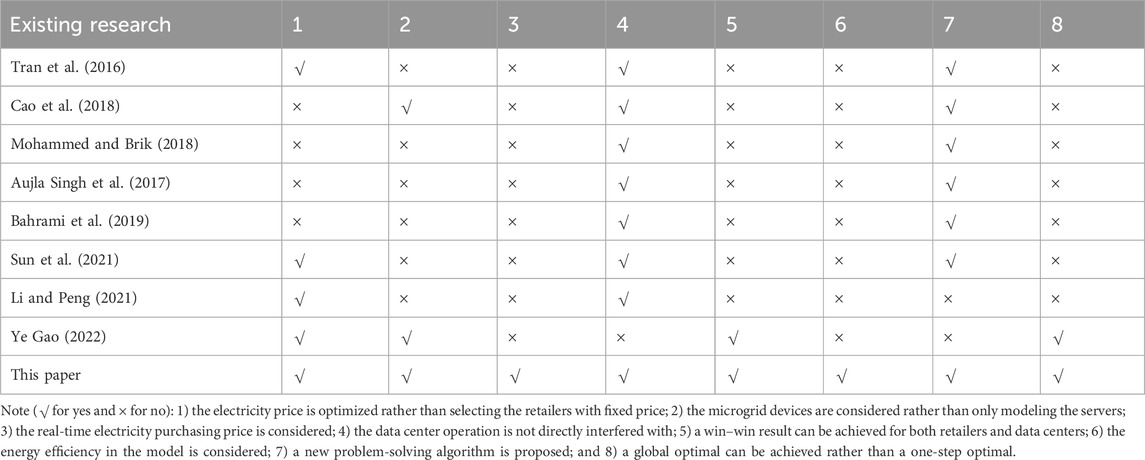
To achieve further cooperation in electricity trading, the game theory is widely used to coordinate the interests of various parties (Li et al., 2019; Huang and Wu, 2022; Wang et al., 2022). Tran et al. (2016) first proposed an electricity pricing method to improve the function of the demand response of the data center, but this method only optimized the electricity price for 1 h in each iteration and ignored the operation optimization of data center microgrid devices, such as generators and ESS, and the electricity purchasing price of the retailer. Cao et al. (2018) proposed a bargaining approach for the data center demand response, which takes renewable energy into consideration, but this method only improved the absorption of renewable energy and social welfare and ignored the benefit of data center operators and electricity retailers. Mohammed and Brik (2018) introduced a game theoretic approach for task scheduling in multiple data centers, yet it did not consider the cooperation with electricity retailers or the impact of varying electricity purchase costs on the optimization results. Aujla Singh et al. (2017) and Bahrami et al. (2019) proposed Stackelberg game methods for the data center workload scheduling, considering local renewable energy output and electricity price, but this method used the game theory to select the retailer with a fixed electricity price rather than to bargain and decide the electricity price. Sun et al. (2021) proposed a workload balance method in deregulated electricity markets and used the iteration gaming method to solve it, and Li et al. (2021) proposed a game theory-based workload management method for distributed data centers, but these models only considered the scheduling of computational workload and ignored the data center microgrid devices. Ye and Gao (2022) proposed a cooperative game-based electricity pricing method for data center and electricity retailer cooperation, where the electricity retailer directly controls the load of the data center, which may not be practical due to security and independent authority issues. The differences in the existing research studies are given in Table 1.

TABLE 1

TABLE 1. Literature comparison.

In summary, the existing research on optimizing data center operations still has certain shortcomings. First, most of the existing research on data center scheduling optimization only achieves microgrid operational optimization under given electricity prices, neglecting the possibility of involving data centers in electricity pricing as major electricity consumers. Second, the existing research on data center electricity pricing ignored the operation of microgrid devices. Third, the variations in electricity purchase costs for retailers at different times are not considered; thus, the revenue for electricity retailers is not fully considered. Therefore, the scheduling flexibility of data center workload is not fully utilized to optimize electricity prices, and the optimized electricity price in the previous research cannot fully benefit both participants in the electricity trading.

This paper innovatively combines data center microgrid operational optimization with electricity pricing, introducing a novel non-cooperative game-based method for coordinating data center electricity pricing and operational scheduling to achieve the global optimum of data center operational costs and revenue for electricity retailers. This paper establishes a Stackelberg game model between electricity retailers and data centers to effectively depict the optimization of electricity prices and data center operations. To effectively model the real-time electricity purchase costs for local electricity retailers, the weighted average electricity procurement cost is introduced into the model, which can accurately describe the impact of data center operational optimization on the electricity purchase costs and revenue for electricity retailers. Furthermore, a novel hybrid problem-solving method combining the genetic algorithm and branch-and-cut algorithm is proposed to solve this optimization problem. The simulation results demonstrate that this method can significantly reduce data center operational costs by 3% while increasing revenue for the electricity retailer by 17%. The innovative contributions are summarized below:

(1) This paper proposes a non-cooperative game theory model for electricity pricing and data center operation optimization in the electricity trading between the data center microgrid and electricity retailer, which considers the characteristics of the data center microgrid and the income of both sides.

(2) To solve the optimization problem, a hybrid problem-solving method combining the genetic algorithm and branch-and-cut algorithm achieves a fast solution.

2 System model and mathematical formulation

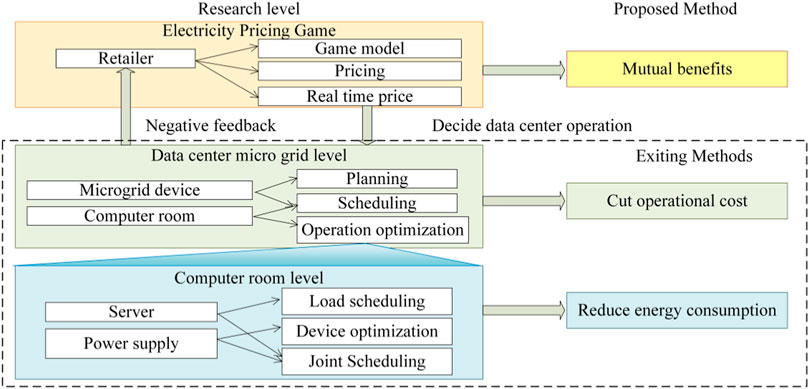
This paper focuses on a data center and a electricity retailer as the research subjects. It comprehensively considers the pricing game between the electricity retailer and the data center in electricity trading, the optimized operation within the data center microgrid, and the load optimization and scheduling within the data center. The study conducts coordinated optimization between the electricity retailer and data center, whose framework and research approach are shown in Figure 1. In contrast to traditional methods, this paper proposes an electricity pricing method tailored to the data center scenario and a real-time electricity price model, which fully considers the flexibility of data center workload scheduling and the potential for real-time operation optimization. As a consequence, a win–win situation for the data center and electricity retailer can be achieved.

FIGURE 1

FIGURE 1. Relationship between electricity pricing and data center operational optimization.

The detailed process of electricity trading is shown in Figure 2. The proposed model comprehensively takes into account data center workload scheduling, data center microgrid operation, and the retailer’s electricity purchase costs and revenue in the transaction. The following analysis focuses on the decision-making of the participants in electricity trading and the transaction process.

FIGURE 2

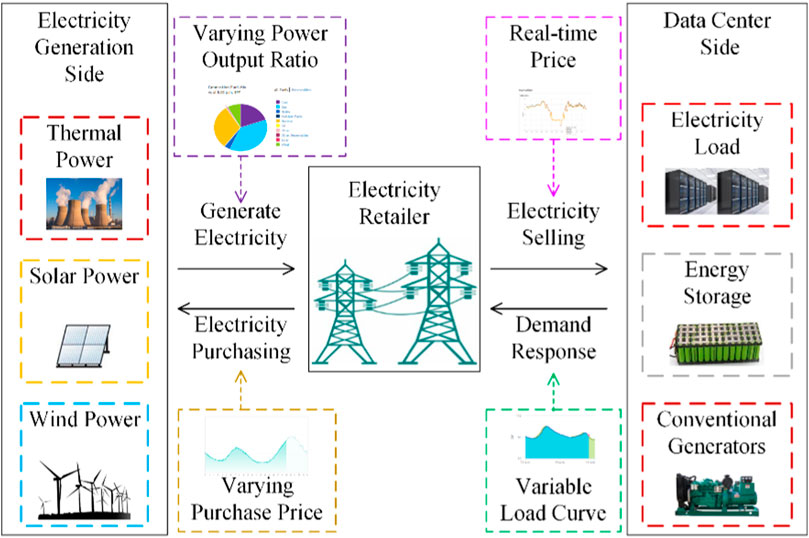
FIGURE 2. Scheme of energy trading between the data center microgrid and local electricity retailer.

2.1 Analysis of the electricity retailer’s game behavior in electricity trading

The electricity retailers act as intermediaries in the electricity market, purchasing electricity from the generation side and selling it to end users. In the proposed model, we only focus on the game between the electricity retailer and a data center, and treat the power grid as an infinite grid. Therefore, the data center’s electricity purchase will not influence the power flow and losses. The primary cost for the electricity retailer is the electricity procurement cost. Due to the stochastic and time-varying nature of renewable generation, the energy composition at different time intervals within a day varies, resulting in different electricity procurement costs.

The electricity retailer’s revenue is solely determined by the data center’s electricity purchases, which are influenced by both the electricity procurement quantity and the real-time electricity pricing. The electricity retailer holds a dominant position in the transaction and can adjust the electricity selling price to further increase the revenue or influence the data center’s electricity consumption behavior.

2.2 Analysis of the data center’s electricity purchasing behavior

The data center is the electricity purchasing entity studied in this paper, and it is an important participant in the electricity pricing game, whose objective is to minimize its own operational cost. Compared to traditional electricity consumers, data centers are major electricity consumers due to their significant annual electricity consumption and, therefore, have more potential for participating in electricity pricing, which makes the negotiation with the local retailer feasible (Jiang, 2018). The operational costs for data centers mainly include electricity purchasing costs and the operating costs of generators. During periods of high electricity prices, data centers utilize on-site generators and energy storage systems to reduce electricity purchases from the grid, which would reduce the electricity purchasing costs but increase generator operational costs. In contrast, during periods of low electricity prices, data centers tend to purchase electricity from the local retailer since the operational cost of the generator exceeds the real-time electricity price.

For instance, in the case of an independent operator in California, electricity procurement involves day-ahead and real-time markets, with the procurement cost being determined by real-time electricity prices and the amount of electricity purchased. The electricity retailer provides time-varying electricity prices to users through a real-time pricing market (Ren et al., 2017; Yang et al., 2019). Meanwhile, the data centers equipped with energy storage units, renewable energy sources, and generators exhibit characteristics of both the load and generator, providing significant optimization opportunities.

3 Proposed game model

This paper fully considers the game between data centers and electricity retailers in the electricity transaction and models it as a Stackelberg game model. In this model, the interactions between data center workload scheduling, data center microgrid operation, and the electricity retailer’s purchase cost and revenue are comprehensively considered. The electricity retailer acts as the leader in the electricity price game, aiming to set an optimal real-time electricity price to achieve higher profits and influence user behavior. The data center, on the other hand, acts as the follower in the game, adjusting its real-time operational mode to reduce electricity and operational costs, thus maximizing its own benefits. By optimizing the real-time electricity prices offered by the electricity retailer to the data center, the data center operational costs can be reduced, and the electricity retailer’s revenue can be increased at the same time, achieving a win–win outcome through cooperation.

3.1 Data center microgrid model

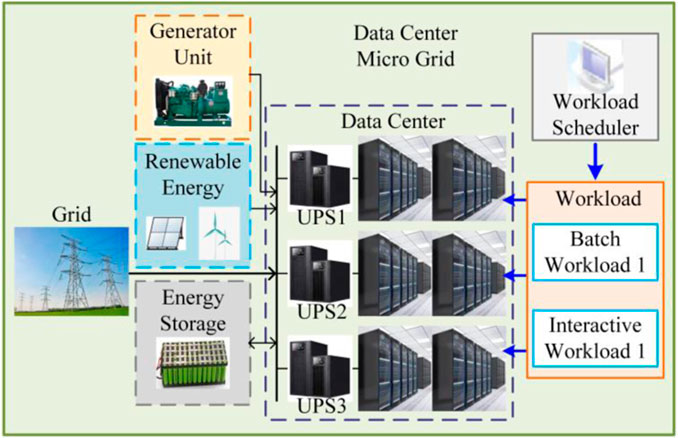
The scheduling of the data center microgrid operation is the lower-level optimization problem in the proposed game model. The basic structure of the data center microgrid is shown in Figure 3. In each microgrid, the servers and UPSs are powered by solar power, wind power, a conventional generator unit, and a utility grid. Energy storage systems are also deployed to reduce the volatility of renewable energy and reduce the electricity cost by making use of the daily electricity price difference. The abovementioned equipment can be classified into electricity load and the microgrid equipment.

FIGURE 3

FIGURE 3. Architecture of an internet data center.

The electrical load in the data center primarily consists of servers and supporting equipment like cooling systems, whose real-time power consumption exhibits an approximate linear relationship with the computational workload. The computational workload can be divided into the interactive workload and batch workload. Interactive workload, such as game services, online shopping, and stock trading, have low tolerance for response delays and should be processed promptly at each moment; otherwise, significant penalties may be incurred. Batch workloads, on the other hand, involve tasks like data processing for large-scale research projects or neural network training, which can tolerate delays of a few minutes or hours. Consequently, the data center’s batch workloads can be integrated into the demand response by adjusting their execution times, thereby regulating the load characteristics of the data center. The electrical load of the data center can be modeled as follows:

${\mathit{\lambda }}_{\mathit{j},\mathit{t}}={\mathit{\zeta }}_{\mathit{j},\mathit{t}}^{\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{r}}+{\displaystyle {\sum }_{\mathit{a}}^{\mathit{A}}}{\mathit{\mu }}_{\mathit{a},\mathit{j},\mathit{t}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}\left(\forall \mathit{j},\mathit{t}\right),(1)$

${\mathbf{0}\le \mathit{\lambda }}_{\mathit{j},\mathit{t}}\le {Cap}_j\left(\forall \mathit{j},\mathit{t}\right),(2)$

${\displaystyle {\sum }_{{\mathit{t}}_{\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}}^{{\mathit{D}}_{\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}}}{\mathit{\mu }}_{\mathit{a},\mathit{j},\mathit{t}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}={\displaystyle {\sum }_{\mathit{a}}^{\mathit{A}}}{\mathit{\mu }}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l},\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}\left(\forall \mathit{a}\in \mathit{A}\right),(3)$

$\mathit{max}\left(∆{\mathit{t}}_{\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}\right)\le {\mathit{T}}_{\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}},(4)$

${\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}\mathit{s}}\le {\mathit{P}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d},\mathit{j}}^{\mathit{U}\mathit{P}\mathit{S}}\left(\forall \mathit{j},\mathit{t}\right).(5)$

In addition, for every time slot, the total real-time power of the node $j$ in the data center is

${\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}\mathit{s}}=M_j\times \left({{\mathit{\phi }}_{\mathit{j}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}}\times \frac{{\mathit{\lambda }}_{\mathit{j},\mathit{t}}}{{Cap}_j}+\mathit{P}}_{\mathit{j}}^{\mathit{i}\mathit{d}\mathit{l}\mathit{e}}\right)\left(\forall \mathit{j},\mathit{t}\right),(6)$

where

${\mathit{\phi }}_{\mathit{j}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}}={{\mathit{P}}_{\mathit{j}}^{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}-\mathit{P}}_{\mathit{j}}^{\mathit{i}\mathit{d}\mathit{l}\mathit{e}}.(7)$

In the above equations, ${\mathit{\lambda }}_{\mathit{j},\mathit{t}}$ represents the total computational workload at time t in the data center. ${\mathit{\mu }}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l},\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}$ is the total workload of the batch workload in the data center. ${\mathit{\mu }}_{\mathit{a},\mathit{j},\mathit{t}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}$ and ${\mathit{\zeta }}_{\mathit{j},\mathit{t}}^{\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{r}}$ are the batch and interactive workloads at each time t in the data center, respectively. ${Cap}_{i,j}$ is the maximum load capacity of the servers. $∆{\mathit{t}}_{\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}$ is the required time for task a to complete, which should be less than the allowable maximum time delay ${\mathit{T}}_{\mathit{a}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}$. ${\mathit{P}}_{\mathit{j}}^{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$ represents the peak power consumption of each server, while ${\mathit{P}}_{\mathit{j}}^{\mathit{i}\mathit{d}\mathit{l}\mathit{e}}$ represents the idle power consumption of the servers. $M_j$ is the total number of servers in the data center. ${\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}\mathit{s}}$ is the real-time power consumption of all servers within the data center.

UPS power loss nonlinearly varies depending on the load rate, which is decided by server power, and can be expressed as follows:

${\mathit{P}}_{\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}={\mathit{P}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d},\mathit{i},\mathit{j}}^{\mathit{L}\mathit{o}\mathit{s}\mathit{s}\_\mathit{U}\mathit{P}\mathit{S}}\times \left[{\mathit{a}}_{\mathbf{0}}+{\mathit{a}}_{\mathbf{1}}\times \frac{{\mathit{P}}_{\mathit{i},\mathit{j},\mathit{t}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}\mathit{s}}}{{\mathit{P}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d},\mathit{i},\mathit{j}}^{\mathit{L}\mathit{o}\mathit{s}\mathit{s}\_\mathit{U}\mathit{P}\mathit{S}}}+{\mathit{a}}_{\mathbf{2}}\times {\left(\frac{{\mathit{P}}_{\mathit{i},\mathit{j},\mathit{t}}^{\mathit{s}\mathit{e}\mathit{r}\mathit{v}\mathit{e}\mathit{r}\mathit{s}}}{{\mathit{P}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d},\mathit{i},\mathit{j}}^{\mathit{L}\mathit{o}\mathit{s}\mathit{s}\_\mathit{U}\mathit{P}\mathit{S}}}\right)}^{\mathbf{2}}\right]\left(\forall \mathit{i},\mathit{j},\mathit{t}\right).(8)$

${\mathit{P}}_{\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}$ is the total power of servers and the corresponding UPSs and is nonlinearly determined by the ratio of real-time server power to rated power ${\mathit{P}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d},\mathit{i},\mathit{j}}^{\mathit{L}\mathit{o}\mathit{s}\mathit{s}\_\mathit{U}\mathit{P}\mathit{S}}$ of power supply devices. In the above equation, a₀ = 0.0455, a₁ = −0.0162, and a₂ = 0.0345, which is obtained from the most classic paper by Pratt et al. (2007).

The microgrid equipment includes the energy storage system, conventional generators, and renewable energy sources. The energy storage system can be modeled as follows:

${\mathit{E}\mathit{S}}_{\mathit{t}+\mathbf{1}}={\mathit{E}\mathit{S}}_{\mathit{t}}+{\mathit{\eta }}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}{\bullet \mathit{P}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}-{\mathit{\eta }}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}{\bullet \mathit{P}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\left(\forall \mathit{t}\right),(9)$

${\mathit{E}\mathit{S}}_{\mathit{min}}\le {\mathit{E}\mathit{S}}_{\mathit{t}}\le {\mathit{E}\mathit{S}}_{\mathit{max}}\left(\forall \mathit{t}\right),(10)$

${\mathit{Z}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}},{\mathit{Z}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\in \left\{\mathbf{0},\mathbf{1}\right\}\left(\forall \mathit{t}\right),(11)$

${\mathit{Z}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}+{\mathit{Z}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\le \mathbf{1}\left(\forall \mathit{t}\right),(12)$

$0\le {\mathit{P}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\le {\mathit{P}}_{\mathit{max}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\bullet {\mathit{Z}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\left(\forall \mathit{t}\right),(13)$

$0\le {\mathit{P}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\le {\mathit{P}}_{\mathit{max}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\bullet {\mathit{Z}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}\left(\forall \mathit{t}\right).(14)$

Eq. 9 represents the relationship between the energy storage capacity of the data center’s energy storage devices and the charging and discharging power. In addition, Eqs 10–14 represent the upper and lower constraints on the energy storage capacity and charging and discharging power. ${\mathit{E}\mathit{S}}_{\mathit{t}}$ represents the state of charge of the energy storage battery in the data center at time t. ${\mathit{Z}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$, ${\mathit{Z}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$, ${\mathit{P}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$, and ${\mathit{P}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$ represent the charging and discharging operations and power of the data center’s energy storage devices, respectively. ${\mathit{\eta }}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$ and ${\mathit{\eta }}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$ represent the efficiency of charging and discharging processes, respectively.

A conventional generator unit commitment decision model can be described as follows (Wang et al., 2022):

${\mathit{P}}_{\mathit{min},\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\bullet {\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\le {\mathit{P}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\le {\mathit{P}}_{\mathit{max},\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\bullet {\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\left(\forall \mathit{j},\mathit{t}\right)-{\mathit{o}}_{\mathit{l},\mathit{t}-\mathbf{1}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}-{\mathit{o}}_{\mathit{l},\mathit{k}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\le \mathbf{0},(15)$

$2\le k-\left(t-1\right)\le {\mathit{M}\mathit{U}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\left(\forall \mathit{j},\mathit{t}\right){\mathit{o}}_{\mathit{l},\mathit{t}-\mathbf{1}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}-{\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{o}}_{\mathit{l},\mathit{k}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\le \mathbf{1},(16)$

$2\le k-\left(t-1\right)\le {\mathit{M}\mathit{D}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\left(\forall \mathit{j},\mathit{t}\right),(17)$

$-{\mathit{o}}_{\mathit{l},\mathit{t}-\mathbf{1}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{u}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\le \mathbf{0}\left(\forall \mathit{j},\mathit{t}\right),(18)$

${\mathit{o}}_{\mathit{l},\mathit{t}-\mathbf{1}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}-{\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{v}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\le \mathbf{0}\left(\forall \mathit{j},\mathit{t}\right),(19)$

${\mathit{P}}_{l,t}^{unit}-{\mathit{P}}_{l,t-1}^{unit}\le \left(2-{\mathit{o}}_{l,t-1}^{unit}-{\mathit{o}}_{l,t}^{unit}\right)·{\mathit{P}}_{\mathit{min},l}^{unit}+\left(1+{\mathit{o}}_{l,t-1}^{unit}-{\mathit{o}}_{l,t}^{unit}\right)·\mathit{U}{\mathit{R}}_l^{unit}\left(\forall \mathit{j},\mathit{t}\right),(20)$

${\mathit{P}}_{l,t-1}^{unit}-{\mathit{P}}_{l,t}^{unit}\le \left(2-{\mathit{o}}_{l,t-1}^{unit}-{\mathit{o}}_{l,t}^{unit}\right)·{\mathit{P}}_{\mathit{min},l}^{unit}+\left(1-{\mathit{o}}_{l,t-1}^{unit}-{\mathit{o}}_{l,t}^{unit}\right)·\mathit{D}{\mathit{R}}_l^{unit}\left(\forall \mathit{j},\mathit{t}\right),(21)$

${\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}},{\mathit{v}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}{,\mathit{u}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\in \left\{\mathbf{0},\mathbf{1}\right\}\left(\forall \mathit{j},\mathit{t}\right).(22)$

${\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, ${\mathit{u}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, and ${\mathit{v}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ represent the operating state and start–stop state of the traditional generator, respectively. ${\mathit{P}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ represents the real-time power output of the generator. ${\mathit{M}\mathit{U}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ and ${\mathit{M}\mathit{D}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ represent the minimum start and stop times of the generator, respectively, while ${\mathit{U}\mathit{R}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ and ${\mathit{D}\mathit{R}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ represent the maximum ramp-up and ramp-down rates during the generator’s start-up and shut-down processes, respectively. Eq. 15 represents the constraints on the maximum and minimum output power of the generator. Eqs 16–19 represent the constraints on the start-stop time of the generator. Eqs 20–22 represent the maximum and minimum ramp rate constraints during the generator’s start-up and shut-down processes.

In implementation, the microgrid prioritizes the utilization of renewable generation to minimize electricity purchases and associated costs. As the renewable generation might be insufficient to meet the entire load demand, the output power of renewable generation, including photovoltaic and wind power, is considered a fixed value in the optimization scheduling for computational simplification, which are represented by ${\mathit{P}}_{\mathit{t}}^{\mathit{P}\mathit{V}}$ and ${\mathit{P}}_{\mathit{t}}^{\mathit{w}\mathit{i}\mathit{n}\mathit{d}}$, respectively.

In the operation of the data center microgrid, it is necessary to satisfy the power balance constraint, which ensures that the real-time power consumed by the loads and energy storage system is equal to the sum of the power generated by microgrid devices and purchased from the grid. Combining the supply side and demand side, the power balance constraints can be obtained as follows:

${\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}={\theta }^{PUE}{\bullet \mathit{P}}_{\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}+{\mathit{\eta }}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}{\bullet \mathit{P}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}-{\mathit{\eta }}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}{\bullet \mathit{P}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}-{\displaystyle {\sum }_{\mathit{l}}^{\mathit{L}}}{\mathit{P}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}-{\mathit{P}}_{\mathit{t}}^{\mathit{P}\mathit{V}}-{\mathit{P}}_{\mathit{t}}^{\mathit{w}\mathit{i}\mathit{n}\mathit{d}}\left(\forall \mathit{t}\right).(23)$

${\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ represents the real-time power, which the data center microgrid purchases from the distribution grid. ${\theta }^{PUE}$ represents the power usage effectiveness, which is used to characterize the relationship between the total electrical load of the data center and the energy consumption of the server and power supply devices in the data center. It is evident that the real-time power purchased by the data center microgrid is jointly determined by the total energy consumption of the data center facility and the operational state of the microgrid.

The aforementioned equations can fully describe the operations of the data center microgrid, which should be optimized in the lower level of the optimization problem. The optimization objective of the lower-level optimization problem is to minimize the operational cost of the data center microgrid, which is represented by ${\mathit{C}}_{\mathit{t}}^{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}$ and consists of the electricity bill ${\mathit{C}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ and the operational cost ${\mathit{C}}_{\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ of the generators in the microgrid, as shown in Eq. 24:

${\mathit{C}}_{\mathit{t}}^{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}={\displaystyle {\sum }_{t=1}^T}{\left(\mathit{C}\right.}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}+{\mathit{C}}_{\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}).(24)$

${\mathit{C}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ in Eq. 24 is decided by the electricity price ${\mathit{\pi }}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ and electricity purchasing amount ${\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$, as shown in Eq. 25:

${\mathit{C}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}={\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}{\bullet \mathit{\pi }}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}\left(\forall \mathit{t}\right).(25)$

${\mathit{C}}_{\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$ is described in Eq. 26, which consists of start-up cost ${\mathit{C}\mathit{U}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, shut-down cost ${\mathit{C}\mathit{D}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, no-load cost ${\mathit{C}\mathit{O}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, and marginal cost ${\mathit{C}\mathit{M}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$. The start-up and shut-down costs represent the cost generated in each start and stop processes of the generators. The no-load cost represents the cost when the generators run without electricity load, and the marginal cost represents the cost required to generate each unit of electricity.

${\mathit{C}}_{\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}={\displaystyle {\sum }_{\mathit{l}=\mathbf{1}}^{\mathit{L}}}\left({\mathit{C}\mathit{U}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}{\bullet \mathit{u}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{C}\mathit{D}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}{\bullet \mathit{v}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{C}\mathit{O}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}{\bullet \mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}+{\mathit{C}\mathit{M}}_{\mathit{l}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}{\bullet \mathit{P}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}\right)\left(\forall \mathit{i},\mathit{t}\right).(26)$

3.2 Electricity pricing and income model for the electricity retailer

The electricity pricing and electricity retailer income optimization is the objective of the upper-level problem in the proposed model. The electricity retailer’s net income in the transaction is as follows:

${\mathit{E}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}={\displaystyle {\sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}}\left({\mathit{S}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}{-\mathit{B}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}\right).(27)$

In this equation, the net income ${\mathit{E}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ for the power retailer is determined by the real-time electricity sales revenue ${\mathit{S}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ and the electricity purchasing cost ${\mathit{B}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$.

Since only one retailer and one electricity consumer are considered in the model, the real-time electricity sales revenue ${\mathit{S}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ is equal to the electricity bill of the data center, as shown below:

${\mathit{S}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}={\mathit{C}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}={\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}{\bullet \mathit{\pi }}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}\left(\forall \mathit{t}\right).(28)$

The electricity purchasing cost is described in Eqs 29 and 30:

${\mathit{B}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}={\mathit{P}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l},\mathit{t}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}{\bullet \mathit{\rho }}_{\mathit{a}\mathit{v}\mathit{e}\mathit{r}\mathit{a}\mathit{g}\mathit{e}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}\left(\forall \mathit{t}\right),(29)$

${\mathit{\rho }}_{\mathit{a}\mathit{v}\mathit{e}\mathit{r}\mathit{a}\mathit{g}\mathit{e}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}={\displaystyle {\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}}\left(\frac{{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}}{{\mathit{P}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l},\mathit{t}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}}{\bullet \mathit{\rho }}_{\mathit{k}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}\right)\left(\forall \mathit{k},\mathit{t}\right).(30)$

As shown in the equation, the cost of electricity purchasing, represented by ${\mathit{B}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$, varies according to the amount of electricity purchased from the energy generation side ${\mathit{P}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l},\mathit{t}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}$ and the real-time electricity purchasing price ${\mathit{\rho }}_{\mathit{a}\mathit{v}\mathit{e}\mathit{r}\mathit{a}\mathit{g}\mathit{e}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}$, which is time-variant and decided by the unit price of energy sources ${\mathit{\rho }}_{\mathit{k}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}$ and the proportion of the corresponding energy source in the total electricity purchasing amount $\frac{{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}}{{\mathit{P}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l},\mathit{t}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}}$ at different time intervals. The average electricity purchase price at each time interval can be calculated using the weighted averaging value.

To increase the revenue of the power retailer, the real-time electricity sales prices ${\mathit{\pi }}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ should be optimized to facilitate electricity trading, and the electricity should be purchased at times when ${\mathit{\rho }}_{\mathit{k}}^{\mathit{p}\mathit{u}\mathit{r}\mathit{c}\mathit{h}\mathit{a}\mathit{s}\mathit{e}}$ is lower. By doing so, the power retailer can maximize its revenue while ensuring efficient electricity trading.

3.3 Optimization problem analysis

In the Stackelberg game, the private information about each market entity is shared and centralized by the system operator for decision-making. It belongs to a multi-level hierarchical decision problem, studying the counter-strategy behaviors of decision-makers at different levels (Huang et al., 2018). The decision mechanism of this game problem is that the upper-level decision-maker first announces its decision variables, which will affect the objective function of the lower-level decision-maker. The lower-level decision-maker then makes decisions that optimize their own objective function under this premise, which, in turn, affects the objective function of the upper-level decision-maker. The upper-level decision-maker then adjusts their decision variables accordingly to achieve the optimal objective.

During the operation of the data center microgrid, the pricing game is mainly dominated by the electricity retailer. The retailer determines the real-time electricity price, and the data center adjusts its load curve and microgrid operations, such as battery charging and discharging, and generator start-up and shutdown based on the electricity price. Subsequently, the electricity retailer further adjusts the electricity price based on the data center’s load status to maximize its own interests. This game problem exhibits a leader–follower decision relationship and can be mathematically formulated as a bi-level programming problem. The upper-level optimization objective is to maximize the electricity retailer’s net income in the electricity transaction, while the lower-level optimization objective is to minimize the data center’s operational cost.

4 Hybrid problem-solving method combining the genetic algorithm and branch-and-cut algorithm

4.1 Necessity for the algorithm design

From a mathematical analysis perspective, the above analyzed Stackelberg game-based electricity pricing problem can be taken as a mixed-integer nonlinear programming problem, which cannot obtain the accurate analytical solution using the existing problem-solving methods.

On one hand, the optimization problem is a cubic-order nonlinear optimization problem, while the existing analytical problem-solving algorithm can only solve the problem whose order is not more than quadratic. In detail, the optimization problem includes two components: electricity price optimization and data center scheduling optimization. The electricity price optimization is the upper-level problem, whose optimal solution is decided by the data center scheduling method. The data center scheduling optimization is the lower-level problem, whose optimization objective is quadratically decided by the decisive variables, in which the electricity price given by the upper-level optimization has significant influence. Therefore, the problem is coupled with the electricity price, which makes the objective a cubic function of the decision variables. When dealing with the optimization problem, the traditional analytical algorithms, such as branch-and-bound or branch-and-cut algorithms, which are dedicated to linear or quadratic programming problems, can only solve the lower-level optimization quickly but cannot handle the entire optimization.

On the other hand, there are instances where continuous variables are multiplied by integer variables in the optimization objective and constraints, so the surface composed of feasible solutions is a discrete curved surface, which makes it hard to solve using the existing problem-solving methods. Intelligent algorithms such as the genetic algorithm can help solve the nonlinear programming problem, but it performs relatively poorly when dealing with the discrete nonlinear programming problem. When the number of variables increases, the feasible solutions that need to be searched increase significantly; therefore, the problem solving time will increase quickly. For example, in the encoding process of the genetic algorithm, a continuous variable can be represented by a float number, while a binary number can represent a 0/1 discrete variable. In the proposed model of the optimization problem, each day is divided into 24 time slots to represent the 24 h in a day, which is the least number of time slots and, thereby, reduce the number of decisive variables, whose number will directly influence the problem solving time. In each time slot, there are five discrete variables, ${\mathit{Z}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$, ${\mathit{Z}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$, ${\mathit{o}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, ${\mathit{u}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, and ${\mathit{v}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, and seven continuous variables, namely, ${\mathit{\mu }}_{\mathit{a},\mathit{i},\mathit{j},\mathit{t}}^{\mathit{b}\mathit{a}\mathit{t}\mathit{c}\mathit{h}}$, ${\mathit{\zeta }}_{\mathit{i},\mathit{j},\mathit{t}}^{\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{r}}$, ${\mathit{P}}_{\mathit{t}}^{\mathit{c}\mathit{h}\mathit{a}\mathit{r}}$, ${\mathit{P}}_{\mathit{t}}^{\mathit{d}\mathit{i}\mathit{s}\mathit{c}\mathit{h}\mathit{a}\mathit{r}},$ ${\mathit{P}}_{\mathit{l},\mathit{t}}^{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}$, ${\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$, and ${\mathit{\pi }}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$. In the optimization problem, a total of 7 × 24 sets of continuous variables and 5 × 24 sets of discrete variables need to be solved, so the problem can be taken as an optimization problem consisting of 5 × 24 continuous nonlinear programming sub-problems involving 7 × 24 sets of continuous variables. Assuming that the solving time for each sub-problem is T₀, the search time required would be T₀×2^5×24. It is obvious that the scale of the genetic algorithm is huge. The genetic algorithm will face significant challenges in application.

4.2 Introduction of the hybrid problem-solving method

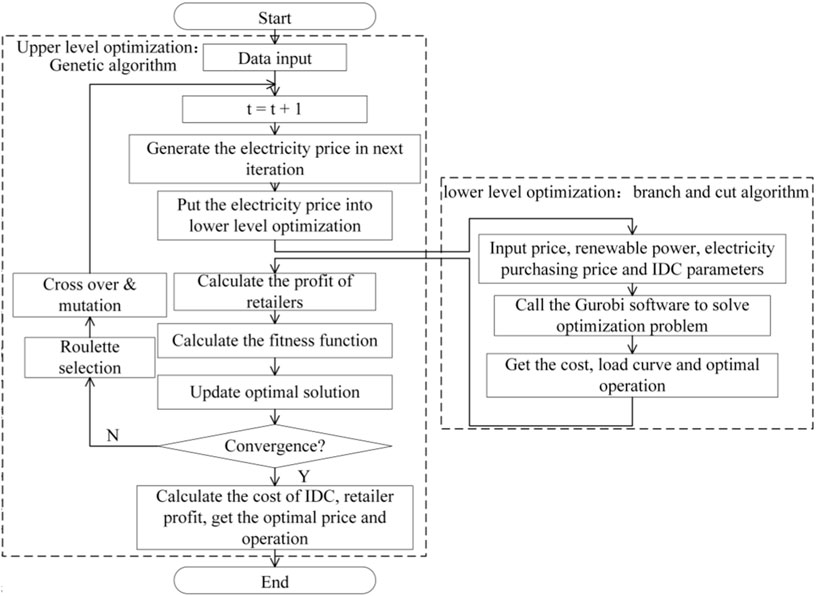
To facilitate the solution of the bi-level programming problem, we propose a hybrid problem-solving method combining the genetic algorithm and branch-and-cut algorithm. In this method, the upper level employs the genetic algorithm to search for optimal real-time price, while the lower level uses the branch-and-cut algorithm to rapidly solve the data center scheduling problem under the given electricity price. The electricity purchase in the optimal solution of the lower-level problem will be fed back to the upper-level optimization, enabling the iterative selection that maximizes benefits. Due to the considerable variation in electricity price data and in order to reduce the number of encoded bits, we adopt true-value encoding in this approach. Specifically, 24 float numbers are used to represent the electricity prices at different time slots during a day, and the genetic algorithm encoding the length is reduced to 24 bits, which significantly reduces the scale of the problem. Assuming a search process involving m iterations, each iteration consists of n genetic encoding sequences and the solution time for the lower-level problem is T₁; the total solving time is m×n×T₁. Obviously, the proposed method can significantly reduce the iterations and number of genes per iteration compared to the direct application of the genetic algorithm and then saving the total solving time.

The algorithm flow chart is shown in Figure 4. In the upper-level optimization process, to maximize the interests of the electricity retailer, the genetic algorithm uses the reciprocal of the electricity retailer’s net income ${\mathit{E}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ in Eq. 27 as the fitness function. In each iteration, it searches and selects the combination of electricity prices that yields the highest value of this fitness function. In the lower-level optimization, the branch-and-cut algorithm aims to minimize the data center’s operational cost ${\mathit{C}}_{\mathit{t}}^{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}$. In each iteration, the genes are selected as parents using the roulette wheel selection method, and offspring individuals are generated through a single-point crossover and single-point mutation for the next iteration. The roulette wheel selection method is a common selection strategy used to choose parent individuals for crossover and mutation operations based on their fitness values. This method simulates a scenario akin to a roulette wheel in a casino, where each individual occupies a segment on the wheel circumference proportional to its fitness value. In the roulette wheel selection process, first, the fitness values of each individual in the population are calculated, typically evaluated through an objective function. Subsequently, these fitness values are normalized to obtain normalized fitness values. Normalized fitness values represent the probability of an individual being selected, meaning individuals with higher fitness values have a greater probability of being chosen. During the roulette wheel selection process, a random number in the range [0,1] is generated. Then, based on the normalized fitness values, the first individual whose cumulative fitness value exceeds or equals the random number is selected as the parent individual. This process mimics the spinning of a roulette wheel in a casino, eventually stopping at a specific individual, who is then chosen as the parent. The roulette wheel selection method possesses stochastic selection probabilities based on fitness, enabling individuals with higher fitness to have a higher chance of being chosen. This increases the representation of high-fitness individuals in the offspring, steering the algorithm toward the evolution of better solutions.

FIGURE 4

FIGURE 4. Flowchart of the proposed hybrid problem-solving method.

In the algorithm, the genetic algorithm first randomly generates the electricity within a certain range, and the electricity price is introduced as a fixed value into the operation optimization problem of the data center microgrid in the lower level. Then, the branch-and-cut algorithm is called to solve the operation optimization problem, and the income of both sides is returned to the genetic algorithm, which uses it to calculate the fitness function and iterate to select the optimal electricity price. In essence, the algorithm reduces the problem-solving time by splitting the large-scale problem into several quadratic programming problems. The specific operation steps are given in Table 2:

TABLE 2

TABLE 2. Hybrid problem-solving method combining the genetic algorithm and branch-and-cut algorithm.

4.3 Convergence analysis

In the proposed algorithm, we adopted the real number-coded genetic algorithm and the roulette wheel method, which is a proportional selection method. The random mutation method is used to enhance the random search, and the branch-and-cut algorithm is used to reduce the dimension of the problem and accelerate the problem-solving process. To prove the convergence of the algorithm, the convergence in probability and metric space is introduced into the proof process.

Definition 1:. Convergence in probability. Assume that $f\left(j\right)$ is the minimum fitness function of all the genes in thepopulation of the $jth$ generation. $minf$ is the minimum value of fitness function $F\left(j\right)$ in the set of all the possible genes $X$. If $f\left(j\right)$ can satisfy Eq. 31,

$\underset{j\to \infty }{\lim }p\left\{f\left(j\right)=minf\right\}=1,(31)$

then, the algorithm can converge to the optimal solution.

Definition 2:. Metric space. Assume that $X$ is a nonempty set, and $d$ is a mapping from $X\times X$ to $R$, and for $\forall x,y,z\in X$, the following equation can be satisfied:$d\left(x,y\right)\ge 0$ and $d\left(x,y\right)=0$ only if $=y$; $d\left(x,y\right)=d\left(y,x\right)$; $d\left(x,y\right)\le d\left(x,z\right)+d\left(z,y\right)$. Then, $d$ can be defined as the metric of $X$, and $\left(X,d\right)$ is the metric space.

Theorem 1:. In the metric space $\left(X,d\right)$, for $\forall x,y,z\in X$, $\left|d\left(x,z\right)\bullet d\left(z,y\right)\right|\le d\left(x,y\right);$for$\forall x,y,x_1,y_1\in X$, $\left|d\left(x,z\right)\bullet d\left(x_1,y_1\right)\right|\le d\left(x,x_1\right)+d\left(y,y_1\right).$

Definition 3:. In the metric space $\left(X,d\right)$, $\left\{x_n\right\}$ is a series. If $\exists N\in N_{+},\forall n>N$ and $d\left(x_n,x\right)<\epsilon$, then $\left\{x_n\right\}$ converges to $x$, recorded as $x_n\to x$.

Definition 4:. In the metric space $\left(X,d\right)$, $\left\{x_n\right\}$ is a series. If $\forall \epsilon >0,\exists N\in N_{+,}\forall m,n>N,$ $d\left(x_m,y_n\right)<\epsilon ,$ then $\left\{x_n\right\}$ is the Cauchy series. If all the $\left\{x_n\right\}$ converge, then $\left(X,d\right)$ is a complete metric space.

Definition 5:. In the metric space $\left(X,d\right)$, for the mapping $f:X\to X,\exists \epsilon \in \left[0,1\right),\forall x,y\in X$, if $d\left(f\left(x\right),f\left(y\right)\right)\le \epsilon \bullet d\left(x,y\right)$, then $f$ is a contraction mapping.

Theorem 2:. (Banach’s contraction mapping theorem): If the metric space $\left(X,d\right)$ is a contraction mapping, then there is only one fixed point $x^{*}\in X$, and for $\forall x_0\in X$, $x^{*}=f^k\left(x_0\right)$, where $f^0\left(x_0\right)=x_0$ and $f^{k-1}\left(x_0\right)$ = $\left.{f(f}^k\left(x_0\right)\right)$.

Based on the above given theory, the convergence of the proposed algorithm is proved below.

Assume that $X$ is a population of the genetic algorithm, and its amount is $p$, which means $X=\left\{x_1,x_2,\dots ,x_p\right\}$. In the genetic algorithm, the roulette wheel method is selected, which is a proportional selection method; the $i$th individual in the $j$th generation can be selected into the next generation by a probability of $p_s\left(j\right)$, which is shown in Eq. 32:

$p_s\left(j\right)=\frac{F\left(j\right)}{{\displaystyle {\sum }_{j=1}^p}F\left(j\right)}\ge \frac{f_{\min }}{p\bullet f_{\max }}=M,(32)$

where $x_i^j$ belongs to the group consisting of the $p$-th individual, which is $F\left(j\right)=\left\{x_1^j,x_2^j,\dots ,x_p^j\right\}$, and $M$ is a constant, which is irrelevant to the number of iteration $j$ and the number of groups in $F\left(j\right)$.

According to the Banach contraction mapping theorem, it is easy to prove that the algorithm can converge to a fixed point $x^{*}\in X$ for $\forall x_0$ as the initial population if there is a metric space $\left(X,d\right)$, which can make the operator consisting of the genetic algorithm and branch-and-cut algorithm a contraction mapping.

Assume that the minimum value of the objective function is $\min f$ and $d$ is a mapping from $X\times X$, which can be described by Eq. 33:

$d\left(X_1,X_2\right)=\left\{\begin{array}{c}0X_1=X_2\\ \left|1+M-F\left(X_1\right)\right|+\left|1+M-F\left(X_2\right)\right|X_1\ne X_2\end{array}\right..(33)$

Then, the mapping $d$ can satisfy

$d\left(X_1,X_2\right)\ge 0\forall X_1,X_2\in X;$

$d\left(X_1,X_2\right)=d\left({X_2,X}_1\right)\forall X_1,X_2\in X;$

$d\left(X_1,X_2\right)\le d\left(X_1,X_3\right)+d\left(X_2,X_3\right)\forall X_1,X_2\in X.$

Therefore, the mapping $d$ is a metric, and $\left(X,d\right)$ is a metric space. Since $X$ is a finite set, each Cauchy series in $X$ will converge. So, $\left(X,d\right)$ is a complete metric space.

The operator, which consists of the genetic algorithm and branch-and-cut algorithm, is defined as $g:X\to X$, and $j$ represents the number of generations. Since the selection method is a proportional selection method, and the gene which leads to infeasibility of the lower-level problem is eliminated before the selection, the average fitness in each generation increases.

Therefore, for the mapping $g$, the Eq. (34) can be satisfied as

$d(g\left(\left.X_1\left(j\right),X_2\left(j\right)\right)\right)=\left|1+M-F\left(g\left(X_1\left(j\right)\right)\right)\right|+\left|1+M-F\left(g\left(X_2\left(j\right)\right)\right)\right|<\epsilon \bullet \left(\left|1+M-F\left(X_1\right)\right|+\left|1+M-F\left(X_2\right)\right|\right)=\epsilon \bullet d\left(g\left(X_1\left(j\right),X_2\left(j\right)\right)\right),\epsilon \in \left(\mathrm{0,1}\right).(34)$

Therefore, $g$ is a contraction mapping, and the proposed algorithm should converge to the only fixed point $x^{*}\in X$ according to the Banach contraction mapping theorem, and the proposed genetic algorithm is convergent.

5 Case study

5.1 Simulation setup

In this study, a data center located in California is selected as the case for analysis (Liu and Peng, 2021; Singh and Saxena, 2021). The data center is powered by a microgrid system, which includes energy storage, photovoltaic (PV) generation, wind power, natural gas, and conventional generators. The specific capacity configuration and operating parameters of the servers, generators, and energy storage are given in Tables 3–6. 2) The data on servers, generators, and ESS are obtained from the papers by Cao and Wang (2019) and Ding et al. (2018). The total computational workload is based on historical data from Alibaba’s data center, with a time delay tolerance of 24 h for the batch workload. 4) The power losses can surely be modeled as a quadratic equation, which is decided by the electrical characteristics of UPS, as shown by Guo et al. (2019). The capacity of PV and wind power is 10 MW. The electricity purchasing and selling prices, as well as the output power of renewable energy sources, are shown in Figure 5. The existing electricity price is obtained from real-time electricity price data on a typical day in July 2022 provided by California Independent System Operator (CAISO). The electricity purchasing prices are calculated based on the real-time weighted average price of different fuel types, while the PV and wind power outputs are calculated using the ratio of wind and solar power to their installed capacities for that specific day. In the study of microgrid scheduling, since the operation of conventional units usually takes no less than 1 h, we set 1 h as a time slot to narrow the dimension of decision variables and simplify problem solving.

TABLE 3

TABLE 3. Number and rated power of servers.

TABLE 4

TABLE 4. Parameters of the energy storage system.

TABLE 5

TABLE 5. Parameters of conventional generator units.

TABLE 6

TABLE 6. Electricity purchasing price.

FIGURE 5

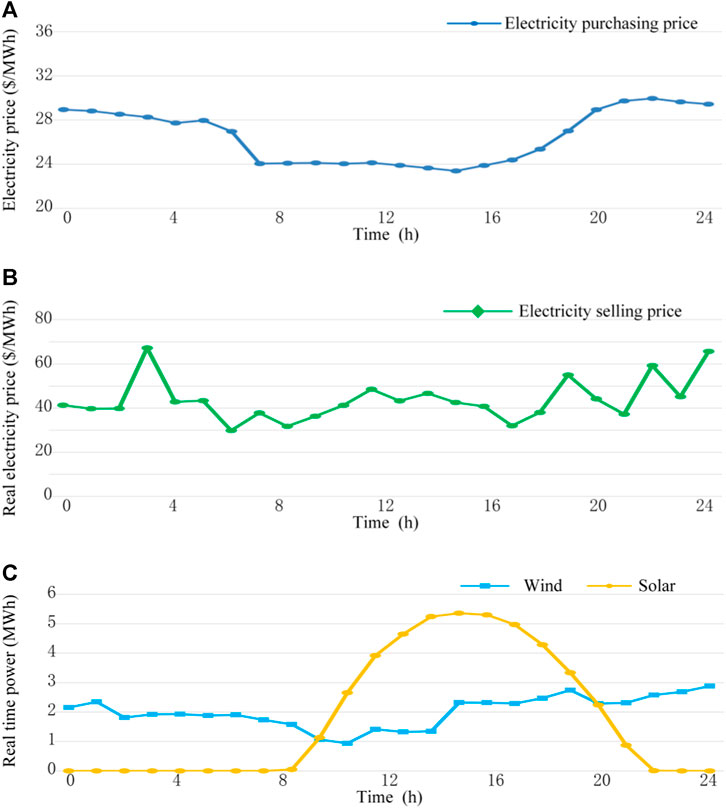
FIGURE 5. Working condition in the game between the data center and local electricity retailer, (A) electricity purchasing price, (B) real-time electricity selling price, and (C) renewable power output.

The aforementioned case study was conducted on a desktop computer equipped with an Intel Core i5-8400 processor and 8 GB RAM. The genetic algorithm used for the upper-level electricity price optimization is coded in PyCharm software, while the lower-level linear optimization problems are solved using Gurobi simulation software. In this simulation, the genetic algorithm is set with a population size of 50 individuals, 20 generations of iterations, a mutation rate of 0.01, and a crossover rate of 0.9.

5.2 Result analysis

Under the aforementioned parameter settings, simulations are conducted for both the case with CAISO’s daily pricing and the case using the proposed game theory-based method. The operating costs and revenues of both the data center and electricity retailer are analyzed, and the simulation results are given in Table 7. It can be observed that after applying the proposed game-theoretic method, the data center’s operating costs decreased by 3%, and the electricity retailer’s profit increased by 17%. This indicates that the proposed method effectively enhances the revenues of both the data center and electricity retailer.

TABLE 7

TABLE 7. Comparison of the benefits.

The electricity price curves and the data center microgrid operations before and after the optimization are shown in Figure 6. Figure 6A displays the real-time electricity price curve before and after optimization. Figure 6B shows the time distribution of the data center’s electricity load before and after optimization. It can be observed that the time distribution of the data center’s electricity load changes with the variation in grid electricity prices, indicating that the electricity consumption behavior of the data center is influenced by adjusting the electricity price. Figure 6C shows the data center’s electricity purchase before and after optimization. A comparison showed that after the electricity price adjustment, the amount of electricity purchased from the grid by the data center significantly increases, and therefore, the electricity retailer gains more revenue through the strategy of small profit but quick turnover. Figure 6D illustrates the variation in the output power of the generators in the data center microgrid before and after optimization. By comparing it with the traditional generator output power in the figure, it can be observed that after the electricity price optimization, the data center generators stop running, and all the electricity is supplied by the renewable energy and the utility grid, resulting in a significant reduction in the additional operating costs.

FIGURE 6

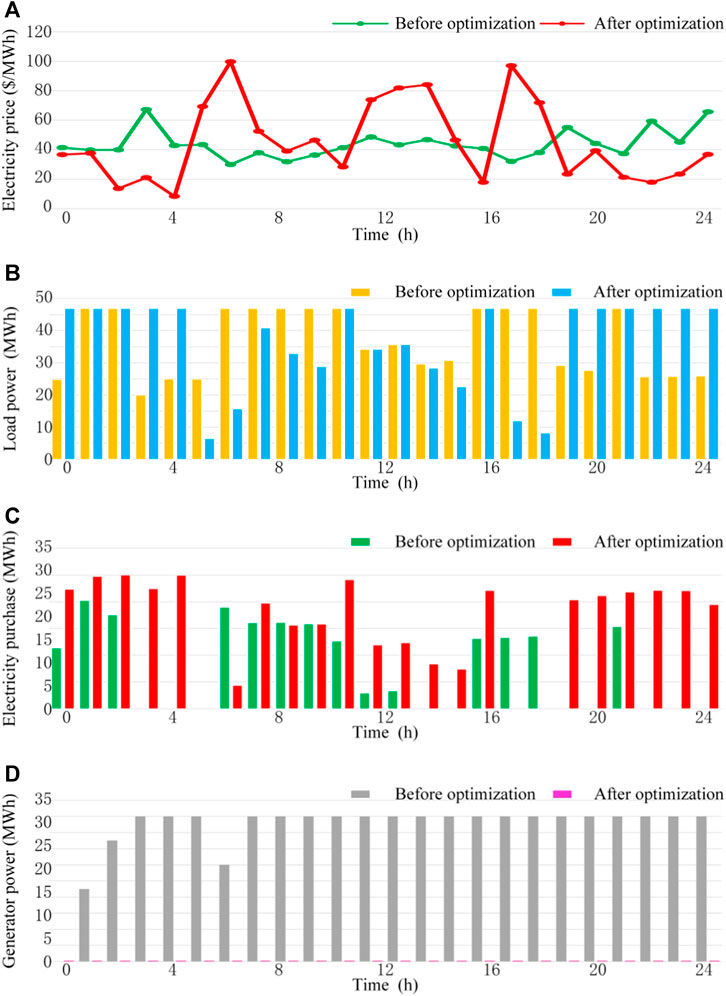
FIGURE 6. Operations of the data center micro grid before and after the optimization, (A) electricity price, (B) load power, (C) electricity purchase amount, and (D) generator power output.

Table 8 presents a comparison of the problem solving times for the genetic algorithm, branch-and-cut algorithm, and the proposed two-layer solution method. Since the problem to be solved is a high-order nonlinear optimization problem, the traditional branch-and-cut algorithm is unable to solve it. Furthermore, the solution time for the traditional genetic algorithm exceeds 1 h because of the large scale of the problem, making it ineffective to be applied in the implementation. In contrast, the newly proposed hybrid problem-solving method combining the genetic algorithm and branch-and-cut algorithm significantly reduces the solution time to 1.5 min, which improves the solution efficiency.

TABLE 8

TABLE 8. Comparison of algorithm performance.

Furthermore, the universality of results can be guaranteed. First, the simulation verification is based on public data which can be found in the website of CAISO (2022), Alibaba, and other related websites. Second, the model and algorithm are coded in PyCharm software and based on an open-source software package, which can be reproduced on other computers. Third, although a random search in the problem-solving process is caused by the genetic algorithm and branch-and-cut algorithm, the convergence of the algorithm proved in Section 4.3 can ensure the recurrence of the results.

6 Conclusion

In this paper, we proposed a non-cooperative game theory-based optimization method for data center electricity procurement negotiation and operation scheduling. The proposed method models the electricity pricing between the electricity retailer and the data center as a Stackelberg game model, and a hybrid problem solving method combining the genetic algorithm and branch-and-cut algorithm is proposed, thus achieving coordinated optimization of electricity pricing and data center microgrid scheduling in the electricity trading process. The simulation results demonstrate that the proposed method reduces the data center operational cost by 3% while improving the retailer’s revenue by 17%, and the problem-solving time is significantly reduced.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JL: conceptualization, data curation, methodology, project administration, software, writing–review and editing, and writing–original draft. GY: visualization and writing–original draft. FG: supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors declare all sources of funding received for the research being submitted.

Conflict of interest

Author JL was employed by Global Mainstream Dynamic Energy Technology Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Hazemi, F., Peng, Y., and Youn, C. (2018). Dynamic allocation of power delivery paths in consolidated data centers based on adaptive UPS switching. Comput. Netw. 144 (24), 254–270. doi:10.1016/j.comnet.2018.08.004

CrossRef Full Text | Google Scholar

Aujla Singh, G., Singh, M., Kumar, N., and Zomaya, A. Y. (2017). Stackelberg game for energy-aware resource allocation to Sustain data centers using RES. IEEE Trans. Cloud Comput. 7 (4), 1109–1123. doi:10.1109/tcc.2017.2715817

CrossRef Full Text | Google Scholar

Bahrami, S., Wong, V. W. S., and Huang, J. (2019). Data center demand response in deregulated electricity markets. IEEE Trans. Smart Grid 10 (3), 2820–2832. doi:10.1109/TSG.2018.2810830

CrossRef Full Text | Google Scholar

Beloglazov, A., Abawajy, J., and Buyya, R. (2012). Energy-aware resource allocation heuristics for efficient management of data centers for cloud computing. F. Gener. Comput. Syst. 28 (5), 755–768. doi:10.1016/j.future.2011.04.017

CrossRef Full Text | Google Scholar

California ISO (2022). California ISO real-time daily market watch report. California, US.

Google Scholar

Cao, F., Wang, Y., Zhu, F., Cao, Y., and Ding, Z. (2019). UPS node-based workload management for data centers considering flexible service requirements. IEEE Trans. Ind. Appl. 55 (6), 5533–5542. doi:10.1109/TIA.2019.2933791

CrossRef Full Text | Google Scholar

Cao, X., Zhang, J., and Poor, H. V. (2018). Data center demand response with on-site renewable generation: a bargaining approach. IEEE/ACM Trans. Net. 26 (6), 2707–2720. doi:10.1109/TNET.2018.2873752

CrossRef Full Text | Google Scholar

Ding, Z., Xie, L., Lu, Y., Wang, P., and Xia, S. (2018). Emission-aware stochastic resource planning Scheme for data center micro grid considering batch workload scheduling and Risk management. IEEE Trans. Ind. Appl. 54 (6), 5599–5608. doi:10.1109/TIA.2018.2851516

CrossRef Full Text | Google Scholar

Guangdong Provincial Development and Reform Commission (2020). Review opinions of Guangdong provincial energy bureau on energy saving report of foshan advanced manufacturing and industrial internet industrial park project. Guangdong, China. available at: http://drc.gd.gov.cn/snyj/tzgg/content/post_3104954.html.

Google Scholar

Guo, F., Wu, Y., Wang, J., et al. (2020). China data center renewable energy application development report (2020). Beijing: Chinese Institute Of Electronics.

Google Scholar

Guo, J., Chang, Z., Wang, S., Ding, H., Feng, Y., Mao, L., et al. (2019). Who limits the resource efficiency of my datacenter: an analysis of alibaba datacenter traces. IWQoS '19. Proc. Int. Symposium Qual. Serv. 39. doi:10.1145/3326285.3329074

CrossRef Full Text | Google Scholar

Huang, H., Li, X., Zou, L., et al. (2018). Stackelberg game model of user interactive operation considering uncertainty. J. N. C. Electr. Power Univ. 55 (20), 82–89. doi:10.3969/j.issn.1001-1390.2018.20.014

CrossRef Full Text | Google Scholar

Huang, Y., Wu, S., et al. (2022). Optimal scheduling of regional integrated energy systems with carbon trading based on incomplete information game. J. N. C. Electr. Power Univ. 1-13. in press.

Google Scholar

Institute for Energy Economics and Financial Analysis (IEEFA) (2020). Google's solar deal for Nevada data center would Be largest of its kind. California, US: Lakewood.

Google Scholar

Jiang, Y. (2018). Research on marketing strategy of key customers of SD electric power company under the background of electricity selling side Reform. (Doctoral dissertation). Shandong University of Finance and Economics.

Google Scholar

Khalaj Habibi, A., and Halgamuge, K. S. (2017). A review on efficient thermal management of air- and liquid-cooled data centers: from chip to the cooling system. Appl. Energy 205 (1), 1165–1188. doi:10.1016/j.apenergy.2017.08.037

CrossRef Full Text | Google Scholar

Li, P., Hu, J., and Tan, Z. (2019). Research on game model of electricity supplier competition strategy under new electricity Reform. J. N. C. Electr. Power Univ. 46 (03), 103–110.

Google Scholar

Li, Z., Wang, R., Zhu, K., Yi, C., Liu, L., and Niyato, D. (2021). “Joint energy and computation workload management for geo-distributed data centers in Smart grid,” in 2021 IEEE 23rd Int Conf on High Performance Computing and Communications; 19th Int Conf on Smart City; (HPCC/SmartCity), Haikou, Hainan, China, 20-22 December 2021, 2410–2416. doi:10.1109/HPCC-DSS-SmartCity-DependSys53884.2021.00363

CrossRef Full Text | Google Scholar

Liu, K., Peng, J., Yu, B., Liu, W., Huang, Z., and Pan, J. (2021). An instance reservation framework for cost-effective services in geo-distributed data centers. IEEE Trans. Svcs, Comput. 14 (2), 356–370. doi:10.1109/TSC.2018.2818121

CrossRef Full Text | Google Scholar

Luo, Y., Andresen, J., Clarke, H., Rajendra, M., and Maroto-Valer, M. (2019). A decision support system for waste heat recovery and energy efficiency improvement in data centres. Appl. Energy 250 (1), 1217–1224. doi:10.1016/j.apenergy.2019.05.029

CrossRef Full Text | Google Scholar

Mohammed, A. B., Brik, B., Esseghir, M., and Merghem-Boulahia, L. (2018). A game based power allocation in cloud computing data centers. Int. Conf. Wirel. Mob. Comput. Netw. Commun. doi:10.1109/WiMOB.2018.8589177

CrossRef Full Text | Google Scholar

Muhammad, A., and Mekhilef, S. (2017). An online transformerless uninterruptible power supply (UPS) system with a smaller battery bank for low-power applications. IEEE Trans. Power Electr. 32 (1), 233–247. doi:10.1109/TPEL.2016.2537834

CrossRef Full Text | Google Scholar

Ohn, S., Yu, J., Burgos, R., Boroyevich, D., and Suryanarayana, H. (2020). Reduced common-mode voltage PWM Scheme for full-SiC three-level uninterruptible power supply with small DC-link capacitors. IEEE Trans. Power Electr. 35 (8), 8638–8651. doi:10.1109/TPEL.2019.2962964

CrossRef Full Text | Google Scholar

Orkowski, M., and Krzysztof, A. (2022). Customized data center cooling system operating at significant outdoor temperature fluctuations. Appl. Energy 306 (1), 1179–1191. doi:10.1016/j.apenergy.2021.117975

CrossRef Full Text | Google Scholar

Peter, A. (2017). Data centers and advanced micro grids [R]. Rueil, France: Schneider Electric.

Google Scholar

Pratt, A., Kumar, P., and Aldridge, T. V. (2007). Evaluation of 400V DC distribution in Telco and data centers to improve energy efficiency. Proc. IEEE Intelec Conf., 32–39.

CrossRef Full Text | Google Scholar

Qi, W., Li, J., Liu, Y., and Liu, C. (2019). Planning of distributed internet data center micro grids. IEEE Trans. Smart Grid 10 (1), 762–771. doi:10.1109/TSG.2017.2751756

CrossRef Full Text | Google Scholar

Qin, Y. (2020). Research on the energy-aware multi-objective virtual resource management in the cloud data center. Jinan: Doctoral dissertation. Shandong Univ.

Google Scholar

Ren, Y., Zhou, M., and Li, G. (2017). Bi-level model of electricity procurement and sale strategies for electricity retailers considering users' demand response. Autom. Electr. Power Syst. 41 (14), 30–36. doi:10.7500/AEPS20170219003

CrossRef Full Text | Google Scholar

Singh, K. A., Saxena, D., Kumar, J., and Gupta, V. (2021). A quantum approach towards the adaptive prediction of cloud workloads. IEEE Trans. Paral. Dist. Syst. 32 (12), 2893–2905. doi:10.1109/TPDS.2021.3079341

CrossRef Full Text | Google Scholar

Sun, J., Chen, S., Giannakis, G. B., Yang, Q., and Yang, Z. (2021). Cross service Providers workload balancing for data centers in deregulated electricity markets. IEEE Trans. Cont. Net. Syst. 8 (2), 803–815. doi:10.1109/TCNS.2021.3053236

CrossRef Full Text | Google Scholar

The Natural Resources Defense Council (2015). America's data centers consuming and wasting growing amounts of energy. New York: The Natural Resources Defense Council.

Google Scholar

Tran, N. H., Tran, D. H., Ren, S., Han, Z., Huh, E.-N., and Hong, C. S. (2016). How geo-distributed data centers do demand response: a game-theoretic approach. IEEE Trans Smart Grid 7 (2), 1–947. doi:10.1109/TSG.2015.2421286

CrossRef Full Text | Google Scholar

Wang, Z., Cui, W., and Li, L. (2022). Research on business model of electric power credit investigation based on evolutionary game. J. N. C. Electr. Power Univ. 49 (5), 101–109.

Google Scholar

Wu, Q., Ishikawa, F., Zhu, Q., and Xia, Y. (2019). Energy and migration cost-aware dynamic virtual machine consolidation in heterogeneous cloud datacenters. IEEE Trans. Serv. Comput. 12 (4), 550–563. doi:10.1109/TSC.2016.2616868

CrossRef Full Text | Google Scholar

Yang, H., Wei, Z., Huang, Y., et al. (2019). Multi-agent purchase and sale master-slave game model in cross-regional spot market. Power Syst. Technol. 43 (8), 2781–2788. doi:10.13335/j.1000-3673.pst.2019.0548

CrossRef Full Text | Google Scholar

Ye, G., and Gao, F. (2022). Coordinated optimization scheduling of data center and electricity retailer based on cooperative game theory. CPSS Trans. Power Electr. Appli. 7 (3), 273–282. doi:10.24295/CPSSTPEA.2022.00025

CrossRef Full Text | Google Scholar

Yu, X., and Song, L. (2019). Data center white paper 2018. Beijing: CAICT. available at: https://www.scdsjzx.cn/scdsjzx/ziliaoxiazai/2022/6/27/5b92a33cc6de4ec18c940410bf7cbdba/files/a71f71e5fbc44be19451fa0d4e45475f.pdf?eqid=d7ed89a800071ca3000000026497bc76.

Google Scholar