A distribution network planning method based on the integration of operation and planning and coordinated with the transmission network

With the increasing integration of renewable energy into the power grid, the traditional roles of the transmission and distribution networks have become less distinct at the operational level. The integration between distribution network planning (DNP) and the transmission and distribution networks operation is crucial to ensure grid stability. Existing research has primarily focused on collaborative operation control between transmission and distribution networks, leaving a gap in integrated DNP, since few works can handle the integer variables. This study proposes a distribution network planning method based on the integration of operation and planning and coordinated with the transmission network. It aims to minimize investment and operational costs while considering local generation units, distributed renewables, and network constraints. Using a heterogeneous decomposition algorithm (HGD), the optimization model alternates between the two networks, assisted by injected parameters for global optimality. A convolutional neural network (CNN) surrogate model is then used to rapidly optimize precise distribution network plans that coordinate with the transmission network. Experimental results on IEEE 30 and IEEE 69 cases demonstrate that the proposed approach offers valuable engineering benefits, reducing iteration counts by up to 20% and improving accuracy compared to other distributed algorithms.

1 Introduction

The DNP could ensure the economic and secure operation of power systems. For a long time, DNP has been closely related to developing and evolving generation-transmission-distribution characteristics (Wang et al., 2020). The emergence of distributed renewable energy has brought uncontrollable, stochastic, and fluctuating issues to power flow (Liu et al., 2022; Lotfi, 2022). The uncertainty of their spatial distribution profoundly impacts DNP, which also needs to consider the renewable energy consumption capacity to optimize the allocation of renewable energy output ratios (Wang et al., 2020).

Compared to DNP, the existing research on coordination optimization of transmission and distribution mainly focuses on four problems (Xie et al., 2023): economic dispatch (Li et al., 2016, 2018b; Loukarakis, Dent and Bialek, 2016; Yu et al., 2019), unit commitment (Kargarian and Fu, 2014; Nawaz and Wang, 2021; Zhang et al., 2022; Zhang et al., 2022), optimal power flow (Li et al., 2018a; Mohammadi, Mehrtash and Kargarian, 2019; Lin et al., 2020; Zuo et al., 2020; Tang et al., 2021), and reactive power optimization (Wang, 2015; Lin et al., 2017; Sun, 2019). These model DNP problems as optimization problems with nonlinear constraints, which contain sparse Jacobian matrix due to different transmission and distribution power grid parameters. Some state-of-the-art optimization techniques are introduced due to the feature of problems. The analytical target cascading method (Kargarian and Fu, 2014; Mohammadi, Mehrtash and Kargarian, 2019; Zhang et al., 2022; Zhang et al., 2022) is proposed in the literature. However, its algorithm suffers from slow convergence speed, easy oscillation around the optimal point, or divergence issues when improper penalty multiplier selection and imbalanced weights among subsystems occur. Relatively, the HGD algorithm, which is based on boundary interaction variables (Li et al., 2016; 2018a), is widely applied in heterogeneous system solving (Yu et al., 2019) and can be combined with sensitivity calculation (Li et al., 2018b) or the alternating direction multiplier method (ADMM) to reach the optimum of more complex multi-period (Loukarakis, Dent and Bialek, 2016) and multi-objective (Zuo et al., 2020) problems. Since the HGD composite algorithm above requires optimization in each iteration (Wang, 2015; Lin et al., 2017; Zhao et al., 2019), calculations can be computationally intensive, especially in the case of large-scale data or complex models, less-iterative (Tang et al., 2021) algorithms, non-iterative (Lin et al., 2020) algorithms, mechanism-based algorithms and heuristic algorithms (Lotfi and Shojaei, 2022) are proposed to substitute for iterative algorithms, wherein the convergence performance of the first two and the generality of the latter two cannot be guaranteed.

Although the reported methods show a certain level of effectiveness in the coordination optimization of transmission and distribution, they offer the following inadequacies:

1) The composite distributed solution algorithm requires customization for specific problems; its solution speed becomes uncontrollable as the problem size increases. Moreover, its global optimality and algorithm convergence cannot be adequately demonstrated.

2) The existing academic literature mainly focuses on dealing with continuous optimization problems, but only some studies on mixed-integer optimization problems are represented by DNP. Only one study in the existing literature addresses the transmission network planning problem using Benders Decomposition for DC power flow constraints (Liu et al., 2021). Still, this method cannot be transferred to distribution network planning problems with nonlinear power flow constraints. Consequently, more research should be conducted on mixed-integer optimization problems related explicitly to DNP.

To fill the above gaps, this paper focuses on the DNP method based on integrating operation and planning and coordinated with the transmission network.

1) An integrated optimization mathematical model is proposed for coordinated operation and planning of the distribution and transmission networks. This model aims to minimize the investment and construction cost of the distribution network, along with the generation cost, load shedding cost, and renewable energy curtailment cost of the transmission and distribution networks (Lotfi, 2020; Lotfi, Ghazi and Naghibi-Sistani, 2020; Lotfi and Ghazi, 2021). The model incorporates heterogeneous DC power flow and distflow constraints in the transmission and distribution networks to achieve this optimization.

2) A heterogeneous decomposition of optimization models for both the transmission and distribution networks was performed, using substations as boundaries. A concise HGD algorithm was employed to achieve distributed solving of the optimization models containing continuous variables. This approach allows for efficient convergence within a limited number of steps.

3) For integer variables, due to their association with the distribution network topology, a correlation matrix is introduced to describe the distribution network topology. A convolutional neural network is employed to learn and extract topological features, enabling the efficient fitting of the non-linear relationship between integer variables and optimization objectives. This significantly reduces the overall computational complexity of the process.

The proposed DNP method has been tested on a benchmark power system constructed of IEEE CASE 30 and CASE 69, including the comparative study with a global optimization algorithm, since there are few relevant studies. The results indicate that, within the allowed precision of the DNP problem, the proposed DNP method achieves optimization results consistent with global optimization algorithms and efficiently completes the optimization process.

2 Specific DNP model in synergy with the transmission network

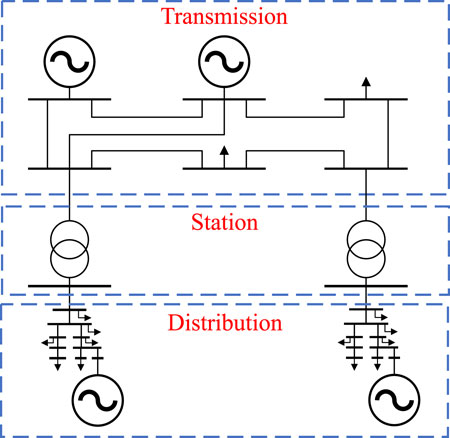
As shown in Figure 1, the power grid is divided into three parts: the transmission network, the substation, and the distribution network. The substation nodes serve as the boundaries between the transmission and distribution networks.

FIGURE 1

FIGURE 1. Structure diagram of power transmission and distribution network.

2.1 Objective function

A DNP model should be built with objective functions constructed from both planning and operation perspectives to establish a coordinated transmission and distribution model for planning and operation. The aim of the planning function should be based on the investment and construction cost of the distribution grid. In contrast, the operation objective function should consider the operating costs of both the transmission grid and the distribution grid. The operational costs of the transmission and distribution grid should include the cost of power generation, the penalty for load shedding, and the cost of renewable energy curtailment. The objective functions can be expressed as follows:

$\min {\delta }^{IC}+{\delta }_{T,c}^{OP}+{\delta }_{T,l}^{OP}+{\delta }_{T,r}^{OP}+{\delta }_{D,c}^{OP}+{\delta }_{D,l}^{OP}+{\delta }_{D,r}^{OP}(1)$

The symbols in the equation represent the following costs: ${\delta }^{IC}$ represents the investment and construction cost for the distribution network; ${\delta }_{T,c}^{OP}$ represents the conventional generation cost for the transmission network; ${\delta }_{T,l}^{OP}$ represents the loss of load penalty cost for the transmission network; ${\delta }_{T,r}^{OP}$ represents the curtailment cost of renewable energy for the transmission network; ${\delta }_{D,c}^{OP}$ represents the conventional generation cost for the distribution network; ${\delta }_{D,l}^{OP}$ represents the loss of load penalty cost for the distribution network; ${\delta }_{D,r}^{OP}$ represents the curtailment cost of renewable energy for the distribution network.

1) Investment and construction costs for the distribution network ${\delta }^{IC}$.

${\delta }^{IC}={\displaystyle \sum _{c\in C^{IC}}}{u}_{IC,c}{b}_c(2)$

The symbols in the equation are defined as follows: $u_{IC,c}$ is the investment cost for building cable in the distribution network; $b_c$ is the decision variable for investing and constructing cables in the distribution network, which is a 0-1 variable and indexed by the index of the cable to be built; $C^{IC}$ is the set of lines to be invested and constructed.

2) Conventional generation cost for the transmission network ${\delta }_{T,c}^{OP}$.

${\delta }_{T,c}^{OP}={\displaystyle \sum _{s\in S}}{\gamma }_{s,c}{\displaystyle \sum _{\forall t\in T}}{\displaystyle \sum _{i\in N_T}}{c}_{i,s}^c{P}_{i,t,s}^c(3)$

In the equation, $S$ represents the set of scenarios; $s$ is the index of the scenario; ${\gamma }_{s,c}$ is the weight of the conventional generator scenario; $T$ represents the set of time sections; $t$ is the index of the time section; $N_T$ represents the set of nodes in the transmission network; $i$ is the index of the node; $c_{i,s}^c$ represents the unit generation cost of the conventional generator at node $i$ under scenario $s$; and $P_{i,t,s}^c$ represents the output of the conventional generator at time $t$ under scenario $s$.

3) Loss of load penalty cost for the transmission network ${\delta }_{T,l}^{OP}$.

${\delta }_{T,l}^{OP}={\displaystyle \sum _{s\in S}}{\gamma }_{s,l}{\displaystyle \sum _{\forall t\in T}}{\displaystyle \sum _{i\in N_T}}{c}_{i,s}^l{P}_{i,t,s}^l(4)$

In the formula, ${\gamma }_{s,l}$ represents the weight of the loss scenario, $c_{i,s}^l$ represents the unit loss cost at the node $i$ under the scenario $s$, and $P_{i,t,s}^l$ represents the amount of loss at the moment $t$ under the scenario $s$.

4) Curtailment cost of renewable energy for the transmission network ${\delta }_{T,l}^{OP}$.

${\delta }_{T,r}^{OP}={\displaystyle \sum _{s\in S}}{\gamma }_{s,r}{\displaystyle \sum _{\forall t\in T}}{\displaystyle \sum _{i\in N_T}}{c}_{i,s}^r\left(P_{i,t,s}^{r,\max }-P_{i,t,s}^r\right)(5)$

In the equation, ${\gamma }_{s,r}$ represents the scenario weight for renewable energy, $c_{i,s}^r$ represents the unit abandonment cost of renewable energy for the node $i$ in the scenario $s$, $P_{i,t,s}^{r,\max }$ represents the maximum output of renewable energy at the node $i$ during the time period $t$ in the scenario $s$, and $P_{i,t,s}^r$ represents the output of renewable energy at the node $i$ during the time period $t$ in the scenario $s$.

5) Conventional generation cost for the distribution network ${\delta }_{D,c}^{OP}$.

${\delta }_{D,c}^{OP}={\displaystyle \sum _{s\in S}}{\gamma }_{s,c}{\displaystyle \sum _{\forall t\in T}}{\displaystyle \sum _{i\in N_D}}{c}_{i,s}^c{P}_{i,t,s}^c(6)$

In the equation, $N_D$ is the set of distribution network nodes.

6) Loss of load penalty cost for the distribution network ${\delta }_{D,l}^{OP}$.

${\delta }_{D,l}^{OP}={\displaystyle \sum _{s\in S}}{\gamma }_{s,l}{\displaystyle \sum _{\forall t\in T}}{\displaystyle \sum _{i\in N_D}}{c}_{i,s}^l{P}_{i,t,s}^l(7)$

7) Curtailment cost of renewable energy for the distribution network ${\delta }_{D,r}^{OP}$.

${\delta }_{D,r}^{OP}={\displaystyle \sum _{s\in S}}{\gamma }_{s,r}{\displaystyle \sum _{\forall t\in T}}{\displaystyle \sum _{i\in N_D}}{c}_{i,s}^r\left(P_{i,t,s}^{r,\max }-P_{i,t,s}^r\right)(8)$

2.2 Constraints

The transmission constraints are described below.

1) Power balance equation for transmission network nodes.

$P_{i,t,s}^c+P_{i,t,s}^l+P_{i,t,s}^r+{\displaystyle \sum _{l\in L_i^e}}{P}_{l,t,s}^f={\displaystyle \sum _{l\in L_i^h}}{P}_{l,t,s}^f+D_{i,t,s},i\in N_T,\forall t,\forall s(9)$

In the equation, $L_i^e$ represents the set of lines connected to node $i$ as the ending point, $L_i^h$ represents the set of lines connected to node $i$ as the starting point, $P_{l,t,s}^f$ represents the flow on line $l$, $D_{i,t,s}$ represents the load at node $i$, and the subscript $l$ represents the index of the line.

2) Power flow equation of transmission network.

$P_{l,i,t,s}^f=B_l\left({\theta }_{t,s}^h-{\theta }_{t,s}^e\right),l\in L^T,\forall t,\forall s(10)$

In the equation, $P_{l,i,t,s}^f$ represents the flow of line $l$, $B_l$ is the reciprocal of the reactance of line $l$, ${\theta }_{t,s}^h$ and ${\theta }_{t,s}^e$ are the phase angles of the starting node and the ending node of line $l$, respectively. $L^T$ is the set of transmission lines in the power grid.

3) Transmission network line capacity constraints.

$P^{f,\min }\le P_{l,i,t,s}^f\le P^{f,\max },l\in L^T,i\in N_T,\forall t,\forall s(11)$

Where: $P^{f,\max }$ and $P^{f,\min }$ are the upper and lower limits of the line transmission power.

4) Generation output constraints in transmission network.

$P_i^{c,\min }\le P_{i,t,s}^c\le P_i^{c,\max },i\in N_T,\forall t,\forall s(12)$

${\vartheta }^{-}{P}_i^{c,\max }\le P_{i,t,s}^c-P_{i,t-1,s}^c\le {\vartheta }^{+}{P}_i^{c,\max },i\in N_T,\forall t,\forall s(13)$

$P_i^{r,\min }\le P_{i,t,s}^r\le P_i^{r,\max },i\in N_T,\forall t,\forall s(14)$

Where: $P_i^{c,\max }$ and $P_i^{c,\min }$ are the upper and lower limits of conventional generation output at node; ${\vartheta }^{+}$ and ${\vartheta }^{-}$ are the maximum change ranges of conventional generation output within a time interval, expressed as a percentage of unit capacity; $P_i^{r,\max }$ and $P_i^{r,\min }$ are the upper and lower limits of renewable generation output.

5) Transmission network load shedding constraint.

$0\le P_{i,t,s}^l\le P_{i,t,s}^{l.\max },i\in N_T,\forall t,\forall s(15)$

In the equation, $P_{i,t,s}^{l.\max }$ represents the maximum load shedding capacity at node $i$.

The distribution constraints are described below.

1) Power balance equation for distribution network nodes.

$P_{i,t,s}^c+P_{i,t,s}^l+P_{i,t,s}^r+{\displaystyle \sum _{l\in L_i^e}}\left(P_{l,t,s}^f-r_l{\iota }_{l,t,s}\right)={\displaystyle \sum _{l\in L_i^h}}{P}_{l,t,s}^f,i\in N_D,\forall t,\forall s(16)$

$Q_{i,t,s}^c+Q_{i,t,s}^r+{\displaystyle \sum _{l\in L_i^e}}\left(Q_{l,t,s}^f-x_l{\iota }_{l,t,s}\right)={\displaystyle \sum _{l\in L_i^h}}{Q}_{l,t,s}^f,i\in N_D,\forall t,\forall s(17)$

${\iota }_{l,t,s}={\left|I_{l,t,s}\right|}^2,\forall l\in L_D,\forall t,\forall s(18)$

In the equation: $Q_{i,t,s}^c$ and $Q_{i,t,s}^r$ are the reactive power output of conventional generators and renewable energy generators, respectively; $Q_{l,t,s}^f$ is the reactive power flow on the line; $r_l$ and $x_l$ are the resistance and reactance of the line, respectively; $I_l$ is the current on the line; $L_D$ is the set of distribution network lines; $l$ is the line index.

2) Distribution network node voltage equation.

$v_{l,t,s}^e=v_{l,t,s}^h-2\left(r_l{P}_{l,i,t,s}^f+x_l{Q}_{l,i,t,s}^f\right)+\left(r_l^2+x_l^2\right){\iota }_{l,t,s},\forall l\in L_D,\forall t,\forall s(19)$

$v_{l,t,s}={\left|V_{l,t,s}\right|}^2,\forall l\in L_D,\forall t,\forall s(20)$

In the equation, $v_{l,t,s}^h$ and $v_{l,t,s}^e$ represent the squared voltage magnitudes at the starting and ending nodes of line $l$, respectively.

3) Power flow equation of transmission network.

${\iota }_{l,t,s}=\frac{{\left(P_{l,t.s}^f\right)}^2+{\left(Q_{l,t.s}^f\right)}^2}{v_{l,t,s}},\forall l\in L_D,\forall t,\forall s(21)$

4) Upper and lower voltage limits for distribution network nodes.

$V^{\min }\le V_{l,t,s}\le V^{\max },\forall l\in L_D,\forall t,\forall s(22)$

Where: $V^{\max }$ and $V^{\min }$ are the upper and lower limits of the distribution network node voltage, respectively.

5) Distributed generation output constraints in transmission network.

$P_i^{c,\min }\le P_{i,t,s}^c\le P_i^{c,\max },i\in N_D,\forall t,\forall s(23)$

${\vartheta }^{-}{P}_i^{c,\max }\le P_{i,t,s}^c-P_{i,t-1,s}^c\le {\vartheta }^{+}{P}_i^{c,\max },i\in N_D,\forall t,\forall s(24)$

$P_i^{r,\min }\le P_{i,t,s}^r\le P_i^{r,\max },i\in N_D,\forall t,\forall s(25)$

6) Distribution network load shedding constraint.

$0\le P_{i,t,s}^l\le P_{i,t,s}^{l.\max },i\in N_D,\forall t,\forall s(26)$

The substation constraints are described below.

1) Power balance equation for substation network nodes.

$P_{i,t,s}^c+P_{i,t,s}^l+P_{i,t,s}^r+{\displaystyle \sum _{l\in L_i^e}}{P}_{l,t,s}^f={\displaystyle \sum _{l\in L_i^h}}{P}_{l,t,s}^f+D_{i,t,s},i\in N_S,\forall t,\forall s(27)$

Where: $N_S$ represents the set of substation nodes.

2) Local generation output constraints in substation network.

$P_i^{c,\min }\le P_{i,t,s}^c\le P_i^{c,\max },i\in N_S,\forall t,\forall s(28)$

${\vartheta }^{-}{P}_i^{c,\max }\le P_{i,t,s}^c-P_{i,t-1,s}^c\le {\vartheta }^{+}{P}_i^{c,\max },i\in N_S,\forall t,\forall s(29)$

3 Solution method

3.1 Construction of a collaborative operation model for transmission and distribution

In traditional DNP, the transmission network and substations are treated as infinite power sources. In collaborative planning between the transmission and distribution networks, a network model is established for the transmission network, including line flows, distributed generation units, and renewable energy, to reflect the real-time operating status of the transmission network. To achieve optimized calculation of the collaborative operation between transmission and distribution, variable exchange is required at the transmission-distribution boundary to achieve the optimal dispatch under the given planning scheme. The construction of the collaborative operation optimization model between transmission and distribution is shown in the following equation:

$\left\{\begin{array}{l}\min O_T^c\left(c_T^v,x_T^v,x_S^v\right)+O_D^c\left(c_D^v,x_D^v,x_S^v\right)\\ g_T\left(c_T^v,x_T^v,x_S^v\right)\ge 0\to {\mu }_T\\ h_T\left(c_T^v,x_T^v,x_S^v\right)=0\to {\lambda }_T\\ g_D\left(c_D^v,x_D^v,x_S^v\right)\ge 0\to {\mu }_D\\ h_D\left(c_D^v,x_D^v,x_S^v\right)=0\to {\lambda }_D\\ g_S\left(c_S^v,x_S^v\right)\ge 0\to {\mu }_S\\ h_S\left(c_D^v,x_D^v,x_T^v,x_S^v\right)=0\to {\lambda }_S\end{array}\right.(30)$

In the equation, $O_T^c\left(c_T^v,x_T^v,x_S^v\right)$ represents the operational cost of the transmission network, corresponding to Eqs 2–4; $O_D^c\left(c_D^v,x_D^v,x_S^v\right)$ represents the operational cost of the distribution network, corresponding to Eqs 5–7; $g$ and $h$ respectively correspond to inequality constraints and equality constraints; $\mu$ and $\lambda$ correspond to Lagrange multipliers for inequality constraints and equality constraints. $c^v$ and $x^v$ represents control variables and represents state variables.

Operating model, the “node splitting” concept is used, and auxiliary functions for the injection of power from substations into the distribution network $y_{SD}$ , the injection of power from the transmission network region into the substation region $f_{TS}$ , and the injection of power from the substation region into the distribution network region $f_{SD}$ are introduced. Therefore, Eq. 27 can be decomposed into the power constraint for the injection of power from the transmission network region into the substation region Eq. 32 and the power constraint for the injection of power from the substation region into the distribution network region Eq. 33. The abstract expression of Eq. 27 is shown in Eq. 31.

$h_S\left(c_D^v,x_D^v,x_T^v,x_S^v\right)=0(31)$

$f_{TS}\left(c_S^v,x_T^v,x_S^v\right)=y_{SD}(32)$

$f_{SD}\left(x_T^v,x_S^v\right)=y_{SD}(33)$

The Lagrange function of Eq. 30 can be expressed as

$\begin{array}{l}L=O_T^c\left(c_T^v,x_T^v,x_S^v\right)+O_D^c\left(c_D^v,x_D^v,x_S^v\right)+{\mu }_T^T{g}_T+{\lambda }_T^T{h}_T+{\mu }_D^T{g}_D+{\lambda }_D^T{h}_D+{\mu }_S^T{g}_S+{\lambda }_{TS}^T\left(f_{TS}-y_{SD}\right)+{\lambda }_{SD}^T\left(y_{SD}-f_{SD}\right)\end{array}(34)$

Further, the Karush Kuhn Tucher (KKT) condition can be expressed as.

1) The partial derivative of each variable is equal to 0;

2) Satisfying equality and inequality constraints;

3) The complementary relaxation condition is satisfied.

3.2 Solution for the collaborative operation model for transmission and distribution

The planning model algorithm utilizes the HGD algorithm for solving. The solving approach is as follows:

The coordinated operation model of transmission and distribution (30) can be decomposed into the sub-model of transmission network operation optimization and the sub-model of distribution network operation optimization with the aid of auxiliary functions. The auxiliary functions are used to ensure that the optimization objectives of the two sub-models after decomposition are consistent with the optimization objective of the original model.

Specifically, the sub-model of transmission network operation optimization can be represented by Eq. 35, and the sub-model of distribution network operation optimization can be represented by Eq. 36.

$\begin{array}{l}\min O_T^c\left(c_T^v,x_T^v,x_S^v\right)+A_T\\ \mathrm{s}.\mathrm{t}.\left(c_T^v,c_S^v,x_T^v,x_S^v\right)\in D_T(y_{SD}^{*})\end{array}(35)$

$\begin{array}{l}\min O_D^c\left(c_D^v,x_D^v,{x_S^v}^{*}\right)+A_D\\ \mathrm{s}.\mathrm{t}.\left(c_D^v,x_D^v,y_{SD}\right)\in D_D\left({x_S^v}^{*}\right)\end{array}(36)$

In the equations: $D_T\left(y_{SD}^{*}\right)$ represents the feasible domain of the sub-model of transmission network operation optimization while $y_{SD}=y_{SD}^{*};$$D_D\left({x_S^v}^{*}\right)$ represents the feasible domain of the sub-model of distribution network operation optimization while $x_S^v={x_S^v}^{*}$; $A_T$ and $A_D$ are auxiliary functions introduced into the decomposed optimization model to ensure the optimality condition of the original model is satisfied.

To satisfy the optimality condition, the auxiliary function should satisfy the following equation:

$\left\{\begin{array}{l}{A}_T\left(x_S\right)=h_{BD}^T{x}_S\\ A_D\left(y_{SD}\right)={\lambda }_{TS}^T{y}_{SD}\end{array}\right.(37)$

Where:

$h_{SD}=\frac{\partial O_D^c}{\partial x_S^v}+\frac{\partial h_D^T}{\partial x_S^v}{\lambda }_D+\frac{\partial g_D^T}{\partial x_S^v}{\mu }_D+\frac{\partial f_{SD}^T}{\partial x_S^v}{\lambda }_{SD}(38)$

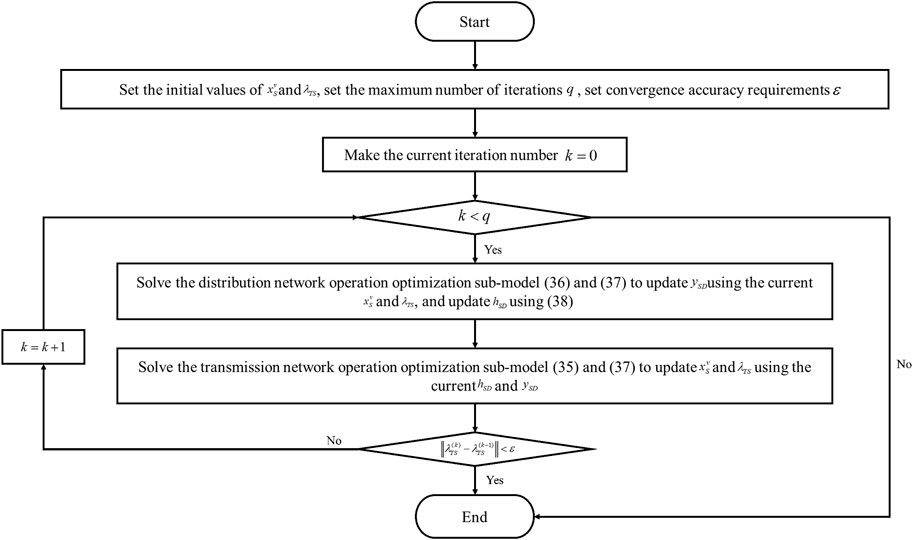
The HGD algorithm solves the operation optimization models of transmission and distribution networks alternately through iterations until the physical quantities related to the boundary region converge. The specific steps for solving the coordinated operation model of transmission and distribution using the HGD algorithm are shown in Figure 2.

FIGURE 2

FIGURE 2. HGD algorithm flowchart.

3.3 Construction and optimization of DNP agent model for coordinated operation of transmission and distribution based on convolutional neural network

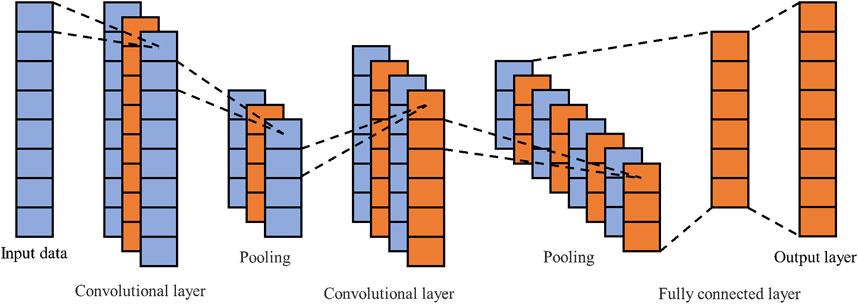
CNN is one of the classical algorithms in deep learning. Its internal structure uses weight sharing and local connectivity, which enables CNN to effectively extract deep-level features contained in data while reducing algorithm complexity. CNN mainly consists of a convolutional layer that performs convolution calculation on the data and extracts potential features and a pooling layer that downsamples and compresses network parameters. The alternating use of convolutional and pooling layers can effectively extract the potential features of the input data and reduce the errors caused by manual feature extraction. The structure diagram of one-dimensional CNN is shown in Figure 3.

FIGURE 3

FIGURE 3. CNN structure diagram.

The construction and solution of the coordinated operation model for the transmission and distribution system described in Section 3.1, Section 3.2 can output the optimal operating cost for a given planning scheme. Combined with the investment and construction cost of the distribution network corresponding to the planning scheme, as shown in Eq. 2, the total cost of the scheme can be obtained. In practical engineering problems, the feasible planning schemes for the stock planning of the distribution network are generated from a planning problem library accumulated over some time. Therefore the number of feasible planning schemes is often limited. In addition, considering the large scale of the distribution network, the introduction of nonlinear constraints in the distribution network power flow, and the growth in the number of operating scenarios, calculating the total cost for each feasible planning scheme and seeking optimization will increase the time and space complexity. However, each planning scheme corresponds to a topological structure of the distribution network, which an adjacency matrix can intuitively represent. Therefore, a convolutional neural network can be introduced to map the topological structure of the distribution network to the total cost, constructing a proxy model for the complex coordinated operation model of the transmission and distribution system and achieving rapid optimization of the total cost for a limited number of planning schemes.

4 Case study

4.1 Case construction

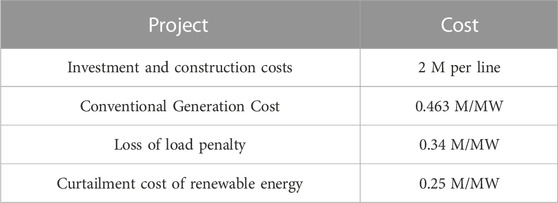
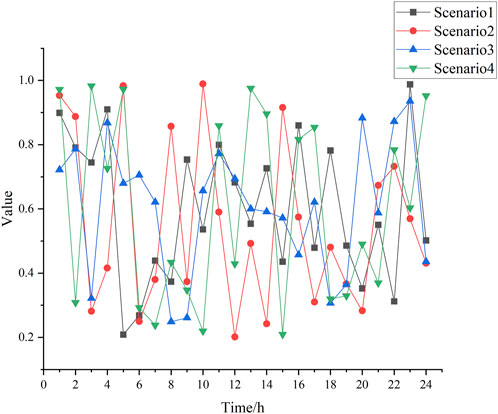
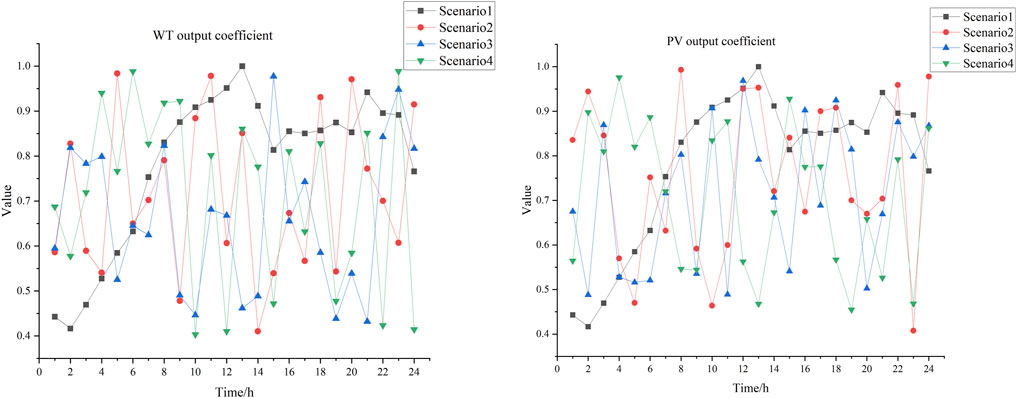
The IEEE transmission network test case CASE 30 and IEEE distribution network test case CASE 69 are concatenated. Specifically, node 30 of CASE 30 is connected to the root node of CASE 69 via a single substation node. The voltage amplitude upper and lower limits for each node in the distribution network are 1.1 p. u. and 0.9 p. u., respectively. In the transmission network test case CASE 30, nodes 1, 2, 22, 23, and 27 are connected to conventional thermal power generation units, while nodes 3, 4, and 6 are connected to renewable energy generation units. In the distribution network test case CASE 69, some nodes are connected to local conventional power generation units and distributed renewable energy sources, whose parameters are listed in Table 1. The costs are showed in Table 2. The load coefficients and renewable energy unit output coefficients are shown in Figures 4, 5. All calculations are performed by Gurobi 10.0.2 API for Python on an Intel Core I7 11700F 2.5 GHz processor.

TABLE 1

TABLE 1. Distributed renewable energy parameters for distribution network.

TABLE 2

TABLE 2. Construction and operation costs.

FIGURE 4

FIGURE 4. Load factor.

FIGURE 5

FIGURE 5. Renewable energy output coefficient.

4.2 Example results and analysis

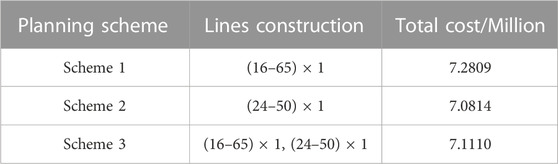
The proposed lines to be built in this case study are (24–50), (24–52), (16–50), (16–65), (16–69), (50–65), (30–52), (28–60), (50–60), and (18–67), which can generate a total of 1024 planning schemes through permutation and combination. The total costs of some planning schemes, calculated by the model described in Chapter 3, are shown in Table 3.

TABLE 3

TABLE 3. Planning schemes and total costs.

From Table 3, it can be seen that three planning schemes can be generated by selecting Line (16–35) and Line (24–50), among which the planning scheme that only constructs Line (24–50) has the lowest total cost. The planning scheme that constructs both Line (16–35) and Line (24–50) is the second cheapest, followed by the planning scheme that only constructs Line (16–35). In the four typical scenarios constructed in this paper, operating costs account for a relatively large proportion of the total cost of the planning scheme. As the number of typical scenarios inputted further increases, the proportion of operating costs in the total cost of the planning scheme will also increase. Theoretically, the more typical scenarios are inputted, the more the planning scheme can reflect its impact on the actual operating costs of various levels of power grids.

Considering the number of typical scenarios increases and the granularity of a single scenario in practical engineering applications as the transmission and distribution network scale increases, the time and space complexity of a single operation of the HGD algorithm, which is mainly based on iterative calculations, will increase significantly. Reducing the calls to the HGD algorithm in the solution algorithm is a vital optimization direction. At this point, the transmission and distribution coordinated operation model has a clear input-output relationship with the planning scheme-total cost. Building a convolutional neural network proxy model can simplify the planning model by “making the complicated simple.”

Selecting the planning schemes to form the training and testing sets, the two-dimensional description of the adjacency matrix corresponding to the planning scheme is extracted as the carrier form of the input of the convolutional neural network. The comparison of the computation speed and accuracy between the trained convolutional neural network proxy model and the original model is shown in Table 4. Both the directly solved optimal construction scheme and the optimal construction scheme found by the neural network proxy model are to invest in line (24–50) and (24–52). Furthermore, the computation time for individual optimization is provided, demonstrating an advantage in computation time. However, its results lack reference value.

TABLE 4

TABLE 4. Comparison of solution methods.

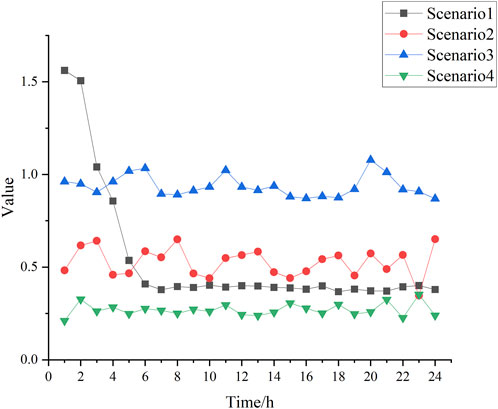
As seen from Table 4, the DNP model that coordinates with the transmission network for optimization will consume a significant amount of time and computing power, even for small-scale network models. However, training a convolutional neural network proxy model makes it possible to achieve optimal planning solutions that meet the required precision by calling multi-iteration solving algorithms on a small scale. Using a convolutional neural network proxy model can effectively capture the topological characteristics corresponding to the planning solutions, map them to the total cost with high precision, and quickly optimize the exponential number of planning solutions composed of numerous lines to be constructed. The optimal solution corresponds to the boundary node line flow of the substation, as shown in Figure 6.

FIGURE 6

FIGURE 6. Boundary substation power flow.

Based on Figure 6, it can be seen that the objective function is constructed with the abandoned energy cost of renewable energy sources. This is reflected in the optimization results by the low power flow values at the boundary nodes of the substation, indicating that the active power injected into the distribution network from the transmission network is relatively low. As a result, the distribution network load is mainly provided by local units and distributed renewable energy output.

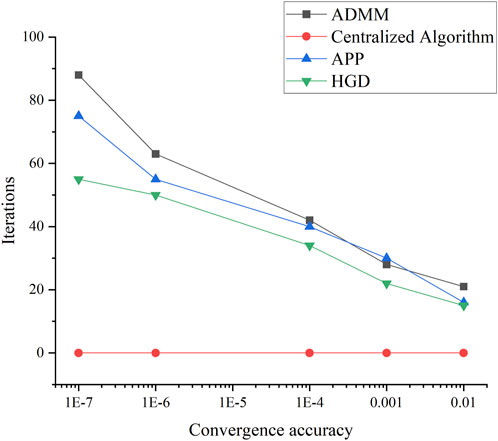
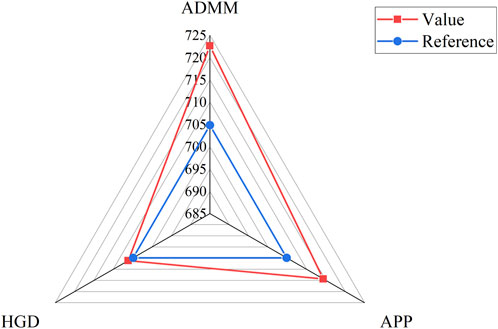
In order to validate the applicability of the algorithm, a comparison between centralized and distributed algorithms was conducted in the given case study. The distributed algorithms included the ADMM and the APP (Auxiliary Problem Principle) methods. Additionally, a comparison of optimization results was performed using a collaborative optimization model involving continuous variables in transmission and distribution systems. The iteration counts for algorithms with varying convergence accuracy are depicted in Figure 7, while the optimization results for different algorithms are presented in Figure 8.

FIGURE 7

FIGURE 7. Iteration counts for algorithms with varying convergence accuracy.

FIGURE 8

FIGURE 8. The optimization results for different algorithms.

From Figures 7, 8 it is evident that the HGD algorithm exhibits a robust convergence performance compared to other commonly used decomposition algorithms. The iteration count of the HGD algorithm is minimally affected by the convergence accuracy. On the other hand, the iteration counts of the ADMM and APP algorithms are significantly influenced by the convergence accuracy; under higher convergence accuracy requirements, their iteration counts are much greater than those of the HGD algorithm employed in this study. When considering the directly solved centralized algorithm as a benchmark, the HGD algorithm demonstrates a more minor computational error by up to 2.34%.

Furthermore, decomposition algorithms like ADMM and APP necessitate the tuning of several constant parameters, the selection of which directly impacts the algorithm’s convergence performance. The optimization and tuning of these parameters also require manual adjustments. In comparison, the HGD algorithm eliminates the need for parameter setting, resulting in stable convergence performance.

5 Conclusion

To adapt to the scenario of high-penetration renewable energy integration into the power grid, where the source-load roles in the operational perspective of transmission and distribution networks are blurred, and to conduct DNP with greater precision, this paper proposes a distribution network planning method based on the integration of operation and planning and coordinated with the transmission network. This method constructs operational models for both the transmission and distribution networks and substation, as well as a planning model for the distribution network. The optimization model with continuous variables is decomposed and solved using the HGD algorithm. To overcome the challenges of optimizing models with integer variables, this paper constructs a distribution network correlation matrix to represent its topological connections for the integer part optimization model and employs a CNN surrogate model for global optimization.

Results from case studies constructed using IEEE 30 and IEEE 69 indicate that the proposed solving method reduces computation time by 43.91% compared to direct solving using centralized algorithms, with an error of only 0.18% from the direct solving results. The HGD algorithm used in this study, when compared to other distributed algorithms like ADMM and APP, achieves convergence with significantly fewer iterations while maintaining the same accuracy level. Additionally, the optimization results using HGD algorithm show a reduction in computation error by 2.34% compared to the mentioned distributed algorithms. The proposed method improves solving efficiency and reduces computation errors to a certain extent, demonstrating its value for engineering applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZC: Supervision, Writing–original draft, Writing–review and editing. KY: Supervision, Writing–original draft, Writing–review and editing. XG: Supervision, Writing–original draft, Writing–review and editing. ZX: Supervision, Writing–original draft, Writing–review and editing. JH: Writing–original draft, Writing–review and editing. WW: Software, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article.

The authors declare that this study received funding from the Special Research Project of Electric Power Planning “Research on the Global Planning Method of Power System Based on Digital Twin Technology (Project number: 030400QQ00220003)”, Guangdong Grid Co. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors ZC, KY, XG, and ZX were employed by the company Zhuhai Power Supply Bureau of Guangdong Power Grid Co., Ltd. Author WW was employed by the company Guangzhou Shuimu Qinghua Technology Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1261028/full#supplementary-material

References

Kargarian, A., and Fu, Y. (2014). System of systems based security-constrained unit commitment incorporating active distribution grids. IEEE Trans. Power Syst. 29 (5), 2489–2498. doi:10.1109/tpwrs.2014.2307863

CrossRef Full Text | Google Scholar

Li, Z., Guo, Q., Sun, H., and Wang, J. (2018b). A new LMP-sensitivity-based heterogeneous decomposition for transmission and distribution coordinated economic dispatch. IEEE Trans. Smart Grid 9 (2), 931–941. doi:10.1109/tsg.2016.2571848

CrossRef Full Text | Google Scholar

Li, Z., Guo, Q., Sun, H., and Wang, J. (2016). Coordinated economic dispatch of coupled transmission and distribution systems using heterogeneous decomposition. IEEE Trans. Power Syst. 31 (6), 4817–4830. doi:10.1109/tpwrs.2016.2515578

CrossRef Full Text | Google Scholar

Li, Z., Guo, Q., Sun, H., and Wang, J. (2018a). Coordinated transmission and distribution AC optimal power flow. IEEE Trans. Smart Grid 9 (2), 1228–1240. doi:10.1109/tsg.2016.2582221

CrossRef Full Text | Google Scholar

Lin, C., Wu, W., Shahidehpour, M., Guo, Y., and Wang, B. (2020). A non-iterative decoupled solution of the coordinated robust OPF in transmission and distribution networks with variable generating units. IEEE Trans. Sustain. Energy 11 (3), 1579–1588. doi:10.1109/tste.2019.2931908

CrossRef Full Text | Google Scholar

Lin, C., Wu, W., Zhang, B., Wang, B., Zheng, W., and Li, Z. (2017). Decentralized reactive power optimization method for transmission and distribution networks accommodating large-scale DG integration. IEEE Trans. Sustain. Energy 8 (1), 363–373. doi:10.1109/tste.2016.2599848

CrossRef Full Text | Google Scholar

Liu, D., Liu, L., Cheng, H., Li, A., Li, G., Zhang, X. K. L. o. C. o. P. T., et al. (2021). Transmission expansion planning coordinated with distribution networks based on generalized master-slave splitting theory. Proc. CSEE 41 (17), 5856–5866. doi:10.13334/j.0258-8013.pcsee.201322

CrossRef Full Text | Google Scholar

Liu, H., Liu, S., Gai, X., Liu, Y., and Yan, Y. (2022). Review of active distribution network planning with high proportion renewable energy. Power Gener. Technol., 1–13. Available at: http://kns.cnki.net/kcms/detail/33.1405.TK.20230213.1059.002.html (accessed August 18, 2023).

Google Scholar

Lotfi, H., Ghazi, R., and Naghibi-Sistani, M. b. (2020). Multi-objective dynamic distribution feeder reconfiguration along with capacitor allocation using a new hybrid evolutionary algorithm. Energy Syst. 11 (3), 779–809. doi:10.1007/s12667-019-00333-3

CrossRef Full Text | Google Scholar

Lotfi, H., and Ghazi, R. (2021). Optimal participation of demand response aggregators in reconfigurable distribution system considering photovoltaic and storage units. J. Ambient Intell. Humaniz. Comput. 12 (2), 2233–2255. doi:10.1007/s12652-020-02322-2

CrossRef Full Text | Google Scholar

Lotfi, H. (2020). Multi-objective energy management approach in distribution grid integrated with energy storage units considering the demand response program. Int. J. Energy Res., 44(13), 10662–10681. doi:10.1002/er.5709

CrossRef Full Text | Google Scholar

Lotfi, H. (2022). Optimal sizing of distributed generation units and shunt capacitors in the distribution system considering uncertainty resources by the modified evolutionary algorithm. J. Ambient Intell. Humaniz. Comput. 13 (10), 4739–4758. doi:10.1007/s12652-021-03194-w

CrossRef Full Text | Google Scholar

Lotfi, H., and Shojaei, A. A. (2022). A dynamic model for multi-objective feeder reconfiguration in distribution network considering demand response program. Energy Syst. doi:10.1007/s12667-022-00507-6

CrossRef Full Text | Google Scholar

Loukarakis, E., Dent, C. J., and Bialek, J. W. (2016). Decentralized multi-period economic dispatch for real-time flexible demand management. IEEE Trans. Power Syst. 31 (1), 672–684. doi:10.1109/tpwrs.2015.2402518

CrossRef Full Text | Google Scholar

Mohammadi, A., Mehrtash, M., and Kargarian, A. (2019). Diagonal quadratic approximation for decentralized collaborative TSO+DSO optimal power flow. IEEE Trans. Smart Grid 10 (3), 2358–2370. doi:10.1109/tsg.2018.2796034

CrossRef Full Text | Google Scholar

Nawaz, A., and Wang, H. (2021). Distributed stochastic security constrained unit commitment for coordinated operation of transmission and distribution system. CSEE J. Power Energy Syst. 7 (4), 11. doi:10.17775/CSEEJPES.2020.02150

CrossRef Full Text | Google Scholar

Sun, Y. (2019). Research on distributed reactive power optimization method for the integrated power transmission and distribution systems considering static voltage security constraints. Jinan, China: Shandong University. https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201902andfilename=1019043093.nh

Google Scholar

Tang, K., Dong, S., Ma, X., Lv, L., and Song, Y. (2021). Chance-Constrained optimal power flow of integrated transmission and distribution networks with limited information interaction. IEEE Trans. Smart Grid 12 (1), 821–833. doi:10.1109/tsg.2020.3021829

CrossRef Full Text | Google Scholar

Wang, C., Wang, R., Yu, H., Song, Y., Yu, L., and Li, P. (2020a). Challenges on coordinated planning of smart distribution networks driven by source network-load evolution. Proc. ofthe CSEE 40 (08), 2385–2396. doi:10.13334/j.0258-8013.pcsee.191699

CrossRef Full Text | Google Scholar

Wang, J., Li, Q., Wang, X., Huang, Q., Liu, S., Qian, T., et al. (2020b). A generation expansion planning method for power systems with large-scale new energy. Proc. CSEE 40 (10), 3114–3124. doi:10.13334/j.0258-8013.pcsee.190011

CrossRef Full Text | Google Scholar

Wang, X. (2015). Static voltage security assessrent and reactive power optimization in joint power transmission and distribution systems. Jinan, China: Shandong University. https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201601andfilename=1015370737.nh

Google Scholar

Xie, D., Liu, M., and Xu, L. (2023). Review and prospect of transmission-distribution Co-optimization of power systems with distributed energy resources. South. Powe Syst. Technol. 17 (04), 25–37. doi:10.13648/j.cnki.issn1674-0629.2023.04.003

CrossRef Full Text | Google Scholar

Yu, J., Li, Z., Guo, Y., and Sun, H. (2019). Decentralized chance-constrained economic dispatch for integrated transmission-district energy systems. IEEE Trans. Smart Grid 10 (6), 6724–6734. doi:10.1109/tsg.2019.2910757

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, Y., Ji, X., Han, X., Yang, M., and Xu, B. (2022a). Synergetic optimized scheduling of transmission and distribution network with electricity-gas-heat integrated energy system. Power Syst. Technol. 46 (11), 4256–4270. doi:10.13335/j.1000-3673.pst.2021.2065

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, X., Ji, X., Han, X., Wang, C., and Yu, Y. C. (2022b). Synergetic unit commitment of transmission and distribution network considering dynamic characteristics of electricity-gas-heat integrated energy system. Proc. CSEE 42 (23), 8576–8592. doi:10.13334/j.0258-8013.pcsee.212034

CrossRef Full Text | Google Scholar

Zhao, J., Zhang, Z., Yao, J., Yang, S., and Wang, K. (2019). Heterogeneous decomposition based distributed reactive power optimization method for global transmission and distribution network. Automation Electr. Power Syst. 43 (03), 108–115. doi:10.7500/AEPS20180111009

CrossRef Full Text | Google Scholar

Zuo, J., Tang, J., Zhong, W., Yang, D., Li, X., and Ma, R.School of, E., Information Engineering, C. U. o. S., and Technology (2020). Multi-objective dynamic random fuzzy optimal power flow of wind integrated power system considering the interaction of transmission-distribution system. J. Electr. Power Sci. Technol. 35 (01), 50–60. doi:10.19781/j.issn.1673-9140.2020.01.006

CrossRef Full Text | Google Scholar