Analysis and modeling magnetic energy harvester with field shaping capacitors

A detailed circuit model is discussed in this paper for the operation of magnetic energy harvesters with field shaping capacitors (FSC) feeding constant voltage load. First an equivalent circuit with nonlinear inductance, current source and a diode bridge was given based on the physical analysis of the harvester. Then detailed analysis of the circuit operation and state transitions under various FSC are provided. A mathematical model is established to replace the circuit model so that the optimization of the system parameters, such as number of turns, load voltage, could be carried out directly. Simulation and experimental results are given in the paper to prove the effectiveness of the proposed circuit analysis method.

1 Introduction

The smart grid requires distributed real-time monitoring network to actively sense the states, to define the problems of the power system, to discover knowledge, and to solve the problems Zhang et al. (2021). This means that more and more smart sensor grids need to be integrated into the power system and its apparatus. Even though the power consumption of both the sensors and the microelectronic chips has decreased in the last decades, life long energy supply is still one of the biggest challenges for the widely distributed and wirelessly enabled sensor systems Moon et al. (2013). A cost-effective and self-sustained smart sensing node system uses energy harvesting to convert ambient energy sources into electric power to supply the electronic systems (Sudevalayam and Kulkarni, 2011; Tang et al., 2018). A variety kinds of energy sources Tang et al. (2018), for example, vibrations Ottman et al. (2002), RF energy Facen and Boni (2006), corona current Shi et al. (2023), thermal and solar Tan and Panda (2011), could be utilized with different techniques, but magnetic energy harvesters based on electromagnetic induction is still the most reliable and cost-effective way to extract energy from the power system itself (Moon et al., 2013; White et al., 2018). The power line goes through the center of a magnetic core and the 50 or 60 Hz alternating current in the power line will induce voltage on the secondary side, similar manner with a current transformer. What is different with a current transformer is that the output of the secondary winding is feeding a low impedance load to extract energy. Usually a rectifier is followed to converter the AC voltage to DC so that it can power the sensors and microelectronics.

One of the most challenging problems for the magnetic energy harvester is the magnetic saturation when the transmission line current is high. Reference Moon and Leeb (2015a) and Moon and Leeb (2015b) have developed a circuit model incorporating the nonlinear behaviour of the core to model and predict the harvester system performance. In the analysis of Moon and Leeb (2015a) and Moon and Leeb (2015c), a constant voltage load other than a pure resistor was used as the load of the energy harvester system, which is of much more practical meaning since the energy harvested is usually used to charge a battery or supercapacitor load. Several groups continued to research on utilizing the saturation region of the core Park et al. (2021) and Gruber et al. (2021). Reference Moon and Leeb (2016) and Moon and Leeb (2014) proposed two methods to increase the energy harvested for a constant voltage load without significantly increasing circuit complexity. One method called transfer window alignment (TWA) is to change the energy harvesting timing while another is to increase the time to reach saturation by shaping the core voltage with a field shaping capacitor (FSC) in series connection with the core. A detailed analysis and control strategy of TWA was given in Moon and Leeb (2015b) and the energy extracting capability improved considerably. However, no detailed circuit analysis was done on FSC technology.

In this paper, a comprehensive circuit analysis for the FSC method is introduced based on the nonlinear model of the magnetic core. The optimization of the core and system design parameters are presented. Simulation and experimental results are given as verifications.

2 Materials and methods

2.1 Circuit model of the magnetic core

The primary side could be viewed as a current source i_P = I_P sin ωt where I_P is the peak amplitude of the wire current. The secondary side of the core has current i_S. From Ampere’s Law, the magnetic field intensity H at radius r is:

$H\left(r\right)=\frac{i_P-N{i}_S}{r}=\frac{1}{r}\left(I_P\sin \omega t-N{i}_S\right)(1)$

where N is the number of turns of the secondary side. The induced AC voltage is rectified to DC voltage by a full bridge rectifier. The full bridge rectifier could be implemented by Schottky diodes or MOSFETs. The rectified DC voltage usually charges an energy storage device, such as a supercapacitor or a battery. Since the charging of an energy storage device is much slower compared with the voltage rectifying dynamics, the load of the harvester could be modelled as a voltage source V_L.

For a ring shape core, B is almost constant across the range under the assumption that H(r) changes little between the outer and inner radius. The flux linkage in the core is:

$\mathrm{\Gamma }=NAB(2)$

where A is the cross section area of the core. The induced voltage of the harvester v_core is the time derivative of the flux linkage:

$v_{\mathit{core}}=\frac{\mathrm{d}\mathrm{\Gamma }}{\mathrm{d}t}(3)$

H is calculated from the primary and secondary currents as shown in 1. Using the equations above, the flux linkage is:

$\mathrm{\Gamma }=NAB=NAf\left(H\right)=NAf\left(\frac{1}{r}\left(I_P\sin \omega t-N{i}_S\right)\right)(4)$

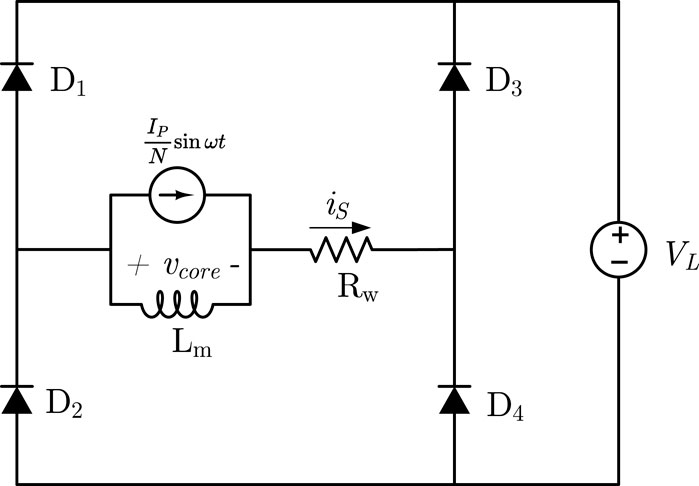
Where B = f(H) is the magnetizing curve. This equation means that the flux linkage in the core relates with the difference between the primary current and the secondary current. Therefore the current transformer of the magnetic energy harvester could be modelled as an ideal current source in parallel with a non-linear magnetizing inductance L_m, as shown in Figure 1.

FIGURE 1

FIGURE 1. Circuit model of a general magnetic energy harvester.

The complicated relationship between B and H determines the harvesting capability of the harvester. In the linear region where B = μH, L_m is:

$L_m=\mu \frac{N^{2}A}{l}(5)$

where μ is the permeability of the core material and l is the effective flux length of the core. Since N is very large, L_m is large enough so that almost no current flows through it in the linear region. The leakage inductance of the harvester could also be ignored since it is much smaller compared to L_m.

In the saturation region, B ≈ B_sat. From 2, Γ ≈ NAB_sat. Eq. 3 shows that the saturation of B or Γ is directly caused by accumulating voltage-seconds which is the time integral of v_core. When feeding a constant voltage load, the time it takes to saturate the core is:

$T_{\mathit{sat}}=\frac{2B_{\mathit{sat}}NA}{V_L}(6)$

The effective permeability of the core decreases dramatically and most of the induced current i_S is bypassed by the magnetizing inductor. Much less energy is harvested at this region. However, crudely dividing the magnetizing curve into linear/non-linear regions is far from accurately predicting the harvested energy. There are several methods to establish mathematical model for a non-linear magnetic core. In Vos (2020) the model is established by treating the core permeance as a complex parameter that includes loss. Kuang et al. (2021) used finite element method in both electromagnetic and electrical system. In Moon and Leeb (2015a), the “arctan” function was used to model the saturation where there was one fitting parameter α. In this research, the Chan model Chan et al. (1991) was chosen since it is relatively easy to implement in circuit simulation tools and provides relatively more freedom to emulate the saturation behavior. The Chan model was defined by three parameters:

$B=\frac{H+H_c}{|H\pm H_c|+H_c\left(\frac{B_{\mathit{sat}}}{B_r}-1\right)}+{\mu }_{0}H(7)$

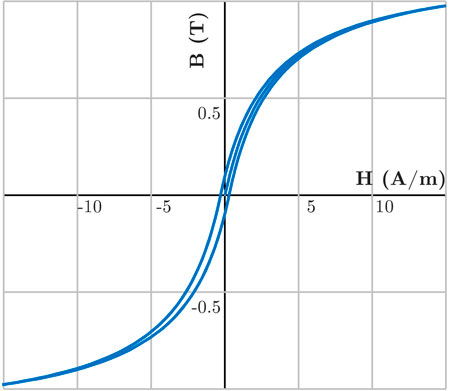
where B_sat is the saturation flux density; B_r is the remnant flux density and H_c is coercive force.

A high permeability amorphous non-crystalline core VITROPERM 500F VacuumSchmelze (2022) was used as the magnetic core. The fitted parameters for this core material are: B_sat = 1.19 T, B_r = 0.1 T, H_c = 0.3 A/m. The simulated B-H curve using the Chan model is shown in Figure 2, which is very close to the curve given in the datasheet. Note that the H of the core starts from 0 and is swept forward and backward. The hysteresis of the material is relatively small so the iron loss of the core is ignored in this paper.

FIGURE 2

FIGURE 2. Numerically calculated B-H curve of the VITROPERM 500F core using the Chan model in 7.

2.2 Circuit model of the magnetic energy harvester

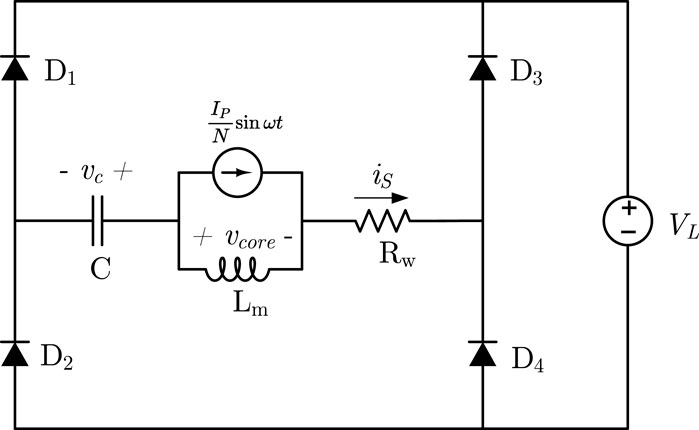
In the circuit of Figure 1, the voltage of the core v_core equals to the load voltage V_L during the linear region when neglecting the voltage drop across diodes. For the rectifier circuit with an FSC as shown in Figure 3, v_core is not constant any more due to the capacitor voltage v_C. Sincev_C lags i_S, v_C might be negative at the start of one period. v_core could be less than V_L at the beginning of the energy transfer. Therefore the total energy transfer time T_sat may extend after adding an FCS.

FIGURE 3

FIGURE 3. Circuit model of the magnetic energy harvester with a field shaping capacitor (FSC).

The voltage and current waveforms of the harvester with and without FSC are shown in Figure 4. The peak value of the primary current is 14 A, the secondary side has N = 200 turns and the load voltage V_L = 7 V. The value of the FSC is 20 μF. The rectifying diodes are Schottky diodes 1N5819 from DIODES whose forward voltage V_F is 0.2 V. As expected, with FSC v_core is smaller than V_L at the beginning of the energy transfer. T_sat is 0.5 ms wider, which means more energy is harvested with FSC. The power harvested at different FSC value (5, 15, and 25 μF) is 80, 125, and 87 mW respectively. The power extracted from the core under a certain operating point does not increase monotonically with the value of FSC. There should be an optimal value for FSC. The waveforms of v_core and v_c are shown in Figure 5. Even though the peak value of v_C and v_core increases as FSC decreases, T_sat first increases and then decreases. The shape of v_C also becomes different at 5 μF. In order to find out the optimized FSC and load voltage V_L under a specified design, a detailed circuit analysis should be carried out.

FIGURE 4

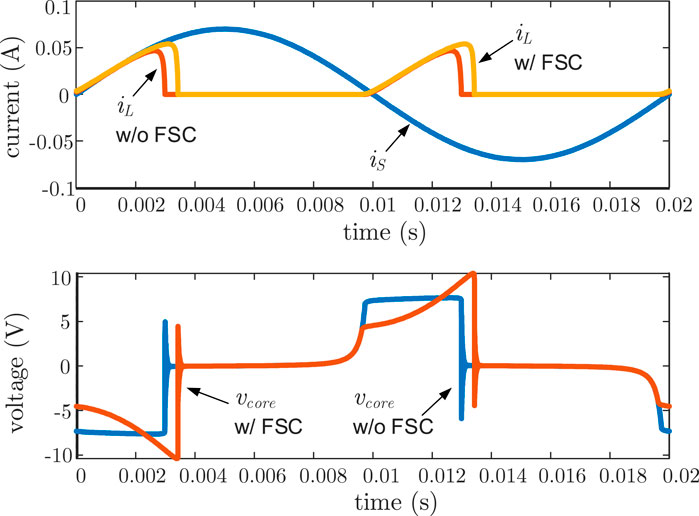
FIGURE 4. Comparison of voltage and current waveforms of the energy harvesters with and without FSC: the waveforms with longer transfer window is with FSC.

FIGURE 5

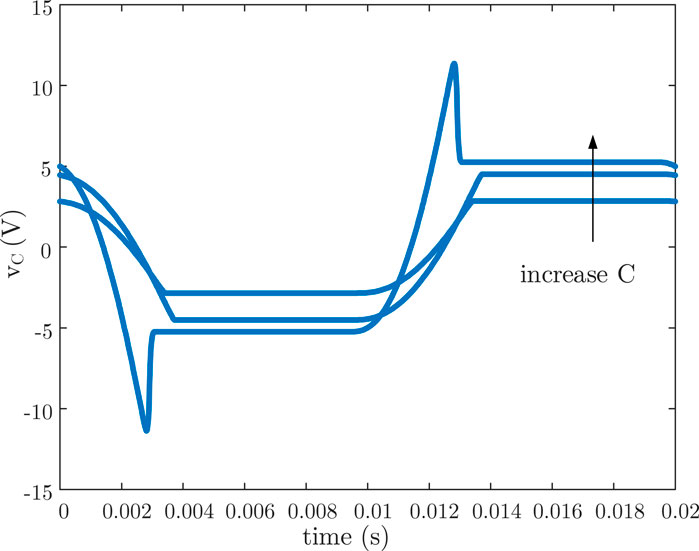
FIGURE 5. Capacitor voltage waveforms of the energy harvesters with different FSC: 5, 15, and 25 μF.

2.3 Circuit analysis of the magnetic energy harvester with FSC

Since the circuit behaves symmetrically at ω ∈ [0, π] and [π, 2π], the analysis will be focused on the first half of the period. At the beginning of a new sinusoidal period, L_m is in its linear region and it is so large that i_S entirely flows through FSC. Diodes D₂ and D₃ turn on. From KVL:

$v_{\mathit{core}}=v_C-v_L+i_S{R}_w-2V_F(8)$

where v_C and v_R are the voltages of FSC and wire resistance respectively, as shown in Figure 3. By integrating i_S, v_C is:

$v_C\left(t\right)=V_{C0}+\frac{I_p}{N\omega C}\left(\cos \omega t-1\right)(9)$

where V_C0 is initial voltage of the FSC at t = 0. Apparently the capacitor voltage at t = T_sat depends on the value of FSC. Therefore, the circuit operation could be divided into two scenarios depending on the value of FSC.

2.3.1 Large FSC

At t = T_sat, L_m enters into saturation region. Its value decreases dramatically and i_S flows entirely into L_m. Based on the reference direction definition in Figure 3, the voltage-seconds accumulating in the core drive it from positive saturation to negative saturation:

${\int }_0^{T_{\mathit{sat}}}{v}_{\mathit{core}}\mathrm{d}t=-2B_{\mathit{sat}}NA(10)$

Diodes D₂ and D₃ turn off at T_sat. v_C keeps unchanged during the rest of the half period since there is no current flowing through it. v_C(T_sat) will be the capacitor voltage initial value for [π, 2π]. From the principle of symmetry:

$v_C\left(T_{\mathit{sat}}\right)=-V_{C0}(11)$

Solving Eqs 8, 10, 11 numerically, the value of T_sat and V_C0 could be obtained. The average power harvested is:

$P_h=\frac{2}{T}{\int }_0^{T_{\mathit{sat}}}{V}_L\frac{I_P}{N}\sin \omega t\mathrm{d}t(12)$

2.3.2 Small FSC

From Figure 5, the capacitor voltage v_C is not continuous when C = 5 μF. The capacitor discharges rapidly once the core enters saturation. Therefore the relationship in Eq. 11 is no longer valid. To solve T_sat and V_C0, the discharging process of the FSC should be examined. At t = T_sat, the current source is bypassed by the magnetizing inductance L_m and diodes D₂ and D₃ turn off. In view of the fact that the value of i_S and L_m is small, the voltage drop on L_m is very small compared to v_C(T_sat). If the absolute value of v_C(T_sat) is larger than V_L, diodes D₁ and D₄ will turn on to discharge the capacitor through the voltage source V_L, magnetizing inductance L_m and wire resistance R_w. This is a classical RLC transient process. The resonance between C and L_m will end when i_C goes back to zero and diode D₁ and D₄ will turn off then. Since the resonant frequency of C and L_m is large compared with the line frequency so the discharging time of the capacitor is very short. After discharging process, v_C stays unchanged since all the diodes are off.

After solving the 2nd order ODE of the RLC circuit, the capacitor voltage during discharging is:

$\begin{array}{cc}\hfill v_C\left(t\right)& =e^{-\alpha t}\left(\frac{\alpha }{{\omega }_d}\left(V_{C0}+V_L+2V_F\right)\sin {\omega }_{d}t\right.\hfill \\ \hfill & +\left.\left(V_{C0}+V_L+2V_F\right)\cos {\omega }_{d}t\right)\hfill \end{array}(13)$

where α is the damping coefficient and ω_d is the oscillation frequency. They could be calculated as:

$\begin{array}{cc}\hfill {\omega }_0& =\frac{1}{\sqrt{LC}}\hfill \\ \hfill \alpha & =\frac{1}{2}\frac{R_w}{L}\hfill \\ \hfill {\omega }_d& =\sqrt{{\alpha }^2-{\omega }_0^2}\hfill \end{array}(14)$

The discharging time for the capacitor is half of the RLC oscillation period π/ω_d. v_C drops to −V_C0 according to the principle of symmetry. Together solving Eqs 10, 13, 14 numerically, the value of T_sat and V_C0 could be obtained. The average power harvested during D₂ and D₃ on is still based on Eq. 12 while the average power harvested during D₁ and D₄ on is:

$P_{h,d}=\frac{2}{T}C\left(V_{C0}+V_L+2V_F\right)V_L\left(1+e^{-\alpha \frac{\pi }{{\omega }_d}}\right)(15)$

It is worth noting that the value of L used in Eqs 13–15 comes from calculation by Eqs 5, 7.

A comparison of the harvested power calculated by the mathematical model presented above and circuit simulation is shown in Figure 6. The simulation condition is the same as Section 2.3: I_p = 14 A, N = 200, C = 15 μF. The two methods output very similar results and the biggest difference is less than 5%. Therefore it is more convenient to use the numerical model to optimize the system design.

FIGURE 6

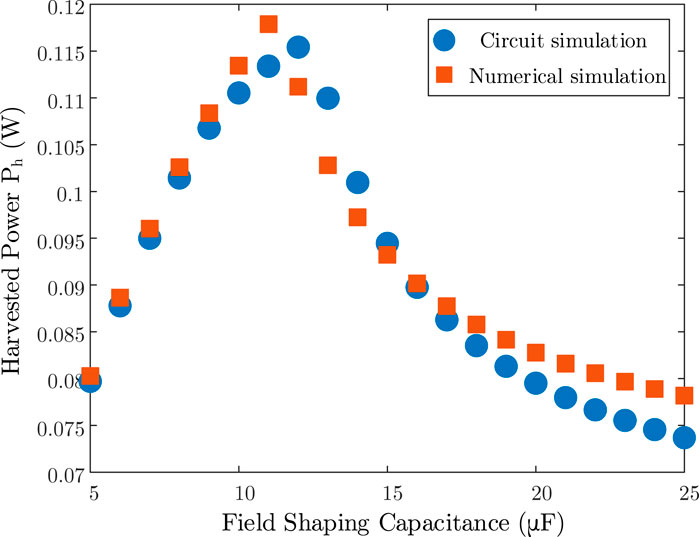
FIGURE 6. Comparison of the harvest power of the harvester with different FSC from SPICE simulation and numerical model.

3 Results

In this section, the optimized field shaping capacitor value C and the harvester core design will be investigated. This equation is valid as long as the primary current is not high enough so the voltage drop on the wire resistance could be ignored. The optimized FSC value with different V_L under the condition (I_p = 14 A, N = 200) is shown in Figure 7. The optimal FSC decreases as the load voltage V_L increases. Note that the optimal power harvested with FSC under different V_L is 0.124, 0.125, 0.118, and 0.111 W respectively. Without FSC, the power harvested is 0.109, 0.099, 0.090, and 0.082 W respectively from 6. A proper FSC can improve the energy extraction capability significantly, especially when the load voltage is high. Since higher V_L results in shorter T_sat, the harvester will extract less power as the load voltage increases if no special voltage shaping techniques are used. Higher V_L also means a stronger voltage shaping, which means a smaller FSC is needed.

FIGURE 7

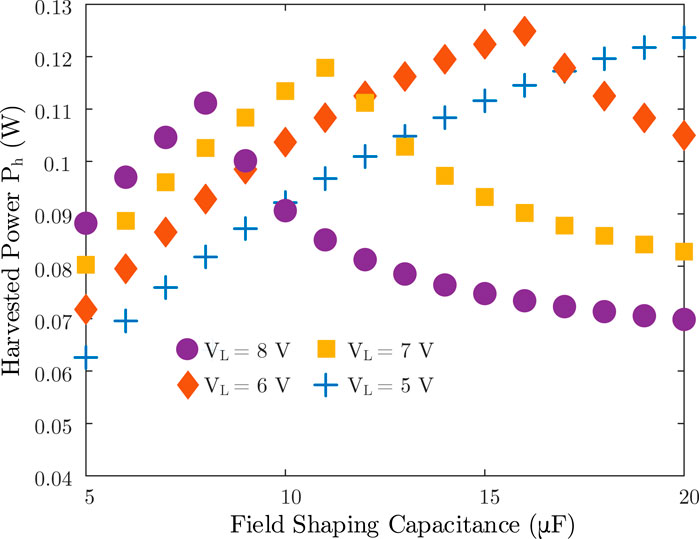
FIGURE 7. Numerical simulation of the harvested power vs. FSC value (I_p = 14 A, N = 200) with different V_L: 5, 6, 7, and 8 V.

The optimized FSC value with different N under the condition (I_p = 14 A, V_L = 6 V) is shown in Figure 8. Figure 8 reveals the fact that N has a very complicated impact on the energy harvesting efficiency. When the number of turns is low, the core is easier to get saturated based on 6 while the secondary current would be too small to effectively charge the load if N is large.

FIGURE 8

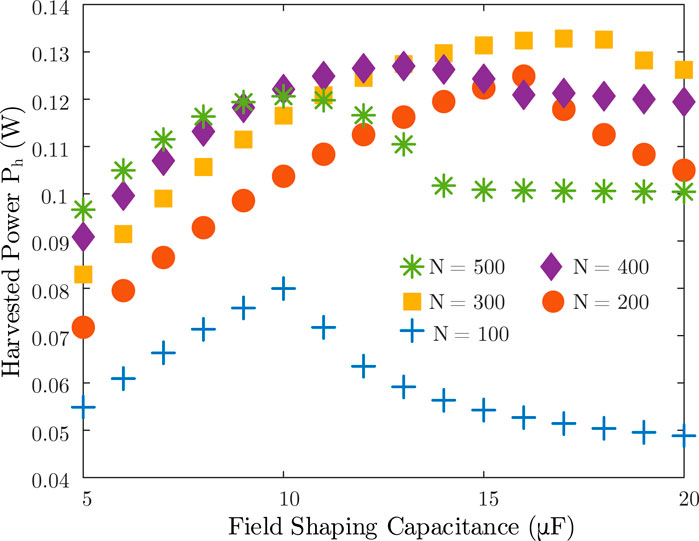
FIGURE 8. Numerical simulation of the harvested power vs. FSC value (I_p = 14 A, V_L = 6 V) with different N: 100, 200, 300, and 400.

The optimized FSC value with different primary current peak value I_P under the condition (V_L = 6 V, N = 200) is shown in Figure 9. The maximum amount of energy harvest is proportional to I_p, as predicted by 12. The optimal FSC changes rapidly as I_p increases, from 5 to 20 μF as I_p increases from 3 to 20 A. This is owing to the fact that small FSC could be easily charged up by large I_P based on Eq. 9, which results a stronger field shaping effect. Figure 10 is the power vs. current plot. The power monotonically increases with primary current, as indicated in Eq. 12.

FIGURE 9

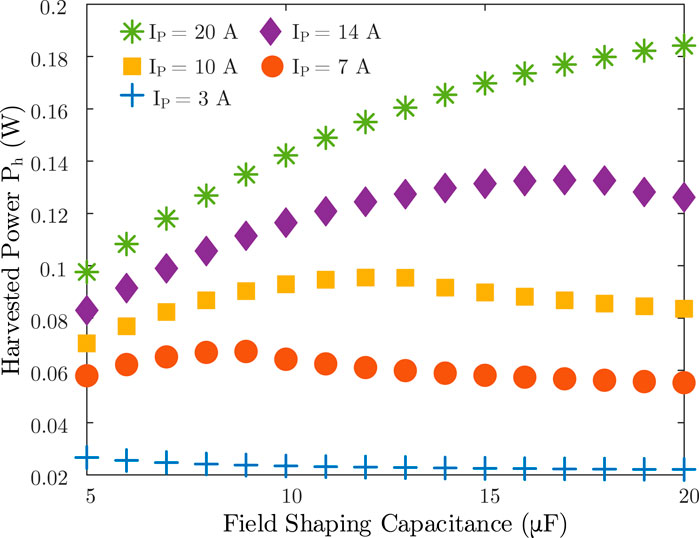
FIGURE 9. Numerical simulation of the harvested power vs. FSC value (V_L = 6 V, N = 200) with different I_p: 3, 7, 10, 14, and 20 A.

FIGURE 10

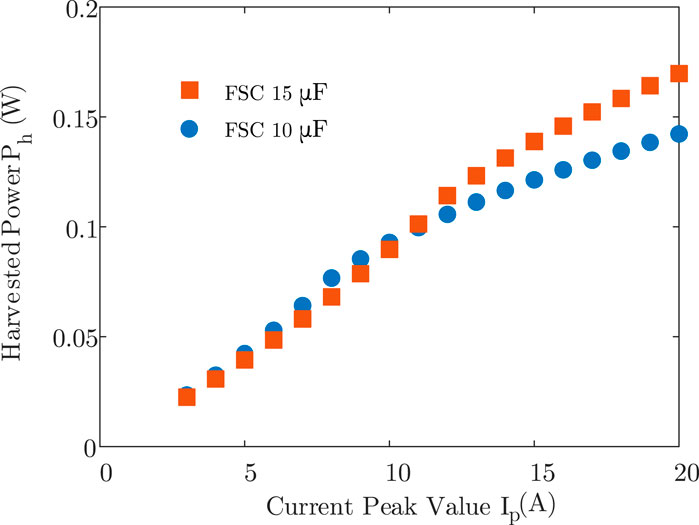
FIGURE 10. Numerical simulation of the harvested power vs. peak current value (V_L = 6 V, N = 200) with different FSC: 10, 15 μF.

An experimental prototype was built to verify the analysis. Figure 11 shows the current/voltage waveforms of the harvester with different FSC. The current of the constant voltage load was measured through a current sensing resistor and differential amplifier. Figures 11A, B show that the power transfer time increases significantly with a 14.7 μF FSC. For small FSC, 4.7 μF for example, as in Figure 11C, the current peak is the result of RLC discharging explained in Eq. 13.

FIGURE 11

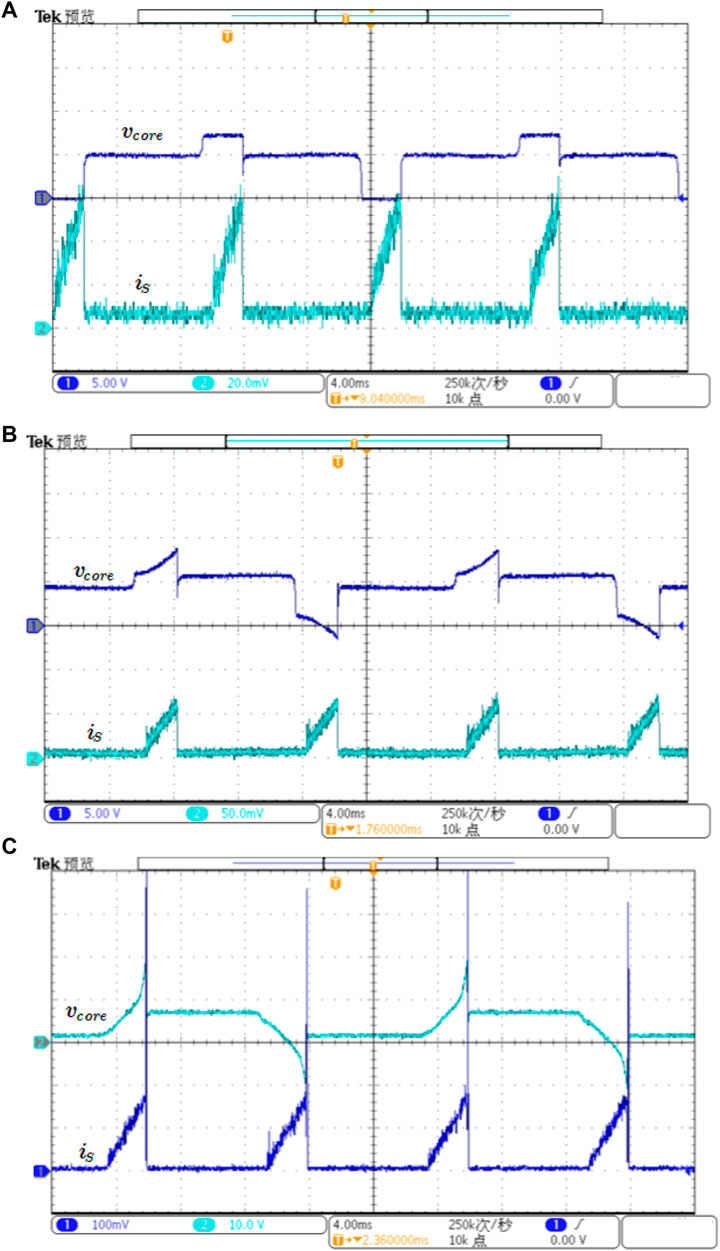
FIGURE 11. Comparison of the voltage/current waveforms of the harvester: (A) without FSC, (B) with 14.1 μF FSC and (C) 4.7 μF FSC.

The harvested power from experiments and numerical calculation with different FSC is shown in Figure 12. The experiment condition is: I_P = 14 A, N = 200, V_L = 5 V. Simulation and experimental results show the same trend. The difference between the experiments and numerical calculation mainly comes from the discrepancies between the piecewise assumption of the magnetic core’s B-H curve in the numerical model and its real saturation curve.

FIGURE 12

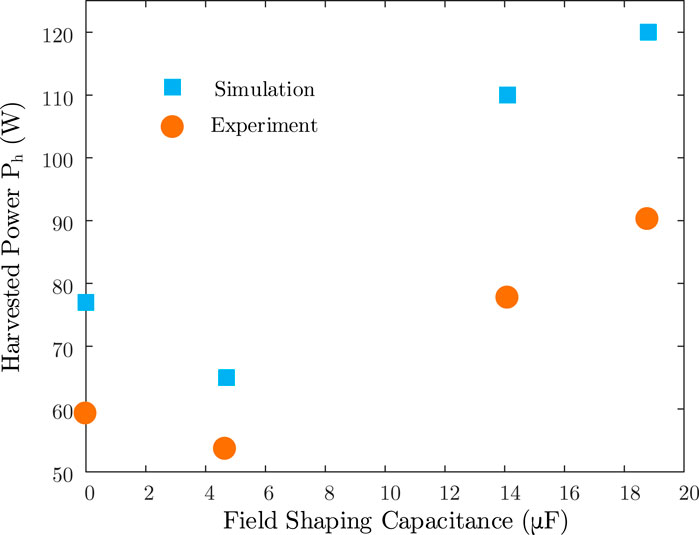
FIGURE 12. Comparison of the harvest power of the harvester with different FSC from numerical model calculation and experiments.

4 Discussion

This paper discusses the modeling and optimization process for the magnetic energy harvester with field shaping capacitors in order to enhance its energy extracting capability. The Chan model is used to emulate the saturation of the magnetic core. Then a circuit model is given to study the behaviour of the harvester system feeding a constant voltage load. Based on the circuit model, a detailed mathematical model is developed based on the value of FSC so that the fast calculation and optimization of the system performance is possible through numerical software. Optimization of the harvester parameters under various operating conditions are discussed. The optimal FSC is sensitive to the operation conditions of the energy harvester: load voltage, number of turns and primary side current. Therefore FSC is especially suitable for applications with almost constant current, for example, harvesting energy on the cable of an induction machine. With the model introduced in this paper, designers could maximize the output power through an optimum design of the harvester: number of turns, size of the core and field shaping capacitors.

Data availability statement

The datasets presented in this article are not readily available because the dataset are not available to the public due to authors’ organization policies. Requests to access the datasets should be directed to bWluc3VuQHVlc3RjLmVkdS5jbg==.

Author contributions

YM, MS, MZ, and JL contributed to conception and design of the study. GC contributes to the theoretical part. YM designed the experiments. ML and MZ performed simulation and experiments. YM wrote the first draft of the manuscript. MS wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

Research reported in this publication was partially supported by the Laboratory Open Fund of Beijing Smart-Chip Microelectronics Technology Co., Ltd., under contract No. SGTYHT/21-JS-223. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author YM was employed by Beijing Smart-Chip Microelectronics Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chan, J., Vladimirescu, A., Gao, X.-C., Liebmann, P., and Valainis, J. (1991). Nonlinear transformer model for circuit simulation. IEEE Trans. Computer-Aided Des. Integr. Circuits Syst.10, 476–482. doi:10.1109/43.75630

CrossRef Full Text | Google Scholar

Facen, A., and Boni, A. (2006). “Power supply generation in cmos passive uhf rfid tags,” in 2006 Ph.D. Research in microelectronics and electronics, 33–36. doi:10.1109/RME.2006.1689889

CrossRef Full Text | Google Scholar

Gruber, G., Neumayer, M., Bretterklieber, T., Siegl, A., and Felsberger, R. (2021). “Miniaturized magnetic energy harvester: Lightweight and safe transformer design,” in 2021 IEEE international instrumentation and measurement technology conference (I2MTC), 1–6. doi:10.1109/I2MTC50364.2021.9460033

CrossRef Full Text | Google Scholar

Kuang, Y., Chew, Z. J., Ruan, T., and Zhu, M. (2021). Magnetic field energy harvesting from current-carrying structures: Electromagnetic-circuit coupled model, validation and application. IEEE Access9, 46280–46291. doi:10.1109/ACCESS.2021.3068472

CrossRef Full Text | Google Scholar

Moon, J., Donnal, J., Paris, J., and Leeb, S. B. (2013). “Vampire: A magnetically self-powered sensor node capable of wireless transmission,” in 2013 twenty-eighth annual IEEE applied power electronics conference and exposition (APEC), 3151–3159. doi:10.1109/APEC.2013.6520751

CrossRef Full Text | Google Scholar

Moon, J., and Leeb, S. B. (2015a). Analysis model for magnetic energy harvesters. IEEE Trans. Power Electron.30, 4302–4311. doi:10.1109/TPEL.2014.2357448

CrossRef Full Text | Google Scholar

Moon, J., and Leeb, S. B. (2015b). “Enhancement on energy extraction from magnetic energy harvesters,” in 2015 IEEE energy conversion congress and exposition (ECCE), 427–433. doi:10.1109/ECCE.2015.7309720

CrossRef Full Text | Google Scholar

Moon, J., and Leeb, S. B. (2016). Power electronic circuits for magnetic energy harvesters. IEEE Trans. Power Electron.31, 270–279. doi:10.1109/TPEL.2015.2401336

CrossRef Full Text | Google Scholar

Moon, J., and Leeb, S. B. (2014). “Power flow control and regulation circuits for magnetic energy harvesters,” in 2014 IEEE 15th workshop on control and modeling for power electronics (COMPEL), 1–8. doi:10.1109/COMPEL.2014.6877207

CrossRef Full Text | Google Scholar

Moon, J., and Leeb, S. B. (2015c). “Power loss analysis with high primary current in magnetic energy harvesters,” in 2015 IEEE 16th workshop on control and modeling for power electronics (COMPEL), 1–8. doi:10.1109/COMPEL.2015.7236503

CrossRef Full Text | Google Scholar

Ottman, G., Hofmann, H., Bhatt, A., and Lesieutre, G. (2002). Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron.17, 669–676. doi:10.1109/TPEL.2002.802194

CrossRef Full Text | Google Scholar

Park, B., Huh, S., Kim, J., Kim, H., Shin, Y., Woo, S., et al. (2021). The magnetic energy harvester with improved power density using saturable magnetizing inductance model for maintenance applications near high voltage power line. IEEE Access9, 82661–82674. doi:10.1109/ACCESS.2021.3085989

CrossRef Full Text | Google Scholar

Shi, Y., Cui, X., Qi, L., Zhang, X., Li, X., and Shen, H. (2023). A novel energy harvesting method for online monitoring sensors in hvdc overhead line. IEEE Trans. Industrial Electron.70, 2139–2143. doi:10.1109/TIE.2022.3158028

CrossRef Full Text | Google Scholar

Sudevalayam, S., and Kulkarni, P. (2011). Energy harvesting sensor nodes: Survey and implications. IEEE Commun. Surv. Tutorials13, 443–461. doi:10.1109/SURV.2011.060710.00094

CrossRef Full Text | Google Scholar

Tan, Y. K., and Panda, S. K. (2011). Energy harvesting from hybrid indoor ambient light and thermal energy sources for enhanced performance of wireless sensor nodes. IEEE Trans. Industrial Electron.58, 4424–4435. doi:10.1109/TIE.2010.2102321

CrossRef Full Text | Google Scholar

Tang, X., Wang, X., Cattley, R., Gu, F., and Ball, A. D. (2018). Energy harvesting technologies for achieving self-powered wireless sensor networks in machine condition monitoring: A review. Sensors18, 4113. doi:10.3390/s18124113

PubMed Abstract | CrossRef Full Text | Google Scholar

VacuumSchmelze, (2022). Nanocrystalline VITROPERM vitroperm 500f.

Google Scholar

Vos, M. J. (2020). A magnetic core permeance model for inductive power harvesting. IEEE Trans. Power Electron.35, 3627–3635. doi:10.1109/TPEL.2019.2933133

CrossRef Full Text | Google Scholar

White, R. M., Nguyen, D.-S., Wu, Z., and Wright, P. K. (2018). Atmospheric sensors and energy harvesters on overhead power lines. Sensors18, 114. doi:10.3390/s18010114

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, N., Ma, G., Guan, Y., Hu, J., Lu, C., Wen, J., et al. (2021). Panoramic information perception and intelligent grid. Proc. CSEE41, 1274–1283. doi:10.13334/j.0258-8013.pcsee.202508

CrossRef Full Text | Google Scholar