Remaining useful life prediction of lithium-ion batteries using CEEMDAN and WOA-SVR model

The remaining useful life (RUL) prediction of Lithium-ion batteries (LIBs) is a crucial element of battery health management. The accurate prediction of RUL enables the maintenance and replacement of batteries with potential safety hazards, which ensures safe and stable battery operation. This paper develops a new method for the RUL prediction of LIBs, which is combined with complete ensemble empirical mode decomposition with adaptive noise (CEEDMAN), whale optimization algorithm (WOA), and support vector regression (SVR). Firstly, the CEEMDAN is employed to perform noise reduction in battery capacity data for prediction accuracy improvement. Then, an SVR model optimized by the WOA is proposed to predict the RUL. Finally, the public battery datasets are selected to validate the performance of the CEEMDAN-WOA-SVR method. The RUL prediction accuracy of the CEEMDAN-WOA-SVR method is better than the WOA-SVR method. In addition, a comparison is made between the proposed method and the existing methods (artificial bee colony algorithm-SVR method, ensemble empirical mode decomposition-gray wolf optimization-SVR method). The results show that the accurate prediction of the proposed method is superior to the two methods.

1 Introduction

Lithium-ion batteries (LIBs), as a green energy source, are characterized by high capacity, high reliability, and high safety. They have been widely used in fields involving electric vehicles, mobile phones, and computers (Xue et al., 2020; Ren L. et al., 2021). However, as the number of LIBs operations increases, the batteries will experience aging problems, and the failed batteries will affect the regular operation of the devices (Chen W. et al., 2021). A LIB’s remaining useful life (RUL) is the number of remaining charge/discharge cycles before the end of life (EOL). The accurate RUL prediction of LIBs could guide timely battery repair and replacement to ensure safe operation. Therefore, the research on RUL prediction of batteries has attracted extensive attention (Bracale et al., 2021).

Recently, many RUL prediction methods have been developed in the research literature, and these methods are mainly divided into two types: model-based methods and data-based methods (Ge et al., 2021). The model-based methods aim to build a mathematical-physical model to estimate the RUL of LIBs based on the failure mechanisms. Xing et al. (2013) presented an ensemble model that integrated an empirical exponential, a polynomial regression, and particle filtering (PF) for the RUL prediction. Su et al. (2017) developed a new method based on the interacting multiple model particle filter for the RUL prediction. Guha and Patra (2018) presented a regression model combined with the reconstructed electrochemical impedance spectrum, which was applied to the PF method to predict the RUL. Deng et al. (2020) proposed an empirical model to predict the RUL and used the PF method to estimate the parameters of the model. Hong et al. (2022) built an iterative model of the generalized Cauchy process with long-range dependence characteristics for the RUL prediction. The model-based methods are built based on the battery failure mechanisms and could obtain high prediction accuracy. However, the battery operating process is a complex and dynamic system, and many parameters require consideration to construct a model with high prediction accuracy.

The data-based methods are different from the model-based methods, which mainly mine the valid information from historical degradation data without considering failure mechanisms. Machine learning techniques such as the support vector machine (SVM) and artificial neural network (ANN) are used to predict the RUL of LIBs. Qin et al. (2019) proposed a fusion model based on the PF algorithm and ANN to predict the RUL. Ren X. et al. (2021) developed a novel method to predict the RUL by combining the deep convolution neural network (CNN) and long-short-term memory, and the experimental results demonstrated the effectiveness of the proposed method. Zhang et al. (2022) presented a hybrid parallel residual CNN model for RUL prediction. Tang and Yuan (2022) extracted the health indicators from all the measured parameters and constructed an ANN model to predict the RUL from three aspects of the shape feature. However, the ANN-based prediction methods have high prediction accuracy, which requires more computing time and computational complexity. The support vector regression (SVR) model, as a type of SVM model, has a simple structure and is widely used for RUL prediction. Zhao et al. (2018) extracted health indicators and proposed an SVR model combined with feature vector selection to achieve the prediction of the RUL. Wei et al. (2018) combined a particle filter with the SVR model for the RUL prediction, and the results showed that the proposed method could achieve an accurate result. Wang et al. (2019) developed a hybrid method based on an artificial bee colony algorithm and SVR (ABC-SVR) to predict the RUL, and the results indicated that an accurate prediction was obtained. Yang et al. (2021) presented a hybrid model to predict the RUL, which combined the ensemble empirical mode decomposition (EEMD), gray wolf optimization, and SVR (GWO-SVR). In a data-driven approach, complex historical data are used to predict the RUL effectively, and the feature information extracted from the historical data is crucial.

Inspired by references (Wei et al., 2018; Wang et al., 2019; Yang et al., 2021), a new data-based method is proposed to predict the RUL in this paper, and the method combines the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), whale optimization algorithm (WOA), and SVR model (WOA-SVR). The CEEMDAN method is used firstly for noise reduction processing of battery capacity data, which effectively improves prediction accuracy. The WOA is a new intelligent optimization algorithm and has excellent search capability compared to other optimization algorithms. The SVR model has the advantages of global optimality and high generalization ability in solving nonlinear problems, but there are still some challenges in selecting the parameters of the SVR model (Wang and Mamo, 2018). To address the issue of selecting the SVR method parameters, the WOA is applied to select the kernel parameters to facilitate the RUL prediction of LIBs. Although the WOA-SVR method has been used to solve signal series data problems in many fields (Li et al., 2020; Tikhamarine et al., 2020; Wang et al., 2021), this method is employed for the RUL prediction for the first time. The proposed method is validated using a public battery dataset provided by the NASA Prognostics Center of Excellence (Goebel et al., 2008). The proposed method accurately predicts the RUL of LIBs according to the experimental results, thus enabling timely battery maintenance and replacement.

The remainder of the paper is organized as follows. In Section 2, the principle of the related theory is described, including the CEEMDAN method, WOA algorithm, and SVR model. Section 3 introduces the RUL prediction for LIBs using the CEEMDAN-WOA-SVR method. Noise reduction processing of the capacity degradation data is analyzed, and the prediction results are discussed in Section 4. Finally, the conclusion and future work are shown in Section 5.

2 Related theory

2.1 Principle of complete ensemble empirical mode decomposition with adaptive noise

Empirical mode decomposition (EMD) is presented as a signal processing method that transforms the signal sequence into several intrinsic mode functions (IMFs) and a residual (Huang et al., 1998). Although the EMD method has been widely used in signal processing, it has significant problems, such as end effect and modal aliasing. As an improvement of EMD, the CEEMDAN method is proposed by the addition of adaptive white Gaussian noise, which efficiently suppresses the end effect and modal aliasing (Zhang and Hong, 2019).

Assuming that the original signal sequence and Gaussian white noise are $s\left(n\right)$ and $\nu \left(n\right)$, respectively, and the i-th composite signal after the addition of Gaussian white noise can be represented as $s^i\left(n\right)=s\left(n\right)+{\nu }^i\left(n\right)$. The detailed steps are given as follows (Chen Z. et al., 2021; Peng et al., 2021):

1) The signal time series $s^i\left(n\right)$ is decomposed by the CEEMDAN method. The calculation of the first modal component is represented as:

$IM{F}_1\left(n\right)=\frac{1}{I}{\displaystyle \sum }_{i=1}^{I}IM{F}_1^i\left(n\right)=\overline{IM{F}_1\left(n\right)}(1)$

where $I$ represents the decomposition time.

2) The residual sequence is calculated, and the first residual sequence is given by:

$r_1\left(n\right)=s\left(n\right)-IM{F}_1\left(n\right)(2)$

3) Adding ${\epsilon }_1{E}_1\left[{\nu }^i\left(n\right)\right]$ to the first residual sequence, the realization $r_1\left(n\right)+{\epsilon }_1{E}_1\left[{\nu }^i\left(n\right)\right],i=\mathrm{1,2},\cdots ,I.$ is achieved. Then, decompose $r_1\left(n\right)+{\epsilon }_1{E}_1\left[{\nu }^i\left(n\right)\right],i=\mathrm{1,2},\cdots ,I$, and the second modal component can be calculated as:

$IM{F}_2\left(n\right)=\frac{1}{I}{\displaystyle \sum }_{i=1}^I{E}_1\left(r_1\left(n\right)\right)+{\epsilon }_1{E}_1\left({\nu }^i\left(n\right)\right)(3)$

4) Similarly, the k-th residue sequence is calculated in the remaining phase. Then, the next modal component can be given by:

$r_k\left(n\right)=r_{k-1}\left(n\right)-IM{F}_k\left(n\right)(4)$

$IM{F}_{k+1}\left(n\right)=\frac{1}{I}{\displaystyle \sum }_{i=1}^I{E}_1\left(r_k\left(n\right)\right)+{\epsilon }_k{E}_k\left({\nu }^i\left(n\right)\right)(5)$

5) The decomposition process is terminated when the residual sequence is unsuitable for further decomposition. The decomposition process is carried out K times, and the final result of the residual sequence is shown as:

$R\left(n\right)=s\left(n\right)-{\displaystyle \sum }_{i=1}^{K}IM{F}_k\left(n\right)(6)$

The original signal series $s\left(n\right)$ can be represented as:

$s\left(n\right)=R\left(n\right)+{\displaystyle \sum }_{i=1}^{K}IM{F}_k\left(n\right)(7)$

2.2 Support vector regression method

SVR is a type of the SVM model developed through statistical learning (Smola and Schölkopf, 2004). The SVR model can effectively express the nonlinear mapping relationship between input and output data, which has been widely used to solve regression and prediction problems (Amroune et al., 2018; Liu et al., 2021).

Supposing that data sample is $D=\left\{\left(x_i,y_i\right)\right\}$, $i=1,\cdots ,N$, where $x_i$ and $y_i$ represent the input and output data, respectively. The nonlinear mapping of sample data can be expressed as (Malik et al., 2021):

$f\left(x\right)=\omega \cdot \phi \left(x\right)+b_c(8)$

where $f\left(\cdot \right)$ denotes the regression function, $\phi \left(\cdot \right)$ indicates the transfer function, $\omega$ is the weight parameter, and $b_c$ represents the intercept parameter.

The regression problem is formulated as:

$\min R\left(\omega ,b,\zeta \right)=\frac{1}{2}{\Vert \omega \Vert }^2+C{\displaystyle \sum }_i^n\left({\xi }_i+{\xi }_i^{\ast }\right)(9)$

$s.t.\{\begin{array}{l}{y}_i-\omega \cdot \phi \left(x\right)-b_c\le \epsilon +{\xi }_i\\ \omega \cdot \phi \left(x\right)+b_c-y_i\le \epsilon +{\xi }_i^{\ast }\\ {\xi }_i,{\xi }_i^{\ast }\ge 0.\end{array}(10)$

where $C$ represents the penalty parameter, ${\xi }_i$ and ${\xi }_i^{*}$ are the slack variables, and $\epsilon$ is the boundary value.

The regression problem is transformed by the Lagrange multipliers and the solution of the nonlinear regression function is obtained by simplification, which can be expressed as:

$f\left(x\right)={\displaystyle \sum }_i^n\left({\alpha }_i-{\alpha }_i^{\ast }\right)K\left(x_i,x\right)+b_c(11)$

where $K\left(x_i,x\right)$ is the kernel function, and ${\alpha }_i$, ${\alpha }_i^{*}$ are Lagrange multipliers.

The kernel function has various forms, and this paper selects the radial basis function, represented as:

$K_{RBF}\left(x_i,x\right)=\exp \left(-\frac{1}{2{\sigma }^2}{\Vert x_i-x\Vert }^2\right)(12)$

where $\sigma$ represents the kernel parameter.

For the SVR model, the parameters $C$ and $\sigma$ affect the complexity and prediction accuracy of the model. Therefore, intelligent optimization algorithms are used for the optimal selection of parameters.

2.3 Whale optimization algorithm algorithm

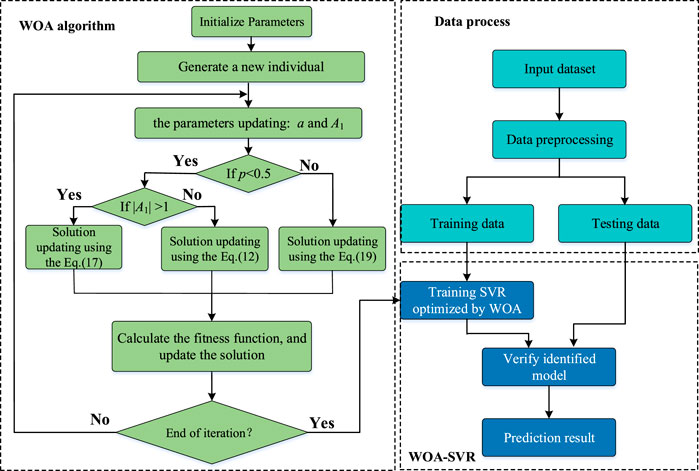
WOA is a novel metaheuristic algorithm inspired by humpback whales (Mirjalili and Lewis, 2016). The WOA is featured with excellent search capability and simple structure, and has been employed for solving practical optimization problems.

In the WOA, there are three stages for finding superiority: searching for prey, encircling prey, and spiral update of position (Saidala and Devarakonda, 2018; Chakraborty et al., 2021).

Encircling prey (p < 0.5 and |A₁| < 1):

$X_{i,t+1}=X_{best}-A_1\cdot D,0\le i\le NP(13)$

$D=\left|C\cdot X_{best}-X_{i,t}\right|(14)$

$A_1=2\cdot a\cdot r-a(15)$

$C=2\cdot r(16)$

$a=2-t\cdot \left(1-t/T_{\max }\right)(17)$

where $X_{i,t}$ denotes the solution in the current generation, $X_{i,t+1}$ represents the solution in the next generation, $X_{best}$ is the best solution, $NP$ is the population number, $t$ is the current number of iterations, $T_{\max }$ is the maximum number of iterations, $p$ and$r$ are random numbers,

Searching for prey (p < 0.5 and |A₁|≥1):

$X_{i,t+1}=X_{rand,t}-A_1\cdot D(18)$

$D=\left|C\cdot X_{rand,t}-X_{i,t}\right|(19)$

where $X_{rand,t}$ represents a random solution in the current generation.

Spiral update of position (p ≥ 0.5):

$X_{i,t+1}=X_{i,t}+D_p\cdot e^{bl}\cdot \cos \left(2\pi l\right)(20)$

$D_p=\left|X_{best}-X_{i,t}\right|(21)$

where $b$ indicates a constant, and $l$ represents a random number in [−1,1].

3 Remaining useful life prediction for lithium batteries based on complete ensemble empirical mode decomposition with adaptive noise and whale optimization algorithm-support vector regression methods

3.1 Whale optimization algorithm-support vector regression model

In the SVR model, the penalty factor $C$ and kernel function parameter $\sigma$ are critical parameters, and they have a direct impact on the performance of the SVR model. Thus, the WOA is used to optimize the kernel parameters of the SVR model. The flowchart of the WOA-SVR method is shown in Figure 1, and the detailed process is described as follows:

FIGURE 1

FIGURE 1. Flowchart of the WOA-SVR method.

Step 1: The parameters setting.

Before the prediction method execution, the population number $N_p$, dimension of variables $D_m$, the maximum iteration number $T$, the optimal range of $C$, and the optimal range of $\sigma$ are set.

Step 2: Data preprocessing.

In this step, the battery capacity datasets are normalized, and the capacity values are mapped in the range [−1, 1] with Eq. 22. The preprocessed data is divided into two parts, one part is training data and the other part is testing data.

$x_i=2\times \frac{x_i-x_{\min }}{x_{\max }-x_{\min }}-1(22)$

where $x_i$ represents the i-th battery capacity value, $x_{\max }$ represents the maximum value of battery capacity, and $x_{\min }$ represents the minimum value of battery capacity.

Step 3: Setting the fitness function.

The fitness function is established with the mean square error (MSE) between the actual and predicted value, which can be expressed as:

$MSE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2(23)$

where ${\widehat{y}}_i$ and $y_i$ represent the predicted value and the actual value at the i-th cycle, respectively. $n$ indicates the cycle time.

Step 4: Optimizing the kernel parameters of the SVR.

According to the search process of the WOA, the parameters of the SVR are selected in the solution space.

Step 5: The RUL prediction of LIBs: The RUL prediction accuracy of the WOA-SVR model is validated by the testing data.

3.2 The remaining useful life prediction of lithium-ion batterie based on CEEMDAN-GWO-SVR

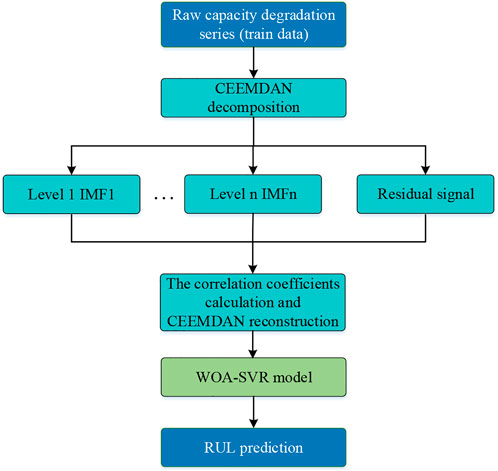
To improve prediction accuracy, the CEEMDAN is firstly used to perform noise reduction in battery capacity series. Figure 2 shows the flowchart of RUL prediction based on CEEMDAN-WOA-SVR, and the detailed steps are introduced as follows:

FIGURE 2

FIGURE 2. Flowchart of RUL prediction based on CEEMDAN-WOA-SVR method.

Step 1: Getting the capacity data.

Step 2: Decomposition of capability degradation series into $IM{F}_i\left(i=\mathrm{1,2},\cdots ,n\right)$ and a residual by applying CEEMDAN.

Step 3: To represent the correlation between each $IM{F}_i$ component and the original signal, the correlation coefficient is utilized and expressed as Eq. 24. The sensitive IMF components are selected when the correlation coefficient is more than the threshold value.

$C_i=\frac{{\displaystyle \sum }_{t=1}^{N-1}IM{F}_i\left(t\right)x\left(t\right)}{\sqrt{{\displaystyle \sum }_{i=1}^{N-1}{\left[IM{F}_i\left(t\right)\right]}^2{\displaystyle \sum }_{i=1}^{N-1}{\left[x\left(t\right)\right]}^2}}(24)$

where $C_i$ denotes the correlation coefficient of the i-th modal component with the original signal, $IM{F}_i\left(t\right)$ represents the i-th modal component, $x\left(t\right)$ represents the original signal sequence value, and $N$ denotes the length of the time series.

Step 4: The battery capacity sequence is reconstructed according to the selected IMF components and the residual. A WOA-SVR model is constructed for the reconstruction sequence.

Step 5: Obtaining the prediction of RUL.

4 Performance evaluation and analysis

4.1 Capacity degradation dataset of lithium-ion batterie

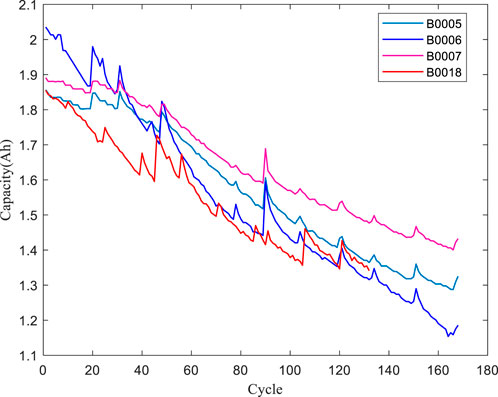
In this section, the public battery datasets provided by the NASA Prognostics Center of Excellence (Goebel et al., 2008) are employed to verify the accuracy and validity of the proposed method. These data were obtained from charge and discharge tests at room temperature (24°C) using 18650 LIBs with a capacity of 2 Ah. In the datasets, there are many parameters such as voltage, current, and capacity. Because the change in battery capacity directly indicates the degree of battery degradation, the capacity can be applied to the RUL prediction of LIBs. The capacity degradation curves of B5, B6, B7, and B18 are shown in Figure 3.

FIGURE 3

FIGURE 3. Curves of Li-ion battery capacity.

Generally, it is considered that the EOL of a battery is reached when the capacity degrades by 30%. In the experiment, the cyclic testing of battery charging and discharging test was terminated when the battery degraded to the EOL. However, for battery B7 degradation at 30%, it does not drop to the EOL, so this study resets the failure threshold of the battery, which is set to 72% of the rated battery capacity (1.44 Ah).

4.2 Evaluation criterion

To assess the proposed method’s performance, the mean absolute error (MAE) and the root mean square error (RMSE) are selected as the evaluation criteria, denoted as (Wang and Mamo, 2018):

$MAE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|\stackrel{\wedge }{y_i}-y_i\right|(25)$

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left|\stackrel{\wedge }{y_i}-y_i\right|}^2}(26)$

where $\stackrel{\wedge }{y_i}$ and $y_i$ represent the i-th predicted and the actual capacity value, respectively. $n$ indicates the estimated number. MAE is the average error of all prediction results. RMSE is the root mean square of all prediction errors. However, MAE and RMSE are applied to reflect the accuracy of the predicted method.

4.3 Noise reduction of lithium-ion batterie capacity sequences

The capacity decay curves of LIBs can be seen that there is a decreasing trend with the charging and discharging cycles, but in some cycles, the capacity of LIB has a fast and short rise, mainly due to random noise disturbance. To reduce the impact of noise, the capacity data need to be processed for noise reduction before the RUL prediction.

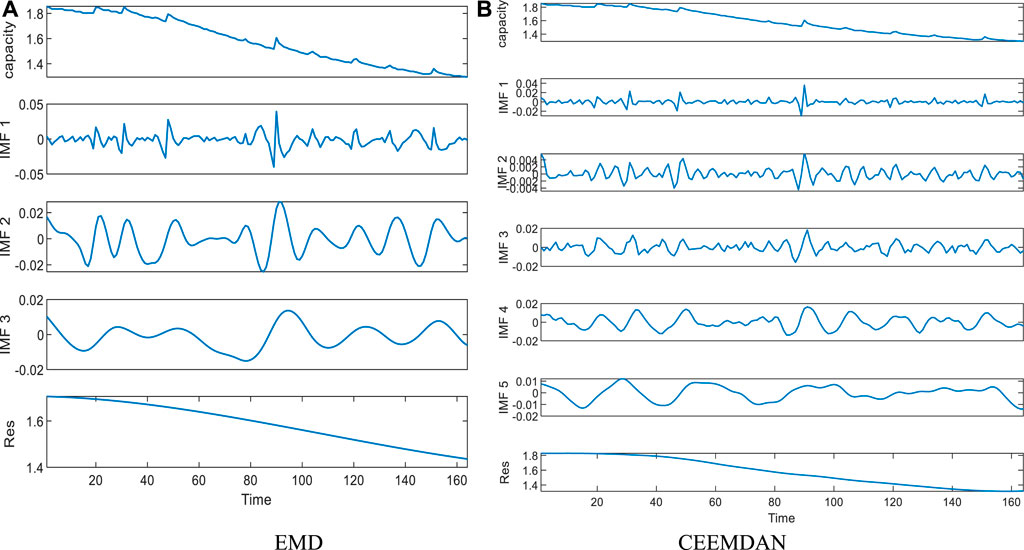
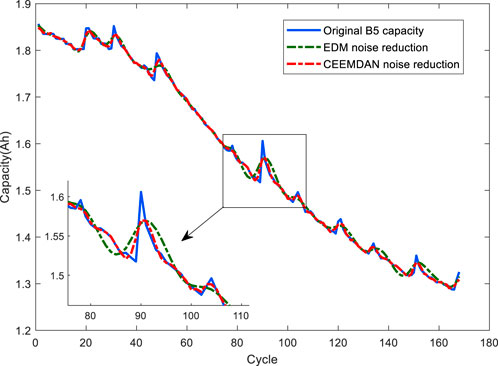
In this paper, the noise reduction process on capacity data is performed using CEEMDAN, and the sensitive IMF components are selected when the threshold value is more than 0.05. In this section, B5 capacity data is chosen to prove the efficacy of the CEEMDAN. Figure 4 shows the decomposition results of EMD and CEEMDAN. The B5 capacity after noise reduction by the EMD and CEEMDAN methods is shown in Figure 5. As can be seen from Figure 5, CEEMDAN can effectively reduce the noise of the capacity data, and the noise reduction effect of CEEMDAN is closer to the original data compared with the EMD method.

FIGURE 4

FIGURE 4. Decomposition results of B5 capacity by EEMD and CEEMDAN. (A) EMD, (B) CEEMDAN.

FIGURE 5

FIGURE 5. Noise reduction results of B5 capacity using EMD and CEEMDAN methods.

4.4 Simulation results analysis

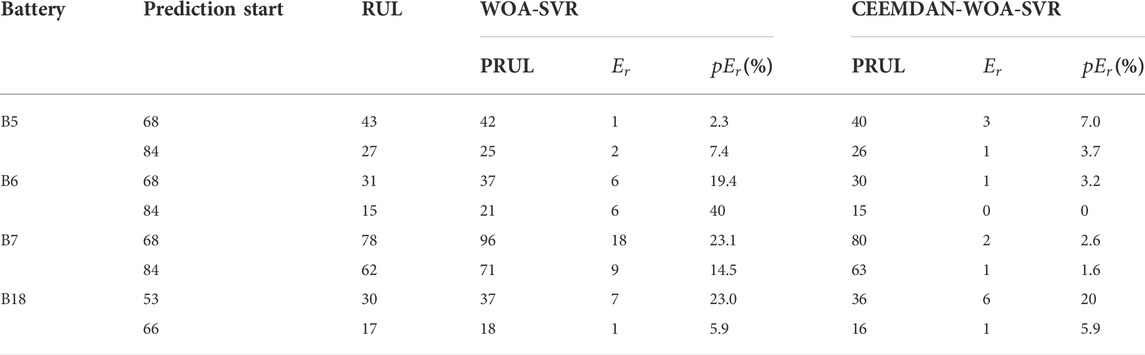
To verify the prediction performance of the proposed method, 40% (prediction start: 68, 68, 68, and 53) and 50% (prediction start: 84, 84, 84, and 66) of the total cycle data were used as training samples for prediction with the WOA-SVR method, respectively. The parameters of the WOA are set in Table 1. The prediction results are shown in Figures 6–9, Tables 2, 3.

TABLE 1

TABLE 1. Parameter setting of the algorithm.

FIGURE 6

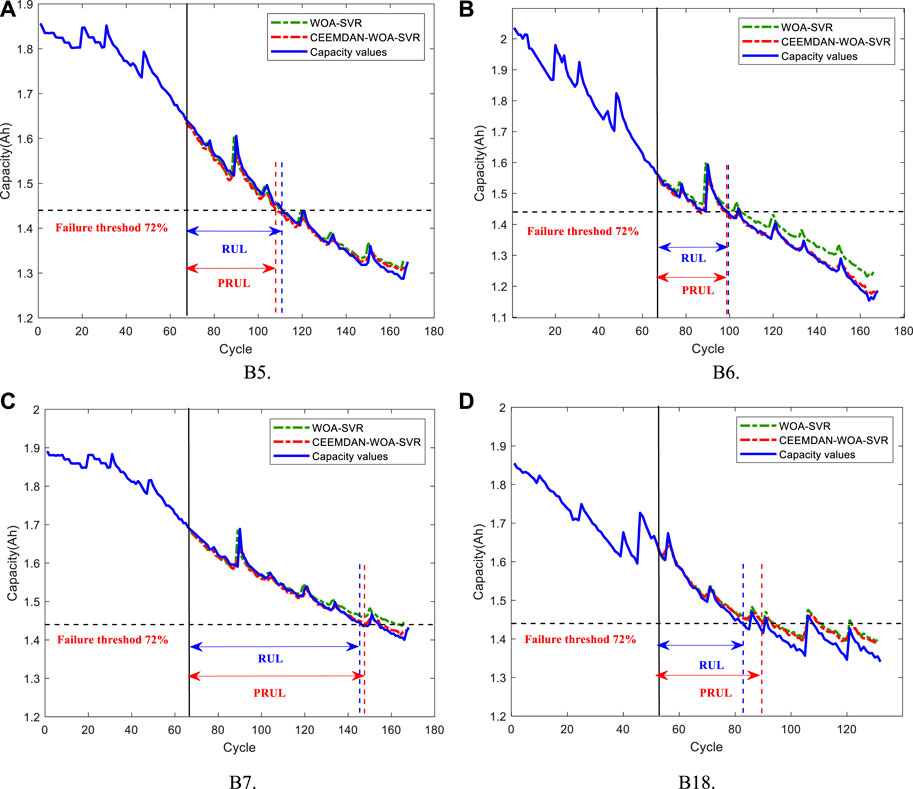
FIGURE 6. Prediction results of WOA-SVR and CEEMDAN-WOA-SVR (training samples with 40% cycle data). (A) B5, (B) B6, (C) B7, (D) B18.

TABLE 2

TABLE 2. The RUL prediction results of WOA-SVR and CEEMDAN-WOA-SVR methods.

TABLE 3

TABLE 3. Results of WOA-SVR and CEEMDAN-WOA-SVR methods for RUL prediction.

When the capacity failure threshold of the LIB is reached, the errors between the predicted remaining useful life (PRUL) and the RUL are calculated as:

$E_r=\left|PRUL-RUL\right|(27)$

$p{E}_r=\frac{\left|PRUL-RUL\right|}{RUL}\times 100\%(28)$

$E_r$ is used to reflect the predicted error of RUL, and $p{E}_r$ is applied to assess the accuracy of RUL prediction.

In Figures 6, 8; Table 2, the $E_r$ and$p{E}_r$ of the CEEMDAN-WOA-SVR method are less than the WOA-SVR method except for B5 (start = 68). Take the B7 battery as an example (start = 68), the $E_r$ and $p{E}_r$ of the WOA-SVR method are 18 and 23.1% respectively, whereas, the $E_r$ and $p{E}_r$ of the CEEMDAN-WOA-SVR method are 2 and 2.6% respectively. Compared with the WOA-SVR method, the $E_r$ and $p{E}_r$ of the CEEMDAN-WOA-SVR method are reduced by 89%.

FIGURE 8

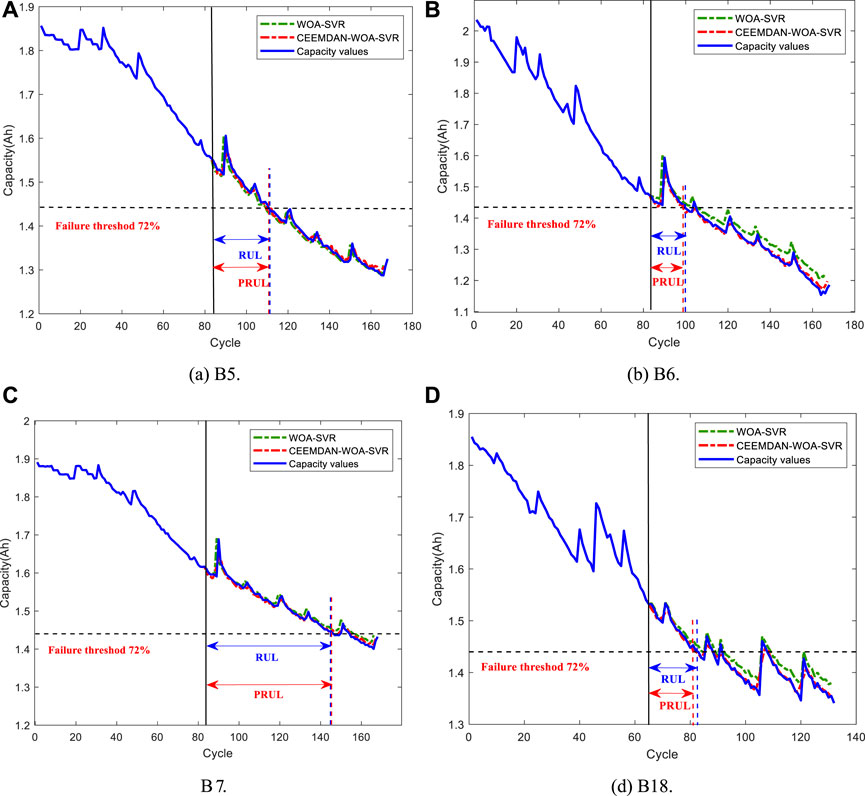
FIGURE 8. Prediction results of WOA-SVR and CEEMDAN-WOA-SVR (training samples with 50% cycle data). (A) B5, (B) B6, (C) B7, (D) B18.

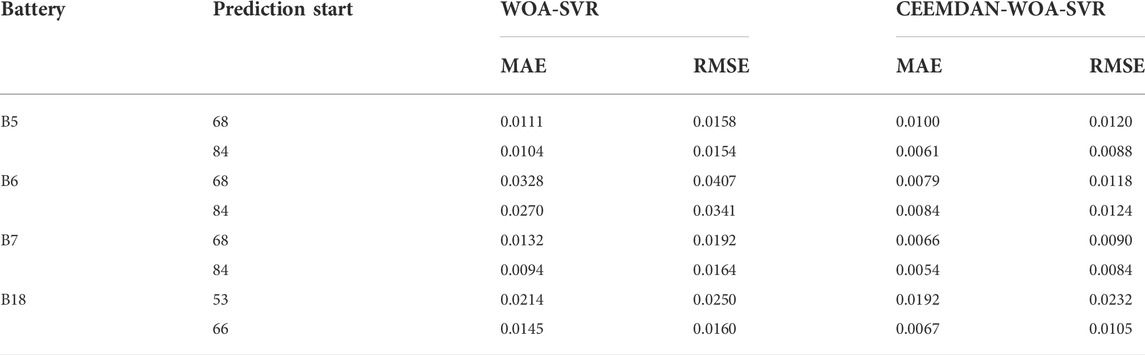
From Figures 7, 9; Table 3, it can be seen that MAEs and RMSEs of the CEEMDAN-WOA-SVR method are less than the WOA-SVR method. For example, when the prediction start number is 84 for the B6 battery, the MAE and RMSE of the WOA-SVR are 0.027 and 0.0341 respectively, whereas, the MAE and RMSE of the CEEMDAN-WOA-SVR are 0.0084 and 0.0124 respectively. Compared with the WOA-SVR method, the MAE of the CEEMDAN-WOA-SVR method is reduced by 69%, and the RMSE is reduced by 64%. Therefore, the accuracy of RUL prediction with the CEEMDAN-WOA-SVR method is better than the WOA-SVR method.

FIGURE 7

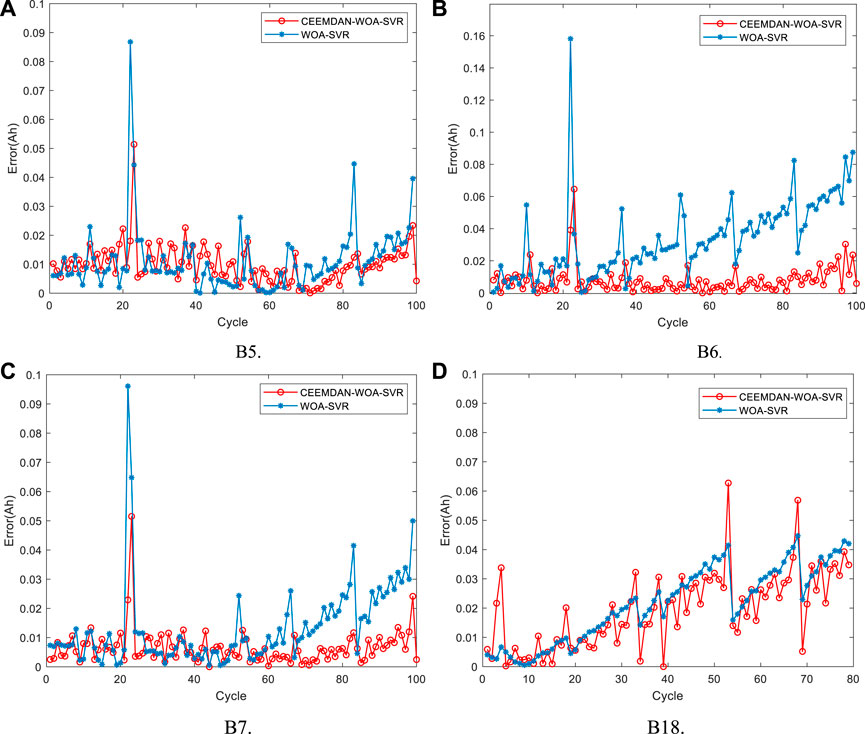
FIGURE 7. Absolute prediction errors of CEEMDAN-WOA-SVR and WOA-SVR (training samples with 40% cycle data). (A) B5, (B) B6, (C) B7, (D) B18.

FIGURE 9

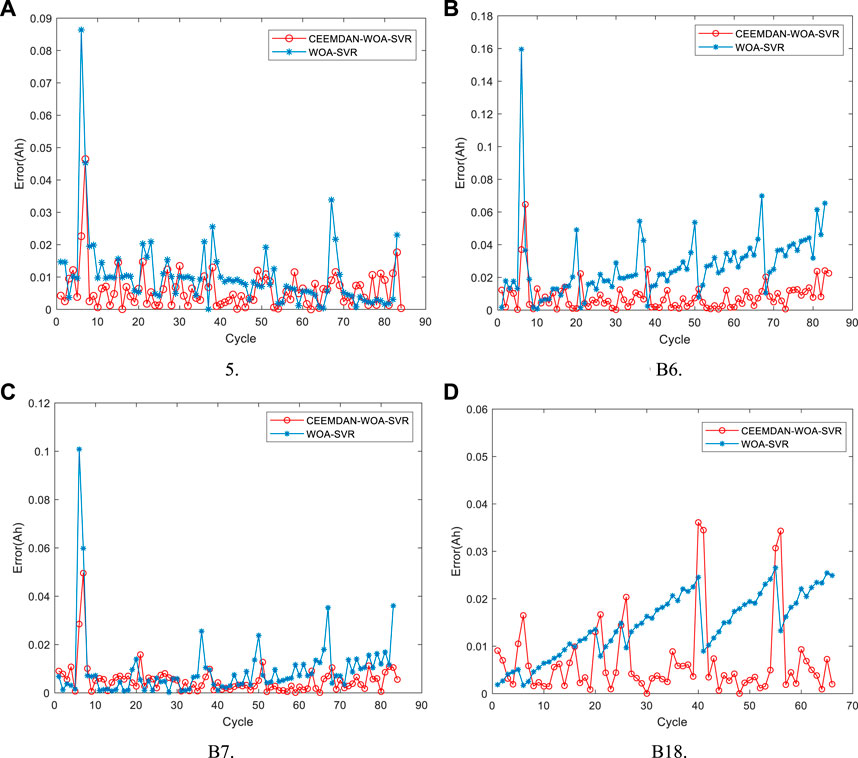
FIGURE 9. Absolute prediction Errors of CEEMDAN-WOA-SVR and WOA-SVR (training samples with 50% cycle data). (A) B5, (B) B6, (C) B7, (D) B18.

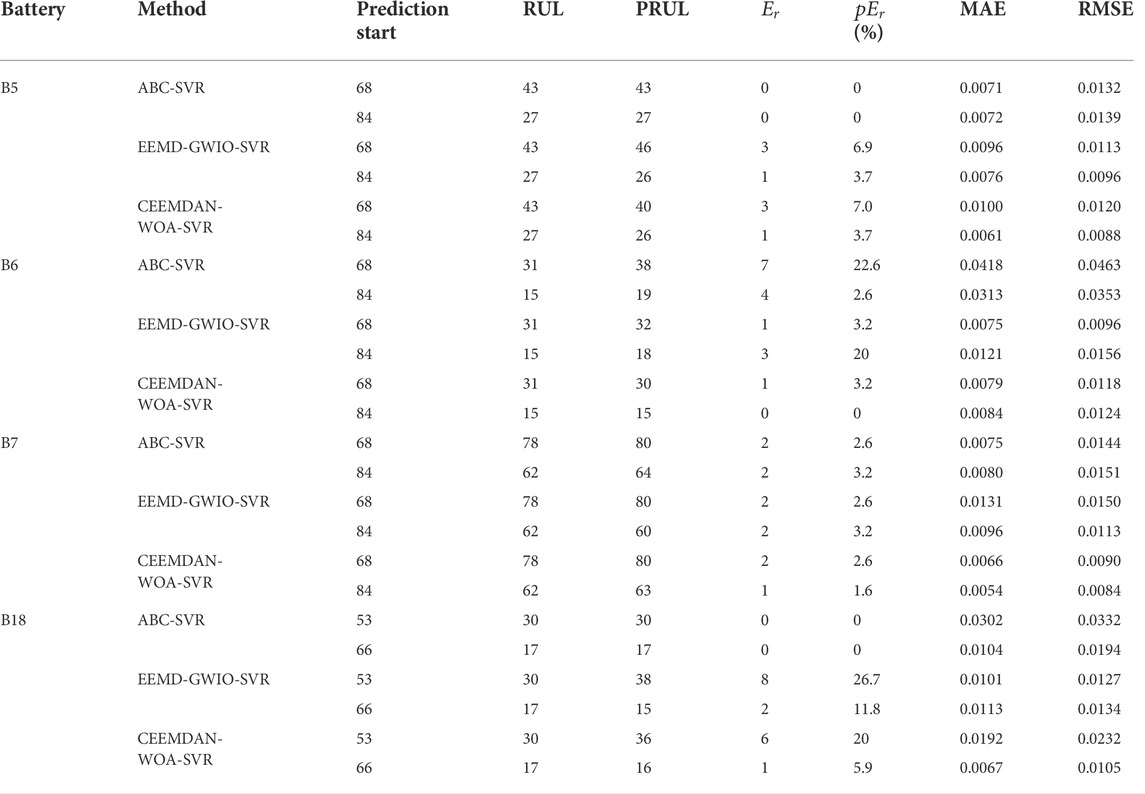
To further verify the effectiveness of the proposed method, the proposed method is compared with the methods in the literature under the same conditions. Wang et al. (2019) proposed an ABC-SVR method to predict the RUL, they employed ABC algorithm to select the kernel parameters of the SVR model. Yang et al. (2021) presented a hybrid model based on EEMD, GWO, and SVR to predict the RUL, they used EEMD to extract the degradation trend of battery capacity and employed the GWO algorithm to search the parameters of the SVR method. Table 4 lists the detailed comparison results of the CEEMDAN-WOA-SVR method and the two methods.

TABLE 4

TABLE 4. The RUL prediction results of CEEMDAN-WOA-SVR and other methods.

From Table 4, it is apparent that the prediction errors of the proposed method are also less than those of the existing methods in the literature. Take the B7 battery as an example (start = 84), the $E_r$, $p{E}_r$, MAE, and RMSE of the EEMD-GWO-SVR method are 1, 1.6%, 0.0054, and 0.0084, respectively. Compared with the two methods, the prediction errors of the proposed method are smaller.

Based on the above discussion, it can be concluded that the CEEMDAND method reduces the influence of noise on the prediction, and the CEEMDAN-WOA-SVR method could effectively improve the RUL prediction accuracy of LIBs.

5 Conclusion

The accurate RUL prediction of LIB is a critical technology for battery health management, which ensures the safe, stable, and efficient operation of the battery. In this study, a new method for the RUL prediction of lithium-ion batteries is proposed, which is combined with the CEEMDAN, WOA, and SVR methods. First, the battery capacity data is processed by CEEMDAN to reduce the impact of noise on the data sequence. Then, the WOA is applied to the SVR model for solving the parameter selection problem. Finally, a new method based on CEEMDAN and WOA-SVR is used for the RUL prediction of LIBs. To verify the efficacy of the CEEMDAN-WOA-SVR method, simulation experiments of LIBs RUL prediction using the WOA-SVR and CEEMDAN-WOA-SVR methods are performed. The results show that the $E_r$ and $p{E}_r$ of CEEMDAN-WOA-SVR method are less than the WOA-SVR method, and MAEs and RMSEs of the proposed method are less than the WOA-SVR method. As a result, the noise of the capacity sequence is reduced by CEEMDAN, which effectively improves the prediction performance. In addition, the prediction experiments are performed using the ABC-SVR and EEMD-GWO-SVR methods, and the results indicate that the errors of the CEEMDAN-WOA-SVR method are also smaller than the ABC-SVR method and EEMD-GWO-SVR method. Therefore, the CEEMDAN-WOA-SVR method is an effective tool for the RUL prediction of LIBs.

In this study, the MAE and RMSE are used to demonstrate the effectiveness of the CEEMDAN-WOA-SVR method. Compared with other SVR-based methods, the predicted results of the proposed method do not appear to be significantly improved. In future work, we will use other prognostics metrics, such as the accuracy index, alpha-lambda, and precision index, to verify the method’s performance. In addition, we will calculate the lower and upper bounds of the RUL prediction and compare them with the threshold value to achieve the prediction of the RUL.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: The datasets provided by the NASA Prognostics Center of Excellence.

Author contributions

XM: methodology, conceptualization, and writing. CC: conceptualization and data curation. YW: conceptualization and editing. QW: software. LT: validation.

Funding

This research is supported by the Anhui Province University Natural Science Research Project of China (Grant Nos. KJ2021A1164 and KJ2021A1165) and the nature research project of Anhui Xinhua University (Grant No. 2021zr002).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amroune, M., Bouktir, T., and Musirin, I. (2018). Power system voltage stability assessment using a hybrid approach combining dragonfly optimization algorithm and support vector regression. Arab. J. Sci. Eng. 43 (6), 3023–3036. doi:10.1007/s13369-017-3046-5

CrossRef Full Text | Google Scholar

Bracale, A., De Falco, P., Di Noia, L. P., and Rizzo, R. (2021). “Probabilistic state of health and remaining useful life prediction for Li-ion batteries,” in 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 02-05 February 2021. doi:10.1109/tpec51183.2021.9384939

CrossRef Full Text | Google Scholar

Chakraborty, S., Sharma, S., Saha, A. K., and Chakraborty, S. (2021). SHADE–WOA: A metaheuristic algorithm for global optimization. Appl. Soft Comput. 113, 107866. doi:10.1016/j.asoc.2021.107866

CrossRef Full Text | Google Scholar

Chen, W., Li, J., Wang, Q., and Han, K. (2021). Measurement, 172. doi:10.1016/j.measurement.2020.108901Fault feature extraction and diagnosis of rolling bearings based on wavelet thresholding denoising with CEEMDAN energy entropy and PSO-LSSVM

CrossRef Full Text | Google Scholar

Chen, Z., Shi, N., Ji, Y., Niu, M., and Wang, Y. (2021). Lithium-ion batteries remaining useful life prediction based on BLS-RVM. Energy 234, 121269. doi:10.1016/j.energy.2021.121269

CrossRef Full Text | Google Scholar

Deng, L., Shen, W., Wang, H., and Wang, S. (2020). A rest-time-based prognostic model for remaining useful life prediction of lithium-ion battery. Neural comput. Appl. 33 (6), 2035–2046. doi:10.1007/s00521-020-05105-0

CrossRef Full Text | Google Scholar

Ge, M.-F., Liu, Y., Jiang, X., and Liu, J. (2021). A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 174, 109057. doi:10.1016/j.measurement.2021.109057

CrossRef Full Text | Google Scholar

Goebel, K., Saha, B., Saxena, A., Celaya, J. R., Christophersen, J. P. J. I. i., and magazine, m. (2008). IEEE Instrum. Meas. Mag. 11 (4), 33–40. doi:10.1109/mim.2008.4579269

CrossRef Full Text

Guha, A., and Patra, A. (2018). Online estimation of the electrochemical impedance spectrum and remaining useful life of lithium-ion batteries. IEEE Trans. Instrum. Meas. 67 (8), 1836–1849. doi:10.1109/tim.2018.2809138

CrossRef Full Text | Google Scholar

Hong, G., Song, W., Gao, Y., Zio, E., and Kudreyko, A. (2022). An iterative model of the generalized Cauchy process for predicting the remaining useful life of lithium-ion batteries. Measurement 187, 110269. doi:10.1016/j.measurement.2021.110269

CrossRef Full Text | Google Scholar

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., et al. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Math. Phys. Eng. Sci. 454 (1971), 903–995. doi:10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

Li, W., Shi, Q., Sibtain, M., Li, D., and Mbanze, D. E. (2020). A hybrid forecasting model for short-term power load based on sample entropy, two-phase decomposition and whale algorithm optimized support vector regression. IEEE Access 8, 166907–166921. doi:10.1109/access.2020.3023143

CrossRef Full Text | Google Scholar

Liu, L., Liu, J., Zhou, Q., and Qu, M. (2021). An SVR-based machine learning model depicting the propagation of gas explosion disaster hazards. Arab. J. Sci. Eng. 46 (10), 10205–10216. doi:10.1007/s13369-021-05616-5

CrossRef Full Text | Google Scholar

Malik, A., Tikhamarine, Y., Souag-Gamane, D., Rai, P., Sammen, S. S., and Kisi, O. (2021). Support vector regression integrated with novel meta-heuristic algorithms for meteorological drought prediction. Meteorol. Atmos. Phys. 133 (3), 891–909. doi:10.1007/s00703-021-00787-0

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Peng, Y., Liu, Y., Zhang, C., and Wu, L. (2021). A novel denoising model of underwater drilling and blasting vibration signal based on CEEMDAN. Arab. J. Sci. Eng. 46 (5), 4857–4865. doi:10.1007/s13369-020-05274-z

CrossRef Full Text | Google Scholar

Qin, W., Lv, H., Liu, C., Nirmalya, D., and Jahanshahi, P. (2019). Remaining useful life prediction for lithium-ion batteries using particle filter and artificial neural network. Industrial Manag. Data Syst. 120 (2), 312–328. doi:10.1108/imds-03-2019-0195

CrossRef Full Text | Google Scholar

Ren L., L., Dong, J., Wang, X., Meng, Z., Zhao, L., and Deen, M. J. (2021). A data-driven auto-CNN-LSTM prediction model for lithium-ion battery remaining useful life. IEEE Trans. Ind. Inf. 17 (5), 3478–3487. doi:10.1109/tii.2020.3008223

CrossRef Full Text | Google Scholar

Ren, X., Liu, S., Yu, X., and Dong, X. (2021). A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 234, 121236. doi:10.1016/j.energy.2021.121236

CrossRef Full Text | Google Scholar

Saidala, R. K., and Devarakonda, N. (2018). “Improved whale optimization algorithm case study: Clinical data of anaemic pregnant woman,” in Data engineering and intelligent computing. Singapore: Springer. doi:10.1007/978-981-10-3223-3_25

CrossRef Full Text | Google Scholar

Smola, A. J., and Schölkopf, B. J. S. (2004). A tutorial on support vector regression. Stat. Comput. 14 (3), 199–222. doi:10.1023/b:stco.0000035301.49549.88

CrossRef Full Text | Google Scholar

Su, X., Wang, S., Pecht, M., Zhao, L., and Ye, Z. (2017). Interacting multiple model particle filter for prognostics of lithium-ion batteries. Microelectron. Reliab. 70, 59–69. doi:10.1016/j.microrel.2017.02.003

CrossRef Full Text | Google Scholar

Tang, T., and Yuan, H. (2022). An indirect remaining useful life prognosis for Li-ion batteries based on health indicator and novel artificial neural network. J. Energy Storage 52, 104701. doi:10.1016/j.est.2022.104701

CrossRef Full Text | Google Scholar

Tikhamarine, Y., Malik, A., Pandey, K., Sammen, S. S., Souag-Gamane, D., Heddam, S., et al. (2020). Monthly evapotranspiration estimation using optimal climatic parameters: Efficacy of hybrid support vector regression integrated with whale optimization algorithm. Environ. Monit. Assess. 192 (11), 696. doi:10.1007/s10661-020-08659-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, F.-K., and Mamo, T. (2018). A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 401, 49–54. doi:10.1016/j.jpowsour.2018.08.073

CrossRef Full Text | Google Scholar

Wang, X., Gao, S., Zhou, S., Guo, Y., Duan, Y., Wu, D., et al. (2021). Prediction of house price index based on bagging integrated WOA-SVR model. Math. Problems Eng. 2021, 1–15. doi:10.1155/2021/3744320

CrossRef Full Text | Google Scholar

Wang, Y., Ni, Y., Lu, S., Wang, J., and Zhang, X. (2019). Remaining useful life prediction of lithium-ion batteries using support vector regression optimized by artificial bee colony. IEEE Trans. Veh. Technol. 68 (10), 9543–9553. doi:10.1109/tvt.2019.2932605

CrossRef Full Text | Google Scholar

Wei, J., Dong, G., and Chen, Z. (2018). Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 65 (7), 5634–5643. doi:10.1109/tie.2017.2782224

CrossRef Full Text | Google Scholar

Xing, Y., Ma, E. W. M., Tsui, K.-L., and Pecht, M. (2013). An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 53 (6), 811–820. doi:10.1016/j.microrel.2012.12.003

CrossRef Full Text | Google Scholar

Xue, Z., Zhang, Y., Cheng, C., and Ma, G. (2020). Remaining useful life prediction of lithium-ion batteries with adaptive unscented kalman filter and optimized support vector regression. Neurocomputing 376, 95–102. doi:10.1016/j.neucom.2019.09.074

CrossRef Full Text | Google Scholar

Yang, Z., Wang, Y., and Kong, C. (2021). Remaining useful life prediction of lithium-ion batteries based on a mixture of ensemble empirical mode decomposition and GWO-SVR model. IEEE Trans. Instrum. Meas. 70, 1–11. doi:10.1109/tim.2021.3125108

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Yang, L., Guo, W., Qiang, J., Peng, C., Li, Q., et al. (2022). A deep learning method for lithium-ion battery remaining useful life prediction based on sparse segment data via cloud computing system. Energy 241, 122716. doi:10.1016/j.energy.2021.122716

CrossRef Full Text | Google Scholar

Zhang, Z., and Hong, W.-C. (2019). Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dyn. 98 (2), 1107–1136. doi:10.1007/s11071-019-05252-7

CrossRef Full Text | Google Scholar

Zhao, Q., Qin, X., Zhao, H., and Feng, W. (2018). A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries. Microelectron. Reliab. 85, 99–108. doi:10.1016/j.microrel.2018.04.007

CrossRef Full Text | Google Scholar

Nomenclature

Variables

$\mathit{b}$ constant number

${\mathit{b}}_{\mathit{c}}$ intercept parameter

$\mathit{C}$ penalty parameter

${\mathit{C}}_{\mathit{i}}$ i-th correlation coefficient

${\mathit{D}}_{\mathit{m}}$ variable dimension

${\mathit{E}}_{\mathit{r}}$ absolute predicted error of RUL

$\mathit{f}\left(\mathit{x}\right)$ regression function

$\mathit{I}$ decomposition time

${\mathit{I}\mathit{M}\mathit{F}}_{\mathit{i}}\left(\mathit{t}\right)$ i-th modal component

$\mathit{K}\left({\mathit{x}}_{\mathit{i}},\mathit{x}\right)$ kernel function

$\mathit{l},\mathit{p},\mathit{r}$ random numbers

$\mathit{n}$ cycle time number

$\mathit{N}$ length of the time series

$\mathit{N}\mathit{P}$ population number

$\mathit{p}{\mathit{E}}_{\mathit{r}}$ relative prediction error of RUL

${\mathit{r}}_1\left(\mathit{n}\right)$ first residual sequence

${\mathit{r}}_{\mathit{k}}\left(\mathit{n}\right)$ k-th residue sequence

$\mathit{R}\left(\mathit{n}\right)$ residual sequence

$\mathit{s}\left(\mathit{n}\right)$ original signal sequence

$\mathit{t}$ current number of iteration

${\mathit{T}}_{\mathbf{max}}$ maximum number of iteration

$\mathit{\nu }\left(\mathit{n}\right)$ Gaussian white noise

${\mathit{x}}_{\mathit{i}}$ i-th battery capacity value

${\mathit{x}}_{\mathbf{max}}$ maximum value of battery capacity

${\mathit{x}}_{\mathbf{min}}$ minimum value of battery capacity

${\mathit{X}}_{\mathit{i},\mathit{t}}$ solution in the current generation

${\mathit{X}}_{\mathit{i},\mathit{t}+1}$ solution in the next generation

${\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}$ best solution in the current generation

${\mathit{X}}_{\mathit{r}\mathit{a}\mathit{n}\mathit{d},\mathit{t}}$ random solution in the current generation

$\mathit{x}\left(\mathit{t}\right)$ original signal sequence value

${\widehat{\mathit{y}}}_{\mathit{i}}$ predicted value at the i-th cycle

${\mathit{y}}_{\mathit{i}}$ actual value at the i-th cycle

$\mathit{\phi }\left(\mathit{x}\right)$ transfer function

$\mathit{\omega }$ weight parameter

${\mathit{\xi }}_{\mathit{i}}$, ${\mathit{\xi }}_{\mathit{i}}^{*}$ slack variables

$\mathit{\epsilon }$ boundary value

$\mathit{\sigma }$ kernel parameter

${\mathit{\alpha }}_{\mathit{i}}$, ${\mathit{\alpha }}_{\mathit{i}}^{*}$ Lagrange multipliers

Abbreviations

ABC artificial bee colony

ANN artificial neural network

CEEMDAN complete ensemble empirical mode decomposition with adaptive noise

CNN convolutional neural networks

EEMD ensemble empirical mode decomposition

EMD empirical mode decomposition

EOL end of life

GWO gray wolf optimization

IMF intrinsic mode function

LIB lithium-ion battery

MAE mean absolute error

MSE mean square error

PF particle filtering

PRUL predicted remaining useful life

RMSE root mean square error

RUL remaining useful life

SVM support vector machine

SVR support vector regression

WOA whale optimization algorithm