Pore-scale phenomena in carbon geological storage (Saline aquifers—Mineralization—Depleted oil reservoirs)

The injection of CO₂ into geological formations triggers inherently coupled thermo-hydro-chemo-mechanical processes. The reservoir pressure and temperature determine the CO₂ density, the CO₂-water interfacial tension, and the solubility of CO₂ in water (hindered by salts and competing gases). The CO₂-water interface experiences marked pinning onto mineral surfaces, and contact angles can range from the asymptotic advancing to receding values, in contrast to the single contact angle predicted by Young’s equation. CO₂ dissolves in water to form carbonic acid and the acidified water dissolves minerals; mineral dissolution enhances porosity and permeability, triggers settlement, may couple with advection to form “wormholes”, produces stress changes and may cause block sliding and shear bands. Convective currents can emerge beneath the CO₂ plume and sustain CO₂ and mineral dissolution processes. On the other hand, mineralization is a self-homogenizing process in advective regimes. The crystallization pressure can exceed the tensile capacity of the host rock and create new surfaces or form grain-displacive lenses. Within the rock matrix, coupled reactive-diffusion-precipitation results in periodic precipitation bands. Adequate seal rocks for CO₂ geological storage must be able to sustain the excess capillary pressure in the buoyant CO₂ plume without experiencing open-mode discontinuities or weakening physico-chemical interactions. CO₂ injection into depleted oil reservoirs benefits from time-proven seals; in addition, CO₂ can mobilize residual oil to simultaneously recover additional oil through oil swelling, ganglia destabilization, the reduction in oil viscosity and even miscible displacement. Rapid CO₂ depressurization near the injection well causes cooling under most anticipated reservoir conditions; cooling can trigger hydrate and ice formation, and reduce permeability. In some cases, effective stress changes associated with the injection pressure and cooling thermoelasticity can reactivate fractures. All forms of carbon geological storage will require large reservoir volumes to hold a meaningful fraction of the CO₂ that will be emitted during the energy transition.

Introduction

We emit ∼40 billion tons of CO₂ per year, however, emissions should decrease to ≤18 billion tons per year to prevent further global warming (IPCC, 2021). This scenario will require reduced fossil fuel consumption and CO₂ capture and geological storage. Currently, the total capacity of operating CO₂ storage facilities is 150 million tons/year (GCCSI, 2021), i.e., three orders of magnitude lower than needed. Therefore, thousands of new geological storage projects must come online in the near future.

The injection of CO₂ into geological formations triggers inherently coupled thermo-hydro-chemo-mechanical processes. In this manuscript, we present a comprehensive review of the underlying physical processes, summarize the properties of bulk phases and interfaces, and analyze the most relevant pore-scale phenomena that can affect the long-term geological storage of CO₂.

CO₂ and aqueous solutions: Properties and interactions

Fluids involved in carbon geological storage exhibit different pressure and temperature-dependent bulk properties, solubilities and capillary response.

Density

The pressure and temperature-dependent CO₂ density determines storage capacity, gravity-driven displacement, instabilities, and capillary pressure against the seal (Van der Meer, 1993; DiCarlo, 2013). Figure 1 shows the density ρ [kg/m³] of water, oil and CO₂ as a function of pressure and temperature: the density of CO₂ varies significantly but remains a buoyant phase, while water is the heavier fluid in high-temperature reservoirs.

FIGURE 1

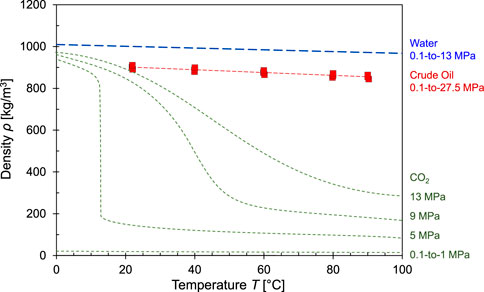
FIGURE 1. Density as a function of pressures and temperature: water, crude oil and CO₂. Data sources: Karnanda et al., 2013, NIST Chemistry WebBook., 2022, Freund et al., 2006.

Geological storage projects can involve gas, liquid and supercritical CO₂ (Figure 2). The gas-liquid phase boundary $P=\mathit{0.0008}{\left(\frac{T}{°C}\right)}^{\mathrm{2}}+\mathit{0.1}\left(\frac{T}{°C}\right)+\mathit{3.5}\mathrm{M}\mathrm{P}\mathrm{a}$ applies until the critical point (T = 31°C and P = 7.37 MPa).In the supercritical regime, beyond the critical point, the Widom line divides the lighter gaseous-like regime from the denser liquid-like regime (Simeoni et al., 2010; Houben et al., 2021). Density gradients in P or T are pronounced across the Widom line, particularly near the critical point; for example, the CO₂ density changes from 661 kg/m³ to 285 kg/m³ when the temperature increases from 35°C to 50°C at a constant pressure of P = 8.5 MPa (see Figure 2).

FIGURE 2

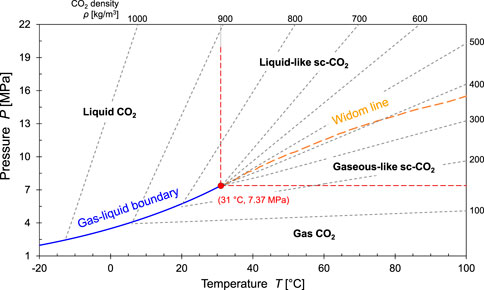
FIGURE 2. Carbon dioxide phase diagram. Note that there are marked changes across the Widom line within the supercritical regime. Data for density lines: Bachu., 2003.

Viscosity

Liquid CO₂ and water are Newtonian fluids, yet most crude oils exhibit some shear thinning. Figure 3 shows the reduction in viscosity μ [μPa⋅s] with temperature for different types of crude oils, water and CO₂ (Note: viscosity shown in log-scale). Molecular vibration acts against intermolecular attraction hence the viscosity of liquids decreases with higher temperature while pressure has a second-order effect. On the other hand, the viscosity of gases tends to increase with temperature and pressure because the collision frequency increases. The viscosity of CO₂ is much lower than water and oil, and it experiences sharp changes across the liquid-gas LG phase boundary and the Widom line WL in agreement with density changes.

FIGURE 3

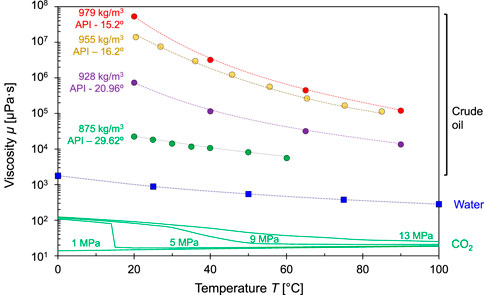
FIGURE 3. Viscosity as a function of temperature: various crude oils (●), water (■) and CO₂ (continue lines - different pressures). Crude oils include heavy (density $\rho$ = 979 kg/m³, 955 kg/m³), medium ($\rho$ = 928 kg/m³) and light oils ($\rho$ = 875 kg/m³). Data sources: water: Schmelzer et al. (2005), crude oil: Gachuz-Muro and Sohrabi., 2013, Akhmadiyarov et al., 2019 and CO₂: NIST Chemistry WebBook., 2022.

Interfacial tension

Interfacial tension γ [mN/m] and contact angle θ [°] determine capillary phenomena between multiphase fluids in porous media. The capillary pressure ΔP is the pressure difference between the non-wetting P_nw [Pa] and the wetting P_w [Pa] fluid; for a spherical interface of radius r [m]

$P_{nw}-P_w=P_c=\frac{\mathrm{2}\gamma \bullet \mathit{cos}\theta }{r}(1)$

The interfacial tension between CO₂ and water is reported as a function of pressure and temperature in most cases. However, intermolecular distance $l_{\mathit{0}}$ [m] determines molecular interaction at the interface, therefore the CO₂ density ρ [kg/m³] which scales as $\rho \propto l_{\mathit{0}}^{-\mathit{3}}$ is a more meaningful parameter to predict the interfacial tension. Figure 4 plots compiled CO₂-water interfacial tension data gathered from the literature and our own studies as a function of CO₂ density (computed from reported pressure and temperature conditions): there is a clear decrease in the interfacial tension with increasing CO₂ density. The remaining spread in the data indicates that thermal vibration affects interfacial tension beyond its role on density(in addition to measurement variability among devices and test protocols).

FIGURE 4

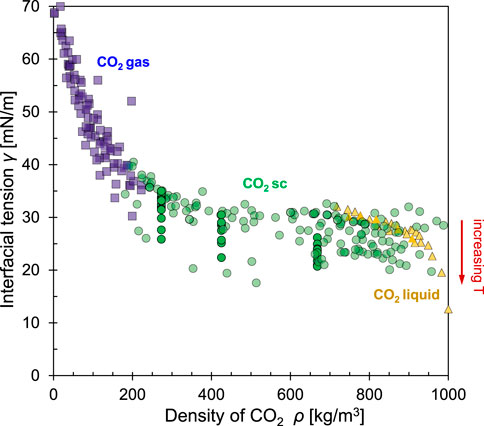
FIGURE 4. The interfacial tension between CO₂ and water as a function of CO₂ density. The dataset combines results for CO₂ in gas (■), super critical (●) and liquid states (▲). Note: density determines molecular proximity for electrical interactions, thus, it emerges as the governing variable. Still, the data spread is due to thermal effects: interfacial tension decreases with increased random vibration. Data sources: Hough et al., 1952, Park et al., 2005, Sutjiadi-Sia et al., 2008, Chun and Wilkinson., 1995, Da Rocha et al., 1999, Hebach et al., 2002, Chiquet et al., 2007, Kvamme et al., 2007, Espinoza and Santamarina., 2010, Georgiadis et al., 2010, and measurements by the authors for this study (2022).

Wettability—contact angles

Wettability captures the interaction between two fluids and the mineral surface. Wettability plays a critical role in capillary phenomena, pore-scale fluid arrangement, and macroscopic multiphase flow in CO₂ geological storage.

Contact angle measurements provide an apparently simple assessment of the otherwise complex physical processes that underline wettability (Sargent et al., 2005; Drelich et al., 2020). Force equilibrium parallel to the mineral surface relates the contact angle to the interfacial tensions γ [N/m] between the fluid F, liquid L and solid S (Young, 1805):

$\sum F_H={\left({\gamma }_{FS}-{\gamma }_{LS}\right)-\gamma }_{LF}\cos \theta (2)$

On the other hand, force equilibrium normal to the substrate surface allows us to anticipate the adhesion A [N/m] between the liquid-fluid interface and the mineral substrate $A={\gamma }_{LF}\sin \theta$. Equilibrium contact angle measurements show that both calcite and quartz are strongly water-wet (Figure 5, Bikkina, 2011; Arif et al., 2017a).

FIGURE 5

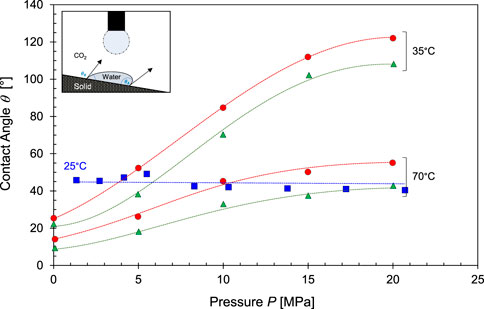
FIGURE 5. Contact angle formed by a water droplet on calcite in a CO₂ atmosphere as function of CO₂ pressure. Advancing contact angle (●), receding contact angle (▲) and static contact angle (■). Data sources: Bikkina, 2011, Arif et al., 2017a. For clarity, only a subset of the dataset is presented in this figure.

In contrast to the single thermodynamic contact angle predicted by Young’s equation, interfaces can exhibit a range of contact angles between two asymptotic values: the advancing contact angle ${\theta }_A$ and the receding contact angle ${\theta }_R$ when it is measured in a quasi-static condition. For example, a deionized water droplet resting on a horizontal smooth calcite surface surrounded by supercritical CO₂ at P = 9 MPa and T = 40°C forms an advancing contact angle ${\theta }_A$ = 138° and a receding contact angle ${\theta }_R=$20° (quasi-static injection/extraction measurements conducted for this study). Even dynamic measurements show marked hysteresis; for example, a water droplet released on a smooth calcite surface in a CO₂ environment at P = 20 MPa and T = 35°C exhibits an advancing contact angle ${\theta }_A$ = 122° and a receding contact angle ${\theta }_R=$108° (see inset in Figure 5—Note: dynamic contact angle measurements based on a sliding droplet do not capture the full pinning effect of the contact line measured in quasi-static tests at the verge of sliding, thus, hysteresis in dynamic tests is smaller than in quasi-static tests—Huhtamäki, et al., 2018).

X-ray CT measurements confirm these observations and show that a wide range of contact angles exist in-situ possibly due to (Andrew et al., 2014): 1) the contact line adhesion A, 2) surface roughness and chemical inhomogeneities on the solid surface (de Gennes, 1985; Eral et al., 2013), and 3) the fact that in-situ contact angles rarely represent equilibrium conditions.

Let’s modify Young’s force equilibrium analysis parallel to the mineral surface to take into consideration the adhesion force A acting against both advancing on receding directions; then the anticipated contact angle hysteresis is ${\cos \theta }_R-{\cos \theta }_A=\mathit{2}A/{\gamma }_{LF}$. Conversely, we can recover the adhesion force from contact angle hysteresis measurements $A={\gamma }_{LF}\left(\cos {\theta }_R-{\cos \theta }_A\right)/\mathit{2}$. Evidently, the adhesion force scales with the liquid-fluid interfacial tension ${\gamma }_{LF}$ and should not be ignored in wettability analyses. For example, consider the water-CO₂-calcite system reported above: the computed adhesion force A = 18.8 mN/m while the water-CO₂ interfacial tension is ${\gamma }_{LF}=$ 22.39 mN/m (${\theta }_A$ = 138°, ${\theta }_R=$20°).

CO₂ solubility in aqueous solutions

While two phases may exhibit interfacial tension, their mutual solubilities can have important implications. For example, CO₂ dissolves in water and enhances carbon geological storage, on the other hand, minerals dissolve in CO₂-acidified water and may trigger internal instabilities (details follow).

The solubility of CO₂ in water increases with pressure but decreases with temperature. Henry’s law relates solubility χ [mol/l] to the partial pressure of CO₂ P_CO2 [kPa] through the temperature dependent Henry’s constant k_H [mol L⁻¹ kPa⁻¹]:

${\chi }_{C{O}_{\mathrm{2}}}=k_H{P}_{C{O}_{\mathrm{2}}}(3)$

where k_H = 3.4 × 10^–4 [mol L⁻¹ kPa⁻¹] at temperature T = 298.15 K. Figure 6A shows the evolving CO₂ solubility in water as a function of pressure for different temperatures.

FIGURE 6

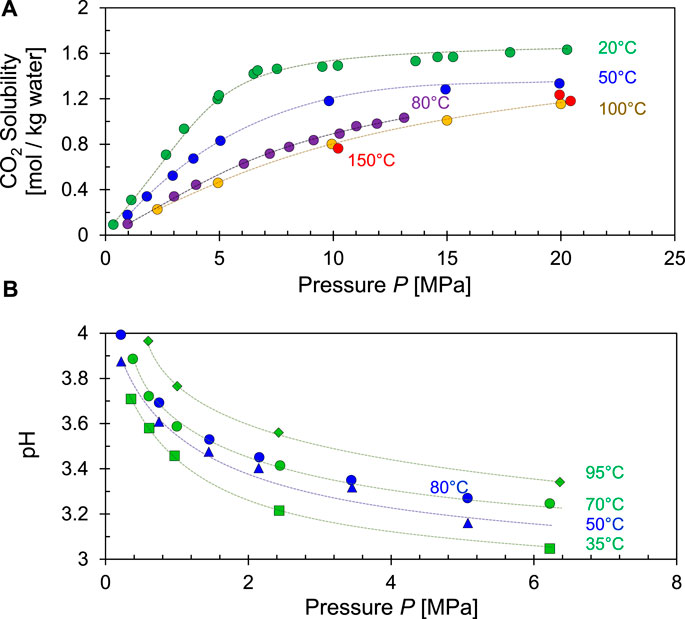
FIGURE 6. Solubility of CO₂ in water and change in pH. (A) CO₂ solubility increases with pressure but decreases with temperatures—Data sources: Duan and Sun., 2003, Sanaei et al., 2019. (B) Equilibrium pH for CO₂ saturated water as a function of pressure and temperatures—Data sources: blue = Haghi et al., 2017; green = Peng et al., 2013.

CO₂ dissolves in water to form aqueous carbon dioxide CO₂ (aq). The ionization of carbonic acid produces H⁺ and decreases the pH:

$\mathrm{C}{\mathrm{O}}_2\left(\mathrm{g}\right)\iff \mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)(4)$

$\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)+{\mathrm{H}}_2\mathrm{O}\iff {\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3\mathrm{Log}{\mathrm{K}}_{25°\mathrm{C}}=-8.23(5)$

${\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3\iff {\mathrm{H}}^{+}+\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{-}\mathrm{Log}{\mathrm{K}}_{25°\mathrm{C}}=-\mathrm{6.38}(6)$

$\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{-}\iff {\mathrm{H}}^{+}+\mathrm{C}{\mathrm{O}}_3^{2-}\mathrm{Log}{\mathrm{K}}_{25°\mathrm{C}}=-\mathrm{10.48}(7)$

Therefore, the equilibrium pH for water with dissolved CO₂ is also a function of pressure and temperature (Figure 6B).

Effect of salinity

High salinity is a common condition in reservoirs considered for CO₂ geological storage, such as saline aquifers, depleted hydrocarbon reservoirs and coalbeds. In general, CO₂ solubility in water may either increase (salting-in effect, e.g. NaClO₄ and K₃PO₄) or decrease (salting-out effect, e.g., salts from strong bases and strong acids such as NaCl, CaCl₂ and MgCl₂ (Yasunishi and Yoshida 1979; García, 2005; García et al., 2005). In most geological settings, CO₂ solubility decreases with salt concentration as water mobility decreases, particularly for small high-valence ions. Consequently, the CO₂ solubility in salt solutions at the same ionic concentration follows the following sequence: highest in KCl solutions → NaCl → CaCl₂ → lowest in MgCl₂ solutions. Figure 7 shows that the solubility of CO₂ decreases by ∼50% for a 3 mol NaCl solution compared to deionized water. Therefore, the storage capacity for dissolved CO₂ decreases by half and the needed reservoir size doubles in brine saturated formations.

FIGURE 7

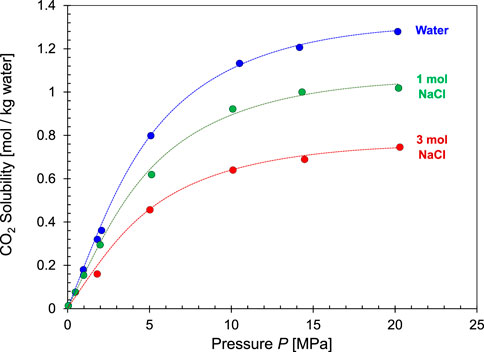
FIGURE 7. The effect of salinity on CO₂ solubility in NaCl solutions as a function of pressures (T = 50°C—Data source: Koschel et al., 2006). Data at p = 101.3 kPa were gathered at T = 25°C thus solubility values are higher than the rest of the trend for T = 50°C (Data sources: Markham and Kobe., 1941; Koschel et al., 2006; Duan et al., 2006; Kiepe et al., 2002).

Effect of mixed gases

Flue gas released at power plants and industrial sources contains N₂ (∼66%), CO₂ (10%–15%), water vapor, other gases such as SO₂, H₂S, NO₂, and light hydrocarbons such as CH₄ (Bell et al., 2021). Separation is costly and the presence of competing gases affects the solubility of CO₂ in water mainly because: (1) the solubility of CO₂ in water depends on its partial pressure which decreases in a mixed gas at constant total pressure, and (2) competing ions. In the case of a N₂-CO₂-water system, N₂ does not react with water, therefore the solubility of CO₂ only depends on its partial pressure or mole fraction in the mixed gas (Figure 8A).

FIGURE 8

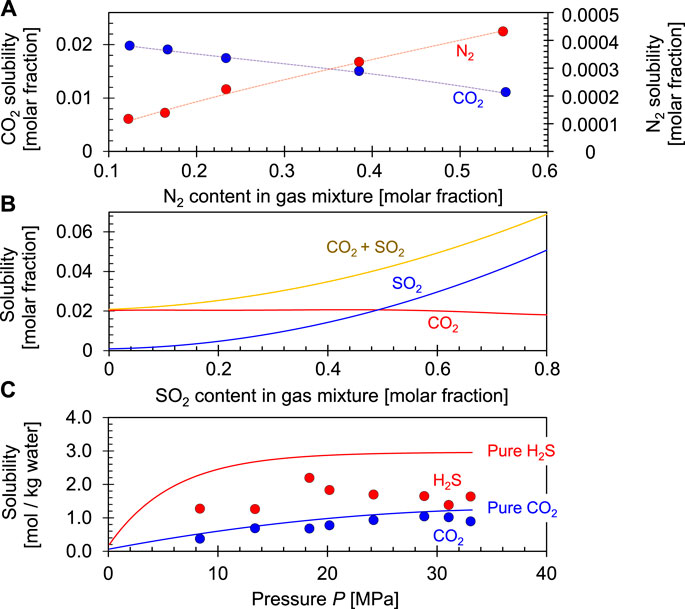
FIGURE 8. Effects mixed gas of CO₂ solubility. (A) CO₂ and N₂ solubilities in the N₂+CO₂+H₂O systems at a T = 34.85°C and p = 8.0 MPa. Data source: Nakhaei-Kohani et al., 2022. (B) CO₂ and SO₂ solubilities in the SO₂+CO₂+H₂O systems at a T = 50°C and p = 10 MPa. Data source: Miri et al., 2014. (C) CO₂ and H₂S solubilities in the H₂S + CO₂+H₂O systems at a T = 120°C. Trends and data from Savary et al., 2012.

Similar to salt, coexisting gases can either promote or inhibit CO₂ solubility, yet competition is more common in carbon storage. For example, the dissolution of SO₂ in water involves the following reactions (Goldberg and Parker., 1985):

$\mathrm{S}{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}_2\mathrm{S}{\mathrm{O}}_3(8)$

${\mathrm{H}}_2\mathrm{S}{\mathrm{O}}_3\rightleftharpoons {\mathrm{H}}^{+}+\mathrm{H}\mathrm{S}{\mathrm{O}}_3^{-}(9)$

$\mathrm{H}\mathrm{S}{\mathrm{O}}_3^{-}\rightleftharpoons {\mathrm{H}}^{+}+\mathrm{S}{\mathrm{O}}_3^{2-}(10)$

$2\mathrm{H}\mathrm{S}{\mathrm{O}}_3^{-}\rightleftharpoons {\mathrm{S}}_2{\mathrm{O}}_5^{2-}+{\mathrm{H}}_2\mathrm{O}(11)$

The generated H⁺ competes with the ionization of carbonic acid and decreases the CO₂ solubility (Figure 8B). Similarly, H₂S dissolution in water inhibits CO₂ dissolution as well (Figure 8C):

${\mathrm{H}}_2\mathrm{S}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}^{+}+\mathrm{H}{\mathrm{S}}^{-}(12)$

$\mathrm{H}{\mathrm{S}}^{-}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}^{+}+{\mathrm{S}}^{2-}(13)$

Fluid-Mineral interaction: Dissolution and precipitation

Water acidifies in the presence of CO₂ and prompts mineral dissolution. The consequences of reactive fluids on the reservoir and seal stability require careful consideration.

Mineral dissolution in CO₂ acidified water

A mineral’s crystal structure determines its susceptibility to dissolution in CO₂ acidified water. In particular, crystallographic orientation may cause spatially heterogeneous dissolution (Daval et al., 2013; Pollet-Villard et al., 2016; Oelkers et al., 2018).

Crystal structure

Silicates and carbonates are the most common minerals in CO₂ geological reservoirs. Others, minerals include oxides, sulfides, sulfate and halide.

Silicates are abundant and chemically reactive with carbonated water, thus, they have become the most promising mineral class for carbon mineralization (O’Connor et al., 2002). The fundamental unit in silicate structures is the silicon-oxygen tetrahedron (SiO₄)^4- (see Figure 9A). Metal ions are present in all silicates except quartz. Other cations with similar dimensions such as Al³⁺, Mg²⁺, Fe²⁺, Fe³⁺, Mn²⁺ and Ti⁴⁺ can replace Si⁴⁺ from tetrahedral groups by isomorphic substitution (Brigatti et al., 2006).

FIGURE 9

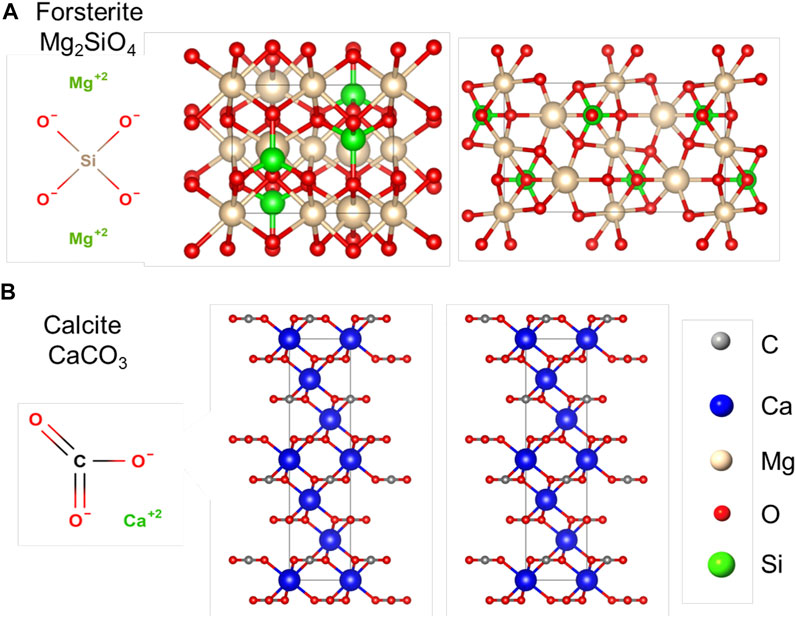
FIGURE 9. Crystal molecular structure. (A) Forsterite Mg₂SiO₄. (B) Calcite CaCO₃. The visualization prepared with the open source software VESTA.

Carbonates are common in most formations currently considered for CO₂ geological storage. The carbonate ion (CO₃^2-) is the basic structural unit of carbonate minerals (see Figure 9B). This anion forms ionic bonds with cations such as Ca²⁺, Mg²⁺, Fe²⁺, Mn²⁺ as well as rare-earth elements e.g., Ba²⁺, Ce³⁺. Calcite CaCO₃, magnesite MgCO₃, rhodochrosite MnCO₃, siderite FeCO₃, and dolomite CaMg(CO₃)₂ are some of the most common carbonate minerals in nature (Effenberger et al., 1981).

Chemical bonds in minerals

Oxygen and metals Ca, Mg, Fe, Mn, Ni become oppositely charged by electron transfer and form ionic bonds, whereas silicon Si, carbon C, sulfur S and oxygen O bond together by sharing electron pairs in covalent bonds. Covalent bonds have higher bond energy than ionic bonds, for example, the bond energy in the covalent bond formed by silicon-oxygen is ∼13,100 kJ/mol, and the bond energy in the ionic bond formed by magnesium-oxygen is ∼3,816 kJ/mol (Huggins and Sun., 1946). Therefore, metal-oxygen bond breakage prevails in mineral dissolution and controls the dissolution rate (Figure 10). In addition, amorphous minerals dissolve more readily than their crystalline counterparts, such as basaltic glass compared with crystalline basalt.

FIGURE 10

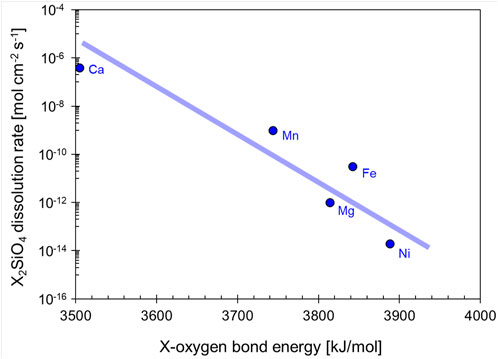
FIGURE 10. Olivine dissolution rate as a function of the metal-oxygen bond energy. X represents one of the metallic ions commonly found in olivine, such as: Ca²⁺, Mn²⁺, Fe²⁺, Mg²⁺, Ni²⁺. Data sources: Huggins and Sun., 1946, Casey., 1991.

Mineral dissolution

In the presence of water, a mineral liberates ions (reactants) that move away from the mineral surface to the bulk solution mainly due to electrical interaction within the Helmholtz layer and random vibration. Ions experience the greatest potential change across the Helmholtz layer, and eventually form activated complexes and new reaction products in the bulk solution (Hayes and Katz., 1996; Crundwell., 2014). Common mineral and glass dissolution reactions in CO₂ acidified water are summarized in Table 1 (see also Espinoza et al., 2011; Kim and Santamarina., 2014). Figure 11 shows the dissolution of forsterite in CO₂ acidified water. Dissolution involves the breaking of magnesium-oxygen bonds and the release of Mg²⁺ and SiO₄^4-; subsequently, Mg²⁺ ions form hydrated ions with water, while SiO₄^4- ions form activated complexes with protons, HSiO₄^3-.

TABLE 1

TABLE 1. Common mineral dissolution reactions in CO₂ acidified water.

FIGURE 11

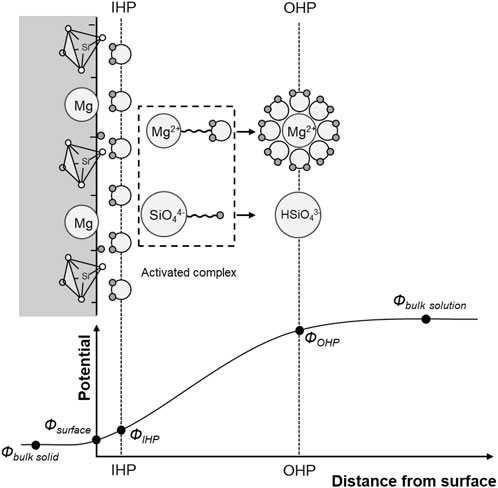
FIGURE 11. Stages in forsterite Mg₂SiO₄ dissolution—OHP: outer Helmholtz plane. IHP: inner Helmholtz plane. After Crundwell., 2014.

Kinetics of mineral dissolution

The rate of dissolution far-from-equilibrium r_d [mol/s] can be estimated as (Arthur et al., 2000):

$r_d=k·s·a_{H^{+}}^{n_{H^{+}}}(14)$

where k [mol m⁻² s⁻¹] is the rate constant for mineral dissolution, s [m²] is the surface area of minerals in a reference volume of solution, and $n_{H^{+}}$[ ] is the reaction order with respect to the activity of protons $a_{H^{+}}$ [ ]. The mineral surface area varies during dissolution (Grandstaff., 1978; Gautier et al., 2001; Fischer et al., 2012).

Table 2 lists kinetic dissolution rates calculated using Eq. 14 and kinetic parameters compiled from the literature for common silicate and carbonate minerals in acid solutions. Clearly, carbonates are more reactive than other minerals, in agreement with their bond energies reported above. Anorthite, fayalite and forsterite have higher reactivity than other silicates due to the relative abundance of ionic metal-oxygen bonds and the absence of silicon-oxygen covalent bonds in these minerals (Angel., 1988; Velbel., 1999). Other parameters affect mineral dissolution rates as well, for example: temperature, pH, CO₂ partial pressure (Stumm and Morgan., 1996), salinity (Pokrovsky et al., 2005), organic ligands (Fredd and Fogler., 1998), and catalysts (e.g., sodium bicarbonate–O’Connor et al., 2001).

TABLE 2

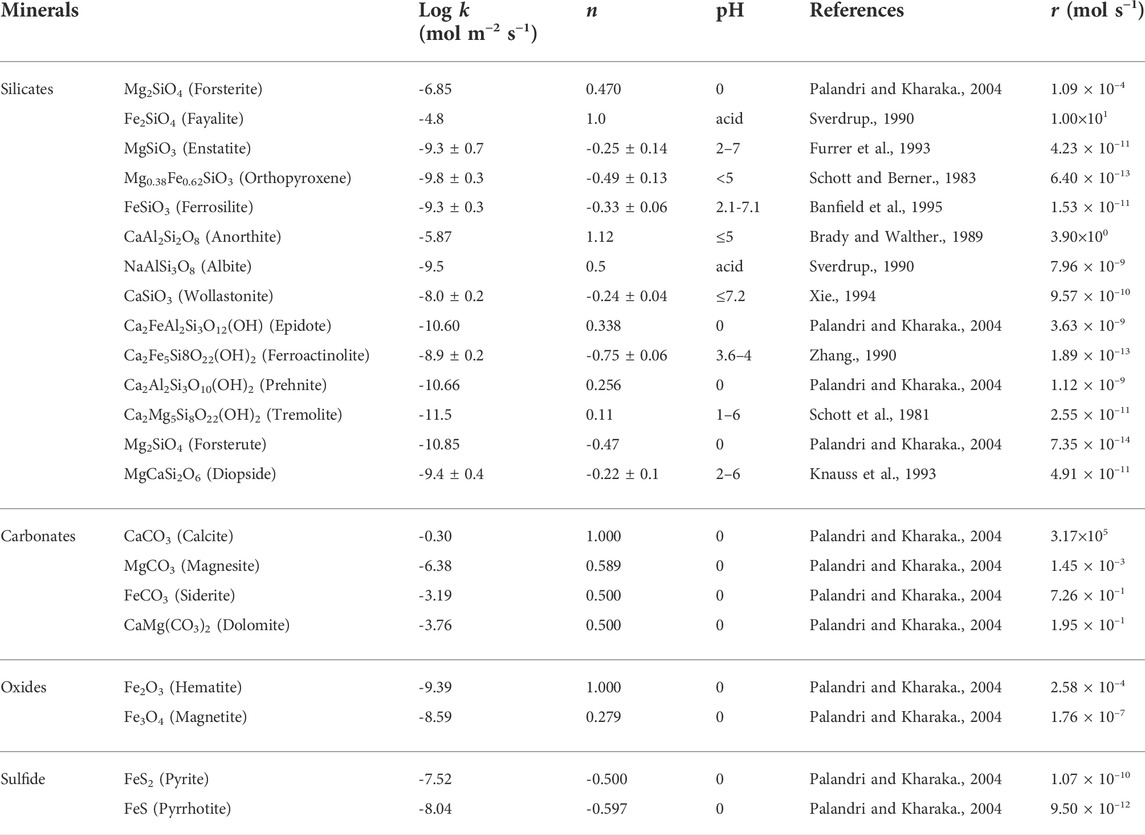
TABLE 2. Kinetic rate parameters for mineral dissolution in acid solutions (T = 25°C) and the calculated dissolution rates r (Eq. 14—Calculations assume 25°C, 0.1 MPa, the pH of CO₂ water is 4.5, the surface area is fixed at 2 m²).

Mineral dissolution: Hydro-chemo-mechanical coupling

Minerals dissolve during CO₂ injection and produce species that are carried away by advection and diffusion. Consequently, mineral dissolution enhances porosity and permeability, and causes settlement and stress changes.

The evolution of mineral dissolution in a porous medium is inherently related to pore size variability and the presence of preferential flow pathways which deliver the majority of the reactants in advective regimes: 10% of pores may be responsible for more than 50% of the total flow rate in sediments (Jang et al., 2011), and flow channeling is even more pronounced in fractured rock masses (National Academies of Sciences Engineering and Medicine, 2020; Cardona et al., 2021). Therefore, dissolution and transport are coupled, and may involve fabric changes. Hydro-chemo-mechanical coupling effects triggered by dissolution are explored next.

Dissolution at constant fabric (no mechanical coupling)

Dissolution and advection lead to increased flow focusing and “wormhole” formation (Kim and Santamarina., 2015; Kim and Santamarina., 2016; Menke et al., 2017; Derr et al., 2020). Two dimensionless ratios combine the three time scales for advection t_adv, diffusion t_diff, and reaction t_r; for a channel length L_ch,

$\mathrm{D}\mathrm{a}\mathrm{m}\mathrm{k}\mathrm{ö}\mathrm{h}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{D}\mathrm{a}=\frac{t_{adv}}{t_r}=\frac{k{L}_{ch}}{v}(15)$

$\mathrm{P}\mathrm{é}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{P}\mathrm{e}=\frac{t_{diff}}{t_{adv}}=\frac{v{L}_{ch}}{D}(16)$

where v [m/s] is the average flow velocity in pores, D [m²/s] is the molecular diffusion coefficient, and the kinetic rate $\kappa \left[1/\mathrm{s}\right]=k{S}_s{M}_m$ is a function of the rate constant for mineral dissolution k [mol m⁻² s⁻¹], the mineral specific surface area S_s [m²/g], and the mineral molar mass M_m [g/mol]. Various dissolution topologies become apparent in the Péclet-Damköhler Pe-Da diagram in Figure 12: compact dissolution, conical wormhole, dominant wormhole, ramified wormhole and uniform dissolution regimes. Low advection velocities, i.e., long t_adv and small Pe, allow reactant consumption near the inlet and instabilities cannot develop; conversely, very high advection velocities, i.e., short t_adv, high Pe and small Da, carry reactants all along the porous medium from inlet to outlet and favor a stable homogeneous dissolution. Wormholes develop at intermediate flow rates, i.e., large Da and Pe, so that reactants act preferentially along flow channels.

FIGURE 12

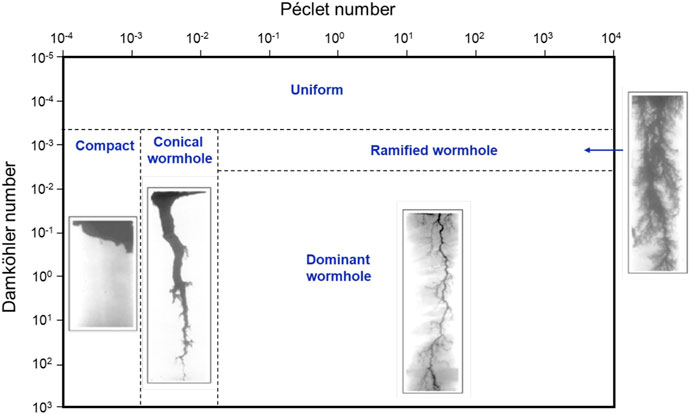
FIGURE 12. Dissolution in rigid porous network—Various regimes in the Péclet-Damköhler space. Modified from Golfier et al., 2002. Source of images: Fredd., 2000.

Similarly, various dissolution regimes emerge when reactive fluids flow through rock fractures (Kim and Santamarina., 2015; Shafabakhsh et al., 2021). A low Da causes a more uniform aperture enlargement along the length of the fracture. On the other hand, most reactants are consumed near the inlet in large Da and low Pe regimes (highly reactive low-advection conditions). Finally, a large fracture aperture slows the diffusive transport of reactants to the mineral fracture surface, and higher reactant concentrations remain along the centerline.

Dissolution-triggered fabric changes (mechanically coupled effects)

Mineral dissolution during CO₂ injection can cause fabric changes in sediments, block sliding in fractured rocks and stress changes in both cases.

The coefficient of lateral earth pressure at rest k₀ = σ_h’/σ_v’| _εh=0 is the stress ratio between the effective horizontal stress σ_h’ and the effective vertical stress σ_v’ under zero lateral strain conditions ε_h = 0. Both experimental and numerical results show that even a small amount of particle dissolution can produce a pronounced drop in k₀ and the state of stress may even reach the Coulomb failure envelope, i.e., Rankine active coefficient k₀→k_a (mixture of soluble and insoluble grains–Shin and Santamarina., 2009). At the grain scale, forces initially carried by dissolving particles get transferred to less soluble neighboring grains, the particle coordination number decreases, and force chains form a brittle honeycomb-like fabric (Figure 13A—Shin et al., 2008; Cha and Santamarina, 2014; Kim et al., 2019). After reaching its lowest value, the stress ratio may gradually recover upon further dissolution to reach a “terminal state”.

FIGURE 13

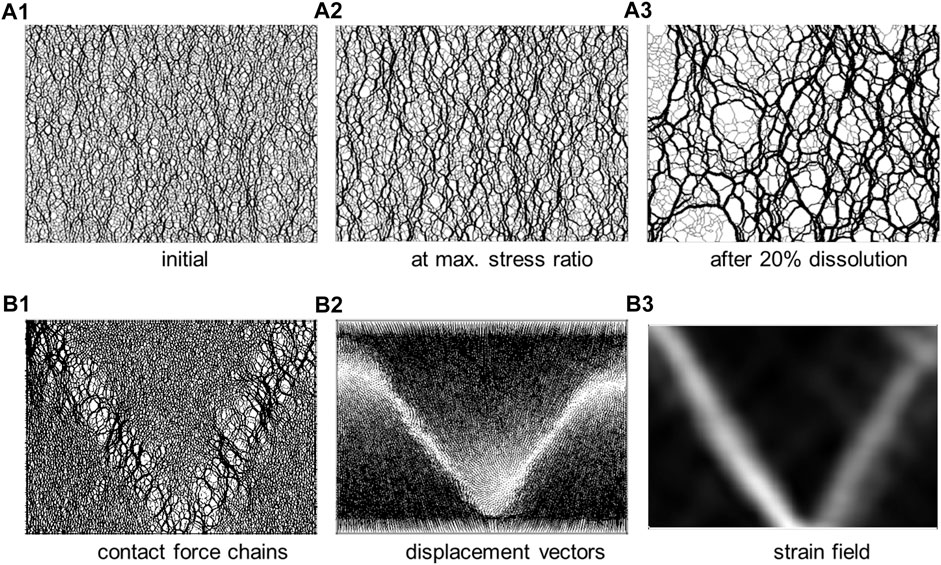
FIGURE 13. Dissolution in granular materials under constant vertical stress and zero lateral strain. (A) Force chain evolution during the dissolution of randomly distributed soluble grains: the evolving brittle “honeycomb” structure exhibits pronounced force chain arching (20% of the grains are soluble—Shin et al., 2008). (B) Pressure-solution whereby the particle dissolution rate is proportional to the normal force: the emergence of shear bands, Cha and Santamarina., 2019.

Stress concentration at grain contacts favors localized dissolution, i.e., “pressure solution” (even in single-mineral systems—Rutter, 1983; Etheridge et al., 1984; Fowler and Yang., 1999). Strong intergranular force chains and force-dependent contact dissolution combine to create a positive feedback mechanism that can lead to shear localization (Cha and Santamarina, 2016—Figure 13B). This sequence of events explains the nontectonic origin of shear discontinuities and polygonal fault systems observed in marine sediments and lacustrine deposits (Cartwright et al., 2003; Shin et al., 2008; Shin et al., 2010).

Let’s assume a carbonate reservoir (mineralogy = 100% calcite, porosity = 0.3) at a depth of 800 m (p = 8 MPa, T = 60 °C) filled with CO₂ saturated water (pH ≈ 3.21, calcite solubility ≈ 4.41 × 10^–5 mol/L). Under these conditions, 1.3 g ∼ 0.5 cm³ of calcite will dissolve for every pore volume of CO₂ saturated water, and cause a volumetric strain of ε = 0.5 × 10^–6. The induced isotropic stress change is Δσ = E × ε ≈ 1 kPa per pore volume of fluid exchange (the Young’s modulus is E ≈ 5 GPa for a carbonate with porosity 0.3—Ng and Santamarina 2022). Thus, the stress change for a single pore volume is small; however, ensuing convective transport and dissolution localization may eventually trigger mechanical instabilities.

Precipitation: Crystallization pressure and matrix filling

Precipitation is a self-homogenizing process in porous media: precipitates reduce the permeability of preferential flow paths and reactive fluids deviate to other pathways. Still, precipitation has other important consequences related to crystallization pressure and ensuing pore habits. These processes play a central role in CO₂ mineralization.

Crystallization pressure: new fractures

New minerals nucleate on preexisting surfaces (heterogeneous nucleation), grow into the pore space, and exert crystallization pressure when growth is constrained by pore and fracture walls (Lee and Kurtis, 2017). A thin film between the crystal and the wall and corner flow (along roughness and crevices which are not occupied by the growing mineral) maintain connectivity with the saturated solution and sustain crystal growth (Becker and Day, 1916; Taber, 1916; Correns, 1949).

The crystal experiences an internal excess pressure ΔP = P_crys–P_sol, where P_crys is the pressure in the growing crystal and P_sol is the hydrostatic pressure of the pore solution. This excess pressure ΔP is a function of the solution supersaturation S = c/c₀, where c and c₀ are the solute concentrations in the supersaturated solution and in the saturated solution respectively:

$∆P=P_{crys}-P_{sol}=\frac{RT}{V_m}lnS(17)$

Other parameters include: the gas constant R [J mol⁻¹ K⁻¹], the absolute temperature T [K], and the molar volume of the precipitated solid phase V_m [m³/mol]. Figure 14 shows the calculated crystallization pressure of quartz SiO₂, cristobalite SiO₂ and calcite CaCO₃ for different degrees of supersaturation (Wiltschko and Morse, 2001).

FIGURE 14

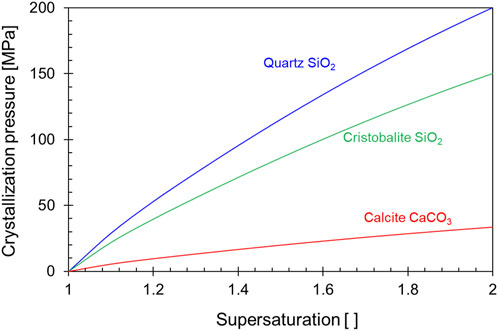
FIGURE 14. Crystallization pressures of quartz, cristobalite, and calcite as a function of supersaturation Trends from Wiltschko and Morse., 2001; formulation in Maliva and Siever., 1988.

The stress field induced by the crystallization pressure in neighboring pores may trigger an opening mode fracture (Anderson, 2017). Similarly, precipitation may form grain-displacive nodules and lenses in sediments when the crystallization pressure exceeds the in situ effective stress (Shin and Santamarina, 2011; Liu and Santamarina, 2022). Note that precipitated carbonates usually occupy a larger volume than the dissolved source minerals (Snæbjörnsdóttir et al., 2018; Snæbjörnsdóttir et al., 2020), therefore volume expansion during local dissolution-precipitation will also cause crystallization pressure.

Recurrent precipitation in the matrix: Liesegang band formation

Crystal growth decreases the local reactant concentration and may locally deplete the reactants that the host medium may contribute. Meanwhile, the reaction front keeps advancing; eventually transported and host rock reactants reach the threshold saturation concentration again and a new round of mineral precipitation starts. Such reactive-diffusion-precipitation process produces a periodic precipitation pattern, known as Liesegang bands (Liesegang, 1896; Rácz, 1999; Panjarian and Sultan, 2001; Nabika et al., 2020). Banded precipitation is found in a wide range of geological settings; Figure 15 shows periodic precipitation patterns in sandstones, carbonate and granite. These field observations are natural analogues for CO₂ mineralization within the rock matrix.

FIGURE 15

FIGURE 15. Diffusive-reactive transport: Liesegang bands. (A) in sandstone - from T McCarron. (B) Orbicular granite—Lahti et al., 2005. (C) Sandstone—Wadi Lajab, Saudi Arabia. (D) Jordanian carbonate.

CO2 mineralization

The general reaction for CO₂ mineralization starts with calcium, magnesium or iron silicates to produce the corresponding carbonates:

$\left(\mathrm{C}\mathrm{a},\mathrm{M}\mathrm{g},\mathrm{F}\mathrm{e}\right)\mathrm{S}\mathrm{i}{\mathrm{O}}_{\mathrm{3}}+\mathrm{C}{O}_{\mathrm{2}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \left(\mathrm{C}\mathrm{a},\mathrm{M}\mathrm{g},\mathrm{F}\mathrm{e}\right)\mathrm{C}{\mathrm{O}}_{\mathrm{3}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{S}\mathrm{i}{\mathrm{O}}_{\mathrm{3}}(18)$

Mafic and ultramafic rocks are silicates; therefore, the ultimate storage ability per cobic meter of rock is determined by the molar mass ratio between CO₂ and silicate M_CO2/M_silic, and the rock density and porosity (M_CO2/M_silic)⋅(1-ϕ)ρ_rock. The molar mass ratios M_CO2/M_silic are: 0.38 for wollastonite CaSiO₃, 0.44 for enstatite MgSiO₃ and 0.33 FeSiO₃ for ferrosilite. Then, the theoretical ultimate storage density values can exceed 500 kg/m³. However, the reaction is time-dependent and more modest values between 30-and-200 kg CO₂ per cubic meter of basalt could be expected within the first 10-to-100 years after injection (e.g., Xiong et al., 2018).

In fact, the reaction rate depends on the mineral reactivity, the available exposed surface area and fracture spacing, and the evolving efficiency of transport processes. Eq. 14 and kinetic parameters in Table 2 show that the characteristic time for carbonation varies in orders of magnitude for different minerals. For example, consider a rock block with a constant exposed surface of 2 m² in contact with CO₂ saturated water (p = 0.1 MPa, T = 25°C, pH = 4.5): it takes around 7 years to dissolve 1 m³ forsterite Mg₂SiO₄ ($\rho$ = 3,270 kg/m³) but 40,000 years for albite NaAlSi₃O₈ ($\rho$ = 2,620 kg/m³). These times are for reaction-limited processes; advection or diffusion-limited transport may eventually determine the rate of mineralization under reservoir conditions.

Other phenomena—reservoirs

The geological storage of CO₂ involves other reservoir-dependent processes, such as zone differentiation and convective currents in saline aquifers, excess pressure due to the buoyant CO₂ plume and altered seal performance, oil mobilization in depleted reservoirs, and near-well drying and cooling. These phenomena are investigated next.

CO₂ injection into saline aquifers

Transport during CO₂ injection into saline aquifers involves advection, dispersion, dissolution, diffusion, and convection (Figure 16). CO₂ is lighter and less viscous than water, therefore, CO₂ injection responds to buoyant, capillary and viscous forces: 1) CO₂ invasion next to the well is most sensitive to stratification and invades by viscous fingering through the most pervious layers, 2) the plume becomes gravity-dominant away from the well (Hesse et al., 2008), and eventually 3) it rests against the top seal by buoyancy and capillary trapping. Then, the reservoir develops various zones according to the saturating fluids: the supercritical CO₂ plume, the capillary transition zone, CO₂-rich brine, and the far-field saturated with the initial brine (Figure 16).

FIGURE 16

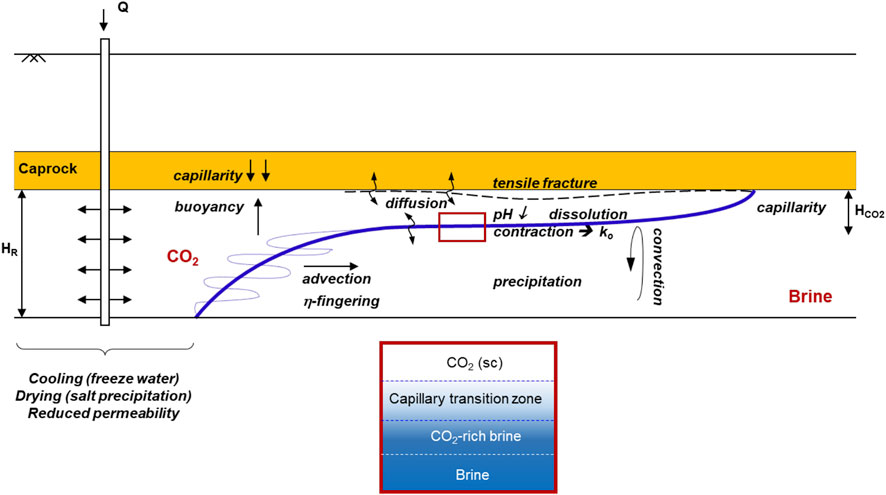
FIGURE 16. Carbon geological storage in saline aquifer: reservoir zones and underlying phenomena near the injection well and in the far field.

During early storage times, the degree of water saturation in the reservoir is a function of the capillary pressure $P_c=\left({\gamma }_w-{\gamma }_{CO\mathit{2}}\right)H_{CO\mathit{2}}$, where H_CO2 is the height of the CO₂ column, as predicted by the reservoir capillarity-saturation response $S_w=f\left(\Delta u\right)$ often captured with Brooks-Corey or van Genuchten models. The degree of water saturation decreases with time as water dissolves in CO₂ and is transported away by diffusion.

Next to the plume lower boundary, stored CO₂ dissolves into the groundwater and convection emerges due to the increased density of water with dissolved CO₂ - between $\Delta \rho /{\rho }_O$ = 0.1 and 1% depending on pressure and temperature (Emami-Meybodi et al., 2015. Note: water acidified with carbonic acid dissolves minerals and experiences an even larger increases in density–see previous sections). The Rayleigh number Ra compares the rate of fluid convection with the rate of diffusive transport:

$\mathrm{R}\mathrm{a}=\frac{k_{hy}g{H}_R\Delta \rho {\rho }_{\mathit{0}}}{{\mu }_{w}D}(19)$

where the governing parameters are the formation permeability k_hy [m²], g = 9.8 m/s², the height of the fluid column H_R [m], the change in fluid density $\Delta \rho$ [kg/m³], the viscosity of water ${\mu }_w$ [Pa⋅s], and the diffusion coefficient of CO₂ in water D [m²/s]. Convection typically occurs when $Ra>\mathit{4}{\pi }^{\mathit{2}}$ (Kneafsey and Pruess, 2010). Figure 17 shows time-lapse images of emerging convective currents when CO₂ gas rests above an aquifer at atmospheric pressure; the pH indicator changes in color from green to yellow at pH = 5. Small fingers initiate at the interface and begin to grow. Then there is an increase in the finger wavelength and a decrease in the number of fingers.

FIGURE 17

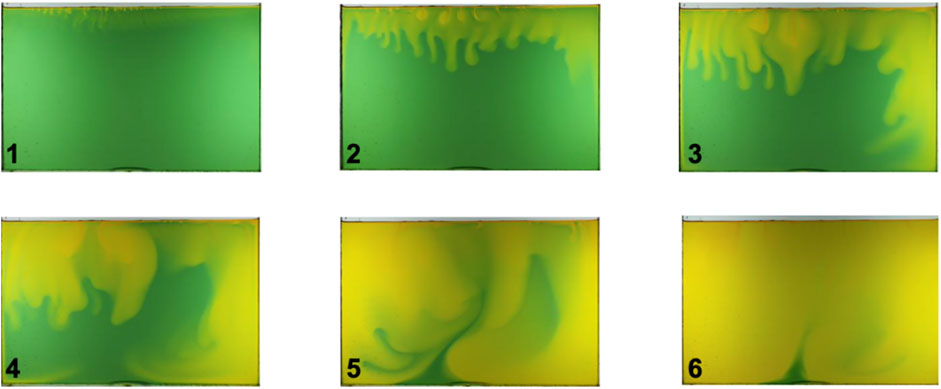
FIGURE 17. CO₂ solute driven convection. Time lapse images of a water bath beneath a CO₂ atmosphere (water with a universal pH indicator—Bang et al., 2012). The time interval between images is 40 min.

The convection period is $t_{cov}=\frac{\mu H_R}{k_{hyd}\mathrm{g}\Delta \rho }$ (Jiang et al., 2019) then, for an aquifer of thickness H_R = 10 m and permeability k_hyd = 20 md, the convection period is t_cov = 150 years assuming $\Delta \rho$ = 10 kg/m³.

Finally, the injection of dry CO₂ into a saline aquifer causes salt precipitation as water evaporates into the supercritical CO₂ near the wellbore (Miri et al., 2015). Salt precipitation can reduce CO₂ injectivity into the reservoir; its impact depends on the injection rate, mode (monotonic vs. cyclic), and brine salinity (Talman et al., 2020; He et al., 2022).

Seal rock: structure trapping

Small pores in high specific surface clay-rich caprocks give rise to the high capillary entry pressure and low permeability needed to hinder the upwards migration of the buoyant CO₂ plume. On the other hand, CO₂ invasion either dissolved in water or as a supercritical phase alters the physiochemical equilibrium in the seal rock.

Capillary pressure against the seal

The plume height h [m] determines the excess pressure in the CO₂ plume at the seal-reservoir interface, $\Delta P=P_{CO\mathit{2}}-P_w=\left({\rho }_w-{\rho }_{co\mathit{2}}\right)gh$. On the other hand, the capillary breakthrough pressure $P_c$ the seal may resist is a function of the interfacial tension $\gamma$ [N/m] between water and CO₂ at reservoir pressure and temperature conditions, the contact angle $\theta$ formed by the water-CO₂ interface on the mineral surface, and the characteristic pore diameter d^* [m] for the percolating path across the seal layer.

$P_c=\frac{\gamma \cos \theta }{d^{*}}(20)$

The characteristic pore diameter d^* is a function of the specific surface area S_s, the void ratio e, the mineral density ${\rho }_m$, a fabric factor ψ and a β factor related to the pore size distribution along percolating paths: $d^{*}=\beta \psi e/\left(Ss.{\rho }_m\right)$ (Espinoza and Santamarina, 2010; Espinoza and Santamarina, 2017). Then, the sealing number ${\Pi }_{seal}$ compares the capillary breakthrough pressure $P_c$ to the buoyant pressure $\Delta P$:

${\mathrm{\Pi }}_{seal}=\frac{P_c}{\Delta P}=\frac{\gamma \cos \theta S_s{\rho }_m}{\beta \psi e\left({\rho }_w-{\rho }_{C{O}_{\mathrm{2}}}\right)gh}(21)$

Sealing numbers ${\Pi }_{seal}\gg \mathit{1}$ are expected for safe storage. Clearly, a high sealing number is found for small plume thickness h, and high specific surface Ss clayey seals.

On the other hand, the higher CO₂ pressure changes the effective stress can trigger fault reactivation and grain-displacive breakthrough. The stability number ${\Pi }_{stability}$compares the initial horizontal effective stress ${\sigma }_{h\mathit{0}}^{\prime }$at the reservoir depth z to the capillary pressure $\Delta P$ created by a CO₂ plume of thickness h.

${\mathrm{\Pi }}_{stability}=\frac{{\sigma }_{h\mathrm{0}}^{\prime }}{\Delta P}=\frac{\left({\sigma }_{z\mathrm{0}}-P_{\mathrm{0}}\right)k_{\mathrm{0}}}{hg\left({\rho }_w-{\rho }_{C{O}_{\mathrm{2}}}\right)}(22)$

where the variables are: the initial total vertical stress σ_z0 and fluid pressure P₀ at the reservoir-seal interface before CO₂ injection, and effective stress ratio k₀ = σ_h’/σ_z’ at zero lateral strain. Safe CO₂ injection requires reservoirs with a high stability number ${\Pi }_{stability}$. The organic matter in a shale is CO₂-wet (Arif et al., 2017b), therefore, low organic content shales are preferred for CO₂ seal.

CO2 interaction with clay-rich caprock

As anticipated by the sealing number ${\Pi }_{seal}$, clayey shales are promising seal layers for CO₂ geological storage. Hence, we must address the hydro-chemo-mechanical coupling between CO₂ and clay minerals. We can anticipate two salient effects:

1) First contact (before SC-CO₂ invasion): CO₂ dissolves in water and acidifies the brine. Low pH promotes protonation, and leads to positively charged surfaces, which will affect the clay fabric.

2) Long term (after SC-CO₂ invasion): CO₂ replaces water and becomes the saturating pore fluid. There will be a reduction in osmotic repulsion, dissolution of residual water in CO₂ and salt precipitation, volumetric contraction driven by capillarity, and a three-fold increase in the Hamaker constant for clay-CO₂-clay as compared to clay-water-clay (Shin and Santamarina, 2010; Espinoza and Santamarina, 2012).

Changes in electrical and capillary forces will induce volumetric changes, thus stress changes in the caprock. Figure 18 shows that a montmorillonite-water paste contracts and experiences desiccation cracks when water evaporates into supercritical CO₂ atmosphere. Sedimentation experiments show that clay particles show strong particle aggregation with heptane and liquid CO₂ which shows that the electrical interaction between clays and water is different than with CO₂ in its different states (Espinoza and Santamarina, 2012).

FIGURE 18

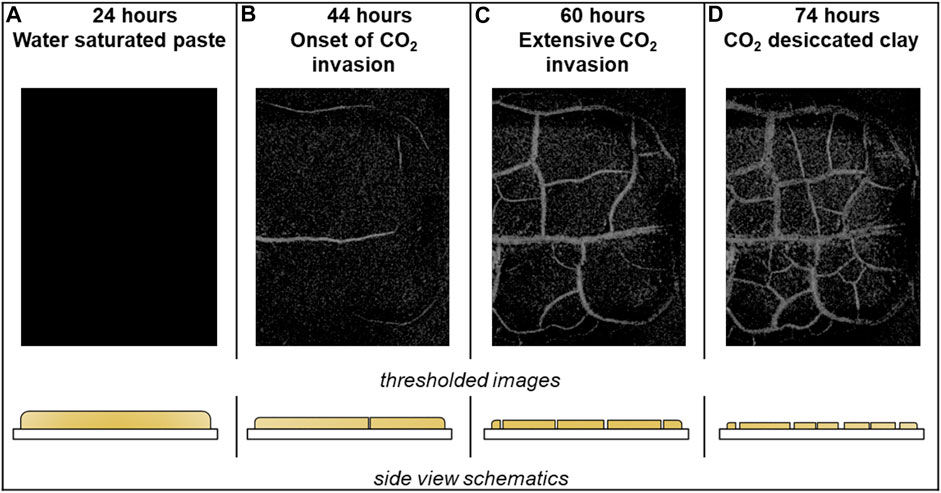
FIGURE 18. Montmorillonite-water paste subjected to a supercritical CO₂ atmosphere (p = 15 MPa and T = 38°C). The photographs and associated sketches show the evolution of desiccation and the formation of capillary-driven fractures: as water evaporates into the CO₂ reservoir, suction increases and the water-CO₂ interface “compresses” the sediment; eventually, supercritical CO₂ invades the sediment and triggers desiccation cracks, Espinoza and Santamarina., 2012.

CO₂ injection into depleted oil reservoirs

CO₂ injection into depleted oil reservoirs benefits from time-proven seals. In addition, CO₂ can mobilize residual oil; in this case, we can simultaneously sequester CO₂ while recovering additional oil. Numerous pore-scale mechanisms affect CO₂-oil displacement processes, including oil swelling, ganglia destabilization, coalescence of disconnected oil blobs into a continuous oil phase, light-component extraction, miscible displacement and asphaltene deposition. Details follow.

Oil density and viscosity

The oil density decreases slightly with temperature, and pressure has a second order effect (Figure 1). On the other hand, the viscosity of crude oils can decrease by an order of magnitude when the temperature increases from 40°C to 80°C (Figure 3).

Oil-water interfacial tension

The interfacial tension between two non-polar fluids such as CO₂ and oil tends to be smaller than when dipolar water molecules are involved. Figure 19 shows the interfacial tension between three different alkanes (decane, dodecane and hexadecane) and CO₂ as a function of CO₂ density. The interfacial tension increases with the number of carbon atoms in alkanes and decreases with increasing CO₂ density.

FIGURE 19

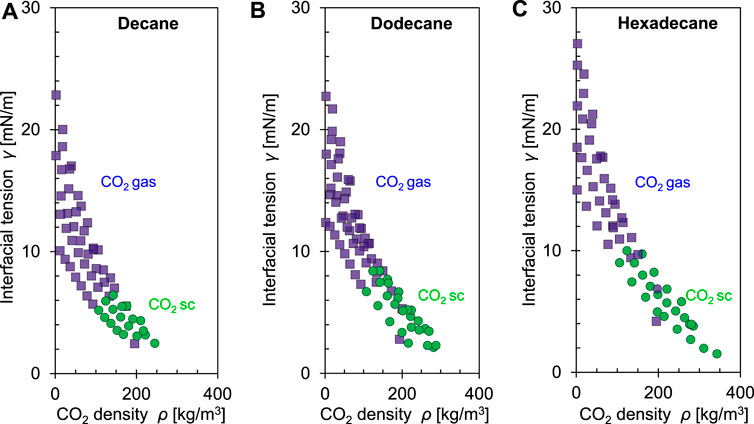
FIGURE 19. Interfacial tension between selected alkanes and CO₂ as a function of the CO₂ density at different pressures and temperatures: (A) Decane, (B) Dodecane and (C) Hexadecane. Symbols: CO₂ gas (■) and CO₂ supercritical (●). Data source: Georgiadis et al., 2010.

CO2 solubility in crude oil - Viscosity

The solubility of CO₂ in crude oil is much higher than in water because of their shared non-polar nature (Schmid, 2001). Solubility is directly dependent on the CO₂ partial pressure (Figure 20A), and is also affected by temperature and oil properties. Oil experiences a pronounced decrease in viscosity as CO₂ dissolves in it (Figure 20B).

FIGURE 20

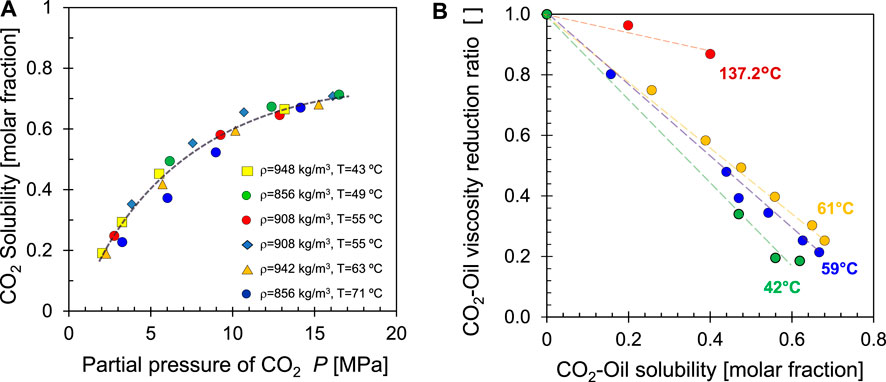
FIGURE 20. CO₂ and oil. (A) Solubility as a function of CO₂ partial pressure for different temperatures. Data source: Simon and Graue., 1965. (B) Oil viscosity with increasing molar fraction of dissolved CO₂. Data source: Barclay and Mishra., 2016.

Crude oil and CO₂ become fully miscible and the interface vanishes when the “minimum miscibility pressure” is reached; Table 3 lists minimum miscibility pressures for various crude oils. Above the minimum miscibility pressure, a transition zone forms in the reservoir. Miscibility is not instantaneous but develops gradually, i.e., “dynamic miscibility” (Verma, 2015).

TABLE 3

TABLE 3. Minimum miscibility pressure for different crude oils and organic compounds.

Swelling and shrinkage

Miscibility results from (1) the dissolution of CO₂ into the reservoir oil causing swelling, and (2) the vaporization of intermediate-molecular-weight hydrocarbons into the injected CO₂ resulting in oil shrinkage. The competitive effects of swelling and shrinkage are evident in the data presented in Figure 21: the oil swelling factor increases with CO₂ pressure until it reaches a maximum volume (at p = 8 MPa when T = 50°C, or at p = 17 MPa when T = 95°C); thereafter, vaporization-extraction becomes dominant at high-pressure and oil shrinks.

FIGURE 21

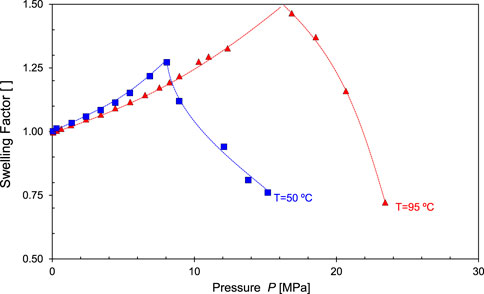
FIGURE 21. Miscibility and oil volume change. There are two competing processes: CO₂ dissolution in oil prevails at low pressure and causes oil swelling; on the other hand, light hydrocarbons vaporize into CO₂ and oil shrinks at high pressure. Data source: Rezk and Foroozesh (2019).

Asphaltene precipitation

Crude oil contains saturated hydrocarbons (single bonds between carbon atoms and saturated with hydrogen), aromatics (planar rings), resins, and asphaltenes. Asphaltenes are polar, polyaromatic and of high molecular weight substances that are insoluble in n-hexane or n-pentane. The size of asphaltenes ranges from less than 1 nm single molecules in light oils to more than 5 nm aggregates in black oils and heavy oils (Mullins, 2010). CO₂ dissolution in oil causes asphaltene precipitation; as asphaltene deposits on mineral surfaces, it changes the wettability of the reservoir causing mostly irreversible formation damage. Experimental studies show that ionic liquids prevent asphaltene precipitation (Hu and Guo, 2005; Zheng et al., 2019).

Thermal effects

The injection of CO₂ triggers thermal changes in surface facilities, the injection well and inside the reservoir (Hoteit et al., 2019).

Joule-Thomson expansion

The CO₂ injection pressure exceeds the formation pressure and rapid quasi-adiabatic expansion of CO₂ takes place near the injection well. When a gas expands from high pressure to low pressure, the temperature change ΔT is related to the pressure change ΔP by the Joule-Thomson coefficient ${\mu }_{JT}$ [K/Pa], which can be expressed in terms of the gas’ molar volume V_m [m³/mol], its molar heat capacity at constant pressure C_p [J K⁻¹ mol⁻¹], and the coefficient of thermal expansion $\alpha$[K⁻¹] as (Demirel., 2014):

$\left(\frac{\Delta T}{\Delta P}\right)\approx {\left(\frac{\partial T}{\partial P}\right)}_H={\mu }_{JT}=\frac{V_m}{C_p}\left(\alpha T-\mathrm{1}\right)(23)$

Gas expansion causes cooling when the Joule-Thomson coefficient ${\mu }_{JT}>\mathit{0}$ and heating when ${\mu }_{JT}<\mathit{0}$. In general, the Joule-Thomson coefficient decreases with increasing pressure and temperature (Han et al., 2010), and it is zero at the inversion point when $\alpha T-\mathit{1}=\mathit{0}$ (Note: the coefficient of thermal expansion $\alpha$ is temperature dependent as well).

The Joule-Thomson coefficient is ${\mu }_{JT}\approx$10°C/MPa for CO₂ at T = 40°C and p = 5 MPa, i.e., five times higher than for air (Phuoc and Massoudi, 2021). Figure 22 shows the Joule-Thomson inversion curve for CO₂; the auxiliary lines correspond to pressure-temperature profiles for a geothermal gradient of 30°C/km. Clearly, CO₂ expansion will cause cooling at most reservoir pressure and temperature conditions, except for injection in the seafloor under deep water columns and beneath permafrost layers.

FIGURE 22

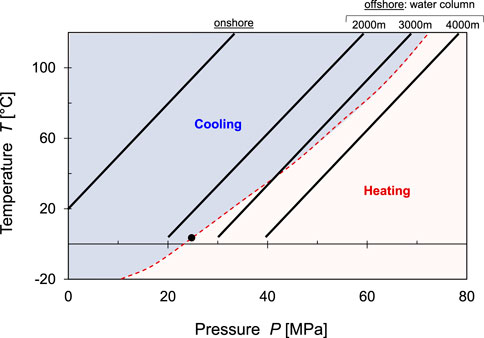
FIGURE 22. Joule-Thompson effect—Near well thermal effects. Cooling is anticipated for most onshore and offshore applications. The “inversion curve” predicts heating for seafloor injections beneath > 2,400 m high water columns.

Other thermal effects

In addition to the Joule-Thomson effect, endothermic water vaporization into supercritical CO₂ takes place mainly near the injection well (Vilarrasa and Rutqvist, 2017), while exothermic dissolution of supercritical CO₂ into the host brine prevails further away from the well ($\Delta H$ = -171.38 kJ/kg of CO₂, at p = 10.5 MPa and T = 50°C–Koschel et al., 2006). These two competing thermal effects continue until both brine and scCO₂ are saturated with the other phase.

Field implications

Under most field conditions, CO₂ injection will cause a significant temperature drop. The extent of cooling scales with the pressure drop and is partially compensated by heat transport in the reservoir (Oldenburg, 2007; Gauteplass et al., 2020). Cooling induces thermo-elastic stresses and triggers hydrate or ice formation when PT-conditions cross the corresponding phase boundary; hydrate and ice hinder fluid flow into the formation (Sloan, 2010). Effective stress changes caused by the injection pressure and thermos-elastic effects can reactivate fractures and improve their transmissivity due to shear dilation (Vilarrasa et al., 2017).

Finally, thermal changes affect density (Figures 1, 2), viscosity (Figure 3), interfacial properties (Figures 4, 5), and solubility and pH (Figure 6). In the supercritical regime, thermally induced density gradients are most pronounced across the Widom line and near the critical point. The induced thermal gradients give rise to thermally driven convection (Islam et al., 2014).

Storage density—reservoir size

The storage capacity per unit volume of the reservoir or ‘storage density’ SD [kg CO₂/m³ of rock] depends on the CO₂ phase and the reservoir porosity ϕ:

$\begin{array}{ccc}\text{Dissolved}:& {\mathit{SC}=\mathit{M}}_{\mathit{CO2}}{\chi }_{\mathit{CO2}}& {\mathit{SD}=4-\text{to}-13\text{kg}/\mathrm{m}}^3\\ {\text{Fluid}\text{CO}}_2:& \mathit{SC}={\rho }_{\mathit{CO2}}& {\mathit{SD}=50-\text{to}-240\text{kg}/\mathrm{m}}^3\\ \text{Hydrate}:& \mathit{SC}=0.234{\rho }_{\text{hyd}}& {\mathit{SD}=25-\text{to}-77\text{kg}/\mathrm{m}}^3\\ \text{Mineralized}:& \mathit{SC}=\mathit{f}\left(\mathit{mineral},\mathit{time},\mathit{flux}\right)& {\mathit{SD}=30-\text{to}-200\text{kg}/\mathrm{m}}^3\end{array}$

The listed SD values correspond to: porosity ϕ = 0.1-to-0.3, CO₂ solubility in fresh water at common reservoir PT conditions ${\chi }_{CO\mathit{2}}$ = 1 mol/l (reduce it to about half for brine—Figure 7), CO₂ molar mass $M_{CO\mathit{2}}$ = 44 g/mol, CO₂ mass density ρ_CO2 = 500-to-800 kg/m³ (from supercritical to liquid—Figure 1), mass fraction of CO₂ in hydrate CO₂⋅8H₂O equal to 0.234, and hydrate density ρ_hyd = 1,100 kg/m³, and attainable mineralization within the first 10-to-100 years after injection.

The annual worldwide CO₂ emission is ∼40 Gt/yr. Let’s consider storing 1 gigaton of CO₂, i.e., a “small fraction” of the total annual emissions: the required volume for CO₂ dissolved in fresh water is equivalent to a 30 m thick porous reservoir 50 km × 50 km wide, assuming high porosity ϕ = 0.3 and a storage density SD = 13 kg/m³. Clearly, higher density CO₂ forms are preferred for efficient storage; still, the storage density SD values listed above imply that all CO₂ geological storage forms will require large reservoir volumes.

Conclusions

The injection of CO₂ into geological formations triggers numerous coupled thermo-hydro-chemo-mechanical processes.

The gas-liquid phase boundary and the Widom line within the supercritical regime divide the lighter gaseous-like regime from the denser liquid-like regime. The density of CO₂ has a first-order effect on the CO₂-water interfacial tension.

The CO₂-water interface pins strongly to mineral surfaces and results in a wide range of contact angles that vary between the advancing and the receding asymptotic values. Soon after injection, the residual water saturation reflects the reservoir capillary pressure vs. saturation response; thereafter, the degree of water saturation decreases with time as water evaporates into CO₂.

The solubility of CO₂ in water increases with pressure but decreases with temperature. In most geological settings, CO₂ solubility decreases with salt concentration particularly when small high-valence ions are involved. Similarly, the presence of competing gases affects the solubility of CO₂ in water because of competing ions and a reduction in the partial pressure of CO₂ (at constant total pressure).

Dissolved CO₂ acidifies water and prompts mineral dissolution (silicates and carbonates). Dissolution couples with preferential advective flow channels, diffusive transport and mechanical effects to cause various dissolution patterns, internal shear failure (even under zero lateral strain conditions), and strains may localize along shear bands. Next to the plume lower boundary, convective currents may emerge due to the increased density of water with dissolved CO₂ and minerals.

CO₂ mineralization homogenizes flow pathways. Crystal growth against pore and fracture walls exert crystallization pressure that can create new fracture surfaces or cause grain-displacive mineral lenses (when the crystallization pressure exceeds the rock tensile strength or the far-field confining stress). Precipitation may also take place within the rock matrix by successive dissolution-diffusion-precipitation sequences that result in periodic precipitation patterns, i.e., Liesegang bands.

Buoyant CO₂ plumes apply excess pressure against the seal caprock and interact with clay minerals through physicochemical processes. The sealing number ${\Pi }_{seal}$ compares the seal capillary breakthrough pressure to the excess buoyant pressure in the CO2 plume. On the other hand, the stability number ${\Pi }_{stability}$ compares the initial effective stress to the excess buoyant pressure. Safe CO₂ storage requires large sealing and stability numbers and careful consideration of physicochemical effects.

CO₂ injection into depleted oil reservoirs benefits from proven seal performance. At the same time, it causes light-component extraction, oil swelling, ganglia destabilization, a reduction in oil viscosity, and miscible displacement. Then, we can simultaneously sequester CO₂ while recovering additional oil through CO₂ gravity-driven enhanced oil recovery.

Rapid CO₂ depressurization near the injection well causes cooling under most anticipated reservoir conditions. Cooling may trigger hydrate and ice formation, and reduce permeability. In some cases, effective stress changes associated with the injection pressure and cooling thermoelasticity can reactivate fractures.

The CO₂ storage density in terms of kg of CO₂ per cubic meter of the reservoir depends on the CO₂ phase and the reservoir porosity ϕ. First order estimates are 4-to-13 kg/m³ for CO₂ dissolved in water, 25-to-77 kg/m³ for CO₂ trapped in hydrate, 30-to-200 kg/m³ for mineralized CO₂ (attainable within the first 10-to-100 years of storage), and 50-to-240 kg/m³ for supercritical-to-liquid CO₂ (most efficient but prone to leakage). In all cases, large reservoir volumes will be required to store a meaningful fraction of the CO₂ that will be emitted during the energy transition (Anderson, 2017; Global status CCS, 2021).

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

G. Abelskamp edited the manuscript. Support for this research was provided by the KAUST Endowment.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akhmadiyarov, A. A., Petrov, A. A., Rakipov, I. T., and Varfolomeev, M. A. (2019). Effect of pressure, temperature and gas phase composition on the rheological properties of heavy crude oil. IOP Conf. Ser. Earth Environ. Sci. 282, 012021. doi:10.1088/1755-1315/282/1/012021

CrossRef Full Text | Google Scholar

Anderson, T. L. (2017). Fracture mechanics. Boca Raton. CRC Press. doi:10.1201/9781315370293

CrossRef Full Text | Google Scholar

Andrew, M., Bijeljic, B., and Blunt, M. J. (2014). Pore-scale contact angle measurements at reservoir conditions using X-ray microtomography. Adv. Water Resour. 68, 24–31. doi:10.1016/j.advwatres.2014.02.014

CrossRef Full Text | Google Scholar

Angel, R. J. (1988). High-pressure structure of anorthite. Am. Mineral. 73, 1114–1119.

Google Scholar

Arif, M., Lebedev, M., Barifcani, A., and Iglauer, S. (2017a). CO2 storage in carbonates: Wettability of calcite. Int. J. Greenh. Gas Control 62, 113–121. doi:10.1016/j.ijggc.2017.04.014

CrossRef Full Text | Google Scholar

Arif, M., Lebedev, M., Barifcani, A., and Iglauer, S. (2017b). Influence of shale-total organic content on CO2 geo-storage potential. Geophys. Res. Lett. 44, 8769–8775. doi:10.1002/2017GL073532

CrossRef Full Text | Google Scholar

Arthur, R. C., Savage, D., Sasamoto, H., Shibata, M., and Yui, M. (2000). Compilation of kinetic data for geochemical calculations. Tokai, Ibaraki (Japan): Japan Nuclear Cycle Development Inst.

Google Scholar

Bachu, S. (2003). Screening and ranking of sedimentary basins for sequestration of CO2 in geological media in response to climate change. Environ. Geol. 44, 277–289. doi:10.1007/s00254-003-0762-9

CrossRef Full Text | Google Scholar

Banfield, J. F., Ferruzzi, G. G., Casey, W. H., and Westrich, H. R. (1995). HRTEM study comparing naturally and experimentally weathered pyroxenoids. Geochim. Cosmochim. Acta 59, 19–31. doi:10.1016/0016-7037(94)00372-S

CrossRef Full Text | Google Scholar

Bang, E. S., Son, J. S., and Santamarina, J. C. (2012). “Subsurface CO2 leakage : Lab-scale study of salient characteristics and assessment of borehole-based detection using resistivity tomography,” in Proceeding of the 4th International Conference on Geotechnical and Geophysical Site Characterization (ISC’4), Porto de Galinhas, Pernambuco – Brazil, January 2013.

Google Scholar

Barclay, T. H., and Mishra, S. (2016). New correlations for CO2-Oil solubility and viscosity reduction for light oils. J. Pet. Explor. Prod. Technol. 6, 815–823. doi:10.1007/s13202-016-0233-y

CrossRef Full Text | Google Scholar

Becker, G. F., and Day, A. L. (1916). Note on the linear force of growing crystals. J. Geol. 24, 313–333. doi:10.1086/622342

CrossRef Full Text | Google Scholar

Bell, J. G., Benham, M. J., and Thomas, K. M. (2021). Adsorption of carbon dioxide, water vapor, nitrogen, and sulfur dioxide on activated carbon for capture from flue gases: Competitive adsorption and selectivity aspects. Energy fuels. 35, 8102–8116. doi:10.1021/acs.energyfuels.1c00339

CrossRef Full Text | Google Scholar

Bikkina, P. (2011). Contact angle measurements of CO2–water–quartz/calcite systems in the perspective of carbon sequestration. Int. J. Greenh. Gas Control 5 (5), 1259–1271. doi:10.1016/j.ijggc.2011.07.001

CrossRef Full Text | Google Scholar

Brady, P. V., and Walther, J. V. (1989). Controls on silicate dissolution rates in neutral and basic pH solutions at 25°C. Geochim. Cosmochim. Acta 53, 2823–2830. doi:10.1016/0016-7037(89)90160-9

CrossRef Full Text | Google Scholar

Brigatti, M. F., Galan, E., and Theng, B. K. G. (2006). Chapter 2 structures and mineralogy of clay minerals. Elsevier. doi:10.1016/S1572-4352(05)01002-0

CrossRef Full Text | Google Scholar

Cardona, A., Finkbeiner, T., and Santamarina, J. C. (2021). Natural rock fractures: From aperture to fluid flow. Rock Mech. Rock Eng. 54, 5827–5844. doi:10.1007/s00603-021-02565-1

CrossRef Full Text | Google Scholar

Cartwright, J., James, D., and Bolton, A. (2003). The Genesis of polygonal fault systems: A review. Geol. Soc. Lond. Spec. Publ. 216, 223–243. doi:10.1144/GSL.SP.2003.216.01.15

CrossRef Full Text | Google Scholar

Casey, W. H. (1991). On the relative dissolution rates of some oxide and orthosilicate minerals. J. Colloid Interface Sci. 146, 586–589. doi:10.1016/0021-9797(91)90225-W

CrossRef Full Text | Google Scholar

Cha, M., and Santamarina, J. C. (2014). Dissolution of randomly distributed soluble grains: Post-dissolution k 0 -loading and shear. Géotechnique 64, 828–836. doi:10.1680/geot.14.P.115

CrossRef Full Text | Google Scholar

Cha, M., and Santamarina, J. C. (2016). Hydro-chemo-mechanical coupling in sediments: Localized mineral dissolution. Geomechanics Energy Environ. 7, 1–9. doi:10.1016/j.gete.2016.06.001

CrossRef Full Text | Google Scholar

Cha, M., and Santamarina, J. C. (2019). Localized dissolution in sediments under stress. Granul. Matter 21, 79–11. doi:10.1007/s10035-019-0932-4

CrossRef Full Text | Google Scholar

Chiquet, P., Daridon, J. L., Broseta, D., and Thibeau, S. (2007). CO2/water interfacial tensions under pressure and temperature conditions of CO2 geological storage. Energy Convers. Manag. 48, 736–744. doi:10.1016/j.enconman.2006.09.011

CrossRef Full Text | Google Scholar

Chun, B. S., and Wilkinson, G. T. (1995). Interfacial tension in high-pressure carbon dioxide mixtures. Ind. Eng. Chem. Res. 34, 4371–4377. doi:10.1021/ie00039a029

CrossRef Full Text | Google Scholar

Correns, C. W. (1949). Growth and dissolution of crystals under linear pressure. Discuss. Faraday Soc. 5, 267. doi:10.1039/df9490500267

CrossRef Full Text | Google Scholar

Crundwell, F. K. (2014). The mechanism of dissolution of minerals in acidic and alkaline solutions: Part I — a new theory of non-oxidation dissolution. Hydrometallurgy 149, 252–264. doi:10.1016/j.hydromet.2014.06.009

CrossRef Full Text | Google Scholar

Da Rocha, S. R. P., Harrison, K. L., and Johnston, K. P. (1999). Effect of surfactants on the interfacial tension and emulsion formation between water and carbon dioxide. Langmuir 15, 419–428. doi:10.1021/la980844k

CrossRef Full Text | Google Scholar

Daval, D., Hellmann, R., Saldi, G. D., Wirth, R., and Knauss, K. G. (2013). Linking nm-scale measurements of the anisotropy of silicate surface reactivity to macroscopic dissolution rate laws: New insights based on diopside. Geochim. Cosmochim. Acta 107, 121–134. doi:10.1016/j.gca.2012.12.045

CrossRef Full Text | Google Scholar

de Gennes, P. G. (1985). Wetting: Statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863. doi:10.1103/revmodphys.57.827

CrossRef Full Text | Google Scholar

Demirel, Y. (2014). Nonequilibrium thermodynamics: Transport and rate processes in physical, chemical and biological systems. Elsevier. doi:10.1016/C2012-0-00459-0

CrossRef Full Text | Google Scholar

Derr, N. J., Fronk, D. C., Weber, C. A., Mahadevan, A., Rycroft, C. H., and Mahadevan, L. (2020). Flow-driven branching in a frangible porous medium. Phys. Rev. Lett. 125, 158002. doi:10.1103/PhysRevLett.125.158002

PubMed Abstract | CrossRef Full Text | Google Scholar

DiCarlo, D. A. (2013). Stability of gravity-driven multiphase flow in porous media: 40 Years of advancements. Water Resour. Res. 49, 4531–4544. doi:10.1002/wrcr.20359

CrossRef Full Text | Google Scholar

Dong, Z., Li, Y., Lin, M., and Li, M. (2013). A study of the mechanism of enhancing oil recovery using supercritical carbon dioxide microemulsions. Pet. Sci. 10, 91–96. doi:10.1007/s12182-013-0254-9

CrossRef Full Text | Google Scholar

Drelich, J. W., Boinovich, L., Chibowski, E., Della Volpe, C., Hołysz, L., Marmur, A., et al. (2020). Contact angles: History of over 200 years of open questions. Surf. Innov. 8, 3–27. doi:10.1680/jsuin.19.00007

CrossRef Full Text | Google Scholar

Duan, Z., and Sun, R. (2003). An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 193, 257–271. doi:10.1016/S0009-2541(02)00263-2

CrossRef Full Text | Google Scholar

Duan, Z., Sun, R., Zhu, C., and Chou, I. M. (2006). An improved model for the calculation of CO2 solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42. Mar. Chem. 98 (2-4), 131–139. doi:10.1016/j.marchem.2005.09.001

CrossRef Full Text | Google Scholar

Effenberger, H., Mereiter, Κ., and Zemann, J. (1981). Crystal structure refinements of magnesite, calcite, rhodochrosite, siderite, smithonite, and dolomite, with discussion of some aspects of the stereochemistry of calcite type carbonates. Z. für Krist. - Cryst. Mat. 156, 233–244. doi:10.1524/zkri.1981.156.14.233

CrossRef Full Text | Google Scholar

Emami-Meybodi, H., Hassanzadeh, H., Green, C. P., and Ennis-King, J. (2015). Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control 40, 238–266. doi:10.1016/j.ijggc.2015.04.003

CrossRef Full Text | Google Scholar

Eral, H. B., ’t Mannetje, D. J. C. M., and Oh, J. M. (2013). Contact angle hysteresis: A review of fundamentals and applications. Colloid Polym. Sci. 291, 247–260. doi:10.1007/s00396-012-2796-6

CrossRef Full Text | Google Scholar

Espinoza, D. N., Kim, S. H., and Santamarina, J. C. (2011). CO2 geological storage—geotechnical implications. KSCE J. Civ. Eng. 15 (4), 707–719. doi:10.1007/s12205-011-0011-9

CrossRef Full Text | Google Scholar

Espinoza, D. N., and Santamarina, J. C. (2010). Water-CO2-mineral systems: Interfacial tension, contact angle, and diffusion - implications to CO2 geological storage. Water Resour. Res. 46, 1–10. doi:10.1029/2009WR008634

CrossRef Full Text | Google Scholar

Espinoza, D. N., and Santamarina, J. C. (2012). Clay interaction with liquid and supercritical CO2: The relevance of electrical and capillary forces. Int. J. Greenh. Gas Control 10, 351–362. doi:10.1016/j.ijggc.2012.06.020

CrossRef Full Text | Google Scholar

Espinoza, D. N., and Santamarina, J. C. (2017). CO2 breakthrough—caprock sealing efficiency and integrity for carbon geological storage. Int. J. Greenh. Gas Control 66, 218–229. doi:10.1016/j.ijggc.2017.09.019

CrossRef Full Text | Google Scholar

Etheridge, M. A., Wall, V. J., Cox, S. F., and Vernon, R. H. (1984). High fluid pressures during regional metamorphism and deformation: Implications for mass transport and deformation mechanisms. J. Geophys. Res. 89, 4344–4358. doi:10.1029/JB089iB06p04344

CrossRef Full Text | Google Scholar

Fischer, C., Arvidson, R. S., and Lüttge, A. (2012). How predictable are dissolution rates of crystalline material? Geochim. Cosmochim. Acta 98, 177–185. doi:10.1016/j.gca.2012.09.011

CrossRef Full Text | Google Scholar

Fowler, A. C., and Yang, X. (1999). Pressure solution and viscous compaction in sedimentary basins. J. Geophys. Res. 104, 12989–12997. doi:10.1029/1998JB900029

CrossRef Full Text | Google Scholar

Fredd, C. N. (2000). “Dynamic model of wormhole formation demonstrates conditions for effective skin reduction during carbonate matrix acidizing,” in Proceeding of the SPE Permian Basin Oil Gas Recover. Conf. Proc., Midland, Texas, March 2000. doi:10.2118/59537-ms

CrossRef Full Text | Google Scholar

Fredd, C. N., and Fogler, H. S. (1998). Alternative stimulation fluids and their impact on carbonate acidizing. SPE J. 3, 34–41. doi:10.2118/31074-PA

CrossRef Full Text | Google Scholar

Freund, P., Bachu, S., and Gupta, M. (2006). Annex I - properties of CO2 and carbon-based fuels. Carbon N. Y., 383–400.

Google Scholar

Furrer, G., Zysset, M., and Schindler, P. W. (1993). “Weathering kinetics of montmorillonite: Investigations in batch and mixed-flow reactors,” in Geochemistry of clay-pore fluid interactions (London: Chapman & Hall), 243–262.

Google Scholar

Gachuz-Muro, H., and Sohrabi, M. (2013). “Effects of brine on crude oil viscosity at different temperature and brine composition - heavy oil/water interaction,” in Proceeding of the 75th Eur. Assoc. Geosci. Eng. Conf. Exhib. 2013 Inc. SPE Eur. 2013 Chang. Front., London, UK, June 2013, 1878–1889. doi:10.2118/164910-ms

CrossRef Full Text | Google Scholar

García, A. V. (2005). Measurement and modelling of scaling minerals.

Google Scholar

García, A. V., Thomsen, K., and Stenby, E. H. (2005). Prediction of mineral scale formation in geothermal and oilfield operations using the extended UNIQUAC model. Geothermics 34, 61–97. doi:10.1016/j.geothermics.2004.11.002

CrossRef Full Text | Google Scholar

Gauteplass, J., Almenningen, S., Barth, T., and Ersland, G. (2020). Hydrate plugging and flow remediation during CO2 injection in sediments. Energies 13, 4511. doi:10.3390/EN13174511

CrossRef Full Text | Google Scholar

Gautier, J.-M., Oelkers, E. H., and Schott, J. (2001). Are quartz dissolution rates proportional to B.E.T. surface areas? Geochim. Cosmochim. Acta 65, 1059–1070. doi:10.1016/S0016-7037(00)00570-6

CrossRef Full Text | Google Scholar

Georgiadis, A., Llovell, F., Bismarck, A., Blas, F. J., Galindo, A., Maitland, G. C., et al. (2010). Interfacial tension measurements and modelling of (carbon dioxide + n-alkane) and (carbon dioxide + water) binary mixtures at elevated pressures and temperatures. J. Supercrit. Fluids 55, 743–754. doi:10.1016/j.supflu.2010.09.028

CrossRef Full Text | Google Scholar

Global status CCS (2021). The global status of CCS 2021. Australia.

Google Scholar

Goldberg, R. N., and Parker, V. B. (1985). Thermodynamics of solution of SO2(g) in water and of aqueous sulfur dioxide solutions. J. Res. Natl. Bur. Stand. (1977). 90, 341. doi:10.6028/jres.090.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D., and Quintard, M. (2002). On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium. J. Fluid Mech. 457, 213–254. doi:10.1017/S0022112002007735

CrossRef Full Text | Google Scholar

Grandstaff, D. E. (1978). Changes in surface area and morphology and the mechanism of forsterite dissolution. Geochim. Cosmochim. Acta 42, 1899–1901. doi:10.1016/0016-7037(78)90245-4

CrossRef Full Text | Google Scholar

Gu, Y., Hou, P., and Luo, W. (2013). Effects of four important factors on the measured minimum miscibility pressure and first-contact miscibility pressure. J. Chem. Eng. Data 58, 1361–1370. doi:10.1021/je4001137

CrossRef Full Text | Google Scholar

Gysi, A. P., and Stefánsson, A. (2012). Experiments and geochemical modeling of CO2 sequestration during hydrothermal basalt alteration. Chem. Geol. 306307, 10–28. doi:10.1016/j.chemgeo.2012.02.016

CrossRef Full Text | Google Scholar

Haghi, R. K., Chapoy, A., Peirera, L. M. C., Yang, J., and Tohidi, B. (2017). pH of CO2 saturated water and CO2 saturated brines: Experimental measurements and modelling. Int. J. Greenh. Gas Control 66, 190–203. doi:10.1016/j.ijggc.2017.10.001

CrossRef Full Text | Google Scholar

Han, W. S., Stillman, G. A., Lu, M., Lu, C., McPherson, B. J., and Park, E. (2010). Evaluation of potential nonisothermal processes and heat transport during CO2 sequestration. J. Geophys. Res. 115, B07209. doi:10.1029/2009JB006745

CrossRef Full Text | Google Scholar

Hayes, K. F., and Katz, L. E. (1996). “Application of X-ray absorption spectroscopy for surface complexation modelling of metal ion sorption,” in Physics and Chemistry of mineral surfaces. Editor P. V. Brady (Baton Rouge): CRC Press), 147–223.

Google Scholar

He, D., Xu, R., Ji, T., and Jiang, P. (2022). Experimental investigation of the mechanism of salt precipitation in the fracture during CO2 geological sequestration. Int. J. Greenh. Gas Control 118, 103693. doi:10.1016/j.ijggc.2022.103693

CrossRef Full Text | Google Scholar

Hebach, A., Oberhof, A., Dahmen, N., Kögel, A., Ederer, H., and Dinjus, E. (2002). Interfacial tension at elevated pressures-measurements and correlations in the water + carbon dioxide system. J. Chem. Eng. Data 47, 1540–1546. doi:10.1021/je025569p

CrossRef Full Text | Google Scholar

Hemmati-Sarapardeh, A., Ayatollahi, S., Ghazanfari, M. H., and Masihi, M. (2014). Experimental determination of interfacial tension and miscibility of the CO2-crude oil system; Temperature, pressure, and composition effects. J. Chem. Eng. Data 59, 61–69. doi:10.1021/je400811h

CrossRef Full Text | Google Scholar

Hesse, M. A., Orr, F. M., and Tchelepi, H. A. (2008). Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60. doi:10.1017/S002211200800219X

CrossRef Full Text | Google Scholar

Hoteit, H., Fahs, M., and Soltanian, M. R. (2019). Assessment of CO2 injectivity during sequestration in depleted gas reservoirs. Geosciences 9 (5), 199. doi:10.3390/geosciences9050199

CrossRef Full Text | Google Scholar

Houben, M., van Geijn, R., van Essen, M., Borneman, Z., and Nijmeijer, K. (2021). Supercritical CO2 permeation in glassy polyimide membranes. J. Memb. Sci. 620, 118922. doi:10.1016/j.memsci.2020.118922

CrossRef Full Text | Google Scholar

Hough, E. W., Wood, B. B., and Rzasa, M. J. (1952). Adsorption at water–helium, –methane and –nitrogen interfaces at pressures to 15, 000 P.s.i.a. J. Phys. Chem. 56, 996–999. doi:10.1021/j150500a017

CrossRef Full Text | Google Scholar

Hu, Y. F., and Guo, T. M. (2005). Effect of the structures of ionic liquids and alkylbenzene-derived amphiphiles on the inhibition of asphaltene precipitation from CO 2-injected reservoir oils. Langmuir 21, 8168–8174. doi:10.1021/la050212f

PubMed Abstract | CrossRef Full Text | Google Scholar

Huggins, M. L., and Sun, K.-H. (1946). Energy additivity in oxygen-containing crystals and glasses. J. Phys. Chem. 50, 319–328. doi:10.1021/j150448a003

CrossRef Full Text | Google Scholar

Huhtamäki, T., Tian, X., Korhonen, J. T., and Ras, R. (2018). Surface-wetting characterization using contact-angle measurements. Nat. Protoc. 13, 1521–1538. doi:10.1038/s41596-018-0003-z

PubMed Abstract | CrossRef Full Text | Google Scholar

IPCC (2021). IPCC. Cambridge, United Kingdom: Cambridge Univ. Press. doi:10.1260/095830507781076194

CrossRef Full Text | Google Scholar

Islam, A., Nia, K. A. K., Sepehrnoori, K., and Patzek, T. (2014). Effects of geochemical reaction on double diffusive natural convection of CO2 in brine saturated geothermal reservoir. Energy Procedia 63, 5357–5377. doi:10.1016/j.egypro.2014.11.568

CrossRef Full Text | Google Scholar

James, L., Palandri, K., Yousif, K., and Kharaka, K. (2004). U.S. GEOLOGICAL SURVEY OPEN FILE REPORT (OF 2004-1068) National Energy Technology Laboratory. Steve Jobs. Menlo Park, NY: Department of Energy.

Google Scholar

Jang, J., Narsilio, G. A., and Santamarina, J. C. (2011). Hydraulic conductivity in spatially varying media-a pore-scale investigation. Geophys. J. Int. 184 (3), 1167–1179. doi:10.1111/j.1365-246x.2010.04893.x

CrossRef Full Text | Google Scholar

Jiang, L., Wang, S., Abudula, A., Liu, Y., and Song, Y. (2019). The effect of density difference on the development of density-driven convection under large Rayleigh number. Int. J. Heat. Mass Transf. 139, 1087–1095. doi:10.1016/j.ijheatmasstransfer.2019.05.027

CrossRef Full Text | Google Scholar

Karnanda, W., Benzagouta, M. S., AlQuraishi, A., and Amro, M. M. (2013). Effect of temperature, pressure, salinity, and surfactant concentration on IFT for surfactant flooding optimization. Arab. J. Geosci. 6, 3535–3544. doi:10.1007/s12517-012-0605-7

CrossRef Full Text | Google Scholar

Kiepe, J., Horstmann, S., Fischer, K., and Gmehling, J. (2002). Experimental determination and prediction of gas solubility data for CO2+H2O mixtures containing NaCl or KCl at temperatures between 313 and 393K and pressures up to 10 MPa. Ind. Eng. Chem. Res. 41 (17), 4393–4398. doi:10.1021/ie020154i

CrossRef Full Text | Google Scholar

Kim, S., Espinoza, D. N., Jung, J., Cha, M., and Santamarina, J. C. (2019). “Carbon geological storage: Coupled processes, engineering and monitoring,” in Science of carbon storage in deep saline formations (Elsevier), 383–407. doi:10.1016/B978-0-12-812752-0.00017-4

CrossRef Full Text | Google Scholar

Kim, S., and Santamarina, J. C. (2014). Engineered CO2 injection: The use of surfactants for enhanced sweep efficiency. Int. J. Greenh. Gas Control 20, 324–332. doi:10.1016/j.ijggc.2013.11.018

CrossRef Full Text | Google Scholar

Kim, S., and Santamarina, J. C. (2015). Reactive fluid flow in CO2 storage reservoirs: A 2-D pore network model study. Greenh. Gas. Sci. Technol. 5, 462–473. doi:10.1002/ghg.1487

CrossRef Full Text | Google Scholar

Kim, S., and Santamarina, J. C. (2016). Geometry‐coupled reactive fluid transport at the fracture scale: Application to CO 2 geologic storage. Geofluids 16 (2), 329–341. doi:10.1111/gfl.12152

CrossRef Full Text | Google Scholar

Knauss, K. G., Nguyen, S. N., and Weed, H. C. (1993). Diopside dissolution kinetics as a function of pH, CO2, temperature, and time. Geochim. Cosmochim. Acta 57, 285–294. doi:10.1016/0016-7037(93)90431-U

CrossRef Full Text | Google Scholar

Kneafsey, T. J., and Pruess, K. (2010). Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Transp. Porous Media 82, 123–139. doi:10.1007/s11242-009-9482-2

CrossRef Full Text | Google Scholar

Koschel, D., Coxam, J.‐Y., Rodier, L., and Majer, V. (2006). Enthalpy and solubility data of CO2 in water and NaCl(aq) at conditions of interest for geological sequestration. Fluid Phase Equilib. 247 (1–2), 107–120. doi:10.1016/j.fluid.2006.06.006

CrossRef Full Text | Google Scholar

Kvamme, B., Kuznetsova, T., Hebach, A., Oberhof, A., and Lunde, E. (2007). Measurements and modelling of interfacial tension for water + carbon dioxide systems at elevated pressures. Comput. Mat. Sci. 38, 506–513. doi:10.1016/j.commatsci.2006.01.020

CrossRef Full Text | Google Scholar

Lahti, S. I., Raivio, P., and Laitakari, I. (2005). Orbicular rocks in Finland, with contributions by paula raivio and ilkka laitakari. Espoo: Geological Survey of Finland.

Google Scholar

Lee, B. Y., and Kurtis, K. E. (2017). Effect of pore structure on salt crystallization damage of cement-based materials: Consideration of w/b and nanoparticle use. Cem. Concr. Res. 98, 61–70. doi:10.1016/j.cemconres.2017.04.002

CrossRef Full Text | Google Scholar

Li, H., Yang, D., and Tontiwachwuthikul, P. (2012). Experimental and theoretical determination of equilibrium interfacial tension for the solvent(s)-CO 2-heavy oil systems. Energy fuels. 26, 1776–1786. doi:10.1021/ef201860f

CrossRef Full Text | Google Scholar

Liesegang, R. E. (1896). Ueber einige Eigenschaften von Gallerten. Naturwissenschaftliche. Wochenschrift 11, 353.

Google Scholar

Liu, Q., and Santamarina, J. C. (2022). Fluid- driven instabilities in granular media: From viscous fingering and dissolution wormholes to desiccation cracks and ice lenses. Front. Mech. Eng. 8, 861554. doi:10.3389/fmech.2022.861554

CrossRef Full Text | Google Scholar

Maliva, R. G., and Siever, R. (1988). Mechanism and controls of silicification of fossils in limestones. J. Geol. 96, 387–398. doi:10.1086/629235

CrossRef Full Text | Google Scholar

Markham, A. E., and Kobe, K. A. (1941). The solubility of carbon dioxide in aqueous solutions of sulfuric and perchloric acids at 25°. J. Am. Chem. Soc. 63, 1165–1166. doi:10.1021/ja01849a507

CrossRef Full Text | Google Scholar

Menke, H. P., Bijeljic, B., and Blunt, M. J. (2017). Dynamic reservoir-condition microtomography of reactive transport in complex carbonates: Effect of initial pore structure and initial brine pH. Geochim. Cosmochim. Acta 204, 267–285. doi:10.1016/j.gca.2017.01.053

CrossRef Full Text | Google Scholar

Miri, R., Aagaard, P., and Hellevang, H. (2014). Examination of CO2 –so 2 solubility in water by SAFT1. Implications for CO2 transport and storage. J. Phys. Chem. B 118, 10214–10223. doi:10.1021/jp505562j

PubMed Abstract | CrossRef Full Text | Google Scholar

Miri, R., van Noort, R., Aagaard, P., and Hellevang, H. (2015). New insights on the physics of salt precipitation during injection of CO2 into saline aquifers. Int. J. Greenh. Gas Control 43, 10–21. doi:10.1016/j.ijggc.2015.10.004

CrossRef Full Text | Google Scholar

Mullins, O. C. (2010). The modified yen model. Energy fuels. 24, 2179–2207. doi:10.1021/ef900975e

CrossRef Full Text | Google Scholar

Nabika, H., Itatani, M., and Lagzi, I. (2020). Pattern formation in precipitation reactions: The Liesegang phenomenon. Langmuir 36, 481–497. doi:10.1021/acs.langmuir.9b03018

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakhaei-Kohani, R., Taslimi-Renani, E., Hadavimoghaddam, F., Mohammadi, M.-R., and Hemmati-Sarapardeh, A. (2022). Modeling solubility of CO2–N2 gas mixtures in aqueous electrolyte systems using artificial intelligence techniques and equations of state. Sci. Rep. 12, 3625. doi:10.1038/s41598-022-07393-z

PubMed Abstract | CrossRef Full Text | Google Scholar

National Academies of Sciences Engineering and Medicine (2020). Characterization, modeling, monitoring, and remediation of fractured rock. Washington, DC: The National Academies Press. doi:10.17226/21742

CrossRef Full Text | Google Scholar

Ng, K., and Santamarina, J. C. (2022). Mechanical and hydraulic properties of carbonate rocks - the critical role of porosity. J. Rock Mech. Geotech. Eng. doi:10.1016/j.jrmge.2022.07.017

CrossRef Full Text | Google Scholar

NIST Chemistry WebBook (2022). NIST stand. Ref. Database number 69.

Google Scholar

Nobakht, M., Moghadam, S., and Gu, Y. (2008). Mutual interactions between crude oil and CO2 under different pressures. Fluid Phase Equilib. 265, 94–103. doi:10.1016/j.fluid.2007.12.009

CrossRef Full Text | Google Scholar

O’Connor, W. K., Dahlin, D. C., Nilsen, D. N., Rush, G. E., and WaltersRichard P Turner, P. C. (2001). “Carbon dioxide sequestration by direct mineral carbonation: Results from recent studies and current status,” in First national conference on carbon sequestration (Washington, DC.

Google Scholar

O’Connor, W. K., Dahlin, D. C., Rush, G. E., Dahlin, C. L., and Collins, W. K. (2002). Carbon dioxide sequestration by direct mineral carbonation: Process mineralogy of feed and products. Min. Metall. Explor. 19, 95–101. doi:10.1007/BF03403262

CrossRef Full Text | Google Scholar

Oelkers, E. H., Declercq, J., Saldi, G. D., Gislason, S. R., and Schott, J. (2018). Olivine dissolution rates: A critical review. Chem. Geol. 500, 1–19. doi:10.1016/j.chemgeo.2018.10.008

CrossRef Full Text | Google Scholar

Oldenburg, C. M. (2007). Joule-Thomson cooling due to CO2 injection into natural gas reservoirs. Energy Convers. Manag. 48, 1808–1815. doi:10.1016/j.enconman.2007.01.010

CrossRef Full Text | Google Scholar

Palandri, J. L., and Kharaka, Y. K. (2004). A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling. Open-File Report. USGS Numbered S.

Google Scholar

Panjarian, S., and Sultan, R. (2001). Crystal selection and Liesegang banding in dynamic precipitate systems. Collect. Czechoslov. Chem. Commun. 66, 541–554. doi:10.1135/cccc20010541

CrossRef Full Text | Google Scholar

Park, J. Y., Lim, J. S., Yoon, C. H., Lee, C. H., and Park, K. P. (2005). Effect of a fluorinated sodium bis(2-ethylhexyl) sulfosuccinate (aerosol-OT, AOT) analogue surfactant on the interfacial tension of CO 2 + water and CO2 + Ni-plating solution in near- and supercritical CO2. J. Chem. Eng. Data 50, 299–308. doi:10.1021/je0499667

CrossRef Full Text | Google Scholar

Peng, C., Crawshaw, J. P., Maitland, G. C., Martin Trusler, J. P., and Vega-Maza, D. (2013). The pH of CO2-saturated water at temperatures between 308 K and 423 K at pressures up to 15 MPa. J. Supercrit. Fluids 82, 129–137. doi:10.1016/j.supflu.2013.07.001

CrossRef Full Text | Google Scholar

Phuoc, T. X., and Massoudi, M. (2021). Using CO2 as a cooling fluid for power plants: A novel approach for CO2 storage and utilization. Appl. Sci. (Basel). 11, 4974. doi:10.3390/APP11114974

CrossRef Full Text | Google Scholar

Pokrovsky, O. S., Golubev, S. V., and Schott, J. (2005). Dissolution kinetics of calcite, dolomite and magnesite at 25 °C and 0 to 50 atm pCO2. Chem. Geol. 217, 239–255. doi:10.1016/j.chemgeo.2004.12.012

CrossRef Full Text | Google Scholar

Pollet-Villard, M., Daval, D., Ackerer, P., Saldi, G. D., Wild, B., Knauss, K. G., et al. (2016). Does crystallographic anisotropy prevent the conventional treatment of aqueous mineral reactivity? A case study based on K-feldspar dissolution kinetics. Geochim. Cosmochim. Acta 190, 294–308. doi:10.1016/j.gca.2016.07.007

CrossRef Full Text | Google Scholar

Rácz, Z. (1999). formation of Liesegang patterns. Phys. A Stat. Mech. its Appl. 274, 50–59. doi:10.1016/S0378-4371(99)00432-X

CrossRef Full Text | Google Scholar

Rezk, M. G., and Foroozesh, J. (2019). Phase behavior and fluid interactions of a CO2-Light oil system at high pressures and temperatures. Heliyon 5, e02057. doi:10.1016/j.heliyon.2019.e02057

PubMed Abstract | CrossRef Full Text | Google Scholar

Rutter, E. H. (1983). Pressure solution in nature, theory and experiment. J. Geol. Soc. Lond. 140, 725–740. doi:10.1144/gsjgs.140.5.0725

CrossRef Full Text | Google Scholar

Sanaei, A., Varavei, A., and Sepehrnoori, K. (2019). Mechanistic modeling of carbonated waterflooding. J. Pet. Sci. Eng. 178, 863–877. doi:10.1016/j.petrol.2019.04.001

CrossRef Full Text | Google Scholar

Sargent, J. P., Tredwell, S., Dixon, D. G., Buxton, A. L., Shanahan, M. E. R., Padday, J. F., et al. (2005). Handbook of adhesion. Chichester, UK: John Wiley & Sons, 579–620. doi:10.1002/0470014229.ch21

CrossRef Full Text | Google Scholar

Savary, V., Berger, G., Dubois, M., Lacharpagne, J.-C., Pages, A., Thibeau, S., et al. (2012). The solubility of CO2+H2S mixtures in water and 2M NaCl at 120°C and pressures up to 35MPa. Int. J. Greenh. Gas Control 10, 123–133. doi:10.1016/j.ijggc.2012.05.021

CrossRef Full Text | Google Scholar

Schmelzer, J. W. P., Zanotto, E. D., and Fokin, V. M. (2005). Pressure dependence of viscosity. J. Chem. Phys. 122, 074511. doi:10.1063/1.1851510

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmid, R. (2001). Recent advances in the description of the structure of water, the hydrophobic effect, and the like-dissolves-like rule. Monatsh. fur Chem. 132, 1295–1326. doi:10.1007/s007060170019

CrossRef Full Text | Google Scholar

Schott, J., Berner, R. A., and Sjöberg, E. L. (1981). Mechanism of pyroxene and amphibole weathering—I. Experimental studies of iron-free minerals. Geochim. Cosmochim. Acta 45, 2123–2135. doi:10.1016/0016-7037(81)90065-X

CrossRef Full Text | Google Scholar

Schott, J., and Berner, R. A. (1983). X-ray photoelectron studies of the mechanism of iron silicate dissolution during weathering. Geochim. Cosmochim. Acta 47, 2233–2240. doi:10.1016/0016-7037(83)90046-7

CrossRef Full Text | Google Scholar

Shafabakhsh, P., Ataie-Ashtiani, B., Simmons, C. T., Younes, A., and Fahs, M. (2021). Convective-reactive transport of dissolved CO2 in fractured-geological formations. Int. J. Greenh. Gas Control 109, 103365. doi:10.1016/j.ijggc.2021.103365

CrossRef Full Text | Google Scholar

Shin, H., Santamarina, J. C., and Cartwright, J. A. (2008). Contraction-driven shear failure in compacting uncemented sediments. Geol. 36, 931. doi:10.1130/G24951A.1

CrossRef Full Text | Google Scholar

Shin, H., Santamarina, J. C., and Cartwright, J. A. (2010). Displacement field in contraction-driven faults. J. Geophys. Res. 115, B07408. doi:10.1029/2009JB006572

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2010). Fluid-driven fractures in uncemented sediments: Underlying particle-level processes. Earth Planet. Sci. Lett. 299 (1-2), 180–189. doi:10.1016/j.epsl.2010.08.033

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2009). Mineral dissolution and the evolution of k0. J. Geotech. Geoenviron. Eng. 135, 1141–1147. doi:10.1061/(ASCE)GT.1943-5606.0000053

CrossRef Full Text | Google Scholar

Shin, H., and Santamarina, J. C. (2011). Open-mode discontinuities in soils. Geotech. Lett. 1, 95–99. doi:10.1680/geolett.11.00014

CrossRef Full Text | Google Scholar

Simeoni, G. G., Bryk, T., Gorelli, F. A., Krisch, M., Ruocco, G., Santoro, M., et al. (2010). The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 6, 503–507. doi:10.1038/nphys1683

CrossRef Full Text | Google Scholar

Simon, R., and Graue, D. J. (1965). Generalized correlations for predicting solubility, swelling and viscosity behavior of CO2 -crude oil systems. J. Pet. Technol. 17, 102–106. doi:10.2118/917-pa

CrossRef Full Text | Google Scholar

Sloan, E. D. (2010). Natural gas hydrates in flow assurance. Burlington, MA: Gulf Professional Publishing. doi:10.1016/C2009-0-62311-4

CrossRef Full Text | Google Scholar

Snæbjörnsdóttir, S. Ó., Gislason, S. R., Galeczka, I. M., and Oelkers, E. H. (2018). Reaction path modelling of in-situ mineralisation of CO2 at the CarbFix site at Hellisheidi, SW-Iceland. Geochim. Cosmochim. Acta 220, 348–366. doi:10.1016/j.gca.2017.09.053

CrossRef Full Text | Google Scholar

Snæbjörnsdóttir, S. Ó., Sigfússon, B., Marieni, C., Goldberg, D., Gislason, S. R., and Oelkers, E. H. (2020). Carbon dioxide storage through mineral carbonation. Nat. Rev. Earth Environ. 1, 90–102. doi:10.1038/s43017-019-0011-8

CrossRef Full Text | Google Scholar

Stumm, W., and Morgan, J. J. (1996). Aquatic Chemistry, Chemical Equilibria and Rates in Natural Waters. J. Chem. Educ. 3rd Edn. New York: 73.

Google Scholar

Sutjiadi-Sia, Y., Jaeger, P., and Eggers, R. (2008). Interfacial phenomena of aqueous systems in dense carbon dioxide. J. Supercrit. Fluids 46, 272–279. doi:10.1016/j.supflu.2008.06.001

CrossRef Full Text | Google Scholar

Sverdrup, H. U. (1990). The kinetics of base cation release due to chemical weathering. Lund, Sweden: Lund University Press.

Google Scholar

Taber, S. (1916). The growth of crystals under external pressure. Am. J. Sci. s4-41, 532–556. doi:10.2475/ajs.s4-41.246.532

CrossRef Full Text | Google Scholar

Talman, S., Shokri, A. R., Chalaturnyk, R., and Nickel, E. (2020). “Salt precipitation at an active CO2 injection site,” in Gas injection into geological formations and related topics (John Wiley & Sons), 183–199. doi:10.1002/9781119593324.ch11

CrossRef Full Text | Google Scholar

Van der Meer, L. G. H. (1993). The conditions limiting CO2 storage in aquifers. Energy Convers. Manag. 34, 959–966. doi:10.1016/0196-8904(93)90042-9

CrossRef Full Text | Google Scholar

Velbel, M. A. (1999). Bond strength and the relative weathering rates of simple orthosilicates. Am. J. Sci. 299, 679–696. doi:10.2475/ajs.299.7-9.679

CrossRef Full Text | Google Scholar

Verma, M. K. (2015). Fundamentals of carbon dioxide-enhanced oil recovery (CO2-EOR): A supporting document of the assessment methodology for hydrocarbon recovery using CO2-EOR associated with carbon sequestration. Washington, DC: US Department of the Interior, US Geological Survey, 19.

Google Scholar

Vilarrasa, V., Rinaldi, A. P., and Rutqvist, J. (2017). Long-term thermal effects on injectivity evolution during CO2 storage. Int. J. Greenh. Gas Control 64, 314–322. doi:10.1016/j.ijggc.2017.07.019

CrossRef Full Text | Google Scholar

Vilarrasa, V., and Rutqvist, J. (2017). Thermal effects on geologic carbon storage. Earth. Sci. Rev. 165, 245–256. doi:10.1016/j.earscirev.2016.12.011

CrossRef Full Text | Google Scholar

Wang, X., Zhang, S., and Gu, Y. (2010). Four important onset pressures for mutual interactions between each of three crude oils and CO2. J. Chem. Eng. Data 55, 4390–4398. doi:10.1021/je1005664

CrossRef Full Text | Google Scholar

Wiltschko, D. V., and Morse, J. W. (2001). Crystallization pressure versus “crack seal” as the mechanism for banded veins. Geology 29, 79. doi:10.1130/0091-7613(2001)029<0079:CPVCSA>2.0.CO;2

CrossRef Full Text | Google Scholar

Xie, Z. (1994). Surface properties of silicates, their stability and dissolution kinetics.

Google Scholar

Xiong, W., Wells, R. K., Horner, J. A., Schaef, H. T., Skemer, P. A., and Giammar, D. E. (2018). CO 2 mineral sequestration in naturally porous basalt. Environ. Sci. Technol. Lett. 5, 142–147. doi:10.1021/acs.estlett.8b00047

CrossRef Full Text | Google Scholar

Yasunishi, A., and Yoshida, F. (1979). Solubility of carbon dioxide in aqueous electrolyte solutions. J. Chem. Eng. Data 24, 11–14. doi:10.1021/je60080a007

CrossRef Full Text | Google Scholar

Young, T. (1805). III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 95, 65–87. doi:10.1098/rstl.1805.0005

CrossRef Full Text | Google Scholar

Zhang, H. (1990). Factors determining the rate and stoichiometry of hornblende dissolution.

Google Scholar

Zheng, C., Brunner, M., Li, H., Zhang, D., and Atkin, R. (2019). Dissolution and suspension of asphaltenes with ionic liquids. Fuel 238, 129–138. doi:10.1016/j.fuel.2018.10.070

CrossRef Full Text | Google Scholar

Zolghadr, A., Escrochi, M., and Ayatollahi, S. (2013). Temperature and composition effect on CO2 miscibility by interfacial tension measurement. J. Chem. Eng. Data 58, 1168–1175. doi:10.1021/je301283e

CrossRef Full Text | Google Scholar

Glossary

$a_{H^{+}}$[] Activity of protons

c [mol/l] Solute concentration (0: at saturation)

C_p [J/K] Heat capacity

D [m²/s] Molecular diffusion coefficient

d* [m] Characteristic pore diameter

Da [] Damköhler number

e [] Void ratio

E [GPa] Young’s modulus

g [m/s] Gravitational acceleration

H [m] Height of the fluid column (CO₂: carbon dioxide column; R: reservoir)

k [mol m⁻² s⁻¹] Rate constant of mineral dissolution

k₀ [] Lateral coefficient earth pressure (0: at rest; a: Rankine’s active case)

k_H [mol L⁻¹ atm⁻¹] Henry’s constant

k_hyd [m²] Permeability

L_ch [m] Channel length

l₀ [m] Intermolecular distance

M [g/mol] Molar mass (CO₂; silic: silicate minerals)

$n_{H^{+}}$ [] Reaction order with respect to the activity of protons

P [Pa] Pressure (0: initial pressure; CO₂: partial pressure CO₂; nw: non-wetting fluid; w: wetting fluid; crys: on a growing crystal; sol: solution)

Pe [] Péclet number

R [J mol⁻¹ K⁻¹] Gas constant

Ra [] Rayleigh number

r [m] Radius of the interface

r_d [mol/s] Mineral dissolution rate

S [] Supersaturation

s [m²] Surface area

S_s [m²/g] Specific surface area

S_w [] Degree of water saturation

SD [kg/m³] Storage density in terms of kg of CO₂ per m³ of the reservoir

T [K] Absolute temperature

T_p [m] Plume thickness

t [s] Time (adv: advection; diff: diffusion; r: reactive)

V_m [m³/mol] Mineral molar volume

v [m/s] Average flow velocity

z [m] Height of the sediment column

z_w [m] Height of the water column above the seafloor

α [K⁻¹] The coefficient of thermal expansion

β [] Factor related to the pore size distribution

γ [N/m] Interfacial tension (FS: fluid-solid; LS: liquid-solid; LF: fluid-liquid)

ΔH [kJ/kg] Enthalpy change in phase transformation

ε[] Strain

θ [°] Contact angle (A: advancing; R: receding)

κ [1/s] Kinetic rate of mineral dissolution

μ [µPa·s] Fluid Viscosity (w: water)

μ_JT [] Joule-Thomson coefficient

Π_seal [] Dimensionless ratio (seal: sealing number; stability: stability number)

ρ [kg/m³] Density (b: bulk; CO₂; hyd: hydrate; m: mineral; W: water; 0: initial fluid density)

σ’ [Pa] Effective stress (h: horizontal; v: vertical; z₀: under zero lateral strain conditions)

χ_CO2 [mol/L] Solubility of CO₂

φ [] Porosity

ψ [] Geometric fabric factor