- 1State Grid Corporation of China, Beijing, China
- 2China Electric Power Research Institute, Beijing, China
- 3State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan, China
In this work, a novel PV station participating FR technique based on PV array reconfiguration and battery energy storage system (BESS) is put forward. Through the PV array reconfiguration under Partial shading condition, photovoltaic (PV) system can adjust the output power according to the power dispatch instruction. And with the help of BESS, The PV station can achieve continuous power output. Specifically, a joint PV energy storage system model combining profit maximization and power deviation minimization is established. In order to two conflicting goals simultaneously, multi-objective golden eagle optimizer and improved ideal point decision making method are applied. And Lagrange function is given to determine the weight coefficients of each objective more fairly. Two cases are designed and tested. In the high frequency response simulation test, the profit is increased by 8.4% and the power deviation from FR signal is decreased by 19.98%; meanwhile the profit is increased by 10.07% and power deviation is decreased by 67.69% in the low frequency response test. Therefore, the simulation results verify that the proposed method contributes to the frequency response of PV station.
Introduction
With the increasing severity of environmental problems and the consumption of fossil fuels, solar energy has become one of the most widely used renewable energy sources due to its huge reserves, clean and environmentally friendly (Yang et al., 2021). Driven by the national strategy of “carbon neutral, emission peak”, the proportion of Photovoltaic (PV) power generation in the power system will continue to grow (Yang et al., 2021) (Kaushika and Gautam, 2003). In the context of high proportion of renewable energy in new power system, the traditional frequency regulation (FR) control means are stretched, as a result PV system participating in power grid FR is inevitable (Sai Krishna and Moger, 2019). Therefore, the research on the FR strategy based on PV reconfiguration coordinated with energy storage carried out in this work has important value for the frequency safety of the new power system.
Partial shading condition (PSC) (Laudani et al., 2018), (Ajmal et al., 2020) is one of the most common environmental factors which effecting the PV power generation efficiency and maximum power point tracking (MPPT) efficiency. Changing the connection topology of PV modules can equivalently disperse the originally concentrated shadows to the entire array, so as to reduce the influence of PSC and improve the output power (Rani et al., 2013). In recent years, researchers have developed a variety of PV array reconfiguration methods, mainly divided into two categories: static and dynamic.
The literature (NamaniRakesh and Madhavaram, 2016) studies the performance of three different topologies (parallel, total-cross-tied (TCT) and bridge structure) of PV array in PSC proposes that TCT topology extract the maximum power of the array. Sudoku scheme is used to reconfigures PV modules in literature (Horoufiany and Ghandehari, 2018). Literature (Shams El-Dein et al., 2013) introduces mathematical formulas based on mixed integer quadratic programming to disperse the shadow of TCT-connected PV arrays. In addition, static technique is a one-time reconfiguration method which can hardly settle time-varying shadow.
However, dynamic reconfiguration can adjust the switch matrix in real time according to the shadow change, so as to achieve the purpose of dynamically changing the electrical topological structure of the array (Deshkar et al., 2015), (Balraj and Stonier, 2020). The literature (Sanseverino et al., 2015) proposes a PV array reconfiguration method based on knapsack problem, and uses additional unshaded PV components to compensate for components that are heavily shaded. In recent years, the application of meta-heuristic algorithms to PV array reconfiguration has become a new trend, such as genetic algorithm (Deshkar et al., 2015), particle swarm optimization (Babu et al., 2018), and grasshopper optimization algorithms (Fathy, 2018), butterfly optimization algorithm (Fathy, 2020) and artificial ecological optimization algorithm (Yousri et al., 2020a).
None of the current PV reconfiguration studies have taken the application of PV reconfiguration techniques to grid frequency regulation into account (Zhang et al., 2021), so this work proposes a PV array reconfiguration of grid frequency regulation strategy based on multi-objective golden eagle optimizer (MOGEO) (Mohammadi-Balani et al., 2021) which has strong global exploration ability and optimization stability. At the same time, the battery energy storage system (BESS) is introduced to coordinate the PV system so that the reconfiguration can achieve linear continuity response to FR instructions (Yousri et al., 2020b) (González-Castaño et al., 2021).
From the view of PV power station, the PV system and BESS are considered to participate frequency regulation at the same time, to provide ancillary services (Krishnan et al., 2020), (Bi et al., 2020). According to the electric price, operation cost, the PV array reconfiguration optimization economic model is established to determine the required energy storage power, power generation planning and charging and discharging strategy of PV power plant under different shadows and frequency regulation capacity, so as to maximize the joint PV energy storage system. Leave out the dynamic interaction with the system frequency, the system frequency is regarded as the known input of the model, so the final model can be solved by heuristic algorithm.
Design of multi-objective golden eagle optimizer
Spiral movement and prey selection
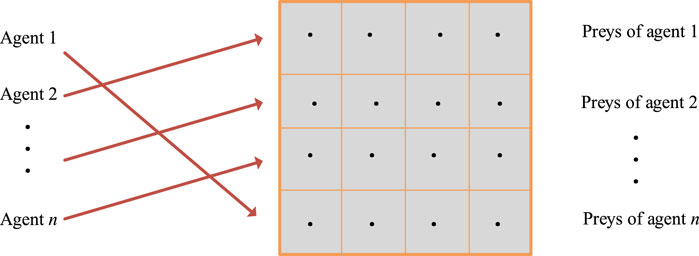
Each golden eagle can remember its best prey and cruises around its own prey or others’ preys. Prey selection strategies play an important role in MOGEO. For the sake of enhancing the exploration efficiency of agents, a one-to-one mapping program is proposed in MOGEO so that each prey can be randomly assigned to only one golden eagle. And then every golden eagle cruises and attacks the chosen prey. And the schematic diagram of one-to-one mapping program is shown in Figure 1.
Exploitation and exploration
The golden eagle’s attack behavior can be viewed as a vector. The starting point of this vector is the current position of the golden eagle and the destination is the prey. So, the attack vector which emphasizes the development stage in MOGEO of agent i can be modeled by Formula (1).
where,
The speed direction of cruising vector is perpendicular to the attack vector. The cruising vector can be obtained only when the equation of the tangent hyperplane is calculated. Hence the expression of the n-dimensional hyperplane can be calculated by Eq. 2.
The steps of golden eagle randomly seeking the destination position C located on a n-dimensional cruising hyperplane are as follows:
Step 1 A variable is randomly selected to assigned as the fixed variable from whole variable set other than whose corresponding attack vector is 0.
Step 2 Except for the pth variable whose value is fixed, appoints random figures to all variables.
Step 3 Use Eq. 3 to acquire the value of the fixed parameter.
where,
Updating of location
The position movement of the golden eagle consists of two parts, attack and cruise, which affect and restrict each other, as shown in the following equation.
where,
When the new position of the golden eagle is better than the original position, the original position is replaced by the new coordinates; Instead, keep the original position. In the next iteration, compute the new attack vector and cruise vector, and move to the new position. Iteration is not stopped until the loop termination condition is met.
Mathematical modeling of combined photovoltaic energy storage system revenue
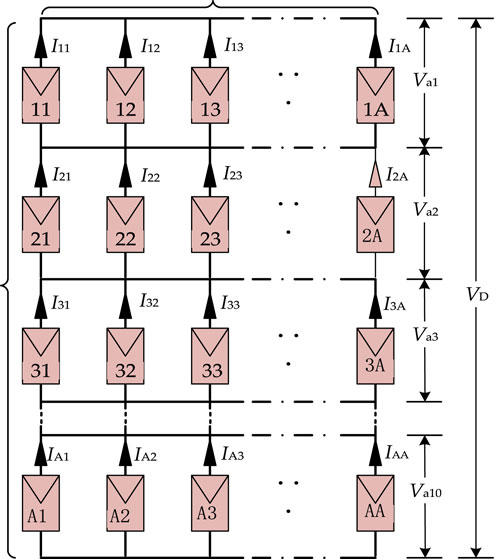
Modeling of total-cross-tied structure photovoltaic arrays
Many individual PV cells form a PV module, and multiple PV modules form a PV array by series and parallel connection, and correspondingly, multiple PV arrays can form a PV system. For ease of study, the PV cell can be seen as a current generator. According to the general model of PV cell, the current of PV cell can be expressed as below:
where
Since the TCT topology is less affected by shadows under PSC, the output power is more stable, which is widely used in the study of PV arrays. A
where
Constraints
1) Constraints of battery.
In order to ensure the safe operation and life of the battery, it is necessary to constrain its charge and discharge power and the remaining capacity of the battery, as shown below:
Where,
2) Balance constraint of frequency regulation power.
The power responded to high frequency and low frequency from joint PV energy storage system is provided by PV array and energy storage systems together, which can be expressed as follows:
where,
3) Full response constraint of frequency regulation power.
As the frequency response is the mandatory auxiliary service of the power system, the frequency regulation power provided by combined PV energy storage system must be satisfied with the frequency regulation capacity calculated according to the grid-connection guidelines requirements.
where,
4) Constraints of PV power sale.
where,
Objective function
In order to increase the power generation income of the PV storage power station and make the power response to the FM signal at the same time, two conflicting goals are considered in this paper, the first goal is to minimize the average power deviation between the power output of the PV array coordinated energy storage battery and the FR signal
Where,
where,
where,
For the convenience of research, the cost of energy storage here only considers the charge and discharge cost of the battery during operation.
where,
During the practical operation process of MOGEO, in order to fit the characteristics of the algorithm, it is necessary to appropriately adjust the objective function so that the fitness function of the algorithm program is calculated as follows:
where,
Application design of photovoltaic reconfiguration solution based on pareto
The MOGEO proposed in this work is a multi-objective intelligent optimization algorithm, so the key problems including variable processing, fitness function, solution screening and compromise decision must be mainly solved in the model solution of joint PV energy storage system (Yousri et al., 2020c).
Variable processing and fitness function
PV array reconfiguration optimization and charge-discharge optimization of BESS contain both continuous and discrete variables (Mahmoud et al., 2019). Continuous variables can be processed according to normal optimization; The discrete variables can be rounded by the values of the continuous space, and the upper and lower limits of the continuous optimization space are the upper and lower limits of the corresponding discrete variables (Horoufiany and Ghandehari, 2017).
The fitness function of the algorithm must effectively combine the objective and constraint conditions of the proposed model, which can be performed by Eq. 17.
Storage and screening of pareto solutions
In the iteration process of MOGEO, the number of Pareto solutions will persistently grow. And the solutions will be put into a finite sized storeroom. The new non-dominant solution obtained by the MOGEO is compared with the non-dominant solution set in the storeroom. Based on the comparison result, the new non-dominant solution is determined whether to put in the storeroom or not. Like the general multi-objective optimization algorithm, the judgment process is divided into the following three situations.
1) If the new solution dominates one or more solutions in the storeroom, replace them with the new solution;
2) If the new solution is dominated by at least one solution in the storeroom, the new solution is discarded;
3) If the new solution does not have a dominant relationship with all the solutions in the storeroom, the new solution is added to the storage pool.
To improve the computing efficiency of the algorithm, the storeroom stores only a limited number of dynamic non-dominant solutions. Therefore, when the number of non-dominant solutions in the storeroom exceeds the threshold, redundant non-dominant solutions need to be removed. In order to screen out non-dominant solutions with crowded distribution, the algorithm removes them according to the number of adjacent solutions of each non-dominant solution. On the basis of obtaining the number of adjacent solutions of each non-dominant solution in the storeroom, the method of roulette is adopted to eliminate the non-dominant solutions whose adjacent solutions exceed the limit amount. The more the number of adjacent solutions of non-dominant solutions is, the greater the probability of being eliminated is.
Improved ideal point decision making method
According to the optimal Pareto front obtained by MEGEO, the target ideal point of the current optimization problem to be solved and the square of the Euclidean distance from each non-dominant solution to the ideal point can be computed. First, the objective function value of the non-dominant solution is normalized, as shown in the formula below.
where,
Therefore, the ideal point of pareto frontier after normalization is (0, 0). So that the squared Euclidean distance from each nondominant solution to the ideal point is calculated by following formula.
where,
The optimal weight model is constructed to give the weight coefficients of each objective more fairly, as shown in Eq. 20.
where,
Hence, the decision compromise solution is determined by the following formula:
In conclusion, the detailed steps of joint PV energy storage system participating frequency regulation is tabulated in Table 1.
Case studies
In order to verify the contribution of the joint PV energy storage system on improving the frequency condition of the grid based on proposed PV plant reconfiguration model, two simulation tests are designed and executed. In the studied cases, the installed capacity of PV power station is 25 MW, and the capacity of BESS is 15 MW. Moreover, the key parameter settings of the joint PV energy storage system model are shown in Table 2.
The PV system consists of 25 subsystems, each of which is the same
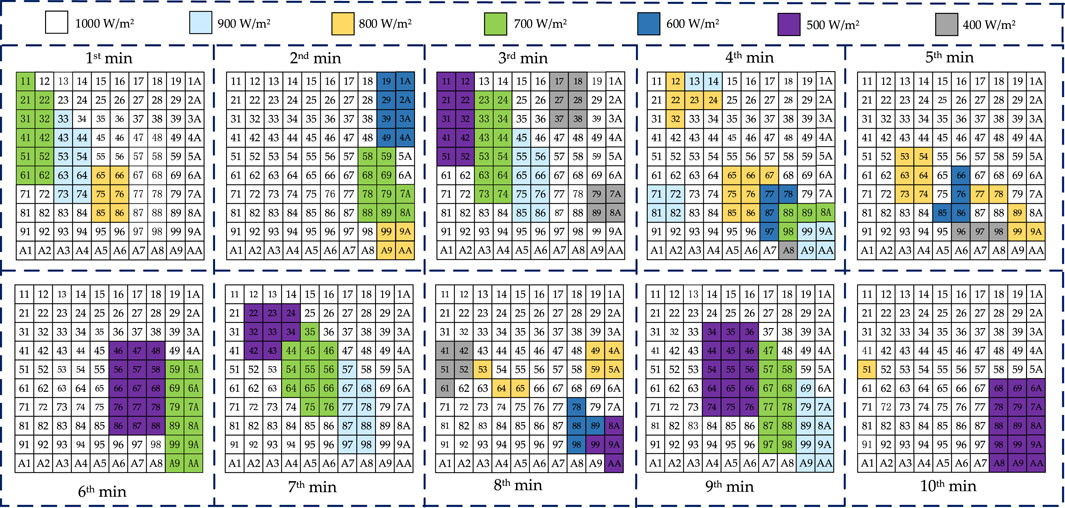
The shading which is varying with time of each subsystem is assumed same, and the shading condition of PV array in 10 minutes is depicted in Figure 3. Besides, all case studies are performed on Matlab R2019b.
Response to high frequency of grid
When the practical frequency of power grid is higher than power frequency, the joint PV energy storage system will receive a FR command of decreasing power output from dispatch department. Therefore, the FR signal under high grid frequency is designed as below:
After the optimization of PV reconfiguration by MOGEO, the shadow is dispersed to the whole array as demonstrated in Figure 4A. Moreover, the power curves of BESS, joint PV-BESS station and PV plant without optimization are depicted in Figure 4B. Obviously, the proposed reconfiguration method based on MOGEO effectively mitigate the impact of PSC and consequently enhance the upper limit of PV output. With the cooperation of BESS, the proposed technique achieves the aim of reducing the deviation between output power of joint PV-BESS and FR signal than that without reconfiguration optimization. In addition, the power biases from FR signal and profits before and after optimization are shown in Figure 4C.
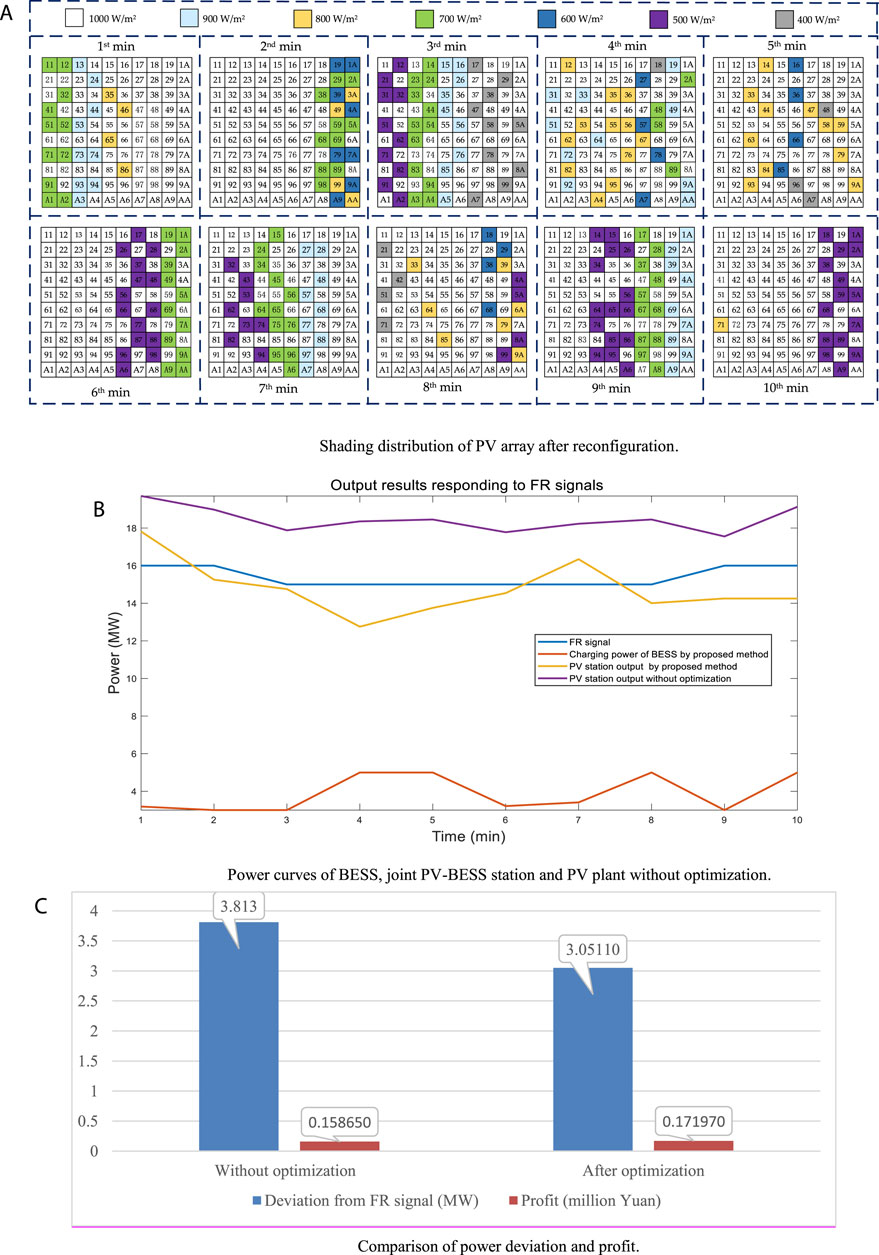
FIGURE 4. (A) Shading distribution of PV array after reconfiguration. (B) Power curves of BESS, joint PV-BESS station and PV plant without optimization. (C) Comparison of power deviation and profit.
Response to low frequency of grid
Apart from high frequency response, the simulation test for low frequency response is also performed, and the FR signal is designed as follows:
The shadow distribution after PV reconfiguration is demonstrated in Figure 5A. Moreover, the power curves of BESS, joint PV-BESS station and PV plant without optimization are depicted in Figure 5B. And the power output of PV station is more closed to FR signal than that of high frequency response. Besides, the proposed reconfiguration model effectively enhances the upper limit of PV output and consequently enhance the margin space of power modulation. What’s more, the power biases from FR signal and profits before and after optimization are shown in Figure 5C.
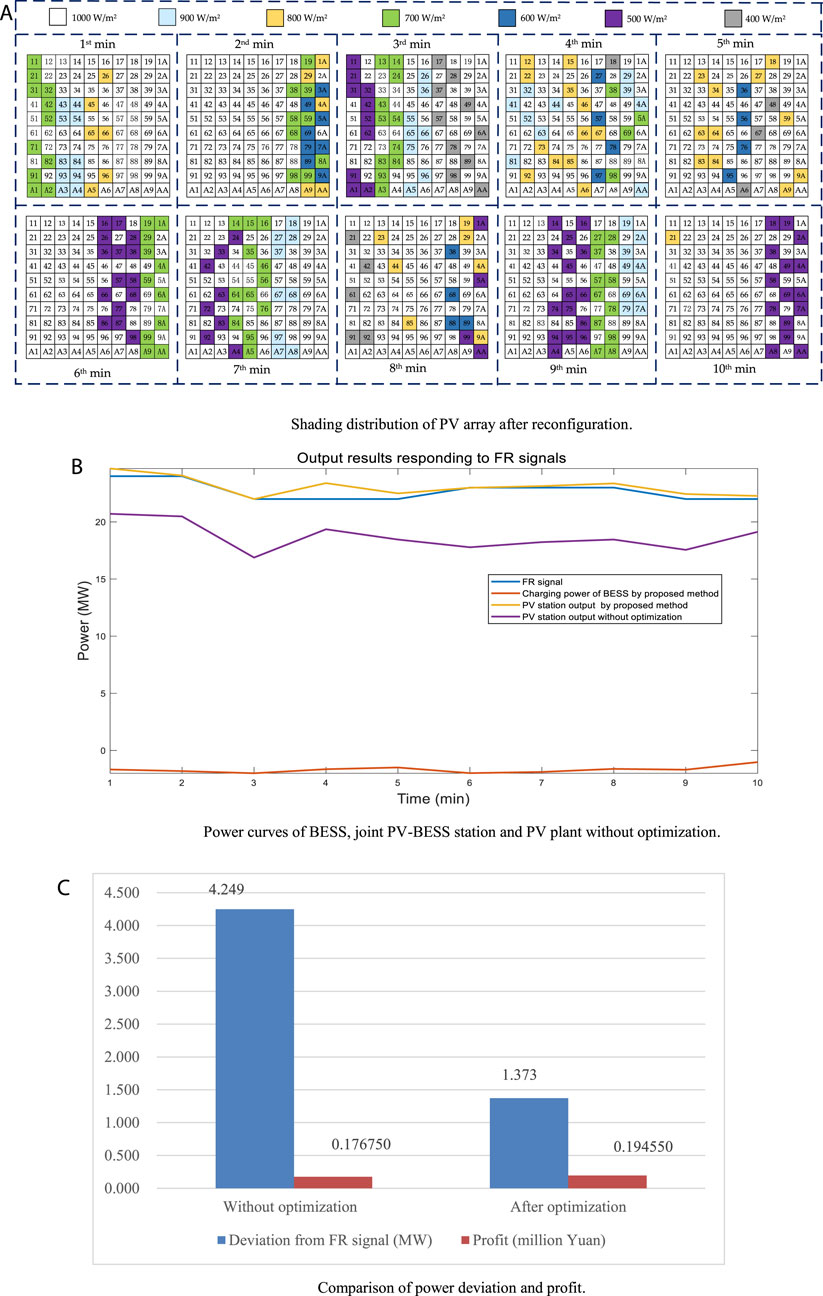
FIGURE 5. (A) Shading distribution of PV array after reconfiguration. (B) Power curves of BESS, joint PV-BESS station and PV plant without optimization. (C) Comparison of power deviation and profit.
Conclusions and perspectives
In this work, a novel PV station participating FR technique based on PV array reconfiguration and BESS is put forward. And the simulation results verify that the proposed method contributes to the frequency response of PV station. Two cases are designed and tested. The main conclusions of this work are summarized as below:
1) MOGEO can effectively find satisfactory solution which can meet both of profit maximization and power deviation minimization;
2) The improved ideal point decision making method is proposed to get optimal weight coefficients of each objective more fairly;
3) By proposed technique, the profit of PV station is increased by 8.4 and 10.07% respectively in the high and low frequency response simulation tests; meanwhile the power deviation from FR signal is decreased by 19.98 and 67.69% in the high and low frequency response tests.
The future works will focus on the following issues:
• Hardware-in-the-loop experiments should be executed to testify the practical influence and algorithm convergence rate of proposed technique;
• Hardware implementation method of PV array reconfiguration deserves more attention.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
JZ: Conceptualization, Writing-Original Draft, Formal analysis; CL: Formal analysis, Software, Supervision; KL: Project administration, Resources.
Conflict of interest
Author JZ was employed by the company State Grid Corporation of China.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ajmal, A. M., Babu, T. S., Ramachandaramurthy, V. K., Yousri, D., and Ekanayake, J. B. (2020). Static and dynamic reconfiguration approaches for mitigation of partial shading influence in photovoltaic arrays. Sustain. Energy Technol. Assessments 40, 100738. doi:10.1016/j.seta.2020.100738
Babu, T. S., Ram, J. P., Dragičević, T., Miyatake, M., Blaabjerg, F., and Rajasekar, N. (2018). Particle swarm optimization based solar PV array reconfiguration of the maximum power extraction under partial shading conditions. IEEE Trans. Sustain. Energy 9 (1), 74–85. doi:10.1109/TSTE.2017.2714905
Balraj, R., and Stonier, A. A. (2020). A novel PV array interconnection scheme to extract maximum power based on global shade dispersion using grey wolf optimization algorithm under partial shading conditions. Circuit World 48, 28–38. doi:10.1108/CW-07-2020-0143
Bi, Z., Ma, J., Wang, K., Man, K. L., Smith, J. S., and Yue, Y. (2020). Identification of partial shading conditions for photovoltaic strings. IEEE Access 8, 75491–75502. doi:10.1109/ACCESS.2020.2988017
Deshkar, S. N., Dhale, S. B., Mukherjee, J. S., Babu, T. S., and Rajasekar, N. (2015). Solar PV array reconfiguration under partial shading conditions for maximum power extraction using genetic algorithm. Renew. Sustain. Energy Rev. 43, 102–110. doi:10.1016/j.rser.2014.10.098
Fathy, A. (2020). Butterfly optimization algorithm based methodology for enhancing the shaded photovoltaic array extracted power via reconfiguration process. Energy Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115
Fathy, A. (2018). Recent meta-heuristic grasshopper optimization algorithm for optimal reconfiguration of partially shaded PV array. Sol. Energy 171, 638–651. doi:10.1016/j.solener.2018.07.014
González-Castaño, C., Restrepo, C., Kouro, S., and Rodriguez, J. (2021). MPPT algorithm based on artificial bee colony for PV system. IEEE Access 9, 43121–43133. doi:10.1109/ACCESS.2021.3066281
Horoufiany, M., and Ghandehari, R. (2017). Optimal fixed reconfiguration scheme for PV arrays power enhancement under mutual shading conditions. IET Renew. Power Gener. 11, 1456–1463. doi:10.1049/iet-rpg.2016.0995
Horoufiany, M., and Ghandehari, R. (2018). Optimization of the sudoku based reconfiguration technique for PV arrays power enhancement under mutual shading conditions. Sol. Energy 159, 1037–1046. doi:10.1016/j.solener.2017.05.059
Kaushika, N. D., and Gautam, N. K. (2003). Energy yield simulations of interconnected solar PV arrays. IEEE Power Eng. Rev. 18 (1), 62. doi:10.1109/MPER.2002.4312475
Krishnan, G. S., Kinattingal, S., Simon, S. P., and Nayak, P. S. R. (2020). MPPT in PV systems using ant colony optimisation with dwindling population. IET Renew. Power Gener. 14 (7), 1105–1112. doi:10.1049/iet-rpg.2019.0875
Laudani, A., Lozito, G. M., Lucaferri, V., Radicioni, M., and Riganti Fulginei, F. (2018). On circuital topologies and reconfiguration strategies for PV systems in partial shading conditions: A review. AIMS Energy 6 (5), 735–763. doi:10.3934/energy.2018.5.735
Mahmoud, A., Shamseldein, M., Hasanien, H., and Abdelaziz, A. (2019). “Photovoltaic array reconfiguration to reduce partial shading losses using water cycle algorithm,” in IEEE Canada Electrical Power and Energy Conference, Montréal, Québec, Canada, 16-18 October 2019, 16–18. doi:10.1109/EPEC47565.2019.9074818
Mohammadi-Balani, A., Nayeri, M. D., Azar, A., and Taghizadeh-Yazdi, M. (2021). Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Industrial Eng. 152, 107050. doi:10.1016/j.cie.2020.107050
NamaniRakesh, T., and Madhavaram, T. V. (2016). Performance enhancement of partially shaded solar PV array using novel shade dispersion technique. Front. Energy 10 (2), 227–239. doi:10.1007/s11708-016-0405-y
Rani, B. I., Ilango, G. S., and Nagamani, C. (2013). Enhanced power generation from PV array under partial shading conditions by shade dispersion using Su Do Ku configuration. IEEE Trans. Sustain. Energy 4 (3), 594–601. doi:10.1109/TSTE.2012.2230033
Sai Krishna, G., and Moger, T. (2019). Reconfiguration strategies for reducing partial shading effects in photovoltaic arrays: State of the art. Sol. Energy 182, 429–452. doi:10.1016/j.solener.2019.02.057
Sanseverino, E. R., Ngoc, T. N., Cardinale, M., Li Vigni, V., Musso, D., Romano, P., et al. (2015). Dynamic programming and Munkres algorithm for optimal photovoltaic arrays reconfiguration. Sol. Energy 122, 347–358. doi:10.1016/j.solener.2015.09.016
Shams El-Dein, M. Z., Kazerani, M., and Salama, M. M. A. (2013). Optimal photovoltaic array reconfiguration to reduce partial shading losses. IEEE Trans. Sustain. Energy 4 (1), 145–153. doi:10.1109/TSTE.2012.2208128
Yang, B., Ye, H., Wang, J., Li, J., Wu, S., Li, Y., et al. (2021). PV arrays reconfiguration for partial shading mitigation: Recent advances, challenges and perspectives. Energy Convers. Manag. 247, 114738. doi:10.1016/j.enconman.2021.114738
Yousri, D., Allam, D., and Eteiba, M. B. (2020). Optimal photovoltaic array reconfiguration for alleviating the partial shading influence based on a modified harris hawks optimizer. Energy Convers. Manag. 206, 112470. doi:10.1016/j.enconman.2020.112470
Yousri, D., Babu, T. S., Beshr, E., Eteiba, M. B., and Allam, D. (2020). A robust strategy based on marine predators algorithm for large scale photovoltaic array reconfiguration to mitigate the partial shading effect on the performance of PV system. IEEE Access 8, 112407–112426. doi:10.1109/ACCESS.2020.3000420
Yousri, D., Babu, T. S., Mirjalili, S., Rajasekar, N., and Elaziz, M. A. (2020). A novel objective function with artificial ecosystem-based optimization for relieving the mismatching power loss of large-scale photovoltaic array. Energy Convers. Manag. 225, 113385. doi:10.1016/j.enconman.2020.113385
Keywords: PV array reconfiguration, battery energy storage system, frequency regulation, multi-objective golden eagle optimizer, optimizing operation
Citation: Zhou J, Liu C and Li K (2022) PV array reconfiguration with electrical energy storage system for power system frequency regulation. Front. Energy Res. 10:971628. doi: 10.3389/fenrg.2022.971628
Received: 17 June 2022; Accepted: 15 July 2022;
Published: 23 August 2022.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Xiaoshun Zhang, Northeastern University, ChinaPuyu Wang, Nanjing University of Science and Technology, China
Copyright © 2022 Zhou, Liu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kun Li, bGlrdW5fYWNAb3V0bG9vay5jb20=
 Jun Zhou1
Jun Zhou1 Kun Li
Kun Li