A Hybrid Data-Driven Method to Predict Battery Capacity of Medical Devices and Analyze Component Effects

Lithium-ion batteries are currently the most utilized power source in medical devices due to their long service life, high energy performance, and being portable. The performance of battery-powered medical devices is heavily dependent on battery capacity, which would be directly affected by related battery component parameters. To widen the application of battery-powered medical devices, it is vital to effectively monitor battery capacity and analyze the effects of battery component parameters. This article derives a hybrid data-driven method to achieve accurate early predictions of battery capacity and reliable analysis of battery component effects. To be specific, a Gaussian process regression-based data-driven model is first developed to efficiently capture the underlying fitting among four component parameters and battery capacity. Then two effect analysis tools including the automatic relevance determination kernel-based weights and tree-based local interpretable model-agnostic explanation are equipped to quantify and analyze both global and local effects of these four component parameters, respectively. Illustrative results show that the designed hybrid data-driven method is able to provide accurate battery capacity predictions with 0.97$R^2$, while both global effects and local effects of four component parameters are successfully quantified. Due to the merits of data-driven characteristics, the designed hybrid data-driven method is capable of efficiently helping users to monitor/predict battery capacity and analyze/understand the effects of interested component parameters. This could further benefit battery-powered medical devices for higher-performance and longer-lifetime applications.

1 Introduction

Lithium-ion (Li-ion) batteries are one of the most popular power sources in medical devices owing to their advantages of long service life, high energy performance, and being portable (Li et al., 2021a; Liu et al., 2022a). The property of the battery such as capacity plays a vital role in affecting battery-powered medical devices’ performance and will be influenced by related component parameters. In light of this, to improve battery operational performance and widen the applications of battery-powered medical devices, it is crucial to monitor/predict battery capacity and analyze/quantify the effects of corresponding component parameters simultaneously (Li et al., 2021b).

However, Li-ion batteries belong to a complicated power source involving numerous chemical, mechanical, and electrical dynamics during their operations (Wu et al., 2019; Chen et al., 2021). To date, the widely used approaches to analyze and understand how component parameters affect battery performance especially for its capacity are mainly based on trial and error solutions, which usually lead to huge cost and time consumption (Li et al., 2016; Yang et al., 2021). Therefore, developing the proper approach to not only predict the battery capacity of medical devices and analyze the corresponding component parameters is a challenging but important task for widening battery-powered medical devices.

With the quick development of data science, artificial intelligence, and cloud platform, data-driven approaches have become a promising and powerful tool in the field of Li-ion battery management (Lucu et al., 2018; Li et al., 2019; Liu et al., 2022b). Specifically, lots of data-driven approaches are derived for estimating the internal states of batteries (Feng et al., 2020a; Feng et al., 2021; Shi et al., 2021; Tang et al., 2021), predicting battery aging trajectories (Hu et al., 2022a; Hu et al., 2022b; Liu et al., 2022c) and remaining useful life (Liu et al., 2020a; Ren et al., 2020; Hu et al., 2021), balancing battery cells (Feng et al., 2020b; Liu et al., 2020b), performing effective battery charging (Liu et al., 2017; Xie et al., 2020), and energy management (Li et al., 2022; Wang et al., 2022; Xie et al., 2022; Zhang et al., 2022). In summary, according to the well-designed data-driven approaches, reliable management could be achieved to improve battery operational performance. However, these approaches are mainly related to battery macro-dynamic rather than micro-dynamic such as its component parameters. Currently, there are still limited research focuses on the analysis of battery component parameters by designing related data-driven methods. For example, according to the cross-industrial standard process, a neural network-based data-driven method is proposed in the study by Schnell et al. (2019) to analyze the dependency between battery component parameters. After using four parameters from battery mixing and coating processes, a Gaussian process regression (GPR)-based data-driven method is developed in the study by Liu et al. (2021a) to predict battery electrode mass loading and analyze the effects of these parameters. To handle the imbalance issue during battery production, an RUBoost-based data-driven method is derived in the study by Liu et al. (2021b) to classify the quality of battery and analyze formulation components. In real battery-powered medical device applications, it should be known that the component parameters will be crucial for determining and influencing battery property, especially for its capacity. To improve the performance of battery-powered medical devices, it therefore becomes necessary to develop an efficient data-driven method to predict battery capacity and analyze how related component parameters would influence the battery capacity.

Based upon the above discussion, to benefit battery-powered medical devices, a hybrid data-driven method is designed in this study to accurately predict battery capacity and analyze both global and local effects of component parameters of the corresponding battery. Several contributions are made as follows: 1) a GPR-based data-driven model is developed to perform accurate battery capacity prediction by using four battery component parameters as the input terms; 2) after equipping the automatic relevance determination (ARD)-based kernel structure, the global effects of these four battery component parameters are quantified and analyzed based on the ARD-based weights; and 3) after equipping tree-based local interpretable model-agnostic explanation (LIME), the local effects of these component parameters are quantified and analyzed for four randomly selected sample points. Due to the pure data-driven nature, the developed hybrid data-driven method can accurately predict battery capacity at the early prediction stage and analyze both global and local effects of corresponding component parameters, generating an effective way to well monitor battery capacity and understand the related component parameters, further benefitting the performance of battery-powered medical devices.

The rest of this article is organized as follows: Both battery key component parameters and related capacity dataset are described in Section 2. The GPR-based data-driven model, two effect analysis tools including ARD-kernel-based weights and tree-based LIME, and related performance indicators are described in Section 3. Section 4 then provides and discusses the results of both battery capacity predictions and component effect analyses. Section 5 summarizes this study finally.

2 Key Battery Components and Related Capacity Dataset

As the main power source to supply energy for numerous medical devices, Li-ion batteries are usually composed of some components including the positive electrode, negative electrode, and electrolyte (Ayerbe et al., 2021; Niri et al., 2021). It should be known that these component parameters play an important role in affecting battery properties such as its capacity, which would then determine the performance of related medical devices. Therefore, in order to ensure the effectiveness of battery-powered medical devices, battery capacity dynamics require to be carefully monitored and how battery component parameters affect battery capacity must be well analyzed (Liu et al., 2022d).

For the battery within medical devices, it generally consists of several electrode component parameters, as shown in Figure 1. To be specific, the battery electrode usually contains the active material components, electrode additive components, and polymeric binder components. For real medical device applications, LTO is usually selected as a widely utilized active material as it has the merits of being nontoxic and adaptive to complicated conditions such as high temperatures and large currents. In addition, electrode additive is another important component parameter for Li-ion batteries (Liu et al., 2022e). In order to increase the intrinsic electronic conductivities of battery electrodes, several conductive fillers such as carbon-black as well as carbon-nanofiber are generally needed within Li-ion batteries. Moreover, to further increase batteries’ mechanical cohesion, polymeric binders are also required. In many battery-powered medical device applications, three types of polymeric binders including polyvinylidene fluoride (PVDF), polyethylene co-ethyl acrylate co-maleic anhydride (TPE), and hydrogenated nitrile butadiene rubber (HNBR) are adopted as they have the advantages of presenting exceptional chemical stabilities and efficient binding properties. All these component parameters are crucial for determining battery electrode properties such as thickness and electronic conductivities, further affecting battery performance, especially for its capacity, which must be carefully monitored and analyzed in battery-powered medical device applications.

FIGURE 1

FIGURE 1. Main component parameters within Li-ion battery for battery-powered medical devices.

In light of this, to ensure the effectiveness of battery-powered medical devices, it is necessary to develop a suitable solution which can not only perform accurate battery capacity prediction but also analyze the effects of these key component parameters on battery capacity dynamics. In this study, a hybrid data-driven method through equipping the GPR data-driven model with effect analysis tools is designed to predict battery capacity and quantify both global as well as local effects of component parameters. To ensure model training effectiveness, the well-proven data (Rynne et al., 2019) from Hawaii Natural Energy Institute Franco are utilized. More information regarding these data and how to carry out an experiment for generating this dataset are referred to (Liu et al., 2021c) for the interested reader. In this study, four basic battery component parameters including LTO-based active materials (LTO) with a formulation weight from 75% to 95%, C65-based carbon black (C65) with a formulation weight from 0% to 20%, CNF with a formulation weight from 0% to 10%, and binders with a formulation weight from 3% to 20% are utilized. To obtain the capacity data of the corresponding battery, the coulomb-counting approach with a C/25 current rate is utilized.

3 Hybrid Data-Driven Method

In this section, the Gaussian process regression (GPR)-based model is first introduced for battery capacity prognostics. Then the effect analysis tools including automatic relevance determination (ARD) kernel weight and tree-based local interpretable model-agnostic explanation (LIME) are derived to analyze the global and local component effects, respectively. Afterward, several performance indicators are given to evaluate the performance of battery capacity prediction via the developed data-driven model.

3.1 Gaussian Process Regression

According to Bayesian theory, GPR is able to give a Gaussian process for non-parametric regression (Tagade et al., 2020; Liu et al., 2021c), whose probability distribution can be described by a mean function $m\left(x\right)$ and a kernel function $k\left(x,x^{\prime }\right)$ as follows:

$f\left(x\right)\sim GPR\left(m\left(x\right),k\left(x,x^{\prime }\right)\right)(1)$

with

$\{\begin{array}{c}m\left(x\right)=E(f\left(x\right))\\ k\left(x,x^{\prime }\right)=E\left[\left(m\left(x\right)-f\left(x^{\prime }\right)\right)\left(m\left(x\right)-f\left(x^{\prime }\right)\right)\right]\end{array}.(2)$

Here, $m\left(x\right)$ is generally set to zero for simplifying computation. For a prediction, the output’s prior distribution can be described by

$y\sim N\left(0,k\left(x,x^{\prime }\right)\right).(3)$

Assuming training dataset $x$ and testing dataset $x^{\prime }$ present similar Gaussian distributions, then the testing output $y^{\prime }$ could show a joint prior distribution with training output $y$ (Williams and Rasmussen, 2006):

$\left[\begin{array}{c}y\\ y^{\prime }\end{array}\right]\sim N\left(0,\left[\begin{array}{cc}k\left(x,x\right)& k\left(x,x^{\prime }\right)\\ k{\left(x,x^{\prime }\right)}^T& k\left(x^{\prime },x^{\prime }\right)\end{array}\right]\right).(4)$

According to this joint prior distribution, predicted output $y^{\prime }$ corresponding to inputs $x^{\prime }$ can be calculated by computing the conditional distribution $p\left(y^{\prime }\text{|}x,y, x^{\prime }\right)$ as

$p\left(y^{\prime }\text{|}x,y, x^{\prime }\right)\sim N\left(y^{\prime }\text{|}{\overline{y}}^{\prime },cov\left(y^{\prime }\right)\right)(5)$

with

$\{\begin{array}{c}{\overline{y}}^{\prime }=k{\left(x,x^{\prime }\right)}^T{\left[k\left(x,x\right)\right]}^{-1}y\\ cov\left(y^{\prime }\right)=k\left(x^{\prime },x^{\prime }\right)-k{\left(x,x^{\prime }\right)}^T{\left[k\left(x,x\right)\right]}^{-1}k\left(x,x^{\prime }\right)\end{array}(6)$

where ${\overline{y}}^{\prime }$ is the mean predicted values, while $cov\left(y^{\prime }\right)$ reflects its variance values.

It can be seen that kernel function $k\left(x,x^{\prime }\right)$ plays an important role in determining GPR’s performance and must be carefully designed. In this study, to ensure the effectiveness of GPR in battery capacity prediction, three kernel functions are explored.

The first one is a classical kernel function called squared exponential (SE) kernel.

$k_{SE}\left(x,x^{\prime }\right) ={\sigma }_{SE}^{2}exp\left(-\frac{{\Vert x-x^{\prime }\Vert }^2}{2{\sigma }_m^2}\right)(7)$

where ${\sigma }_{SE}$ and ${\sigma }_m$ are its two hyperparameters for determining the amplitude and length of the SE kernel function.

In general, the SE kernel function is easy to cause smooth distribution. To further enhance the performance of GPR in fitting nonlinear relations, another two classical kernel functions including Mater5/2 kernel function $k_{M5/2}\left(x,x^{\prime }\right)$ and quadratic kernel function $k_{Quadratic}\left(x,x^{\prime }\right)$ could be used as follows:

$k_{M5/2}\left(x,x^{\prime }\right) ={\sigma }_{M5/2}^2\left(1+\frac{\sqrt{5}\Vert x-x^{\prime }\Vert }{{\sigma }_m}+\frac{5{\Vert x-x^{\prime }\Vert }^2}{3{\sigma }_m^2}\right)exp\left(-\frac{\sqrt{5}\Vert x-x^{\prime }\Vert }{{\sigma }_m}\right)(8)$

$k_{Quadratic}\left(x,x^{\prime }\right) ={\sigma }_Q^2{\left(1+\frac{{\Vert x-x^{\prime }\Vert }^2}{2\alpha {\sigma }_m^2}\right)}^{-\alpha }(9)$

where ${\sigma }_{M5/2}$ and ${\text{σ}}_{\text{Q}}$ are hyperparameters to determine Matern5/2 kernel and quadratic kernel functions’ amplitudes, respectively. ${\sigma }_m$ is the hyperparameter to determine their length.

3.2 Effect Analysis Tools

After developing a GPR-based data-driven model for battery capacity prediction, to further quantify and analyze the effects of corresponding component parameters, two data-driven-based effect analysis tools including the ARD kernel weight and local interpretable model-agnostic explanations need to be adopted.

3.2.1 ARD Kernel Weight

To equip the GPR model with the capability of quantifying the global effects of parameters of interest, the classical kernel functions including SE kernel, Matern5/2 kernel, and the quadratic kernel can be enhanced with the ARD structures (Zhao et al., 2018) as follows:

$k_{SE\_ARD}\left(x,x^{\prime }\right) ={\sigma }_{SE}^{2}exp\left[-\frac{1}{2}\left(\frac{{\Vert x_{LTO}-x_{LTO}^{\prime }\Vert }^2}{{\sigma }_{LTO}^2}+\frac{{\Vert x_{Binder}-x_{Binder}^{\prime }\Vert }^2}{{\sigma }_{Binder}^2}+\frac{{\Vert x_{C65}-x_{C65}^{\prime }\Vert }^2}{{\sigma }_{C65}^2}+\frac{{\Vert x_{CNF}-x_{CNF}^{\prime }\Vert }^2}{{\sigma }_{CNF}^2}\right)\right](10)$

$\{\begin{array}{c}{k}_{5/2\_ARD}\left(i,i^{\prime }\right) ={\sigma }_{5/2}^2\left(1+\sqrt{5}r+\frac{5}{3}{r}^2\right)\exp \left(-\sqrt{5}r\right)\\ r=\sqrt{\frac{{\Vert x_{LTO}-x_{LTO}^{\prime }\Vert }^2}{{\sigma }_{LTO}^2}+\frac{{\Vert x_{Binder}-x_{Binder}^{\prime }\Vert }^2}{{\sigma }_{Binder}^2}+\frac{{\Vert x_{C65}-x_{C65}^{\prime }\Vert }^2}{{\sigma }_{C65}^2}+\frac{{\Vert x_{CNF}-x_{CNF}^{\prime }\Vert }^2}{{\sigma }_{CNF}^2}}\end{array},(11)$

$\{\begin{array}{c}{k}_{Quadratic\_ARD}\left(i,i^{\prime }\right) ={\sigma }_Q^2{\left(1+\frac{r^2}{2\alpha {\sigma }_l^2}\right)}^{-\alpha }\\ r=\sqrt{\frac{{\Vert x_{LTO}-x_{LTO}^{\prime }\Vert }^2}{{\sigma }_{LTO}^2}+\frac{{\Vert x_{Binder}-x_{Binder}^{\prime }\Vert }^2}{{\sigma }_{Binder}^2}+\frac{{\Vert x_{C65}-x_{C65}^{\prime }\Vert }^2}{{\sigma }_{C65}^2}+\frac{{\Vert x_{CNF}-x_{CNF}^{\prime }\Vert }^2}{{\sigma }_{CNF}^2}}\end{array}.(12)$

Obviously, compared with classical kernels, the ARD structure-based kernels have an individual hyperparameter for each input term. The values of these individual hyperparameters could reflect how important this input term will affect the prediction results (Zhao et al., 2018). In light of this, the global effects of component parameters on battery capacity can be quantified directly by using the ARD kernel-based GPR model. Theoretically, a larger hyperparameter ${\sigma }_i$ ($i=LTO, Binder, C65, CNF$) would lead to a smaller ARD kernel weight, which indicates the lower global effect on the predicted battery capacity output.

3.2.2 Local Interpretable Model-Agnostic Explanation

After using ARD kernel weight to quantify the global effects of component parameters, to further analyze the local effects of these parameters on the specific samples, an effective data-driven tool named the local interpretable model-agnostic explanation (LIME) (Zafar and Khan, 2021) will be adopted. According to the developed GPR-based data-driven model, a detailed procedure to equip LIME for local effect analysis is illustrated in Table 1.

Algorithm 1. Detailed procedure to equip LIME for local effect analysis of component parameters.

In summary, based upon four key processes, LIME is able to quantify the local effect of a sample point as follows: 1) generating several new samples around the interested sample $S$, as shown in step 3; 2) performing capacity prediction of these generated samples based on the developed GPR-based data-driven model, as illustrated in step 4; 3) constructing a local prediction model by using the generated samples and predicted points from GPR-based data-driven model, as shown in line 5; and 4) using the coefficients from this local prediction model to quantify the effects and importance of component parameters on the capacity prediction from the GPR-based data-driven model.

3.3 Data-Driven Structure

Based upon the effective data-driven tools mentioned earlier, to well predict battery capacity and analyze the effects of battery component parameters of interest, a hybrid data-driven structure is developed by equipping a GPR-based data-driven model, ARD kernel-based weights, and tree-based LIME, as illustrated in Figure 2.

FIGURE 2

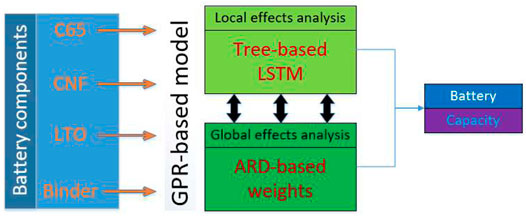
FIGURE 2. Hybrid data-driven method structure to predict battery capacities and analyze both global and local effects of component parameters.

To be specific, the input terms of this data-driven structure are four battery component parameters including LTO, binder, C65, and CNF, while the output term of this structure is the corresponding battery capacity. After well training GPR-based data-driven model by minimizing its negative log marginal likelihood, the ARD kernel-based weights can be used to reflect the global effects of these four component parameters on battery capacity. Through equipping the tree-based LIME, the local effects for some specific sample points can also be quantified and analyzed.

3.4 Model Performance Indicators

To directly reflect the battery capacity prediction performance of GPR-based data-driven model, the following typical performance indicators (Šeruga et al., 2021) are used:

1) Mean absolute error (MAE): Supposing $T$ is the total number of all samples, $Y_t$ stands for the real battery capacity value, while ${\widehat{Y}}_t$ is the predicted capacity value from the GPR-based data-driven model, MAE can be expressed as follows:

$MAE=\frac{1}{T}{\displaystyle {\sum }_{t=1}^T\left|Y_t-{\widehat{Y}}_t\right|}(13)$

2) Root mean square error (RMSE): as another typical performance indicator, RMSE is calculated by

$RMSE=\sqrt{\frac{1}{T}{{\displaystyle {\sum }_{t=1}^T\left(Y_t-{\widehat{Y}}_t\right)}}^2}(14)$

3) $R^2$: let $\overline{Y}$ reflect the average value of all predicted battery capacities, $R^2$ can be calculated by

$R^2=1-{{\displaystyle {\sum }_{t=1}^T\left(Y_t-{\widehat{Y}}_t\right)}}^2/{{\displaystyle {\sum }_{t=1}^T\left(Y_t-\overline{Y}\right)}}^2(15)$

It should be known that for real battery capacity prediction, when the predicted values get close to the actual values, MAE and RMSE would become close to 0, while $R^2$ will reach 1.

4 Result and Discussion

In order to evaluate the capacity prediction performance of using a GPR-based data-driven model, this section first presents and discusses the battery capacity prediction results via three different ARD kernels. Then the tests using ARD kernel-based weights and tree-based LIME are carried out to quantify the local effect and global effect analyses of all four battery components, respectively.

4.1 Capacity Prediction via GPR

We first focus on the battery capacity predictions by using four component parameters as inputs to the GPR-based data-driven model with three different ARD kernels. After performing six-fold cross-validation, the capacity prediction results of using SE-based GPR, Matern5/2-based GPR, and quadratic-based GPR are illustrated in Figure 3, while their corresponding performance indicators are illustrated in Table 2. According to Figure 3, it can be seen that all three GPR-based data-driven models can capture most of battery capacity sample points, indicating the effective performance of ARD-based kernel functions. To be specific, SE-based GPR presents the worst prediction results with 4.52 $mAh$ RMSE and 0.91 $R^2$ value, which is 57.5% and 5.2% worse than those from Matern5/2-based GPR. In comparison, quadratic-based GPR presents the best results for battery capacity prediction, whose RMSE and $R^2$ values are 2.43 $mAh$ and 0.97, respectively, which are 15.3% and 1.1% better than those of Matern5/2-based GPR. It can be concluded that four battery component parameters (LTO, binder, C65, and CNF) and battery capacity present strong nonlinear relations as the smooth SE kernel cannot well capture their underlying mapping. By using non-smooth kernel functions like Matern5/2 and quadratic kernels, the capacity prediction performance can be improved.

FIGURE 3

FIGURE 3. Battery capacity predictions by using a GPR-based data-driven model with different ARD kernels: (A) SE kernel, (B) Matern5/2 kernel, and (C) quadratic kernel.

TABLE 1

TABLE 1. Performance indicators for battery capacity predictions by using the GPR-based data-driven model with different ARD kernels.

To further explore these battery capacity prediction results using GPR-based data-driven models, the prediction versus true plots for all GPR-based data-driven cases are illustrated in Figure 4. In theory, the farthest observation in the prediction versus true plots could make the prediction line toward that sample. The more accurate a model is, the observations from this model should get closer to the perfect prediction line. In this study, it can be seen that most observations can get close to the perfect prediction line by using GPR-based data-driven models. But there still exist several observations that are away from the perfect prediction line this is mainly caused by the overfitting issue of the data-driven model and can be improved when more corresponding data are available.

FIGURE 4

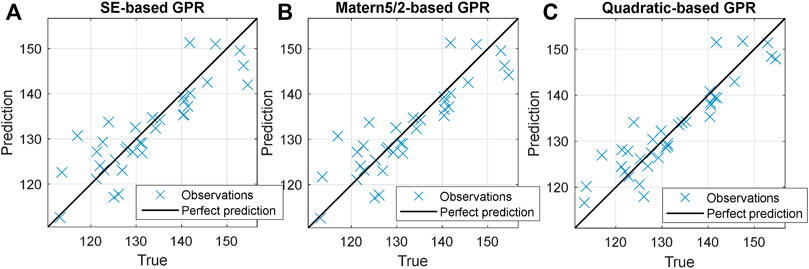
FIGURE 4. Prediction versus true plots using a GPR-based data-driven model with different ARD kernels: (A) SE kernel, (B) Matern5/2 kernel, and (C) quadratic kernel.

4.2 Component Effect Analyses

Next, after developing the GPR-based data-driven model to effectively predict battery capacity, the ARD-based kernel weight and tree-based LIME would be carried out to analyze both the global effects and local effects of four component parameters, respectively.

4.2.1 Analysis of Global Effects

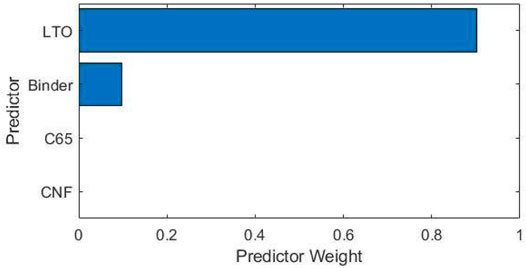
To quantify the global effects of component parameters for all observation samples, the hyperparameters of the quadratic-based GPR model are utilized as this GPR model gives the best results for battery capacity prediction. For global effect analysis, after normalizing the weights of the ARD-based kernel, the importance of four component parameters (LTO, binder, C65, and CNF) are quantified and plotted in Figure 5. It can be obvious that the LTO term provides the largest importance weight with 0.89 value for the battery capacity prediction. Binder term gives the second largest importance weight with 0.09 value. In comparison, the importance weights of both C65 and CNF are too small, which means their global effects can be negligible for this battery capacity prediction.

FIGURE 5

FIGURE 5. Analysis of global effects of all four components.

4.2.2 Analysis of Local Effects

Next, to further explore the local effects of component parameters for some specific sample points, the tree-based LIME is adopted. Here four sample points are randomly selected for further local effect exploration with the detailed information shown in Table 3. It can be seen that these sample points are composed of different values of LTO, C65, CNF, and binder.

TABLE 2

TABLE 2. Randomly selected sample points for the analysis of local component effects.

To analyze the local effects of four battery component parameters (LTO, C65, CNF, and binder) on predicting battery capacity of these four case points, the quantified parameter effects through using tree-based LIME are illustrated in Figure 6. Here the predicted model within LIME is the decision tree. Both the capacity prediction results of the GPR-based data-driven model and tree-based LIME are shown for all four case points to reflect their prediction difference. According to Figure 6, although there exist a few differences between the quantified effects of these four sample points, their quantified local effects all present a similar trend. Specifically, the LTO term always gives the largest quantified effect, while the binder term gives the second largest effect. In comparison, the CNF term always gives the smallest quantified effect for all these four sample points. The trend of local effects is similar to the trend of global effects, which indicates that our hybrid data-driven method effectively quantifies both global and local effects of these four component parameters. Moreover, it can be obviously observed that the predicted battery capacity values from tree-based model prediction are all close to the predicted values from the GPR-based data-driven model, which indicates that the tree-based LIME is able to well predict battery capacity and the related local effect analysis can also be well explained.

FIGURE 6

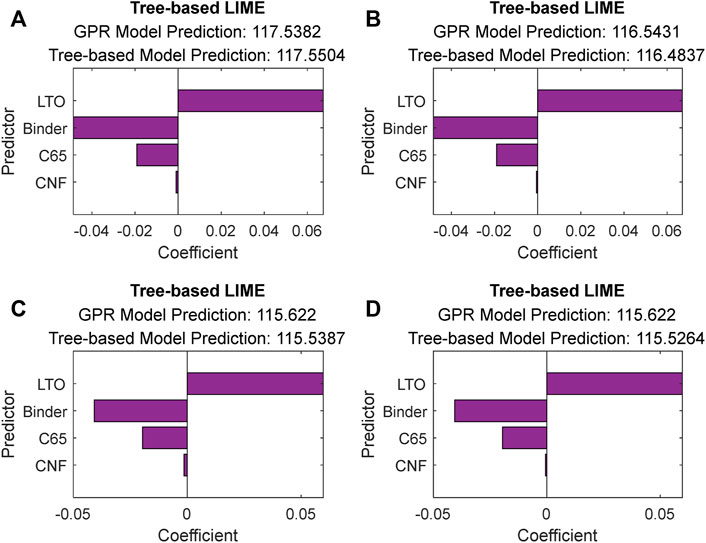
FIGURE 6. Analysis of local component effects for four randomly selected sample points: (A) Sample 1, (B) Sample 2, (C) Sample 3, and (D) Sample 4.

5 Conclusion

Li-ion batteries are the most popular power source and are widely utilized in medical devices to supply power and energy. As the performance of battery-powered medical devices is highly affected by battery capacity, this study focuses on the accurate monitoring/prediction of battery capacity and the explainable analysis of related component parameters. To achieve this, a hybrid data-driven method using the GPR-based data-driven model and effect analysis tools is developed. Illustrative results indicate that the designed GPR-based data-driven model is capable of accurately predicting battery capacity with 0.97 $R^2$ by using the quadratic-based kernel. Through equipping ARD kernel-based weights and tree-based LIME, both the global effects and local effects of four main component parameters including LTO, C65, CNF, and binder can be successfully quantified and analyzed. Specifically, LTO and binder provide the first and second most important ranking for both global and local effects, while CNF gives the smallest contribution to battery capacity prediction. Due to the merits of the data-driven nature, the designed hybrid data-driven method is capable of efficiently helping users to monitor/predict battery capacity at the early prediction stage and analyze/understand both global and local effects of interested component parameters. This could further benefit battery-powered medical devices for wider and longer-life applications.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

RF and QP contributed to the conception and design of the study. RF wrote the first draft of the manuscript. CL, HQ, LZ, and QP contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ayerbe, E., Berecibar, M., Clark, S., Franco, A. A., and Ruhland, J. (2021). Digitalization of Battery Manufacturing: Current Status, Challenges, and Opportunities. Adv. Energy Mater. 12, 2102696. doi:10.1002/aenm.202102696

CrossRef Full Text | Google Scholar

Chen, T., Song, M., Hui, H., and Long, H. (2021). Battery Electrode Mass Loading Prognostics and Analysis for Lithium-Ion Battery–Based Energy Storage Systems. Front. Energy Res. 9, 543. doi:10.3389/fenrg.2021.754317

CrossRef Full Text | Google Scholar

Feng, F., Hu, X., Liu, K., Che, Y., Linc, X., Jin, G., et al. (2020). A Practical and Comprehensive Evaluation Method for Series-Connected Battery Pack Models. IEEE Trans. Transp. Electrification. 455, 227935. doi:10.1109/TTE.2020.2983846

CrossRef Full Text | Google Scholar

Feng, F., Teng, S., Liu, K., Xie, J., Xie, Y., Liu, B., et al. (2020). Co-estimation of Lithium-Ion Battery State of Charge and State of Temperature Based on a Hybrid Electrochemical-Thermal-Neural-Network Model. J. Power Sources 455, 227935. doi:10.1016/j.jpowsour.2020.227935

CrossRef Full Text | Google Scholar

Feng, H., Wang, Z., and Zhang, F. (2021). A Comprehensive Evaluation of the Influence of Major Hysteresis on State of Charge Prediction of LiNiMnCoO2 Battery. Front. Energy Res., 159. doi:10.3389/fenrg.2021.666092

CrossRef Full Text | Google Scholar

Hu, T., Ma, H., Liu, K., and Sun, H. (2022). Lithium-ion Battery Calendar Health Prognostics Based on Knowledge-Data-Driven Attention. IEEE Trans. Industrial Electron. doi:10.1109/tie.2022.3148743

CrossRef Full Text | Google Scholar

Hu, T., Ma, H., Sun, H., and Liu, K. (2022). Electrochemical-Theory-Guided Modelling of the Conditional Generative Adversarial Network for Battery Calendar Ageing Forecast. IEEE J. Emerg. Sel. Top. Power Electron. doi:10.1109/jestpe.2022.3154785

CrossRef Full Text | Google Scholar

Hu, X., Yang, X., Feng, F., Liu, K., and Lin, X. (2021). A Particle Filter and Long Short-Term Memory Fusion Technique for Lithium-Ion Battery Remaining Useful Life Prediction. J. Dyn. Syst. Meas. Control 143, 6. doi:10.1115/1.4049234

CrossRef Full Text | Google Scholar

J. Li, S. Zhou, and Y. Han (Editors) (2016). Advances in Battery Manufacturing, Service, and Management Systems (New Jersey, United States: John Wiley & Sons).

Google Scholar

Li, J., Liu, K., Zhou, Q., Meng, J., Ge, Y., and Xu, H. (2022). Electrothermal Dynamics-Conscious Many-Objective Modular Design for Power-Split Plug-In Hybrid Electric Vehicles. IEEE/ASME Trans. Mechatronics. doi:10.1109/TMECH.2022.3156535

CrossRef Full Text | Google Scholar

Li, R., Li, W., Zhang, H., Zhou, Y., and Tian, W. (2021). On-Line Estimation Method of Lithium-Ion Battery Health Status Based on PSO-SVM. Front. Energy Res, 401. doi:10.3389/fenrg.2021.693249

CrossRef Full Text | Google Scholar

Li, Y., Li, K., Liu, X., Wang, Y., and Zhang, L. (2021). Lithium-ion Battery Capacity Estimation—A Pruned Convolutional Neural Network Approach Assisted with Transfer Learning. Appl. Energy 285, 116410. doi:10.3389/fenrg.2021.693249

CrossRef Full Text | Google Scholar

Li, Y., Liu, K., Foley, A. M., Zülke, A., Berecibar, M., Nanini-Maury, E., et al. (2019). Data-driven Health Estimation and Lifetime Prediction of Lithium-Ion Batteries: A Review. Renew. Sustain. Energy Rev. 113, 109254. doi:10.1016/j.rser.2019.109254

CrossRef Full Text | Google Scholar

Liu, K., Gao, Y., Zhu, C., Li, K., Fei, M., Peng, C., et al. (2022). Electrochemical Modeling and Parameterization towards Control-Oriented Management of Lithium-Ion Batteries. Control Eng. Pract. 124, 105176. doi:10.1016/j.conengprac.2022.105176

CrossRef Full Text | Google Scholar

Liu, K., Hu, X., Meng, J., Guerrero, J. M., and Teodorescu, R. (2021). RUBoost-Based Ensemble Machine Learning for Electrode Quality Classification in Li-Ion Battery Manufacturing. IEEE/ASME Trans. Mechatronics. 37 (2), 1282–1291. doi:10.1109/TEC.2021.3130600

CrossRef Full Text | Google Scholar

Liu, K., Li, K., and Zhang, C. (2017). Constrained Generalized Predictive Control of Battery Charging Process Based on a Coupled Thermoelectric Model. J. Power Sources 347, 145–158. doi:10.1016/j.jpowsour.2017.02.039

CrossRef Full Text | Google Scholar

Liu, K., Peng, Q., Sun, H., Fei, M., Ma, H., and Hu, T. (2022). A Transferred Recurrent Neural Network for Battery Calendar Health Prognostics of Energy-Transportation Systems. IEEE Trans. Industrial Inf. doi:10.1109/tii.2022.3145573

CrossRef Full Text | Google Scholar

Liu, K., Shang, Y., Ouyang, Q., and Widanage, W. D. (2020). A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-Ion Battery. IEEE Trans. Industrial Electron. 68 (4), 3170–3180. doi:10.1109/TIE.2020.2973876

CrossRef Full Text | Google Scholar

Liu, K., Tang, X., Teodorescu, R., Gao, F., and Meng, J. (2021). Future Ageing Trajectory Prediction for Lithium-Ion Battery Considering the Knee Point Effect. IEEE Trans. Energy Convers 289, 125159. doi:10.1016/j.jclepro.2020.125159

CrossRef Full Text | Google Scholar

Liu, K., Wang, Y., and Lai, X. (2022). Data Science-Based Full-Lifespan Management of Lithium-Ion Battery: Manufacturing, Operation and Reutilization. Berlin, Germany: Springer Nature.

Google Scholar

Liu, K., Wei, Z., Yang, Z., and Li, K. (2021). Mass Load Prediction for Lithium-Ion Battery Electrode Clean Production: a Machine Learning Approach. J. Clean. Prod. 289, 125159. doi:10.1109/TMECH.2021.3115997

CrossRef Full Text | Google Scholar

Liu, K., Wei, Z., Zhang, C., Shang, Y., Teodorescu, R., and Han, Q. L. (2022). Towards Long Lifetime Battery: AI-Based Manufacturing and Management. IEEE/CAA J. Automatica Sinica. doi:10.1109/jas.2022.105599

CrossRef Full Text | Google Scholar

Liu, K., Yang, Z., Tang, X., and Cao, W. (2020). Automotive Battery Equalizers Based on Joint Switched-Capacitor and Buck-Boost Converters. IEEE Trans. Veh. Technol. 69 (11), 12716–12724. doi:10.1109/tvt.2020.3019347

CrossRef Full Text | Google Scholar

Liu, R., Peng, Q., Li, K., and Chen, T. (2022). Li‐Ion Battery. Automot. Innov., 1–46. doi:10.1002/9783527830053.ch1

CrossRef Full Text | Google Scholar

Lucu, M., Martinez-Laserna, E., Gandiaga, I., and Camblong, H. (2018). A Critical Review on Self-Adaptive Li-Ion Battery Ageing Models. J. Power Sources 401, 85–101. doi:10.1016/j.jpowsour.2018.08.064

CrossRef Full Text | Google Scholar

Niri, M. F., Liu, K., Apachitei, G., Ramirez, L. R., Lain, M., Widanage, D., et al. (2021). Machine Learning for Optimised and Clean Li-Ion Battery Manufacturing: Revealing the Dependency between Electrode and Cell Characteristics. J. Clean. Prod. 324, 129272. doi:10.1016/j.jclepro.2021.129272

CrossRef Full Text | Google Scholar

Ren, L., Dong, J., Wang, X., Meng, Z., Zhao, L., and Deen, M. J. (2020). A Data-Driven Auto-Cnn-Lstm Prediction Model for Lithium-Ion Battery Remaining Useful Life. IEEE Trans. Industrial Inf. 17 (5), 3478–3487. doi:10.1109/TII.2020.3008223

CrossRef Full Text | Google Scholar

Rynne, O., Dubarry, M., Molson, C., Lepage, D., Prébé, A., Aymé-Perrot, D., et al. (2019). Designs of Experiments for Beginners-A Quick Start Guide for Application to Electrode Formulation. Batteries 5 (4), 72. doi:10.3390/batteries5040072

CrossRef Full Text | Google Scholar

Schnell, J., Nentwich, C., Endres, F., Kollenda, A., Distel, F., Knoche, T., et al. (2019). Data Mining in Lithium-Ion Battery Cell Production. J. Power Sources 413, 360–366. doi:10.1016/j.jpowsour.2018.12.062

CrossRef Full Text | Google Scholar

Šeruga, D., Gosar, A., Sweeney, C. A., Jaguemont, J., Mierlo, J. V., and Nagode, M. (2021). Continuous Modelling of Cyclic Ageing for Lithium-Ion Batteries. Energy 215, 119079. doi:10.1016/j.energy.2020.119079

CrossRef Full Text | Google Scholar

Shi, G., Chen, S., Yuan, H., You, H., Wang, X., Dai, H., et al. (2021). Determination of Optimal Indicators Based on Statistical Analysis for the State of Health Estimation of a Lithium-Ion Battery. Front. Energy Res. 9, 262. doi:10.3389/fenrg.2021.690266

CrossRef Full Text | Google Scholar

Tagade, P., Hariharan, K. S., Ramachandran, S., Khandelwal, A., Naha, A., Kolake, S. M., et al. (2020). Deep Gaussian Process Regression for Lithium-Ion Battery Health Prognosis and Degradation Mode Diagnosis. J. Power Sources 445, 227281. doi:10.1016/j.jpowsour.2019.227281

CrossRef Full Text | Google Scholar

Tang, X., Gao, F., Liu, K., Liu, Q., and Foley, A. M. (2021). A Balancing Current Ratio Based State-Of-Health Estimation Solution for Lithium-Ion Battery Pack. IEEE Trans. Industrial Electron. 69 (8), 8055–8065. doi:10.1109/TIE.2021.3108715

CrossRef Full Text | Google Scholar

Wang, Y., Dan, D., Xie, Y., Li, W., Guo, H., and Zhang, Y. (2022). Study on the Influence of Flat Heat Pipe Structural Parameters in Battery Thermal Management System. Front. Energy Res. 9, 1–18. doi:10.3389/fenrg.2021.797664

CrossRef Full Text | Google Scholar

Williams, C. K. I., and Rasmussen, C. E. (2006). Gaussian Processes for Machine Learning. Cambridge, MA: MIT press.

Google Scholar

Wu, X., Song, K., Zhang, X., Hu, N., Li, L., Li, W., et al. (2019). Safety Issues in Lithium Ion Batteries: Materials and Cell Design. Front. Energy Res. 7, 65. doi:10.3389/fenrg.2019.00065

CrossRef Full Text | Google Scholar

Xie, W., Liu, X., He, R., Li, Y., Gao, X., Li, X., et al. (2020). Challenges and Opportunities toward Fast-Charging of Lithium-Ion Batteries. J. Energy Storage 32, 101837. doi:10.1016/j.est.2020.101837

CrossRef Full Text | Google Scholar

Xie, Y., Yang, R., Li, W., Liu, K., Chen, B., Qian, Y., et al. (2022). A Comprehensive Study on Influence of Battery Thermal Behavior on Degradation and Consistency. IEEE Trans. Transp. Electrification. doi:10.1109/TTE.2022.3148335

CrossRef Full Text | Google Scholar

Yang, Y., Okonkwo, E. G., Huang, G., Xu, S., Sun, W., and He, Y. (2021). On the Sustainability of Lithium Ion Battery Industry–A Review and Perspective. Energy Storage Mater. 36, 186–212. doi:10.1016/j.ensm.2020.12.019

CrossRef Full Text | Google Scholar

Zafar, M. R., and Khan, N. (2021). Deterministic Local Interpretable Model-Agnostic Explanations for Stable Explainability. Make 3, 525–541. doi:10.3390/make3030027

CrossRef Full Text | Google Scholar

Zhang, F., Xiao, L., Coskun, S., Pang, H., Xie, S., Liu, K., et al. (2022). Comparative Study of Energy Management in Parallel Hybrid Electric Vehicles Considering Battery Ageing. Energy, 123219. doi:10.1016/j.energy.2022.123219

CrossRef Full Text | Google Scholar

Zhao, J., Chen, L., Pedrycz, W., and Wang, W. (2018). Variational Inference-Based Automatic Relevance Determination Kernel for Embedded Feature Selection of Noisy Industrial Data. IEEE Trans. Industrial Electron. 66 (1), 416–428. doi:10.1109/tie.2018.2815997

CrossRef Full Text | Google Scholar