Robust Strong Structural Controllability of Complex Power Systems

Ensuring the control of power systems is crucial for their safe operation. This paper analyses the robust controllability of complex power systems from the structural sighta structural point of view. Stressing the dominant role of generators in the control of power systems, we propose three kinds of controllable networks by generator nodes. Additionally, the satisfied conditions and the relevant proof of zero forcing set in the controllable networks by generator nodes and extra nodes are given. Besides, tThe satisfied conditions and the relevant proofs of the largest set of removable edges that have no -effect on the strong structural controllability in three kinds of controllable networks by generator nodes are also proposed. Finally, the robustness of strong structural controllability of IEEE 39 bus system and IEEE 14 bus system have been analyzed. The zero-forcing set and the largest set of removable edges of IEEE 39 bus system and IEEE 14 bus system are provided.

1 Introduction

With the development of economy and society, the scale of power systems grows rapidlyZhang et al. (2019), ensuring the safe and stable power transmission has thus become a hot research issue Kiaei et al. (2021). There is a growing demand for power systems with high robustness, that is, they can withstand large disturbances, such as transmission line damage, accidental loss of large generators, or heavy load loss Mahmud et al. (2017). Many researches on the control of power systems at the device level have been proposed, such as braking resistor Rubaai et al. (2005), fast valving of turbines Hassan et al. (1999), utilizing reactor and capacitor units Taylor and Leuven (1996), flexible ac transmission system devices Haque (2004), power system stabilizers Chung et al. (2002), and energy storage systems Kiaei et al. (2021). In addition, as the power system as is a special complex network, complex network theory is also an important tool to study its controllability Chu and lu (2017). The controllability analysis of power systems has the question that capturing the time-dependent interactions between the components, which is difficult. Fortunately, the controllability study is based on the complex network theory regardless of the coupling strength between the components.

In complex networks, structural controllability (weak structural controllability) and strong structural controllability are two basic directions of network controllability analysis. The week structural controllability was first proposed by Lin (1974), that means almost all networks of the identical topology have the same controllability. Nevertheless, the dependencies between system parameters in actual networks leads to networks being uncontrollable, although it is weekly structurally controllable. Thus, the notion of strong structural controllability was proposed by Mayeda and Yamada (1979). The network is strong structurally controllable if alladmissible numerical realizations of its coupling matrix and control input matrix are controllable. Bowden et al. (2012) extended the strong structural controllability to multiple entry systems. Whereafter, the strong structural controllability were further investigated by constrained matchings Chapman and Mesbahi (2013) and cycle families Jarczyk et al. (2011).

Group (2008) was first proposed the concept of zero-forcing set (ZFS) to investigate the minimum rank problem for symmetric patterned matrices, which is connected with a particular coloring of nodes in a graph. Then, zero forcing set was extended to directed graphs by Barioli et al. (2009). Furthermore, Monshizadeh et al. (2014) has shown the correspondence between zero-forcing sets and the strong structural controllability by the view of a network-centric point. Subsequently, ZFS was widely used in the analysis of strong structural controllability of undirected networks Mousavi and Mesbahi (2018), networks with missing connection information, Jia et al. (2021) and other networks.

When complex network theory is applied to a power system, the accuracy of analysis will be affected by oversimplification of the influence of electrical characteristics Hines et al. (2010), but too much consideration of electrical characteristics will greatly increase the computational complexity. Therefore, the reasonable combination of structural characteristics and electrical characteristics is still an unsolved problem. Li et al. (2015) investigated the weak structural controllability of power systems. The minimum input theorem was used to find the drive node set that makes the network weakly structurally controllable in an unweighted directed model. However, the absent of electrical characteristics makes the research results deviate from the actual situation. Yang et al. (2020) established a directed network model that can reflect the intrinsic direction of the power system for weak structural controllability analysis. The edge weighs were considered in the search method of maximum weak controllable scope. Nevertheless, this work didn’t did not consider the different functions of different nodes in control. In particular, the special status of generator nodes is was ignored. In the modern power industry, the control of generators can realize active power control and frequency response, voltage/reactive power control, and ride-through for both voltage and frequency Hatziargyriou et al. (2021). Thus, generator nodes play a dominant role in the control of power systems.

Based on the above research gaps, the main contributions of this paper are as follows:

1. Considering the dominant role of generators in the control of power systems, precisely controllable networks by generator nodes, redundantly controllable networks by generator nodes, and controllable networks by generator nodes, and extra nodes are defined.

2. The satisfied conditions and the relevant proof of zero-forcing set in the controllable networks by generator nodes and extra nodes are given.

3. The satisfied conditions and the relevant proofs of the largest set of removable edges in three kinds of controllable networks by generator nodes are given.

The remains of this paper are organized as follows: Section 2 introduces the network modeling method of power systems. Section 3 analyzses the strong structural controllability of power systems. Section 4 analyzses the robustness of controllable networks by generator nodes. Section 5 concludes the paper with discussions.

2 Network Modelling of Power Systems

In this paper, the power system is abstracted as a digraph. Network modeling is the critical prerequisite of structural controllability analysis. The accuracy of structural controllability analysis is closely related to the described natures of power systems in a network model. We assume that the construction structure of power systems and the configuration of generators and loads are known correctly.

2.1 Basic Model Topology Principles

The dynamic characteristics of power systems are so tanglesome entangled that a generic dynamical equation that describes them all is out of the question. Prosperously, the controllability of nonlinear system and its linearized dynamics is are often structurally similar. The power system is described as a digraph D (V, E) with nodes and edges, V = {v₁, … , v_N} is the node set, and the E = {(v_i, v_j), v_i, v_j ∈ V} is the edge set, N is the scale of networks. According to Ohm’s law, a power system with scale N can be writed written as linear equations, as follows:

$\left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill ⋮\hfill \\ \hfill U_N\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill Z_{11}\hfill & \hfill Z_{12}\hfill & \hfill \cdots \hfill & \hfill Z_{1N}\hfill \\ \hfill Z_{21}\hfill & \hfill Z_{22}\hfill & \hfill \cdots \hfill & \hfill Z_{2N}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill Z_{N1}\hfill & \hfill Z_{N2}\hfill & \hfill \cdots \hfill & \hfill Z_{NN}\hfill \end{array}\right]\left[\begin{array}{c}\hfill I_1\hfill \\ \hfill I_2\hfill \\ \hfill ⋮\hfill \\ \hfill I_N\hfill \end{array}\right](1)$

where Z_ij is the impedance of transmission lines. If there is a transmission line from node v_i to node v_j, then Z_ij = Z_ji ≠ 0 or else Z_ij = Z_ji = 0. U_i is the voltage of bus, and I_i is the injection current of bus.

The basic topology of the network model is constructed based on the transmission line architecture of power systems. Topology principles in this paper are described as follows.

• The buses of power plants, substations, and loads are abstracted to nodes. The node set is classified into generator node set V_G, transmission node set V_T, and load node set V_L.

• The high voltage transmission lines are abstracted as edges, only the lines whose voltage above 110 KV are considered.

• Parallel transmission lines on the same tower and neglecting shunt capacitor lines are merged to prevent multiple edges in the basic topology model and generate a simple topology model.

• The influences of the relay protection devices and the stability control devices in power systems are not under consideration.

2.2 Definition of Edge Direction

The direction of power flowing was defined as the direction of edges in the network model in some literatures Liu et al. (2018); Dey et al. (2016). However, the direction of power flowing is time-variant, which and only describes the direction of edges in power systems at a certain time. The network model proposed in this paper wants to have an edge direction which can express the intrinsic properties of power systems. Therefore, the author’s previous definition of edge direction in a network model of a power system Yang et al. (2020) is used again in this paper, where the direction of an edge is determined by its electrical betweenness.

In graph theory, the betweenness of edges is an important global geometric quantity that reflects the influence of edges in the whole network Freeman (1978). Betweenness of an edge is defined as the portion of the number of shortest paths between all nodes pairs that pass through the edges divided by the number of shortest paths between all node pairs. However, the power is transmitted in complex power systems in accordance with electrical characteristics. The power from node v_i to node v_j flows through every edges in complex power systems. Thus, betweenness in graph theory is unfit for evaluating edges in power systems.

Electrical betweenness of edges is an evaluation index Wang et al. (2011) that, which is related to the network structure and the configuration of generators and loads.

If there is a unit current supplied from the generator node v_i to the load node v_j (I_i = 1, I_j = −1), the voltage of node v_k can be writed as

$U_k=Z_{ki}-Z_{kj},(2)$

The electrical betweenness of edge (v_m, v_n) is the sum of the currents flowing through the edge for all node pairs of generator and load that have unit current transmitted in complex power systems. Then, the electrical betweenness of edge (v_m, v_n) is depicted as follows.

$B_e\left(m,n\right)=\sum _{V_{i\in V_G},V_{j\in V_L}}\sqrt{W_i{W}_j}{I}_{mn}\left(i,j\right)(3)$

W_i is the capacity of generator node v_i, and W_j is the maximal demand of load node v_j. I_mn(i, j) is the generated current in the edge (v_m, v_n) when an unit current is supplied from the generator node v_i to the load node v_j. $\sqrt{W_i{W}_j}$ is the weight coefficient of I_mn(i, j).

Assuming that the admittance of edge (v_m, v_n) is y_mn, I_mn(i, j) can be obtained

$\begin{array}{cc}\hfill I_{mn}\left(i,j\right)& =y_{mn}\left(U_m-U_n\right)\hfill \\ \hfill & =y_{mn}\left[\left(Z_{mi}-Z_{mj}\right)-\left(Z_{ni}-Z_{nj}\right)\right],\hfill \end{array}(4)$

where y_mn is admittance.

The electrical betweenness matrix of edges is isomorphic with the impedance matrix, which is an antisymmetric matrix with B_e (m, n) = −B_e (m,n)^T. The electrical betweenness matrix is rewrited as:

$B_e\left(m,n\right)=\left\{\begin{array}{c}{B}_e\left(m,n\right)B_e\left(m,n\right)>0\hfill \\ \hfill \\ 0B_e\left(m,n\right)<0\hfill \end{array}\right.(5)$

The edge direction in the network model: If B_e (m, n) > 0, there is an edge from node v_m to node v_n in the network model.

3 Strong Structural Controllabity of Power Systems

3.1 Weak Structural Controllability and Strong Structural Controllabity

Consider the linear-time-invariant system:

$\dot{\mathbf{x}}\left(t\right)=\mathbf{A}\mathbf{x}\left(t\right)+\mathbf{B}\mathbf{u}\left(t\right)(6)$

where $\mathbf{x}={(x_1,\dots ,x_N)}^T$ is the node states vector; N is the scale of the system; $\mathbf{A}=\left[a_{ij}\right]\in R^{N\times N}$ is the coupling matrix between nodes; a_ij describes the strength of coupling between nodes; $\mathbf{u}={(u_1,u_2,\dots ,u_m)}^T$ describes the states of m controllers; and B ∈ R^N×m is the control input matrix.

A system is controllable if it can be moves from its initial state x₀ to any desired final state within a limited time. Due to many models of physical and technical systems are being structured, dynamics of nonlinear-time-invariant system is often linear-time-invariant.

Then, let $\bar{\mathbf{A}}=\left[\overline{a_{ij}}\right]\in {\{0,*\}}_{N\times N}$ denotes the structure pattern of A, and $\bar{\mathbf{B}}\in {\{0,*\}}^{N\times m}$ represents the structure pattern of B; the element in matrix $\bar{\mathbf{A}}$ or $\bar{\mathbf{B}}$ is equal to zero if the corresponding element in matrix A or B is equal to zero, and the other value otherwise.

Based on the network model of power systems in section 2, the structure pattern of a power system coupling matrix can be experessed as:

$\overline{a_{ij}}=\left\{\begin{array}{c}*B_e\left(m,n\right)>0\hfill \\ \hfill \\ 0B_e\left(m,n\right)=0\hfill \end{array}\right.(7)$

The system $(\bar{A},\bar{B})$ is weak structurally controllable, which means that the admissible numerical realization (A, B) is existed in $A\in \bar{A}$ and $B\in \bar{B}$. The weak structural controllability is such a generic property that almost all systems of the same structure have identical controllability properties. However, the physical dependencies between system parameters in actual systems leads to systems being uncontrollable although it is weekly structurally controllable. Thus, the concept of strong structural controllability was introduced. In this paper, the strong structural controllability of power systems is mainly considered.

The system $(\bar{A},\bar{B})$ is strong structurally controllable if the admissible numerical realization (A, B) is controllable for all $A\in \bar{A}$ and $B\in \bar{B}$.

Theorem 1 Trentelman et al. (2012): A class of systems defined by the structure matrices $\bar{A}$ and $\bar{B}$ is said to be strong structural controllable if rank (A− λIB) = n for all admissible numerical realizations $A\in \bar{A}$, $B\in \bar{B}$, and all eigenvalue λ_i, i = 1, … , n of A.

Graph theory is also the main direction of analyzing strong structural controllability. Concepts mentioned in this paper are introduced in the following passage, strong structurally controllable is reduced to controllable.

Out-neighbor: If (v_m, v_n) ∈ E, then node v_n is the out-neighbor of node v_m. In Figure 1A, v₄ is the out-neighbor of v₂.

FIGURE 1

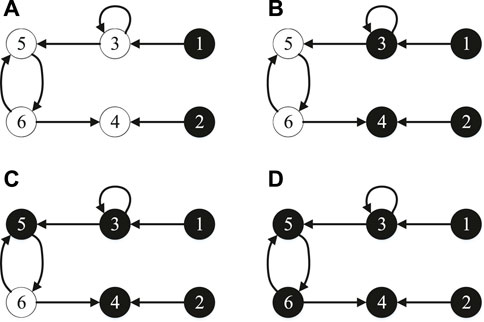
FIGURE 1. A forcing process based on color change rule in a digraph with six nodes and seven edges. (A) A graph with drive node set V_D = {v₁, v₂}; (B) v₁ force v₃ to be black and v₂ force v₄ to be black; (C) v₃ force v₅ to be black; (D) v₅ force v₆ to be black.

Color change rule: There are white nodes and black nodes in a directed graph D (V, E). If a black node v_m ∈ V has only out-neighbor v_n ∈ V, it forces v_n to be black. In Figures 1A,B, v₁ force v₃ to be black and v₂ force v₄ to be black.

Forcing process: The color change process that repeaterepeats the color change rule until no more color changes is called a forcing process. Figures 1A–D is a forcing process. In the first step, v₁ forces v₃ to be black and v₂ forces v₄ to be black. In the second step, v₃ forces v₅ to be black. In the final step, v₅ forces v₆ to be black.

Drive node set: let V_D ⊂ V is the set of initially black nodes in V, then V_D is drive node set. In Figure 1A, drive node set is V_D = {v₁, v₂}.

Controllable node set: The set of final black nodes after the forcing process is called the controllable node set V_C(V_D) of drive node set V_D. In Figure 1, controllable node set of V_D = {v₁, v₂} is V_C(V_D) = {v₁, v₂, v₃, v₄, v₅, v₆}.

Zero forcing set (ZFS): If V_C(V_D) = V, then V_D is a zero-forcing set (ZFS). In Figure 1, drive node set V_D = {v₁, v₂} is a zero-forcing set.

Theorem 2 Monshizadeh et al. (2014): A network system with dynamics 6) is strong structural controllable if and only if V_D ⊂ V is a zero-forcing set of the structure described digraph D (V, E) of system 6).

3.2 Drive Node set in Power Systems

3.2.1 Controllable Networks by Generator Nodes

The energy flow along the transmission line of a power system changes in real time. The system coupling matrixs of power systems have innumerable numerical implementations with the same zero-nonzero pattern. Therefore, the power system with the driver nodes’ configuration that realizes the weak structure control of the system is possible uncontrollable at a time. Power system is the most important social infrastructure network. It is very important to keep it under control for the safe and stable operation of power systems. Thus, the configuration of drive nodes with strong structural controllability is more in line with the control requirements of a power system.

Power systems areis a complex network with special physical characteristics. As shown in the previous network modeling, different nodes have different properties. Therefore, the strong structural controllability analysis of power systems should fully consider the differences between nodes.

In the modern power industry, synchronous generators are widely used in wind power generation, hydroelectric power generation, diesel power generation, and nuclear power generation. Synchronous generators play a dominant role in power systems. Synchronous generators convert part of the mechanical energy into sinusoidal AC electrical energy, while the other part is stored as kinetic energy in the huge rotating mass of the rotor. When the power system is disturbed, the rotor absorbs or releases energy to maintain the internal energy balance of the system. With the development of the power system, it has progressively become more dependent on fast response power electronic devices. The converter interfaces generation technologies can provide numerous services, such as active power control and frequency response, voltage/reactive power control, and ride-through for both voltage and frequency. In a nutshell, the generator node must be a drive node in the digraph of power systems. Then, we have V_G ⊂ V_D in the strong structural control of power systems.

Due to the special status of generator nodes in power system control, there are three different situations of strong structural controllability of a power network, which are defined as follows.

Definition 1 (precisely controllable networks by generator nodes) A structure described digraph of power systems is a precisely controllable network by generator nodes if the following conditions hold:

• The generator node set in the power system happens to be a zero-forcing set (V_C(V_G) = V).

• All proper subsets of generator nodes are not zero-forcing sets (V_C(V_D)⫋V for all V_D⫋V_G).

As despicted in Figure 2A digraph of power system with the generator node set V_G = {v₄, v₅}. Let V_D = V_G, then V_c(V_D) = V. Furthermore, if V_D = {v₄}, V_C(V_D) = {v₃, v₄}⫋V, and if V_D = {v₅}, V_C(V_D) = {v₂, v₅}⫋V. Thus, the power system in Figure 2A is the a precisely controllable networks by generator nodes.

FIGURE 2

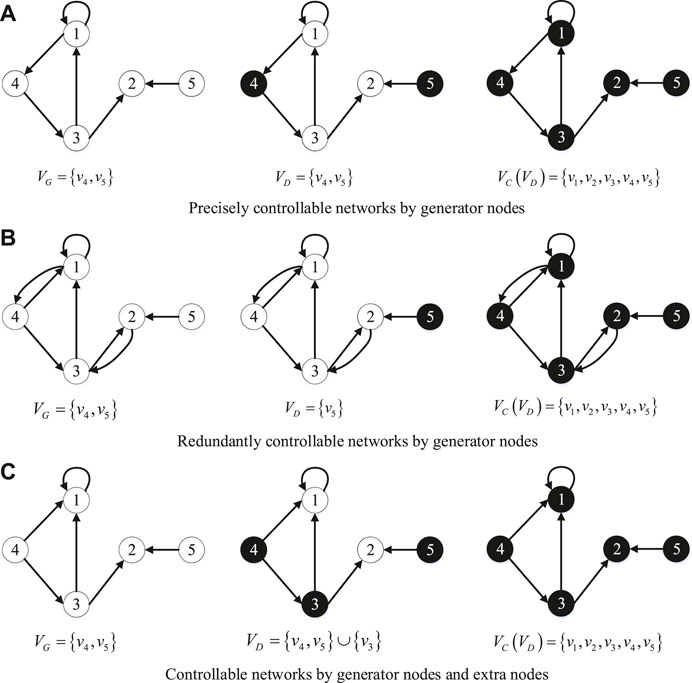
FIGURE 2. Three kind of controllable networks by generator nodes. (A) Precisely controllable networks by generator nodes; (B) Redundantly controllable networks by generator nodes; (C) Controllable networks by generator nodes and extra nodes.

Definition 2 (redundantly controllable networks by generator nodes) A structure described digraph of power systems is a redundantly controllable network by generator nodes if there is at least one zero-forcing set is in the proper subset of the generator node set in the power system (∃ZFS⫋V_G).

As despicted in Figures 2A,B digraph of power system with the generator node set V_G = {v₄, v₅}. Let V_D = {v₅}, then V_C(V_D) = V. Thus, the power system in Figure 2B is the redundantly controllable networks by generator nodes.

Definition 3 (controllable networks by generator nodes and extra nodes) A structure described digraph of power systems is a controllable networks by generator nodes and extra nodes if the controllable node set of generator node set is the proper subset of node set (V_C(V_G)⫋V).

The extra nodes belong to the transmission node set V_T or the load node set V_L. In actual power systems, the substation realizes system control through load station transfer and load cutting strategies. Load nodes achieve system control through demand response.

As despicted in Figures 2A,C digraph of power system with the generator node set V_G = {v₄, v₅}. Let V_D = V_G, then V_C(V_D) = {v₁, v₂, v₄, v₅}⫋V. Furthermore, when V_D = V_G ∪ {v₄}, V_C(V_D) = {v₁, v₂, v₃, v₄, v₅} = V. Thus, the power system in Figure 2C is the controllable networks by generator nodes and extra nodes.

3.2.2 Zero-Forcing Set of Controllable Networks by Generator Nodes and Extra Nodes

In this section, we focus on the zero-forcing set of controllable networks by generator nodes and extra nodes. Because this kind of networks cannot achieve strong structural controllability through generator nodes alone, we will investigate the conditions satisfied to satisfy of extra nodes in their zero-forcing set.

Then, we will introduce some of the concepts used in the follows.

A path is a special kind of graph consists consisting of disjoint edges and nodes.

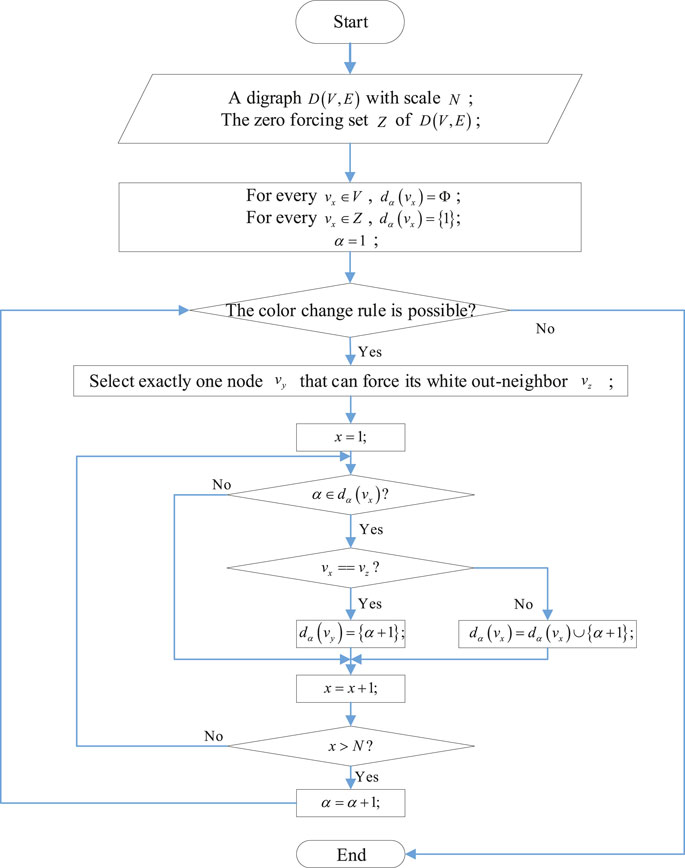
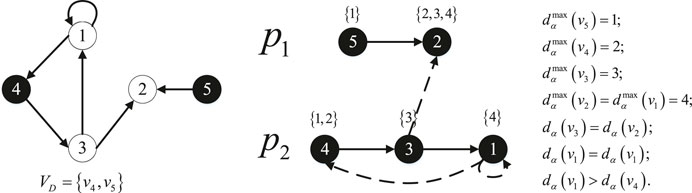
Distribution of integers on a path: let p = (V_p, E_p) is be a directed path with scale N_p. Let α ≥ N_p is be an integer. Let D_p denotes the distribution of integers from 1 to α among N_p nodes of p in a way, and every node is endowed at least one number. Besides, for i = 1, … , α − 1, two integers i and i + 1 are either assigned to one node, or i is given to a node and i + 1 is given to its out-neighbor. Thus, every node v ∈ V_p is given a set of successive integers, denoted by d_α(v). For every 1 ≤ β ≤ α, let v_α(β, p) is be the node v ∈ V_p and β ∈ d_α(v). Let v_α(1, p) be the start node of p. Furthermore, let $d_{\alpha }^{\max }(v)=\max \{\beta :\beta \in d_{\alpha }(v)\}$ and $d_{\alpha }^{\min }(v)=\min \{\beta :\beta \in d_{\alpha }(v)\}$.

For two path p₁ and p₂ with integer distribution $D_{p_1}$ and $D_{p_2}$. For v ∈ p₁ and u ∈ p₂, we define d_α(v) = d_α(u) if d_α(v) ∩ d_α(u) ≠ ∅; d_α(v) > d_α(u) if $d_{\alpha }^{\min }(v)>d_{\alpha }^{\max }(u)$; d_α(v) ≥ d_α(u) if either d_α(v) > d_α(u) or d_α(v) = d_α(u); d_α(v) < d_α(u) otherwise.

For a distinct directed path set p = {p₁, … , p_m}, where $p_i=(V_{p_i},E_{p_i})$ is a path of size $N_{p_i}$, i = 1, 2, … , m. For $\alpha \ge \max (N_{p_i})$, let $D_{\alpha }^{\sum }=\{D_{p_1},\dots ,D_{p_m}\}$ be the set of distribution of integers from 1 to α in P. Besides, the start nodes of p are the union of start nodes of p_i, $V_{\alpha }(\beta ,P)={\cup }_{i=1}^m{v}_{\alpha }(\beta ,p_i)$.

An efficient set of distribution $E{D}_{\alpha }^{\sum }$ is a set of distribution with $\alpha =1-m+{\sum }_{i=1}^m{N}_{p_i}$, where m is the number of paths. For every 1 ≤ j < α, the distributions $D_{p_i}$, i = 1, … , m have exactly one node in ${\cup }_{i=1}^m{V}_{p_i}$ such that $d_{\alpha }^{\max }(v)=j$.

The distribution algorithm that gives every node a successive set of integers of a digraph with a zero-forcing set is depicted in Figure 3. As shown in Figure 4, a digraph D (V, E) is forced by drive nodes V_D = {v₄, v₅}. After the forcing process, the distribution of integers on two paths $p_1=\{V_{p_1},E_{p_1}\}$, $p_2=\{V_{p_2},E_{p_2}\}$ are depicted in Figure 4. According to the above definition, the set of distribution $D_{\alpha }^{\sum }=\{D_{p_1},D_{p_2}\}$ is an efficient set of distribution. Furthermore, all edges $(u,v)\in E-E_{p_1}-E_{p_2}$ all have d_α(u) ≥ d_α(v).

FIGURE 3

FIGURE 3. The flowchart of distribution algorithm.

FIGURE 4

FIGURE 4. The schematic diagram of successive integers’ distribution process.

Definition 4 (precisely controllable subnetworks by generator nodes D_g (V_g, E_g)) In controllable networks by generator nodes and extra nodes D_{V, E}, let generator nodes be black nodes and other nodes be white. After the forcing process, the final black nodes are denoted in V_g. The edge set E_g is defined, such that E_g = {(v_m, v_n) (v_m, v_n) ∈ E and v_m, v_n ∈ V_g}. Then, the precisely controllable subnetworks by generator nodes is consist of node set V_g and edge set E_g, and V_G is a ZFS of D_g.

Theorem 3: The precisely controllable subnetworks by generator nodes D_g (V_g, E_g) is consist of a set of paths $P=\{p_1,\dots ,p_{N_G}\}$ $(p_i=\{V_{p_i},E_{p_i}\})$ with start node set V_G, which has an efficient set of distribution $E{D}_{\alpha }^{\sum }$. Besides, the edges $(u,v)\in E_g-{\cup }_{i=1}^{N_G}{E}_{p_i}$ all have d_α(u) ≥ d_α(v). Where N_G is the number of generator nodes in V_G.

Proof: V_G with |V_G| = N_G is a zero-forcing set of D_g. $P=\{p_1,\dots ,p_{N_G}\}$ is the set of paths with the maximum forcing chain of V_G with the set of distribution of successive integers $D_{\alpha }^{\sum }=\{D_{p_1},\dots ,D_{p_{N_G}}\}$, which are obtained from the distribution algorithm in Figure 3. Furthermore, $\alpha =1-N_G+{\sum }_{i=1}^{N_G}{N}_{p_i}$, $N_{p_i}$ is the number of nodes in p_i.

As described in the distribution algorithm, the nodes in V_G are given {1} in Step 1. Then, exactly one node in D_g is forced to be black in other eachstep. Let v_m be the last black node of p_i in step j − 1, then j − 1 ∈ d_α(v_m). If in step j, v_m can force v_m+1 to be black, then d_α(v_m+1) = {j}. Otherwise, d_α(v_m) = d_α(v_m) ∪ {j}, and v_m is still the last black node of p_i. Thus, for x = 1, … , α − 1, we have only one node v ∈ V_g such that $d_{\alpha }^{\max }(v)=x$. Hence, the set of distribution $D_{\alpha }^{\sum }$ is efficient.

Suppose that the edges $(u,v)\in E_g-{\cup }_{i=1}^{N_G}{E}_{p_i}$ all have d_α(u) ≥ d_α(v) is not true. Then we have $d_{\alpha }^{\max }(u)<d_{\alpha }^{\min }(v)$ for $(u,v)\in E_g-{\cup }_{i=1}^{N_G}{E}_{p_i}$, v is a out-neighbor of u, and $d_{\alpha }^{\max }(u)<\alpha$.

If two nodes u and v belong to different path p_i and p_j, respectively. u is not the end node of p_i, because $d_{\alpha }^{\max }(u)<\alpha$. According to the integer distribution algorithm in Figure 3, u is the last black node of p_i in Step $d_{\alpha }^{\max }(u)$, and it will forces its white out-neighbor in Step $d_{\alpha }^{\max }(u)+1$. However, due to $d_{\alpha }^{\max }(u)<d_{\alpha }^{\min }(v)$, v is still a white node in Step $d_{\alpha }^{\max }(u)+1$. Then, u has two white out-neighbor nodes, and the color change rule cannot be performed. Hence, there is a contradiction.

If two nodes, u and v, belong to a path p_i, as mentioned above, v is a white put-neighbor of u in Step $d_{\alpha }^{\max }(u)+1$ in p_i. u will forces v be black in Step $d_{\alpha }^{\max }(u)+1$ in p_i. Thus, $(u,v)\in E_{p_i}$. However, $(u,v)\in E_g-{\cup }_{i=1}^{N_G}{E}_{p_i}$. There is also a contradiction.

Based on Theorem 3, we can make the inference of the zero-forcing set Z of controllable networks by generator nodes and extra nodes, as shown in Lemma 1.

Lemma 1: The zero-forcing set Z of controllable networks by generator nodes and extra nodes D (V, E) (|V| = N) is consists of two parts, Z = V_G ∪ V_EN. We have the precisely controllable subnetworks by generator nodes D_g (V_g, E_g). All nodes in set V − V_g can form a set of paths $P^{\prime }=\{p_1,\dots ,p_{N_{EN}}\}$ with start node set V_EN, where N_EN is the number of nodes in V_EN. The set of paths $P^{\sum }=P\cup P^{\prime }=\{p_1,\dots ,p_{N_G}\}\cup \{p_1,\dots ,p_{N_{EN}}\}$ also has an efficient set of distribution ${\overline{ED}}_{\alpha }^{\sum }$. The edge $(u,v)\in E_g-{\cup }_{i=1}^{N_G+N_{EN}}{E}_{p_i}$ all have d_α(u) ≥ d_α(v). Where $\alpha =1-(N_G+N_{EN})+{\sum }_{i=1}^{N_G+N_{EN}}{N}_{p_i}$. $N_{p_i}$ is the number of nodes in p_i.

Remark 1: According to Theorem 3, we can infer that for every digraph with a zero-forcing set, all nodes in the digraph can consist of a forcing path set with the start nodes in the zero-forcing set, and the forcing path set has an efficient distribution. Moreover, except for the forcing path set, any edge (u, v) in the digraph satisfies d_α(u) ≥ d_α(v). The controllable networks by generator nodes and extra nodes is a digraph with the zero-forcing set V_G ∪ V_EN. Thus, all nodes in the digraph can consist of a forcing path set with the start nodes in V_G ∪ V_EN, and all the other edges (u, v) in the network satisfies d_α(u) ≥ d_α(v).

4 Robustness of Controllable Networks by Generator Nodes

Transmission lines in a power system can be damaged and disconnected from the system due to factors such as natural disasters or a perceived deliberate attack. Damage to a transmission line causes edges to be removed from its network model. The structural change of a network model also leads to the change of strong structural controllability of networks. Therefore, this paper analyzes the robustness of three kinds of controllable networks by generator nodes.

Definition 5 (The largest set of removable edges) The largest set of removable edges E_r is the subset of E in the controllable networks by generator nodes D (V, E) with zero-forcing set Z. Remove If any subsets of E_r are removed, the strong structural controllability of D (V, E) from Z remains. We define N_R = |E_r| as the robustness evaluation parameters of strong structural controllability.

Theorem 4: The largest set of removable edges E_r of precisely controllable networks D (V, E) by generator nodes is $E-{\cup }_{i=1}^{N_G}{E}_{p_i}$. Where $p_i(V_{p_i},E_{p_i})\in P=\{p_1,\dots ,p_{N_G}\}$. p is the set of paths forced by generator node set V_G, |V_G| = N_G.

Proof: According to the color change rule and Theorem 2, the subnetwork $D_s(V_s,E_s)={\cup }_{i=1}^{N_G}{p}_i$ is controllable by V_G. Suppose there exists an edge (u, v) ∈ E_s, such that V_G is still the zero-forcing set of D_s − {(u, v)}. We know that D_s consists of N_G disjointed paths, and D_s − {(u, v)} consists of N_G + 1 disjointed paths. It is clear that the size of zero-forcing set Z of D_s − {(u, v)} should greater than N_G. Thus, V_G is not a zero-forcing set of D_s − {(u, v)}. And D_s − {(u, v)} can not be controlled by V_G.

Based on Theorem 4, we can get the largest set of removable edges E_r of controllable networks D (V, E) by generator nodes and extra nodes, as shown in Lemma 2.

Lemma 2: The largest set of removable edges E_r of controllable networks D (V, E) by generator nodes and extra nodes is $E-{\cup }_{i=1}^{N_G+N_{EN}}{E}_{p_i}$. Where $p_i(V_{p_i},E_{p_i})\in P=\{p_1,\dots ,p_{N_G+N_{EN}}\}$. p is the set of paths forced by generator node set V_G and extra node set V_EN, |V_G| = N_G and |V_EN| = N_EN.

Remark 2: According to Theorem 4, we can infer that for a digraph in which drive node set is a zero-forcing set, the largest set of removable edges contains all edge in the digraph except the edges in the forcing paths that the start nodes belong to its zero-forcing set. The controllable network by generator nodes and extra nodes is a digraph in which the drive node set and the zero-forcing set are both V_G ∪ V_EN. Thus, the largest set of removable edges of the network contains all edges in the digraph except the edges in the forcing paths that the start nodes belong to V_G ∪ V_EN.

Theorem 5: There exists a zero-forcing set Z⫋V_G of redundantly controllable networks D (V, E) by generator nodes. The largest set of removable edges E_r of redundantly controllable networks D (V, E) by generator nodes is $E-{\cup }_{i=1}^{|Z|}{E}_{p_i}+{\cup }_{j=1}^{N_G-|Z|}(v_x,v_j)$. Where $p_i(V_{p_i},E_{p_i})\in P=\{p_1,\dots ,p_{|Z|}\}$, and $v_j\in V_G-Z,(v_x,v_j)\in {\cup }_{i=1}^{|Z|}{E}_{p_i}$. p is the set of paths forced by the zero-forcing set Z⫋V_G.

Proof: According to the color change rule and Theorem 2, the subnetwork $D_s^{\prime }(V_s^{\prime },E_s^{\prime })={\cup }_{i=1}^{|Z|}{p}_i$ is controllable by Z. The subnetwork $D_s^{\prime }-{\cup }_{j=1}^{N_G-|Z|}(v_x,v_j)$ is a set of paths with the start nodes of $V_G{D}_s^{\prime }-{\cup }_{j=1}^{N_G-|Z|}(v_x,v_j)=\{p_1,\dots ,p_{N_G}\}$. According to Theorem 4, $D_s^{\prime }-{\cup }_{j=1}^{N_G-|Z|}(v_x,v_j)={\cup }_{i=1}^{|Z|}{p}_i$ is controllable by V_G, and removing any edge $(u,v)\in D_s^{\prime }-{\cup }_{j=1}^{N_G-|Z|}(v_x,v_j)$, $D_s^{\prime }-{\cup }_{j=1}^{N_G-|Z|}(v_x,v_j)$ is not controllable by V_G.

5 Instance Analysis

5.1 Instance of Controllable Network by Generator Nodes and Extra Nodes

In this subsection, IEEE 39 bus system is selected to analysis analyze the strong structural controllability and the robustness of strong structural controllability in this paper. There are 39 buses, 10 generator nodes, and 46 edges in the system. The wiring diagram and the network model of IEEE 39 bus system are depicted in Figures 5A,B, respectively, where the red nodes are generator nodes.

FIGURE 5

FIGURE 5. (A) Wiring diagram of IEEE 39 bus system; (B) Network model of IEEE 39 bus system. The red nodes are generator nodes.

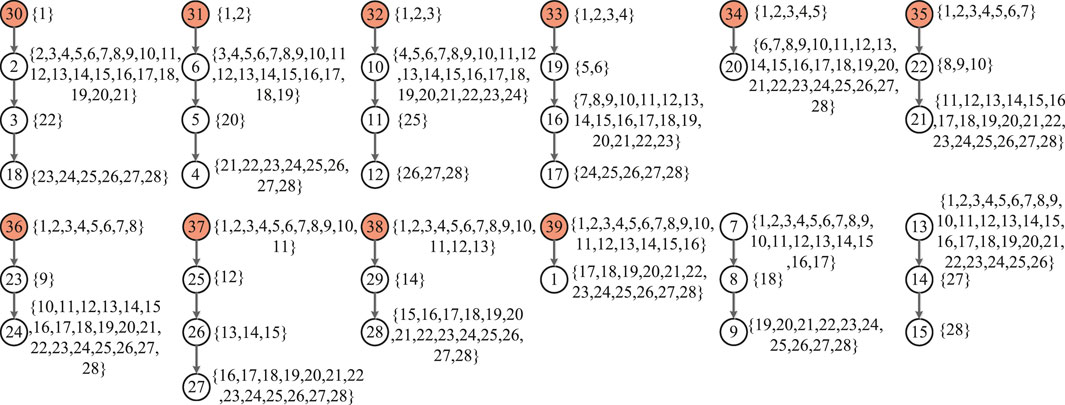
According to the above definition, the IEEE 39 bus system is the a controllable network s by generator nodes and extra nodes. A zero-forcing set of the system is Z = V_G ∪ V_EN = {v₃₀, v₃₁, v₃₂, v₃₃, v₃₄, v₃₅, v₃₆, v₃₇, v₃₈, v₃₉} ∪ {v₇, v₁₃}. The forcing paths are depicted in Figure 6, where solid lines are edges in path sand dotted lines are other edges in the system. The integer’s distribution on these forcing paths are given in Figure 7, which is an efficient set of distribution. α = 1–12 + 39 = 28. For every 1 ≤ j < 28, there are is exactly one node in this path set such that $d_{\alpha }^{\max }(v)=j$. According to the lemma 2, the largest set of removable edges E_r of IEEE 39 bus system is $E-{\cup }_{i=1}^{10,+,2}{E}_{p_i}$, which are dotted lines in Figure 6. E_r = {(v₂, v₁) (v₂, v₂₅) (v₃, v₄) (v₅, v₈) (v₆, v₇) (v₉, v₃₉) (v₁₀, v₁₃) (v₁₁, v₆) (v₁₃, v₁₂) (v₁₄, v₄) (v₁₅, v₁₆) (v₁₆, v₂₁) (v₁₆, v₂₄) (v₁₇, v₂₇) (v₁₈, v₁₇ (v₁₉, v₂₀) (v₂₂, v₂₃) (v₂₆, v₂₈) (v₂₉, v₂₆))}.

FIGURE 6

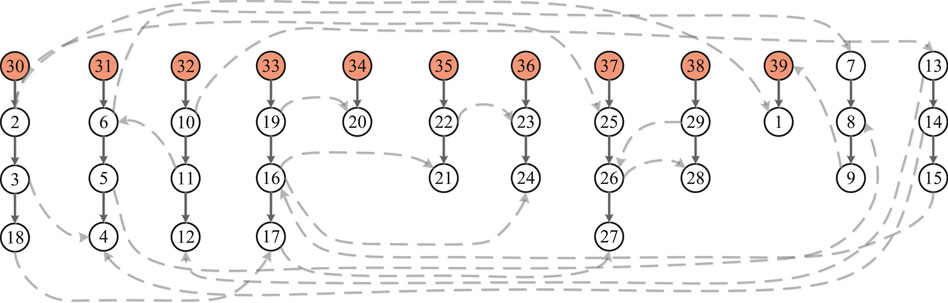
FIGURE 6. The forcing paths in the IEEE 39 bus system. Solid lines are edges in paths and dotted lines are other edges in the system.

FIGURE 7

FIGURE 7. The integer’s distribution on the forcing paths of the IEEE 39 bus system.

5.2 Instance of Redundantly Controllable Networks by Generator Nodes

In this subsection, IEEE 14 bus system is selected to analysis analyze the strong structural controllability and the robustness of strong structural controllability in this paper. There are 14 buses, five generator nodes, and 20 edges in the system. The wiring diagram and the network model of IEEE 14 bus system are depicted in Figures 8A,B, respectively, where the red nodes are generator nodes.

FIGURE 8

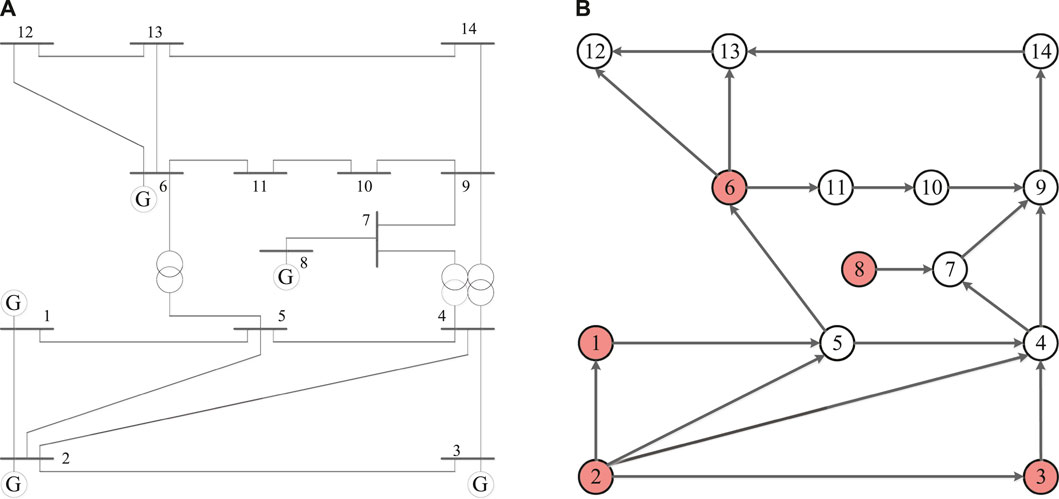
FIGURE 8. (A) Wiring diagram of IEEE 14 bus system; (B) Network model of IEEE 14 bus system. The red nodes are generator nodes.

According to the above definition, the IEEE 14 bus system is the a redundantly controllable networks by generator nodes. A zero-forcing set of the system is Z ⊂ V_G = {v₁, v₂, v₆, v₈}. The forcing paths are depicted in Figure 9A. The integer’s distribution on the forcing paths of four drive nodes are given in Figure 9B, which is an efficient set of distribution. α₁ = 1–4 + 14 = 11. For every 1 ≤ j < 11, there are is exactly one node in this path set such that $d_{{\alpha }_1}^{\max }(v)=j$.

FIGURE 9

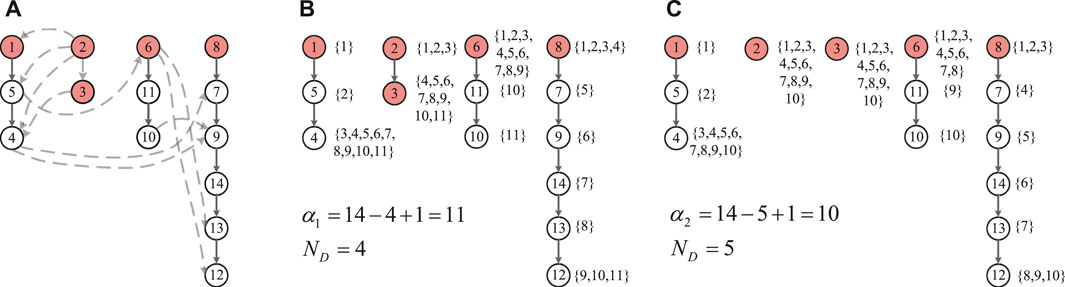
FIGURE 9. (A) The forcing paths of four drive nodes in the IEEE 14 bus system. (B) The integer’s distribution on the forcing paths of four drive nodes in the IEEE 14 bus system. (C)The integer’s distribution on the forcing paths of five drive nodes in the IEEE 14 bus system.

According to the Theorem 5, the largest set of removable edges E_r of IEEE 14 bus system is $E-{\cup }_{i=1}^4{E}_{p_i}+{\cup }_{j=1}^{5-4}(v_x,v_j)$, which are dotted lines in Figure 9A. E_r = {(v₂, v₁) (v₂, v₃) (v₂, v₄) (v₂, v₅) (v₃, v₄) (v₄, v₇) (v₄, v₉) (v₅, v₆) (v₆, v₁₂) (v₆, v₁₃) (v₁₀, v₉)}. Due to v₃ is being a generator node, when all edges in E_r are removed from the IEEE 14 bus system, the system is still strong structuallystructurally controllable. At this point, the zero-forcing set of the system is Z = V_G = {v₁, v₂, v₃, v₆, v₈}. The integer’s distribution on the forcing paths of five drive nodes are given in Figure 9C, which is an efficient set of distribution. α₂ = 1–5 + 14 = 10. For every 1 ≤ j < 10, there are is exactly one node in this path set such that $d_{{\alpha }_2}^{\max }(v)=j$.

6 Conclusion

This paper analyses analyzes the robust strong structural controllability of complex power systems. Considering the dominant role of generators in the control of power systems, we define three kinds of controllable networks by generator nodes, precisely controllable networks by generator nodes, redundantly controllable networks by generator nodes, and controllable networks by generator nodes and extra nodes. Additionally, the satisfied conditions of zero-forcing set in the controllable networks by generator nodes and extra nodes are given in Theorem 3 and Lemma 1, and the relevant proof is also given. Besides, the robustness of strong structural controllability in three kinds of controllable networks by generator nodes are analyzed. We give the satisfied conditions and the relevant proofs of the largest set of removable edges in three kinds of controllable networks by generator nodes. Finally, the robust strong structural controllability of the IEEE 39 bus system is investigated. We have found that the IEEE 39 bus system is the a controllable networks by generator nodes and extra nodes, and the scale of the largest set of removable edges is 19.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YS and DY contributed to the theorem derivation and proof. YS wrote the first draft of the manuscript. XG and JQ contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (U1908217), the Liaoning Revitalization Talents Program (XLYC1902055), National Key Research and Development Project (2018YFB1700500), and the Fundamental Research Funds for the Central Universities (N180415004).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barioli, F., Fallat, S., Hall, H., Hershkowitz, D., Hogben, L., Van der Holst, H., et al. (2009). On the Minimum Rank of Not Necessarily Symmetric Matrices: a Preliminary Study. Electronic. J. Linear. Algebra. 18, 126–145. doi:10.13001/1081-3810.1300

CrossRef Full Text | Google Scholar

Bowden, C., Holderbaum, W., and Becerra, V. M. (2012). Strong Structural Controllability and the Multilink Inverted Pendulum. IEEE Trans. Autom. Contr. 57, 2891–2896. doi:10.1109/TAC.2012.2191180

CrossRef Full Text | Google Scholar

Chapman, A., and Mesbahi, M. (2013). On Strong Structural Controllability of Networked Systems: a Constrained Matching Approach.” in Proc. American Control Conf (IEEE), 6126. doi:10.1109/acc.2013.6580798

CrossRef Full Text | Google Scholar

Ching-Tai Lin, C. T. (1974). Structural Controllability. IEEE Trans. Autom. Contr. 19, 201–208. doi:10.1109/tac.1974.1100557

CrossRef Full Text | Google Scholar

Chu, C.-C., and Iu, H. H.-C. (2017). Complex Networks Theory for Modern Smart Grid Applications: A Survey. IEEE J. Emerg. Sel. Top. Circuits Syst. 7, 177–191. doi:10.1109/JETCAS.2017.2692243

CrossRef Full Text | Google Scholar

Chung, C. Y., Wang, K. W., Tse, C. T., and Niu, R. (2002). Power-system Stabilizer (Pss) Design by Probabilistic Sensitivity Indexes (Psis). IEEE Trans. Power Syst. 17, 688–693. doi:10.1109/TPWRS.2002.800914

CrossRef Full Text | Google Scholar

Dey, P., Mehra, R., Kazi, F., Wagh, S., and Singh, N. M. (2016). Impact of Topology on the Propagation of Cascading Failure in Power Grid. IEEE Trans. Smart Grid 7, 1970–1978. doi:10.1109/TSG.2016.2558465

CrossRef Full Text | Google Scholar

Freeman, L. C. (1978). Centrality in Social Networks Conceptual Clarification. Soc. Netw. 1, 215–239. doi:10.1016/0378-8733(78)90021-7

CrossRef Full Text | Google Scholar

Group, A. M. R. G. W. (2008). Zero Forcing Sets and the Minimum Rank of Graphs. Linear Algebra its Appl. 428, 1628–1648. doi:10.1016/j.laa.2007.10.009

CrossRef Full Text | Google Scholar

Haque, M. H. (2004). Improvement of First Swing Stability Limit by Utilizing Full Benefit of Shunt Facts Devices. IEEE Trans. Power Syst. 19, 1894–1902. doi:10.1109/TPWRS.2004.836243

CrossRef Full Text | Google Scholar

Hassan, F. F., Balasubramanian, R., and Bhatti, T. S. (1999). New Fast Valving Scheme Using Parallel Valves for Transient Stability Improvement. IEE Proc. Gener. Transm. Distrib. 146, 330–336. doi:10.1049/ip-gtd:19990176

CrossRef Full Text | Google Scholar

Hatziargyriou, N., Milanovic, J., Rahmann, C., Ajjarapu, V., Canizares, C., Erlich, I., et al. (2021). Definition and Classification of Power System Stability - Revisited & Extended. IEEE Trans. Power Syst. 36, 3271–3281. doi:10.1109/TPWRS.2020.3041774

CrossRef Full Text | Google Scholar

Hines, P., Cotilla-Sanchez, E., and Blumsack, S. (2010). Do topological Models Provide Good Information about Electricity Infrastructure Vulnerability? Chaos 20, 033122. doi:10.1063/1.3489887

PubMed Abstract | CrossRef Full Text | Google Scholar

Jarczyk, J. C., Svaricek, F., and Alt, B. (2011). “Strong Structural Controllability of Linear Systems Revisited,” in Proc. 50th IEEE Conf. on Decision and Control and Eur. Control Conf (IEEE), 1213. doi:10.1109/cdc.2011.6160392

CrossRef Full Text | Google Scholar

Jia, J., van Waarde, H. J., Trentelman, H. L., and Camlibel, M. K. (2021). A Unifying Framework for Strong Structural Controllability. IEEE Trans. Autom. Contr. 66, 391–398. doi:10.1109/TAC.2020.2981425

CrossRef Full Text | Google Scholar

Kiaei, I., Rostami, M., and Lotfifard, S. (2021). Robust Decentralized Control of Synchronous Generators for Improving Transient Stability of Multimachine Power Grids. IEEE Syst. J. 15, 3470–3479. doi:10.1109/JSYST.2020.3025028

CrossRef Full Text | Google Scholar

Li, Y.-S., Ma, D.-Z., Zhang, H.-G., and Sun, Q.-Y. (2015). Critical Nodes Identification of Power Systems Based on Controllability of Complex Networks. Appl. Sci. 5, 622–636. doi:10.3390/app5030622

CrossRef Full Text | Google Scholar

Liu, B., Li, Z., Chen, X., Huang, Y., and Liu, X. (2018). Recognition and Vulnerability Analysis of Key Nodes in Power Grid Based on Complex Network Centrality. IEEE Trans. Circuits Syst. II 65, 346–350. doi:10.1109/TCSII.2017.2705482

CrossRef Full Text | Google Scholar

Mahmud, M. A., Hossain, M. J., Pota, H. R., and Oo, A. M. T. (2017). Robust Partial Feedback Linearizing Excitation Controller Design for Multimachine Power Systems. IEEE Trans. Power Syst. 32, 3–16. doi:10.1109/TPWRS.2016.2555379

CrossRef Full Text | Google Scholar

Mayeda, H., and Yamada, T. (1979). Strong Structural Controllability. SIAM J. Control Optim. 17, 123–138. doi:10.1137/0317010

CrossRef Full Text | Google Scholar

Monshizadeh, N., Zhang, S., and Camlibel, M. K. (2014). Zero Forcing Sets and Controllability of Dynamical Systems Defined on Graphs. IEEE Trans. Autom. Contr. 59, 2562–2567. doi:10.1109/TAC.2014.2308619

CrossRef Full Text | Google Scholar

Mousavi, S. S., Haeri, M., and Mesbahi, M. (2018). On the Structural and Strong Structural Controllability of Undirected Networks. IEEE Trans. Autom. Contr. 63, 2234–2241. doi:10.1109/TAC.2017.2762620

CrossRef Full Text | Google Scholar

Rubaai, A., Ofoli, A. R., Cobbinah, D., and Kankam, M. D. (2005). Two-layer Supervisory Controller-Based Thyristor-Controlled Braking Resistor for Transient Stability Crisis. IEEE Trans. Ind. Appl. 41, 1539–1547. doi:10.1109/TIA.2005.857465

CrossRef Full Text | Google Scholar

Taylor, C. W., and Van Leuven, A. L. (1996). Caps: Improving Power System Stability Using the Time-Overvoltage Capability of Large Shunt Capacitor Banks. IEEE Trans. Power Deliv. 11, 783–792. doi:10.1109/61.489335

CrossRef Full Text | Google Scholar

Trentelman, H., Stoorvogel, A., and Hautus, M. (2012). Control Theory for Linear Systems. Berlin, Germany: Springer.

Google Scholar

Wang, K., Zhang, B.-h., Zhang, Z., Yin, X.-g., and Wang, B. (2011). An Electrical Betweenness Approach for Vulnerability Assessment of Power Grids Considering the Capacity of Generators and Load. Phys. A Stat. Mech. its Appl. 390, 4692–4701. doi:10.1016/j.physa.2011.07.031

CrossRef Full Text | Google Scholar

Yang, D.-S., Sun, Y.-H., Zhou, B.-W., Gao, X.-T., and Zhang, H.-G. (2020). Critical Nodes Identification of Complex Power Systems Based on Electric Cactus Structure. IEEE Syst. J. 14, 4477–4488. doi:10.1109/JSYST.2020.2967403

CrossRef Full Text | Google Scholar

Zhang, Z., Qiao, W., and Hui, Q. (2019). Power System Stabilization Using Energy-Dissipating Hybrid Control. IEEE Trans. Power Syst. 34, 215–224. doi:10.1109/TPWRS.2018.2866839

CrossRef Full Text | Google Scholar