- 1Power Grid Planning Center of Guangdong Power Grid CO., LTD, Guangzhou, China
- 2New Energy Service Center of Guangdong Power Grid CO., LTD, Guangzhou, China
- 3School of Electric Power Engineering, South China University of Technology, Guangzhou, China
- 4Energy Development Research Institute of China Southern Power Grid, Guangzhou, China
Accurate forecasting of short-term photovoltaic power output is vital for enhancing the operation efficiency of photovoltaic (PV) power stations and ensuring the safety and stable operation of grid-connected PV plants. Therefore, a short-term power forecasting model based on a backpropagation neural network with atom search optimization optimizes the weights and thresholds. Meanwhile, the Pearson correlation coefficient formula is introduced to screen the key meteorological factors and eliminate redundant factors, i.e., total irradiance, temperature, humidity, and direct irradiance are taken as the input of the prediction model. Moreover, the Euclidean distance formula is used to establish a customized training set for each test data which improves the dependability of the training set. Lastly, with the simulations of actual data from a solar farm in Yunnan, China, it is verified that the proposed ASO-BPNN model is competent to forecast the PV power generation.
1 Introduction
Energy is the foundation for the existence of industrial society (Bozorg et al., 2020; Yang et al., 2021a). At present, the energy crisis is becoming increasingly severe, and many countries are vigorously developing clean power technology (Kemmoku et al., 1999; Almonacid et al., 2014). For a continuous power grid safe operation and regional power optimization dispatching, a variety of clean power generation, e.g., the solar energy, the wind energy, the hydropower station, and the tidal energy, are connected to the power grid (Olujobi, 2020; Yang et al., 2021b). Especially in the peak period of power consumption, the grid connection of clean energy can effectively relieve the dispatching pressure of the grid and ensure the continuous and efficient operation of the power system (Mayer and Gróf, 2020; Collino and Ronzio, 2021). Among various alternative energy sources, solar energy draws much attention because of its huge reserves and eco-friendly peculiarity (Li et al., 2020). In the background of a carbon-neutral strategy, solar power generation technology has become a significant method to solve the problem of resource scarcity and improve China’s energy consumption structure (Xue and Shen, 2020).
However, photovoltaic (PV) power generation is susceptible to solar azimuth motion and meteorological factors in the field operation, and its time fluctuation also brings new challenges to the security and economy of the grid (Li et al., 2017). Therefore, improving the prediction accuracy of PV power is of great significance in two aspects: dispatch operation and market competition. The dispatching plan and the operating costs can be optimized according to the prediction results of the PV power system, and the high accuracy of short-term forecast performance is in favor of the competition of solar power in the electric power market (Yildiz et al., 2017; Yang et al., 2021c). An accurate and reasonable scheduling plan can not only ensure the power balance and power quality of the power system but also reduce the rotating spare capacity of the power system, which reduces the operation cost of the grid and improve the utilization efficiency of solar energy (Huang et al., 2018; Qing and Niu, 2018). In short, with the continuous expansion of grid-connected PV systems, solar power forecasting technology has important practical and guiding significance for grid dispatching operation, electrical load coordination, planning of conventional energy, and PV generation (Meenal and Selvakumar, 2018).
Nowadays, short-term PV power prediction is in the stage of extensive research, which is mainly divided into the following two categories (Chang et al., 2020): indirect prediction and direct prediction in view of the principle of forecasting methods as illustrated in Figure 1. The indirect method establishes a physical prediction model according to the detailed parameters of the PV module and geographic information. This method has high prediction accuracy but depends on a complex model of the PV power generation system and the accurate weather forecast information which restricts its application range. The indirect prediction method is only suitable for stable conditions, while the prediction performance will be badly affected under unpredictable weather conditions. Moreover, significant inaccuracies could be generated by improper utilization of the empirical formula when the PV component parameters change, which further increases the difficulty of short-term prediction. In contrast, the direct prediction method is simpler in modeling, which only requires the mapping relationship between historical training samples and PV power generation data. Moreover, it has a strong nonlinear fitting ability (Liu et al., 2015).
At present, the main solar forecasting methods are as follows: the backpropagation neural network (BPNN) method, the gray forecast model, the multiple linear regression method, the autoregressive integrated moving average (ARIMA) prediction technique, the Markov chain, the support vector machine (SVM) method, the fuzzy cluster analysis, and so on. Lorenz et al. (2009) used the forecast data of radiation intensity provided by the weather forecast center for the next 3 days and the measured data of the PV power station to predict the PV power generation, and the monthly relative root means square error could reach 22%. Almonacid et al. (2009) fully considered the influence of the PV panel temperature and irradiation intensity on the PV output power. They established the function among the PV module temperature, irradiation intensity, and outputs of the PV station based on the I/V curve attained by a neural network. The case studies verify that the correlation coefficient between the predicted value and the actual power is as high as 0.998. Kudo et al. (2009) adopted the multiple regression analysis method to realize an hourly power prediction of the PV plant for the next day based on the historical power generation data and corresponding meteorological data. Particularly, in order to reduce the prediction accuracy dependence on the meteorological data accuracy, a novel forecasting scheme that combined measured data, prediction, and late correction is proposed. The results show that the prediction error of average hourly power generation is 30.53% and the average daily power generation is 25.6%. The BPNN model is suitable for the power prediction of PV power generation (Liu et al., 2017), but BPNN has the drawback of low convergence rate and easily falling into local extremums since it is trained by the gradient descent method. To overcome the above problems, swarm intelligence algorithms are often used to optimize the BPNN parameters. Tao and Chen ( 2014) used the genetic algorithm (GA) to optimize the connection weight and the threshold value between various layers in the BP neural network model. Ant colony optimization (ACO) is proposed to optimize the structure of BPNN in Netsanet et al., 2022. In the aforementioned pieces of literature, the selection of the training set is relatively rough and the accuracy is not high because only the average dominant meteorological factor is utilized to filter the similar days as the training set. As a result, the training samples in the aforementioned studies could not reflect the meteorological characteristics for the predicted days. Moreover, the parameters of the selected optimization algorithm are complicated, which leads to low accuracy and poor robustness of the solar power prediction model in unstable weather conditions (Benmouiza and Cheknane, 2019).
Atom search optimization (ASO), a novel swarm intelligence optimization algorithm that has the advantages of good stability, strong global searchability, and few parameters (Zhao et al., 2019), is applied to optimize the weights and bias of BPNN. The simulation tests verify the good forecasting performance and less prediction error of the proposed ASO-BPNN model.
This work is structured as follows: The screening of meteorological factors and training samples is elaborated in Section 2. The principle of the BPNN modeling of the ASO-BPNN PV power forecasting model is constructed in Section 3. Simulation tests of the original BPNN and ASO-BPNN algorithms are carried out in Section 4, and the analysis of the simulation results is detailed and discussed in Section 5. Finally, the conclusions are given in Section 6.
2 Screening of Meteorological Factors and Training Samples
2.1 Screening of Meteorological Factors
There are numerous factors related to PV power generation, but the redundant factors will increase the complexity of solar power forecasting if considered. To improve the convergence speed and accuracy, the core factors influencing the PV power should be picked out. In this work, the historical power generation and corresponding meteorological data for 3 months of a PV plant are collected for correlation analysis. In order to avoid the influence of redundant meteorological factors on the PV output, the Pearson correlation coefficient formula is used to extract meteorological factors which are highly correlated with the PV power generation as the input of the forecasting model. Particularly, the formula of the Pearson coefficient method is as follows:
where
After the calculation, four meteorological factors, i.e., the total irradiance, temperature, humidity, and direct irradiance, are kept as the input variables for higher coefficients. The Pearson correlation coefficients of the whole seven indexes are shown in Table 1.
2.2 Screening of Training Samples
In previous studies, the daily average dominant meteorological factors of similar days were usually regarded as the training set. However, due to the great fluctuation of meteorological factors, the average dominant meteorological factors could hardly accurately reflect the weather fluctuation characteristics of the inflection point. Also, the prediction model trained by average dominant factors had a poor prediction accuracy of the model under unstable weather conditions. Therefore, in this study, the Euclidean distance formula is used to calculate the temporal sequence similarity of each piece of test data and then the independent training set is screened one by one. On account of the similarities between the meteorological characteristics of the predicted points and those of the historical samples, the selected training samples can accurately track the variation meteorological characteristics of the predicted points and, thus, the robustness of the prediction model is improved. The screening formula of the training set is calculated as follows:
where
The former k (
where
3 ASO-BPNN Prediction Model
3.1 Principle of BPNN
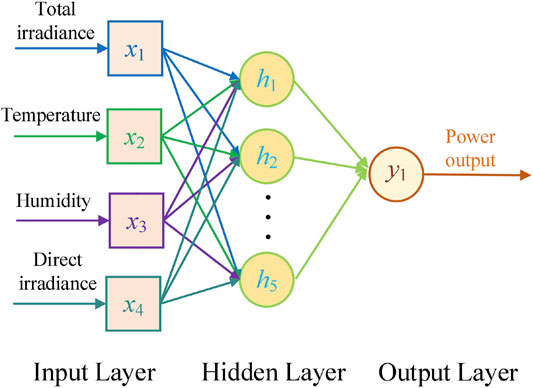
BPNN is a complex nonlinear network system based on imitating the structure and function of the biological brain and applying mathematical and physical methods (Kaushika et al., 2014). It has good nonlinearity, strong robustness, fault tolerance, and self-learning ability, and hence it is very suitable for high dimensional and nonlinear problems such as the PV power generation prediction. The common structure of BPNN is a three-layer network, which is shown in Figure 2.
According to the analysis results in Section 2.1, the total irradiance, temperature, humidity, and direct irradiance are taken as the inputs of the BPNN-based prediction model, and the output power of the PV station is regarded as the outputs of the prediction model. In addition, the number of nodes in the hidden layer is determined by an empirical formula as follows:
where
The training of the BPNN model can be divided into two phases: the input signal forward propagation stage and the error signal backpropagation stage. First, the input data are input through the input layer and then pass through the hidden layer to the output layer. When the difference between the output value and the expected value does not meet the accuracy requirements, the error signal will enter the stage of reverse propagation, that is, the deviation of the output value from the expected value will be reverse propagated through the output layer. Based on this deviation signal, BPNN adjusts the weights and bias of each layer through the gradient descent algorithm. The cycle repeats until the error between the output value and the expected value meets the accuracy requirement or reaches the maximum number of iterations.
BPNN utilizes the error backpropagation algorithm to adjust parameters whose initial parameters are random numbers, so it is easy to fall into the local optimum in the training process. Therefore, it is necessary to improve the structure of BPNN to enhance the prediction accuracy of the PV power prediction model.
3.2 Modeling of ASO-BPNN
In this study, ASO which has a strong macro exploration ability and good global optimization performance is introduced to optimize the weights and bias of BPNN. As one of the physically inspired metaheuristic optimizers, ASO is inspired by basic molecular dynamics models and imitates patterns of atomic motion in nature, in which atoms interact through the Lennard–Jones potential and binding interactions through bond growth potential. ASO is simple and easy to perform (Yang et al., 2020).
3.2.1 Principle of ASO
ASO is inspired by basic molecular dynamics. All substances in nature are composed of atoms with mass and volume. In an atomic system, all atoms interact with each other and are in a constant state of motion, and atoms’ microscopic interactions are very complex. The atomic motion follows the laws of classical mechanics, and the interaction force between atoms has two main characteristics in the atomic system: first, when the close contact between atoms produces compression, the atoms produce mutual repulsion; the other is the attraction between the atoms that holds them together. The potential energy of atoms is a good explanation for these two features, and the Lennard–Jones potential is used to mimic the interaction between a pair of atoms. In the repulsive region, the repulsive force between atoms increases rapidly as the distance between two atoms decrease. In the attractive region, the attraction gradually drops to zero as the distance between the two atoms increases. When the two atoms reach the equilibrium distance, the potential energy between the atoms reaches a minimum, and the interaction force between the atoms is equal to zero. Therefore, the total interaction force
where
In ASO, the position of each atom in the searching space represents a solution that is related to the atomic mass. Heavier masses of atoms mean better solutions and vice versa. All the atoms in the swarm attract or repel each other depending on the distance between two atoms, causing the lighter atoms to move toward the heavier ones. Heavy atoms, with smaller accelerations, seek better solutions in local space. In other words, lighter atoms have higher accelerations, which drives them to explore the global searching space for better solutions. Apart from the interaction force
The velocity and position of atoms are as shown in Eqs 8 and 9, respectively:
In addition, the drift factor is introduced into ASO to enable the algorithm to drift from the exploration stage to the exploitation stage, which is expressed as follows:
where
3.2.2 Process of ASO-BPNN
After exploration and exploitation of ASO, the optimal solution sought by ASO is assigned to the initial weights and bias of BPNN for enhancing its prediction accuracy. In conclusion, the specific steps of the solar energy forecasting model based on ASO-BPNN are as follows:
(1) Set the atomic population size N and randomly initialize the position and speed of each atom each of which represents a potential solution to the optimization problem;
(2) Calculate the fitness value of each atom (fitness is the average absolute percentage error between the real value and the predicted value after each iteration);
(3) Compute the acceleration and mass of each atom in the swarm using Eqs 6 and 7;
(4) Update the velocity and position using Eqs 8 and 9;
(5) If the maximum number of iterations is reached, export the best atom’s position; otherwise, repeat steps (2) to (4);
(6) Assign the position of the optimal atom which contains the initial weights and bias to BPNN;
(7) Adjust the individual weight and threshold by model training until the error precision is satisfied;
(8) Forecast simulation of PV power generation.
4 Simulation Test
4.1 Establishment of the Sample Set
The experimental data in this work are acquired from a solar farm in Yunnan, China. The selected sample data include the PV power generation data and the corresponding meteorological data within the time interval from March 1, 2020, to May 31, 2017, and the temporal resolution of data collection is 15 min. The forecasting time period is between 06:00 and 20:00. The input variables of the solar power forecasting model include four meteorological indicators, i.e., total irradiance, temperature, humidity, and direct irradiance. After screening and sorting, the summation of the sample data is 5239, containing 5182 pieces of training data to train ASO-BPNN, and 59 pieces of test data to verify the prediction performance.
4.2 Prediction Error Indicator
In order to accurately evaluate the prediction performance of each proposed model, root mean squared error (RMSE) (Zhang et al., 2021) and mean absolute percentage error (MAPE) (Yang et al., 2015) are introduced to quantitatively compare and analyze the prediction effect of each power forecasting model. Particularly, the specific formulae of RMSE and MAPE are as follows:
where n is the number of total data in the test set;
4.3 Parameter Setting of the Prediction Model
The sample data of the PV prediction model are trained by the original BPNN and ASO-BPNN, respectively, and the test results and model performance are compared and analyzed. According to the time sequence similarity calculated by the Euclidean distance formula in descending order, the former 2000 pieces of data are selected as the training set of each model, and then the data on May 31, 2017, are regarded as the test set. Moreover, after repeated imitation tests, the parameter settings of each prediction model are shown in Table 2; meanwhile, the rest of the parameters use the default values or remain the same. In particular, all simulation tests are performed using Matlab 2019b on a personal computer with IntelR CoreTMi7 CPU at 2.0 GHz and 32 GB of RAM.
5 Analysis of Simulation Results
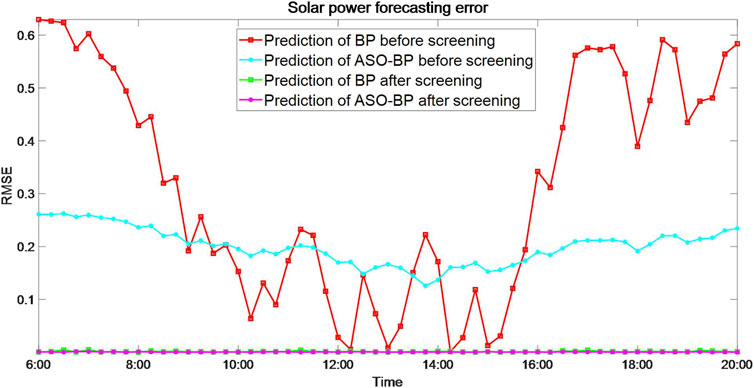
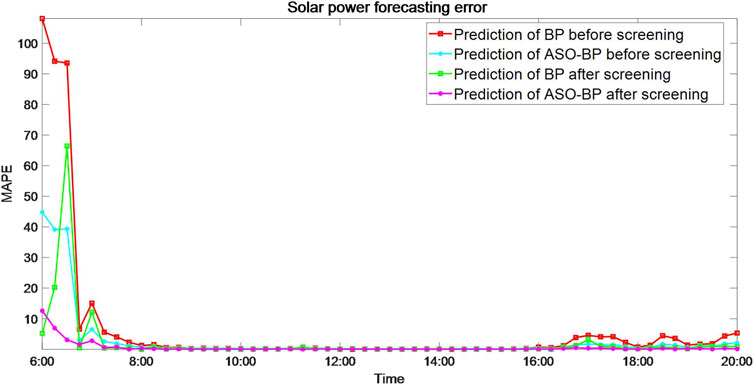
The neuron number for input, hidden, and output layers of each network are 4, 5, and 1, respectively. Except for the simulation results based on the screened and sorted sample, the simulation data based on the original sample was provided to verify the effectiveness and necessity of data screening by the Pearson correlation analysis and the Euclidean distance. Figure 3A shows the forecasting results by BPNN based on two samples. The simulation shows that the predicted values in 6:00–10:00 and 16:00–20:00 based on the original sample are far from measured values, and that based on a screened sample are slightly improved but still unsatisfactory. Figure 3B shows the forecasting results by ASO-BPNN based on two samples which verify the effectiveness of data screening as well. Figure 3C shows four curves of two forecasting network models based on two samples. Simulation results show that the forecasting results of the ASO-BPNN model based on a screened sample are best; the forecasting results of BPNN based on a screened sample are slightly worse than that of ASO-BPNN based on an original sample in 6:00–7:00 and 17:00–20:00, but better in the remaining time. Moreover, the RMSE and MAPE curves of the two forecasting network models based on two samples are depicted in Figures 4 and 5, respectively. Moreover, the corresponding mean forecasting error of the two models based on two samples are tabulated in Table 3.
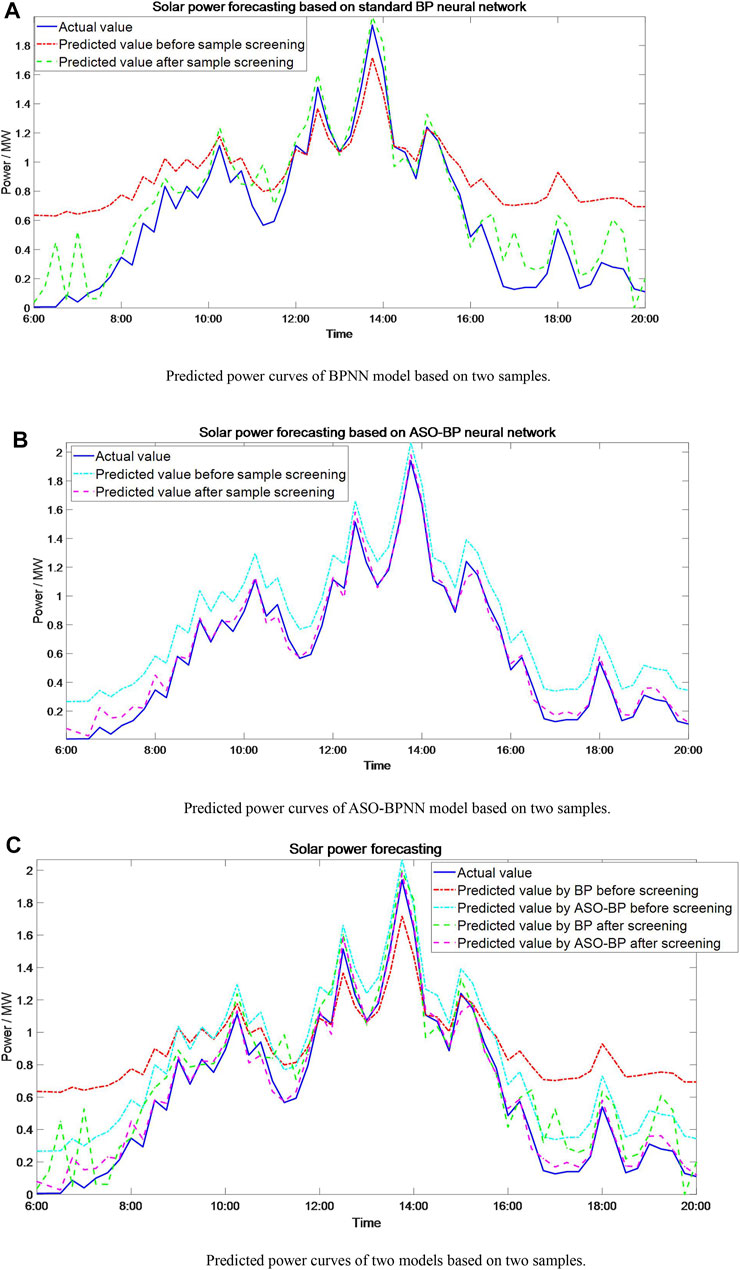
FIGURE 3. (A) Predicted power curves of the BPNN model based on two samples. (B) Predicted power curves of the ASO-BPNN model based on two samples. (C) Predicted power curves of two models based on two samples.
According to the comparison power curves in Figure 3 and the forecasting error in Table 3, it can be inferred that ASO effectively improves the weights and bias of BPNN and thus observably enhance the forecasting accuracy of the solar power prediction model. Particularly, the ASO-BPNN model based on the screened sample has the smallest values in two error indexes of RMSE and MAPE which verify that the ASO-BPNN model has good adaptability and outstanding predictive performance. It is worth mentioning that the screening of training samples by using the Pearson correlation analysis and the Euclidean distance has contributed to decreasing the prediction error of the ASO-BPNN model.
6 Conclusion
In this study, given the lack of the gradient descent algorithm in the traditional BPNN forecasting model resulting in easy trapping into local extremum, low convergence rate, and the undesirable prediction error, ASO is applied to optimize the weights and bias of BPNN and further enhance the accuracy and robustness of the solar farm power model. Thus, the short-term power forecasting model based on ASO-BPNN is established. Meanwhile, the training samples to train the network are screened and sorted which mitigates the adverse impact on the prediction precision of redundant meteorological factors. The following conclusions are stated as follows:
• According to the analysis results of the Pearson correlation coefficient formula, the meteorological factors of total irradiance, temperature, humidity, and direct irradiance are taken as the input of the prediction model, which reduces the complexity of the prediction model and effectively avoids the redundancy of meteorological factors;
• Combined with the Pearson correlation analysis results, the Euclidean distance formula is used to calculate temporal sequence similarity to accurately screen training samples. The screened training samples accurately track the meteorological characteristics;
• The ASO-BPNN prediction model has a desirable forecasting accuracy and is competent to carry out the short-term power prediction work for this aforementioned solar farm in Yunnan.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
HC: conceptualization, writing-original draft, and formal analysis; TW: supervision, writing-review, and editing; PC: visualization and validation; WC: data curation and visualization; YC: formal analysis and software; ZL: project administration and resources.
Funding
This work was supported by China Southern Power Grid Science and Technology Project 037700KK52210022 (GDKJXM20212051).
Conflict of Interest
HC, PC, and WC are employed with the Power Grid Planning Center of Guangdong Power Grid CO., LTD, and TW is employed with the New Energy Service Center of Guangdong Power Grid CO., LTD.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Almonacid, F., Pérez-Higueras, P. J., Fernández, E. F., and Hontoria, L. (2014). A Methodology Based on Dynamic Artificial Neural Network for Short-Term Forecasting of the Power Output of a PV Generator. Energ. Convers. Manag. 85 (9), 389–398. doi:10.1016/j.enconman.2014.05.090
Almonacid, F., Rus, C., Perez, P. J., and Hontoria, L. (2009). Estimation of the Energy of a PV Generator Using Artificial Neural Network. Renew. Energ. 34 (12), 2743–2750. doi:10.1016/j.renene.2009.05.020
Benmouiza, K., and Cheknane, A. (2019). Clustered ANFIS Network Using Fuzzy C-Means, Subtractive Clustering, and Grid Partitioning for Hourly Solar Radiation Forecasting. Theor. Appl. climatology 137, 31–43. doi:10.1007/s00704-018-2576-4
Bozorg, M., Bracale, A., and Caramia, P. (2020). Bayesian Bootstrap Quantile Regression for Probabilistic Photovoltaic Power Forecasting. Prot. Control. Mod. Power Syst. 5 (3), 218–229. doi:10.1186/s41601-020-00167-7
Chang, X., Li, W., and Ma, J. (2020). “Interpretable Machine Learning in Sustainable Edge Computing: a Case Study of Short-Term Photovoltaic Power Output Prediction,” in 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (Barcelona, Spain: IEEE), 8981–8985. doi:10.1109/icassp40776.2020.9054088
Collino, E., and Ronzio, D. (2021). Exploitation of a New Short-Term Multimodel Photovoltaic Power Forecasting Method in the Very Short-Term Horizon to Derive a Multi-Time Scale Forecasting System. Energies 14 (3), 789. doi:10.3390/en14030789
Huang, N., Li, R., Lin, L., Yu, Z., and Cai, G. (2018). Low Redundancy Feature Selection of Short Term Solar Irradiance Prediction Using Conditional Mutual Information and Gauss Process Regression. Sustainability 10 (8), 2889. doi:10.3390/su10082889
Kaushika, N. D., Tomar, R. K., and Kaushik, S. C. (2014). Artificial Neural Network Model Based on Interrelationship of Direct, Diffuse and Global Solar Radiations. Solar Energy 103, 327–342. doi:10.1016/j.solener.2014.02.015
Kemmoku, Y., Orita, S., Nakagawa, S., and Sakakibara, T. (1999). Daily Insolation Forecasting Using a Multi-Stage Neural Network. Solar energy 66 (3), 193–199. doi:10.1016/S0038-092X(99)00017-1
Kudo, M., Takeuchi, A., Nozaki, Y., and Endo, H. (2009). Forecasting Electric Power Generation in a Photovoltaic Power System for an Energy Network. Electr. Eng. Jpn. l67 (4), 16–23. doi:10.1002/eej.20755
Li, R., Wong, P., and Wang, K. (2020). Power Quality Enhancement and Engineering Application with High Permeability Distributed Photovoltaic Access to Low-Voltage Distribution Networks in Australia. Prot. Control. Mod. Power Syst. 5 (3), 183–189. doi:10.1186/s41601-020-00163-x
Li, X., Li, C., and Cong, L. (2017). Short-term Load Forecasting Based on Dynamic Weight Similar Day Selection Algorithm. Power Syst. Prot. Control 45 (6), 1–8.
Liu, J., Fang, W., and Zhang, X. (2015). An Improved Photovoltaic Power Forecasting Model with the Assistance of Aerosol Index Data. IEEE Trans. Sust. Energ. 6 (2), 1–9. doi:10.1109/tste.2014.2381224
Liu, L., Liu, D., Sun, Q., Wennersten, R., and Li, H. (2017). Forecasting Power Output of Photovoltaic System Using a BP Network Method. Energ. Proced. 142, 780–786. doi:10.1016/j.egypro.2017.12.126
Lorenz, E., Hurka, J., Heinemann, D., and Hans Georg, B. (2009). Irradiance Forecasting for the Power Prediction of Grid-Connected Photovoltaic Systems. IEEE J. Selected Top. Appl. Earth Observations Remote Sensing 2 (1), 2–10. doi:10.1109/jstars.2009.2020300
Mayer, M. J., and Gróf, G. (2020). Extensive Comparison of Physical Models for Photovoltaic Power Forecasting. Appl. Energ. 283 (12), 116239. doi:10.1016/j.apenergy.2020.116239
Meenal, R., and Selvakumar, A. I. (2018). Assessment of SVM, Empirical and ANN Based Solar Radiation Prediction Models with Most Influencing Input Parameters. Renew. Energ. 121, 324–343. doi:10.1016/j.renene.2017.12.005
Netsanet, S., Zheng, D., and Zhang, W. (2022). Short-term PV Power Forecasting Using Variational Mode Decomposition Integrated with Ant colony Optimization and Neural Network. Energ. Rep. 8, 2022–2035. doi:10.1016/j.egyr.2022.01.120
Olujobi, J. O. (2020). The Legal Sustainability of Energy Substitution in Nigeria’s Electric Power Sector: Renewable Energy as Alternative. Prot. Control. Mod. Power Syst. 5 (4), 358–369. doi:10.1186/s41601-020-00179-3
Qing, X., and Niu, Y. (2018). Hourly Day-Ahead Solar Irradiance Prediction Using Weather Forecasts by LSTM. Energy 148, 461–468. doi:10.1016/j.energy.2018.01.177
Tao, Y., and Chen, Y. (2014). “Distributed PV Power Forecasting Using Genetic Algorithm Based Neural Network Approach,” in IEEE 2014 International Conference on Advanced Mechatronic Systems (ICAMechS) (Japan: IEEE), 557–560. doi:10.1109/icamechs.2014.6911608
Xue, J., and Shen, B. (2020). A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 8 (1), 22–34. doi:10.1080/21642583.2019.1708830
Yang, B., Guo, Z., Yang, Y., Chen, Y., Zhang, R., Su, K., et al. (2021). Extreme Learning Machine Based Meta-Heuristic Algorithms for Parameter Extraction of Solid Oxide Fuel Cells. Appl. Energ. 303, 117630. doi:10.1016/j.apenergy.2021.117630
Yang, B., Jiang, L., and Yao, W. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012
Yang, B., Ye, H., Wang, J., Li, J., Wu, S., Li, Y., et al. (2021). PV Arrays Reconfiguration for Partial Shading Mitigation: Recent Advances, Challenges, and Perspectives. Energ. Convers. Manag. 247, 114738. doi:10.1016/j.enconman.2021.114738
Yang, B., Zhang, M., and Zhang, X. (2020). Fast Atom Search Optimization Based MPPT Design of Centralized Thermoelectric Generation System under Heterogeneous Temperature Difference. J. Clean. Prod. 248, 119301. doi:10.1016/j.jclepro.2019.119301
Yang, B., Zhu, T., Cao, P., Guo, Z., Zeng, C., Li, D., et al. (2021). “Classification and Summarization of Solar Irradiance and Power Forecasting Methods: a Thorough Review,” in CSEE Journal of Power and Energy Systems (Beijing: CSEE), 1–19. doi:10.17775/CSEEJPES.2020.04930
Yildiz, B., Bilbao, J. I., and Sproul, A. B. (2017). A Review and Analysis of Regression and Machine Learning Models on Commercial Building Electricity Load Forecasting. Renew. Sustain. Energ. Rev. 73, 1104–1122. doi:10.1016/j.rser.2017.02.023
Zhang, K., Zhou, B., and Or, S. W. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Industry Appl. 58, 2728–2739. doi:10.1109/TIA.2021.3093841
Keywords: solar energy short-term forecasting, backpropagation neural network, ASO-BPNN algorithm, Pearson correlation coefficient, PV power generation
Citation: Cao H, Wang T, Chen P, Cheng W, Cao Y and Liu Z (2022) Solar Energy Forecasting in Short Term Based on the ASO-BPNN Model. Front. Energy Res. 10:902486. doi: 10.3389/fenrg.2022.902486
Received: 23 March 2022; Accepted: 08 April 2022;
Published: 13 May 2022.
Edited by:
Yaxing Ren, University of Warwick, United KingdomReviewed by:
Yixuan Chen, The University of Hong Kong, Hong Kong SAR, ChinaKai Shi, University of Warwick, United Kingdom
Copyright © 2022 Cao, Wang, Chen, Cheng, Cao and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peidong Chen, Nzk4NTk3OTA5QHFxLmNvbQ==
 Huazhen Cao1
Huazhen Cao1 Peidong Chen
Peidong Chen Weitian Cheng
Weitian Cheng