- Department of Electrical Engineering, School of Automation, Guangdong University of Technology, Guangzhou, China
With the flexible integration of local renewable energy with the smart distribution network system, the problems of high operating costs and power shortage can be effectively solved. However, taking the industrial park microgrid with high penetration photovoltaic as an example, due to the uncertainties and fluctuations arising from the meteorological conditions and the load demands, the safe and reliable operation of the microgrid system has been threatened significantly. Operators often need to pay additional unnecessary costs to maintain stable operations of the microgrid. Therefore, in this study, a dispatch strategy based on robust model predictive control considering low-carbon cost is designed to reduce the adverse effects of uncertainties. First, a low-carbon energy management scheme is formulated based on short-term source and load forecast information in which a two-stage robust optimization solution method is used to generate the optimal dispatch scheme under the worst scenario. Then, an intraday real-time strategy with a closed-loop feedback mechanism is formed based on the model predictive control. Finally, the feasibility of the proposed strategy is simulated and analyzed based on the measured data of the photovoltaic microgrid in the industrial park. The results show that compared with the general intraday scheduling strategy and the day-ahead robust strategy, the proposed strategy can effectively get low-carbon scheduling plans considering the uncertainty of source and load while efficiently balancing the robustness and economy of the grid-connected industrial park photovoltaic microgrid system operation.
1 Introduction
Decentralization and low-carbon energy reformation are promoted continuously with the increasing scale and intricate operating conditions of modern power grids (Basak et al., 2012; Morstyn et al., 2018). As a single modular system, the microgrid (MG) can flexibly dispatch distributed generation (DG) such as photovoltaics (PVs) and wind turbines (WTs) to provide power for its regional load demand (Alipour et al., 2015; Zia et al., 2018). Compared with the traditional distribution network, the electrical distance between generator units and the consumers is much closer, which can increase power quality and economic benefits. Because of the plug-and-play characteristics of these distributed devices, microgrids are considered the foundation for further expansion of the power grids.
Microgrid operators are management platforms responsible for energy flow within the region, which need to consider the principles of profitability while ensuring the balance of power supply and demand in the whole region (Zhou et al., 2021). However, due to the uncertainties of meteorological conditions and load demands, it is difficult for microgrid operators to use accurate forecast information to formulate scheduling plans (Kou et al., 2018). Therefore, microgrid operators need to use a more appropriate dispatch strategy in their energy management system (EMS) to ensure the normal and stable operation of the microgrid (Raya-Armenta et al., 2021). At the same time, to achieve the objective of low-carbon environmental protection, various regions have begun to implement carbon trading policies aiming to meet the carbon indexes. In addition to purchasing electricity from the main grid, large-scale consumers of the distribution network can also trade carbon to deal with the rest of carbon consumption apart from allocated carbon indexes (Lu et al., 2013). Therefore, the low-carbon dispatch operation of microgrids also needs further improvement.
The microgrid in the industrial park is dominated by industrial loads, which have the characteristics of large load demand and higher requirement of power supply reliability (Yu et al., 2016). To minimize the operating cost, the traditional day-ahead dispatch strategy can make an economic optimal dispatch plan based on the forecast data. However, these strategies lack consideration of uncertainty in actual operation; it is tough to make timely and rational adjustments, which leads to a higher requirement for the accuracy of the prediction model of renewable sources and load. On the other hand, operators need to pay extra costs for forecast deviations due to sudden uncertain fluctuations and tolerate the damage of power balance and the safe operation.
Therefore, in order to adapt to the dynamic characteristics of various devices in the microgrid, various types of scheduling strategies have been designed in various literature studies to cope with different uncertain information (Yang and Su, 2021). Robust optimization (RO) strategy ensures the stable operation of the microgrid in a complex operating environment by finding the worst scenario for the scheduling plan (Liu et al., 2020; Choi et al., 2019). In Liu et al. (2020), a two-stage robust model is proposed for an integrated power–heat–gas microgrid to achieve the optimal day-ahead economic scheduling considering the uncertainty of wind power scenarios. In Li et al. (2021a), a data-driven set–based robust optimization (DSRO) model considering the uncertainties of wind power and multiple demand response programs (DRPs) has been proposed, and a combined cooling, heating, and power (CCHP) microgrid with the power-to-gas (P2G) device is used to verify its feasibility. In Choi et al. (2019), the robust optimal control strategy for an energy storage system (ESS) of a grid-connected microgrid is proposed. The mixed-integer linear programming and the non-linear efficiency map method are considered to cope with different external conditions. These aforementioned studies effectively improve the safety margin and robustness of scheduling plan through RO strategy. However, these strategies are still day-ahead scheduling strategies, which are limited by insufficient flexibility in operation. Meanwhile, on account of the requirements to consider the amount of information throughout the whole day, the computational burden on the central controller will be aggravated.
Model predictive control (MPC) utilizes the idea based on closed-loop rolling optimization to respond to the fluctuation of renewable energy and realize adaptive optimization with the time rolls (Li et al., 2018; Wu et al., 2021). In Li et al. (2018), a multi-time scale–based three-layer coordination optimal scheduling system is designed. In Garcia-Torres and Bordons (2015), a control strategy using MPC for renewable energy microgrids with hybrid ESS is proposed in which the MPC is built within the market framework in different time scales to maximize the economic benefit of the microgrid. A multi-renewable-to-hydrogen production method is proposed to enhance the green H2 production efficiency in Zhang et al. (2022), and a hierarchical coordinated control strategy is also developed based on MPC to suppress high fluctuations in electrolysis current caused by uncertainty from PV and WT. In summary, the optimal scheduling strategy based on MPC intraday strategy can effectively deal with the uncertainty of renewable energy. However, the aforementioned literature is more inclined toward constructing the intraday rolling strategy, and there are few descriptions of the MPC feedback module, which is an essential means to deal with the uncertainty of renewable energy. With the increasing penetration of renewable energy, the effectiveness and the advantage of the strategy will be reduced.
An online optimal operation approach for CCHP microgrids based on MPC with feedback correction to compensate for prediction error was proposed in Gu et al. (2017a). Moreover, as a flexible framework based on the combination of multiple modules with different time scales, MPC provides the feasibility of its combination with a variety of traditional optimization strategies (Cai et al., 2020). An optimal scheduling model considering the demand responses is proposed in Zhang et al. (2021) in which a multi-time scale economic scheduling method based on day-ahead robust optimization and intraday MPC is designed. A battery/flywheel hybrid ESS stochastic model predictive control (SMPC) method is proposed in He et al. (2022) to improve the automatic generation control performance of thermal power units in which a scenario tree generation approach is proposed to simulate operation scenario. In Wu et al. (2021), the results of multiple uncertainty samplings are used to simulate the future characteristics of aggregated electric vehicles, and a two-layer strategy framework is proposed for the optimization issue. These studies provide some methods for further combating the uncertainty of renewable energy, but the analysis and processing of uncertain data are focused on the day ahead or before the optimization. Therefore, it results in the online optimization stage of MPC still aiming at the pursuit of economy alone, which has the lack of flexibility to deal with real-time changing operating scenarios.
Therefore, in order to better cope with the impact of uncertainty from high penetration of renewable energy and load demand and further flexibly balance the robustness and economy of the microgrid online dispatch plan, a dispatch strategy for the photovoltaic microgrid in an industrial park is designed based on low-carbon robust model predictive control (RMPC) in this study. First, the dynamic model and cost function of operation is built and the two-stage RO method is used to find the low-carbon scheduling scheme under the worst scenario considering uncertainty, where the introduction of the carbon index cost target makes the environmental protection and economy of the microgrid are further comprehensively considered. Second, the feedback mechanism based on MPC is designed to respond to the fluctuation of PV in an ultra-short term time scale, which effectively combats the uncertainty of renewable energy. Finally, the MPC strategy framework is used to form the intraday scheduling plan of the microgrid, which can balance the robustness and economy of the microgrid by combining the RO and MPC strategy. Moreover, the feasibility and effectiveness of the proposed RMPC strategy are verified by simulation experiments.
2 Dynamic Model of the Photovoltaic Industrial Park Microgrid
2.1 Typical Photovoltaic Microgrid Structure
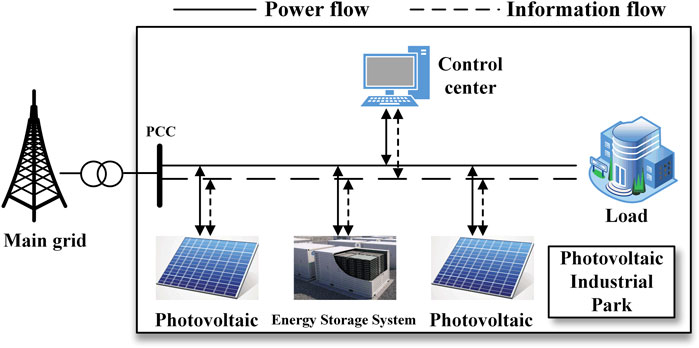
Figure 1 shows a typical structure of the microgrid in a photovoltaic industrial park. The park is connected to the main grid through the point of common coupling (PCC); thus, stable electricity power can be purchased from the main grid to meet the large load demand. A large number of distributed PV generation units are built to obtain the renewable energy, and surplus or lack of electrical energy can be stored or released in an energy storage system (ESS). As an important auxiliary power device, ESS can handle excess renewable energy in time, which simultaneously takes into account both economy and stability of the system. Moreover, the dispatch plan and control operation of the microgrid will be formulated and sent by the control center. It should be noted that despite the existence of different devices to obtain power, renewable energy like PV is hopefully used in priority by operators meeting the load considering the electricity price and low-carbon objective.
2.2 Deterministic Dynamic Model
The deterministic power generation unit in the microgrid can provide stable and high-quality electricity power, such as generator, ESS, and the power from the main grid. The dynamic model of the devices based on the proposed background is as follows:
Eq. 1 represents the power transaction between the microgrid and the main grid in which the value of the traded power at
In order to reduce integer variables during optimization, an intermediate variable
where
Moreover, the operating constraints are as follows:
Eq. 6 is the limit constraints representing the PCC tie-line power limitation and the energy storage constraint, respectively. In order to ensure that the microgrid system can switch to the island operation mode at any time,
2.3 Uncertainty Dynamic Model
Uncertain equipment in the microgrid refers to the renewable energy generation units and loads with volatility and uncertainty. In this study, the high penetration of the PV is the main reason to cause a great challenge to the safe and stable operation of the microgrid, where the dispatching scheme did not match the actual power output. The uncertainty model is described as follows:
Equation 9 represents the uncertainty model of the PV and load.
where
3 Low-Carbon Robust Predictive Dispatch Strategy
3.1 Low-Carbon Optimization Layer
As mentioned in the introduction, the MPC strategy incorporates the idea of rolling optimization, which can be more flexibly integrated with other algorithms reasonably. Therefore, the original optimal economic problem in MPC is transformed into a “min–max–min” robust optimization problem to obtain the robust scheduling plan under the worst scenario.
Equation 12 represents the objective function of the microgrid in the optimization layer;
Under the robust uncertainty model in Eq. 11, the primary goal of operation in microgrid remains economic while meeting both the supply and demand balance and a certain degree of robustness, and the microgrid operation cost is shown in Eq. 14, Eq. 15.
To be specific, Eq. 13 indicates the carbon emission cost. In the industrial park, the microgrid needs to undertake the purchase of carbon emission quotas mainly based on CO2. In Eq. 13,
To mobilize the enthusiasm of all power generation units and prevent the damage to the battery caused by the excessive or low energy storage, the relationship between the charging/discharging cost coefficient and the remaining energy of the ESS is shown in Eq. 15.
From the aforementioned equations, after converting Eqs 1–15 into the standard form of robust optimization, Eq. 12 can be solved by a two-stage robust optimization problem based on the column constraint generation (C&CG) algorithm. The main problem is described as follows:
The constraints from Eqs 6–8 can be written as the standard constraint expression in Eq. 16.
On the other hand, the strong duality theory is used to linearize the constraints in the subproblem, which the hard-to-solve “max–min” optimization problem in the subproblem is transformed into a “max” problem. This transformed Lagrange dual problem is shown in Eq. 17:
Finally, the optimization problem iterates between the two subproblems until the optimal scheduling plan is found even in the worst scenario which is still feasible. The whole process is shown in Figure 2.
3.2 Robust Model Predictive Control Rolling Layer
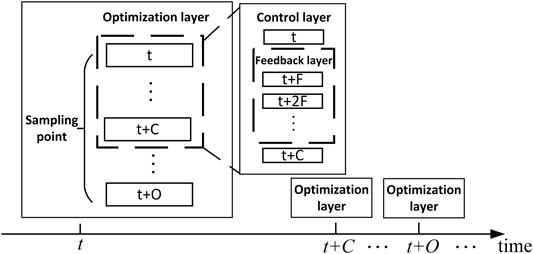
The intraday scheduling strategy based on rolling optimization rolls forward with time in a day. The RMPC framework based on time flow is shown in Figure 3.
In Figure 3, the RMPC framework is divided into three stages. First, the time horizon for the optimization layer is from
3.3 Low-Carbon Robust Model Predictive Control Feedback Layer
In the optimization layer, the robust optimization ensures the feasibility of the schedule plan in the worst scenario, but the problem solved without predicted data has a certain probability that it may not match the real operation conditions of the microgrid. Therefore, in a shorter time scale, the feedback mechanism of MPC is used to form a closed-loop control system that can timely forecast the predictive deviation of the uncertain information and make a response. The feedback mechanism is divided into two stages: the prediction correction and the output correction.
In the prediction correction module, the actual output value in the past is collected for feedback, and then the prediction output in an ultra-short term will be corrected. In other words, when the latest actual output is obtained at a certain feedback sampling point, the prediction module in the feedback layer will update the predicted variation of the renewable energy output at the next feedback point. At the same time, the prediction model is also revised to obtain more accurate planning in the next optimization stage. Such prediction model is generally obtained by the gray model or neural network. This study selects the wavelet decomposition convolutional neural networks (WDCNN) to form the prediction model which is widely used in prediction research (Li et al., 2021b; Yan et al., 2021).
The corrected prediction output will be sent to the output correction module. Under the ultra-short time scale, the overloaded tie lines may suffer excess uncertainty fluctuations if there is no protective action in the schedule plan, and it will pose a great threat to the safe operation of the microgrid. Therefore, the redistribution principle in the output correction module is designed, which is more inclined to the safe operation than the pursuit of economy. Therefore, the minimum pressure of the remaining power generation capacity of each equipment is regard as the goal shown in Eq. 18, (Zhao et al., 2021). The dispatch plan will be adjusted in the ultra-short time scale based on the predicted values.
In Eq. 18,
4 Simulation Results
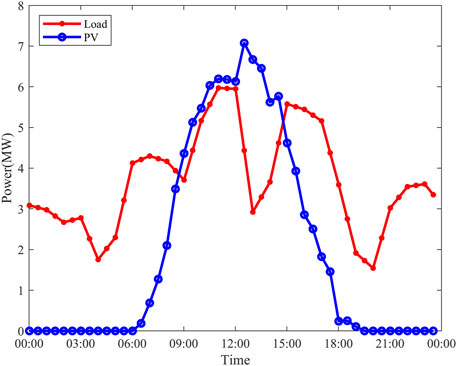
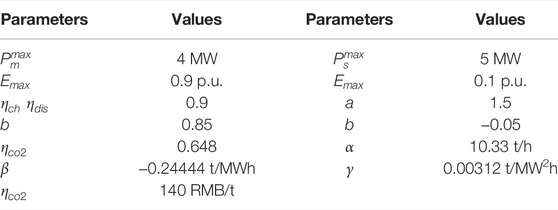
This study takes a typical industrial park photovoltaic microgrid as an example, and the microgrid will be operated within a day through the RMPC strategy proposed. Figure 4 shows the forecast curves of PV and load for a typical day with a time interval of 30 min. In the simulation environment with MATLAB 2019a, we set the rolling layer
4.1 Feasibility Analysis of Robust Model Predictive Control Strategy
Figure 6 shows the scheduling scheme of the photovoltaic microgrid in the industrial park using the proposed RMPC strategy. The uncertainty coefficients of photovoltaic and load in Eq. 11 are both four, which is the moderate value of robust expectation. The allowable ranges of prediction error in Eq. 10 are both 5%. The operation goal of the microgrid in industrial parks is to achieve internal supply and demand balance and can maintain stable operation even if the forecast data has errors. That is the significance of introducing a robust optimization mechanism.
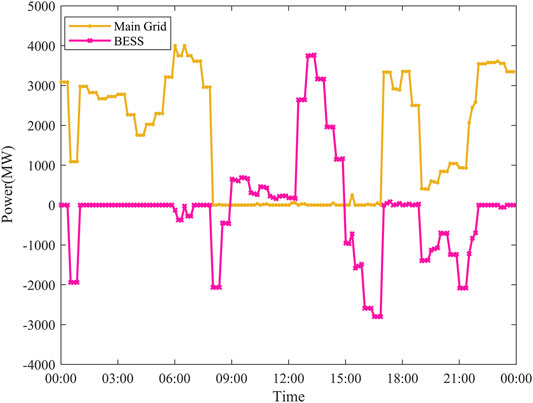
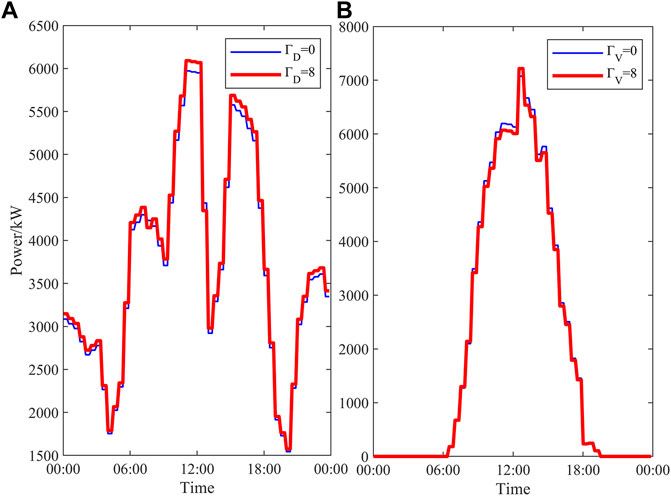
As shown in Figure 4, although the power output from PV has a strong arch-shaped output law in a day, the shortcomings of this are also obvious. With the lack of sunlight, the PV has little output in the morning and evening. It makes the microgrid to purchase a large amount of power from the main grid and use the BESS as an auxiliary power output device to meet the large load demand.
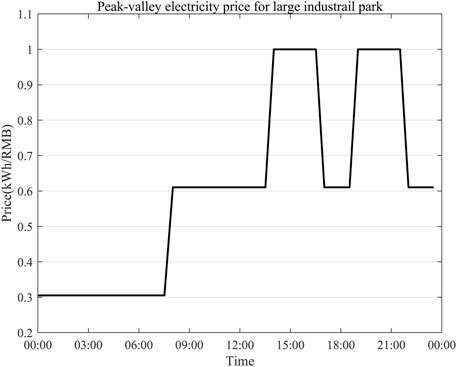
For example, as shown in Figure 6, from 0:00 a.m. to 6:00 a.m., there is no energy output from PV. Therefore, the load is nearly satisfied by the power purchased from the main grid considering the economy because of the lowest electricity price in the whole day, and the BESS is scheduled to contribute energy as little as possible. After that, the PV starts to generate electric power, and the electrical price of the main grid reaches the parity zone. Therefore, the power balance will be met by the BESS from 8:00 a.m. to 10:00 a.m. From 10:00 a.m. to 3:00 p.m., the PV reaches its peak period, which could promptly replenish the BESS by the surplus energy. It makes it possible to avoid the expensive period of electricity price in the afternoon while satisfying the self-sufficiency expectation of renewable energy in the industrial park. The proposed strategy efficiently improves the economy of the photovoltaic microgrid in industrial parks.
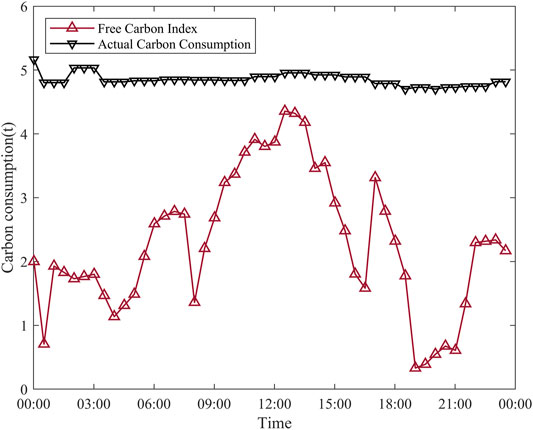
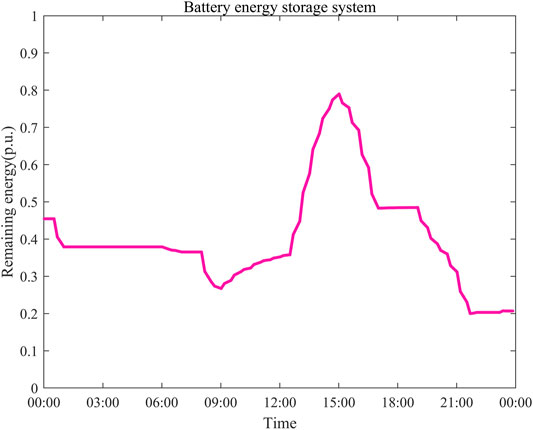
Figure 7 shows the changing curves of the carbon index and carbon consumption in the microgrid. Due to the added carbon index in the optimization goal, the power purchased from the main grid is more restrained. Thus, the microgrid is encouraged to consider larger-scale renewable energy sources in the projecting stage to increase their advantage in the future carbon index trading market. And the application of the carbon index could also meet the environmental protection targets and low-carbon operating goals reasonably for the photovoltaic microgrid in the industrial park. Furthermore, Figure 8 shows the change of the energy storage in the BESS. Except for periods when renewable energy is extremely abundant, the power storage in ESS can always maintain a healthy value for system operation, even it has fluctuation.
4.2 Effectiveness Analysis for Strategy Considering Uncertainty
As mentioned in Section 3.3, while the robust dispatch scheme satisfies the basic requirements of the economic operation, the feedback mechanism in MPC is proposed to avoid the damage to the stable operation of the microgrid caused by the error of the prediction information.
The ability to fight the uncertainty of input information depends on the accuracy of the correction model. Therefore, the proposed rolling feedback mechanism based on historical and real-time data can make the error correction curve under the ultra-short time scale closer to the actual output situation. Secondly, in the proposed output correction module, due to the setting of the redistribution objective in Eq. 18, the output adjustment pressure of the equipment is fairly distributed to each controllable power generation beforehand. Thereby, it could improve the safety margin of the operation (Zhao et al., 2021).
The calculation results of the average relative error of the net load (Gu et al., 2017b) are shown in Figure 9. It can be seen from Figure 9 that the error calculation result based on the MPC strategy is obviously better than the rolling optimization strategy which pursues the economy completely. This is because the introduction of the feedback mechanism makes the prediction curve closer to the actual one, and the relative prediction error naturally decreases. However, it can be also found from Figure 9 that the relative error value increases slightly with the RMPC strategy compared with the MPC strategy. This is because the worst-case scenario predicted by robust optimization is not based on the actual data, but rather on the operating state of the devices. Therefore, it does not necessarily match the actual operation scenario, which may lead to more operation errors.
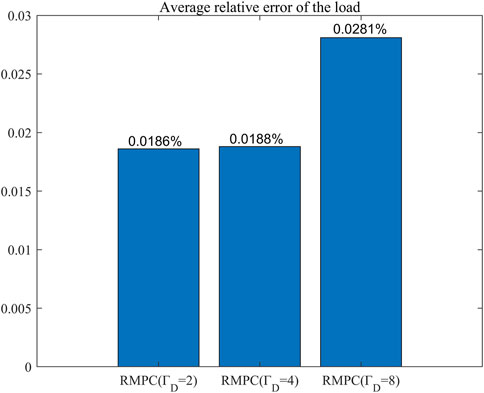
Figure 10 shows the average relative error of the load under the uncertainty model compared with the day-ahead forecast value of load which
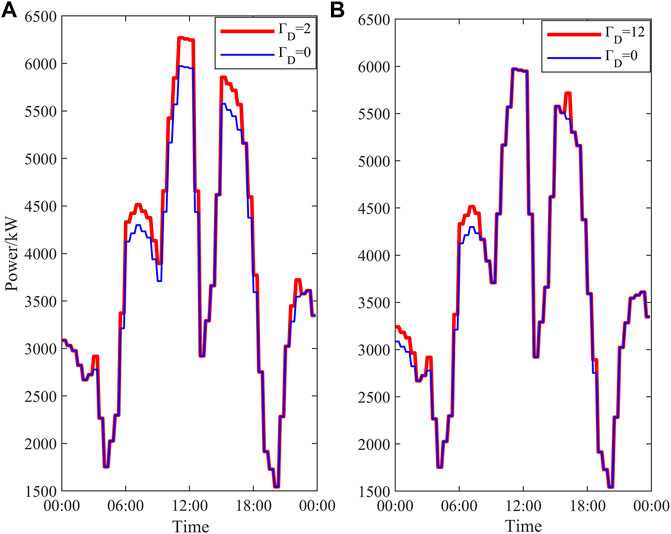
If it is assumed that these points that are forced to deviate are called robust point, the case with the most robust points (
Figure 12 shows the worst scenario for day-ahead RO and rolling RO with the same ratio of uncertainty degree. Taking
4.3 Economic Analysis
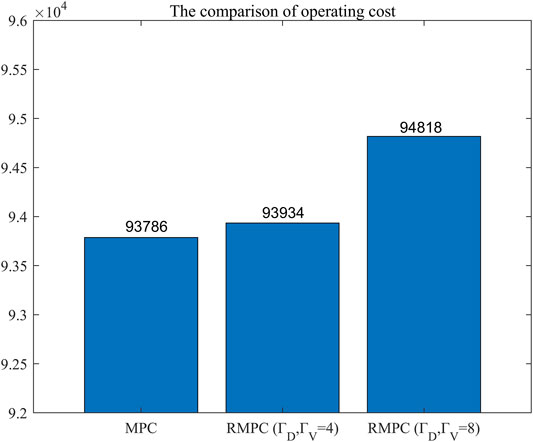
Since the intraday scheduling scheme is a real-time optimization strategy that rolls with the time flow, the uncertainty degree of the system can be flexibly adjusted. Compared with the day-ahead robust optimization strategy, the worst scheduling scenario is just for the short-term period, which has greater operability and accuracy. At the same time, RO and MPC strategies can respond to the uncertainty of renewable energy at different time scales, respectively. But this ability has to pay the cost of certain economic losses, as shown in Figure 13, which is the comparison of the cost with different strategy and uncertainty degree. Compared with the RMPC strategy, the MPC strategy pursues cost minimization in the short-term scheduling stage, so that the total cost can be kept lower.
And it can be seen from Figure 13 that with the increase of uncertainty degree, the economy gradually decreases. From the change of
These also confirm what we discussed in the previous section, robustness and economy of the operation of the microgrid are two opposite directions that operators cannot get both at the same time. The prevention of the worst-case scenario in exchange for part of economic losses can make the microgrid with a high proportion of renewable energy access more reliable.
Moreover, if the operator wants to eliminate the impact of robust optimization on economy, they can consider increasing the benefits of microgrid operations in other aspects, such as power transactions, cooperation with other microgrids, electricity price games between operators and users, etc. In short, how to balance risks and benefits depends on the operator’s thoughts and their operation goals for microgrids in the region. The proposed RMPC strategy can flexibly balance the robustness and economy of PV microgrid operation in industrial parks, which gives operators more options to achieve their desired microgrid management target.
5 Conclusion
This study proposes a low-carbon robust predictive dispatch strategy for a photovoltaic microgrid in industrial parks, which combines the advantages of robust optimization strategy and MPC strategy. Based on establishing the dynamic model of power generation equipment and the uncertainty model of renewable energy and load, an energy management strategy based on RMPC is designed for the photovoltaic microgrid. The proposed strategy ensures the independent and stable operation of the microgrid and has the ability to combat the uncertainty through two-stage robust optimization method and an MPC feedback mechanism at different time scales. These two methods cooperate with each other and improve both robustness and the safe operation of the microgrid at the expense of part of the economy. At the same time, due to the characteristics of the real-time strategy, the uncertainty degree is adjustable, which allows operators to balance robustness and economy more flexibly. In addition, the introduction of the carbon index mechanism effectively increases the inhibition of the use of polluting energy. Thus, the operators have to consider the environmental cost while pursuing the operation economy so as to achieve the goal of low carbon emissions. Finally, simulations using real data are carried out to verify the effectiveness of the proposed strategy. By comparing with other strategies, the characteristics of the proposed strategy are analyzed, which provides an important reference for the application and further development of this strategy.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Conceptualization and methodology: ZZ; software: JG and SG; modeling: JG, and JX; formal analysis: JG and XL; validation: JG, JW and QY; writing—original draft preparation: JG and ZZ; writing review and editing: ZZ and LL; supervision: ZZ; and project administration: ZZ.
Funding
This work was supported by the National Natural Science Foundation of China 51907031; Guangdong Basic and Applied Basic Research Foundation (Guangdong-Guangxi Joint Foundation) 2021A1515410009.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alipour, M., Mohammadi-Ivatloo, B., and Zare, K. (2015). Stochastic Scheduling of Renewable and CHP-Based Microgrids. IEEE Trans. Ind. Inf. 11 (5), 1049–1058. doi:10.1109/TII.2015.2462296
Basak, P., Chowdhury, S., Halder nee Dey, S., and Chowdhury, S. P. (2012). A Literature Review on Integration of Distributed Energy Resources in the Perspective of Control, protection and Stability of Microgrid. Renew. Sustain. Energ. Rev. 16 (8), 5545–5556. doi:10.1016/j.rser.2012.05.043
Cai, S., Xie, Y., Wu, Q., and Xiang, Z. (2020). Robust MPC-Based Microgrid Scheduling for Resilience Enhancement of Distribution System. Int. J. Electr. Power Energ. Syst. 121 (2), 106068. doi:10.1016/j.ijepes.2020.106068
Choi, J., Shin, Y., Choi, M., Park, W.-K., and Lee, I.-W. (2019). Robust Control of a Microgrid Energy Storage System Using Various Approaches. IEEE Trans. Smart Grid 10 (3), 2702–2712. doi:10.1109/TSG.2018.2808914
Garcia-Torres, F., and Bordons, C. (2015). Optimal Economical Schedule of Hydrogen-Based Microgrids with Hybrid Storage Using Model Predictive Control. IEEE Trans. Ind. Electron. 62 (8), 5195–5207. doi:10.1109/TIE.2015.2412524
Gu, W., Wang, Z., Wu, Z., Luo, Z., Tang, Y., and Wang, J. (2017). An Online Optimal Dispatch Schedule for Cchp Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 8 (5), 2332–2342. doi:10.1109/TSG.2016.2523504
Gu, W., Wang, Z., Wu, Z., Luo, Z., Tang, Y., and Wang, J. (2017). An Online Optimal Dispatch Schedule for CCHP Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 8 (5), 2332–2342. doi:10.1109/TSG.2016.2523504
He, J., Shi, C., Wei, T., and Jia, D. (2022). Stochastic Model Predictive Control of Hybrid Energy Storage for Improving Agc Performance of thermal Generators. IEEE Trans. Smart Grid 13 (1), 393–405. doi:10.1109/TSG.2021.3111610
Kou, P., Liang, D., and Gao, L. (2018). Stochastic Energy Scheduling in Microgrids Considering the Uncertainties in Both Supply and Demand. IEEE Syst. J. 12 (3), 2589–2600. doi:10.1109/JSYST.2016.2614723
Li, Y., Fan, X., Cai, Z., and Yu, B. (2018). Optimal Active Power Dispatching of Microgrid and Distribution Network Based on Model Predictive Control. Tinshhua Sci. Technol. 23 (3), 266–276. doi:10.26599/TST.2018.9010083
Li, Y., Zhang, F., Li, Y., and Wang, Y. (2021). An Improved Two-Stage Robust Optimization Model for Cchp-P2g Microgrid System Considering Multi-Energy Operation under Wind Power Outputs Uncertainties. Energy 223, 120048. doi:10.1016/j.energy.2021.120048
Li, Z., Li, Y., Liu, Y., Wang, P., Lu, R., and Gooi, H. B. (2021). Deep Learning Based Densely Connected Network for Load Forecasting. IEEE Trans. Power Syst. 36 (4), 2829–2840. doi:10.1109/TPWRS.2020.3048359
Liu, Y., Ye, Y., Chen, X., Li, H., and Huang, Y. (2020). Robust Day-Ahead Dispatch for Integrated Power-Heat-Gas Microgrid Considering Wind Power Uncertainty. Math. Probl. Eng. 2020, 1–12. doi:10.1155/2020/4215906
Lu, S., Lou, S., Wu, Y., and Yin, X. (2013). Power System Economic Dispatch under Low‐carbon Economy with Carbon Capture Plants Considered. IET Generation, Transm. & Distribution 7, 991–1001. doi:10.1049/iet-gtd.2012.0590
Morstyn, T. B., Hredzak, B., and Agelidis, V. G. (2018). Control Strategies for Microgrids with Distributed Energy Storage Systems: an Overview. IEEE Trans. Smart Grid 9 (4), 3652–3666. doi:10.1109/TSG.2016.2637958
Parisio, A., Rikos, E., and Glielmo, L. (2014). A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Contr. Syst. Technol. 22 (5), 1813–1827. doi:10.1109/TCST.2013.2295737
Raya-Armenta, J. M., Bazmohammadi, N., Avina-Cervantes, J. G., Sáez, D., Vasquez, J. C., and Guerrero, J. M. (2021). Energy Management System Optimization in Islanded Microgrids: An Overview and Future Trends. Renew. Sustain. Energ. Rev. 149 (4), 111327. doi:10.1016/j.rser.2021.111327
Saber, A. Y., and Venayagamoorthy, G. K. (2011). Plug-In Vehicles and Renewable Energy Sources for Cost and Emission Reductions. IEEE Trans. Ind. Electron. 58 (4), 1229–1238. doi:10.1109/TIE.2010.2047828
Wu, C., Gao, S., Liu, Y., Song, T. E., and Han, H. (2021). A Model Predictive Control Approach in Microgrid Considering Multi-Uncertainty of Electric Vehicles. Renew. Energ. 163, 1385–1396. doi:10.1016/j.renene.2020.08.137
Yan, J., Hu, L., Zhen, Z., Wang, F., Qiu, G., Li, Y., et al. (2021). Frequency-Domain Decomposition and Deep Learning Based Solar PV Power Ultra-short-term Forecasting Model. IEEE Trans. Ind. Applicat. 57 (4), 3282–3295. doi:10.1109/TIA.2021.3073652
Yang, J., and Su, C. (2021). Robust Optimization of Microgrid Based on Renewable Distributed Power Generation and Load Demand Uncertainty. Energy 223 (6), 120043. doi:10.1016/j.energy.2021.120043
Yu, N., Kang, J.-S., Chang, C.-C., Lee, T.-Y., and Lee, D.-Y. (2016). Robust Economic Optimization and Environmental Policy Analysis for Microgrid Planning: an Application to Taichung Industrial Park, Taiwan. Energy 113, 671–682. doi:10.1016/j.energy.2016.07.066
Zhang, J., Qin, D., Ye, Y., He, Y., Fu, X., Yang, J., et al. (2021). Multi-Time Scale Economic Scheduling Method Based on Day-Ahead Robust Optimization and Intraday Mpc Rolling Optimization for Microgrid. IEEE Access 9, 140315–140324. doi:10.1109/ACCESS.2021.3118716
Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. (2022). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat. 58 (2), 2728–2739. doi:10.1109/TIA.2021.3093841
Zhao, Z., Guo, J., Lai, C. S., Xiao, H., Zhou, K., and Lai, L. L. (2021). Distributed Model Predictive Control Strategy for Islands Multimicrogrids Based on Noncooperative Game. IEEE Trans. Ind. Inf. 17 (6), 3803–3814. doi:10.1109/TII.2020.3013102
Zhou, B., Zou, J., Yung Chung, C., Wang, H., Liu, N., Voropai, N., et al. (2021). Multi-Microgrid Energy Management Systems: Architecture, Communication, and Scheduling Strategies. J. Mod. Power Syst. Clean Energ. 9 (3), 463–476. doi:10.35833/MPCE.2019.000237
Keywords: microgrid, feedback mechanism, robust optimization, rolling optimization, low-carbon dispatching
Citation: Guo J, Gong S, Xie J, Luo X, Wu J, Yang Q, Zhao Z and Lai LL (2022) Low-Carbon Robust Predictive Dispatch Strategy of Photovoltaic Microgrids in Industrial Parks. Front. Energy Res. 10:900503. doi: 10.3389/fenrg.2022.900503
Received: 20 March 2022; Accepted: 08 April 2022;
Published: 22 July 2022.
Edited by:
Bin Zhou, Hunan University, ChinaCopyright © 2022 Guo, Gong, Xie, Luo, Wu, Yang, Zhao and Lai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhuoli Zhao, emh1b2xpLnpoYW9AZ2R1dC5lZHUuY24=
 Juntao Guo
Juntao Guo Zhuoli Zhao
Zhuoli Zhao Loi Lei Lai
Loi Lei Lai