Improving Parameter Estimation of Fuel Cell Using Honey Badger Optimization Algorithm

In this study, we proposed an alternative method to determine the parameter of the proton exchange membrane fuel cell (PEMFC) since there are multiple variable quantities with diverse nonlinear characteristics included in the PEMFC design, which is specified correctly to ensure effective modeling. The distinctive model of FCs is critical in determining the effectiveness of the cells’ inquiry. The design of FC has a significant influence on the simulation research of such methods, which have been used in a variety of applications. The developed method depends on using the honey badger algorithm (HBA) as a new identification approach for identifying the parameters of the PEMFC. In the presented method, the minimal value of the sum square error (SSE) is applied to determine the optimal fitness function. A set of experimental series has been conducted utilizing three datasets entitled 250-W stack, BCS 500-W, and NedStack PS6 to justify the usage of the HBA to determine the PEMFC’s parameters. The results of the competitive algorithms are assessed using SSE and standard deviation metrics after numerous independent runs. The findings revealed that the presented approach produced promising results and outperformed the other comparison approaches.

1 Introduction

The technology of the fuel cell (FC) is an essential energy exporter due to its extraordinary production and reduced carbon effects. Also, in contrast to wind and photovoltaic power origins, the production of power from the FC is autonomous of the climatologic conditions. Thus, it can be used for perpetual power generation. Different models of the FC are revealed; their system is carried out based on the characteristics of the electrolyte applied. Among the numerous types of FCs are the chemical-based FC approach (CFC) (McLean et al., 2002), PEMFC (Eisman, 1989), solid-based oxide FC (SOFC) (Kawada et al., 1990), etc. One of the most well-known types of FCs is the PEMFC. Their active start is recognized because of their economic temperature and yield ranging between 30 and 60%. The PEMFCs are utilized in different disciplines (Messaoud et al., 2021). The escalating cost of human energy has a hazardous impression on the atmosphere. Electricity requirements contribute primarily to ecological degeneration while consuming nonrenewable supplies (Nain et al., 2021). The portion of renewable electricity from the universal energy production is 26% approximately. Various varieties of power references for providing hydrogen exist. Now, most of the hydrogen composition is generated by solar power (37%) and comes behind conventional fossil fuel (26%), as shown in Figure 1 (Fathy et al., 2020b). These H2 results guide to reasonable prices and more critical appropriate solutions via hydrogen in the real world (Kayfeci et al., 2019).

FIGURE 1

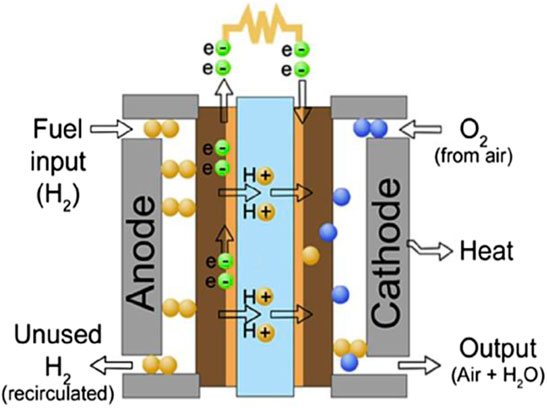
FIGURE 1. PEMFC arrangement (Famouri and Gemmen, 2003).

FC-based energy production methods can meet the anticipations of very low emanations and comparatively high conductivity (Mo et al., 2006). FC is characterized by more economical contamination and more extraordinary performance than traditional power origins; however, they have an excellent dynamic reaction, sound balance, and moderate noise (Ramos-Paja et al., 2010). Between several systems of FCs, because of their approximately low running temperature, quick reaction, small volume, high popular mass, no loss, and in case of explicit hydrogen zero emission is generated, PEMFC can be an excellent option for energy-producing origins in the future, particularly in the automation applications, shared power production, and transferable photoelectric applicability (Askarzadeh and Rezazadeh, 2011).

Despite substantial advancements in the previous few years, the financial performance of PEMFCs is still a point of contention among support and opposition (Alizadeh and Torabi, 2021). The improvement of PEMFC performance is critical for the marketing of the technology and achieving significant market adoption (Kahraman and Orhan, 2017). Generally, the performance of the FC is regarded as the essential aspect of end-user acceptability (J. Wang et al., 2018). Many published articles show that numerous structural and operational factors (parameters) highly influence the performance of the PEMFC. The most efficient methods that have successfully proved their ability to extract the parameters are the optimization methods (Eid et al., 2021; Hassan et al., 2021; Wang et al., 2021). This field still needs further investigation to find a more efficient approach to tackle this problem.

As presented in the relevant studies, Priya et al. (2015) presented a unique presentation for the efficient estimation of FC parameters. The parameters’ values of FC were determined based on the genetic algorithm, and the obtained results proved its ability to find better results than several other methods in this domain. İnci and Caliskan(2020) proposed a new enhanced energy extraction-based optimization method to tackle the FC parameters. The presented technique is based on using an improved cuckoo optimizer. The proposed technique achieved better convergence acceleration than traditional techniques. Kandidayeni et al. (2019) used several optimization techniques to solve PEMFC. The proposed method reduced squared errors among the included and measured voltage for two possible test cases. The proposed SFLA method got better results in terms of precision and repeatability than the other comparative methods.

Fathy et al. (2020a) introduced a hybrid of differential evolution and vortex search algorithms for determining the optimum parameters of the FC, called VSADE. The achieved results established the superiority of the introduced VSADE method. This study aimed to provide a new, simpler, and accurate model of the proton electrolyte membrane FC (Seleem et al., 2021). The suggested approach drastically lowers the number of unknown factors in such models, resulting in a more straightforward model. It discloses just four design factors within the model in this regard. This model’s great effectiveness is tested both in steady-state and dynamic operating situations. It is possible to build a highly exact PEMFC model using the suggested approach. Menesy et al. (2020) suggested an enhanced artificial ecosystem optimizer to determine the problem of the FC parameters. According to the results, it is proved that the presented optimizer has high performance in obtaining the optimal parameters compared with the other comparative methods.

As mentioned before, metaheuristic optimization algorithms proved their ability to deal with various problems such as bioinformatics (Issa, 2021a; Issa and Abd Elaziz, 2020; Issa and Hassanien, 2017; Issa et al., 2018a; Issa et al., 2018b; Issa and Helmi, 2021; Issa et al., 2022), control engineering (Issa, 2021b; Issa et al., 2019), passive suspension system (Issa and Samn, 2022), and digital watermarking (Abualigah and Diabat, 2021; Issa, 2018). To estimate the model parameters of the PEMFC, an efficient method compared to the existing method is needed. This research work proposed a new parameter extraction technique to deal with the FC modeling optimization problem. The proposed method is based on the honey badger algorithm (HBA), a technique recently proposed by Hashim et al.(2021) inspired by the creative foraging habits of the honey badger in real life. The mathematical modeling of the HBA is produced using efficient search operators to deal with highly complicated problems which motivate to use it for the parameter estimation of PEMFCs. The balancing between diversification and intensification of the search space of the HBA is the main merit and motivation to use it in this work. The primary fitness function that is used in the proposed method is to minimize the integral squared errors. The high effectiveness of the presented technique is verified using dynamic and steady-state operating conditions. The results illustrated that the presented method using the HBA achieved promising results in comparison with several relevant study parameter extraction methods used in the literature.

The main contributions and novelties of this study are concluded as following:

1. The optimal values of the PEMFC model parameters were adjusted based on the HBA.

2. Three PEMFC datasets (NedStack PS6, 250 W, and BCS 500 W) were used in the experimental tests.

3. The results of the developed method were compared with well-known methods.

The remaining sections of this article are organized as follows: Section 2 proposes the background of the used optimization methods. Section 3 shows the procedure of the proposed FC parameter extraction using the honey badger algorithm. In Section 4, experiments and results are given. Finally, Section 5 presents the conclusions and future potential works.

2 Background

In this part, the primary mathematical representation of the PEMFC design is explained. It includes a cathode, negative charges, charged anode, and electrolyte, as described in Figure 1. In the PEMFC system, the hydrogen data are divided into two main parts utilizing a catalyst: protons and electrons. Moreover, the cathode pulls the protons, and the electrons produce the output charge by moving along the exterior circuit. The mathematical notations of the chemical stability produced in the FC are presented as follows (Alizadeh and Torabi, 2021):

$H_2\to 2H^{+}+2e^{-},(1)$

$O_2+4e^{-}\to 2O^{-2},(2)$

$H_2+\frac{1}{2}{O}_2\to H_{2}O+electricalenergy+Heat.(3)$

In the PEMFC system, three drops normally happen during the voltage process, called activation (V_act), ohmic (V_ohm), and concentration (V_con). Thus, Eq. 4 is used to calculate the FC terminal voltage.

$V_{FC}=E_{Nernest}-V_{act}-V_{ohm}-V_{con},(4)$

where E_Nernest is the double-faced open circuit charge voltage, which is calculated as follows (Yuan et al., 2020):

$E_{Nernest}=\mathit{1.229}-\mathit{8.5}\times {\mathit{10}}^{-4}\left(T-\mathit{298.15}\right)+\mathit{4.385}\times {\mathit{10}}^{-5}T\mathit{ln}\left(P_{H2}+\mathit{0.5}\mathit{ln}{P}_{\mathit{O}\mathit{2}}\right),(5)$

where RP_O2 presents the pressure of the O2, RP_H2 presents the pressure of H₂, and T represents the cell temperature value used in this research. The activation voltage loss value (V_act) is calculated as follows:

$V_{act}=-\left[{\xi }_1+{\xi }_{2}T+{\xi }_{3}T\ln \left(C_{02}\right)+ {\xi }_{4}T\ln \left(I_{FC}\right)\right],(6)$

where I_FC is the present value of the FC and ξ₁, ξ₂, ξ₃, and ξ₄ denote the coefficient values. C_O2 presents the condensation value of oxygen (mol/cm³) calculated as follows:

${\text{C}}_{\text{O}2}=\frac{{\text{P}}_{\text{O}2}}{{5.08}^{\ast }{10}^{6\ast }{e}^{\left(\frac{-498}{\text{T}}\right)}}.(7)$

The V_ohm is calculated using Eq. 8, which is resulted from the equivalent resistance of the FC value.

$V_{ohm}=I_{FC}\left(R_M+R_C\right),(8)$

where R_C presents the connection resistance and R_M presents the membrane resistances calculated as follows:

$R_M=\frac{{\rho }_M.l}{A},(9)$

${\rho }_M=\frac{181.6\left[1+0.03\left(\frac{I_{FC}}{A}\right)+0.0062\left(\frac{T}{303}\right){\left(\frac{I_{FC}}{A}\right)}^{2.5}\right]}{\left[{\lambda }_m-0.634-3\left(\frac{I_{FC}}{A}\right)\right]exp\left[4.18\left(\frac{T-303}{T}\right)\right]},(10)$

where ${\rho }_M$ presents the measure of the resisting power of the membrane (Ω.cm), l presents the density value of the membrane (cm), A presents the effective range of the cell (cm²), and ${\lambda }_m$ presents the membrane water fulfilled. The V_con value is calculated using Eq. 11.

$V_{con}=-b\ln \left\{1-\frac{\left(\frac{I_{FC}}{A}\right)}{I_{max}}\right\},(11)$

where $b$ presents a constant value and $I_{max}$ is the present maximum destiny value. So, the stack includes a series value of $n$ FCs, and the stack voltage value is calculated as follows.

$V_{stack}=n.V_{FC}=n.\left(E_{Nernest}-V_{act}-V_{ohm}-V_{con}\right).(12)$

Figure 2 presents the FC polarization detour.

FIGURE 2

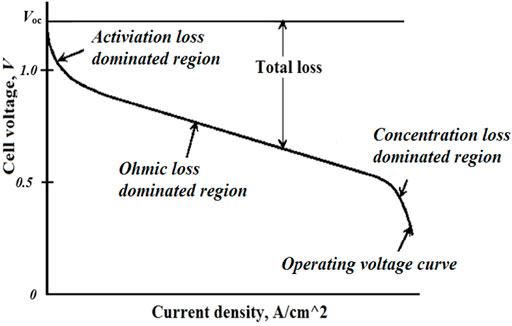
FIGURE 2. Polarization detour of the PEMFC system (Famouri and Gemmen, 2003) slowly while using digging for catching it. The optimization process of HBA is based on two modes.

2.1 Honey Badger Algorithm

The HBA mimicked the locating of prey operation of the honey badger that lives in rainforests and semideserts of Southwest Asia, the Indian subcontinent, and Africa. For locating a prey, it depends on its smelling skills and moving.

- Digging phase: In this phase, the honey badger depends on its smelling sense for locating the prey and the suitable place to catch it.

- Honey phase: In this phase, the honey badger tracks the honey bird for locating the beehive.

The HBA starts with the initialization of the solutions within the lower boundary (lb) and upper boundary (ub) according to Eq. (13).

$x^i=l{b}_i+r_1\ast \left(u{b}_i-l{b}_i\right),(13)$

where (xⁱ) represents the solution of the honey badger agent (i) where (i = 1:N) and (r₁) is a random number within (0,1). For balancing between the exploration and exploitation of the HBA, a density factor (α) is defined in Eq. (14).

$a=C\ast ex{p}^{\left(-\frac{t}{T}\right)},(14)$

where C represents a constant with a value more than (1), T represents the total number of iterations, and t represents the current iteration.

In the HBA, there are two phases for updating the movements of solutions.

- Digging phase: In this phase, the movements are updated according to a cardioid shape [2], which is represented in Eq. (15).

${\mathrm{x}}^{\text{new}}={\mathrm{x}}^{\text{prey}}+\text{F}\ast \text{β}\ast \text{l}\ast {\mathrm{x}}^{\text{prey}}+\text{F}\ast \text{α}\ast {\text{d}}^i\ast {\text{r}}_3\ast \left|\cos \left(2\text{π}{\text{r}}_4\right)\ast \left[1-\cos \left(2\text{π}{\text{r}}_5\right)\right]\right|,(15)$

where ${\text{x}}^{\text{new}}$ is the new updated value of xⁱ; x^prey is the best-founded solution; (F) controls the direction of the search according to Eq. (16); r₃, r₄, r₅, and r₆ are uniformly generated random numbers within the range (0,1); (B) is a constant number having a value greater than (1); and (I) is the smell intensity of the prey, which expresses the remoteness between the prey and the honey badger.

It was estimated according to Eq. (17) and (18), where (d_i) represents the remoteness between the prey and the honey badger and (S) expresses the source strength.

$F=\{\begin{array}{cc}1& If\left(r_6\le 0.5\right)\\ -1& Else\end{array} ,(16)$

$I_i=r_2 \frac{S}{4 \pi d_i^2},(17)$

$\begin{array}{cc}S={\left(x^i-x^{i+1}\right)}^2,& d_i=x^{prey}-x_i\end{array}.(18)$

- Honey Phase: This phase simulates the tracking of the honey badger for the honey guide bird to find the beehive, and this operation is simulated as in Eq. (19).

$x^{new}=x^{prey}+F\ast r_7\ast \alpha \ast d_i,(19)$

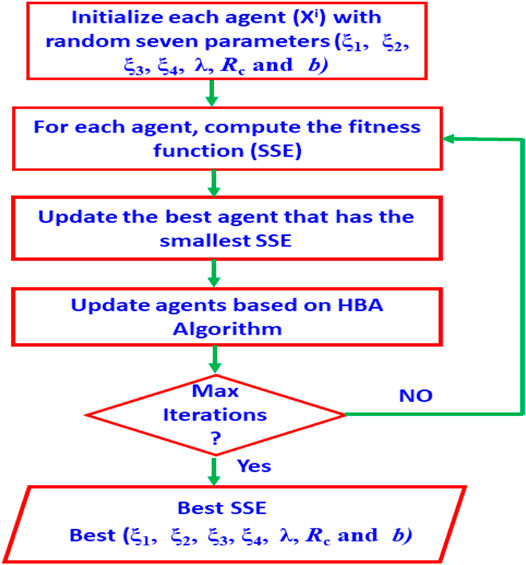
where r₇ is a uniform random number within the range (0,1). The procedure of the HBA is expressed as in algorithm (1). Figure 3 shows the flowchart of HBA. HBA’s time complexity is O (T x N x C_cost), where T is the total number of iterations, N represents the population size, and C_cost is the needed execution time for updating solutions.

FIGURE 3

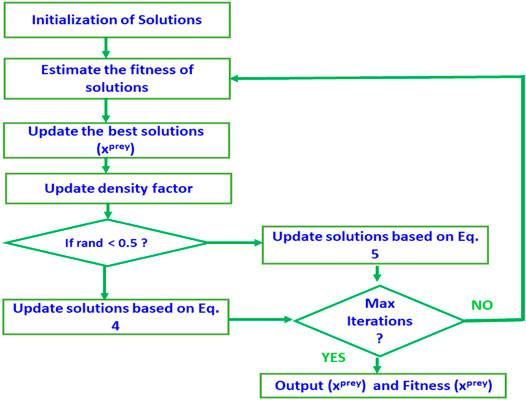
FIGURE 3. Flowchart of HBA (Hashim et al., 2022).

Algorithm 1. HBA procedure

The balancing between diversification and intensification of the search space of the HBA is the main merit and motivation to use it in this work. The balancing is performed through three main parameters:

1 - Intensity $\left(\mathrm{I}\right)$: It controls the transfer between exploration to exploitation and the reverse through the distance between the prey and the other solutions, which may be increased or decreased. In addition, there is another issue that controls the exploration/exploitation process that is the distance between two neighbors of solutions. These interactions increase the possibility of escaping from local minima.

2 - Density factor (α): This parameter decreases with time, which achieves the trade-off between diversification and intensification of the search space.

3 - Flag $\left(\mathrm{F}\right)$: It controls the direction of the movements of the solutions, which increase the diversity of the generated solutions, which enhance the exploration.

3 PEMFC Model Parameter Estimations Based on HBA

The HBA was used for tuning the best parameters’ values of PEMFCs where each agent has a total of the seven parameters (λ, Rc, ξ₁, ξ₂, ξ₃, ξ₄, and b), and the best agent is the agent that produces the best fitness. The fitness function used to evaluate the search is the sum square error (SSE) function, which represents the integral square of the subtraction between experimental and estimated voltages. The representation of the SSE function as proposed in Eq. (20), where Vexp and Vest represent the experimental and estimated voltages, respectively.

$SSE={\left(V_{exp}-V_{est}\right)}^2.(20)$

Figure 4 shows the flowchart of parameter estimation of PEMFCs based on the HBA. The initial random solutions are initialized according to satisfying conditions and input into the HBA’s block. The output of the HBA is the best solution found that achieves the smallest SSE.

FIGURE 4

FIGURE 4. PEMFC model parameter estimation based on HBA.

4 Numerical Analysis

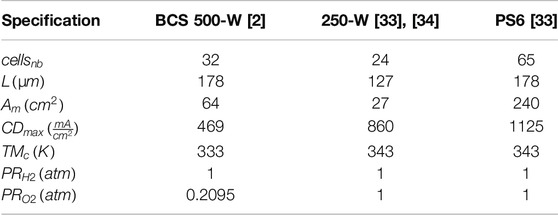
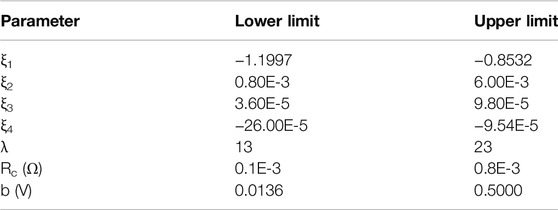
The efficiency of the created HBA used for estimating PEMFC model parameters is assessed in this part using three datasets: PEMFC 250-W stack, NedStack PS6, and BCS 500-W, and their electrical specification are listed in Table 1. In addition, Table 2 presents the parameters’ boundaries (lower bound and higher bound) (Zhang and Liu, 2010).

TABLE 1

TABLE 1. PEMFC dataset’s electrical specifications.

TABLE 2

TABLE 2. Two parameter ranges of PEMFC parameters.

The HBA is compared to other MH techniques such as grey wolf optimization (GWO) (Ali et al., 2017; Mirjalili et al., 2014), Hunger Games Search (HGS) (Yang et al., 2021), sine cosine algorithm (SCA) (Mirjalili, 2016), and Harris hawk optimization (HHO) (Heidari et al., 2019) to demonstrate its capability. The values of each algorithm’s parameters are assigned depending on the algorithm’s original implementation. The conventional settings for the number of populations and iterations are 50 and 500, respectively.

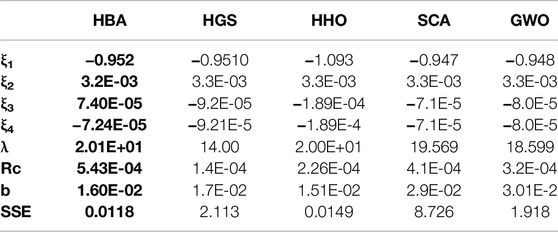
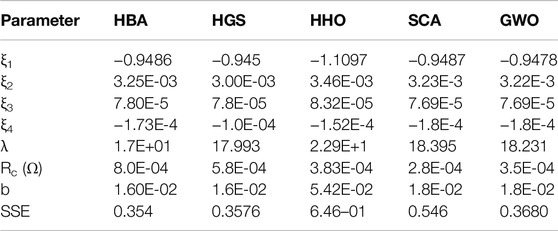
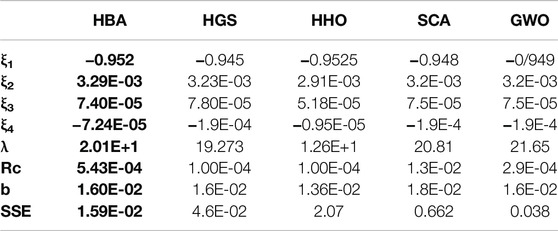
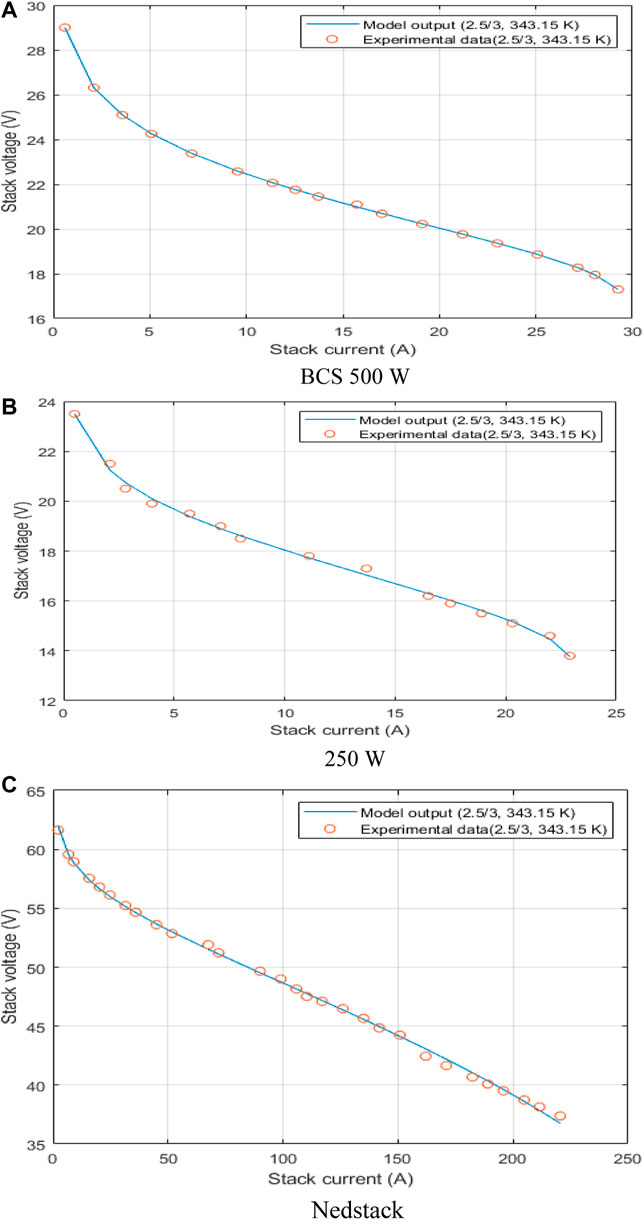
Tables 3–7 and Figures 5–9 using the three datasets show the comparison between the HBA and other approaches. Table 3 shows the estimated parameters derived by each algorithm and their SSE values in general. The performance of the HBA in terms of SSE is superior to other MH approaches among the datasets studied, as can be seen from these results. HBA’s SSE value with BCS 500-W, 250-W, and NedStack PS6 is, for example, 0.0118, 0.3378, and 1.38E+00, respectively.

TABLE 3

TABLE 3. Estimated BSC 500 W’s parameters.

TABLE 4

TABLE 4. Estimated 250 W’s parameters.

TABLE 5

TABLE 5. Estimated Nedstack PS6’s parameters.

TABLE 6

TABLE 6. Statistical values for each method.

TABLE 7

TABLE 7. p-value for comparison between HBA and other methods.

FIGURE 5

FIGURE 5. Convergence curve of SSE of datasets. (A) BSC 500, (B) 250 W, and (C) Nedstack.

FIGURE 6

FIGURE 6. Error % of datasets: (A) BCS 500 W, (B) 250 W module, and (C) Nedstack module.

FIGURE 7

FIGURE 7. I-V curves of datasets: (A) BCS 500 W, (B) 250 W, and (C) Nedstack.

FIGURE 8

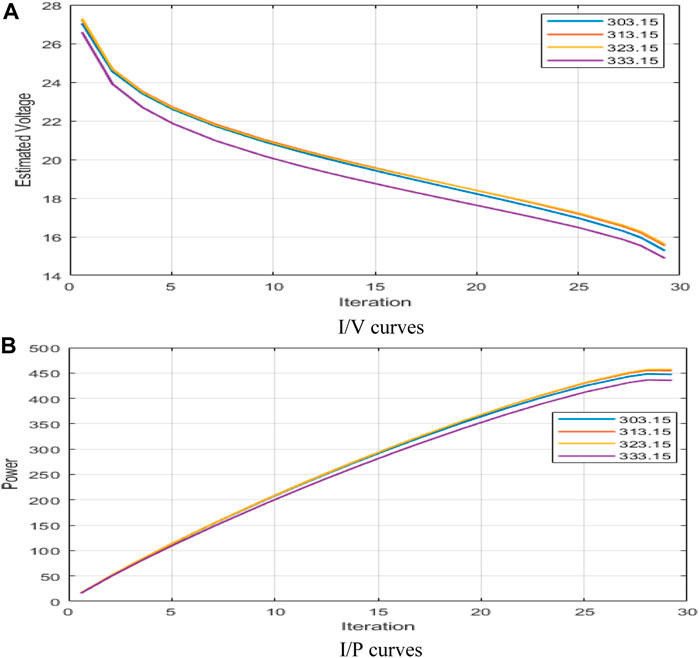
FIGURE 8. Curves under different temperatures for BCS 500 W using HBA. (A) I/V curves and (B) I/P curves.

FIGURE 9

FIGURE 9. Different RP_H2 and RP_O2 for BCS 500 W using HBA. (A) Different RP_O2. (B) Different RP_H2.

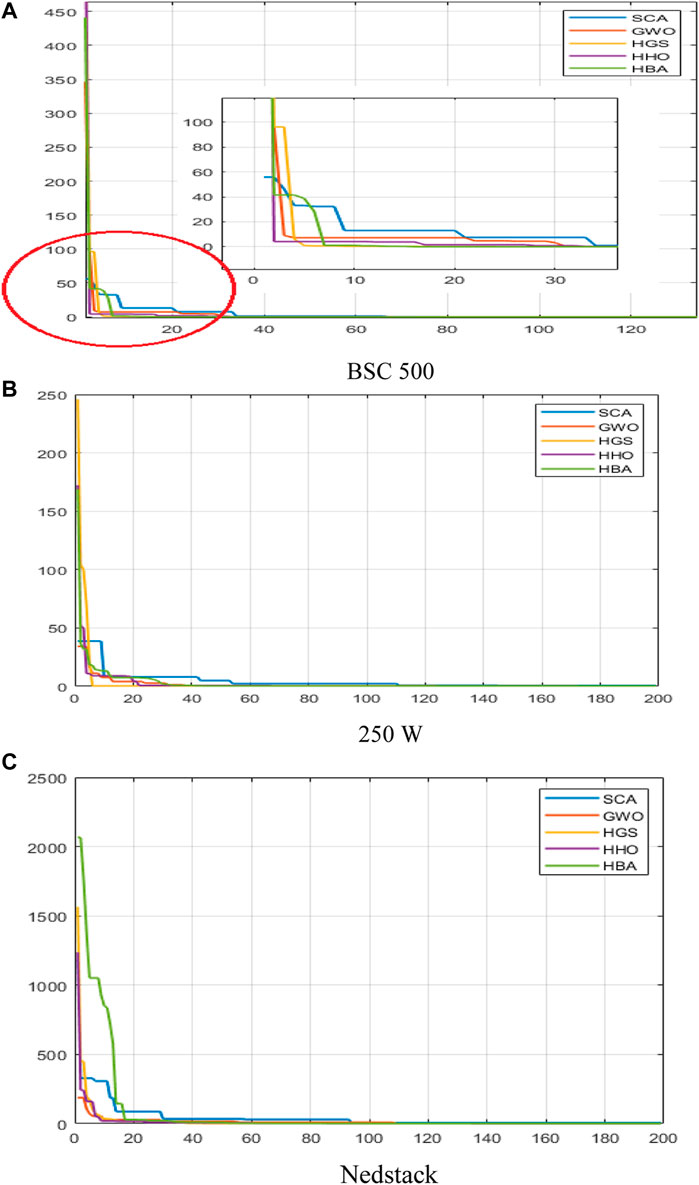
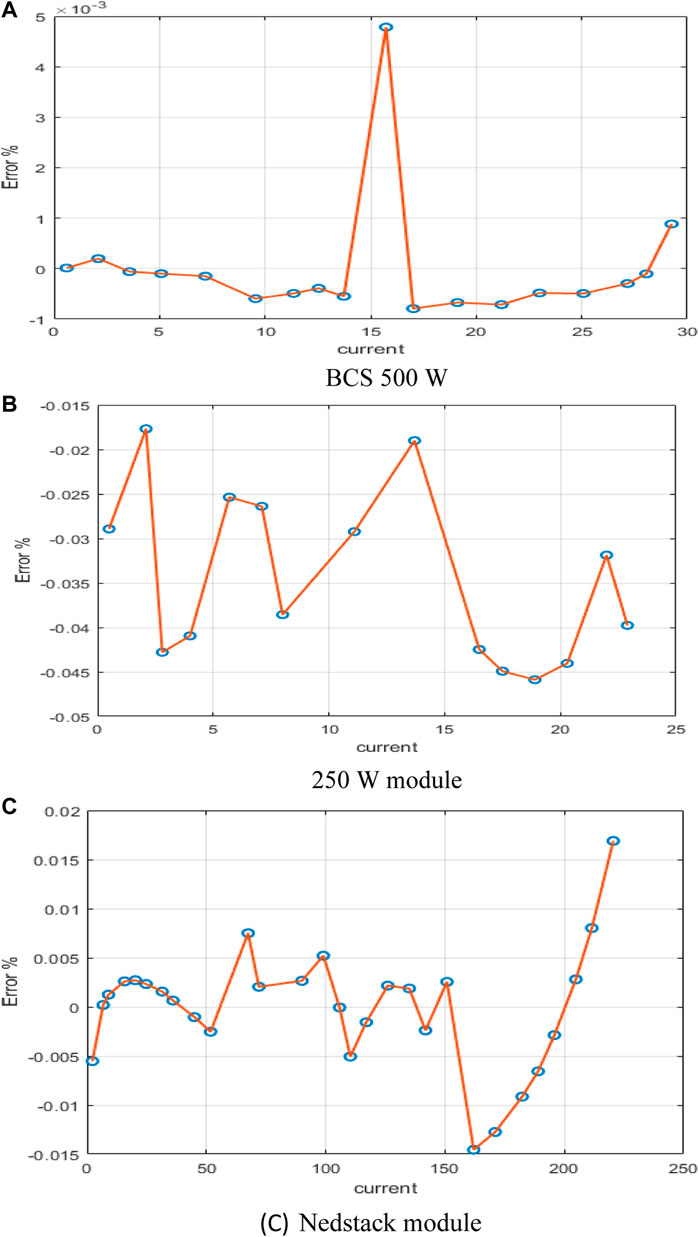
Furthermore, the values of SSE over the iterations for SCA, GWO, HGS, HHO, and HBA are presented in Figure 5 among the three datasets for SCA, GWO, HGS, and HBA to justify the produced HBA’s convergence rate. These charts show that the HBA has a higher convergence rate than other approaches, especially in the NedStack PS6 dataset. Figure 6 also displays the voltage and measured I/V polarization percentage errors, where the percentage error was estimated as the difference between estimated and measured voltage relative to the measured voltage. The percentage error of the HBA is nearly -0.9E-3 to 4.8E-3 for BCS 500 W and from -0.012 to.015 for 250 W module, according to these curves. Finally, the percentage errors for the NedStack PS6 range from -0.012 to +0.012.

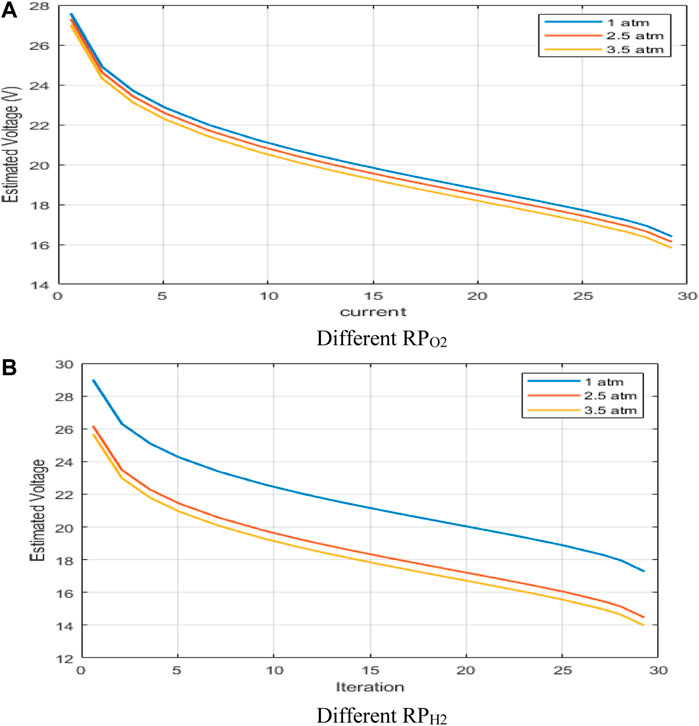
The obtained results in Figure 8A,B depict the effect of the three temperature values on the I/V and I/P polarization curves, respectively. The pressures RP_O2 and RP_H2 were set to justify the effect of temperature on the performance of the PEMFC stack as shown in Figure 9A,B.

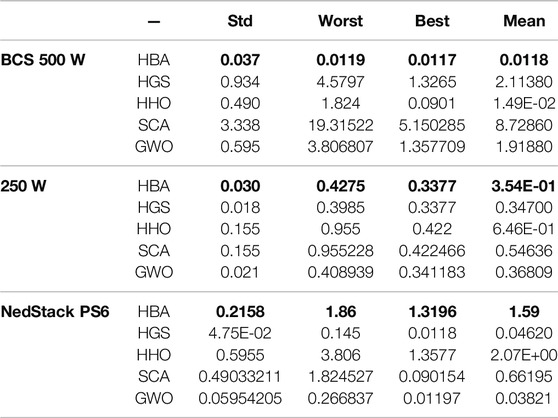
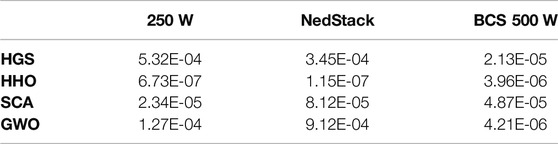
Various statistical parameters such as mean, standard deviation, best, and worst of the SSE are calculated to further examine the effectiveness of HBA as a PEMFC model, as shown in Table 6. From these metrics, it is clear that the HBA is better at finding optimal settings than other approaches, as evidenced by the examined datasets. We also utilized the Wilcoxon nonparametric test to see if there was a significant difference between the HBA and other approaches. Table 7 shows the Wilcoxon test p-value at a significance level of 0.05. These results show that there is a considerable difference in overall datasets between the HBA and other approaches.

5 Conclusion

In this study, an alternative approach for estimating the model parameters of a PEMFC under various operating conditions is described. This method is based on the HBA. This algorithm has proven its efficacy in a variety of applications, which prompted us to use it. The main motivation for using the HBA for estimating the PEMFC’s parameters is the advantage of balance between exploration and exploitation of the search space, which avoids trapping in local minima. A set of experimental series has been conducted utilizing three datasets entitled 250-W stack, BCS 500-W, and NedStack PS6 to justify the usage of the HBA to determine the PEMFC’s parameters (i.e., λ, Rc, ξ₁, ξ₂, ξ₃, ξ₄, and b). HBA’s results have also been compared to those of other metaheuristic techniques such as HGS and SCA. In terms of performance measures, the results showed that the HBA outperformed other MH approaches. The findings revealed that the presented approach produced promising results and outperformed the other pproaches. The main limitation of using the HBA for estimating the parameters of PEMFCs is it was tested on three modules only. More modules are needed to be used in the experimental tests for efficient verification of the performance of the HBA. Apart from the findings generated by the HBA, it may be employed in a variety of applications, such as PV parameter estimation, mechanical engineering, and other challenges such as cloud computing and picture segmentation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All the authors have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R197), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abualigah, L., and Diabat, A. (2021). Advances in Sine Cosine Algorithm: a Comprehensive Survey. Artif. Intell. Rev. 54, 1–42. doi:10.1007/s10462-020-09909-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, M., El-Hameed, M. A., and Farahat, M. A. (2017). Effective Parameters' Identification for Polymer Electrolyte Membrane Fuel Cell Models Using Grey Wolf Optimizer. Renew. Energy 111, 455–462. doi:10.1016/j.renene.2017.04.036

CrossRef Full Text | Google Scholar

Alizadeh, M., and Torabi, F. (2021). Precise PEM Fuel Cell Parameter Extraction Based on a Self-Consistent Model and SCCSA Optimization Algorithm. Energy Convers. Manag. 229, 113777. doi:10.1016/j.enconman.2020.113777

CrossRef Full Text | Google Scholar

Askarzadeh, A., and Rezazadeh, A. (2011). Artificial Immune System-Based Parameter Extraction of Proton Exchange Membrane Fuel Cell. Int. J. Electr. Power & Energy Syst. 33 (4), 933–938. doi:10.1016/j.ijepes.2010.12.036

CrossRef Full Text | Google Scholar

Ben Messaoud, R., Midouni, A., and Hajji, S. (2021). PEM Fuel Cell Model Parameters Extraction Based on Moth-Flame Optimization. Chem. Eng. Sci. 229, 116100. doi:10.1016/j.ces.2020.116100

CrossRef Full Text | Google Scholar

Eid, A., Kamel, S., and Abualigah, L. (2021). Marine Predators Algorithm for Optimal Allocation of Active and Reactive Power Resources in Distribution Networks. Neural Comput. Appl. 33, 1–29. doi:10.1007/s00521-021-06078-4

CrossRef Full Text | Google Scholar

Eisman, G. (1989). “The Application of Dow Chemical's Perfluorinated Membranes in Proton-Exchange Membrane Fuel Cells,” in Paper presented at the Space Electrochemical Research and Technology Conference, Freeport, TX, United States, January 1, 1989.

Google Scholar

Famouri, P., and Gemmen, R. S. (2003). “Electrochemical Circuit Model of a PEM Fuel Cell,” in Proceeding of the IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, July 2003 (IEEE). Paper presented at the 2003.

Google Scholar

Fathy, A., Elaziz, M. A., and Alharbi, A. G. (2020a). A Novel Approach Based on Hybrid Vortex Search Algorithm and Differential Evolution for Identifying the Optimal Parameters of PEM Fuel Cell. Renew. Energy 146, 1833–1845. doi:10.1016/j.renene.2019.08.046

CrossRef Full Text | Google Scholar

Fathy, A., Rezk, H., and Mohamed Ramadan, H. S. (2020b). Recent Moth-Flame Optimizer for Enhanced Solid Oxide Fuel Cell Output Power via Optimal Parameters Extraction Process. Energy 207, 118326. doi:10.1016/j.energy.2020.118326

CrossRef Full Text | Google Scholar

Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., and Al-Atabany, W. (2021). Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 192, 84–110. doi:10.1016/j.matcom.2021.08.013

CrossRef Full Text | Google Scholar

Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., and Al-Atabany, W. (2022). Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 192, 84–110. doi:10.1016/j.matcom.2021.08.013

CrossRef Full Text | Google Scholar

Hassan, M. H., Kamel, S., Abualigah, L., and Eid, A. (2021). Development and Application of Slime Mould Algorithm for Optimal Economic Emission Dispatch. Expert Syst. Appl. 182, 115205. doi:10.1016/j.eswa.2021.115205

CrossRef Full Text | Google Scholar

Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028

CrossRef Full Text | Google Scholar

İnci, M., and Caliskan, A. (2020). Performance Enhancement of Energy Extraction Capability for Fuel Cell Implementations with Improved Cuckoo Search Algorithm. Int. J. Hydrogen Energy 45 (19), 11309–11320. doi:10.1016/j.ijhydene.2020.02.069

CrossRef Full Text | Google Scholar

Issa, M. (2018). “Digital Image Watermarking Performance Improvement Using Bio-Inspired Algorithms,” in Advances in Soft Computing and Machine Learning in Image Processing (Springer), 683–698. doi:10.1007/978-3-319-63754-9_30

CrossRef Full Text | Google Scholar

Issa, M. (2021a). Expeditious Covid-19 Similarity Measure Tool Based on Consolidated SCA Algorithm with Mutation and Opposition Operators. Appl. Soft Comput. 104, 107197. doi:10.1016/j.asoc.2021.107197

PubMed Abstract | CrossRef Full Text | Google Scholar

Issa, M. (2021b). “Performance Optimization of PID Controller Based on Parameters Estimation Using Meta-Heuristic Techniques: A Comparative Study,” in Metaheuristics in Machine Learning: Theory and Applications (Springer), 691–709. doi:10.1007/978-3-030-70542-8_28

CrossRef Full Text | Google Scholar

Issa, M., Hassanien, A. E., Helmi, A., Ziedan, I., and Alzohairy, A. (2018a). “Pairwise Global Sequence Alignment Using Sine-Cosine Optimization Algorithm,” in Paper presented at the International Conference on Advanced Machine Learning Technologies and Applications, January 2018, 102–111.

CrossRef Full Text | Google Scholar

Issa, M., Hassanien, A. E., Oliva, D., Helmi, A., Ziedan, I., and Alzohairy, A. (2018b). ASCA-PSO: Adaptive Sine Cosine Optimization Algorithm Integrated with Particle Swarm for Pairwise Local Sequence Alignment. Expert Syst. Appl. 99, 56–70. doi:10.1016/j.eswa.2018.01.019

CrossRef Full Text | Google Scholar

Issa, M., Elbaset, A. A., Hassanien, A. E., and Ziedan, I. (2019). “PID Controller Tuning Parameters Using Meta-Heuristics Algorithms: Comparative Analysis,” in Machine Learning Paradigms: Theory and Application (Springer), 413–430. doi:10.1007/978-3-030-02357-7_20

CrossRef Full Text | Google Scholar

Issa, M., Helmi, A. M., Elsheikh, A. H., and Abd Elaziz, M. (2022). A Biological Sub-sequences Detection Using Integrated BA-PSO Based on Infection Propagation Mechanism: Case Study COVID-19. Expert Syst. Appl. 189, 116063. doi:10.1016/j.eswa.2021.116063

PubMed Abstract | CrossRef Full Text | Google Scholar

Issa, M., and Elaziz, M. A. (2020). Analyzing COVID-19 Virus Based on Enhanced Fragmented Biological Local Aligner Using Improved Ions Motion Optimization Algorithm. Appl. Soft Comput. 96, 106683. doi:10.1016/j.asoc.2020.106683

PubMed Abstract | CrossRef Full Text | Google Scholar

Issa, M., and Hassanien, A. E. (2017). “Multiple Sequence Alignment Optimization Using Meta-Heuristic Techniques,” in Handbook of Research on Machine Learning Innovations and Trends (Hershey, Pennsylvania: IGI Global), 409–423. doi:10.4018/978-1-5225-2229-4.ch018

CrossRef Full Text | Google Scholar

Issa, M., and Helmi, A. (2021). “Two Layer Hybrid Scheme of IMO and PSO for Optimization of Local Aligner: COVID-19 as a Case Study,” in Artificial Intelligence for COVID-19 (Springer), 363–381. doi:10.1007/978-3-030-69744-0_21

CrossRef Full Text | Google Scholar

Issa, M., and Samn, A. (2022). Passive Vehicle Suspension System Optimization Using Harris Hawk Optimization Algorithm. Math. Comput. Simul. 191, 328–345. doi:10.1016/j.matcom.2021.08.016

CrossRef Full Text | Google Scholar

Kahraman, H., and Orhan, M. F. (2017). Flow Field Bipolar Plates in a Proton Exchange Membrane Fuel Cell: Analysis & Modeling. Energy Convers. Manag. 133, 363–384. doi:10.1016/j.enconman.2016.10.053

CrossRef Full Text | Google Scholar

Kandidayeni, M., Macias, A., Khalatbarisoltani, A., Boulon, L., and Kelouwani, S. (2019). Benchmark of Proton Exchange Membrane Fuel Cell Parameters Extraction with Metaheuristic Optimization Algorithms. Energy 183, 912–925. doi:10.1016/j.energy.2019.06.152

CrossRef Full Text | Google Scholar

Kawada, T., Sakai, N., Yokokawa, H., Dokiya, M., Mori, M., and Iwata, T. (1990). Structure and Polarization Characteristics of Solid Oxide Fuel Cell Anodes. Solid State Ionics 40-41, 402–406. doi:10.1016/0167-2738(90)90367-z

CrossRef Full Text | Google Scholar

Kayfeci, M., Keçebaş, A., and Bayat, M. (2019). “Hydrogen Production,” in Solar Hydrogen Production (Elsevier), 45–83. doi:10.1016/b978-0-12-814853-2.00003-5

CrossRef Full Text | Google Scholar

McLean, G., Niet, T., Prince-Richard, S., and Djilali, N. (2002). An Assessment of Alkaline Fuel Cell Technology. Int. J. hydrogen energy 27 (5), 507–526. doi:10.1016/s0360-3199(01)00181-1

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey Wolf Optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mirjalili, S. (2016). SCA: a Sine Cosine Algorithm for Solving Optimization Problems. Knowledge-Based Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022

CrossRef Full Text | Google Scholar

Mo, Z.-J., Zhu, X.-J., Wei, L.-Y., and Cao, G.-Y. (2006). Parameter Optimization for a PEMFC Model with a Hybrid Genetic Algorithm. Int. J. Energy Res. 30 (8), 585–597. doi:10.1002/er.1170

CrossRef Full Text | Google Scholar

Nain, A., Banerjee, A., and Melkania, N. P. (2021). “Effects of Green Buildings on the Environment,” in Digital Cities Roadmap: IoT‐Based Architecture and Sustainable Buildings, 477–507. doi:10.1002/9781119792079.ch15

CrossRef Full Text | Google Scholar

Priya, K., Sudhakar Babu, T., Balasubramanian, K., Sathish Kumar, K., and Rajasekar, N. (2015). A Novel Approach for Fuel Cell Parameter Estimation Using Simple Genetic Algorithm. Sustain. Energy Technol. assessments 12, 46–52. doi:10.1016/j.seta.2015.09.001

CrossRef Full Text | Google Scholar

Ramos-Paja, C. A., Romero, A., Giral, R., Calvente, J., and Martinez-Salamero, L. (2010). Mathematical Analysis of Hybrid Topologies Efficiency for PEM Fuel Cell Power Systems Design. Int. J. Electr. Power & Energy Syst. 32 (9), 1049–1061. doi:10.1016/j.ijepes.2010.01.032

CrossRef Full Text | Google Scholar

S. Menesy, A., Sultan, H. M., Korashy, A., Banakhr, F. A., G. Ashmawy, M., and Kamel, S. (2020). Effective Parameter Extraction of Different Polymer Electrolyte Membrane Fuel Cell Stack Models Using a Modified Artificial Ecosystem Optimization Algorithm. IEEE Access 8, 31892–31909. doi:10.1109/access.2020.2973351

CrossRef Full Text | Google Scholar

Seleem, S. I., Hasanien, H. M., and El-Fergany, A. A. (2021). Equilibrium Optimizer for Parameter Extraction of a Fuel Cell Dynamic Model. Renew. Energy 169, 117–128. doi:10.1016/j.renene.2020.12.131

CrossRef Full Text | Google Scholar

Wang, J., Wang, H., and Fan, Y. (2018). Techno-economic Challenges of Fuel Cell Commercialization. Engineering 4 (3), 352–360. doi:10.1016/j.eng.2018.05.007

CrossRef Full Text | Google Scholar

Wang, S., Liu, Q., Liu, Y., Jia, H., Abualigah, L., Zheng, R., et al. (2021). A Hybrid SSA and SMA with Mutation Opposition-Based Learning for Constrained Engineering Problems. Comput. Intell. Neurosci. 2021, 1–21. doi:10.1155/2021/6379469

CrossRef Full Text | Google Scholar

Yang, Y., Chen, H., Heidari, A. A., and Gandomi, A. H. (2021). Hunger Games Search: Visions, Conception, Implementation, Deep Analysis, Perspectives, and towards Performance Shifts. Expert Syst. Appl. 177, 114864. doi:10.1016/j.eswa.2021.114864

CrossRef Full Text | Google Scholar

Yuan, Z., Wang, W., Wang, H., and Ashourian, M. (2020). Parameter Identification of PEMFC Based on Convolutional Neural Network Optimized by Balanced Deer Hunting Optimization Algorithm. Energy Rep. 6, 1572–1580. doi:10.1016/j.egyr.2020.06.011

CrossRef Full Text | Google Scholar

Zhang, P.-Y., and Liu, Z.-L. (2010). Experimental Study of the Microbial Fuel Cell Internal Resistance. J. power sources 195 (24), 8013–8018. doi:10.1016/j.jpowsour.2010.06.062

CrossRef Full Text | Google Scholar