Energy Management and Pricing Strategy of Building Cluster Energy System Based on Two-Stage Optimization

With the application of advanced information and communication technology in building cluster energy system (BCES), energy management based on two-way interaction has become an effective method to improve its operation efficiency. BCES can quickly respond to the mismatch between supply and demand by adjusting flexible load and system operation strategy, which can improve operation reliability and reduce energy cost. This paper proposes an energy management and pricing framework of BCES based on two-Stage optimization method. First, on the basis of profit-seeking modeling of energy service provider (ESP) and building clusters (BCs), a dynamic pricing decision-making framework for energy management in a hierarchical energy market is proposed, which considers both ESP’s energy supply income and BCs’ comprehensive benefit. The dynamic pricing problem is formulated as a discrete finite Markov decision process (MDP), and Q-learning algorithm is adopted to solve the MDP problem. Moreover, an operation optimization model of the BCES based on the obtained optimal price decision is established, and the established model is solved by the alternating direction multiplier method algorithm (ADMM). Through numerical simulation case studies, it is demonstrated that the proposed method can achieve the optimal pricing decision-making closer to the psychological needs of ESP and BCs, and can significantly reduce the cost of BCs and improve the operational efficiency of BCES.

1 Introduction

1.1 Background and Motivation

With the rapid development of urban economy and the large-scale application of smart energy technology, Building Cluster Energy System (BCES) plays an increasingly important role in the construction of smart cities. On the one hand, with the increasing number of commercial and residential urban complexes, the energy demand of building energy system is also increasing, and its energy consumption accounts for more than 40% of the total urban energy consumption (Winkler et al., 2020). At the same time, it faces the problems that the energy structure of building system is unreasonable, and it is easy to increase the peak-valley difference of urban power grid load. On the other hand, the diversified energy supply mode and flexible terminal equipment of the BCES make it a smart energy body with strong flexibility and adjustability, which greatly increases its potential to participate in the energy management and regulation of urban energy systems. Therefore, the wide application of multi-energy coupling technology in buildings and the increasing demand for diversified energy use make the energy supply-demand relationship and energy management of BCES more complex (Li et al., 2021a; Lombardi et al., 2021).

BCES has great adjustable potential to participate in demand response (DR) programme and energy optimization of urban energy system due to its diversity of energy supply and flexibility of terminal equipment (Li et al., 2021a). Building clusters can strengthen the information interaction with external urban energy networks and optimize energy consumption mode, which can reduce the peak load of urban energy networks and realize building energy conservation. With the deepening of energy market reform and the transformation of urban energy consumption patterns, the emerging energy supply patterns are developing continuously. In 2015, the Rocky Mountain Research Institute put forward a more innovative energy service provider (ESP) model in the design process of net zero energy consumption urban comprehensive development zone in the United States. The innovative highlight of this model is that it uses a user-centered one-stop solution for resource integration and coordinated energy supply management. In this new mode of energy supply and management, ESP can not only aggregate and guide BCs to participate in the energy management of urban energy networks, but also directly participate in the energy supply of urban energy networks and building clusters as an energy supplier (Xie et al., 2018). In this process of energy interaction, the ultimate goal of BCs is to optimize the energy consumption mode and reduce the energy cost as much as possible while satisfying its own comfort. ESP seeks the maximum benefit between utility grid and BCs. The key to achieve this goal lies in the reasonable pricing strategy of ESP for BCs and the best operating conditions of energy supply equipment. Therefore, reasonable pricing strategy, optimal energy consumption mode and optimal equipment operation strategy are the key to realize the efficient and economic operation of urban energy system with the participation of building energy BCs and ESP.

1.2 Literature Review

To resolve the above-mentioned key problems, some scholars and institutions have conducted research on building cluster energy management from the aspects of building energy modeling, power grid optimization with BCES participation, demand response and so on. Literature (Mason and Grijalva, 2019) presents a model for energy management system of a building microgrid coupled with a battery energy storage. The model can be used to dispatch the battery as a flexible energy resource using a market-based setting. Energy management is one of the main challenges in Microgrids (MGs) applied to Smart Buildings (SBs). Literature (Antoniadou-Plytaria et al., 2020) proposes a novel energy management architecture model based on complete Supervisory Control and Data Acquisition system duties in an educational building. Literature (Kermani et al., 2021) presents a hardware testbed for testing the building energy management system based-on the multi agent system and the objective is to maximize user comfort while minimizing the energy extracted from the grid. Literature (Ma et al., 2019) put forwards an energy management method to optimally control the energy supply and the temperature settings of distributed heating and ventilation systems for residential buildings. Literature (Paul and Padhy, 2019) elaborates a real-time energy management strategy for a smart residential apartment building and designs a distributed energy management algorithm. Literature (Shakeri et al., 2020) introduces a trading energy management framework for the residential buildings to address grid overloading and building cost optimization problem.

In addition, with the application of data acquisition terminals and communication equipment in smart buildings, advanced technologies such as big data and artificial intelligence have been widely used in building energy system optimization and control. Data-driven method is one of the effective solutions used for control problems and has had many successful applications in the area of building energy management. Literature (Soetedjo et al., 2019) summarizes the application of reinforcement learning algorithm in building indoor environment control system, and analyzes application of multi-agent reinforcement learning algorithm in building comfort control. Literature (Nizami et al., 2020) prospects the application of machine learning algorithm in building thermal comfort prediction model, and puts forward the application of artificial intelligence algorithm in building thermal comfort control. Literature (Rezaei and Dagdougui, 2020) analyzes the application of artificial intelligence and big data technology in energy saving of commercial/residential building design and operation, and verifies that the combination of artificial intelligence and big data technology can improve building energy efficiency and cost-effectiveness.

The above research focuses on energy management method and the application of artificial intelligence in building energy system, but few studies consider the impact of pricing decision-making between ESP and BCs on energy management. Dynamic pricing is a business strategy that adjusts the energy price in time, to allocate the right service to the right customer at the right time. Exploring the principle of demand response pricing is the key for ESP to make reasonable price strategies and gain benefit. Literature (Zhong et al., 2021) presents a deep reinforcement learning framework for dynamic pricing demand response of regenerative electric heating. Literature (Taherian et al., 2021) studies the dynamic pricing of electricity service provider in the day-ahead spot market. Literature (Lu et al., 2018) presents a dynamic pricing DR algorithm using reinforcement learning in smart grid. From the perspective of residential users, Literature (Wang et al., 2021) establishes a residential user evaluation system by selecting indicators related to user characteristics and electricity consumption data, and as well proposes a new interactive real-time pricing mechanism. Literature (Lu et al., 2021) proposes a pricing method that combines long short-term memory networks and reinforcement learning to solve the pricing problem of service providers. Literature (Xu et al., 2020) establishes a decision system for end-user to choose electricity price schemes. Literature (Kong et al., 2020) presents data-driven-based dynamic pricing method for sharing rooftop photovoltaic energy in a single apartment building.

From the above-mentioned literatures, it can conclude that the focus of building cluster energy management is to find the balance of interests between ESP and BCs, which is the key point for ESP to participate in building cluster energy management and for BCs to actively respond to ESP energy management strategy. However, there are few studies on the dynamic pricing between ESP and BCs, and the related studies do not consider the influence of dynamic pricing and energy consumption characteristics of BCs on energy management effect.

1.3 Paper Contributions and Structure

To deal with the above-mentioned limitations, this paper proposes an energy management and pricing strategy of BCES based on two-Stage optimization method. The main contributions of this paper include the following:

1) Proposed a dynamic pricing method by Markov decision in a regional energy market composed of ESP and BCs. Reinforcement learning is used to illustrate the pricing decision-making framework, and Q-learning is adopted to solve this Markov decision-making problem.

2) Focusing on the energy interaction under the dynamic pricing mechanism, a building cluster energy management framework under the guidance of ESP is proposed, and a distributed scheduling strategy is formulated based on the alternating direction multiplier method (ADMM). The ESP and BCs sub-problems are solved by transferring a few parameters to update the operation state, so as to realize the energy optimal utilization, reduce the operational pressure of ESP and protect the privacy information of BCs.

The rest of this paper is organized as follows: Section 2 describes the framework and mechanism, Section 3 presents the model and research approach, Section 4 discusses simulation results, Section 5 presents the main conclusions of this paper.

2 System Framework and Energy Management Mechanism

2.1 System Architecture

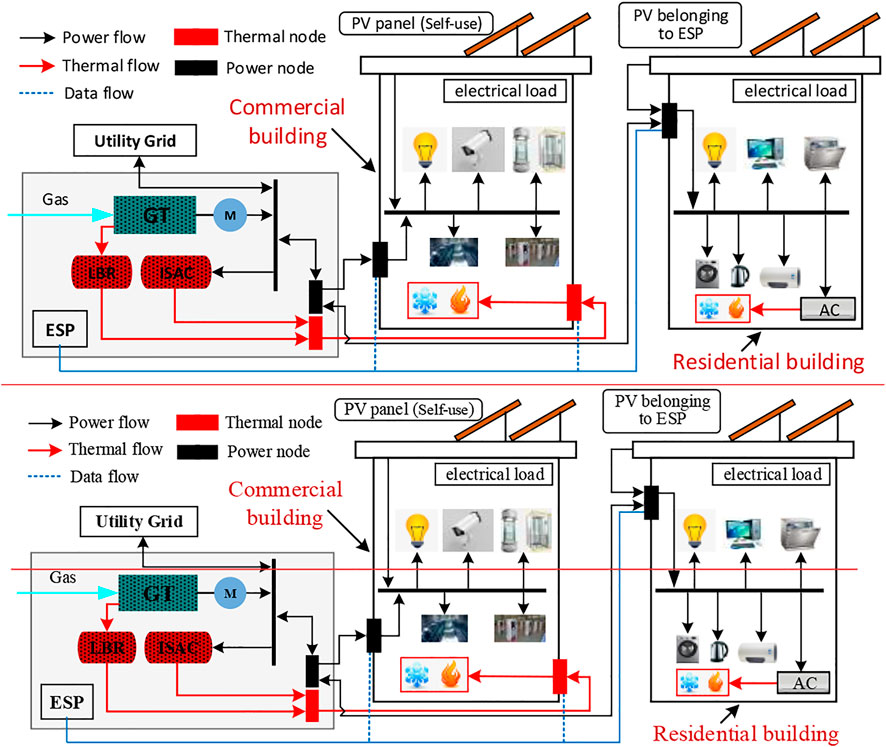
In this paper, a typical thermal-electrical hybrid energy system structure of building cluster is constructed, as shown in Figure 1.

FIGURE 1

FIGURE 1. Energy system structure of building cluster.

The system includes two stakeholders: ESP and BCs. ESP is equipped with Combined Cooling Heating and Power (CCHP) units and distributed photovoltaics (PV, installed on residential roofs), which are responsible for supplying electricity and thermal energy to commercial and residential buildings in the BCES. Commercial buildings are generally installed with PV, but ESP is still needed to supply insufficient electricity, thermal and cooling demand. There is no energy generation equipment in residential building, and its energy demand is completely met by ESP.

2.2 Pricing and Energy Management Framework

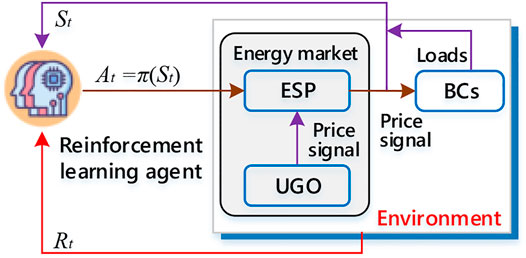
As shown in Figure 1, ESP is the most important operating entity in BCES, and the effectiveness of its energy management scheme is directly affected by the price strategy. Figure 2 shows the pricing decision-making and energy management framework in the BCES.

FIGURE 2

FIGURE 2. Pricing and energy management framework.

As shown in Figure 2, the Utility Grid Operator (UGO) calculates and announces the wholesale electricity prices to the ESP though internal optimization algorithms, considering the procurement cost and electricity generation capacity. Upon the receipt of wholesale electricity prices from UGO, the ESP will launch the DR program to its enrolled BCs. In specific, the ESP will firstly collect the energy demand and private parameters from BCs at the precondition of taking actions on behalf of BCs (Step1). Then ESP will calculate the optimal retail electricity and thermal prices for BCs by maximizing energy sales revenue via reinforcement learning method. Once getting the optimal retail prices, the ESP will announce these prices to its BCs (Step2). At the same time, ESP will formulate the best operation strategy of equipment and report the energy consumption information to UGO in line with its maximum benefit (Step3), and BCs finally form the actual consumption strategy of electric-thermal energy.

It is important to note that in the second stage, the RL method can simulate the social behavior of ESP and BCs, and work out the transaction prices that meet the psychological expectations of both parties.

3 Energy Collaborative Management Model Based on Markov Decision

3.1 Building Energy Cluster Model

3.1.1 Electrical Load Model

Electrical load profiles of BCs can be classified as critical and adjustable loads according to priorities (Yuan et al., 2021).

Critical load: it is very important that these electricity demands of BCs are met, such as consumption of electricity usage of fire control monitoring centers.

$E_{n,de}^{critic}\left(t\right)=E_{n,co}^{critic}\left(t\right)(1)$

Here, $E_{n,de}^{critic}\left(t\right)$ and $E_{n,co}^{critic}\left(t\right)$ indicate the energy demand and energy consumption of nth BC at time t.

Adjustable load: Compared with critical load, electricity demands such as heating, ventilation and electric vehicles of BCs usually decrease as the electricity price increases, these loads are uniformly classified as adjustable load, including transferable load and reducible load. The adjustable load model established in this paper not only considers BC’s willingness to adjust energy consumption behavior due to demand response price, but also considers the negative impact of ESP’s low energy price strategy. The consumed energy of the adjustable load for nth BC at time t is defined as:

${\displaystyle \sum _{t=1}^{T=24}{E}_n^{trans}\left(t\right)}-{\displaystyle \sum _{t=1}^{T=24}{E}_n^{\overline{trans}}\left(t\right)}=0(2)$

$E_n^{reduc}\left(t\right)=\overline{E_n^{reduc}\left(t\right)}\cdot {\zeta }_n^e\left(t\right)\cdot \left\{1-\frac{p_{buy}^{ugo,e}\left(t\right)-p_{buy}^e\left(t\right)}{p_{buy}^{ugo,e}\left(t\right)}\right\}(3)$

Here, $E_n^{trans}\left(t\right)$ and $E_n^{\overline{trans}}\left(t\right)$ indicate the transferable load after and before demand response of nth BC at time t. $E_n^{reduc}\left(t\right)$ indicates the reducible load. ${\zeta }_n^e\left(t\right)$ indicates electric elasticity coefficient of nth BC at time t. $p_{buy}^e\left(t\right)$ indicates the ESP electric selling price at time t. $p_{buy}^{ugo,e}\left(t\right)$ indicates the UGO electric selling price at time t. $\overline{E_n^{reduc}\left(t\right)}$ indicates the upper limit for reducible load at time t.

3.1.2 Thermal Load Model

Thermal load of BCs is defined as air heating or cooling load of commercial or office buildings in this paper. Thermal load profiles of BCs can be classified as critical and adjustable loads according to priorities (Liu et al., 2019).

Critical load: it is very important that these thermal demands of BCs are met. It is directly related to the living standards of BCs and generally cannot be affected.

$H_{n,de}^{critic}\left(t\right)=H_{n,co}^{critic}\left(t\right)(4)$

Here, $H_{n,de}^{critic}\left(t\right)$ and $H_{n,co}^{critic}\left(t\right)$ indicate the thermal demand and consumption of nth BC at time t.

Adjustable load: The load characteristics are closely related to ambient temperature and building characteristics.

${\theta }_n^{in}(t+1)={\theta }_n^{in}\left(t\right)e^{\frac{-\mathrm{\Delta }t}{RC}}+\left({\theta }_n^{out}(t+1)-R{H}_{AC,n}^{inj}\left(t\right)\right)(1-e^{\frac{-\mathrm{\Delta }t}{R\cdot C}})(5)$

$H_N^{total}\left(t\right)={\displaystyle \sum _{n=1}^N\frac{{\mathrm{\Phi }}_h\left({\theta }_n^{out}\left(t\right)-{\theta }_n^{in,set}\left(t\right)\right)}{R}}(6)$

Here, ${\theta }_n^{in}$ and ${\theta }_n^{out}$ indicate the indoor and outdoor temperatures. $R$ indicates the thermal resistance material. $C$ indicates the specific heat capacity of air. $H_{AC,n}^{inj}\left(t\right)$ indicates the thermal power injected into the room at time slot t. $H_n^{total}\left(t\right)$ indicates total thermal power required to ensure temperature at time t. $N$ indicates the number of users in BC. ${\Phi }_h$ indicates simultaneity factor. ${\theta }_n^{in,set}\left(t\right)$ indicates equipment temperature value set by user at time slot t.

In this paper, the thermal load of BCs is mainly used for indoor heating or cooling, which is non-transferable. In a certain range, changing the temperature of indoor heating or cooling has little impact on BCs. Therefore, the thermal load of BC can be scheduled by adjust heating or cooling power.

$H_{AC,n}^{inj-DR}\left(t\right)=\overline{H_{AC,n}^{inj}\left(t\right)}\cdot \left\{1-\frac{p_{buy}^{ugo,t}\left(t\right)-p_{buy}^t\left(t\right)}{p_{buy}^{ugo,t}\left(t\right)}\right\}(7)$

Here, $H_{AC,n}^{inj-DR}\left(t\right)$ indicates the amount of thermal load demand response at time t. $p_{buy}^t\left(t\right)$ indicates the ESP thermal selling price at time t. $p_{buy}^{ugo,t}\left(t\right)$ indicates the UGO thermal selling price at time t. $\overline{H_{AC,n}^{inj}\left(t\right)}$ indicates the upper limit for thermal load that nth BC can make adjustment at time t.

3.1.3 Comprehensive Benefit Model

The comprehensive benefit of BCs consists of utility function, satisfaction loss function and cost function (Wei et al., 2017; Li et al., 2021b). The utility of BCs is defined as the sum of satisfaction obtained by consuming various kinds of energy, which is commonly expressed by quadratic function.

$U_n^E\left(t\right)={\partial }_n^E{P}_{n,co}^E\left(t\right)-{\beta }_n^E{\left(P_{n,co}^E\left(t\right)\right)}^2(8)$

$U_n^T\left(t\right)={\partial }_n^T{P}_{n,co}^T\left(t\right)-{\beta }_n^T{\left(P_{n,co}^T\left(t\right)\right)}^2(9)$

Here, ${\partial }_n^E$ and ${\beta }_n^E$ indicate the satisfaction coefficient of electric energy consuming for nth BC. ${\partial }_n^T$ and ${\beta }_n^T$ indicate the satisfaction coefficient of thermal energy consuming for nth BC.

The BCs has the most suitable energy consumption in each period, and it deviates from the most suitable energy consumption, there will be a loss of utility.

$\{\begin{array}{c}{U}_n^{SL,E}\left(t\right)=\frac{1}{2}{\lambda }_n^E{\left(\mathrm{\Delta }{E}_n\left(t\right)\right)}^2+{\eta }_n^E\mathrm{\Delta }{E}_n\left(t\right)\\ \mathrm{\Delta }{E}_n\left(t\right)=\left|P_{n,co}^E\left(t\right)-E_{n,co}^{critic}\left(t\right)\right|\end{array}(10)$

$\{\begin{array}{c}{U}_n^{SL,T}\left(t\right)=\frac{1}{2}{\lambda }_n^T{\left(\mathrm{\Delta }{H}_n\left(t\right)\right)}^2+{\eta }_n^T\mathrm{\Delta }{H}_n\left(t\right)\\ \mathrm{\Delta }{H}_n\left(t\right)=\left|P_{n,co}^T\left(t\right)-H_{n,co}^{critic}\left(t\right)\right|\end{array}(11)$

Here, $U_n^{SL,E}\left(t\right)$ and $U_n^{SL,T}\left(t\right)$ indicate the utility loss for electric and thermal loads of nth BC at time t. $\Delta E_n\left(t\right)$ and $\Delta H_n\left(t\right)$ indicate the deviation for electric and thermal loads of nth BC at time t. $P_{n,co}^E\left(t\right)$ and $P_{n,co}^T\left(t\right)$ indicate the actual consumption for electric and thermal loads of BC n at time slot t. ${\lambda }_n^E$ and ${\eta }_n^E$ indicate the loss coefficient of electric load utility for nth BC. ${\lambda }_n^T$ and ${\eta }_n^T$ indicate the loss coefficient of thermal load utility for nth BC.

The energy cost of BCs mainly includes the cost of purchasing electricity and thermal from ESP.

$C_n^{energy}\left(t\right)=p_{buy}^e\left(t\right)P_{n,co}^E\left(t\right)+p_{buy}^t\left(t\right)P_{n,co}^T\left(t\right)(12)$

Here, $C_n^{energy}\left(t\right)$ indicates the energy cost of nth BC at time t.

To sum up, the interest pursuit of BCs can be expressed as the maximized comprehensive benefit function.

$\mathit{Max }{\mathit{F}}_{BC,n}={\displaystyle \sum _{t=1}^{T=24}\left\{U_n^E\left(t\right)+U_n^T\left(t\right)-U_n^{SL,E}\left(t\right)-U_n^{SL,T}\left(t\right)-C_n^{energy}\right\}}(13)$

3.2 Energy Service Provider Model

3.2.1 Operating Condition Model

3.2.1.1 Distributed Photovoltaic

PV is an important renewable energy power generation unit in the BCES. The output power of PV depends on the illumination intensity and the temperature of photovoltaic module.

$P_{pv}\left(t\right)=P_{STC}\frac{G_{pv}\left(t\right)}{G_{STC}}\left[1+{\alpha }_p\left(T_{pv}\left(t\right)-T_r\right)\right](14)$

Here, $P_{pv}\left(t\right)$ indicates the output power of PV at time slot t. $G_{pv}\left(t\right)$ indicates the light intensity at time slot t. $P_{STC}$ indicates the maximum output power of PV under standard test conditions. $G_{STC}$ indicates the light intensity under standard test conditions. ${\alpha }_p$ indicates power temperature coefficient. $T_{pv}\left(t\right)$ indicates the actual surface temperature of PV module. $T_r$ indicates the rate temperature of PV module under standard test conditions.

3.2.1.2 Ice Storage Air Conditioner System [25]

ISAC is composed of refrigeration unit and storage tank. In the period of low power consumption and low electricity price, ISAC can make ice and store cold by electric power, and then melt ice flexibly to supply cooling, thus reducing the electric power consumption during the peak period. The mathematical model of its refrigeration unit is as follows.

$P_{ISAC}\left(t\right)=\frac{H_{ISAC}\left(t\right)}{F_{CO{P}_{co}}\left[c{\left(\frac{H_{ISAC}\left(t\right)}{\overline{H_{ISAC}}}\right)}^2+b\frac{H_{ISAC}\left(t\right)}{\overline{H_{ISAC}}}+a\right]}(15)$

Here, $P_{ISAC}\left(t\right)$ and $H_{ISAC}\left(t\right)$ indicate the electric power and cooling power of ISAC at time t. $F_{CO{P}_{co}}$ indicates the rated energy efficiency ratio of ISAC system. $\overline{H_{ISAC}}$ indicates the maximum cooling power of ISAC system. $a$, $b$ and $c$ are the fitting coefficients of dynamic energy efficiency ratio of ISAC system.

3.2.1.3 Combined Cooling Heating and Power System

CCHP is a key energy production equipment, which burns natural gas to provide electricity energy, thermal energy and cooling energy at the same time. CCHP is mainly composed of micro gas turbine (MT), WHR and LBR. In this paper, we only consider the relationship between output power and fuel consumption of CCHP.

$P_{mt}^T\left(t\right)=\frac{P_{mt}^E\left(t\right)(1-{\eta }_e-{\eta }_l)}{{\eta }_e}(16)$

$P_{whr}^T\left(t\right)=P_{mt}^T\left(t\right){\eta }_{whr}(17)$

$V_{ng}\left(t\right)=\frac{P_{mt}^E\left(t\right)}{{\eta }_e\times LH{V}_{NG}}(18)$

Here, $P_{mt}^E\left(t\right)$ and $P_{mt}^T\left(t\right)$ indicate electrical and thermal power of MT at time t. ${\eta }_e$ and ${\eta }_l$ indicate operating efficiency and thermal loss coefficient of MT. $P_{whr}^T\left(t\right)$ indicates the thermal power of WHR at time t. ${\eta }_{whr}$ indicates the thermal recovery efficiency of WHR. $V_{ng}\left(t\right)$ indicates the natural gas consumption of MT. $LH{V}_{NG}$ indicates the low calorific value of natural gas.

LBR is a thermal-driven refrigeration equipment, and its main parameters are thermal consumption, cold output and coefficient of performance.

$P_{lbr}^T\left(t\right)=CO{P}_T{P}_{in}^T\left(t\right)(19)$

Here, $P_{lbr}^T\left(t\right)$ indicates the cooling power of LBR at time t. $CO{P}_T$ indicates the coefficient of performance of LBR. $P_{in}^T\left(t\right)$ indicates the thermal energy input into LBR at time t.

3.2.2 Comprehensive Benefit Model

The comprehensive benefit of ESP consists of revenue function and cost function. ESP’s revenue is defined as the sales revenue of ESP supplying energy to BCs.

$R_{ESP}^{energy}={\displaystyle \sum _{t=1}^{T=24}\left[p_{buy}^e\left(t\right)P_{n,co}^E\left(t\right)+p_{buy}^t\left(t\right)P_{n,co}^T\left(t\right)\right]}(20)$

Here, $R_{ESP}^{energy}\left(t\right)$ indicates the sales revenue of ESP at time t.

The cost of ESP mainly includes transaction cost with UGO, fuel cost, equipment operation cost and environmental cost.

$\begin{array}{l}{C}_{ESP}^{total}={\displaystyle \sum _{t=1}^{T=24}[p_{sell}^{ugo,e}\left(t\right)\max (-P_{ugo}^E\left(t\right),0)+p_{buy}^{ugo,e}\left(t\right)\max (P_{ugo}^E\left(t\right),0)]}\\ \begin{array}{cc}& \end{array}+{\displaystyle \sum _{t=1}^{T=24}{p}_{buy}^{ng}\left(t\right)V_{ng}\left(t\right)}+{\displaystyle \sum _{t=1}^{T=24}{\displaystyle \sum _{i=1}^N{p}_i^{op}{P}_i\left(t\right)}}+{\displaystyle \sum _{t=1}^{T=24}{\displaystyle \sum _{m=1}^M{p}_m^{en}{\theta }_m^{en}{V}_{ng}\left(t\right)}}\end{array}(21)$

Here, $C_{ESP}^{total}$ indicates the total cost of ESP. $p_{buy}^{ugo,e}\left(t\right)$ and $p_{sell}^{ugo,e}\left(t\right)$ indicate the price at which ESP buys and sells electric energy from UGO. $P_{ugo}^E\left(t\right)$ indicates the exchange of power between ESP and UGO at time t. $p_{buy}^{ng}$ indicates the nature gas price. $p_i^{op}$ indicates the operating cost per unit power of equipment i. $P_i\left(t\right)$ indicates the power of equipment i. $p_m^{en}$ indicates the emission cost per unit mass of pollutant m. ${\theta }_m^{en}$ indicates the emissions of pollutant m produced by unit volume of natural gas.

Therefore, the interest pursuit of ESP can be expressed as the maximized comprehensive benefit function.

$\mathit{Max }{\mathit{F}}_{ESP}=R_{ESP}^{energy}-C_{ESP}^{total}(22)$

3.3 Pricing MDP Model Based on RL Algorithm

In this paper, the dynamic retail pricing problem is modeled as a discrete finite horizon Markov decision process (MDP). In this pricing decision-making MDP model for ESP, the reward and electricity and thermal energy consumption depend only on the energy demand and retail price at the corresponding time slot but not on the historical data. Figure 3 shows the framework and mechanism of the MDP dynamic pricing model.

FIGURE 3

FIGURE 3. Framework of the MDP dynamic pricing model.

As shown in the Figure 3, where the price-energy interaction process between ESP and BCs constitutes an environment for reinforcement learning agent. ESP pricing strategy denotes the action that the ESP sends to the BCs, the load information of the BCs represent the state, and the comprehensive benefit of ESP and BCs indicate the reward.

MDP is usually described by state space S, action space A, reward function R and state transition rate P (Zhang et al., 2019; Lu et al., 2021). According to the MDP pricing model between ESP and BCs discussed in this paper, the main elements are modeled as follows.

3.3.1 Selection of State Space

For the state space $S$ in this paper, it mainly includes the power consumption of electrical load of BCs, the power consumption of thermal load of BCs, and the adjustment of electric load and thermal load. For BCs, the state space $S_t$ at sampling time $t$ can be defined as:

$S_t=\left[P_{n,co}^E\left(t\right),P_{n,co}^T\left(t\right),E_n^{trans}\left(t\right),E_n^{reduc}\left(t\right),H_{AC,n}^{inj-DR}\left(t\right),t\right](23)$

At each transaction time, BCs will formulate load response strategy and load consumption strategy according to the ESP pricing information and the operation state information such as energy demand collected and reported by each BC, and then update the whole state space.

3.3.2 Selection of Action Strategy Set

In the process of energy trading between ESP and BCs, ESP is always in a dominant position, and is willing to gain the maximum benefit for itself by adjusting the energy price strategy. For ESP, the action strategy space $A_t$ at sampling time $t$ can be defined as:

$A_t=\left[p_{buy}^e\left(t\right),p_{buy}^t\left(t\right),t\right](24)$

However, the advantages of ESP are not unlimited. Energy pricing strategy is also limited to some extent:

$p_{buy,\min }^{ugo,e}\le \overline{\overline{p_{buy}^e}}\le p_{buy,\max }^{ugo,e}(25)$

$\overline{\overline{p_{buy}^t}}\le p_{buy,\max }^{ugo,t}(26)$

Here, $p_{buy,\min }^{ugo,e}$ and $p_{buy,\max }^{ugo,e}$ indicate minimum and maximum value of UGO wholesale electricity price. $p_{buy,\max }^{ugo,t}$ indicates the maximum value of UGO thermal wholesale price. $\overline{\overline{p_{buy}^e}}$ and $\overline{\overline{p_{buy}^t}}$ indicate the ESP average electric and thermal selling price.

At each transaction moment, ESP will update the pricing strategy and action space. Then agent calculate the current transaction reward value and cumulative reward value.

3.3.3 Selection of Reward Function

It is precisely because the energy trading behavior between ESP and BCs is similar to a price game behavior, and the benefits generated by both sides should be considered in the pricing decision-making process. Therefore, we consider both ESP’s benefit and BCs’ benefit as the components of reward function (Rajaei et al., 2021).

$R_t=\mathit{Max }{\displaystyle \sum _{n=1}^N{\displaystyle \sum _{t=1}^{T=24}\left(\left(1-r\right)F_{BC,n}+r{R}_{ESP}^{energy}\right)}}(27)$

Here, $r\in \left[\mathrm{0,1}\right]$ indicates the weighting factor of relative importance between ESP’s benefit and BCs’ benefit.

3.3.4 MDP Process Based on RL Algorithm

In most cases, the state transition rate is difficult to estimate, and the traditional model-based methods such as dynamic programming are difficult to solve. In particular, the energy consumption behavior of BCs is regarded as the environment of ESP pricing decision-making, which cannot be modeled, because the BCs energy consumption behavior is integrated with information, society and physics, and it cannot be accurately described by mathematical model.

Therefore, this paper adopts the model-free reinforcement learning method, which can effectively deal with model-free problems and does not need information such as state transition rate. In this paper, a model-free Q-learning algorithm is chosen to solve the MDP problem and basic theory of Q-learning algorithm can be referred to (Lu et al., 2021). Table 1 shows the flowchart for implementing the Q-learning mechanism.

TABLE 1

TABLE 1. Flowchart for implementing the Q-learning mechanism.

3.4 Optimized Scheduling Model Based on ADMM Algorithm

3.4.1 Distributed Solution Mechanism of Energy Management Problem for ESP and BCs

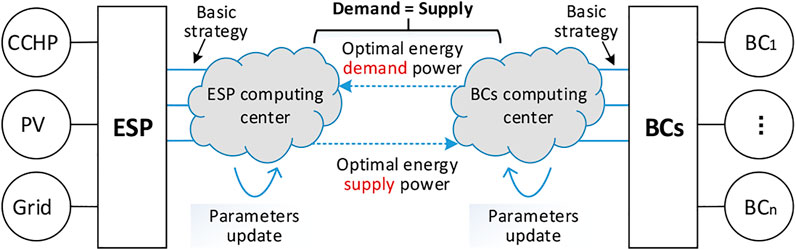
The core of energy management problem between ESP and BSs is that two sides form optimal operation strategy and energy consumption strategy driven by interests. Mechanism of ESP and BCs energy management problems is shown in Figure 4.

FIGURE 4

FIGURE 4. Mechanism of ESP and BCs energy management problems.

ESP and BCs have their own virtual computing centers, ESP will upload its current policy parameters to the computing center, and the computing center will issue ESP energy supply strategy and update the parameters according to the solution results. The calculation centers of both sides will transfer the calculated shared variable values to each other, and update the shared variable values and energy supply and demand.

In order to avoid the problems of complex model and excessive traffic, this paper uses ADMM algorithm to solve the energy management problem between ESP and BCs. The ADMM algorithm has the characteristics of fast convergence and good convergence performance, which has been widely applied in the field of energy system optimization. The basic principle of ADMM algorithm can be referenced to (Wang et al., 2019).

Based on this solution mechanism, the transmission power at the junction of ESP and BCs is selected as the shared variable, which is the energy supply power at ESP side and the energy demand power at BCs side. Equation 28 is used to characterize the coupling relationship between the two subjects.

$\left[\begin{array}{c}{P}_{\text{de},bc}\\ H_{\text{de},bc}\end{array}\right]-\left[\begin{array}{c}{P}_{\sup ,esp}\\ H_{\sup ,esp}\end{array}\right]=0(28)$

Here, $P_{\text{de},bc}$ and $H_{\text{de},bc}$ indicate the electric and thermal demand of BCs. $P_{\sup ,esp}$ and $H_{\sup ,esp}$ indicate the electric and thermal supply of ESP.

3.4.2 Distributed Optimization of BCES Based on ADMM

According to the ADMM algorithm, the energy management problem is decomposed into two sub-problems: ESP optimal operation and BCs optimal consumption. Each sub-problem aims at the maximum benefit. Then the energy management model of the whole BCES is solved, and the optimal energy management strategy is obtained. The energy management problem between ESP and BCs is deduced as the standard form of ADMM.

$\mathbf{max}\left(F_{ESP}+F_{BCs}\right)(29)$

$F_{BCs}={\displaystyle \sum _{n=1}^N{F}_{BC,n}}(30)$

Considering the physical boundary of system energy management, the related variables should not only satisfy the constraints in Part A and Part B, but also satisfy the power balance constraints of system.

$P_{\text{de},bc}={\displaystyle \sum \left(P_{pv}+P_{mt}^E+P_{ugo}^E-P_{ISAC}\right)}(31)$

$H_{\text{de},bc}={\displaystyle \sum \left(H_{ISAC}+P_{mt}^T\right)}(32)$

Constraints 31) and 32) ensure that the actual electricity and thermal supply of ESP are equal to the expected energy consumption of BCs, so as to minimize the total operating cost. According to the principle of ADMM algorithm, the iterative form of each sub-problem can be deduced.

${\mathit{x}}^{k+1}=\underset{\mathbf{w}}{\arg \max }\left(F_{ESP}+\frac{\rho }{2}{\Vert \left[\begin{array}{c}{\mathit{P}}_{de,bc}\\ {\mathit{H}}_{de,bc}\end{array}\right]-\left[\begin{array}{c}{\mathit{P}}_{\sup ,esp}^k\\ {\mathit{H}}_{\sup ,esp}^k\end{array}\right]+{\mathbf{u}}^k\Vert }_2^2\right)(33)$

${\mathbf{w}}^{k+1}=\underset{\mathbf{w}}{\mathrm{argmin}}\left(F_{BCs}+\frac{\rho }{2}{\Vert \left[\begin{array}{c}{\mathit{P}}_{de,bc}^{k+1}\\ {\mathit{H}}_{de,bc}^{k+1}\end{array}\right]-\left[\begin{array}{c}{\mathit{P}}_{\sup ,esp}\\ {\mathit{H}}_{\sup ,esp}\end{array}\right]+{\mathit{u}}^k\Vert }_2^2\right)(34)$

${\mathbf{u}}^{k+1}={\mathbf{u}}^k+\left[\begin{array}{c}{\mathit{P}}_{de,bc}^{k+1}\\ {\mathit{H}}_{de,bc}^{k+1}\end{array}\right]-\left[\begin{array}{c}{\mathit{P}}_{\sup ,esp}^{k+1}\\ {\mathit{H}}_{\sup ,esp}^{k+1}\end{array}\right](35)$

$\mathbf{w}=\left[P_{pv},P_{mt}^E,P_{ugo}^E,P_{ISAC},P_{\sup ,esp},H_{ISAC},P_{mt}^T,H_{\sup ,esp}\right](36)$

$\mathbf{x}=\left[P_{\text{de},bc},H_{\text{de},bc}\right](37)$

Here, $\rho$ indicates the penalty coefficient. $k$ indicates the iterations. ${\mathbf{u}}^k$ indicates the Lagrange multiplier vector in the iteration $k$.

According to the solving rules of ADMM algorithm, original residual $r^k$ and dual residual $s^k$ are taken as the convergence conditions.

${\Vert r^k\Vert }_2^2={\Vert \left[\begin{array}{c}{P}_{de,bc}^{k+1}\\ H_{de,bc}^{k+1}\end{array}\right]-\left[\begin{array}{c}{P}_{\sup ,esp}^{k+1}\\ H_{\sup ,esp}^{k+1}\end{array}\right]\Vert }_2^2\le {\mathit{\epsilon }}^{pri}(38)$

${\Vert s^k\Vert }_2^2={\Vert \rho ({\mathbf{w}}^k-{\mathbf{w}}^{k-1})\Vert }_2^2\le {\epsilon }^{dual}(39)$

Here, ${\epsilon }^{pri}$ and ${\epsilon }^{dual}$ indicate the set value of convergence error corresponding to the original residual and the dual residual.

In the process of optimization, BCs performs optimization scheduling to obtain the electricity consumption of each user, the electric energy and thermal energy that BCs expect ESP to provide, and upload the optimized expected energy supply to ESP. Secondly, considering the expected value of BCs, ESP performs distributed iteration on the cost, optimizes equipment output and broadcasts it to BCs, while the Lagrange multipliers are updated independently by ESP and BCs. Table 2 shows the solution flow of ADMM algorithm in optimal scheduling stage.

TABLE 2

TABLE 2. Solution flow of ADMM algorithm in optimal scheduling stage.

4 Case Study

4.1 Basic Data

In this paper, a BCES comprising of one commercial building, one residential building and one hotel building is selected as the study case. All the load data are collected from the smart meters of buildings in Guangzhou, China in summer. Considering that the energy system studied in this paper involves power system, thermal system and gas system, and different systems operate in different dynamic processes and time scales. In this paper, the optimization time scale is set to 1 h ().

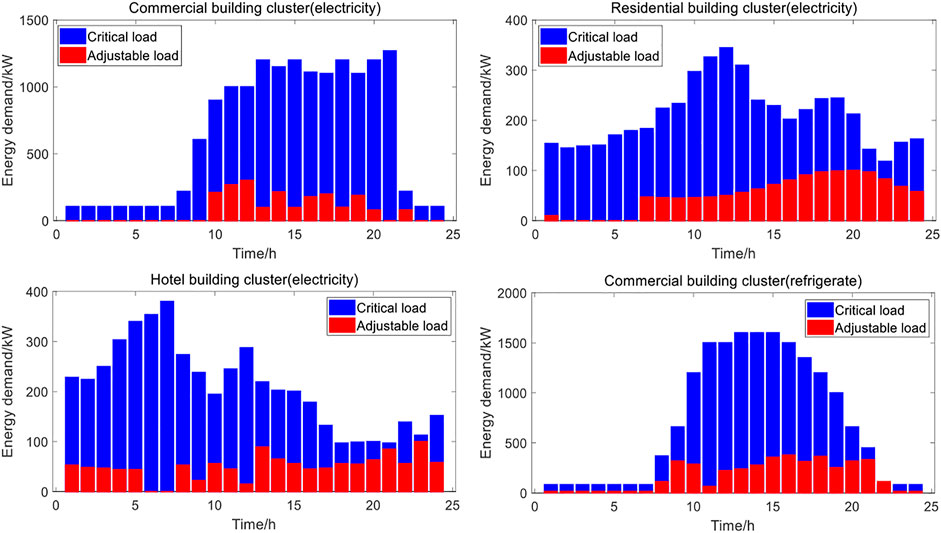
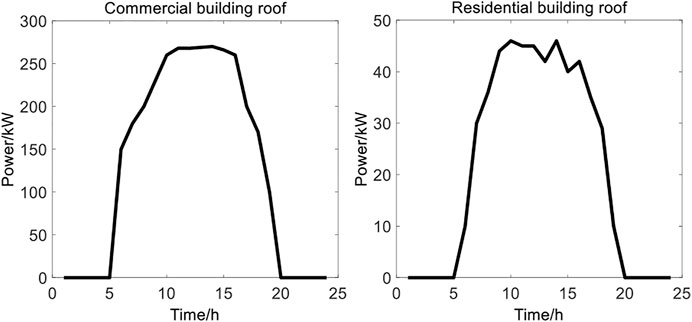
The daily load curves of these buildings are shown in Figure 5. The ESP is responsible for the energy supply, and it has distributed PV (Installed on the residential roof) and CCHP systems. The equipment attribution and load demand of the BCES system are shown in Table 3. Figure 6 shows the rated photovoltaic output at different installation positions.

FIGURE 5

FIGURE 5. Energy demand profile of three building clusters.

TABLE 3

TABLE 3. Equipment capacity and energy demand.

FIGURE 6

FIGURE 6. Rated photovoltaic output at different installation positions.

It can be seen from the physical characteristics of the system in Table 3 that ESP has an absolute dominant advantage in this BCES. Nevertheless, ESP’s pricing strategy still needs to be influenced and restricted by UGO. Table 4 shows the wholesale prices of UGO on a typical day.

TABLE 4

TABLE 4. UGO wholesale prices on a typical day CNY/kWh.

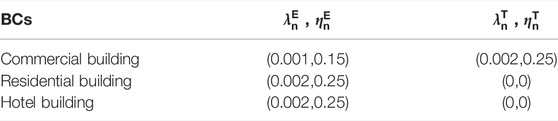
Table 5 shows the load preference parameters of different BCs, and Table 6 shows the electrical load elastic coefficient ${\zeta }_n^E$ for different BCs. Table 7 shows the equipment parameters.

TABLE 5

TABLE 5. Load preference parameters of BCs.

TABLE 6

TABLE 6. Electrical load elastic coefficient for different BCs.

TABLE 7

TABLE 7. Equipment parameters in the BCES.

4.2 Simulation Results

4.2.1 ESP and BCs Pricing Results

This section presents numerical simulation results to assess the performance of the proposed pricing decision-making MDP model according to the algorithm flow shown in Table 1. And the parameters required are shown in Section 3.1.

In the simulation of this section, the value of weighting factor $r$ (Relative importance between ESP’s benefit and BCs’ benefit) is taken as 0.5. Figures 7–9 show the pricing decision-making and load adjustment willingness results of commercial building, residential building and hotel building respectively.

FIGURE 7

FIGURE 7. Pricing decision-making results of Commercial building cluster.

FIGURE 8

FIGURE 8. Pricing decision-making results of residential building cluster.

FIGURE 9

FIGURE 9. Pricing decision-making results of hotel building cluster.

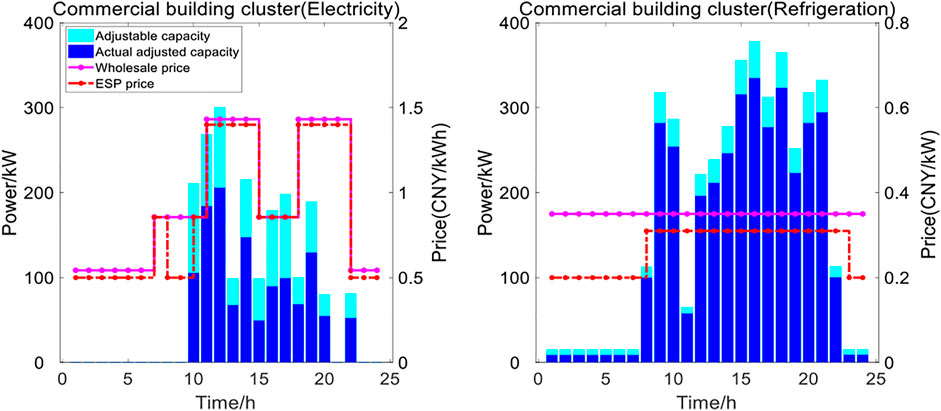
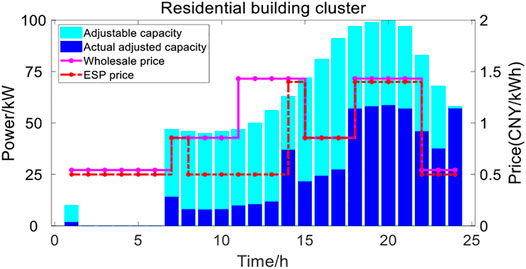
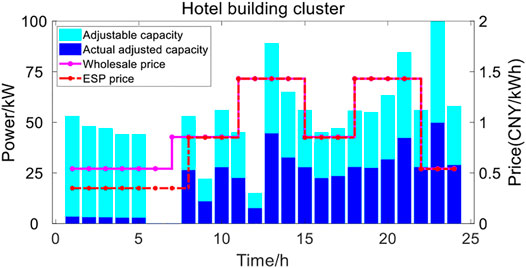
The wholesale price of UGO is a widely known information for both ESP and BCs. For BC, it will evaluate its own energy consumption behavior under the influence of such open information, which leads to BC’s willingness to adjust its own load according to the wholesale energy price in the market, namely BC’s load adjustable capacity. This willingness is constrained by BC’s own electricity consumption behavior and comfort, which can be represented by load elastic coefficient. In order to increase income, ESP will guide BCs to adjust energy consumption behavior by setting energy prices, whose average value is less than the UGO wholesale price, and the ESP prices curve can be seen from the Figures 7–9.

The above factors will lead to some unusual phenomena in the MDP pricing stage of ESP and BCs, and BCs will weaken the willingness of load reduction due to the wholesale price of the market driven by the psychology of interest balance. In this phenomenon, the psychological desires of ESP and BCs will be satisfied. Due to the above reasons, the actual load adjustment of commercial cluster, residential cluster and building cluster is less than the expected adjustable capacity, as shown in the Figures 7–9.

In this stage of interaction, ESP and BCs made energy transaction pricing decisions under influence of profit-seeking psychology. ESP gives BCs the acceptable energy price within its own profit range, and BCs feeds back the actual energy consumption demand that can satisfy profit-seeking psychology of ESP. In a word, the real transaction intention between ESP and BCs is solved by the established MDP pricing model.

4.2.2 Optimal Scheduling Results of BCES

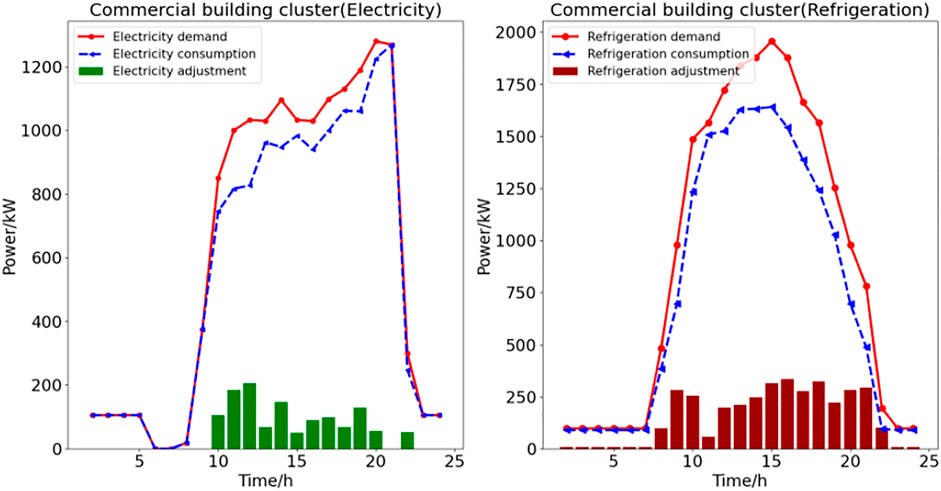
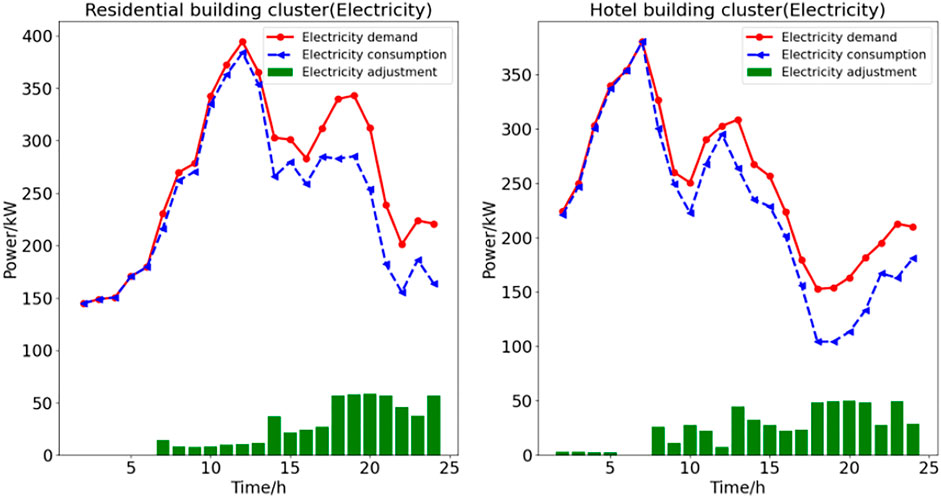
In this section, the energy management of BCES is carried out through the established optimal scheduling model on the basis of obtaining the trading willingness of both parties. Figures 10, 11 show the real energy consumption curves of three building clusters, and Figure 12 shows the electro-thermal equipment operating conditions of ESP.

FIGURE 10

FIGURE 10. Energy consumption curves of commercial BC.

FIGURE 11

FIGURE 11. Real energy consumption curves of other BCs.

FIGURE 12

FIGURE 12. Equipment operating conditions of ESP.

As shown in Figure 10, the commercial building reduced the electrical load and refrigeration load greatly from 10: 00–20: 00. In this period, commercial building is in the business stage, and the gap between ESP price and UGO wholesale price is small. Therefore, the commercial building has carried out load adjustment in a way close to the maximum load reduction intention. However, the energy demand of commercial building is relatively small in other periods, and the lower energy price of ESP does not affect its energy consumption behavior.

Compared with commercial building, residents building and hotel building show different energy consumption behaviors, which are caused by their operating habits and ESP price stimulation.

For the resident building, ESP gives an energy price far lower than the wholesale price from 8: 00–13: 00, which makes the resident building give up the original load reduction plan (As shown in the figure, the load curve of the resident building is hardly adjusted in this period). In other periods, ESP electricity price is almost close to wholesale price, and resident building is not active in changing its plan. Similarly, hotel building shows similar behavior to resident building, because their operating habits are similar.

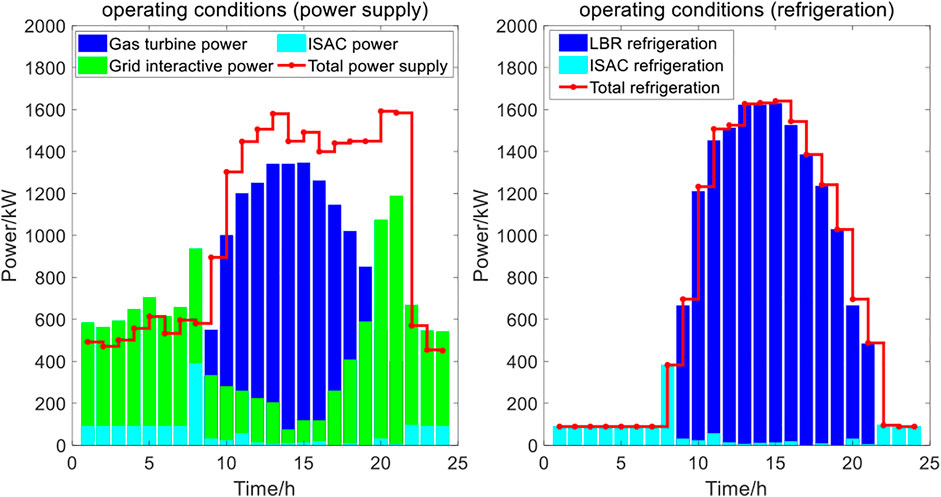
Figure 12 shows the best operation strategy of ESP equipment under the condition of meeting the electricity and cooling demands of 3 BCs. ESP gives priority to dispatching CCHP and PV in the system to supply the power demand of BCs and ISAC. However, the gas turbine is constrained by the operating cost and environmental emissions, and the power output by the gas turbine and PV cannot meet all the power demands, and the insufficient power is obtained by trading with UGO. It can be seen from Figure 12 that ESP buys a large amount of electricity from UGO during the period of low wholesale price at 1: 00–8: 00 and 22: 00–24: 00. At the same time, the refrigeration demand in the system is preferentially met by CCHP system, and the insufficient part is provided by ISAC.

4.3 Discussion and Analysis

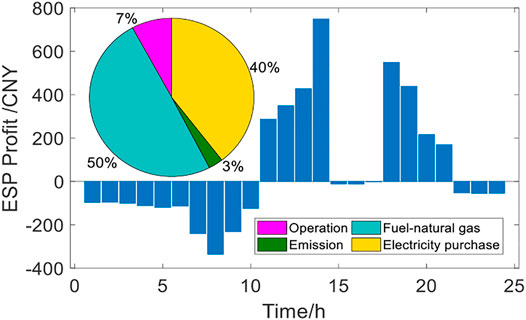
As mentioned earlier, this paper makes pricing decision and system operation optimization in BCES system in order to improve the operation efficiency of ESP and BCs. The economic results of energy management are shown in Table 8 and Figure 13.

TABLE 8

TABLE 8. Optimal results of the ESP.

FIGURE 13

FIGURE 13. Cost composition and hourly benefit of ESP.

As shown in Table 8, ESP can obtain a total benefit of 1429.08 CNY in the optimization of a typical day. The benefit of ESP is the remaining part of energy supply income obtained from BCs excluding the total operating cost. Figure 13 shows the cost composition and hourly benefit of ESP.

Figure 13 shows in detail the change trend of ESP benefit in 1 day. During 1:00–10:00 and 22:00–24:00, ESP is in a state of benefit loss. During these periods, the electricity and refrigeration demand of BCs are small. ESP shut down CCHP in order to avoid the gas turbine running under a low load state. As a result, the energy supply in the system must depend on UGO, which makes ESP have to pay high electricity bills and ISAC operating expenses. This benefit trend of ESP is consistent with the operating conditions of the electric-thermal unit shown in Figure 12.

In addition, from Figure 13, we can clearly observe the daily cost composition of ESP, in which fuel cost and electricity purchase cost account for almost 90% of the total cost. At the same time, commercial building, resident building and hotel building need to pay 20,611.39 CNY, 4382.92 CNY and 4354.75.77CNY energy costs respectively. Compared with direct acquisition of electric energy and thermal energy from UGO, their energy costs have been reduced by 2.11, 24.71 and 10.86%, respectively.

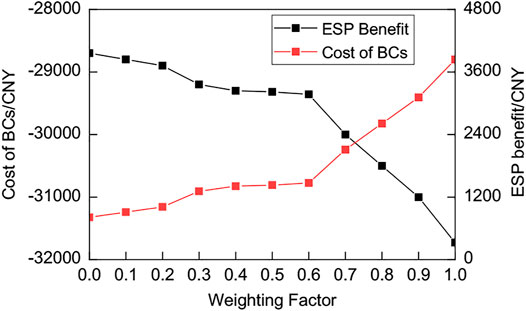
The above-mentioned economic dispatching results of ESP and BCs are obtained when the reward weight factor $r$ in MDP is 0.5, in which case ESP and BCs have equal importance in pricing decision-making. However, in the actual energy trading market, each trading subject has different positions, which leads to the fact that this weighting factor is not necessarily fair to all parties. Figure 14 shows the impact of reward weight factor in MDP on economic dispatch results.

FIGURE 14

FIGURE 14. Impact of reward weight factor on economic dispatch results.

From Figure 14, we can observe that an increase in $r$ from 0 to 1 lead to a decrease of the ESP benefit and the BCs’ energy cost. The reason is obvious: as weight factor increases, the BCs’ costs become more important compared to the ESP benefit. In particular, in the case when $r$ = 1, the system tends to minimize the BCs’ costs, and the ESP chooses relatively low energy prices to the BCs. On the contrary, when $r$ = 0, the ESP aims at maximizing its own benefit that does not consider the BCs’ costs. Hence, the ESP chooses relatively high retail prices. The above-mentioned reward weight factor finally leads to the trend shown by the curve in the Figure 14 as the ESP benefit and BCs cost change with the reward weight factor in the system operation optimization stage.

In addition, it can be seen from the Figure 14 that when the reward weight factor changes in the range of 0.3–0.6, the system economic dispatching result fluctuates less, while in other ranges, it will change greatly. However, even in the extreme case where the reward weight factor is 1 or 0, the optimization result is still strictly constrained. For example, when the reward weight factor is 0, it can still ensure that the energy cost of BCs is not higher than the cost of purchasing energy from UGO. Moreover, when the reward weight factor is 1, ESP can still be guaranteed to be profitable. This is because the strategies of ESP and BCs are clearly and reasonably constrained in the pricing decision-making stage.

5 Conclusion

In this paper, a dynamic pricing decision-making and energy management framework is proposed for BCES with ESP and different BCs based on two-Stage optimization method. First, this paper establishes the comprehensive benefit models that can reflect the characteristics and profit-seeking psychology of ESP and BCs, and put forward a dynamic pricing decision-making method between ESP and BCs in a hierarchical energy market, wherein the ESP can adaptively decide the retail energy price using the data driven methodology according to the BCs’ benefit and the UGO wholesale prices. Then, an operation optimization model of the BCES is established to optimize the energy consumption behavior of BCs and formulate best operation strategy of ESP’ equipment, and put forward a distributed solution framework, in which ADMM algorithm is used to solve the operation optimization problem.

The simulation cases have shown the benefits of the dynamic pricing decision-making and energy management framework of the BCES. In the stage of pricing decision-making, the pricing decision-making simulation process constructed by reinforcement learning method can make energy prices that not only meet the energy consumption habits and consumption psychology of commercial building, resident building and hotel building, but also meet the operation interest needs of ESP. In the operation optimization stage, the optimization model based on ADMM algorithm can realize the economical and efficient operation of the system and minimize the energy cost of BCs. Compared with directly obtaining energy from UGO, BCs’ costs have been reduced by 2.11, 24.71 and 10.86%, respectively. In addition, through numerical analysis, we also find the relationship between energy management results and the reward weight factors in MDP, and the economic boundary of system energy management in some extreme cases.

The pricing strategy proposed in this paper mainly focuses on electricity price and thermal price. With the gradual implementation of the carbon trading mechanism in the energy market, the trading and pricing of carbon emission quota will become the key factor in the future energy trading market. Therefore, in the future research, we will consider the carbon trading prices into the multi-energy pricing strategy.(Du et al., 2017).

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

1) LM: Modeling, writing and simulation 2) JL: instructor 3) QW: Modeling.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

ADMM, Alternating Direction Multiplier Method Algorithm; BCES, Building Cluster Energy System; BCs, Building Clusters; CCHP, Combined Cooling Heating and Power; ESP, Energy Service Provider; GT, Gas Turbine; ISAC, Ice Storage Air Conditioner System; LBR, Lithium Bromide Refrigerator; MDP, Markov Decision Process; RL, Reinforcement Learning; UGO, Utility Grid Operator; WHR, Waste Heat Recovery Device.

References

Antoniadou-Plytaria, K., Steen, D., Tuan, L. A., Carlson, O, and Fotouhi Ghazvini, M. A., (2020). Market-based Energy Management Model of a Building Microgrid Considering Battery Degradation. IEEE T Smart Grid 12 (2), 1794–1804.

Google Scholar

Du, Y., Gai, W.-m., Jin, L.-z., and Sheng, W. (2017). Thermal comfort Model Analysis and Optimization Performance Evaluation of a Multifunctional Ice Storage Air Conditioning System in a Confined Mine Refuge Chamber. Energy 141, 964–974. doi:10.1016/j.energy.2017.09.123

CrossRef Full Text | Google Scholar

Kermani, M., Adelmanesh, B., Shirdare, E., Sima, C. A., Carnì, D. L., and Martirano, L. (2021). Intelligent Energy Management Based on SCADA System in a Real Microgrid for Smart Building Applications. Renew. Energ. 171, 1115–1127. doi:10.1016/j.renene.2021.03.008

CrossRef Full Text | Google Scholar

Kong, X., Kong, D., Yao, J., Bai, L., and Xiao, J. (2020). Online Pricing of Demand Response Based on Long Short-Term Memory and Reinforcement Learning. Appl. Energ. 271, 114945. doi:10.1016/j.apenergy.2020.114945

CrossRef Full Text | Google Scholar

Li, A., Xiao, F., Zhang, C., and Fan, C. (2021). Attention-based Interpretable Neural Network for Building Cooling Load Prediction. Appl. Energ. 299 (10), 117238. doi:10.1016/j.apenergy.2021.117238

CrossRef Full Text | Google Scholar

Li, P., Wu, D., and Li, Y. (2021). Optimal Scheduling Strategy of Multi-Microgrid Integrated Energy System Based on Comprehensive Demand Response and Master-Slave Game. Proc. CSEE 41 (04), 1307–1321+1538.

Google Scholar

Liu, P., Ding, T., Zou, Z., and Yang, Y. (2019). Integrated Demand Response for a Load Serving Entity in Multi-Energy Market Considering Network Constraints. Appl. Energ. 250, 512–529. doi:10.1016/j.apenergy.2019.05.003

CrossRef Full Text | Google Scholar

Lombardi, F., Roccoa, M. V., Belussi, L., Danza, L., Magni, C., Colombo, E., et al. (2021). Weather-induced Variability of Country-Scale Space Heating Demand under Different Refurbishment Scenarios for Residential Buildings. Energy 239, 122152.

Google Scholar

Lu, R., Hong, S. H., and Zhang, X. (2018). A Dynamic Pricing Demand Response Algorithm for Smart Grid: Reinforcement Learning Approach. Appl. Energ. 220 (JUN.15), 220–230. doi:10.1016/j.apenergy.2018.03.072

CrossRef Full Text | Google Scholar

Lu, T., Chen, X., Mcelroy, M. B., Nielsen, C. P., Wu, Q., and Ai, Q. (2021). A Reinforcement Learning-Based Decision System for Electricity Pricing Plan Selection by Smart Grid End Users. IEEE Trans. Smart Grid 12 (3), 2176–2187. doi:10.1109/tsg.2020.3027728

CrossRef Full Text | Google Scholar

Ma, K., Yu, Y., Yang, B., and Yang, J. (2019). Demand-Side Energy Management Considering Price Oscillations for Residential Building Heating and Ventilation Systems. IEEE Trans. Ind. Inf. 15 (8), 4742–4752. doi:10.1109/tii.2019.2901306

CrossRef Full Text | Google Scholar

Mason, K., and Grijalva, S. (2019). A Review of Reinforcement Learning for Autonomous Building Energy Management. Comput. Electr. Eng. 78, 300–312. doi:10.1016/j.compeleceng.2019.07.019

CrossRef Full Text | Google Scholar

Nizami, M. S. H., Hossain, M. J., and Fernandez, E. (2020). Multiagent-Based Transactive Energy Management Systems for Residential Buildings with Distributed Energy Resources. IEEE Trans. Ind. Inf. 16 (3), 1836–1847. doi:10.1109/tii.2019.2932109

CrossRef Full Text | Google Scholar

Paul, S., and Padhy, N. P. (2019). Real Time Bi-level Energy Management of Smart Residential Apartment Building. IEEE T Ind. Inform. 16 (6), 3708–3720.

Google Scholar

Rajaei, A., Fattaheian-Dehkordi, S., Fotuhi-Firuzabad, M., and Moeini-Aghtaie, M. (2021). Decentralized Transactive Energy Management of Multi-Microgrid Distribution Systems Based on ADMM. Int. J. Electr. Power Energ. Syst. 132, 107126. doi:10.1016/j.ijepes.2021.107126

CrossRef Full Text | Google Scholar

Rezaei, E., and Dagdougui, H. (2020). Optimal Real-Time Energy Management in Apartment Building-Integrating Microgrid with Multi-Zone HVAC Control. IEEE T Ind. Inform. doi:10.1109/tii.2020.2972803

CrossRef Full Text | Google Scholar

Shakeri, M., upuleti, J., Amin, N., Rokonuzzaman, M., Low, F. W., Yaw, C. T., et al. (2020). An Overview of the Building Energy Management System Considering the Demand Response Programs, Smart Strategies and Smart Grid. Energies 13 (13), 3299. doi:10.3390/en13133299

CrossRef Full Text | Google Scholar

Soetedjo, A., Nakhoda, Y. I., and Saleh, C. (2019). An Embedded Platform for Testbed Implementation of Multi-Agent System in Building Energy Management System. Energies 12 (9), 3655. doi:10.3390/en12193655

CrossRef Full Text | Google Scholar

Taherian, H., Aghaebrahimi, M. R., Baringo, L., and Reza Goldani, S., (2021). Optimal Dynamic Pricing for an Electricity Retailer in the price-responsive Environment of Smart Grid. Int. J. Elec Power, 130. doi:10.1016/j.ijepes.2021.107004

CrossRef Full Text | Google Scholar

Wang, Y., Wang, Y., Huang, Y., Yang, J., Ma, Y., Yu, H., et al. (2019). Operation Optimization of Regional Integrated Energy System Based on the Modeling of electricity-thermal-natural Gas Network. Appl. Energ. 251, 113410. doi:10.1016/j.apenergy.2019.113410

CrossRef Full Text | Google Scholar

Wang, Z., Sun, M., Gao, C., Wang, X., and Ampimah, B. C. (2021). A New Interactive Real-Time Pricing Mechanism of Demand Response Based on an Evaluation Model. Appl. Energ. 295, 117052. doi:10.1016/j.apenergy.2021.117052

CrossRef Full Text | Google Scholar

Wei, F., Jing, Z. X., Wu, P. Z., and Wu, Q. H. (2017). A Stackelberg Game Approach for Multiple Energies Trading in Integrated Energy Systems. Appl. Energ. 200, 315–329. doi:10.1016/j.apenergy.2017.05.001

CrossRef Full Text | Google Scholar

Winkler, M., Yadav, A., and Chitu, C., (2020). Spiel und Pädagogik. IEEE, 265–276. doi:10.2307/j.ctvvb7m51.25

CrossRef Full Text | Google Scholar

Xie, Z., Weili, H. U., Tan, J., Xiao, J., Wu, G., and Liu, Y., (2018). Demand Response Optimization Strategy of Intelligent Buildings for Regional Energy Service Providers. Electric Power Construction.

Google Scholar

Xu, X., Xu, Z., Zhang, R., Chai, S., and Li, J. (2020). Data‐driven‐based Dynamic Pricing Method for Sharing Rooftop Photovoltaic Energy in a Single Apartment Building. IET Generation, Transm. & Distribution 14 (24), 5720–5727. doi:10.1049/iet-gtd.2020.0606

CrossRef Full Text | Google Scholar

Yuan, G., Gao, Y., and Ye, B. (2021). Optimal Dispatching Strategy and Real-Time Pricing for Multi-Regional Integrated Energy Systems Based on Demand Response. Renew. Energ. 179, 1424–1446. doi:10.1016/j.renene.2021.07.036

CrossRef Full Text | Google Scholar

Zhang, B., Hu, W., Cao, D., Huang, Q., Chen, Z., and Blaabjerg, F. (2019). Deep Reinforcement Learning-Based Approach for Optimizing Energy Conversion in Integrated Electrical and Heating System with Renewable Energy. Energ. Convers. Manag. 202, 112199. doi:10.1016/j.enconman.2019.112199

CrossRef Full Text | Google Scholar

Zhong, S., Wang, X., Zhao, J., Li, W., Li, H., Wang, Y., et al. (2021). Deep Reinforcement Learning Framework for Dynamic Pricing Demand Response of Regenerative Electric Heating. Appl. Energ. 288, 116623. doi:10.1016/j.apenergy.2021.116623

CrossRef Full Text | Google Scholar