A Solution Method for Many-Objective Security-Constrained Unit Commitment Considering Flexibility

With the increasing penetration of wind power into power systems and the random fluctuation of the wind farm (WF) output, system flexibility must be considered in the optimal generation dispatch. Based on the extreme scenarios of the WF output, we proposed a flexibility risk index to evaluate the system flexibility of each time interval. We established a five-objective security-constrained unit commitment (SCUC) model of a power system with WFs, thermal generation plants, battery energy storage stations, and pumped storage hydro stations. The objectives were to minimize the system flexibility risk, total network loss, operation cost, power purchase cost, and pollutant gas emissions. To obtain the Pareto optimal solutions of the model, based on the objective selection and ε-constraint methods, we proposed two methods to reduce the dimension of objectives and transformed the five-objective optimization model into a series of three-objective optimization models. Then, we used the normalized normal constraint method to solve the Pareto frontier surface of each three-objective optimization model. We used a color column to represent the value change of the two upper layer objectives and visualized the Pareto frontier of the five-objective SCUC model in the three-dimensional ordinate space. Case studies on the modified IEEE-9 bus system and an actual power grid demonstrated the effectiveness and high computational efficiency of the proposed method.

1 Introduction

With the increasing penetration of intermittent renewable energy into power systems, flexibility is becoming more and more important to the secure operation of power systems. The International Energy Agency (IEA) suggests that a flexible power system can respond reliably and rapidly to violent fluctuations in both supply and demand (Agency, 2009). The North American Electric Reliability Corporation (NERC) proposes that a flexible power system can provide a real-time balance of supply and demand (North American Electric Reliability Corporation, 2010), (Adams et al., 2010), that is, it can accommodate uncertainties within an acceptable time range under different constraints (Zhao et al., 2016). Because of the high penetration of wind power, power systems need to reserve sufficient flexible resources to balance the random fluctuations of the wind farm (WF) output. Thus, the optimal generation dispatch method needs to ensure that flexibility supply resources can satisfy the flexibility demands of the power system.

Many scholars have studied the optimal generation dispatch of power systems with renewable energy considering flexibility. For example, Zhao et al. (2015) proposed a dispatch framework for variable energy resources (VERs) using the “do not exceed” (DNE) limit, which is the largest VER output that the system can accommodate under the worst-case scenario. They also propose three approaches to solve the DNE limit problem. In the study by Pourahmadi et al. (2019), Farzaneh et al. proposed a novel robust-based framework to quantify the economically optimal uncertainty set such that both feasibility and optimality robustness are guaranteed. To improve the flexibility of the power grid, Yun et al. (2019) proposed an electricity–heat–hydrogen multi-energy storage system (EHH-MESS) and its coordinated optimal operation model. The simulation results showed that the EHH-MESS has better regulation flexibility and economy of the power grid. Tang et al. (2019) proposed an operational flexibility metric based on the ramping capacity for a combined heat and power microgrid and an intraday rolling dispatch model including the operation flexibility constraints. Chen et al. (2016) proposed an economic dispatch model for power systems with wind-storage combined systems and battery energy storage (BES). The calculation results showed that the integration of energy storage effectively improved the wind power utilization and operation efficiency. These studies focused on how to use flexibility resources to improve system flexibility, but none included quantitative evaluations of system flexibility considering the extreme power output scenario of renewable energy. In addition to flexibility, other objectives, such as lowering costs, saving energy, and reducing emissions, must be considered for optimal generation dispatch. Hence, the formulation of optimal generation dispatch must consider multiple optimization objectives while ensuring the secure operation of the system. However, conflicts always exist among multiple optimization objectives, meaning they cannot all be optimized simultaneously. Thus, the result of the multi-objective optimization problem (MOP) is a set of solutions, which are called the Pareto optimal solutions. Methods for obtaining the Pareto optimal solutions of MOPs include heuristic algorithms and traditional optimization algorithms. Heuristic algorithms include particle swarm optimization (Reyes and Coello, 2006), the differential evolution algorithm (Storn and Price, 1997), and the non-dominated sorting genetic algorithm (NSGA) (Deb et al., 2002). Heuristic algorithms can obtain multiple Pareto optimal solutions at the same time and are suitable for non-convex and discontinuous problems. However, they have low computational efficiency for solving large-scale MOPs, such as the multi-objective optimal generation dispatch problem of an actual large-scale power system. Traditional optimization algorithms include the linear weighted sum method (Milano et al., 2003), ideal point method (Bryson and Mobolurin, 1996), ε-constraint method (Nezhad et al., 2014), normal boundary intersection (NBI) method (Das and Dennis, 1998), (Roman and Rosehart, 2006), and normalized normal constraint (NNC) method (Lin et al., 2017), (Li et al., 2015). These algorithms can transform an MOP into a series of single-objective optimization problems to obtain their optimal solutions. Traditional algorithms can obtain a series of evenly distributed Pareto optimal solutions and have high computational efficiency for solving large-scale MOPs. Traditional algorithms are mainly used to solve MOPs with few objectives, that is, only two or three objectives. Thus, understanding how to extend traditional optimization algorithms to solve many-objective optimization problems (MaOPs) is important.

In most of the existing literature studies, MaOPs are solved by heuristic algorithms, among which the elitist NSGA (NSGA-II) (Deb and Jain, 2014), (Jain and Deb, 2014) and the multi-objective evolutionary algorithm based on decomposition (Zhang and Li, 2007) have good computational performance. However, when the number of objectives is large, the size of the solution space of heuristic algorithms increases exponentially, resulting in a long computation time. Thus, most approaches reduce the dimension of the objectives first and then solve the optimization model. To simplify MaOPs, non-linear correlation information entropy with the covariance method was proposed in the study by Wang and Yao. (2016) to analyze the conflicts among the objectives. In the studies by Kou et al. (2017) and Zheng et al. (2019), a conflicting objective-selection method and an objective reduction algorithm were proposed, in which the most conflicting objective subset can be selected, and the dimension of the MaOP can be reduced. In these studies, the MaOPs are solved by first analyzing the relationship among the objectives and then aggregating or eliminating some of the objectives to reduce the dimension of the problem. However, the information of the objectives will be inevitably lost during the process of aggregation or eliminating the objectives, resulting in incomplete Pareto optimal solutions of MaOPs. At present, few studies have adopted the traditional algorithms to solve the Pareto optimal solutions of MaOPs. Therefore, it is important to propose an efficient algorithm based on the traditional optimization algorithms to solve the Pareto optimal solutions of MaOPs while also retaining the information integrity of all the objectives.

This study makes three contributions:

1) Based on the extreme scenarios of uncertain WF output, a flexibility risk index (i.e., the risk cost of the unsecure operation of the system due to the lack of flexibility) is proposed to evaluate the system flexibility. Then, a five-objective SCUC model of a power system with WFs, thermal generation (TG) plants, BES stations, and pumped storage hydro (PSH) stations is established to minimize the system flexibility risk, network loss, operation cost, power purchase cost, and pollutant emissions.

2) A convex hull relaxation optimization method is used to relax the power balance equation with quadratic terms of power loss into convex inequalities in the SCUC model, and the SCUC model is then transformed into a mixed integer convex programming (MICP) model.

3) According to the objective selection and ε-constraint methods, two-objective dimension reduction methods are proposed to transform the five-objective SCUC model into a series of three-objective optimization models. Then, the Pareto frontier surface of each three-objective optimization model is solved by the NNC method. A color column is used to represent the value change of two upper layer objectives, and the Pareto frontier of the five-objective SCUC model is visualized in the three-dimensional coordinate space.

The rest of this article is organized as follows: the Flexibility Risk Index section proposes a flexibility risk index. The Five-Objective SCUC Model section proposes a five-objective SCUC model considering the aforementioned flexibility risk index. The Solution Methods section proposes an algorithm for solving the Pareto frontier of the five-objective SCUC model. The Case Studies section presents case studies and analyzes the obtained results. The Conclusion section offers the conclusions.

2 Flexibility Risk Index

In the SCUC model considering the uncertain WF output, the uncertain WF output is always modeled by sampling numerous scenarios or establishing an uncertainty set, which refer to the stochastic SCUC model (Zhao and Guan, 2013) and the robust SCUC model (Chen et al., 2020), (Chen et al., 2019). In this study, the uncertain WF output is simulated by sampling numerous scenarios. In the scenario-based stochastic SCUC model (Zhao and Guan, 2013), the on/off states of normal units are the same in different scenarios, but their power outputs are different to balance the random fluctuation of the WF output. To reduce the scale of the scenario-based stochastic SCUC model and reflect the worst case of the random WF output, many sampling scenarios are replaced with extreme scenarios (Xu et al., 2019). It is assumed that there are N_w WFs in the system, and 2^Nw extreme scenarios will be generated. It is also assumed that the WF outputs obey a normal distribution N (μ,σ²) with the predicted value as the expected value. The confidence level can reach 95.45% when the confidence interval of the WF output is [μ − 2σ, μ + 2σ]. Thus, 2^Nw extreme scenarios can be obtained by making the lower and upper bounds of the WF output equal to μ − 2σ and μ + 2σ.

The flexibility risk index R_t at time interval t is defined in Eq. 1, which considers the occurrence probability of each extreme scenario of the WF output and the regulating cost of unsecure operation of the system under this scenario:

$R_t={\displaystyle {\sum }_{w=1}^{N_w}{\lambda }_w\left({\widehat{P}}_{w,t}^0-P_{w,t}^0\right)}+Q_{\mathrm{lack},t}^0+{\displaystyle {\sum }_{sc=1}^{2^{N_{\text{w}}}}{p}^{sc}\left[{\displaystyle {\sum }_{w=1}^{N_w}{\lambda }_w\left({\widehat{P}}_{w,t}^{sc}-P_{w,t}^{sc}\right)}+{\displaystyle {\sum }_{i=1}^{N_1}{D}_{i,t}^{sc}}+{\displaystyle {\sum }_{b=1}^{N_2}{D}_{b,t}^{sc}}\right]},(1)$

where λ_w is the penalty cost coefficient of the wind curtailment of WF w. sc is the index of the scenario, where sc = 0 indicates the forecast scenario, and other values of sc indicate the extreme scenarios. In the following part of this article, superscript 0 represents the variables under the forecast scenario, and superscript sc represents the variables under the extreme scenario sc. $P_{w,t}^0$ and $P_{w,t}^{sc}$ are the dispatch power output of WF w at time interval t, ${\widehat{P}}_{w,t}^0$ is the predicted power, and ${\widehat{P}}_{w,t}^{sc}$ is the maximum power under the extreme scenario sc. $Q_{\mathrm{lack},t}^0$ is the penalty cost of the system flexibility shortage, which is expressed as Eq. 2. p^sc is the occurrence probability of the extreme scenario sc, and it is assumed that p^sc = $1/2^{N_w}$; N₁ is the total number of TG units, that is, the total number of coal-fired units and gas-fired units; N₂ is the total number of BES stations. $D_{i,t}^{sc}/D_{b,t}^{sc}$ is the flexible dispatch cost of the TG unit i/BES station b at time t, which includes the dispatch cost caused by regulating their power output of the extreme scenario from the power output of the forecast scenario, as shown in Eq. 3. Here, the flexible dispatch cost includes only the dispatch cost of TG units and BES stations. This is because only the startup/shutdown costs of PSH units are considered, and their power output regulation costs are not considered. The on/off states of PSH units under the extreme scenarios are the same as those of the forecast scenario, but the power outputs are different; hence, the flexible dispatch cost of PSH units is 0.

$Q_{\mathrm{lack},t}^0={\lambda }_{\mathrm{lack}}\left(\text{Δ}{P}_{\mathrm{lku},t}^0+\text{Δ}{P}_{\mathrm{lkd},t}^0\right),(2)$

where λ_lack is the penalty cost coefficient of the system flexibility shortage, and $\Delta P_{\mathrm{lku},t}^0/\Delta P_{\mathrm{lkd},t}^0$ is the up/down system flexibility shortage at time t.

$\{\begin{array}{c}{D}_{i,t}^{sc}\ge F_{i,t}^{sc}-F_{i,t}^0,D_{i,t}^{sc}\ge 0\\ D_{b,t}^{sc}\ge F_{b,t}^{sc}-F_{b,t}^0,D_{b,t}^{sc}\ge 0\end{array}sc=1,\mathrm{...},N_{sc},(3)$

where $F_{i,t}^{sc}$ and $F_{i,t}^0$ are the fuel costs of the TG unit i at time t, which can be expressed as Eq. 4 and approximated by the piecewise linear inequality as Eq. 5. $F_{b,t}^{sc}$ and $F_{b,t}^0$ are the operation costs of the BES station b at time t, which can be expressed as Eq. 6.

$F_{i,t}^{sc}=A_{i,2}{\left(P_{i,t}^{sc}\right)}^2+A_{i,1}{P}_{i,t}^{sc}+A_{i,0}{I}_{i,t},(4)$

$F_{i,t}^{sc}\ge {\alpha }_{i,k}{P}_{i,t}^{sc}+{\beta }_{i,k}{I}_{i,t},k=\mathrm{1,2},\dots ,M,(5)$

where $P_{i,t}^{sc}$ is the output of the TG unit i at time t; A_i,2, A_i,1, and A_i,0 are the fuel cost coefficients of the TG unit i; and I_i,t is the on/off state of the TG unit i at time t, where 1/0 represents the on/off state. α_i,k/β_i,k is the slope/intercept of segment k of the fuel cost of the TG unit t; and M is the total number of segments.

$F_{b,t}^{sc}=C_{\text{dis},b}{P}_{\text{dis},b,t}^{sc}+C_{\text{ch},b}{P}_{\text{ch},b,t}^{sc},(6)$

where $P_{\text{dis},b,t}^{sc}/P_{\text{ch},b,t}^{sc}$ is the discharging/charging power of the BES station b at time t, and C_dis,b/C_ch,b is the discharging/charging cost coefficient of the BES station b.

3 Five-Objective SCUC Model

3.1 Objectives

In the actual operation and dispatch of a power system, security, economy, efficiency, and environment friendliness are required to be considered. In addition, the system flexibility is also required to be considered to balance the random fluctuations of the WF output. Thus, we established a five-objective SCUC model to minimize the total flexibility risk, network loss, operation cost, power purchase cost, and pollutant emissions.

3.1.1 Total Flexibility Risk z₁

$z_1={\displaystyle {\sum }_{t=1}^T{R}_t},(7)$

where T is the total number of time intervals in the dispatch period. Taking 1 day as the dispatch period and each time interval as 15 min, then T = 96.

3.1.2 Total Network Loss z₂

$z_2={\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{l=1}^{N_L}{P}_{\text{Los},l,t}^0}},(8)$

where N_L is the total number of branches in the system; and $P_{\mathrm{Los},l,t}^0$ is the network loss of the branch l at time t, which can be expressed as follows (Lin et al., 2017):

$P_{\mathrm{Los},l,t}^0={\mathrm{g}}_{km}{\left[{\displaystyle {\sum }_{i\in \psi }\left(X_{ki}-X_{mi}\right)P_{i,t}^0}-{\displaystyle {\sum }_{r\in L}\left(X_{kr}-X_{mr}\right)P_{\text{ld}r,t}}\right]}^2,(9)$

where k and m are the buses at both ends of the branch l; g_km is the conductance of the branch l; X_ki, X_mi, X_kr, and X_mr are the elements of the node impedance matrix in the DC power flow model; ψ is the set of generator buses and injected power buses connecting external power grids; L is the set of load buses; and P_ldr,t is the active power of the load bus r at time t.

3.1.3 Total Operating Cost z₃

$z_3={\displaystyle {\sum }_{t=1}^T\left[{\displaystyle {\sum }_{i=1}^{N_1}\left(F_{i,t}^0+C_{i\text{U},t}+C_{i\text{D},t}\right)}+{\displaystyle {\sum }_{b=1}^{N_2}{F}_{b,t}^0}+{\displaystyle {\sum }_{s=1}^{N_3}\left(C_{s\text{U},t}+C_{s\text{D},t}\right)}\right]},(10)$

where N₃ is the total number of PSH units. C_iU,t/C_iD,t and C_sU,t/C_sD,t are the startup/shutdown cost of the TG unit i and PSH unit s at time t, which can be expressed as follows:

$\{\begin{array}{cc}{C}_{i\mathrm{U},t}\ge K_i\left(I_{i,t}-I_{i,t-1}\right),& C_{i\mathrm{U},t}\ge 0\\ C_{s\mathrm{U},t}\ge K_s\left(Z_{s,t}-Z_{s,t-1}\right),& C_{s\mathrm{U},t}\ge 0\\ C_{i\mathrm{D},t}\ge J_i\left(I_{i,t-1}-I_{i,t}\right),& C_{i\mathrm{D},t}\ge 0\\ C_{s\mathrm{D},t}\ge J_s\left(Z_{s,t-1}-Z_{s,t}\right),& C_{s\mathrm{D},t}\ge 0\end{array},(11)$

where K_i/J_i and K_s/J_s are the startup/shutdown cost of the TG unit i and PSH unit s. Z_s,t is the on/off state of the PSH unit s at time t, where 1/0 represents the on/off state.

3.1.4 Total Power Purchase Cost z₄

$z_4={\displaystyle {\sum }_{t=1}^T({\displaystyle {\sum }_{i=1}^{N_1}{C}_{i,t}{P}_{i,t}^0}}+{\displaystyle {\sum }_{w=1}^{N_w}{C}_{w,t}{P}_{w,t}^0}),(12)$

where C_i,t and C_w,t are the power purchase prices of the TG unit i and the WF w at time t.

3.1.5 Total Pollutant Emissions z₅

$z_5={\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{i=1}^{N_1}\left(B_{i,1}{P}_{i,t}^0+B_{i,0}{I}_{i,t}\right)}},(13)$

where B_i,1 and B_i,0 are the polluted gas emission coefficients of the TG unit i. Because of the small amount of polluted gas emissions of gas-fired units, their coefficients are B_i,1 = B_i,0 = 0.

3.2 Constraints

3.2.1 Fundamental Constraints

The power balance constraint is expressed as Eq. 14:

${\displaystyle {\sum }_{i=1}^{N_1}{P}_{i,t}^{sc}}+{\displaystyle {\sum }_{b=1}^{N_2}\left(P_{\mathrm{dis},\text{b},t}^{sc}+P_{\mathrm{ch},b,t}^{sc}\right)}+{\displaystyle {\sum }_{s=1}^{N_3}\left(P_{\mathrm{pg},s,t}^{sc}+P_{\mathrm{pp},s,t}^{sc}\right)}=P_{\mathrm{nld},t}^{sc}+{\displaystyle {\sum }_{l=1}^{N_L}{P}_{\mathrm{Los},l,t}^{sc}},(14)$

where $P_{\mathrm{pg},s,t}^{sc}/P_{\mathrm{pp},s,t}^{sc}$ is the generating/pumping power of the PSH unit s at time t; $P_{\mathrm{Los},l,t}^{sc}$ can be calculated similar to $P_{\mathrm{Los},l,t}^0$ as in Eq. 9; and $P_{\mathrm{nld},t}^{sc}$ is the system net load at time t, which is equal to the difference between the total load forecast value and the total WF output value, expressed as Eq. 15:

$P_{\text{nld},t}^{sc}={\displaystyle {\sum }_{r=1}^{N_{\text{LD}}}{P}_{\text{ld}r,t}}-{\displaystyle {\sum }_{w=1}^{N_w}{P}_{w,t}^{sc}}.(15)$

The constraints of generators’ output are expressed as follows:

$\{\begin{array}{l}{I}_{i,t}{P}_{i,\min }\le P_{i,t}^{sc}\le I_{i,t}{P}_{i,\max }\\ 0\le P_{w,t}^{sc}\le {\widehat{P}}_{w,t}^{sc}\\ P_{i,t}^{sc}-P_{i,t-1}^{sc}\le r_{ui}{T}_{15}{I}_{i,t-1}+P_{i,\min }\left(I_{i,t}-I_{i,t-1}\right)\\ P_{i,t-1}^{sc}-P_{i,t}^{sc}\le r_{di}{T}_{15}{I}_{i,t}+P_{i,\min }\left(I_{i,t-1}-I_{i,t}\right)\end{array},(16)$

$\{\begin{array}{l}{P}_{i,t}^0-P_{i,t}^{sc}\le r_{ui}{T}_{10}{I}_{i,t}\\ P_{i,t}^{sc}-P_{i,t}^0\le r_{di}{T}_{10}{I}_{i,t}\end{array}sc=1,\mathrm{...},N_{sc},(17)$

where P_i,min/P_i,max is the minimum/maximum output of the TG unit i, and r_ui/r_di is its ramp up/down rate. T₁₅ is the length of each time interval, which is 15 min. In Eq. 16, the unit maintains the minimum output in the first time interval after starting up and the last time interval before shutting down. T₁₀ is the response time of the regulating power of the TG units, which is 10 min.

The constraints of minimum continual on/off time of TG units can be expressed as follows (Carrion and Arroyo, 2006):

$\{\begin{array}{l}{I}_{i,t}=1,t\in \left[1,U_i\right],U_i=\min \left\{T,\left(T_{\text{on}i}-X_{\text{on}i,0}\right)I_{i,0}\right\}\\ {\displaystyle {\sum }_{n=t}^{t+T_{\text{on}i}-1}{I}_{i,n}\ge T_{\text{on}i}\left(I_{i,t}-I_{i,t-1}\right)},t\in \left[U_i+1,T-T_{\text{on}i}+1\right]\\ {\displaystyle {\sum }_{n=t}^T\left[I_{i,n}-\left(I_{i,t}-I_{i,t-1}\right)\right]}\ge 0,t\in \left[T-T_{\text{on}i}+2,T\right]\\ I_{i,t}=0,t\in \left[1,D_i\right],D_i=\min \left\{T,\left(T_{\text{off}i}-X_{\text{off}i,0}\right)\left(1-I_{i,0}\right)\right\}\\ {\displaystyle {\sum }_{n=t}^{t+T_{\text{off}i}-1}\left(1-I_{i,n}\right)\ge T_{\text{off}i}\left(I_{i,t-1}-I_{i,t}\right)},t\in \left[D_i+1,T-T_{\text{off}i}+1\right]\\ {\displaystyle {\sum }_{n=t}^T\left[1-I_{i,n}-\left(I_{i,t-1}-I_{i,t}\right)\right]}\ge 0,t\in \left[T-T_{\text{off}i}+2,T\right]\end{array},(18)$

where U_i/D_i is the number of time intervals during which the unit i must stay on/stay off at the beginning of the dispatch period, which is related to the unit states at the end of the last dispatch period; T_oni/T_offi is the minimum number of continual on/off time intervals of the unit i; and X_oni,0/X_offi,0 is the number of continual on/off time intervals of the unit i at the beginning of the dispatch period.

3.2.2 Constraints of Network Security

The network security constraints represented by the DC power flow model are as follows:

$\{\begin{array}{l}{P}_{l,km,t}^{sc}={\displaystyle \sum _{i\in \psi }\left(\frac{X_{ki}-X_{mi}}{x_{km}}\right)P_{i,t}^{sc}}-{\displaystyle \sum _{r\in L}\left(\frac{X_{kr}-X_{mr}}{x_{km}}\right)P_{\text{ld}r,t}}\\ -{\overline{P}}_{l,km}\le P_{l,km,t}^{sc}\le {\overline{P}}_{l,km}\end{array},(19)$

where $P_{l,km,t}^{sc}$ is the transmission power of the branch l at time interval t; x_km is the reactance of the branch l; and ${\overline{P}}_{l,km}$ is the maximum transmission power of the branch l.

3.2.3 Operation Constraints of PSH Stations

The constraints of the power output are as follows:

$\{\begin{array}{l}0\le P_{\text{pg},s,t}^{sc}\le P_{\text{pg},s,\max }\cdot Z_{\text{pg},s,t}\\ P_{\text{pp},s,\max }\cdot Z_{\text{pp},s,t}\le P_{\text{pp},s,t}^{sc}\le 0\end{array},(20)$

where P_pg,s,max/P_pp,s,max is the maximum generating/pumping power of the PSH unit s, and Z_pg,s,t/Z_pp,s,t is the generating/pumping state of the PSH unit s at time interval t.

The complementary constraint of operating states is as follows:

$Z_{s,t}=Z_{\text{pg},s,t}+Z_{\text{pp},s,t}\le 1.(21)$

The constraint of energy balance within a day is as follows:

${\displaystyle {\sum }_{t=1}^T{P}_{\text{pg},s,t}^{sc}}+\xi \cdot {\displaystyle {\sum }_{t=1}^T{P}_{\text{pp},s,t}^{sc}}=0,(22)$

where $\xi$ is the conversion efficiency of PSH units, which is 75% in this study.

The constraints of switching time of operating states are as follows:

$\{\begin{array}{cc}{Z}_{\text{pg},s,t}+Z_{\text{pp},s,t+1}\le 1& t=\mathrm{1,2},\cdots ,\left(T-1\right)\\ Z_{\text{pg},s,t}+Z_{\text{pp},s,t+2}\le 1& t=\mathrm{1,2},\cdots ,\left(T-2\right)\\ Z_{\text{pp},s,t}+Z_{\text{pg},s,t+1}\le 1& t=\mathrm{1,2},\cdots ,\left(T-1\right)\\ Z_{\text{pp},s,t}+Z_{\text{pg},s,t+2}\le 1& t=\mathrm{1,2},\cdots ,\left(T-2\right)\end{array}.(23)$

3.2.4 Operation Constraints of BES Stations

The constraints of discharging/charging power are as follows:

$\{\begin{array}{l}0\le P_{\text{dis},b,t}^{sc}\le P_{\text{dis},b,\max }\cdot Z_{\text{dis},b,t}\\ P_{\text{ch},b,\max }\cdot Z_{\text{ch},b,t}\le P_{\text{ch},b,t}^{sc}\le 0\end{array},(24)$

where P_dis,b,max/P_ch,b,max is the maximum discharging/charging power of the BES station b, and Z_dis,s,t/Z_ch,s,t is the discharging/charging state of the BES station b at time interval t.

The complementary constraint of operating state is as follows:

$Z_{b,t}=Z_{\text{dis},b,t}+Z_{\text{ch},b,t}\le 1.(25)$

The constraints of the remaining energy are as follows:

$\{\begin{array}{l}{E}_{b,t}^{sc}=E_{b,t-1}^{sc}+\left(-P_{\text{dis},b,t}^{sc}/{\eta }_{\text{dis},b}-P_{\text{ch},b,t}^{sc}{\eta }_{\text{ch},b}\right)T_{15}\\ 0\le E_{b,t}^{sc}\le E_{b,\max }\end{array},(26)$

where η_dis,b/η_ch,b is the discharging/charging efficiency of the BES station b, and $E_{b,t}^{sc}$ is the stored remaining energy of the BES station b at time interval t.

3.2.5 System Flexibility Constraints

The system flexibility demand needs to consider not only the uncertainties of the load power and WF output in each time interval but also the change of the net load power in adjacent time intervals. Thus, the upward and downward system flexibility demand constraints are expressed as follows:

$\{\begin{array}{l}{P}_{\text{nld},t+1}^0-P_{\text{nld},t}^0+L_{\text{u}}\%P_{\text{ld},t+1}+w_{\text{u}}\%{\displaystyle {\sum }_{w=1}^{N_w}{P}_{w,t+1}^0}\le \text{Δ}{P}_{\text{fu},t}^0+\text{Δ}{P}_{\text{lku},t}^0\\ P_{\text{nld},t}^0-P_{\text{nld},t+1}^0+L_{\text{d}}\%P_{\text{ld},t+1}+w_{\text{d}}\%{\displaystyle {\sum }_{w=1}^{N_w}\left({\widehat{P}}_{w,t+1}-P_{w,t+1}^0\right)}\le \text{Δ}{P}_{\text{fd},t}^0+\text{Δ}{P}_{\text{lkd},t}^0\end{array},(27)$

where L_u%/L_d% is the percentage of the upward/downward system flexibility demand due to the load forecast deviation; w_u%/w_d% is the percentage of the upward/downward system flexibility demand due to the wind power forecast deviation; and $\Delta P_{\text{fu},t}^0/\Delta P_{\text{fd},t}^0$ is the upward/downward system flexibility supply capacity at time interval t.

The system flexibility supply capacity is the sum of the flexibility supply capacity provided by all units, as follows:

$\{\begin{array}{l}\text{Δ}{P}_{\text{fu},t}^0={\displaystyle {\sum }_{i=1}^{N_1}\text{Δ}{P}_{\text{u},i,t}^0}+{\displaystyle {\sum }_{b=1}^{N_2}\text{Δ}{P}_{\text{u},b,t}^0}+{\displaystyle {\sum }_{s=1}^{N_3}\text{Δ}{P}_{\text{u},s,t}^0}\\ \text{Δ}{P}_{\text{fd},t}^0={\displaystyle {\sum }_{i=1}^{N_1}\text{Δ}{P}_{\text{d},i,t}^0}+{\displaystyle {\sum }_{b=1}^{N_2}\text{Δ}{P}_{\text{d},b,t}^0}+{\displaystyle {\sum }_{s=1}^{N_3}\text{Δ}{P}_{\text{d},s,t}^0}\end{array},(28)$

where $\Delta P_{\text{u},i,t}^0/\Delta P_{\text{u},s,t}^0/\Delta P_{\text{u},b,t}^0$ is the upward flexibility supply capacity provided by the TG unit i/PSH unit s/BES station b at time interval t, and $\Delta P_{\text{d},i,t}^0/\Delta P_{\text{d},s,t}^0/\Delta P_{\text{d},b,t}^0$ is the corresponding downward flexibility supply capacity.

The flexibility supply capacities provided by different units can be expressed as follows:

$\{\begin{array}{l}0\le \text{Δ}{P}_{\text{u},i,t}^0\le \min \left(P_{i,\max }{I}_{i,t}-P_{i,t}^0,r_{\text{u}i}{T}_{10}{I}_{i,t}\right)\\ 0\le \text{Δ}{P}_{\text{d},i,t}^0\le \min \left(P_{i,t}^0-P_{i,\min }{I}_{i,t},r_{\text{d}i}{T}_{10}{I}_{i,t}\right)\\ 0\le \text{Δ}{P}_{\text{u},s,t}^0\le P_{\text{pg},s,\max }{Z}_{\text{pg},s,t}-P_{\text{pg},s,t}^0-P_{\text{pp},s,t}^0\\ 0\le \text{Δ}{P}_{\text{d},s,t}^0\le P_{\text{pg},s,t}^0+P_{\text{pp},s,t}^0-P_{\text{pp},s,\max }{Z}_{\text{pp},s,t}\\ 0\le \text{Δ}{P}_{\text{u},b,t}^0\le P_{\text{dis},b,\max }-\left(P_{\text{dis},b,t}^0+P_{\text{ch},b,t}^0\right)\\ 0\le \text{Δ}{P}_{\text{d},b,t}^0\le P_{\text{dis},b,t}^0+P_{\text{ch},b,t}^0-P_{\text{ch},b,\max }\end{array}.(29)$

4 Solution Methods

4.1 Convex Relaxation of Network Loss

The SCUC model consists of objectives Eqs 7, 8, 10, 12, 13 and constraints Eqs 1–3, 5, 6, 9, 11, 14–29. Because it includes the discrete decision variable of on/off states of units and the network loss term in Eq. 14 is represented by a quadratic equation Eq. 9, the SCUC model is a mixed integer non-linear non-convex programming (MINNP) model. The MINNP is attributed to the NP-hard problem and is difficult to solve. For the actual large-scale power grid, the SCUC model’s scale is very large. If solvers such as DICOPT or SBB in the commercial optimization software GAMS are directly used to solve the problem, the computational efficiency will be very low, and the global optimal solution always cannot be obtained. Recent studies have shown that the MINNP model can be transformed into an MICP model by the convex relaxation technique to reduce the computational complexity (Jabr et al., 2012). To ensure that the solution of the optimization model after convex relaxation has high accuracy compared with that of the original optimization model, a convex hull relaxation method that can obtain the tight convex relaxation of the original optimization model is applied (Li and Vittal, 2016). Thus, we used the convex hull relaxation method to transform the quadratic equality constraint into convex constraints.

Taking the quadratic equality (Eq. 30) as an example, it can be expressed equivalently as Eqs. 31, 32, where Eq. 31 is convex and Eq. 32 is non-convex.

$y=a{x}^2+bx+c,a>0,(30)$

$y\ge a{x}^2+bx+c,a>0,(31)$

$y\le a{x}^2+bx+c,a>0.(32)$

Generally, the minimum/maximum value of x (i.e., x_min/x_max) is known, and the corresponding value of y is y_min/y_max. Then, the equation of the straight line determined by two points (x_min, y_min) and (x_max, y_max) is shown in Eq. 33.

$y-y_{\min }=\frac{y_{\max }-y_{\min }}{x_{\max }-x_{\min }}\cdot \left(x-x_{\min }\right).(33)$

The convex hull relaxation of Eq. 32 is a linear inequality constraint as Eq. 34. Therefore, the quadratic equality constraint Eq. 30 can be relaxed as Eq. 31 and Eq. 34.

$y\le y_{\min }+\frac{y_{\max }-y_{\min }}{x_{\max }-x_{\min }}\cdot \left(x-x_{\min }\right).(34)$

The network loss in Eq. 9 can be written as Eq. 35

$\{\begin{array}{c}{P}_{\mathrm{Los},l,t}^{sc}=g_{km}{{\displaystyle {\theta }_{km,t}^{sc}}}^2\\ {\theta }_{km,t}^{sc}={\displaystyle {\sum }_{i\in \psi }\left(X_{ki}-X_{mi}\right)P_{i,t}^{sc}}-{\displaystyle {\sum }_{r\in L}\left(X_{kr}-X_{mr}\right)P_{\text{ld}r,t}}\end{array},(35)$

where ${\theta }_{km,t}^{sc}$ is the voltage angle difference between buses k and m at time interval t.

Therefore, the first formula of Eq. 35 can be relaxed as follows:

$\{\begin{array}{c}{P}_{\mathrm{Los},l,t}^{sc}\ge g_{km}{{\displaystyle {\theta }_{km,t}^{sc}}}^2\\ P_{\mathrm{Los},l,t}^{sc}\le P_{\mathrm{Los},l,\min }+\frac{P_{\mathrm{Los},l,\max }-P_{\mathrm{Los},l,\min }}{{\theta }_{\text{km,}\max }-{\theta }_{\text{km,}\min }}\left({\theta }_{km,t}^{sc}-{\theta }_{\text{km,}\min }\right)\end{array},(36)$

where θ_km,min/θ_km,max is the minimum/maximum value of θ_km,t, and the corresponding value of P_Los,_lt is P_Los,_lmin/P_Los,_lmax.

By convex hull relaxation, the SCUC model can be transformed from the original MINNP model into the MICP model. Hence, the GUROBI solver in GAMS can be used to solve the MICP model with higher computational efficiency and reliability.

4.2 Objective Selection Method Based on the Spearman Correlation Coefficient

To reduce the dimension of the objectives in the MaOP, an objective selection method is required. Based on the objective selection method (Kou et al., 2017), (Zheng et al., 2019), we proposed the following objective dimension reduction method: the most conflicting objectives were selected as the upper layer optimization objectives, and the remaining objectives were taken as the lower layer optimization objectives. Combined with the ε-constraint method, the upper layer objectives are added into the constraints of the lower layer optimization model. Thus, the original MaOP was transformed into a series of low-dimension MOPs. The pseudocode of the objective selection method is as follows:

According to the Spearman correlation coefficient matrix among different objectives, we selected the most conflicting objective, that is, the objective with the largest absolute value of the sum of negative correlation coefficients. This objective was moved from S_t to S_c, and then, the next most conflicting objective was selected from the remaining objectives. We repeated this selection process until the terminal condition was satisfied. In the pseudocode, S_t is the intermediate set, which is used to store the unselected objectives; S_c is the most selected conflicting objective set; and C^M(i, j) is the Spearman correlation coefficient between the ith and jth objectives.

By using the objective selection method, we selected the two most conflicting objectives as the upper layer optimization objectives and the other three objectives as the lower layer optimization objectives. Thus, the dimension of the five-objective SCUC model was reduced hierarchically.

4.3 Grid-Based Five-Objective ε-Constraint Method

We used the objective selection method based on Spearman correlation coefficients to select the most conflicting objective as the first-level conflicting objective, and then, we selected the most conflicting objective among the remaining objectives as the second-level conflicting objective. The five-objective SCUC model can be transformed into a series of three-objective SCUC models by the ε-constraint method constraints. The specific process is as follows.

The five-objective SCUC model in the Five-Objective SCUC Model section can be written in a compact form as follows:

$\{\begin{array}{l}\min \left\{z_1\left(\mathit{x}\right),z_2\left(\mathit{x}\right),z_3\left(\mathit{x}\right),z_4\left(\mathit{x}\right),z_5\left(\mathit{x}\right)\right\}\\ \text{s}.\text{t}.\mathit{h}\left(\mathit{x}\right)=0\\ \underset{¯}{\mathit{g}}\left(\mathit{x}\right)\le \mathit{g}\left(\mathit{x}\right)\le \overline{\mathit{g}}\left(\mathit{x}\right)\end{array},(37)$

where h(x) and g(x) are the equality and inequality constraints of the five-objective SCUC model, respectively.

Assuming that z₅ is the first-level conflicting objective, z₄ is the second-level conflicting objective, and the other three objectives z₁, z₂, and z₃ are the lower layer objectives, steps for transforming the five-objective optimization model (Eq. 37) into a series of three-objective optimization models are as follows:

Step 1The two single-objective models max z₅(x) and min z₅(x) are solved to determine the maximum and minimum values of z₅, that is, z_5max and z_5min, and then, the value range of z₅, that is, Δz₅ = z_5max − z_5min is calculated.

Step 2The value range Δz₅ is divided into q₁ equal segments to obtain q₁ + 1 points, and the value of the kth point is z_5k = z_5min + k Δz₅/q₁, k = 0, 1, … , q₁.

Step 3According to the ε-constraint method, the two single-objective models (Eq. 38) and (Eq. 39) are solved to determine the maximum and minimum values of z₄ at the point z₅ = z_5k, that is, z_4,5kmax and z_4,5kmin, and then, the value range of z₄, that is, Δz_4,5k = z_4,5kmax − z_4,5kmin is calculated.

$\begin{array}{c}\max z_4\left(\mathit{x}\right)-l_0{v}_{5b}/\text{Δ}{z}_5\\ s.t.z_5\left(\mathit{x}\right)=z_{5k}+v_{5b},v_{5b}\ge 0\\ \mathit{h}\left(\mathit{x}\right)=0\\ \underset{¯}{\mathit{g}}\left(\mathit{x}\right)\le \mathit{g}\left(\mathit{x}\right)\le \overline{\mathit{g}}\left(\mathit{x}\right)\end{array},(38)$

$\begin{array}{c}\min z_4\left(\mathit{x}\right)+l_0{v}_{5b}/\text{Δ}{z}_5\\ s.t.z_5\left(\mathit{x}\right)=z_{5k}+v_{5b},v_{5b}\ge 0\\ \mathit{h}\left(\mathit{x}\right)=0\\ \underset{¯}{\mathit{g}}\left(\mathit{x}\right)\le \mathit{g}\left(x\right)\le \overline{\mathit{g}}\left(\mathit{x}\right)\end{array},(39)$

where l₀ is a constant between 10^–3 and 10^–1; and v_5b is an auxiliary variable of the objective z₅, which is introduced to find a feasible solution between adjacent value points. To make the z₅ value of the obtained solution equal to the selected point z_5k, the value of v_5b should be as close to zero as possible. Thus, in the objective function of the maximization problem (Eq. 38), the term $l_0{v}_{5\text{b}}/\Delta z_5$ is subtracted, and in the objective function of the minimization problem (Eq. 39), the term $l_0{v}_{5\text{b}}/\Delta z_5$ is added.

Step 4. The value range Δz_4,5k is divided into q₂ equal segments to obtain q₂ + 1 points. The value of the jth point is z_4j,5k = z_4,5kmin + j Δz_4,5k/q₂, j = 0, 1, … , q₂.

Step 5. According to the ε-constraint method, the Pareto frontier surface of the lower layer three-objective optimization model is solved corresponding to the grid points z₅ = z_5k and z₄ = z_4j,5k, expressed as follows:

$\begin{array}{c}\min \{z_1\left(\mathit{x}\right)+l_1\left(v_{4b}/\text{Δ}{z}_{\mathrm{4,5}k}+v_{5b}/\text{Δ}{z}_5\right),z_2\left(\mathit{x}\right)+l_1\left(v_{4b}/\text{Δ}{z}_{\mathrm{4,5}k}+v_{5b}/\text{Δ}{z}_5\right)\\ z_3\left(\mathit{x}\right)+l_1\left(v_{4b}/\text{Δ}{z}_{\mathrm{4,5}k}+v_{5b}/\text{Δ}{z}_5\right)\}\\ s.t.z_5\left(\mathit{x}\right)=z_{5k}+v_{5b},v_{5b}\ge 0\\ z_4\left(\mathit{x}\right)=z_{4j,5k}+v_{4b},v_{4b}\ge 0\\ \mathit{h}\left(\mathit{x}\right)=0\\ \underset{¯}{\mathit{g}}\left(\mathit{x}\right)\le \mathit{g}\left(\mathit{x}\right)\le \overline{\mathit{g}}\left(x\right)\end{array},(40)$

where l₁ is a constant between 10^–3 and 10^–1; and v_4b is an auxiliary variable of the objective z₄, which is introduced to find a feasible solution between adjacent value points. By gathering all the Pareto optimal solutions of solving the lower layer three-objective optimization model (Eq. 40) corresponding to each grid point, the Pareto optimal solutions of the five-objective SCUC model are obtained.

4.4 Curve-Based Five-Objective ε-Constraint Method

We used the objective selection method based on Spearman correlation coefficients to select the two most conflicting objectives as the upper layer objectives and the remaining three objectives as the lower layer objectives. The five-objective SCUC model was decomposed into two low-dimension multiple-objective optimization subproblems. Taking the five-objective optimization model (Eq. 37) as an example, we assumed that z₄ and z₅ are the upper layer objectives, and the other three objectives (i.e., z₁, z₂, and z₃) are the lower layer objectives. The steps of transforming the five-objective optimization model (Eq. 37) into a series of three-objective optimization models are as follows:

Step 1The Pareto frontier curve of the upper layer two-objective optimization model (Eq. 41)is solved, which includes m Pareto optimal solutions. The maximum and minimum values of z₄ and z₅ are determined on the Pareto frontier curve (i.e., z_4max, z_4min, z_5max, and z_5min).

$\{\begin{array}{l}\min \left\{z_4\left(\mathit{x}\right),z_5\left(\mathit{x}\right)\right\}\\ \text{s}\text{.t}\text{.}\mathit{h}\left(\mathit{x}\right)=0\\ \underset{¯}{\mathit{g}}\left(\mathit{x}\right)\le \mathit{g}\left(\mathit{x}\right)\le \overline{\mathit{g}}\left(\mathit{x}\right)\end{array}.(41)$

Step 2The value ranges of z₄ and z₅ are calculated on the upper layer Pareto frontier curve, Δz₄ = z_4max − z_4min and Δz₅ = z_5max − z_5min. The points are arranged on the curve with the endpoint (z_4min, z_5max) as the first point and the endpoint (z_4max, z_5min) as the last point. Thus, when the order of points increases, z₄ increases and z₅ decreases. The kth Pareto point is recorded as (z_4,k, z_5,k).

Step 3According to the ε-constraint method, the Pareto frontier surface of the lower layer three-objective optimization model is solved corresponding to each point (z_4,k, z_5,k), which is expressed as follows:

$\begin{array}{c}\min \{z_1\left(\mathit{x}\right)+l_2\left(u_{4a}/\text{Δ}{z}_4+u_{5a}/\text{Δ}{z}_5\right),z_2\left(\mathit{x}\right)+l_2\left(u_{4a}/\text{Δ}{z}_4+u_{5a}/\text{Δ}{z}_5\right),\\ z_3\left(\mathit{x}\right)+l_2\left(u_{4a}/\text{Δ}{z}_4+u_{5a}/\text{Δ}{z}_5\right)\}\\ \text{s}\text{.t}\text{.}{z}_4\left(\mathit{x}\right)=z_{4,k}+u_{4a},u_{4a}\ge 0,1\le k\le m\\ z_5\left(\mathit{x}\right)=z_{5,k}-u_{5a},u_{5a}\ge 0,1\le k\le m\\ \mathit{h}\left(\mathit{x}\right)=0\\ \underset{¯}{\mathit{g}}\left(\mathit{x}\right)\le \mathit{g}\left(\mathit{x}\right)\le \overline{\mathit{g}}\left(\mathit{x}\right)\end{array},(42)$

where l₂ is a constant between 10^–3 and 10^–1; and u_4a and u_5a are auxiliary variables of the objectives z₄ and z₅, which are introduced to obtain a feasible solution between the adjacent points in the Pareto frontier curve of the upper layer optimization model. With the increase of the point order k, z₄ increases and z₅ decreases. Thus, a positive sign appears before u_4a, and a negative sign appears before u_5a in the constraints of Eq. 42.Obviously, compared with the method of obtaining the grid points from the upper layer two objectives, the number of points obtained from the Pareto frontier curve of the upper layer two-objective optimization model is significantly reduced, and the computational burden is also smaller. Thus, the calculation efficiency was significantly improved.

4.5 NNC Method for Solving the Lower Layer Three-Objective Optimization Model

The NNC method is used to solve the Pareto frontier of each lower layer three-objective optimization model (Lin et al., 2017). With the NNC method, the three-objective optimization model is transformed into a series of single-objective optimization models. By solving each single-objective optimization model, the complete Pareto frontier surface of the three-objective optimization model can be obtained.

After obtaining the Pareto optimal solutions of the five-objective SCUC problem, we used the entropy weight method to determine a compromise optimal solution (COS) from Pareto optimal solutions as the final optimal decision scheme (Tan et al., 2013). The obtained COS has the maximum comprehensive optimization degree λ value in the Pareto optimal solutions.

5 Case Studies

We demonstrated the proposed many-objective optimization method in case studies on a modified IEEE-9 bus system and an actual power grid. We used a Dell workstation with a 3.50 GHz Intel(R) Xeon(R) CPU E3-1270 v3 (8 cores) and 16 GB RAM in these case studies. The software platform was GAMS 24.4.3.

5.1 The Modified IEEE-9 Bus System

The modified IEEE-9 bus system is shown in Figure 1, which includes one PSH unit, one coal-fired TG unit, one gas-fired TG unit, one BES station, and one WF. Parameters of the units are given in Supplementary Table A1. The forecast power of the WF output and total load are shown in Supplementary Figure A1. According to the active power proportion of each load bus in the BPA data of the IEEE-9 bus system, we obtained the forecast load curve of each load bus from the forecast total load curve. The power purchase prices of TG units 2 and 3 were 0.17 ¥/kWh and 0.21 ¥/kWh, respectively. The power purchase price of the WF was 0.51 ¥/kWh, and the penalty cost coefficient of the wind curtailment λ_w was set as 2.6 ¥/kWh. The rated power and energy of the BES station were 5 MW and 10 MWh, the charge/discharge efficiency was 96%, and the charge/discharge cost was 0.8 ¥/kWh. The coefficients were set as L_u% = 3%, L_d% = 1%, w_u% = 20%, and w_d% = 20%.

FIGURE 1

FIGURE 1. Modified IEEE-9 bus system.

5.1.1 Comparative Results of Convex and Non-Convex Models

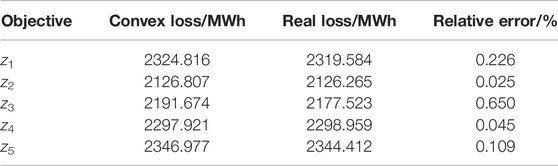
Taking z₁, z₂, z₃, z₄, and z₅ as the optimization objectives of the SCUC model, we used the GUROBI solver to solve each single-objective optimization problem (SOP) after convex relaxation of quadratic terms of network loss. We compared the obtained network loss after optimization with the real network loss calculated by substituting the obtained optimal power outputs of units into Eq. 9, and the results are given in Table 1. It is evident that the difference between the network loss obtained by the convex relaxation method and the real network loss was very small, and the maximum relative error was only 0.224%, which demonstrated that the proposed convex hull relaxation method for the quadratic term of network loss had high computational accuracy.

TABLE 1

TABLE 1. Comparison of the convex and real network loss of SOPs.

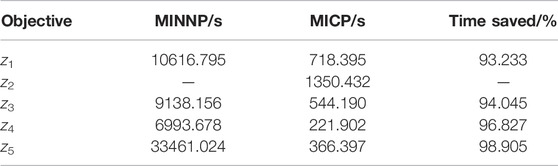
We used the SBB solver to solve the original MINNP of the SCUC model. We compared the CPU time of solving the MINNP model with that of solving the MICP model, as shown in Table 2. We observed that the CPU time of the MICP model decreased more than 75%. Moreover, for the SOP with z₄ as the objective, the optimal solution could not be obtained by solving the MINNP model, but it could be obtained by solving the MICP model. Thus, the proposed convex hull relaxation method could significantly improve the computational efficiency, and the optimal solution of the SCUC model could be obtained more reliably.

TABLE 2

TABLE 2. Comparison of CPU time of the MINNP and MICP models.

5.1.2 Solution of the Pareto Frontier and the COS

We analyzed the correlation between the objective functions. We solved each of the five SOPs, and the objective function values of the five optimal solutions are shown in Table 3. We used these five optimal solutions to calculate Spearman correlation coefficients between the optimization objectives and the sum of the negative correlation coefficients of each optimization objective. The results are given in Supplementray Table A2. From Supplementray Table A2, we selected the objective with the largest absolute value of the sum of negative correlation coefficients (i.e., z₅) as the first-level conflicting objective and selected the objective with the next largest absolute value of the sum of negative correlation coefficients (i.e., z₄) as the second-level conflicting objective. Thus, we obtained the most conflicting objective set S_c = [z₄, z₅] by the objective selection method, and z₅ and z₄ were the upper layer optimization objectives.

TABLE 3

TABLE 3. Objective function values of the SOP solutions.

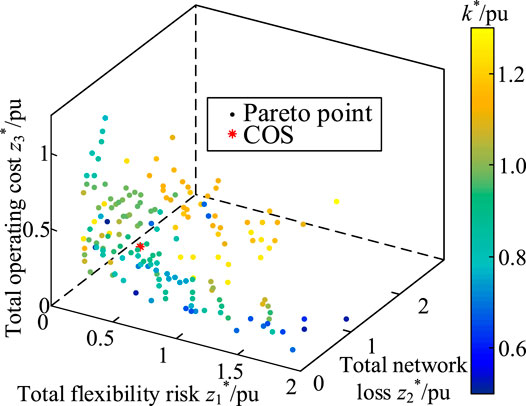
Then, we solved the Pareto frontier of the five-objective SCUC model by the two proposed ε-constraint methods and the NSGA-II algorithm. Considering the value differences of different objectives, we defined the color column coordinates k^* = z₄^*/z₅^* = (z₄/z_4min)/(z₅/z_5min); thus, as k^* increases, z₄ increases and z₅ decreases.

1) Grid-based five-objective ε-constraint method.

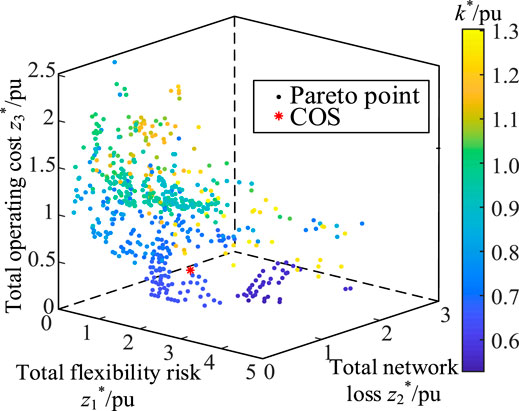
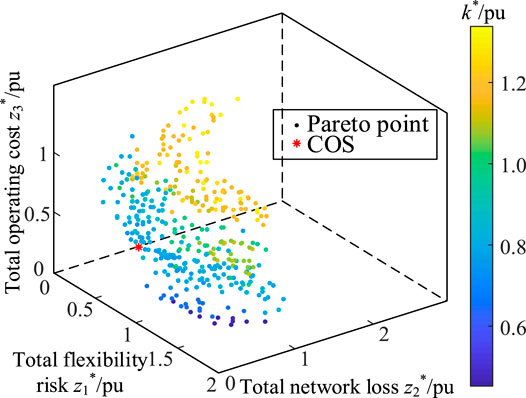
We calculated z_5max and z_5min and obtained the four points of z₅ by setting q₁ = 3. Then, for each z_5k, according to Eq. 38 and Eq. 38, we obtained z_4,5kmax and z_4,5kmin and obtained the four points of z₄ by setting q₂ = 3. Thus, the total number of grid points of the upper layer two objectives was 16. The Pareto frontier surface of the lower layer three-objective optimization model (Eq. 40) corresponding to each grid point was solved. After gathering all the obtained optimal solutions and removing the dominated solutions, we obtained the Pareto frontier composed of 427 non-dominated solutions, as shown in Figure 2. The COS is also obtained and is shown as the red-colored point in Figure 2.

2) Curve-based five-objective ε-constraint method.

FIGURE 2

FIGURE 2. Pareto frontier obtained by the grid-based ε-constraint method.

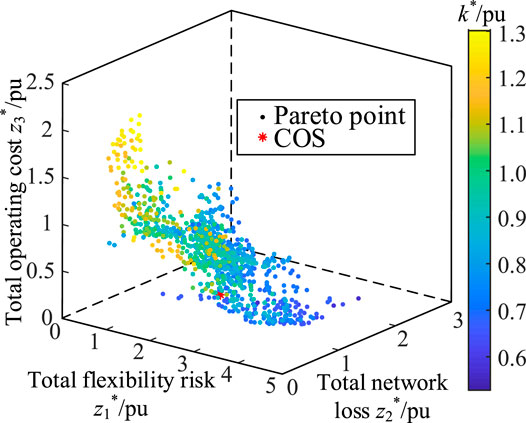
We used the NNC method to solve the upper layer two-objective optimization model (Eq. 41). Letting m = 11, the obtained Pareto frontier curve is shown in Supplementary Figure A2. We added the kth point (z_4,k, z_5,k) values to the lower layer three-objective optimization model (Eq. 42) as constraints and solved the Pareto frontier surface of the model (Eq. 42) corresponding to each point (z_4,k, z_5,k). Finally, we obtained the Pareto frontier composed of 595 non-dominated points, as shown in Figure 3. We also obtained the COS, which is shown as the red-colored point in Figure 3.

FIGURE 3

FIGURE 3. Pareto frontier obtained by the curve-based ε-constraint method.

By comparing the computational process and results of the aforementioned two methods, it can be seen that the curve-based ε-constraint method obtained more non-dominated solutions and more compact Pareto frontier surfaces. This is because when the curve-based ε-constraint method was used to solve the five-objective SCUC model, the selected points were within the Pareto frontier curve of the upper layer two objectives and had a good non-dominated relationship. However, for the grid-based ε-constraint method, although the hierarchical division of grid points seemed to be uniform, it ignored the conflicting relationship between these two objectives, resulting in more dominated points being computed in the lower layer three-objective optimization. Thus, the curve-based ε-constraint method could obtain better results because it could obtain more Pareto optimal solutions and supply more trade-off relationship information of different objectives for the final decision of the five-objective SCUC problem.

3) NSGA-II algorithm.

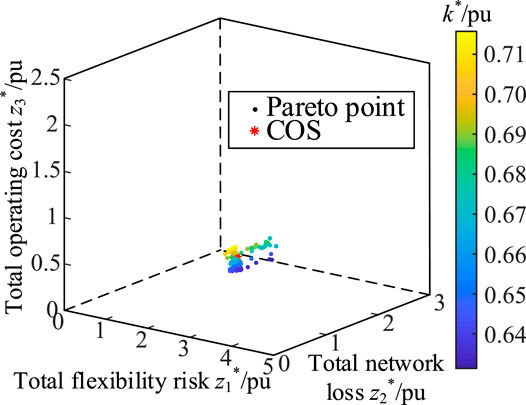
We used the gamultiobj (.) function of the NSGA-II algorithm in MATLAB to solve the Pareto frontier of the five-objective SCUC model, which included 100 non-dominated solutions, as shown in Figure 4. The obtained Pareto optimal solutions were concentrated and supplied with little trade-off relationship information for the final decision of the five-objective SCUC problem.

FIGURE 4

FIGURE 4. Pareto frontier obtained by the NSGA-II algorithm.

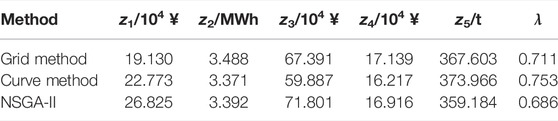
We compared the CPU time and COSs of the three methods. The CPU times of the grid-based ε-constraint method, curve-based ε-constraint method, and NSGA-II algorithm were 56,703.958 s, 33,561.423 s, and 117,618.003 s, respectively. The two proposed methods had higher computational efficiency, among which the curve-based ε-constraint method had the highest computational efficiency. Since different Pareto optimal solutions can be calculated independently in the two proposed methods, thus, the parallel calculation technique for opening eight threads in the eight cores of the used computer was used to improve the computational efficiency. By the parallel calculation, the CPU times of the grid-based ε-constraint method and the curve-based ε-constraint method were reduced to 7,260.439 s and 4570.952 s, and the acceleration ratios were 7.810 and 7.342. These demonstrated that the two proposed methods had good computational performance for solving the five-objective SCUC model, and they were more suitable for solving MaOPs. The COSs of the three methods are shown in Table 4. The λ value corresponding to the curve-based ε-constraint method was the largest, which indicated that the obtained COS was the best in the coordinate optimization of the five objectives. Thus, this analysis showed that the curve based ε-constraint method could obtain the Pareto frontier and the COS more efficiently, and the obtained COS had a better optimization degree.

TABLE 4

TABLE 4. Comparisons of the COSs by different methods.

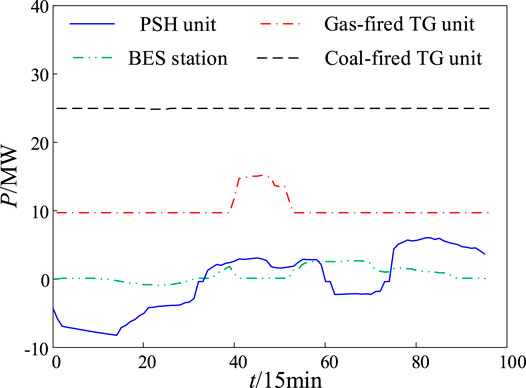
The power output schedule of the units corresponding to the COS obtained by the curve-based ε-constraint method is shown in Figure 5. The PSH and BES stations pumped water and charged energy, respectively, during the low-load time intervals, and they generated electricity and discharged energy, respectively, during the high-load time intervals, which has high flexibility for regulating power rapidly.

FIGURE 5

FIGURE 5. Power output schedule of the units.

5.2 An Actual Power Grid

The actual power grid includes 1,563 buses, 733 lines, and 1,675 transformers. The main network structure, including several 110 kV power plants and lines, is shown in Supplementary Figure B1. The units included two PSH units, six coal-fired TG units, 32 gas-fired TG units, four garbage-fired units, one BES station, and one WF. The parameters of parts of the units are given in Supplementary Table B1. There are five tie lines for power exchange between the grid and outer grids. The power transmission plan curve and total load forecast curve of each tie line are shown in Supplementary Figure B2. The forecast load of each node was determined according to the load percentage in BPA operation data. The forecast output of the WF is shown in Supplementary Figure B3. The values of L_u%, L_d%, w_u%, w_d%, and λ_w are the same as those given in the Convex Relaxation of Network Loss section. For the BES station, the rated power and capacity were 5 MW and 10 MWh, C_dis,b/C_ch,b = 0.8 ¥/kWh, and η_dis,b/η_ch,b = 96%.

5.2.1 Comparison of Convex and Non-convex Models

Comparative results of the network loss of the five SOPs are shown in Table 5, demonstrating the high computational accuracy of the proposed convex hull relaxation method for the quadratic term of network loss in large-scale SCUC problems. Comparison of the CPU time of the original MINNP model with the MICP model is shown in Table 6. The CPU time of the MICP model decreased by more than 90%, and the convergence problem of the MINNP model was also addressed, which demonstrated the high-computational efficiency and convergence of the proposed convex hull relaxation method.

TABLE 5

TABLE 5. Comparison of convex and real loss of the SOPs.

TABLE 6

TABLE 6. Comparison of the CPU time of the MINNP and MICP models.

5.2.2 Solution of the Pareto Frontier and the COS

We calculated Spearman correlation coefficients among the five objective functions and the sum of the negative correlation coefficients of each objective, which are shown in Supplementary Table B2. The absolute sums of the negative correlation coefficients of z₄ and z₅ were the largest. Thus, we selected S_c = [z₄, z₅] as the first-level conflicting objective and z₄ as the second-level conflicting objective.

The NSGA-II algorithm cannot solve this large-scale five-objective SCUC problem because of the huge size of the optimization model. Thus, we compared only the results of the two proposed ε-constraint methods. For the grid-based five-objective ε-constraint method, by setting q₁ = q₂ = 2, the total number of grid points of the upper layer two objectives was nine. The Pareto frontier surface of the lower layer three-objective optimization model corresponding to each grid point was obtained by solving Eq. 40. The final Pareto frontier of the five-objective SCUC model is shown in Figure 6. For the curve-based ε-constraint method, the NNC method was used to solve the Pareto frontier curve of the upper layer two-objective optimization model (Eq. 41) by setting m = 6. Then, the Pareto frontier surface of the lower layer three-objective optimization model corresponding to each point (z_4,k, z_5,k) was obtained by solving Eq. 42. The final Pareto frontier of the five-objective SCUC model is shown in Figure 7. From Figures 6, 7, it can be seen that more Pareto optimal solutions were obtained by the curve-based ε-constraint method than by the grid-based ε-constraint method. We compared the CPU time of the two methods, the CPU times of the grid-based and curve-based ε-constraint methods by the parallel calculation technique were 24765.4 and 16,792.8 s, respectively. This demonstrated that the curve-based ε-constraint method had higher computational efficiency than the grid-based ε-constraint method. Obviously, if the used computer has more cores, the computational efficiency of the proposed curve-based ε-constraint method will be further increased to satisfy the requirement of actual application. Although the grid-based ε-constraint method solved a higher number of lower layer three-objective optimization models and consumed more CPU time, many dominated solutions in the obtained results had to be deleted in the final Pareto frontier of the five-objective SCUC model. Thus, the curve-based ε-constraint method had better results and higher computational efficiency than the grid-based ε-constraint method.

FIGURE 6

FIGURE 6. Pareto frontier obtained by the grid-based ε-constraint method.

FIGURE 7

FIGURE 7. Pareto frontier obtained by the curve-based ε-constraint method.

The objective functions of the COSs obtained by the two proposed methods and the five single-objective optimal solutions are shown in Table 7. The λ value of each solution is also listed in the table. The COS obtained by the curve-based ε-constraint method was the best because it had the largest λ value. The results demonstrated that the proposed curve-based ε-constraint method could obtain a COS with a better comprehensive optimization degree in the coordinate optimization of the five objectives.

TABLE 7

TABLE 7. Comparison of the single-objective solutions and the COS.

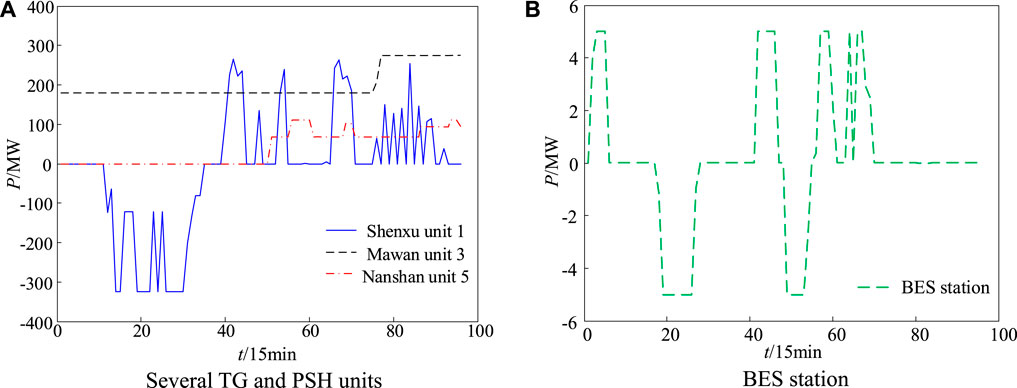
The power output schedules of several units and the BES station corresponding to the COS of the curve-based ε-constraint method are shown in Figure 8. The schedules reflected the high flexibility of PSH and BES stations to rapidly regulate their power output.

FIGURE 8

FIGURE 8. Power output schedules of some units. (A) Several TG and PSH units. (B) BES station.

5.3 Results Analysis

From the aforementioned results, the proposed convex hull relaxation method for the quadratic equality of network loss had high computational accuracy, and it could obtain the optimal solution of the SCUC model more efficiently and reliably. For solving the Pareto optimal solutions of the proposed five-objective SCUC model, the proposed curve-based ε-constraint method had higher computational efficiency than the proposed grid-based ε-constraint method and the NSGA-II algorithm. Moreover, the obtained COS of the proposed curve-based ε-constraint method had a better optimization degree than the other two algorithms. By the parallel computation technique, the computational efficiency of the proposed curve-based ε-constraint method for solving the Pareto optimal solutions of the five-objective SCUC model can be greatly increased to satisfy the requirement of actual application.

6 Conclusion

In this study, we proposed a system flexibility risk index to quantify power system flexibility under the uncertain fluctuation of wind power, including in extreme wind power output scenarios. Then, we established a five-objective SCUC model considering system flexibility. We used the convex hull relaxation method to relax the quadratic equality constraints of network loss in this model and transformed the original MINNP model into the MICP model. According to objective selection and ε-constraint methods, we proposed a two-objective dimension reduction method to transform the five-objective SCUC model into a series of three-objective SCUC models. We used the NNC method to obtain the evenly distributed Pareto frontier surface of each three-objective SCUC model. Results of case studies on the modified IEEE-9 bus system and an actual power grid demonstrated that the proposed curve-based five-objective ε-constraint method could solve the five-objective SCUC problem with higher computational efficiency and obtain a better COS than the grid-based ε-constraint method. The proposed method also was superior to the NSGA-II algorithm, which was unable to solve the problem altogether.

In future work, we may explore how to extend the proposed method to solve the Pareto frontier of the many-objective SCUC model with more than five objectives and seek to visualize the Pareto frontier in the three-dimensional ordinate space.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. SL carried out model and methodology construction, supervision, and writing; HW carried out case computation and writing; the contribution of JL and WL is investigation; YL and ML were responsible for supervision.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 51977080 and 51207056).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.857520/full#supplementary-material

References

Adams, J., O’Malley, M., and Hanson, K. (2010). Flexibility Requirements and Potential Metrics for Variable Generation: Implocations for System Planning Studies. Princeton, American: North American Electric Reliability Corporation, 14–17.

Google Scholar

Agency, I. E. (2009). Empowering Variable Renewables-Options for Flexible Electricity Systems. Paris, France: OECD Publishing, 13–14.

Google Scholar

Bryson, N., and Mobolurin, A. (1996). An Action Learning Evaluation Procedure for Multiple Criteria Decision Making Problems. Eur. J. Oper. Res. 96 (2), 379–386.

Google Scholar

Carrion, M., and Arroyo, J. M. (2006). A Computationally Efficient Mixed-Integer Linear Formulation for the thermal Unit Commitment Problem. IEEE Trans. Power Syst. 21 (3), 1371–1378. doi:10.1109/TPWRS.2006.876672

CrossRef Full Text | Google Scholar

Chen, H., Zhang, R., Li, G., Bai, L., and Li, F. (2016). Economic Dispatch of Wind Integrated Power Systems with Energy Storage Considering Composite Operating Costs. IET Gener. Transm. Distrib. 10 (5), 1294–1303. doi:10.1049/iet-gtd.2015.0410

CrossRef Full Text | Google Scholar

Chen, Y., Zhang, Z., Chen, H., and Zheng, H. (2020). Robust UC Model Based on Multi‐band Uncertainty Set Considering the Temporal Correlation of Wind/load Prediction Errors. IET Generation, Transm. Distribution 14 (2), 180–190. doi:10.1049/iet-gtd.2019.1439

CrossRef Full Text | Google Scholar

Chen, Y., Zhang, Z., Liu, Z., Zhang, P., Ding, Q., Liu, X., et al. (2019). Robust N - K CCUC Model Considering the Fault Outage Probability of Units and Transmission Lines. IET Generation, Transm. Distribution 13 (17), 3782–3791. doi:10.1049/iet-gtd.2019.0780

CrossRef Full Text | Google Scholar

Das, I., and Dennis, J. E. (1998). Normal-boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM J. Optim. 8 (3), 631–657. doi:10.1137/S1052623496307510

CrossRef Full Text | Google Scholar

Deb, K., and Jain, H. (2014). An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Computat. 18 (4), 577–601. doi:10.1109/TEVC.2013.2281535

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Computat. 6 (2), 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

Jabr, R. A., Singh, R., and Pal, B. C. (2012). Minimum Loss Network Reconfiguration Using Mixed-Integer Convex Programming. IEEE Trans. Power Syst. 27 (2), 1106–1115. doi:10.1109/TPWRS.2011.2180406

CrossRef Full Text | Google Scholar

Jain, H., and Deb, K. (2014). An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Computat. 18 (4), 602–622. doi:10.1109/TEVC.2013.2281534

CrossRef Full Text | Google Scholar

Kou, Y. N., Zheng, J. H., Li, Z., and Wu, Q. H. (2017). Many-objective Optimization for Coordinated Operation of Integrated Electricity and Gas Network. J. Mod. Power Syst. Clean. Energ. 5 (3), 350–363. doi:10.1007/s40565-017-0279-y

CrossRef Full Text | Google Scholar

Li, Q., Liu, M., and Liu, H. (2015). Piecewise Normalized Normal Constraint Method Applied to Minimization of Voltage Deviation and Active Power Loss in an AC-DC Hybrid Power System. IEEE Trans. Power Syst. 30 (3), 1243–1251. doi:10.1109/TPWRS.2014.2343625

CrossRef Full Text | Google Scholar

Li, Q., and Vittal, V. (2016). The Convex hull of the AC Power Flow Equations in Rectangular Coordinates. IEEE Power & Energy Society General Meeting Boston.

CrossRef Full Text | Google Scholar

Lin, S., Liu, M., Li, Q., Lu, W., Yan, Y., and Liu, C. (2017). Normalised normal Constraint Algorithm Applied to Multi‐objective Security‐constrained Optimal Generation Dispatch of Large‐scale Power Systems with Wind Farms and Pumped‐storage Hydroelectric Stations. IET Generation, Transm. Distribution 11 (6), 1539–1548. doi:10.1049/iet-gtd.2016.1386

CrossRef Full Text | Google Scholar

Milano, F., Canizares, C. A., and Invernizzi, M. (2003). Multiobjective Optimization for Pricing System Security in Electricity Markets. IEEE Trans. Power Syst. 18 (2), 596–604. doi:10.1109/TPWRS.2003.810897

CrossRef Full Text | Google Scholar

Nezhad, A. E., Javadi, M. S., and Rahimi, E. (2014). Applying Augmented Ɛ-Constraint Approach and Lexicographic Optimization to Solve Multi-Objective Hydrothermal Generation Scheduling Considering the Impacts of Pumped-Storage Units. Int. J. Electr. Power Energ. Syst. 55, 195–204. doi:10.1016/j.ijepes.2013.09.006

CrossRef Full Text | Google Scholar

North American Electric Reliability Corporation (2010). Special Report: Accommodating High Levels of Variable Generation. Princeton, American: North American Electric Reliability Corporation, 2–6.

Google Scholar

Pourahmadi, F., Hosseini, S. H., and Fotuhi-Firuzabad, M. (2019). Economically Optimal Uncertainty Set Characterization for Power System Operational Flexibility. IEEE Trans. Ind. Inf. 15 (10), 5456–5465. doi:10.1109/TII.2019.2906058

CrossRef Full Text | Google Scholar

Reyes, S. M., and Coello, C. C. (2006). Multi-objective Particle Swarm Optimizers: a Survey of the State of the Art. Int. J. Comput. Intelligence Res. 2 (3), 287–308.

Google Scholar

Roman, C., and Rosehart, W. (2006). Evenly Distributed Pareto Points in Multi-Objective Optimal Power Flow. IEEE Trans. Power Syst. 21 (2), 1011–1012. doi:10.1109/TPWRS.2006.873010

CrossRef Full Text | Google Scholar

Storn, R., and Price, K. (1997). Differential Evolution - a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optimization 11 (4), 341–359. doi:10.1023/A:1008202821328

CrossRef Full Text | Google Scholar

Tan, S., Lin, S., Yang, L., Zhang, A., Shi, W., and Feng, H. (2013). Multi-objective Optimal Power Flow Model for Power System Operation Dispatching. Hong Kong, China: APPEEC, 1–6.

Google Scholar

Tang, J., Ding, M., Lu, S., Li, S., Huang, J., and Gu, W. (2019). Operational Flexibility Constrained Intraday Rolling Dispatch Strategy for CHP Microgrid. IEEE Access 7, 96639–96649. doi:10.1109/ACCESS.2019.2929623

CrossRef Full Text | Google Scholar

Wang, H., and Yao, X. (2016). Objective Reduction Based on Nonlinear Correlation Information Entropy. Soft Comput. 20, 2393–2407. doi:10.1007/s00500-015-1648-y

CrossRef Full Text | Google Scholar

Xu, J., Wang, B., Sun, Y., Xu, Q., Liu, J., Cao, H., et al. (2019). A Day-Ahead Economic Dispatch Method Considering Extreme Scenarios Based on a Wind Power Uncertainty Set. Csee Jpes 5 (2), 224–233. doi:10.17775/CSEEJPES.2016.00620

CrossRef Full Text | Google Scholar

Yun, T., Zedi, W., Zedi, W., Yan, L., Qian, M., Qian, H., et al. (2019). A Multi Energy Storage System Model Based on Electricity Heat and Hydrogen Coordinated Optimization for Power Grid Flexibility. Csee Jpes 5 (2), 266–274. doi:10.17775/CSEEJPES.2019.00190

CrossRef Full Text | Google Scholar

Zhang, Q., and Li, H. (2007). MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Computat. 11 (6), 712–731. doi:10.1109/TEVC.2007.892759

CrossRef Full Text | Google Scholar

Zhao, C., and Guan, Y. (2013). Unified Stochastic and Robust Unit Commitment. IEEE Trans. Power Syst. 28 (1), 3353–3361. doi:10.1109/TPWRS.2013.2251916

CrossRef Full Text | Google Scholar

Zhao, J., Zheng, T., and Litvinov, E. (2016). A Unified Framework for Defining and Measuring Flexibility in Power System. IEEE Trans. Power Syst. 31 (3), 339–347. doi:10.1109/TPWRS.2015.2390038

CrossRef Full Text | Google Scholar

Zhao, J., Zheng, T., and Litvinov, E. (2015). Variable Resource Dispatch through Do-Not-Exceed Limit. IEEE Trans. Power Syst. 30 (2), 820–828. doi:10.1109/TPWRS.2014.2333367

CrossRef Full Text | Google Scholar

Zheng, J. H., Kou, Y. N., Jing, Z. X., and Wu, Q. H. (2019). Towards many-objective Optimization: Objective Analysis, Multi-Objective Optimization and Decision-Making. IEEE Access 7, 93742–93751. doi:10.1109/ACCESS.2019.2926493

CrossRef Full Text | Google Scholar