Multi-Objective Mayfly Optimization-Based Frequency Regulation for Power Grid With Wind Energy Penetration

With the continuous development of society and under the background of sustainable development and resource conservation, the proportion of renewable energy in the global energy structure is increasing. At the same time, wind power has been widely used in many regions of the world because wind power technology is more advanced and mature than other renewable energy sources. In addition, with a large number of wind turbines connected to the grid, it not only helps automatic generation control (AGC) of power systems but also brings new challenges and difficulties. In this study, a multi-source cooperative control model of wind power participating in AGC frequency regulation is established to solve the dynamic problem of power distribution from real-time total power command to different AGC units. This study presents an optimal AGC-coordinated control method based on the multi-objective mayfly optimization (MMO) algorithm, which makes the fitting degree of power command output and actual output curve high and the adjustment mileage payment minimum, so as to achieve the best AGC performance. Finally, the simulation results show that this method can effectively decrease the total power deviation and adjustment mileage payment in the multi-source-coordinated control of AGC.

1 Introduction

Nowadays, renewable energy such as wind power, solar energy, and tidal energy, are developing rapidly, under the background of pursuing energy conservation, emission reduction, and sustainable development (Zhang et al., 2015; Yang et al., 2020a; Yang et al., 2020b; Xiong et al., 2020; Zhang et al., 2021a; Shetty and Priyam, 2021). Therefore, the world energy structure is changing to an energy structure dominated by renewable energy (Yang et al., 2015; Dong et al., 2022). Wind power generation technology has been leading in the development of renewable energy and has been widely used in all regions of the world (Yang et al., 2018; Ye et al., 2018; Attig-Bahar et al., 2021). In recent years, with the increasing popularity of wind power generation, although wind power brings green and clean energy for social development, wind power generation is greatly affected by climate conditions and power output fluctuations, which brings great pressure to the frequency control of power systems (Bevrani et al., 2010; He et al., 2015; Wu et al., 2018; Huang et al., 2021).

Generally, the task of automatic generation control (AGC) is undertaken by hydro power plants and thermal power plants. Its main control objective is to maintain the system frequency and tie line power within the allowable error range (IbraheemKumar and Kothari, 2005; Xu et al., 2016; Zhang et al., 2016; Rahman et al., 2017; YiranMa et al., 2020). With the increasing proportion of wind power in the power grid, it is inevitable for wind farms to participate in the AGC process. Compared with traditional hydro power units and thermal power units, wind turbines have higher response speed and higher climbing speed (Yang et al., 2016; Yang et al., 2017; Zhang et al., 2018; Lu et al., 2021). However, wind power generation is vulnerable to weather, resulting in large power fluctuations (Li et al., 2020). At present, the research on the participation of renewable energy in AGC is mainly about the design of controller and gain optimization, and the coordinated operation of renewable energy and traditional hydro/thermal power units is not considered (Suresh Kumar et al., 2017; Nizamuddin et al., 2018; Yogendra, 2018; Celik, 2020; Pillai et al., 2020; An and Nishat, 2021; Arya et al., 2021; Gaber et al., 2022). In Nizamuddin et al. (2018), a genetic optimization algorithm was used to obtain the optimal gain of AGC controllers. In Arya et al. (2021), a control strategy of fractional connected fuzzy proportional integral differential (PID) combination filter controllers was proposed to solve the coordinated control problem of AGC with multi-source participation. In Lal et al. (2016), in the AGC system, a gray wolf optimization algorithm was used to obtain the optimal gain of PID controllers of the AGC system, so as to quickly attenuate the oscillation frequency of the area and tie line power.

When wind power is highly involved in AGC frequency regulations, this study considers achieving the coordinated control between wind turbines and traditional water/thermal power units by reasonably distributing power output commands. Aiming at minimizing power deviation and regulating mileage, a multi-objective optimization model of AGC multi-source cooperative control was established (Zhang et al., 2021b; He et al., 2021; Li et al., 2021; Li et al., 2022). The cooperative AGC process with the participation of multiple frequency regulation power plants is a complex non-linear problem (Mukherjee and Shiva, 2016; Pan et al., 2019). In practical application, most AGC processes distribute power only according to the adjustable capacity and the climbing speed. When wind power participates in frequency regulation, it does not make full use of the advantages of high response speeds and climbing speeds of wind power and consider the characteristics of large fluctuations of wind turbine’s output power, so it is impossible to achieve the optimal control of AGC systems. For the cooperative optimal AGC problem of wind turbines and traditional frequency regulation units, although the traditional mathematical optimization method has high solution speed, it is difficult to obtain an optimal solution because of its poor global search ability. In contrast, a meta-heuristic algorithm is more flexible and has stronger global search ability (Yang et al., 2019), such as the genetic algorithm (GA) (Pajak et al., 2020) and the particle swarm optimization (PSO) algorithm (Gu et al., 2022).

For the sake of improving the dynamic response ability of AGC, the biological target of complementary control of energy storage resources with high participation is established in He et al. (2021). Zhang et al. (2021b) used an adaptive distributed auction algorithm to optimize AGC scheduling commands to minimize the deviation between power command output and actual output. The optimal scheduling scheme is obtained by using the strength Pareto evolutionary algorithm and gray target decision. The simulation results show that this method can effectively reduce power deviation and adjustment mileage payment. Li et al. (2022) proposed a multi-agent deep learning algorithm to realize the frequency regulation of power systems. The simulation results show that this method can not only improve the control effect but also reduce the adjustment mileage payment. In Li et al. (2021), in order to reduce the random power disturbance in energy systems, a multi-experience pool replay double delay deep deterministic method gradient is proposed to reduce control deviation and adjustment mileage payment.

This study presents a multi-objective mayfly optimization (MMO) algorithm. This algorithm is used to optimize the power command distribution link in the working process of AGC, make full use of the advantages of high response speeds of upper wind turbines, and weaken the disadvantages of large fluctuations of wind turbine’s output, so as to achieve the coordinated control problem between wind turbines and traditional water/thermal power units (Bhattacharyya et al., 2020; Zervoudakis and Tsafarakis, 2020). In addition, because each control interval can only assign one AGC scheduling signal to each unit, an appropriate decision method is needed to select an optimal scheme from the Pareto solution set. In this study, the gray target decision-making method is used to select the best decision scheme, which is one of the effective methods to solve the multi-objective optimization problem (Li et al., 2018; Liu et al., 2019).

The contents of this article are as follows: the second section introduces the multi-source-coordinated control model of AGC. The third section introduces MMO. In the fourth section, the simulation results and discussion of multi-objective mayfly algorithm are given. The fifth section summarizes the work results of this study.

2 AGC Multi-Source Cooperative Control Model

2.1 AGC Framework

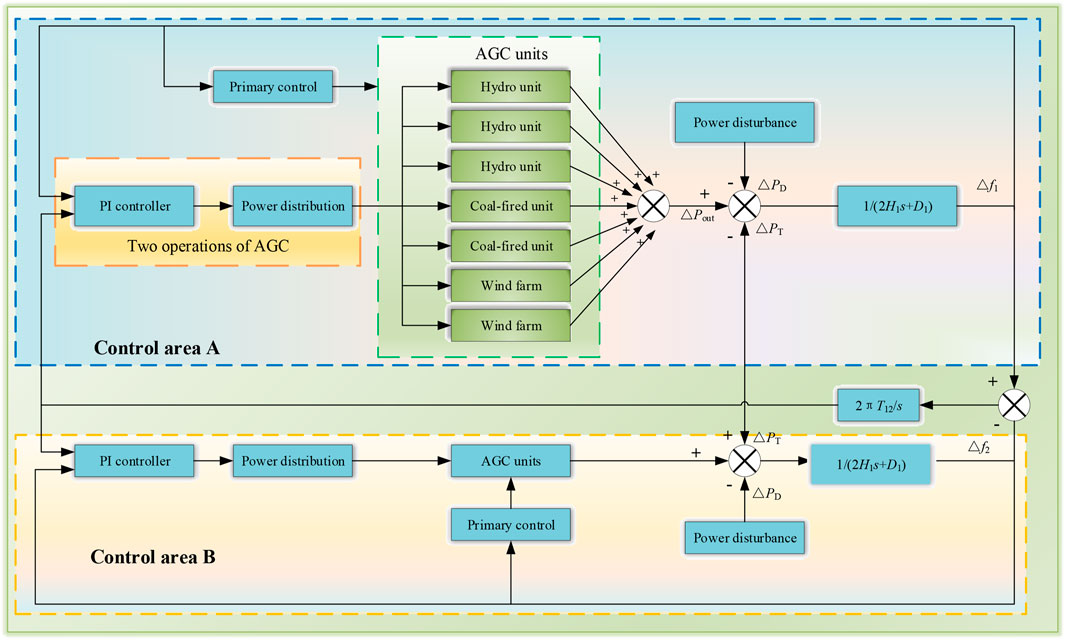
The two-area load frequency control (LFC) model adopted in this study is shown in Figure 1. The AGC working process mainly includes two links: controller and power distribution. The controller usually adopts the PI control strategy. The controller converts the real-time acquisition frequency deviation and tie-line power deviation into regional control deviation, and finally outputs the real-time total regulated power $\mathrm{\Delta }P$; then it allocates $\mathrm{\Delta }P$ to each AGC unit according to the distribution algorithm. The focus of this study is the allocation process of the second link. An MMO algorithm is used to optimize the power allocation process and achieve the optimal power allocation scheme.

FIGURE 1

FIGURE 1. AGC structure of the two-area LFC model.

In Figure 1, $\mathrm{\Delta }{P}_{\text{T}}$ is defined as the power exchange deviation of the connecting line; $\mathrm{\Delta }f$ is defined as the deviation of real-time frequency; $\mathrm{\Delta }{P}_{\text{out}}$ is defined as the practical adjusted power output; and $\mathrm{\Delta }{P}_{\text{D}}$ is defined as power disturbance.

2.2 Constraints

In the working process of AGC systems (Zhang et al., 2020), the following two constraints need to be considered.

2.2.1 Power Balance Constraint

The total power output command of the control is equal to the sum of commands received by all AGC units, as follows:

${\displaystyle {\sum }_{i=1}^n\mathrm{\Delta }{P}_i^{\text{in}}\left(k\right)-\mathrm{\Delta }{P}_{\text{c}}\left(k\right)=0},(1)$

where $\mathrm{\Delta }{P}_i^{\text{in}}$ is defined as the input instruction received by the ith unit of the kth control interval and $\mathrm{\Delta }{P}_{\text{c}}$ is output of the controller.

2.2.2. Generation Ramp Constraint

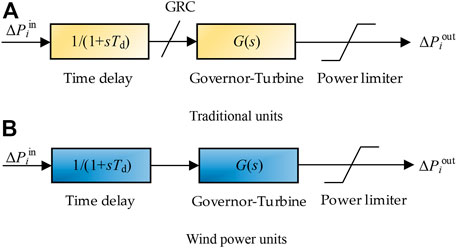
Different types of AGC units have different response time delays, as shown in Table 1 (Yu et al., 2011). Wind energy does not have generation ramp constraint (GRC), and the function of dynamic response is shown in Figure 2. The actual regulated power output is related to the Laplace inverse transfer function, which can be expressed as follows:

$\mathrm{\Delta }{P}_i^{\text{out}}\left(t\right)=L^{-1}\left\{\frac{G_i\left(s\right)}{s\left(1+T_d^{i}s\right)}{\displaystyle {\sum }_{k=1}^N\left[{\text{e}}^{-\mathrm{\Delta }T\left(k-1\right)s}{M}_i^{\text{in}}\left(k\right)\right]}\right\},(2)$

$\mathrm{\Delta }{P}_i^{\text{out}}\left(t\right)=\mathrm{\Delta }{P}_i^{\text{out}}\left(t=k\cdot \mathrm{\Delta }T\right),(3)$

$M_i^{\text{in}}\left(k\right)=\mathrm{\Delta }{P}_i^{\text{in}}\left(k\right)-\mathrm{\Delta }{P}_i^{\text{in}}\left(k-1\right),(4)$

where $G_i\left(s\right)$ is the energy transfer function, $\mathrm{\Delta }T$ is the delay time constant, and $M_i^{\text{in}}\left(k\right)$ is the adjustment mileage input.

TABLE 1

TABLE 1. Types of transfer functions for various units.

FIGURE 2

FIGURE 2. Dynamic response models. (A) Traditional units. (B) Wind power units.

Considering GRC and power limiter, the output of the control can be shown as follows:

$\mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)=\{\begin{array}{c}{P}_i^{\text{out}}\left(k-1\right)+R_i^{\text{min}},if\mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)<R_i^{\text{min}}\\ \mathrm{\Delta }{P}_i^{\text{out}}\left(k\right),if{R}_i^{\text{min}}\le \mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)\le R_i^{\text{max}}\\ P_i^{\text{out}}\left(k-1\right)+R_i^{\text{max}}, if\mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)>R_i^{\text{min}}\end{array},(5)$

$R_i^{\text{min}}=\{\begin{array}{c}0,if{M}_{\text{c}}\left(k\right)\ge 0\\ \max \left[-\mathrm{\Delta }{P}_i^{\text{rate}}\cdot \mathrm{\Delta }T,\mathrm{\Delta }{P}_i^{\text{min}}-\mathrm{\Delta }{P}_i^{\text{out}}\left(k-1\right)\right], if{M}_{\text{c}}\left(k\right)<0\end{array},(6)$

$R_i^{\text{max}}=\{\begin{array}{c}\min \left[\mathrm{\Delta }{P}_i^{\text{rate}}\cdot \mathrm{\Delta }T, \mathrm{\Delta }{P}_i^{\text{max}}-\mathrm{\Delta }{P}_i^{\text{out}}\left(k-1\right)\right], if{M}_{\text{c}}\left(k\right)\ge 0\\ 0,if{M}_{\text{c}}\left(k\right)<0\end{array},(7)$

where $\mathrm{\Delta }{P}_i^{\text{min}}$ and $\mathrm{\Delta }{P}_i^{\text{max}}$ are defined as minimum and maximum adjust capacity, respectively; $R_i^{\text{min}}$ and $R_i^{\text{max}}$ are defined as the minimum and maximum power regulation range; and $\mathrm{\Delta }{P}_i^{\text{rate}}$ is the maximum ramp rate.

2.3 Objective Function

According to the two control objectives of this study, the fitting degree of power command output and actual output curve is higher and the adjustment mileage payment is smaller. Therefore, the objective function can be as follows:

$\{\begin{array}{c}\mathrm{m}\mathrm{i}\mathrm{n}{f}_1={\displaystyle {\sum }_{k=1}^N\left|\mathrm{\Delta }{P}_{\text{c}}\left(k\right)-{\displaystyle {\sum }_{i=1}^n\mathrm{\Delta }{P}_i^{\text{out}}(k+1)}\right|}\\ \mathrm{m}\mathrm{i}\mathrm{n}{f}_2={\displaystyle {\sum }_{k=1}^n{R}_i} \end{array},(8)$

where $R_i$ is the adjustment mileage payment, as follows:

$R_i={\displaystyle {\sum }_{k=1}^N\gamma S_i^P{M}_i^{\text{out}}\left(k\right)},(9)$

$M_i^{\text{out}}\left(k\right)=\left|\mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)-\mathrm{\Delta }{P}_i^{\text{out}}\left(k-1\right)\right|,(10)$

where $\gamma$ is defined as the price per mileage, $S_i^P$ is defined as the performance effect, $\mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)$ is defined as the actual output of regulated power, and $M_i^{\text{out}}\left(k\right)$ is defined as the adjusted mileage output.

3 Multi-Objective Mayfly Algorithm

3.1 Movements of the Male Mayfly

For solving the LFC model, this study tries to make the search ability stronger and use higher convergence speeds to find the solution of the MMO; it can get more widely and more uniformly distributed Pareto frontier, and based on the office weight method, the design of gray target decision objectively chooses compromise solution so that you can get optimal economic conditions and have minimal power response total deviation for power allocation schemes. The clustering of male mayflies means that each male adjusts his position according to his own and his neighbors’ appropriate values. Suppose $x_i^t$ is the current position of the ith mayfly in the search space at the time t, then by changing the position by adding velocity $v_i^{t+1}$, it can be expressed as follows (Zervoudakis and Tsafarakis, 2020):

$x_i^{t+1}=x_i^t+v_i^{t+1}.(11)$

Also, the speed of the male mayfly can be expressed as follows (Zervoudakis and Tsafarakis, 2020):

$v_{ij}^{t+1}=v_{ij}^t+a_1{\text{e}}^{-\beta r_p^2}\left(pbes{t}_{ij}-x_{ij}^t\right)+a_2{\text{e}}^{-\beta r_g^2}\left(gbes{t}_j-x_{ij}^t\right),(12)$

where $v_{ij}^t$ is the velocity of the ith mayfly at time t in the jth dimension, $x_{ij}^t$ represents the position at time t, $a_1$ and $a_2$ are positive attraction coefficients of social effects, $pbes{t}_{ij}$ represents ephemera history in place, and $gbes{t}_j$ represents the best mayfly location. The distance can be expressed as follows (Zervoudakis and Tsafarakis, 2020):

$\Vert x_i-X_i\Vert =\sqrt{{\displaystyle {\sum }_{j=1}^n{\left(x_{ij}-X_{ij}\right)}^2}}.(13)$

The best mayflies must constantly change their speed to improve their global search, as follows:

$v_{ij}^{t+1}=v_{ij}^t+d\ast r,(14)$

where $d$ is the dance coefficient and $r$ is the random number between [−1,1].

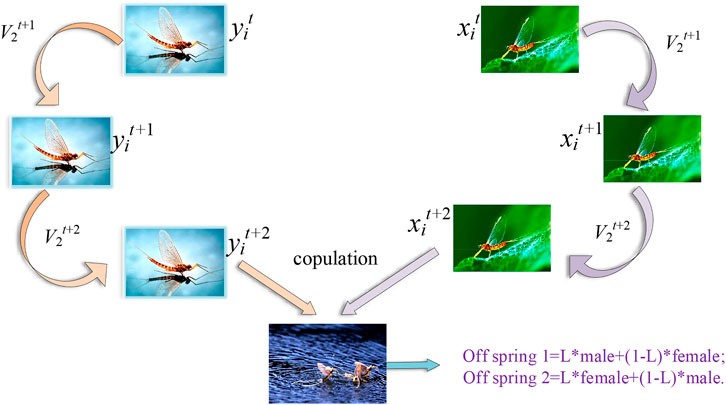
3.2 The Movement of the Female Mayfly

Suppose $y_i^t$ is the ith mayfly at time t, whose position is updated by increasing the speed (Zervoudakis and Tsafarakis, 2020), then the following is obtained:

$y_i^{t+1}=y_i^t+v_i^{t+1}.(15)$

Since the process of attraction is random, the best females should be attracted to the best males, the second best females should be attracted to the second best males, and so on, based on their fitness properties. Therefore, considering the minimization problem, the velocity is calculated as follows (Zervoudakis and Tsafarakis, 2020):

$v_{ij}^{t+1}=\{\begin{array}{c}{v}_{ij}^t+a_2{e}^{-\beta r_{\text{mf}}^2}\left(x_{ij}^t-y_{ij}^t\right), iff\left(y_i\right)>f\left(x_i\right)\\ v_{ij}^t+fl\ast r,iff\left(y_i\right)\le f\left(x_i\right)\end{array},(16)$

where $r_{\text{mf}}$ is the distance between the female and the male.

Crossover results in two offspring, which are produced, are as follows:

$\begin{array}{c}offspring1=\mathit{L}\ast male+\left(1-L\right)\ast female \\ offspring2=L\ast female+\left(1-L\right)\ast male \end{array},(17)$

where L is a random number of a certain range.

3.3 Crowding Distance

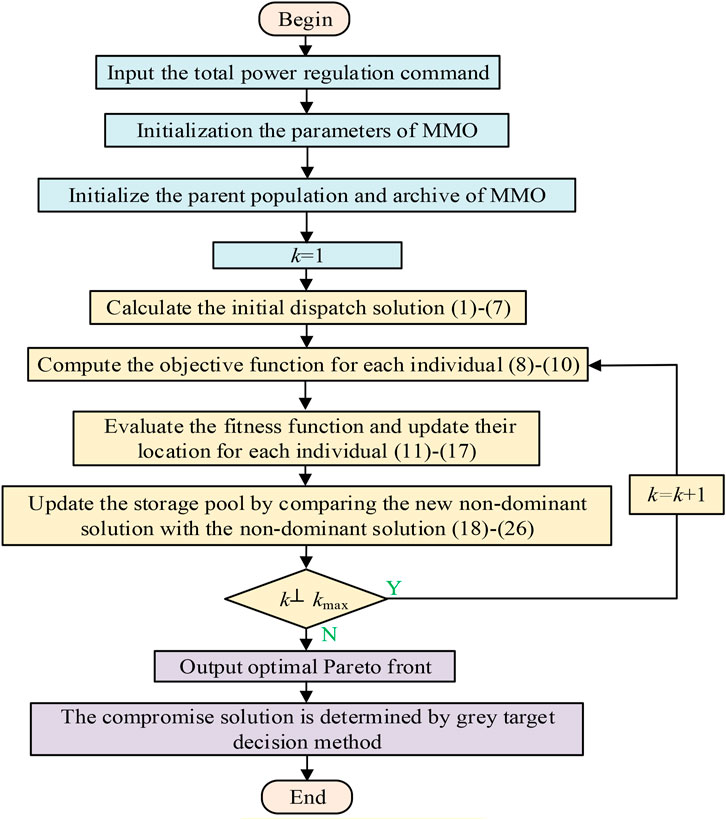
The repository has the maximum size to store non-dominant solutions. In order to sort mayfly and retain the best, a fast non-dominated sort is performed using the crowding distance. The crowding distance provides an estimate of the largest cuboid enclosing a solution by calculating the Euclidean distance between adjacent individuals, without including any other solutions. Boundary solutions with lowest and highest objective function values are always selected by giving an infinite crowding distance value. In addition, the optimization principle of MMO is demonstrated in Figure 3.

FIGURE 3

FIGURE 3. Optimization principle of MMO.

3.4 Design of Gray Targets Decision-Making

The Pareto solution set X based on MMO is a matrix with n rows and m columns, and the absolute value of each solution in X can be taken as one of the decision-making indexes, or as the unit solution output of Pareto frontier, as shown below (Yu et al., 2011):

$X^{\prime }\left(i,j\right)=\left|X\left(i,j\right)\right|, i=\mathrm{1,2},\mathrm{..},n,j=\mathrm{1,2},\dots ,N.(18)$

In order to consider reducing the total power deviation and adjustment mileage payment, two objective function values F₁ and F₂ were used as one of the evaluation indicators.

We considered adding an index D to limit the change of the output of each unit, as follows (Yu et al., 2011):

$D_i=\sqrt{{\displaystyle {\sum }_{j=1}^{m}X\prime {\left(i,j\right)}^2}}.(19)$

Therefore, the effect sample matrix is expressed as follows (Yu et al., 2011):

$X^{\text{″}}=\left[X^{\text{′}}{F}_1{F}_2\text{D}\right].(20)$

The operator $Z_j$ is calculated as follows (Yu et al., 2011):

$Z_j=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\mathit{X}}^{\text{″}}\left(i,j\right),j=\mathrm{1,2},\dots ,m+3}.(21)$

The decision-making matrix V is calculated as follows (Yu et al., 2011):

$v_{ij}=\frac{z_{ij}-x_{ij}}{\text{max}\left\{\underset{1\le i\le n}{\max }\left\{x_{ij}\right\}-z_j,z_j-\underset{1\le i\le n}{\min }\left\{x_{ij}\right\}\right\}}.(22)$

Then the decision matrix can be obtained as follows: $V={\left(v_{ij}\right)}_{n\times \left(m+3\right)}$. Here, $v_j^0=\text{max}\left\{v_j^i|1\le i\le n\right\},j=\mathrm{1,2},\dots .,\left(m+3\right)$. Therefore, the selected bullseye vector is as follows: $v^0=\left\{v_1^0,v_2^0,\dots ,v_{m+3}^0\right\}$.

We calculated the weight $y_{ij}$ and entropy $E_j$ according to the index value of each program, as follows (Yu et al., 2011):

$y_{ij}=x_{ij}/{\displaystyle {\sum }_{i=1}^n{x}_{ij},x_{ij}\ge 0},(23)$

$E_j=-\frac{1}{\text{ln}n}{\displaystyle {\sum }_{i=1}^n{y}_{ij}\text{ln}{y}_{ij},E_j>0},(24)$

${\omega }_j=\left(1-E_j\right)/{\displaystyle {\sum }_{j=1}^{m+3}\left(1-E_j\right)},(25)$

According to the bullseye vector $v^0=\left\{v_1^0,v_2^0,\dots ,v_{m+3}^0\right\}$ (Huang et al., 2021), the bullseye distance of each program can be expressed as follows (Yu et al., 2011):

$d_i=\left|v_i-v^0\right|=\left|\sqrt{{\displaystyle {\sum }_{j=1}^{m+3}{\omega }_j{\left(v_{ij}-v_j^0\right)}^2}}\right|.(26)$

The principle of screening programs is that the closer the indicator is to the bullseye, the better the solution. In addition, the flow chart of MMO is shown in Figure 4.

FIGURE 4

FIGURE 4. Flowchart of MMO.

4 Case Studies

In order to verify the effectiveness of MMO, the extended two-area LFC model is tested in this study, and the multi-objective immune algorithm with non-dominated neighbor-based selection is introduced (NNIA) (Gong et al., 2014) along with the non-dominated sorting genetic algorithm II (NSGA-II) (Deb et al., 2002) and the improved strength Pareto evolutionary algorithm (SPEA2) (Corne et al., 2001). In order to fairly compare the search performance of each algorithm, the population size and maximum iteration of all algorithms were set as N = 50 and k_max = 50, respectively. Among them, the time cycle of frequency regulation control is 4 s, and the price of frequency regulation mileage is 2 MW/$. In addition, transfer function parameters of each unit are shown in Table 2, and main parameters of each unit are given in Table 3. In addition, the simulation is executed on MATLAB/Simulink 2019 using a personal computer with an Intel^R Core™ i7 CPU at 2.2 GHz and 16 GB of RAM, and ode23 was selected as the solver, the sampling rate was set to .001 s.

TABLE 2

TABLE 2. Transfer function parameters of AGC units.

TABLE 3

TABLE 3. Main parameters of AGC units in area A of the two-area LFC model.

4.1 Algorithm Performance Test

In order to test the adjustment ability of the algorithm when it encounters load disturbance, load disturbance of ∆P_D = −120 MW is adopted. In addition, Figure 5 compares the Pareto front obtained by each algorithm. It can be seen that the solutions obtained by NNIA deviate from the ideal Pareto frontier. In addition, the Pareto front obtained by NNIA, NSGA-II, and SPEA2 has poor performance. MMO can obtain the most evenly distributed and extensive Pareto front under power disturbances.

FIGURE 5

FIGURE 5. Comparison of the Pareto front.

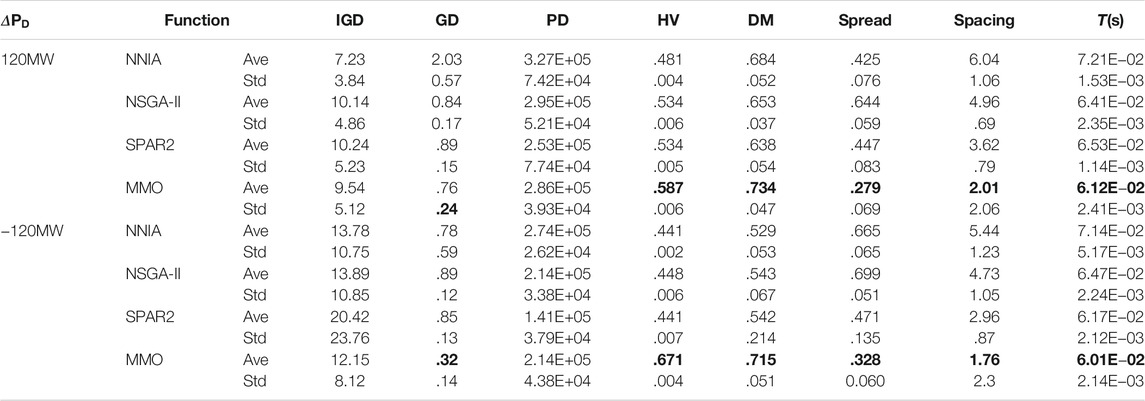
Table 4 shows that after running each algorithm 10 times, inverted generational distance (IGD), generational distance (DG), pure diversity (PD), hyper volume (HV), diversity metric (DM), breadth, spacing, and average running time T(s) were used (Deb and Jain, 2002; While et al., 2006; Wang et al., 2017), so as to compare the search performance of each algorithm; hence, it can be seen as follows:

(1) Among the GD average values of all algorithms, MMO has the smallest value, so its convergence performance is the best. It is worth noting that the GD average for MMO is only 42%, 90%, and 85% of the NNIA, NSGA-II, and SPAR2, respectively;

(2) The average DM and HV values of MMO are significantly higher than those of other algorithms, which prove that MMO has a good performance of Pareto front. In particular, the average DM for MMO was 1.07, 1.12, and 1.15 times higher than the NNIA, NSGA-II, and SPAR2, respectively;

(3) MMO has the minimum universality and average spacing, which can prove that the distribution of Pareto front obtained by MMO is the most uniform and extensive. In particular, the spacing average for MMO is only 33%, 40%, and 55% for NNIA, NSGA-II, and SPAR2, respectively;

(4) MMO has the minimum average running time, so it can converge to the Pareto front the fastest, to respond to the power regulation command in the shortest time.

TABLE 4

TABLE 4. Comparison of performance metrics of algorithms.

4.2 Step Load Disturbance

In order to further verify the effectiveness of MMO and gray target decision method, load disturbances of ∆P_D = 120 MW and ∆P_D = −120 MW are used to test and compare with the proportion method (PROP). Therefore, the output of the ith unit in the kth control cycle is calculated as follows:

$\mathrm{\Delta }{P}_i^{\text{out}}\left(k\right)=\{\begin{array}{c}\mathrm{\Delta }{P}_{\text{c}}\left(k\right)\cdot \mathrm{\Delta }{P}_i^{\text{max}}/{\displaystyle {\sum }_{i=1}^{n_g}\mathrm{\Delta }{P}_i^{\text{max}}},\text{if}\mathrm{\Delta }{P}_{\text{c}}\left(k\right)\ge 0\\ \mathrm{\Delta }{P}_{\text{c}}\left(k\right)\cdot \mathrm{\Delta }{P}_i^{\text{min}}/{\displaystyle {\sum }_{i=1}^{n_g}\mathrm{\Delta }{P}_i^{\text{min}}},\text{if}\mathrm{\Delta }{P}_{\text{c}}\left(k\right)<0\end{array}.(27)$

It can be seen from Figure 6A that MMO can well coordinate the power output among all units. When ∆P_D = 120 MW, the total power deviation obtained is obviously low. The overshoot of the total power command is reduced, and the total power output curve is much closer to the total command curve. It makes the system more stable and can quickly recover the disturbed power system. In addition, Figure 6B shows the power response curve of each unit. Wind power resources have a higher response speed, while hydro power resources have a higher output. Under the mutual cooperation of all resources, the disturbed power system can be well restored. Figure 6C shows the frequency deviation controlled by MMO and PROP. It can be found that MMO has a strong multi-objective search ability, which can further effectively reduce the frequency deviation of the system.

FIGURE 6

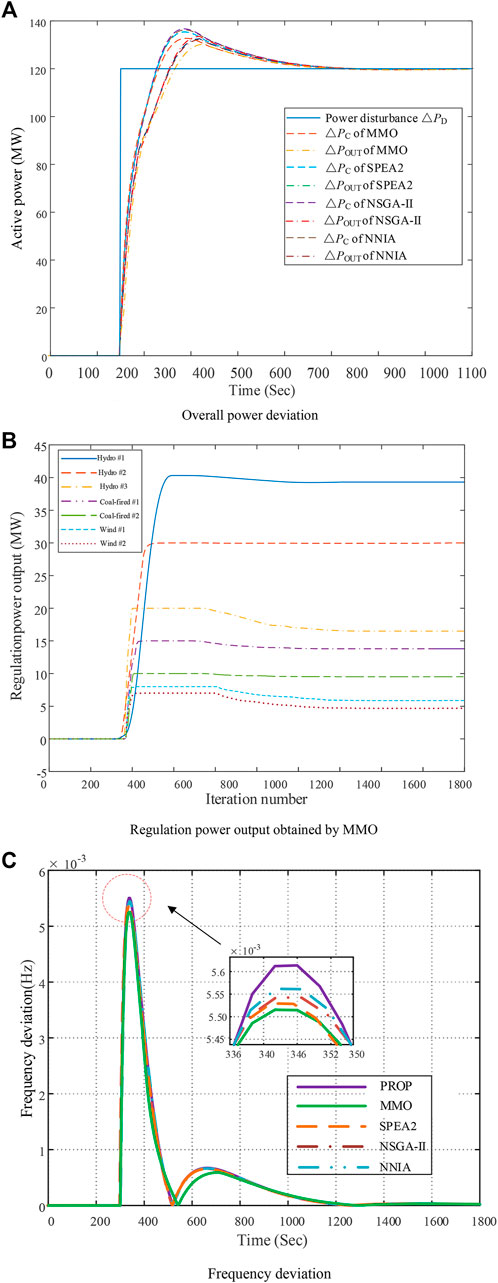
FIGURE 6. Real-time optimization results under ∆P_D = 120 MW. (A) Overall power deviation. (B) Regulation power output obtained by MMO. (C) Frequency deviation.

In addition, Figure 7 shows the system response when the disturbance is −120 WM. It can be seen that the error between the total input power and the total output power can be reduced under MMO adjustment, and the peak of frequency deviation can be slightly reduced. In this case, the recovery ability of the system under different disturbances is further verified. It can be seen that the wind turbine has a high response speed, which makes up for the slow response speed of hydro power and thermal power resources. Under the optimization of MMO, the frequency deviation of the system is further reduced. It is worth noting that the hydro power unit has the best peak shaving capacity, and its response speed is slightly lower than that of the wind turbine, but it can maximize the power gap.

FIGURE 7

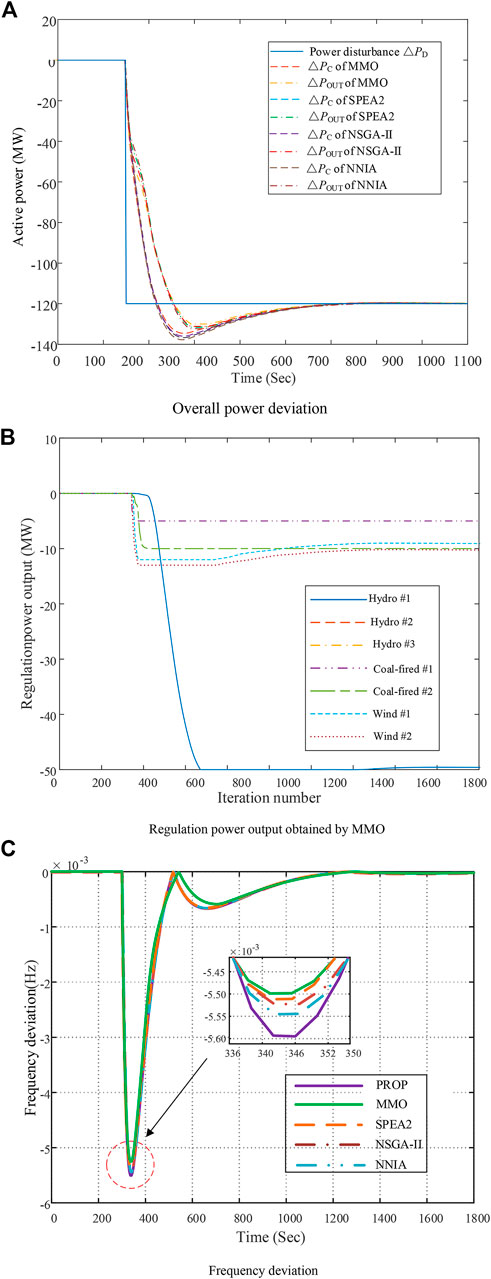
FIGURE 7. Real-time optimization results under ∆P_D = −120 MW. (A) Overall power deviation. (B) Regulation power output obtained by MMO. (C) Frequency deviation.

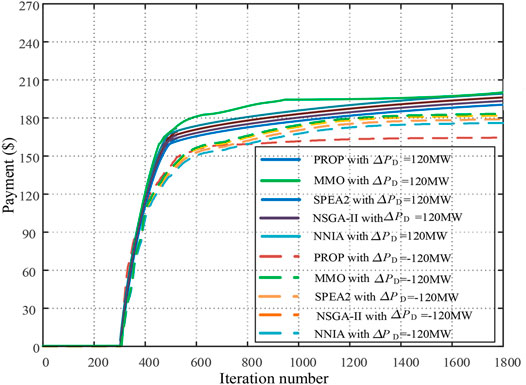
Figure 8 shows the variation of frequency adjustment mileage expenditure under different perturbations. Based on Figures 6–8, it can be seen that MMO can significantly improve power quality on the premise of taking into account the frequency regulation mileage expenditure. Thus, MMO can significantly increase the frequency regulation capability of their systems at a slightly higher price for frequency regulation miles.

FIGURE 8

FIGURE 8. Adjustment mileage payment under four perturbations cases.

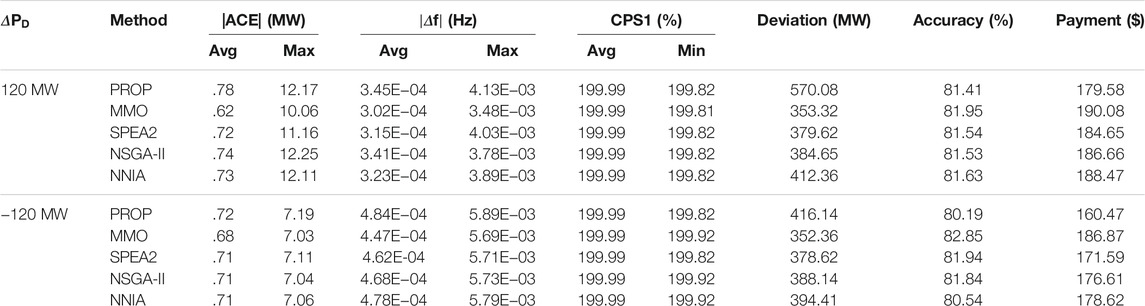
Finally, the comparison of the two kinds of Table 5 conditions of online optimization results shows that the method can effectively reduce power response total deviation, reduce the average as |∆f| and |ACE|, and effectively improve the dynamic response performance of the system. Particularly, area control error (ACE) of MMO is only 79.48%, 81.11%, 84.78%, and 84.93% than that of PROP, SPEA2, NSGA-II, and NNIA, respectively, in $\mathrm{\Delta }{P}_{\text{D}}=120\text{MW}$. In addition, |Δf| of MMO is only 92.36%, 96.75%, 95.51%, and 93.51% than that of PROP, SPEA2, NSGA-II, and NNIA, respectively, in $\mathrm{\Delta }{P}_{\text{D}}=120\text{MW}$. Payment of MMO is only 105.84%, 102.94%, 101.83%, and 100.85% than that of PROP, SPEA2, NSGA-II, and NNIA, respectively, in $\mathrm{\Delta }{P}_{\text{D}}=120\text{MW}$. Deviation of MMO is only 61.98%, 93.07%, 91.85%, and 85.68% than that of PROP, SPEA2, NSGA-II, and NNIA, respectively, in $\mathrm{\Delta }{P}_{\text{D}}=-120\text{MW}$. Particularly, Payment of MMO is only 116.45%, 108.90%, 105.80%, and 104.61% than that of PROP, SPEA2, NSGA-II, and NNIA, respectively, in $\mathrm{\Delta }{P}_{\text{D}}=-120\text{MW}$.

TABLE 5

TABLE 5. Result comparison of online optimization under different disturbances.

5 Conclusion

This study proposes a multi-source optimal cooperative frequency regulation strategy based on MMO. The main contributions can be summarized as follows:

(1) The strategy can effectively reduce the total power deviation and optimize the allocation of various frequency regulation resources under the premise of optimal economic benefits. Particularly, the power deviation, average $\left|\mathrm{\Delta }f\right|$, and $\left|\text{ACE}\right|$ obtained by MMO reduce to 38.1%, 7.6%, and 20.5%, respectively, compared with PROP in $\mathrm{\Delta }{P}_{\text{D}}=120\text{MW}$;

(2) The MMO can obtain the most evenly distributed and extensive ideal Pareto front in the shortest time, while the gray target decision method based on the entropy weight method can objectively select the compromise solution, giving full play to the advantages of various frequency regulation resources;

(3) For extension of two regional load frequency control model test, the result shows that |ACE|, average $\left|\mathrm{\Delta }f\right|$, and total power deviation decreases, to obtain the best efficiency and improve dynamic response performance, proving that the strategy can effectively solve the multi-objective optimization problem.

In order to further improve economic benefits and system response speed, a renewable energy system equipped with an energy storage system will be studied in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CL: conceptualization and writing–reviewing and editing; QQL: writing–original draft preparation and Investigation; XST: supervision; LJW: conceptualization and resource collection; YNC: writing–reviewing and editing and software; CGL assisted with supervision.

Funding

This was supported in part by the National Natural Science Foundation of China (U1966208, 52007174).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

ACE, area control error; AGC, automatic generation control; DM, diversity metric; GA, genetic algorithm; GD, generational distance; GRC, generation ramp constraint; HV, hyper volume; IGD, inverted generational distance; LFC, load frequency control; MMO, multi-objective mayfly optimization; NNIA, multi-objective immune algorithm with non-dominated neighbor-based selection; NSGA-II, non-dominated sorting genetic algorithm II; PD, pure diversity; PID, proportional integral differential; PROP, proportion method; PSO, particle swarm optimization; SPEA2, improved strength Pareto evolutionary algorithm.

References

An, K. M., and Nishat, A. S. (2021). Sliding Mode Controller Design for Frequency Regulation in an Interconnected Power System. Prot. Control. Mod. Power Syst. 6 (1), 77–88. doi:10.1186/s41601-021-00183-1

Arya, Y., Dahiya, P., Celik, E., Sharma, G., Gözde, H., and Nasiruddin, I. (2021). AGC Performance Amelioration in Multi-Area Interconnected thermal and thermal-hydro-gas Power Systems Using a Novel Controller - ScienceDirect. Eng. Sci. Technol. Int. J. 24 (2021), 384–396. doi:10.1016/j.jestch.2020.08.015

Attig-Bahar, F., Ritschel, U., Akari, P., Abdeljelil, I., and Amairi, M. (2021). Wind Energy Deployment in Tunisia: Status, Drivers, Barriers and Research Gaps-A Comprehensive Review. Energ. Rep. 7, 7374–7389. doi:10.1016/j.egyr.2021.10.087

Bevrani, H., Ghosh, A., and Ledwich, G. (2010). Renewable Energy Sources and Frequency Regulation: Survey and New Perspectives. IET Renew. Power Gener. 4 (5), 438–457. doi:10.1049/iet-rpg.2009.0049

Bhattacharyya, T., Chatterjee, B., Singh, P. K., Yoon, J. H., Geem, Z. W., and Sarkar, R. (2020). Mayfly in Harmony: A New Hybrid Meta-Heuristic Feature Selection Algorithm. IEEE Access 8, 195929–195945. doi:10.1109/access.2020.3031718

Celik, E. (2020). Improved Stochastic Fractal Search Algorithm and Modified Cost Function for Automatic Generation Control of Interconnected Electric Power Systems. Eng. Appl. Artif. Intelligence 88 (Feb.), 103407.1–103407.20. doi:10.1016/j.engappai.2019.103407

Corne, D. W., Jerram, N. R., Knowles, J. D., and Oates, M. J. (2001). “PESA-II: Region-Based Selection in Evolutionary Multiobjective Optimization,” in Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco California, July 2001 (Burlington, Massachusetts, United States: Morgan Kaufmann Publishers Inc), 283–290.

Deb, K., and Jain, S. (2002). “Running Performance Metrics for Evolutionary Multi-Objective Optimizations,” in Proceedings of the Fourth Asia-Pacific Conference on Simulated Evolution and Learning, Singapore, 2002, 13–20.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Computat. 6 (2), 182–197. doi:10.1109/4235.996017

Dong, F., Li, Y., Gao, Y., Zhu, J., Qin, C., and Zhang, X. (2022). Energy Transition and Carbon Neutrality: Exploring the Non-linear Impact of Renewable Energy Development on Carbon Emission Efficiency in Developed Countries. Resour. Conservation Recycling 177, 106002. doi:10.1016/j.resconrec.2021.106002

Gaber, M., Abualkasim, B., and Mohammed, A. (2022). Superconducting Energy Storage Technology-Based Synthetic Inertia System Control to Enhance Frequency Dynamic Performance in Microgrids with High Renewable Penetration. Prot. Control. Mod. Power Syst. 6 (4), 460–472. doi:10.1186/s41601-021-00212-z

Gong, M., Jiao, L., Du, H., and Bo, L. (2014). Multiobjective Immune Algorithm with Nondominated Neighbor-Based Selection. Evol. Comput. 16 (2), 225–255. doi:10.1162/evco.2008.16.2.225

Gu, Q., Liu, Y., Chen, L., and Xiong, N. (2022). An Improved Competitive Particle Swarm Optimization for many-objective Optimization Problems. Expert Syst. Appl. 189, 116118. doi:10.1016/j.eswa.2021.116118

He, C., Wang, H., Wei, Z., and Wang, C. (2015). Distributed Coordinated Real-Time Control of Wind Farm and AGC Units. Proc. Chin. Soc. Electr. Eng. 35 (2), 302–309. doi:10.13334/j.0258-8013.pcsee.2015.02.006

He, T. Y., Li, S. N., Wu, S. J., Li, C., and Xu, B. (2021). Biobjective Optimization-Based Frequency Regulation of Power Grids with High-Participated Renewable Energy and Energy Storage Systems. Math. Probl. Eng. 2021, 5526492. doi:10.1155/2021/5526492

Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for VSC-HVDC Connected Offshore Wind Farm. IEEE Trans. Ind. Inf. 17, 8165–8176. doi:10.1109/TII.2021.3065375

Ibraheem,, , Kumar, P., and Kothari, D. P. (2005). Recent Philosophies of Automatic Generation Control Strategies in Power Systems. IEEE Trans. Power Syst. 20 (1), 346–357. doi:10.1109/tpwrs.2004.840438

Lal, D. K., Barisal, A. K., and Tripathy, M. (2016). Grey Wolf Optimizer Algorithm Based Fuzzy PID Controller for AGC of Multi-Area Power System with TCPS. Proced. Comp. Sci. 92, 99–105. doi:10.1016/j.procs.2016.07.329

Li, J., Liu, C., Zhang, P., Wang, Y., and Rong, J. (2020). Difference between Grid Connections of Large-Scale Wind Power and Conventional Synchronous Generation. Glob. Energ. Interconnection 3 (5), 486–493. doi:10.1016/j.gloei.2020.11.008

Li, J., Yu, T., and Zhang, X. (2022). Coordinated Load Frequency Control of Multi-Area Integrated Energy System Using Multi-Agent Deep Reinforcement Learning. Appl. Energ. 306 (A), 117900. doi:10.1016/j.apenergy.2021.117900

Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021). Efficient Experience Replay Based Deep Deterministic Policy Gradient for AGC Dispatch in Integrated Energy System. Appl. Energ. 285, 116386. doi:10.1016/j.apenergy.2020.116386

Li, R., Jiang, Z., Ji, C., Li, A., and Yu, S. (2018). An Improved Risk-Benefit Collaborative Grey Target Decision Model and its Application in the Decision Making of Load Adjustment Schemes. Energy 156, 387–400. doi:10.1016/j.energy.2018.05.119

Liu, Y., Du, J.-l., and Wang, Y.-h. (2019). An Improved Grey Group Decision-Making Approach. Appl. Soft Comput. 76, 78–88. doi:10.1016/j.asoc.2018.12.010

Lu, P., Ye, L., Zhao, Y., Dai, B., Pei, M., and Tang, Y. (2021). Review of Meta-Heuristic Algorithms for Wind Power Prediction: Methodologies, Applications and Challenges. Appl. Energ. 301 (1), 117446. doi:10.1016/j.apenergy.2021.117446

Mukherjee, V., and Shiva, C. K. (2016). Design and Analysis of Multi-Source Multi-Area Deregulated Power System for Automatic Generation Control Using Quasi-Oppositional harmony Search Algorithm. Int. J. Electr. Power Energ. Syst. 80, 382–395. doi:10.1016/j.ijepes.2015.11.051

Nizamuddin, H., Anita, K., and Kumar, G. J. (2018). Centralized and Decentralized AGC Schemes in 2-area Interconnected Power System Considering Multi Source Power Plants in Each Area. J. King Saud Univ. Eng. Sci. 32 (2), 123–132.

Pajak, M., Buchaniec, S., Kimijima, S., Szmyd, J. S., and Brus, G. (2020). A Multiobjective Optimization of a Catalyst Distribution in a Methane/steam Reforming Reactor Using a Genetic Algorithm. Int. J. Hydrogen Energ. 46 (38), 20183–20197. doi:10.1016/j.ijhydene.2020.02.228

Pan, L., Li, F., and Liu, J. (2019). “Combined Simulation Method of Multi-Source Automatic Generation Control,” in IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), ChangSha, China, 8-10 Nov. 2019. doi:10.1109/EI247390.2019.9062107

Pillai, A. G., Samuel, E. R., and Unnikrishnan, A. (2020). Optimal Load Frequency Control through Combined State and Control Gain Estimation for Noisy Measurements. Prot. Control. Mod. Power Syst. 5 (3), 66–78. doi:10.1186/s41601-020-00169-5

Rahman, A., Saikia, L. C., and Sinha, N. (2017). Automatic Generation Control of an Interconnected Two-Area Hybrid thermal System Considering Dish-stirling Solar thermal and Wind Turbine System. Renew. Energ. 105, 41–54. doi:10.1016/j.renene.2016.12.048

Shetty, C., and Priyam, A. (2021). A Review on Tidal Energy Technologies. Materialstoday: Proc. doi:10.1016/j.matpr.2021.10.020

Suresh Kumar, L. V., Nagesh Kumar, G. V., and Madichetty, S. (2017). Pattern Search Algorithm Based Automatic Online Parameter Estimation for AGC with Effects of Wind Power. Int. J. Electr. Power Energ. Syst. 84, 135–142. doi:10.1016/j.ijepes.2016.05.009

Wang, H., Jin, Y., and Yao, X. (2017). Diversity Assessment in many-objective Optimization. IEEE Trans. Cybernetics 47 (6), 1510–1522. doi:10.1109/TCYB.2016.2550502

While, L., Hingston, P., Barone, L., and Huband, S. (2006). A Faster Algorithm for Calculating Hypervolume. IEEE Trans. Evol. Computat. 10 (1), 29–38. doi:10.1109/tevc.2005.851275

Wu, X., Pei, W., Deng, W., Kong, L., and Ye, H. (2018). Collaborative Optimal Distribution Strategy of AGC with Participation of ESS and Controllable Load. Energ. Proced. 145, 103–108. doi:10.1016/j.egypro.2018.04.017

Xiong, L. S., Liu, X. K., Liu, Y. H., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: a Review. Csee Jpes, 1–18. doi:10.17775/CSEEJPES.2020.03590

Xu, Y., Li, F., Jin, Z., and Variani, M. H. (2016). Dynamic Gain-Tuning Control (DGTC) Approach for AGC with Effects of Wind Power. IEEE Trans. Power Syst. 31 (5), 1–10. doi:10.1109/tpwrs.2015.2489562

Yang, B., Jiang, L., Wu, Q. H., and Wu, Q. H. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036

Yang, B., Wang, J., Zhang, X., Wang, J., Shu, H., Li, S., et al. (2020). Applications of Battery/supercapacitor Hybrid Energy Storage Systems for Electric Vehicles Using Perturbation Observer Based Robust Control. J. Power Sourc. 448, 227444. doi:10.1016/j.jpowsour.2019.227444

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047

Yang, B., Zhang, X., Yu, T., Shu, H., and Fang, Z. (2017). Grouped Grey Wolf Optimizer for Maximum Power point Tracking of Doubly-Fed Induction Generator Based Wind Turbine. Energ. Convers. Manag. 133, 427–443. doi:10.1016/j.enconman.2016.10.062

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

Ye, L., Zhang, C., Xue, H., Li, J., Lu, P., and Zhao, Y. (2018). Study of Assessment on Capability of Wind Power Accommodation in Regional Power Grids. Renew. Energ. 133, 647–662. doi:10.1016/j.renene.2018.10.042

Yiran,, , Ma, X., Han, M., Yang, W. J., and Lee, (2020). Multi-timescale Robust Dispatching for Coordinated Automatic Generation Control and Energy Storage. Glob. Energ. Interconnection 3 (4), 355–364.

Yogendra, A. (2018). Improvement in Automatic Generation Control of Two-Area Electric Power Systems via a New Fuzzy Aided Optimal PIDN-FOI Controller. ISA Trans. 80, 475–490. doi:10.1016/j.isatra.2018.07.028

Yu, T., Wang, Y. M., Ye, W. J., Zhou, B., and Chan, K. W. (2011). Stochastic Optimal Generation Command Dispatch Based on Improved Hierarchical Reinforcement Learning Approach. IET Gener. Transm. Distrib. 5 (8), 789–797. doi:10.1049/iet-gtd.2010.0600

Zervoudakis, K., and Tsafarakis, S. (2020). A Mayfly Optimization Algorithm. Comput. Ind. Eng. 145, 106559. doi:10.1016/j.cie.2020.106559

Zhang, J., Chen, J., Kong, X., Song, W., Zhang, Z., Wang, Z., et al. (2018). Research on Active Power Automatic Control Strategy of Wind Farm Energy Station Access System. Energ. Proced. 152, 1033–1038. doi:10.1016/j.egypro.2018.09.115

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat., 1. doi:10.1109/TIA.2021.3093841

Zhang, X. S., Tan, T., Yu, T., Yang, B., and Huang, X. (2020). Bi-objective Optimization of Real-Time AGC Dispatch in a Performance-Based Frequency Regulation Market. CSEE J. Power Energ. Syst., 1–9.

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

Zhang, X., Yu, T., Yang, B., and Li, L. (2016). Virtual Generation Tribe Based Robust Collaborative Consensus Algorithm for Dynamic Generation Command Dispatch Optimization of Smart Grid. Energy 101, 34–51. doi:10.1016/j.energy.2016.02.009

Zhang, X., Yu, T., Yang, B., Zheng, L., and Huang, L. (2015). Approximate Ideal Multi-Objective Solution Q(λ) Learning for Optimal Carbon-Energy Combined-Flow in Multi-Energy Power Systems. Energ. Convers. Manag. 106, 543–556. doi:10.1016/j.enconman.2015.09.049

U1966208 52007174