- 1School of Environmental and Municipal Engineering, Qingdao University of Technology, Qingdao, China
- 2School of Energy and Power Engineering, Chongqing University, Chongqing, China
- 3School of Environmental and Material Engineering, Yantai University, Yantai, China
The tail gas with relatively high calorific value, generated from the depleted reduction of copper slag, can be used as fuel for gas turbines. In this study, the flame speed calculation module in PREMIX of CHEMKIN was used to simulate the combustion characteristics of the tail gas after sulfide removal, the effects of equivalence ratio, gas preheating temperature, and the CO2 concentration on the flame propagation speed and the flame combustion temperature were mainly investigated. Results show that the flame propagation speed and the flame combustion temperature increase continuously with the increase in preheating temperature, while it decreases continuously with the increase in CO2 concentration. Additionally, the peak flame combustion temperature appears at an equivalent ratio of 1.1, while the peak flame propagation speed appears at an equivalent ratio of 2.0, which indicates that the flame combustion temperature is not the main factor affecting flame propagation speed for tail gas.
1 Introduction
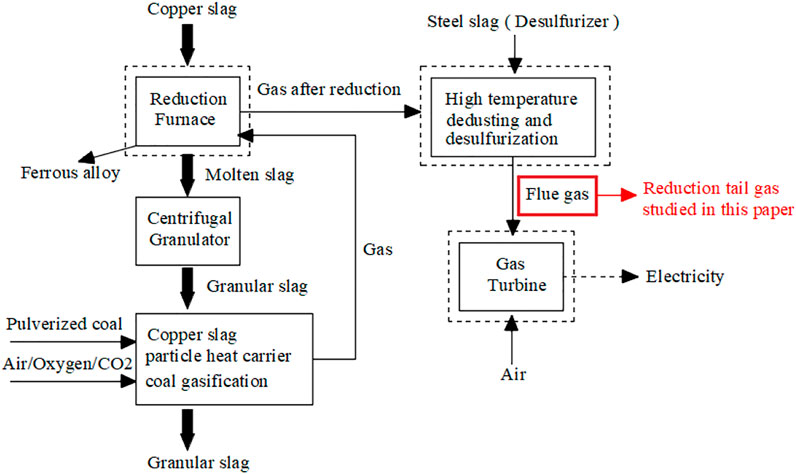
Copper slag, a by-product of the copper smelting industry, contains a large amount of sensible heat and is composed of some metal oxides, which exhibit preferable catalytic performance in improving coal gasification (Du et al., 2010; Li et al., 2021). A heat recovery system from the heat of copper slag, which generates reducing tail gas via the endothermic reactions of gasification, was presented. The specific technology is shown in Figure 1. Copper slag itself is composed of a variety of metal oxides, so it has a certain catalytic reforming ability for low-molecular alkanes (He et al., 2002; Wang and Yu, 2018; Wang et al., 2021), and as a result, the composition of the tail gas changes greatly compared with the gas before reduction. The gas is mainly composed of H2, CO, CO2, and CnHm, which can be used as the reducing gas of copper slag for recycling valuable metals. While this reduction tail gas has a certain calorific value, it can also be used as fuel for gas turbines (Yalikunjiang·Tursun and Yue, 2019). Therefore, tail gas has received a particular interest in recent years.
Laminar flame propagation velocity is a basic parameter of fuel combustion, which can comprehensively reflect the exothermic capacity, diffusivity, and chemical reaction rate of the combustible gas mixture system (Hu and Yu, 2018; Shang et al., 2019). Laminar flame propagation velocity is not only an important basis for studying complex combustion but also an important parameter for verifying the chemical dynamic mechanism and guiding burner safety design (Dong et al., 2002; Bao and Liu, 2011). Flame temperature is also a basic parameter of combustion and a key factor of overall efficiency of the combustion system, which affects all aspects of the material strength, structure, and design of the burner. Studying the combustion characteristics of laminar flame can help us better understand and interpret the actual combustion phenomenon together with the law of combustion reaction. Furthermore, understanding the laminar flame propagation mechanism is also the basis for the study of turbulent flame propagation mechanism (Kishore et al., 2008; Burluka et al., 2010; Zhang et al., 2010).
In recent years, domestic and foreign scholars have also done many experiments and model developments for laminar flame combustion characteristics. Among the study of the basic flame properties required for gas combustion, basic flame speed is very important because it provides detailed information on the thermochemical processes controlling fuel combustion (Bouvet et al., 2011; Zeng et al., 2019). A great deal of previous research into the laminar combustion velocity has focused on the Bunsen burner method (Lee et al., 2002; Pareja et al., 2009; Bouvet et al., 2011; Zhang et al., 2016), whose base-wood principle is to determine the laminar combustion velocity using a premixed flame cone. Research over the last decade indicates that laminar flame propagation velocity of gas can be affected by hydrogen volume fraction, CO2 concentration, preheating temperature, and other factors (Han et al., 2016; Dai et al., 2020). In addition, some domestic and foreign scholars have used CHEMKIN software to simulate the flame combustion characteristics, and the simulation results are consistent with the results obtained by the basic experiments (Mueller et al., 2000; Natarajan et al., 2007, 2008; Ouimette and Seers, 2008; Krejci et al., 2013). At present, some studies have been carried out to simulate the flame propagation velocity of natural gas by using the raw lamp experiment method and CHEMKIN simulation software combined with GRI-3.0 reaction mechanism (Li et al., 2004). The results show that the GRI-3.0 reaction mechanism is more suitable for the simulation of methane combustion characteristics.
In general, there have been plenty of studies on the combustion of single gas. The laws of laminar flame combustion characteristics of natural gas have been proved previously; however, the results cannot be used directly on the analysis of the tail gas, and the studies on the laminar flame combustion characteristics of the tail gas are seldom referred to.
This study aims to use the flame speed calculation module in PREMIX of CHEMKIN to simulate the combustion characteristics of the tail gas after sulfide removal, to mainly discuss the influence law of the equivalence ratio, gas preheating temperature, and the CO2 concentration on the flame propagation speed and the flame combustion temperature. In this simulation, the reduced tail gas is generated from the endothermic gasification reacting in a heat recovery system. Therefore, this work will lay the foundation and provide basic data for the promotion and application of reducing gas combustion technology.
2 CHEMKIN Simulation Method
2.1 Reaction Model
CHEMKIN is a chemical reaction kinetics package, which simulates gas-phase reactions and surface reactions by using detailed primitive reactions. The PREMIX model can be divided into two modules: burner stabilized flame module (BSF) and flame speed calculation module (FSC). The BSF module is suitable for solving the flame temperature distribution curve and the material concentration curve when the mass flow of premixed gas is known. The FSC module is suitable for pressure constant, premixed gas temperature, and known proportion. The flame temperature distribution and flame propagation velocity curve distribution can be conveniently obtained. In this study, the FSC module is used to simulate the combustion characteristics of the tail gas because the atmospheric pressure is constant and the gas temperature and ratio are known.
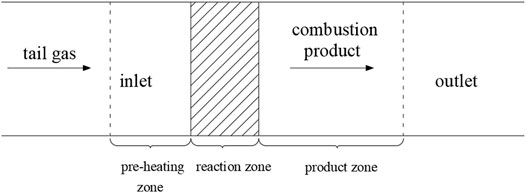
The one-dimensional laminar flame combustion physical model is shown in Figure 2. The tail gas from the copper slag depleted reduction enters the preheating zone from the inlet, and the gas temperature rises continuously, while the chemical reaction proceeds slowly. After the gas reaches the combustion temperature, it burns vigorously in the reaction zone, the chemical reaction proceeds violently, and the reaction reaches a dynamic equilibrium. The rise of gas temperature gradually slows down, and the final temperature tends to be certain in the product zone. Then, the chemical reaction rate drops rapidly, and the combustion products are finally discharged from the outlet.
2.2 Reaction Mechanism
All calculations in CHEMKIN software are based on the mechanism file. This is because the reaction of each primitive and its related parameters, the data of thermodynamic properties of each component, and the data of transport properties are included in the reaction mechanism file. The CO/H2/NOX mechanism file proposed by the National University of Ireland in collaboration with Xi’an Jiaotong University was used for this simulation, which is capable of simulating various reaction systems including H2/O2/N2, N2O pyrolysis, H2/N2O, H2/NOX/O2, CO/H2O/NOX/O2, and H2/CO/H2O/NOX/O2 (Frassoldati et al., 2007; Zhang et al., 2017). Meanwhile, the mechanism contains a large amount of experimental data, including 104 excitation tube datasets, 87 JSR datasets, 87 FR datasets, and six laminar flame velocity datasets with more than 3,000 experimental points. In general, the mechanism file can simulate the combustion process of the tail gas well and has good simulation effect, so this mechanism file is chosen to simulate the combustion characteristics.
Assuming that the gas inlet is a one-dimensional steady flow, the governing equation can be simplified as follows:
Continuity:
Energy:
Species:
Equation of state:
where
2.3 Grid Model Establishment and Independence Test
According to the one-dimensional laminar flame physical model, the exhaust gas passes through the preheating zone, the reaction zone, and the product zone in turn. The path of the gas that passes through is established as a one-dimensional model, and the number of grids is divided. The number of grids is an important basis to determine the calculation accuracy and simulation time. If the number of grids is too small, the simulation accuracy is too poor, while if the number of grids is too large, the simulation calculation time is too long. Meanwhile, the temperature gradient and concentration gradient are smaller in the preheating zone and product zone but larger in the reaction zone. Therefore, the grid cannot be divided equally. According to the gradient, the number of grids in the reaction zone is the densest, followed by the product zone, and the number of grids in the preheating zone is the least. The grid division of the laminar flame is shown in Figure 3.
Table 1 shows the results of the grid independence test of the tail gas under simulated conditions of pressure 1 atm, preheating temperature 598 K, and equivalence ratio 1.0 by using TWOPNT function self-meshing principle.
It can be concluded from the aforementioned table that when the number of grids changes from 100 to 300; the changing ranges of flame propagation speed are 0.105, 0.111, and 0.215, respectively; and the error is large. When the number of grids increases from 300 to 500, the changing range of flame propagation speed is 0.074 and the error is small. Therefore, when the number of grids is 300, the truncation error is small and the amount of computation is reduced, and the simulation accuracy and simulation time reach the best balance.
2.4 Materials and Calculation Conditions
The tail gas used in this simulation is generated by the endothermic reaction of copper slag gasification. The specific process technology is shown in Figure 1. Table 2 shows the main gas composition of the tail gas used in this simulation.
In this article, the effects of the equivalence ratio, preheating temperature, and the CO2 concentration on the combustion characteristics of a one-dimensional laminar premixed flame were investigated. During the calculation, the pressure was kept at 1 atm, the premixed gas inlet velocity was set at 40 cm/s, and the ordinary air at 298 K, and 1 atm was used for calculation air. Other conditions for the simulation are shown in Table 3.
3 Results and Discussion
3.1 Flame Temperature Distribution
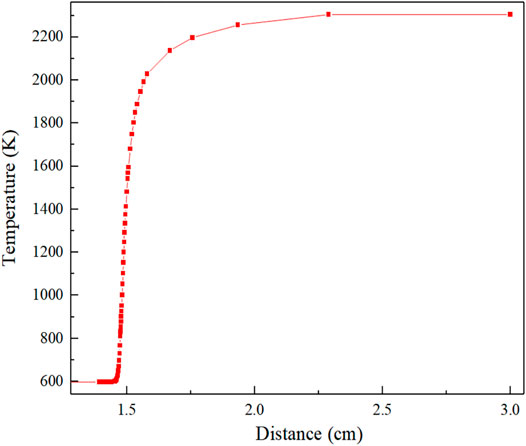
Figure 4 shows the flame temperature distribution curve. Based on the grid self-division function, the analysis is carried out with the curve of equivalent ratio = 1.0. The preheating zone is 0–1.42 cm, and the flame temperature gradient is close to 0. The reaction zone is 1.42–1.66 cm. In this zone, intense heat and mass exchange occur, and when X = 1.66 cm, the temperature reaches 88% of the complete reaction temperature (2305 K). After X = 1.66 cm is the product region, in which the flame combustion temperature rises slowly, the heat–mass exchange gradually reaches equilibrium, and the chemical reaction through a longer product zone to reach equilibrium. The calculation results show that when X = 3.00 cm, the temperature reaches stability and the maximum reaction temperature is 2169 K.
3.2 Simulation of Flame Combustion Characteristics at Different Equivalence Ratios
3.2.1 Effect of the Equivalence Ratio on the Flame Combustion Temperature
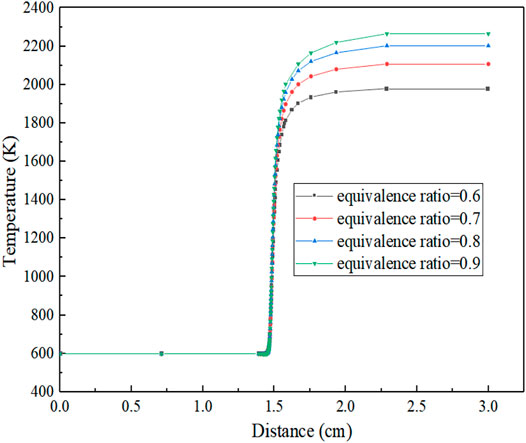
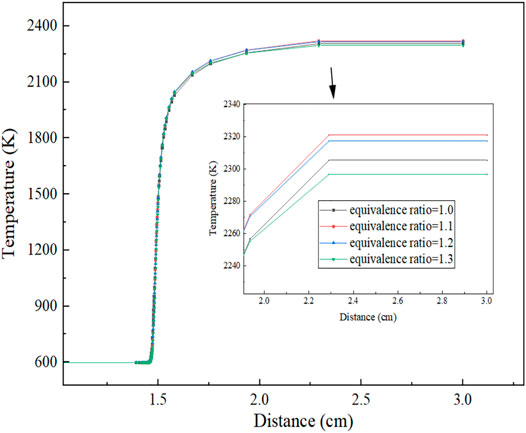
Figure 5 shows the temperature distribution under oxygen-enriched combustion. It can be observed that the ranges of preheating zone, reaction zone, and exothermic zone are basically similar for different equivalence ratios, and there is little change in the distance. The equivalence ratio mainly affects the flame combustion temperature and flame temperature gradient. When the equivalence ratio is less than 1.0, the temperature gradient decreases with the decrease in the equivalence ratio, the flame temperature slowly increases with the increase of distance, and finally, the reaction equilibrium temperature gets lower and lower. This is because with the decrease in equivalence ratio, the amount of substances in the air is more than that of fuel, and finally, the air is in a surplus state. However, the lower the concentration of fuel, the slower the reaction speed and the slower the heat release. Therefore, in an adiabatic condition, the accumulated heat is lower, which leads to the lower and lower equilibrium reaction temperature at the macro-level.
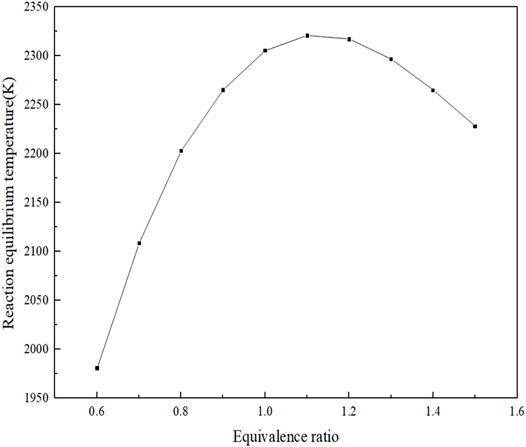
As can be clearly seen from Figure 6, when the equivalent ratio is 1.1, the equilibrium reaction temperature is the highest, about 2321 K; when the equivalent ratio is less than 1.1, the reaction equilibrium temperature gradually decreases and the flame temperature rises slowly. The lower the air concentration and the lower the accumulated heat under adiabatic conditions, the lower the equilibrium reaction temperature at the macro-level. Calculations show that the temperature gradient is 0 when X = 3.0 cm and the reaction temperature reaches equilibrium. The relationship between the specific reaction equilibrium temperature and the equivalence ratio is shown in Figure 7, from which it can be clearly seen that when the equivalence ratio is 1.1, the equilibrium reaction temperature reaches the maximum.
3.2.2 Effect of the Equivalence Ratio on the Flame Propagation Speed
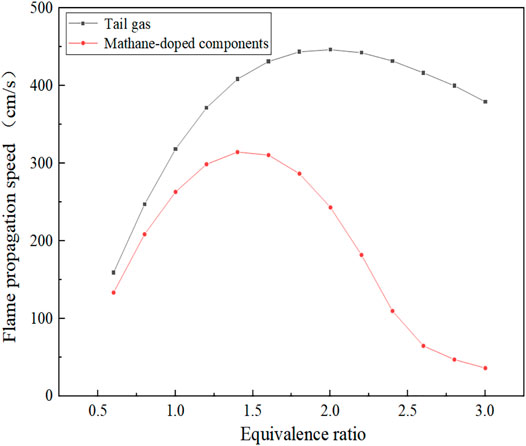
Figure 8 shows the comparison of the tail gas with a typical methane flame propagation speed law. It can be seen that the flame propagation speed increases at first with the increase in the equivalence ratio and then decreases. When the equivalence ratio changes from 0.6 to 2.0, the flame propagation speed rises rapidly; while in the range of 2.0–3.0, the flame propagation speed decreases slowly. As the equivalence ratio changed to 2.1, the flame propagation speed achieved a maximum speed of 446.58 cm/s. According to the variation trend of flame propagation velocity of typical methane component, the maximum flame propagation velocity is achieved at the equivalence ratio of 1.4 after the methane component is mixed in the fuel component. Compared with the fuel tail gas, the flame propagation velocity rises at the equivalence ratio of 0.6–1.4 while it falls at the equivalence ratio of 1.4–3.0. In addition, the gradient of the falling phase is significantly larger than the gradient of the rising phase, that is, the flame propagation velocity decreases extremely fast, and the maximum value of flame propagation velocity is smaller than that of the fuel components in this study.
The reason for the aforementioned differences mainly lies in the composition of the fuel components, when the fuel contains a certain amount of CH4, and the equivalence ratio corresponding to the maximum flame propagation velocity moves from the fuel-rich region to 1.0. From the point of view of chemical kinetics, the increase in laminar flame propagation speed has a strong correlation with the maximum value of free radicals such as H, O, and OH. When CH4 is added, the reaction rate of the chain branching reaction (H + O2 = O + OH) with the largest generation rate of OH radicals decreases, while the reaction rate of the main oxidation reaction (CO + OH = CO2 + H) decreases, and the sensitivity coefficient also decreases. At the same time, CH4 and CH3 consume highly active H and OH, resulting in the decrease in laminar flame propagation speed. As the experimental results obtained by Liu Jiaqi et al. using the Bunsen burner method, the equivalence ratios of the maximum flame propagation velocities were 1.3, 1.2, and 1.1 for 2, 5, and 8% of the methane blending mass, respectively. The gas is affected by the thermodynamic dilution effect of H2O, resulting in the aforementioned phenomenon (Liu, 2018). After the addition of CH4, the molar share of H2 decreases, which makes the decrease in flame propagation speed accordingly (Xiao et al., 2020). As can be seen from Figure 7, the peak adiabatic combustion temperature occurs at an equivalence ratio of 1.1, while the peak flame propagation velocity occurs at an equivalence ratio of 2.0. Therefore, for the fuel components in this article, the adiabatic combustion temperature is not the main factor affecting the flame propagation velocity.
3.3 Simulation of Flame Combustion Characteristics at Different Preheating Temperatures
3.3.1 Effect of the Preheating Temperature on the Flame Combustion Temperature
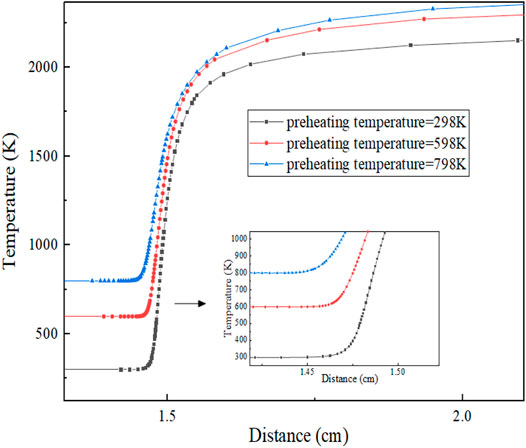
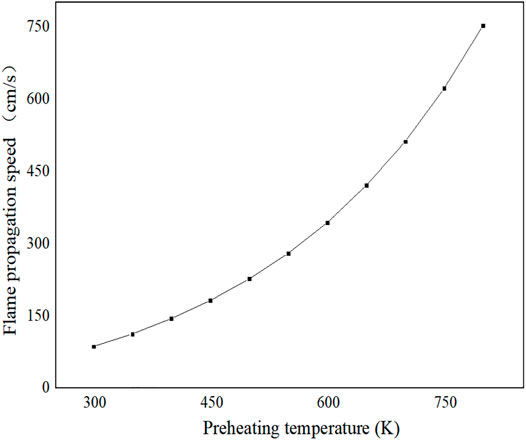
Figure 9 shows the variation of flame temperature with preheating temperature. It can be seen from the figure that the reaction zone decreases with the increase in preheating temperature, while the reaction temperature rises with the increase in preheating temperature, and the specific reaction zones are shown in Table 4. The reason for the aforementioned phenomenon is that with the increase in preheating temperature, the number of activating molecules increases, the activation energy required for the reaction decreases, and the basic reaction becomes more intense. Finally, at the macro-level, the higher the equilibrium temperature of the reaction, the larger the temperature gradient and the smaller the reaction area.
It can be seen from Figure 9 that with the increase in preheating temperature, the starting position of the reaction zone is approaching coordinate zero. This is because the increase in temperature increases the number of activated molecules in the preheating zone and the probability and intensity of collisions between molecules, so it is easier to start the reaction. And the closer the starting position of the reaction zone is to the coordinate zero. In other words, the preheating zone decreases, while the product zone increases.
3.3.2 Effect of the Preheating Temperature on the Flame Propagation Speed
The influence of preheating temperature on laminar flame velocity can be described by the following formula:
where
Figure 10 shows the variation law of flame propagation speed with the preheating temperature. From Figure 10, it can be concluded that the flame propagation element is directly proportional to the preheating temperature. The reason is that the increase in preheating temperature increases the number of active molecules and reduces the activation energy of the reaction. Therefore, the reaction can proceed quickly and the heat as well as the mass exchange is violent, resulting in a faster flame propagation.
3.4 Simulation of Flame Combustion Characteristics at Different CO2 Concentrations
3.4.1 Effect of CO2 Concentration on the Flame Combustion Temperature
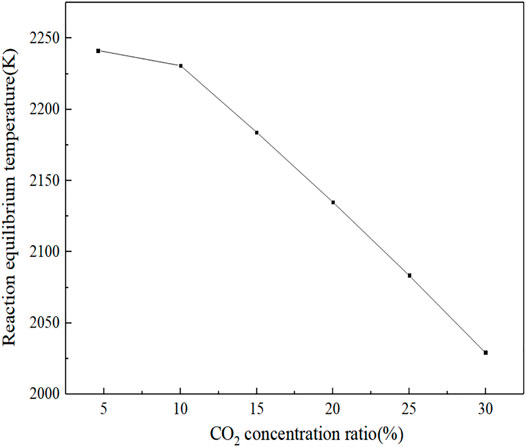
Figure 11 shows the law of the influence of CO2 concentration on the flame burning rate. As the gas enters the reaction zone, the flame burning temperature starts to change. In the range of 1.4468–1.4767 cm, the flame burning rate increases with the increase in CO2 concentration, and when X > 1.4767 cm, the flame burning temperature decreases with the increase in CO2 concentration. The final equilibrium temperature of the reaction decreases with the increase in carbon dioxide concentration, as shown in Figure 12. The reaction equilibrium temperature decreases linearly with CO2. The reason is that CO2 is a non-combustible component. When combustible components burn and release heat, CO2 will absorb the heat released in the reaction process but will not spontaneously burn and release heat. Therefore, the higher the concentration of CO2, the lower the flame combustion temperature and even the non-combustible situation will occur.
3.4.2 Effect of the CO2 Concentration on the Flame Propagation Speed
The thermodynamic effect of CO2 on the flame velocity is mainly to reduce the total amount of reactants and the overall heat release, increase the specific heat capacity of the mixture, reduce the flame temperature, and change the transport properties of the mixture. But CO2 is not just an inert diluent; on the contrary, it can participate in chemical reactions.
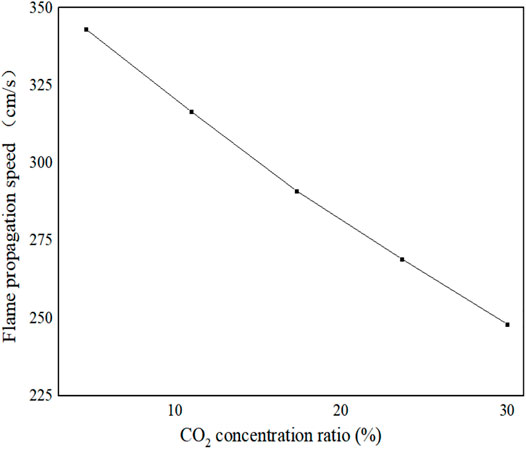
Figure 13 shows the variation of flame propagation velocity with CO2 concentration. It can be seen from Figure 13 that the flame propagation velocity decreases with the increase in CO2 concentration. This is because when the CO2 component is involved in the chemical reaction, the suppression of flame propagation speed by CO2 component mainly comes from two aspects: First, the thermodynamic properties of CO2; when the CO2 is used as a fuel component, it is non-combustible, thus causing an overall reduction in fuel heat generation, which increases the specific heat capacity of the resulting mixture as well as lowers the adiabatic temperature, to suppress the flame propagation rate. Second, the chemical effect of CO2, unlike the typical inert component N2, is directly involved in the process of radical reaction, for instance, CO + OH = CO2 + H, which inhibits the oxidative combustion reaction of CO but also competes with the branching radical reaction H + O2 = O + OH for H. In this way, active free radicals such as O, OH, and H are reduced, thereby reducing the flame propagation speed, which is consistent with the results of Han and Zhang (Zhang et al., 2011; Han et al., 2016).
4 Conclusion
In this study, the thermal properties of combustion of the reduced tail gas were simulated by CHEMKIN, and the basic parameters of flame combustion were studied. The main findings have been summarized as follows:
(1) The flame propagation speed and the flame combustion temperature increase continuously with the increase in preheating temperature, while they decrease continuously with the increase in CO2 concentration.
(2) Compared with the typical methane flame propagation velocity distribution, the results show that the gradient of the decreasing phase of flame propagation velocity of the tail gas is significantly lower than that of methane flame. However, the maximum value of flame propagation velocity of the tail gas is higher than that of a typical methane flame, indicating that the flame propagation velocity decreased due to the addition of CH4 for the tail gas component.
(3) The peak flame combustion temperature appears at an equivalent ratio of 1.1, while the peak flame propagation speed appears at an equivalent ratio of 2.0, which indicates that the flame combustion temperature is not the main factor affecting flame propagation speed for the tail gas.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
HS performed the data analysis and wrote the manuscript. HX performed the simulations using software. SL provided ideas and directed the analysis of the data. WZ and ZZ provided constructive comments on revisions to the manuscript. XG interpreted the results.
Funding
This work supported by 2020 science and technology project of Qingdao West Coast New Area (Science and technology benefiting the people) (2020-99) and the National Key Research and Development of China (2020YFD1100302).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bao, X., and Liu, F. (2011). Experimental Measurement and Simulation Calculation of Laminar Combustion Velocity of Hydrogen/air Mixture. Combustion Sci. Technology 17 (05), 407–413. CNKI:SUN:RSKX.0.2011-05-004.
Bouvet, N., Chauveau, C., Gökalp, I., and Halter, F. (2011). Experimental Studies of the Fundamental Flame Speeds of Syngas (H2/CO)/air Mixtures. Proc. Combustion Inst. 33 (1), 913–920. doi:10.1016/j.proci.2010.05.088
Burluka, A. A., Harker, M., Osman, H., Sheppard, C. G. W., and Konnov, A. A. (2010). Laminar Burning Velocities of Three C3H6O Isomers at Atmospheric Pressure. Fuel 89 (10), 2864–2872. doi:10.1016/j.fuel.2010.02.004
Dai, L., Wang, K., Xu, P., and Hu, X. (2020). Experimental Study of Laminar Flame Propagation Velocity of CH4/H2 Mixture in O2/CO2 Atmosphere. Metallurgical Energy 39 (03), 29–32+64. CNKI:SUN:YJLY.0.2020-03-007.
Dong, G., Liu, H., and Chen, Y. (2002). Semi-detailed Chemical Kinetic Mechanism of Generalized Methane Laminar Flow Premixed Flame. Combustion Sci. Technology 8 (01), 44–48. doi:10.3321/j.issn:1006-8740.2002.01.011
Du, W., Yu, Q., and Li, P. (2010). “Research Progress of Chemical Sensible Heat Recovery Technology of Blast Furnace Slag,” in 2010 National Academic Conference on Energy and Thermal Engineering, 5.
Frassoldati, A., Faravelli, T., and Ranzi, E. (2007). The Ignition, Combustion and Flame Structure of Carbon Monoxide/hydrogen Mixtures. Note 1: Detailed Kinetic Modeling of Syngas Combustion Also in Presence of Nitrogen Compounds. Int. J. Hydrogen Energ. 32 (15), 3471–3485. doi:10.1016/j.ijhydene.2007.01.011
Han, M., Ai, Y., Chen, Z., Wang, Y., and Kong, W. (2016). Laminar Flame Propagation Characteristics of H2/CO/O2/CO2 at Different Preheating Temperatures. J. Eng. Thermophys. 37 (01), 189–193. CNKI:SUN:GCRB.0.2016-01-041.
He, P., Yu, Y., Guo, S., Zhang, X., Jia, J., and Yin, C. (2002). Combustion Test in the Lifting Section of Solid Heat Carrier Coal Gasification Pilot Plant. Metallurgical Energy 21 (03), 52–55. doi:10.3969/j.issn.1001-1617.2002.03.015
Hu, X., and Yu, Q. (2018). Effect of the Elevated Initial Temperature on the Laminar Flame Speeds of Oxy-Methane Mixtures. Energy 147, 876–883. doi:10.1016/j.energy.2018.01.088
Krejci, M. C., Mathieu, O., Vissotski, A. J., Ravi, S., Sikes, T. G., Petersen, E. L., et al. (2013). Laminar Flame Speed and Ignition Delay Time Data for the Kinetic Modeling of Hydrogen and Syngas Fuel Blends. J. Eng. Gas Turbines Power 135 (2). doi:10.1115/1.4007737
Lee, C.-E., Oh, C.-B., Jung, I.-S., and Park, J. (2002). A Study on the Determination of Burning Velocities of LFG and LFG-Mixed Fuels. Fuel 81 (13). doi:10.1016/S0016-2361(02)00049-2
Li, J., Zhao, Z., Kazakov, A., and Dryer, F. L. (2004). An Updated Comprehensive Kinetic Model of Hydrogen Combustion. Int. J. Chem. Kinet. 36 (10), 566–575. doi:10.1002/kin.20026
Li, X., Dou, Z., Zhang, T., and Liu, Y. (2021). Progress of Comprehensive Utilization of Copper Smelting Slag. Nonferrous Met. (Smelting Part) (04), 108–118. doi:10.3969/j.issn.1007-7545.2021.04.018
Liu, J. (2018). Study on CO/H2/CH4 Laminar Flame Propagation Velocity under O2/H2O Condition. Harbin Municipality: Harbin Institute of Technology. master's degree.
Mueller, M. A., Gatto, J. L., Yetter, R. A., and Dryer, F. L. (2000). Hydrogen/nitrogen Dioxide Kinetics: Derived Rate Data for the Reaction H 2 + NO 2 = HONO + H at 833 K. Combustion and Flame 120 (4). doi:10.1016/S0010-2180(99)00118-2
Natarajan, J., Lieuwen, T., and Seitzman, J. (2008). Laminar Flame Speeds and Strain Sensitivities of Mixtures of H2∕O2∕N2 at Elevated Preheat Temperatures. J. Eng. Gas Turbines Power 130 (6). doi:10.1115/1.2943180
Natarajan, J., Lieuwen, T., and Seitzman, J. (2007). Laminar Flame Speeds of H2/CO Mixtures: Effect of CO2 Dilution, Preheat Temperature, and Pressure. Combustion and Flame 151 (1), 104–119. doi:10.1016/j.combustflame.2007.05.003
Ouimette, P., and Seers, P. (2009). Numerical Comparison of Premixed Laminar Flame Velocity of Methane and wood Syngas. Fuel 88 (3), 528–533. doi:10.1016/j.fuel.2008.10.008
Pareja, J., Burbano, H. J., and Ogami, Y. (2010). Measurements of the Laminar Burning Velocity of Hydrogen-Air Premixed Flames. Int. J. Hydrogen Energ. 35 (4), 1812–1818. doi:10.1016/j.ijhydene.2009.12.031
Ratna Kishore, V., Duhan, N., Ravi, M. R., and Ray, A. (2008). Measurement of Adiabatic Burning Velocity in Natural Gas-like Mixtures. Exp. Therm. Fluid Sci. 33 (1), 10–16. doi:10.1016/j.expthermflusci.2008.06.001
Shang, R., Yang, Y., Gao, J., and Li, G. (2019). Experimental Study of Flame Propagation Velocity of Hydrogen-Doped Natural Gas Laminar Flow. Chin. J. Saf. Sci. 29 (11), 103–108. doi:10.16265/j.cnki.issn1003-3033.2019.11.017
Wang, H., Fan, F., Li, P., and Pan, S. (2021). Analysis of Modern Coal Gasification Technology Progress and Industrial Status. Coal Chem. Industry 49 (04), 52–56. doi:10.19889/j.cnki.10059598.2021.04.012
Wang, H., and Yu, Q. (2018). Experimental Study of Self-Heating Hot Carrier Coal Gasification. Metallurgical Energy 37 (06), 19–24. doi:10.3969/j.issn.1001-1617.2018.06.005
Xiao, P., Lee, C.-f., Wu, H., and Liu, F. (2020). Effects of Hydrogen Addition on the Laminar Methanol-Air Flame under Different Initial Temperatures. Renew. Energ. 154, 209–222. doi:10.1016/j.renene.2020.03.037
Yalikunjiang·Tursun, A·A., and Yue, P. (2019). Characterization of Coal Gasification with Pyrolysis-Reforming-Combustion Decoupling. J. Chem. Eng. 70 (08), 3040–3049.
Zeng, W., Liu, J., Ma, H., Liu, A., Liu, K., Liang, S., et al. (2019). Effect of Nitrogen Dilution Gas on the Combustion Characteristics of Natural Gas. Therm. Sci. Technology 18 (03), 219–227. doi:10.13738/j.issn.1671-8097.018098
Zhang, H., Bai, X., Jeong, D., Cho, G., Choi, S., and Lee, J. (2010). Fuel Combustion Test in Constant Volume Combustion Chamber with Built-In Adaptor. Sci. China Technol. Sci. 53 (4), 1000–1007. doi:10.1007/s11431-009-0407-7
Zhang, W., Chen, Z., and Kong, W. (2012). Effects of Diluents on the Ignition of Premixed H2/air Mixtures. Combustion and Flame 159 (1), 151–160. doi:10.1016/j.combustflame.2011.05.017
Zhang, Y., Lu, H., Wang, Q., Yu, S., and Gao, W. (2016). Simulation and Experimental Testing of Natural Gas normal Flame Propagation Velocity. Gas Heat 36 (05), 17–22+33. doi:10.13608/j.cnki.1000-4416.2016.05.005
Keywords: tail gas, copper slag, CHEMKIN, flame propagation speed, flame combustion temperature
Citation: Sun H, Xie H, Luo S, Zhang W, Zuo Z and Xianjun G (2022) Numerical Simulation of Flame Combustion Characteristics of Tail Gas From the Copper Slag Depleted Reduction. Front. Energy Res. 10:840383. doi: 10.3389/fenrg.2022.840383
Received: 05 January 2022; Accepted: 08 March 2022;
Published: 06 April 2022.
Edited by:
Chungen Yin, Aalborg University, DenmarkReviewed by:
Yiheng Tong, China Space Foundation, ChinaCopyright © 2022 Sun, Xie, Luo, Zhang, Zuo and Xianjun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Siyi Luo, bHVvc2l5aTY2NkAxMjYuY29t
 Huiping Sun
Huiping Sun Haojie Xie
Haojie Xie Siyi Luo
Siyi Luo Weiwei Zhang
Weiwei Zhang Zongliang Zuo
Zongliang Zuo Guo Xianjun
Guo Xianjun