Capacity Configuration Method of Hybrid Energy Storage Participating in AGC Based on Improved Meta-Model Optimization Algorithm

To improve the performance and economy of the hybrid energy storage system (HESS) coordinating thermal generators to participate in automatic generation control (AGC), a HESS bi-layer capacity configuration model that considers the control strategy and net benefits of HESS is proposed. In addition, an improved mode-pursuing sampling (MPS) optimization algorithm based on meta-model is presented to improve the accuracy of model solving. In the lower layer, to improve the performance of HESS participating in AGC, a model predictive control (MPC) strategy is presented to distribute HESS power reasonably. Based on this, the upper layer develops a life-cycle net benefit model of HESS participating in AGC to improve its economy. The bi-layer model realizes iterative optimization of HESS capacity and operation through parameter transmission. Furthermore, to improve the solution accuracy of the bi-layer model, the convergence speed of the MPS algorithm is improved, so that the global search and local convergence speed can be taken into account. The case study results show that the bi-layer model can comprehensively consider the interaction between the economy and operating strategy of HESS. The proposed MPC strategy has better frequency regulation performance and the improved MPS algorithm has better solution performance.

Introduction

Presently, with the increase of renewables penetration, the adjustment of automatic generation control (AGC) commands is more intense (Akram et al., 2020; Ashouri-Zadeh et al., 2020; Bevrani et al., 2021; Liu et al., 2021). However, the power response performance of traditional thermal generators is poor and it is difficult to meet the frequency regulation requirements of power systems with high penetration of renewable energy (Bryant et al., 2021), (Zhang et al., 2021). Generally, a hybrid energy storage system (HESS) is composed of power-type energy storage with small energy and energy-type energy storage with slow power response. It has the advantages of power and energy response of various types of energy storage systems (ESS) and has better economy (Joshi et al., 2021), (Luo et al., 2021). Coordinating the power of thermal generators through the HESS is an effective way to improve the AGC performance of generators, which has a good engineering application prospect. It can not only improve the power response performance of thermal generators, but also increase the income of ancillary service (He et al., 2021). However, the capacity configuration cost and performance of HESS are contradictory. Meanwhile, the control strategy of HESS is the key to improving the AGC performance. Therefore, to improve the performance and economy of HESS, the capacity configuration and control strategy of HESS are key issues for HESS participating in AGC.

Researchers have been paying attention to the related fields of ESS involved in frequency regulation. Relevant references have studied the features of AGC commands and developed AGC models, which provide a basis for further control and scheduling of AGC participants (Qiu et al., 2021)–(Donadee and Wang, 2014). In (Qiu et al., 2021), stochastic differential equations were used to model the uncertainty of AGC commands, which can be used for AGC optimal scheduling or other issues. In (Zhang et al., 2019), an AGC dynamics-constrained economic dispatch model was proposed to provide a more reliable and economical regulation reserve schedule. It can be applied to short-term prediction or as a benchmark based on historical data.

The control strategy of HESS is one of the key issues in its participation in AGC. The key issue to the HESS control strategy is to improve the AGC performance of the “HESS-generator” system, avoid the energy limitation of HESS, and prolong its lifetime. Most existing studies are based on ESS as an independent AGC participant, directly scheduled by the AGC controller (Yang et al., 2022)–(Cheng et al., 2014). In (Yang et al., 2022), to complete the frequency regulation service of battery energy storage (BES) and effectively manage its state of charge (SOC), a BES multi-state control strategy was proposed, which considered the interdependency between frequency regulation performance, SOC, and lifetime of the BES. In (Xiong et al., 2020), to improve the consistency of each ESS participating in AGC, a discrete prescribed time consensus control strategy was proposed and an event triggered communication protocol was presented to reduce the information interaction between ESSs. In (Mégel et al., 2018), to improve the dynamic performance of distributed batteries when following AGC commands, a distributed battery energy management method considering storage efficiency was proposed. However, it is also an effective approach for ESS to participate in AGC by aiding generators to respond to AGC commands (Xie et al., 2018)–(He et al., 2022). Compared with ESS as an independent AGC participant, this approach has many advantages, such as, easier system update, will not affect existing controls, and the capacity configuration is smaller. For example, based on this approach, (Xie et al., 2018) proposed a method for BES to participate in frequency regulation to improve the AGC performance of thermal generators. In (Doenges et al., 2020), a BES control strategy was proposed to improve AGC performance by minimizing the rate of non-compliance with the corresponding dynamic performance criteria. At present, there are few studies on ESS coordinated generators and how they respond to AGC commands and most of them are based on a single BES and there are even fewer studies on capacity configuration and control strategies based on HESS.

Although HESS has advantages in power response, participation in AGC may have a great impact on its lifetime, resulting in high frequency regulation costs. To improve the economy of HESS participating in AGC, optimizing its capacity configuration is another key issue (Chen et al., 2016), (Wang et al., 2022). (Chen et al., 2016) studied the BES capacity configuration through a series of system-level performance tests with different BES penetration rates. Furthermore, the response effect of BES under different interference levels was analyzed. (Wang et al., 2022) considered the interaction between the battery degradation and the market clearing process and a bi-level optimization model was proposed to optimize the economics of ESS participating in frequency regulation services. Since the operating strategy and capacity configuration of HESS are related to each other, it is necessary to jointly optimize them to improve the performance of HESS. However, there is little research on it at present.

In this paper, considering the interaction between the economy and operation strategy of HESS, an HESS bi-layer capacity configuration method is proposed for HESS to coordinate thermal generators to participate in AGC. First of all, a bi-layer optimization model of HESS is formulated. In the lower layer, to improve the AGC performance of HESS participating in AGC, an MPC strategy is presented to distribute HESS power. Based on this, the upper layer develops a HESS net benefit model to optimize the economy of HESS. The bi-layer model implements the iterative optimization of HESS capacity and operation through parameter transmission. Furthermore, to improve the solution accuracy of the bi-layer optimization model, an improved MPS algorithm based on the meta-model is presented. Simulation results based on historical data show that the proposed HESS bi-layer capacity configuration method is effective in both the economy and operation control. The main contributions of this paper are summarized as follows:

1) A bi-layer capacity configuration model of HESS is presented to jointly optimize the economy and control strategy of HESS.

2) A model predictive control strategy of HESS is presented to improve the performance of HESS participating in AGC.

3) A MPS algorithm with improved convergence speed is presented, which take into account both the global search and the local convergence speed.

The rest of this paper is organized as follows: Section 2 introduces the overview of the bi-layer capacity configuration method, Section 3 introduces the presented MPC strategy in the lower layer, HESS net benefit model in the upper layer is presented in Section 4, the improved MPS algorithm is discussed in Section 5, Section 6 presents the case study results, and finally, conclusions are presented in Section 7.

Overview of Hybrid Energy Storage System Bi-layer Capacity Configuration Method

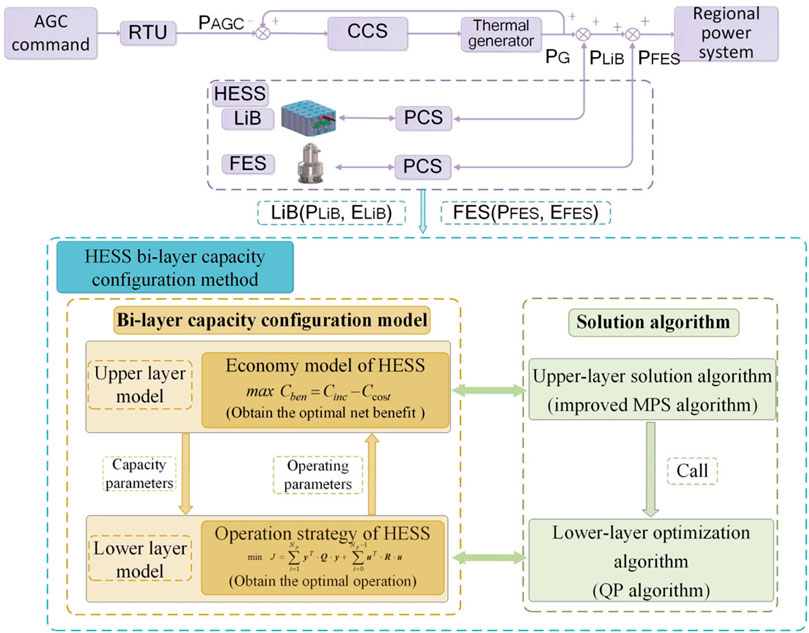
In this paper, HESS is composed of flywheel energy storage (FES) and lithium-ion batteries (LiB). Figure 1 presents the approach of HESS-aided AGC and the proposed bi-layer capacity configuration method. In this approach, HESS is not directly controlled by the AGC controller but coordinates the generator to improve its AGC performance.

FIGURE 1

FIGURE 1. Overview of the proposed bi-layer capacity configuration method.

At present, the AGC performance evaluation of the State Grid in North China implements the “Two Detailed Rules,” which is formulated by the North China Power Regulatory Bureau (North China Power Regulat, 2019). In the “Two Detailed Rules,” the AGC performance index K_p is the comprehensive performance of the three indexes of regulation rate K₁, regulation accuracy K₂, and response rate K₃, which respectively represent the performance of different stages in an AGC cycle. The performance index K_p of the ith adjustment $K_p^i$ is calculated as follows.

$K_p^i=K_1^i\cdot K_2^i\cdot K_3^i(1)$

According to the “Two Detailed Rules,” the performance index K_p can be better improved only by comprehensively improving the performance of the three indexes, rather than one or two indexes. However, in an AGC cycle, due to the energy limitation of FES, it is difficult to completely compensate the power difference between the generator and the AGC command. Therefore, a reasonable distribution of HESS power is the key to improving its performance. Based on the prediction model of the controlled object, MPC can minimize the impact of possible future operating conditions by solving an optimal cost function. The goal of HESS power distribution is consistent with the features of the MPC strategy. Therefore, it is feasible to implement the MPC strategy to realize the optimal control of HESS.

Another goal of HESS participating in AGC is to increase the income of frequency regulation services. The economic benefits of HESS include its cost and the increased frequency regulation income due to the implementation of HESS. Therefore, in this paper, the upper layer optimization model is formulated based on the annualized net benefits of HESS in the project operating time.

In addition, because the bi-layer model is computationally intensive and nonlinear, the solution requires a large amount of computational consumption. Although the solution efficiency of the MPS algorithm based on the meta-model is high (Xiao et al., 2018), (Liu et al., 2018), it has the problem of aggressive convergence evaluation, which is easy to fall into a local optimum before generating enough exploratory points (Wang et al., 2004). Therefore, in this paper, the convergence evaluation index is modified and the convergence speed is dynamically adjusted, so that the improved MPS algorithm can take into account the global search and local convergence speed. All of these efforts are to improve the accuracy and efficiency of solving the bi-layer model.

Model Predictive Control Strategy of Hybrid Energy Storage System in Lower Layer

In this paper, the HESS compensates the power difference between AGC commands and the power output of thermal generators. Its control objective is to reasonably distribute the HESS power to coordinate thermal generators, so as to improve AGC performance, prolong the lifetime of LiB, and improve economy.

System Model of Hybrid Energy Storage System-Aided Automatic Generation Control

Assuming that the power demand of HESS at time k is P_d(k), then

$P_d\left(k\right)=P_{bat}\left(k\right)+P_{fl}\left(k\right)+P_{dif}\left(k\right)(2)$

Where P_bat (k) and P_fl (k) are the power of LiB and FES at time k, respectively, and P_dif is the power difference between the AGC command and the “HESS-generator” system.

The SOC of LiB and FES at k + 1 can be determined as follows:

$SO{C}_{bat}(k+1)=SO{C}_{bat}\left(k\right)-P_{bat}\left(k\right)\cdot \text{Δ}t/E_{bat}(3)$

$SO{C}_{fl}(k+1)=SO{C}_{fl}\left(k\right)-P_{fl}\left(k\right)\cdot \text{Δ}t/E_{fl}(4)$

Where SOC_bat and SOC_fl are the SOC of LiB and FES respectively, and Δt is the control cycle of the system. P_bat and E_bat are the power capacity, and energy capacity of LiB, respectively, and P_fl and E_fl are the power capacity and energy capacity of FES, respectively.

According to (2–4), the SOC of HESS is used as a state vector and an output vector, such that x (k) = [SOC_bat (k) SOC_fl (k)]^T, y (k) = [SOC_bat (k) SOC_fl (k)]^T. The LiB power and the power difference after compensation are used as a control vector, such that u (k) = [P_bat (k) P_dif (k)]^T. The power demand of HESS is the disturbance, such that w (k) = P_d (k), which can be obtained according to the rated ramp rate of the generator. Therefore, the system state-space model can be formulated as follows:

$\{\begin{array}{c}x(k+1)=\mathit{A}\mathit{x}\left(k\right)+\mathit{B}\mathit{u}\left(k\right)+{\mathit{B}}_{\mathit{2}}\mathit{w}\left(k\right)\\ \mathit{y}\left(k\right)=\mathit{C}\mathit{x}\left(k\right)\end{array}(5)$

_Where $\mathit{A}=\mathit{C}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$_, $\mathit{B}=\left[\begin{array}{cc}-\mathrm{\Delta }t/E_{bat}& 0\\ \mathrm{\Delta }t/E_{fl}& \mathrm{\Delta }t/E_{fl}\end{array}\right]$_, ${\mathit{B}}_2=\left[\begin{array}{c}0\\ -\mathrm{\Delta }t/E_{fl}\end{array}\right]$_.

Model Predictive Control Strategy for Hybrid Energy Storage System

It is a multi-objective optimization problem for HESS-aided AGC. The goal is to improve the AGC performance of the generator, reduce the power fluctuation of LiB and the compensated power difference, and keep the SOC of HESS within a reasonable range. In summary, according to the principle of MPC strategy, the cost function is formulated as follows:

$\min J={\displaystyle \sum _{i=1}^{N_p}{(y(k+i)-y_{ref})}^T}\cdot \mathit{Q}\cdot (y(k+i)-y_{ref})+{\displaystyle \sum _{i=0}^{N_p-1}\mathit{u}{(k+i)}^T\cdot \mathit{R}\cdot \mathit{u}(k+i)}(6)$

Where N_p is the prediction horizon. y (k + i) and u (k + i) are the output vector and control vector of the ith prediction step at k, respectively, y_ref is the reference of the output vector. Q and R are the weight coefficient matrix of the cost function, respectively. Q, R, and y_ref are as follows:

$\{\begin{array}{c}\mathit{Q}=\left[\begin{array}{cc}{Q}_{bat}^{soc}& 0\\ 0& Q_{fl}^{soc}\end{array}\right]\\ \mathit{R}=\left[\begin{array}{cc}{R}_{bat}^p& 0\\ 0& R_{dif}^p\end{array}\right]\\ {\left[y_{ref}\left(k\right)\right]}_1=SO{C}_{bat}\left(k\right)\\ {\left[y_{ref}\left(k\right)\right]}_2=SO{C}_{fl}\left(k\right)\end{array}(7)$

Where $Q_{bat}^{soc}$, $Q_{fl}^{soc}$, $R_{bat}^p$, and $R_{dif}^p$ are all greater than zero.

The four weight coefficients in the cost function will influence different objectives and even contradict each other in different scenarios. The larger the $Q_{bat}^{soc}$, the smaller the SOC change of LiB, so the degradation of LiB can be reduced to prolong its lifetime. Similarly, $Q_{fl}^{soc}$ affects the SOC change of FES. The larger the weight coefficient $R_{bat}^p$, the smaller the SOC change of LiB. Similarly, the larger $R_{dif}^p$ is, the output of “HESS-generator” is as close to the power demand P_d as possible. Therefore, when implementing the presented MPC strategy, it is necessary to adjust them reasonably according to the performance.

To implement the presented MPC strategy, the state vector and control vector of the system must meet certain constraints.

s.t. 1) SOC constraints. In every prediction step, the state of the system must meet the SOC constraints of HESS, such that

$\{\begin{array}{c}SO{C}_{bat}^{min}<y_1\left(k\right)<SO{C}_{bat}^{max}\\ SO{C}_{fl}^{min}<y_2\left(k\right)<SO{C}_{fl}^{max}\end{array}(8)$

Where $SO{C}_{bat}^{min}$ and $SO{C}_{bat}^{max}$ are the minimum and maximum SOC constraints of LiB, respectively. $SO{C}_{fl}^{min}$ and $SO{C}_{fl}^{max}$ are the minimum and maximum SOC constraints of FES, respectively.

2) Power constraints. In every prediction step, the state of the system must meet the power constraints of HESS, such that

$\{\begin{array}{c}-P_{bat}^{max}<P_{bat}\left(k\right)<P_{bat}^{max}\\ -P_{fl}^{max}<P_{fl}\left(k\right)<P_{fl}^{max}\end{array}(9)$

Where $P_{bat}^{max}$ and $P_{fl}^{max}$ are the maximum power constraints of LiB and FES, respectively.

3) System model constraints. To avoid the power circulation inside the HESS and reduce the unnecessary charging/discharging, $P_d$, $P_{bat}$, $P_{fl}$, and $P_{dif}$, should be the same positive or negative values, such that

$\{\begin{array}{c}{P}_d\left(k\right)\cdot P_{dif}\left(k\right)\text{>0}\\ \begin{array}{l}{P}_d\left(k\right)\cdot P_{bat}\left(k\right)\text{>0}\\ P_d\left(k\right)\cdot P_{fl}\left(k\right)\text{>0}\end{array}\end{array}(10)$

The optimization problem of Equations 6–10 can be transformed into a standard quadratic programming (QP) problem to obtain the control vector u_i. The specific transformation process can be found in the Supplementary Material. Since the proposed MPC strategy of HESS is implemented through a computer, it can be easily applied to real-time control. Once the control vector u_i is obtained, the control vector u₀ is used as the power output of the HESS to compensate the generator.

In addition, based on the presented MPC strategy, 1-day historical power response data of a thermal generator is used to implement HESS-aided AGC. Once the compensation results are obtained, the operating parameters of the lower layer can be obtained, which are the lifetime of LiB T_lt and the 1-day AGC performance index $K_{p\_day}$, respectively. The T_lt can be obtained from the SOC change of LiB in 1 day by the rain flow counting method (Li et al., 2015), and the $K_{p\_day}$ can be obtained from the compensation results based on the “Two Detailed Rules.”

Economic optimization model of Hybrid Energy Storage System in upper layer

Increasing the income of frequency regulation services is one of the goals of HESS participating in AGC. The economy of HESS includes the cost of HESS and the increased frequency regulation income due to the implement of HESS. Therefore, the upper layer takes the maximum annualized net benefits of HESS as the optimization goal. The cost function is formulated as follows:

$\text{max}{C}_{ben}=C_{inc}-C_{cost}(11)$

Where $C_{ben}$ is the annualized net benefit of HESS participating in AGC, $C_{inc}$ is the annual frequency regulation income of HESS, and $C_{\cos t}$ is the annualized cost of HESS.

Annual Frequency Regulation Income of Hybrid Energy Storage System ${\mathit{C}}_{\mathit{inc}}$

According to the “Two Detailed Rules”, the annual income of the “HESS-generator” system G_AGC when configuring HESS is as follows:

$G_{AGC}={\displaystyle \sum _{i=1}^{365}(\ln K_{p\_day}^i+1)\cdot D_{day}^i\cdot Y_{AGC}\cdot {\eta }_i}+{\displaystyle \sum _{j=1}^{365}{Y}_{hour}\cdot \mathbf{24}}\cdot {\eta }_j(12)$

Where $K_{p\_day}^i$ is the K_p value on the ith day, Y_AGC is the payment standard for generators participating in AGC, and Y_hour is the payment standard for the available time of generators, both of which are formulated by the local regulatory agency. η is the proportion of the daily operation time of generators, and $D_{day}^i$ is the daily regulation depth of the generator on the ith day.

Similarly, the annual income of frequency regulation services without HESS can be calculated as follows:

$G_{AGC}^{\prime }={\displaystyle \sum _{i=1}^{365}(\ln K_{p\_day}^{\prime i}+1)\cdot D_{day}^{\prime i}\cdot Y_{AGC}\cdot {\eta }_i}+{\displaystyle \sum _{j=1}^{365}{Y}_{hour}\cdot 24}\cdot {\eta }_j(13)$

Where $K_{p\_day}^{\prime i}$ and $D_{day}^{\prime i}$ are the daily K_p value and daily regulation depth of the generator without HESS, respectively.

The daily regulation depth is the sum of the power adjustments of the “HESS-generator” system in response to AGC commands in 1 day, which can be obtained as follows

$D_{day}^i={\displaystyle \sum _{j=1}^b{D}_j}={\displaystyle \sum _{j=1}^b\left|P_j-P_{j-1}\right|}(14)$

When the power output of the system reaches the jth AGC command, P_j in (14) is equal to the jth AGC command. When not reached, P_j is the power output of the system when the (j + 1)-th AGC command is received.

In summary, the annual frequency regulation income of HESS is as follows:

$C_{inc}=G_{AGC}-G_{AGC}^{\prime }(15)$

Annualized Cost of Hybrid Energy Storage System ${\mathit{C}}_{\mathit{cost}}$

The annualized cost of HESS is the sum of annualized capital cost, annual replacement cost, and annual maintenance cost. The annualized capital cost of HESS is as follows:

$C_{cap}=(c_{pb}\cdot P_{bat}+c_{eb}\cdot E_{bat}+c_{pf}\cdot P_{fl}+c_{ef}\cdot E_{fl})\cdot {\gamma }_{CRF}(16)$

${\gamma }_{CRF}=\frac{\gamma \cdot {\left(1+\gamma \right)}^{T_{rt}}}{{\left(1+\gamma \right)}^{T_{rt}}-1}(17)$

Where c_pb and c_eb are the unit power cost and unit energy cost of LiB, respectively, c_pf and c_ef are the unit power cost and unit energy cost of FES, respectively. P_bat and E_bat are the power and energy of LiB, respectively. P_fl and E_fl are the power and energy of FES, respectively. γ is the interest rate. T_rt is the operation time of the “HESS-generator” project.

The replacement cost of HESS within the project operation time is as follows:

$C_{rep}=(c_{pb}\cdot P_{bat}+c_{eb}\cdot E_{bat})\cdot n_{bat}\cdot {\gamma }_{CRF}(18)$

Where n_bat is times of LiB replacement in T_rt, which can be obtained according to the lifetime of the LiB T_lt, the calculation is as follows:

$n_{bat}=ceil\left(T_{rt}/T_{lt}-1\right)(19)$

Where the ceil (x) function refers to the smallest integer greater than or equal to x,

since the lifetime of FES generally exceeds 20 years, the replacement cost of FES is not considered.

The maintenance cost of HESS is as follows:

$C_{pm}=c_{pm\_bat}\cdot E_{bat}+c_{pm\_fl}\cdot E_{fl}(20)$

Where c_{pm_bat} and c_{pm_fl} are the annual maintenance cost of LiB and FES per unit capacity, respectively.

To meet the optimal power distribution in the lower layer, the capacity configuration of HESS in the upper layer needs to meet certain minimum power capacity and energy capacity constraints.

s.t. 1) The power capacity and energy capacity limits of HESS should be reasonably set according to the actual operating conditions.

$\{\begin{array}{c}0<P_{bat}<P_{bat}^{max}\\ 0<E_{bat}<E_{bat}^{max}\\ 0<P_{fl}<P_{fl}^{max}\\ 0<E_{fl}<E_{fl}^{max}\end{array}(21)$

Where $P_{bat}^{max}$, $E_{bat}^{max}$, $P_{fl}^{max}$ and $E_{fl}^{max}$ are the maximum power capacity and energy capacity limits of LiB and FES according to the actual operating conditions, respectively.

2) To improve the economy of HESS, according to Equation 2, the sum of the power capacity of P_bat and P_fl should be less than the maximum HESS power demand, which can be obtained according to the historical data of AGC commands and generators, such that

$0<P_{bat}+P_{fl}\le P_d^{max}(22)$

Where $P_d^{max}$ is the maximum HESS power demand in the historical data.

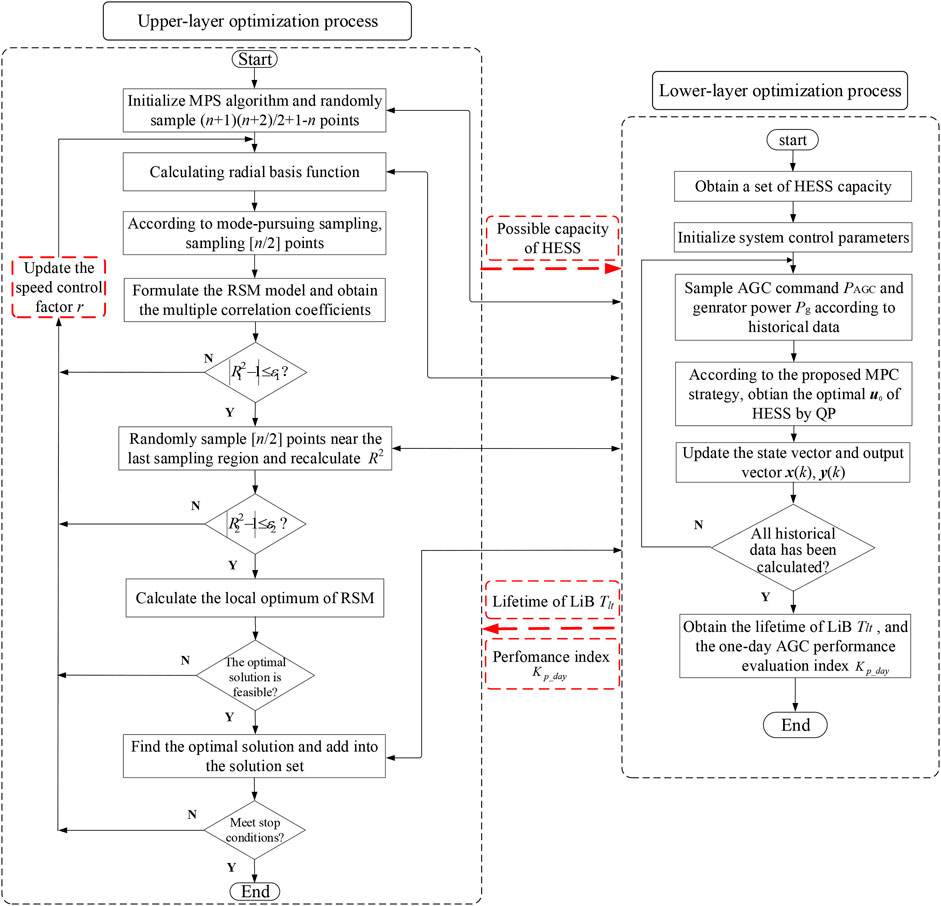
The optimization variables of the upper-layer cost function are the capacity parameters of HESS P_bat, E_bat, P_fl, and E_fl. When the upper layer is optimized to obtain a set of HESS capacity, the lower layer is called to realize the optimal control of HESS. Then, the optimal results of the lower layer are updated and returned to the upper layer to repeat the upper-layer optimization, so as to realize iterative optimization.

Improved Model Predictive Control Algorithm

In the bi-layer optimization model, the lower layer is a QP optimization problem. Although it is easy to solve, in this paper, to obtain the control results of HESS in 1 day, it will lead to a large amount of calculation consumption. As a result, when solving the outer layer, traditional heuristic optimization algorithms [such as particle swarm optimization (PSO)] need a large number of calls to the lower-layer model, resulting in reduced calculation accuracy or low efficiency. The key of meta model-based optimization algorithm is to formulate a meta model to replace the original complex model for calculation. It can effectively reduce expensive calculation times and improve solution efficiency.

In this paper, the MPS algorithm based on meta-model is adopted, which is effective in solving computation-intensive black box optimization problems. The MPS algorithm uses multi-correlation coefficient R² to evaluate the global convergence and control the convergence speed. However, the author also pointed out that it is risky (Wang et al., 2004) because the index R² may be aggressive for convergence speed control and the optimization process may converge to a local optimum before generating enough exploratory points. Therefore, an improvement of convergence speed control factor is implemented to address this issue in this paper.

The modification of the convergence speed control factor in MPS is divided into two parts, which are the modification of the multi-correlation coefficient R² and the modification of the convergence speed factor based on modified R².

Modification of Multi-Correlation Coefficient R²

In the process of formulating the response surface model (RSM) in the MPS algorithm, the accuracy evaluation index of RSM $R^2\in (0,1)$. The more R² tends to 1, the higher the fitting accuracy of the RSM model. However, an increase in the number of variables tends to increase R², but this does not mean that the RSM model has been well fitted. That is, R² approaching 1 does not necessarily mean a better fit, but it is also related to the number of variables. Therefore, the global convergence based on R² evaluation index may cause the optimization process to converge prematurely before generating enough exploratory points, thus falling into a local optimal solution.

Therefore, to be able to consider the influence of the number of variables, the evaluation index R² can be modified as follows:

$R_{adj}^2=1-\frac{{\displaystyle \sum _{i=1}^{n_s}{({\widehat{y}}_i-\overline{y})}^2/{(n_s-n{}_t-1)}^2}}{{\displaystyle \sum _{i=1}^{n_s}{(y_i-\overline{y})}^2/n_s^2}}(23)$

Where $R_{adj}^2$ is the modified accuracy evaluation index of RSM, n_s is the sample size, and n_t is the number of variables.

In (23), the quadratic form of n_t is introduced to correct the multi-correlation coefficient R². The corrected R² dynamically decreases with the increase of the number of the sample size, so as to increase more exploration points and avoid premature convergence to a local optimum.

Modification of the Convergence Speed Control Factor

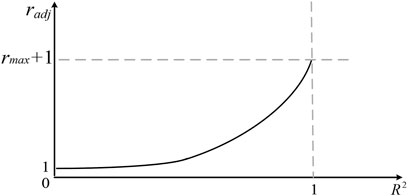
The function of the convergence speed control factor is to dynamically adjust the range of the search region according to the accuracy of the RSM model. The increase of R² means the increase of the fitting accuracy of the RSM model, so the speed control factor r will increase to generate more sample points in the current region, thereby accelerating the convergence process. On the contrary, if R² decreases, r will tend to 1, thereby expanding the sampling region to search for the global optimum. Based on the above analysis, the Sigmoid function has strong nonlinearity and its curve features are consistent with the dynamic change requirements of r. Therefore, based on the Sigmoid function, the r can be modified as follows:

$r_{adj}=\frac{2\cdot r_{max}}{1+e^{-\alpha \cdot (R_{adj}^2-1)}}+1(24)$

Where r_max is the maximum value of r_adj, which can be set as an empirical value through the MPS algorithm, α is an adjustment coefficient, which can be adjusted according to r_max.

The nonlinear characteristic of the curve in (24) is shown in Figure 2.

FIGURE 2

FIGURE 2. Characteristic diagram of speed control factor r_adj (α = 5).

According to the above two step modification, the “greediness” of the convergence speed control factor is dynamically adjusted, so as to avoid the problems of premature convergence to a local optimum and slow convergence when finally converging to the local optimum region.

The flow diagram of the proposed bi-layer capacity configuration method is shown in Figure 3. The bi-layer model realizes mutual iterative optimization through parameter transmission. When the lower-layer LiB lifetime T_lt and AGC performance index $K_{p\_day}$ are obtained, the upper layer optimizes the capacity configuration of HESS. When the HESS capacity configuration of the upper layer is obtained, the lower layer optimizes the power distribution of the HESS. The final optimization results meet both the optimal capacity configuration and optimal HESS control.

FIGURE 3

FIGURE 3. The flow diagram of the proposed bi-layer capacity configuration method.

Case Study

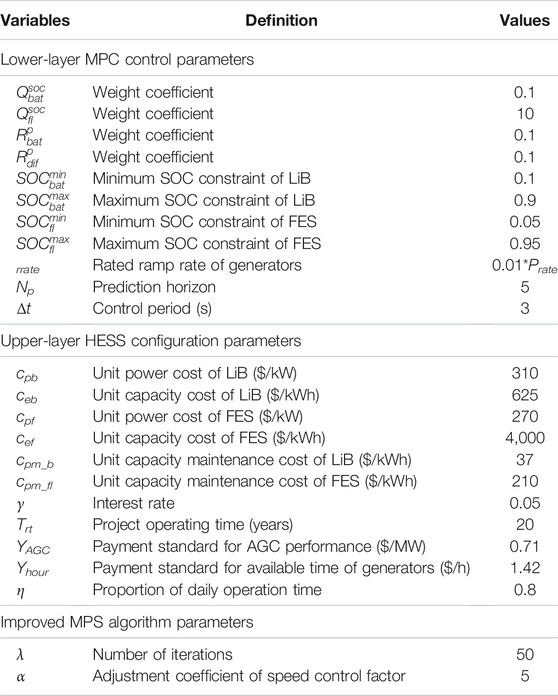
To verify the effectiveness of the proposed bi-layer capacity configuration method, in this section, the historical data of a thermal generator with poor AGC performance is used for simulation analysis. The rated power P_rate of the generator is 330 MW, located in North China. The control period Δt of the generator is 3 s, the data sampling period is 1 s, and the generator participates in AGC throughout the day. The historical power curves of thermal generators in response to AGC commands and the capacity configuration analysis of HESS are presented in Supplementary Material. The proposed models and algorithm were validated based on MATLAB, and the parameter settings (Zhang et al., 2020), (Han et al., 2014) are shown in Table 1.

TABLE 1

TABLE 1. Parameter settings in case study.

Optimization Results of the Bi-Layer Model

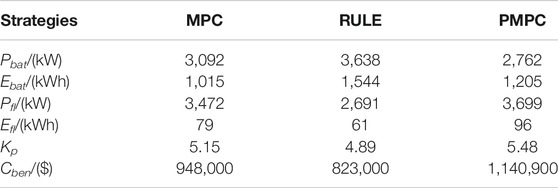
Table 2 shows the HESS capacity results obtained using the bi-layer capacity configuration method. Figure 4 shows the partial results of the lower-layer optimization control under the optimal capacity, where Figure 4A shows the HESS compensation results, Figure 4B shows the power distribution of HESS, and Figure 4C shows the SOC change of HESS in 1 day.

TABLE 2

TABLE 2. Capacity configuration results of HESS.

FIGURE 4

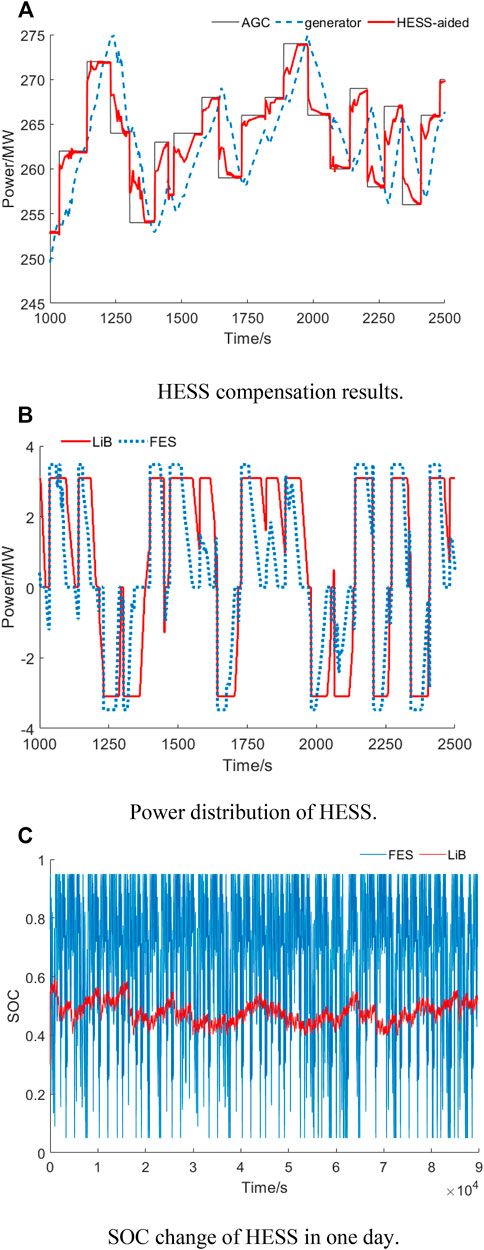
FIGURE 4. Results of the lower-layer optimization control (partial results). (A) HESS compensation results. (B) Power distribution of HESS. (C) SOC, change of HESS, in 1 day.

According to Figure 4B and Figure 4C, although the AGC command fluctuates constantly, its average change is close to zero. The HESS compensates for the power difference between AGC commands and the generator. Its power output is continuously charged and discharged with the change of AGC commands, so the energy requirement of HESS is not high. This feature also determines that a power-type ESS with a longer cycle life can be used for compensation, so as to improve its economy.

According to the results in Figure 4 and Table 2, compared with the AGC performance compensated by the generator alone, the K_p is increased by 114% when HESS is configured using the proposed method. Meanwhile, the annual frequency regulation income of “HESS-generator” system is increased by 78.8%. Both the AGC performance and frequency regulation income are significantly improved. In addition, the annual net benefit of HESS is US$ 948,000.

Performance Comparison of Different Control Strategies

To verify the effectiveness of the presented MPC strategy, under the optimal capacity configuration of HESS in Section 6.1, two other control strategies are used for power compensation.

1) RULE: common rule-based strategy (Xie et al., 2018), (Zhang et al., 2020) is used for comparison.

2) PMPC: MPC strategy based on prescient information is used for comparison. It is assumed that the power demand of HESS can be obtained in advance and participate in the control. It is an ideal case and is usually used as a benchmark for comparing the limits of the MPC strategy.

3) No HESS: the power response is completely dependent on generators without configuring HESS.

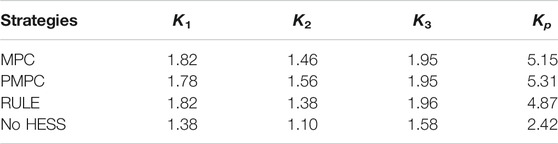
Table 3 shows the results of the AGC performance index K_p within 1 day under different strategies. Figure 5 shows the comparison of compensation results between the MPC strategy and other strategies.

TABLE 3

TABLE 3. AGC performance within 1 day under different strategies.

FIGURE 5

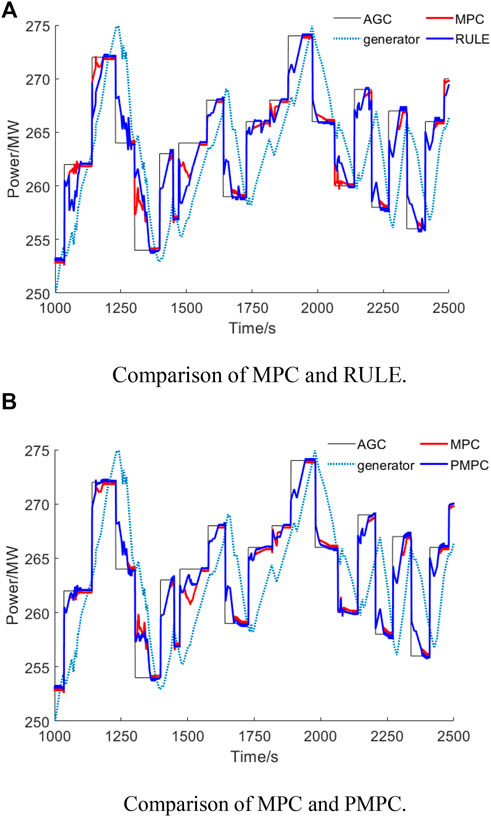
FIGURE 5. Compensation results under different strategies. (A) Comparison of MPC and RULE. (B) Comparison of MPC and PMPC.

The performance index K_p under different strategies is significantly higher than that without HESS configuration. Under the optimal capacity, the K_p of the presented MPC strategy is 5.7% higher than that of the rule-based strategy. This is because in the “Two Detailed Rules”, the AGC performance index K_p is a comprehensive evaluation of different stages of an AGC cycle. However, the RULE strategy requires that the difference between AGC commands and the generator power be fully compensated as much as possible. The compensation performance of the RULE strategy strongly depends on the energy capacity of HESS, especially the energy of FES. As a result, the RULE strategy uses most of the energy of FES to compensate for the initial stage of the AGC command but it does little to improve the performance of K₃. However, in the later stage of K₁ stage and K₂ stage, due to the energy limitation of FES, it is difficult to continue compensation, or even withdraw the compensation suddenly, resulting in secondary disturbance. It will affect the overall performance of K_p. In contrast, the MPC strategy solves this problem better. For example, in the multiple AGC cycles from 1,600 s to 1,800 s in Figure 5A, the power compensated by HESS under the RULE strategy fluctuates significantly in the K₂ stage, which leads to a decrease in K₂ and thus affects K_p. However, under the MPC strategy, the fluctuation of the compensated power in K₂ stage is smaller. Based on the future power demand of HESS, the decision of MPC strategy considers the system state of N_p cycles in the future. Therefore, MPC can optimize the power output of the HESS at the current time according to the control target to prolong the compensation time, so as to improve the performance of K₁ and K₂ stages.

Since the actual power response of the generator may not operate completely at the rated ramp rate, the MPC strategy was compared with the ideal PMPC strategy. The K_p performance under the MPC strategy is only 3.0% lower than that of the PMPC strategy. The PMPC strategy uses the actual historical power data of the generator to replace the rated ramp rate. Under the same parameters, its power output is the ideal result of the MPC strategy. Compared with PMPC strategy, MPC has lower K₂ and higher K₁. This means that MPC consumes more energy in the K₁ stage, which leads to a decrease in the performance of the K₂ stage. This is consistent with the analysis of the HESS compensation process in Section 2 and at the same time verifies the effectiveness of the presented MPC strategy.

Influence of Different Control Strategies on Capacity Configuration

To analyze the interaction between the bi-layer models and their influence on the performance of HESS participating in AGC, different strategies were used to configure the capacity of HESS. The results are shown in Table 4.

TABLE 4

TABLE 4. Capacity configuration results under different strategies.

As shown in Table 4, under different control strategies, the results of HESS capacity and economy are significantly different. The optimal result of the annual net benefit of HESS under the MPC strategy is 15.1% higher than that under the RULE strategy. According to the HESS capacity configuration results, compared with the MPC strategy, the LiB capacity under the RULE strategy is larger and FES capacity is smaller. This means that due to the high capital cost of FES, it is more economical to configure higher LiB capacity under the RULE strategy. In addition, because the RULE strategy needs to fully compensate the power difference, it has higher requirements for the capacity of HESS, which affects its economy.

The optimal result of the annual net benefit of HESS under the MPC strategy is 16.8% lower than that under the PMPC strategy. The main reason for the higher economy of HESS under the PMPC strategy is that the power distribution of HESS is more reasonable, which can obtain better performance benefits. Meanwhile, under the PMPC strategy, the optimal capacity of HESS increases the LiB energy capacity and the FES capacity. As a result, the lifetime of LiB T_lt under the PMPC strategy is 10.8 years, while that under the MPC strategy is 5.6 years. The increase in HESS capacity further increases K_p and reduces the replacement cost of HESS, thereby increasing the net benefit of HESS. The results verify that the proposed bi-layer model can comprehensively take into account the influence of HESS operation control and economic benefits.

Furthermore, the influence of the key operating parameters of the lower layer on the economy of HESS is analyzed in this paper. Figure 6 shows the variations in the annual net benefit of HESS under different parameters, which are the proportion of the daily operation time of HESS η and payment standard Y_AGC. It can be seen from Figure 6 that under different operating parameters, the annual net benefit of HESS presents nonlinear changes. With the increase of η and Y_AGC, the annual net benefit of HESS increases faster. Compared with η, the annual net benefit of HESS is more sensitive to the change of Y_AGC.

FIGURE 6

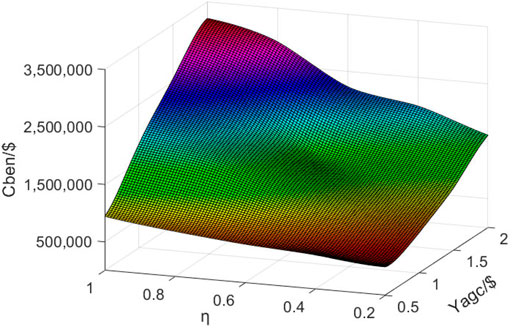
FIGURE 6. Annual net benefit changes of HESS under different operating parameters. Results of different optimization algorithms.

Results of Different Optimization Algorithms

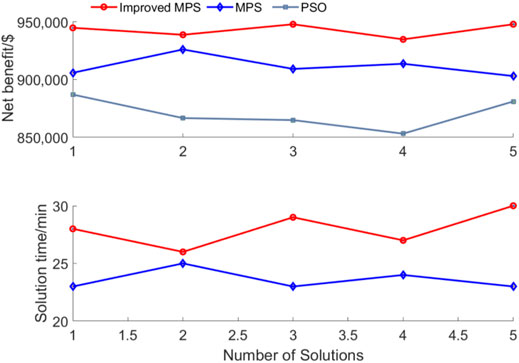
To verify the effectiveness of the improved MPS optimization algorithm, the PSO algorithm and standard MPS algorithm were used to solve the bi-layer model. The parameters of the PSO algorithm are set to the default value, such that the particle swarm size is 20, the minimum inertia weight is 0.4, the maximum inertia weight is 0.8, and the learning factor is 1.5. The number of iterations of all algorithms is set to 50, and all algorithms are calculated five times. Table 5 shows the optimization results of different optimization algorithms. Figure 7 shows the comparison of five calculation results of different algorithms. (Since the solution time of the PSO algorithm is almost fixed, it is not shown in the figure).

TABLE 5

TABLE 5. Results of different optimization algorithms.

FIGURE 7

FIGURE 7. Comparison of five calculation results of three algorithms.

According to Table 5, the improved MPS algorithm has a higher annual net benefit, which is $22,000 and $61,000 higher than that under the standard MPS and PSO, respectively. According to Figure 7, the improved MPS algorithm improves the accuracy and robustness of the model solution. At the same time, the average solution time of the improved MPS is only 1/6 of that of the PSO algorithm and is slightly slower than that of the standard MPS algorithm.

In this paper, the convergence speed of the MPS algorithm is improved. By modifying the global convergence evaluation index and using a nonlinear curve as the speed control factor, the improved MPS dynamically adjusts the convergence region to avoid premature convergence to a local optimal region. The improved MPS algorithm only calls the lower-layer model 168 times for evaluation but it can obtain higher solution accuracy. This is because the improved MPS algorithm is more efficient in global sampling. Firstly, when the sampling points increase, the multi-correlation coefficient $R_{adj}^2$ is modified, which reduces the impact of the increase of variables on the convergence evaluation index. Secondly, when speed control factor r_adj is small, the search region can be quickly expanded for more exploration points, and when r_adj is close to the threshold, the search region can be quickly reduced to promote algorithm convergence. Therefore, the improved MPS algorithm can effectively expand the search region and sample more exploration points to determine the global optimum and avoid premature convergence. At the same time, the solution time is basically the same as that of the standard MPS algorithm. If the other two algorithms improve the solution accuracy, it is necessary to increase the number of iterations to increase the sampling points but this also reduces the solution efficiency.

Conclusion

To improve the performance and economy of HESS participating in AGC, a bi-layer capacity optimization method considering the operating strategy and net benefits of HESS is proposed in this paper. In addition, an improved MPS algorithm is presented to improve the accuracy of model solving. In an AGC cycle, to reasonably distribute the HESS power to improve AGC performance in the lower layer, an MPC strategy of HESS is presented to coordinate the power of generators. In the upper layer, the net benefit optimization model of HESS is formulated to improve its economy. Through bi-layer mutual iterative optimization, the optimization results obtained meet both the optimal capacity and optimal control of HESS. Furthermore, to improve the solution accuracy of the bi-layer model, the convergence speed of the MPS algorithm is improved, so that the global search and local convergence speed can be taken into account. The case study results show that the bi-layer model can comprehensively consider the interaction between the economy and operating strategy of HESS. Compared with the commonly used RULE strategy, the presented MPC strategy not only has better AGC performance, but also has better economic benefits. The improved MPS algorithm has higher solution accuracy. Compared with the results of the standard MPS algorithm, the annual net benefits of HESS increased by $22,000.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JH: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing-original draft, Visualization. CS Conceptualization, Resources, Writing-review and editing. QW: Writing-review and editing; WZ: Writing-review and editing, Visualization; YG: Writing-review and editing, Visualization.

Funding

This work was supported by the Strategic Priority Research Program of Chinese Academy of Sciences, China(XDA21050302) and Protection system development of high-voltage feeder switch for mining mobile substations (Grant Number:2019109).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.828913/full#supplementary-material

References

Akram, U., Nadarajah, M., and Shah, R. (2020). A Review on Rapid Responsive Energy Storage Technologies for Frequency Regulation in Modern Power Systems. Renew. Sust. Energ. Rev. 120, 109626. doi:10.1016/j.rser.2019.109626

CrossRef Full Text | Google Scholar

Ashouri-Zadeh, A., Toulabi, M., and Dobakhshari, A. (2020). Frequency Stability Improvement in Wind-thermal Dominated Power Grids. IET Generation Transm. Distribution 14 (4), 619–627. doi:10.1049/iet-gtd.2019.0875

CrossRef Full Text | Google Scholar

Bevrani, H., Golpîra, H., Messina, A., Hatziargyriou, N., Milano, F., and Ise, T. (2021). Power System Frequency Control: An Updated Review of Current Solutions and New Challenges. Electric Power Syst. Res. 194, 107114. doi:10.1016/j.epsr.2021.107114

CrossRef Full Text | Google Scholar

Bryant, J. S., Sokolowski, P., Jennings, R., and Meegahapola, L. (2021). Synchronous Generator Governor Response: Performance Implications under High Share of Inverter-Based Renewable Energy Sources. IEEE Trans. Power Syst. 36 (3), 2721–2724. doi:10.1109/tpwrs.2021.3054251

CrossRef Full Text | Google Scholar

Chen, S., Zhang, T., Gooi, H. B., Masiello, R. D., and Katzenstein, W. (2016). Penetration Rate and Effectiveness Studies of Aggregated BESS for Frequency Regulation. IEEE Trans. Smart Grid 7 (1), 167–177. doi:10.1109/tsg.2015.2426017

CrossRef Full Text | Google Scholar

Cheng, Y., Tabrizi, M., Sahni, M., Povedano, A., and Nichols, D. (2014). Dynamic Available AGC Based Approach for Enhancing Utility Scale Energy Storage Performance. IEEE Trans. Smart Grid 5 (2), 1070–1078. doi:10.1109/tsg.2013.2289380

CrossRef Full Text | Google Scholar

Doenges, K., Egido, I., Sigrist, L., Lobato Miguelez, E., and Rouco, L. (2020). Improving AGC Performance in Power Systems with Regulation Response Accuracy Margins Using Battery Energy Storage System (BESS). IEEE Trans. Power Syst. 35 (4), 2816–2825. doi:10.1109/tpwrs.2019.2960450

CrossRef Full Text | Google Scholar

Donadee, J., and Wang, J. (2014). AGC Signal Modeling for Energy Storage Operations. IEEE Trans. Power Syst. 29 (5), 2567–2568. doi:10.1109/tpwrs.2014.2301592

CrossRef Full Text | Google Scholar

Han, S., Han, S., and Aki, H. (2014). A Practical Battery Wear Model for Electric Vehicle Charging Applications. Appl. Energ. 113, 1100–1108. doi:10.1016/j.apenergy.2013.08.062

CrossRef Full Text | Google Scholar

He, J., Shi, C., Wei, T., and Jia, D. (2022). Stochastic Model Predictive Control of Hybrid Energy Storage for Improving AGC Performance of thermal Generators. IEEE Trans. Smart Grid 13 (1), 393–405. doi:10.1109/tsg.2021.3111610

CrossRef Full Text | Google Scholar

He, J., Shi, C., Wei, T., Peng, X., and Guan, Y. (2021). Hierarchical Optimal Energy Management Strategy of Hybrid Energy Storage Considering Uncertainty for a 100% Clean Energy Town. J. Energ. Storage 41, 102917. doi:10.1016/j.est.2021.102917

CrossRef Full Text | Google Scholar

Joshi, A., Suresh, A., and Kamalasadan, S. (2021). Grid Frequency Regulation Based on point of Common Coupling Angle Deviation Control of Distributed Energy Resources with Fully Active Hybrid Energy Storage System. IEEE Trans. Industry Appl. 57 (5), 4473–4485. doi:10.1109/tia.2021.3089559

CrossRef Full Text | Google Scholar

Li, J., Gee, A. M., Zhang, M., and Yuan, W. (2015). Analysis of Battery Lifetime Extension in a SMES-Battery Hybrid Energy Storage System Using a Novel Battery Lifetime Model. Energy 86, 175–185. doi:10.1016/j.energy.2015.03.132

CrossRef Full Text | Google Scholar

Liu, J., Dong, H., and Jin, T. (2018). Optimization of Hybrid Energy Storage Systems for Vehicles with Dynamic On-Off Power Loads Using a Nested Formulation. Energies 11 (2), 2699–2724. doi:10.3390/en11102699

CrossRef Full Text | Google Scholar

Liu, L., Hu, Z., Duan, X., and Pathak, N. (2021). Data-driven Distributionally Robust Optimization for Real-Time Economic Dispatch Considering Secondary Frequency Regulation Cost. IEEE Trans. Power Syst. 36 (5), 4172–4184. doi:10.1109/tpwrs.2021.3056390

CrossRef Full Text | Google Scholar

Luo, Y., Chen, C., Kadavil, R., Liaw, B., Muljadi, E., Wu, X., et al. (2021). A Novel Framework for Optimizing Ramping Capability of Hybrid Energy Storage Systems. IEEE Trans. Smart Grid 12 (2), 1651–1662. doi:10.1109/tsg.2020.3023712

CrossRef Full Text | Google Scholar

Mégel, O., Liu, T., Hill, D., and Andersson, G. (2018). Distributed Secondary Frequency Control Algorithm Considering Storage Efficiency. IEEE Trans. Smart Grid 9 (6), 6214–6228. doi:10.1109/tsg.2017.2706979

CrossRef Full Text | Google Scholar

North China Power Regulatory Bureau (2019). Implementation Rules for Auxiliary Service Management of Grid Connected Power Plants in North China. Available at: http://hbj.nea.gov.cn/frontIndex/index.do.

Google Scholar

Qiu, Y., Lin, J., Liu, F., Dai, N., and Song, Y. (2021). Continuous Random Process Modeling of AGC Signals Based on Stochastic Differential Equations. IEEE Trans. Power Syst. 36 (5), 4575–4587. doi:10.1109/tpwrs.2021.3058681

CrossRef Full Text | Google Scholar

Wang, L., Shan, S., and Wang, G. G. (2004). Mode-pursuing Sampling Method for Global Optimization on Expensive Black-Box Functions. Eng. Optimization 36 (4), 419–438. doi:10.1080/03052150410001686486

CrossRef Full Text | Google Scholar

Wang, X., Ying, L., Wen, K., and Lu, S. (2022). Bi-level Non-convex Joint Optimization Model of Energy Storage in Energy and Primary Frequency Regulation Markets. Int. J. Electr. Power Energ. Syst. 134, 107408. doi:10.1016/j.ijepes.2021.107408

CrossRef Full Text | Google Scholar

Xiao, H., Pei, W., Pei, W., Dong, Z., and Kong, L. (2018). Bi-level Planning for Integrated Energy Systems Incorporating Demand Response and Energy Storage under Uncertain Environments Using Novel Metamodel. Csee Jpes 4 (2), 155–167. doi:10.17775/cseejpes.2017.01260

CrossRef Full Text | Google Scholar

Xie, X., Guo, Y., Wang, B., Dong, Y., Mou, L., and Xue, F. (2018). Improving AGC Performance of Coal-Fueled thermal Generators Using Multi-MW Scale BESS: a Practical Application. IEEE Trans. Smart Grid 9 (3), 1769–1777. doi:10.1109/tsg.2016.2599579

CrossRef Full Text | Google Scholar

Xiong, L., Yang, S., Li, P., Huang, S., Wang, C., and Wang, J. (2020). Discrete Specified Time Consensus Control of Aggregated Energy Storage for Load Frequency Regulation. Int. J. Electr. Power Energ. Syst. 123, 106224. doi:10.1016/j.ijepes.2020.106224

CrossRef Full Text | Google Scholar

Yang, W., Wen, Y., Pandžić, H., and Zhang, W. (2022). A Multi-State Control Strategy for Battery Energy Storage Based on the State-Of-Charge and Frequency Disturbance Conditions. Int. J. Electr. Power Energ. Syst. 135, 107600. doi:10.1016/j.ijepes.2021.107600

CrossRef Full Text | Google Scholar

Zhang, C., Liu, L., Cheng, H., Liu, D., Zhang, J., and Li, G. (2021). Frequency-constrained Co-planning of Generation and Energy Storage with High-Penetration Renewable Energy. J. Mod. Power Syst. Clean Energ. 9 (4), 760–775. doi:10.35833/mpce.2020.000743

CrossRef Full Text | Google Scholar

Zhang, F., Hu, Z., Meng, K., Ding, L., and Dong, Z. (2020). HESS Sizing Methodology for an Existing thermal Generator for the Promotion of AGC Response Ability. IEEE Trans. Sustain. Energ. 11 (2), 608–617. doi:10.1109/tste.2019.2898998

CrossRef Full Text | Google Scholar

Zhang, G., McCalley, J., and Wang, Q. (2019). An AGC Dynamics-Constrained Economic Dispatch Model. IEEE Trans. Power Syst. 34 (5), 3931–3940. doi:10.1109/tpwrs.2019.2908988

CrossRef Full Text | Google Scholar