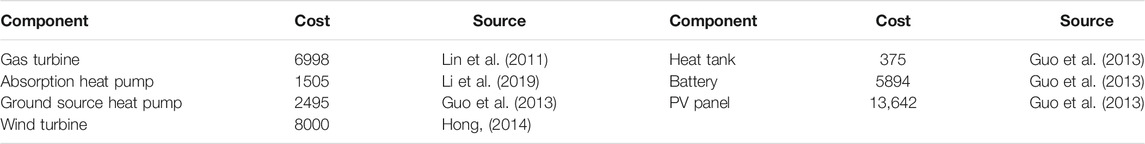Robust Optimization of Micro-Grid of Natural Gas and Renewable Energies Considering Operational Performances and Flexibility

The micro-grid based on renewable and fossil energies relieves environmental pollution due to fuel pollutant emission and offsets renewable energies’ instabilities. A micro-grid integrated with wind, solar, and natural gas is proposed. Primary energy saving rate, annual total cost saving rate, and carbon dioxide emission reduction rate are employed to evaluate the energetic, economic, and environmental performances of micro-grid, and grid integration level and net interaction level between micro-grid and national grid are used to show its system operational flexibility. The multi-objective robust optimization model considering these indicators in non-dominated sorting genetic algorithm II is constructed, in which the linear regression models fitted using points in the neighborhood of each candidate solution are used to present sensitivity analysis for the selection process of optimal solutions. The simulations in a case study demonstrate the validation of the proposed optimization model. The results show that the primary energy saving rate, annual total cost-saving rate, and CO₂ reduction rate are decreased by 1.7, 19.8, and 1.2%, respectively, when integrating system flexibility into optimization objectives.

1 Introduction

Distributed energy or micro-grid is an advanced energy system, which is close to users. Natural gas combined cooling, heating, and power system is its primary form, which has the characteristics of energy-saving, environmental protection, and economy (Jin et al., 2016). Developing and strengthening the comprehensive utilization of renewable energy has become a common consensus globally with the depletion of fossil energy and environmental pollution, and other issues, improving energy efficiency. The combination of microgrid and wind, solar, natural gas, and other energy sources can meet the needs of industrial parks, public, commercial, and civil buildings for heating, cooling, electricity, steam, and hot water. The above methods can also be applied to different energy production, conversion, transmission, storage, and other links. The micro-grid can meet the multiple energy needs of users by combining the renewable energy available at the user terminal. Also, it can realize the cascade utilization of energy to a certain extent, which has a positive significance to reduce the consumption of fossil energy and pollutant emissions, meets the requirements of sustainable development, and has broad development prospects (Liang, 2018).

Distributed micro-grid is a multi-module, multi-process, and multi-level complex coupling system with complex structure and various operation modes. The uncertainty of the renewable energy side and user demand side has a significant impact. Therefore, how to realize the optimal planning and operation of the micro-grid according to the user’s energy demand is the leading technical problem faced by the distributed energy supply system. Many scholars have carried out a series of related research at present. For example, in the aspect of system configuration planning, Ren et al. (2019) constructed the optimization model of solar energy, natural gas, a geothermal micro-grid system based on a genetic algorithm, and Cao et al. (2020) proposed a multi-stage planning method of the multi-energy complementary system considering construction sequence. In terms of operational optimization. Ma et al. (2017) based on the general model of an energy hub, collaborative optimization of a micro-grid’s day-ahead scheduling strategy. Ding et al. (2018) formulated the optimal economical operation strategy for a park’s energy Internet. The research results have a certain guiding significance for the safe and economic operation of the multi-energy complementary systems. In addition, the results of system configuration and operation optimization are closely related to the optimization objectives. Financial costs (Ding et al., 2018) or benefits (Chen et al., 2019), energy consumption (Faeze et al., 2015) or utilization rate (Chen et al., 2019), and carbon dioxide (Liang, 2018) are often used in the form of a single objective or multi-objective. Multi-objective optimization usually needs to make optimal decisions by balancing multiple conflicting objectives, making it more challenging to solve.

With the high proportion of renewable energy penetration and the gradual advancement of power market reform, the uncertainty factors of distributed multi-energy complementary systems are increasing. There are many uncertain parameters in the optimization model, which significantly aggravates the uncertainty of the optimization results. Scholars have proposed various methods to deal with uncertain factors, among which stochastic optimization and robust optimization have been widely concerned. Generally, stochastic optimization is based on the probability that random variables obey specific uncertainty distribution. With the help of Monte Carlo simulation (Davood and Hassan, 2019) and other methods, a large number of discrete scenarios are generated, and the increase of calculation scales results from a more extended optimization solution time. However, the designs can be reduced by the clustering method (Dong et al., 2019). It also faces the challenge of representativeness. Robust optimization does not need accurate probability distribution but only needs to construct the boundary information of the uncertainty set to find a solution with good performance for the uncertainty factors, which makes the model have certain robustness and dramatically improves the solution speeds (He et al., 2020).

At present, the robust optimization of distributed multi-energy complementary systems or micro-grids is generally divided into three categories according to the uncertainty factors considered (Zhu et al., 2017): (1) considering the “source-load” uncertainty, (2) considering the fault uncertainty, and (3) considering the uncertainty of market factors. Static robust optimization based on single-stage is widely used because of its simple model and solution process. The robust optimization considering wind and light uncertainties proposed in references (Qin et al., 2016) and (Peng et al., 2014) all adopt a particular method to deal with the equality balance constraint problem, simplifying the solution process. Still the corresponding optimal solution is only the approximate optimal solution. The two-stage robust optimization can contain equality constraints, and the stag decision-making can reduce the conservatism of the model solution. It is a typical multi-stage robust optimization model, which has been widely used in multi-energy complementarity (Jiang et al., 2012), unit commitment (Lin et al., 2018), operation scheduling (Ding et al., 2017), and other aspects. The multi-stage robust optimization solution process is more complex and computational efficiency is low. Complete optimization does not contain the available probability information about uncertain factors, so it has some limitations. In recent years, distributed robust optimization considering the worst probability distribution of uncertain factors has been paid more and more attention, that is, multiple discrete scenarios (He et al., 2020), Wasserstein distance (Wang Y et al., 2020), moment information (Zhao et al., 2020), and other measures are used to consider the uncertainty of probability distribution of uncertain variables, which makes robust optimization have the advantages of stochastic optimization, but also brings complex problems of model solving.

In addition, the uncertain data has great influences on optimization solutions. In multi-objective optimization, the Pareto-optimal solutions are nondominated to each other. If a global optimal solution is sensitive to variable perturbation, the implemental solution may result in a different set of objective values (Deb and Gupta, 2006). Therefore, finding a global robust solution is the key factor in multi-objective optimization. The solving algorithm will be of importance to obtain the robust solutions, which are classified to the derivative-based approaches and derivative-free approaches. The steepest descent method and quasi-Newton method are the derivative-based optimization. But the derivative information is not easily obtained. On the contrary, the derivative free optimization is repeated evaluation of objective function without derivatives.

To sum up, most of the current research on robust optimization of micro-grids focuses on the source load, equipment failure, market parameters, and other uncertain factors to carry out operation scheduling optimization. Referring to the idea of robust optimization, this paper proposes a robust optimization model based on nondominated sorting genetic algorithm II (NSGA II) for the uncertain parameters in the optimization model to improve the robustness of the optimal solution. The integrated optimization of system configuration and operation strategy is carried out for a micro-grid based on natural gas and renewable energies by a case study. The system configuration and operation strategy considers system economy, energy efficiency, emissions, and other optimization goals and flexibility are discussed.

2 Micro-grid Based on Natural Gas and Renewable Energies

2.1 Energy Flows of Micro-grid

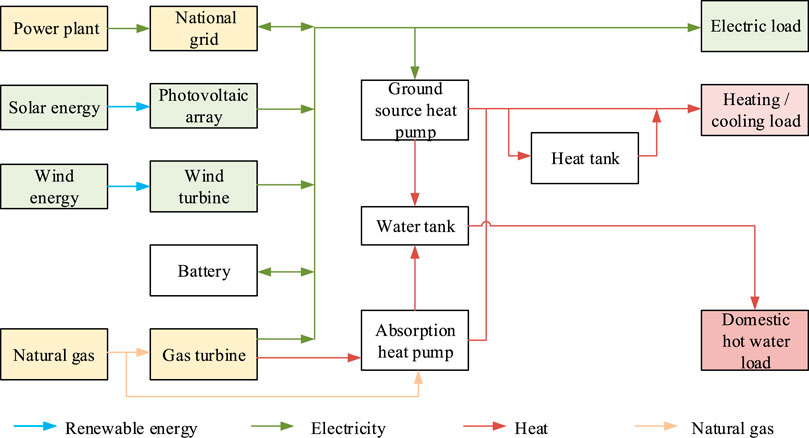
Figure 1 shows the energy flows of the micro-grid. The power technologies include a gas turbine, wind turbine, and solar photovoltaic (PV) panels. The national grid is also a supplementary method to supply electricity when the micro-grid does not satisfy the electric demand of users. The waste heat from the gas turbine and the absorption heat pump with the combustion of natural gas both supply the heat and cooling needs. In addition, the storage components such as battery and heat water tank and the ground source heat pump being a transfer component between electricity and heat are integrated into the micro-grid, which improves the operational flexibility of the micro-grid to adopt the dynamic loads.

FIGURE 1

FIGURE 1. Energy flows of a micro-grid integrated with natural gas and renewable energies.

The electric demands of users are mainly satisfied by the gas turbine, wind turbine, and PV panels. When the generated electricity is less than the user’s demand, the national grid supplies the shortage. On the contrary, the surplus electricity of the micro-grid is sold back to the national grid. The battery is employed to store the extra electricity or supplement the electricity deficiency.

The cooling and heat loads are supplied by the absorption heat pump driven by high-temperature exhaust gas. The ground source heat pump consumes power to produce chilled water or heat water for cooling and heating, respectively, which is an efficient method to balance the power to heat ratio. If the exhaust heat is not enough to satisfy the heat demand, the absorption heat pump consumes natural gas to produce. On the contrary, surplus heat is stored in the heat tank when the waste heat is more than the demand. The heat tank can supplement the heat deficiency.

From the energy flows of the micro-grid, the national grid, heat tank, and battery are effective assistances for improving the operation reliability of the micro-grid. Their integrations play essential roles in increasing the operational flexibility of the micro-grid.

2.2 Thermodynamic Models of Components

The thermodynamic models of components are constructed, and the main equations are listed in Table 1. The symbols are explained as follows: P represents the power of ingredients (kW), E and Q represent electricity and heat (kW), respectively, F represents fuel consumption (kW), t represents time (hour), A represents the area (m²), COP is the coefficient of performance, T represents temperature (°C), G represents solar radiation, $\alpha$ is the temperature coefficient (%/°C), S represents storage, $N$ is the number, $f$ is the power derating factor of PV, v represents the ratio of gas turbine’s consumption in total fuel consumption, $\eta$ represents efficiency (%), $\epsilon$ is the control factor (1 or 0), the subscripts GT, WT, PV, grid, GSHP, AHP, B, and TS represent gas turbine, wind turbine, solar PV panels, national grid, ground source heat pump, absorption heat pump, battery, and thermal storage of heat tank, respectively, and the superscript nom represents the nominal value.

TABLE 1

TABLE 1. Energy principles of components

In these components, the gas turbine is the key component, whose part load efficiency with the dynamic loads has influences on the fuel consumptions and the ratio of power and heat. Herein, its part load efficiency is ignored due to less capacity, and moreover, the gas turbine is limited to operate in the larger load factor by operation control (the constraints can be seen in Section 3.2). Thus, its part load efficiency is not considered. The power efficiency of PV panel is influenced by ambient temperature, which is expressed in the temperature coefficient in Equation (3). When the waste heat from the gas turbine is not enough for the absorption heat pump, the additional natural gas $(1-\nu )F_{ng,t}$ is consumed to supplement heat.

2.3 Problem Definition

The performance of the micro-grid is influenced by the types and capacities of the selected components, including energy converter and energy storage units. The challenge of designing the micro-grid is to select the appropriate unit from different candidate components, determine components’ capacities, and attain a synergic operation of all selected components.

According to the energy flows of the micro-grid in Figure 1, the problem can be expressed to:

1) determine the optimal device types from the candidate devices, and (2) determine the optimal capacity size of serial devices,

in the given conditions such as the users’ loads of electricity, heating, and cooling, the energy purchase price including electrical power and natural gas, and the technical and economic parameters for potential candidate energy converter and storage components. Thus, the capacities of components in Figure 1 are selected to be decision variables. In addition, considering the flexible operation of ground source heat pump and absorption heat pump, the ratio of ground source heat pump, $\gamma$ is defined to:

$\gamma =Q_{GSHP,t}/Q_t(9)$

where $Q_{GSHP,t}$ and $Q_t$ represent the generated heat from the ground source heat pump and total heat demand at the time t (kW), respectively. Considering the simplification of computation, $\gamma$ is set to a constant number. When it is larger, the electric demand is more significant, and the heat demand of the absorption heat pump is lower.

Thus, the decision variables in the optimization problem can be expressed as:

$X={[P_{GT}^{nom},P_{WT}^{nom},P_{PV}^{nom},P_{grid}^{nom},P_{GSHP}^{nom},P_{AHP}^{nom},S_B^{nom},S_{TS}^{nom},\gamma ]}^T(10)$

The operational performance of the micro-grid is closely related to its operating strategy. Herein, the following rules are set to determine the run of the micro-grid:

1) The generated electricity from renewable technologies is first consumed, and the stored power in the battery is also finished.

2) The gas turbine does not output excess electricity to reduce the battery’s capacity or the interaction between the micro-grid and the national grid.

3) The gas turbine does not run when its load factor is less than its start-up coefficient, which avoids too low generation efficiency.

4) When the waste heat from the gas turbine is more considerable than the heat demand, the surplus heat is stored in the heat tank. If there is still excess heat after storage, the remained waste heat is exhausted to the atmosphere.

5) When the waste heat from the gas turbine is less than the heat demand, the heat shortage is supplemented by an absorption heat pump or heat tank.

6) The cooling and heating loads are provided by the absorption heat pump and ground source heat pump.

3 Model Formulation and Solving Methodology

3.1 Multi-Objective Functions

1) Energetic performance.

In comparison to the conventional separation production system, the energetic performance of the micro-grid is evaluated in the primary energy saving rate (PESR), and it is calculated as:

$PESR=\left(1-\frac{{\displaystyle \sum _{t=1}^n{F}_t^{MG}}}{{\displaystyle \sum _{t=1}^n{F}_t^R}}\right)\times 100\%(11)$

In which n represents the annual operation hours, the superscript MG and R represent the micro-grid and reference system, respectively. The fuel consumption is calculated as:

$F_t=F_{c,t}+F_{ng,t}=E_{grid.t}/{\eta }_e^R+F_{ng,t}(12)$

$F_c$ and $F_{ng}$ are the fuel consumption of the national gird and the natural gas consumption in the micro-grid. $E_{grid.t}$ is the purchased electricity from the national grid, and ${\eta }_e^R$ is the power generation efficiency of the central power plant.

2) Economic performance.

Similarly, the economic benefit of the micro-grid is assessed in the annual cost saving rate (ACSR) of the micro-grid in comparison to the reference system, and it is expressed as:

$ATCSR=\left(1-\frac{AT{C}^{MG}}{AT{C}^R}\right)\times 100\%(13)$

where ATC is the annual total cost, and it is calculated as:

$\begin{array}{l}ATC=C_{cap}+C_{om}+C_{ng}+C_{grid}-C_{sgrid}\\ ={\displaystyle \sum _{m=1}^l{P}_m^{nom}{C}_m}\frac{i{\left(1+i\right)}^{\beta }}{{\left(1+i\right)}^{\beta }-1}+\lambda {\displaystyle \sum _{m=1}^l{P}_m^{nom}{C}_m}+C_{png}{\displaystyle \sum _{t=1}^n{F}_{ng,t}}+{\displaystyle \sum _{t=1}^n{C}_{pe,t}{E}_{grid,t}}-{\displaystyle \sum _{t=1}^n{C}_{se,t}{E}_{exc,t}}\end{array}(14)$

where $C_{cap},C_{om},C_{ng},C_{grid}$, and $C_{sgrid}$ are the cost of investment, operation, natural gas, electricity purchased from the national grid, and the earning of selling electricity to the national grid, respectively. $P_m$ is the installation capacity of the mth elements, $C_m$ is the unit investment cost, l is the number of ingredients, $i$ is the interest rate, $\beta$ is the service life of components (the service life of the battery is set to 9 years, and other components have 20 years for service (Andreas et al., 2018)), and $\lambda$ is the coefficient of operation cost to investment cost and it is set to 0.02 (Guo et al., 2013). $C_{png}$, $C_{pe}$, and $C_{se}$ are the unit cost of natural gas, purchased electricity, and selling electricity, respectively.

3.2 Environmental Performance

Global warming due to greenhouse gases is a critical environmental issue, and the environmental performance of the micro-grid because of the integration of renewable energies is assessed in carbon dioxide emission reduction rate (CDERR) as

$CDERR=\left(1-\frac{{\displaystyle \sum _{t=1}^{n}CD{E}_t^{MG}}}{{\displaystyle \sum _{t=1}^{n}CD{E}_t^R}}\right)\times 100\%(15)$

in which the lifecycle carbon dioxide emission (CDE) from the renewable energy technologies is not considered, and the CDE during the operation is calculated as:

$CD{E}_t=E_{grid,t}{\lambda }_{C{O}_2,c}+F_{ng,t}{\lambda }_{C{O}_2,ng}(16)$

in which ${\lambda }_{C{O}_2,c}$ and ${\lambda }_{C{O}_2,ng}$ are the unit emission factors of electricity of the national grid and natural gas, respectively. They are set to 0.968 kg/kWh electricity and 0.220 kg/kWh heat (Wang et al., 2010), respectively.

3.3 Flexibility Performance

The flexibility of the micro-grid can be assessed in its interaction with the national grid. If the interaction is less, it is shown that the micro-grid has higher operational flexibility (Perera et al., 2013). Usually, the interaction can be evaluated in the grid integration level and the net interaction level, and they are respectively defined as (Wang J et al., 2020):

$GIL=\frac{{\displaystyle \sum _{t=1}^{n}r{E}_{grid,t}}}{{\displaystyle \sum _{t=1}^n{P}_{L,t}}}\times 100\%r=\{\begin{array}{c}1E_{grid,t}\ge 0\\ 0E_{grid,t}<0\end{array}(17)$

and

$NIL=\frac{{\displaystyle \sum _{t=1}^n\left|E_{grid,t}\right|}}{{\displaystyle \sum _{t=1}^n{P}_{L,t}}}\times 100\%(18)$

in which $P_L$ is the electricity load of users.

The multi-objective functions are adopted to evaluate the performances of the micro-grid, and there are two cases to be constructed as follows:

Case 1. Maximizing the energetic, economic, and environmental performances as:

$\text{max }\left\{PESR\left(P\right),ATCSR\left(P\right),CDERR\left(P\right)\right\}(19)$

Case 2 Both maximizing the energetic, economic, and environmental performances AND minimizing the interaction between the micro-grid and the national grid as:

$\text{max}\left\{PESR\left(P\right),ATCSR\left(P\right),CDERR\left(P\right)\right\}\mathrm{and}\text{min}\left\{GIL\left(P\right),NIL\left(P\right)\right\}(20)$

3.4 Constraints

1) Power balances of electricity and heat

$P_{GT,t}+P_{PV,t}+P_{WT4t}+P_{B,t}+P_{grid,t}=P_{GSHP,t}+P_{L,t}(21)$

$Q_{GT,t}+Q_{GSHP,t}+Q_{TS,t}\ge Q_{L,t}(22)$

where $Q_L$ is the heat load of users, the negative values of $P_{B,t}$ and $Q_{TS,t}$ represent the charge states of battery and heat tank, respectively, while the positive values represent the discharge, and the negative $P_{grid,t}$ represents that the excess electricity is sent back to the national grid. In contrast, the positive value represents the purchased electricity from the national grid.

2) Capacities of components

$0\le P_{i,t}\le P_i^{nom}{\epsilon }_{i,t},\epsilon \in \left(\mathrm{0,1}\right)(23)$

When each component runs, $\epsilon =1$ and its output is not larger than its capacity. If the component does not run, $\epsilon$ is equal to 0.

3) Constraints of the heat tank

$S_{TS,t}\le S_{TS}^{nom}(24)$

$0\le Q_{TS,i,t}\le Q_{TS,i}^{\max }(25)$

$0\le Q_{TS,o.t}\le Q_{TS,o}^{\max }(26)$

in which the stored heat is always less than its capacity, and the power of charge and discharge is less than their maximum powers ($Q_{TS,i}^{\max }$ and $Q_{TS,o}^{\max }$), respectively.

4) Constraints of battery

$S_B^{\min }\le S_{B,t}\le S_B^{\max }(27)$

$0\le P_{B,i,t}\le P_{B,i}^{\max }(28)$

$0\le P_{B,o,t}\le P_{B,o}^{\max }(29)$

in which the stored electricity is always less than its capacity, and the power of charge and discharge is less than their maximum powers ($P_{B,i}^{\max }$ and $P_{B,o}^{\max }$), respectively.

5) Operation and climbing of components.

The generation efficiency of the gas turbine is declined with the decreasing power, and the following constraint is set to avoid too low power factor:

${\vartheta }_{GT}{P}_{GT}^{nom}\le P_{GT,t}\le P_{GT}^{nom}(30)$

in which ${\vartheta }_{GT}$ is the off coefficient of the gas turbine. The climbing constraints of the gas turbine and the heat pump are expressed as:

$P_{i,t-1}-r_i^{down}\Delta t\le P_{i,t}\le P_{i,t-1}+r_i^{up}\Delta t(31)$

$Q_{i,t-1}-r_i^{down}\Delta t\le Q_{i,t}\le Q_{i,t-1}+r_i^{up}\Delta t(32)$

in which $r_i^{down}$ and $r_i^{up}$ are the up and bottom limitations of climbing, respectively.

3.5 Robust Solving Algorithm

A robust Pareto Frontier is defined as one that has to demonstrate its insensitivity to the perturbations in the optimization variables in their neighborhoods. The robust optimization problem on Equation (8) can be defined as:

$\begin{array}{c}\underset{P}{\min /\max }O\left(P\right),\\ \begin{array}{l}\text{subject to }\frac{\Vert O^{eff}\left(P\right)-O\left(P\right)\Vert }{\Vert O\left(P\right)\Vert }\le \beta \\ P\in S\end{array}\end{array}\}(33)$

where O represents the objective function, $\beta$ is the threshold vector to adjust robustness, and it can be directly controlled to the desired robustness by the user, $O^{eff}$ is the anxious function value that could be the mean practical function value or the worst function value in the neighborhood. For example, the solutions P with sensitivity larger than the threshold of $\beta$ are considered unfeasible. The $\Vert \cdot \Vert$ operator can be any suitable norm measure.

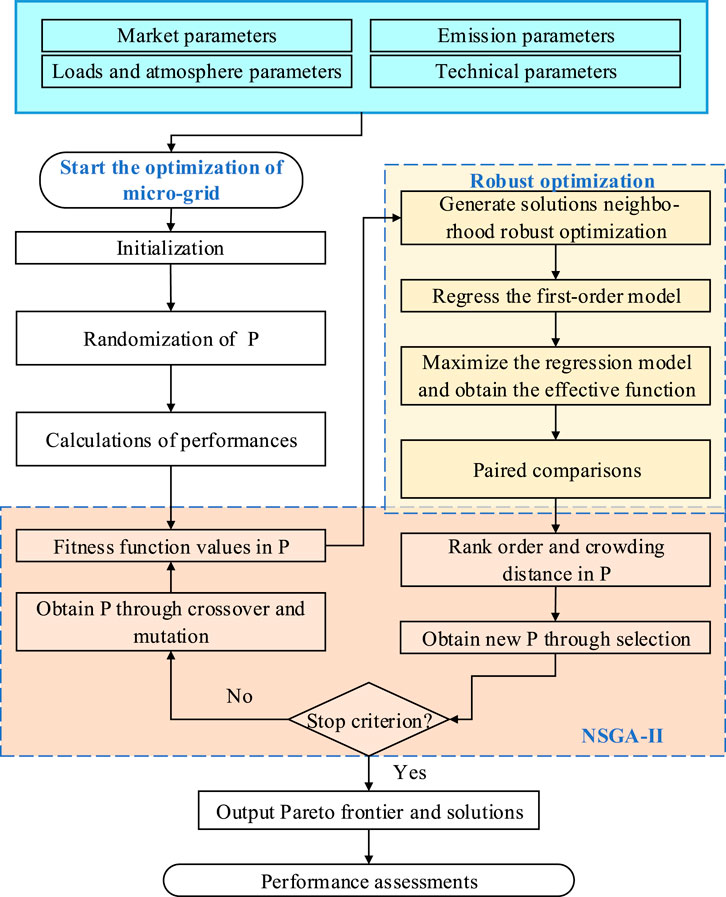
In this study, the NSGA II was employed to solve this problem, and the procedures are displayed in Figure 2. The NSGA II has apparent advantages in multi-objective optimization, which combines the parent scheme with its offspring schemes and competes together to produce the next generation population, reducing the computational complexity. The elite strategy prevents the excellent solutions from being discarded in the evolution. The mutation operation is an essential guarantee for jumping out of the local optimum and facing global optimization. The Pareto solution set obtained by the calculation keeps the diversity of populations.

FIGURE 2

FIGURE 2. Robust NSGA II optimization.

The detailed procedures are shown as follows:

Step 1 Initialization. Some parameters are initialized, including system parameters such as technical and economic parameters, and NSGA-II parameters such as population size, number of iterations, and probabilities of crossover and mutation.

Step 2 Randomization of the population P. Based on the input parameters and the ranges of decision variables, the initial P is obtained.

Step 3 Calculate the fitness functions of each individual in the population. This value can be calculated according to the objective functions.

Step 4 Perform the robustness calculations with the worst function values through sensitivity analysis of population P as follows:The N solutions in the neighborhood $(P,\Delta P)$ are generated in the feasible range, and the following three steps are performed:

1) The first-order linear regression model of each $O_j$ is fitted using the points in the neighborhood, and $c_j$ denotes the resulting coefficients’ vector.

2) The following liner program is solved using an optimization algorithm (the simplex method is adopted in this study):

$\begin{array}{c}\text{max }{c}_j^T{y}_j\\ \text{subject to }{y}_j\ge P-\Delta P/2\\ y_j\le P+\Delta P/2\end{array}\}(34)$

3) The optimal solution $y_j^{\ast }$ is obtained and the value of the effective function is calculated as:

$O_j^{eff}\left(P\right)=\max (O_j\left(y_j^{\ast }\right),\max O_j\left(P\right))(35)$

After the practical function values are obtained, the paired comparisons ($\mu (\cdot )=\frac{\Vert O^{eff}\left(P\right)-O\left(P\right)\Vert }{\Vert O\left(P\right)\Vert }$) between each current solution and its specific challenges in the selection phase are implemented. Then, the new population is selected according to the following rules:

· If both points have $\mu (\cdot )>\beta$, the solution with the lowest $\mu (\cdot )$ is included in the new population;

· If only one point has $\mu (\cdot )\le \beta$, only this point is included;

· If both points have $\mu (\cdot )\le \beta$, the Pareto-dominated solution is included. If they are mutually non-dominated, both of them are included.

Step 5 Determine the rank value and crowding distance of each individual in the population according to the fitness function. Then, a new population is obtained from the population according to rank value and crowding distance.

Step 6 If the stop criterion is not satisfied, the new population P2 is obtained through crossover and mutation operations of P1. Then, the fitness of individuals in the population (P1, P2) is, thus, determined, and the sensitivity of solutions in the population (P1, P2) is analyzed. The procedure ends until the stop criterion is satisfied.

4 Results and Discussions

A case study was performed to demonstrate the validation of the proposed robust optimization model in the micro-grid in this section, and the used software to implement the optimization algorithm is MATLAB software.

A typical commercial area with hotel and office buildings in North China was selected as a case, and the micro-gird was designed using the proposed optimization. The typical hourly ambient temperature, wind velocity, and solar radiation are shown in Figure 3 and Figure 4, respectively.

FIGURE 3

FIGURE 3. Daily solar radiation.

FIGURE 4

FIGURE 4. Daily atmosphere temperature and wind speed.

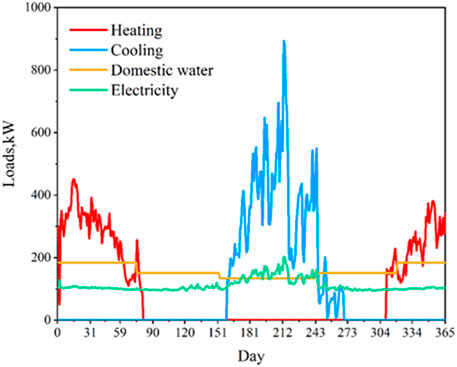
The hourly loads of electricity, cooling, heating, and domestic hot water are displayed in Figure 5. Other initial parameters are set as follows:

FIGURE 5

FIGURE 5. Daily loads of cooling, heating, power, and domestic hot water.

1) The available installation area of solar PV panels is 2000 m² (Liu et al., 2012).

2) The economic parameters of components are summarized in Table 2 (Lin et al., 2011; Guo et al., 2013; Hong, 2014; Li et al., 2019).

TABLE 2

TABLE 2. Investment costs (Yuan/kW or Yuan/kWh)

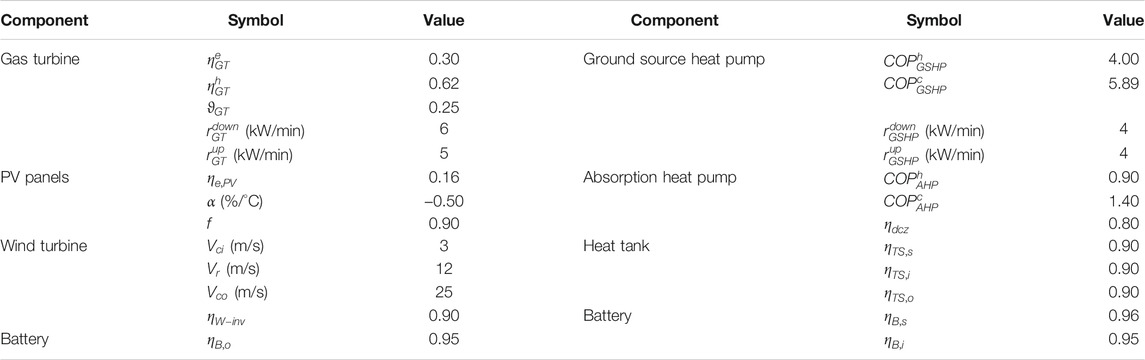
3) The technical parameters of components are listed in Table 3 (Lin et al., 2011; Perera et al., 2013; Dou, 2018; Alamgir et al., 2019; Li et al., 2019; Ren et al., 2019).

TABLE 3

TABLE 3. Technical parameters

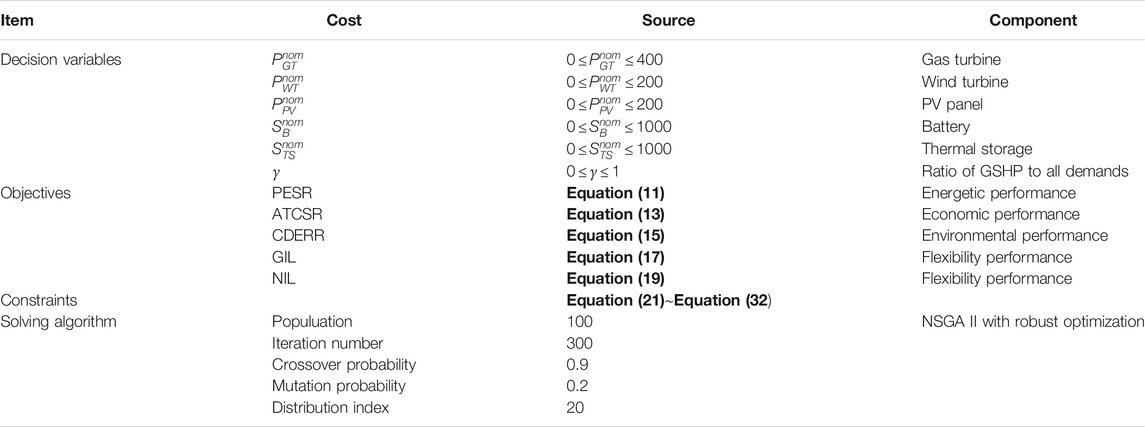
4) The optimization model and parameters of NSGA-II are set in Table 4.

TABLE 4

TABLE 4. The optimization model for the micro-grid

5) The hourly electricity prices are 1.51 (11:00–13:00, 16:00–17:00), 1.38 (10:00–11:00, 13:00–15:00, 18:00–21:00), 0.86 (7:00–10:00, 15:00–16:00, 17:00–18:00, 21:00–23:00) and 0.37 (23:00–7:00) Yuan/kWh (Peng et al., 2020).

6) The price of natural gas is 2.9 Yuan/Nm³ (Peng et al., 2020), and the low heating value is 42 MJ/Nm³.

7) The reference system is set to the following configurations and operation: electricity is supplied by the national electric grid (the power generation efficiency is set to 0.35 and the transmission efficiency is 0.92), the ground source heat pump satisfies the hot and chilled water for heating and cooling loads, respectively, and the boiler provides the heat required for domestic hot water (the heat efficiency is set to 0.80).

4.1 Results

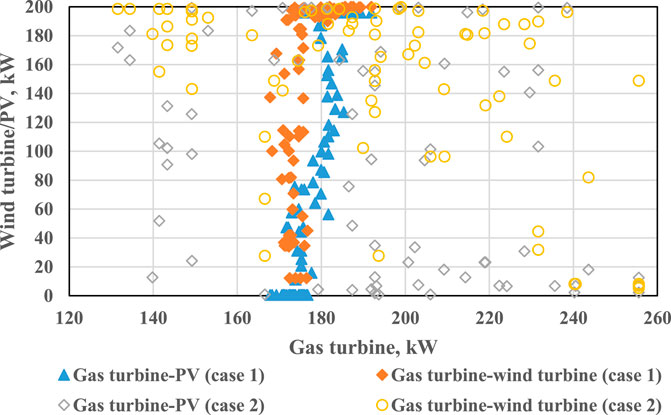
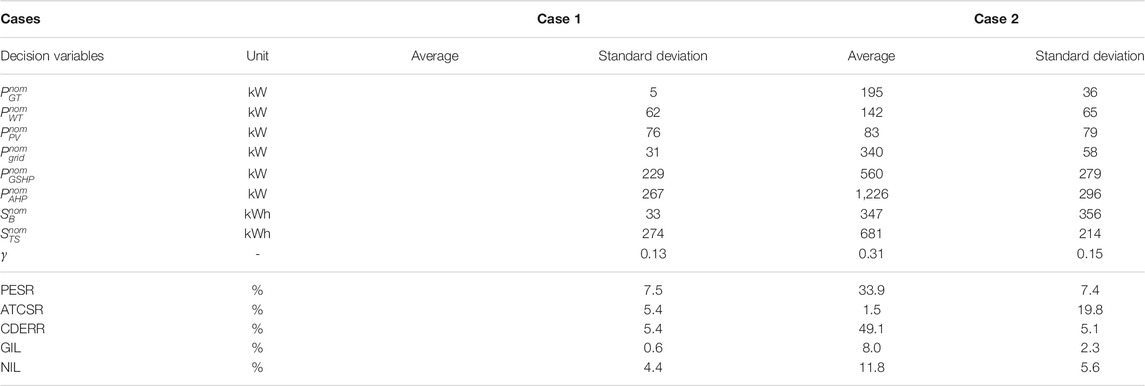
To discuss the optimization results under different optimization objective functions, three indicators of PESR, ATCSR, and CDERR (without considering the operational flexibility in case (1) and five indicators of PESR, ATCSR, CDERR, GIL, and NIL (considering the operational flexibility in case (2) for optimization goals. Through the multi-objective robust optimization algorithm and using 100 Pareto solutions in the optimization, the system power generation equipment (gas turbine, wind power, and photovoltaic) is shown in Figure 6. It is observed that when the system operation flexibility is not considered, the gas turbine capacity is concentrated between 168 kW and 192 kW. When the system operation flexibility is considered, the gas turbine capacity range is expanded from 132 kW to 256 kW. The distributions of the mean and standard deviation corresponding to the 100 groups of optimal solutions are shown in Table 5. When considering the operating flexibility of the system, except for the minor standard deviation of the heat storage device, the standard deviations of other variables all increase, indicating that the Pareto optimal solution distribution is more discrete. When the GI and NI decreased by 0.2 and 2.3%, respectively, the PESR, ATCSR, and CDERR were reduced by 1.6, 19.8, and 1.2%, respectively, and the economic performance decreased significantly.

FIGURE 6

FIGURE 6. Optimal configurations of power technologies of two cases.

TABLE 5

TABLE 5. Distributions of optimal solutions of two cases

The configuration of equipment capacity is optimized based on local resource conditions and user load. Therefore, the degree of wind and photovoltaic power generation equipment is closely related to weather conditions such as wind speed and irradiation. The annual utilization hours are 1406 and 1221, respectively. The annual utilization hours of gas turbines are different in 100 sets of optimal solutions. When operating flexibility is not considered, the average utilization hours are 4174, and when working flexibility is considered, it is reduced to 3863. The decrease of annual utilization hours is mainly due to the increase in the configuration capabilities of the gas turbine when operating flexibility is considered.

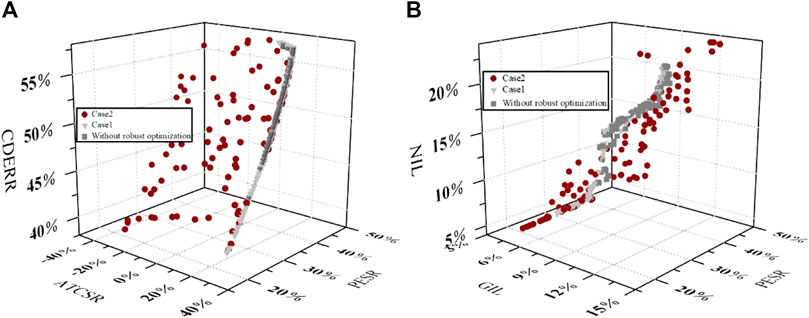
The performances in the optimal cases are shown in Figure 7. When flexibility is not considered in case 1, the PESR ranges from 20.8 to 45.3% Figure 7A. The increasing PESR means the decrease in fuel consumption, and the CDERR is also increased from 39.6 to 57.4%. Also, the ratio of renewable energy is increased, resulting in worse economic performance due to the larger investment cost of PV and wind turbines. The ATCSR is declined from 27.1 to 6.3%. At case 1, the GIL and NIR in Figure 7B are [7.2%, 9.2%] and [7.2%, 20.4%], respectively. The NIL increases with the increasing PESR, and its increase is relatively large, whereas the increase of GIL is slight.

FIGURE 7

FIGURE 7. Comparisons of Pareto frontiers of optimal systems considering different objectives.

When the flexibility is considered in the optimization of case 2, the performance distributions are not in a Pareto Frontier. There are specific relationships between PESR, ATCSR, and CDERR, and their change ranges are [19.3%, 35.3%], [-40.7%, 27.0%], and [39.0%, 57.5%]. Compared to case 1, the economic performance declined dramatically, reducing to -40.7%, which is worse than the reference system. In case 2, the change ranges of GIL are [4.7%, 13.6%] and that of Nil are [4.7%, 24.0%]. Obviously, their lowest values decrease 2.5%, and their largest values increase, resulting from the conflict between five optimization objectives. Comprehensively, the average values of GIL and NIL are declined by 0.2 and 2.3%, respectively. This point demonstrates that the optimization considering operational flexibility obtains the obvious benefits, and the proposed robust optimization is feasible.

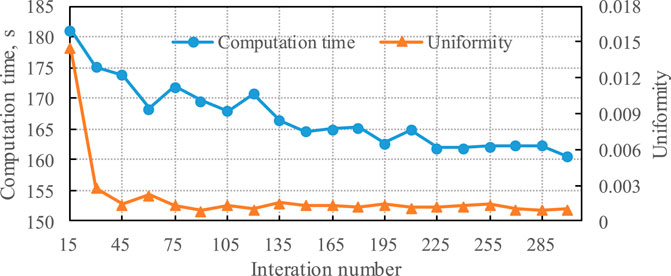
Case 1was optimized without the robust optimization to evaluate the benefit of the proposed optimization model, and the Pareto frontier is shown in Figure 7. The results show that the more extensive ranges of Pareto solution in the robust optimization are obtained, and the PESR, ATCSR, and CDERR are increased by 6.5, 4.3, and 4.7%, respectively. The validation of the proposed method is also indicated.In addition, the performance of solving algorithms is assessed in the convergence, uniformity, and breadth of solutions. Considering no real Pareto Frontier, the uniformity of keys is selected and used to determine the algorithm. The program was performed in the personal computer of 3.40-GHz I7-6700 CPU and 8-GB, and the computation time of each step and the standard deviation are shown in Figure 8. It is seen that the distributions of solutions will be uniform when the iteration number reaches 45, and the computation time decreases with the increasing iteration. When the iteration increases from 15 to 300, the consumed time is declined by 11.3%. But the total time is increased. The suitable maximum iteration is set to about 45, which considers both the computation cost and solution distributions.

FIGURE 8

FIGURE 8. Impacts of iteration generation on computation time and uniformity of solutions.

4.2 Discussion

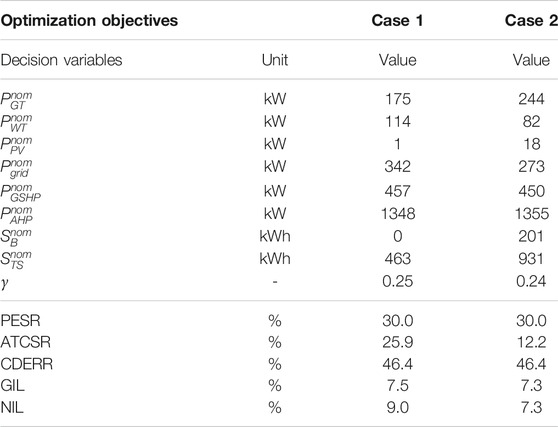
Two optimal solutions with similar PESR are selected from the 100 solutions of the Pareto Frontier to compare the operation strategies of two cases considering different optimization objectives, and their configurations and performances are displayed in Table 6. Their PESR are similar, and the arrangements in other aspects are as same as the analysis in Section 4.2. When the GIL and NIL of operational flexibility are both considered, the ATCSR of the micro-grid is reduced.

TABLE 6

TABLE 6. Typical system configurations and performances in different optimization objectives

Figure 9 displays the electricity balances of the cases in Table 6 on a typical summer day. It is observed that the electric demands are not different because of the different cooling ratios of the ground source heat pump in the two cases. Analyzed their total supplies of power technologies, the gas turbine supplies more than 51.1% of total electricity demand. The wind turbine plays an essential role in providing electricity, and its ratio reaches 25.5% when considering operation flexibility. The national grid is an important supplementary source of the micro-grid, and its ratios in two cases are 11.1 and 16.3%, respectively. Because of the consideration of flexibility of micro-grid, the national grid decreases the supply by 5.2%. In addition, it is seen that the capacities of PV panels are both low in two cases in Table 6, and their supply ratios are only 1.6 and 0.1%. Compared to selling electricity from the micro-grid to the national grid (4:00–6:00), there is excess electricity to be sold back to the national grid because of the larger capacity of the wind turbine in case 1 in Figure 9A without considering flexibility, indicating that it has more extensive dependence on the national grid.

FIGURE 9

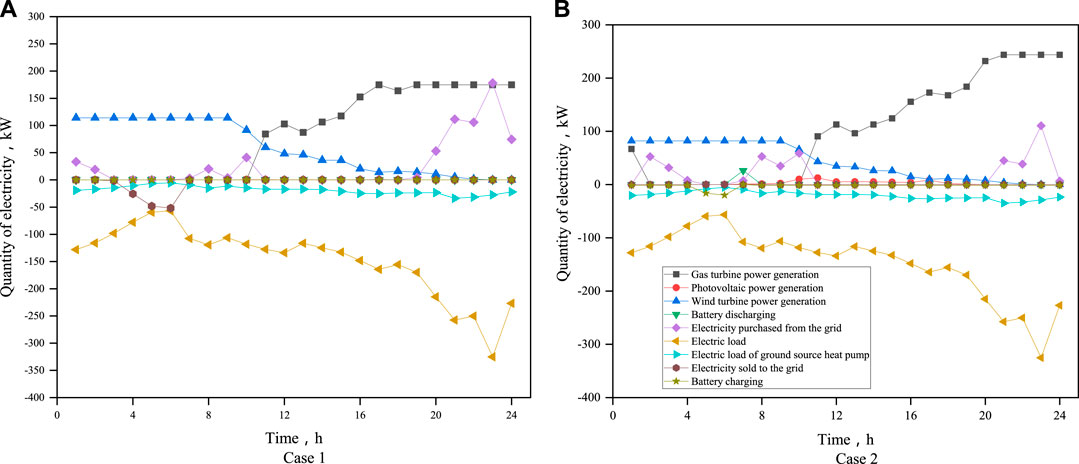
FIGURE 9. Comparisons of operational modes of power components in a typical summer day considering different objectives.

The cooling and domestic hot water loads are converted to thermal demand, and the heat balances in two cases of Table 6 are shown in Figure 10. The generated power determines the exhaust waste heat from the gas turbine, and their heat ratios reach 46.7% in case 1 without operational flexibility Figure 10A and 55.3% in case 2 in Figure 10B with flexibility. The second unit to supply more heat is the absorption heat pump, and their ratios reach 30.6 and 19.8%, respectively. The ground source heat pump delivers about 20.0% of total heat demand. Because the capacity of the heater tank is more prominent in case 2 when considering flexibility, its ratio is 4.9%, which is more significant than in case 1.

FIGURE 10

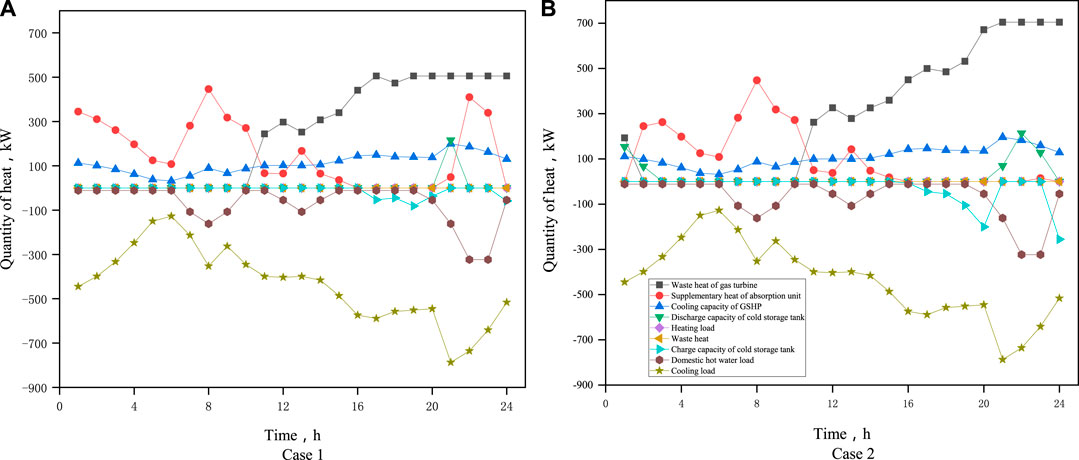
FIGURE 10. Comparisons of operational modes of thermal components in a typical summer day considering different objectives.

5 Conclusion

This paper constructed a robust optimization model of micro-grid of natural gas and renewable energies. The multi-aspect performances, including energy, economic, environmental, and operation flexibility of the micro-grid, were considered. The optimal configurations and implementations were discussed in the different optimization objectives by a case study. The following main conclusions are obtained:

1) When the PESR, ATCSR, and CDERR are considered for optimization, Pareto solutions’ performances are related. The CDERR is increased with the increasing PESR, whereas the ATCSR is declined with the increase of PESR.

2) When the operational flexibility of the micro-grid is considered in the optimization, the micro-grid decreases its dependence on the national grid, and the flexibility is improved. But the Pareto solutions are discrete.

3) In the specific case study in this paper, the micro-gird optimized in energetic, economic, and environmental performances averagely reduces the fuel consumption by 35.5%, economic cost of 21.3%, and carbon dioxide emission of 50.3%. When the operational flexibility using the indicators of GIL and NIL is as the optimization objective, the gird integration level is averagely decreased by 0.2%, and the net interaction level is averagely declined by 2.3%. But the improvement of flexibility of the micro-grid results in the decreases of PESR, ATCSR, and CDERR. They are reduced by 1.6, 19.8, and 1.2%, respectively.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

Author TZ was employed by the company China Energy Investment Corporation (China Energy).

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alamgir, H. M., Pota, H. R., and Stefano, S. (2019). Energy Scheduling of Community Microgrid with Battery Cost Using Particle Swarm Optimisation. Appl. Energ. 254, 113723. doi:10.1016/j.apenergy.2019.113723

CrossRef Full Text | Google Scholar

Andreas, B., Wolf-Peter, S., and Alexander, Z. (2018). Power-to-heat for Renewable Energy Integration: A Review of Technologies, Modeling Approaches, and Flexibility Potentials. Appl. Energ. 212, 1611–1626. doi:10.1016/j.apenergy.2017.12.073

CrossRef Full Text | Google Scholar

Cao, Y., Mu, Y., and Jia, H. (2020). Multi-stage Planning of Park-Level Integrated Energy System Considering Construction Time Sequence. Proc. CSEE 40 (21), 6815–6828. (in Chinese). doi:10.13334/j.0258-8013.pcsee.200622

CrossRef Full Text | Google Scholar

Chen, L., Lin, X., and Xu, Y. (2019). Modeling and Multi-Objective Optimal Dispatch of Micro Energy Grid Based on Energy Hub. Power Syst. Prot. Control. 47 (06), 9–16. (in Chinese).

Google Scholar

Davood, R., and Hassan, B. (2019). Probabilistic Optimization in Operation of Energy Hub with Participation of Renewable Energy Resources and Demand Response. Energy 173, 384–399. doi:10.1016/j.energy.2019.02.021

CrossRef Full Text | Google Scholar

Deb, K., and Gupta, H. (2006). Introducing Robustness in Multi-Objective Optimization. Evol. Comput. 14 (4), 463–494. doi:10.1162/evco.2006.14.4.463

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, T., Li, C., Yang, Y., Jiang, J., Bie, Z., and Blaabjerg, F. (2017). A Two-Stage Robust Optimization for Centralized-Optimal Dispatch of Photovoltaic Inverters in Active Distribution Networks. IEEE Trans. Sustain. Energ. 8 (2), 744–754. doi:10.1109/tste.2016.2605926

CrossRef Full Text | Google Scholar

Ding, Z., Chen, B., and Zhou, Y. (2018). The Research on Operation Optimization of Regional Energy Internet Based on Detailed Model. Renew. Energ. Resour. 36 (09), 1362–1368. (in Chinese). doi:10.13941/j.cnki.21-1469/tk.2018.09.016

CrossRef Full Text | Google Scholar

Dong, X., Sun, Y., and Pu, T. (2019). An Optimal Scenario Reduction Method Based on Wasserstein Distance and Validity index. Proc. CSEE 39 (16), 4650–4658+4968. (in Chinese). doi:10.13334/j.0258-8013.pcsee.181494

CrossRef Full Text | Google Scholar

Dou, Chao. (2018). Study of Combined Cooling Heating and Power System Coupled with Ground Source Heat pump. Baoding: North China Electric Power University. (in Chinese).

Google Scholar

Faeze, B., Masoud, H., and Shahram, J. (2015). Optimal Electrical and thermal Energy Management of a Residential Energy Hub, Integrating Demand Response and Energy Storage System. Energy & Buildings 90, 65–75. doi:10.1016/j.enbuild.2014.12.039

CrossRef Full Text | Google Scholar

Guo, L., Liu, W., Cai, J., Hong, B., and Wang, C. (2013). A Two-Stage Optimal Planning and Design Method for Combined Cooling, Heat and Power Microgrid System. Energ. Convers. Manag. 74, 433–445. doi:10.1016/j.enconman.2013.06.051

CrossRef Full Text | Google Scholar

He, S., Ruan, H., and Gao, H. (2020). Overview on Theory Analysis and Application of Distributionally Robust Optimization Method in Power System. Automation Electric Power Syst. 44 (14), 179–192. (in Chinese).

Google Scholar

Hong, B. (2014). Research on Dispatch Model and Method of Microgrid. Tianjin: Tianjin University. (in Chinese).

Google Scholar

Jiang, R., Wang, J., and Guan, Y. (2012). Robust Unit Commitment with Wind Power and Pumped Storage Hydro. IEEE Trans. Power Syst. 27 (2), 800–810. doi:10.1109/tpwrs.2011.2169817

CrossRef Full Text | Google Scholar

Jin, H., Sui, J., and Xu, C. (2016). Research on Theory and Method of Multi-Energy Complementary Distributed CCHP System. Proc. CSEE 36 (12), 3150–3160. (in Chinese). doi:10.13334/j.0258-8013.pcsee.161259

CrossRef Full Text | Google Scholar

Li, Z., Qin, Z., and Wang, H. (2019). Research on Wind Power Cost Level and its Influencing Factors in China. Price:Theory. Practice. (10), 24–29+166. (in Chinese). doi:10.19851/j.cnki.cn11-1010/f.2019.10.005

CrossRef Full Text | Google Scholar

Liang, W. (2018). Modeling and Optimization of the Distributed Energy System with Complementation of Multiple Energy. Guangzhou: South China University of Technology.

Google Scholar

Lin, Y., Zhang, S., and Xiao, Y. (2011). Optimal Design and Operational Strategies of Hybrid CCHP-Groundwater Heat Pump System. Heat. Ventilating Air Conditioning 41 (10), 84–90.

Google Scholar

Lin, Z., Zhao, L., and Zhu, D. (2018). Robust Optimization Model for Electricity Production Planning and its Application. Electric Power Sci. Eng. 34 (12), 1–9. (in Chinese).

Google Scholar

Liu, M., Shi, Y., and Fang, F. (2012). A New Operation Strategy for CCHP Systems with Hybrid Chillers. Appl. Energ. 95, 164–173. doi:10.1016/j.apenergy.2012.02.035

CrossRef Full Text | Google Scholar

Ma, T., Wu, J., and Hao, L. (2017). Energy Flow Modeling and Optimal Operation Analysis of the Micro Energy Grid Based on Energy Hub. Energ. Convers. Manag. 133, 292–306. doi:10.1016/j.enconman.2016.12.011

CrossRef Full Text | Google Scholar

Peng, C., Xie, P., and Chen, C. (2014). Adjustable Robust Optimal Dispatch of Power System with Large-Scale Photovoltaic Power Stations. Proc. CSEE 34 (25), 4324–4332. (in Chinese). doi:10.13334/j.0258-8013.pcsee.2014.25.015

CrossRef Full Text | Google Scholar

Peng, C., Zheng, C., and Chen, J. (2020). Robust Optimal Dispatching of Integrated Energy System Based on Confidence gap Decision. Proc. CSEE, 1–10. (in Chinese). doi:10.13334/j.0258-8013.pcsee.20122

CrossRef Full Text | Google Scholar

Perera, A. T. D., Attalage, R. A., Perera, K. K. C. K., and Dassanayake, V. P. C. (2013). A Hybrid Tool to Combine Multi-Objective Optimization and Multi-Criterion Decision Making in Designing Standalone Hybrid Energy Systems. Appl. Energ. 107, 412–425. doi:10.1016/j.apenergy.2013.02.049

CrossRef Full Text | Google Scholar

Qin, L., Lin, J., and Dai, S. (2016). Improved Light Robust Optimization Model Based Wind-thermal Unit Commitment. Proc. CSEE 36 (15), 4108–4119. (in Chinese). doi:10.13334/j.0258-8013.pcsee.142829

CrossRef Full Text | Google Scholar

Ren, F., Wang, J., Zhu, S., and Chen, Y. (2019). Multi-objective Optimization of Combined Cooling, Heating and Power System Integrated with Solar and Geothermal Energies. Energ. Convers. Manag. 197, 111866. doi:10.1016/j.enconman.2019.111866

CrossRef Full Text | Google Scholar

Wang, J., Liu, Y., Ren, F., and Lu, S. (2020). Multi-objective Optimization and Selection of Hybrid Combined Cooling, Heating and Power Systems Considering Operational Flexibility. Energy 197, 117313. doi:10.1016/j.energy.2020.117313

CrossRef Full Text | Google Scholar

Wang, J., Zhai, Z., Jing, Y., and Zhang, C. (2010). Particle Swarm Optimization for Redundant Building Cooling Heating and Power System. Appl. Energ. 87 (12), 3668–3679. doi:10.1016/j.apenergy.2010.06.021

CrossRef Full Text | Google Scholar

Wang, Y., Yang, Y., Tang, L., Sun, W., and Li, B. (2020). A Wasserstein Based Two-Stage Distributionally Robust Optimization Model for Optimal Operation of CCHP Micro-grid under Uncertainties. Int. J. Electr. Power Energ. Syst. 119, 105941. doi:10.1016/j.ijepes.2020.105941

CrossRef Full Text | Google Scholar

Zhao, P., Gu, C., Huo, D., Shen, Y., and Hernando-Gil, I. (2020). Two-Stage Distributionally Robust Optimization for Energy Hub Systems. IEEE Trans. Ind. Inf. 16 (5), 3460–3469. doi:10.1109/tii.2019.2938444

CrossRef Full Text | Google Scholar

Zhu, G., Lin, J., and Luo, Z. (2017). Review of Robust Optimization for Generation Scheduling in Power Systems. Proc. CSEE 37 (20), 5881–5892. (in Chinese). doi:10.13334/j.0258-8013.pcsee.161950

CrossRef Full Text | Google Scholar