Statistical Machine Learning Model for Uncertainty Planning of Distributed Renewable Energy Sources in Distribution Networks

New energy power systems with high-permeability photovoltaic and wind power are high-dimensional dynamic large-scale systems with nonlinear, uncertain and complex operating characteristics. The uncertainty of new energies creates challenges in detailed analyses of operating conditions and the efficient planning of distribution networks. Probabilistic power flows (PPFs) are effective tools for uncertainty analyses of distribution networks, and they can be applied in stochastic programming, risk assessment and other fields. We propose different forms of PPFs, which are origin moments rather than means and variances, based on point estimation. We design a stochastic programming model suitable for new energy planning in practice, and the PPF results can be used to improve energy stochastic programming methods by considering the principle of maximum entropy (POME) and quadratic fourth-order moment (QFM) estimation. The origin moments of PPFs are transformed into central moments as inputs of QFM based on probability theory. QFM can efficiently estimate the constraint probability levels of stochastic optimal planning models, and the proposed method is verified based on an IEEE 33-node distribution network.

Introduction

In the context of smart grids and low-carbon power, the broad application of intermittent renewable distributed generation (DG) has led to uncertainty in distribution network planning (Injeti and Thunuguntla, 2020). Hydrogen production from renewable energy has become a hot spot of new energy application because of its low energy consumption (Zhang et al., 2021). The impact of new energy uncertainty on the operation optimization of distribution networks cannot be ignored, and high requirements for planning and design have been proposed. The stochastic optimal planning of distribution networks has become one of the key problems in the development of smart grids. The impacts of various uncertain processes on distribution network planning results can be formulated as part of a complex, nonlinear mixed-integer programming problem. The traditional planning method is based on typical daily deterministic scenarios, and the influence of uncertain factors is often not considered. The main methods that include uncertain programming in power systems are robust programming and stochastic programming.

Robust power system planning commonly combines the worst-case scenario approach and interval optimization theory (Liu et al., 2016). Roldán et al. presented an adaptive robust optimization theory in which correlated uncertainty and the worst-case operating cost are fully considered (Roldán et al., 2019). Considering the uncertainty of DG and the corresponding demand, Chatthaworn and Chaitusaney presented a robust model for transmission network expansion planning in which all possible scenarios are analyzed (Chatthaworn and Chaitusaney, 2015). Zhang et al. presented a sequential quadratic interval programming model for reactive power optimization based on the interval uncertainty of DG (Zhang et al., 2019). To efficiently solve reactive power planning problems, the applied planning model often approximated as a linear model (Zhang et al., 2018). Zhang et al. presented a scenario method for reactive power optimization, and the uncertainty of DG was obtained from distribution functions (Zhang et al., 2016). Compared with deterministic programming, robust programming can ensure the security of power grid systems under extreme conditions. However, the fluctuations in DG uncertainty considerably influence robust programming. When the fluctuations in uncertain factors are small, the superiority of robust programming may not be apparent. When the fluctuations in uncertain factors exceed the corresponding threshold values, robust programming may not yield sufficient planning results. In addition, for safety, robust programming may be too extreme in many scenarios.

With respect to stochastic programming, probability distributions are often used in uncertain programming modeling. Gan et al. presented a wind farm planning method based on a linearized bilevel model that was solved using a linear solver (Gan et al., 2016). The mixed-integer linear stochastic model has become a popular stochastic planning model for distribution networks, and various scenarios should be considered to capture DG uncertainty (Jooshaki et al., 2020). Park et al. presented a two-stage stochastic mixed-integer programming model that considers DG uncertainty (Park et al., 2015). Haghighat and Zeng presented a two-stage stochastic programming model in which correlations among uncertainties are reflected by a Gaussian copula (Haghighat and Zeng, 2018). In regard to new energy power systems, the operation scenario of power systems is often determined according to the DG outputs. Chen et al. suggested that the operation scenario should be established according to the relevant state variables (Chen et al., 2020). The uncertainty of DG is considered in stochastic programming, so decision makers can assess the relationship between risk and benefits, which can help balance the economy and security of distribution networks. However, the probability distribution of DG uncertainty in stochastic programming models is limited by the amount of historical data available, and this limitation can bias the empirical distribution. In addition, nonlinear stochastic programming methods often have poor solution efficiency. Thus, establishing an efficient planning model is important and is the research motivation of this paper.

Scholars conducted research in the stochastic planning and inquiry field. The decision variables of the stochastic planning scenario are related to DG levels, reactive power devices, PEV charging stations, etc. The decision variables include the optimal site, size, quantity or level. To decrease wind power (WP) curtailment, a novel reactive power allocation scheme was presented in (Niu et al., 2017) based on autonomous voltage security regions. To solve the problem of reactive power imbalance associated with DG, a robust reactive power potential estimation method was presented in (Li et al., 20196) based on two-stage robust optimization. To improve the efficiency of stochastic programming under the premise of fully considering refined scenarios, a new stochastic programming theory was presented in (Fu et al., 2020) based on statistical machine learning. To maximize the profit of PEV charging stations, a bilevel optimization model was formulated in (Zhao et al., 2020), and the optimal sites and station sizes were calculated. It can be concluded that the consideration of equivalence in programming models is a key to solving stochastic programming problems.

In uncertainty analyses of power systems, probabilistic digital information is important. Many works use probabilistic power flow (PPF) calculations to evaluate the influence of uncertainty on the power grid, and the final results include the mean and variance (Tang et al., 2016; Ren et al., 2017; Lin et al., 2020). In this paper, a novel concept is proposed for the stochastic planning of power grids. In stochastic programming models, the central moment is used instead of the mean and variance.

The innovation of this paper lies in: 1) PPF is applied to uncertain programming for the first time, which verifies the application value of PPF theory. Instead of the mean and variance, we use central moments as the results of the PPF calculation, and they are used to estimate the opportunity constraint levels in stochastic programming problems. 2) The principle of maximum entropy (POME) is applied twice to uncertain planning of distributed renewable energy sources in distribution networks. The first involves estimating the probability characteristics of temperature, which can influence photovoltaic (PV) power generation, and the second involves estimating the probability level of constraint satisfaction in stochastic programming. 3) We propose a novel uncertain planning model with the mean value as the objective function and confidence levels as constraints. The practical significance of the planning model is clear and can be expanded for real problems.

The remainder of this paper is organized as follows. First, a statistical model for uncertainty planning of distributed renewable energy sources is proposed based on statistical machine learning in Stochastic Programming Model Section. Second, uncertainty calculation method is given for expanding PPF results into a stochastic programming model with the proposed method in Uncertainty Calculation Method Section. Specifically, we propose methods for weather uncertainty calculation, PPF calculation and uncertainty constraint calculation. Finally, three cases are simulated in MATLAB to verify the effectiveness of the proposed statistical model and solution method in Simulation Section. Specifically, we successively verify the effectiveness of uncertainty constraints, PPF and uncertainty programming.

Stochastic Programming Model

Stochastic programming is an important part of uncertain programming, and it regards random variables as uncertain parameters. Combined with probability theory, the new energy system can be planned based on stochastic programming. We first introduce the stochastic programming problem and then introduce the stochastic programming model used in this paper.

Problem Description

As shown in Figure 1, the uncertain components of new energy distributions network are important to consider. The energy sources of PV and WP are natural, but these sources are highly unpredictable. When new renewable energy capacity is added to the grid, the uncertainty of the distribution network will increase, and the operation scenario become increasingly complex, thus creating challenges related to the efficient planning and use of new energies. In stochastic programming, decision variables can only take certain values, thereby limiting the potential operating scenarios.

FIGURE 1

FIGURE 1. Uncertainty in a new energy distribution network.

Programming Model

We propose a PPF-based stochastic programming model for new energies in distribution networks as follows:

$f_{\mathbf{obj}}\left(nu{m}_{\mathbf{PV}},p_{\mathbf{PV}},nu{m}_{\mathbf{WP}},p_{\mathbf{WP}}\right)=\min E\left(p_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right),(1)$

subject to

$0\le Y_{\mathbf{PV}}\le Y_{\mathbf{PV}}^{-},(2)$

$0\le Y_{\mathbf{WP}}\le Y_{\mathbf{WP}}^{-},(3)$

$2\le nu{m}_{\mathbf{PV}}<nu{m}_{sys},(4)$

$2\le nu{m}_{\mathrm{WP}}<nu{m}_{sys},(5)$

$\mathrm{Pr}\left(V_i>V_{-}\right)>\alpha ,(6)$

where f_obj (•) is the objective function of the planning scheme, p_loss is the total active power loss in distribution and can be changed to other economic indicators based on the relevant decision-making requirements, E (•) is the mean function, Y_PV is a decision variable and represents the rated capacity of PV power, Y_PV⁻ is the upper limit of the PV planning capacity, Y_WP is another decision variable that represents the rated capacity of the WP, Y_WP⁻ is the upper limit of the WP planning capacity, num is the number of buses with new energy grid connections, num_sys is the number of distribution network buses, V_i is the ith bus voltage amplitude, V_{_} is the allowable lower limit of v_i, Pr (•) is a probability function, and α is the confidence probability.

The above formula cannot clearly explain how the decision variables affect the objective and constraint functions. Therefore, we will explain these relations through the following formula.

$E\left(p_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)=PPF\left(nu{m}_{\mathbf{PV}},p_{\mathbf{PV}},nu{m}_{\mathbf{WP}},p_{\mathbf{WP}}\right),(7)$

where PPF(•) is the PPF estimation method, which is a point estimation method (PEM) in this paper. Additionally, p_PV is the active PV power, and p_WP is the active WP power.

The power generated by new energy must be a function of the planned capacity, as shown below (Rohani and Nour, 2014).

$p_{\mathbf{PV}}=Y_{\mathbf{PV}}{f}_{\mathbf{PV}}\left(\frac{G}{G_{\mathbf{STC}}}\right)\left[1+{\alpha }_{\mathbf{p}}\left(T_{\mathbf{C}}-T_{\mathbf{C,STC}}\right)\right](8)$

$T_{\mathbf{c}}=\frac{T_{\mathbf{a}}+\left(T_{\mathbf{c,NOCT}}-T_{\mathbf{a,NOCT}}\right)\frac{G}{G_{\mathbf{NOCT}}}\left[1-\frac{{\eta }_{\mathbf{mp,STC}}\left(1-{\alpha }_p{T}_{\text{c,STC}}\right)}{\tau {\alpha }_{\mathbf{ab}}}\right]}{\mathbf{1}+\left(T_{\text{c,NOCT}}-T_{\text{a,NOCT}}\right)\frac{G}{G_{\mathbf{T,NOCT}}}\frac{{\alpha }_p{\eta }_{\mathbf{mp,STC}}}{\tau {\alpha }_{\mathbf{ab}}}}(9)$

$p_{\text{WP}}=\{\begin{array}{l}0v\text{<}{v}_{\text{ci}}\text{or}v\ge {\text{v}}_{\text{co}}\\ \frac{v^3-v_{\text{ci}}^3}{v_{\text{r}}^3-v_{\text{ci}}^3}{Y}_{\text{WP}}{v}_{\text{ci}}\le v\text{<}{v}_{\text{r}}\\ Y_{\text{WP}}{v}_{\text{r}}\le v\text{<}{v}_{\text{co}}\end{array}(10)$

where f_PV is the PV derating factor, G is the amount of current solar radiation, STC is a subscript that represents standard test conditions, α_p is the temperature coefficient, T_C is the PV cell temperature, NOCT is a subscript that represents the nominal operating cell temperature, T_a is the ambient temperature, ηmp is the maximum power efficiency, τ is the solar transmittance of a PV cell, α_ab is the solar absorptance of a PV cell, v is the current wind speed, v_r is the nominal wind speed, v_ci is the cut-in wind speed, and v_co is the cut-out wind speed.

By substituting Equations 8–10 into Eq. 7 and treating the capacities and locations of new energies as decision variables, we can obtain

$E\left(p_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)=PPF\left(nu{m}_{\text{PV}},Y_{\text{PV}},nu{m}_{\text{WP}},Y_{\text{WP}}\right),(11)$

Now, let us summarize the stochastic programming model for new energies in distribution networks. Notably, (2), (3), (4), and (5) are the upper and lower limits of decision variables, and these constraints can be implemented by limiting the feasible region when solving the stochastic programming model for new energies in distribution networks.

Remark 1: The key to the solution is to efficiently and accurately solve Eqs 6, 11. As in the estimation in Eq. 1 based on Eqs 6, 11 can also be estimated based on a PPF. The solution processes for (6) and (11) are discussed in detail in the next section.

Uncertainty Calculation Method

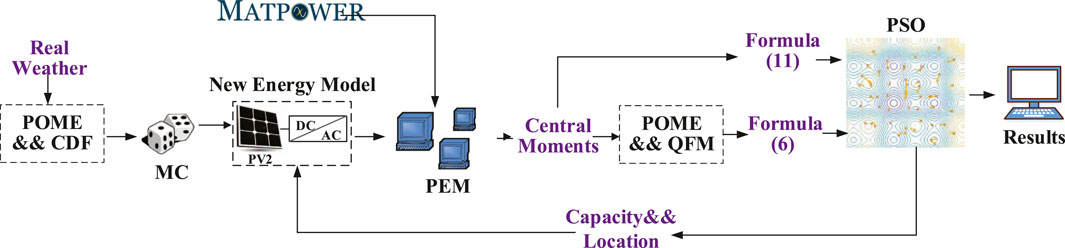
First, we introduce simulated weather data, which are the inputs of Eqs 8–10. Second, the PPF method is introduced, and the results are origin moments. Finally, the method used to solve Eq. 6 is introduced based on central moments and particle swarm optimization (PSO). The proposed methodology is briefly shown in Figure 2.

FIGURE 2

FIGURE 2. Schematic diagram of the proposed methodology.

Uncertainty Weather

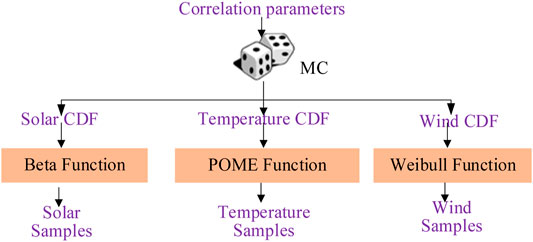
The weather simulation is based on a copula function, marginal probability distributions and logic, as shown in Figure 3. First, we introduce the marginal probability distributions for different weather types. Second, the copula function is introduced.

FIGURE 3

FIGURE 3. Flow chart of weather simulation.

The marginal probability distribution of G can be expressed as (Karaki et al., 1999):

$pdf\left(G\right)=\frac{\mathrm{\Gamma }\left(\alpha +\beta \right)}{\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }\left(\beta \right)}{\left(\frac{G}{G_{\max }}\right)}^{\alpha -1}{\left(1-\frac{G}{G_{\max }}\right)}^{\beta -1}(12)$

where pdf (•) is a probability density function (PDF), α and β are shape parameters, Г is the gamma function, and G_max is the maximum solar radiation.

The marginal probability distribution of v can be expressed as (Karaki et al., 1999):

$pdf\left(v\right)=\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left[-{\left(\frac{v}{c}\right)}^k\right](13)$

where k is a shape parameter and c is a scale parameter.

The marginal probability distribution of T_a can be expressed using POME in (Shore and Johnson, 1980):

$\max H\left(T_a\right)=-{\displaystyle \int pdf\left(T_a\right)\ln pdf\left(T_a\right)}d{T}_a,(14)$

subject to

${\displaystyle \int pdf\left(T_a\right)}d{T}_a=1,(15)$

${\displaystyle \int g_k\left(T_a\right)pdf\left(T_a\right)}d{T}_a={\mu }_k,k=0,\mathrm{...},m,(16)$

$pdf\left(T_a\right)={\mathrm{e}}^{{\displaystyle {\sum _{k=0}^m}^{{\lambda }_k{g}_k\left(T_a\right)}}},(17)$

where H (•) is the entropy function, ${\mu }_k$ is the kth given expectation, g_k (•) is the kth known function, and λ_k is the kth Lagrange parameter.

λ_k in Eq. 18 can be estimated using the program in (Mohammad-Djafari et al., 1992).

${\displaystyle \int g_k\left(T_a\right){\mathrm{e}}^{-{\displaystyle {\sum _{k=0}^m}^{{\lambda }_k{g}_k\left(T_a\right)}}}}d{T}_a={\mu }_k,k=0,\mathrm{...},m(18)$

A Gaussian copula function is used to model the correlation among G, v and T_a. We estimate rho for the matrix of linear correlation parameters using real weather data.

$rho=\mathbf{copulafit}\left(cdf\left(G\right),cdf\left(v\right),cdf\left(T_a\right)\right),(19)$

where rho is a coefficient estimated for a matrix of linear correlation parameters based on a Gaussian copula, copulafit (•) is a fitting function, and cdf (•) is a cumulative distribution function (CDF).

The Monte Carlo (MC) method is used to generate random weather simulation samples from the Gaussian copula with rho.

$\left[cdf\left(G^s\right),cdf\left(v^s\right),cdf\left(T_a^s\right)\right]=\mathbf{copularnd}\left(rho\right),(20)$

where s is a superscript that indicates that a variable is simulated and copularnd (•) represents the generation of random vectors using a MC approach. According to the simulated CDFs, we can obtain the simulated weather samples.

Remark 2: We input the weather variables into the model so that the research results can be applied to power grid planning under different weather conditions. There are classical probability functions for solar radiation and wind speed. With respect to the simulation of temperature, POME is used to estimate the unknown probability distribution.

PPF Calculation

PEM uses samples to obtain estimates. We can determine the statistical moments of the population using the PEM. The statistical moments of power flow solutions can be obtained from weighted samples at different positions. MATPOWER in (Zimmerman et al., 2011) is used for deterministic power flow (DPF) calculations. A two-point estimation (2PEM) approach is applied, and two values are determined on both sides of the mean value of each uncertain variable.

$x_{i\mathbf{,}k}=X_{\mathrm{mean,}i}+s{p}_{i,k}\times X_{\mathrm{standard,}i},(21)$

$s{p}_{i,k}=s{k}_i/2+{\left(-1\right)}^{\left(3-k\right)}\times \sqrt{m+{\left(s{k}_i/2\right)}^2},(22)$

where x_i is the ith uncertain variable (i.e., p_PV or p_WP), i = 1,2,…,m, m is the number of uncertain variables, X_mean,i is the mean of x_i, X_standard,i is the standard deviation of x_i, k = 1 or 2 (where 2 reflects the values on both sides of X_mean,i), sk_i is the sample skewness of x_i, and sp_ik is a location-specific measurement.

We introduce the following data into the DPF calculation using MATPOWER.

$P_{i,k}=\left[X_{\mathrm{mean,1,}}{X}_{\mathrm{mean,2}},\mathrm{...},X_{i,k},\mathrm{...},X_{\mathrm{mean,m}}\right],(23)$

$u_{i,k}=dpf\left(P_{i,k}\right),(24)$

where dpf (•) is the DPF calculated using MATPOWER and u is the obtained voltage, power flow, or other variable.

Next, we give the origin moment formula for u:

$M_{\mathrm{origin}}^j\left(u\right)={\displaystyle \sum _i^m{\displaystyle \sum _k^2{w}_{i,k}}}\times u_{i,k}^j,(25)$

$w_{i,k}=\frac{1}{m}\times {\left(-1\right)}^k\frac{s{p}_{i,3-k}}{{\delta }_i},(26)$

${\delta }_i=2\times \sqrt{m+{\left(s{k}_i/2\right)}^2}(27)$

where M_origin (•) is the function for the origin moment of order j and w_ik represents the weights for a given location set.

From Eq. 25, we can obtain the following equations:

$E\left(p_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)=M_{\mathrm{origin}}^1\left(p_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right),(28)$

$V_{om,j}=M_{\text{origin}}^j\left(V\right),j=\mathrm{1,2,3,4,}(29)$

where p_loss is one type of u, V is the PQ node voltage set related to u, and V_om,j is the origin moment of order j.

At this point, we have obtained the objective function formula, that is, (28), using the PPF calculation based on 2PEM. The next problem to address is how to transform PPF results into constrained probabilities. The quadratic fourth-order moment (QFM) estimation method is introduced for this probability transformation by converting 29) into (6). However, the inputs of QFM are central moments. Hence, we convert the origin moments to central moments. It is well known that

${\mu }_j\left(V\right)=E\left\{{\left[V-E\left(V\right)\right]}^j\right\},(30)$

where μ_j (•) is the function for a central moment of order j.

This equation can be used to obtain

${\mu }_1\left(V\right)=0,(31)$

${\mu }_2\left(V\right)=V_{\text{om},2}-V_{\text{om},1}^2,(32)$

${\mu }_3\left(V\right)=V_{\text{om},3}-3V_{\text{om},1}{V}_{\text{om},2}+2V_{\text{om},1}^3,(33)$

${\mu }_4\left(V\right)=V_{\text{om},4}-4V_{\text{om},3}{V}_{\text{om},1}+6V_{\text{om},2}{V}_{\text{om},1}^2-3V_{\text{om},1}^4.(34)$

Remark 3: PEM can be used to quickly and accurately obtain moment information for the output random variables, but Gram-Charlier series fitting is needed to obtain the PDFs of the output random variables. The proposed method combines PEM and QFM in stochastic programming to encompass the advantages of PEM (quick and accurate) and avoid the corresponding disadvantages (series expansion).

Uncertainty Constraint

A method for solving 6) with the QRM and central moments is introduced below. QRM is a theory for estimating failure probability, and we estimate the qualified voltage probability based on the principle that the sum of failure probability and qualified probability is equal to one.

$P_{\mathbf{f}}=1-\alpha ,(35)$

where P_f is the failure probability, which is an unqualified concept.

The limit state function for the voltage amplitude is expressed as:

$Z_i=g\left(V\right)=V_i-V_{-},(36)$

By expanding g (V_i) to a Taylor’s series at V_i*, we obtain the following equation:

$Z_i=g\left({\mathit{V}}_{\mathit{i}}^{\ast }\right)+{\left({\mathit{V}}_i-{\mathit{V}}_{\mathit{i}}^{\ast }\right)}^{\text{T}}\nabla g\left({\mathit{V}}_{\mathit{i}}^{\ast }\right)+\frac{1}{2}{\left({\mathit{V}}_i-{\mathit{V}}_{\mathit{i}}^{\ast }\right)}^{\text{T}}{\nabla }^{2}g\left({\mathit{V}}_{\mathit{i}}^{\mathrm{*}}\right)\left({\mathit{V}}_i-{\mathit{V}}_{\mathit{i}}^{\ast }\right)(37)$

where ∇g (•) is a gradient function and ∇²g (•) is a Hessian matrix function. The moments of Z are

$E\left(Z_i\right)=g\left(V_{\mathbf{om},1}\right)+\frac{1}{2}{\displaystyle \sum _{i=1}^n\frac{{\partial }^{2}g\left(V_{\mathrm{om},1}\right)}{\partial V_i^2}}{\mu }_2\left(V_i\right),(38)$

$\begin{array}{c}{\mu }_2\left(Z_i\right)={{\displaystyle \sum _{i=1}^n\left[\frac{\partial g\left(V_{\mathbf{om},1}\right)}{\partial V_i}\right]}}^2{\mu }_2\left(V_i\right)+{\displaystyle \sum _{i=1}^n\frac{\partial g\left(V_{\mathbf{om},1}\right)}{\partial V_i}\frac{{\partial }^{2}g\left(V_{\mathbf{om},1}\right)}{\partial V_i^2}}{\mu }_3\left(V_i\right)\\ +\frac{1}{4}{{\displaystyle \sum _{i=1}^n\left[\frac{{\partial }^{2}g\left(V_{\mathbf{om},1}\right)}{\partial V_{\mathrm{i}}^{\mathrm{2}}}\right]}}^2\left[{\mu }_4\left(V_i\right)-3{\mu }_2^2\left(V_i\right)\right]\\ +\frac{1}{2}{\displaystyle \sum _{i=1}^n{{\displaystyle \sum _{j=1}^n\left[\frac{{\partial }^{2}g\left(V_{\mathbf{om},1}\right)}{\partial V_i\partial V_j}\right]}}^2{\mu }_2\left(V_i\right){\mu }_2\left(V_j\right)},\end{array}(39)$

$\begin{array}{c}{\mu }_3\left(Z_i\right)={{\displaystyle \sum _{i=1}^n\left[\frac{\partial g\left(V_{\mathbf{om},1}\right)}{\partial V_i}\right]}}^3{\mu }_3\left(V_i\right)\\ +\frac{3}{2}{{\displaystyle \sum _{i=1}^n\left[\frac{\partial g\left(V_{\mathbf{om},1}\right)}{\partial V_i}\right]}}^2\frac{{\partial }^{2}g\left(V_{\mathbf{om},1}\right)}{\partial V_i^2}\left({\mu }_4\left(V_i\right)-3{\mu }_2^2\left(V_i\right)\right)\\ +3{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\frac{\partial g\left(V_{\mathbf{om},1}\right)}{\partial V_i}\frac{\partial g\left(V_{\mathbf{om},1}\right)}{\partial V_j}\frac{{\partial }^{2}g\left(V_{\mathbf{om},1}\right)}{\partial V_i\partial V_j}}{\mu }_2\left(V_i\right){\mu }_2\left(V_j\right),}\end{array}(40)$

$\begin{array}{c}{\mu }_4\left(Z_i\right)={{\displaystyle \sum _{i=1}^n\left[\frac{\partial g\left(V_{\text{om},1}\right)}{\partial V_i}\right]}}^4\left({\mu }_4\left(V_i\right)-3{\mu }_{X2,i}^2\right)\\ +3{\displaystyle \sum _{i=1}^n{{\displaystyle \sum _{j=1}^n{\left[\frac{\partial g\left(V_{\text{om},1}\right)}{\partial V_i}\right]}^2\left[\frac{\partial g\left(V_{\text{om},1}\right)}{\partial V_j}\right]}}^2}{\mu }_2\left(V_i\right){\mu }_2\left(V_j\right),\end{array}(41)$

We change the moments of the voltage amplitude into the moments of voltage amplitude constraints via (38)-(41).

The following formulas no longer limit the number of buses, and a portion of Z is removed. We transform moments to other digital features.

$Z_{\text{standard}}=\sqrt{E\left(Z\right)},(42)$

$csZ=\frac{{\mu }_3\left(Z\right)}{Z_{\text{standard}}^3},(43)$

$ckZ=\frac{{\mu }_4\left(Z\right)}{Z_{\text{standard}}^4},(44)$

where csz is the skewness coefficient and cks is the kurtosis coefficient.

We transform Z to a standard normal vector Y, and the moments of Y are calculated with

${\mu }_j\left(Z\right)={\sigma }^j\left(Z\right)\mathrm{E}\left(Y^j\right),(45)$

where Y is a standard normal vector and σ(•) is the standard deviation function.

From Eq. 42, we can obtain the moments of Y, as follows:

${\mu }_3\left(Z\right)=csZ,(46)$

${\mu }_4\left(Z\right)=ckZ,(47)$

After the second step in the POME approach with four moments, we obtain

${\displaystyle {\int }_{-\infty }^{\infty }{y}^i}pdf\left(y\right)dy={\mu }_j\left(Y\right),(48)$

$pdf\left(y\right)=\exp \left(-{\displaystyle \sum _{j=0}^m{\lambda }_j{y}^j}\right)(49)$

where (48) and (17) have the same form but different physical meanings. By inserting (46), (47), and (49) into Eq. 48, λ_k can be estimated.

P_f can be obtained using pdf(y):

$P_{\text{f}}=P\left(z\le 0\right)={\displaystyle {\int }_{-\infty }^{-\frac{E\left(Z\right)}{Z_{\text{standard}}}}pdf\left(y\right)}dy,(50)$

By inserting Eq. 50 into Eqs 6, 35 can be estimated. The voltage constraints for each node in the distribution network can be solved according to the above formula. Now, both 6) and 11) can be adjusted for a set of specific solutions. PSO in (Fu et al., 2020) is used to find the minimum to 11) while satisfying 6) by searching the solutions of Eqs 2–5.

Remark 4: The voltage probability information is transformed into voltage constraints via the QFM approach, which is a new way to apply PPFs to obtain constraint solutions in stochastic programming.

Simulation

Verification is performed in a step-by-step manner in this study, and the specific examples are as follows. Case 1 verifies the feasibility of estimating confidence levels using central moments from the perspective of pure mathematics, and we show that the QFM approach is suitable for solving the constraint satisfaction probability problem. Case 2 verifies the correctness of the proposed method for estimating different forms of PPF results. Case 3 uses the power quality qualification as a constraint to verify the effectiveness of the proposed method in stochastic programming for distribution networks.

Case 1

The result of the stochastic programming constraint function is a confidence level. The index accompanying the confidence level is the failure probability, which is a common reliability index, and the sum of the two is equal to 1. In using different methods to estimate the variable disqualification probability (i.e., failure probability), we make the following assumptions.

1) X₁ and X₂ are two uncertain variables, both of which obey normal distributions. The reason why we assume a normal distribution is that there are many algorithms that are based on the normal distribution; thus, the effectiveness of the proposed method can be verified. It should be noted that the normal distribution does not have to be used based on the use conditions of the proposed method.

2) We assume that the limit state equation with independent variables X₁ and X₂ is

$\mathbf{Z}={\mathbf{X}}_1-{\mathbf{X}}_2.(51)$

3) The original sample set is shown in Figure 4, and the number of samples is one thousand.

FIGURE 4

FIGURE 4. Original samples studied.

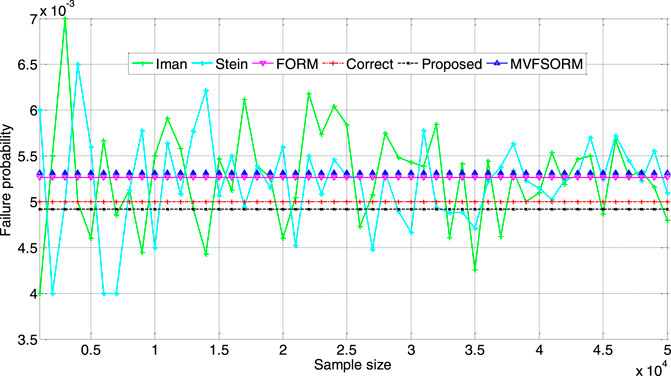
We compared the proposed method (QFM estimation method) with classic, mature and effective methods that have been previously published, including the Iman method in (Iman and Conover, 1982), the Stein method in (Stein, 1987), the first-order reliability method (FORM) in (Sankararaman et al., 2014), and the mean value first-order second moment (MVFSORM) method in (Du and Huang, 2008), as references to verify the proposed method. Considering the need for sampling, the Iman and Stein methods are applied with step size of 100–5,000. The simulation results are shown in Figure 5.

FIGURE 5

FIGURE 5. Failure probability calculated with different algorithms.

The results of different algorithms vary. Compared with those of other algorithms, the results of the proposed method are closest to the real values. The simulation results are related to the information that each algorithm considers and the algorithm design. The usage conditions and input probability information for the different algorithms are shown in Table 1.

TABLE 1

TABLE 1. Input probability information for the different algorithms.

It should be noted that the central moments can be calculated from the mean, standard deviation, skewness, and kurtosis. We can also obtain central moments using origin moments. The mean is an origin moment, and another origin moment (standard deviation, which is the arithmetic square root of the variance) is the second central moment.

The mean and standard deviation are the first two moments. Both MVFSORM and the proposed method do not use a probability distribution function, so they are not limited by a certain probability distribution and have high practical value.

More probability information is used when considering four moments than when considering two moments, so the proposed method based on four moments is more accurate than the MVFSORM method based on two moments. Compared with the Iman, Stein, and FORM methods, the proposed method does not need to solve the probability distribution function. In addition, the Iman and Stein methods are only suitable for the normal distribution, but the proposed method does not have this limitation. When the probability distribution is unknown, the proposed method can still determine the reliability or chance constraint level.

Discussion 1: This case shows how to transform digital features into unqualified probabilities, and qualified probabilities are used in the constraint conditions in stochastic programming. The typical results of PPF calculations are the mean and variance, which are first-order and second-order moments. However, the above results indicate that it is not appropriate to rely only on the mean and variance to estimate unqualified probabilities. Specifically, it is necessary to use additional central moments from the PPF results to estimate the probability of constraint satisfaction in stochastic programming.

Case 2

The main advantage of the proposed method is its computational efficiency. The computing time depends on both the efficiency of the algorithm and the hardware configuration of the computer. The simulations in cases 2 and 3 were performed on a ThinkBook with an Intel(R) Core (TM) i7-1065G7 CPU @ 1.50 GHz and 15.7 GB of available memory.

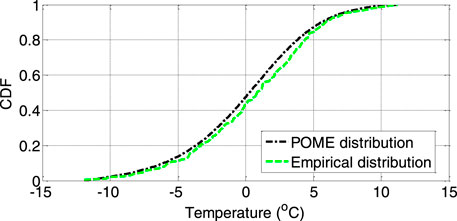
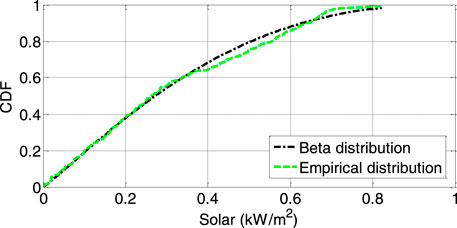
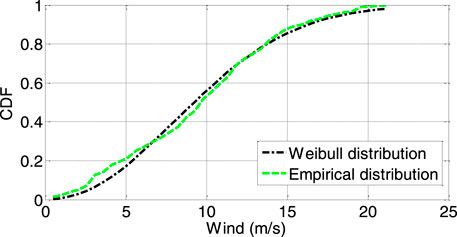
POME is used to describe the cumulative distribution function (CDF) of the ambient temperature, which affects the PV cell temperature. We calculate the Lagrange multipliers of the maximum entropy probability density functions from the knowledge of the four-moment constraints (i.e., the first, second, third and fourth central sample moments of the values at a given ambient temperature). Lambda is a vector containing the resulting Lagrange parameters, and the lambda vector in this case is [2.4003, -0.0447, 0.0292, 0.0008, -0.0001]. The solar radiation that reaches a PV array is simulated using a beta distribution. The maximum likelihood estimates of the parameters of the beta distribution for solar radiation are α = 1.1112 and β = 2.4690. The maximum likelihood estimates for the parameters of the Weibull distribution for wind speed are as follows: scale parameter = 1.1112 and shape parameter = 2.4690.

As shown in Figures 6–8, the POME, beta and Weibull distributions are very similar to the empirical distributions, so the simulated ambient temperature, solar radiation and wind speed values are generally accurate. We use a Gaussian copula to model the correlation among the three weather CDFs. The MC method is used for sampling, and the sample size for sets of weather variables is 10,000.

FIGURE 6

FIGURE 6. CDF of the ambient temperature.

FIGURE 7

FIGURE 7. CDF of solar radiation.

FIGURE 8

FIGURE 8. CDF of wind speed.

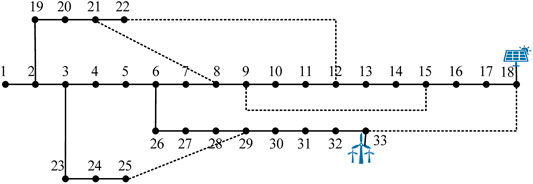
The IEEE 33-bus distribution system from (Baran and Wu, 1989) is used to demonstrate the proposed method. We assume that both the PV and WP rated capacities are 2,000 kW, and the access buses are shown in Figure 9.

FIGURE 9

FIGURE 9. An IEEE 33-bus distribution system.

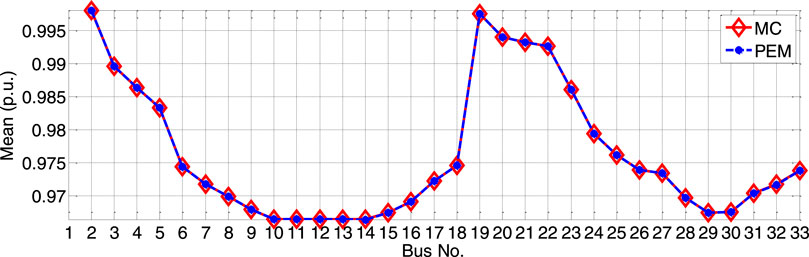
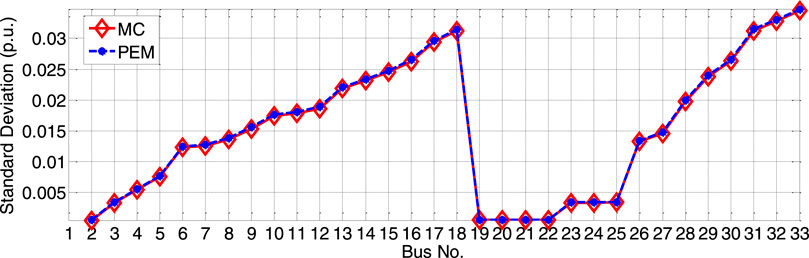
Figures 10, 11 cannot be used to verify the appropriateness of the PEM theory but do verify the suitability of the point PEM formula and the corresponding programming method in this paper. The proposed PEM method provides results that can support subsequent simulation analyses. The MC simulation takes 266.829 s, and the PEM simulation takes 0.147 s; thus, the disadvantage of MC is the comparatively longer computing time.

FIGURE 10

FIGURE 10. Mean value of the elements from bus voltage profiles.

FIGURE 11

FIGURE 11. Standard deviation of the elements from bus voltage profiles.

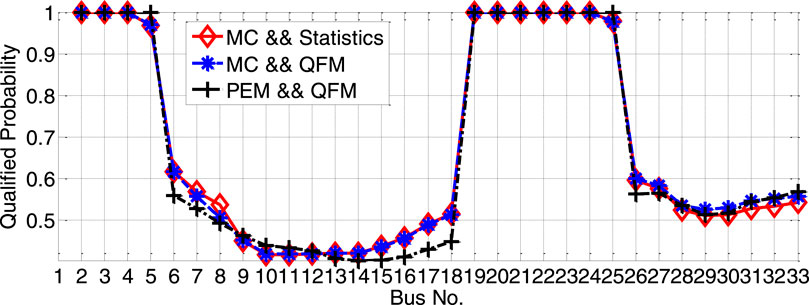
&& stands for logical AND. It should be noted that the proposed method refers to PEM&&QFM. In essence, the proposed method transforms the digital characteristics of PEMs to other digital characteristics that are suitable for stochastic programming. The purpose of assessing the simulation results of MC&&QFM is to verify the accuracy of the QFM approach and the proposed method. As shown in Figure 12, the voltage qualification probability of MC&&QFM is almost the same as that of MC&&Statistics (i.e., direct statistical qualification probability for the voltage amplitude), and it can be used as a reference standard. The voltage qualification probability of PEM&&QFM is close to that of MC&&Statistics.

FIGURE 12

FIGURE 12. Simulation results for the qualified probability of the voltage amplitude.

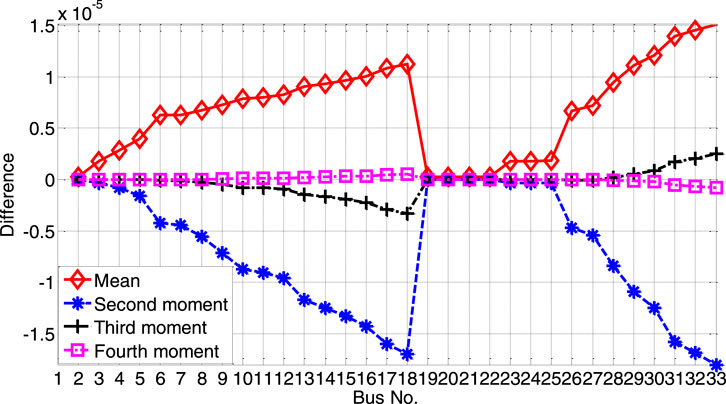
As shown in Figure 13, although the PEM result is very similar to the MC result, there are still some errors associated with the mean value and the second, third and fourth central moments of the voltage amplitude. The errors in the voltage amplitude moments lead to differences in the qualified probability of the voltage amplitude in the MC&&QFM and PEM&&QFM cases, as shown in Figure 12.

FIGURE 13

FIGURE 13. Digital characteristic error of voltage variables.

Discussion 2: We use the maximum entropy principle to transform the quadratic fourth-order moment of the voltage amplitude into probability density function (PDF) information and then solve for the voltage qualification probability. The most important contribution of this paper is the novel PPF results, which include the mean loss and the probability of voltage qualification. These results provide the basis for the stochastic planning of distribution networks because traditional PPF results cannot be used directly in stochastic programming.

Case 3

What we want to verify in this case is the efficiency of achieving a feasible solution to the objective function and constraint functions in programming. To verify the effectiveness of the proposed method, we compare the accuracy of some specific solutions, as listed in Table 2. We assume that the rated capacities of PV and WP are the same, and the access buses are shown in Figure 9.

TABLE 2

TABLE 2. Input simulation results for the objective and constraint functions.

It should be noted that one hundred percent accuracy is logically impossible for an efficient approximation solution algorithm. Stochastic optimal planning allows for certain error margins, and the error problem in power grid dispatching can be solved with this relative approach. It can be concluded that the proposed method supports stochastic programming in distribution networks. The simulation results using PSO are listed in Table 3. Compared with the values in Table 2, the values in Table 3 are better.

TABLE 3

TABLE 3. Optimum planning results.

Discussion 3: We consider mean loss in the objective function in stochastic programming, and the probability of a constraint meeting a certain confidence threshold is a programming constraint based on a quadratic fourth-order moment. Our goal is not to improve the programming algorithm but to improve the efficiency of estimating the probabilistic numerical characteristics of objective functions and constraint functions corresponding to feasible solutions.

The superiorities of the proposed method can be summarized as follows. 1) The results of case 1 show that the proposed QFM method are more precise than other algorithms, and it is not limited by a certain probability distribution. 2) The results of case 2 show that the proposed PEM method spend much less time than MC, but PEM can achieve accuracy levels equivalent to MC. The proposed method can save more than 266 s 3) The results of case 3 show that PPF can be used in uncertainty planning of distributed renewable energy sources in distribution networks. It takes only 4,989 s for optimization solution, and the importance of simplifying the planning model is verified. Compared with the traditional programming methods, we improve the uncertainty planning model rather than the optimization solver.

Conclusion

The mean, variance and probability distribution function are commonly obtained from PPF calculations. However, the conventional PPF calculation results cannot be used to directly solve many actual operation and planning problems. The PPF results in this paper are central moments that are used to model objective and constraint functions in stochastic programming and provide a feasible way to address uncertainty problems in smart grid planning. The essence of uncertain planning is to achieve optimal economic performance under safety constraints. It is reasonable to use different statistical machine learning theories such as PPF, PEM and QFM to obtain probability values for uncertainty planning of distributed renewable energy sources.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XF organized case studies and wrote the manuscript. XW and NL contributed to the theoretical research of this paper. All authors contributed to manuscript, and approved the submitted version.

Funding

This study is supported by the State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (Grant No. LAPS21016), the National Natural Science Foundation of China (Grant No. 52007193), and The 2115 Talent Development Program of China Agricultural University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baran, M. E., and Wu, F. F. (1989). Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing. IEEE Trans. Power Deliv. 4 (2), 1401–1407. doi:10.1109/61.25627

CrossRef Full Text | Google Scholar

Chatthaworn, R., and Chaitusaney, S. (2015). Improving Method of Robust Transmission Network Expansion Planning Considering Intermittent Renewable Energy Generation and Loads. IET Generation, Transm. Distribution 9 (13), 1621–1627. doi:10.1049/iet-gtd.2015.0363

CrossRef Full Text | Google Scholar

Chen, Z., Shi, G., Li, Y., and Fu, X. (2020). “Optimal Planning Method for a Multi-Energy Complementary System with New Energies Considering Energy Supply Reliability,” in 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29-31 May 2020, 952–956. doi:10.1109/aeees48850.2020.9121425

CrossRef Full Text | Google Scholar

Du, X., and Huang, B. (2008). Probabilistic Uncertainty Analysis by Mean-Value First Order Saddlepoint Approximation. Reliability Eng. Syst. Saf. 93 (2), 325–336. doi:10.1016/j.ress.2006.10.021

CrossRef Full Text | Google Scholar

Fu, X., Guo, Q., and Sun, H. (2020). Statistical Machine Learning Model for Stochastic Optimal Planning of Distribution Networks Considering a Dynamic Correlation and Dimension Reduction. IEEE Trans. Smart Grid 11 (4), 2904–2917. doi:10.1109/tsg.2020.2974021

CrossRef Full Text | Google Scholar

Gan, L., Li, G., and Zhou, M. (2016). Coordinated Planning of Large-Scale Wind Farm Integration System and Transmission Network. CSEE Power Energ. Syst. 2 (1), 19–29. doi:10.17775/cseejpes.2016.00005

CrossRef Full Text | Google Scholar

Haghighat, H., and Zeng, B. (2018). Stochastic and Chance-Constrained Conic Distribution System Expansion Planning Using Bilinear Benders Decomposition. IEEE Trans. Power Syst. 33 (3), 2696–2705. doi:10.1109/tpwrs.2017.2751514

CrossRef Full Text | Google Scholar

Iman, R. L., and Conover, W. J. (1982). A Distribution-free Approach to Inducing Rank Correlation Among Input Variables. Commun. Stat. - Simulation Comput. 11 (3), 311–334. doi:10.1080/03610918208812265

CrossRef Full Text | Google Scholar

Injeti, S., and Thunuguntla, V. (2020). Optimal Integration of DGs into Radial Distribution Network in the Presence of Plug-In Electric Vehicles to Minimize Daily Active Power Losses and to Improve the Voltage Profile of the System Using Bioinspired Optimization Algorithms. Prot. Control. Mod. Power Syst 5 (1), 21–35. doi:10.1186/s41601-019-0149-x

CrossRef Full Text | Google Scholar

Jooshaki, M., Farzin, H., Abbaspour, A., Fotuhi-Firuzabad, M., and Lehtonen, M. (2020). A Model for Stochastic Planning of Distribution Network and Autonomous DG Units. IEEE Trans. Ind. Inf. 16 (6), 3685–3696. doi:10.1109/tii.2019.2936280

CrossRef Full Text | Google Scholar

Karaki, S. H., Chedid, R. B., and Ramadan, R. (1999). Probabilistic Performance Assessment of Autonomous Solar-Wind Energy Conversion Systems. IEEE Trans. Energy Convers. 14 (3), 766–772. doi:10.1109/60.790949

CrossRef Full Text | Google Scholar

Li, Z., Wang, J., Sun, H., Qiu, F., and Guo, Q. (2019). Robust Estimation of Reactive Power for an Active Distribution System. IEEE Trans. Power Syst. 34 (5), 3395–3407. doi:10.1109/tpwrs.2019.2902136

CrossRef Full Text | Google Scholar

Lin, C., Bie, Z., Pan, C., and Liu, S. (2020). Fast Cumulant Method for Probabilistic Power Flow Considering the Nonlinear Relationship of Wind Power Generation. IEEE Trans. Power Syst. 35 (4), 2537–2548. doi:10.1109/tpwrs.2019.2959404

CrossRef Full Text | Google Scholar

Liu, C., Lee, C., Chen, H., and Mehrotra, S. (2016). Stochastic Robust Mathematical Programming Model for Power System Optimization. IEEE Trans. Power Syst. 31 (1), 821–822. doi:10.1109/tpwrs.2015.2394320

CrossRef Full Text | Google Scholar

Mohammad-Djafari, A. (1992). “A Matlab Program to Calculate the Maximum Entropy Distributions,” in Maximum Entropy and Bayesian Methods. Editors C.R. Smith, G.J. Erickson, and P.O. Neudorfer (New York, NY, USA: Springer), 221–233. doi:10.1007/978-94-017-2219-3_16

CrossRef Full Text | Google Scholar

Niu, T., Guo, Q., Jin, H., Sun, H., Zhang, B., and Liu, H. (2017). Dynamic Reactive Power Optimal Allocation to Decrease Wind Power Curtailment in a Large‐Scale Wind Power Integration Area. IET Renew. Power Generation 11 (13), 1667–1678. doi:10.1049/iet-rpg.2017.0144

CrossRef Full Text | Google Scholar

Park, H., Baldick, R., and Morton, D. P. (2015). A Stochastic Transmission Planning Model with Dependent Load and Wind Forecasts. IEEE Trans. Power Syst. 30 (6), 3003–3011. doi:10.1109/tpwrs.2014.2385861

CrossRef Full Text | Google Scholar

Ren, Z., Wang, K., Li, W., Jin, L., and Dai, Y. (2017). Probabilistic Power Flow Analysis of Power Systems Incorporating Tidal Current Generation. IEEE Trans. Sustain. Energ. 8 (3), 1195–1203. doi:10.1109/tste.2017.2669139

CrossRef Full Text | Google Scholar

Rohani, G., and Nour, M. (2014). Techno-Economical Analysis of Stand-Alone Hybrid Renewable Power System for Ras Musherib in United Arab Emirates. Energy 64, 828–841. doi:10.1016/j.energy.2013.10.065

CrossRef Full Text | Google Scholar

Roldán, C., Mínguez, R., García-Bertrand, R., and Arroyo, J. M. (2019). Robust Transmission Network Expansion Planning under Correlated Uncertainty. IEEE Trans. Power Syst. 34 (3), 2071–2082. doi:10.1109/TPWRS.2018.2889032

CrossRef Full Text | Google Scholar

Sankararaman, S., Daigle, M. J., and Goebel, K. (2014). Uncertainty Quantification in Remaining Useful Life Prediction Using First-Order Reliability Methods. IEEE Trans. Rel. 63 (2), 603–619. doi:10.1109/tr.2014.2313801

CrossRef Full Text | Google Scholar

Shore, J., and Johnson, R. (1980). Axiomatic Derivation of the Principle of Maximum Entropy and the Principle of Minimum Cross-Entropy. IEEE Trans. Inform. Theor. 26 (1), 26–37. doi:10.1109/tit.1980.1056144

CrossRef Full Text | Google Scholar

Stein, M. (1987). Large Sample Properties of Simulations Using Latin Hypercube Sampling. Technometrics 29 (2), 143–151. doi:10.1080/00401706.1987.10488205

CrossRef Full Text | Google Scholar

Tang, J., Ni, F., Ponci, F., and Monti, A. (2016). Dimension-Adaptive Sparse Grid Interpolation for Uncertainty Quantification in Modern Power Systems: Probabilistic Power Flow. IEEE Trans. Power Syst. 31 (2), 907–919. doi:10.1109/tpwrs.2015.2404841

CrossRef Full Text | Google Scholar

Zhang, C., Chen, H., Liang, Z., Guo, M., Hua, D., and Ngan, H. (2018). Reactive Power Optimization under Interval Uncertainty by the Linear Approximation Method and its Modified Method. IEEE Trans. Smart Grid 9 (5), 4587–4600. doi:10.1109/tsg.2017.2664816

CrossRef Full Text | Google Scholar

Zhang, C., Chen, H., and Ngan, H. (2016). Reactive Power Optimisation Considering Wind Farms Based on an Optimal Scenario Method. IET Generation, Transm. Distribution 10 (15), 3736–3744. doi:10.1049/iet-gtd.2016.0036

CrossRef Full Text | Google Scholar

Zhang, C., Chen, H., Shi, K., Liang, Z., Mo, W., and Hua, D. (2019). A Multi-Time Reactive Power Optimization under Interval Uncertainty of Renewable Power Generation by an Interval Sequential Quadratic Programming Method. IEEE Trans. Sustain. Energ. 10 (3), 1086–1097. doi:10.1109/tste.2018.2860901

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat., 1. doi:10.1109/TIA.2021.3093841 Available at: https://ieeexplore.ieee.org/document/9468931/authors#authors.

CrossRef Full Text | Google Scholar

Zhao, Y., Guo, Y., Guo, Q., Zhang, H., and Sun, H. (2020). Deployment of the Electric Vehicle Charging Station Considering Existing Competitors. IEEE Trans. Smart Grid 11 (5), 4236–4248. doi:10.1109/tsg.2020.2991232

CrossRef Full Text | Google Scholar

Zimmerman, R. D., Murillo-Sanchez, C. E., and Thomas, R. J. (2011). MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 26 (1), 12–19. doi:10.1109/tpwrs.2010.2051168

CrossRef Full Text | Google Scholar