
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 24 December 2021
Sec. Process and Energy Systems Engineering
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.809024
This article is part of the Research TopicAdvanced Technologies for Planning and Operation of Prosumer Energy SystemsView all 111 articles
The integrated energy system is an important strategic direction in the world’s future energy field, which will become the main carrier form of the energy future of human society in the next 30–50 years, directly affecting or even determining the future energy strategy pattern of the world. There are many types of integrated energy system. In the study of optimal dispatching of energy storage, the integrated energy system is modeled according to the energy transmission characteristics of the integrated energy system, which mainly includes the combined cooling, heating and power system and the multi-type energy storage system containing electricity and heat storage. Then, a two-tier optimal scheduling model for an integrated energy system with multiple types of energy storage as the core is established, divided into the day-head scheduling layer and the real-time dispatch layer. At the day-head scheduling layer, an optimization model has been proposed with the minimum cost of the optimization goal and the power network, heating network, cooling network, energy storage operation constraints and carbon constraints as constraints. Then at the real-time dispatch layer, utilize the fuzzy controller to dispatch and control the electric storage system and the thermal storage system. Finally, the verification simulation experiment is carried out in an industrial park. Besides, the energy efficiency, economy and environmental performance before and after the integrated energy system connected to the multi-energy storage device are compared and analyzed, and different scheduling methods are used to compare and prove the advantages of the scheduling method.
Due to historical development, the energy supply systems of electricity, heat and natural gas in most countries are independently planned, designed and operated, lacking coordination and control among each other, resulting in low overall energy utilization efficiency and difficulty in ensuring energy reliability (Zhang et al., 2021).
As a clean, low-carbon, energy-efficient, safe and reliable energy supply system to meet the diverse needs of energy consumers, the integrated energy system has become one of the important measures taken by many countries in the world to deal with energy issues. The integrated energy system is mainly composed of a power network (e.g., power supply, gas supply, and cooling/heat network), the energy exchange link (e.g., CCHP unit, generator, boiler, air conditioner, heat pump), the energy storage link (storage, gas storage and heat storage, cold storage), terminal units and a large number of terminal users (Guerrero et al., 2013). It breaks the existing mode of independent design and operation of each energy system and integrates a variety of energy systems, to realize the overall energy design planning and optimal operation. Due to the fact that the different resource conditions and energy needs, a multi-energy complementary energy system can be built through the coordinated optimization control of the integrated energy system, to improve the consumption of renewable energy, promote the reform of energy structure and achieve the goal of energy conservation and emission reduction. However, as a variety of energy sources can interact with each other, the operation of a single energy system is constrained by its coupling system. Meanwhile, the coupling equipment can also affect the energy flow of the energy systems. Therefore, the optimal operation of IES is considered a non-trivial task that needs to be addressed.
In recent years, the environmental concerns of energy systems have promoted the development of micro-grid, and the rapid deployment of micro-grid accelerates the integration of renewable energy, distributed energy (DERs) and distributed energy storage systems in modern power systems (Injeti and Thunuguntla, 2020; Ming et al., 2020). The existing studies (e.g., (Huang et al., 2021) have well addressed the optimal control of the power systems considering the interconnection with the large-scale renewable sources. Unlike the operational scenarios of large-scale renewable generations, the high share of renewable distributed generation (DG) in microgrids reduces operating costs and carbon dioxide emissions in addition to reducing reliance on fossil fuels. The recovery and utilization of waste heat from cogeneration units have improved the comprehensive utilization efficiency of fuel and significantly improved the economic feasibility of microgrids (Gu et al., 2014). Although renewable distributed generation has many benefits, the intermittency and uncertainty of renewable power generation pose great challenges to the power balance control and reliable operation of microgrids. Considering the scheduling of multi-energy microgrids, the energy flow between distributed energy sources and the load related to electricity, heat, and cold energy further aggravates the complexity of operation and control (Hatziargyriou et al., 2007). Advanced modeling and scheduling techniques, as well as innovative energy storage and management systems, are still needed to fully model the uncertainties and energy flow in multi-energy microgrids. An energy storage system is the key equipment in the comprehensive energy system. It plays an important role in the stable operation and loads transfer of the system. It is of great strategic significance for ensuring the security of the power grid, increasing the proportion of renewable energy, improving energy utilization efficiency and realizing the sustainable development of energy (Katiraei et al., 2008). To effectively manage real-time energy storage of integrated energy systems, two key problems need to be solved: real-time regulation cost assessment and multi-period coordinated scheduling.
To increase the energy efficiency of IES and increase the consumption ratio of renewable energy, existing researches mainly focus on the economic dispatch and optimization operation of IES by combining renewable energy, energy flow characteristics and related coupling equipment. Scheduling generally includes day-ahead scheduling and real-time scheduling (Yang et al., 2019). Day-ahead scheduling refers to making short-term generation plans based on load and renewable generation forecasts. In literature (Piagi and Lasseter, 2006), based on the regional grid connection system of electro-thermal joint dispatching, CPLEX optimization software was used to obtain the optimal output and operation cost of multiple energy sources within the dispatching cycle. The authors in (Qadrdan et al., 2015) considered the thermal dynamic characteristics such as heat pipe transmission time delay and heat loss in the thermal system, as well as the flexibility of users’ heating demands, and established the electric-thermal IES optimal scheduling model. In (Geidl et al., 2007), the work proposed a multi-objective optimization scheduling model of IES on gas-electricity interconnection with electricity to gas and found that the change of natural gas load has a great impact on power system scheduling, and thus affects the system economy and pollution emission. Literature (Kanchev et al., 2011) puts forward a new electric-gas IES optimal scheduling model considering the demand side load response and dynamic natural gas flow and obtains the conclusion that the introduction of response can improve the economy of IES operation. The study in (Mohamed and Koivo, 2010) proposed an IES response mechanism based on the comprehensive demand of electric heating load in the park. The results showed that the application of the comprehensive demand response improved the flexibility of the thermal power production of the micro-grid in the park. These models optimize the charging and discharging modes of energy storage by scheduling 1 day in advance. Energy storage stores energy in off-peak hours when the electricity price is low and returns the energy to the microgrid in peak load hours. The high penetration of renewable energy in a microgrid brings about great power fluctuation. Therefore, it is necessary to track these unpredictable changes in micro-networks through real-time corrective scheduling. In (Ji et al., 2019) - (Jiang et al., 2013), a number of solutions of real-time micro-grid scheduling are studied. The work in (Ji et al., 2019) proposed an energy management approach for real-time scheduling of an MG based on deep reinforcement learning considering the uncertainty of the load demand, renewable energy, and electricity price. In (Abdulgalil et al., 2019), the stochastic programming technique is applied to the optimization algorithm of micro-grid online power generation scheduling. In (Jiang et al., 2013), an agent-based energy management technology is developed, which calculates the cost of the storage system according to the accumulative charging cost of the storage system. However, these methods cannot accurately evaluate the economic benefits of energy storage systems.
As the one-step real-time scheduling method cannot deal with the economic efficiency of energy storage in multiple periods, a two-layer scheduling model is proposed that consists of a day-ahead scheduling layer and a real-time scheduling layer. In (Mahmoodi et al., 2015), day-ahead scheduling formulates economic power generation schemes based on forecast data, and prediction errors are processed by real-time scheduling. The goal of real-time scheduling is to minimize the cost of power regulation and make the real-time scheduling follow the scheduling scheme as much as possible. In (Zhang et al., 2017), in day-ahead scheduling, real-time unbalanced power is mainly matched by energy storage. Energy storage, as an explicit cost and as a function of charge and discharge power (Vasilj et al., 2019), is widely considered in microgrids. In fact, since the energy storage operations are coupled over multiple periods, it cannot be directly used to judge the economic efficiency of energy storage charge and discharge in real-time. In (Paatero and Lund, 2007), from the perspective of real-time operation, two hidden costs of energy storage, namely opportunity cost of discharge and marginal charge cost, are proposed and modeled, to improve the coordination efficiency between energy storage and controllable generator, and a two-layer model of real-time operation of the microgrid is proposed. In (Brekken et al., 2011), a comprehensive day-ahead heating and electric power dispatching model for residential micro-grid is proposed, which considered the economic factors, power supply safety, quality and technical factors and consumer preference under the condition of power market opening. The day-ahead scheduling model is supplemented by the real-time Economic Model Predictive Control (MPC) model, which is used for the scheduling results of subsequent control 1 day in advance. However, in these efforts, there has been no study of multiple sources of energy and electricity, heating and cooling loads.
The main technical contributions can be summarized as follows:
A two-tier scheduling optimization model for integrated energy systems based on energy storage is proposed to deal with the uncertainty of wind and photovoltaic power generation and energy requirements for electricity, heating and cooling.
The developed energy management model consists of a prospective scheduling layer and a real-time scheduling layer. The former optimizes the controllable generator and energy storage system to balance the predicted load, wind power and photovoltaic power generation. The latter is based on the comparison between the actual and predicted values of load and generation after solving the advanced scheduling problem, and the real-time scheduling of electrical and thermal energy storage is carried out by using fuzzy control. This solution effectively combines the power flow and heat transfer equation to model the complex energy flow among power, heating and cooling energy and load. The distributed energy combinations studied include wind turbines, photovoltaic power generation, cell storage devices, gas-fired boilers, heat storage tanks, cogeneration devices, electric freezers and absorption freezers.
The heat storage value in the regenerator is transferred from long-term scheduling to real-time control. Since storage usually presents periodic patterns on its designed time scale, the significantly lower time scale cannot capture these longer phenomena. The combination of scheduling and real-time control can be coordinated to address the energy management challenge.
The reminder of the paper is organized as follows: Section 2 Outlines the proposed physical model of an integrated energy system. Section 3 introduces the two-layer scheduling optimization model, including day-ahead scheduling and real-time scheduling. Section 4 carries on the simulation research. Finally, Section 5 provides the conclusive remarks.
The integrated energy system model is shown in Figure 1. The load demand is formed by the electrical loads, heating loads and cooling loads, where the electrical loads are delivered by the wind turbines, photovoltaic, CHP and battery storage units, the heating loads are supplied by the gas-fired boilers, CHP and thermal storage units, the cooling loads are provided by the electric chillers and absorption chillers. In addition to this, the battery and thermal storage units also have the function of storing electric energy and heat energy during times of extra power production.
1) Power and Heat Output
Considering the complicated dynamic processes of the CHP units (Teleke et al., 2010), we design a simple CHP model without crossover and reheat, which is completely represented by the produced power
where
2) Electrical Energy Storage System
Given the relatively mature battery technology and its advantages of low cost, large capacity, and long-term power supply, it is chosen to be the energy storage unit (Teleke et al., 2010). In consideration of the extremely short time scale of the battery charging/discharging processes, it is generally believed that battery dynamics is instantaneous, therefore a sufficient model of the battery is provided by Equation 3. To monitor the charging and discharging process of the battery, the state of charge (SOC) of the battery is utilized to reflect its remaining energy, with the specific model at time t shown in Eq. 4 (charging state) and Eq. 5 (discharging state).
Where
3) Thermal Energy Storage System
The thermal energy storage system is mainly realized in the form of water storage, which can store temporary excess thermal energy, realize load peak and valley filling, reduce boiler capacity configuration, and improve energy utilization and energy supply security (Demirören et al., 2006). The dynamics of the selected heat storage model are described by (Eq. 6), and it utilizes the stored energy from boilers and CHP (
where
In this work, the proposed two-layer energy management solution for IES is illustrated in Figure 2. It consists of two stages as follows: the day-ahead scheduling and the real-time dispatch. In the first stage, the day-ahead scheduling in the upper level is a stochastic optimal control problem. Based on the predicted cooling, heating and power load, photovoltaic power generation and wind power generation, considering the system dynamics and the uncertainty of prediction, it optimizes the CHP, boilers, energy storage, thermal storage and electric/absorption chillers to determine the submitted power spectrum. In the second stage, the real-time dispatch is a decision-making problem, considering the available actual values of load and power generation and the specified CHP power production. In the low layer, the energy storage and thermal storage are adjusted with the fuzzy control to apply for real-time dispatch.
The day-ahead scheduling aims to solve the CHP-ICE commitment problem of the IES in multiple periods, to determine the status of the CHP-ICE. In the energy scheduling process, the energy storage system cooperates with renewable energy and user energy requirements to achieve optimal energy scheduling in both space and time dimensions. Considering reliability, economy and environmental protection, under the premise of ensuring the reliability of energy supply, achieve the purpose of reducing energy costs and carbon emissions by minimizing the purchase of electricity from the grid and the consumption of the fuel with the increased consumption of renewable energy.
The objective function is formulated as (Eq. 7), which accounts for the fuel costs
where h denotes a collection of fuel-using units, h
Multiple operating constraints are considered in this model to minimize the system cost while ensuring the reliability of the energy supply and meeting the carbon emission target. All these constraints are as follows:
1) Electrical network constraints: The electrical network constraints are composed of the electrical balance constraints (Eq. 13), and CHP operating constraints (Eq. 15)–(Eq. 16). Constraint (Eq. 13) ensures that the power demand, namely electrical loads
where
2) Heating network constraints: The heating network constraints contain the heat balance constraint (Eq. 17) and heat piping capacity constraint (Eq. 18). The constraints (Eq. 17) enforce the power balance between the heat supply and demand, accounting for the boiler heat
where
3) Cooling network constraints: The cooling network constraints are about the cooling power balance constraint (Eq. 19) and the operating temperature constraint (Eq. 20). The constraint (Eq. 19) guarantees the power balance between the cooling power supply and demand, consisting of the output of the absorption chillers, the electric chillers and the cooling load
4) Storage system constraints: The storage system constraints consist of the electrical storage operating constraints and the thermal storage operating constraints, covering the capacity boundary limit (Eq. 21) and charge-discharge rate limit of the storage units (Eq. 22).
where
5) Carbon constraint: Considering that the actual overall carbon emissions should not exceed the prescribed amount, constraint (Eq. 23) restricts the annual carbon emissions (Clerc and Kennedy, 2002). And the regulated amount is obtained by multiplying the specified total carbon emission standard
where
In real-time dispatch, due to the relatively short prediction period, random parameters can be approximated as a scene, and the problem becomes deterministic. In consideration of the power errors between the actual and predicted variety of load and output of photovoltaic and wind turbines, the real-time dispatch aims to utilize the electric storage and thermal storages to perform a corrective dispatch according to the day-ahead scheduling results, to minimize the purchase electricity from grid, satisfy the real demand for the electrical/heating/cooling load and guarantee the basic reliability of energy supply.
In the lower layer, the fuzzy controller is proposed for the IES, which is divided into two steps: the fuzzy control of the thermal storage system and the fuzzy control of the electrical storage system based on the previous step. In the first step, the designed fuzzy controller samples the state of the thermal storage system
In this work, the proposed fuzzy controller for TES is composed of the fuzzy process, inference process and defuzzy process (Bouleimen and Lecocq, 2003).
1) Membership Function and Fuzzy Vectors
The role of membership function (MF) is to quantitatively describe the “fuzziness” of fuzzy sets, so it occupies an important position in fuzzy control. It can be determined by fuzzy statistical method, expert experience method, relative comparison method and neural network method (Jin et al., 2005). And for different ranges of input values, the membership function can be roughly divided into three categories: Z function, S function and Π function, such as the drop semi Cauchy distribution function (Eq. 24), the rise semi Cauchy distribution function (Eq. 25) and the symmetric normal distribution function (Eq. 26) correspond to the cases where the input value in the Universe is small, large and in the middle value respectively.
where
It is wildly known that during the actual deployment process, under the premise of satisfying the completeness of fuzzy control, the fewer the number of fuzzy segmentation of language variables, the fewer the number of fuzzy rules, the lower the complexity of implementation, and the higher the efficiency of the decision-making process. In this work, the input variables
Given any sampling time, the explicit inputs
2) Fuzzy Inferences
In this paper, an improved inference is proposed for the fuzzy decision controller with the export control rules and the fuzzy inference result
where
For the TES fuzzy decision system, the fuzzy control rule base is established with M expert control rules, and the rules are a set of language sentences based on IF-THEN sentences which can be described as: “If
Based on (Eq. 30), the inference result
And the fuzzy implications of each rule
And given the sampling variables, the current state of the system can be further expressed as:
3) Defuzzification
The
4) Establishment of Fuzzy Control General Table
Considering the real-time requirements of the control system, the design stage of the fuzzy controller is usually separated, and the corresponding fuzzy control summary table is established in an offline manner, which can be expressed in the form of a graph (Zhang et al., 2014).
For the ESS fuzzy decision control, it is in some way analogous to the TES fuzzy decision controller design consisting of the fuzzy process, inference process and defuzzy process.
In the fuzzy process, the input variables are composed of the electric storage unit state
The input variable
In the fuzzy inferences process, the EES fuzzy control rule base is set up with N expert control rules, and the total fuzzy implications
In the defuzzification process, the weighted average method to defuzzify is utilized to obtain the output
In this section, small-scale terminal integrated energy systems such as microgrids are selected as the simulation verification object to evaluate and verify the effectiveness of the proposed two-layer model.
The studied microgrid system includes CHP, gas boilers, distributed renewable energy represented by photovoltaics and wind turbines, electric storage and thermal energy storage, absorption refrigerator and electric refrigerator, whose parameters are shown in Table 1. In addition, there are four internal combustion engines in the integrated energy system with the minimum load rate of 0.3, the rated power capacity of a single internal combustion engine is 125kW, the operation and maintenance cost is 7.8$/MWh; the electric energy storage device adopts the lithium iron phosphate battery model, and the self-discharge rate is 0.04, the state of charge is 0.2–0.9; the heat storage tank is selected as the thermal energy storage device, the self-heat release rate is 0.1, the upper limit of the energy storage level is 0.9, and the lower limit of the energy storage level is 0.2. The CO2 emission coefficient of the electricity purchased from the large power grid is 889$/MWh, and the fuel price of CHP and boiler is 0.0569$/kWh.
The power generation of PV and wind, the demand and pricing profiles are obtained from1,2,3. In this study, the curves of the forecasting data are illustrated in Figure 3 on a typical winter day, consisting of the day-ahead power load, heat load and cooling load, PV and WT generation obtained by the time series forecasting method and the electricity price equal to the expected price. Among them, the electric load, photovoltaic and wind are predicted by the improved genetic algorithm neural network model, which not only classifies the local weather and environment but also considers the factors affecting solar and wind power generation, to optimize the error and adjust the parameters. To ensure the accuracy of prediction, heating load and cooling load are indirectly predicted through physical forecasting models. For instance, heating load is predicted by an equivalent thermal parameter model in the case of determining the comfortable range of indoor temperature, grasping the outdoor temperature of the day through weather forecast, and utilizing the coupling relationship between temperature difference and heating load are used. The electricity price is to predict the specific expected electricity value at each forecast time point through the time series method, and the current price is estimated by combining the previous price and the history of external factors including electricity and weather.
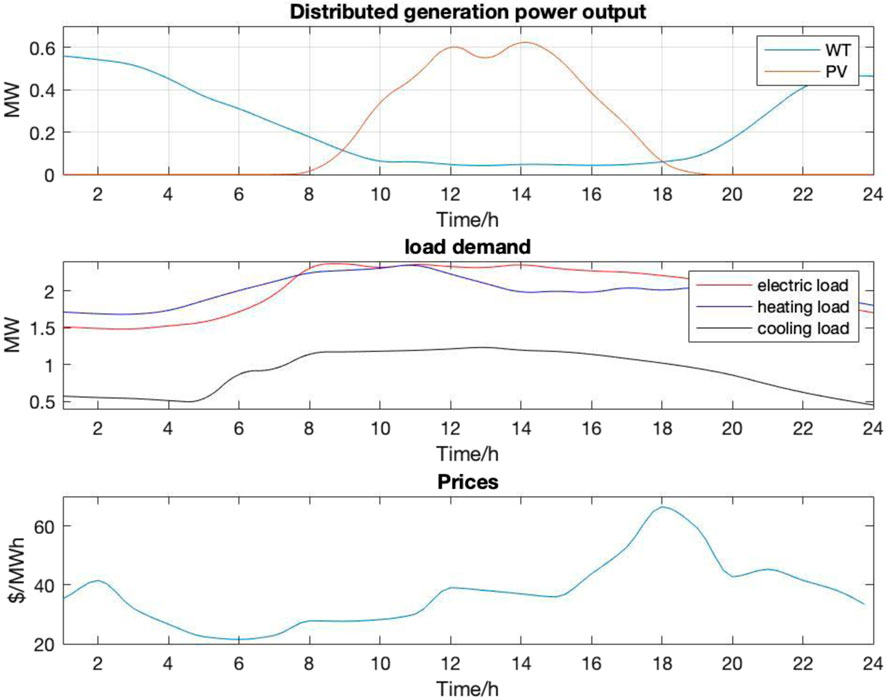
FIGURE 3. The day ahead electric load, heating load, cooling load, generation, WT, and prices forecasting.
In this paper, the design and implementation of fuzzy decision controllers are constructed as follows to realize the proposed energy dispatch solution. For the TES fuzzy design controller, the state of the thermal storage system
The design of control rules is important for the performance of fuzzy decision-making schemes. Based on the design presented in Section 3, the principles of energy dispatch are described as follows:
1) Considering different time scales, TES fuzzy control is once an hour, and ESS fuzzy control is once every 15 min.
2) When the output of the CHP and the gas boiler meet the thermal load demand, the excess energy is absorbed by the heat storage; when the CHP and the boiler meet the thermal load demand and the surplus is significant, if the cooling load deficit is significant, give priority to supplying absorption chillers, otherwise, the heat storage Prioritize energy absorption.
3) When the CHP and boiler cannot meet the heat load demand, if the cooling load surplus is significant, the lack of heat load is obtained by reducing the input of the absorption chiller, otherwise, the lack of heat load is first provided by the heat storage; when the CHP and boiler cannot When the thermal load demand is met and the shortage is obvious the thermal storage releases energy;
4) When CHP, PV and WT meet the demand of electric load and electric refrigerator, the excess energy is absorbed by electric storage; when CHP, PV and WT meet the demand of electric load and electric refrigerator and the surplus is significant, if the real-time electricity price is lower If it is high, it will be sold to the grid first, otherwise the excess energy will be absorbed by the electricity storage first;
5) When CHP, PV and WT cannot meet the demand of electric load and electric refrigerator, the electric storage releases energy; when CHP, PV and WT cannot meet the demand of electric load and electric refrigerator and the shortage is high if the real-time electricity price is higher if it is low, it will give priority to purchasing from the grid, otherwise it will give priority to the release of energy from electric storage;
6) When the remaining energy of the energy storage is low, even if the energy supply is insufficient, the energy storage will not discharge; when the energy storage state is high, even if the energy supply is excessive, the energy storage will not charge; this can effectively prevent overcharging of the energy storage or over-discharge.
The above principles aim to maximize economic efficiency and the penetration rate of renewable energy. The control rules of all scheduling principles (case #1∼#6) are shown in Table 2 and Table 3 respectively with their control surfaces shown in Figure 5 and Figure 6.
According to the scheduling strategy in this paper, the simulation scheduling results are shown in Figures 7, 8, 9. In winter, the heat load and electric load are mainly concentrated at night, which is the opposite of the time when renewable energy sources concentrate on providing electric power during the day. However, the energy storage system can transfer energy in two dimensions, space-time and space, so the excess energy is stored first and then released when users need it, thereby increasing the consumption rate of renewable energy.
The electric load is provided by a mixture of wind turbines, photovoltaic generators, CHP, battery units and large grids, while the power demand is composed of the main electric load and the energy consumed by the electric refrigerator. The optimized dispatch results are shown in Figure 7. In winter, the number of hours during the day is significantly reduced, resulting in a reduction in photovoltaic power generation, which is offset by greater wind power generation throughout the day. At night when the real-time electricity price is at a valley value, wind resources are abundant, the output power of the gas generator in the CHP is small, and the electrical load is mainly provided by the power purchase from the grid through wind power generation and the system. At this time, the real-time electricity price is low. When the wind energy output cannot meet the demand, the system first purchases surplus electric energy from the grid for power supply, and stores the surplus electric energy in the electric storage device. In the daytime, the electricity price is at the level and peak stage, the output power of gas generators is relatively large, and the power load of the system is mainly provided by CHP, photovoltaic and wind power output. The peaks of grid electricity prices appear from 9 to 12 am and from 6 to 9 pm, so the electric energy storage system mainly releases energy in these two time periods to meet user needs. In the period from 9 am to 12 o’clock, the grid electricity price reaches its peak, but the user’s electrical load demand is not high, so the system sells part of the stored electricity to the large grid to achieve low storage and high power arbitrage. In the period from 6 to 9 in the afternoon, the grid electricity price reaches its peak and the electricity demand also reaches the maximum. Due to the limitation of the rated discharge power, the energy storage system can only release a limited amount of electrical energy per unit time, which cannot fully meet the current user’s needs. Demand, so users still need to buy electricity from the large grid.
The heat load is provided by the waste heat generated by the gas boiler and the CHP system. The heat demand mainly includes the heat load and the heat load consumption required for the energy supply of the absorption chiller. The optimal scheduling of the heat power is shown in Figure 8. The heat recovery of cogeneration is related to the power distribution and heating method of the integrated energy system. The heat demand in winter is much higher than in summer, and the combined heat and power system and boilers operate all day to meet the high demand for heat. At night, the heat load demand is very large, mainly provided by the boiler, the gas generator plays an auxiliary role, and the thermal energy storage system releases the stored energy to play a regulatory role. During the day, the heat load of the system is mainly provided by gas generators, and gas boilers play an auxiliary role. If there are surplus energy, the thermal energy storage system converts and stores energy. Between two o’clock and five o’clock in the afternoon, the heat load demand is small, and the thermal energy storage system absorbs energy for storage. From five to eight in the evening, as the temperature decreases, the heat load demand reaches a peak, and the thermal energy storage system continues to release energy to ensure a reliable supply of thermal energy. In the whole process, the effect of peak shaving and valley filling of the thermal energy storage system is more obvious.
The cooling load is mainly provided by electric refrigerators and absorption refrigerators, and the optimal scheduling results are shown in Figure 9. Generally speaking, considering that the energy efficiency ratio of electric refrigerators is much greater than that of absorption refrigerators if the electric refrigerators can provide the total load, the absorption refrigerators will be turned off and the energy consumption will be zero. Otherwise, the unsatisfied cooling load will be provided by the absorption chiller. Compared with summer, the refrigeration demand on cloudy days in winter is significantly lower, so only electric refrigerators can meet the refrigeration requirements, without the need for absorption chillers.
In this section, to illustrate the importance of multiple types of energy storage technology in an integrated energy system, it is compared with a multi-energy microgrid without energy storage. At the same time, to illustrate the effectiveness of the two-tier scheduling model proposed in this chapter, it is compared with the other two scheduling methods commonly used in the existing literature.
For energy systems, energy efficiency, economy and environmental protection are significant evaluation indicators. Therefore, for the above-mentioned integrated energy system, the performance of the stripped energy storage device is compared and analyzed in the same environment.
Here, the energy utilization efficiency is calculated based on the consumption rate of renewable energy, and the ratio of the consumption of renewable energy to the total output of renewable energy is utilized as the energy utilization efficiency index; the economic index only considers the operation and maintenance cost of the integrated energy system, which mainly includes the cost of purchasing electricity from the large power grid and the operation and maintenance cost of the system. The environmental protection index is to consider the carbon dioxide emissions caused by the operation of the system, mainly considering the carbon dioxide emissions caused by the power purchase of the large grid and the fuel consumption of the cogeneration system. The comparison results can be seen in Table 4.

TABLE 4. Performance comparison of integrated energy systems before and after access to multiple types of energy storage.
It can be observed that the integrated energy system connected to the energy storage device has a better economy and environmental protection, and its renewable energy consumption rate has also been improved. Compared with the system without energy storage, the integrated energy system with an energy storage device can store the excess energy when the energy is abundant and supply it when needed later, which greatly improves the energy consumption rate; therefore, it reduces the cost of purchasing electricity from the large grid during the operation of the system, and can even sell it to the grid when the electricity price is high when the price of energy storage electricity is low, which has better economic efficiency; the power supply of the large grid is mainly thermal power generation and carbon emissions. The energy storage system increases the consumption rate of renewable energy on the one hand, and on the other hand reduces the purchase of electricity from the large power grid, which greatly reduces carbon emissions.
To intuitively reflect the advantages of the proposed two-tier scheduling model, two common scheduling methods are selected for comparison. The first comparison method is day-ahead scheduling. Based on a multi-objective optimal scheduling model, the forecast data is used to obtain the best output and operating cost of multiple energy sources within the scheduling period. The second comparison method is real-time scheduling, which uses the fuzzy control method to schedule the energy storage system based on real-time data. The simulation result is shown in Figure 10.
It is shown that the method proposed outperforms method 1 and comparison method 2, and has lower operating costs. For instance, when the root mean square error of load forecasting is 10%, the total operating cost of the two-tier optimization model is $1,726, which is lower than the total operating cost of Comparative Method 1 and Method 2 with $1772 and $1745, respectively. As the load forecasting error increases, the economic benefits of this method become more and more significant.
This paper proposes a two-tier scheduling optimization model for an integrated energy system based on energy storage to deal with the uncertainty of wind power and photovoltaic power generation and the energy demand for electricity, heating and cooling. The model consists of a forward-looking dispatch layer and a real-time dispatch layer and considers the different time scales of electric storage and thermal storage. The upper-level advanced dispatch optimizes the CHP and energy storage system to balance the predicted load, wind power and photovoltaic power. The lower-level real-time dispatch uses fuzzy control to dispatch electric energy storage and thermal energy storage in a real-time fashion based on the comparison of actual load and predicted power generation. To verify the effectiveness of the proposed scheduling model, a case study was carried out based on a microgrid test system. It is confirmed that the proposed solution can fully utilize the flexibility of renewable energy and energy storage system to adjust the peak load of the system while ensuring the balance of energy supply and demand of the system, optimize the period of renewable energy utilization, and effectively reduce the energy cost of users, improve the energy utilization efficiency.
The scheduling scheme proposed in this work provides a feasible solution for realizing a low-cost and low-carbon integrated energy system. On this basis, future research directions and challenges are proposed. The energy storage system scheduling strategy adopted in this paper relies on real-time electricity prices, but the coupling relationship between real-time electricity prices and demand-side response is not considered, and it is only used as a lever to regulate the scheduling of energy storage systems. The proposed solution still needs to be further investigated to promote its performance. A number of research directions are considered worth further research effort. The future work can study real-time electricity prices based on this article, adding dynamic real-time electricity prices. With the continuous development of the integrated energy system, pilot projects can be established to apply the above simulation results in actual scenarios, and combine actual operating conditions to further improve the model. In addition, considering the rise of flexible loads, e.g., smart home appliances and electric vehicles, reasonable control of demand-side response is required to retain the social and economic benefits brought by the balance of supply and demand and also meet the maximization of users’ energy efficiency and minimization of costs.
Publicly available datasets were analyzed in this study. This data can be found here: http://energyalmanac.ca.gov/renewables/solar/pv.html.
QG and MY conceived and designed the experiments; XZ and MY performed the experiments and analyzed the data; XC, HZ, and MY contributed reagents/materials/analysis tools; QY and MY wrote the paper.
This work is supported in part by the Science and Technology Project of State Grid Zhejiang Electric Power Co., Ltd. (5211TZ 1900S5) and the Fundamental Research Funds for the Central Universities (Zhejiang University NGICS Platform).
QG, XZ, and HZ were employed by the company State Grid Zhejiang Electric Power Co. Ltd., Taizhou Power Supply Company.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1Electricity price and demand, AEMO (Online). Available: http://www.aemo.com.au/Electricity/Data/Price-and-Demand
2The California Energy Almanac (Online). Available: http://energyalmanac.ca.gov/renewables/solar/pv.html
3Wind power (Online). Available: http://www.thewindpower.net/
Abdulgalil, M. A., Khalid, M., and Alismail, F. (2019). Optimal Sizing of Battery Energy Storage for a Grid-Connected Microgrid Subjected to Wind Uncertainties. Energies 12 (12), 2412. doi:10.3390/en12122412
Bouleimen, K., and Lecocq, H. (2003). A New Efficient Simulated Annealing Algorithm for the Resource-Constrained Project Scheduling Problem and its Multiple Mode Version. Eur. J. Oper. Res. 149 (2), 268–281. doi:10.1016/s0377-2217(02)00761-0
Brekken, T. K. A., Yokochi, A., Jouanne, A. V., Yen, Z. Z., Hapke, H. M., and Halamay, D. A. (2011). Optimal Energy Storage Sizing and Control for Wind Power Applications. IEEE Trans. Sustain. Energ. 2 (1), 69–77. doi:10.1109/TSTE.2010.2066294
Clerc, M., and Kennedy, J. (2002). The Particle Swarm - Explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Trans. Evol. Computat. 6, 58–73. doi:10.1109/4235.985692
Demirören, A., Zeynelgil, H. L., and Sengör, S. N. (2006). The Application of Neural Network Controller to Power System with SMES for Transient Stability Enhancement. Int. Trans. Electr. Energ. Syst. 16 (6), 629–646.
Geidl, M., Koeppel, G., Favre-Perrod, P., Klockl, B., Andersson, G., and Frohlich, K. (2007). Energy Hubs for the Future. IEEE Power Energ. Mag. 5 (1), 24–30. doi:10.1109/mpae.2007.264850
Gu, W., Wu, Z., Bo, R., Liu, W., Zhou, G., Chen, W., et al. (2014). Modeling, Planning and Optimal Energy Management of Combined Cooling, Heating and Power Microgrid: A Review. Int. J. Electr. Power Energ. Syst. 54, 26–37. doi:10.1016/j.ijepes.2013.06.028
Guerrero, J. M., Chandorkar, M., Lee, T.-L., and Loh, P. C. (2013). Advanced Control Architectures for Intelligent Microgrids-Part I: Decentralized and Hierarchical Control. IEEE Trans. Ind. Electron. 60, 1254–1262. doi:10.1109/tie.2012.2194969
Hatziargyriou, N., Asano, H., Iravani, R., and Marnay, C. (2007). Microgrids. IEEE Power Energ. Mag. 5, 78–94. doi:10.1109/mpae.2007.376583
Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for VSC-HVDC Connected Offshore Wind Farm. IEEE Trans. Ind. Inf. 17, 8165–8176. doi:10.1109/TII.2021.3065375
Injeti, S. K., and Thunuguntla, V. K. (2020). Optimal Integration of DGs into Radial Distribution Network in the Presence of Plug-In Electric Vehicles to Minimize Daily Active Power Losses and to Improve the Voltage Profile of the System Using Bioinspired Optimization Algorithms. Prot. Control. Mod. Power Syst. 5 (1), 21–35. doi:10.1186/s41601-019-0149-x
Ji, Y., Wang, J., Xu, J., Fang, X., and Zhang, H. (2019). Real-Time Energy Management of a Microgrid Using Deep Reinforcement Learning. Energies 12 (12), 2291. doi:10.3390/en12122291
Jiang, Q., Xue, M., and Geng, G. (2013). Energy Management of Microgrid in Grid-Connected and Stand-Alone Modes. IEEE Trans. Power Syst. 28 (3), 3380–3389. doi:10.1109/tpwrs.2013.2244104
Jin, H., Hong, H., Wang, B., Han, W., and Lin, R. (2005). A New Principle of Synthetic cascade Utilization of Chemical Energy and Physical Energy. Sci. China Ser. E 48 (2), 163–179. doi:10.1360/04ye0234
Kanchev, H., Lu, D., Colas, F., Lazarov, V., and Francois, B. (2011). Energy Management and Operational Planning of a Microgrid with a PV-Based Active Generator for Smart Grid Applications. IEEE Trans. Ind. Electron. 58 (10), 4583–4592. doi:10.1109/tie.2011.2119451
Katiraei, F., Iravani, R., Hatziargyriou, N., and Dimeas, A. (2008). Microgrids Management. IEEE Power Energ. Mag. 6, 54–65. doi:10.1109/mpe.2008.918702
Mahmoodi, M., Shamsi, P., and Fahimi, B. (2015). Economic Dispatch of a Hybrid Microgrid with Distributed Energy Storage. IEEE Trans. Smart Grid 6 (6), 2607–2614. doi:10.1109/tsg.2014.2384031
Ming, H., Xia, B., Lee, K-Y., Adepoju, A., Srinivas, S., and Xie, L. (2020). Prediction and Assessment of Demand Response Potential with Coupon Incentives in Highly Renewable Power Systems. Prot. Control. Mod. Power Syst. 5 (2), 124–137. doi:10.1186/s41601-020-00155-x
Mohamed, F. A., and Koivo, H. N. (2010). System Modelling and Online Optimal Management of MicroGrid Using Mesh Adaptive Direct Search. Int. J. Electr. Power Energ. Syst. 32 (5), 398–407. doi:10.1016/j.ijepes.2009.11.003
Paatero, J. V., and Lund, P. D. (2007). Effects of Large-Scale Photovoltaic Power Integration on Electricity Distribution Networks. Renew. Energ. 32 (2), 216–234. doi:10.1016/j.renene.2006.01.005
Piagi, P., and Lasseter, R. H. (2006). Autonomous Control of Microgrids. Montreal: IEEE Power Eng. Soc. Gen. Meet., 1–6.
Qadrdan, M., Abeysekera, M., Chaudry, M., Wu, J., and Jenkins, N. (2015). Role of Power-To-Gas in an Integrated Gas and Electricity System in Great Britain. Int. J. Hydrogen Energ. 40 (17), 5763–5775. doi:10.1016/j.ijhydene.2015.03.004
Teleke, S., Baran, M. E., Bhattacharya, S., and Huang, A. Q. (2010). Optimal Control of Battery Energy Storage for Wind Farm Dispatching. IEEE Trans. Energ. Convers. 25 (3), 787–794. doi:10.1109/tec.2010.2041550
Turton, H., and Moura, F. (2008). Vehicle-to-grid Systems for Sustainable Development: An Integrated Energy Analysis. Technol. Forecast. Soc. Change 75 (8), 1091–1108. doi:10.1016/j.techfore.2007.11.013
Vasilj, J., Gros, S., Jakus, D., and Zanon, M. (2019). Day-Ahead Scheduling and Real-Time Economic MPC of CHP Unit in Microgrid with Smart Buildings. IEEE Trans. Smart Grid 10 (2), 1992–2001. doi:10.1109/tsg.2017.2785500
Yang, Y., Bremner, S., Menictas, C., and Kay, M. (2019). A Mixed Receding Horizon Control Strategy for Battery Energy Storage System Scheduling in a Hybrid PV and Wind Power Plant with Different Forecast Techniques. Energies 12 (12), 2326. doi:10.3390/en12122326
Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat. 2021, 1. doi:10.1109/TIA.2021.3093841
Zhang, X., Karady, G. G., and Ariaratnam, S. T. (2014). Optimal Allocation of CHP-Based Distributed Generation on Urban Energy Distribution Networks. IEEE Trans. Sustain. Energ. 5 (1), 246–253. doi:10.1109/tste.2013.2278693
Zhang, Z., Wang, J., and Ding, T. (2017). A Two-Layer Model for Microgrid Real-Time Dispatch Based on Energy Storage System Charging/Discharging Hidden Costs. IEEE Trans. Sustain. Energ. 8, 33. doi:10.1109/TSTE.2016.2577040
Keywords: multi-energy storage technology, integrated energy system, two-layer scheduling, fuzzy control, energy dispatch
Citation: Gao Q, Zhang X, Yang M, Chen X, Zhou H and Yang Q (2021) Fuzzy Decision-Based Optimal Energy Dispatch for Integrated Energy Systems With Energy Storage. Front. Energy Res. 9:809024. doi: 10.3389/fenrg.2021.809024
Received: 04 November 2021; Accepted: 26 November 2021;
Published: 24 December 2021.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Xueqian Fu, China Agricultural University, ChinaCopyright © 2021 Gao, Zhang, Yang, Chen, Zhou and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qiang Yang, cXlhbmdAemp1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.