Ridwan O. Agbaoye1*
Sherifdeen Bolarinwa2
Kolawole Olubunmi Akiode3
Abibat A. Adekoya-Olowofela4
Lateefat Modupe Habeeb5
Omolola Myriam Balogun1
Paul O. Adebambo6
Stephane Kenmoe7*
Gboyega A. Adebayo6*- 1Applied Science Department, Federal College of Dental Technology and Therapy Enugu, Enugu, Nigeria
- 2Department of Physics, King Abdul Aziz University, Jeddah, Saudi Arabia
- 3Department of Chemistry, Federal University of Agriculture, Abeokuta, Nigeria
- 4Department of Physics, University of South Florida, Tampa, FL, United States
- 5Environmental Health Science Department, Kwara State University, Malete, Nigeria
- 6Department of Physics, Federal University of Agriculture, Abeokuta, Nigeria
- 7Department of Theoretical Chemistry, University of Duisburg-Essen, Essen, Germany
The search for stable and highly efficient solar cell absorbers has revealed interesting materials; however, the ideal solar cell absorber is yet to be discovered. This research aims to explore the potentials of dimethylammonium lead iodide (CH3NH2CH3PbI3) as an efficient solar cell absorber. (CH3NH2CH3PbI3) was modeled from the ideal organic–inorganic perovskite cubic crystal structure and optimized to its ground state. Considering the spin-orbit coupling (SOC) effects on heavy metals, the electronic band structure and bandgaps were calculated using the density functional theory (DFT). In contrast, bandgap correction was achieved by using the GW quasiparticle methods of the many-body perturbation theory. The optical absorption spectra were calculated from the real and imaginary dielectric tensors, which are determined by solving the Bethe–Salpeter equations of the many-body perturbation theory. Spin-orbit coupling induces band splitting and bandgap reduction in both DFT and GW methods, while the GW method improves the DFT bandgap. We report a DFT band gap of 1.55 eV, while the effect of spin-orbit coupling reduces the bandgap to 0.50 eV. Similarly, the self-consistent GW quasiparticle method recorded a bandgap of 2.27 eV, while the effect of spin-orbit coupling on the self-consistent GW quasiparticle method reported a bandgap of 1.20 eV. The projected density of states result reveals that the (CH3NH2CH3PbI3) does not participate in bands around the gap, with the iodine (I) p orbital and the lead (Pb) p orbital showing most prominence in the valence band and the conduction band. The absorption coefficient reaches 106 in the ultraviolet, visible, and near-infrared regions, which is higher than the absorption coefficient of CH3NH3PbI3. The spectroscopic limited maximum efficiency predicts a high maximum efficiency of about 62% at room temperature and an absorber thickness of about 10–1 to 102 μm, suggesting that (CH3NH2CH3PbI3) has an outstanding prospect as a solar cell absorber.
1 Introduction
The ability to explore materials for different technological applications allows us to improve the efficiency of various materials. Amongst these applications, materials are engineered to have a high figure of merits for viable thermoelectric generators (He et al., 2015; Adebambo et al., 2021; Jouhara et al., 2021), which can efficiently convert heat energy to electricity. Similarly, material engineering has the potential of discovering catalysts (Zhao et al., 2021a; Wang et al., 2021) which will reduce the activation barrier and speed up the rate of chemical reactions. For solar cell applications, materials could be engineered to scale up the power conversion efficiency. In all of these applications, the stability of these materials at varying temperatures, humidity, and other environmental conditions needs to be improved to withstand varying environmental conditions and enhance longevity (Aftab and Ahmad, 2021; Baranowska-Korczyc et al., 2021; Cha and Wu, 2021). For decades, a lot of success has been achieved from experimental and theoretical research in power generation from solar cells. Among these successes is the increased power conversion efficiency, from 4% to a maximum efficiency of 38.9% (Mancini et al., 2016; Akman et al., 2021; Zhao et al., 2021b; Zhang et al., 2021). A fascinating family of materials that plays a significant role in the increment of solar cell efficiency is the perovskite material (Park, 2016; Akman et al., 2021; Zhao et al., 2021a; Zhang et al., 2021). Alongside perovskites’ increased power conversion efficiency, inorganic and hybrid perovskites with a general formula, ABX3, have hundreds of thousands of members as the A and B sites are filled with monovalent and divalent cations, while the X site is filled with either oxides or halides, allowing experimental and computational screening of potentials materials for solar cell absorbers and other technological applications. The success of perovskite materials is primarily attributed to the high carrier mobility, strong broadband absorption, long electron-hole diffusion length, design flexibility, and bandgap tunability of the absorbing materials (Kojima et al., 2009; Stoumpos et al., 2013; Snaith et al., 2014; Yin et al., 2014; Christians et al., 2015; Snaith and Hacke, 2018). Bandgap engineering is a well-demonstrated approach for modulating the power conversion efficiency of hybrid perovskites by substituting the X site element with other halides to form a mixed halide alloy (Hao et al., 2014; Ogomi et al., 2014; Mancini et al., 2015). Conversely, altering the A-site composition in a stoichiometric approach enhances the bandgap (Eperon et al., 2014). However, efforts to replace the A site in the ABX3 perovskite compound (Im et al., 2012; Stoumpos et al., 2015) have served as a playground for further insights into the search for highly efficient perovskite materials. Lately, the quest for a stable and more efficient solar cell absorber has birthed the use of
2 Computational Procedure
The CH3NH2CH3PbI3 structure was modeled after the ideal cubic perovskite structure, where the lead (Pb) atom occupies the (0.0, 0.0, 0.0) position, the iodine (I) atoms occupy the (0.5, 0.0, 0.0), (0.0, 0.5, 0.0), and (0.0, 0.0, 0.5) positions in units of lattice vectors, while the dimethylammonium cation (CH3NH2CH3)+ was placed in the middle of the cubic cage at (0.5, 0.5, 0.5) (Agbaoye et al., 2020; Agbaoye et al., 2021). The final structure is such that the NH2 points toward the upper part of the cubic cage, while the two CH3 arms point downward toward the sides of the cubic cage. In order to describe the dispersion forces, energy, and structure of the system accurately (Barone et al., 2009), the van der Waals interaction between the dimethylammonium molecule and the cubic cage was treated with the grimme-d2 semiempirical van der Waals correction (Grimme, 2006; Barone et al., 2009). The stable crystal structure of (CH3)2NH2PbI3 was achieved by optimizing the cut-off for the wavefunction to 115 Ry, and then kpoint optimization shows that the 16 × 16 × 16 Monkhorst–Pack kpoint mesh (Monkhorst and Pack, 1976) is sufficient to describe the system, while at minimum energy, a lattice parameter of 6.20 Å was achieved. The most stable pseudo-cubic structure is achieved using the Broyden–Fletcher–Goldfarb–Shannon quasi-newton algorithm (Shanno, 1970), which relaxed the position of atoms and the size of the lattice. The density functional theory (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) and the GW quasiparticle (Marini et al., 2009; Sangalli et al., 2019; Rangel et al., 2020) band structure were performed using the Perdew–Burke–Enzenhoff (Perdew et al., 1992; Perdew et al., 2008) exchange-correlation functional of the generalized gradient approximation (Perdew and Yue, 1986; Perdew et al., 1996) as implemented in the quantum espresso package (Scandolo et al., 2005; Giannozzi et al., 2009). The band structures are calculated along the Gamma (0.00, 0.00, 0.00); X (0.00, 0.50, 0.00); M (0.50, 0.50, 0.00); G (0.0, 0.0, 0.0); R (0.50, 0.50, 0.50); and X (0.00, 0.50, 0.00) high symmetry points, while the projected density of states was calculated using the tetrahedra method (Blöchl et al., 1994). A denser Monkhorst–Pack kpoint mesh of 20 × 20 × 20 and 12 × 12 × 12 was used to calculate the density of states in the non–spin-orbit calculation and the spin-orbit calculations, respectively (Monkhorst and Pack, 1976). The non–spin-orbit and the spin-orbit coupling–based calculations (lattice optimizations, variable cell relaxation, electronic band structures, density of states, and optical absorption spectra) were carried out using the norm-conserving Troullier–Martins (Troullier and Martins, 1991a; Troullier and Martins, 1991b) scalar relativistic pseudopotentials (Pb.pbe-n-nc.UPF, I.pbe-n-nc.UPF, C.pbe-nc.UPF, H.pbe-n-nc.UPF, and N.pbe-nc.UPF) and the fully relativistic pseudopotentials (Pb.rel-pbe-n-nc.UPF, I.rel-pbe-n-nc.UPF, C.rel-pbe-nc.UPF, H.rel-pbe-n-nc.UPF, and N.rel-pbe-nc.UPF) (Hamann et al., 1979; Kresse and Hafner, 1994; Dal Corso, 2014) (Hamann et al., 1979; Kresse and Hafner, 1994; Dal Corso, 2014), respectively. For both non–spin-orbit and spin-orbit coupling GW band structures, the ground state calculation was carried out using a 6 × 6 × 6 Monkhorst–Pack kpoint grid and a cut-off for a wavefunction of 30 Ry, and the number of Gvectors in the exchange term was optimized to 40 Ry and 30 Ry for non–spin-orbit coupling and spin-orbit coupling–based calculations, respectively. In comparison, the number of Gvector blocks in the dielectric constant was optimized to 5 Ry and 6 Ry for non–spin-orbit coupling and spin-orbit coupling–based calculations. The number of bands in the independent response function was optimized as 90 bands and 100 bands for non–spin-orbit coupling and spin-orbit coupling–based calculations. The GW band structures were calculated with six (6) empty and six (6) filled bands for non–spin-orbit coupling–based calculations, while seven (7) empty and seven (7) filled bands were used for the spin-orbit coupling–based calculations as implemented in the YAMBO code (Marini et al., 2009; Sangalli et al., 2019; Rangel et al., 2020). The Bethe–Salpeter equation optical properties were carried out with the 4 × 4 × 4 and 6 × 6 × 6 Monkhorst–Pack kpoint grid to determine the effect of kpoint optimization on the optical absorption spectra. The macroscopic dielectric matrix was calculated with eight (8) occupied and seventeen (17) unoccupied bands for the non–spin-orbit coupling calculation and fourteen (14) unoccupied and ten (10) occupied bands for spin-orbit coupling–based calculations as implemented in the YAMBO code (Marini et al., 2009; Sangalli et al., 2019; Rangel et al., 2020). Furthermore, the absorption and extinction coefficients, transmittance, reflectivity, refractive index, and absorbance were calculated from the real and imaginary parts of the dielectric tensor. We also determine the spectroscopy limited maximum efficiency, which could screen potential photovoltaic absorbers based on intrinsic properties such as absorption coefficient, temperature, direct and indirect allowed gap, and thickness of the absorber (Yu and Zunger, 2012).
3 Results
3.1 Structure of CH3NH2CH3PbI3
The structure of the perovskite cubic cage is similar to the conventional perovskite structure modeled in previous articles (Filip and Giustino, 2014; Lang et al., 2014; Agbaoye et al., 2020; Agbaoye et al., 2021), with the Pb atom placed at the edge of the crystal, forming an octahedra with the I3 atoms and the organic cation placed in the middle of the cubic cage (Filip and Giustino, 2014; Lang et al., 2014). At the same time, the dimethylammonium ion (CH3NH2CH3)+ is optimized such that the amino group (H-N-H) and the methyl group (H-C-H2) have a bond angle of 109.40 and 109.50, respectively. Thus, the H-N and H-C bond length is reported as 1.15
In this study, the CH3NH2CH3PbI3 crystal displayed in Figure 1 is optimized such that the lattice size and the atomic positions are at the ground state. The variation in the lattice parameter reported in this study and in the work of Kim et al. (Kim et al., 2017), shown in table 1, is within about 5% agreement with the theoretical study of Kim et al. (2017); this slight variation could be a result of lattice size and atomic position being in a local minimum and the difference in the Perdew–Burke–Enzenhoff exchange-correlation functional used in this study and the refitted Perdew–Wang 86 exchange-correlation functional used by Kim et al. (2017) and Shastri and Pandey (2018). However, the slight difference in the lattice parameter tends to affect the bandgap, magnetic properties, and other superconducting properties (Bagayoko and Callaway, 1983; Wang et al., 1996; Kim et al., 2017).
FIGURE 1. Cubic crystal structure of (CH3)NH2CH3PbI3.
TABLE 1. Lattice parameters of pseudo-cubic CH3NH2CH3PbI3.
3.2 Electronic Structure
The density functional theory band structure has its maximum valence band and its minimum conduction band at the R high symmetry point, resulting in a direct bandgap of 1.55 eV as shown in Figure 2. The DFT band structure calculated without spin-orbit coupling shows a dense band around 2 eV along the Γ−X−M−Γ−R−X high symmetry point in the valence band, but less dense bands were noticed along the Γ−X−M−Γ−R−X high symmetry point in the conduction band, as shown in Figure 2. The density of states calculated without spin-orbit coupling shows a similar amount of available states, which results in sharp peaks around the 2 eV of the valence band, while smaller peaks that result from fewer states and relate to fewer bands in the band structure are reported in the total density of states. The projected density of states indicates that the iodine (I) p orbital is most responsible in the valence band, while the lead (Pb) p orbital shows dominance in the conduction band, which is in agreement with previous studies (Crespo, 2019; Agbaoye et al., 2020; Agbaoye et al., 2021). Hybridization of other orbitals accounts for the other available states as reported for the non–spin-orbit coupling– and the spin-orbit coupling–based density of states. The dimethylammonium cation does not contribute significantly to the band edges at the maximum valence band and the minimum conduction bands as shown in the available state of the projected density of states in agreement with previous studies (Filip and Giustino, 2014; Im et al., 2015; Crespo, 2019). The spin-orbit coupling–based DFT band structure recorded a lower bandgap of 0.50 eV at R high symmetry; band splitting inherent to spin-orbit coupling is noticed in the spin-orbit–based DFT band structure. The spin-orbit coupling effect creates a gap between the first and the second band in the conduction region at R and M high symmetry points for both DFT-soc and GW-soc band structure calculations.
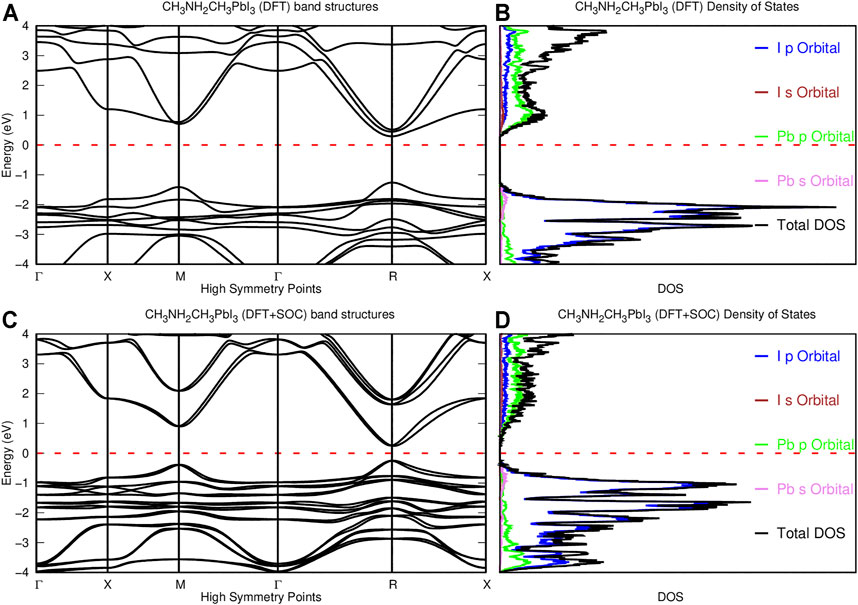
FIGURE 2. DFT band structure and density of states of pseudo-cubic CH3NH2CH3PbI3. (A) DFT band structure of CH3NH2CH3PbI3. (B) DFT density of states of CH3NH2CH3PbI3. (C) DFT + SOC band structure of CH3NH2CH3PbI3. (D) DFT + SOC density of states of (CH3)NH2CH3PbI3.
The DFT method underestimates the bandgap of semiconductors and insulators as a result of self-interaction error (Einollahzadeh et al., 2016; Morales-García et al., 2017; Crespo, 2019), while materials with d and f orbitals require more advanced formalism like DFT + U for accurate bandgaps (Morales-García et al., 2017). Although DFT + U improves semiconductors’ bandgaps, they sometimes fail due to the parameterization of the Hubbard parameter (U) and the fact that U is sometimes fitted to the experimental bandgaps (Morales-García et al., 2017). Furthermore, hybrid functionals which mix a portion of the Fock exchange with DFT functionals are often used to improve the bandgaps of semiconductors, but the material dependence of hybrid functionals and the associated high computation cost count as its demerit (Morales-García et al., 2017). This study also performs the self-consistent GW calculations on the system’s eigenvalues for both G and W. This method is known to reproduce the experimental bandgap of materials accurately (Morales-García et al., 2017). Although self-consistent GW calculations can be calculated on both the eigenvalues and the wavefunctions, the eigenvalue-based self-consistent GW calculations give results that are comparable to those of experimental studies since DFT calculations produce good wavefunctions. The GW and GW-soc band structures shown in Figure 3 also show identical bands, comparable with the DFT band structures. The G0W0 and the spin-based G0W0-soc band structure reported a bandgap of 2.25 and 1.10 eV, respectively, while self-consistent GW and GW-soc calculations reported a direct gap of 2.27 eV for G1W1, 1.18 eV for G1W1-soc, and 1.20 eV for G2W2-soc at the R high symmetry point as shown in Table 2. The self-consistent GW and GW-soc calculations reported bands at a similar energy range in the valence band region, while the effect of the GW self-consistency was noticed in the conduction band, as shown in Figure 3.
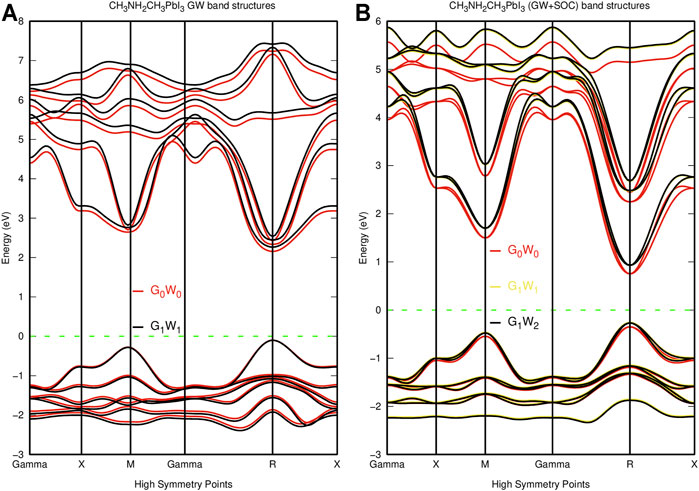
FIGURE 3. GW band structure of pseudo-cubic CH3NH2CH3PbI3. (A) GW band structure of CH3NH2CH3PbI3. (B) GW + SOC band structure of CH3NH2CH3PbI3.
TABLE 2. DFT and self-consistent GW bandgaps of pseudo-cubic CH3NH2CH3PbI3.
The self-consistent GW method improves the GW bandgaps by increasing the G0W0 bandgap by up to 0.5 eV (Filip and Giustino, 2014). In this work, the results suggest that the self-consistency in the GW method improves the G0W0 bandgap without spin-orbit by 0.02 eV, while the bandgap with spin-orbit coupling improves by 0.1 eV in agreement with Filip and Giustini’s findings (Filip and Giustino, 2014; Katan et al., 2015). Alongside the band splitting, the spin-orbit coupling also reduces the bandgap gap by pushing the valence bands upward in the DFT band structure as shown in Figure 2, but both the valence band and the conduction band are pushed downward in the GW band structure calculation as shown in Figure 3. In the DFT band structure, the spin-orbit effect reduces the bandgap of CH3NH2CH3PbI3 by 0.94 eV (65%), in agreement with previous studies (Filip and Giustino, 2014; Agbaoye et al., 2020; Agbaoye et al., 2021). Similarly, the effect of spin-orbit reduces the bandgap of the GW band structure by 1.15 eV (51%), similar to the bandgap difference of 1.18 eV reported by Filip and Giustino (Filip and Giustino, 2014). Hence, the accurate bandgap of perovskites requires fully relativistic spin-orbit correction coupled with the GW quasiparticle method (Filip and Giustino, 2014). The DFT, DFT-soc, GW, and GW-soc band structures recorded similar band curvature, which indicates that although the DFT band structure underestimates the bandgap, it gives accurate band curvature. The DFT bandgap reported in this study is lower than the bandgaps reported by Crespo (2019) and Kim et al. (2017), as shown in table 2. The difference in the bandgaps reported in this study and the work of (Crespo, 2019) could be a result of the difference in lattice parameters and lattice coordinates, which is known to produce variation in the value of bandgaps (Bagayoko and Callaway, 1983; Wang et al., 1996; Kim et al., 2017). Alternatively, the difference in the bandgaps reported in this study and the study of Kim et al. (2017) may be associated with the difference in the Perdew–Burke–Enzenhoff exchange-correlation functional treated with the Grimme-d2 dispersion correction used in this study and the projected augmented wavefunction (PAW) formalism of the generalized gradient approximation method and the refitted Perdew–Wang 86 exchange-correlation functional used by Kim et al. (2017).
3.3 Optical Absorption
Similar optical spectra were reported by the 6 × 6 × 6 and the 4 × 4 × 4 Monkhorst–Pack kpoint scheme based Bethe–Salpeter equation method (BSE) without spin-orbit coupling. Furthermore, the 4 × 4 × 4 and 6 × 6 × 6 Monkhorst–Pack kpoint mesh optical spectra also show similar spectra in the spin-orbit coupling–based calculation. However, the optical spectra calculated using the 6 × 6 × 6 Monkhorst–Pack kpoint grid do not agree completely with the 4 × 4 × 4 Monkhorst–Pack kpoint grid; this could be a result of the kpoint convergence dependence in the Bethe–Salpeter equation method. The spin-orbit coupling–based optical spectra calculated with the 6 × 6 × 6 and 4 × 4 × 4 kpoint mesh record a redshift compared to the non–spin-orbit coupling–based optical spectra.
The 4 × 4 × 4 based optical spectra have sharper and more prominent absorption peaks compared to the results of the 6 × 6 × 6 optical spectra in both spin-orbit coupling and non–spin-orbit coupling calculation. The non–spin-orbit coupling–based optical spectra show higher and sharper absorption peaks in the 6 × 6 × 6 and 4 × 4 × 4 Monkhorst–Pack mesh than the spin-orbit coupling–based optical spectra. The optical absorption onsets in the real dielectric tensor and refractive index were noticed from the 6 × 6 × 6 and 4 × 4 × 4 kpoint mesh–based BSE calculation without spin-orbit coupling at 423 nm, 386 nm, 355 nm and 435 nm, 372 nm, and 349 nm, respectively. Alternatively, for non–spin-orbit coupling–based BSE calculation of the imaginary dielectric tensor, extinction coefficient, reflectivity, and absorbance, we report absorption peaks at 412 nm, 375 nm, 338 nm, 306 nm and 420 nm, 359 nm, 333 nm, and 306 nm for 6 × 6 × 6 and 4 × 4 × 4 kpoint mesh calculations, respectively. In the spin-orbit coupling–based BSE calculations, the real dielectric tensor and reflectivity have optical absorption peaks at 711 and 458 nm for the 4 × 4 × 4 kpoint mesh–based calculations and 793 nm, 567 nm, and 410 nm for the 6 × 6 × 6 kpoint mesh–based calculations. Similarly, the imaginary dielectric tensor, extinction coefficient, reflectivity, and absorbance have absorption peaks at 658 nm, 600 nm, and 448 nm for 4 × 4 × 4 kpoint mesh–based calculations and 687 nm, 538 nm, and 394 nm for 6 × 6 × 6 kpoint mesh–based calculation. The 4 × 4 × 4 (color red) and 6 × 6 × 6 (color blue) kpoint mesh–based spin-orbit coupling absorption coefficient of CH3NH2CH3PbI3 increases from 103 to 106 within the ultraviolet region. In contrast, the absorption coefficient remains steady at 106 along the visible spectrum toward the near-infrared region. The 4 × 4 × 4 (color black) and 6 × 6 × 6 (color green) kpoint mesh–based non–spin-orbit coupling reported its absorption coefficient in the order of 106 cm−1 along the ultraviolet region and toward the visible spectrum. The absorption coefficient attenuates to 103 cm−1 along the visible and toward the near-infrared region. Similar attenuation was reported in our previous study (Agbaoye et al., 2020) and the result of silicon (Green and Keevers, 1995), shown in Figure 4F. The absorption coefficient of CH3NH2CH3PbI3 calculated with and without spin-orbit coupling recorded lower values at the ultraviolet region than silicon’s absorption coefficient (Green and Keevers, 1995).
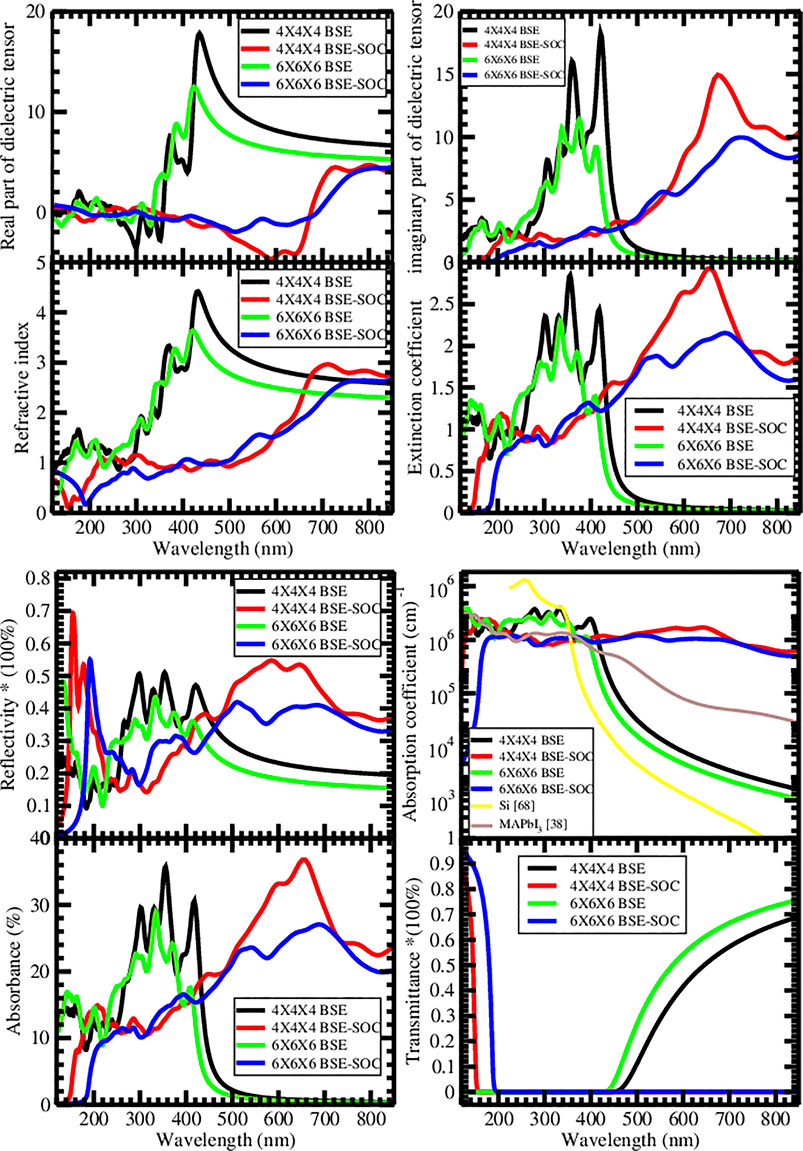
FIGURE 4. Optical spectra of pseudo-cubic CH3NH2CH3PbI3. (A) Real part of the dielectric tensor. (B) Imaginary part of the dielectric tensor. (C) Refractive index (n). (D) Extinction coefficient (k). (E) Reflectivity. (F) Absorption coefficient. (G) Absorbance. (H) Transmittance.
However, the absorption coefficient of CH3NH2CH3PbI3 recorded higher values along the visible and the near-infrared region, in agreement with the result of previous studies (Agbaoye et al., 2020; Agbaoye et al., 2021), and this compensates for the lower value of the absorption coefficient along the ultraviolet region, which suggests that CH3NH2CH3PbI3 could have comparable solar cell efficiency with silicon. The absorption onset at 418 nm from the absorption coefficient of the 6 × 6 × 6 kpoint mesh–based BSE calculation agrees with the absorption onset at 3 eV in the absorption coefficient reported by Crespo (2019). The spin-orbit coupling–based transmittance calculated with 6 × 6 × 6 (color blue) and 4 × 4 × 4 (color red) kpoint mesh reports a blue shift of the non–spin-orbit coupling–based transmittance and suggests that CH3NH2CH3PbI3 will transmit only the short wavelength of the ultraviolet region due to the transmittance result up to 100% from 150 to 200 nm. Alternatively, the non–spin-orbit coupling–based transmittance can only transmit in the visible and the near-infrared region due to the exponential increase in the transmission value from 0 to 80% within 450–800 nm. The spectroscopic limited maximum efficiency predicted a maximum efficiency of 30% at a thickness of 10–2 μm, which increases linearly to 62.7% at a thickness of 10–1 μm, and then remains constant as the thickness increases, as shown in Figure 5. These interesting maximum efficiency limits are calculated at room temperature (293.15 K), a direct allowed bandgap of 1 eV, an indirect allowed bandgap of 1.97 eV, and the BSE-soc absorption coefficient reported in Figure 4.
FIGURE 5. Spectroscopic limited maximum efficiency of CH3NH2CH3PbI3 at 293.15 K.
4 Conclusion
This study reveals the electronic structure and the optical absorption spectra of CH3NH2CH3PbI3, the lattice parameters, and the DFT bandgap of the pseudo-cubic ground state structure were reported in agreement with previous studies (Kim et al., 2017; Crespo, 2019). The spin-orbit coupling effect was introduced to both the electronic structure and optical spectra to cater for the presence of heavy metals such as lead (Pb); the spin-orbit coupling effect causes band splitting and bandgap reduction in agreement with the previous studies (Filip and Giustino, 2014; Agbaoye et al., 2020; Agbaoye et al., 2021). The projected density of states reveals that the dimethylammonium cation does not contribute to the bands around the maximum valence band and the minimum conduction band, while the lead (Pb) p orbital and the iodine (I) p orbital play the most significant roles in the conduction and the valence band, respectively. The spin-orbit coupling–based self-consistent GW bandgaps were calculated to correct the deficiency of DFT bandgaps, giving a more accurate bandgap of 1.20 eV, which is within the highest Schockly–Quisser maximum efficiency limit of about 33% (Queisser, 2009; Sha et al., 2015). The spin-orbit coupling–based optical spectra show a redshift of the non–spin-orbit coupling spectra, while the size of the kpoint mesh plays a significant role in the size and position of the absorption peaks. The absorption coefficients were reported in the order of 105 along the ultraviolet region, lower than silicon, but increased absorption coefficients in the order of 106 higher than silicon were recorded along the visible spectrum. The spectroscopic limited maximum efficiency predicts an attractive maximum efficiency of about 62.7% within 10–1 to 102 μm thickness, which affirms that CH3NH2CH3PbI3 will be a highly efficient solar cell absorber.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
RA, SB, PA, SK, and GA contributed to conception and design of the study. AK, A-OA, HM, and BM prepared the input files and literatures. RA, SB, AK, A-OA, HM, and BM wrote sections and the first draft of the manuscript. RA, PA, SK, and GA performed review and editing. RA, SK, and GA performed supervision, validation, and resources. All authors contributed to manuscript revision and read and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors acknowledge the Abdus Salam International Centre for Theoretical Physics for computational access. S. Kenmoe thanks the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for funding 388390466 - TRR 247.
References
Adebambo, P. O., Osafile, O. E., Laoye, J. A., Idowu, M. A., and Adebayo, G. A. (2021). Electronic Fitness Function, Effective Mass and Thermoelectric Properties of Rh-Based (-ScTe; -TiSb; -VSn) Alloys for Thermoelectric Generator Applications. Comput. Condensed Matter 26, e00523. doi:10.1016/j.cocom.2020.e00523
Aftab, A., and Ahmad, M. I. (2021). A Review of Stability and Progress in Tin Halide Perovskite Solar Cell. Solar Energy 216, 26–47. doi:10.1016/j.solener.2020.12.065
Agbaoye, R. O., Adebayo, G. A., and Kenmoe, S. (2021). Band Structure and Absorption Spectra of NH4XI3 (X = Pb, Mg) Based Hybrid Perovskite for UV ray Protector and Electrochromic Materials Applications. J. Phys. Chem. Sol. 151, 109860. doi:10.1016/j.jpcs.2020.109860
Agbaoye, R. O., Akinlami, J. O., Afolabi, T. A., and Adebayo, G. A. (2020). Unraveling the Stable Phase, High Absorption Coefficient, Optical and Mechanical Properties of Hybrid Perovskite CH3NH3PbxMg1-xI3: Density Functional Approach. J. Inorg. Organomet. Polym. 30 (2), 299–309. doi:10.1007/s10904-019-01187-z
Akman, E., Shalan, A. E., Sadegh, F., and Akin, S. (2021). Moisture-Resistant FAPbI3 Perovskite Solar Cell with 22.25 % Power Conversion Efficiency through Pentafluorobenzyl Phosphonic Acid Passivation. ChemSusChem 14 (4), 1176–1183. doi:10.1002/cssc.202002707
AndrewE_R_and Canepa, P. C. (19691972). A Proton Magnetic Resonance Investigation of Solid Mono-, Di-, Tri-and Tetra-Methylammonium Chlorides. J. Magn. Reson. 7 (4), 429–441. doi:10.1016/0022-2364(72)90208-9
Bagayoko, D., and Callaway, J. (1983). Lattice-parameter Dependence of Ferromagnetism in Bcc and Fcc Iron. Phys. Rev. B 28 (10), 5419–5422. doi:10.1103/PhysRevB.28.5419
Baranowska-Korczyc, A., Mackiewicz, E., Ranoszek-Soliwoda, K., Nejman, A., Trasobares, S., Grobelny, J., et al. (2021). A SnO2 Shell for High Environmental Stability of Ag Nanowires Applied for thermal Management. RSC Adv. 11 (7), 4174–4185. doi:10.1039/D0RA10040D
Barone, V., Casarin, M., Forrer, D., Pavone, M., Sambi, M., and Vittadini, A. (2009). Role and Effective Treatment of Dispersive Forces in Materials: Polyethylene and Graphite Crystals as Test Cases. J. Comput. Chem. 30 (6), 934–939. doi:10.1002/jcc.21112
Blöchl, P. E., Jepsen, O., and Andersen, O. K. (1994). Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 49 (23), 16223–16233. doi:10.1103/PhysRevB.49.16223
Cha, H., and Wu, J. (2021). Understanding what Determines the Organic Solar Cell Stability. Joule 5 (6), 1322–1325. doi:10.1016/j.joule.2021.05.020
Christians, J. A., Miranda Herrera, P. A., Kamat, P. V., and Kamat, P. V. (2015). Transformation of the Excited State and Photovoltaic Efficiency of CH3NH3PbI3 Perovskite upon Controlled Exposure to Humidified Air. J. Am. Chem. Soc.ACS Publications 137 (4), 1530–1538. doi:10.1021/ja511132a
Crespo, C. T. (2019). Effect of the Organic Cation on the Optical Properties of lead Iodine Perovskites. Solar Energ. Mater. Solar Cell 200, 110022. doi:10.1016/j.solmat.2019.110022
Dal Corso, A. (2014). Pseudopotentials Periodic Table: From H to Pu. Comput. Mater. Sci. 95, 337–350. doi:10.1016/j.commatsci.2014.07.043
Einollahzadeh, H., Dariani, R. S., and Fazeli, S. M. (2016). Computing the Band Structure and Energy gap of Penta-Graphene by Using DFT and G0W0 Approximations. Solid State. Commun. 229, 1–4. doi:10.1016/j.ssc.2015.12.012
Eperon, G. E., Stone, K. H., Mundt, L. E., Schloemer, T. H., Habisreutinger, S. N., Dunfield, S. P., et al. (2020). The Role of Dimethylammonium in Bandgap Modulation for Stable Halide Perovskites. ACS Energ. Lett. 5 (6), 1856–1864. doi:10.1021/acsenergylett.0c00872
Eperon, G. E., Stranks, S. D., Menelaou, C., Johnston, M. B., Herz, L. M., Snaith, H. J., et al. (2014). Formamidinium lead Trihalide: a Broadly Tunable Perovskite for Efficient Planar Heterojunction Solar Cells. Energy Environ. Sci. 7 (3), 982–988. doi:10.1039/10.1039/c3ee43822h
Filip, M. R., and Giustino, F. (2014). GWquasiparticle Band gap of the Hybrid Organic-Inorganic perovskiteCH3NH3PbI3: Effect of Spin-Orbit Interaction, Semicore Electrons, and Self-Consistency. Phys. Rev. B 90 (24), 245145. doi:10.1103/PhysRevB.90.245145
García-Fernández, A., Bermúdez-García, J. M., Castro-García, S., Llamas-Saiz, A. L., Artiaga, R., López-Beceiro, J., et al. (2017). Phase Transition, Dielectric Properties, and Ionic Transport in the [(CH3)2NH2]PbI3 Organic-Inorganic Hybrid with 2H-Hexagonal Perovskite Structure. Inorg. Chem. 56 (9), 4918–4927. doi:10.1021/acs.inorgchem.6b03095
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: a Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 21 (39), 395502. doi:10.1088/0953-8984/21/39/395502
Green, M. A., and Keevers, M. J. (1995). Optical Properties of Intrinsic Silicon at 300 K. Prog. Photovolt: Res. Appl. 3 (3), 189–192. doi:10.1002/pip.4670030303
Grimme, S. (2006). Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 27 (15), 1787–1799. doi:10.1002/jcc.20495
Hamann, D. R., Schlüter, M., and Chiang, C. (1979). Norm-conserving Pseudopotentials. Phys. Rev. Lett. 43 (20), 1494–1497. doi:10.1103/PhysRevLett.43.1494
Hao, F., Stoumpos, C. C., Chang, R. P. H., Kanatzidis, M. G., and Mercouri, G. (2014). Anomalous Band gap Behavior in Mixed Sn and Pb Perovskites Enables Broadening of Absorption Spectrum in Solar Cells. J. Am. Chem. Soc. 136 (22), 8094–8099. doi:10.1021/ja5033259
He, W., Zhang, G., Zhang, X., Ji, J., Li, G., and Zhao, X. (2015). Recent Development and Application of Thermoelectric Generator and Cooler. Appl. Energ. 143, 1–25. doi:10.1016/j.apenergy.2014.12.075
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, 3BB864–B871. doi:10.1103/PhysRev.136.B864
Im, J.-H., Chung, J., Kim, S.-J., and Park, N.-G. (2012). Synthesis, Structure, and Photovoltaic Property of a Nanocrystalline 2H Perovskite-type Novel Sensitizer (CH3CH2NH3)PbI3. Nanoscale Res. Lett. 7 (1), 1–7. doi:10.1186/1556-276X-7-353
Im, J., Stoumpos, C. C., Jin, H., Freeman, A. J., Kanatzidis, M. G., and Mercouri, G. (2015). Antagonism between Spin-Orbit Coupling and Steric Effects Causes Anomalous Band Gap Evolution in the Perovskite Photovoltaic Materials CH3NH3Sn1-xPbxI3. J. Phys. Chem. Lett. 6 (17), 3503–3509. doi:10.1021/acs.jpclett.5b01738
Jouhara, H., Żabnieńska-Góra, A., Khordehgah, N., Doraghi, Q., Ahmad, L., Norman, L., et al. (2021). Thermoelectric Generator (TEG) Technologies and Applications. Int. J. Thermofluids 9, 100063. doi:10.1016/j.ijft.2021.100063
Katan, C., Pedesseau, L., Kepenekian, M., Rolland, A., and Even, J. (2015). Interplay of Spin-Orbit Coupling and Lattice Distortion in Metal Substituted 3D Tri-chloride Hybrid Perovskites. J. Mater. Chem. A. 3 (17), 9232–9240. doi:10.1039/C4TA06418F
Kim, C., Huan, T. D., Krishnan, S., and Ramprasad, R. (2017). A Hybrid Organic-Inorganic Perovskite Dataset. Sci. Data 4 (1), 1–11. doi:10.1038/sdata.2017.57
Kohn, W., and Sham, L. J. (1965). Self-consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, 4AA1133–A1138. doi:10.1103/PhysRev.140.A1133
Kojima, A., Teshima, K., Shirai, Y., and Miyasaka, T. (2009). Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 131 (17), 6050–6051. doi:10.1021/ja809598r
Kresse, G., and Hafner, J. (1994). Norm-conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements. J. Phys. Condens. Matter 6 (40), 8245–8257. doi:10.1088/0953-8984/6/40/015
Lang, L., Yang, J.-H., Liu, H.-R., Xiang, H. J., and Gong, X. G. (2014). First-principles Study on the Electronic and Optical Properties of Cubic ABX3 Halide Perovskites. Phys. Lett. A 378 (3), 290–293. doi:10.1016/j.physleta.2013.11.018
Mancini, A., Quadrelli, P., Amoroso, G., Milanese, C., Boiocchi, M., Sironi, A., et al. (2016). Synthesis, Structural and Optical Characterization of APbX3 (A=methylammonium, Dimethylammonium, Trimethylammonium; X=I, Br, Cl) Hybrid Organic-Inorganic Materials. J. Solid State. Chem. 240, 55–60. doi:10.1016/j.jssc.2016.05.015
Mancini, A., Quadrelli, P., Milanese, C., Patrini, M., Guizzetti, G., and Malavasi, L. (2015). CH3NH3SnxPb1-xBr3 Hybrid Perovskite Solid Solution: Synthesis, Structure, and Optical Properties. Inorg. Chem. 54 (18), 8893–8895. doi:10.1021/acs.inorgchem.5b01843
Marini, A., Hogan, C., Grüning, M., and Varsano, D. (2009). Yambo: an Ab Initio Tool for Excited State Calculations. Comp. Phys. Commun. 180 (8), 1392–1403. doi:10.1016/j.cpc.2009.02.003
Marshall, A. R., Sansom, H. C., McCarthy, M. M., Warby, J. H., Ashton, O. J., Wenger, B., et al. (2021). Dimethylammonium: An A‐Site Cation for Modifying CsPbI 3. Sol. RRL 5 (1), 2000599. https://onlinelibrary.wiley.com/doi/epdf/10.1002/solr.202000599. doi:10.1002/solr.202000599
Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/PhysRevB.13.5188
Morales-García, Á., Valero, R., and Illas, F. (2017). An Empirical, yet Practical Way to Predict the Band gap in Solids by Using Density Functional Band Structure Calculations. J. Phys. Chem. C 121 (34), 18862–18866. doi:10.1021/acs.jpcc.7b07421
Ogomi, Y., Morita, A., Tsukamoto, S., Saitho, T., Fujikawa, N., Shen, Q., et al. (2014). CH3NH3SnxPb(1-x)I3 Perovskite Solar Cells Covering up to 1060 Nm. J. Phys. Chem. Lett. 5 (6), 1004–1011. doi:10.1021/jz5002117
Park, N.-G. (2016). Methodologies for High Efficiency Perovskite Solar Cells. Nano convergence 3 (1), 1–13. doi:10.1186/s40580-016-0074-x
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865
Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., et al. (1992). Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 46 (11), 6671–6687. doi:10.1103/PhysRevB.46.6671
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 100 (13), 136406. doi:10.1103/PhysRevLett.100.136406
Perdew, J. P., and Yue, W. (1986). Accurate and Simple Density Functional for the Electronic Exchange Energy: Generalized Gradient Approximation. Phys. Rev. B 33 (12), 8800–8802. doi:10.1103/PhysRevB.33.8800
Queisser, H. J. (2009). Detailed Balance Limit for Solar Cell Efficiency. Mater. Sci. Eng. B 159-160, 322–328. doi:10.1016/j.mseb.2008.06.033
Rangel, T., Del Ben, M., Varsano, D., Antonius, G., Bruneval, F., da Jornada, F. H., et al. (2020). Reproducibility in G0W0 Calculations for Solids. Comp. Phys. Commun. 255, 107242. doi:10.1016/j.cpc.2020.107242
Sangalli, D., Ferretti, A., Miranda, H., Attaccalite, C., Marri, I., Cannuccia, E., et al. (2019). Many-body Perturbation Theory Calculations Using the Yambo Code. J. Phys. Condens. Matter 31 (32), 325902. doi:10.1088/1361-648X/ab15d0
Scandolo, S., Giannozzi, P., Cavazzoni, C., de Gironcoli, S., Pasquarello, A., and Baroni, S. (2005). First-principles Codes for Computational Crystallography in the Quantum-ESPRESSO Package. Z. für Kristallographie-Crystalline Mater. 220 (5-6), 574–579. doi:10.1524/zkri.220.5.574.65062
Sha, W. E. I., Ren, X., Chen, L., and Choy, W. C. H. (2015). The Efficiency Limit of CH3NH3PbI3 Perovskite Solar Cells. Appl. Phys. Lett. 106 (22), 221104. doi:10.1063/1.4922150
Shanno, D. F. (1970). Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comp. 24 (111), 647–656. doi:10.1090/S0025-5718-1970-0274029-X
Shastri, S. S., and Pandey, S. K. (2018). A Comparative Study of Different Exchange-Correlation Functionals in Understanding Structural, Electronic and Thermoelectric Properties of Fe2VAl and Fe2TiSn Compounds. Comput. Mater. Sci. 143, 316–324. doi:10.1016/j.commatsci.2017.10.053
Shockley, W., and Queisser, H. J. (1961). Detailed Balance Limit of Efficiency of P‐n Junction Solar Cells. J. Appl. Phys. 32 (3), 510–519. doi:10.1063/1.1736034
Snaith, H. J., Abate, A., Ball, J. M., Eperon, G. E., Leijtens, T., Noel, N. K., et al. (2014). Anomalous Hysteresis in Perovskite Solar Cells. J. Phys. Chem. Lett. 5 (9), 1511–1515. doi:10.1021/jz500113x
Snaith, H. J., and Hacke, P. (2018). Enabling Reliability Assessments of Pre-commercial Perovskite Photovoltaics with Lessons Learned from Industrial Standards. Nat. Energ. 3 (6), 459–465. doi:10.1038/s41560-018-0174-4
Stoumpos, C. C., Frazer, L., Clark, D. J., Kim, Y. S., Rhim, S. H., Freeman, A. J., et al. (2015). Hybrid Germanium Iodide Perovskite Semiconductors: Active Lone Pairs, Structural Distortions, Direct and Indirect Energy Gaps, and strong Nonlinear Optical Properties. J. Am. Chem. Soc. 137 (21), 6804–6819. doi:10.1021/jacs.5b01025
Stoumpos, C. C., Malliakas, C. D., Kanatzidis, M. G., and Mercouri, G. (2013). Semiconducting Tin and lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 52 (15), 9019–9038. doi:10.1021/ic401215x
Thomas, S. A., Hamill Jr, , Loo, S. J. O. Y. L., White, S. J. O., and Loo, Y. L. (2021). Chemical and Structural Degradation of CH 3 NH 3 PbI 3 Propagate from PEDOT:PSS Interface in the Presence of Humidity. Adv. Mater. Inter. 8 (16), 2100505. doi:10.1002/admi.202100505
Troullier, N. J. L., and Martins, J. L. (1991). Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 43 (3), 1993–2006. doi:10.1103/PhysRevB.43.1993
Troullier, N., and Martins, J. L. (1991). Efficient Pseudopotentials for Plane-Wave Calculations. II. Operators for Fast Iterative Diagonalization. Phys. Rev. B 43 (11), 8861–8869. doi:10.1103/PhysRevB.43.8861
Wang, P., Wang, J., An, X., Shi, J., Shangguan, W., Hao, X., et al. (2021). Generation of Abundant Defects in Mn-Co Mixed Oxides by a Facile agar-gel Method for Highly Efficient Catalysis of Total Toluene Oxidation. Appl. Catal. B: Environ. 282, 119560. doi:10.1016/j.apcatb.2020.119560
Wang, Y., Liu, X., Zhang, T., Wang, X., Kan, M., Shi, J., et al. (2019). The Role of Dimethylammonium Iodide in CsPbI 3 Perovskite Fabrication: Additive or Dopant. Angew. Chem. 131 (46), 16844–16849. doi:10.1002/ange.201910800
Wang, Z., Kawakami, A., Uzawa, Y., and Komiyama, B. (1996). Superconducting Properties and crystal Structures of Single‐crystal Niobium Nitride Thin Films Deposited at Ambient Substrate Temperature. J. Appl. Phys. 79 (10), 7837–7842. doi:10.1063/1.362392
Yin, W.-J., Shi, T., and Yan, Y. (2014). Unique Properties of Halide Perovskites as Possible Origins of the superior Solar Cell Performance. Adv. Mater. 26 (27), 4653–4658. doi:10.1002/adma.201306281
Yu, L., and Zunger, A. (2012). Identification of Potential Photovoltaic Absorbers Based on First-Principles Spectroscopic Screening of Materials. Phys. Rev. Lett. 108 (6), 068701. doi:10.1103/PhysRevLett.108.068701
Zhang, Y., Xiong, R., Sa, B., Zhou, J., and Sun, Z. (2021). MXenes: Promising Donor and Acceptor Materials for High-Efficiency Heterostructure Solar Cells. Sust. Energ. Fuels 5 (1), 135–143. doi:10.1039/D0SE01443E
Zhao, J., Yi, J., Yang, C., Wan, K., Duan, X., Tang, S., et al. (2021). A Novel Strategy of Homogeneous Catalysis and Highly Efficient Recycling of Aqueous Catalyst for the Hydroformylation of Higher Olefins Based on a Simple Methanol/Water Mixed Solvent. Catal. Lett. 151 (5), 1273–1281. doi:10.1007/s10562-020-03385-8
Keywords: spin-orbit coupling, GW quasiparticle method, absorption spectra, perovskites, solar cell
Citation: Agbaoye RO, Bolarinwa S, Akiode KO, Adekoya-Olowofela AA, Habeeb LM, Balogun OM, Adebambo PO, Kenmoe S and Adebayo GA (2021) Bandgap Correction and Spin-Orbit Coupling Induced Absorption Spectra of Dimethylammonium Lead Iodide for Solar Cell Absorber. Front. Energy Res. 9:778865. doi: 10.3389/fenrg.2021.778865
Received: 17 September 2021; Accepted: 05 November 2021;
Published: 06 December 2021.
Edited by:
K. Sudhakar, Universiti Malaysia Pahang, MalaysiaReviewed by:
Bjoern Baumeier, Eindhoven University of Technology, NetherlandsSouraya Goumri-Said, Alfaisal University, Saudi Arabia
Copyright © 2021 Agbaoye, Bolarinwa, Akiode, Adekoya-Olowofela, Habeeb, Balogun, Adebambo, Kenmoe and Adebayo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ridwan O. Agbaoye, YWdiYW95ZUBmZWRjb2R0dGVuLmVkdS5uZw==; Stephane Kenmoe, c3RlcGhhbmUua2VubW9lQHVuaS1kdWUuZGU=; Gboyega A. Adebayo, YWRlYmF5b0BkYWFkLWFsdW1uaS5kZQ==