- 1School of Electronic and Electrical Engineering, Lingnan Normal University, Zhanjiang, China
- 2School of Astronautics, Harbin Institute of Technology, Harbin, China
Power systems are crucial for low-carbon energy applications. Condition maintenance plays a vital role in reducing the maintenance cost of renewable power systems without sacrificing system reliability. This paper proposes a hybrid method to effectively deal with the operational changes and uncertainties of state maintenance within the power system of renewable energy applications. Specifically, a multi-objective evolutionary algorithm is first adopted to maintain key components when only considering system variables and overall performance. During operation, numerous variations in offshore substations are detected from power grids and other equipment, such as continuous aging, weather, load factors, measurement, and human-judgment factors. Then, the advisor implements a system optimization maintenance plan in the substation, which can predict changes in load reliability based on the type 2 fuzzy logic and hidden Markov model technology. The reliability of the load point of each substation would also be obtained. Illustrative results indicate that these serious deteriorations would cause substation for the re-optimization maintenance and optimization activities to meet expected reliability. Through connecting an offshore substation to a medium-sized offshore substation, the uncertainties in condition-based maintenance of renewable energy applications can be well handled.
Introduction
A reasonable state maintenance solution is crucial for extending the service life of a power system in renewable energy applications. However, due to the lack of data updates, uncertainties in the reliability of power system components generally exist (Mohanta et al., 2004). Therefore, in order to make continuous monitoring more convenient, more powerful tools are required to deal with these uncertainties (Mechefske and Wang, 2003; Lu et al., 2007; Strachan et al., 2007; Wang et al., 2008). Reliability analysis is an important part of condition maintenance (Endrenyi et al., 2001). When the condition changes, it is often difficult to obtain accurate reliability indicators by using traditional reliability analysis methods due to the uncertainties inside and outside equipment. Zadeh (1965) utilized the fuzzy set theory to represent and process inaccurate information, and to generate correct decisions by using approximate information, further imitating human reasoning under uncertain conditions. This method is called the type 1 fuzzy logic, which has been successfully applied in many application fields (Chang et al., 1997; Mendel, 2001; Tan and Kamal, 2006). In order to analyze the uncertainty of power system maintenance, the type 1 fuzzy logic has been adopted (Suresh et al., 1994; Tanrioven et al., 2004; Mohanta et al., 2005; Khanlari et al., 2008) to estimate the consistency of reliability measures. The fuzzy Markov model is used to describe the transition rates, and the fuzzy mean time to failure and fuzzy mean time to repair could be adopted to deal with the uncertainty related to the generating units (Tanrioven et al., 2004; Mohanta et al., 2005). Then, the type 2 fuzzy logic is further proposed by Zadeh (1975), which presents greater design freedom and success rate than type 1 fuzzy sets in dealing with uncertainties (Zadeh, 1975; Uncu and Türks, 2007; Hwang and Rhee, 2007; Mendel et al., 2006; Noor and McDonald, 1996).
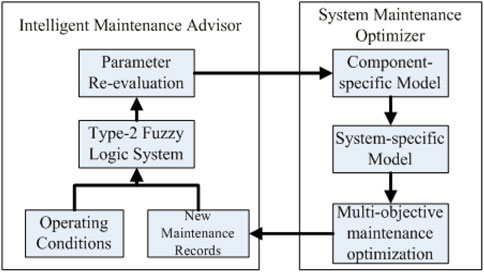
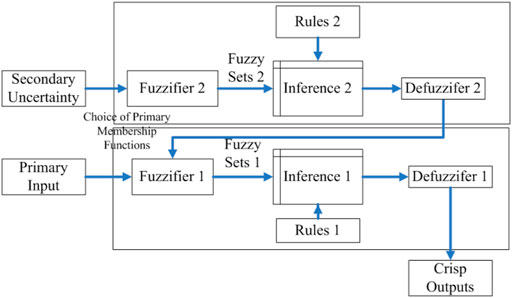
Besides, as another powerful tool, the hidden Markov model has been widely used in many applications such as system monitoring, partial discharge, image classification, and fuzzy spatial pattern processing (Satish and Gururaj, 1993; IEEE APM Subcommittee, 1999; Li et al., 2000; Xu and Ge, 2004; Popescu et al., 2006). Through combining the type 2 fuzzy logic learning analysis system with the hidden Markov model, this paper proposes a hybrid method of using the type 2 fuzzy hidden Markov model to analyze the reliability indicators of the offshore power systems (Anders et al., 1990; Grall et al., 2002; Papoulis and UnnikrishnaPillai, 2002; Yang et al., 2008). In the previous work, the maintenance optimizer is proposed by formulating the best maintenance plan to achieve the suitable balance between grid reliability and cost, further providing a self-contained system for offshore substations based on the maintenance consultant (Billinton et al., 1985; Endrenyi et al., 1998; Garibaldi et al., 2005; Garibaldi and Jaroszewski, 2008; Wang et al., 2009). In this study, the previous work is extended by linking the uncertain type 2 fuzzy intelligent maintenance consultant with the system maintenance optimizer, as shown in Figure 1. Specifically, the maintenance advisor receives the updated maintenance plan from the system maintenance optimizer, which considers the optimization of maintenance activities from two aspects of main system variables and the overall system performance. During operation, the offshore substation will be affected by many factors and produce uncertainty, such as the continuous aging of components, weather, load, measurement, and human subjective judgment. The variations of reliability parameters caused by the operational changes and uncertainties of key components would be sent to the maintenance optimizer. Then, the reliability of the load point will be evaluated, and any variations in the substation can be reported to re-optimize the maintenance activities of the substation for meeting the expected reliability during operation. To achieve reliability modeling of operational changes and uncertainties in offshore substation condition maintenance, type 2 fuzzy logic is adopted here.
Reliability Models in System Maintenance Optimizer
Hidden Markov Model for Individual Component
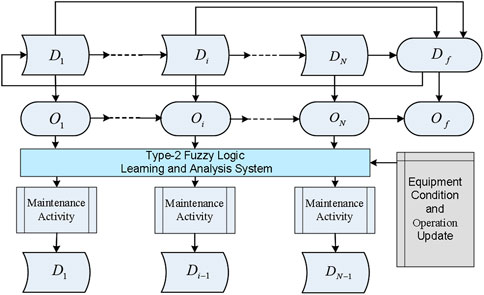
Figure 2 outlines the type 2 fuzzy hidden Markov model for individual offshore power equipment.
Different from the regular Markov model, the state
where
System-Specific Model
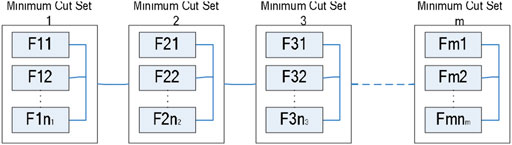
The configuration of the power system with suitable protection solutions would directly affect the reliability of related renewable energy systems. In this study, the minimum cut set method is used to analyze the impact of configuration on system reliability. According to the definition, the minimal cut set belongs to a group of irreducible components whose failure could definitely lead to system failure. The method from Yang et al. (2008) has been applied to the reliability estimation of complex systems, which cannot be simplified to a simple configuration.
From the perspective of reliability, the reliability of a system can be expressed as the block diagram of the minimum cut set that causes system failure, as shown in Figure 3. Here, Fmn represents the fault n in the minimum cut set m. As can be seen from Figure 3, all faults within a minimum cut set can be regarded as parallel, and all minimum cut sets are in series. Therefore, the reliability of the system can be easily evaluated according to the rules for a simple configuration.
It should be noted that the failure modes include the first-order fault events, second-order passive fault, and main protection fault. In a substation with multiple loads, each load will be assigned a different priority to ensure that the load can be transferred to a more important load first. After meeting the higher priority load requirements, the excess load will be transferred to other loads.
The unavailable energy
where
Intelligent Maintenance Advisor With Type 2 Fuzzy Logic System
General Scheme of Quadratic Uncertain Variant Type 2 Fuzzy Logic System
In a fuzzy logic system, the rule-based expert system can capture the overall impact of uncertainty on reliability, and the method of spreading uncertainty between rules is very important for the reasoning engine and is accomplished by the experts who are well acquainted with the operational characteristics of power systems. The input and output of the fuzzy logic system can be combined by experts using the “if-then” rule given by the fuzzy reasoning engine to obtain fuzzy output. Then, the output is defuzzified to get a clear value.
The format of the rule is as follows: If the input is [(the working environment is good) and (the load factor is low), and (the time from previous maintenance is short) and (the equipment age is old)], then the output is [(the transition rates will be decreased by a related percentage value)].
We take an example to show how this fuzzy logic works. A transformer with the operation hours less than 8,760*16 h is considered “young,” while the one with operation hours between 8,760*12 and 8,760*40 is considered “middle-aged.” Therefore, a transformer with the operation hours of 8,760*14 is considered both “young” and “middle-aged” with different levels of confidence. And this particular component is more reliable because of its slower deterioration rate than the older ones if the other operational variations are the same.
Unlike type 1 fuzzy sets with a single membership value, type 2 fuzzy sets are specially designed to deal with secondary uncertainties by introducing a membership value range associated with each value of the main variable. However, due to the significant increase of computational complexity, their implementations are limited.
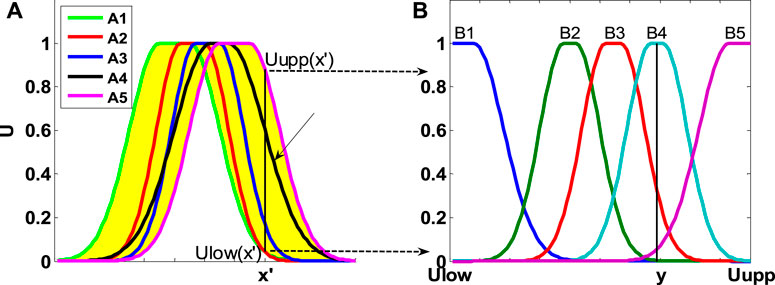
In this study, a simpler method to realize type 2 fuzzy logic is proposed, that is, type 2 fuzzy logic system with quadratic uncertainty change. Secondary uncertainties are captured by initializing a set of primary membership functions. As shown in Figure 4, for a specific value, the membership function takes the value at the position where it intersects the vertical line. As a result, there are a certain range of membership values at
If the input is secondary uncertainty and Y is
With these rules, the number of primary membership functions for each primary linguistic variable equals the number of linguistic variables of its associated secondary uncertainty. As shown in Figure 4, five primary membership functions correspond to the five linguistic variables for secondary uncertainty, respectively.
Membership functions are required for secondary uncertainty, which is the third dimension of type 2 fuzzy logic. In addition, the domain of the secondary membership functions at input
Although many factors affect reliability, this study mainly focuses on the effects of component aging, load, and different maintenance strategies for individual components, which are “primary variables.” The “primary variables” are taken as input to this type 2 fuzzy logic system. The uncertainty in the primary variables is “primary uncertainty.” Besides, additional uncertainty of variations is treated as “secondary uncertainty.” Taking one of the primary variables, time from previous maintenance, as an example, the secondary uncertainty comes from different maintenance extent (minor, medium, and major maintenance).
Figure 5 is a schematic diagram of the type 2 fuzzy logic system of the second uncertainty change. As shown in Figure 5, the implementation of the fuzzy logic system includes two steps: 1) the choice of primary membership functions and 2) mapping the primary input to output. For example, if the input time from previous maintenance is “short” and the previous maintenance is “secondary maintenance,” the primary membership function is first selected and then sent to fuzzier 1. After that, information 1 will map this primary input to an output based on Rule 1. If we want to consider more operation changes, we can combine their influences by more fuzzy inputs and modify the fuzzy inference engine.
Figures 6, 7 show the membership functions of type 2 fuzzy logic systems for transformers and circuit breakers, respectively. The uncertainty caused by various operation changes will affect the reliability of transformers and circuit breakers (annual MTTF and annual failure probability). Table 1 lists the major and minor uncertainties of operational changes.
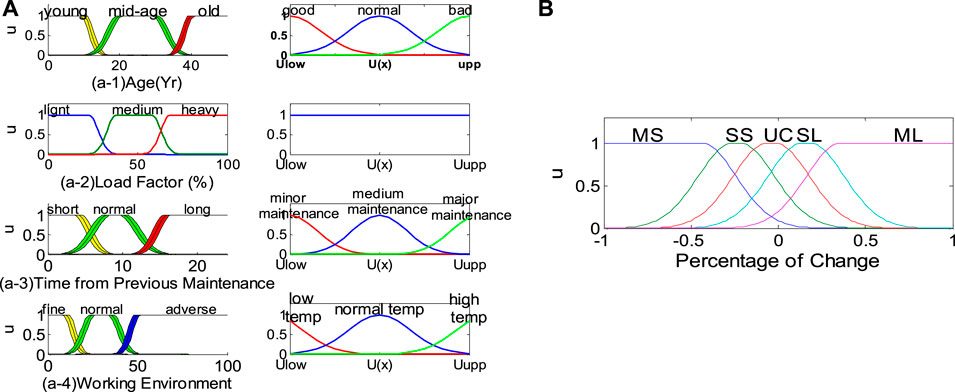
FIGURE 6. Membership functions for transformers: (A) primary and secondary membership functions of inputs (age, load factor, time from previous maintenance, and working environment); (B) membership functions of output (percentage of change to the transition rates of the Markov model).
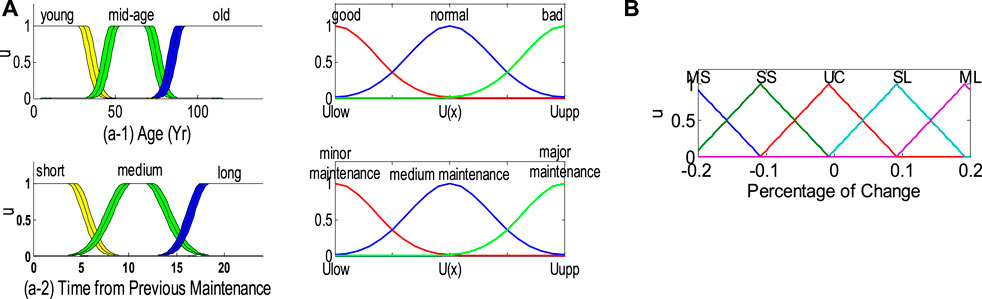
FIGURE 7. Membership functions for circuit breakers: (A) primary and secondary membership functions of inputs (age and time from previous maintenance); (B) membership functions of output (percentage of change to the transition rates of the Markov model).
Generally, the reliability of the transformer will decrease with the aging of insulation. The discourse range of each fuzzy variable is quantified as many overlapping fuzzy sets. These variables are called linguistic variables, as shown in Figure 6(a-1), and are represented by Gaussian membership functions. For the fuzzy variable “insulation age,” the discourse range is the service life of the transformer about 50 years, which is quantified into three linguistic variables, namely, “young,” “middle-aged,” and “old.” Similarly, the age-specific secondary uncertainty (component condition) is quantified as three linguistic variables, namely, “good,” “normal,” and “poor.” For the “young” transformer, if its state is “good,” the membership degree of “young” is higher than that of “bad” state at the same age, so the reliability is higher. The increase of load will reduce the reliability of the transformer. Therefore, as shown in Figure 6(a-2), the other major variable “load” is quantified into three variables, “light,” “medium,” and “heavy.” There is no quadratic uncertainty associated with this variable.
The reliability of the transformer will decrease with the increase of previous maintenance time. Figure 6(a-3) shows the third major variable “time of previous maintenance,” which is quantified as three variables: "short,” “normal,” and “long.” In addition, compared with small-scale maintenance, the improvement of reliability is more significant in large-scale maintenance. Therefore, the influence of maintenance degree is a secondary uncertainty, which is represented by the Gaussian membership function.
The reliability of the transformer is also affected by the working environment as the fourth main variable. As shown in Figure 6(a-4), the “working environment” is quantified into three variables: "fine,” “normal,” and “adverse.” For offshore power plants, ambient temperature is one of the most important factors. Therefore, weather is selected as the factor to bring the secondary uncertainty into the operating environment. The membership function of weather is also shown in Figure 6(a-4).
The reliability output of the transformer and the change percentage of the transition rate of Markov model (
For circuit breakers, the main variables we focus on are the time and duration of previous maintenance because the reliability of circuit breakers is not sensitive to weather or load. Similar to transformers, age is quantified as three variables: “young,” “middle-aged,” and “old.” The secondary uncertainty of age is the component condition, i.e., “good,” “normal,” or “bad,” as shown in Figure 7(a-1). The second “main variable,” the time of previous maintenance, is quantified as “short,” “normal,” and “long.” The secondary uncertainty factor is “maintenance degree,” i.e., “minor maintenance,” “medium maintenance,” or “major maintenance” [Figure 7(a-2)]. The output variables are the same as the transformer variables but are represented by triangular membership functions, as shown in Figure 7B.
Results and Discussion
Case Study and Parameters
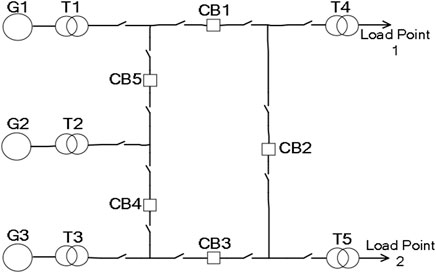
Figure 8 shows the ring configuration of bus 07 in the IEEE-RTS, which can be regarded as an offshore substation. The reliability of the load point is affected by the reliability of the transformer and circuit breaker in the substation. The adaptive maintenance consultant first obtains the initial maintenance plan from the system maintenance optimizer. The research period is set at 20 years.
Table 2 lists the basic fault data of transformers and circuit breakers without any maintenance during the first maintenance interval, which are obtained from the existing work (Billinton et al., 1985). Different priorities are assigned to each load point to reflect the importance of the load they transmit. In this study, load point 2 has priority 1 because it transfers the load back to the medium-sized system to which it is connected, while load point 1 has lower priority because it provides the load to individual customers.
Advantage of Secondary-Uncertainty–Varying Type 2 Fuzzy Logic
Taking the fuzzy logic system designed for the transformer as an example, it is shown that the proposed type 2 fuzzy logic system is easy to implement. Several items including the age, load, last maintenance time, working environment, load factor, and maintenance information have been utilized as the inputs of the transformer. In this type 2 fuzzy system, each input has three membership functions. Three additional uncertainties are superimposed on three inputs, which are represented by three fuzzy sets. In a word, the two kinds of fuzzy systems generate rules. Class 1 fuzzy systems with rules can represent the same uncertainty. Therefore, in dealing with other uncertainties, type 2 fuzzy logic is superior to type 1 fuzzy logic in computational complexity.
Impacts of Operational Variations and Their Secondary Uncertainties
Figures 9, 10 are used as the inputs of quadratic uncertainty type 2 fuzzy logic to calculate the reliability index of each component. When maintenance is not carried out, the Markov model is used to calculate the annual MTTF and failure probability.
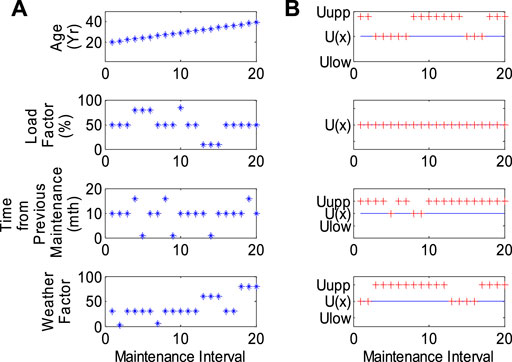
FIGURE 9. Varying operation conditions of transformers: (A) operation variations; (B) secondary uncertainty of each operation variation.
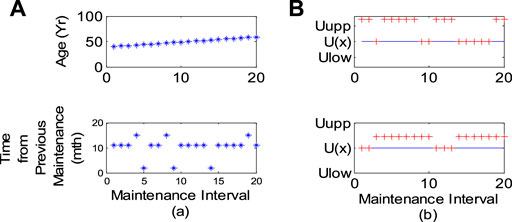
FIGURE 10. Varying operation conditions of circuit breakers: (A) operation variations; (B) secondary uncertainty of each operation variation.
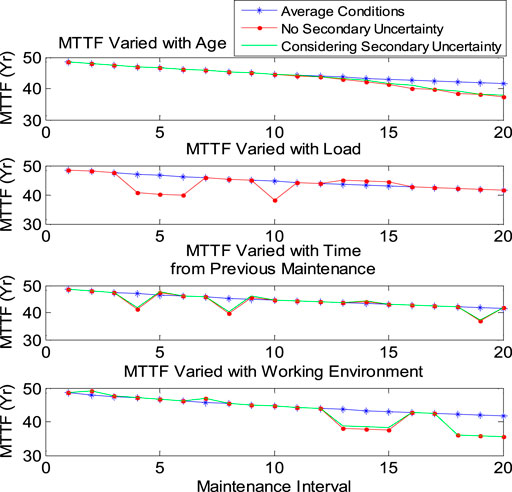
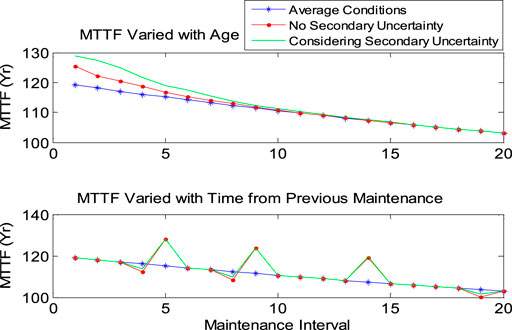
When calculating the MTTF and failure probability, the operation change and its secondary uncertainty should be considered and then compared with the MTTF and failure probability under average conditions (Table 3). Figures 11, 12 show the changes of failure probability and MTTF of the transformer under different service life, load, time from previous maintenance, and working environment, respectively. Considering the secondary uncertainty, these two reliability indexes are different from those only considering the main operation differences. The results show that the second fuzzy logic system successfully captures the quadratic uncertainty. Similar results for circuit breakers are shown in Figures 13, 14.
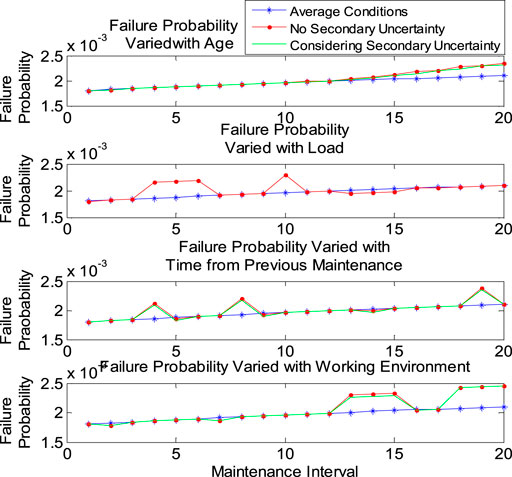
FIGURE 11. Failure probability variation of the transformer with each individual operation condition.
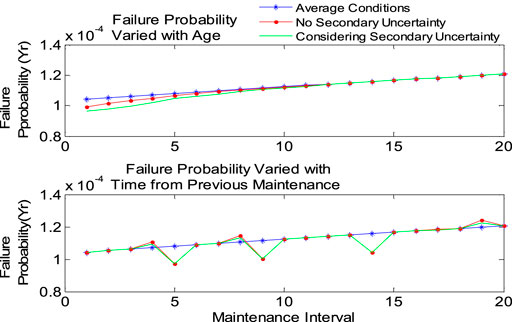
FIGURE 14. Failure probability variation of circuit breakers with each individual operation condition.
Impacts of Operational Variations and Their Secondary Uncertainties
These conditions may vary from time to time due to component aging, weather conditions, load requirements, and previous maintenance times. Therefore, it is not enough to carry out maintenance according to the schedule set at the beginning of the long-term maintenance plan. The purpose of the maintenance plan is to achieve the best reliability at the lowest operating cost under any different conditions. The maintenance plan is carried out under the same three conditions: 1) average condition; 2) considering operational changes without secondary uncertainties; and 3) considering secondary uncertainty.
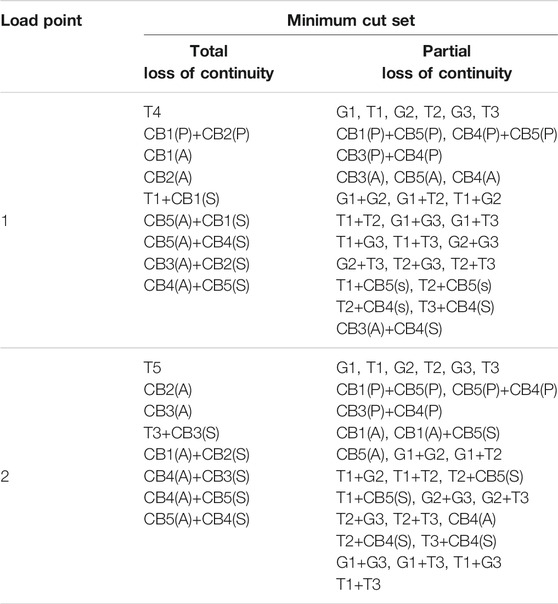
In order to evaluate the reliability of the whole system, it is necessary to determine the minimum cut-off points of each load point, which are listed in Table 4.
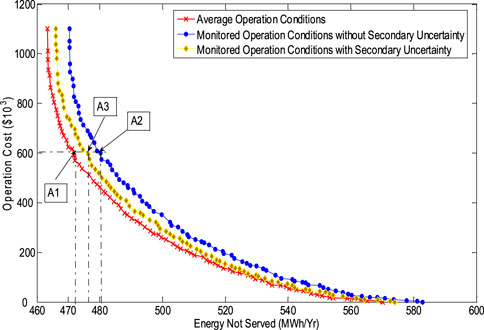
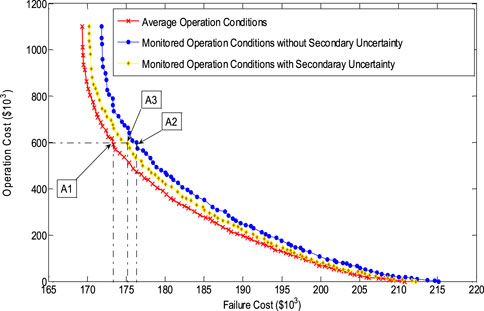
The effects of operational variations on maintenance scheduling are shown in Figures 15, 16. As can be seen in Figure 16, the positions of the two Pareto fronts with varied operation conditions are allocated above the one with average conditions. As a result, in order to achieve the same reliability or budget, the maintenance schedule should be changed according to the operation variations. For example, in order to maintain the operation cost at $6*105 when the operation conditions vary from average conditions, the maintenance schedule A2 should be chosen instead of A1, and the energy not served will be 480 MWh/Yr, which is 9 MWh/Yr higher than the one with average conditions. The higher energy not served also indicates that the monitored conditions which are more severe than average will cause worse reliability. A similar change also happens on the Pareto fronts in Figure 16.
Furthermore, the secondary uncertainty of the operational variations can also be well handled in the maintenance scheduling problem by this type 2 maintenance advisor. Figure 16 shows that the secondary uncertainty of the operational conditions also leads to the change of maintenance schedules. For example, in Figures 15, 16, the schedule A2 will be replaced by A3 because of the secondary uncertainty in the operational conditions.
Conclusion
Power systems are crucial for low-carbon energy applications. This paper proposes a hybrid method for implementing system optimization maintenance plans in offshore substations and estimating the reliability changes at load points due to operational variations and the uncertainty of key components. The maintenance consultant will report any sharp drop in the reliability of load point in the substation, which may lead to re-optimization of the substation’s maintenance activities for achieving the required reliability during operation. Facts have proved that when modeling the operational changes and uncertainties of substation transformers, type 2 fuzzy logic is better than type 1 fuzzy logic. Breaker failure and substation configuration have a significant impact on the reliability of the load point. Another contribution of this study is to propose a type 2 fuzzy hidden Markov model for offshore substations, which is used to model the relationship between non-linear performance characteristics and offshore equipment in the power system, further benefitting low-carbon renewable energy applications.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.
Author Contributions
LX curated the data and supervised the work. LX and HS investigated the data and wrote the original draft of the manuscript. FQ visualized the results and reviewed and edited the paper.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Anders, G. J., Endrenyi, J., Ford, G. L., and Stone, G. C. (1990). A Probabilistic Model for Evaluating the Remaining Life of Evaluating the Remaining Life of Electrical Insulation in Rotating Machines. IEEE Trans. Energy Convers. 5, 761–767. doi:10.1109/60.63150
Billinton, R., Vohra, P. K., and Kumar, S. (1985). Effect of Station Originated Outages in a Composite System Adequate Evaluation of the IEEE Reliability Test System. IEEE Trans. Power Apparatus Syst. PAS-100, 3870–3878. doi:10.1109/TPAS.1981.316982
Chang, C. S., Chen, J. M., Srinivasan, D., Wen, F. S., and Liew, A. C. (1997). Fuzzy Logic Approach in Power System Fault Section Identification. IEE Proc. Gener. Transm. Distrib. 144, 406–414. doi:10.1049/ip-gtd:19971278
Endrenyi, J., Aboresheid, S., Allan, R. N., Anders, G. J., Asgarpoor, S., Billinton, R., et al. (2001). The Present Status of Maintenance Strategies and the Impact of Maintenance on Reliability. IEEE Trans. Power Syst. 16 (11), 638–646. doi:10.1109/59.962408
Endrenyi, J., Anders, G. J., Leite, A. M., and da Silva, A. M. (1998). Probabilistic Evaluation of the Effect of Maintenance on Reliability. An Application [to Power Systems]. IEEE Trans. Power Syst. 13, 576–583. doi:10.1109/59.667385
Garibaldi, J. M., Musikasuwan, A., and Ozen, T. (2005). “The Associationg between Non-stationary and Interval Type-2 Fuzzy Sets: A Case Study,” in 2005 International Conference on Fuzzy Systems (Reno, USA: IEEE), 224–229. doi:10.1109/FUZZY.2005.1452397
Garibaldi, J. M., and Jaroszewski, M. (2008). “Generalisation of the Concept of a Non-stationary Fuzzy Set – a Starting Point to a Formal Discussion,” in IEEE World Congress on Computational Intelligence (Hong Kong, China: IEEE), 2313–2319. doi:10.1109/FUZZY.2008.4630691
Grall, A., Dieulle, L., Bérenguer, C., and Roussignol, M. (2002). Continuous-time Predictive-Maintenance Scheduling for a Deteriorating System. IEEE Trans. Rel. 51, 141–150. doi:10.1109/tr.2002.1011518
Hwang, C., and Rhee, F. C.-H. (2007). Uncertain Fuzzy Clustering: Interval Type-2 Fuzzy Approach to $C$-Means. IEEE Trans. Fuzzy Syst. 15 (1), 107–120. doi:10.1109/tfuzz.2006.889763
IEEE APM Subcommittee, (1999). The IEEE Reliability Test System-1996. IEEE Trans. Power Syst. 14 (3), 1010–1020. doi:10.1109/59.780914
Khanlari, A., Mohammadi, K., and Sohrabi, B. (2008). Prioritizing Equipments for Preventive Maintenance (PM) Activities Using Fuzzy Rules. Comput. Ind. Eng. 54 (2), 169–184. doi:10.1016/j.cie.2007.07.002
Li, J., Najmi, A., and Gray, R. M. (2000). Image Classification by a Two-Dimensional Hidden Markov Model. IEEE Trans. Signal Process. 48 (n 2), 517–533. doi:10.1109/78.823977
Lu, S., Tu, Y.-C., and Lu, H. (2007). Predictive Condition-Based Maintenance for Continuously Deteriorating Systems. Qual. Reliab. Engng. Int. 23 (1), 71–81. doi:10.1002/qre.823
Mechefske, C. K., and Wang, Z. (2003). Using Fuzzy Linguistics to Select Optimum Maintenance and Condition Monitoring Strategies. Mech. Syst. Signal Process. 17 (2), 305–316. doi:10.1006/mssp.2001.1395
Mendel, J. M. (2001). Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions. Upper Saddle River, NJ: Prentice-Hall.
Mendel, J. M., John, R. I., and Liu, F. (2006). Interval Type-2 Fuzzy Logic Systems Made Simple. IEEE Trans. Fuzzy Syst. 14 (6), 808–821. doi:10.1109/tfuzz.2006.879986
Mohanta, D. K., Kumar Sadhu, P., and Chakrabarti, R. (2004). Fuzzy Markov Model for Determination of Fuzzy State Probabilities of Generating Units Including the Effect of Maintenance Scheduling. IEEE Trans. Power Syst. 20, 2117–2124. doi:10.1109/TPWRS.2005.857932
Mohanta, D. K., Sadhu, P. K., and Chakrabarti, R. (2005). Fuzzy Markov Model for Determination of Fuzzy State Probabilities of Generating Units Including the Effect of Maintenance Scheduling. IEEE Trans. Power Syst. 20 (4), 2117–2124. doi:10.1109/tpwrs.2005.857932
Noor, S. F., and McDonald, J. R. (1996). Forced-outage Rates of Generating Units Based on Expert Evaluation. IEEE Trans. Rel. 45 (1), 138–140. doi:10.1109/24.488931
Papoulis, A., and Unnikrishna Pillai, S. (2002). Probability, Random Variables, and Stochastic Processes. Dubuque, Iowa: McGraw-Hill.
Popescu, M., Gader, P., and Keller, J. M. (2006). Fuzzy Spatial Pattern Processing Using Linguistic Hidden Markov Models. IEEE Trans. Fuzzy Syst. 14 (n 1), 81–92. doi:10.1109/tfuzz.2005.861615
Satish, L., and Gururaj, B. I. (1993). Use of Hidden Markov Models for Partial Discharge Pattern Classification. IEEE Trans. Electr. Insul. 28 (n 2), 172–182. doi:10.1109/14.212242
Strachan, S. M., McArthur, S. D. J., Stephen, B., McDonald, J. R., and Campbell, A. (2007). Providing Decision Support for the Condition-Based Maintenance of Circuit Breakers through Data Mining of Trip Coil Current Signatures. IEEE Trans. Power Deliv. 22 (1), 178–186. doi:10.1109/tpwrd.2006.883001
Suresh, P. V., Chaudhuri, D., and Rao, B. V. A. (1994). Fuzzy-set Approach to Select Maintenance Strategies for Multistate Equipment. IEEE Trans. Rel. 43 (3), 451–456. doi:10.1109/24.326445
Tan, W. W., and Kamal, D. H. (2006). “On-line Learning Rules for Type-2 Fuzzy Controller,” in IEEE International Conference on Fuzzy Systems (IEEE), 513–520. doi:10.1109/fuzzy.2006.1681760
Tanrioven, M., Wu, Q. H., Turner, D. R., Kocatepe, C., and Wang, J. (2004). A New Approach to Real-Time Reliability Analysis of Transmission System Using Fuzzy Markov Model. Int. J. Electr. Power Energ. Syst. 26 (10), 821–832. doi:10.1016/j.ijepes.2004.07.004
Uncu, O., and Türks, I. B. (2007). Discrete Interval Type 2 Fuzzy System Models Using Uncertainty in Learning Parameters. IEEE Tran. Fuzzy Syst. 15 (1), 91–105. doi:10.1109/tfuzz.2006.889765
Wang, Z-X., Chang, C. S., Yang, F., and Tan, W. W. (2009). “Adaptive Type-2 Fuzzy Maintenance Advisor for Offshore Power Systems,” in 2009 IEEE International Conference on Systems, Man, and Cybernetics (Texas, USA: IEEE), 11–14. doi:10.1109/icsmc.2009.5346899
Wang, Z.-X., Yang, F., Tan, W. W., and Chang, C. S. (2008). “Intelligent Maintenance Advisor for marine Power System Using Type-2 Fuzzy Logic for Handling Condition Updates and Operation Uncertainties,” in 5th International Conference on Engine and Condition Monitoring, (Invited Paper) (Singapore: Springer), 9–10.
Xu, Y., and Ge, M. (2004). Hidden Markov Model-Based Process Monitoring System. J. Intell. Manufacturing 15 (n 3), 337–350. doi:10.1023/b:jims.0000026572.03164.64
Yang, F., Kwan, C. M., and Chang, C. S. (2008). Multiobjective Evolutionary Optimization of Substation Maintenance Using Decision-Varying Markov Model. IEEE Trans. Power Syst. 23 (3), 1328–1335. doi:10.1109/tpwrs.2008.922637
Keywords: renewable energy, power system, offshore substation, multi-objective evolutionary algorithm, type 2 fuzzy logic, minimum cut set
Citation: Xiang L, Sang H and Qu F (2021) A Type 2 Fuzzy Logic–Based Maintenance Solution for Power System in Renewable Energy Applications. Front. Energy Res. 9:762360. doi: 10.3389/fenrg.2021.762360
Received: 21 August 2021; Accepted: 22 September 2021;
Published: 03 December 2021.
Edited by:
Zhile Yang, Shenzhen Institutes of Advanced Technology (CAS), ChinaReviewed by:
Yihuan Li, University of Leeds, United KingdomQiao Peng, Queen’s University Belfast, United Kingdom
Copyright © 2021 Xiang, Sang and Qu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haitao Sang, c2FuZ2h0QGxpbmduYW4uZWR1LmNu
 Li Xiang1
Li Xiang1 Haitao Sang
Haitao Sang