Practical Method for Data-Driven User Phase Identification in Low-Voltage Distribution Networks

For low-voltage distribution networks (LVDNs), accurate models depicting network and phase connectivity are crucial to the analysis, planning, and operation of these networks. However, phase connectivity data in the LVDN are usually incorrect or missing. Wrong or incomplete phase information collected could lead to unbalanced operation of three-phase distribution systems and increased power loss. Based on the advanced measurement infrastructure (AMI) in the development of smart grids, in this study, a novel data-driven phase identification algorithm is proposed. Firstly, the method involves extracting features from voltage–time matrices using a non-linear dimension reduction algorithm. Secondly, the density-based spatial clustering of applications with noise (DBSCAN) algorithm is used to divide customers into clusters with arbitrary shape. Finally, the algorithms were tested with the IEEE European Low Voltage Test Feeder of the IEEE PES AMPS DSAS Test Feeder working group. The results showed an accuracy of over 90% for the method.

Introduction

Since the introduction of the concept of “Digital Power Grid” (Islam, 2016) and the development of measurement technology, how to deal with electrical data in smart grids has become a focus of research. At the same time, distributed energy resources (DERs) are being deployed in the electric power distribution systems at an unprecedented pace (Yang et al., 2016; Yang et al., 2017; Yang et al., 2018; Yang et al., 2019a). To fully exploit the benefits of the DERs, the distribution network must be actively managed (Yang et al., 2019b; Xi et al., 2020; Yang et al., 2020; Li et al., 2021). The low-voltage distribution network is the last link to connect users in the whole power system. Therefore, the network’s level of information interaction ability directly affects the user experience. The distribution network must be actively managed.

The introduction of the smart grid and advanced measurement infrastructure (AMI) concepts has brought new opportunities for developing distribution networks. To operate the distribution system in an efficient and reliable manner, distribution system operators typically need to perform a series of tasks, including three-phase optimal power flow, distribution system restoration and reconfiguration, and three-phase unbalance degree. Although network connectivity models are often accurate, phasing errors are common. Therefore, an accurate phase identification method is needed.

Electric utility companies typically do not have accurate information on phase connectivity. Moreover, phase connectivity of a distribution network may change when new distribution lines are constructed and included in the network. Correct phase connectivity data are essential to the efficient and reliable operation of a distribution system, especially when more advanced applications are connected. A model has been established to identify transformers and user phases based on voltage correlation using linear regression (Short, 2013). The correlation between a circuit and transformers in it can be determined by analyzing the correlation in voltage between buses and user meters from the perspective of power flow (Luan et al., 2013; Tang and Milanovic, 2018). Topology can also be identified by analyzing the correlation in load between lines at upper and lower levels (Pappu et al., 2018; Lisowski et al., 2019). Most of these studies focus on medium-voltage distribution networks, while the identification of topology in LVDNs is yet to be studied. There are two methods to identify the phase in LVDNs. The first method is based on the law of conservation of energy. With all possible user phases listed, the mixed integer programming model is used to find the optimal solution, taking into consideration the degree of three-phase unbalance and line loss (Tian et al., 2016; Tang and Milanovic, 2018; Zhou et al., 2020). The method requires complex calculation, and the electrical features of users in the same phase sequence are not considered. When there are missing user power values, accuracy is not guaranteed. The other method is based on the clustering algorithm in machine learning. User phases in an LVDN are identified by establishing clusters among three-phase users (Wen et al., 2015; Wang et al., 2016; Liu et al., 2020). However, the difference in load fluctuation between phases is not intuitive enough after three-phase treatment in LVDNs.

To address the problem of the existing solutions, the current study proposes a data-driven phase identification algorithm based on the advanced metering infrastructure (AMI) that allows for in-depth exploitation of data features. Then, the LargeVis (Large-scale Visualizing Data) dimensionality reduction algorithm is used to extract data from high-dimensional time–voltage matrices of LVDN users, resulting in low-dimension data which retain only the main features. Finally, the DBSCAN (density-based spatial clustering of application with noise) algorithm is used to analyze the features of users in clusters and identify the specific user phases. The method may improve the efficiency and accuracy of topology identification.

Topology of Low-Voltage Distribution Networks

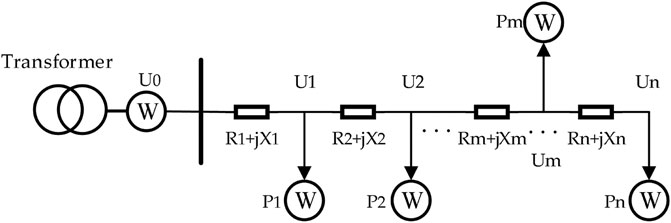
Through the high-voltage transmission line, the electric energy is transmitted to the distribution network. After the distribution transformer is stepped down to 400 V, the electric energy is transmitted to the clients through the three-phase feeder.

Three-phase gate ammeters are installed at the outlet of the distribution transformer to record voltage, current, active power, reactive power, load, and other values for each of the three-phase electrical data information of the feeder. Figure 1 shows the relationship between the gate ammeter at the bus and the meter of each user in a singer-phase line.

FIGURE 1

FIGURE 1. Schematic diagram of single-phase power flow.

As low-voltage distribution feeders extend to a shorter distance than high-voltage lines, no more than 500 m in most cases, the influence of line reactance is not considered in this study. Reactive power effects that exist on the lines are not considered neither, as they are negligible in well-managed networks:

$U_1=U_0-\frac{R_1{P}_1}{U_0},(1)$

$U_m=U_0-\frac{R_1{P}_1}{U_0}-\frac{R_2{P}_2}{U_1}-\cdot \cdot \cdot \hspace{0.17em}\frac{R_m{P}_m}{U_{m-1}}=U_0-{\displaystyle \sum }_{i=1}^m\frac{R_i{P}_i}{U_{i-1}},(2)$

$△U_m=U_m-U_{m-1}=-\frac{R_m{P}_m}{U_{m-1}}<0,(3)$

where $U_0$ represents the voltage at the bus node; $U_1, U_{m-1}, U_m, U_n$ are the voltage values at the corresponding node; $R_1, R_2, R_m, R_n$ are the impedance values of the corresponding line; and $△U_m$ is the voltage difference between adjacent nodes $m$ and $m-1$.

The voltage of users closest to the bus is related only to the bus voltage and their own load. When positioned with short electrical intervals, adjacent nodes in the same feeder will have similar voltage values and the coefficient of correlation is higher than that when they are in different feeders. By analyzing the changes of user voltage values in time sequences, the phase relationships of users can be identified.

Data Pre-Processing and Phase Recognition Algorithm

Time-Series Voltage Data Pre-Processing

The users’ smart meter collects voltage data at a given interval and uploads them to the terminal. The time-series variation matrix of voltage amplitude of users in the station area is obtained from the historical data in the terminal. If some data are missing, and the interpolation method is used to complete the missing values, $U\in R^{N\times M}$ is shown as follows:

$U=\left[\begin{array}{cccc}{u}_{1,t_1}& u_{1,t_2}& \cdot \cdot \cdot & u_{1,t_M}\\ u_{2,t_1}& u_{2,t_2}& \cdot \cdot \cdot & u_{2,t_M}\\ ⋮& ⋮& ⋮& ⋮\\ u_{N,t_1}& u_{N,t_2}& \cdot \cdot \cdot & u_{N,t_M}\end{array}\right],(4)$

where $u_{i,t_j}$ represents the measured voltage of user $i$ at time $t_j$, $N$is the total number of users, and $M$ represents the number of voltage collection times within the analysis period.

For user nodes near the bus, since their voltage is only affected by the bus voltage and their own load, their voltage timing curve will be close to that of the bus if the value of their own load is low. This will cause great disturbance to the subsequent clustering. To avoid this problem, these nodes are distinguished from the rest of the matrix and put into a separate cluster based on their correlation with the bus in terms of voltage and their voltage amplitude. The rest of the data are standardized to eliminate the influence of variation in voltage fluctuation at different phases. The dimensionality of the time–voltage matrix does not change after standardization. The formula used for standardization is as follows:

$U_{t_j}^{\prime }=\frac{U_{t_j}-\mu \left(U_{t_j}\right)}{\sigma \left(U_{t_j}\right)},(5)$

where $U_{t_j}^{\prime }$ represents standardization of voltage at $t_j$; $U_{t_j}$ represents initial values of the voltage at $t_j$; $\mu \left(U_{t_j}\right)$ represents the mean value of voltage at all measurement points at $t_j$; $\sigma \left(U_{t_j}\right)$ represents the voltage standard deviation at all measurement points at $t_j$; and $U^{\prime }$ represents the standardized user voltage dataset.

Feature Dimension Reduction Based on LargeVis

As the time for data collection mounts, the dimensionality of time–voltage matrices also increases. High-dimensional datasets contain excessively redundant information and data noise and require more complex and time-consuming computation.

PCA linear dimension reduction first conducts projection transformation and then finds the low-dimensional space that maximizes its goal. The purpose is to maintain the maximum variance of samples in the low-dimensional space, and the processing speed is fast, but the information loss is serious when the dimension is low. In this study, the LargeVis method is used to reduce the dimensionality of the data, keeping only the main features. It can reduce the high-dimensional dataset of the user voltage matrix to two or three dimensional spaces for visualization and retain the distribution characteristics of the original voltage dataset. The above problems should be improved by means of the feature dimension reduction method.

LargeVis (Tang et al., 2016) is a non-linear reductive dimension algorithm, which can reduce the high-dimensional dataset of the user voltage matrix to two or three dimensional spaces for visualization and retain the distribution characteristics of the original dataset. This algorithm was proposed by Professor Tang Jian in 2016. The dimension reduction process is as follows:

1) In high-dimensional space, LargeVis retains only the weight of KNN edges in the process of mapping. These edges are called positive edges, while nodes that are not directly adjacent are called negative edges. In high-dimensional space, the Euclidean distance between users is transformed into probability similarity, and the formula is as follows:

$p_{j|i}=\frac{\exp \left(-{\Vert X_i^{\prime }-X_j^{\prime }\Vert }^2/2{\sigma }_i^2\right)}{{{\displaystyle \sum }}_{k\ne i}\exp \left(-{\Vert X_i^{\prime }-X_k^{\prime }\Vert }^2/2{\sigma }_i^2\right)},(6)$

$w_{ij}=\frac{p_{j|i}+p_{i|j}}{2L},(7)$

$W_i=\left[w_{i1},w_{i2},w_{i3}\dots ,w_{iL}\right],(8)$

where $w_{ij}$ is the probability similarity between user $i$ and user $j$, to avoid the outlier node, getting it by adding conditional probabilities. $W_i$ is the similarity matrix between user$i$ and other users in the same station. $W$ is the Gaussian probability distribution matrix of the normalized voltage dataset. ${\sigma }_i$ is the standard deviation of the Gaussian model.

2) In low-dimensional space, the low-dimensional coordinates are determined by the probability of observation, and the probability of an edge connection between two points is set as follows:

$P\left(e_{ij}=1\right)=f\left(\Vert y_i-y_j\Vert \right),(9)$

$f\left(x\right)=\frac{1}{1+\exp \left(x^2\right)},(10)$

$P\left(e_{ij}=w_{ij}\right)=P{\left(e_{ij}=1\right)}^{w_{ij}},(11)$

where $e_{ij}$ represents the edge weight between two nodes and $f\left(x\right)$ is a probability function, indicating the distance between vertices $y_i$ and $y_j$. The closer the points are in higher dimensions, the closer the points are in lower dimensions.

3) In the dimension reduction process, the final objective function is as follows:

$O={\displaystyle \sum _{\left(i,k\right)\in E}{w}_{ij}\log p\left(e_{ij}=1\right)}+{\displaystyle \sum _{k=1}^m{E}_{jk}\sim P_n\left(j\right)\gamma \log \left(1-p\left(e_{jk}=1\right)\right)},(12)$

where $E$ is the set of positive edges, $\bar{E}$ is a complement to $E$, and $\gamma$ is the uniform weight assigned to the negative edge.

Using LINE technology (Tang et al., 2015), the weighted edge is regarded as the $w_{ij}$ unit edge. All positive edges are sampled directly, and the weight of the edge is trained to obtain the low-dimensional feature set $Y$. $Y$ is consistent with the characteristic distribution of the standardized voltage dataset $U_{L\times M}^{\prime }$.

Phase Identification Based on DBSCAN Algorithm

Clustering of unlabeled voltage–time datasets can be performed with unsupervised learning algorithms. DBSCAN (density-based spatial clustering of applications with noise) as a density-based clustering algorithm can divide regions with enough density into clusters and identify clusters of arbitrary shape in spatial databases with noise.

After dimension reduction, the Euclidian distance between two points is used as the distance between them. Users at the same phase have relatively shorter distances between them and will form a cluster. Therefore, the DBSCAN method is suitable.

The core point of DBSCAN is determined by setting parameters, including the neighborhood radius (Eps) and the minimum number of sample points (MinPts). To limit the space of density clustering and achieve better visual performance, the maximum and minimum values of the feature set Y after dimension reduction are normalized. The formula is as follows:

$y_{ij}^{\prime }=\frac{y_{ij}-\min \left(y_{\text{*}j}\right)}{\max \left(y_{\text{*}j}\right)-\min \left(y_{\text{*}j}\right)},(13)$

where $y_{ij}$ is a member of matrix $Y$, $\max \left(y_{\ast j}\right)$ is the maximum value of the $j$ column vector in the $Y$ dataset, $\min \left(y_{\ast j}\right)$ is the minimum value of the $j$ column vector in the $Y$ dataset, and $y_{ij}^{\prime }$ belongs to the normalized dataset $Y^{\prime }$.

Based on the dataset $Y^{\prime }$, the distance between all nodes in the dataset is calculated to form a matrix D$\in R^{L\times L}$. The calculation formulas are as follows:

$D_i={\left[d\left(Y_i^{\prime },Y_1^{\prime }\right),d\left(Y_i^{\prime },Y_2^{\prime }\right),\dots ,d\left(Y_i^{\prime },Y_L^{\prime }\right)\right]}^T,(14)$

$D=\left[D_1,D_2,\dots ,D_L\right].(15)$

Here, $d\left(Y_i,Y_j\right)$ indicates the Euclidean distance between $Y_i$ and $Y_j$.

To establish DBSCAN parameters Eps and MinPts, the calculation formulas are as follows:

$\mathrm{Eps}=\frac{\stackrel{\underset{L}{i=1}}{\min }\left\{\stackrel{\underset{L}{j=1}}{\max }\left[D_j\right]\right\}}{Z},(16)$

$MinPts=\frac{\min \left(\stackrel{\underset{L}{i=1}}{count}\left(D_i<Eps\right)\right)}{Z}.(17)$

Here, $Z$ is the number of predicted clusters and $count\left(D_i<Eps\right)$ is the number of nodes whose distance between adjacent and surrounding nodes is less than Eps in the distance vector $D_j$.

After that, set a certain step size, adjust the values of Eps (0.01) and MinPts (1), and determine the most suitable parameter coefficient according to the silhouette coefficient. The formula for calculating the silhouette coefficient is as follows:

$s\left(i\right)=\frac{b\left(i\right)-a\left(i\right)}{\max \left\{a\left(i\right),b\left(i\right)\right\}}.(18)$

Here, $a\left(i\right)$ represents the average distance between node $i$ and other nodes in the same cluster and $b\left(i\right)$ represents the average distance between node $i$ and other cluster nodes. The closer $s\left(i\right)$ is to 1, the more reasonable the clustering result is. In other words, the closer $s\left(i\right)$ is to -1, the more unreasonable the clustering result is.

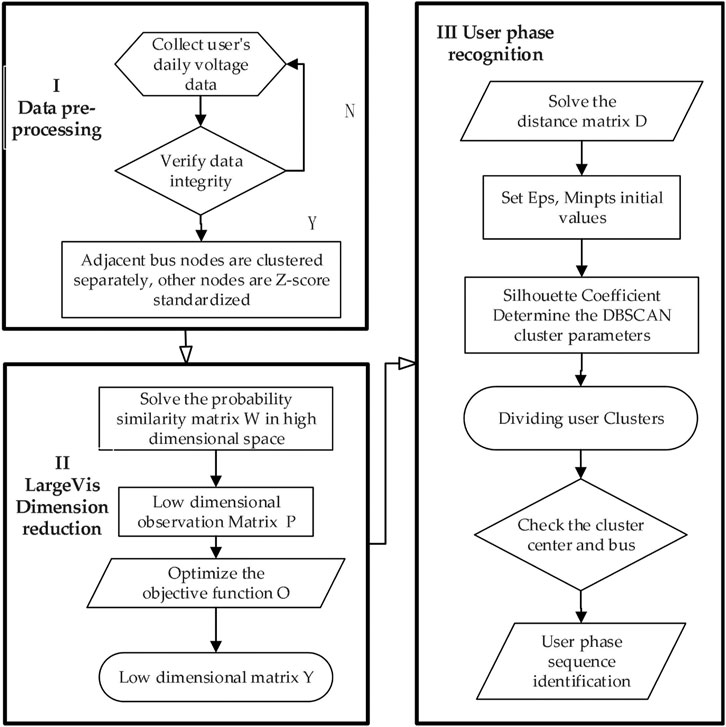
After clustering, each cluster group is obtained, and the phase recognition results of users are tested according to the phase tags of clustering results. The specific flow chart is shown in Figure 2.

FIGURE 2

FIGURE 2. Phase recognition algorithm process.

Analysis of Examples

The dataset used in this paper is the IEEE European Low Voltage Test Feeder of the IEEE PES AMPS DSAS Test Feeder working group (IEEE and PES, 2019). The low-voltage test feeder is a radial distribution feeder with a base frequency of 50 Hz. The feeder is connected to the medium-voltage power system through the transformer of the substation, which makes the voltage from 11 kV to 416 V. There are 55 users in total, and all of them are single-phase users. There are 21 households with phase A load, 19 households with phase B load, and 15 households with phase C load.

According to the configuration file, the power factor of all loads was set to be 0.95 in the whole simulation range. According to the power load curve of 55 users, the power flow calculation was carried out by OpenDSS software, and the voltage curve lasting 24 h with a resolution of 1 minute was obtained.

Parameter Settings of LargeVis and DBSCAN

In the actual environment, the situation of smart meter measurement may be more complicated, and the error is inevitable. To evaluate the effectiveness of the algorithm in the actual environment, we need to test it in a noisy dataset. Smart meters have a non-negligible uncertainty, and their accuracy levels vary in different countries. According to the measurement, the accuracy can be roughly divided into the following grades: 0.2, 0.5, 1, and 2, which means the uncertainty of 0.2, 0.5, 1, and 2%, respectively.

The number of nodes near the bus caused by error clustering accounted for 5∼8% of the total number of nodes. According to the correlation between voltage amplitude and bus, related nodes will be classified separately. The voltage timing matrix composed of other meters has been standardized by the Z-score to obtain the matrix $U^{\prime }$. The LargeVis algorithm is used to reduce the dimension of the user timing voltage matrix $U^{\prime }$. After dimension reduction, the low-dimensional voltage characteristic matrix $Y$ is obtained. The low-dimensional $Y$ is maximally and minimally normalized to $Y^{\prime }$. Calculating the distance matrix between each node of the user, Z is 3 to obtain the initial DBSCAN parameter value (Eps = 0.126, MinPts = 4). Eps changes with the step size of 0.005, MinPts changes with the step size of 1, and the specific values of cluster parameters are determined by the profile coefficient method.

Analysis of Numerical Example Results

Eps = 0.131, MinPts = 3, as the final cluster input parameter. Three clusters are formed after clustering. After comparing the correlation coefficient between the user voltage in the cluster center and the bus voltage, the phase sequence of the users in the station area can be determined.

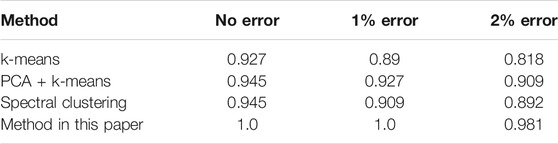
To further prove the accuracy of the proposed method in phase recognition, the proposed method is compared with k-means, PCA, and k-means (Wen et al., 2015) and spectral clustering algorithm (Wang et al., 2016). The cluster number of each method is preset as 3. The recognition accuracy of the results is shown in Table 1.

TABLE 1

TABLE 1. Accuracy comparison of phase recognition methods.

The method proposed in this study showed the highest accuracy compared with the other methods. One of the reasons might be that the users near the bus were put into a separate cluster to avoid interference. Moreover, the LargeVis algorithm is able to retain data features after dimensionality reduction and the DBSCAN algorithm can cluster data points of arbitrary density, making them more suitable for processing datasets. For k-means, errors with ammeters may cause excessively redundant information in the time–voltage matrix, resulting in the instability of clustering results. For PCA, the linear dimensionality reduction approach they use to remove redundant information may lead to loss of data details and thus decreased accuracy. As for spectral clustering, the clustering effect directly depends on the similarity matrix generated in advance, which requires high precision of the original data.

To verify the usability of the proposed algorithms in engineering problems, disturbance errors were set for accuracy analysis under different sampling frequencies. The sampling frequency of the ammeters was set to 15 min, 30 min, 1 h, or 2 h, and the disturbance error was set to no error, 1%, or 2%. The results are shown in Table 2.

TABLE 2

TABLE 2. Evaluation indicators of phase identification in different cases.

When the metering error is small, the identification accuracy of the algorithm in this paper decreases. When the metering error increases, the accuracy of phase sequence identification can be guaranteed only on high sampling frequency (15 min). The decrease of acquisition frequency will decrease the accuracy of recognition rate. When the collection frequency is reduced to 2 h, the identification cannot be completed, which indicates that a certain sampling frequency should be guaranteed for phase identification based on users’ daily voltage variation characteristics.

Conclusion and Discussion

This paper presents a data-driven method for user phase identification in LVDNs. The LargeVis reductive dimension method is used to extract features from the standardized timing voltage matrix. Then, based on the DBSCAN method, the low-dimensional dataset is clustered as a result of user phase identification. Simulations show that the proposed method is more reliable than other unsupervised learning algorithms for single-phase user identification in LVDNs. The method used in this paper only needs to collect the user’s load data for analysis, without additional hardware equipment costs and special personnel to check users one by one, so it can save the cost of user phase verification in the low-voltage distribution network.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

HY involved in conceptualization, performed the methodology, and wrote the article. YW curated the data. WG involved in formal analysis. QL investigated the data. TY obtained the resources and acquired the funding.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge the support of science and technology project by China Southern Power Grid (GDKJXM20172939).

References

IEEEPES. (2019). Distribution Test Feeders. Available at: http://sites.ieee.org/pes-testfeeders/resources/. (still can Accessed June 10, 2021)

Google Scholar

Islam, S. (2016). “Digital Applications in Implementation of Smart Grid,” in International Conference on Accessibility to Digital World (ICADW), Guwahati, India, Dec, 2016, 3–7. doi:10.1109/icadw.2016.7942504

CrossRef Full Text | Google Scholar

Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021). Efficient Experience Replay Based Deep Deterministic Policy Gradient for AGC Dispatch in Integrated Energy System. Appl. Energ. 285, 116386. doi:10.1016/j.apenergy.2020.116386

CrossRef Full Text | Google Scholar

Lisowski, M., Masnicki, R., and Mindykowski, J. (2019). PLC-enabled Low Voltage Distribution Network Topology Monitoring. IEEE Trans. Smart Grid. 10 (6), 6436–6448. doi:10.1109/tsg.2019.2904681

CrossRef Full Text | Google Scholar

Liu, S., Jin, R., Qiu, H., Cui, X., Lin, Z., Lian, Z., et al. (2020). Practical Method for Mitigating Three-phase Unbalance Based on Data-Driven User Phase Identification. IEEE Trans. Power Syst. 35, 1653–1656. doi:10.1109/tpwrs.2020.2965770

CrossRef Full Text | Google Scholar

Luan, W., Peng, J., Maras, M., and Lo, J. (2013). “Distribution Network Topology Error Correction Using Smart Meter Data Analytics,” in IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, July, 2013. doi:10.1109/pesmg.2013.6672786

CrossRef Full Text | Google Scholar

Pappu, S. J., Bhatt, N., and RajeswaranPasumarthy, A. (2018). Identifying Topology of Low Voltage Distribution Networks Based on Smart Meter Data. IEEE Trans. Smart Grid. 9, 5113–5122. doi:10.1109/tsg.2017.2680542

CrossRef Full Text | Google Scholar

Short, T. A. (2013). Advanced Metering for Phase Identification, Transformer Identification, and Secondary Modeling. IEEE Trans. Smart Grid. 4 (2), 651–658. doi:10.1109/tsg.2012.2219081

CrossRef Full Text | Google Scholar

Tang, X., and Milanovic, J. V. (2018). “Phase Identification of LV Distribution Network with Smart Meter Data,” in IEEE Power & Energy Society General Meeting, Portland, OR, USA, Aug, 2018.

CrossRef Full Text | Google Scholar

Tang, J., Liu, J., Zhang, M., and Mei, Q. (2016). “Visualizing Large-Scale and High-Dimensional Data,” in Proceedings of the 25th International World Wide Web Conference, WWW, Montreal, Canada, April 11-15, 2016, 287–297. doi:10.1145/2872427.2883041

CrossRef Full Text | Google Scholar

Tang, J., Qu, M., Wang, M., Zhang, M., Yan, J., and Mei, Q. (2015). “LINE: Large-Scale Information Network Embedding,” in Proceedings of the 24th International Conference on world wide web, Montreal, Canada, April 11-15, 2016,1067.

Google Scholar

Tian, Z., Wu, W., and Zhang, B. (2016). A Mixed Integer Quadratic Programming Model for Topology Identification in Distribution Network. IEEE Trans. Power Syst. 31, 823–824. doi:10.1109/tpwrs.2015.2394454

CrossRef Full Text | Google Scholar

Wang, W., Yu, N., Foggo, B., Davis, J., and Li, J. (2016). “Phase Identification in Electric Power Distribution Systems by Clustering of Smart Meter Data,” in Proceedings. 2016 15th IEEE International Conference on Machine Learning and Applications, ICMLA. Anaheim, CA, USA, Dec, 2016, 259–265. doi:10.1109/icmla.2016.0050

CrossRef Full Text | Google Scholar

Wen, M., Arghandeh, R., Meier, A., Poolla, K., and Li, V. (2015). “Phase Identification in Distribution Networks with Micro-synchrophasors,” in Power and Energy Society General Meeting, Denver, CO, USA, July, 2015.

CrossRef Full Text | Google Scholar

Xi, L., Wu, J., Xu, Y., and Sun, H. (2020). Automatic Generation Control Based on Multiple Neural Networks with Actor-Critic Strategy. IEEE Trans. Neural Netw. Learn. Syst. 32 (6), 2483–2493. doi:10.1109/TNNLS.2020.3006080

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on Pv Cell Parameter Identification. Energ. Convers. Manage. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019). Dynamic Leader Based Collective Intelligence for Maximum Power point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manage. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zhang, X., Yu, T., Shu, H., and Fang, Z. (2017). Grouped Grey Wolf Optimizer for Maximum Power point Tracking of Doubly-Fed Induction Generator Based Wind Turbine. Energ. Convers. Manag. 133, 427–443. doi:10.1016/j.enconman.2016.10.062

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Zhou, L., Zhang, Y., Liu, S., Li, K., Li, C., Yi, Y., et al. (2020). Consumer Phase Identification in Low-Voltage Distribution Network Considering Vacant Users. Int. J. Electr. Power Energ. Syst. 121, 106079. doi:10.1016/j.ijepes.2020.106079

CrossRef Full Text | Google Scholar