First-Principles Design of Rutile Oxide Heterostructures for Oxygen Evolution Reactions

The oxygen evolution reaction (OER) plays a key role in the determination of overall water-splitting rate. Lowering the high overpotential of the OER of transition metal oxides (TMOs), which are used as conventional OER electrocatalysts, has been the focus of many studies. The OER activity of TMOs can be tuned via the strategic formation of a heterostructure with another TMO substrate. We screened 11 rutile-type TMOs (i.e., MO₂; M = V, Cr, Mn, Nb, Ru, Rh, Sn, Ta, Os, Ir, and Pt) on a rutile (110) substrate using density functional theory calculations to determine their OER activities. The conventional volcano approach based on simple binding energies of reaction intermediates was implemented; in addition, the electrochemical-step symmetry index was employed to screen heterostructures for use as electrode materials. The results show that RuO₂ and IrO₂ are the most promising catalysts among all candidates. The scaling results provide insights into the intrinsic properties of the heterostructure as well as materials that can be used to lower the overpotential of the OER.

Introduction

Green hydrogen production remains a challenge that must be overcome to achieve a hydrogen economy (Turner, 2004). Water electrolysis is one of the approaches toward hydrogen eco-friendliness. It is based on the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) as cathodic and anodic reactions, respectively. However, the slow kinetics of the OER limit the commercialization of this approach. Oxide systems based on Ir or Ru (i.e., IrO_x or RuO_x) are known to have the best OER performances (Lee et al., 2012; Frydendal et al., 2014; Suen et al., 2017). However, these materials are expensive. Therefore, many studies have been conducted to identify a cost-effective alternative oxide material with high activity. For example, transition-metal substitution (García-Mota et al., 2011) and the introduction of oxygen vacancies (Xiao et al., 2020) have been studied as means to control the compositions of expensive materials. However, transition-metal substitution and oxygen vacancies only locally affect the active sites.

To activate the metal oxide, support materials are mixed with the oxide to enhance the electrical conductivity and activity of the electrocatalytic reaction (Kumar et al., 2016; Qingxiang et al., 2018; Bu et al., 2019; Lu et al., 2019). In addition, research on heterostructures is conducted with the goal of activating the material on the substrate. Modifications are mainly based on the strain effect and charge transfer due to the formation of an interface between the support material and catalyst. For instance, the heterostructure of La_0.5Sr_0.5CoO_3-δ and MoSe₂ induces the phase transition of MoSe₂ from the 2H to the 1T phase (Oh et al., 2019). In addition, the charge transfer from the Co ion to Mo ion improves the electrochemical activity. The results of another study showed that the heterostructure of IrO_x and SrIrO₃ outperforms iridium or ruthenium oxide systems (Seitz et al., 2016). Based on density functional theory (DFT) calculations, IrO₃ or anatase IrO₂ motifs are formed during strontium leaching in the outermost surface layers of SrIrO₃ and contribute to the high activity. Another strength of the heterostructure is that it can possibly contribute to reducing the use of precious metals by replacing them into low-cost metals while maintaining similar intrinsic activity of each active site (Esposito et al., 2010; Zhou et al., 2014; Wang et al., 2015; Jin et al., 2016). Rutile (TiO₂) is a well-known substrate material for metal oxide systems because of its high structural stability and simple structure (Hanaor et al., 2012). It is suitable for the growth of oxide films, facilitating the fabrication of heterostructures with various metal oxides. In addition, rutile affects the catalytic activity of metal oxides and has a high cost effectiveness (Seitsonen and Over, 2010; Stacchiola et al., 2013; Wei et al., 2015; Sun et al., 2016; Li et al., 2017). However, the effect of the rutile support on the activity remains unclear due to difficulties with respect to the characterization of the heterostructure during experiments (Stacchiola et al., 2013).

In this study, we performed DFT calculations to theoretically investigate the effect of the TiO₂ substrate on the heterostructure and thus on the OER. We screened the OERs of heterostructures consisting of various rutile-type metal oxides (i.e., VO₂, CrO₂, MnO₂, NbO₂, RuO₂, RhO₂, SnO₂, TaO₂, OsO₂, IrO₂, and PtO₂) and a TiO₂ substrate. The results show that these rutile heterostructures follow the universal scaling relations of metals and oxides; however, the binding strengths of the O^* intermediates increase due to the TiO₂ substrate. The volcano plot and electrochemical-step symmetry index (ESSI) show that the RuO₂ and IrO₂ are the closest to an ideal catalyst. The results of our computational screening provide insights into the effects of support materials on electrocatalytic reactions.

Methods

Spin-polarized DFT calculations were performed with the projector-augmented wave (PAW) method (Blochl, 1994) and Vienna Ab initio Simulation Package (VASP) (Kresse and Furthmiiller, 1996). The electron exchange–correlation energy was treated within the generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof functional (Perdew et al., 1997). To determine the trend of the OER activity, the DFT + U method within Liechtenstein’s approach (Anisimovdag et al., 1997) was used and the following correction parameters were employed: U = 4.95 eV for Ti, 2 eV for V, 7.15 eV for Cr, 6.63 eV for Mn, 3.32 eV for Nb, 6.73 eV for Ru, 5.97 eV for Rh, 5.91 eV for Ir, and 6.25 eV for Pt (Xu et al., 2015). The energy cutoff for the plane wave basis set was set at 520 eV. The geometry was optimized using the residual minimization method and the direct inversion in the iterative subspace method (RMM–DIIS) algorithm until the net force on each atom was below 0.02 eV·Å⁻¹, and the total energy was 10^–6 eV per atom. Dipole slab corrections were also applied to all slab model calculations. The k-point sampling of the Brillouin zone was done with a 4 × 4 × 1 for bulk calculations and 6 × 6 × 8 for slab calculations.

Results and Discussion

To theoretically investigate the OER activities of rutile-type heterostructures, we considered the heterostructures of 11 rutile-type oxides (i.e., MO₂, where M = V, Cr, Mn, Nb, Ru, Rh, Sn, Ta, Os, Ir, and Pt) with a TiO₂ substrate. To accurately illustrate the OER activity, the following magnetic structures were used for all calculations according to Xu et al.’s work: nonmagnetic (NM) for TiO₂, NbO₂, RuO₂, RhO₂, IrO₂, and PtO₂, and ferromagnetic (FM) for CrO₂ and MnO₂ (Xu et al., 2015). Furthermore, the ground state magnetic configurations of the other candidate models were identified as FM for VO₂ and NM for SnO₂, TaO₂, and OsO₂, respectively (Supplementary Figure S1). Surface models, that is, six-layer stoichiometric slabs, were built by using the 2 × 1 supercell of the optimized unit cell. The vacuum of ∼15 Å was applied in the (110) direction, which is the most stable facet of rutile-type oxides (Figure 1A; Kung, 1989). Note that a tri-layer consisting of oxygen–metal–oxygen (O–M–O) atomic layers was considered to be a single layer in our slab models. The top four layers of the slab models were allowed to fully relax. The two layers at the bottom were fixed to represent the bulk state. For heterostructures, the top three layers of the TiO₂ slab model were replaced with MO₂ layers while maintaining the cell dimensions of the TiO₂ substrate. The coordinatively unsaturated sites (CUS) of the metal atoms at the top surface were considered to be the adsorption sites for each intermediate (i.e., OH^*, O^*, and OOH^*) for the OER. To examine the oxygen coverage effect on the OER activity, the pristine and fully O^* covered surfaces were representatively compared (i.e., denoted as 2O_b and 2O_b 2O_c, where the subscripts “b” and “c” represent the bridge sites and CUS, respectively).

FIGURE 1

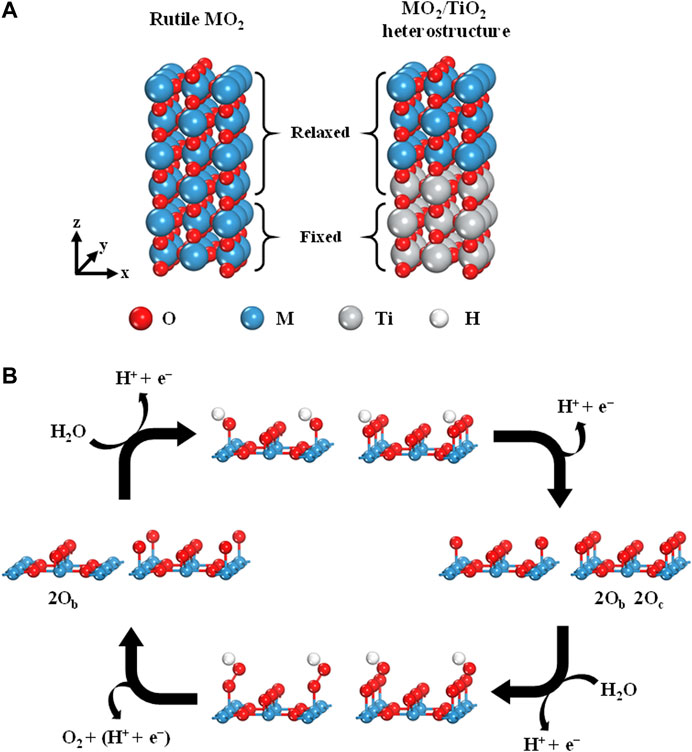
FIGURE 1. (A) Six-layered (110) surface of rutile-type MO₂(left) and MO₂/TiO₂ heterostructure (right). (B) OER scheme of four elementary reaction steps on the rutile-type (110) surface with 2O_b and 2O_b 2O_c.

The overall OER process consists of four elementary steps involving proton-coupled electron transfer (PCET; Figure 1B) (Hammes-Schiffer, 2015; Costentin and Savéant, 2017). In this study, we followed the conventional four-electron pathways with respect to the OER of rutile heterostructures, which can be described as follows:

${\text{H}}_2{\text{O}}_{\left(\text{l}\right)}+\text{M}\to {\text{MOH}}^{*}+\left({\text{H}}^{+}+{\text{e}}^{-}\right)(1)$

${\text{MOH}}^{\text{*}}\to {\text{MO}}^{\text{*}}+\left({\text{H}}^{+}+{\text{e}}^{-}\right)(2)$

${\text{MO}}^{\text{*}}+{\text{H}}_2{\text{O}}_{\left(\text{l}\right)}\to {\text{MOOH}}^{\text{*}}+\left({\text{H}}^{+}+{\text{e}}^{-}\right)(3)$

${\text{MOOH}}^{\text{*}}\to \text{M}+{\text{O}}_{2\left(\text{g}\right)}+({\text{H}}^{+}+{\text{e}}^{-}).(4)$

The adsorption free energy was calculated using the following equation:

$\Delta G=\Delta E+\Delta ZPE-T\Delta S-eU+k_{\text{B}}T\ln a_{{\text{H}}^{+}},(5)$

where $\Delta E$ is the binding energy of each reaction intermediate; $\Delta ZPE$ is the zero-point vibrational enthalpy; $-T\Delta S$ is the entropic correction at room temperature, $-eU$ is the energy shift by the electrode potential, where U is the electrode applied potential relative to the standard hydrogen electrode (SHE) and e is the elementary charge transferred; and $k_{\text{B}}T\ln a_{H^{+}}$ is used as correction for the free energy of H⁺ ions, where $a_{{\text{H}}^{+}}$ is the activity of the proton. In this study, we considered the standard conditions for Gibbs free energy calculations (i.e., T = 298 K and pH = 0). Free energy correction values were taken from Valdes et al.’s work (Valdes et al., 2008). The binding energy for each reaction intermediate (i.e., $\Delta E_{{\text{OH}}^{*}}$, $\Delta E_{{\text{O}}^{\text{*}}}$, and $\Delta E_{{\text{OOH}}^{*}}$) was calculated as follows:

$\Delta E_{{\text{OH}}^{\text{*}}}=E\left({\text{OH}}^{\text{*}}\right)-E(\ast )-\left[E\left({\text{H}}_2\text{O}\right)-0.5E\left({\text{H}}_2\right)\right](6)$

$\Delta E_{{\text{O}}^{\text{*}}}=E\left({\text{O}}^{\text{*}}\right)-E(\ast )-\left[E\left({\text{H}}_2\text{O}\right)-E\left({\text{H}}_2\right)\right](7)$

$\Delta E_{{\text{OOH}}^{\text{*}}}=E\left({\text{OOH}}^{\text{*}}\right)-E(\ast )-\left[2E\left({\text{H}}_2\text{O}\right)-1.5E\left({\text{H}}_2\right)\right],(8)$

where $E\left({\text{OH}}^{\text{*}}\right)$, $E\left({\text{O}}^{\text{*}}\right)$, and $E\left({\text{OOH}}^{\text{*}}\right)$ represent the total energies of the slab models for each adsorbate, $E(\ast )$ is the total energy of the bare slab, and $E\left({\text{H}}_2\text{O}\right)$ and $E\left({\text{H}}_2\right)$ represent the total energies of an isolated water molecule and hydrogen gas, respectively. The differences in the Gibbs free energy (ΔG) of each step were calculated as follows:

$\Delta G_1=\Delta G_{{\text{OH}}^{\text{*}}}(9)$

$\Delta G_2=\Delta G_{{\text{O}}^{*}}-\Delta G_{{\text{OH}}^{\text{*}}}(10)$

$\Delta G_3=\Delta G_{{\text{OOH}}^{\text{*}}}-\Delta G_{{\text{O}}^{\text{*}}}(11)$

$\Delta G_4=4.92-\Delta G_{{\text{OOH}}^{\text{*}}}(12)$

Finally, the theoretical overpotential of the OER $\left({\eta }_{\text{OER}}\right)$ can be calculated as follows:

${\eta }_{\text{OER}}=\max \left(\left[\text{Δ}{G}_1,\text{Δ}{G}_2,\text{Δ}{G}_3,\text{Δ}{G}_4\right]/e\right)-U_{eq},(13)$

where $U_{eq}$ indicates the equilibrium potential of the OER (i.e., 1.23 V vs. reversible hydrogen electrode). Eqs 1–13 assume that thermodynamics of the reaction steps is a valid descriptor for reaction kinetics based on the Brønsted–Evans–Polanyi (BEP) relations (Vojvodic et al., 2011), which refer to that a free-energy change in the transition states (kinetics) follows a change in the reaction heat (thermodynamics). Note that the connection between thermodynamics and kinetics is not always established (Kuo et al., 2017; Kuo et al., 2018), which requires further kinetic experiments or microkinetic modeling based on the activation barrier calculations for all plausible transition states.

We examined the scaling relations between the adsorption free energies of the reaction intermediates (i.e., OH^*, O^*, and OOH^*; Supplementary Table S2) for all rutile-type catalysts of interest (Figure 2A). The binding energies of OOH^* and OH^* are linearly correlated, with an offset of 3.20 eV. Note that our scaling trend is similar to the “universal” scaling relation reported by Man et al. [i.e., ΔE_OOH* = ΔE_OH* + 3.20 (±0.20 eV)] (Man et al., 2011), implying that all rutile-type systems, including heterostructures, follow the conventional scaling relations for metals and oxide surfaces. Based on the best fit, 68% of the points are within ±0.35 eV (1σ) and 95% are within ±0.70 eV (2σ). The scaling relationship between ΔE_O* and ΔE_OH* exhibits a slope of 1.39 (blue solid line), that is, it is much less steep than the slope of two (blue dashed line), which is the indicator line of the double bonding nature of O^* (Rossmeisl et al., 2007).

FIGURE 2

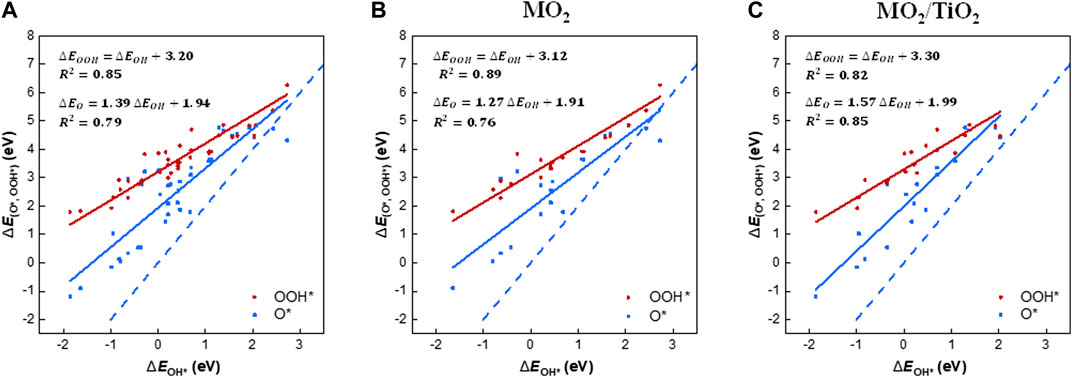
FIGURE 2. Scaling relations of the binding energies of the OER intermediates (i.e., OH^*, O^*, and OOH^*) with the binding energy of OH^*, which is the first intermediate for the OER. The diagrams contain the binding energies on the (110) surface of (A) all rutile-type oxides in this study, (B) MO₂, and (C) MO₂/TiO₂ heterostructures, respectively. The solid lines are the linear trends of the binding energies of OOH^* (red) and O^* (blue) with respect to the binding energy of OH^*. The blue dashed line in all diagrams is the guideline of the O^* intermediate, which indicates the double bonding nature on the surface, with a slope of 2.

To analyze the substrate effect of TiO₂ on the heterostructures, we divided the scaling relations into two groups, that is, (110) surfaces of MO₂ and MO₂/TiO₂ heterostructures (Figure 2B,C). Notably, the binding energies of OOH^* and O^* on the MO₂/TiO₂ (110) surface are more concentrated than those of MO₂. The scaling relation between OOH^* and OH^* of MO₂/TiO₂ (red solid line) shows an increased intercept by 0.18 compared with the corresponding scaling relation of MO₂, implying slightly weakened interactions between OOH^* and the surface. Note that the scaling relations between the binding strengths of O^* and OH^* species on MO₂ and MO₂/TiO₂ (blue solid lines) apparently differ. The slopes of MO₂/TiO₂ (110) heterostructures are closer to 2 (i.e., double bonding nature of O^*) than those of MO₂ (110) surfaces (Rossmeisl et al., 2007). This is due to the intensified binding strengths of O^* intermediates in heterostructures compared with MO₂ surfaces (Divanis et al., 2020). This indicates that the TiO₂ substrate generally stabilizes the O^* intermediates, which might lead to a decrease in ${\eta }_{\text{OER}}$ of rutile oxides involving weakly bound O^* intermediates.

Based on the scaling relations between the binding energies of the reaction intermediates, a volcano plot was constructed, as shown in Figure 3A. We chose $\Delta G_{{\text{O}}^{\text{*}}}-\Delta G_{{\text{OH}}^{\text{*}}}$ (denoted as $\Delta G_2$) as a descriptor, which is commonly used to predict the OER activity of the 4 e⁻ reaction (Man et al., 2011; Krishnamurthy et al., 2018). The plot shows that the O^* bonds of PtO₂, OsO₂, TaO₂, and RhO₂ on the TiO₂ substrate are stronger than those without the TiO₂ substrate, and the activities change along the volcano curve. In the cases of both oxygen coverages of PtO₂/TiO₂ and RhO₂/TiO₂, $\Delta G_2$, which is the potential-determining step for each system, was reduced, exhibiting the improved OER activities (i.e., smaller $\left|{\eta }_{\text{OER}}\right|$) compared to those of PtO₂ and RhO₂, respectively. In the cases of OsO₂, TaO₂, and NbO₂, the bonds of the O^* intermediates are too strong in the presence of the TiO₂ substrate, resulting in a decreased OER activity.

FIGURE 3

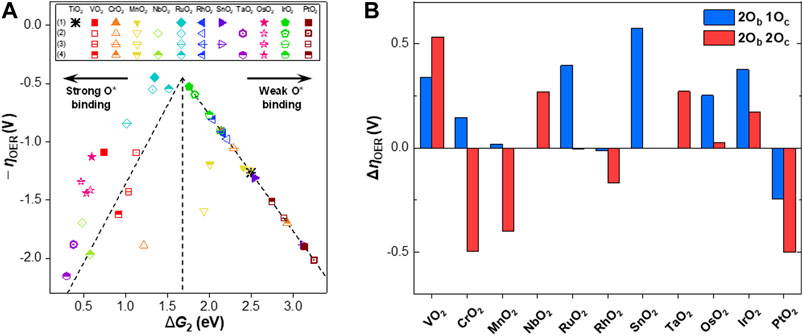
FIGURE 3. (A) Volcano plot for the negative overpotential of the OER $\left(-{\eta }_{\text{OER}}\right)$ as a function of $\Delta G_2$. The numbers in the inset indicate each surface: 1) 2O_b of MO₂, 2) 2O_b 2O_c of MO₂, 3) 2O_b of MO₂/TiO₂, and 4) 2O_b 2O_c of MO₂/TiO₂. (cf. Supplementary Table S2). (B) Difference between the overpotentials of MO₂ and MO₂/TiO₂$\left[\Delta {\eta }_{\text{OER}}={\eta }_{\text{OER}}\left({\text{MO}}_2/{\text{TiO}}_2\right)-{\eta }_{\text{OER}}\left({\text{MO}}_2\right)\right]$. A positive value of $\Delta {\eta }_{\text{OER}}$ indicates the decrease in the OER activity and a negative $\Delta {\eta }_{\text{OER}}$ reflects an enhancement.

Similar to the previous studies (Rossmeisl et al., 2007; Man et al., 2011), RuO₂ and IrO₂ were both identified as the active OER catalysts among the MO₂ candidates (i.e., ${\eta }_{\text{OER}}<\sim 0.5\text{V}$, Figure 3A). In the case of 2O_b 2O_c of RuO₂, the OER activity maintains similarity in the presence of TiO₂ substrate, which is located near the top of the volcano. In general, the TiO₂ substrate stabilizes the adsorbates (i.e., OOH^*, O^*, and OH^*) on 2O_b 2O_c of RuO₂, which appears as stronger adsorption free energies by 0.54–0.70 eV (Supplementary Table S1). Nevertheless, ${\eta }_{OER}$ is almost unchanged (i.e., $\Delta {\eta }_{\text{OER}}=-0.01\text{V}$) because the free energy change in the potential determining step (i.e., ΔG_OOH* − ΔG_O*) remains similar (Supplementary Table S2). In addition, it is also noteworthy that ${\eta }_{\text{OER}}$ for 2O_b 2O_c of IrO₂ is relatively similar, still exhibiting higher activity than other candidates except RuO₂.

The changes in ${\eta }_{\text{OER}}$ induced by the TiO₂ substrate are summarized in Figure 3B. As the value becomes more negative, the activity of MO₂/TiO₂ improves compared with that of MO₂. Notably, 2O_b 2O_c of CrO₂, MnO₂, RuO₂, RhO₂, and PtO₂ shows an enhanced activity. In addition, 2O_b of RhO₂ and PtO₂ also shows an improved activity on the TiO₂ substrate. However, regardless of the coverage, the TiO₂ substrate decreases the OER activity of VO₂, OsO₂, and IrO₂. In particular, 2O_b 2O_c of VO₂ and 2O_b of SnO₂ exhibit significantly increased overpotentials ($\Delta {\eta }_{\text{OER}}$ of 0.53 and 0.57 V, respectively).

To determine the promising free-energy regime for the OER, we further analyzed the free energies of the steps in terms of the ESSI, as suggested by Calle-Vallejo and coworkers (Govindarajan et al., 2018). The ESSI is an energetic descriptor that indicates the degree of similarity with an ideal catalyst, where all OER steps are perfectly symmetric at 1.23 eV. The ESSI is defined by the following equation and is only applied to steps with $\Delta G_i\left(i=\mathrm{1,2,3,4}\right)\ge 1.23\text{eV}$ (denoted as $\Delta G_i^{\ast }$):

$\text{ESSI}=\frac{1}{n}{\displaystyle \sum _i^n(\Delta G_i^{\ast }-1.23).}(14)$

Figure 4A shows ${\eta }_{\text{OER}}$ of each model as a function of the ESSI, representing a good linear correlation. 2O_b of RuO₂ is the closest model to the ideal catalyst, followed by 2O_b 2O_c of RuO₂ and RuO₂/TiO₂. The 2O_b of PtO₂ appears on the ${\eta }_{\text{OER}}$ = ESSI (red dashed line) and has a null bar with respect to the ESSI, which means that only a single step is greater than 1.23 V (i.e., $\Delta G_2$ = 3.13 eV). In the presence of the TiO₂ substrate, $\Delta G_2$ for 2O_b of PtO₂ is reduced, leading to a decrease of the ESSI and ${\eta }_{\text{OER}}$. Meanwhile, 2O_b 2O_c of PtO₂ lies relatively far from the line of ${\eta }_{\text{OER}}=\text{ESSI}$, which has a wide bar with respect to the ESSI, and thus corresponds to a good candidate for optimization (Govindarajan et al., 2018). In practice, the TiO₂ substrate on 2O_b 2O_c of PtO₂ works for enhancing the OER activity with a decrease in both ${\eta }_{\text{OER}}$ and ESSI.

FIGURE 4

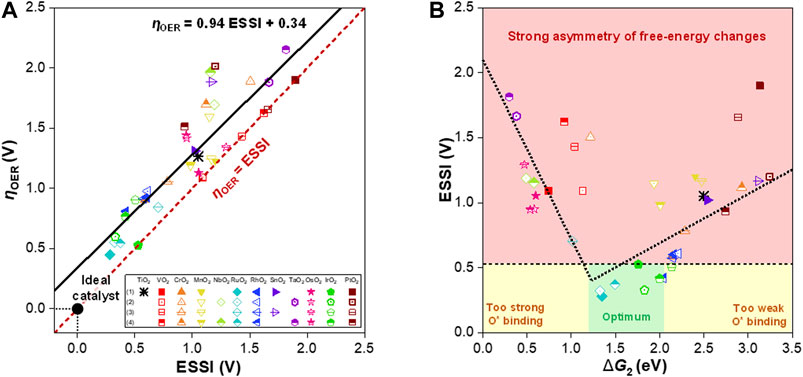
FIGURE 4. (A)${\eta }_{\text{OER}}$ as a function of the ESSI. Black solid line indicates the linear relation between ${\eta }_{\text{OER}}$ and ESSI. Red dotted line indicates the guideline of ${\eta }_{\text{OER}}$ = ESSI. (B) ESSI-$\Delta G_2$ activity map. Three regions are classified depending on the OER activity—green area of 1.2 eV < $\Delta G_2$ < 2.06 eV with ESSI < 0.53 V; yellow area of $\Delta G_2$ < 1.2 eV or $\Delta G_2$ > 2.06 eV with ESSI < 0. 53 V; and red area of ESSI > 0.53 V.

Based on the scaling relation between the ESSIs and ${\eta }_{OER}$’s, we determined a promising group of OER catalysts using the ESSI-$\Delta G_2$ activity map introduced by Exner (Exner, 2019; Figure 4B). The activity map is used to identify OER candidates by adjusting the ESSI threshold. The ESSI threshold (< 0.53 V) was determined from Supplementary Figure S2 by applying ${\eta }_{\text{OER}}$ of IrO₂, which is the conventional OER catalyst. The free-energy regime was set to 1.20 eV < $\Delta G_2$ < 2.06 eV by applying the standard deviation of $\pm$ 0.43 eV of the scaling relationship between $\Delta G_2$ and $\Delta G_3$ (Supplementary Figure S3) on 1.63 eV. The median value of 1.63 eV in the free-energy regime is determined by assuming the threshold electrode potential as the point where the experimental Tafel slope exceeds 59 mV/dec (i.e., ${\eta }_{\text{OER}}$ > 0.4 V), accounting for kinetics (Exner and Over, 2019). The green-colored area includes 2O_b of RuO₂, 2O_b 2O_c of RuO₂, 2O_b 2O_c of RuO₂/TiO₂, 2O_b of IrO₂, 2O_b 2O_c of IrO₂, 2O_b 2O_c of IrO₂/TiO₂, and 2O_b 2O_c of RhO₂, which are the most promising candidates. Particularly, a portion of promising candidates for the OER (i.e., RuO₂, RuO₂/TiO₂, IrO₂, IrO₂/TiO₂, and RhO₂/TiO₂) are more evidently classified on the ESSI-$\text{Δ}{G}_2$ map (Figure 4B), while they are somewhat deviated from the apex in the volcano plot (Figure 3A). This implies that conventional volcano analysis does not guarantee to predict the most active OER catalyst, whereas the ESSI-$\Delta G_2$ activity map, which is based on the kinetic scaling relations, is a more robust descriptor for the OER (Exner, 2019; Exner and Over, 2019). The 2O_b 2O_c surface of IrO₂ exhibits high symmetry of the reaction steps comparable to RuO₂. On the 2O_b and 2O_b 2O_c surfaces of RhO₂/TiO₂, the values of $\Delta G_2$ decrease compared to those of RhO₂. Accordingly, the free-energy differences of the other steps are adjusted to compensate for the decrease in $\Delta G_2$, while maintaining $\Delta G_2$ as a potential-determining step with reduced ${\eta }_{\text{OER}}$ (cf. Supplementary Table S2). Next, 2O_b of IrO₂/TiO₂ belongs to the yellow-colored region, which needs to be reconsidered for activity optimization (Govindarajan et al., 2019). The candidates in the region of ESSI > 0.53 V (i.e., red-highlighted region in Figure 4B) are classified as an inferior group, showing poor OER activities over all ranges of $\Delta G_2$ due to the highly asymmetric free-energy changes of the OER intermediates (Exner, 2019).

Conclusion

We screened a variety of rutile oxide heterostructures based on a TiO₂ substrate using scaling relations and relevant descriptors to identify a promising OER catalyst. The scaling relations between the reaction intermediates demonstrate that the rutile-type MO₂ heterostructures follow the universal scaling relationship of metal oxides. In addition, the TiO₂ substrate stabilizes the O^* bond on the (110) metal oxide surface. Based on the conventional volcano plot, RuO₂ and IrO₂ are found to be highly active OER catalysts as previously reported. Based on the ESSI descriptor, the superior activity of the RuO₂ can be attributed to the high symmetry of the reaction steps. Furthermore, based on the ESSI-ΔG₂ activity map, the candidates can be classified into an optimum group, a second promising group of OER catalysts with potential for optimization, and an inferior group that does not require particular attention.

The results of our computational screening using the scaling relations of rutile-type heterostructures provide valuable insights into the effect of the support material on the overpotential and thus guidelines for the design of a promising OER catalyst.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

All calculations and data analyses were performed by HYL. All authors contributed to the discussion of the results and wrote and revised the manuscript. SKK and GYJ supervised the project.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (Ministry of Science and ICT) (NRF-2019M1A2A2065614) and the Global PhD Fellowship Program (NRF-2019H1A2A1076827 and NRF-2016H1A2A1908137). SKK acknowledges the UNIST grant (2.200487.01) for the support of the publication. Computational resources were provided by UNIST High Performance Computing (HPC) systems and Korea Institute of Science and Technology Information (KISTI) (KSC-2019-CRE-0255).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.606313/full#supplementary-material.

References

Anisimovdag, V. I., Aryasetiawan, F., and Lichtenstein, A. I. (1997). First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method. J. Phys. Condens. Matter 9, 767–808. doi:10.1088/0953-8984/9/4/002

CrossRef Full Text | Google Scholar

Blochl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Bu, Y., Jang, H., Gwon, O., Kim, S. H., Joo, S. H., Nam, G., et al. (2019). Synergistic interaction of perovskite oxides and N-doped graphene in versatile electrocatalyst. J. Mater. Chem. A 7 (5), 2048–2054. doi:10.1039/c8ta09919g

CrossRef Full Text | Google Scholar

Costentin, C., and Savéant, J.-M. (2017). Theoretical and mechanistic aspects of proton-coupled electron transfer in electrochemistry. Curr. Opin. Electrochem. 1, 104–109. doi:10.1016/j.coelec.2016.11.001

CrossRef Full Text | Google Scholar

Divanis, S., Kutlusoy, T., Boye, I. M. I., Man, I. C., and Rossmeisl, J. (2020). Oxygen evolution reaction: a perspective on a decade of atomic scale simulations. Chem. Sci. 11, 2943. doi:10.1039/c9sc05897d

CrossRef Full Text | Google Scholar

Esposito, D. V., Hunt, S. T., Stottlemyer, A. L., Dobson, K. D., McCandless, B. E., Birkmire, R. W., et al. (2010). Low-cost hydrogen-evolution catalysts based on monolayer platinum on tungsten monocarbide substrates. Angew. Chem. Int. Ed. 49, 9859–9862. doi:10.1002/anie.201004718

PubMed Abstract | CrossRef Full Text | Google Scholar

Exner, K. S. (2019). Design criteria for oxygen evolution electrocatalysts from first principles: introduction of a unifying material-screening approach. ACS Appl. Energy Mater. 2, 11. doi:10.1021/acsaem.9b01480

CrossRef Full Text | Google Scholar

Exner, K. S., and Over, H. (2019). Beyond the rate-determining step in the oxygen evolution reaction over a single-crystalline IrO₂ (110) model electrode: kinetic scaling relations. ACS Catal. 9, 6755–6765. doi:10.1021/acscatal.9b01564

CrossRef Full Text | Google Scholar

Frydendal, R., Paoli, E. A., Knudsen, B. P., Wickman, B., Malacrida, P., Stephens, I. E. L., et al. (2014). Benchmarking the stability of oxygen evolution reaction catalysts: the importance of monitoring mass losses. ChemElectroChem. 1, 2075–2081. doi:10.1002/celc.201402262

CrossRef Full Text | Google Scholar

García‐Mota, M., Vojvodic, A., Metiu, H., Man, I. C., Su, H.‐Y., Rossmeisl, J., et al. (2011). Tailoring the activity for oxygen evolution electrocatalysis on rutile TiO₂(110) by transition-metal substitution. ChemCatChem. 3, 1607–1611. doi:10.1002/cctc.201100160

CrossRef Full Text | Google Scholar

Govindarajan, N., Garcia-Lastra, J. M., Meijer, E. A., and Calle-Vallejo, F. (2018). Does the breaking of adsorption-energy scaling relations guarantee enhanced electrocatalysis? Curr. Opin. Electrochem. 8, 110–117. doi:10.1016/j.coelec.2018.03.025

CrossRef Full Text | Google Scholar

Govindarajan, N., Koper, M. T. M., Meijer, E. J., and Calle-Vallejo, F. (2019). Outlining the scaling-based and scaling-free optimization of electrocatalysts. ACS Catal. 9, 4218–4225. doi:10.1021/acscatal.9b00532

CrossRef Full Text | Google Scholar

Hammes-Schiffer, S. (2015). Proton-coupled electron transfer: moving together and charging forward. J. Am. Chem. Soc. 137, 8860–8871. doi:10.1021/jacs.5b04087

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanaor, D. A. H., Xu, W., Ferry, M., and Sorrell, C. C. (2012). Abnormal grain growth of rutile TiO₂ induced by ZrSiO₄. J. Cryst. Growth 359, 83–91. doi:10.1016/j.jcrysgro.2012.08.015

CrossRef Full Text | Google Scholar

Jin, B., Zhou, X., Huang, L., Licklederer, M., Yang, M., and Schmuki, P. (2016). Aligned MoO_x/MoS₂ core–shell nanotubular structures with a high density of reactive sites based on self-ordered anodic molybdenum oxide nanotubes. Angew. Chem., Int. Ed. Engl. 55, 12252. doi:10.1002/anie.201605551

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmiiller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Krishnamurthy, D., Sumaria, V., and Viswanathan, V. (2018). Maximal predictability approach for identifying the right descriptors for electrocatalytic reactions. J. Phys. Chem. Lett. 9, 588–595. doi:10.1021/acs.jpclett.7b02895

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, K., Canaff, C., Rousseau, J., Arrii-Clacens, S., Napporn, T. W., Habrioux, A., et al. (2016). Effect of the oxide−carbon heterointerface on the Activity of Co₃O₄/NRGO nanocomposites toward ORR and OER. J. Phys. Chem. C 120 (15), 7949–7958. doi:10.1021/acs.jpcc.6b00313

CrossRef Full Text | Google Scholar

Kung, H. H. (1989). Transition metal oxides: surface chemistry and catalysis. Amsterdam: Elsevier Science.

Kuo, D. Y., Kawasaki, J. K., Nelson, J. N., Kloppenburg, J., Hautier, G., Shen, K. M., et al. (2017). Influence of surface adsorption on the oxygen evolution reaction on IrO₂(110). J. Am. Chem. Soc. 139, 3473–3479. doi:10.1021/jacs.6b11932

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuo, D. Y., Paik, H., Kloppenburg, J., Faeth, B., Shen, K. M., Schlom, D. G., et al. (2018). Measurements of oxygen electroadsorption energies and oxygen evolution reaction on RuO₂(110): a discussion of the sabatier principle and its role in electrocatalysis. J. Am. Chem. Soc. 140, 17597–17605. doi:10.1021/jacs.8b09657

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y., Suntivich, J., May, K. J., Perry, E. E., and Shao-Horn, Y. (2012). Synthesis and activities of rutile IrO₂ and RuO₂ nanoparticles for oxygen evolution in acid and alkaline solutions. J. Phys. Chem. Lett. 3 (3), 399–404. doi:10.1021/jz2016507

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Sun, X., Xu, X., Liu, W., Peng, H., Fang, X., et al. (2017). CO oxidation on PdO catalysts with perfect and defective rutile-TiO₂ as supports: elucidating the role of oxygen vacancy in support by DFT calculations. Appl. Surf. Sci. 401, 49–56. doi:10.1016/j.apsusc.2016.12.210

CrossRef Full Text | Google Scholar

Lu, X. F., Chen, Y., Wang, S. B., Gao, S. Y., and Lou, X. W. (2019). Interfacing manganese oxide and cobalt in porous graphitic carbon polyhedrons boosts oxygen electrocatalysis for Zn–Air batteries. Adv. Mater. 31 (39), 1902339. doi:10.1002/adma.201902339

CrossRef Full Text | Google Scholar

Man, I. C., Su, H.‐Y., Calle‐Vallejo, F., Hansen, H. A., Martínez, J. I., Inoglu, N. G., et al. (2011). Universality in oxygen evolution electrocatalysis on oxide surfaces. ChemCatChem. 3, 1159–1165. doi:10.1002/cctc.201000397

CrossRef Full Text | Google Scholar

Oh, N. K., Kim, C., Lee, J., Kwon, O., Choi, Y., Jung, G. Y., et al. (2019). In-situ local phase-transitioned MoSe₂ in La_0.5Sr_0.5CoO_3-δ heterostructure and stable overall water electrolysis over 1000 hours. Nat. Commun. 10, 1723. doi:10.1038/s41467-019-09339-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865. doi:10.1103/PhysRevLett.77.3865

CrossRef Full Text | Google Scholar

Qingxiang, W., Dastafkan, K., and Chuan, Z. (2018). Design strategies for non-precious metal oxide electrocatalysts for oxygen evolution reactions. Curr. Opin. Electrochem. 10, 16–23. doi:10.1016/j.coelec.2018.03.015

CrossRef Full Text | Google Scholar

Rossmeisl, J., Qu, Z.-W., Zhu, H., Kroes, G.-J., and Nørskov, J. K. (2007). Electrolysis of water on oxide surfaces. Electroanal. Chem. 607, 83. doi:10.1016/j.jelechem.2006.11.008

CrossRef Full Text | Google Scholar

Seitsonen, A. P., and Over, H. (2010). Oxidation of HCl over TiO₂-supported RuO₂: a density functional theory study. J. Phys. Chem. C 114, 22624–22629. doi:10.1021/jp108603a

CrossRef Full Text | Google Scholar

Seitz, L. C., Dickens, C. F., Nishio, K., Hikita, Y., Montoya, J., Doyle, A., et al. (2016). A highly active and stable IrO_x/SrIrO₃ catalyst for the oxygen evolution reaction. Science 353 (6303), 1011–1014. doi:10.1126/science.aaf5050

PubMed Abstract | CrossRef Full Text | Google Scholar

Stacchiola, D. J., Senanayake, S. D., Liu, P., and Rodriguez, J. A. (2013). Fundamental studies of well-defined surfaces of mixed-metal oxides: special properties of MO_x/TiO₂(110) {M = V, Ru, Ce, or W}. Chem. Rev. 113, 4373–4390. doi:10.1021/cr300316v

PubMed Abstract | CrossRef Full Text | Google Scholar

Suen, N.-T., Hung, S.-F., Quan, Q., Zhang, N., Xu, Y.-J., and Chen, H. M. (2017). Electrocatalysis for the oxygen evolution reaction: recent development and future perspectives. Chem. Soc. Rev. 46 (337), 337–365. doi:10.1039/c6cs00328a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, X., Peng, X., Xu, X., Jin, H., Wang, H., and Wang, X. (2016). H₂ adsorption and dissociation on PdO(101) films supported on rutile TiO₂(110) facet: elucidating the support effect by DFT calculations. J. Mol. Model. 22, 204. doi:10.1007/s00894-016-3072-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Turner, J. A. (2004). Sustainable hydrogen production. Science 305, 972–974. doi:10.1126/science.1103197

PubMed Abstract | CrossRef Full Text | Google Scholar

Valdes, A., Qu, Z.-W., Kroes, G.-J., Rossmeisl, J., and Norskov, J. K. (2008). Oxidation and photo-oxidation of water on TiO₂ surface. J. Phys. Chem. C 2, 9872–9879. doi:10.1021/jp711929d

CrossRef Full Text | Google Scholar

Vojvodic, A., Calle-Vallejo, F., Guo, W., Wang, S., Toftelund, A., Studt, F., et al. (2011). On the behavior of Brønsted-Evans-Polanyi relations for transition metal oxides. J. Chem. Phys. 134, 244509. doi:10.1063/1.3602323

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D. Y., Gong, M., Chou, H. L., Pan, C. J., Chen, H. A., Wu, Y., et al. (2015). Highly active and stable hybrid catalyst of cobalt-doped FeS₂ nanosheets–carbon nanotubes for hydrogen evolution reaction. J. Am. Chem. Soc. 137, 1587. doi:10.1021/jacs.5b07788

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, W., Dai, Y., Huang, B., Li, X., Nagele, F., Over, H., et al. (2015). Density functional characterization of the electronic structures and band bending of rutile RuO₂/TiO₂(110) heterostructures. J. Phys. Chem. C 119, 12394–12399. doi:10.1021/acs.jpcc.5b01884

CrossRef Full Text | Google Scholar

Xiao, Z., Huang, Y.-C., Dong, C.-L., Xie, C., Liu, Z., Du, S., et al. (2020). Operando identification of the dynamic behavior of oxygen vacancy-rich Co₃O₄ for oxygen evolution reaction. J. Am. Chem. Soc. 142, 12087. doi:10.1021/jacs.0c00257

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z., Rossmeisl, J., and Kitchin, J. R. (2015). A linear response DFT+U study of trends in the oxygen evolution activity of transition metal rutile dioxides. J. Phys. Chem. C 119, 4827–4833. doi:10.1021/jp511426q

CrossRef Full Text | Google Scholar

Zhou, W., Hou, D., Sang, Y., Yao, S., Zhou, J., Li, G., et al. (2014). MoO₂ nanobelts@nitrogen self-doped MoS₂ nanosheets as effective electrocatalysts for hydrogen evolution reaction. J. Mater. Chem. A 2, 11358. doi:10.1039/c4ta01898b

CrossRef Full Text | Google Scholar