Time domain analysis of flyback EMI based on distributed parameters theory

The electromagnetic interference (EMI) is a key issue for most of electric or electronic devices, the researches of suitable analysis methods and solutions absorb much attentions. The research about electromagnetic interference (EMI) is normally based on two approaches (i.e., time domain analysis and frequency domain analysis). The frequency domain analysis is easier to apply theoretical model to analyze the circuit loop impedance of EMI noise which can provide guidance of EMI suppression, but it cannot reflect the real amplitude of EMI noise without the real waveforms of noise sources. The time domain analysis is usually based on circuit simulation to get the EMI noise directly, but it is time consuming. In order to combine the advantages of these two approaches, this paper proposes a high frequency equivalent circuit model of flyback converter and analyze the effect of each distributed parameters on the common mode (CM) and differential mode (DM) noise. The experimental result verified the accuracy and efficiency of the proposed method, which not only can correctly reflect the real waveforms of the circuit, but also can predict the EMI noise based on the constructed waveforms.

1 Introduction

In switch-mode power supplies (SMPS), to realize high power density design of power converters, the distance between components should be reduced which could strengthen the electromagnetic field coupling among the components, making the EMI issues more prominent. Therefore, effectively analyzing the mechanisms of EMI noise and proposing corresponding effective solutions are crucial for achieving high power density designs in SMPS.

The essential reason of EMI noise arises from the voltage transitions and current ripples induced by switching actions of the power converters. Consequently, constructing the switching waveforms of the main components in the power converters can effectively reflect the characteristics of the EMI noises. However, since the impact of EMI noises span high frequency bands, various distributed parameters of the circuit significantly influence the switching waveforms, rendering the corresponding differential equations exceedingly complex. As a result, current theoretical analyses of EMI noise are typically based on frequency domain analysis. Time domain analysis is mainly based on circuit simulation, but building and debugging a circuit simulation system has certain complexities. Therefore, it is of great significance to construct time-domain waveforms theoretically to analyze and predict EMI noise (Trinchero et al., 2015; Yang et al., 2020; Fu, 2019; Zhu et al., 2020; Takahashi et al., 2019; Ma et al., 2008; Liu et al., 2015; Emami et al., 2010; Kai et al., 2024; Fakhafkh and Ammous, 2017; Wang et al., 2012; Liang et al., 2012).

This paper utilizes the flyback converter as a platform, and based on its high frequency equivalent circuit model, provides a detailed analysis and solution of the differential equations corresponding to each switching process. This establishes the theoretical solution model for the switching waveforms in the flyback circuit. Building upon this foundation, this paper thoroughly examines the impact of various distributed parameters of the flyback circuit on the waveforms of different components, thereby deducing their influence on EMI noises (differential mode and common mode noises). Finally, through experimental verification, it is confirmed that the theoretically constructed switching waveforms of the flyback converter are highly accurate and can be effectively used to analyze the impact of distributed parameters on EMI noises.

2 EMI noise mechanisms of flyback circuit

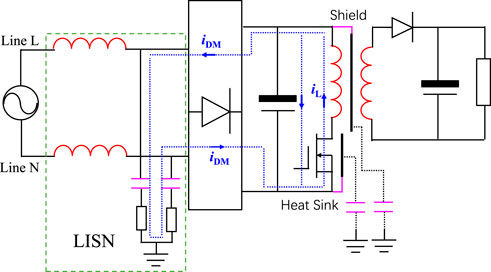
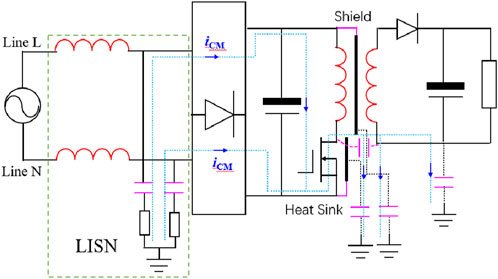
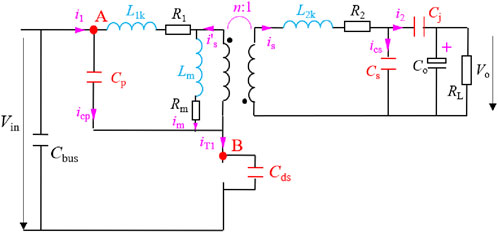
When analyzing EMI noise in switch-mode power supply circuits, it is common to categorize the noise into differential mode and common mode components due to their distinct causes and transmission paths. Differential mode noise primarily originates from current ripples in the power loop of the circuits, thus its main transmission path lies between the line L and line N within the power loop. The DM noise transmission path of the flyback circuit is illustrated in Figure 1. Common mode noise, on the other hand, mainly arises from potential jumps during the switching process, leading to ground displacement currents. Therefore, its transmission path involves the loops between the line L and ground, as well as the line N and ground. In a flyback circuit, both the MOSFET of primary side and the diode of secondary side experience potential jumps during the switching instant, which can generate common mode noise. Figures 2, 3 show the transmission path of common-mode noise generated from the primary side and secondary side separately.

Figure 1

Figure 1. The differential-mode noise transmission path of the flyback circuit.

Figure 2

Figure 2. The primary side’s common-mode noise transmission path of the flyback circuit.

Figure 3

Figure 3. The secondary side’s common-mode noise transmission path of the flyback circuit.

Based on the noise transmission paths shown in Figures 1–3, one can intuitively analyze the impact of circuit’s distributed parameters on EMI noise propagation in the frequency domain. However, this method only reflects the effect of distributed parameters on noise within a given frequency band. In the absence of the original noise’s spectral information, this approach is suitable for qualitatively analyzing the impact of distributed parameters on EMI noise but does not facilitate predictive analysis of EMI during the design process of switch-mode power supplies. Generally, the waveforms at various points in the circuit are obtained via simulation and used for EMI prediction and design. However, constructing a waveform model that considers distributed parameters through circuit theory would be more beneficial for an in-depth analysis of these parameters' impact on EMI. Therefore, this paper will analyze the influence of distributed parameters on EMI noise sources by theoretically constructing the switching waveforms of the flyback circuit.

3 Theoretical model of flyback circuit waveforms

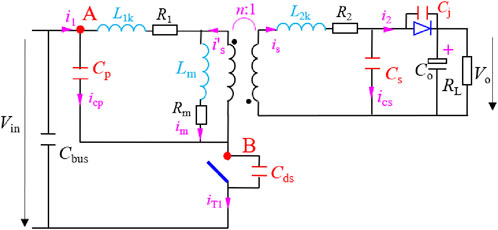
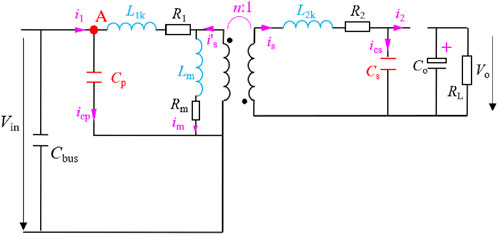
To construct relatively accurate switching waveforms for the flyback circuit, it is necessary to fully consider the effects of distributed parameters. For this purpose, the high-frequency equivalent circuit of the flyback transformer shown in Figure 4 is adopted in this paper. This circuit not only takes into account the leakage inductance, parasitic capacitance, excitation inductance, winding resistance, and core equivalent resistance, but also considers the impact of the parasitic capacitance of the primary side switch and the secondary side diode. This approach can more comprehensively reflect the influence of distributed parameters on the switching waveforms. Due to the majority of current mainstream flyback power supplies operate in DCM (Discontinuous Conduction Mode), which is in order to reduce winding losses and improve efficiency, this paper will use DCM as an example. Based on Figure 4, we will conduct a detailed analysis and construct the switching waveforms corresponding to each switching process.

Figure 4

Figure 4. High frequency equivalent circuit model of flyback.

3.1 The waveforms of flyback circuit at turn off moment

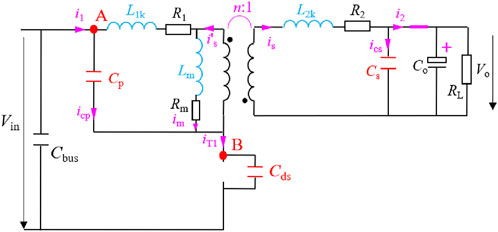
At the turn-off moment of the flyback circuit, the primary switch is turned off and the secondary diode conducts (with a voltage drop V_D). The voltage of the magnetizing inductance L_m is clamped by the output voltage, causing resonance between the primary leakage inductance L_k1, the primary capacitance C_p, and the switch’s drain-source capacitance C_ds, as shown in Figure 5 which represents the equivalent circuit during the turn-off period of the flyback circuit. Based on Figure 5, the Equation 1 for the turn-off moment can be derived. In solving for the magnetizing inductance voltage V_{Lm_off1}(t), the influence of the secondary side resistance R₂ and the magnetizing resistance R_m is neglected, assuming that the magnetizing current decreases linearly at this time.

Figure 5

Figure 5. The equivalent circuit of flyback circuit at the turn off moment.

By applying the Laplace transform to solve Equation 1, the time-domain equations for the switch capacitance voltage and magnetizing current at the turn-off moment can be obtained. Substituting these into Equation 2 allows further solution of the key circuit waveforms.

It is important to note that to completely solve Equation 1, the initial values of the switch junction capacitance voltage, the current through the switch, and the magnetizing current must be determined. At the turn-off moment, the current through the switch instantaneously transfers to the secondary side for “freewheeling,” meaning the magnetizing current remains constant (reaching its peak value I_peak) and the switch current becomes zero. The voltage across the switch junction capacitance C_ds) cannot change instantaneously and remains at zero. Therefore, at the turn-off moment, the initial values of the switch junction capacitance voltage, the current through the switch, and the magnetizing current satisfy Equation 3.

It should be noted that the oscillation frequencies corresponding to each switching process are different. Since resistance is frequency-dependent, a fixed resistance value cannot represent the actual winding resistance (such as R₁ and R₂) or core equivalent resistance (such as R_m) for each process. These values need to be estimated based on the oscillation frequency. At the turn-off moment, the resonance frequency of the primary circuit can be estimated using Equation 4. These resistances mainly act as damping during the LC resonance process. As long as their values do not affect the nature of the resonance (such as underdamped, critically damped, and overdamped resonance), they will not impact the analysis of the influence of other distributed parameters (such as transformer leakage inductance and parasitic capacitance) on the switch waveform. Therefore, the estimated value range for these resistances can be quite broad.

$\left\{\begin{array}{l}{L}_{C1}\cdot \frac{d^2}{d{t}^2}{V}_{cds\_off1}\left(t\right)+R_{C1}\cdot \frac{d}{dt}{V}_{cds\_off1}\left(t\right)+V_{cds\_off1}\left(t\right)=V_{in}+V_{F1}\\ L_m\frac{d}{dt}{i}_{m\_off1}\left(t\right)+R_m\cdot i_{m\_off1}\left(t\right)=-V_{F1}\\ L_{C1}=L_{1k}\cdot \left(C_p+C_{ds}\right)\\ R_{C1}=R_1\cdot \left(C_p+C_{ds}\right)\\ V_{F1}=\frac{n\cdot \left(V_o+V_D\right)}{1+n^2\cdot L_{2k}/L_m}\end{array}\right.(1)$

$\left\{\begin{array}{l}{V}_{cp\_off1}\left(t\right)=V_{in}-V_{cds\_off1}\left(t\right)\\ i_{cp\_off1}\left(t\right)=C_p\frac{d}{dt}{V}_{cp\_off1}\left(t\right)\\ i_{s\_off1}\left(t\right)=n\cdot \left(i_{cp\_off1}\left(t\right)+i_{m\_off1}\left(t\right)-i_{1\_off1}\left(t\right)\right)\end{array}\right.(2)$

$\left\{\begin{array}{l}{V}_{cds\_off1}\left(0\right)=0\\ \frac{d}{dt}{V}_{cds\_off1}\left(0\right)=0\\ i_{m\_off1}\left(0\right)=I_{peak}\end{array}\right.(3)$

$f_{r1}=\frac{1}{2\pi \sqrt{L_{1k}\cdot \left(C_p+C_{ds}\right)}}(4)$

3.2 The waveforms of flyback circuit at discontinuous interval

During the discontinuous conduction period of the flyback circuit, the secondary side diode turns off, and the magnetizing inductance is no longer clamped by the output voltage. Instead, it participates in the resonance of the primary side circuit along with the primary leakage inductance L_1k, the primary winding capacitance C_p, and the switch drain-source capacitance C_ds. The resonant frequency can be calculated using Equation 5. As shown in Figure 6, the equivalent circuit during the discontinuous conduction period can be used to derive the corresponding circuit equations, as given in Equation 6. When the freewheeling time t_off of the secondary side diode is determined, the initial values of the voltages and currents across the switch and the secondary winding during this period satisfy Equation 7.

Figure 6

Figure 6. The equivalent circuit of flyback circuit at discontinuous interval.

Using the Laplace transform to solve Equation 6, the time-domain equations for the voltages across the switch and the secondary winding during the discontinuous conduction period can be obtained. Substituting these time-domain equations into Equation 8 allows the key waveforms of the circuit during the discontinuous conduction period to be determined.

$f_{r2}=\frac{1}{2\pi \sqrt{\left(L_{1k}+L_m\right)\cdot \left(C_p+C_{ds}\right)}}(5)$

$\left\{\begin{array}{l}{L}_{C11}\frac{d^2}{d{t}^2}{V}_{cds\_off2}\left(t\right)+R_{C11}\frac{d}{dt}{V}_{cds\_off2}\left(t\right)+V_{cds\_off2}\left(t\right)=V_{in}-L_{C12}\frac{d^2}{d{t}^2}{V}_{cs\_off2}\left(t\right)-R_{C12}\frac{d}{dt}{V}_{cs\_off2}\left(t\right)\\ L_{C21}\frac{d^2}{d{t}^2}{V}_{cds\_off2}\left(t\right)+R_{C21}\frac{d}{dt}{V}_{cds\_off2}\left(t\right)+L_{C22}\frac{d^2}{d{t}^2}{V}_{cs\_off2}\left(t\right)+R_{C22}\frac{d}{dt}{V}_{cs\_off2}\left(t\right)+V_{cs\_off2}\left(t\right)=0\\ L_{C11}=\left(L_{1k}+L_m\right)\cdot \left(C_{ds}+C_p\right)\\ L_{C12}=\frac{L_m\left(C_s+C_j\right)}{n}\\ L_{C21}=\frac{L_m\left(C_p+C_{ds}\right)}{n}\\ L_{C22}=\left(L_{2k}+L_m/n^2\right)\cdot \left(C_s+C_j\right)\\ R_{C11}=\left(R_1+R_m\right)\cdot \left(C_{ds}+C_p\right)\\ R_{C12}=\frac{R_m\cdot \left(C_s+C_j\right)}{n}\\ R_{C21}=\frac{R_m\cdot \left(C_p+C_{ds}\right)}{n}\\ R_{C22}=\left(R_2+R_m/n^2\right)\cdot \left(C_s+C_j\right)\end{array}\right.(6)$

$\left\{\begin{array}{l}{V}_{cds\_off2}\left(0\right)=V_{cds\_off1}\left(t_{off}\right)\\ \frac{d}{dt}{V}_{cds\_off2}\left(0\right)=\frac{d}{dt}{V}_{cds\_off1}\left(t_{off}\right)\\ V_{cs\_off2}\left(0\right)=V_{cs\_off1}\left(t_{off}\right)\\ \frac{d}{dt}{V}_{cs\_off2}\left(0\right)=\frac{d}{dt}{V}_{cs\_off1}\left(t_{off}\right)\end{array}\right.(7)$

$\left\{\begin{array}{l}{V}_{cp\_off2}\left(t\right)=V_{in}-V_{cds\_off2}\left(t\right)\\ V_{D\_off2}\left(t\right)=V_{cs\_off2}\left(t\right)-V_o\\ i_{1\_off2}\left(t\right)=C_{ds}\frac{d}{dt}{V}_{cds\_off2}\left(t\right)\\ i_{s\_off2}\left(t\right)=\left(C_s+C_j\right)\frac{d}{dt}{V}_{cs\_off2}\left(t\right)\end{array}\right.(8)$

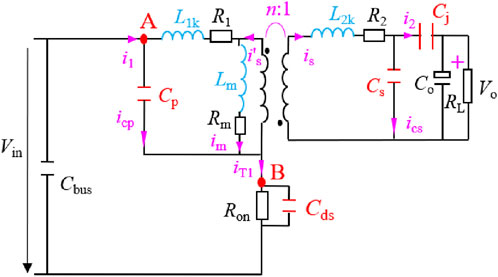
3.3 The waveforms of flyback circuit at turn on moment

During turn on moment, the switch can be approximately represented as a conducting resistance R_on, and in view of its small value, it can be shorted. At this moment, to prevent a sudden change in the voltage across the primary parasitic capacitance of the transformer, a lead inductance L_1w, which can be extracted by PCB simulation, is introduced for analysis. As shown in Figure 7, this is the equivalent circuit at the turn-on moment. The charging current also exhibits a steep spike due to the rate of change of the V_cp potential approaching a sudden change. Additionally, since the magnetizing inductance is large at the turn-on instant and the magnetizing current remains essentially constant, the current changes occurring in the circuit can be considered not to flow through the magnetizing loop. Therefore, the magnetizing inductance is effectively disconnected, which is why it is not reflected in the equivalent circuit shown in Figure 7.

Figure 7

Figure 7. The equivalent circuit of flyback circuit at the turn on moment.

Based on Figure 7, the Equation 9 can be derived. When the duration t_d of the discontinuous stage is determined, the initial values of the voltage and current across the primary and secondary winding parasitic capacitors at the moment of turn-on satisfy Equation 10. By applying the Laplace transform to solve Equation 9, the time-domain equations for the port voltages (i.e., parasitic capacitor voltages) of the primary and secondary windings at the moment of turn-on can be obtained. Substituting these into Equation 11 allows further solution of other key waveforms in the flyback circuit at this moment.

At the turn-on moment, a peak in the primary current occurs, and the secondary side also experiences voltage and current oscillations. However, at this time, the oscillation frequencies of the primary and secondary sides are different. Their resonance frequencies are determined by their circuit parameters respectively and can be estimated using Equation 12, where f_rp represents the primary resonance frequency and f_rs represents the secondary resonance frequency.

$\left\{\begin{array}{l}{L}_{1w}\frac{d}{dt}{i}_{1\_on1}\left(t\right)+V_{cp\_on1}\left(t\right)=V_{in}\\ L_{2k}\frac{d}{dt}{i}_{s\_on1}\left(t\right)+R_2\cdot i_{s\_on1}\left(t\right)+V_{cs\_on1}\left(t\right)+\frac{V_{Lm\_on1}\left(t\right)}{n}=0\\ V_{Lm\_on1}\left(t\right)=\frac{L_{1k}}{n}\frac{d}{dt}{i}_{s\_on1}\left(t\right)+\frac{R_1}{n}{i}_{s\_on1}\left(t\right)+V_{cp\_on1}\left(t\right)\\ i_{cp\_on1}\left(t\right)=i_{1\_on1}\left(t\right)+\frac{i_{s\_on1}\left(t\right)}{n}\\ i_{s\_on1}\left(t\right)=\left(C_s+C_j\right)\frac{d}{dt}{V}_{cs\_on1}\left(t\right)\end{array}\right.(9)$

$\left\{\begin{array}{l}{V}_{cp\_on1}\left(0\right)=V_{cp\_off2}\left(t_d\right)\\ \frac{d}{dt}{V}_{cp\_on1}\left(0\right)=\frac{d}{dt}{V}_{cp\_off2}\left(t_d\right)\\ V_{cs\_on1}\left(0\right)=V_{cs\_off2}\left(t_d\right)\\ \frac{d}{dt}{V}_{cs\_on1}\left(0\right)=\frac{d}{dt}{V}_{cs\_off2}\left(t_d\right)\end{array}\right.(10)$

$\left\{\begin{array}{l}{i}_{s\_on1}\left(t\right)=\left(C_s+C_j\right)\cdot \frac{d}{dt}{V}_{cs\_on1}\left(t\right)\\ i_{1\_on1}\left(t\right)=C_p\frac{d}{dt}{V}_{cp\_on1}\left(t\right)-\frac{i_{s\_on1}\left(t\right)}{n}\\ V_{D\_on1}\left(t\right)=V_{cs\_on1}\left(t\right)-V_o\\ V_{cds\_on1}\left(t\right)=0\end{array}\right.(11)$

$\left\{\begin{array}{l}{f}_{rp}=\frac{1}{2\pi \sqrt{L_{1w}\cdot C_p}}\\ f_{rs}=\frac{1}{2\pi \sqrt{\left(L_{2k}+\frac{L_{1k}}{n^2}\right)\cdot \left(C_s+C_j\right)}}\end{array}\right.(12)$

3.4 The waveforms of flyback circuit at conduction interval

This article suggests that during the conduction period, the voltage of primary-side capacitor V_cp is clamped by the input voltage, and the magnetizing current can be considered to steadily increase under constant voltage excitation, while the secondary-side current is zero. Therefore, the equivalent circuit during the conduction period needs to consider the influence of the magnetizing loop, as shown in Figure 8. Based on this, the corresponding circuit Equation 13 can be derived, which can be simplified to Equation 14. In DCM mode, it can be assumed that the initial value of the primary current i_{1_on2} (0) is zero. However, when the oscillation time t_rn at the moment of turn-on is determined, Equation 15 can also be used to estimate i_{1_on2} (0).

$\left\{\begin{array}{l}{L}_{1k}\frac{d}{dt}{i}_{L1k\_on2}\left(t\right)+R_1\cdot i_{L1k\_on2}\left(t\right)+L_m\frac{d}{dt}{i}_{m\_on2}\left(t\right)+R_m\cdot i_{m\_on2}\left(t\right)=V_{in}\\ i_{1\_on2}\left(t\right)=i_{cp\_on2}\left(t\right)+i_{L1k\_on2}\left(t\right)\\ i_{m\_on2}\left(t\right)=i_{L1k\_on2}\left(t\right)+\frac{i_{s\_on2}\left(t\right)}{n}\end{array}\right.(13)$

$\left(R_1+R_m\right)\cdot i_{1\_on2}\left(t\right)+\left(L_{1k}+L_m\right)\cdot \frac{d}{dt}{i}_{1\_on2}\left(t\right)=V_{in}(14)$

$i_{1\_on2}\left(0\right)=i_{1\_on1}\left(t_{rn}\right)(15)$

Figure 8

Figure 8. The equivalent circuit of flyback circuit at the conduction interval.

3.5 The waveforms of flyback circuit during full period

The previous sections have introduced the circuit equations and their solution methods for each switching process in the flyback circuit, which can be used to construct the main waveform characteristics of the circuit during each switching process. However, to fully draw the switch waveforms for the entire cycle, it is necessary to determine the duration of each switching process.

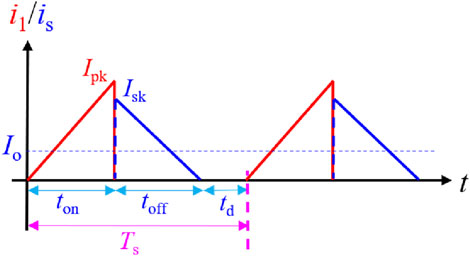
When analyzing the duration of each switching process, this article estimates using ideal primary and secondary current waveforms, as shown in Figure 9, ignoring the influence of winding resistances R₁ and R₂ on the switch waveforms. Although in the DCM mode of the flyback circuit, the circuit operation can be divided into four states: turn-off moment, discontinuous period, turn-on moment, and conduction period, considering that the waveform oscillation at the turn-on moment is relatively short, this article ignores its time proportion during analysis. Therefore, in Figure 9, only three time periods are shown: the conduction time ton, the diode freewheeling time t_off, and the discontinuous time t_d.

Figure 9

Figure 9. The input and output current waveforms with ideal assumption.

Given the output power P_o and output voltage V_o, the average output current I_o can be calculated using Equation 16. According to Figure 9, Io also satisfies Equation 17. During the period of t_off, when ignoring the effect of R₂, Equation 18 can be derived. During the period of t_on, when ignoring the effect of R₁, Equation 19 can be derived. The input peak current I_pk and the output peak current I_sk satisfy the rule of ampere-turns balance, as shown in Equation 20. By combining Equations 16, 20, the conduction time t_on and the output diode freewheeling time t_off can be determined, as shown in Equation 21. The discontinuous time t_d is then equal to the switching cycle minus t_on and t_off, as shown in Equation 22.

Based on the above analysis and combining the time-domain equations for each stage, the required circuit waveforms for the entire cycle can be written. Taking the voltage of the primary-side MOSFET and the secondary-side diode as examples, their equations for the entire cycle can be represented by Equations 23, 24, respectively.

$I_o=\frac{P_o}{V_o}(16)$

$I_o=\frac{I_{sk}\cdot t_{off}}{2\cdot T_s}(17)$

$\left(L_{2k}+\frac{L_m}{n^2}\right)\cdot \frac{I_{sk}}{t_{off}}=V_o+V_D(18)$

$\left(L_{1k}+L_m\right)\cdot \frac{I_{pk}}{t_{on}}=V_{in}(19)$

$n\cdot I_{pk}=I_{sk}(20)$

$\left\{\begin{array}{l}{t}_{off}=\sqrt{\frac{2\cdot P_o\cdot T_s\cdot \left(L_{2k}+L_m/n^2\right)}{V_o\cdot \left(V_o+V_D\right)}}\\ t_{on}=\frac{2\cdot I_o\cdot T_s\cdot \left(L_{1k}+L_m\right)}{n\cdot V_{in}\cdot t_{off}}\end{array}\right.(21)$

$t_d=T_s-t_{on}-t_{off}(22)$

$V_{cds}\left(t\right)=\left\{\begin{array}{ll}{V}_{cds\_off1}\left(t\right)& 0\le t\le t_{off}\\ V_{cds\_off2}\left(t\right)& t_{off}\le t\le t_{off}+t_d\\ 0& t_{off}+t_d\le t\le T_s\end{array}\right.(23)$

$V_D\left(t\right)=\left\{\begin{array}{ll}{V}_{D\_off1}\left(t\right)& 0\le t\le t_{off}\\ V_{D\_off2}\left(t\right)& t_{off}\le t\le t_{off}+t_d\\ V_{D\_on1}\left(\mathrm{t}\right)& t_{off}+t_d\le t\le t_{off}+t_d+t_{rn}\\ V_{D\_on2}\left(\mathrm{t}\right)& t_{off}+t_d+t_{rn}\le t\le T_s\end{array}\right.(24)$

To specifically draw the switch waveforms, it is accepted to assume the following parameters: an output power P_o of 28 W, an input voltage V_in of 380 V, an output voltage V_o of 12 V, a switching frequency f_s of 65 kHz, primary and secondary winding turns ratio of 40:10, a load resistance R_o of 5.1Ω, a secondary-side diode forward voltage V_D of 0.5 V, and relevant distributed parameters as shown in Table 1.

Table 1

Table 1. The distributed parameters of flyback circuit.

According to the analysis in Section 3-1, the values of R₁, R₂, and R_m are affected by frequency. Based on the given parameters, the resonant frequency f_r1 of the primary circuit at the turn-off moment can be calculated as 5.18 MHz. Accordingly, it is assumed that at this time, R₁ = 30Ω, R_m = 2Ω, and R₂ = 5Ω. During the discontinuous period, the primary resonant frequency f_r2 is 741 kHz, and it is assumed that at this time, R₁ = 10Ω, R_m = 1Ω, and R₂ = 3Ω. At the turn-on moment, it is assumed that R₁ = 30Ω, R_m = 30Ω, R₂ = 5Ω, L_1w = 10nH, and R_1w = 5Ω. During the conduction period, it is assumed that R₁ = 30Ω, R_m = 30Ω, and R₂ = 1Ω.

Based on the given parameters and combining Equations 23, 24, the complete cycle waveforms of the switch transistor’s drain-source voltage and the secondary-side diode voltage can be plotted, as shown in Figure 10.

Figure 10

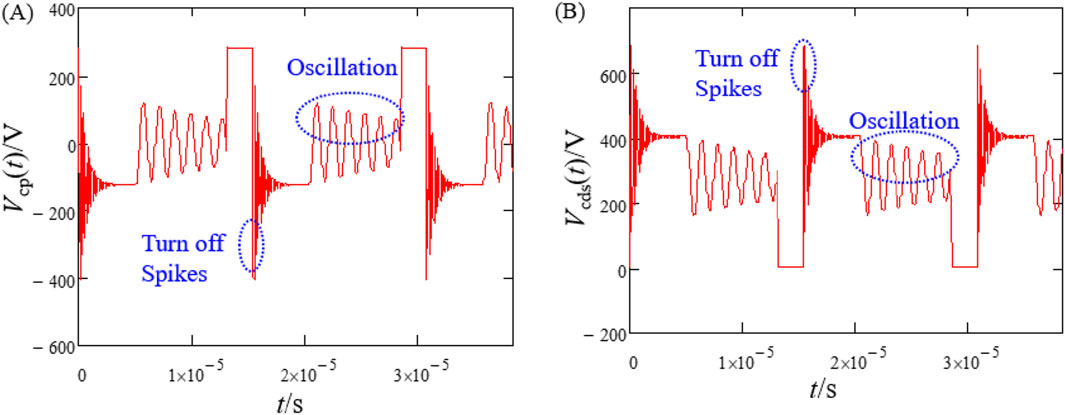
Figure 10. The complete cycle waveform of the primary-side MOSFET’s drain-source voltage and secondary-side diode voltage. (A) Voltage waveform of primary-side MOSFET’s drain-source. (B) Voltage waveform of secondary-side diode.

4 The distributed parameters influence on differential and common-mode noise

According to the analysis in Section 3, the distributed parameters of the flyback circuit have a significant impact on various voltage and current waveforms. The spikes and oscillations in these waveforms are also the fundamental causes of EMI noise generation. Therefore, performing Fourier decomposition on these voltage and current waveforms can reveal the distribution of the noise spectrum they generate.

According to the analysis in Section 3-1, the generation mechanism of differential-mode noise is mainly due to the current ripple in the primary power loop. Therefore, to analyze the impact of distributed parameters on differential-mode noise, Fast Fourier Transform (FFT) can be performed on the primary current i₁. Common-mode noise is primarily caused by ground distribution currents arising from potential jumps in the circuit. Thus, to analyze the impact of distributed parameters on common-mode noise, FFT can be performed on the primary switch transistor voltage V_cds and the secondary diode voltage V_D.

4.1 The distributed parameters influence on differential mode noise

Based on the analysis in Section 3, different primary current waveforms corresponding to various distributed parameters can be constructed and subjected to FFT decomposition to obtain the corresponding noise spectrum, as shown in Figure 11. It can be concluded that an increase in capacitance C_p, C_ds, and primary leakage inductance L_1k will worsen the differential-mode noise in the low-frequency range but improve it in the high-frequency range. It is observed that due to the smaller value of C_p, its impact is much less than that of C_ds. Moreover, as C_p, C_ds, and L_1k increase, the frequency corresponding to the noise peaks in the mid-to-high frequency range of differential-mode noise decrease. This undoubtedly requires the filter to enhance its low-frequency filtering performance, increasing the difficulty of filter design. The distributed parameters L_2k and C_s of the secondary circuit have essentially no effect on differential-mode noise.

Figure 11

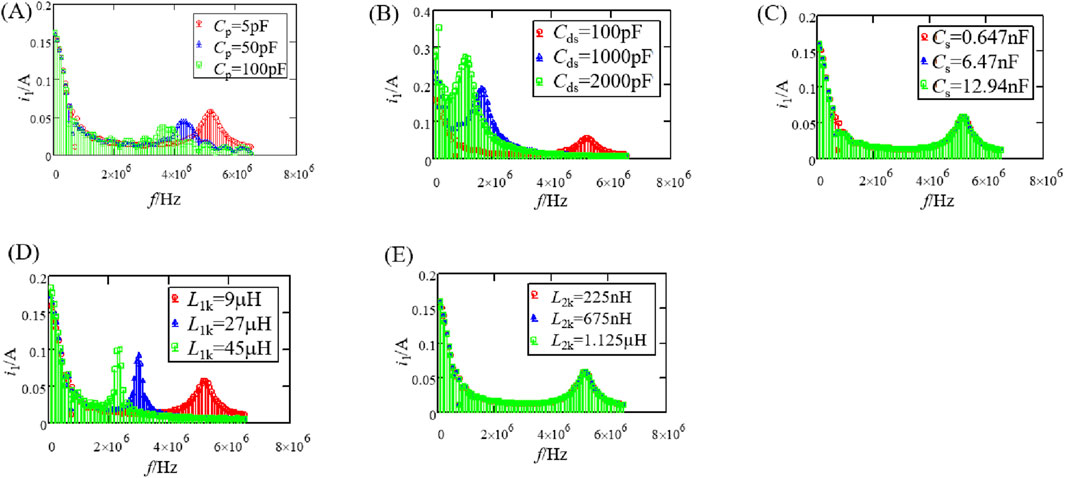
Figure 11. FFT results of the primary current i₁ under different parasitic parameters. (A) Different values of C_p. (B) Different values of C_ds. (C) Different values of C_s. (D) Different values of L_1k. (E) Different values of L_2k.

4.2 The distributed parameters influence on common mode noise

Similarly, by constructing the primary switch transistor voltage waveforms and secondary diode voltage waveforms corresponding to different distributed parameters, and performing FFT decomposition to obtain the corresponding common-mode noise spectrum, as shown in Figures 12, 13, the following conclusions can be drawn:

(1) Due to changes in the secondary winding leakage inductance L_2k and parasitic capacitance C_s, the FFT results of V_cds and V_D remain essentially unchanged. Therefore, the secondary circuit parameters have essentially no effect on common-mode noise.

(2) When the primary winding parasitic capacitance C_p and leakage inductance L_1k increase, the frequency corresponding to the peaks of common-mode noise in the mid-to-high frequency range decrease, while the high-frequency common-mode noise is reduced. However, the impact on low-frequency common-mode noise is relatively minor.

Figure 12

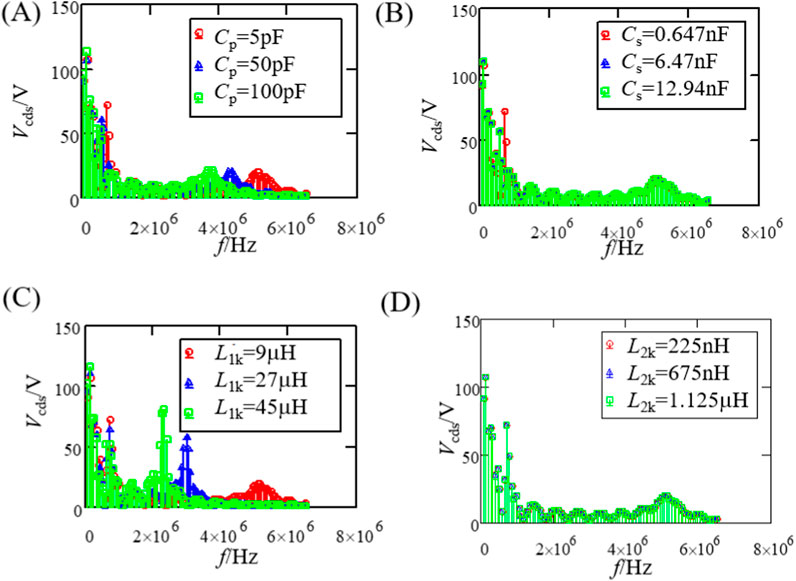
Figure 12. FFT results of the MOSFET voltage V_cds under different parasitic parameters. (A) Different values of C_p. (B) Different values of C_s. (C) Different values of L_1k. (D) Different values of L_2k.

Figure 13

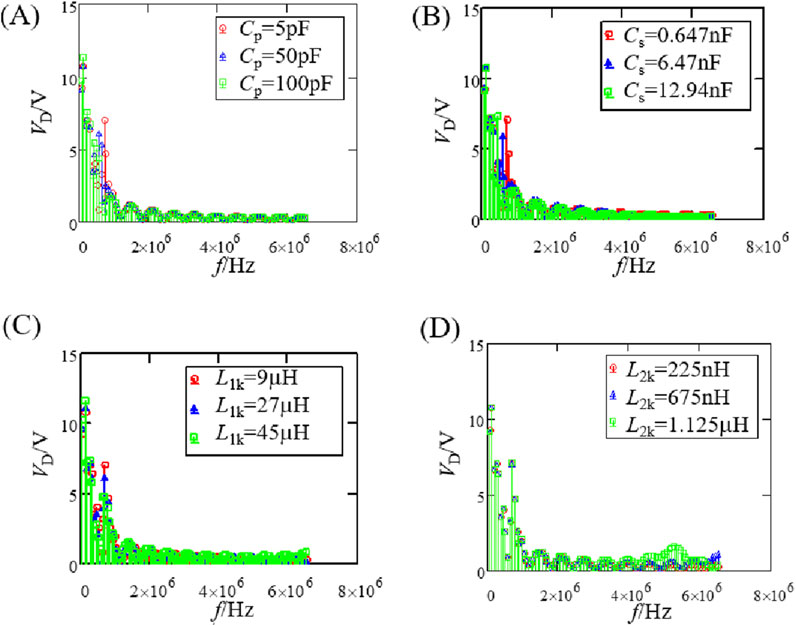
Figure 13. FFT results of the diode voltage V_D under different parasitic parameters. (A) Different values of C_p. (B) Different values of C_s. (C) Different values of L_1k. (D) Different values of L_2k.

5 Experimental verification

The main purpose of this experiment is to verify two aspects, one is to confirm the accuracy of the theoretically constructed switching waveforms, and the other is to validate the effectiveness of analyzing the impact of distributed parameters on EMI noise based on these theoretically constructed switching waveforms. The flyback converter prototype used in this chapter is shown in Figure 14, and its circuit distributed parameter data as shown in Table 1.

Figure 14

Figure 14. The prototype of flyback converter.

As shown in Figure 15, it includes comparison diagrams between the theoretically calculated main switching waveforms and the measured waveforms. It can be seen that the theoretically calculated switching waveforms accurately reflect the characteristics of each switching waveform during every switching process. There are some differences in peak amplitudes, mainly because there are errors between the values of circuit parameters used in the theoretical analysis and their actual values. However, this does not hinder the use of theoretical switching waveforms for analyzing the impact of flyback distributed parameters on its EMI noise. It should be noted that the time corresponding to each stage of these theoretically calculated waveforms is given based on the measured values, rather than calculated according to the formulas in Section 3–5. This is because Equations 21, 22 ignore the effect of winding resistance, and due to errors in the values of parameters such as leakage inductance and magnetizing inductance, it is impossible to achieve the same calculation results for each stage time as the measured values. To facilitate the comparison of theoretical switching waveforms and measured waveforms, this paper uses the actual measured values of each duration in the theoretical analysis.

Figure 15

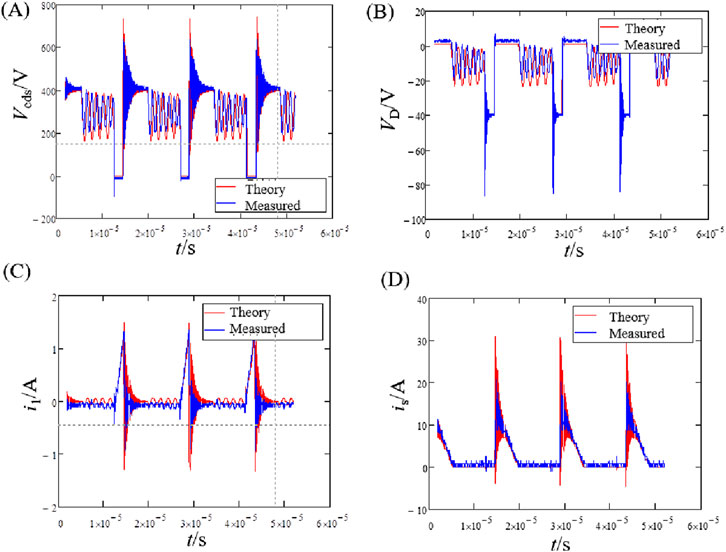
Figure 15. Comparisons of theoretical waveforms and measured waveforms. (A) Waveform of V_cds. (B) Waveform of V_D. (C) Waveform of I₁. (D) Waveform of I_s.

To verify the correctness of using the constructed switching waveforms to analyze the impact of distributed parameters on EMI noise, this paper measured the differential and common-mode noise for different values of primary winding capacitance C_p and secondary winding capacitance C_s, as shown in Figure 16. It can be concluded that as C_p increases, its impact on low-frequency differential and common-mode noise is relatively minor, and the frequency corresponding to the peaks of differential and common-mode noise at mid-to-high frequency decrease. In contrast, changes in C_s have essentially no effect on the differential and common-mode noise of the entire converter. This conclusion is consistent with the results of theoretical analysis, further validating the effectiveness of the proposed theoretical method for time-domain analysis of the impact of flyback distributed parameters on EMI noise.

Figure 16

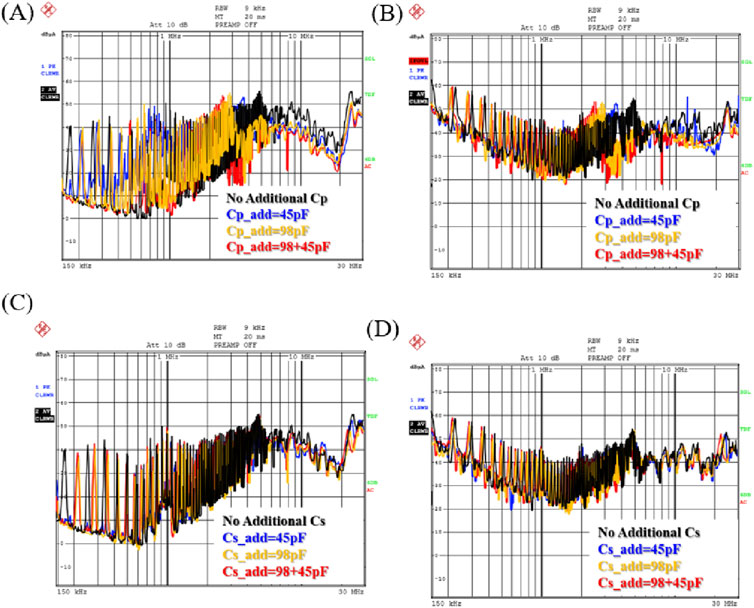
Figure 16. Experimental results of parasitic parameters’ effect on DM and CM noise. (A) The effect of C_p on CM noise. (B) The effect of C_p on DM noise. (C) The effect of C_s on CM noise. (D) The effect of C_s on DM noise.

6 Conclusion

This paper constructs theoretical time-domain waveforms for the flyback circuit considering transformer distributed parameters, analyzes the impact of transformer distributed parameters on voltage and current waveforms, as well as their effect on EMI noise. Experimental validation confirms the correctness and effectiveness of the established model. The following conclusions can be drawn:

(1) The constructed theoretical time-domain waveforms match the measured results, accurately expressing the details of the entire cycle’s voltage and current waveforms, such as the oscillation characteristics of each part.

(2) Analyzing the impact of flyback circuit distrib1uted parameters on differential and common-mode noise based on the constructed theoretical waveforms aligns with the trends of the measured noise results, which can guide the design of transformer distributed parameters and EMI rectification.

(3) The distributed parameters of the primary circuit in the flyback circuit have a larger impact on its EMI noise, while those of the secondary circuit have a smaller effect.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BL: Writing–original draft. RL: Writing–review and editing. JJ: Writing–review and editing. YW: Writing–review and editing. PX: Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors BL, JJ, YW, and PX were employed by Ginlong Technologies Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Emami, Z., Farzanefard, H., and Motahari, S. R. (2010). “Precise prediction of conducted EMI in PWM flyback converters,” in 2010 18th Iranian conference on electrical engineering, 765–771.

Google Scholar

Fakhafkh, L., and Ammous, A. (2017). New simplified model for predicting conducted EMI in DC/DC converters. Electr. Eng. 3, 1087–1097. doi:10.1007/s00202-016-0474-2

CrossRef Full Text | Google Scholar

Fu, K. C. W. (2019). Evaluation method of flyback converter behaviors on common-mode noise. IEEE Access 7, 28019–28030. doi:10.1109/access.2019.2902462

CrossRef Full Text | Google Scholar

Kai, T., Kashihara, T., and Kobayashi, K. (2024). “EMI noise analysis using frequency domain simulation considering dynamic semiconductor characteristics in flyback converter circuits,” in 2024 IEEE joint international symposium on electromagnetic compatibility, signal and power integrity: EMC Japan/asia-pacific international symposium on electromagnetic compatibility (EMC Japan/APEMC okinawa), 156–158.

Google Scholar

Liang, B., Wei, K., and Yue, Y. (2012). Prediction of the conducted EMI in PWM converter system with parasitic parameters considered. Sci. China-Technological Sci. 10, 2829–2836. doi:10.1007/s11431-012-4925-3

CrossRef Full Text | Google Scholar

Liu, J., Wang, Y., Jiang, D., and Cao, Q. (2015). “Fast prediction for conducted EMI in flyback converters,” in 2015 IEEE international conference on computational electromagnetics, 247–249.

Google Scholar

Ma, W., Zhao, Z., Meng, J., Pan, Q., and Zhang, L. (2008). Precise methods for conducted EMI modeling, analysis, and prediction. Sci. China 6, 641–655. doi:10.1007/s11431-008-0082-0

CrossRef Full Text | Google Scholar

Takahashi, K., Ibuchi, T., and Funaki, T. (2019). Frequency-domain EMI simulation of power electronic converter with voltage-source and current source noise models. IEICE Trans. Commun. 9, 1853–1861. doi:10.1587/transcom.2018ebp3301

CrossRef Full Text | Google Scholar

Trinchero, R., Stievano, I. S., and Canavero, F. G. (2015). EMI prediction of switching converters. IEEE Trans. Electromagn. Compat. 5, 1270–1273. doi:10.1109/temc.2015.2419974

CrossRef Full Text | Google Scholar

Wang, Z., Wang, S., Kong, P., and Lee, F. C. (2012). DM EMI noise prediction for constant on-time, critical mode power factor correction converters. IEEE Trans. Power Electron. 7, 3150–3157. doi:10.1109/tpel.2011.2182059

CrossRef Full Text | Google Scholar

Yang, L., Wang, S., Zhao, H., and Zhi, Y. (2020). Prediction and analysis of EMI spectrum based on the operating principle of EMC spectrum analyzers. IEEE Trans. Power Electron. 1, 263–275. doi:10.1109/tpel.2019.2914468

CrossRef Full Text | Google Scholar

Zhu, R., Lin, N., Dinavahi, V., and Liang, G. (2020). An accurate and fast method for conducted EMI modeling and simulation of MMC-based HVdc converter station. IEEE Trans. Power Electron. 5, 4689–4702. doi:10.1109/tpel.2019.2945931

CrossRef Full Text | Google Scholar