Transverse resonance technique for analysis of a symmetrical open stub in a microstrip transmission line

Open stubs in a strip (microstrip) transmission line are one of the most common elements of planar circuits used in numerous devices in the various types of wireless systems. Therefore, the urgent problem is to develop an analyzing method for discontinuities in the form of the open stub in a microstrip transmission line at frequencies at which the high-frequency effects must be considered. In the paper, a technique of scattering characteristics calculating on a symmetrical microstrip open stub by transverse resonance method is presented. Boundary value problems for a rectangular volume resonator based on a microstrip transmission line with a symmetric open stub are solved for the three options boundary conditions in the symmetry plane and on the longitudinal boundaries. The intersection of the spectral curves obtained by the numerical solution of the “electric” and “magnetic” boundary value problems determines the minima of a reflection or transmission coefficients of fundamental wave on discontinuities. To algebraize the boundary value problems for the eigen frequencies of volume resonator with discontinuity, the corresponding two-dimensional functions of the magnetic potential are constructed, through which the components of the current density on the strip are determined. The functions of magnetic potential were defined by decomposing them into expansion by Fourier series, which ensures stable convergence of the series and numerical calculation algorithm. The developed technique has been tested by calculating the eigenfrequency spectra of an open microstrip stub using the transverse resonance method on the example of an open stub in a microstrip transmission line with a resonant frequency of about 3.0 GHz. Also, a technique for numerical solutions of “electric” and “magnetic” boundary-value problems for resonators with two electrodynamically coupled symmetric open stubs in a microstrip transmission line is developed.

1 Introduction

Open or short-circuit stubs in a strip (microstrip) transmission line are one of the most common elements of planar circuits used in numerous devices in the microwave frequency range: various types of filters, couplers, power amplifiers, antennas, sensors, wireless energy transfer systems, etc. Modern planar circuits in the microwave frequency range already contain stubs of a complex shape and a complex pattern inside the microstrip line (Yang et al., 2022; Martín et al., 2003; Boutejdar et al., 2009; MezaalY et al., 2018; Fan et al., 2018; Deshmukh et al., 2012; Deb Roy et al., 2018; Henderson et al., 2018).

The scattering characteristics of ordinary rectangular stubs in a microstrip line are easily determined by transmission line theory by which calculates the input admittance of the stub. A more accurate analysis of such discontinuity, which considers edge and other effects of a microwave circuit with an open or shorted stub, is already a difficult problem of applied electrodynamics. Given the computing capabilities of modern computer technology, complex planar circuits are analyzed using commercial programs by numerical methods, mostly by the moment’s method followed by the construction of an equivalent discontinuity circuit. Rigorous analysis of stub discontinuities in strip and microstrip lines can be carried out using the mode matching method, which is based on the decomposition method and describes the field in them by the eigenwaves of each partial region. But that is a cumbersome method.

More promising for rigorous analysis of such discontinuities, in our opinion, is the transverse resonance method, which was introduced by Sorrentino and Itoh (Sorrentino, 1989) and allows analyzing complex structures without breaking the microwave circuit into small elements. The idea of the method is that there is a relationship between the eigenfrequencies of the volume resonator, in which the discontinuity is located, and the scattering matrix elements on this discontinuity. The transverse resonance method is a universal method for analyzing waveguide and planar circuits, which calculates both the dispersion characteristics of regular transmission lines and the scattering characteristics of unregular distributed circuits (Uwano et al., 1987; Alessandri et al., 1992; Bornemann, 1991; Schwab and Menzel, 1992; Tao, 1992; Green, 1989; Barlabe et al., 2000; Varela and Esteban, 2011). Using the example of the periodic structures scattering characteristics (Rassokhina and Krizhanovski, 2009), it was shown that for symmetrical in the transverse direction discontinuities, the intersection points of the eigenfrequency spectra obtained from the solutions of boundary value problems with two different conditions in the symmetry plane directly indicate the zeros or poles of the scattering characteristics. We are talking about the conditions of the electric and magnetic walls (e.w. and m. w.) in the symmetry plane and on the longitudinal boundaries of the resonator, according to which the boundary value problems with such boundary conditions are called “electric” and “magnetic” boundary value problems, respectively (Rassokhina and Krizhanovski, 2018).

The aim of the study is to develop a technique of algebraization of boundary value problems for the analysis of distributed discontinuity in the form of a symmetric open stub in a microstrip transmission line by the transverse resonance method.

2 Formulation and solution of boundary value problems

The topology of the two-layer planar structure under consideration is provided in Figure 1, which shows a symmetrical open stub in a microstrip transmission line. According to the transverse resonance method, to determine the resonant interaction frequencies of the fed transmission line 1 with discontinuity 2-3, the two boundary value problems with electric and magnetic wall conditions (e.w. or m. w.) in the plane of symmetry $z=0$ must be solved. At the resonator boundary $z=L$ the conditions of an electric or magnetic wall must also be fulfilled.

Figure 1

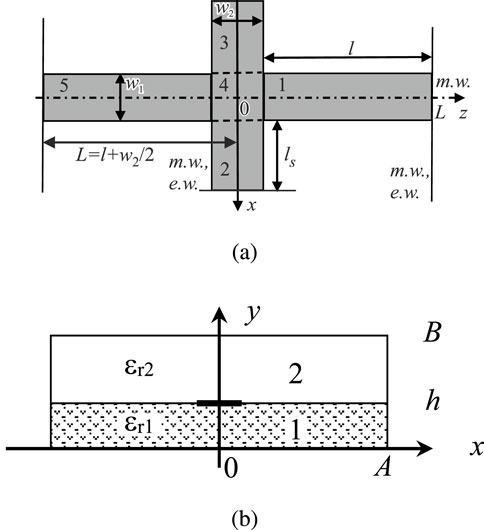
Figure 1. (A) Topology of a symmetrical open stub in a microstrip line, top view, and (B) cross section of volume resonator with a microstrip line.

Consider the solution of the boundary value problem for the current density ${\vec{J}}_{\tau }$ of a microstrip resonator expressed in terms of magnetic type potentials: $J_{h,n}\left(x,z\right)$:

${\vec{J}}_{\tau }\left(x,z\right)=-\frac{1}{j\cdot k_0}{\displaystyle \sum _{n=1}^P}\mathrm{\nabla }{J}_{h,n}\left(x,z\right)C_{h,n}(1)$

where $k_0={\omega }_0/c$ - wavenumber, $J_{h,n}$ are eigenfunctions of the magnetic potential for the current density, $C_{h,n}$ is unknown expansion coefficient, P is the order of series reducing.

The electromagnetic field components in the shielded structure satisfy the Helmholtz equation in Cartesian coordinates. The current density distribution function in the microstrip line is determined by the difference of the magnetic field’s tangent components and therefore also satisfies the Helholtz equation.

Polynomial solutions of the Helmholtz equation were studied in (Burskii and Buryachenko, 2013) as dual problem for high-order hyperbolic problems in elliptic planar domains. For simple discontinuities such as microstrip step discontinuity, the function can be constructed as a series of orthogonal polynomials (Rassokhina and Krizhanovski, 2018; 2023). For a more complex topology to avoid the cumbersome calculations, the current density distribution function in partial regions should be described in the form of Fourier series.

The current density distribution function for a strip line with an open stub satisfies the Helmholtz equation:

$\frac{{\partial }^2{J}_{h,n}}{\partial x^2}+\frac{{\partial }^2{J}_{h,n}}{\partial z^2}+{\chi }_{h,n}^2{J}_{h,n}=0,$

when $\frac{\partial J_{h,n}}{\partial \vec{n}}=0$ by free boundaries in partial regions 1–4, $\frac{\partial J_{h,n}\left(0,z\right)}{\partial x}=0$ in symmetry plane, $J_{h,n}\left(x,0\right)=J_{h,n}\left(x,L\right)=0$ for the “electric” boundary value problem and $\frac{\partial J_{h,n}\left(x,0\right)}{\partial z}=\frac{\partial J_{h,n}\left(x,L\right)}{\partial z}=0$ for the “magnetic” boundary value problem.

Considering the above, the two-dimensional function for the magnetic potential $J_{h,n}\left(x,z\right)$ of the “electric” boundary value problem in partial regions 1-4 can be presented in a Fourier series form:

$J_{h1}\left(x,z\right)={\displaystyle \sum _{k=0}^M}{A}_{1k}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\cdot \frac{\sin k_{\mathit{z1k}}\left(L-z\right)}{k_{\mathit{z1k}}\cos k_{\mathit{z1k}}l}$

for $\left|x\right|\le w_1/2$, $w_2/2\le z\le L$, where $L=l+w_2/2$,

$J_{h2}\left(x,z\right)={\displaystyle \sum _{k=0}^M}{A}_{2k}\sqrt{\frac{2}{w_2}}\sin \frac{\pi \left(2k+1\right)}{w_2}z\frac{\cos k_{\mathit{x1k}}\left(L_s-x\right)}{k_{\mathit{x1k}}\sin k_{\mathit{x1k}}{l}_s}$

for $\left|z\right|\le w_2/2$, $w_1/2\le x\le L_s$, where $L_s=l_s+w_1/2$,

$J_{h3}\left(x,z\right)={\displaystyle \sum _{k=0}^M}{A}_{3k}\sqrt{\frac{2}{w_2}}\sin \frac{\pi \left(2k+1\right)}{w_2}z\frac{\cos k_{\mathit{x1k}}\left(L_s+x\right)}{k_{\mathit{x1k}}\sin k_{\mathit{x1k}}{l}_s}$

for $-w_1/2\le x\le -L_s$. In partial region 4, the solution of the Helmholtz equation consists of the sum of two functions with boundary conditions at $x=0$, $x=w_1/2$ and $z=0$, $z=w_2/2$, respectively:

$J_{h4}\left(x,z\right)={\displaystyle \sum _{k=0}^M}{A}_{\mathit{41k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\frac{\sin k_{\mathit{z1k}}z}{k_{\mathit{z1k}}\cos \left(k_{\mathit{z1k}}{w}_2/2\right)}+$

$+{\displaystyle \sum _{k=0}^M}{A}_{\mathit{42k}}\sqrt{\frac{2}{w_2}}\sin \frac{\pi \left(2k+1\right)}{w_2}z\frac{\cos k_{\mathit{x1k}}x}{k_{\mathit{x1k}}\sin \left(k_{\mathit{x1k}}{w}_1/2\right)}(2)$

for $\left|x\right|\le w_1/2$, $\left|z\right|\le w_2/2$. There $k_{z1,k}^2={\chi }_{hn}^2-{\left(\frac{2\pi k}{w_1}\right)}^2$, $k_{x1,k}^2={\chi }_{hn}^2-{\left(\frac{\pi \left(2k+1\right)}{w_2}\right)}^2$ and ${\chi }_{hn}$ are eigenvalues of the eigenfunction $J_{h,n}\left(x,z\right)$, which is found from the solution of the boundary value problem.

From the continuity conditions of the functions on the partial domains boundaries, a system of linear algebraic equations (SLAE) is obtained in the form:

${\displaystyle \sum _{m=0}}{A}_{\mathit{41m}}\left[F_{1k}\left(k_{\mathit{z1k}}\right){\delta }_{km}-{\displaystyle \sum _{n=0}}\frac{1}{F_{2n}}{S}_{1,kn}{S}_{2,nm}\right]=0.(3)$

Equating the determinant of SLAE Equation 3 to zero, we obtain a spectrum of eigenvalues ${\chi }_{hn}$ and, accordingly, eigenfunctions for the magnetic vector potential $J_{h,n}\left(x,z\right)$, which determines the components of the current density on the strip. Expressions for matrix elements in Equation 3 have the form:

$F_{1k}\left(k_{\mathit{z1k}}\right)=\frac{\tan k_{\mathit{z1k}}l}{k_{\mathit{z1k}}}+\frac{\tan \left(k_{\mathit{z1k}}{w}_2/2\right)}{k_{\mathit{z1k}}},$

$F_{2n}\left(k_{\mathit{x1n}}\right)=\frac{\cot k_{\mathit{x1n}}{l}_s}{k_{\mathit{x1n}}}+\frac{\cot \left(k_{\mathit{x1n}}{w}_1/2\right)}{k_{\mathit{x1n}}}.$

The expansion coefficients $A_{\mathit{41m}},A_{\mathit{42m}}$ of the functions according to the trigonometric basis are calculated with accuracy up to some constant factor, which is determined from the normalization condition of the magnetic potential basis functions (integration over the area of the microstrip $S_{\mathit{MSL}}$):

${\int }_{S_{\mathit{MSL}}}{\left[\mathrm{\nabla }{J}_{h,n}\left(x,z\right)\right]}^{2}dS={\chi }_{h,n}^2{\int }_{S_{\mathit{MSL}}}{J}_{h,n}^2\left(x,z\right)dS=1.$

It is worth noting that the “electrical” boundary value problem also has a solution by ${\chi }_{h,n}=0$, which must be considered by rigorous solving of the boundary problem.

For the “electric-magnetic” boundary value problem under the condition of a magnetic wall in the symmetry plane $z=0$ and an electric wall at the longitudinal boundary $z=L$, the magnetic potential eigenfunctions in partial regions 1-4 can be determined as:

$J_{h1}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{1k}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\cdot \frac{\sin k_{\mathit{z1k}}\left(L-z\right)}{k_{\mathit{z1k}}\cos k_{\mathit{z1k}}l},$

$J_{h2}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{2k}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_2}}\cos \frac{2\pi k}{w_2}z\cdot \frac{\cos k_{\mathit{x1k}}\left(L_s-x\right)}{k_{\mathit{x1k}}\sin k_{\mathit{x1k}}{l}_s},$

$J_{h3}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{3k}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_2}}\cos \frac{2\pi k}{w_2}z\frac{\cos k_{\mathit{x1k}}\left(L_s+x\right)}{k_{\mathit{x1k}}\sin k_{\mathit{x1k}}{l}_s},$

$J_{h4}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{\mathit{41k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\frac{\cos k_{\mathit{z1k}}z}{k_{\mathit{z1k}}\sin \left(k_{\mathit{z1k}}{w}_2/2\right)}+$

$+{\displaystyle \sum _{k=0}}{A}_{\mathit{42k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_2}}\cos \frac{2\pi k}{w_2}z\frac{\cos k_{\mathit{x1k}}x}{k_{\mathit{x1k}}\sin \left(k_{\mathit{x1k}}{w}_1/2\right)},$

where $k_{z1,k}^2={\chi }_{hn}^2-{\left(\frac{2\pi k}{w_1}\right)}^2$, $k_{x1,k}^2={\chi }_{hn}^2-{\left(\frac{2\pi k}{w_2}\right)}^2$. The SLAE for determining the eigenvalues and expansion’s coefficients into series of the magnetic potential has the form:

${\displaystyle \sum _{m=0}}{A}_{\mathit{42m}}\left[F_2\left(k_{\mathit{x1k}}\right){\delta }_{km}+{\displaystyle \sum _{n=0}}\frac{1}{F_{1n}\left(k_{\mathit{z1n}}\right)}{S}_{\mathit{2kn}}{S}_{\mathit{1nm}}\right]=0,(4)$

where, by analogy with the “electrical” boundary problem,

$F_{1k}\left(k_{\mathit{z1k}}\right)=\frac{\tan k_{\mathit{z1k}}l}{k_{\mathit{z1k}}}-\frac{\cot \left(k_{\mathit{z1k}}{w}_2/2\right)}{k_{\mathit{z1k}}},$

$F_{2n}\left(k_{\mathit{x1n}}\right)=\frac{\cot k_{\mathit{x1n}}{l}_s}{k_{\mathit{x1n}}}+\frac{\cot \left(k_{\mathit{x1n}}{w}_1/2\right)}{k_{\mathit{x1n}}}.$

In the same way, the two-dimensional function of the magnetic potential is defined for the boundary value problem with boundary conditions of the magnetic wall in the plane of symmetry and on the longitudinal boundary of the volume resonator (“magnetic” boundary problem).

The boundary value problems solving for current density eigenfunctions in an irregular microstrip line is used for solving of boundary problem for rectangular volume resonators with this discontinuity. In this case, the discontinuity is an open symmetric stub in the microstrip transmission line.

According to the transverse resonance method, the points of spectral curves intersection, corresponding to the solutions of the electric and magnetic–electric boundary value problem, determine the minimum transmission coefficient points (Rassokhina and Krizhanovski, 2009). And the points of spectral curves intersection, corresponding to the solutions of the electric and magnetic boundary value problem, determine the minimum reflection coefficient points.

The Helmholtz equation and boundary conditions for an electric $A_{ey,i}$ and magnetic $A_{hy,i}$ vector potentials for field in volume resonator (Figure 1B) are follows (Collin, 1990):

$\mathrm{\Delta }{A}_{h\left(e\right)y,i}+k_0^2{\epsilon }_{r,i}{A}_{h\left(e\right)y,i}=0,i=\mathrm{1,2},$

where $A_{ey,i}\left(A,y,z\right)=0$, $\frac{\partial }{\partial y}{A}_{ey,i}\left(x,0,z\right)=\frac{\partial }{\partial y}{A}_{ey,i}\left(x,B,z\right)=0$, $A_{ey,i}\left(x,y,0\right)=A_{ey,i}\left(x,y,L\right)=0$ for “electric” boundary value problem and $\frac{\partial }{\partial z}{A}_{ey,i}\left(x,y,0\right)=\frac{\partial }{\partial z}{A}_{ey,i}\left(x,y,L\right)=0$ for “magnetic” boundary value problem; $\frac{\partial }{\partial x}{A}_{hy,i}\left(A,y,z\right)=0$, $A_{hy,i}\left(x,0,z\right)=A_{hy,i}\left(x,B,z\right)=0$, $\frac{\partial }{\partial z}{A}_{hy,i}\left(x,y,0\right)=\frac{\partial }{\partial z}{A}_{hy,i}\left(x,y,L\right)=0$ for “electric” boundary value problem and $A_{hy,i}\left(x,y,0\right)=A_{hy,i}\left(x,y,L\right)=0$ for “magnetic” boundary value problem.

The electric and magnetic vector potentials of a rectangular volume resonator are presented in the form of double Fourier series:

$\begin{array}{c}\hfill A_{ey,i}={\displaystyle {\sum }_{m=1}^N}{\displaystyle {\sum }_{n=1\left(0\right)}^N}{\varphi }_{mn}\left(x,z\right)F_{ei,mn}\left(k_{yi,mn}y\right),\hfill \\ \hfill A_{hy,i}={\displaystyle {\sum }_{m=1}^N}{\displaystyle {\sum }_{n=0\left(1\right)}^N}{\psi }_{mn}\left(x,z\right)F_{hi,mn}\left(k_{yi,mn}y\right),\hfill \end{array}(5)$

where $k_{yi,mn}^2=k_0^2{\epsilon }_{ri}-{\chi }_{mn}^2$, $i=\mathrm{1,2}$ is a partial area number, $N$ is order of series reduction, and

$F_{e1,mn}\left(y\right)=\frac{\cos \left(k_{y1,mn}y\right)}{k_{y1,mn}\sin \left(k_{y1,mn}h\right)}{R}_{\mathit{1mn}},$

$F_{e2,mn}\left(y\right)=\frac{\cos \left(k_{y2,mn}\left(B-y\right)\right)}{k_{y2,mn}\sin \left(k_{y2,mn}{b}_1\right)}{R}_{\mathit{2mn}},$

$F_{h1,mn}\left(y\right)=\frac{\sin \left(k_{y1,mn}y\right)}{\sin \left(k_{y1,mn}h\right)}{T}_{\mathit{1mn}},$

$F_{h2,mn}\left(y\right)=\frac{\sin \left(k_{y2,mn}\left(B-y\right)\right)}{\sin \left(k_{y2,mn}{b}_1\right)}{T}_{\mathit{2mn}},$

when $R_{1(2)mn}$, $T_{1(2)mn}$ is unknown coefficients of expansion into series.

The coupling integrals ${\alpha }_{h,q,mn}^m$, ${\beta }_{h,q,mn}^m$ between a strip resonator with discontinuity and a volume resonator are calculated by the formulas Rassokhina and Krizhanovski (2018):

$\begin{array}{c}\hfill {\alpha }_{h,q,mn}^m={\int }_{S_{\mathit{MSL}}}\nabla J_{h,q}\left(x,z\right)\left[\nabla {\psi }_{mn}\left(x,z\right)\times e_y\right]dS,\hfill \\ \hfill {\beta }_{h,q,mn}^m={\int }_{S_{\mathit{MSL}}}\nabla J_{h,q}\left(x,z\right)\nabla {\varphi }_{mn}\left(x,z\right)dS,\hfill \end{array}(6)$

where ${\psi }_{mn}$, ${\varphi }_{mn}$ are basis functions of the electric and magnetic vector potential of a volume resonator, $k_{xm}=\pi \left(2m-1\right)/2A$, $k_{zn}=\pi n/L$ for the “electric” and “magnetic” boundary value problem or $k_{zn}=\pi \left(2n-1\right)/2L$ for the “magnetic-electric” problem:

${\varphi }_{mn}\left(x,z\right)=\left\{\begin{array}{c}{P}_{mn}\cos k_{xm}x\sin k_{zn}z,ew-ew,\hfill \\ \hfill P_{mn}\cos k_{xm}x\cos k_{zn}z,mw-mw,\hfill \end{array}\right.$

${\psi }_{mn}\left(x,z\right)=\left\{\begin{array}{c}\hfill P_{mn}\sin k_{xm}x\cos k_{zn}z,ew-ew,\hfill \\ \hfill P_{mn}\sin k_{xm}x\sin k_{zn}z,mw-mw,\hfill \end{array}\right.$

$P_{mn}=\sqrt{\frac{2}{A}}\sqrt{\frac{2-{\delta }_{n0}}{L}}\frac{1}{{\chi }_{mn}},{\chi }_{mn}^2=k_{xm}^2+k_{zn}^2.$

The SLAE for the eigenfrequencies of a three-dimensional resonator is as follows:

${\displaystyle \sum _{q=1}}{C}_{h,q}{\displaystyle \sum _{m=1}}{\displaystyle \sum _{n=0}}\left[{\alpha }_{h,q,mn}^m{\alpha }_{h,l,mn}^m\frac{1}{F_{h,mn}}+\frac{1}{k_0^2{\epsilon }_r}{\beta }_{h,q,mn}^m{\beta }_{h,l,mn}^m\frac{1}{F_{e,mn}}\right]=0,(7)$

where

$F_{h,mn}=k_{\mathit{y1l}}\cot k_{\mathit{y1l}}h+k_{\mathit{y2l}}\cot k_{\mathit{y2l}}{b}_1,$

$F_{e,mn}=\frac{\cot k_{\mathit{y1mn}}h}{k_{\mathit{y1mn}}}+\frac{1}{{\epsilon }_r}\frac{\cot k_{\mathit{y2mn}}{b}_1}{k_{\mathit{y2mn}}}.$

From the condition that the determinant of system Equation 7 of equations is zero, we obtain the eigenfrequencies $k_0$ of the volume resonator.

3 Algorithm testing and results of symmetric open stub analysis

The algorithms were developed and tested on the example of a two-dimensional planar structure on a Ro3010 laminate with a thickness of $h=0.635$ mm with dielectric constant ${\epsilon }_r=10.2$, the width and height of the grounding volume resonator are equal, respectively $A=15.0$ mm and $b_1=8.0$ mm, other parameters of the structure: $w_1=w_2=w=0.58$ mm (the characteristic impedance of the main transmission line is $Z_0=50$ Ohm). With a constant number $M=5$ of basis functions by Fourier series Equation 2 considered and reduction of series Equation 1 by eigenfunctions of vector potentials up to $P=3$, sufficient algorithm convergence is observed when reduction of series Equation 5 up to $N=150$. The Newton method was used to determine the zeros of the SLAE determinants Equations 4, 7.

Numerical calculations have shown that using trigonometric basis in the expansion of the current density distribution function provided uniform convergence of the algorithms for calculating eigenvalues and, accordingly, eigenfunctions $J_{h,n}\left(x,z\right)$. This led to the uniform convergence of the algorithm for numerical calculation of the eigenfrequency spectrum of a volume resonator with discontinuity in it.

Eigenvalues of a strip resonator with a symmetric open stub of length $l_s=10.5$ mm and $l_s=8.5$ mm, which were obtained from solutions of three boundary value problems, are shown in Figure 2. In the first approximation, the wave numbers of the “electric” resonator correspond to the values ${\chi }_{h,n}^{\left(e.w.\right)}=\pi n/L$ for the magnetic-electric problem ${\chi }_{h,n}^{\left(m.w.-e.w.\right)}=\pi n/2\left(L+l_s\right)$ and for the magnetic problem ${\chi }_{h,n}^{\left(m.w.\right)}=\pi n/\left(L+l_s\right)$.

Figure 2

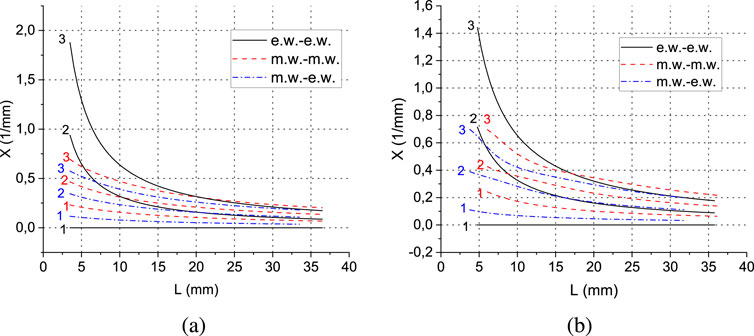
Figure 2. The first three eigenvalues ${\chi }_{h,n}$ of magnetic potential basic functions for a strip resonator with a symmetrical open stub, obtained from the solutions of the electrical, magnetic-electrical and magnetic boundary value problems. Dimensions, in mm: (A) – $w_2=0.58$, $l_s=10.5$; (B) – $w_2=1.16$, $l_s=8.5.$

According to the approximation of the transmission lines theory, the input conductivity of a symmetrical open stub is equal to:

$Y_{in}=2j\cdot Y_0\tan {\theta }_s,$

where $Y_0=1/Z_0$, ${\theta }_s=\omega l_s\cdot \chi /c$ is the wave delay factor, which for this material is equal to about $\chi \approx 2.62$. Resonant frequency of the stub with length $l_s$ (that is, the frequency at which the electric length is ${\theta }_s=\pi /2$) calculated by transmission lines theory is $f_{\mathit{res}}=2.85$ GHz.

For an MSI personal computer with an Intel(R) Core(TM) i3 CPU 2.13 GHz processor, the time to calculate the one points for one root of the characteristic Equation 7 by accuracy $\epsilon ={10}^{-6}$ 1/mm on average is 8 s. The quickness of calculation of the resonator eigenfrequency spectra is ensured by the fact that at each iteration step the coupling integrals Equation 6 are calculated only once.

Figure 3A shows the spectra of the resonator’s eigenfrequencies obtained from solutions of three boundary value problems for a volume resonator with discontinuity in the form of a symmetric open stub in a microstrip transmission line. The intersection point of the spectral curves of the “electric” and “magnetic-electric” boundary value problems corresponds to the frequency at which the minimum of the transmission coefficient is observed $S_{21}$ (about 3.08 GHz), and the point of intersection of the spectral curves of the “electric” and “magnetic” boundary value problems corresponds to the minimum of the reflection coefficient $S_{11}$ at frequency about 5.8 GHz.

Figure 3

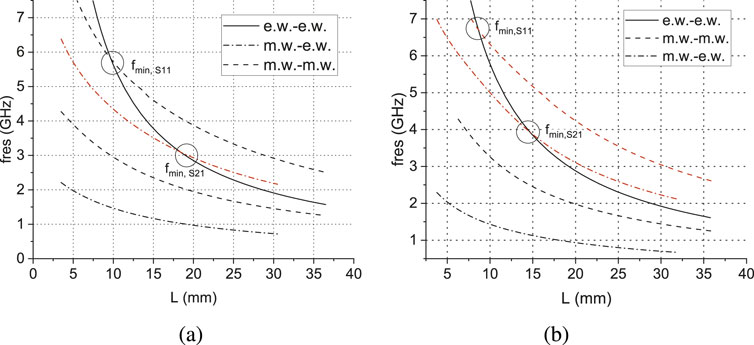
Figure 3. Spectrum of eigenfrequencies of a three-dimensional rectangular resonator based on an microstrip line with a symmetrical open stub, obtained from the solutions of boundary value problems with parameters (in mm): (A) $w=0.58$, $l_s=10.2$; (B) $w_1=0.58$, $w_2=2w_1$, $l_s=8.5$.

Figure 3B shows the spectra of the resonator’s eigenfrequencies with a stub width $w_2=2w_1$ in microstrip transmission line. Such stubs are called capacitive stubs and serve to increase the frequencies of resonant interaction in the microwave circuit.

The results of the scattering characteristics calculations were verified using the microwave design software. The values of the frequencies of resonance interaction obtained from the eigenfrequency spectra and full-wave electrodynamic modeling are almost in agreement.

Thus, according to the results of numerical calculation, a physically correct result was obtained for the scattering characteristics on a symmetrical stub in a microstrip transmission line, considering high-frequency effects, namely, dispersion and marginal capacitance of the open stub.

In Figure 4 the dependence of the resonance frequency on the stub width is shown. As expected from physical considerations, the frequency of resonance reflection increases with the ratio $w_1/w_2$ increase, the frequency of resonant interaction also increases.

Figure 4

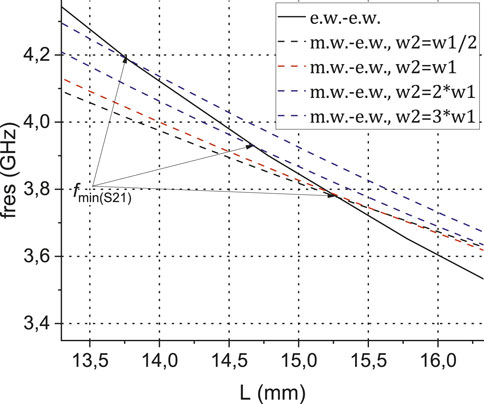
Figure 4. Frequency shift of the of eigen frequencies spectrum of a volume resonator with a symmetric open stub in microstrip line depending on the stub width $w_2$ with parameters (in mm): $w_1=0.58$, $l_s=8.5.$

4 Electromagnetically coupled open microstrip stubs

Electromagnetically coupled discontinuities in planar circuits can also be analyzed by the transverse resonance method. For this purpose, the planar scheme is symmetrized and two boundary value problems are solved under the conditions of an “electric” and “magnetic” wall in the symmetry plane.

The analyzed structure is shown in Figure 5. The plane of symmetry is located at $z=0$, the distance between the stubs is $2z_0$. The figure also shows the geometric parameters and numbering of partial regions for calculating the current density potentials.

Figure 5

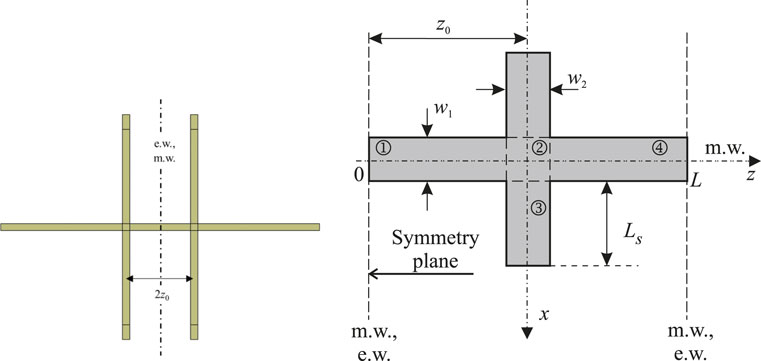
Figure 5. The coupled microstrip stubs: principal scheme of analyzing structure and their decomposition in partial regions.

For the “electrical” boundary value problem, the expressions for the current density potential are as follows:

$J_{h1}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{\mathit{h1k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\frac{\sin k_{\mathit{z1k}}z}{k_{\mathit{z1k}}\cos k_{\mathit{z1k}}{l}_1},$

where $l_1=z_0-w_{2}2$, $k_{z1,k}^2={\chi }_{hn}^2-{\left(\frac{2\pi k}{w_1}\right)}^2$,

$\begin{array}{c}{J}_{h2}\left(x,z\right)={\displaystyle \sum _{k=0}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\left(B_{\mathit{h21k}}\frac{\cos k_{\mathit{z1k}}\left(z-z_0\right)}{k_{\mathit{z1k}}\sin k_{\mathit{z1k}}{w}_{2}2}+B_{\mathit{h22k}}\frac{\sin k_{\mathit{z1k}}\left(z-z_0\right)}{k_{\mathit{z1k}}\cos k_{\mathit{z1k}}{w}_{2}2}\right)+\\ +{\displaystyle \sum _{k=0}}{C}_{\mathit{h2k}}\sqrt{\frac{2-{\delta }_{k0}}{w_2}}\cos \frac{\pi k}{w_2}\left(z-z_0+\frac{w_2}{2}\right)\frac{\cos k_{\mathit{x1k}}x}{k_{\mathit{x1k}}\sin \left(k_{\mathit{x1k}}{w}_{1}2\right)},\end{array}$

$J_{h3}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{\mathit{h3k}}\sqrt{\frac{2-{\delta }_{k0}}{w_2}}\cos \frac{\pi k}{w_2}\left(z-z_0+\frac{w_2}{2}\right)\frac{\cos k_{\mathit{x1k}}\left(L_s+\frac{w_1}{2}-x\right)}{k_{\mathit{x1k}}\sin \left(k_{\mathit{x1k}}{L}_s\right)},$

$J_{h4}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{\mathit{h4k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\frac{\sin k_{\mathit{z1k}}\left(L-z\right)}{k_{\mathit{z1k}}\cos k_{\mathit{z1k}}{l}_2},$

where $k_{x1,k}^2={\chi }_{hn}^2-{\left(\frac{\pi k}{w_2}\right)}^2$, $l_2=L-\left(z_0+w_{2}2\right)$.

From the continuity conditions of the basis function and its derivatives at the partial regions boundaries, a homogeneous SLAE is obtained, the condition for the solution of which is the equality of its determinant to zero, from which the spectrum of eigenvalues ${\chi }_{hn}$ is determined. To solve the “electrical” boundary value problem with zero eigenvalue ${\chi }_{hn}=0$, the expression for the current density distribution function on the microstrip line is simplified to the potential of the current density of an ordinary regular microstrip line of width $w_1$ and length $L$. Taking into account the condition of eigenfunctions normalization, this expression will take the form:

$J_{h,0}\left(x,z\right)=\sqrt{\frac{2}{w_1}}\sqrt{\frac{3}{L}}\cdot \frac{z}{L}.$

The coupling integrals with the basic functions of volume resonance are calculated according by Equation 6.

For the “magnetic” boundary value problem, only the expressions for the current density potentials in partial regions 1 and 4 are changed:

$J_{h1}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{\mathit{h1k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\frac{\cos k_{\mathit{z1k}}z}{k_{\mathit{z1k}}\sin k_{\mathit{z1k}}{l}_1},$

$J_{h4}\left(x,z\right)={\displaystyle \sum _{k=0}}{A}_{\mathit{h4k}}\sqrt{\frac{4-2\cdot {\delta }_{k0}}{w_1}}\cos \frac{2\pi k}{w_1}x\frac{\cos k_{\mathit{z1k}}\left(L-z\right)}{k_{\mathit{z1k}}\sin k_{\mathit{z1k}}{l}_2}.$

The results of calculations of eigen frequencies of the resonator, obtained from the solution of the “electric” and “magnetic” boundary value problem, are shown in Figure 6, where the spectrum of eigen frequencies for two different distances values $z_0$ between symmetrical stubs of a planar structure with two coupled open stubs of the width $w_{1(2)}=w=0.58$ mm and the length $L_s=6.0$ mm are presented. By $z_0=1.5$ mm (Figure 6A) we have a case of uncoupled open stubs, since the distance between them is $l=2z_0\approx 5w$. The coupling between discontinuities by $z_0=0.5$ mm (Figure 6B) is manifested, firstly, in the fact that as this distance decreases, the interval between the two frequencies of resonant interaction of the discontinuity with the main transmission line decreases. Second, the relationship between discontinuities determines the X-shaped forms of the spectral curves.

Figure 6

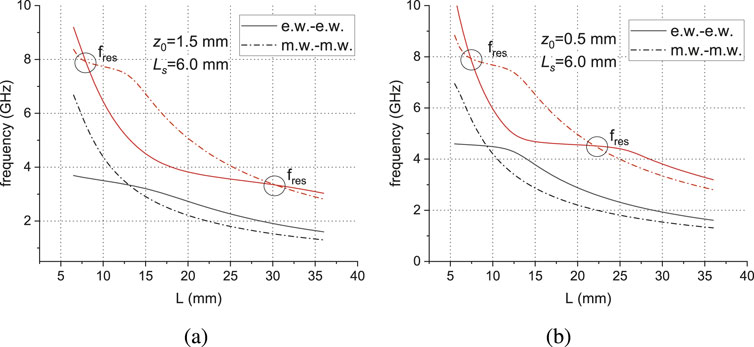
Figure 6. Spectrum of eigenfrequencies of a volume resonator based on an microstrip line with two coupled symmetrical open stubs, obtained from the solutions of boundary value problems with parameters (in mm): $w_1=w_2=0.58$, $L_s=6.0$; (A) $z_0=1.5$, (B) $z_0=0.5$.

Figures 7A, B also shows the spectrum of eigen frequencies of a planar structure with two coupled symmetrical stubs of width $w=0.58$ mm, $L_s=8.5$ mm. In this case also, several frequencies of resonant transmission of the signal are also observed, in comparison with a single discontinuity. With closely spaced stubs $z_0=0.5$ mm, the resonant reflection and resonant transmission frequencies of the signal are close to each other, which is inconvenient for practical use. At distance $z_0=1.89$ mm, we have three frequencies with a minimum reflection coefficient $\left|S_{11}\right|$, and in the upper frequency range we have a bandpass filter. These areas are separated by a broadband bandstop filter with a minimum transmission coefficient $\left|S_{21}\right|$.

Figure 7

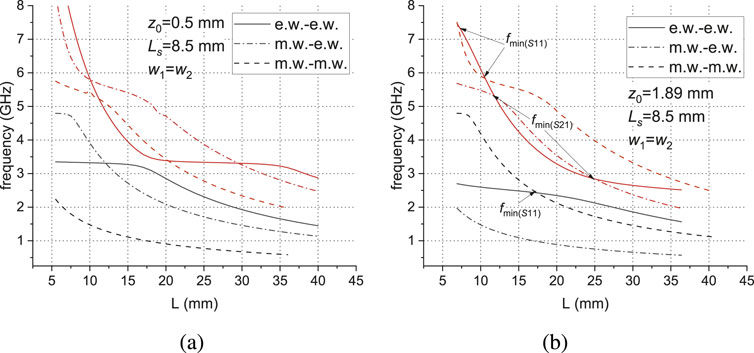
Figure 7. Spectrum of a volume resonator eigenfrequencies based on an microstrip line with two coupled symmetrical open stubs, obtained from the solutions of three boundary value problems with parameters (in mm): $w_1=w_2=0.58$, $L_s=8.5$; (A) $z_0=0.5$, (B) $z_0=1.89$.

Thus, the resonator’s spectral characteristics with discontinuity fully determine the frequencies of resonant interaction of microstrip stubs with the main transmission line.

5 Conclusion

A method of an open stubs analyzing, single and electrodynamically coupled, in a microstrip transmission line by the transverse resonance technique is proposed. To implement the method, the boundary problems for the eigenfunctions of the strip resonator’s current density with a symmetrical open stub were previously solved under the condition of an electric and magnetic wall in the symmetry plane and at the longitudinal boundary. To determine the eigenfunctions of the current density, the trigonometric basis was used, which ensures fast and uniform convergence of numerical calculation algorithms for the eigenfunctions. The use of the trigonometric basis led to the uniform and stable convergence of the algorithm for numerical calculation of the eigen frequency spectrum of a volume cavity with a discontinuity in it.

From the study of the eigenfrequency spectra of volume resonators containing a planar circuit calculated under two different conditions in the symmetry plane, preliminary information about the frequencies of resonant interaction of the discontinuity with the fed microstrip transmission line is obtained. The developed technique of algebraization of boundary value problems for a microstrip line with discontinuity can be applied to the analysis of more complex topologies of microstrip stubs, multi-plane discontinuities and the development of various devices in the microwave frequency range.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YR: Writing–original draft, Conceptualization, Investigation, Methodology, Visualization, Software. VK: Writing–review and editing, Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

This research was supported by the project of Volkswagen Foundation” From modelling and analysis to approximation” (2020–2023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alessandri, F., Baini, G., D’Inzeo, G., and Sorrentino, R. (1992). Conductor loss computation in multiconductor mic’s by transverse resonance technique and modified perturbational method. IEEE Microw. Guid. Wave Lett. 2, 250–252. doi:10.1109/75.136522

CrossRef Full Text | Google Scholar

Barlabe, A., Comeron, A., and Pradell, L. (2000). Generalized transverse resonance analysis of planar discontinuities considering the edge effect. IEEE Microw. Guid. Wave Lett. 10, 517–519. doi:10.1109/75.895088

CrossRef Full Text | Google Scholar

Bornemann, J. (1991). A scattering-type transverse resonance technique for the calculation of (m) mic transmission line characteristics. IEEE Trans. Microw. Theory Tech. 39, 2083–2088. doi:10.1109/22.106550

CrossRef Full Text | Google Scholar

Boutejdar, A., Omar, A., Batmanov, A., and Burte, E. (2009). Design of compact low-pass filter with with wide rejection band using cascaded arrowhead-dgs and multilayer-technique, in 2009 German microwave conference (IEEE), 1–4. doi:10.1109/gemic.2009.4815903

CrossRef Full Text | Google Scholar

Burskii, V. P., and Buryachenko, K. A. (2013). On the breakdown of the uniqueness of a solution of the dirichlet problem for typeless differential equations of arbitrary even order in a disk. J. Math. Sci. 190, 539–566. doi:10.1007/s10958-013-1270-4

CrossRef Full Text | Google Scholar

Collin, R. E. (1990). Field theory of guided waves. IEEE. doi:10.1109/9780470544648

CrossRef Full Text | Google Scholar

Deb Roy, S., Batabyal, S., Chakraborty, S., Chakraborty, M., and Bhattacharjee, A. K. (2018). “Control of higher order modes and their radiation in microstrip antenna using extremely compact defected ground structure symmetric stub,” in 2018 2nd international conference on electronics, materials engineering amp; nano-technology (IEMENTech) (IEEE), 1–5. doi:10.1109/iementech.2018.8465287

CrossRef Full Text | Google Scholar

Deshmukh, A., S, S., and Ray, K. (2012). “Analysis of stub loaded circular microstrip antennas,” in 2012 international conference on advances in computing and communications (IEEE), 282–285. doi:10.1109/icacc.2012.65

CrossRef Full Text | Google Scholar

Fan, L., Qian, H. J., Yangl, B., Wang, G., and Luo, X. (2018). Filtering power divider with wide stopband using open-stub loaded coupled-line and hybrid microstrip t-stub/dgs cell, in 2018 IEEE/MTT-S international microwave symposium - ims, 1–4. doi:10.1109/mwsym.2018.8439433

CrossRef Full Text | Google Scholar

Green, H. (1989). Determination of the cutoff of the first higher order mode in a coaxial line by the transverse resonance technique. IEEE Trans. Microw. Theory Tech. 37, 1652–1653. doi:10.1109/22.41018

CrossRef Full Text | Google Scholar

Henderson, K. Q., Latif, S. I., Lazarou, G., Sharma, S. K., Tabbal, A., and Saial, S. (2018). Dual-stub loaded microstrip line-fed multi-slot printed antenna for l te bands, in 2018 IEEE international Symposium on Antennas and Propagation amp; USNC/URSI national radio science meeting, 1743–1744. doi:10.1109/apusncursinrsm.2018.8608453

CrossRef Full Text | Google Scholar

Martín, F., Falcone, F., Bonache, J., Lopetegi, T., Laso, M. A. G., and Sorolla, M. (2003). New cpw low-pass filter based on a slow wave structure. Microw. Opt. Technol. Lett. 38, 190–193. doi:10.1002/mop.11011

CrossRef Full Text | Google Scholar

Mezaal, Y., S., Hashim, S., A., Al-fatlawi, H., and Hussein, A. (2018). New microstrip diplexer for recent wireless applications. Int. J. Eng. amp; Technol. 7, 96. doi:10.14419/ijet.v7i3.4.16754

CrossRef Full Text | Google Scholar

Rassokhina, Y., and Krizhanovski, V. (2009). Periodic structure on the slot resonators in microstrip transmission line. IEEE Trans. Microw. Theory Tech. 57, 1694–1699. doi:10.1109/tmtt.2009.2022814

CrossRef Full Text | Google Scholar

Rassokhina, Y. V., and Krizhanovski, V. G. (2018). The microstrop line step discontinuity analysis by transverse resonance technique: method of boundary value problem algebraization, in 2018 14th international Conference on advanced Trends in radioelecrtronics, Telecommunications and computer engineering (TCSET), 632–636. doi:10.1109/tcset.2018.8336281

CrossRef Full Text | Google Scholar

Rassokhina, Y. V., and Krizhanovski, V. G. (2023). Transverse resonance technique for analysis of symmetrical stub in microstrip transmission line. Visnyk NTUU KPI Seriia - Radiotekhnika Radioaparatobuduvannia 92, 5–11. doi:10.20535/RADAP.2023.92.5-11

CrossRef Full Text | Google Scholar

Schwab, W., and Menzel, W. (1992). On the design of planar microwave components using multilayer structures. IEEE Trans. Microw. Theory Tech. 40, 67–72. doi:10.1109/22.108324

CrossRef Full Text | Google Scholar

Sorrentino, R. (1989). Numerical techniques for microwave and millimeter-wave passive structures, ch. 1L. Wiley, New York, 637–693. chap. Transverse Resonance Technique.

Google Scholar

Tao, J.-W. (1992). A modified transverse resonance method for the analysis of multilayered, multiconductor quasiplanar structures with finite conductor thickness and mounting grooves. IEEE Trans. Microw. Theory Tech. 40, 1966–1970. doi:10.1109/22.159636

CrossRef Full Text | Google Scholar

Uwano, T., Sorrentino, R., and Itoh, T. (1987). Characterization of strip line crossing by transverse resonance analysis. IEEE Trans. Microw. Theory Tech. 35, 1369–1376. doi:10.1109/tmtt.1987.1133862

CrossRef Full Text | Google Scholar

Varela, J. E., and Esteban, J. (2011). Analysis of laterally open periodic waveguides by means of a generalized transverse resonance approach. IEEE Trans. Microw. Theory Tech. 59, 816–826. doi:10.1109/tmtt.2011.2111379

CrossRef Full Text | Google Scholar

Yang, S., Zhang, L., Chen, Y., Li, B., and Wang, L. (2022). Analysis of septuple-band ngd circuit using an e-shaped defected microstrip structure and two t-shaped open stubs. IEEE Trans. Microw. Theory Tech. 70, 3065–3073. doi:10.1109/tmtt.2022.3164873

CrossRef Full Text | Google Scholar